Derivation of Canopy Resistance in Turbulent Flow from First-Order Closure Models
Abstract
1. Introduction
2. Theory
2.1. Vegetation Resistance
2.1.1. Drag Coefficient
2.1.2. Reference Velocity
2.1.3. A Friction Formula
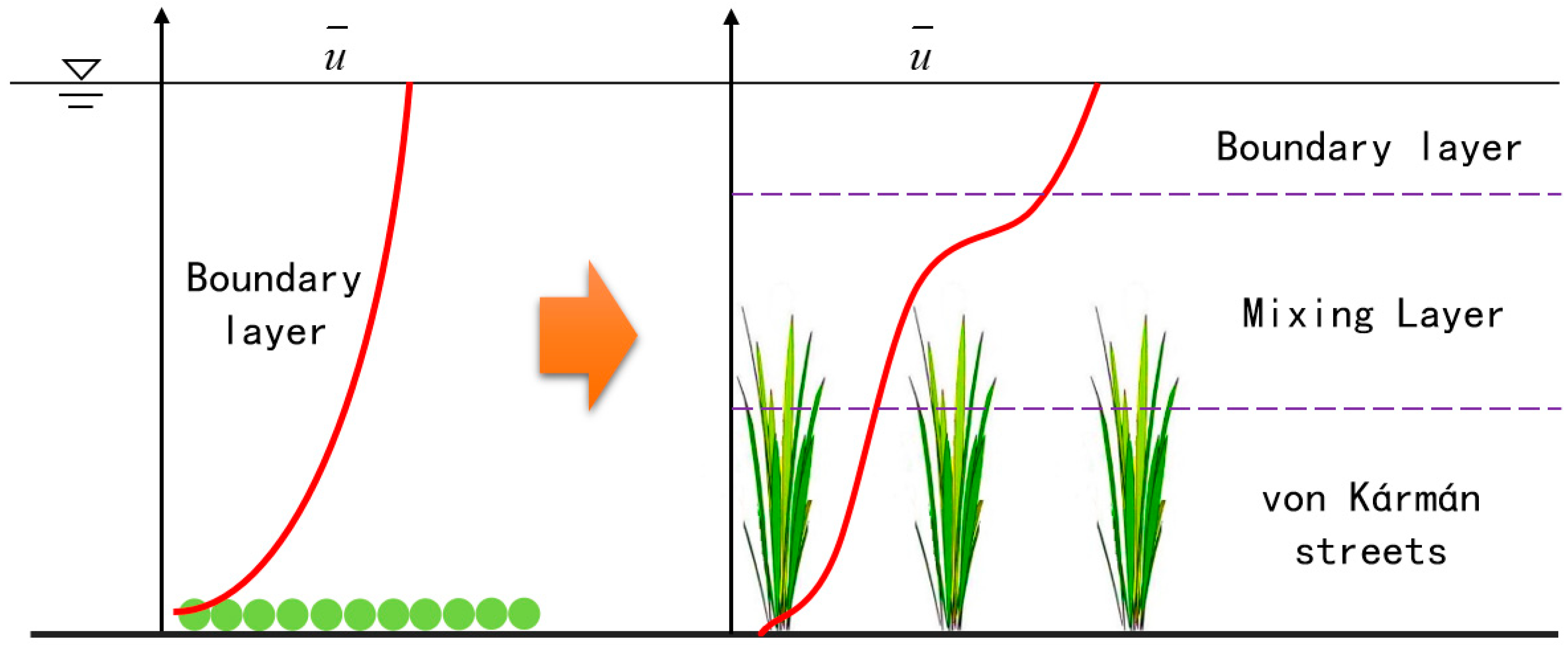
2.2. First-Order Closure Models
3. Laboratory Experiments
4. First-Order Closure Model Runs
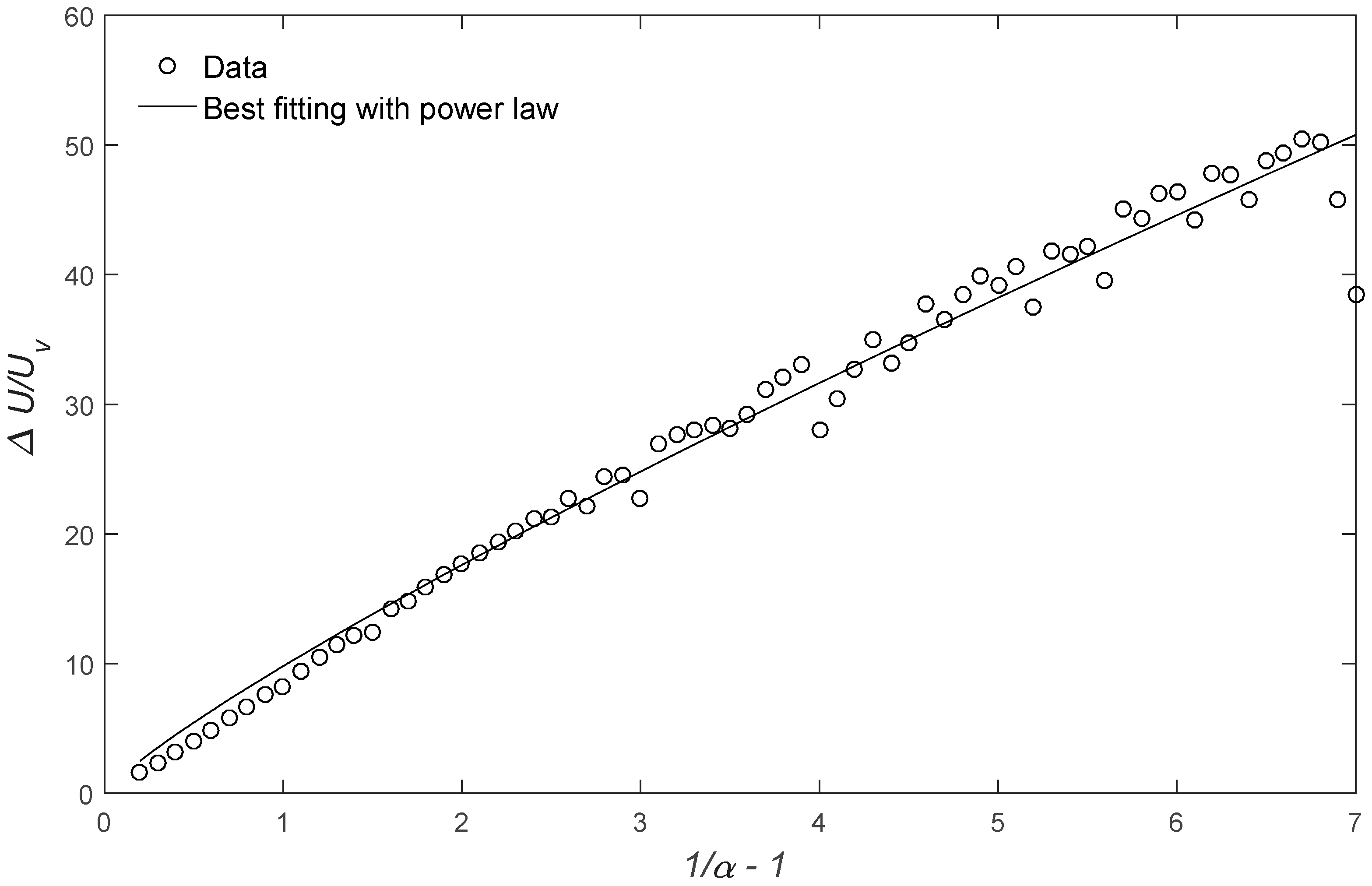
4.1. Scale Analysis with Submergence
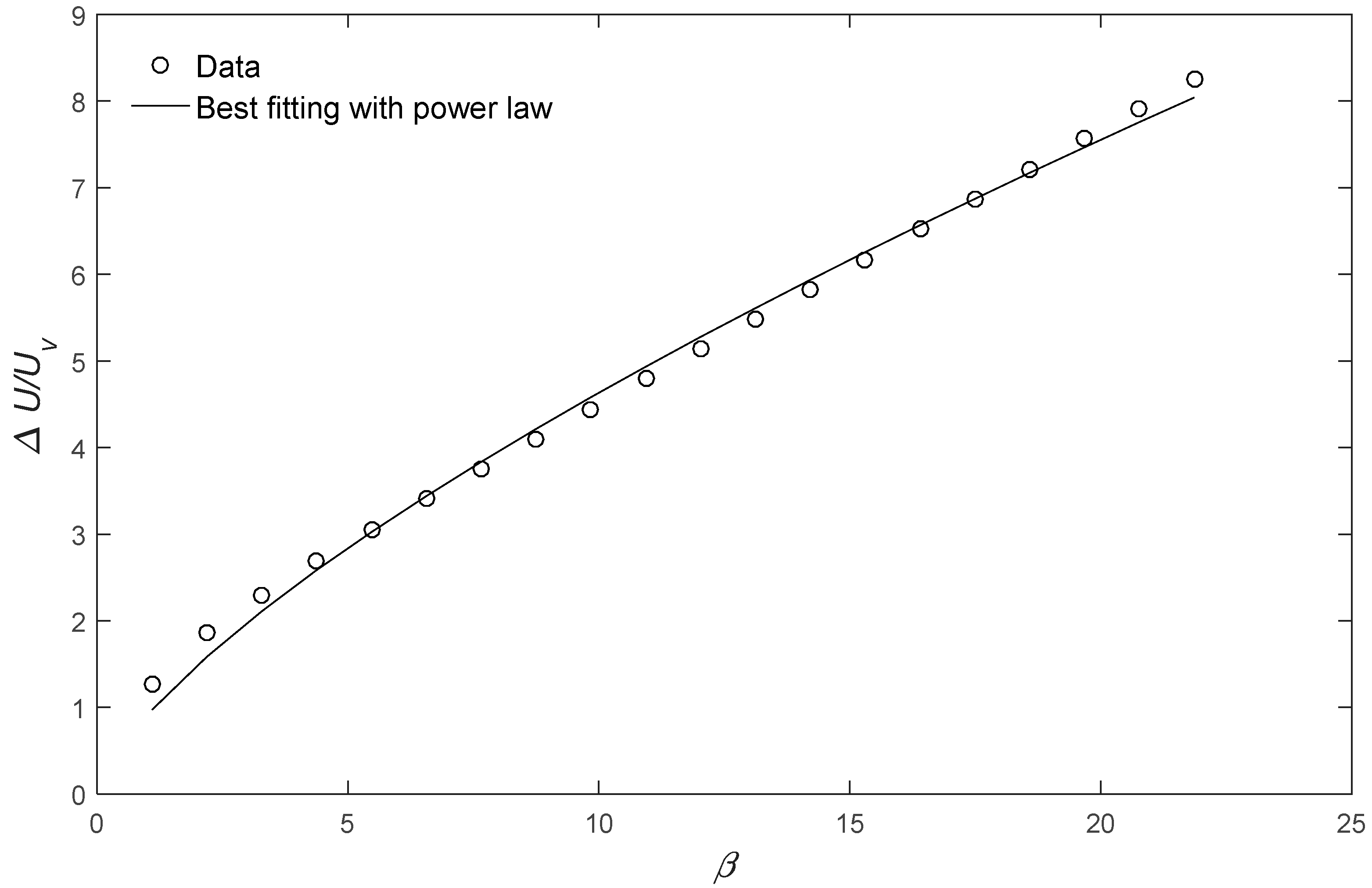
4.2. Scale Analysis with Vegetation Attributes
4.3. Expression for the Combined Influences of Submergence and Vegetation
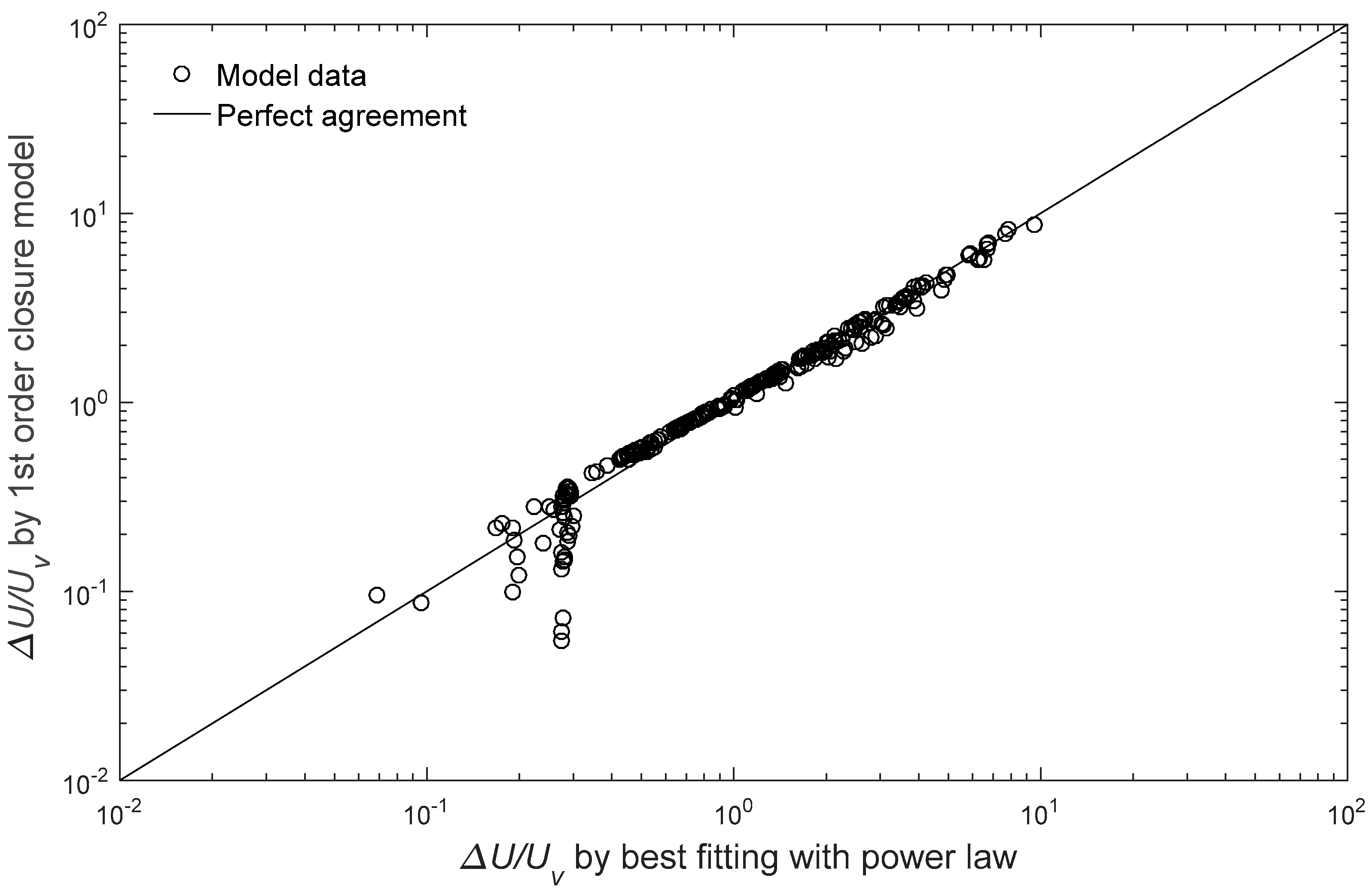
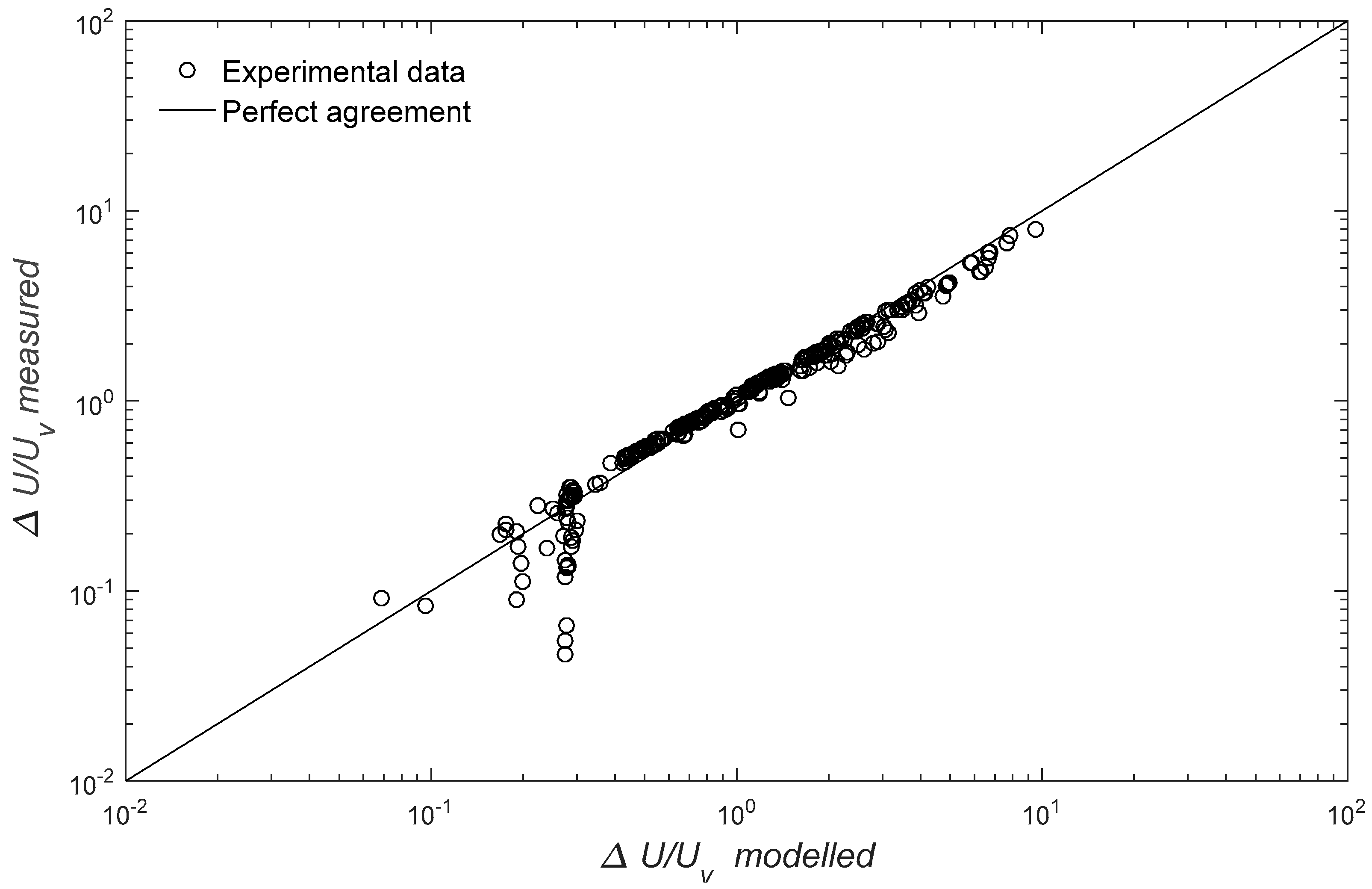
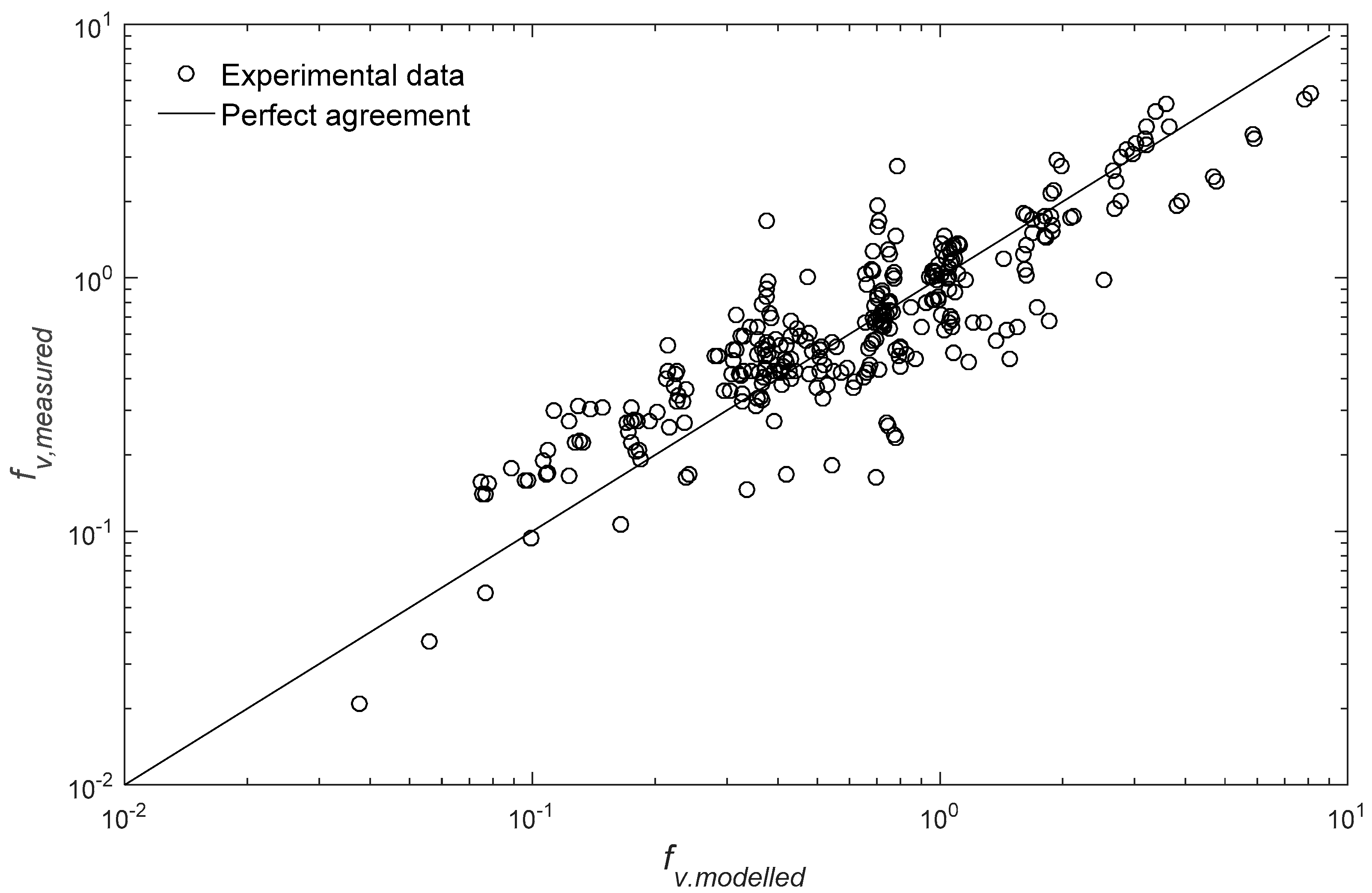
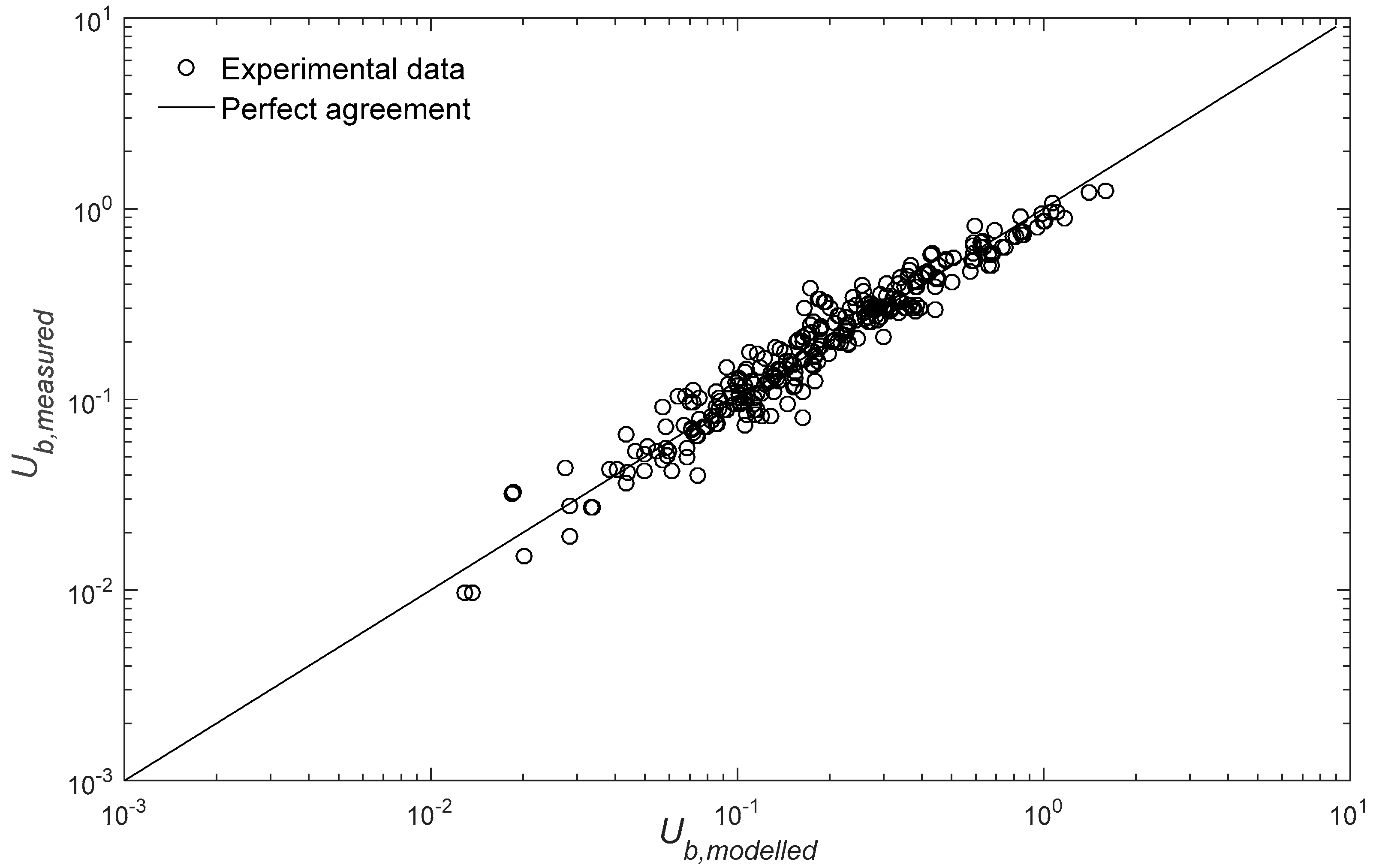
5. Model Validation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- De Serio, F.; Meftah, M.B.; Mossa, M.; Termini, D. Experimental investigation on dispersion mechanisms in rigid and flexible vegetated beds. Adv. Water Resour. 2018, 120, 98–113. [Google Scholar] [CrossRef]
- Mossa, M.; Meftah, M.B.; De Serio, F.; Nepf, H.M. How vegetation in flows modifies the turbulent mixing and spreading of jets. Sci. Rep. 2017, 7, 6587. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Jiang, C.; Nepf, H. Flow adjustment at the leading edge of a submerged aquatic canopy. Water Resour. Res. 2013, 49, 5537–5551. [Google Scholar] [CrossRef]
- Huai, W.-X.; Wang, W.-J.; Hu, Y.; Zeng, Y.; Yang, Z. Analytical model of the mean velocity distribution in an open channel with double-layered rigid vegetation. Adv. Water Resour. 2014, 69, 106–113. [Google Scholar] [CrossRef]
- Wang, P.; Chen, G.Q. Environmental dispersion in a tidal wetland with sorption by vegetation. Commun. Nonlinear Sci. Numer. Simul. 2015, 22, 348–366. [Google Scholar] [CrossRef]
- Thompson, S.; Katul, G.; Konings, A.; Ridolfi, L. Unsteady overland flow on flat surfaces induced by spatial permeability contrasts. Adv. Water Resour. 2011, 34, 1049–1058. [Google Scholar] [CrossRef]
- Wang, W.-J.; Huai, W.-X.; Thompson, S.; Peng, W.-Q.; Katul, G.G. Drag coefficient estimation using flume experiments in shallow non-uniform water flow within emergent vegetation during rainfall. Ecol. Indic. 2018, 92, 367–378. [Google Scholar] [CrossRef]
- Katul, G.G.; Poggi, D.; Ridolfi, L. A flow resistance model for assessing the impact of vegetation on flood routing mechanics. Water Resour. Res. 2011, 47, 427–438. [Google Scholar] [CrossRef]
- Wang, W.-J.; Huai, W.-X.; Thompson, S.; Katul, G.G. Steady nonuniform shallow flow within emergent vegetation. Water Resour. Res. 2015, 51, 10047–10064. [Google Scholar] [CrossRef]
- Moussa, R.; Bocquillon, C. On the use of the diffusive wave for modelling extreme flood events with overbank flow in the floodplain. J. Hydrol. 2009, 374, 116–135. [Google Scholar] [CrossRef]
- Gioia, G.; Bombardelli, F. Scaling and similarity in rough channel flows. Phys. Rev. Lett. 2001, 88, 014501. [Google Scholar] [CrossRef]
- Bonetti, S.; Manoli, G.; Manes, C.; Porporato, A.; Katul, G.G. Manning’s formula and Strickler’s scaling explained by a co-spectral budget model. J. Fluid Mech. 2017, 812, 1189–1212. [Google Scholar] [CrossRef]
- Baptist, M.; Babovic, V.; Rodríguez Uthurburu, J.; Keijzer, M.; Uittenbogaard, R.; Mynett, A.; Verwey, A. On inducing equations for vegetation resistance. J. Hydraul. Res. 2007, 45, 435–450. [Google Scholar] [CrossRef]
- Katul, G.G.; Wiberg, P.; Albertson, J.; Hornberger, G. A mixing layer theory for flow resistance in shallow streams. Water Resour. Res. 2002, 38, 1250. [Google Scholar] [CrossRef]
- Poggi, D.; Porporato, A.; Ridolfi, L.; Albertson, J.; Katul, G. The effect of vegetation density on canopy sub-layer turbulence. Bound.-Layer Meteorol. 2004, 111, 565–587. [Google Scholar] [CrossRef]
- Raupach, M.R.; Finnigan, J.J.; Brunet, Y. Coherent eddies and turbulence in vegetation canopies: The mixing-layer analogy. Bound.Layer Meteorol. 1996, 78, 351–382. [Google Scholar] [CrossRef]
- Finnigan, J. Turbulence in Plant Canopies. Annu. Rev. Fluid Mech. 2000, 32, 519–571. [Google Scholar] [CrossRef]
- Poggi, D.; Katul, G.G. Micro-and macro-dispersive fluxes in canopy flows. Acta Geophys. 2008, 56, 778–799. [Google Scholar] [CrossRef]
- Huai, W.X.; Zeng, Y.H.; Xu, Z.G.; Yang, Z.H. Three-layer model for vertical velocity distribution in open channel flow with submerged rigid vegetation. Adv. Water Resour. 2009, 32, 487–492. [Google Scholar] [CrossRef]
- Wang, W.-J.; Huai, W.-X.; Zeng, Y.-H.; Zhou, J.-F. Analytical solution of velocity distribution for flow through submerged large deflection flexible vegetation. Appl. Math. Mech. 2015, 36, 107–120. [Google Scholar] [CrossRef]
- Nepf, H.M. Flow and transport in regions with aquatic vegetation. Annu. Rev. Fluid Mech. 2012, 44, 123–142. [Google Scholar] [CrossRef]
- Konings, A.G.; Katul, G.G.; Thompson, S.E. A phenomenological model for the flow resistance over submerged vegetation. Water Resour. Res. 2012, 48, W02522. [Google Scholar] [CrossRef]
- Stoesser, T.; Kim, S.; Diplas, P. Turbulent flow through idealized emergent vegetation. J. Hydraul. Eng. 2010, 136, 1003–1017. [Google Scholar] [CrossRef]
- Luhar, M.; Rominger, J.; Nepf, H. Interaction between flow, transport and vegetation spatial structure. Environ. Fluid Mech. 2008, 8, 423–439. [Google Scholar] [CrossRef]
- Kubrak, E.; Kubrak, J.; Rowiński, P. Influence of a method of evaluation of the curvature of flexible vegetation elements on vertical distributions of flow velocities. Acta Geophys. 2012, 60, 1098–1119. [Google Scholar] [CrossRef]
- Liu, Z.W.; Chen, Y.C.; Zhu, D.J.; Hui, E.Q.; Jiang, C.B. Analytical model for vertical velocity profiles in flows with submerged shrub-like vegetation. Environ. Fluid Mech. 2012, 12, 341–346. [Google Scholar] [CrossRef]
- Huthoff, F.; Augustijn, D.; Hulscher, S.J. Analytical solution of the depth-averaged flow velocity in case of submerged rigid cylindrical vegetation. Water Resour. Res. 2007, 43, W06413. [Google Scholar] [CrossRef]
- Huai, W.; Hu, Y.; Zeng, Y.; Han, J. Velocity distribution for open channel flows with suspended vegetation. Adv. Water Resour. 2012, 49, 56–61. [Google Scholar] [CrossRef]
- Huai, W.; Xue, W.; Qian, Z. Large-eddy simulation of turbulent rectangular open-channel flow with an emergent rigid vegetation patch. Adv. Water Resour. 2015, 80, 30–42. [Google Scholar] [CrossRef]
- Cheng, N.-S. Calculation of drag coefficient for arrays of emergent circular cylinders with pseudofluid model. J. Hydraul. Eng. 2012, 139, 602–611. [Google Scholar] [CrossRef]
- Poggi, D.; Katul, G.; Albertson, J. Momentum transfer and turbulent kinetic energy budgets within a dense model canopy. Bound.-Layer Meteorol. 2004, 111, 589–614. [Google Scholar] [CrossRef]
- Boller, M.L.; Carrington, E. The hydrodynamic effects of shape and size change during reconfiguration of a flexible macroalga. J. Exp. Biol. 2006, 209, 1894–1903. [Google Scholar] [CrossRef] [PubMed]
- Carollo, F.G.; Ferro, V.; Termini, D. Flow resistance law in channels with flexible submerged vegetation. J. Hydraul. Eng. 2005, 131, 554–564. [Google Scholar] [CrossRef]
- Järvelä, J. Flow resistance of flexible and stiff vegetation: a flume study with natural plants. J. Hydrol. 2002, 269, 44–54. [Google Scholar] [CrossRef]
- Hui, E.-Q.; Hu, X.-E.; Jiang, C.-B.; Ma, F.-K.; Zhu, Z.-D. A study of drag coefficient related with vegetation based on the flume experiment. J. Hydrodyn. 2010, 22, 329–337. [Google Scholar] [CrossRef]
- Stone, B.M.; Shen, H.T. Hydraulic resistance of flow in channels with cylindrical roughness. J. Hydraul. Eng. 2002, 128, 500–506. [Google Scholar] [CrossRef]
- Tanino, Y.; Nepf, H.M. Laboratory investigation of mean drag in a random array of rigid, emergent cylinders. J. Hydraul. Eng. 2008, 134, 34–41. [Google Scholar] [CrossRef]
- Cheng, N.-S.; Nguyen, H.T. Hydraulic radius for evaluating resistance induced by simulated emergent vegetation in open-channel flows. J. Hydraul. Eng. 2010, 137, 995–1004. [Google Scholar] [CrossRef]
- Ishikawa, Y.; Mizuhara, K.; Ashida, S. Effect of density of trees on drag exerted on trees in river channels. J. For. Res. 2000, 5, 271–279. [Google Scholar] [CrossRef]
- James, C.S.; Birkhead, A.L.; Jordanova, A.A.; O’Sullivan, J.J. Flow resistance of emergent vegetation. J. Hydraul. Res. 2004, 42, 390–398. [Google Scholar] [CrossRef]
- Liu, D.; Diplas, P.; Fairbanks, J.D.; Hodges, C.C. An experimental study of flow through rigid vegetation. J. Geophys. Res. Earth Surf. 2008, 113. [Google Scholar] [CrossRef]
- Ferreira, R.M.; Ricardo, A.M.; Franca, M.J. Discussion of “Laboratory investigation of mean drag in a random array of rigid, emergent cylinders” by Yukie Tanino and Heidi M. Nepf. J. Hydraul. Eng. 2009, 135, 690–693. [Google Scholar] [CrossRef]
- Kothyari, U.C.; Hayashi, K.; Hashimoto, H. Drag coefficient of unsubmerged rigid vegetation stems in open channel flows. J. Hydraul. Res. 2009, 47, 691–699. [Google Scholar] [CrossRef]
- Lee, J.K.; Roig, L.C.; Jenter, H.L.; Visser, H.M. Drag coefficients for modeling flow through emergent vegetation in the Florida Everglades. Ecol. Eng. 2004, 22, 237–248. [Google Scholar] [CrossRef]
- Wu, F.-C.; Shen, H.W.; Chou, Y.J. Variation of roughness coefficients for unsubmerged and submerged vegetation. J. Hydraul. Eng. 1999, 125, 934–942. [Google Scholar] [CrossRef]
- Zhao, K.; Cheng, N.; Wang, X.; Tan, S. Measurements of fluctuation in drag acting on rigid cylinder array in open channel flow. J. Hydraul. Eng. 2013, 140, 48–55. [Google Scholar] [CrossRef]
- Etminan, V.; Lowe, R.J.; Ghisalberti, M. A new model for predicting the drag exerted by vegetation canopies. Water Resour. Res. 2017, 53, 3179–3196. [Google Scholar] [CrossRef]
- Wang, W.-J.; Peng, W.-Q.; Huai, W.-X.; Qu, X.-D.; Dong, F.; Feng, J. Roughness height of submerged vegetation in flow based on spatial structure. J. Hydrodyn. 2018, 30, 754–757. [Google Scholar] [CrossRef]
- Poggi, D.; Krug, C.; Katul, G.G. Hydraulic resistance of submerged rigid vegetation derived from first-order closure models. Water Resour.Res. 2009, 45, 2381–2386. [Google Scholar] [CrossRef]
- Poggi, D.; Katul, G.G.; Albertson, J.D. A note on the contribution of dispersive fluxes to momentum transfer within canopies. Bound.-Layer Meteorol. 2004, 111, 615–621. [Google Scholar] [CrossRef]
- Jackson, P.S. On the Displacement Height in the Logarithmic Velocity Profile. J. Fluid Mech. 1981, 111, 15–25. [Google Scholar] [CrossRef]
- Dunn, C. Experimental Determination of Drag Coefficients in Open Channel with Simulated Vegetation. Master’s Thesis, University of Illinois, Urbana-Champaign, Urbana, IL, USA, 1996. [Google Scholar]
- Ghisalberti, M.; Nepf, H. The limited growth of vegetated shear layers. Water Resour. Res. 2004, 40, 196–212. [Google Scholar] [CrossRef]
- López, F.; García, M.H. Mean flow and turbulence structure of open-channel flow through non-emergent vegetation. J. Hydraul. Eng. 2001, 127, 392–402. [Google Scholar] [CrossRef]
- Meijer, D. Flumes Studies of Submerged Vegetation; PR121.10; HKV: Lelystad, The Netherlands, 1998. (In Dutch) [Google Scholar]
- Meijer, D.; Van Velzen, E. Prototype-scale flume experiments on hydraulic roughness of submerged vegetation. In Proceedings of the 28th International IAHR Conference, Graz, Austria, 22–27 August 1999. [Google Scholar]
- Murphy, E.; Ghisalberti, M.; Nepf, H. Model and laboratory study of dispersion in flows with submerged vegetation. Water Resour. Res. 2007, 43, 687–696. [Google Scholar] [CrossRef]
- Nezu, I.; Sanjou, M. Turburence structure and coherent motion in vegetated canopy open-channel flows. J. Hydro-Environ. Res. 2008, 2, 62–90. [Google Scholar] [CrossRef]
- Shimizu, Y.; Tsujimoto, T.; Nakagawa, H.; Kitamura, T. Experimental study on flow over rigid vegetation simulated by cylinders with equi-spacing. Proc. JSCE 1991, 438, 31–40. [Google Scholar]
- Yan, J. Experimental Study of Flow Resistance and Turbulence Characteristics of Open Channel Flow with Vegetation. Ph.D. Thesis, Hohai University, Nanjing, China, 2008. [Google Scholar]
- Yang, W. Experimental Study of Turbulent Open-Channel Flows with Submerged Vegetation. Ph.D. Thesis, Yonsei University, Seoul, Korea, 2008. [Google Scholar]
- Yang, W.; Choi, S.-U. A two-layer approach for depth-limited open-channel flows with submerged vegetation. J. Hydraul. Res. 2010, 48, 466–475. [Google Scholar] [CrossRef]

| Authors | Stem Shape | Flow Condition | Q (m3/s) | B (m) | So (%) | hw (m) | hv (m) | D (m) | m (Stems/m2) | Cd,array | Red | Fr |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dunn [52] | cylindrical | uniform | 0.046–0.181 | 0.91 | 0.36–1.61 | 0.164–0.391 | 0.118 | 0.006 | 43–387 | 0.84–1.06 | 1891–5421 | 0.2057–0.5649 |
| Ghisalberti and Nepf [53] | cylindrical | uniform | 0.002–0.014 | 0.38 | 0.0002–0.01 | 0.467 | 0.138–0.139 | 0.006 | 391–1250 | 1.66–6.35 | 61–516 | 0.0045–0.0377 |
| Liu et al. [41] | cylindrical | uniform | 0.011 | 0.3 | 0.3 | 0.087–0.119 | 0.076 | 0.006 | 97–496 | 0.89–1.11 | 2028–2774 | 0.2957–0.4730 |
| López and García [54] | cylindrical | uniform | 0.046–0.181 | 0.91 | 0.36–1.61 | 0.164–0.391 | 0.12 | 0.006 | 42–384 | 0.84–1.06 | 1906–5463 | 0.2057–0.5649 |
| Meijer [55] | cylindrical | nonuniform | 0.866–8.98 | 3 | 0.055–0.205 | 0.990–2.500 | 0.45–1.5 | 0.008 | 64–256 | 0.89–1.13 | 1400–9936 | 0.0397–0.2767 |
| Meijer and Velzen [56] | cylindrical | nonuniform | 3.557 | 3 | 0.138 | 2.08 | 0.9 | 0.008 | 256 | 1.08 | 4560 | 0.1263 |
| Murphy et al. [57] | cylindrical | nonuniform | 0.002–0.014 | 0.38 | 0.0003–0.1340 | 0.088–0.467 | 0.070–0.140 | 0.006 | 417–1333 | 1.11–3.63 | 90–1060 | 0.0088–0.1546 |
| Nezu and Sanjou [58] | flat strip | uniform | 0.003–0.008 | 0.4 | 0.0196–0.1553 | 0.063–0.200 | 0.05 | 0.008 | 947–3676 | 1.42–4.44 | 800–960 | 0.0714–0.1278 |
| Poggi et al. [15] | cylindrical | nonuniform | 0.162 | 0.9 | 0.004–0.0320 | 0.6 | 0.12 | 0.004 | 67–1072 | 0.96–1.38 | 1200 | 0.1237 |
| Shimizu et al. [59] | cylindrical | uniform | 0.002–0.016 | 0.40–0.50 | 0.0660–0.7000 | 0.050–0.106 | 0.041–0.046 | 0.01–0.02 | 2501–9995 | 1.09–1.83 | 65–496 | 0.0826–0.3529 |
| Stone and Shen [36] | cylindrical | uniform | 0.002–0.065 | 0.45 | 0.009–4.400 | 0.151–0.314 | 0.124 | 0.003–0.013 | 166–692 | 0.91–1.60 | 126–5405 | 0.0279–0.4436 |
| Yan [60] | cylindrical | uniform | 0.014–0.038 | 0.42 | 0.065–1.280 | 0.120–0.300 | 0.06 | 0.006 | 500–2000 | 1.09–1.87 | 1714–1845 | 0.1703–0.2763 |
| Yang [61] | cylindrical | uniform | 0.008–0.011 | 0.45 | 0.141–0.269 | 0.075 | 0.035 | 0.002 | 1400 | 1.09–1.12 | 444–622 | 0.2592–0.3629 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.-J.; Peng, W.-Q.; Huai, W.-X.; Katul, G.; Liu, X.-B.; Dong, F.; Qu, X.-D.; Zhang, H.-P. Derivation of Canopy Resistance in Turbulent Flow from First-Order Closure Models. Water 2018, 10, 1782. https://doi.org/10.3390/w10121782
Wang W-J, Peng W-Q, Huai W-X, Katul G, Liu X-B, Dong F, Qu X-D, Zhang H-P. Derivation of Canopy Resistance in Turbulent Flow from First-Order Closure Models. Water. 2018; 10(12):1782. https://doi.org/10.3390/w10121782
Chicago/Turabian StyleWang, Wei-Jie, Wen-Qi Peng, Wen-Xin Huai, Gabriel Katul, Xiao-Bo Liu, Fei Dong, Xiao-Dong Qu, and Hai-Ping Zhang. 2018. "Derivation of Canopy Resistance in Turbulent Flow from First-Order Closure Models" Water 10, no. 12: 1782. https://doi.org/10.3390/w10121782
APA StyleWang, W.-J., Peng, W.-Q., Huai, W.-X., Katul, G., Liu, X.-B., Dong, F., Qu, X.-D., & Zhang, H.-P. (2018). Derivation of Canopy Resistance in Turbulent Flow from First-Order Closure Models. Water, 10(12), 1782. https://doi.org/10.3390/w10121782







