Uncertainty in Rainfall Intensity Duration Frequency Curves of Peninsular Malaysia under Changing Climate Scenarios
Abstract
1. Introduction
2. Study Area and Datasets
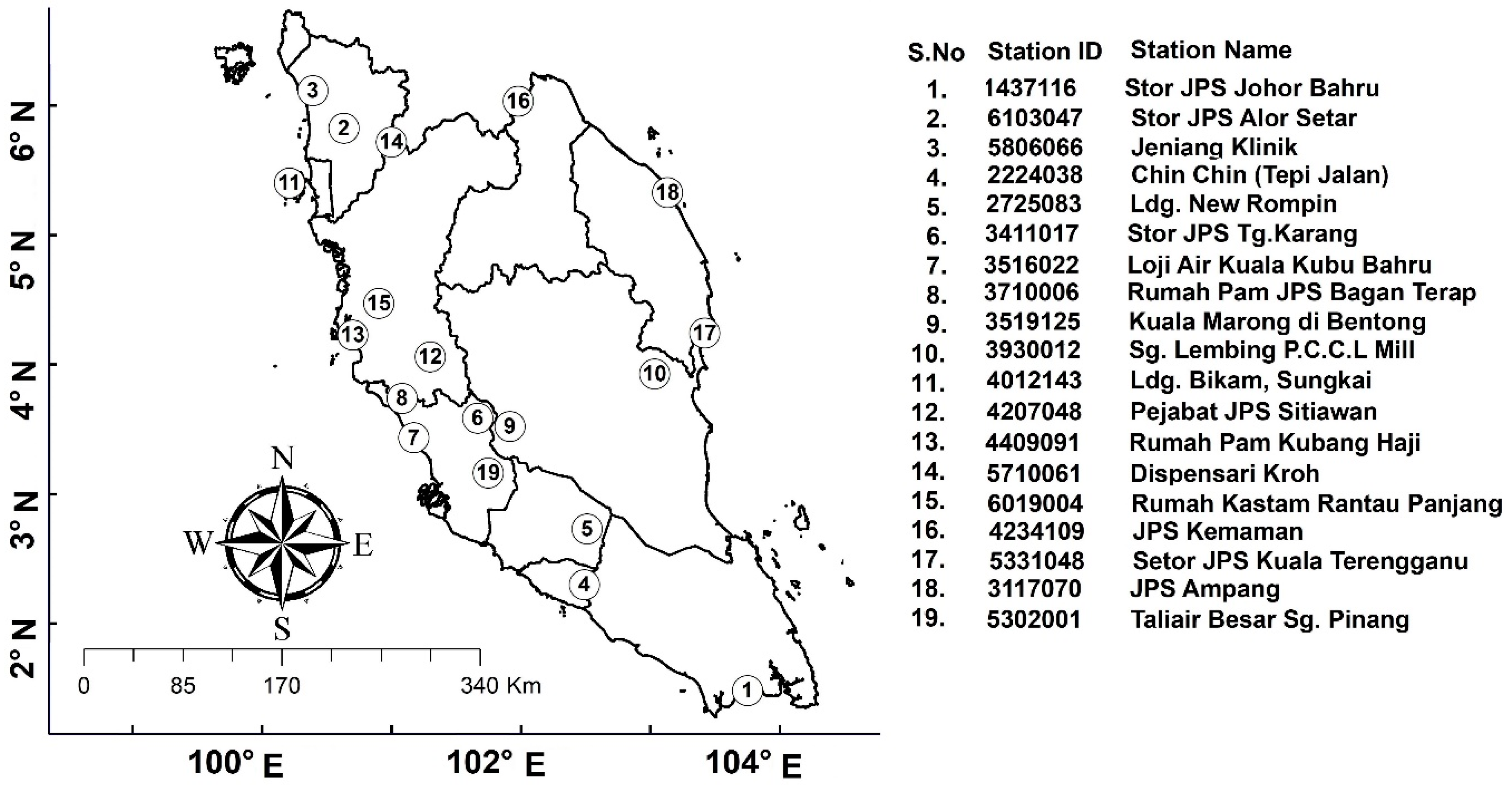
2.1. Study Area
2.2. Data and Sources
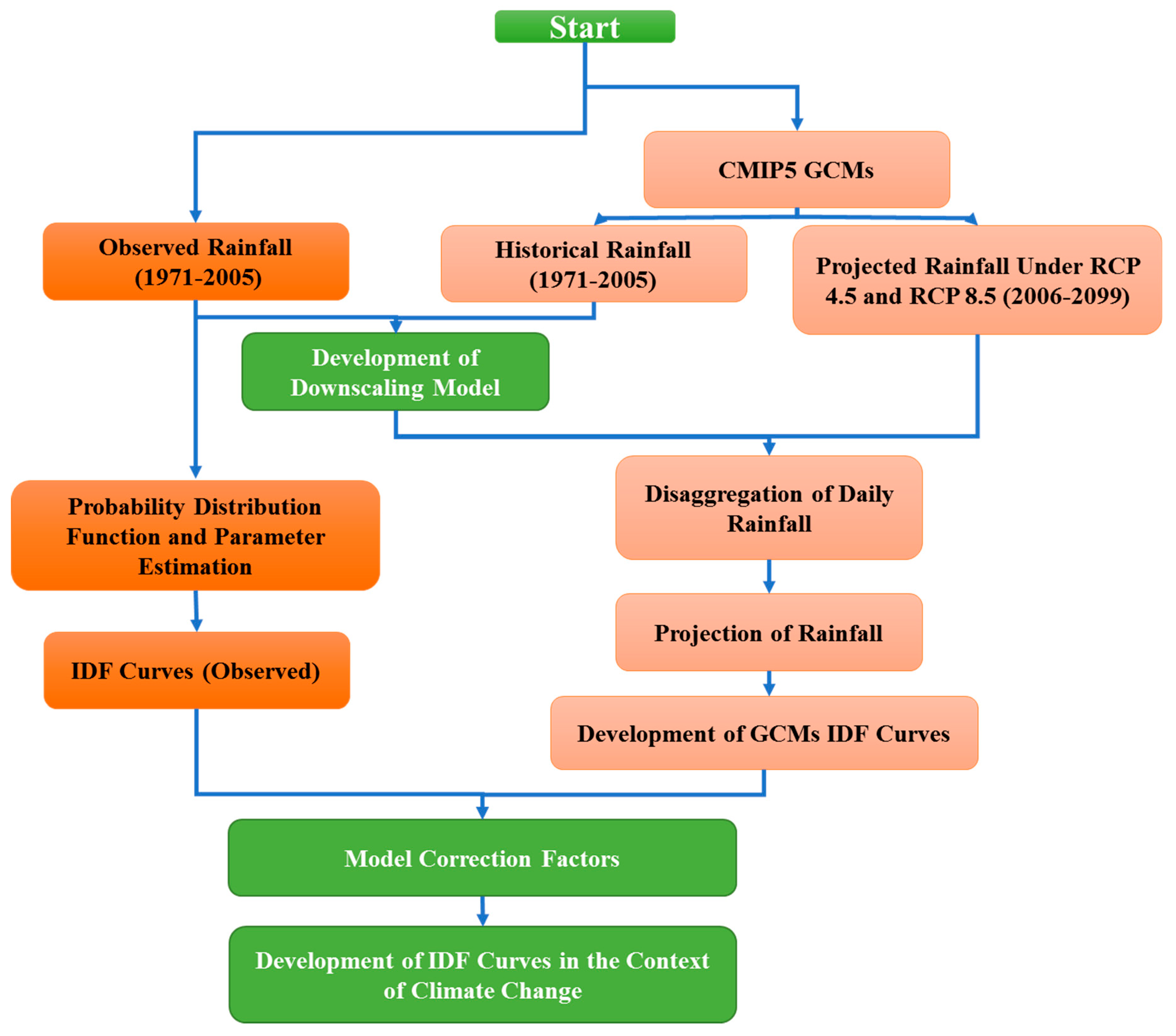
3. Methodology
3.1. Procedure
- The GCM simulations for historical (1971–2010) and future (2006–2099) periods are interpolated to observed locations.
- MOS downscaling model is developed where quantile mapping (QM) is used to derive the bias correction factors by comparing GCM simulated rainfall with observed rainfall for the period (1971–2005).
- The bias correction factors derived from the historical period (1971–2005) are then applied on simulated GCM rainfall for different RCPs for the period 2006–2099.
- An artificial neural network (ANN) model is developed to disaggregate daily rainfall data to hourly rainfall data. The model is calibrated and validated with observe hourly rainfall data for the period 1971–2005.
- The ANN disaggregation model is used to generate hourly rainfall data from daily rainfall projected for the period 2006–2099.
- IDF curves are generated by fitting observed annual maximum of hourly rainfall data (1971–2005) with most suitable probability density function (PDF) and parameter estimation method.
- The disaggregated rainfall data are used to generate time series of annual maximum of hourly rainfall to develop IDF curves for climate change scenarios.
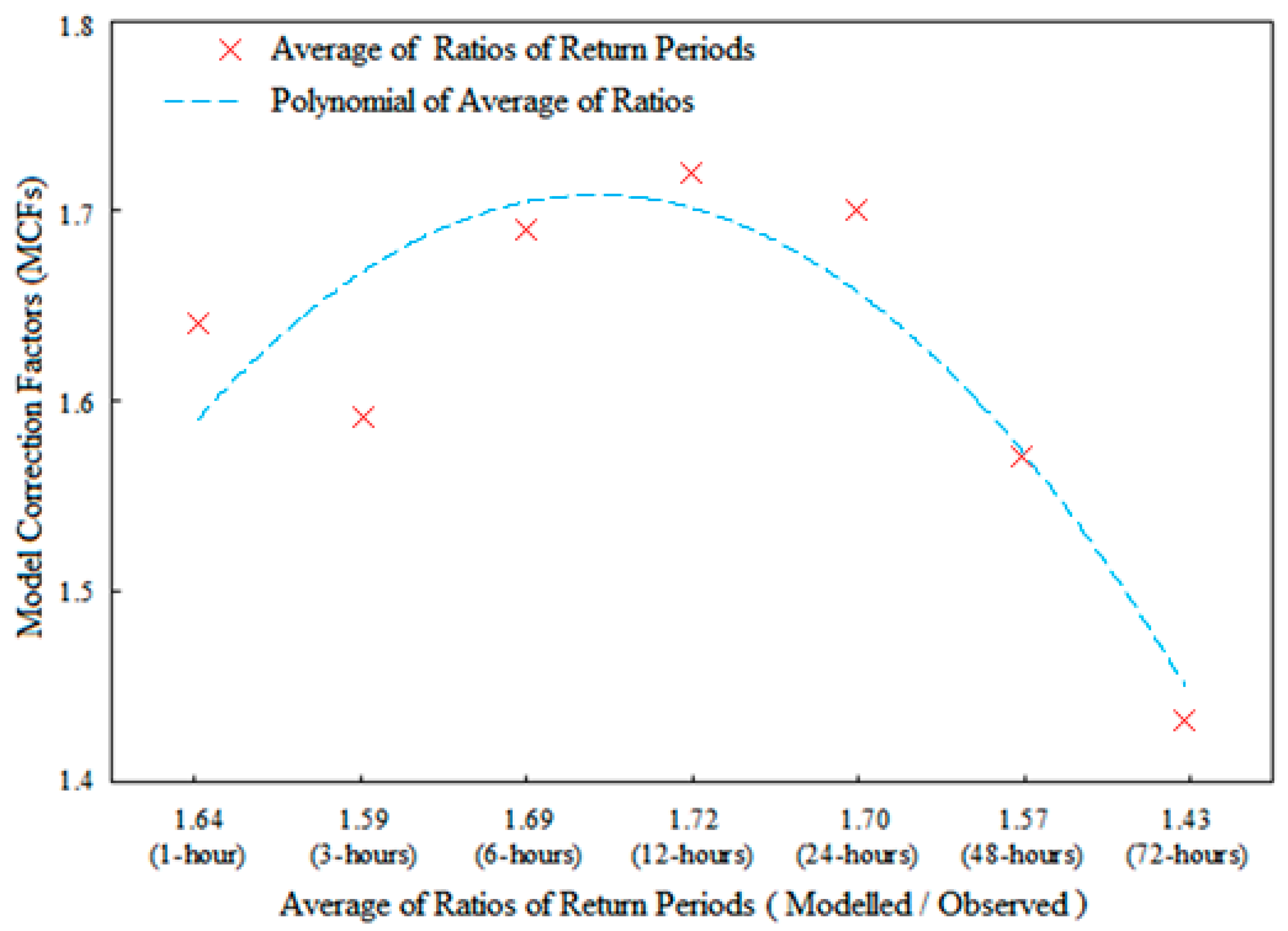
- The model correction factors (MCFs) are estimated for all the durations of rainfall by fitting the average of the ratios of the projected return periods to observed return periods in a polynomial equation.
- The MCFs are applied on the return periods of rainfall durations for future period to generate the IDF curves. The IDF curves are generated for all the 8 GCMs for both the RCP 4.5 and RCP 8.5, separately.
- Finally, the IDF curves are developed with uncertainty level, by estimating the 1st quartile, median and 3rd quartile of the return periods of different rainfall durations obtained from IDF curves generated for eight GCMs.
3.2. Selection of Appropriate Probability Density Function and Paramter Estmation Method
3.3. Rainfall Downscaling and Projections
- The GCM simulated rainfall is interpolated at each station using inverse an weighting distance method to generate GCM simulations at the observed location.
- The QM is used to compute the biases in GCMs by comparing 70% of the randomly-selected observed and GCM simulated daily rainfall for the period 1971–2005. The QM bias correction parameters are validated with the remaining 30% of observed and GCM simulated daily rainfall for the period 1971–2005.
- The derived QM parameters are used to correct the biases in the simulated daily rainfall of GCMs for both the RCP 4.5 and RCP 8.5 for the period 2006–2099.
3.4. Disaggregation of Daily Rainfall and Generation of Projected IDF Curves
3.5. Model Correction Factors
4. Results and Discussion
4.1. Determination of Probability Density Function & Parameter Estimation Method
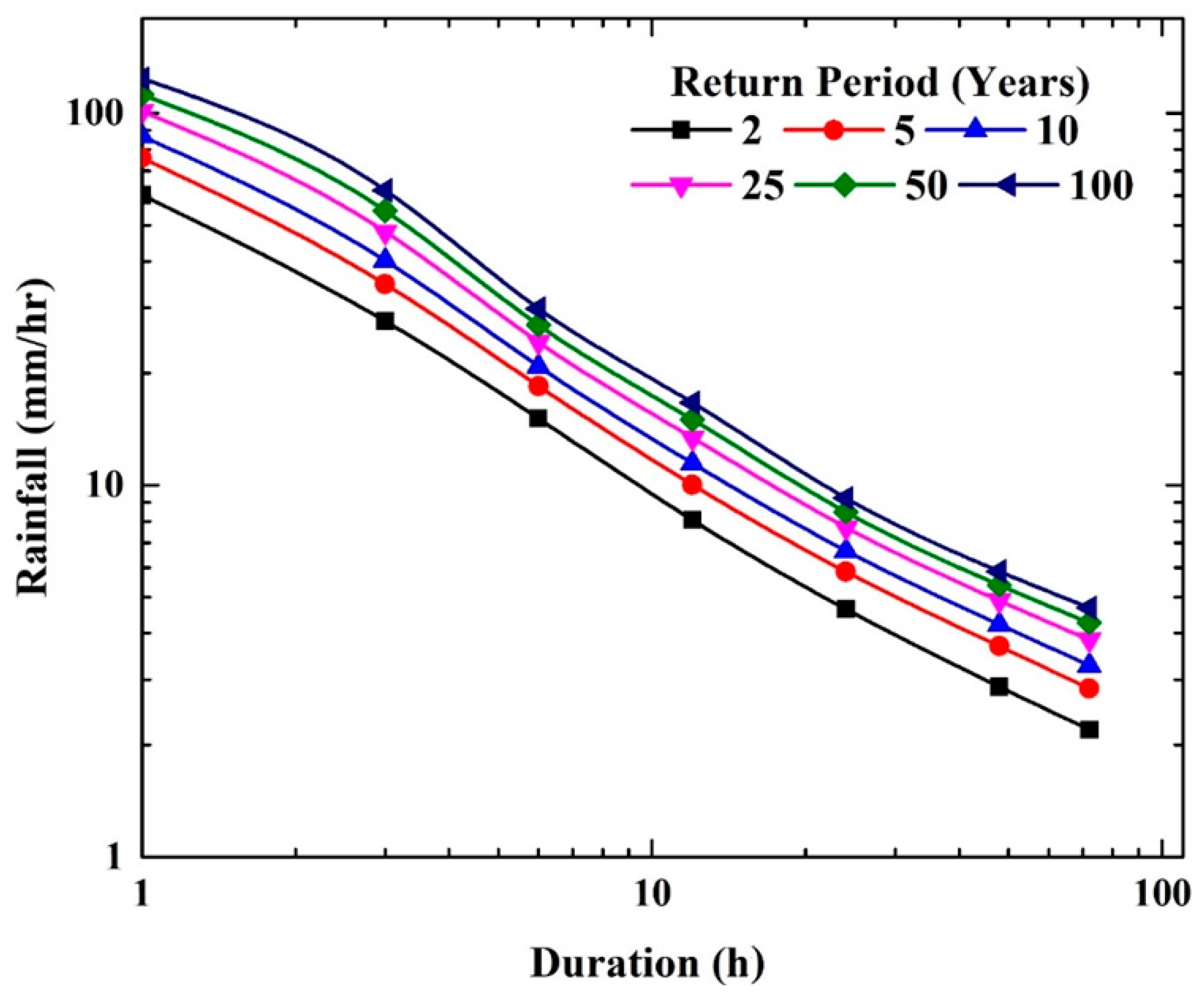
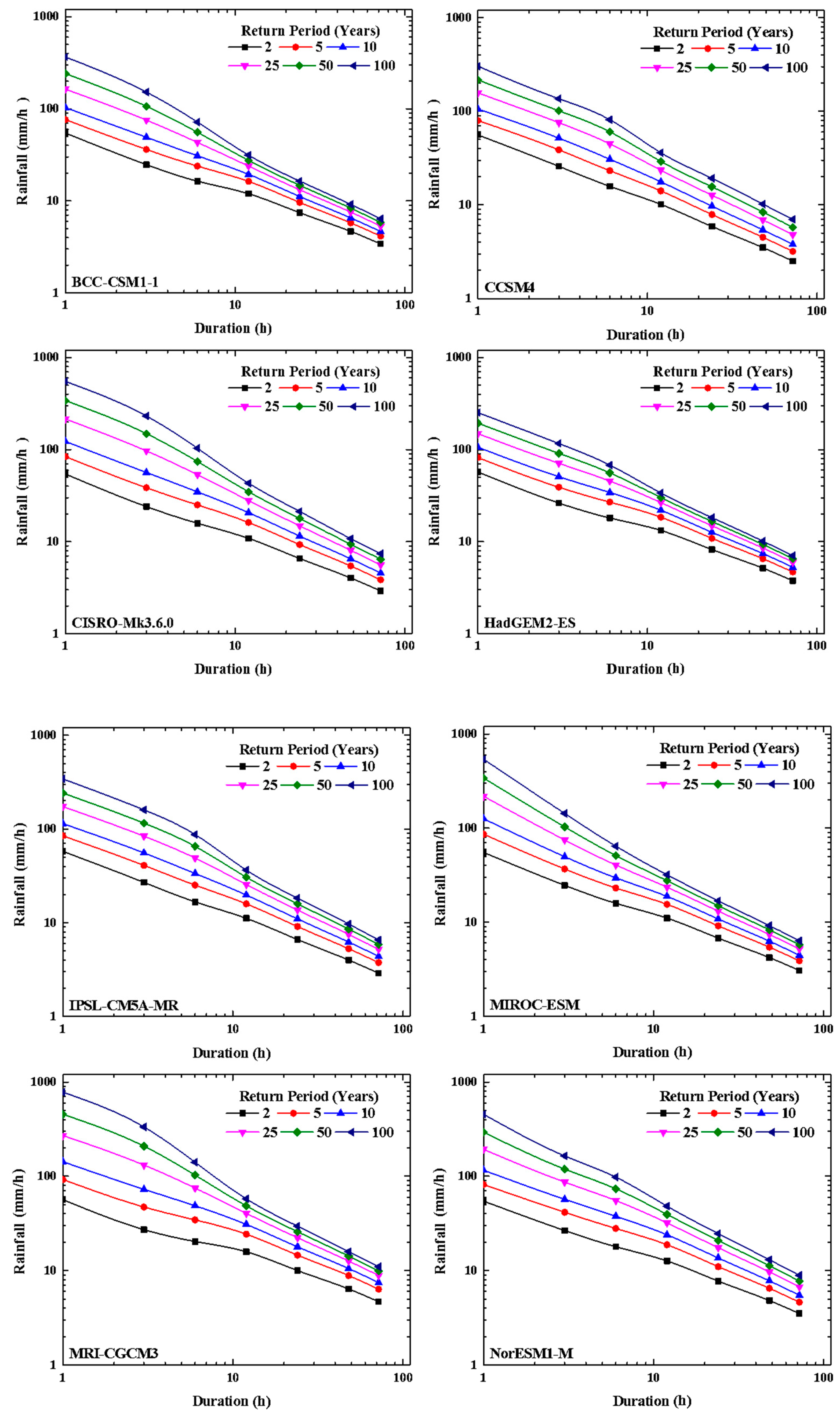
4.2. The IDF Curves based on Historical Rainfall
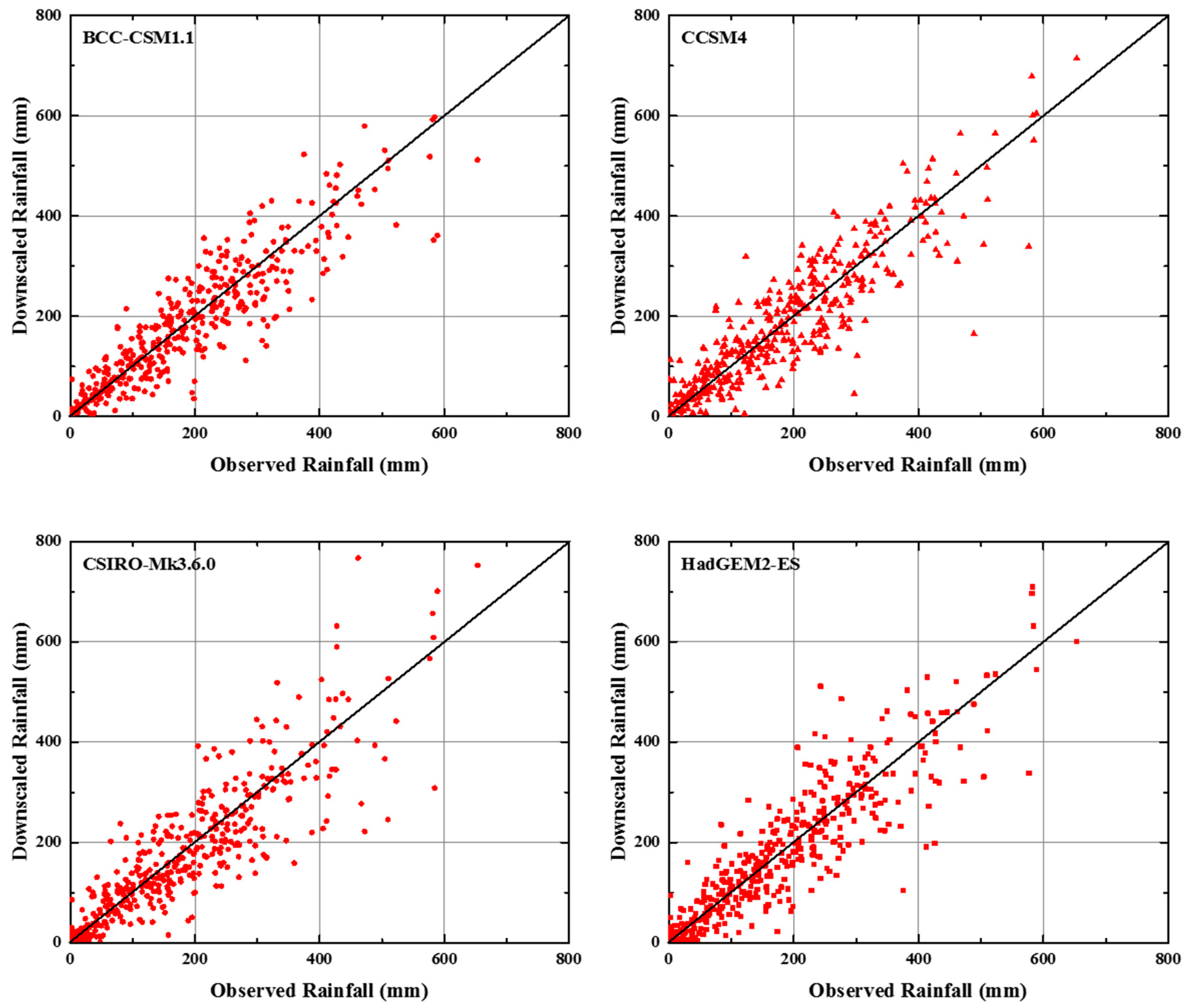
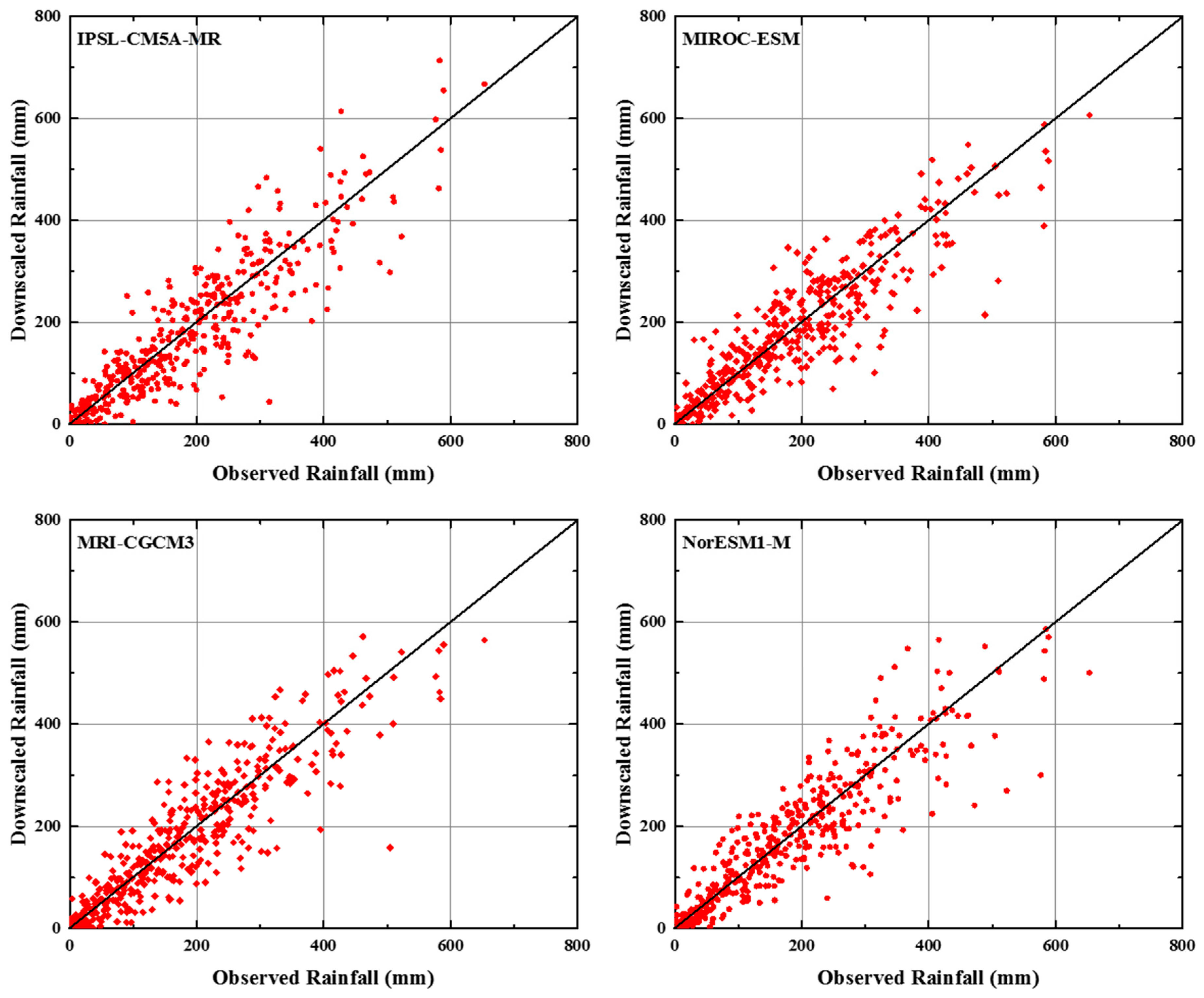
4.3. Climate Downscaling and Projections
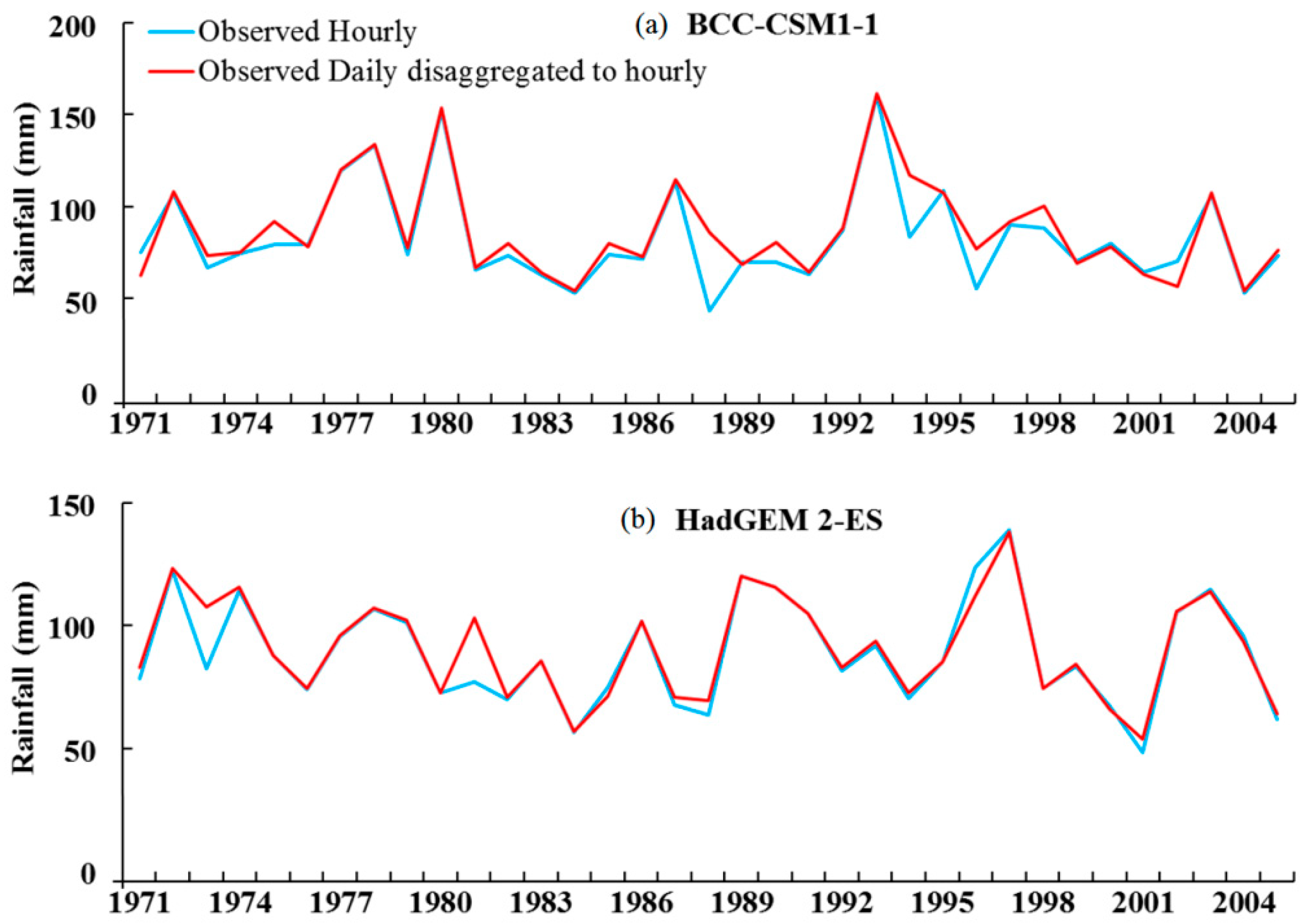
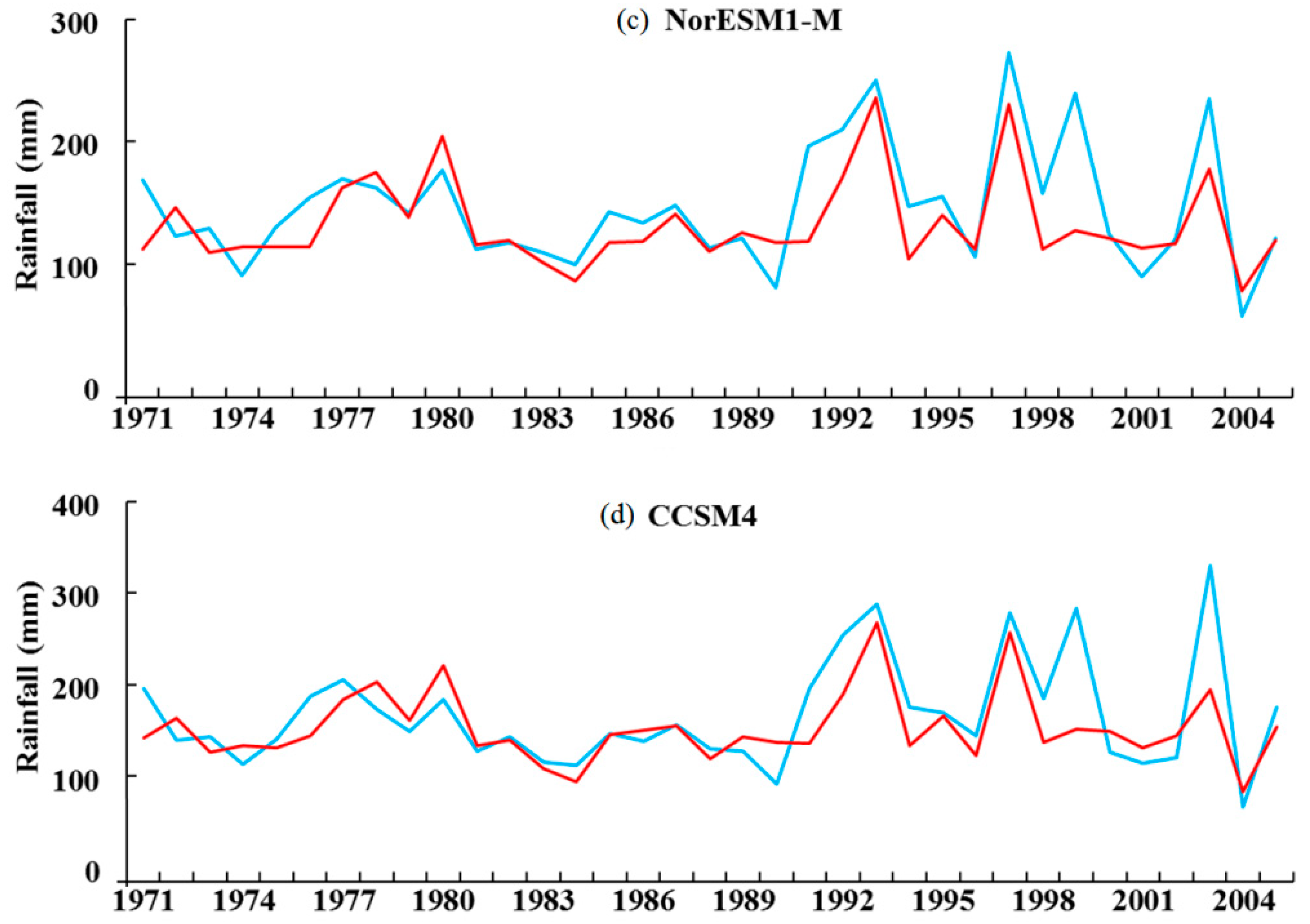
4.4. Disaggregation of Rainfall
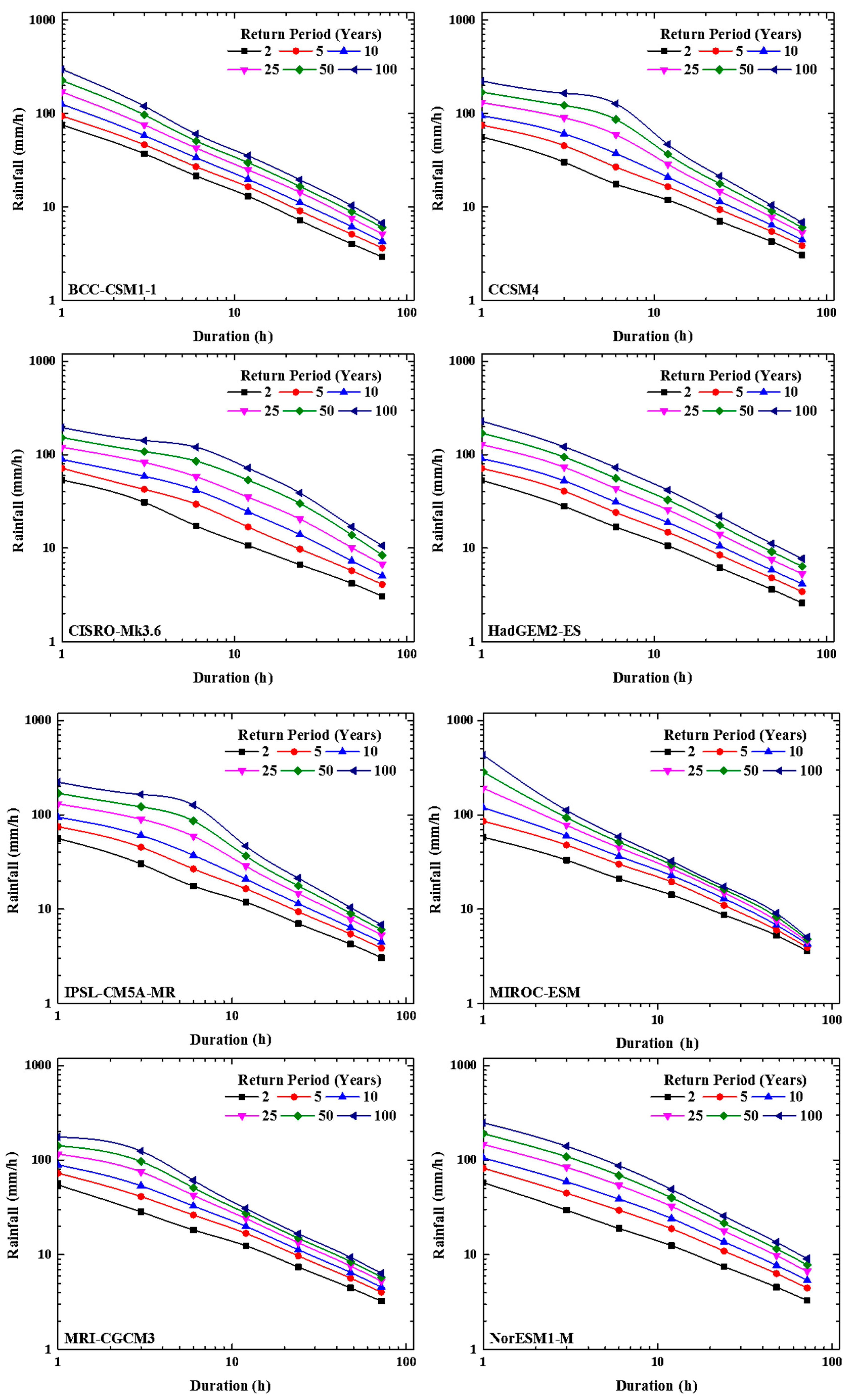
4.5. Development of IDF Curves under Climate Change Scenarios
Model Correction Factor
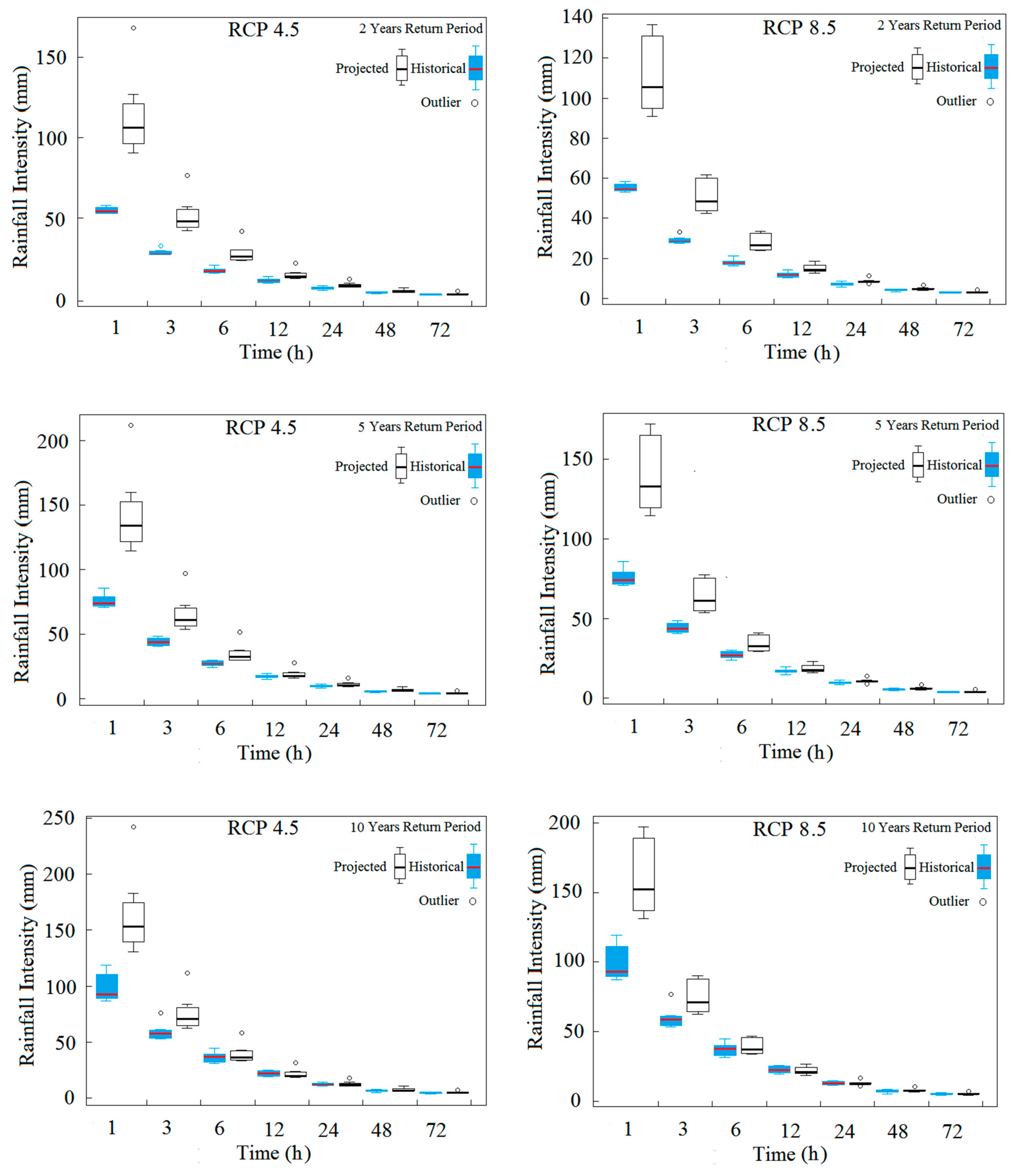
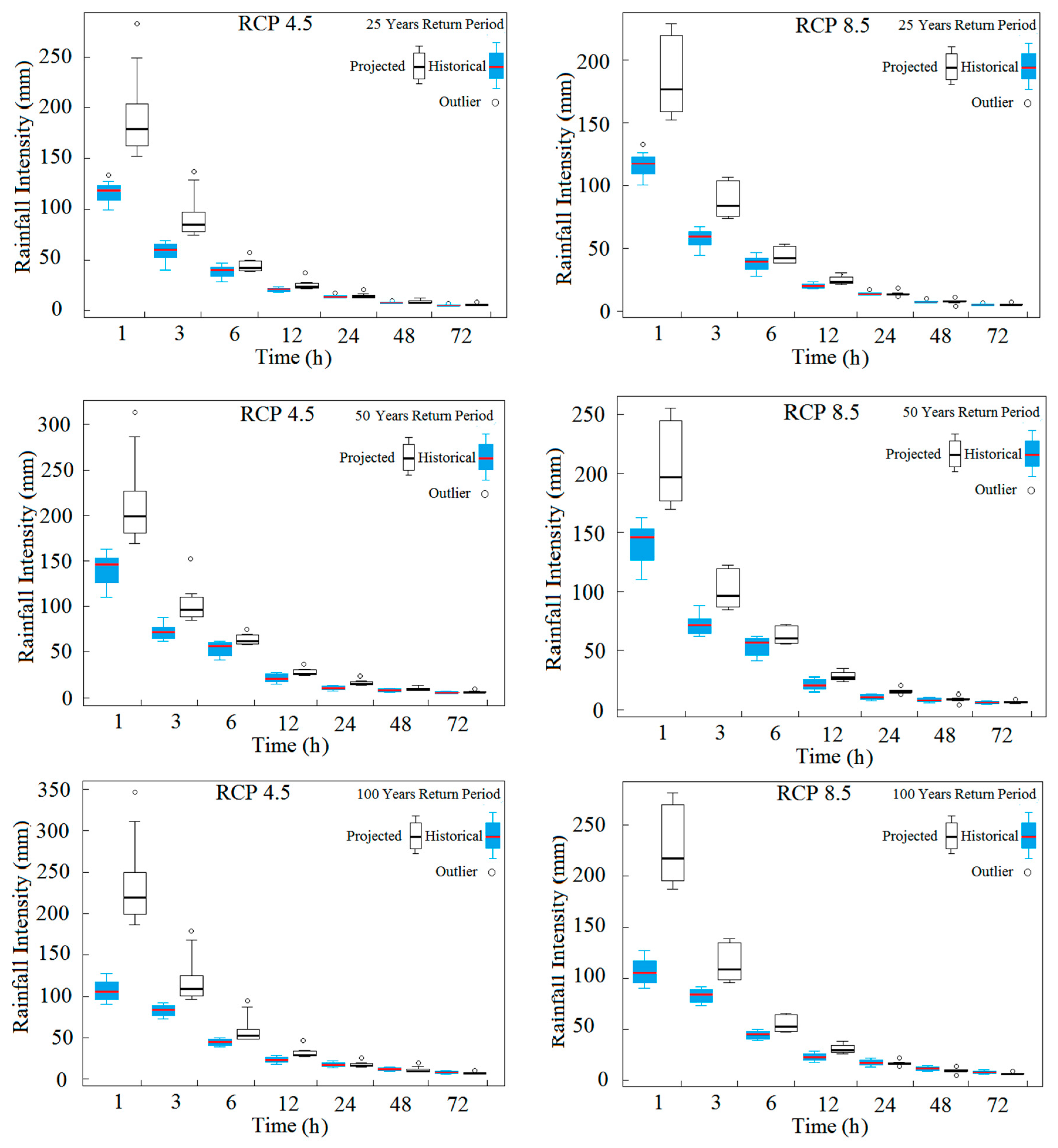
4.6. Development IDF Curves with Uncertainty
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Koutsoyiannis, D.; Kozonis, D.; Manetas, A. A mathematical framework for studying rainfall intensity-duration-frequency relationships. J. Hydrol. 1998, 206, 118–135. [Google Scholar] [CrossRef]
- Simonovic, S.P.; Schardong, A.; Sandink, D. Mapping extreme rainfall statistics for Canada under climate change using updated Intensity-Duration-Frequency curves. J. Water Resour. Plan. Manag. 2016, 143, 04016078. [Google Scholar] [CrossRef]
- Rodríguez, R.; Navarro, X.; Casas, M.C.; Ribalaygua, J.; Russo, B.; Pouget, L.; Redaño, A. Influence of climate change on IDF curves for the metropolitan area of Barcelona (Spain). Int. J. Climatol. 2014, 34, 643–654. [Google Scholar] [CrossRef]
- Willems, P. Revision of urban drainage design rules after assessment of climate change impacts on precipitation extremes at Uccle, Belgium. J. Hydrol. 2013, 496, 166–177. [Google Scholar] [CrossRef]
- Watt, E.; Marsalek, J. Critical review of the evolution of the design storm event concept. Can. J. Civ. Eng. 2013, 40, 105–113. [Google Scholar] [CrossRef]
- Tfwala, C.; van Rensburg, L.; Schall, R.; Mosia, S.; Dlamini, P. Precipitation intensity-duration-frequency curves and their uncertainties for Ghaap plateau. Clim. Risk Manag. 2017, 16, 1–9. [Google Scholar] [CrossRef]
- Ashley, R.M.; Balmforth, D.J.; Saul, A.J.; Blanskby, J. Flooding in the future–predicting climate change, risks and responses in urban areas. Water Sci. Technol. 2005, 52, 265–273. [Google Scholar] [CrossRef] [PubMed]
- He, J.; Valeo, C.; Bouchart, F.-C. Enhancing urban infrastructure investment planning practices for a changing climate. Water Sci. Technol. 2006, 53, 13–20. [Google Scholar] [CrossRef] [PubMed]
- Semadeni-Davies, A.; Hernebring, C.; Svensson, G.; Gustafsson, L.-G. The impacts of climate change and urbanisation on drainage in Helsingborg, Sweden: Combined sewer system. J. Hydrol. 2008, 350, 100–113. [Google Scholar] [CrossRef]
- Mailhot, A.; Duchesne, S. Design criteria of urban drainage infrastructures under climate change. J. Water Resour. Plan. Manag. 2009, 136, 201–208. [Google Scholar] [CrossRef]
- Wernstedt, K.; Carlet, F. Climate change, urban development, and storm water: Perspectives from the field. J. Water Resour. Plan. Manag. 2012, 140, 543–552. [Google Scholar] [CrossRef]
- Vu, M.; Raghavan, S.; Liu, J.; Liong, S.Y. Constructing short-duration IDF curves using coupled dynamical–statistical approach to assess climate change impacts. Int. J. Climatol. 2018. [Google Scholar] [CrossRef]
- Hall, J.W.; Brown, S.; Nicholls, R.J.; Pidgeon, N.F.; Watson, R.T. Proportionate adaptation. Nat. Clim. Chang. 2012, 2, 833. [Google Scholar] [CrossRef]
- Giuliani, M.; Castelletti, A.; Pianosi, F.; Mason, E.; Reed, P.M. Curses, tradeoffs, and scalable management: Advancing evolutionary multiobjective direct policy search to improve water reservoir operations. J. Water Resour. Plan. Manag. 2015, 142, 04015050. [Google Scholar] [CrossRef]
- Hughes, G.; Chinowsky, P.; Strzepek, K. The costs of adaptation to climate change for water infrastructure in OECD countries. Util. Policy 2010, 18, 142–153. [Google Scholar] [CrossRef]
- Borgomeo, E.; Mortazavi-Naeini, M.; Hall, J.W.; Guillod, B.P. Risk, Robustness and Water Resources Planning Under Uncertainty. Earth’s Futur. 2018, 6, 468–487. [Google Scholar] [CrossRef]
- Borgomeo, E.; Mortazavi-Naeini, M.; Hall, J.W.; O’Sullivan, M.J.; Watson, T. Trading-off tolerable risk with climate change adaptation costs in water supply systems. Water Resour. Res. 2016, 52, 622–643. [Google Scholar] [CrossRef]
- Shahid, S.; Alamgir, M.; Wang, X.-J.; Eslamian, S. Climate Change Impacts on and Adaptation to Groundwater. In Handbook of Drought and Water Scarcity; CRC Press: Boca Raton, FL, USA, 2017; pp. 121–138. [Google Scholar]
- Pour, S.H.; Harun, S.B.; Shahid, S. Genetic programming for the downscaling of extreme rainfall events on the east coast of peninsular Malaysia. Atmosphere 2014, 5, 914–936. [Google Scholar] [CrossRef]
- Ahmed, K.; Shahid, S.; bin Harun, S.; Ismail, T.; Nawaz, N.; Shamsudin, S. Assessment of groundwater potential zones in an arid region based on catastrophe theory. Earth Sci. Informat. 2015, 8, 539–549. [Google Scholar] [CrossRef]
- Sa’adi, Z.; Shahid, S.; Chung, E.-S.; bin Ismail, T. Projection of spatial and temporal changes of rainfall in Sarawak of Borneo Island using statistical downscaling of CMIP5 models. Atmos. Res. 2017, 197, 446–460. [Google Scholar] [CrossRef]
- Sachindra, D.; Perera, B. Annual statistical downscaling of precipitation and evaporation and monthly disaggregation. Theor. Appl. Climatol. 2018, 131, 181–200. [Google Scholar] [CrossRef]
- Pour, S.H.; Shahid, S.; Chung, E.-S. A Hybrid Model for Statistical Downscaling of Daily Rainfall. Procedia Eng. 2016, 154, 1424–1430. [Google Scholar] [CrossRef]
- Sachindra, D.; Ahmed, K.; Rashid, M.M.; Shahid, S.; Perera, B. Statistical downscaling of precipitation using machine learning techniques. Atmos. Res. 2018, 212, 240–258. [Google Scholar] [CrossRef]
- Sachindra, D.; Huang, F.; Barton, A.; Perera, B. Statistical downscaling of general circulation model outputs to precipitation—Part 2: Bias-correction and future projections. Int. J. Climatol. 2014, 34, 3282–3303. [Google Scholar] [CrossRef]
- Pour, S.H.; Shahid, S.; Chung, E.-S.; Wang, X.-J. Model output statistics downscaling using support vector machine for the projection of spatial and temporal changes in rainfall of Bangladesh. Atmos. Res. 2018, 213, 149–162. [Google Scholar] [CrossRef]
- Maraun, D.; Wetterhall, F.; Ireson, A.; Chandler, R.; Kendon, E.; Widmann, M.; Brienen, S.; Rust, H.; Sauter, T.; Themeßl, M. Precipitation downscaling under climate change: Recent developments to bridge the gap between dynamical models and the end user. Rev. Geophys. 2010, 48. [Google Scholar] [CrossRef]
- Salman, S.A.; Shahid, S.; Ismail, T.; Ahmed, K.; Wang, X.-J. Selection of climate models for projection of spatiotemporal changes in temperature of Iraq with uncertainties. Atmos. Res. 2018, 213, 509–522. [Google Scholar] [CrossRef]
- Schoof, J.T.; Robeson, S.M. Projecting changes in regional temperature and precipitation extremes in the United States. Weather Clim. Extrem. 2016, 11, 28–40. [Google Scholar] [CrossRef]
- Addor, N.; Rohrer, M.; Furrer, R.; Seibert, J. Propagation of biases in climate models from the synoptic to the regional scale: Implications for bias adjustment. J. Geophys. Res. Atmos. 2016, 121, 2075–2089. [Google Scholar] [CrossRef]
- Campozano, L.; Tenelanda, D.; Sanchez, E.; Samaniego, E.; Feyen, J. Comparison of Statistical Downscaling Methods for Monthly Total Precipitation: Case Study for the Paute River Basin in Southern Ecuador. Adv. Meteorol. 2016, 2016, 6526341. [Google Scholar] [CrossRef]
- Mehrotra, R.; Sharma, A. A Multivariate Quantile-Matching Bias Correction Approach with Auto-and Cross-Dependence across Multiple Time Scales: Implications for Downscaling. J. Clim. 2016, 29, 3519–3539. [Google Scholar] [CrossRef]
- Mayowa, O.O.; Pour, S.H.; Shahid, S.; Mohsenipour, M.; Harun, S.B.; Heryansyah, A.; Ismail, T. Trends in rainfall and rainfall-related extremes in the east coast of peninsular Malaysia. J. Earth Syst. Sci. 2015, 124, 1609–1622. [Google Scholar] [CrossRef]
- Shahid, S.; Pour, S.H.; Wang, X.; Shourav, S.A.; Minhans, A.; Ismail, T.b. Impacts and adaptation to climate change in Malaysian real estate. Int. J. Clim. Chang. Strateg. Manag. 2017, 9, 87–103. [Google Scholar] [CrossRef]
- Ahmed, K.; Chung, E.-S.; Song, J.-Y.; Shahid, S. Effective design and planning specification of low impact development practices using Water Management Analysis Module (WMAM): Case of Malaysia. Water 2017, 9, 173. [Google Scholar] [CrossRef]
- Nashwan, M.; Shahid, S.; Chung, E.-S.; Ahmed, K.; Song, Y. Development of Climate-Based Index for Hydrologic Hazard Susceptibility. Sustainability 2018, 10, 2182. [Google Scholar] [CrossRef]
- McSweeney, C.; Jones, R.; Lee, R.W.; Rowell, D. Selecting CMIP5 GCMs for downscaling over multiple regions. Clim. Dyn. 2015, 44, 3237–3260. [Google Scholar] [CrossRef]
- Thomson, A.M.; Calvin, K.V.; Smith, S.J.; Kyle, G.P.; Volke, A.; Patel, P.; Delgado-Arias, S.; Bond-Lamberty, B.; Wise, M.A.; Clarke, L.E. RCP4. 5: A pathway for stabilization of radiative forcing by 2100. Clim. Chang. 2011, 109, 77. [Google Scholar] [CrossRef]
- Wang, L.; Ranasinghe, R.; Maskey, S.; van Gelder, P.; Vrijling, J. Comparison of empirical statistical methods for downscaling daily climate projections from CMIP5 GCMs: A case study of the Huai River Basin, China. Int. J. Climatol. 2016, 36, 145–164. [Google Scholar] [CrossRef]
- Rahman, A.S.; Rahman, A.; Zaman, M.A.; Haddad, K.; Ahsan, A.; Imteaz, M. A study on selection of probability distributions for at-site flood frequency analysis in Australia. Nat. Hazards 2013, 69, 1803–1813. [Google Scholar] [CrossRef]
- Burian, S.J.; Durrans, S.R.; Tomic, S.; Pimmel, R.L.; Wai, C.N. Rainfall disaggregation using artificial neural networks. J. Hydrol. Eng. 2000, 5, 299–307. [Google Scholar] [CrossRef]
- Burian, S.; Durrans, S. Evaluation of an artificial neural network rainfall disaggregation model. Water Sci. Technol. 2002, 45, 99–104. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Murch, R.R.; Ross, M.A.; Ganguly, A.R.; Nachabe, M. Evaluation of statistical rainfall disaggregation methods using rain-gauge information for West-Central Florida. J. Hydrol. Eng. 2008, 13, 1158–1169. [Google Scholar] [CrossRef]
- Mirhosseini, G.; Srivastava, P.; Fang, X. Developing rainfall intensity-duration-frequency curves for Alabama under future climate scenarios using artificial neural networks. J. Hydrol. Eng. 2014, 19, 04014022. [Google Scholar] [CrossRef]
- Kim, S.; Singh, V.P. Spatial disaggregation of areal rainfall using two different artificial neural networks models. Water 2015, 7, 2707–2727. [Google Scholar] [CrossRef]
- Mirhosseini, G.; Srivastava, P.; Sharifi, A. Developing probability-based IDF curves using kernel density estimator. J. Hydrol. Eng. 2015, 20, 04015002. [Google Scholar] [CrossRef]
- Kim, S.; Kisi, O.; Seo, Y.; Singh, V.P.; Lee, C.-J. Assessment of rainfall aggregation and disaggregation using data-driven models and wavelet decomposition. Hydrol. Res. 2017, 48, 99–116. [Google Scholar] [CrossRef]
- Kim, S.; Seo, Y.; Lee, C.-J. Modeling of Rainfall by Combining Neural Computation and Wavelet Technique. Procedia Eng. 2016, 154, 1231–1236. [Google Scholar] [CrossRef]
- Young, C.B.; McEnroe, B.M. Sampling adjustment factors for rainfall recorded at fixed time intervals. J. Hydrol. Eng. 2003, 8, 294–296. [Google Scholar] [CrossRef]
- Veneziano, D.; Lepore, C.; Langousis, A.; Furcolo, P. Marginal methods of intensity-duration-frequency estimation in scaling and nonscaling rainfall. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Shrestha, A.; Babel, M.S.; Weesakul, S.; Vojinovic, Z. Developing Intensity–Duration–Frequency (IDF) Curves under Climate Change Uncertainty: The Case of Bangkok, Thailand. Water 2017, 9, 145. [Google Scholar] [CrossRef]
- Wilby, R.L.; Dawson, C.W.; Barrow, E.M. SDSM—A decision support tool for the assessment of regional climate change impacts. Environ. Model. Softw. 2002, 17, 145–157. [Google Scholar] [CrossRef]
- Tripathi, S.; Srinivas, V.; Nanjundiah, R.S. Downscaling of precipitation for climate change scenarios: A support vector machine approach. J. Hydrol. 2006, 330, 621–640. [Google Scholar] [CrossRef]
- Ismail, T.; Harun, S.; Zainudin, Z.M.; Shahid, S.; Fadzil, A.B.; Sheikh, U.U. Development of an optimal reservoir pumping operation for adaptation to climate change. KSCE J. Civ. Eng. 2017, 21, 467–476. [Google Scholar] [CrossRef]
- Obaid, H.A.; Shahid, S. Soil erosion susceptibility of Johor River basin. Water Environ. J. 2017, 31, 367–374. [Google Scholar] [CrossRef]
- Masselink, R.; Temme, A.J.; Giménez, R.; Casalí, J.; Keesstra, S.D. Assessing hillslope-channel connectivity in an agricultural catchment using rare-earth oxide tracers and random forests models. Cuad. Investig. Geogr. 2017, 43, 17–39. [Google Scholar] [CrossRef]
- Kirchhoff, M.; Rodrigo-Comino, J.; Seeger, M.; Ries, J.B. Soil erosion in sloping vineyards under conventional and organic land use managements (Saar-Mosel valley, Germany). Cuad. Investig. Geogr. 2017, 43, 119–140. [Google Scholar] [CrossRef]
- Keesstra, S.D.; Temme, A.J.; Schoorl, J.M.; Visser, S.M. Evaluating the hydrological component of the new catchment-scale sediment delivery model LAPSUS-D. Geomorphology 2014, 212, 97–107. [Google Scholar] [CrossRef]
| Centre(s) | Model | Resolution (Lat × Long) |
|---|---|---|
| Beijing Climate Center China | BCC-CSM1.1 | 2.8° × 2.8° |
| Commonwealth Scientific and Industrial Research Organization/Queensland Climate Change Centre of Excellence Australia | CSIRO-Mk3.6.0 | 1.8° × 1.8° |
| Institut Pierre Simon Laplace France | IPSL-CM5A-MR | 1.25° × 2.5° |
| Atmosphere and Ocean Research Institute (The University of Tokyo), National Institute for Environmental Studies, and Japan Agency for Marine-Earth Science and Technology, Japan | MIROC-ESM | 2.8° × 2.8° |
| Met Office Hadley Centre UK | HadGEM2-ES | 1.25° × 1.875° |
| Meteorological Research Institute Japan | MRI-CGCM3 | 1.12° × 1.125° |
| National Center for Atmospheric Research USA | CCSM4 | 0.94° ×1.25° |
| Bjerknes Centre for Climate Research, Norwegian Meteorological Institute, Norway | NorESM1-M | 1.90° × 2.5° |
| Functions | Equations | Parameters |
|---|---|---|
| GEV | where, and k = shape parameter μ = location parameter σ = scale parameter | |
| Exponential | ||
| GP | ||
| Gumbel |
| Estimators | Functions (PDFs) | Durations (Hour) | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 h | 3 h | 6 h | 12 h | 24 h | 48 h | 72 h | ||
| MLE | GEV | 294.88 | 302.74 | 302.46 | 307.9 | 319.75 | 333.06 | 341.18 |
| Gumbel | 295.05 | 302.81 | 302.77 | 308.17 | 319.79 | 333.12 | 341.2 | |
| Exp | 331.19 | 348.82 | 352.79 | 355.99 | 362.27 | 372.3 | 379.05 | |
| GP | 324.23 | 335.72 | 348.73 | 350.64 | 348.4 | 380.8 | 378.85 | |
| GMLE | GEV | 296.32 | 303.97 | 302.84 | 308.29 | 320.88 | 335.53 | 342.74 |
| Gumbel | 295.05 | 302.81 | 302.77 | 308.17 | 319.79 | 333.12 | 341.2 | |
| Exp | 331.19 | 348.82 | 352.79 | 355.99 | 362.27 | 372.3 | 379.05 | |
| GP | 445.27 | 493.66 | 505.88 | 504.24 | 498.67 | 504.61 | 504.26 | |
| L-moments | GEV | 296.32 | 303.97 | 302.84 | 308.29 | 320.88 | 335.53 | 342.74 |
| Gumbel | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | |
| Exp | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | |
| GP | 445.27 | 493.66 | 505.88 | 504.24 | 498.67 | 504.61 | 504.26 | |
| Bayesian | GEV | 5395.3 | 6183.1 | 6027.8 | 6743.8 | 9059.1 | 12867 | 14697 |
| Gumbel | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | |
| Exp | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | |
| GP | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | |
| Station ID | State | 1 h | 3 h | 6 h | 12 h | 24 h | 72 h |
|---|---|---|---|---|---|---|---|
| 1437116 | Johor Bahru | A | A | A | B | B | B |
| 5806066 | Kedah | A | A | A | A | A | A |
| 6103047 | Kedah | A | A | A | A | A | A |
| 2224038 | Melaka | A | A | A | A | B | B |
| 2725083 | Niger Sembilan | A | A | A | A | A | A |
| 3516022 | Selangor | A | A | A | A | A | A |
| 3411017 | Selangor | B | B | B | B | A | A |
| 3710006 | Selangor | A | A | A | A | A | A |
| 3519125 | Pahang | A | A | A | A | A | A |
| 3930012 | Pahang | A | A | A | A | A | A |
| 5302001 | Pinang | B | C | B | C | C | B |
| 4012143 | Perak | A | A | A | A | A | A |
| 4207048 | Perak | A | A | A | A | A | A |
| 5710061 | Perak | A | A | A | A | E | E |
| 4409091 | Perak | D | D | D | D | D | F |
| 6019004 | Kelantan | D | D | F | F | F | D |
| 4234109 | Terengganu | A | A | A | A | A | A |
| 5331048 | Terengganu | A | A | A | A | A | A |
| 3117070 | W. Persekutuan | A | A | D | D | D | A |
| Station ID | Indices | Model | MAE | NRMSE % | PBIAS % | NSE | R2 |
|---|---|---|---|---|---|---|---|
| Kedah 5806066 | Calibration | BCC-CSM1.1 | 0.31 | 12.1 | 1.1 | 0.95 | 0.91 |
| CCSM4 | 0.27 | 12 | 0.6 | 0.97 | 0.93 | ||
| CSIRO-Mk3.6.0 | 0.34 | 13.1 | 2.1 | 0.94 | 0.95 | ||
| HadGEM2-ES | 0.36 | 14.6 | 0.3 | 0.94 | 0.93 | ||
| IPSL-CM5A-MR | 0.33 | 12.1 | 3.1 | 0.92 | 0.92 | ||
| MIROC-ESM | 0.21 | 8.8 | 0.2 | 0.91 | 0.96 | ||
| MRI-CGCM3 | 0.34 | 12.9 | 1.3 | 0.94 | 0.95 | ||
| NorESM1-M | 0.15 | 6.1 | 0.5 | 0.91 | 0.93 | ||
| Validation | BCC-CSM1.1 | 0.45 | 20.6 | 2.1 | 0.93 | 0.92 | |
| CCSM4 | 0.54 | 21.3 | 1.9 | 0.95 | 0.90 | ||
| CSIRO-Mk3.6.0 | 0.56 | 21 | 0.1 | 0.96 | 0.91 | ||
| HadGEM2-ES | 0.4 | 17.2 | 4.1 | 0.94 | 0.94 | ||
| IPSL-CM5A-MR | 0.42 | 19 | 1.3 | 0.93 | 0.93 | ||
| MIROC-ESM | 0.42 | 17.9 | 1.1 | 0.93 | 0.95 | ||
| MRI-CGCM3 | 0.42 | 19.2 | 1 | 0.92 | 0.93 | ||
| NorESM1-M | 0.45 | 17.8 | 1.9 | 0.94 | 0.93 |
| Return Period (Years) | Duration (Hours) | ||||||
|---|---|---|---|---|---|---|---|
| 1 h | 3 h | 6 h | 12 h | 24 h | 48 h | 72 h | |
| 2 | 0.91 | 0.90 | 1.09 | 1.48 | 1.61 | 1.63 | 1.55 |
| 5 | 1.01 | 1.05 | 1.29 | 1.62 | 1.65 | 1.56 | 1.46 |
| 10 | 1.19 | 1.45 | 1.48 | 1.70 | 1.68 | 1.55 | 1.42 |
| 25 | 1.62 | 1.59 | 1.78 | 1.78 | 1.72 | 1.54 | 1.39 |
| 50 | 2.15 | 1.97 | 2.07 | 1.83 | 1.75 | 1.55 | 1.37 |
| 100 | 2.95 | 2.56 | 2.41 | 1.88 | 1.78 | 1.56 | 1.37 |
| Average of ratios of Return Period | 1.64 | 1.59 | 1.69 | 1.72 | 1.70 | 1.57 | 1.43 |
| Model | Duration (Hours) | ||||||
|---|---|---|---|---|---|---|---|
| 1 h | 3 h | 6 h | 12 h | 24 h | 48 h | 72 h | |
| BCC-CSM1.1 | 1.64 | 1.59 | 1.69 | 1.72 | 1.70 | 1.57 | 1.43 |
| CCSM4 | 1.52 | 1.5 | 1.77 | 1.68 | 1.61 | 1.41 | 1.25 |
| CSIRO-Mk3.6 | 2.17 | 1.98 | 2.09 | 1.96 | 1.85 | 1.61 | 1.44 |
| HadGEM2-ES | 1.41 | 1.49 | 1.75 | 1.91 | 1.9 | 1.76 | 1.6 |
| IPSL-CM5A-MR | 1.67 | 1.66 | 1.91 | 1.81 | 1.71 | 1.52 | 1.35 |
| MIROC-ESM | 2.18 | 1.49 | 1.58 | 1.68 | 1.66 | 1.51 | 1.37 |
| MRI-CGCM3 | 2.81 | 2.68 | 2.86 | 2.8 | 2.75 | 2.51 | 2.27 |
| NorESM1-M | 1.92 | 1.7 | 2.13 | 2.24 | 2.17 | 1.93 | 1.73 |
| Models | Polynomial Equations | |
|---|---|---|
| BCC-CSM1.1 | y = −0.02 x2 + 0.14 x + 1.47 | where, x is the average of the ratios of return periods and y is the Model correction factor (MCF) |
| CCSM4 | y = −0.04 x2 + 0.25 x + 1.27 | |
| CSIRO-Mk3.6 | y = −0.02 x2 + 0.04 x + 2.09 | |
| HadGEM2-ES | y = −0.04 x2 + 0.38 x + 1.00 | |
| IPSL-CM5A-MR | y = −0.04 x2 + 0.23 x + 1.44 | |
| MIROC-ESM | y = 0.02 x2 − 0.21 x + 2.16 | |
| MRI-CGCM3 | y = −0.03 x2 + 0.18 x + 2.59 | |
| NorESM1-M | y = −0.04 x2 + 0.34 x + 1.47 |
| Model | Duration (Hours) | ||||||
|---|---|---|---|---|---|---|---|
| 1 h | 3 h | 6 h | 12 h | 24 h | 48 h | 72 h | |
| BCC-CSM1.1 | 1.65 | 1.64 | 1.65 | 1.65 | 1.65 | 1.64 | 1.63 |
| CCSM4 | 1.56 | 1.56 | 1.59 | 1.58 | 1.57 | 1.54 | 1.52 |
| CSIRO-Mk3.6 | 2.08 | 2.09 | 2.09 | 2.09 | 2.10 | 2.10 | 2.11 |
| HadGEM2-ES | 1.46 | 1.48 | 1.54 | 1.58 | 1.58 | 1.54 | 1.51 |
| IPSL-CM5A-MR | 1.71 | 1.71 | 1.73 | 1.73 | 1.72 | 1.70 | 1.68 |
| MIROC-ESM | 1.80 | 1.89 | 1.88 | 1.86 | 1.87 | 1.89 | 1.91 |
| MRI-CGCM3 | 2.86 | 2.86 | 2.86 | 2.86 | 2.86 | 2.85 | 2.84 |
| NorESM1-M | 1.98 | 1.93 | 2.01 | 2.03 | 2.02 | 1.98 | 1.94 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Noor, M.; Ismail, T.; Chung, E.-S.; Shahid, S.; Sung, J.H. Uncertainty in Rainfall Intensity Duration Frequency Curves of Peninsular Malaysia under Changing Climate Scenarios. Water 2018, 10, 1750. https://doi.org/10.3390/w10121750
Noor M, Ismail T, Chung E-S, Shahid S, Sung JH. Uncertainty in Rainfall Intensity Duration Frequency Curves of Peninsular Malaysia under Changing Climate Scenarios. Water. 2018; 10(12):1750. https://doi.org/10.3390/w10121750
Chicago/Turabian StyleNoor, Muhammad, Tarmizi Ismail, Eun-Sung Chung, Shamsuddin Shahid, and Jang Hyun Sung. 2018. "Uncertainty in Rainfall Intensity Duration Frequency Curves of Peninsular Malaysia under Changing Climate Scenarios" Water 10, no. 12: 1750. https://doi.org/10.3390/w10121750
APA StyleNoor, M., Ismail, T., Chung, E.-S., Shahid, S., & Sung, J. H. (2018). Uncertainty in Rainfall Intensity Duration Frequency Curves of Peninsular Malaysia under Changing Climate Scenarios. Water, 10(12), 1750. https://doi.org/10.3390/w10121750








