The Numerical Modeling of Coupled Motions of a Moored Floating Body in Waves
Abstract
:1. Introduction
2. Numerical Methods
2.1. Fluid Flow Governing Equations
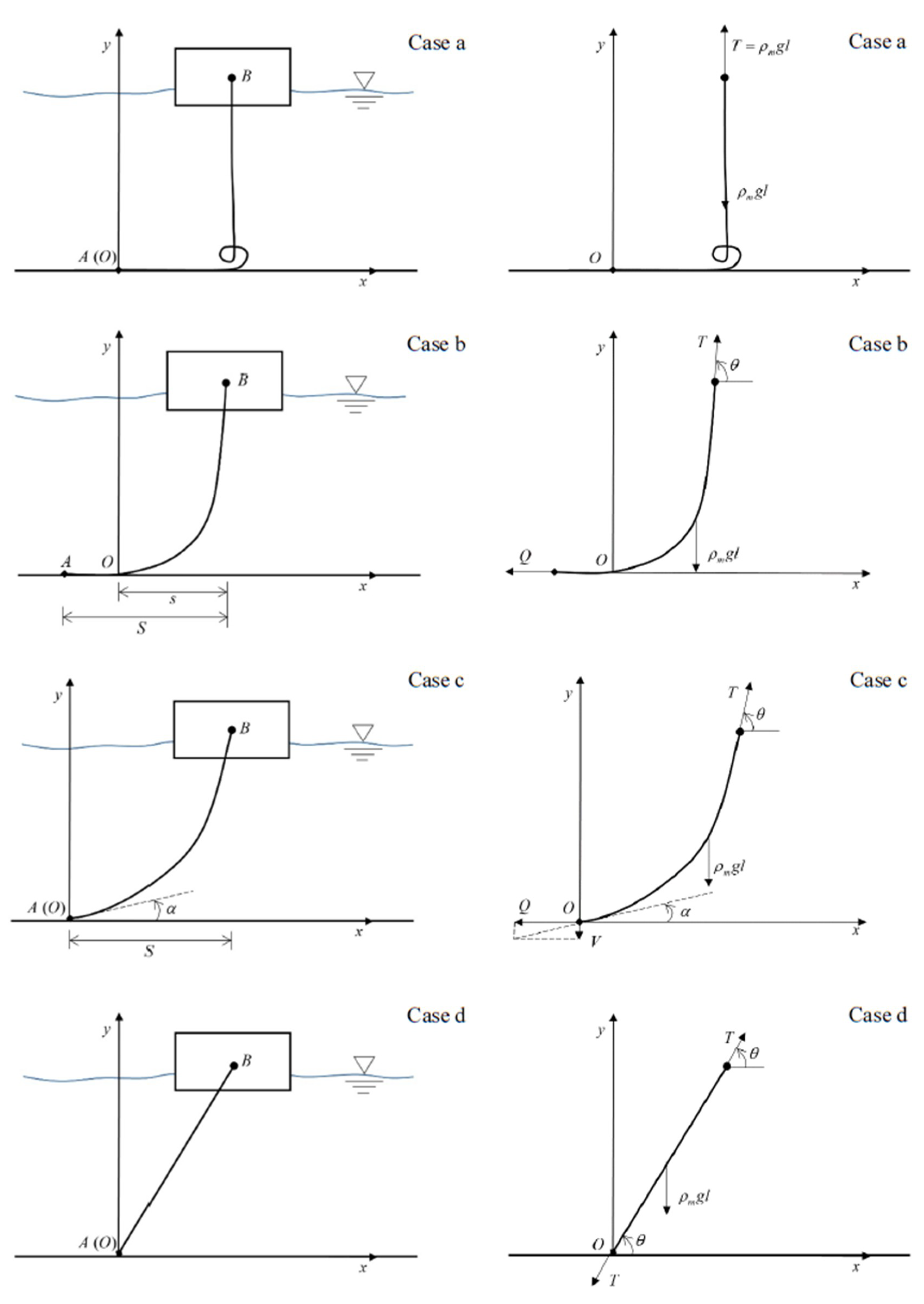
2.2. Equations for Mooring Line Dynamics
2.3. Equations for Floating Body Dynamics
2.4. Numerical Stability Criterion
3. Numerical Validation and Discussion
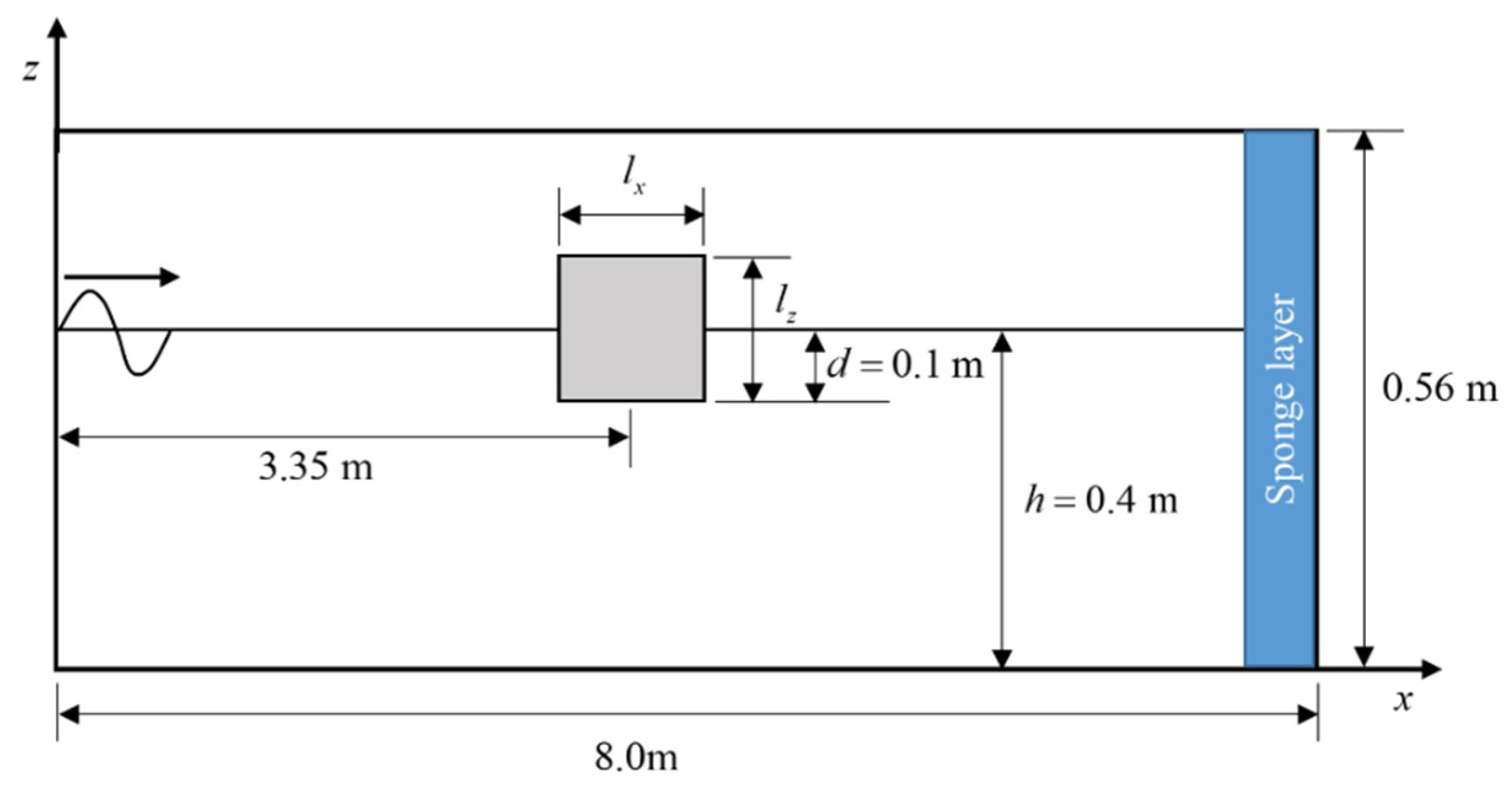
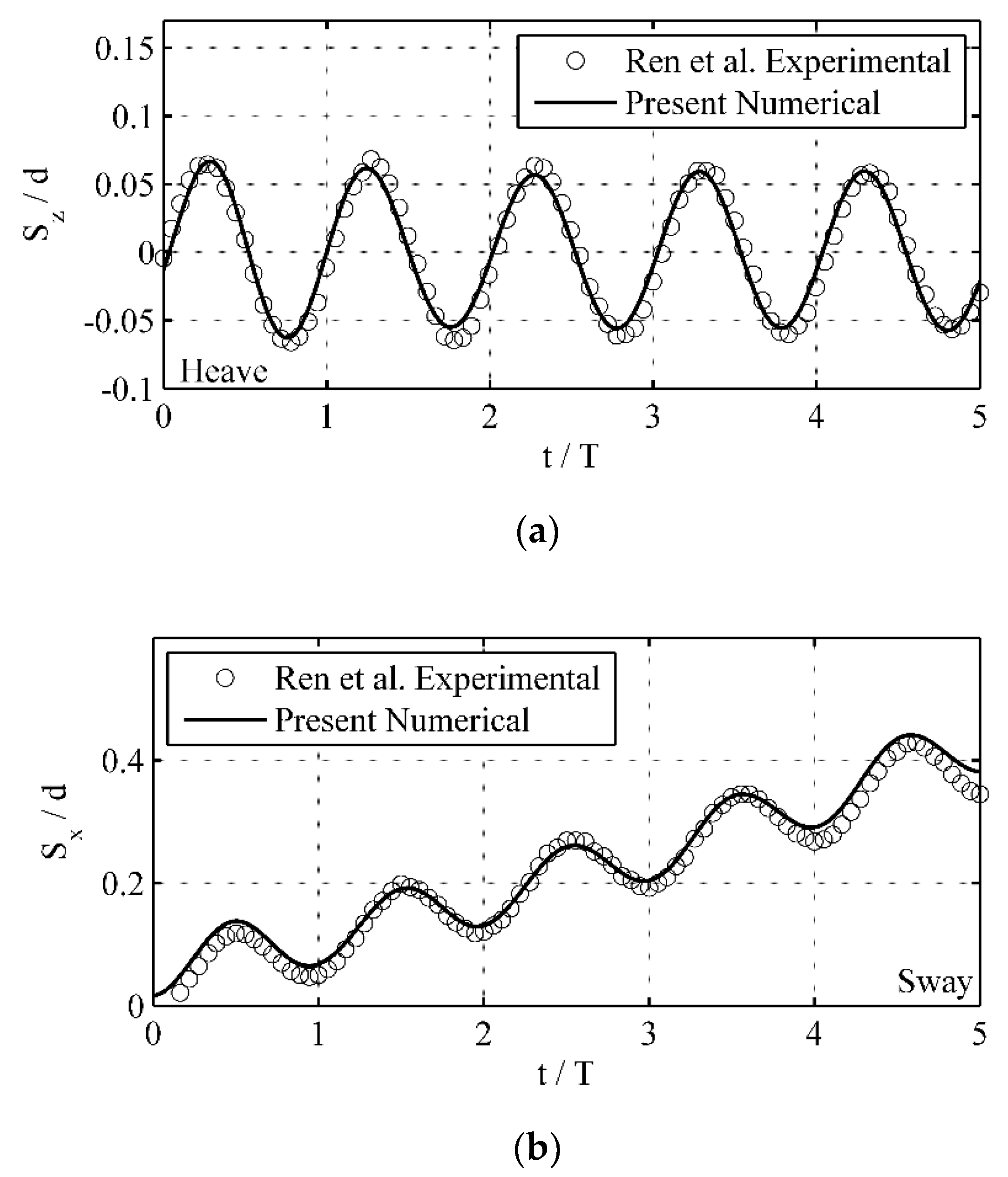
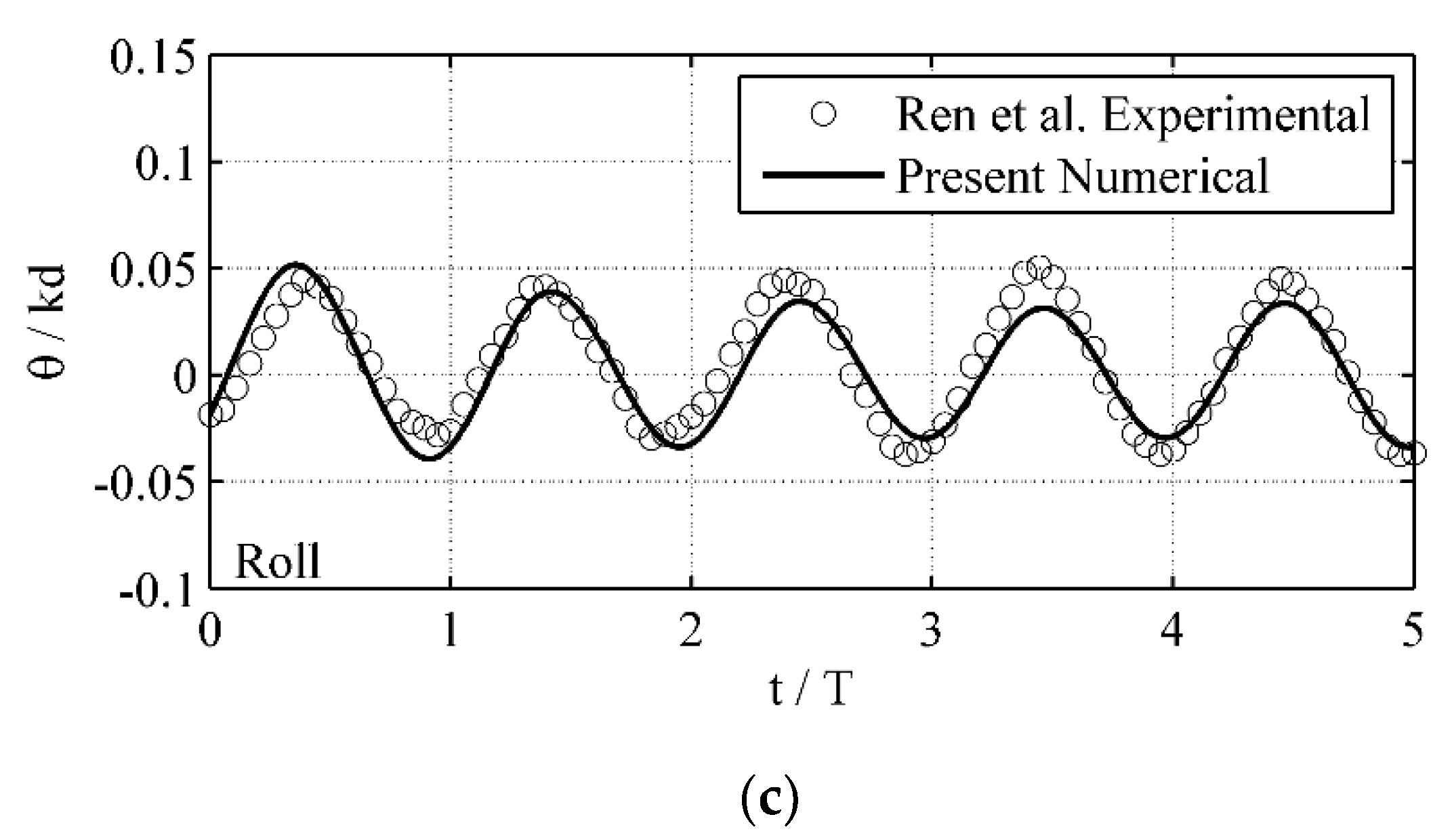
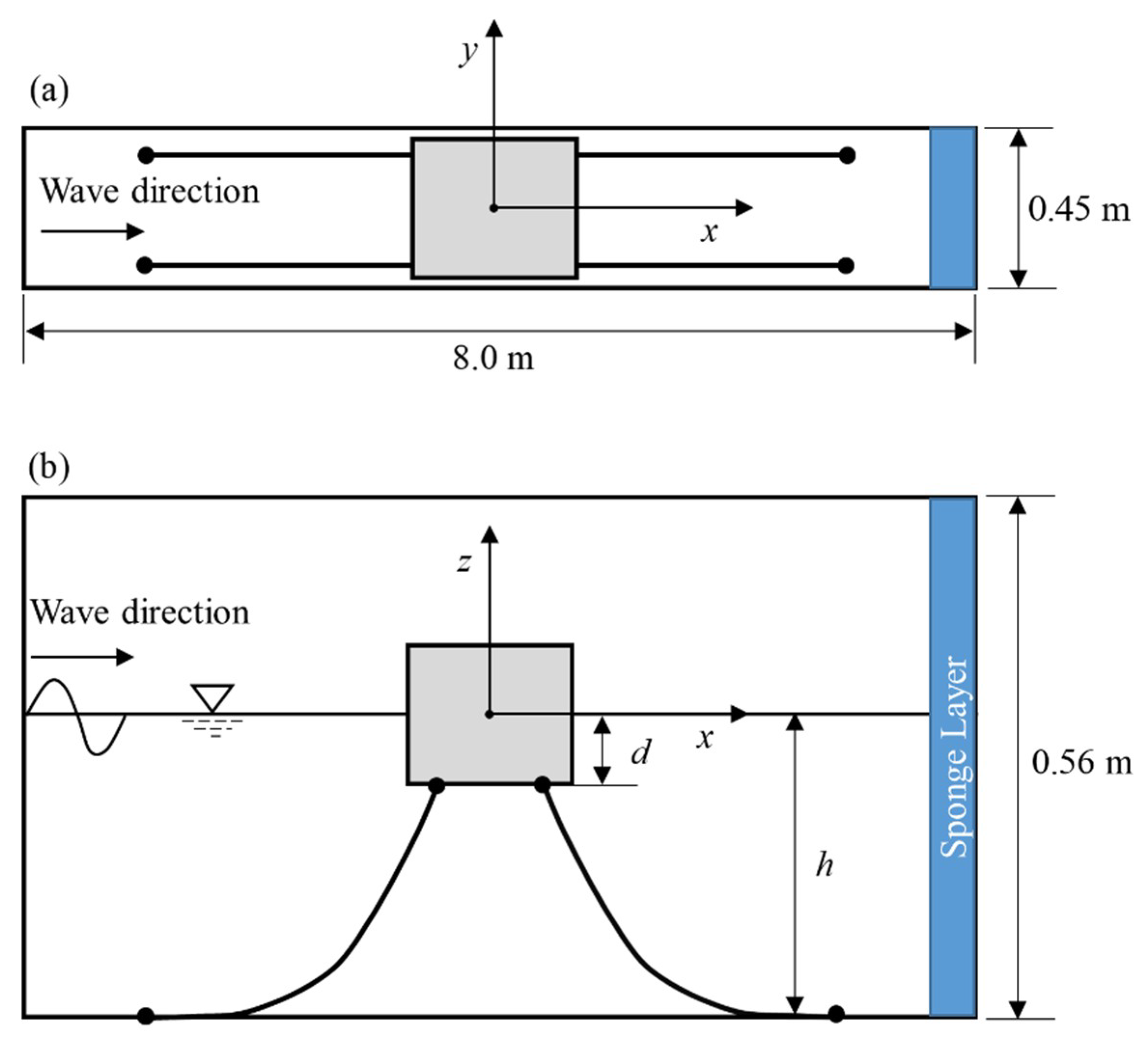
3.1. Motions of a Free-Floating Box in Waves
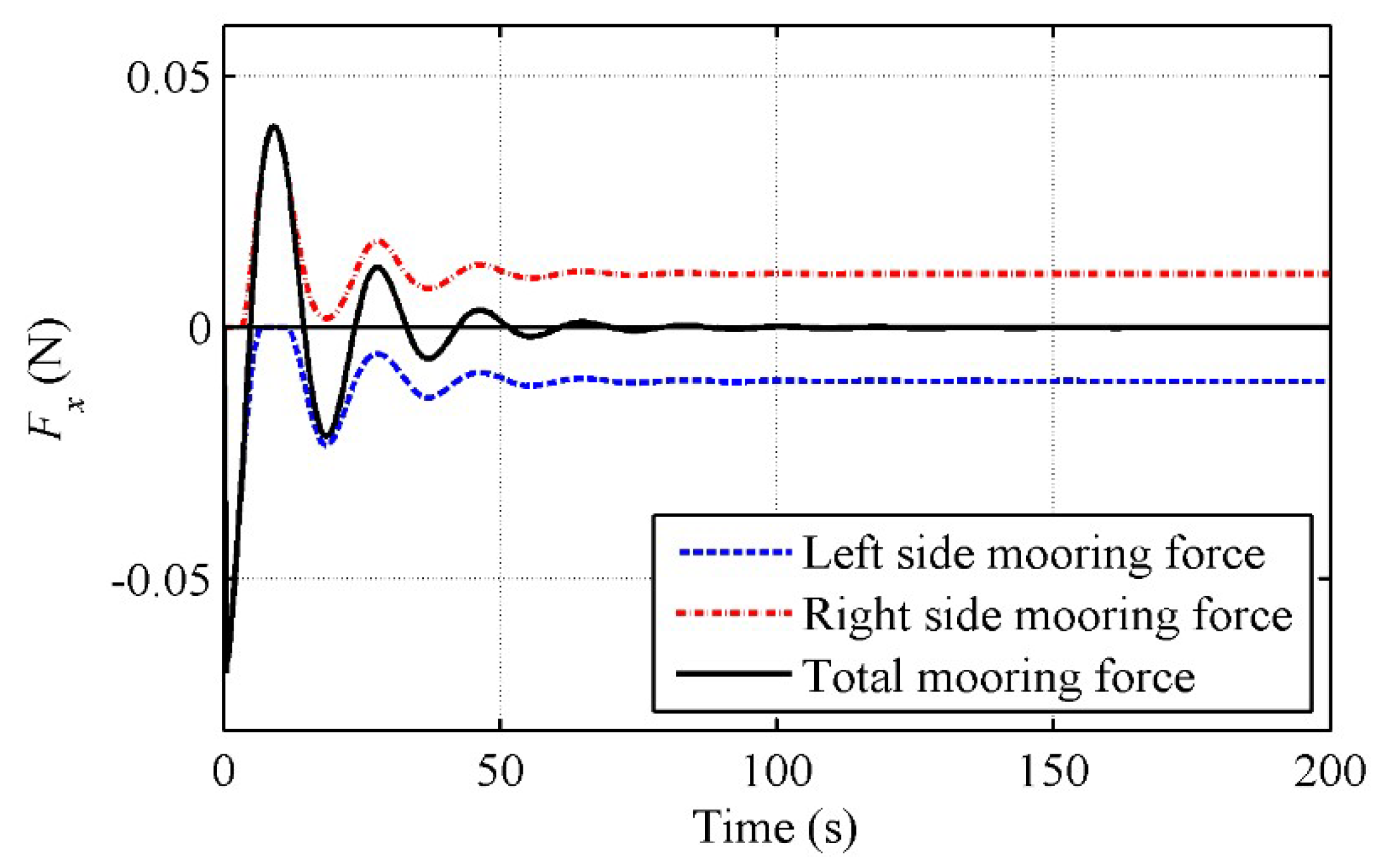
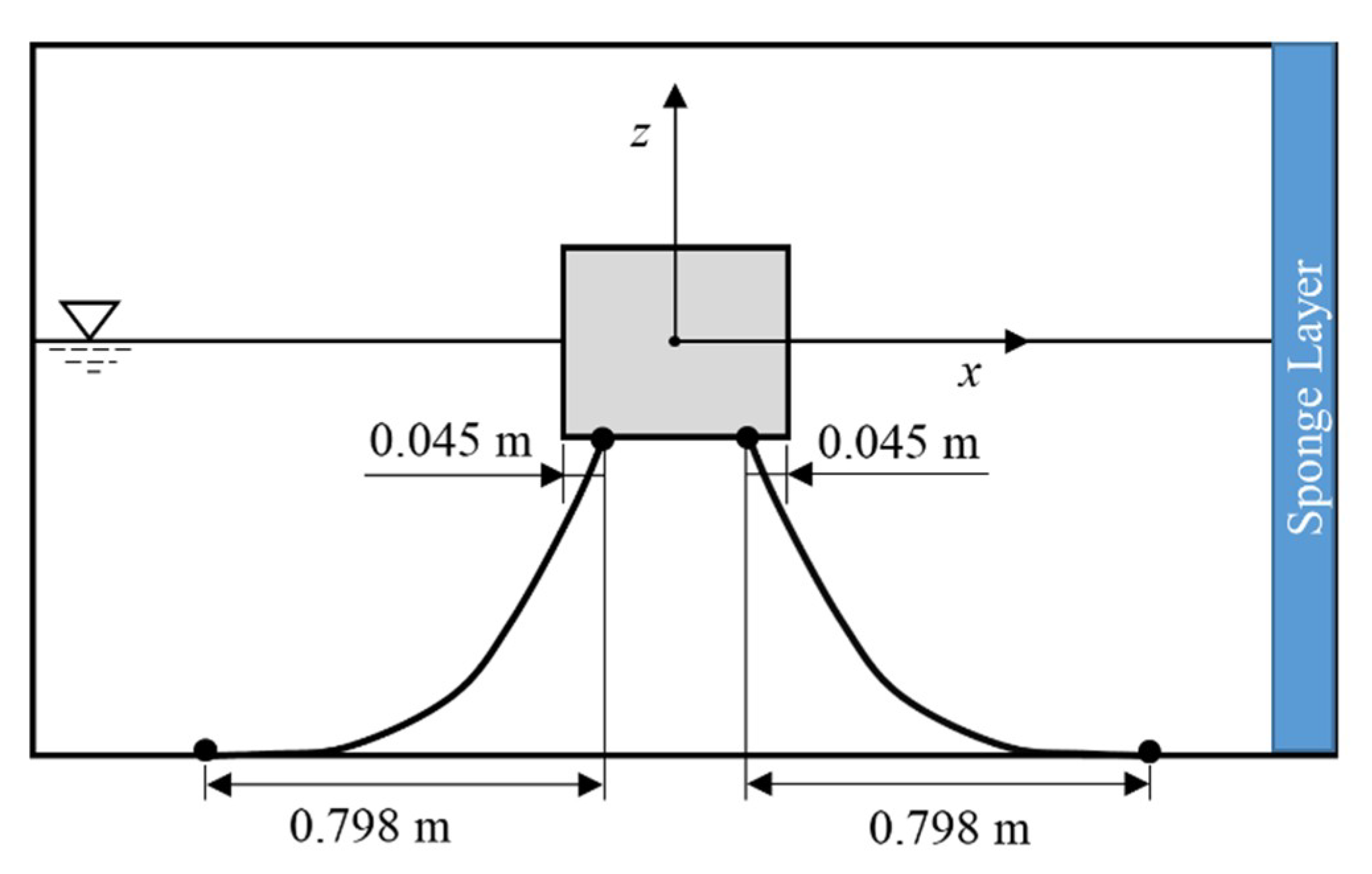
3.2. Motions of a Moored Floating Box in Still Water
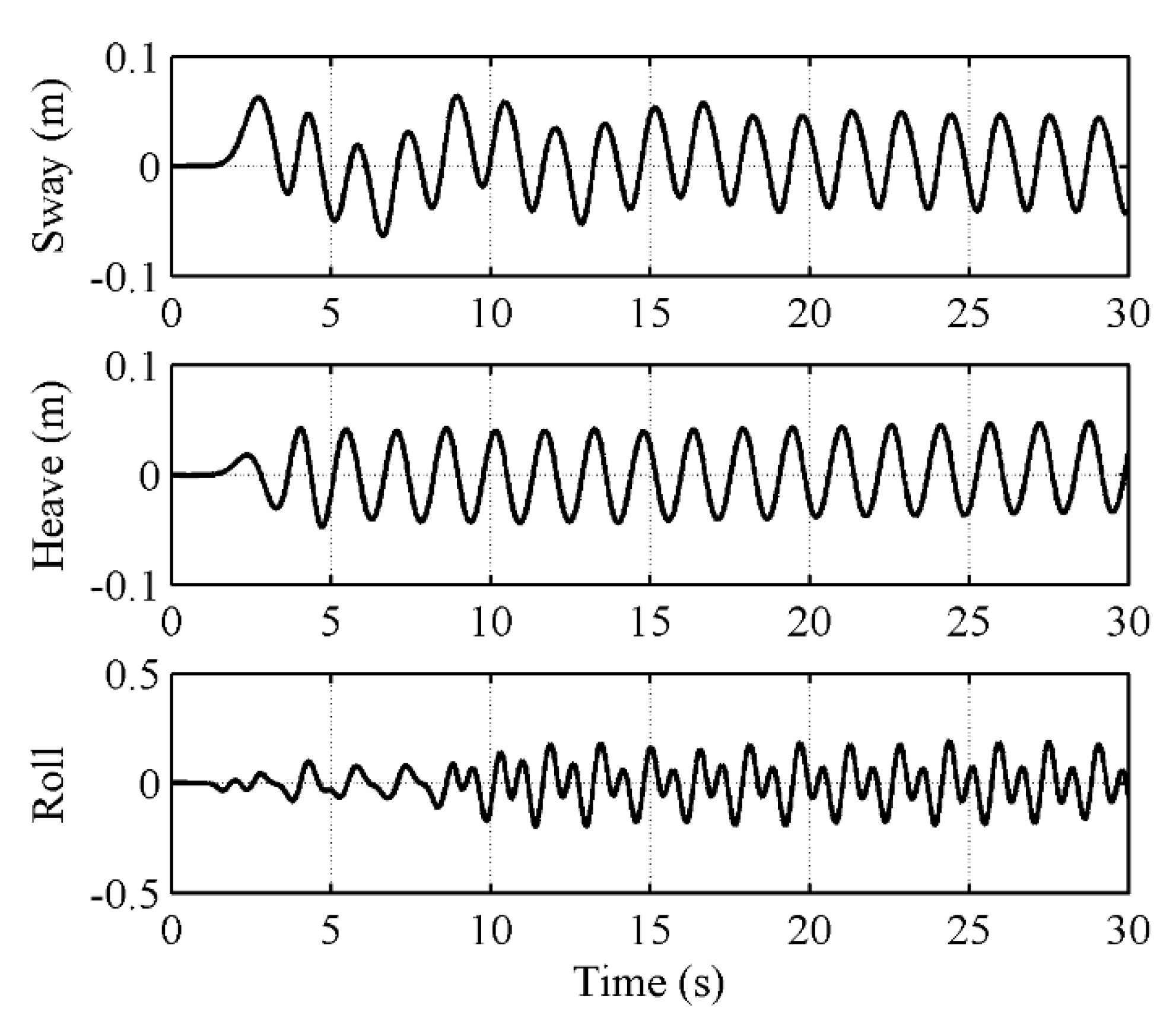
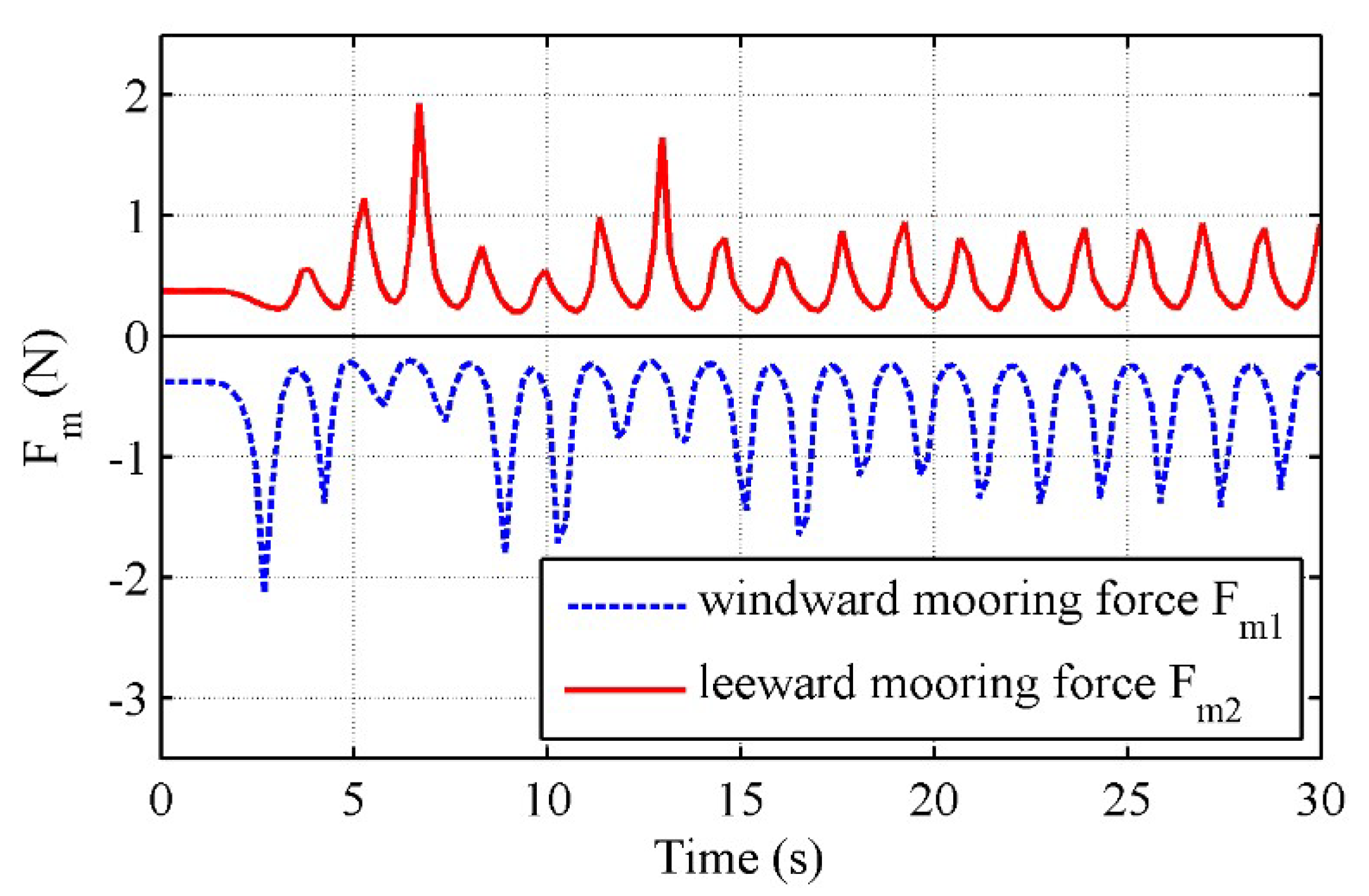
3.3. Motions of a Moored Floating Box in Waves
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Williams, A.; Abul-Azm, A. Dual pontoon floating breakwater. Ocean Eng. 1997, 24, 465–478. [Google Scholar] [CrossRef]
- Sannasiraj, S.; Sundar, V.; Sundaravadivelu, R. Mooring forces and motion responses of pontoon-type floating breakwaters. Ocean Eng. 1998, 25, 27–48. [Google Scholar] [CrossRef]
- Williams, A.; Lee, H.; Huang, Z. Floating pontoon breakwaters. Ocean Eng. 2000, 27, 221–240. [Google Scholar] [CrossRef]
- Chen, X.; Wu, Y.; Cui, W.; Tang, X. Nonlinear hydroelastic analysis of a moored floating body. Ocean Eng. 2003, 30, 965–1003. [Google Scholar] [CrossRef]
- Wen, J. Numerical and Experimental Study on the Interaction between Waves and Two Floating Bodies. Master’s Thesis, Dalian University of Technology, Dalian, China, 2012. [Google Scholar]
- Ku, N.; Cha, J.-H. A Study on Moored Floating Body Using Non-Linear FEM Analysis. In Proceedings of the Twelfth ISOPE Pacific/Asia Offshore Mechanics Symposium, Gold Coast, Australia, 4–7 October 2016; International Society of Offshore and Polar Engineers: Mountain View, CA, USA, 2016. [Google Scholar]
- Zhang, X.; Wolgamot, H.; Draper, S.; Zhao, W.; Cheng, L. The role of overtopping duration in greenwater loading. In Proceedings of the 33rd International Workshop on Water Waves and Floating Bodies, Guidel-Plages, France, 4–7 April 2018. [Google Scholar]
- Zhang, X.; Draper, S.; Wolgamot, H.; Zhao, W.; Cheng, L. Numerical Investigation of Effects of Bow Flare Angle on Greenwater Overtopping a Fixed Offshore Vessel. In Proceedings of the ASME 2018 37th International Conference on Ocean, Offshore and Arctic Engineering, American Society of Mechanical Engineers, Madrid, Spain, 17–22 June 2018; p. V001T01A002. [Google Scholar]
- Xue, M.; Lin, P.; Zheng, J.; Ma, Y.; Yuan, X.; Nguyen, V. Effects of perforated baffle on reducing sloshing in rectangular tank: Experimental and numerical study. China Ocean Eng. 2013, 27, 615–628. [Google Scholar] [CrossRef]
- Xue, M.; Zheng, J.; Lin, P.; Xiao, Z. Violent transient sloshing-wave interaction with a baffle in a three-dimensional numerical tank. J. Ocean Univ. China 2017, 16, 661–673. [Google Scholar] [CrossRef]
- Xue, M.; Zheng, J.; Lin, P.; Yuan, X. Experimental study on vertical baffles of different configurations in suppressing sloshing pressure. Ocean Eng. 2017, 136, 178–189. [Google Scholar] [CrossRef]
- Rahman, M.A.; Mizutani, N.; Kawasaki, K. Numerical modeling of dynamic responses and mooring forces of submerged floating breakwater. Coast. Eng. 2006, 53, 799–815. [Google Scholar] [CrossRef]
- Peng, W.; Lee, K.-H.; Shin, S.-H.; Mizutani, N. Numerical simulation of interactions between water waves and inclined-moored submerged floating breakwaters. Coast. Eng. 2013, 82, 76–87. [Google Scholar] [CrossRef]
- Loukogeorgaki, E.; Angelides, D.C. Stiffness of mooring lines and performance of floating breakwater in three dimensions. Appl. Ocean Res. 2005, 27, 187–208. [Google Scholar] [CrossRef]
- Ji, C.-Y.; Chen, X.; Cui, J.; Yuan, Z.-M.; Incecik, A. Experimental study of a new type of floating breakwater. Ocean Eng. 2015, 105, 295–303. [Google Scholar] [CrossRef] [Green Version]
- Ji, C.-Y.; Guo, Y.-C.; Cui, J.; Yuan, Z.-M.; Ma, X.-J. 3D experimental study on a cylindrical floating breakwater system. Ocean Eng. 2016, 125, 38–50. [Google Scholar] [CrossRef]
- Ji, C.; Cheng, Y.; Yang, K.; Oleg, G. Numerical and experimental investigation of hydrodynamic performance of a cylindrical dual pontoon-net floating breakwater. Coast. Eng. 2017, 129, 1–16. [Google Scholar] [CrossRef]
- Liu, D.; Lin, P. A numerical study of three-dimensional liquid sloshing in tanks. J. Comput. Phys. 2008, 227, 3921–3939. [Google Scholar] [CrossRef]
- Liu, D.; Lin, P. Three-dimensional liquid sloshing in a tank with baffles. Ocean Eng. 2009, 36, 202–212. [Google Scholar] [CrossRef]
- Xue, M.-A.; Lin, P. Numerical study of ring baffle effects on reducing violent liquid sloshing. Comput. Fluids 2011, 52, 116–129. [Google Scholar] [CrossRef]
- Lin, P.; Cheng, L.; Liu, D. A two-phase flow model for wave-structure interaction using a virtual boundary force method. Comput. Fluids 2016, 129, 101–110. [Google Scholar] [CrossRef]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics—The Finite Volume Method, 2nd ed.; Pearson: London, UK, 2007. [Google Scholar]
- Lin, P.; Li, C.-W. Wave–current interaction with a vertical square cylinder. Ocean Eng. 2003, 30, 855–876. [Google Scholar] [CrossRef]
- Gueyffier, D.; Li, J.; Nadim, A.; Scardovelli, R.; Zaleski, S. Volume-of-fluid interface tracking with smoothed surface stress methods for three-dimensional flows. J. Comput. Phys. 1999, 152, 423–456. [Google Scholar] [CrossRef]
- Ren, B.; He, M.; Dong, P.; Wen, H. Nonlinear simulations of wave-induced motions of a freely floating body using WCSPH method. Appl. Ocean Res. 2015, 50, 1–12. [Google Scholar] [CrossRef]
- Hou, Y. Experimental Study on Hydrodynamic Performance of Single Pontoon-Mooring Line Floating Breakwater. Master’s Thesis, Dalian University of Technology, Dalian, China, 2008. [Google Scholar]
- Park, J.; Kim, M.; Miyata, H. Fully non-linear free-surface simulations by a 3D viscous numerical wave tank. Int. J. Numer. Methods Fluids 1999, 29, 685–703. [Google Scholar] [CrossRef]
- Lin, P.; Liu, P.L.F. Discussion of “Vertical variation of the flow across the surf zone”. Coast Eng. 2004, 50, 161–164. [Google Scholar] [CrossRef]
- Dalrymple, R.A.; Dean, R.G. Water Wave Mechanics for Engineers and Scientists; Prentice-Hall: Upper Saddle River, NJ, USA, 1991. [Google Scholar]
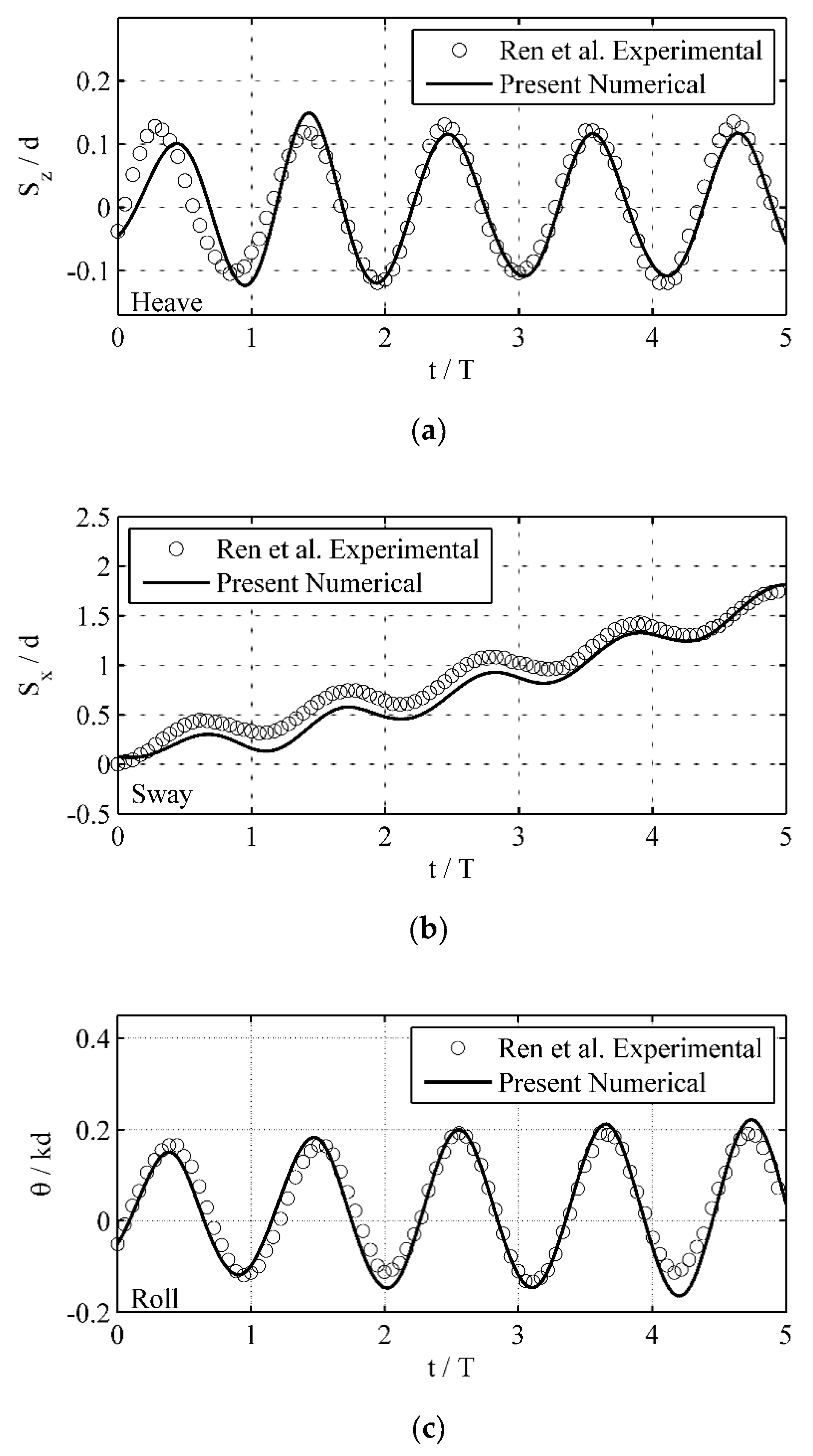
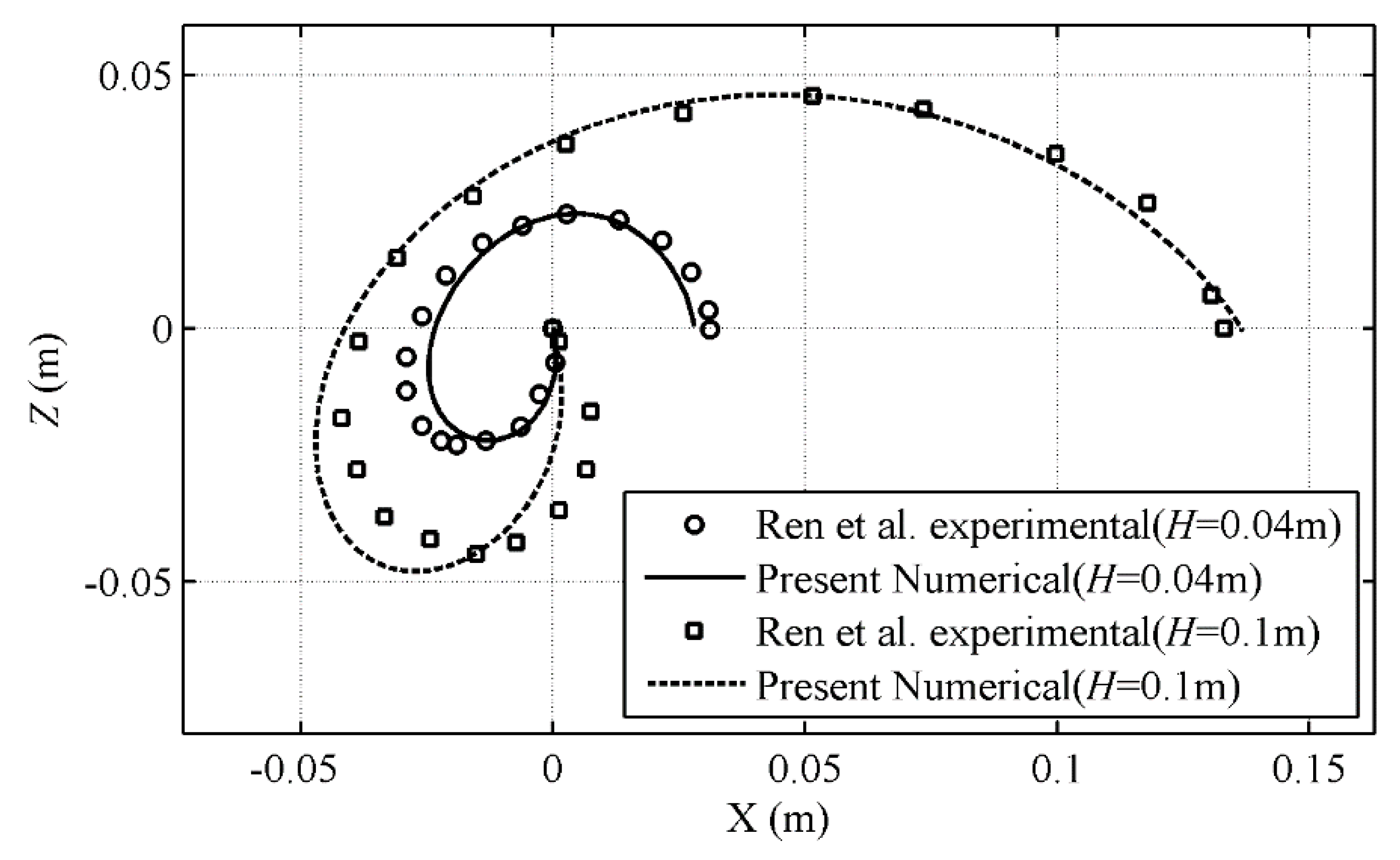
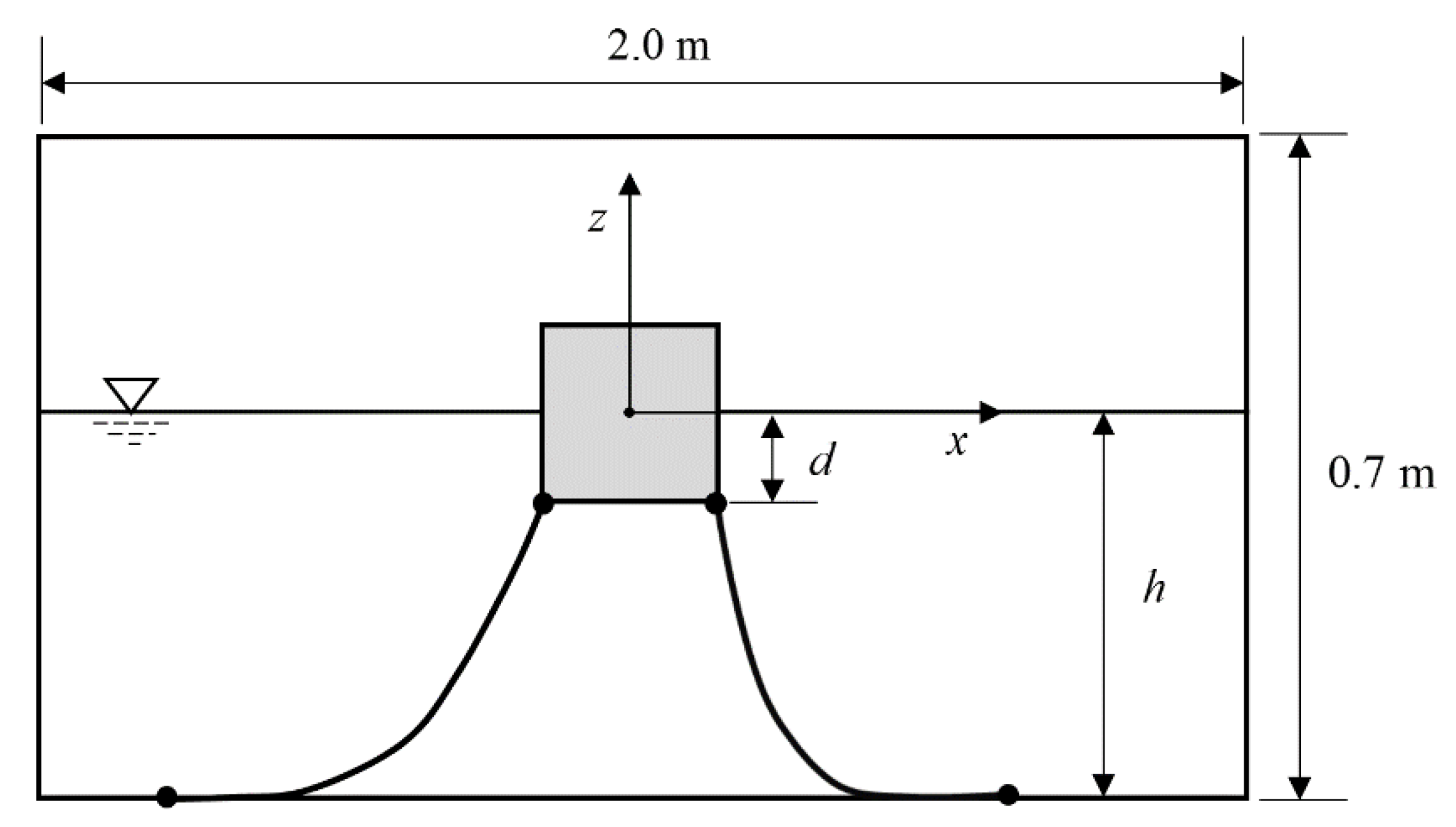
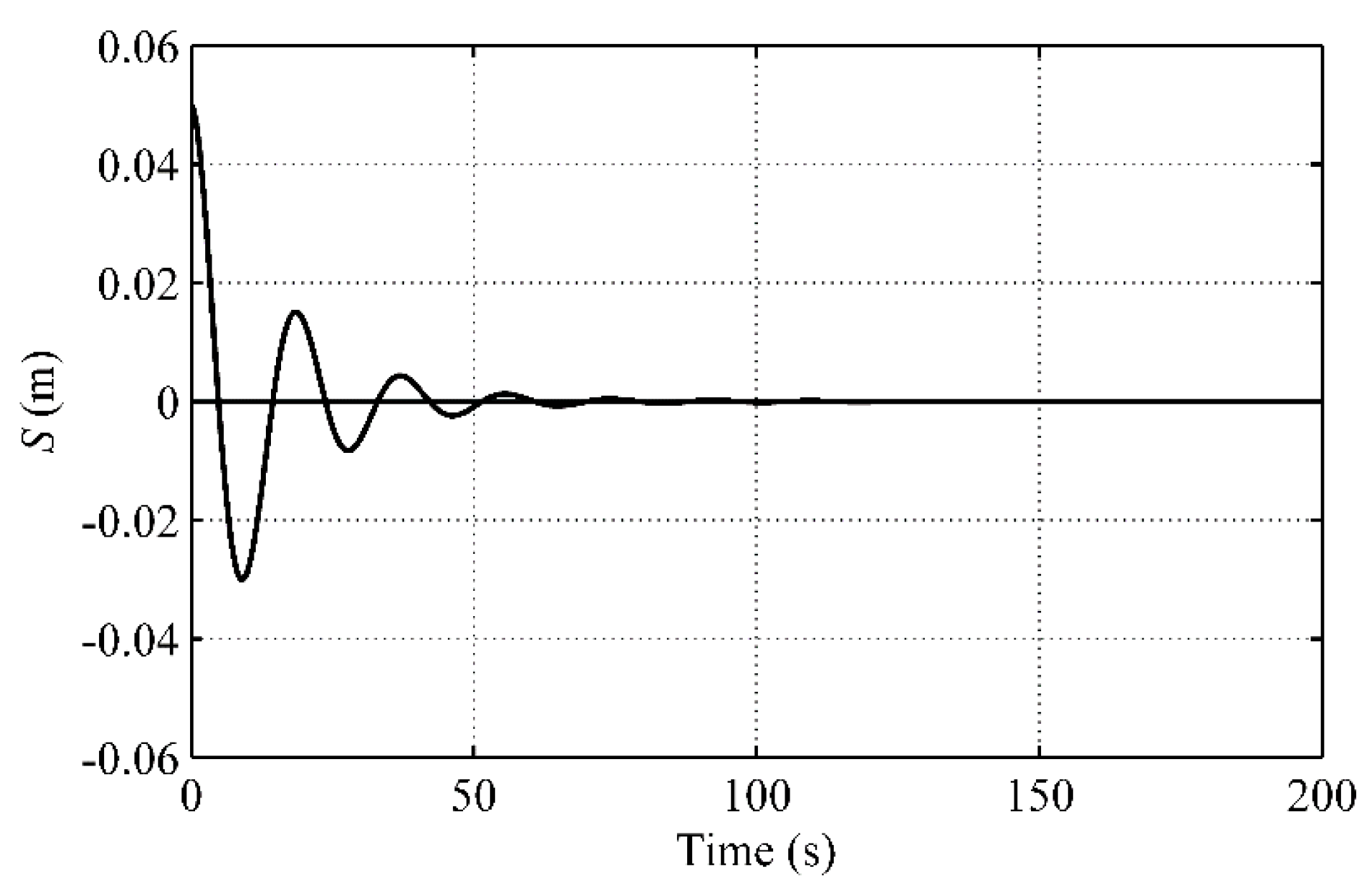
| RAO | Experimental Data [26] | Present Result |
|---|---|---|
| RAO (sway) | 1.17 | 1.23 |
| RAO (heave) | 1.14 | 1.19 |
| RAO (roll): °/cm | 1.42 | 2.09 |
| RAO | Experimental Data [26] | Present Result |
|---|---|---|
| RAO (Fm1): | 0.392 | 0.390 |
| RAO (Fm2): | 0.392 | 0.245 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, L.; Lin, P. The Numerical Modeling of Coupled Motions of a Moored Floating Body in Waves. Water 2018, 10, 1748. https://doi.org/10.3390/w10121748
Cheng L, Lin P. The Numerical Modeling of Coupled Motions of a Moored Floating Body in Waves. Water. 2018; 10(12):1748. https://doi.org/10.3390/w10121748
Chicago/Turabian StyleCheng, Lin, and Pengzhi Lin. 2018. "The Numerical Modeling of Coupled Motions of a Moored Floating Body in Waves" Water 10, no. 12: 1748. https://doi.org/10.3390/w10121748
APA StyleCheng, L., & Lin, P. (2018). The Numerical Modeling of Coupled Motions of a Moored Floating Body in Waves. Water, 10(12), 1748. https://doi.org/10.3390/w10121748




