A Support Vector Machine Forecasting Model for Typhoon Flood Inundation Mapping and Early Flood Warning Systems
Abstract
:1. Introduction
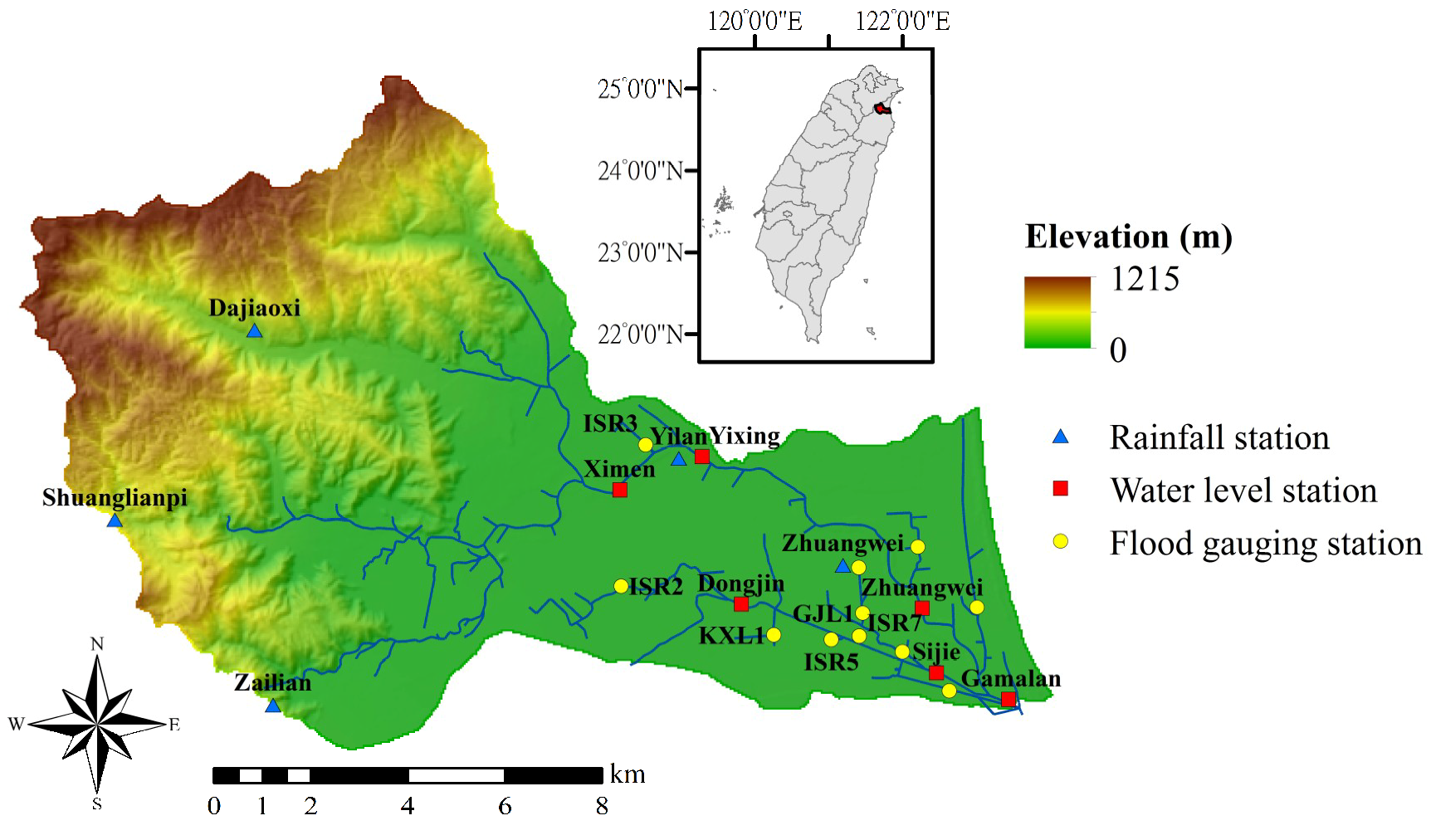
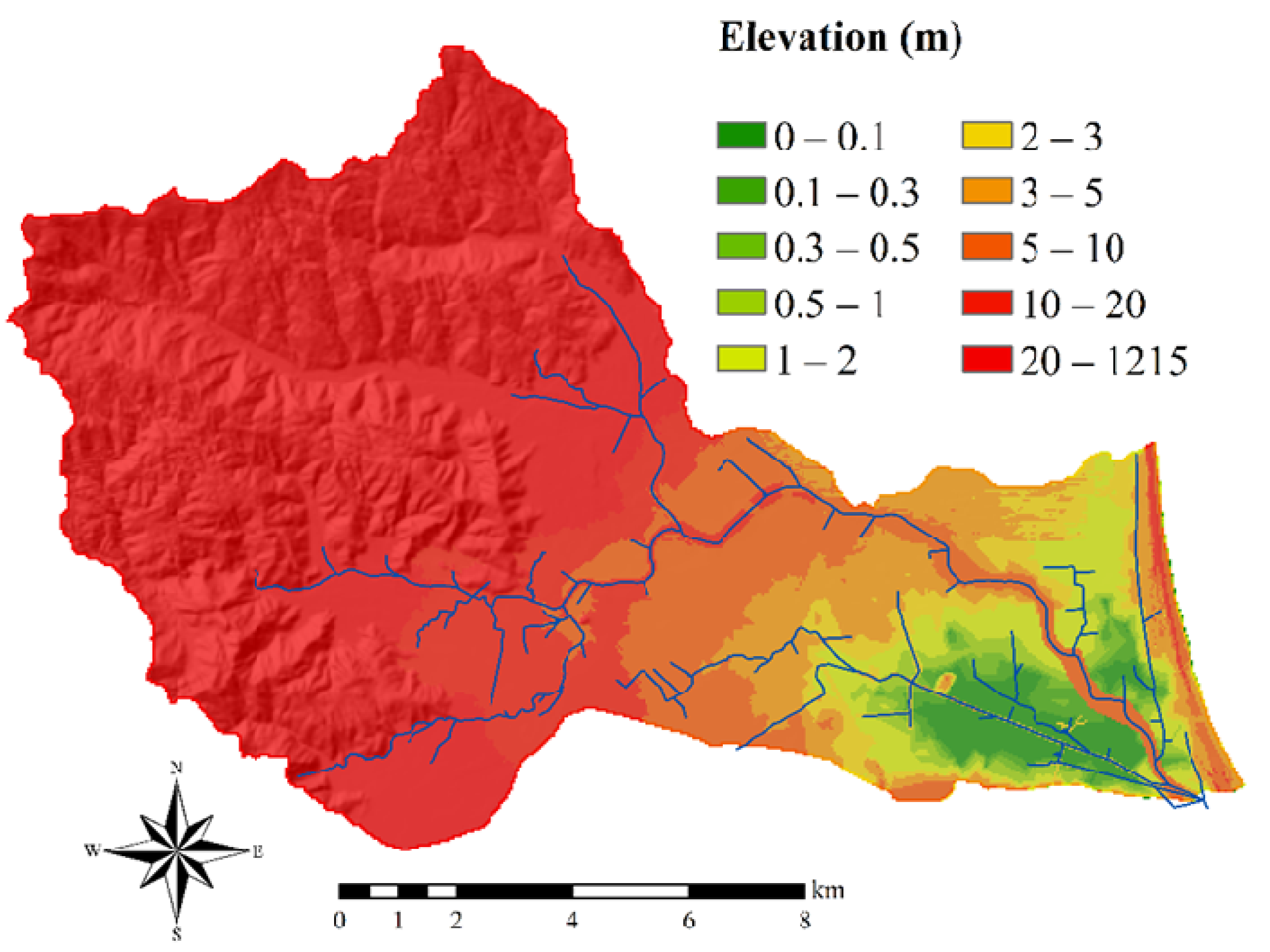
2. Study Area and Hydrological Data
3. Methodology Development
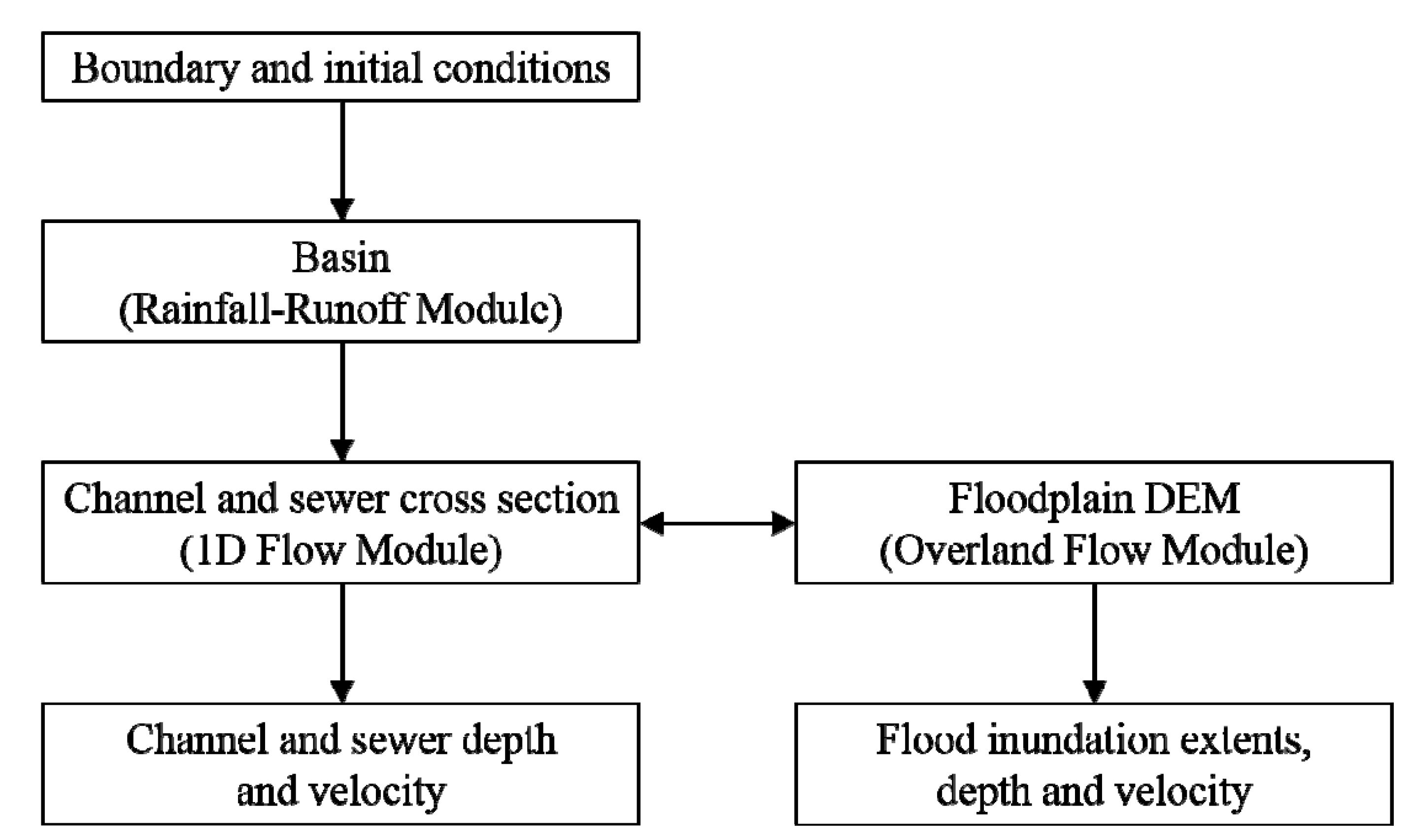
3.1. Hydrodynamic Simulation
3.2. k-means Clustering Algorithm
3.3. Support Vector Machine
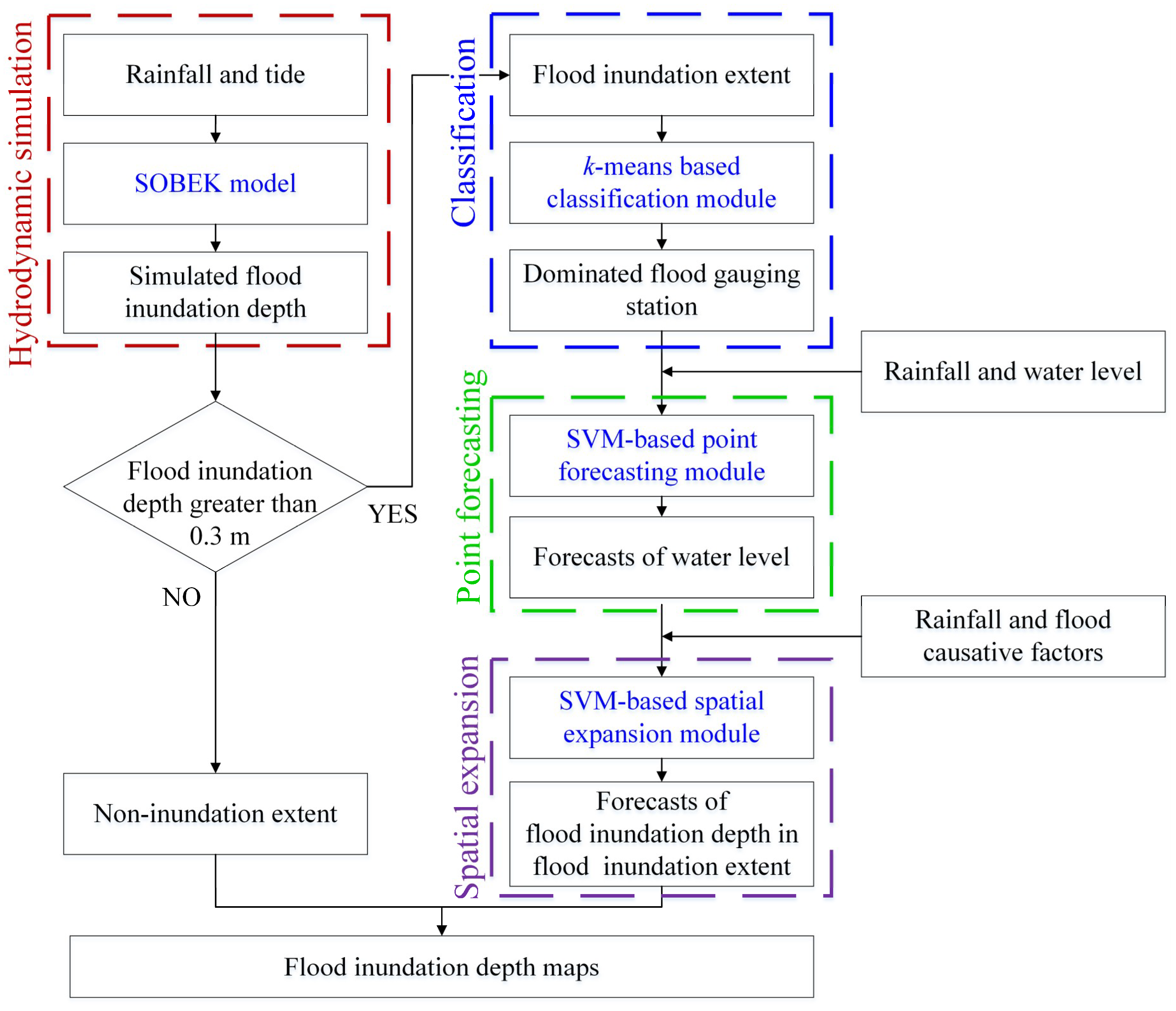
3.4. Methodology Construction
3.4.1. Hydrodynamic simulation step
3.4.2. Classification Step
3.4.3. Point Forecasting Step
3.4.4. Spatial Expansion Step
3.5. Model Evaluation and Cross Validation
4. Results and Discussion
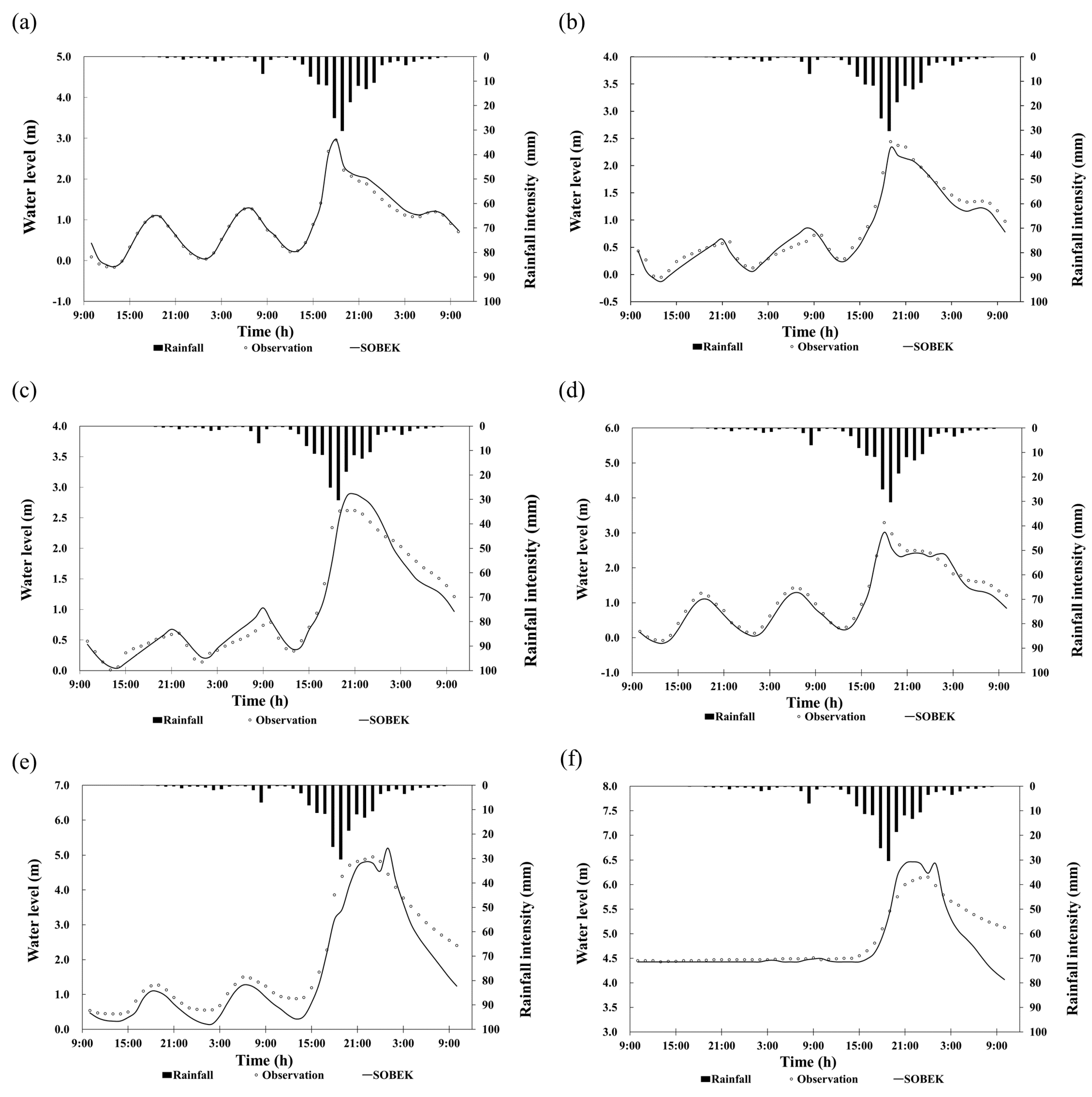
4.1. Calibration and Validation of SOBEK
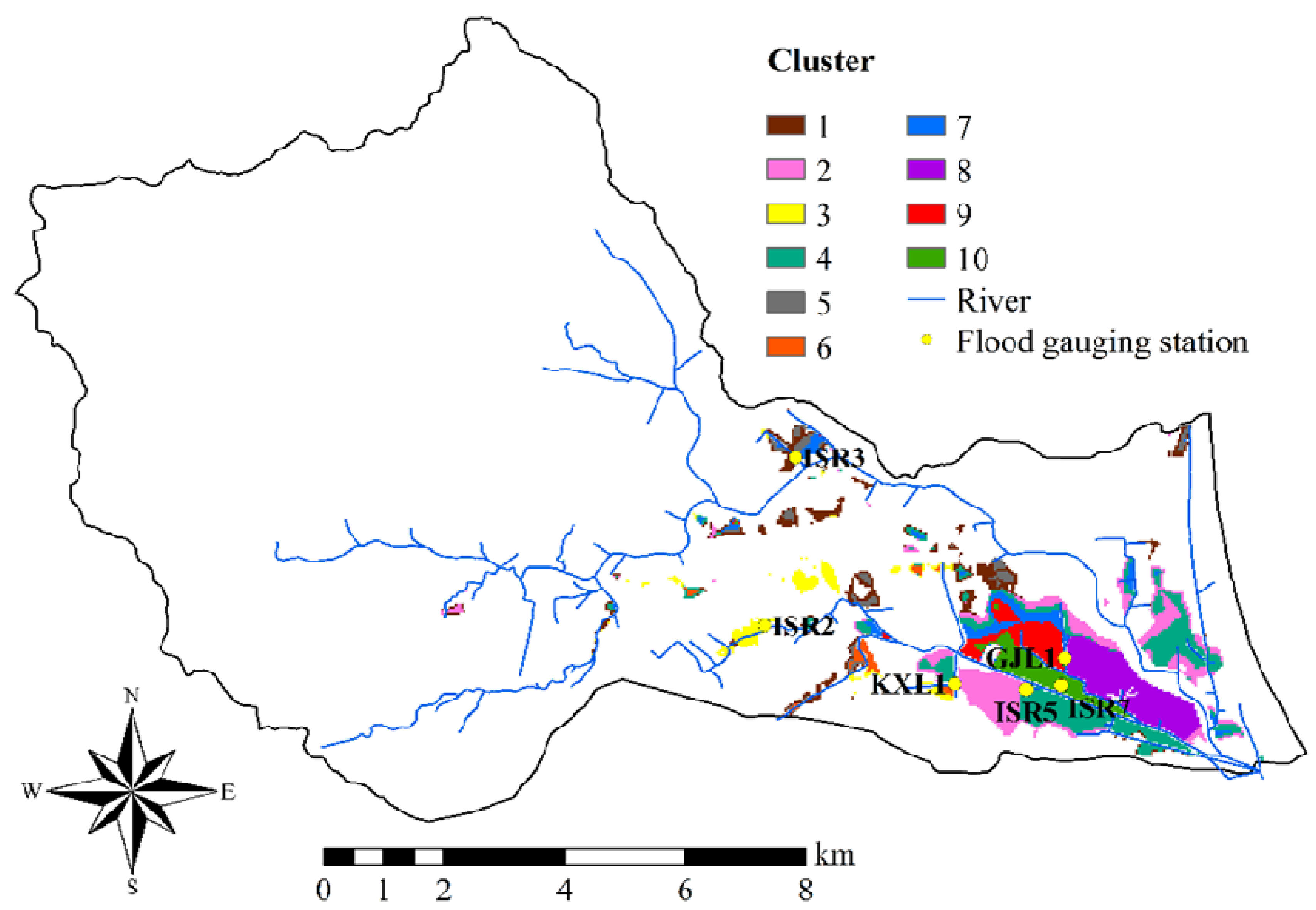
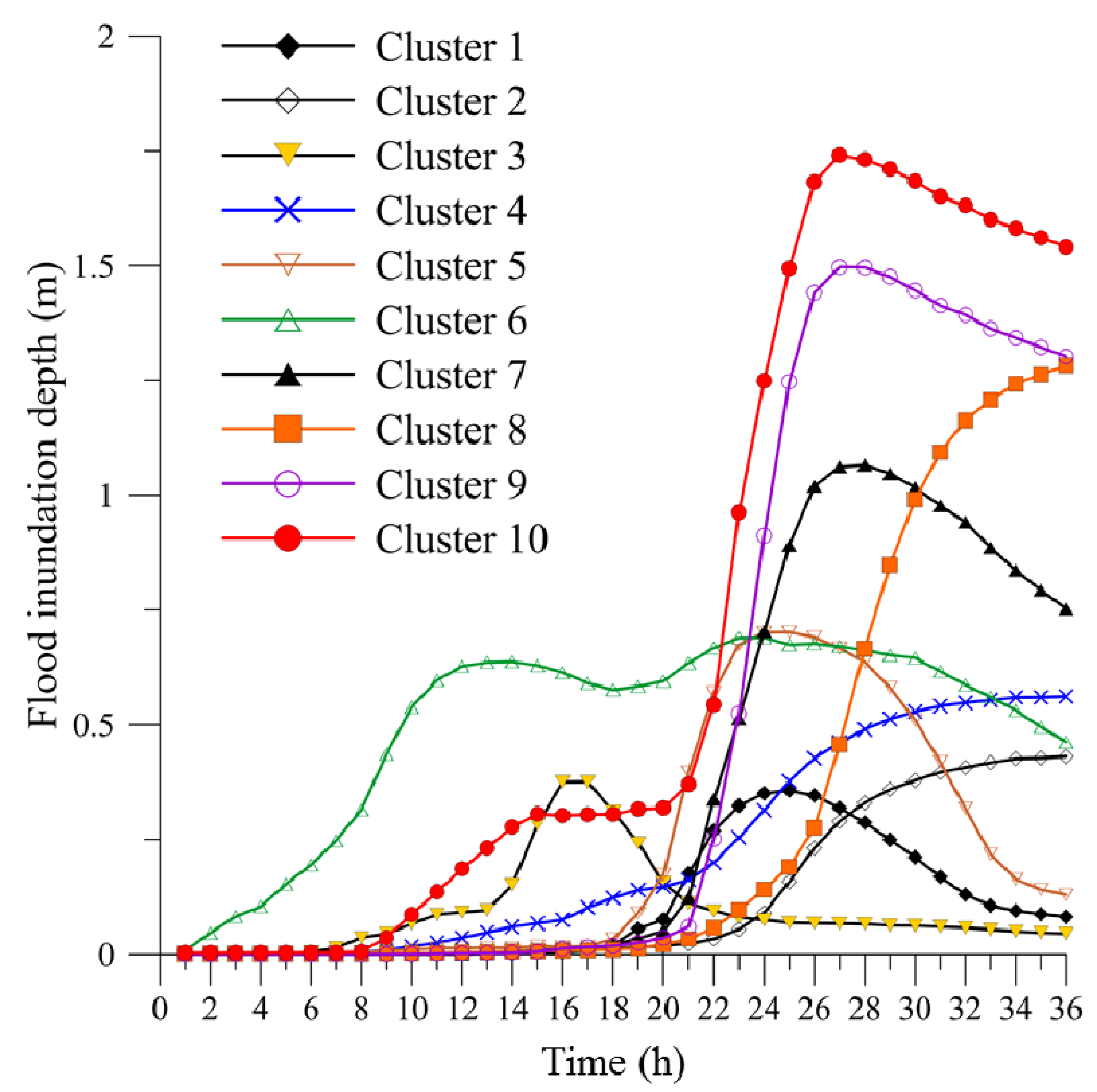
4.2. Identification of Clusters
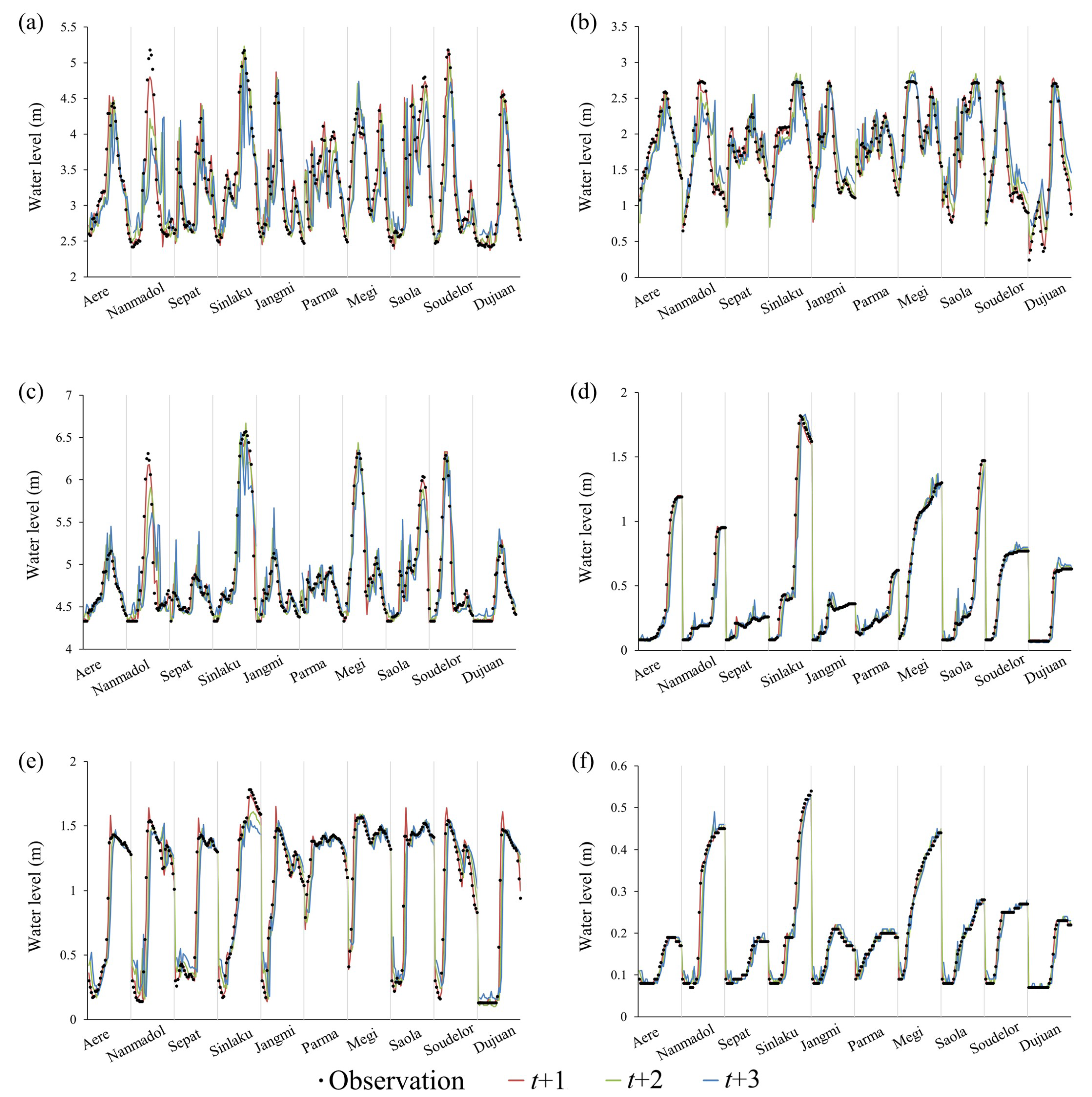
4.3. Performance of the Point Forecasting Module
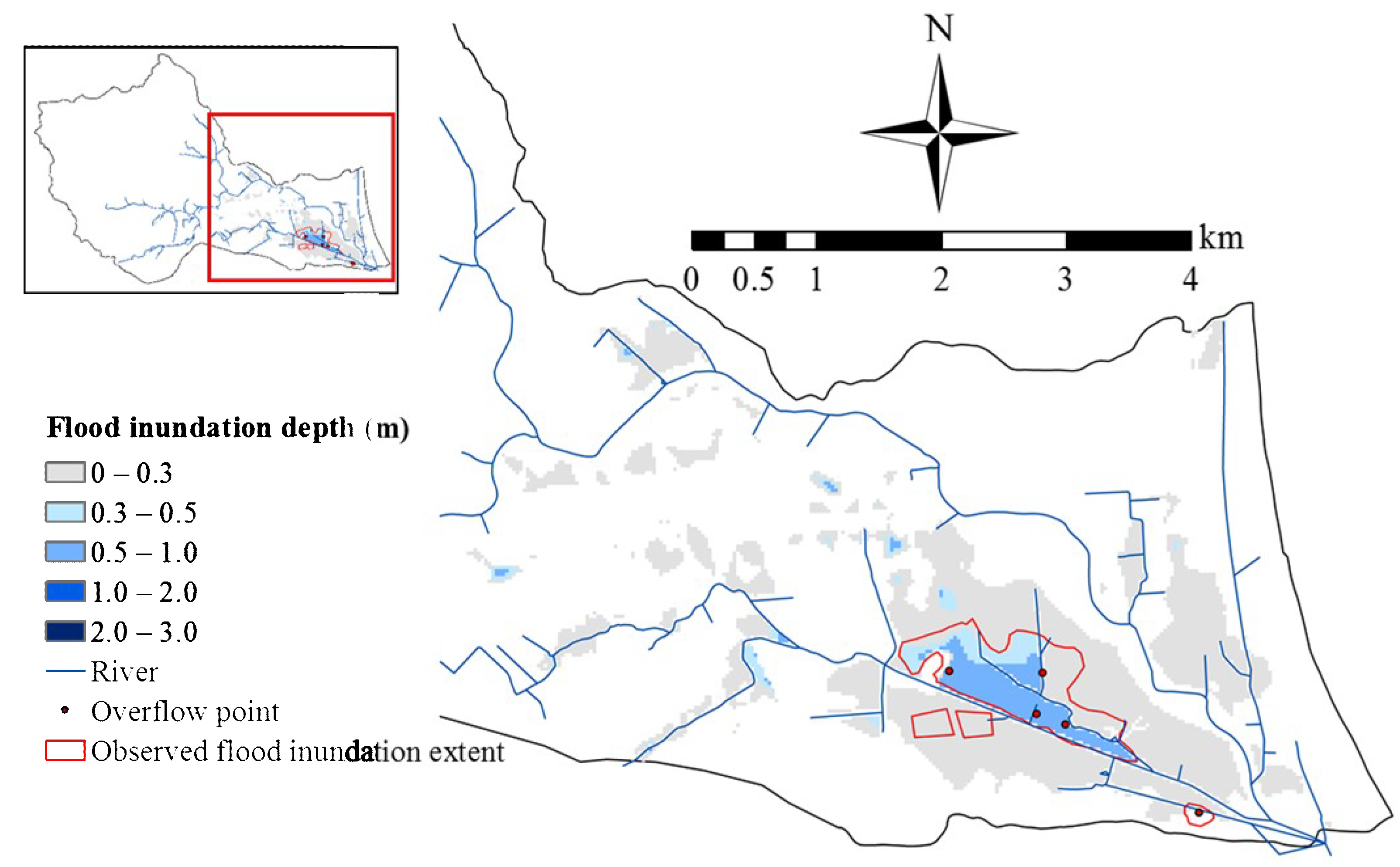
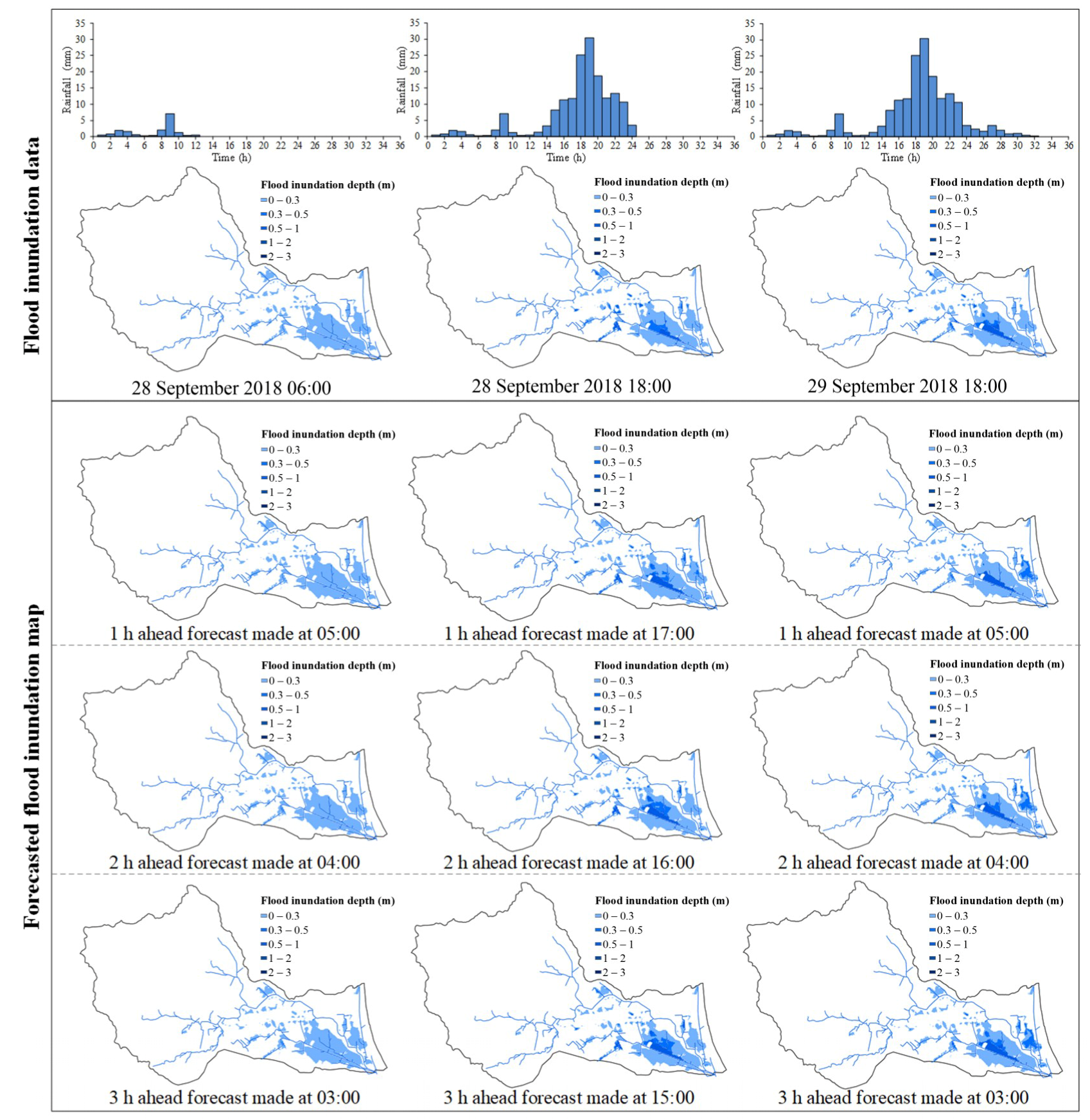
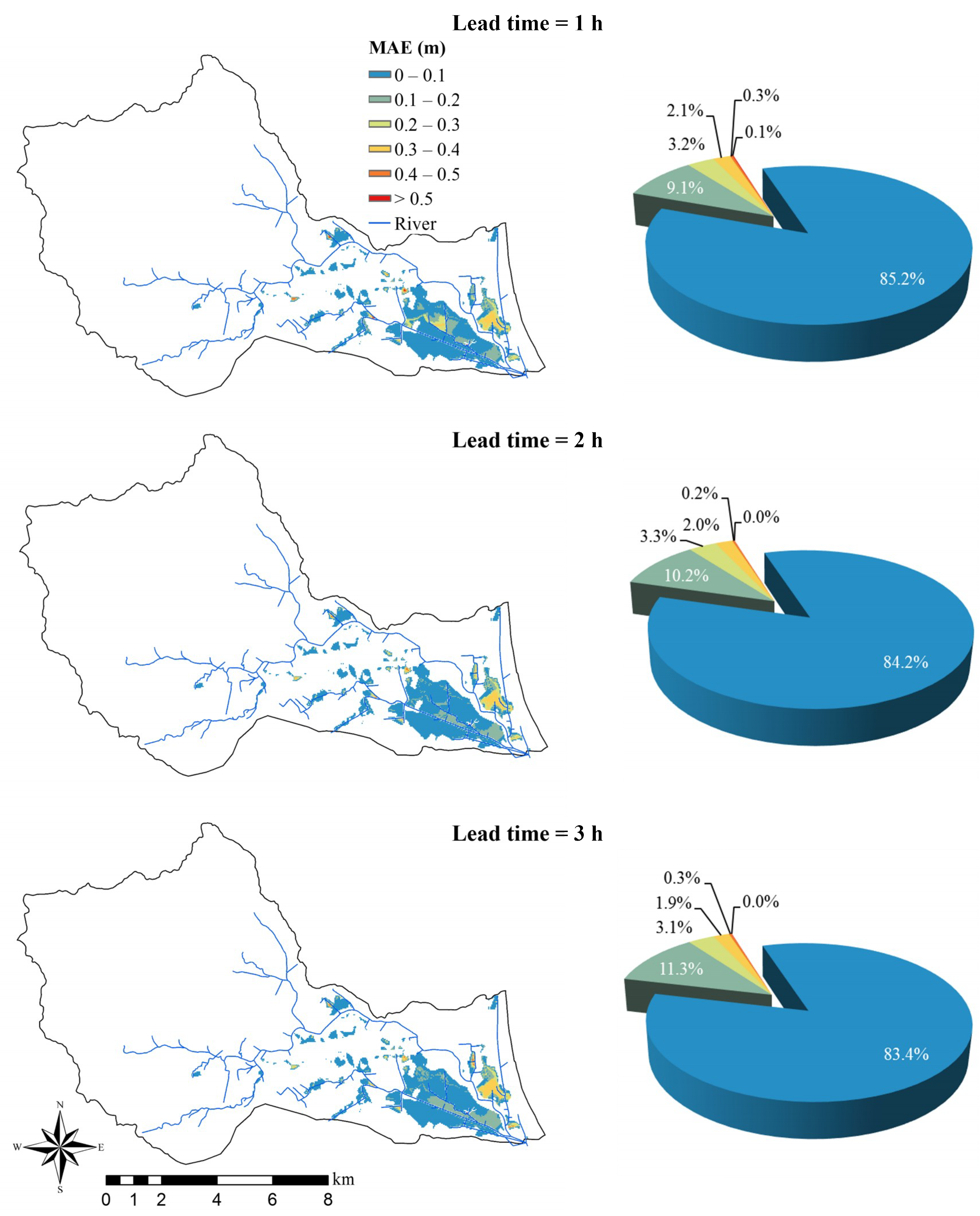
4.4. Performance of the Spatial Expansion Module
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wu, C.C.; Kuo, Y.H. Typhoons affecting Taiwan: Current understanding and future challenges. Bull. Am. Meteorol. Soc. 1999, 80, 67–80. [Google Scholar] [CrossRef]
- WRA (Water Resources Agency). Hydrological year book of Taiwan, Republic of China, 2016; Part I-Rainfall, Taipei, Taiwan; Water Resources Agency, Ministry of Economic Affairs: Taipei, Taiwan, 2015; pp. 5–7.
- Carsell, K.M.; Pingel, N.D.; Ford, D.T. Quantifying the benefit of a flood warning system. Nat. Hazards Rev. 2004, 5, 131–140. [Google Scholar] [CrossRef]
- Delft Hydraulics. SOBEK Software User’s Manual; WL|Delft Hydraulics: Delft, The Netherlands, 2013. [Google Scholar]
- Prinsen, G.F.; Becker, B.P.J. Application of SOBEK hydraulic surface water models in the Netherlands Hydrological Modelling Instrument. Irrig. Drain. 2011, 60, 35–41. [Google Scholar] [CrossRef]
- Yang, S.N.; Chan, M.H.; Chang, C.H.; Chang, L.F. The damage assessment of flood risk transfer effect on surrounding areas arising from the land development in Tainan, Taiwan. Water 2018, 10, 473. [Google Scholar] [CrossRef]
- Risi, R.D.; Paola, F.D.; Turpie, J.; Kroeger, T. Life cycle cost and return on investment as complementary decision variables for urban flood risk management in developing countries. Int. J. Disaster Risk Reduction. 2018, 28, 88–106. [Google Scholar] [CrossRef]
- Rigby, E.; Van Drie, R. ANUGA: A new free and open source hydrodynamic model. In Proceedings of Water Down Under 2008; Engineers Australia: Modbury, Australia, 2008. [Google Scholar]
- Lai, J.S.; Chang, H.K. Inundation Scenario Simulation due to Levee Breach and Overbank Flow in the Keelung River (II); Ministry of Science and Technology: Taipei, Taiwan, 2001.
- Chang, H.K.; Lin, Y.J.; Lai, J.S. Methodology to set trigger levels in an urban drainage flood warning system—An application to Jhonghe, Taiwan. Hydrol. Sci. J. 2017, 63, 31–49. [Google Scholar] [CrossRef]
- Chang, H.K.; Tan, Y.C.; Lai, J.S.; Pan, T.Y.; Liu, T.M.; Tung, C.P. Improvement of a drainage system for flood management with assessment of the potential effects of climate change. Hydrol. Sci. J. 2013, 58, 1581–1597. [Google Scholar] [CrossRef] [Green Version]
- Chang, T.J.; Wang, C.H.; Chen, A.S. A novel approach to model dynamic flow interactions between storm sewer system and overland surface for different land covers in urban areas. J. Hydrol. 2015, 524, 662–679. [Google Scholar] [CrossRef] [Green Version]
- Doong, D.J.; Lo, W.; Vojinovic, Z.; Lee, W.L.; Lee, S.P. Development of a new generation of flood inundation maps—A case study of the coastal city of Tainan, Taiwan. Water 2016, 8, 521. [Google Scholar] [CrossRef]
- Kuntiyawichai, K.; Schultz, B.; Uhlenbrook, S.; Suryadi, F.X.; Van Griensven, A. Comparison of flood management options for the Yang River Basin, Thailand. Irrig. Drain. 2011, 60, 526–543. [Google Scholar] [CrossRef]
- Verwey, A.; Muttil, N.; Liong, S.Y.; He, S. Implementing an urban rainfall-runoff concept in SOBEK for a catchment in Singapore. In Proceedings of Water Down Under; Engineers Australia: Modbury, Australia, 2008; p. 36. [Google Scholar]
- Dimitriadis, P.; Tegos, A.; Oikonomou, A.; Pagana, V.; Koukouvinos, A.; Mamassis, N.; Koutsoyiannis, D.; Efstratiadis, A. Comparative evaluation of 1D and quasi-2D hydraulic models based on benchmark and real-world applications for uncertainty assessment in flood mapping. J. Hydrol. 2016, 534, 478–492. [Google Scholar] [CrossRef]
- Liu, W.C.; Chung, C.E. Enhancing the predicting accuracy of the water stage using a physical-based model and an artificial neural network-genetic algorithm in a river system. Water 2014, 6, 1642–1661. [Google Scholar] [CrossRef]
- Chang, L.C.; Shen, H.Y.; Chang, F.J. Regional flood inundation nowcast using hybrid SOM and dynamic neural networks. J. Hydrol. 2014, 519, 476–489. [Google Scholar] [CrossRef]
- Cheng, C.T.; Feng, Z.K.; Niu, W.J.; Liao, S.L. Heuristic methods for reservoir monthly inflow forecasting: A case study of Xinfeng-jiang Reservoir in Pearl River, China. Water 2015, 7, 4477–4495. [Google Scholar] [CrossRef]
- Pan, T.Y.; Lai, J.S.; Chang, T.J.; Chang, H.K.; Chang, K.C.; Tan, Y.C. Hybrid neural networks in rainfall-inundation forecasting based on a synthetic potential inundation database. Nat. Hazard Earth Syst. 2011, 11, 771. [Google Scholar] [CrossRef]
- Wu, M.C.; Lin, G.F. An hourly streamflow forecasting model coupled with an enforced learning strategy. Water 2015, 7, 5876–5895. [Google Scholar] [CrossRef]
- Chang, L.C.; Amin, M.; Yang, S.N.; Chang, F.J. Building ANN-based regional multi-step-ahead flood inundation forecast models. Water 2018, 10, 1283. [Google Scholar] [CrossRef]
- Chang, L.C.; Shen, H.Y.; Wang, Y.F.; Huang, J.Y.; Lin, Y.T. Clustering-based hybrid inundation model for forecasting flood inundation depths. J. Hydrol. 2010, 385, 257–268. [Google Scholar] [CrossRef]
- Jhong, Y.D.; Chen, C.S.; Lin, H.P.; Chen, S.T. Physical hybrid neural network model to forecast typhoon floods. Water 2018, 10, 632. [Google Scholar] [CrossRef]
- Chen, W.B.; Liu, W.C.; Hsu, M.H. Comparison of ANN approach with 2D and 3D hydrodynamic models for simulating estuary water stage. Adv. Eng. Softw. 2012, 45, 69–79. [Google Scholar] [CrossRef]
- Ahooghalandari, M.; Khiadani, M.; Kothapalli, G. Assessment of artificial neural networks and IHACRES models for simulating streamflow in Marillana catchment in the Pilbara, Western Australia. Australas. J. Water Resour. 2005, 19, 116–126. [Google Scholar] [CrossRef]
- Lin, G.F.; Lin, H.Y.; Chou, Y.C. Development of a real-time regional-inundation forecasting model for the inundation warning system. J. Hydroinform. 2013, 15, 1391–1407. [Google Scholar] [CrossRef]
- Hong, H.; Tsangaratos, P.; Ilia, I.; Liu, J.; Zhu, A.X.; Chen, W. Application of fuzzy weight of evidence and data mining techniques in construction of flood susceptibility map of Poyang County, China. Sci. Total Environ. 2018, 625, 575–588. [Google Scholar] [CrossRef] [PubMed]
- Lai, C.; Shao, Q.; Chen, X.; Wang, Z.; Zhou, X.; Yang, B.; Zhang, L. Flood risk zoning using a rule mining based on ant colony algorithm. J. Hydrol. 2016, 542, 268–280. [Google Scholar] [CrossRef]
- Nandi, A.; Mandal, A.; Wilson, M.; Smith, D. Flood hazard mapping in Jamaica using principal component analysis and logistic regression. Environ. Earth Sci. 2016, 75, 465. [Google Scholar] [CrossRef]
- Tehrany, M.S.; Pradhan, B.; Mansor, S.; Ahmad, N. Flood susceptibility assessment using GIS-based support vector machine model with different kernel types. Catena 2015, 125, 91–101. [Google Scholar] [CrossRef]
- Tehrany, M.S.; Shabani, F.; Neamah Jebur, M.; Hong, H.; Chen, W.; Xie, X. GIS-based spatial prediction of flood prone areas using standalone frequency ratio, logistic regression, weight of evidence and their ensemble techniques. Geomatics Nat. Hazards Risk 2017, 8, 1538–1561. [Google Scholar] [CrossRef] [Green Version]
- MacQueen, J.B. Some methods for classification and analysis of multivariate observations. In 5-th Berkeley Symposium on Mathematical Statistics and Probability; University of California Press: Berkeley, CA, USA, 1967; pp. 281–297. [Google Scholar]
- Liu, C.L.; Hsaio, W.H.; Chang, T.H. Locality Sensitive K-means Clustering. J. Inf. Sci. Eng. 2018, 34, 289–305. [Google Scholar]
- Neshatpour, K.; Malik, M.; Sasan, A.; Rafatirad, S.; Mohsenin, T.; Ghasemzadeh, H.; Homayoun, H. Energy-efficient acceleration of map reduce applications using FPGAs. J. Parallel Distrib. Comput. 2018, 119, 1–17. [Google Scholar] [CrossRef]
- Wei, W.; Chen, L.; Fu, B.; Huang, Z.; Wu, D.; Gui, L. The effect of land uses and rainfall regimes on runoff and soil erosion in the semi-arid loess hilly area, China. J. Hydrol. 2007, 335, 247–258. [Google Scholar] [CrossRef] [Green Version]
- Johnson, R.A.; Wichern, D.W. Applied Multivariate Statistical Analysis, 5th ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Brad, J.F. An efficient point algorithm for a linear two-stage optimization problem. Oper. Res. 1983, 31, 670–684. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer science and business media: New York, NY, USA, 1995. [Google Scholar]
- Chua, L.H.C.; Wong, T.S.W. Runoff forecasting for an asphalt plane by artificial neural networks and comparisons with kinematic wave and autoregressive moving average models. J. Hydrol. 2011, 397, 191–201. [Google Scholar] [CrossRef]
- Lin, G.F.; Chen, L.H. A non-linear rainfall–runoff model using radial basis function network. J. Hydrol. 2004, 289, 1–8. [Google Scholar] [CrossRef]
- Adnan, R.; Ruslan, F.A.; Samad, A.M.; Zain, Z.M. New artificial neural network and extended kalman filter hybrid model of flood prediction system. In Proceedings of the 2013 IEEE 9th International Colloquium on Signal Processing and its Applications, Kuala Lumpur, Malaysia, 8–10 March 2013; pp. 252–257. [Google Scholar]
- Chang, L.C.; Chang, F.J.; Wang, Y.P. Auto-configuring radial basis function networks for chaotic time series and flood forecasting. Hydrol. Process. 2009, 23, 2450–2459. [Google Scholar] [CrossRef]
- Chen, C.S.; Chen, B.P.T.; Chou, F.N.F.; Yang, C.C. Development and application of a decision group Back-Propagation Neural Network for flood forecasting. J. Hydrol. 2010, 385, 173–182. [Google Scholar] [CrossRef]
- Chidthong, Y.; Tanaka, H.; Supharatid, S. Developing a hybrid multi-model for peak flood forecasting. Hydrol. Process. 2009, 23, 1725–1738. [Google Scholar] [CrossRef]
- Cristianini, N.; Shaw-Taylor, J. An Introduction to Support Vector Machines and Other Kernel-Based Learning Methods; Cambridge University Press: New York, NY, USA, 2000. [Google Scholar]
- Geisser, S. Predictive Inference; Chapman and Hall: New York, NY, USA, 1993. [Google Scholar]
- Dahm, R.; Hsu, C.T.; Lien, H.C.; Chang, C.H.; Prinsen, G. Next Generation Flood Modelling using 3Di: A Case Study in Taiwan. In Proceedings of the DSD International Conference, Hong Kong, China, 12–14 November 2014. [Google Scholar]
- Liu, W.C. Monitoring and Applications in the Yilan and Dianbo River Experimental Watersheds; Water Resources Planning Institute: Taichung, Taiwan, 2015.
| Event | Date (yyyy/mm/dd) | Duration (h) | Cumulative Maximum within 36 h Rainfall (mm) | Inundation Extent (km2) |
|---|---|---|---|---|
| Aere | 2004/08/23 | 80 | 350.4 | 0.82 |
| Nanmadol | 2004/12/03 | 35 | 300.4 | 1.36 |
| Sepat | 2007/08/16 | 77 | 186.6 | 1.75 |
| Sinlaku | 2008/09/11 | 125 | 454.1 | 7.33 |
| Jangmi | 2008/09/27 | 71 | 185.6 | 0.10 |
| Parma | 2009/10/03 | 83 | 305.6 | 5.51 |
| Megi | 2010/10/21 | 68 | 416.0 | 6.35 |
| Saola | 2012/07/30 | 89 | 379.8 | 5.22 |
| Soudelor | 2015/08/06 | 80 | 214.9 | 0.87 |
| Dujuan | 2015/09/27 | 56 | 179.9 | 0.54 |
| Water Level Station | ETp (h) | EWp (%) | CE | RMSE (m) |
|---|---|---|---|---|
| Gamalan | 0 | 0.34 | 0.98 | 0.09 |
| Sijie | 0 | 4.92 | 0.97 | 0.16 |
| Dongjin | 0 | 10.18 | 0.95 | 0.18 |
| Zhuangwei | 0 | 8.16 | 0.96 | 0.30 |
| Yixing | 2 | 5.07 | 0.90 | 0.76 |
| Ximen | 2 | 5.10 | 0.74 | 1.09 |
| Flood Gauging Station | Maximum Water Level (m) | Minimum Water Level (m) | Range of Water Levels (m) | Dominant Cluster |
|---|---|---|---|---|
| ISR2 | 5.18 | 2.37 | 2.81 | 3 |
| KXL1 | 2.73 | 0.22 | 2.51 | 6 |
| ISR3 | 6.57 | 4.33 | 2.24 | 1, 5 |
| ISR7 | 1.81 | 0.07 | 1.74 | 10 |
| GJL1 | 1.77 | 0.13 | 1.64 | 7, 8, 9 |
| Lead Time (h) | ISR2 | KXL1 | ISR3 | ISR7 | GJL1 | ISR5 |
|---|---|---|---|---|---|---|
| RMSE (m) | ||||||
| t + 1 | 0.19 | 0.12 | 0.09 | 0.03 | 0.07 | 0.01 |
| t + 2 | 0.41 | 0.26 | 0.19 | 0.07 | 0.17 | 0.02 |
| t + 3 | 0.55 | 0.36 | 0.27 | 0.10 | 0.24 | 0.02 |
| CE | ||||||
| t + 1 | 0.90 | 0.92 | 0.93 | 0.98 | 0.97 | 0.99 |
| t + 2 | 0.57 | 0.69 | 0.67 | 0.91 | 0.81 | 0.94 |
| t + 3 | 0.26 | 0.37 | 0.29 | 0.79 | 0.56 | 0.88 |
| Lead Time (h) | Cluster | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| RMSE (m) | ||||||||||
| t + 1 | 0.07 | 0.09 | 0.08 | 0.13 | 0.14 | 0.20 | 0.20 | 0.13 | 0.35 | 0.11 |
| t + 2 | 0.07 | 0.08 | 0.08 | 0.13 | 0.15 | 0.18 | 0.19 | 0.12 | 0.32 | 0.13 |
| t + 3 | 0.07 | 0.08 | 0.08 | 0.13 | 0.14 | 0.18 | 0.20 | 0.12 | 0.31 | 0.16 |
| MAE (m) | ||||||||||
| t + 1 | 0.05 | 0.05 | 0.05 | 0.09 | 0.09 | 0.15 | 0.14 | 0.10 | 0.26 | 0.07 |
| t + 2 | 0.05 | 0.05 | 0.05 | 0.08 | 0.10 | 0.13 | 0.13 | 0.09 | 0.24 | 0.09 |
| t + 3 | 0.04 | 0.05 | 0.05 | 0.09 | 0.09 | 0.13 | 0.13 | 0.09 | 0.24 | 0.11 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, M.-J.; Chang, H.-K.; Chen, Y.-C.; Lin, G.-F.; Chen, P.-A.; Lai, J.-S.; Tan, Y.-C. A Support Vector Machine Forecasting Model for Typhoon Flood Inundation Mapping and Early Flood Warning Systems. Water 2018, 10, 1734. https://doi.org/10.3390/w10121734
Chang M-J, Chang H-K, Chen Y-C, Lin G-F, Chen P-A, Lai J-S, Tan Y-C. A Support Vector Machine Forecasting Model for Typhoon Flood Inundation Mapping and Early Flood Warning Systems. Water. 2018; 10(12):1734. https://doi.org/10.3390/w10121734
Chicago/Turabian StyleChang, Ming-Jui, Hsiang-Kuan Chang, Yun-Chun Chen, Gwo-Fong Lin, Peng-An Chen, Jihn-Sung Lai, and Yih-Chi Tan. 2018. "A Support Vector Machine Forecasting Model for Typhoon Flood Inundation Mapping and Early Flood Warning Systems" Water 10, no. 12: 1734. https://doi.org/10.3390/w10121734
APA StyleChang, M.-J., Chang, H.-K., Chen, Y.-C., Lin, G.-F., Chen, P.-A., Lai, J.-S., & Tan, Y.-C. (2018). A Support Vector Machine Forecasting Model for Typhoon Flood Inundation Mapping and Early Flood Warning Systems. Water, 10(12), 1734. https://doi.org/10.3390/w10121734






