Barrier-based Longitudinal Connectivity Index for Managing Urban Rivers
Abstract
1. Introduction
2. Study Area and Field Data Collection
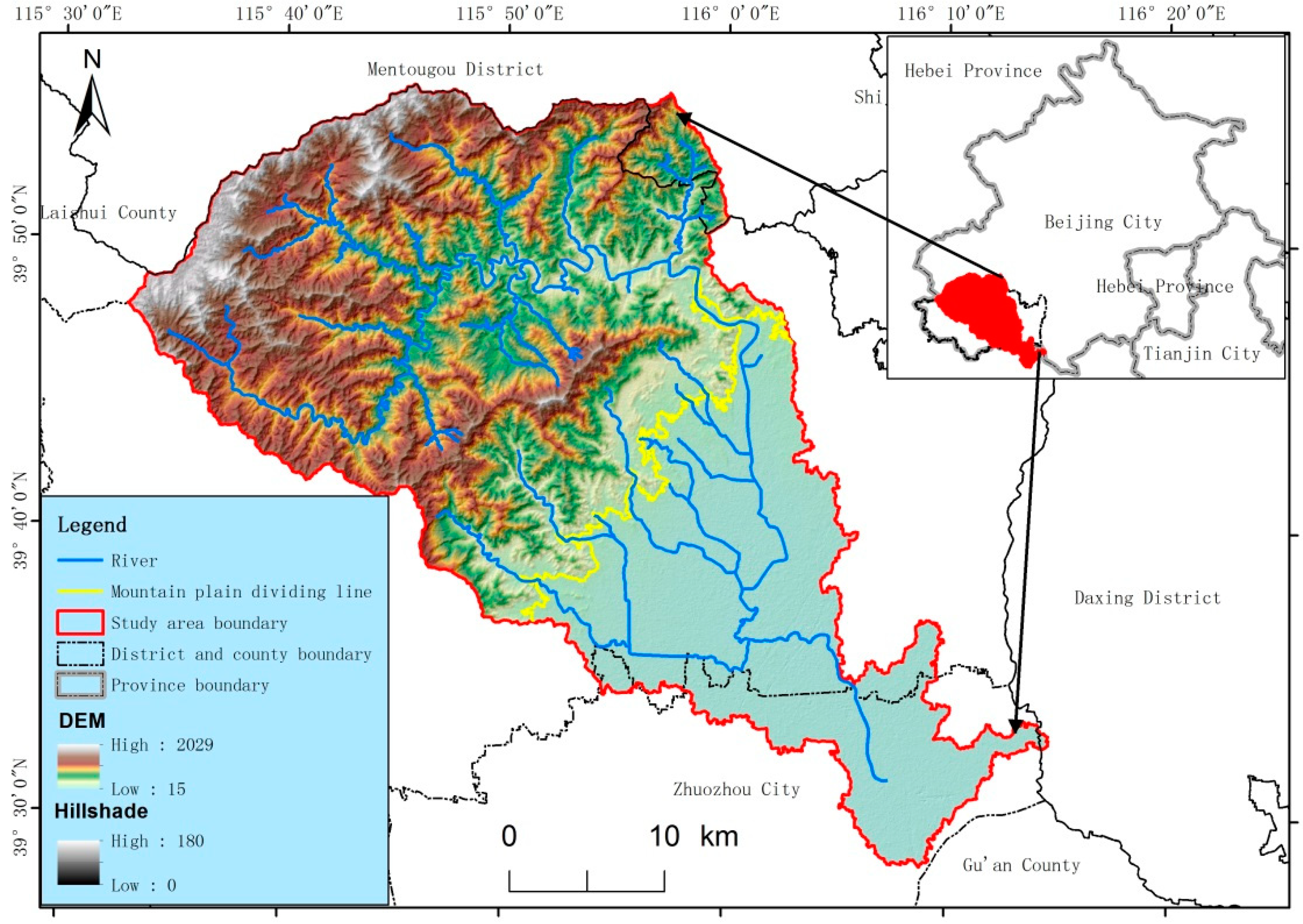
2.1. Study Area
2.2. Data Sources and Preprocessing
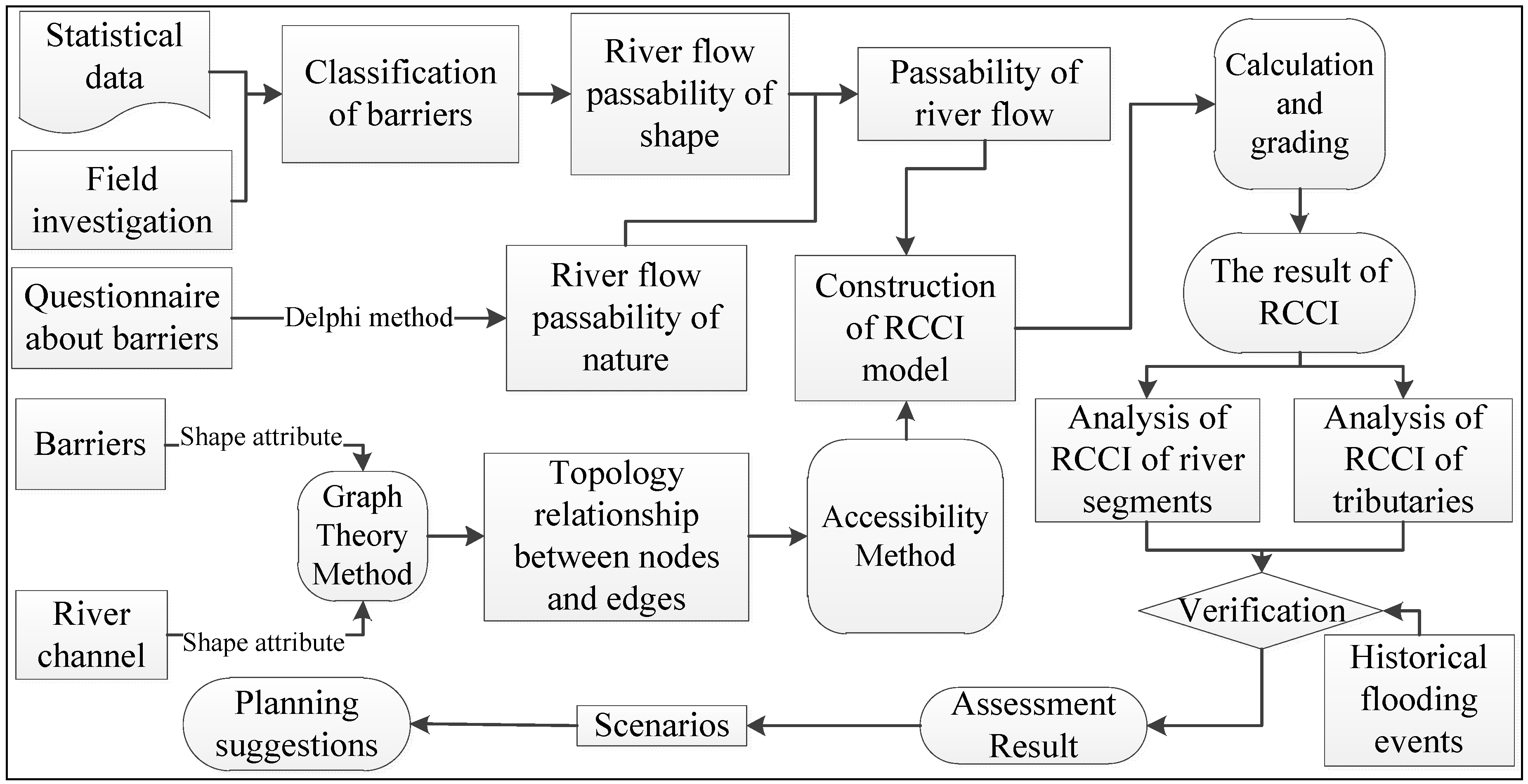
3. Methodology
3.1. Classification and Weight Assignment of Barriers
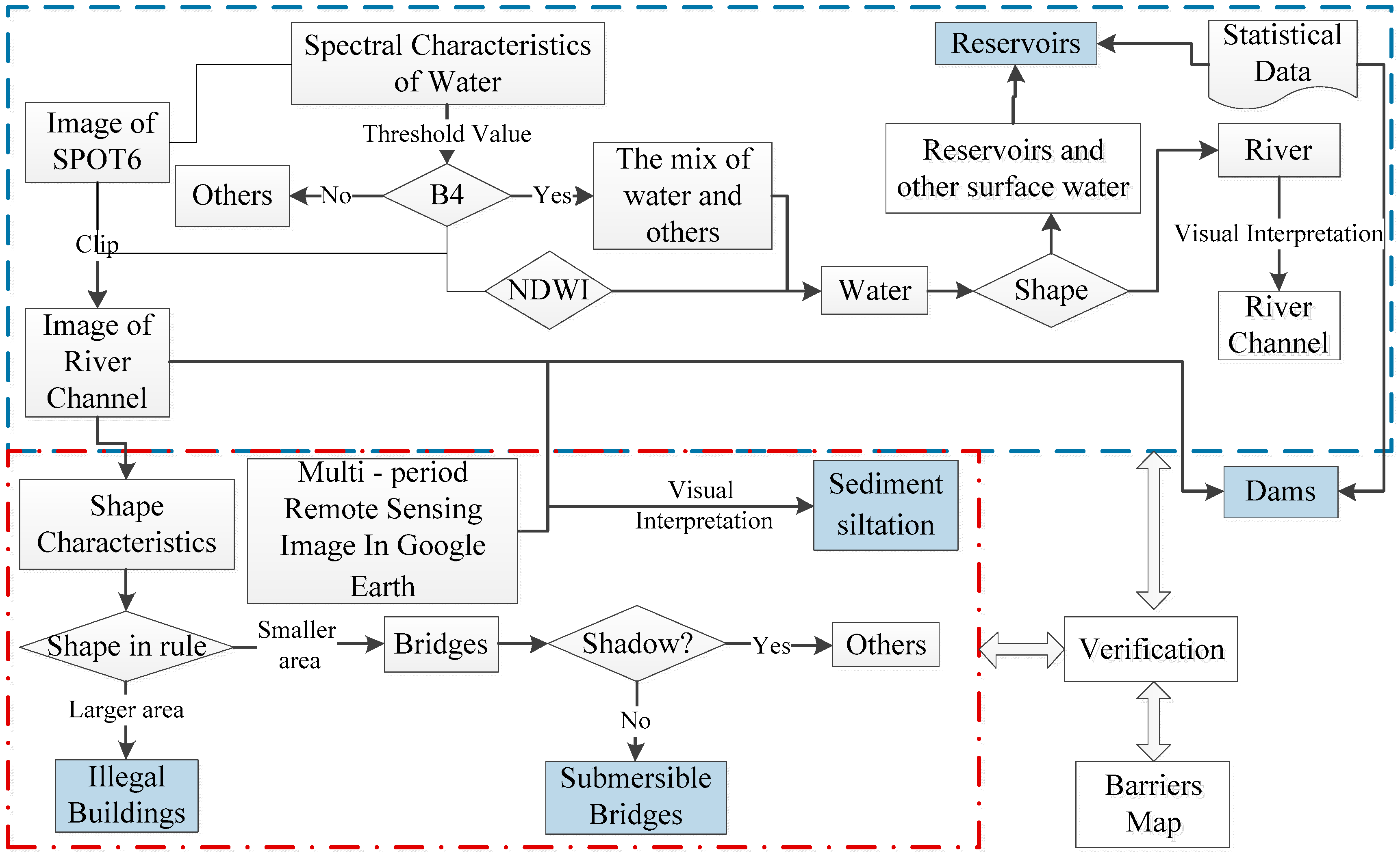
3.2. Identification of River Channels and Barriers
3.3. Definition and Calculation of RCCI
4. Results
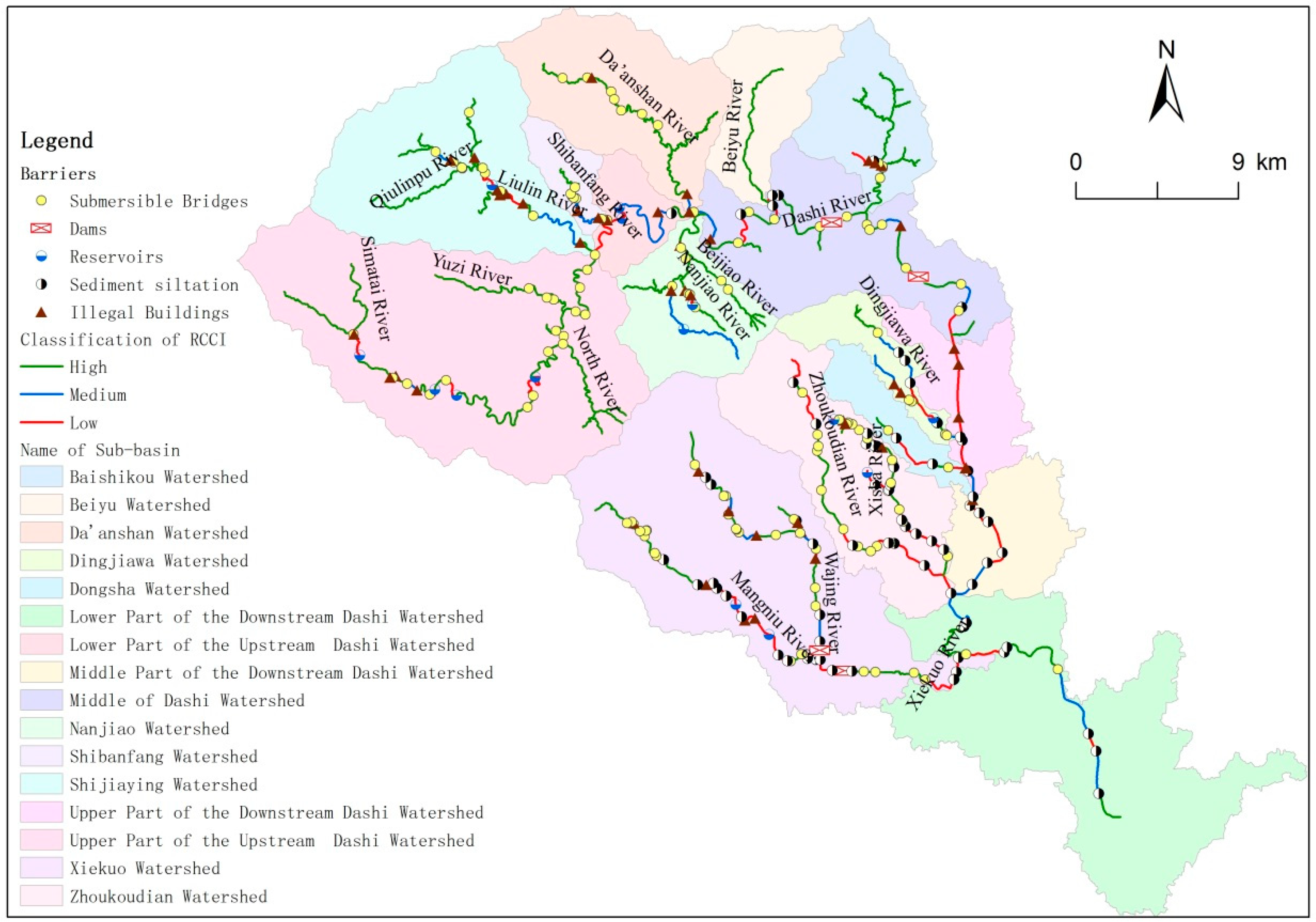
4.1. Spatial Distribution of Barriers in the Watershed
4.2. Assessment Results of RCCI in the Watershed
4.2.1. RCCI Assessment Results for River Segments
4.2.2. RCCI Result for Tributaries
4.3. Verification of RCCI Assessment Results
4.4. Scenario Results
5. Discussion
5.1. The Application of RCCI in Other Rivers
5.2. Verification of RCCI Assessment Results by Flood Data
5.3. Reliability Analysis Based on the Time Accessibility Method
5.4. The Weakness of the RCCI Model
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cote, D.; Kehler, D.G.; Bourne, C.; Wiersma, Y.F. A new measure of longitudinal connectivity for stream networks. Landsc. Ecol. 2009, 24, 101–113. [Google Scholar] [CrossRef]
- Jackson, C.R.; Pringle, C.M. Ecological benefits of reduced hydrologic connectivity in intensively developed landscapes. BioScience 2010, 60, 37–46. [Google Scholar] [CrossRef]
- Buddendorf, W.B.; Malcolm, I.A.; Geris, J.; Wilkinson, M.E.; Soulsby, C. Metrics to assess how longitudinal channel network connectivity and in-stream Atlantic salmon habitats are impacted by hydropower regulation. Hydrol. Process. 2017, 31, 2132–2142. [Google Scholar] [CrossRef]
- Bracken, L.J.; Wainwright, J.; Ali, G.A.; Tetzlaff, D.; Smith, M.W.; Reaney, S.M.; Roy, A.G. Concepts of hydrological connectivity: Research approaches, pathways and future agendas. Earth Sci. Rev. 2013, 119, 17–34. [Google Scholar] [CrossRef]
- Pringle, C. What is hydrologic connectivity and why is it ecologically important? Hydrol. Process. 2003, 17, 2685–2689. [Google Scholar] [CrossRef]
- Nadeau, T.L.; Rains, M.C. Hydrological connectivity between headwater streams and downstream waters: How science can inform policy. J. Am. Water Resour. Assoc. 2007, 43, 118–133. [Google Scholar] [CrossRef]
- Hohl, A.; Václavík, T.; Meentemeyer, R.K. Go with the flow: Geospatial analytics to quantify hydrologic landscape connectivity for passively dispersed microorganisms. Int. J. Geogr. Inf. Sci. 2014, 28, 1626–1641. [Google Scholar] [CrossRef]
- Jacobson, R.B.; Janke, T.P.; Skold, J.J. Hydrologic and geomorphic considerations in restoration of river-floodplain connectivity in a highly altered river system, Lower Missouri River, USA. Wetl. Ecol. Manag. 2011, 19, 295–316. [Google Scholar] [CrossRef]
- Trigg, M.A.; Michaelides, K.; Neal, J.C.; Bates, P.D. Surface water connectivity dynamics of a large scale extreme flood. J. Hydrol. 2013, 505, 138–149. [Google Scholar] [CrossRef]
- Wohl, E.; Rathburn, S.; Chignell, S.; Garrett, K.; Laurel, D.; Livers, B.; Patton, A.; Records, R.; Richards, M.; Schook, D.M.; et al. Mapping longitudinal stream connectivity in the North St. Vrain Creek watershed of Colorado. Geomorphology 2016, 277, 171–181. [Google Scholar] [CrossRef]
- Lane, S.N.; Reaney, S.M.; Heathwaite, A.L. Representation of landscape hydrological connectivity using a topographically driven surface flow index. Water Resour. Res. 2009, 45, 2263–2289. [Google Scholar] [CrossRef]
- Borselli, L.; Cassi, P.; Torri, D. Prolegomena to sediment and flow connectivity in the landscape: A GIS and field numerical assessment. Catena 2008, 75, 268–277. [Google Scholar] [CrossRef]
- Shore, M.; Mechan, S.; Cushen, M.; Jordan, P.; Mellander, P.E.; Kelly-Quinn, M.; Melland, A. Extent and role of ditches in affecting hydrological connectivity in agricultural landscapes. In Proceedings of the EGU General Assembly Conference, Vienna, Austria, 22–27 April 2012; p. 4956. [Google Scholar]
- Cavalli, M.; Trevisani, S.; Comiti, F.; Marchi, L. Geomorphometric assessment of spatial sediment connectivity in small Alpine catchments. Geomorphology 2013, 188, 31–41. [Google Scholar] [CrossRef]
- Cook, E.A. Landscape structure indices for assessing urban ecological networks. Landsc. Urban Plan. 2002, 58, 269–280. [Google Scholar] [CrossRef]
- Pascual-Hortal, L.; Saura, S. Comparison and development of new graph-based connectivity indices: Towards the prioritization of habitat patches and corridors for conservation. Landsc. Ecol. 2006, 21, 959–967. [Google Scholar] [CrossRef]
- Thompson, C.J.; Fryirs, K.; Croke, J. The disconnected sediment conveyor belt: Patterns of longitudinal and lateral erosion and deposition during a catastrophic flood in the Lockyer Valley, South East Queensland, Australia. River Res. Appl. 2016, 32, 540–551. [Google Scholar] [CrossRef]
- Ward, J.V.; Stanford, J.A. The four-dimensional nature of lotic ecosystems. J. N. Am. Benthol. Soc. 1989, 8, 2–8. [Google Scholar] [CrossRef]
- Segurado, P.; Branco, P.; Ferreira, M.T. Prioritizing restoration of structural connectivity in rivers: A graph based approach. Landsc. Ecol. 2013, 28, 1231–1238. [Google Scholar] [CrossRef]
- Mahlum, S.; Kehler, D.; Cote, D.; Wiersma, Y.F.; Stanfield, L. Assessing the biological relevance of aquatic connectivity to stream fish communities. Can. J. Fish. Aquat. Sci. 2014, 71, 1852–1863. [Google Scholar] [CrossRef]
- Grill, G.; Lehner, B.; Lumsdon, A.E.; MacDonald, G.K.; Zarfl, C.; Liermann, C.R. An index-based framework for assessing patterns and trends in river fragmentation and flow regulation by global dams at multiple scales. Environ. Res. Lett. 2015, 10, 55–60. [Google Scholar] [CrossRef]
- Fuller, M.R.; Doyle, M.W.; Strayer, D.L. Causes and consequences of habitat fragmentation in river networks. Ann. N. Y. Acad. Sci. 2015, 1355, 31–51. [Google Scholar] [CrossRef] [PubMed]
- Bourne, C.M.; Kehler, D.G.; Wiersma, Y.F.; Cote, D. Barriers to fish passage and barriers to fish passage assessments: The impact of assessment methods and assumptions on barrier identification and quantification of watershed connectivity. Aquat. Ecol. 2011, 4, 389–403. [Google Scholar] [CrossRef]
- Favaro, C.; Moore, J.W. Fish assemblages and barriers in an urban stream network. Freshw. Sci. 2015, 34, 991–1005. [Google Scholar] [CrossRef]
- Cheng, S.T.; Herricks, E.E.; Tsai, W.P.; Chang, F.J. Assessing the natural and anthropogenic influences on basin-wide fish species richness. Sci. Total Environ. 2016, 572, 825–836. [Google Scholar] [CrossRef] [PubMed]
- Mahlum, S.; Cote, D.; Wiersma, Y.F.; Kehler, D.; Clarke, K.D. Evaluating the barrier assessment technique derived from FishXing software and the upstream movement of brook trout through road culverts. Trans. Am. Fish. Soc. 2014, 143, 39–48. [Google Scholar] [CrossRef]
- Kim, J.; Mohanty, B.P. A physically based hydrological connectivity algorithm for describing spatial patterns of soil moisture in the unsaturated zone. J. Geophys. Res. Atmos. 2017, 122, 2096–2114. [Google Scholar] [CrossRef]
- Forman, R.T.T. Land Mosaics: The Ecology of Landscapes and Regions; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Sánchez-Montoya, M.M.; Moleón, M.; Sánchez-Zapata, J.A.; Tockner, K. Dry riverbeds: Corridors for terrestrial vertebrates. Ecosphere 2016, 7, 10–24. [Google Scholar] [CrossRef]
- Liu, T.G.; Li, F. Study on optimization of water resources in Dashi River. Beijing Water Resour. 2004, 6, 45–47. [Google Scholar]
- Water Resources Authority of Fangshan District. Flood and Drought Disasters in Fangshan District; China Water & Power Press: Beijing, China, 2003. [Google Scholar]
- Liu, Y.K. Dictionary of Water Affairs in Beijing; China Water & Power Press: Beijing, China, 2008. [Google Scholar]
- Beijing Institute of Water; Fangshan Water Authority. Report of Flood Control Planning in Fangshan District; China Water & Power Press: Beijing, China, 2015. [Google Scholar]
- Wang, D.Q.; Tang, L.H.; Gu, Z.C.; Zheng, X.; Jiang, W.K. Malaria Transmission Potential in the Three Gorges Reservoir of the Yangtze River, China. Biomed. Environ. Sci. 2013, 26, 54–62. [Google Scholar] [PubMed]
- Williams, P.L.; Webb, C. The Delphi technique: A methodological discussion. J. Adv. Nurs. 1994, 19, 180–186. [Google Scholar] [CrossRef] [PubMed]
- Graham, B.; Regehr, G.; Wright, J.G. Delphi as a method to establish consensus for diagnostic criteria. J. Clin. Epidemiol. 2003, 56, 1150–1156. [Google Scholar] [CrossRef]
- Hansen, W.G. How accessibility shapes land-use. J. Am. Inst. Plan. 1959, 25, 73–76. [Google Scholar] [CrossRef]
- Zhang, L.; Lu, Y.Q. Regional accessibility of land traffic network in the Yangtze River Delta. J. Geogr. Sci. 2007, 17, 351–364. [Google Scholar] [CrossRef]
- Jiang, B.; Chu, N.C.; Xiu, C.L. Comprehensive evaluation and comparative analysis of accessibility in the four vertical and four horizontal HSR networks in China. Acta Geogr. Sin. 2016, 71, 591–604. [Google Scholar]
- Rushlow, C.R.; Godsey, S.E. Rainfall–runoff responses on Arctic hillslopes underlain by continuous permafrost, North Slope, Alaska, USA. Hydrol. Process. 2017, 31, 4092–4106. [Google Scholar] [CrossRef]
- Golosov, V.; Collins, A.L.; Tang, Q.; Zhang, X.; Zhou, P.; He, X.; Wen, A. Sediment transfer at different spatial and temporal scales in the Sichuan Hilly Basin, China: Synthesizing data from multiple approaches and preliminary interpretation in the context of climatic and anthropogenic drivers. Sci. Total Environ. 2017, 598, 319–329. [Google Scholar] [CrossRef] [PubMed]
- Peñuela, A.; Javaux, M.; Bielders, C.L. How do slope and surface roughness affect plot-scale overland flow connectivity? J. Hydrol. 2015, 528, 192–205. [Google Scholar] [CrossRef]
- Zhang, Z.T.; Gao, C.; Liu, Q.; Zhai, J.; Wang, Y.; Su, B.; Tian, H. Risk assessment on storm flood disasters of different return periods in Huaihe River basin. Geogr. Res. 2014, 33, 1361–1372. [Google Scholar]
- Słapińska, M.; Chormański, J.; Glińska-Lewczuk, K. Relation between inundation frequency and habitat Conditions of floodplain lakes—A case study of the lowland Biebrza River (ne Poland). Environ. Eng. Manag. J. 2016, 15, 1311–1321. [Google Scholar]


| Types | Names | Description | |
|---|---|---|---|
| Reservoirs | Medium-sized | Storage capacity is more than 10 million m3. | 0.30 |
| Small-(I)-sized | Storage capacity is of 1–10 million m3. | 0.40 | |
| Small-(II)-sized | Storage capacity is of 0.1–1 million m3. | 0.50 | |
| Pond | The pond is a small water storage built in mountainous or hilly areas, and its storage capacity of local runoff is less than 100,000 m3. | 0.60 | |
| Dams | Sluices | The grading standards are the same as the reservoir. The storage capacities of the two sluices are equivalent to the medium-sized reservoir in Dashi Watershed. | 0.30 |
| Rubber Dam | Also known as a rubber sluice, crest can overflow. The storage capacities of the two rubber dams are equivalent to the small-(II)-sized reservoir in Dashi Watershed. | 0.50 | |
| Submersible Bridges | Submersible bridges are simple ordinary bridges, which are constructed across the river channel. When water rises slightly, river flow will go through above the bridge. | 0.60 | |
| Deposits in a river channel | Illegal Buildings | Illegal buildings are built in the river channel partly or wholly, such as village houses or cemeteries, etc. | 0.60 |
| Sediment siltation | The sediment siltation in a river channel is produced naturally or man-made, such as sand mining activity. | 0.70 |
| Name | Photo | Image |
|---|---|---|
| Reservoir |  | |
| Rubber Dam |  | 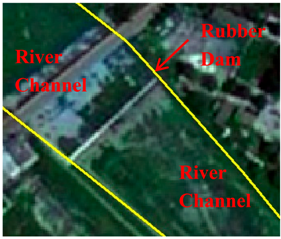 |
| Submersible Bridge |  |  |
| Illegal Buildings |  | |
| Sediment siltation |  | 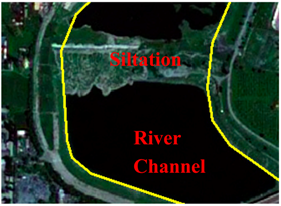 |
| Types | The Whole Region | Mountainous Area | Plain Area | ||||
|---|---|---|---|---|---|---|---|
| Number | Ratio | Number | Ratio | Number | Ratio | ||
| Reservoirs | 15 | 5% | 11 | 7% | 4 | 3% | |
| Dams | 4 | 1% | 2 | 1% | 2 | 2% | |
| Submersible Bridges | 138 | 50% | 93 | 59% | 45 | 37% | |
| Deposits in a river channel | Sediment siltation | 75 | 27% | 18 | 11% | 57 | 47% |
| Illegal Buildings | 48 | 17% | 34 | 22% | 14 | 11% | |
| Total | 280 | 100% | 158 | 100% | 122 | 100% | |
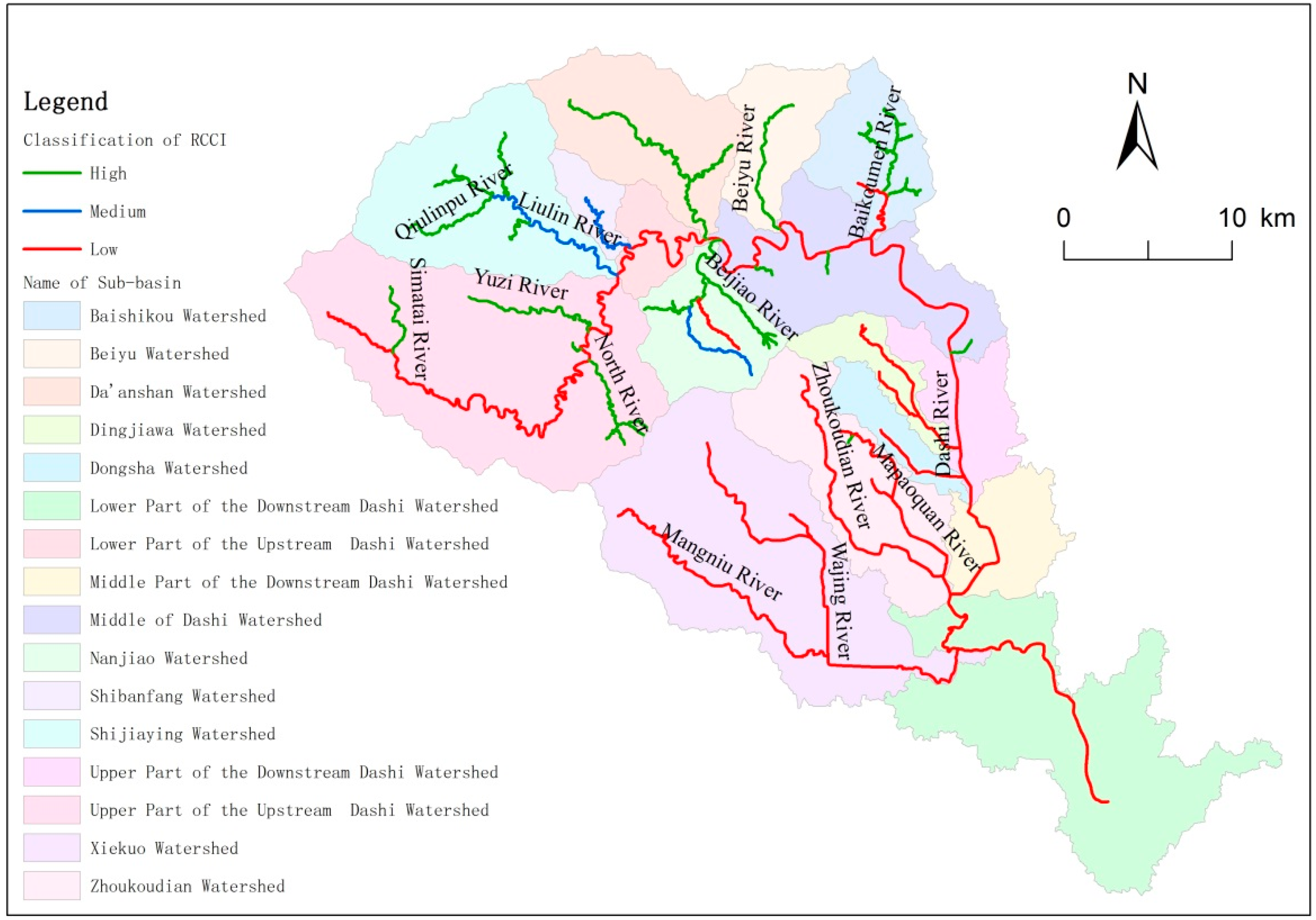
| Name of Sub-Basin | Segments | The Percentage of Each Level Segments in Number | The Length of Segment/m | The Percentage of Each Level Segments in Length | Classification | Basic Morphological Types | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| High/% | Medium/% | Low/% | High/% | Medium/% | Low/% | |||||
| Upper Part of the Downstream Dashi Watershed | 7 | 0 | 14 | 86 | 8617 | 0 | 18 | 82 | Low | Plain |
| Middle Part of the Downstream Dashi Watershed | 7 | 0 | 28 | 72 | 6571 | 23 | 0 | 77 | Low | Plain |
| Zhoukoudian Watershed | 58 | 40 | 8 | 52 | 35,907 | 46 | 1 | 53 | Low | Plain |
| Dongsha Watershed | 6 | 50 | 0 | 50 | 6328 | 30 | 0 | 70 | Low | Plain |
| Lower Part of the Downstream Dashi Watershed | 9 | 33 | 22 | 45 | 24,808 | 41 | 43 | 16 | Low | Plain |
| Xiekuo Watershed | 73 | 41 | 15 | 44 | 51,763 | 53 | 10 | 37 | Low | Plain |
| Dingjiawa Watershed | 18 | 33 | 28 | 39 | 14,983 | 32 | 41 | 27 | Low | Plain |
| Lower Part of the Upstream Dashi Watershed | 5 | 20 | 40 | 40 | 13,914 | 14 | 50 | 36 | Low | Mountain |
| Middle of Dashi Watershed | 28 | 57 | 11 | 32 | 35,714 | 66 | 16 | 18 | High | Mountain |
| Shijiaying Watershed | 24 | 63 | 16 | 21 | 33,969 | 72 | 19 | 9 | High | Mountain |
| Nanjiao Watershed | 23 | 65 | 18 | 17 | 31,133 | 74 | 22 | 4 | High | Mountain |
| Baishikou Watershed | 23 | 70 | 13 | 17 | 22,461 | 91 | 1 | 8 | High | Mountain |
| Shibanfang Watershed | 12 | 50 | 33 | 17 | 6749 | 48 | 47 | 5 | High | Mountain |
| Upper Part of the Upstream Dashi Watershed | 35 | 83 | 6 | 11 | 69,987 | 90 | 2 | 8 | High | Mountain |
| Da’anshan Watershed | 12 | 84 | 8 | 8 | 23,630 | 94 | 5 | 1 | High | Mountain |
| Beiyu Watershed | 1 | 100 | 0 | 0 | 10,001 | 100 | 0 | 0 | High | Mountain |
| Name | Scenario A | Scenario B | Scenario C | Scenario D | Scenario E | Scenario F | Actual RCCI |
|---|---|---|---|---|---|---|---|
| Beiyu River | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| North River | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Baikoumen River | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Shangshuiyu River | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Yanglin Rvier | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Qiulinpu River | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Shijiaying1 River | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Jinjitai River | 1.000 | 0.997 | 1.000 | 0.999 | 1.000 | 1.000 | 0.996 |
| Yuzi River | 1.000 | 1.000 | 0.990 | 0.990 | 0.990 | 0.990 | 0.990 |
| Zhongjiao River | 1.000 | 0.988 | 0.990 | 0.998 | 0.990 | 0.990 | 0.987 |
| Beijiao River | 1.000 | 1.000 | 0.990 | 0.990 | 0.990 | 0.990 | 0.990 |
| Simatai River | 1.000 | 0.990 | 0.990 | 1.000 | 0.990 | 0.990 | 0.990 |
| Da’anshan River | 1.000 | 0.990 | 0.980 | 1.000 | 0.980 | 0.980 | 0.980 |
| Shijiaying2 River | 1.000 | 0.989 | 0.980 | 0.998 | 0.980 | 0.980 | 0.980 |
| Shibanfang River | 1.000 | 0.972 | 0.970 | 0.996 | 0.970 | 0.970 | 0.970 |
| Mao’ershan River | 1.000 | 0.930 | 0.930 | 0.950 | 0.980 | 0.930 | 0.930 |
| Liulin River | 1.000 | 0.921 | 0.920 | 0.970 | 0.945 | 0.920 | 0.920 |
| Nanjiao River | 1.000 | 0.904 | 0.902 | 0.949 | 0.945 | 0.902 | 0.902 |
| Baishikou River | 1.000 | 0.903 | 0.930 | 0.970 | 0.900 | 0.900 | 0.900 |
| Dashi River | 1.000 | 0.900 | 0.930 | 0.920 | 0.940 | 0.894 | 0.890 |
| Dongsha River | 1.000 | 0.881 | 0.980 | 0.890 | 0.880 | 0.880 | 0.880 |
| Shuangquan River | 1.000 | 0.881 | 0.880 | 1.000 | 0.880 | 0.880 | 0.880 |
| Wajing River | 1.000 | 0.878 | 0.910 | 0.960 | 0.876 | 0.880 | 0.876 |
| Xiekuo River | 1.000 | 0.871 | 0.998 | 0.870 | 0.870 | 0.870 | 0.869 |
| Zhoukoudian River | 1.000 | 0.860 | 1.000 | 0.860 | 0.860 | 0.860 | 0.858 |
| Dingjiawa River | 1.000 | 0.854 | 0.900 | 0.852 | 0.940 | 0.852 | 0.852 |
| Xisha River | 1.000 | 0.793 | 0.930 | 0.810 | 0.810 | 0.789 | 0.789 |
| Mapaoquan River | 1.000 | 0.779 | 0.960 | 0.778 | 0.800 | 0.778 | 0.778 |
| Mangniu River | 1.000 | 0.744 | 0.810 | 0.760 | 0.870 | 0.743 | 0.743 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Zhou, D.; Hu, S.; Zhang, J.; Jiang, Y.; Zhang, Y. Barrier-based Longitudinal Connectivity Index for Managing Urban Rivers. Water 2018, 10, 1701. https://doi.org/10.3390/w10111701
Li H, Zhou D, Hu S, Zhang J, Jiang Y, Zhang Y. Barrier-based Longitudinal Connectivity Index for Managing Urban Rivers. Water. 2018; 10(11):1701. https://doi.org/10.3390/w10111701
Chicago/Turabian StyleLi, Heying, Demin Zhou, Shanshan Hu, Jianchen Zhang, Yuemei Jiang, and Yue Zhang. 2018. "Barrier-based Longitudinal Connectivity Index for Managing Urban Rivers" Water 10, no. 11: 1701. https://doi.org/10.3390/w10111701
APA StyleLi, H., Zhou, D., Hu, S., Zhang, J., Jiang, Y., & Zhang, Y. (2018). Barrier-based Longitudinal Connectivity Index for Managing Urban Rivers. Water, 10(11), 1701. https://doi.org/10.3390/w10111701





