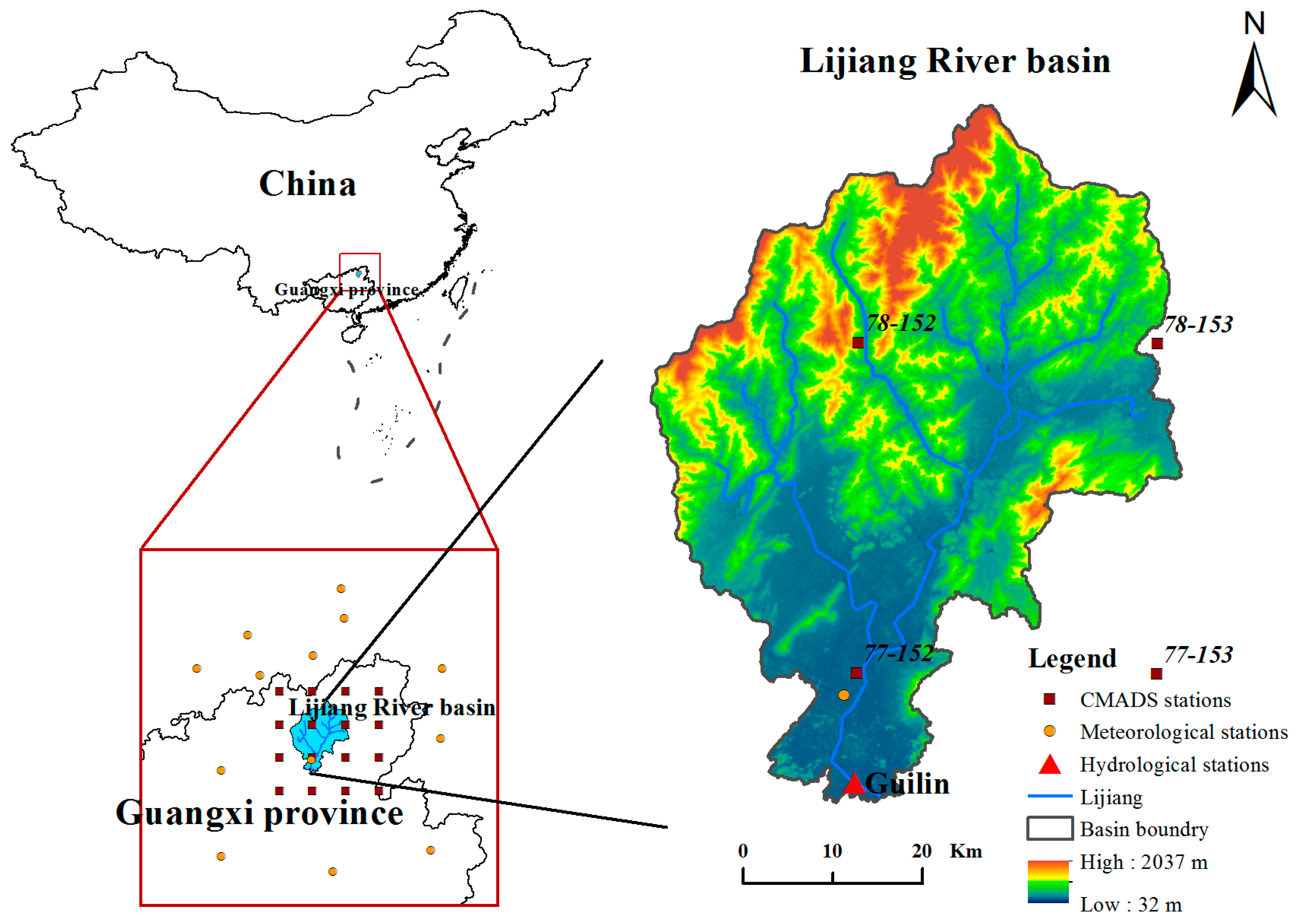
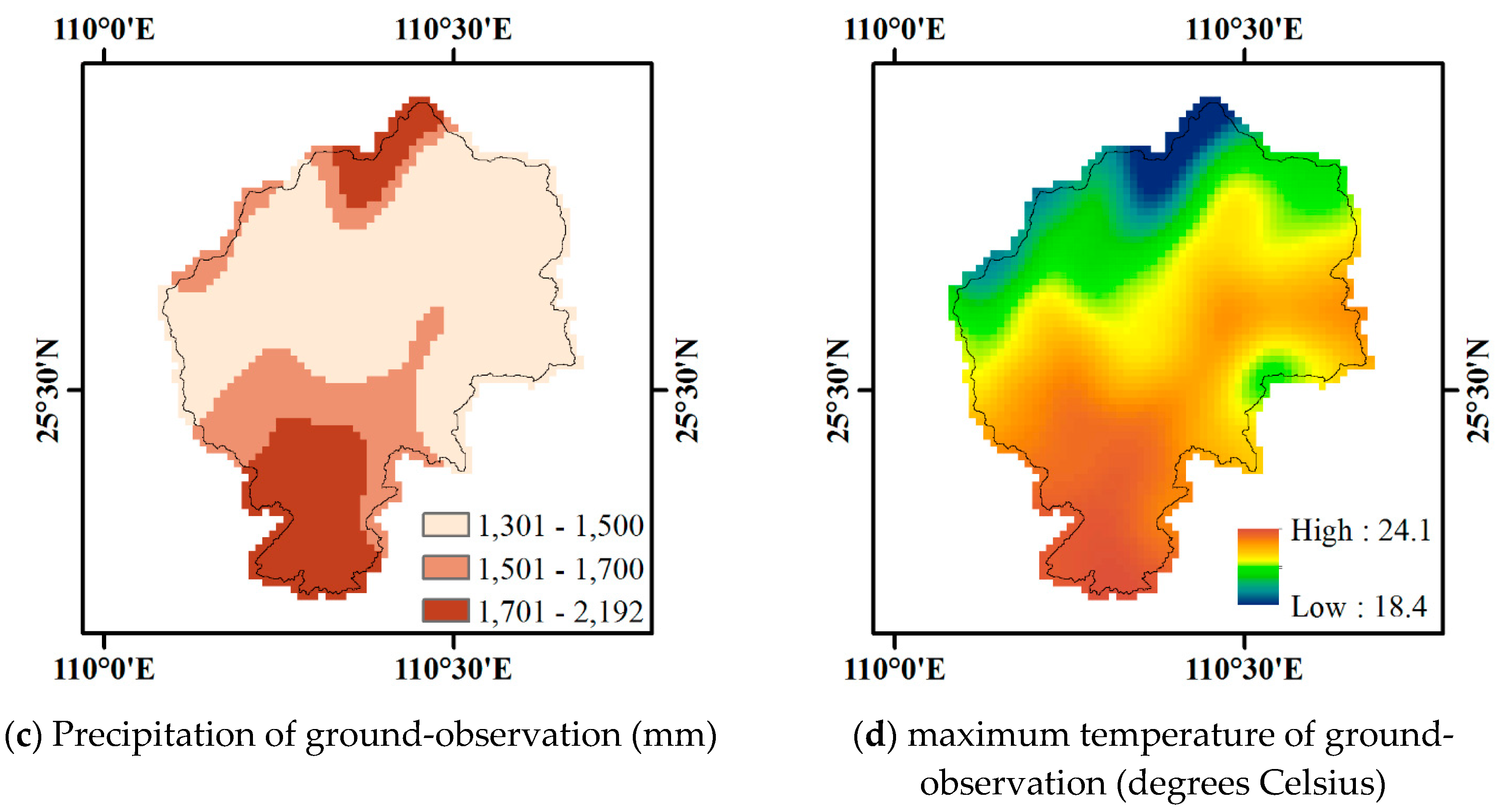
1. Introduction
Hydrologic models are essential tools for understanding processes of the hydrologic cycle and provide useful information for sustainable water-resource management [
1]. Precipitation is the main driving factor of hydrologic processes. Accurate estimation of precipitation is crucial for reliable hydrologic predictions [
2]. Traditionally, precipitation data from a ground observational network have been used as the source of areal precipitation estimates used in watershed modelling. However, ground-based precipitation observation networks are sparsely distributed and may be unable to represent the spatial variability of the precipitation completely. Moreover, precipitation measurements are frequently missing because of malfunctioning of devices [
3]. Remote sensing [
4] and modelling [
5] of precipitation have become viable approaches to address these problems effectively and are often used as input data to hydrologic models.
With regard to the development of remote-sensing technology, satellite-derived precipitation data are an attractive alternative in data-sparse regions because of the relatively high resolution and complete spatial coverage. A number of such remotely sensed precipitation products are currently available. These include, for example, the Climate Prediction Center morphing method (CMORPH, [
6]), the Global Satellite Mapping of Precipitation (GSMaP) project [
7], the Tropical Rainfall Measuring Mission (TRMM) Multi-satellite Precipitation Analysis (TMPA) [
8] and the Global Precipitation Measurement (GPM) products [
9]. Among them, the TMPA products developed by the National Aeronautics and Space Administration (NASA) Goddard Space Flight Center (GSFC), with a spatial resolution of 0.25° × 0.25° for multiple timescales (3 hourly, daily and monthly), has received much more attention [
10]; the latest research product of TMPA for post-real-time research (3B42) is version 7. Most of the applications using the TMPA-3B42V7 product indicate an excellent potential to supply reasonably high spatial and temporal resolution data for hydrometeorological applications [
10,
11,
12,
13]. However, remotely sensed precipitation data suffer from uncertainty in their retrieval algorithms and observation errors [
14] due to the inference of rainfall based on observations of the conditions at the top of clouds.
While precipitation modelling is fairly accurate for coarse-scale (global-scale), organized, synoptic systems, the modelling accuracy decreases rapidly for more localized events as spatial and temporal features cannot be explicitly resolved by global models [
2]. Reanalysis datasets, which are produced by assimilating multi-source data into a climate model, are a viable option of deriving reliable precipitation estimates [
5]. Commonly used reanalysis datasets include the Climate Forecast System Reanalysis (CFSR) [
15] from National Center for Environmental Prediction (NCEP), the European Centre for Medium-Range Weather Forecasts (ECMWF) Reanalysis from September 1957 to August 2002 (ERA-40 [
16]) and the ECMWF Reanalysis-Interim (ERA-Interim [
17]) products. While these reanalysis datasets provide important basic data for global researchers for the analysis of climate–water cycles, the spatial resolution of global reanalysis datasets is often too coarse to be used reliably in local-scale studies. Hydrologic modelling forced by reanalysis datasets has been conducted by, for example, Andreadis et al. (2017) [
5], who reproduced flooding over large scales by using the Twentieth Century Reanalysis (20CRv2, [
18]) dataset and downscaling techniques. Fuka et al. (2014) found the CFSR precipitation product provides a relatively reliable precipitation input for the hydrologic modelling of large-area basins.
Given the strongly underconstrained nature of precipitation inversion, data assimilation based on the large number of stations on regional scales has the potential to resolve fine-scale structures and microphysical processes with more details. The China Meteorological Assimilation Driving Datasets for the Soil and Water Assessment Tool (SWAT) model (CMADS,) developed by Dr. Xianyong Meng from the China Agricultural University (CAU), has received worldwide attention [
19,
20]. CMADS incorporate Space and Time Mesoscale Analysis System (STMAS) assimilation techniques [
21,
22] and multiple other techniques, such as loop nesting of data, projection of resampling models and bilinear interpolation. The precipitation data of the CMADS product is generated by the assimilation of multi-satellite data and precipitation from ground stations. Using CMORPH satellite products as the background field, the CMADS product assimilates hourly precipitation products of nearly 40,000 regional automatic stations and 2421 national automatic stations in China. Relative studies found the CMADS product significantly reduces the uncertainties of precipitation input for the hydrologic modelling [
19]. CMADS has been verified in several basins in China and Korea [
20,
23,
24,
25,
26,
27,
28,
29]. However, reanalysis datasets are limited by the quality of precipitation observations and the uncertainty from the assimilation model.
A number of spatial-interpolation methods [
30] are commonly used for estimating precipitation based on ground-observation data, even in data-sparse regions [
31,
32]. Conventional interpolation methods, such as the Thiessen polygon [
33,
34] and inverse-distance weighting [
35], are widely used for precipitation interpolation [
32]. Ordinary kriging [
36] is a geostatistical technique requiring prior calibration of a semivariogram for its parameters (range, nugget and sill). These methods are suitable for application over relatively flat areas. These methods assume that other potential drivers (particularly topography) of the spatial variation in rainfall is captured by the gauge data and information on other drivers is not needed. In data-sparse regions this is not correct and methods that explicitly include the topography are preferred. Hutchinson found that the interpolating accuracy of a precipitation surface would be enhanced significantly with an appropriate digital elevation model (DEM) [
37,
38,
39]. The advantages of the ANUSPLIN package (Hutchinson and Xu, 2013) over kriging are its simplicity and there is no requirement of a separate calibration of the spatial-covariance structure. The ANUSPLIN interpolation technique has been applied in a number of studies, proving to be one of the best techniques for interpolating point precipitation data [
40,
41,
42]. However, if the meteorological stations are very sparse, obtaining an accurate distribution of precipitation values through interpolation is impossible. The low density of precipitation stations is a major uncertainty source, which potentially impacts the result. Moreover, interpolation of precipitation data is unable to capture some extreme weather conditions. All interpolation techniques have difficulty in simulating sharply varying climate transitions.
Spatially distributed precipitation datasets incorporate uncertainties or errors resulting from the interpolation and retrieval algorithms, the quality of precipitation observations and the uncertainty from the assimilation model. As different precipitation datasets are limited by quantitative inaccuracies, they exhibit significant bias [
43]. Smith and Kummerow [
44] analyzed the water budgets of precipitation datasets from in situ, reanalysis and satellite data over the upper Colorado River basin and found the reanalysis datasets tend to overestimate in situ data, while satellite-derived precipitation data underestimate in situ data. Pfeifroth et al. [
45] evaluated satellite-based and reanalysis precipitation data in the tropical Pacific and found reanalysis products overestimate small and medium precipitation amounts but underestimate high amounts. Some studies have found that runoff-generation is highly sensitive to the spatial and temporal variability of precipitation data, as a result this is found to be the main source of uncertainty in rainfall–runoff modelling [
46]. Therefore, assessing the accuracy of different precipitation products and their applicability and uncertainty for hydrologic models is of great importance; the uncertainties associated with hydrologic models also play a role in the performance of hydrologic simulations [
47].
Our main objective here is to assess and evaluate three general precipitation datasets in terms of their accuracy and efficacy, including the CMADS, TMPA-3B42V7 and gauge-interpolated product. The assessment is based on the simulation results from two well-known hydrologic models (IHACRES and Sacramento models). In addition, the precipitation detection capability of TRMA-3B42V7 and CMADS datasets is also evaluated through their pixel-to-point comparison to the ground-based data. The applicability of these two models is assessed. Moreover, the parameter uncertainty of each hydrologic model is also explored as this is another source of uncertainty in modelling streamflow. This research will provide more insight into precipitation analyses and hydrologic modelling.
3. Results
3.1. Evaluation of Model Performance
By setting one year as the warm-up period, with 2008–2012 as the calibration period and
NSE as the objective function, the shuffled complex evolution algorithm is used to calibrate the parameter values of the two hydrologic models. Using the resulting calibrated parameters, the overall performance (
NSE) of observed and simulated values for the precipitation datasets and models for the period 2008–2016 is shown in
Table 4.
Table 5 and
Table 6 depict the calibrated optimal parameters sets and daily
NSE for each precipitation dataset applied respectively to the IHACRES model and Sacramento model (2008–2012).
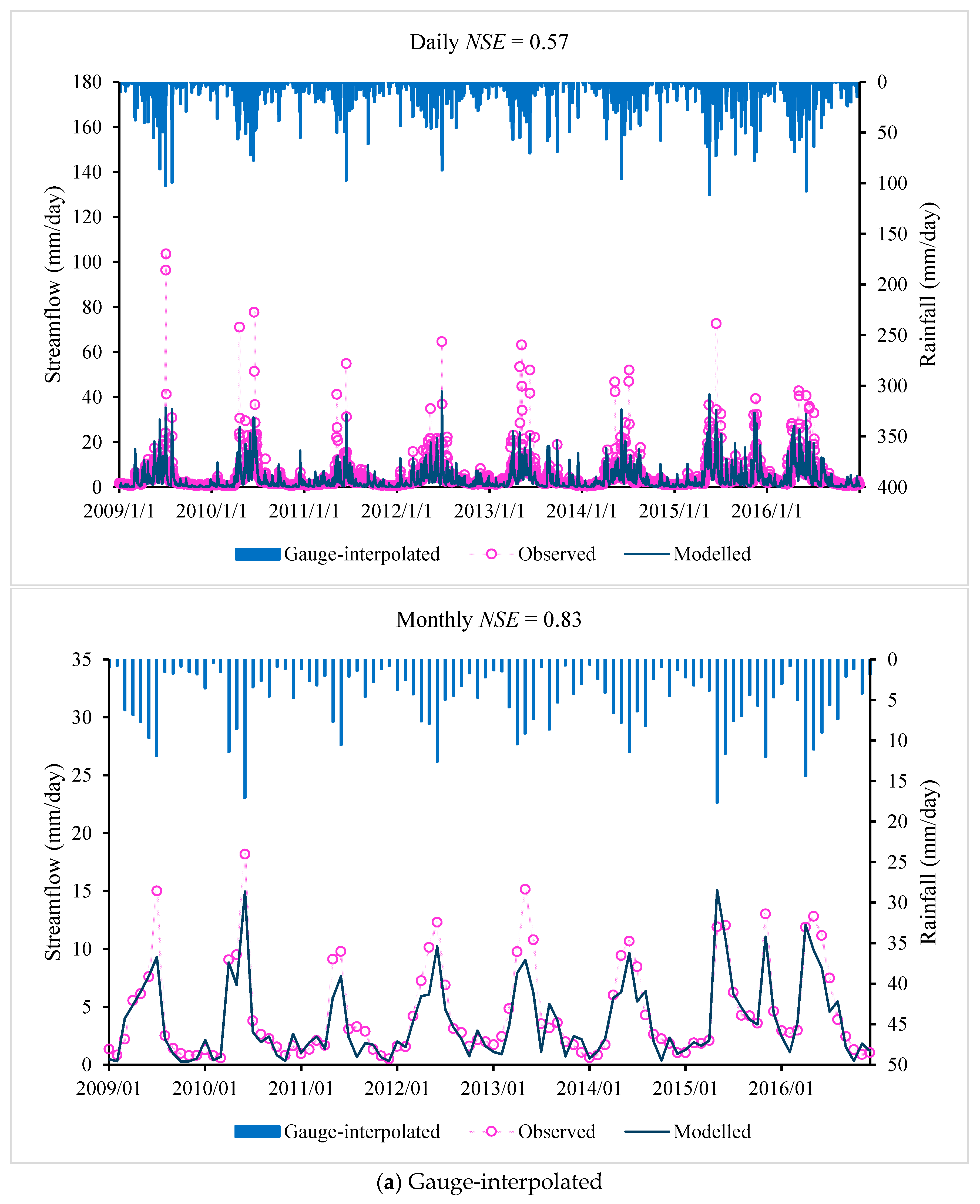
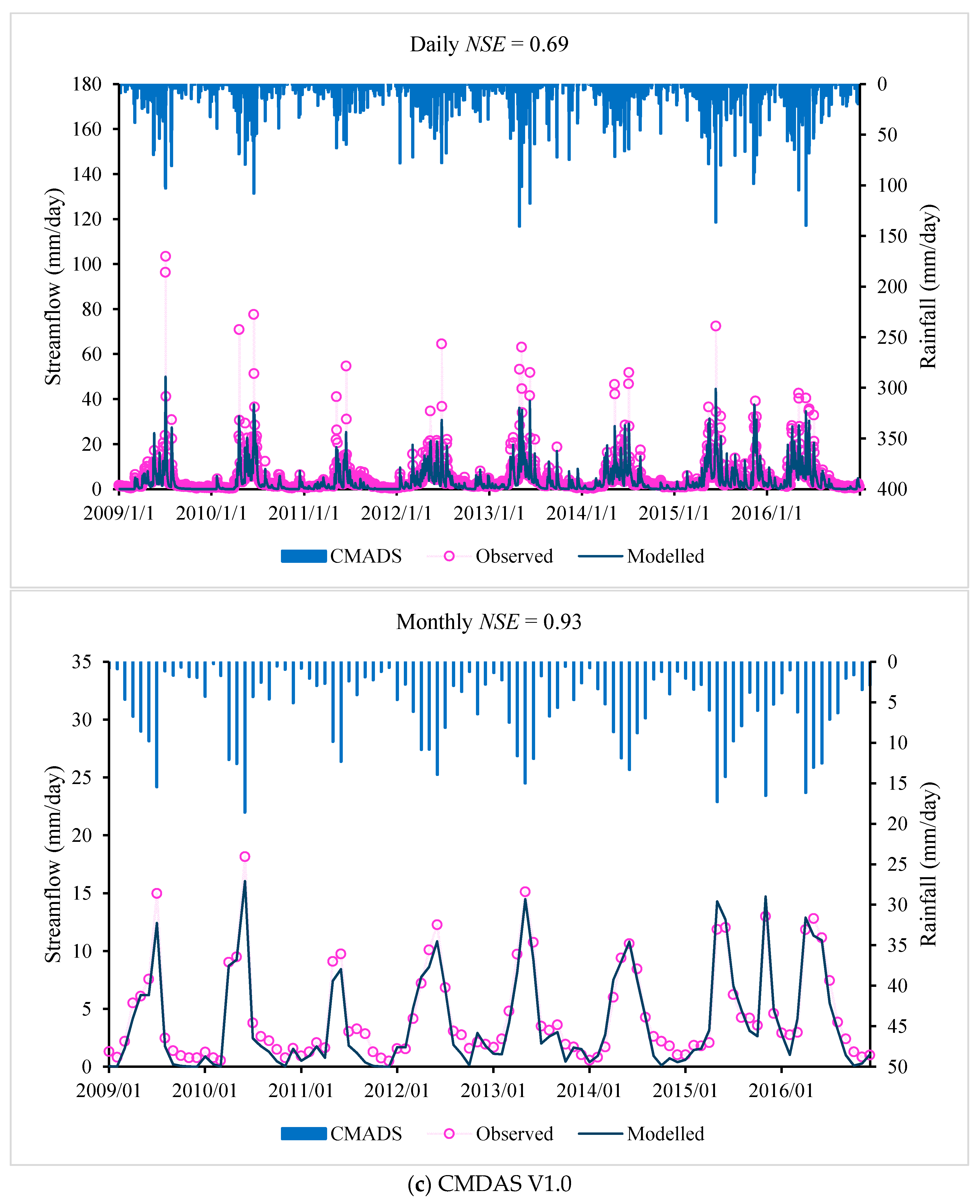
Selecting the years 2008–2012 as the calibration period and the years 2012–2016 as the validation period, the daily and monthly performance of the IHACRES model for different precipitation products are shown in
Table 7, with daily and monthly observed and modelled flow and rainfall shown in
Figure 3. The additive merit of
NSEsq and
NSElog is also calculated. Since
NSEsq and
NSElog shift the focus from high flows to progressively lower flows, using
NSEsq and
NSElog help us judge the performance of the models in simulating over a broader range of flows. The performance of the IHACRES model shows that the CMADS dataset has the best performance among all three precipitation products during the calibration period. The TMPA-3B42V7 and gauge-interpolated product have a similar performance but perform slightly worse than the CMADS dataset. During the validation period, the
NSE,
NSEsq and
NSElog values when using the CMADS dataset show a better performance than other precipitation datasets, which indicates the CMADS dataset performs better than other precipitation datasets in simulating both high flow and low flows. Overall, all the three precipitation datasets perform well, with the CMADS dataset performing slightly better.
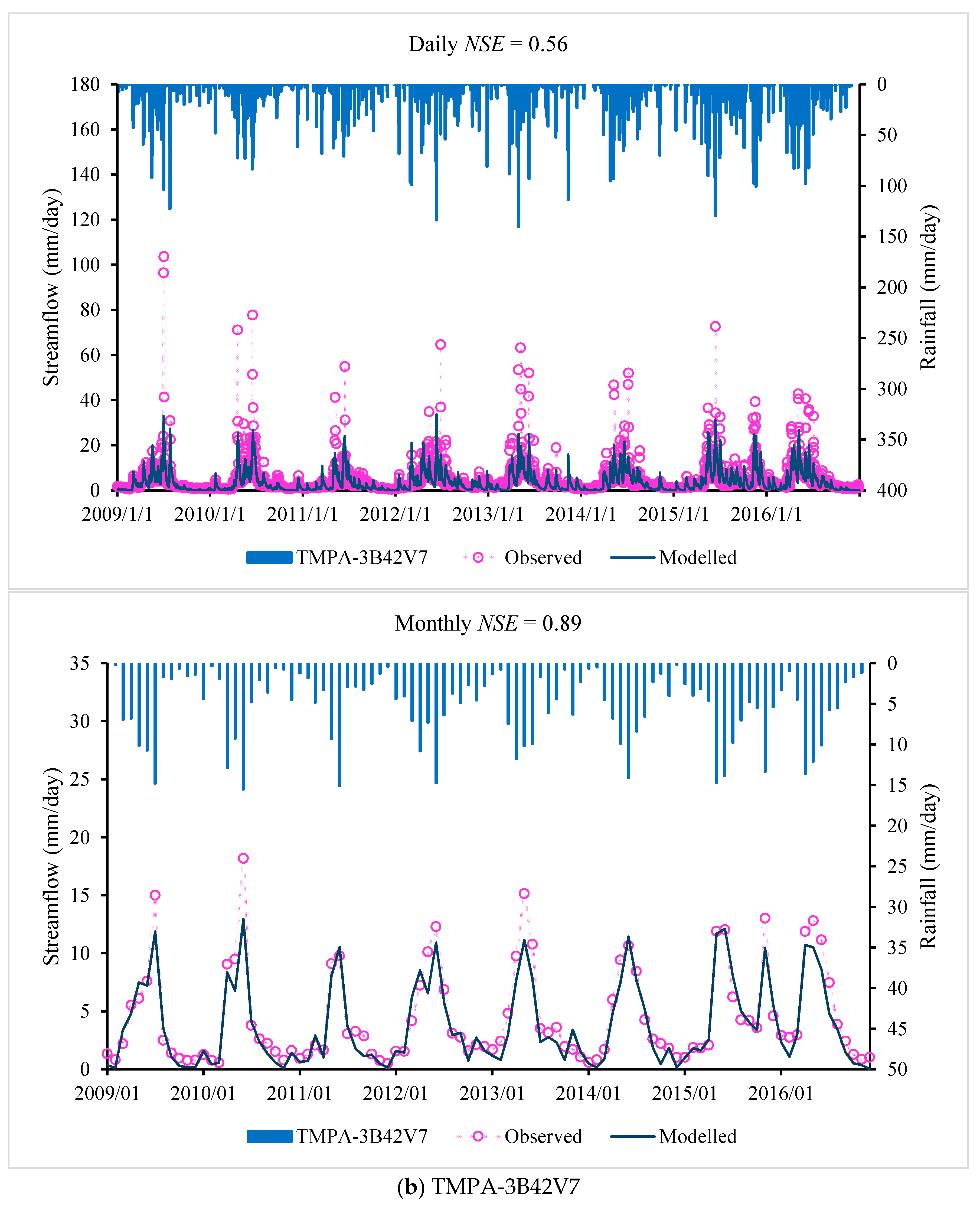
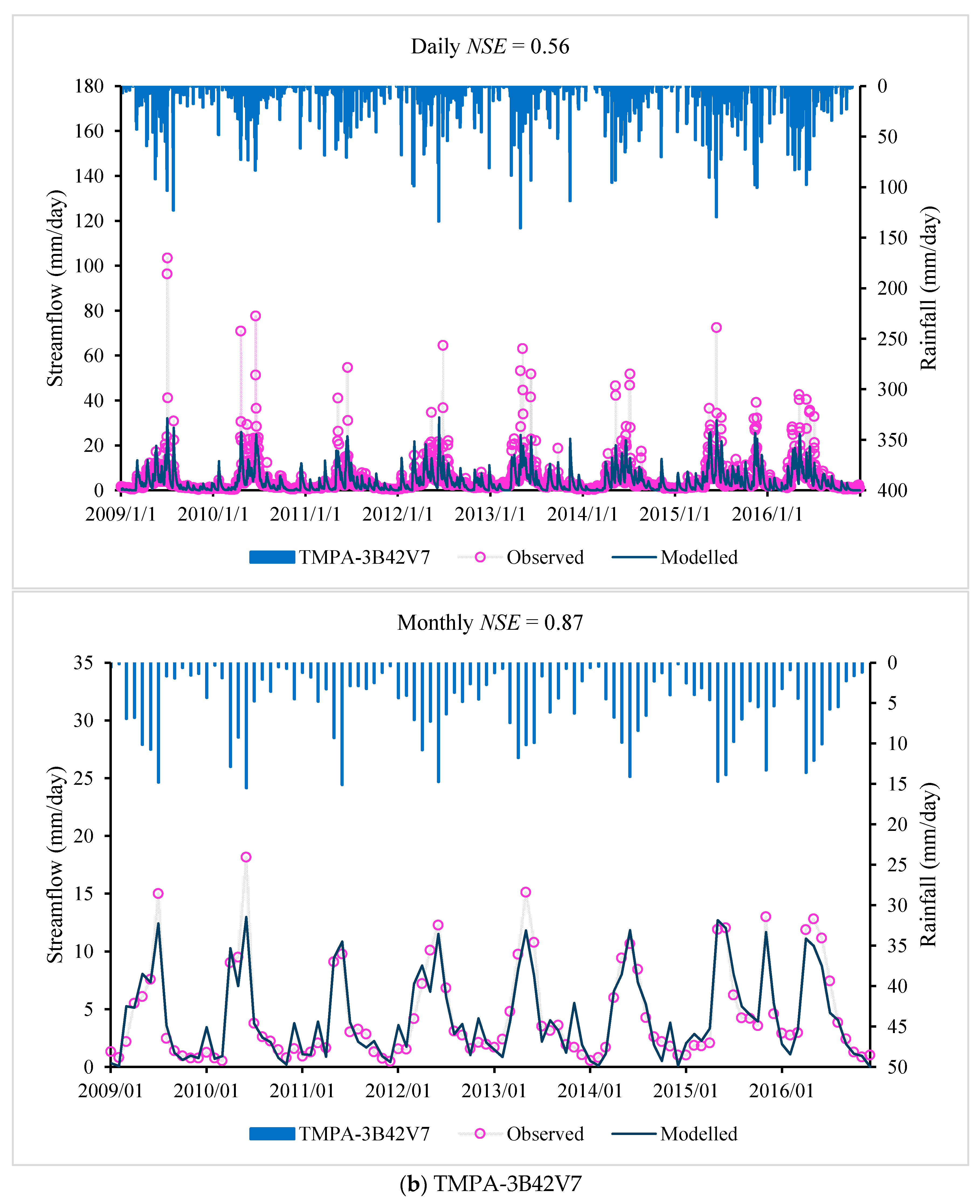
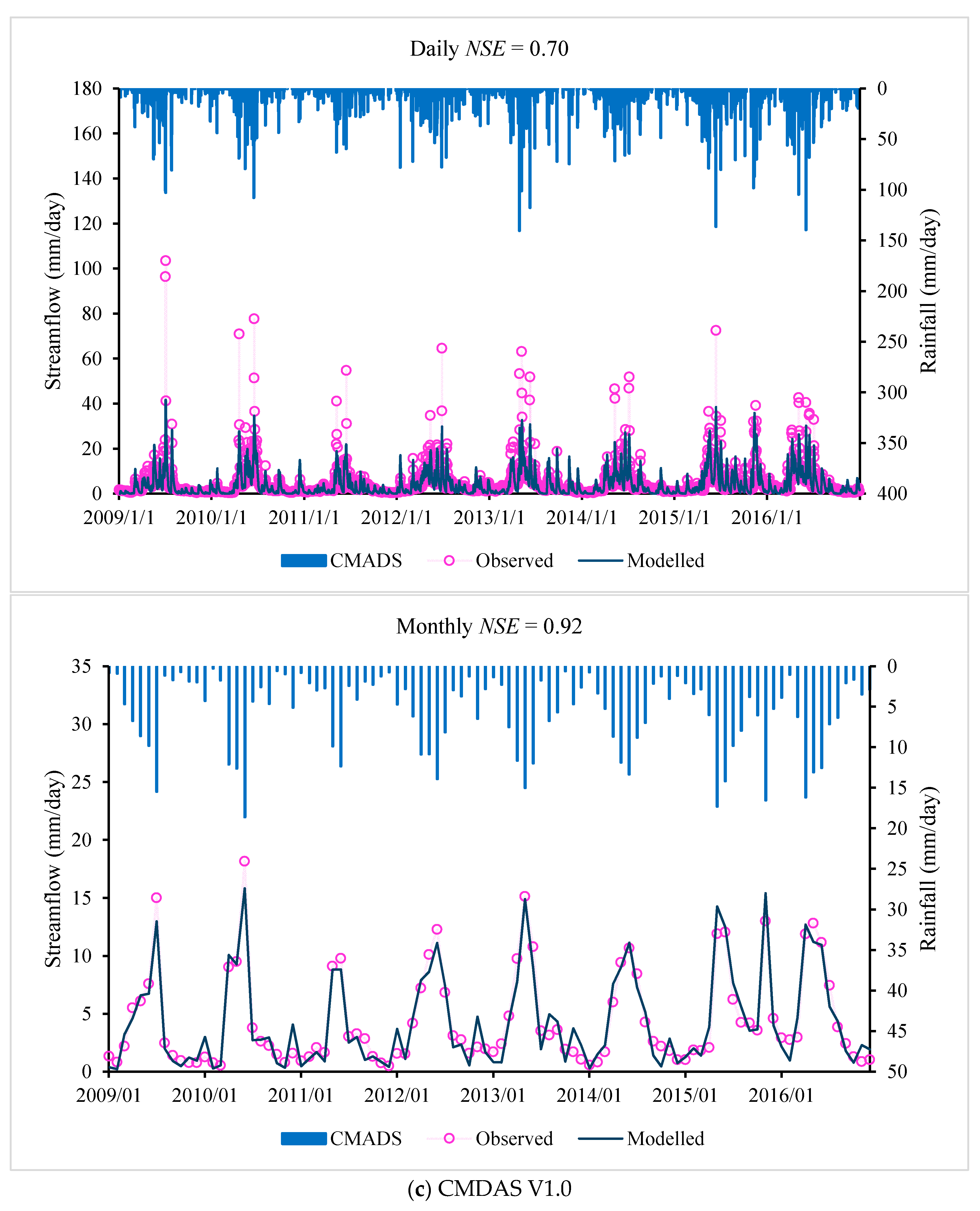
The daily and monthly model performance of the Sacramento model for different precipitation products are shown in
Table 8, with time series plotted in
Figure 4. Again, the performance of the Sacramento model show that the precipitation product of the CMADS dataset performs best for both the calibration and validation periods, followed by the TMPA-3B42V7 datasets, with the performance of the gauge-interpolated product slightly worse.
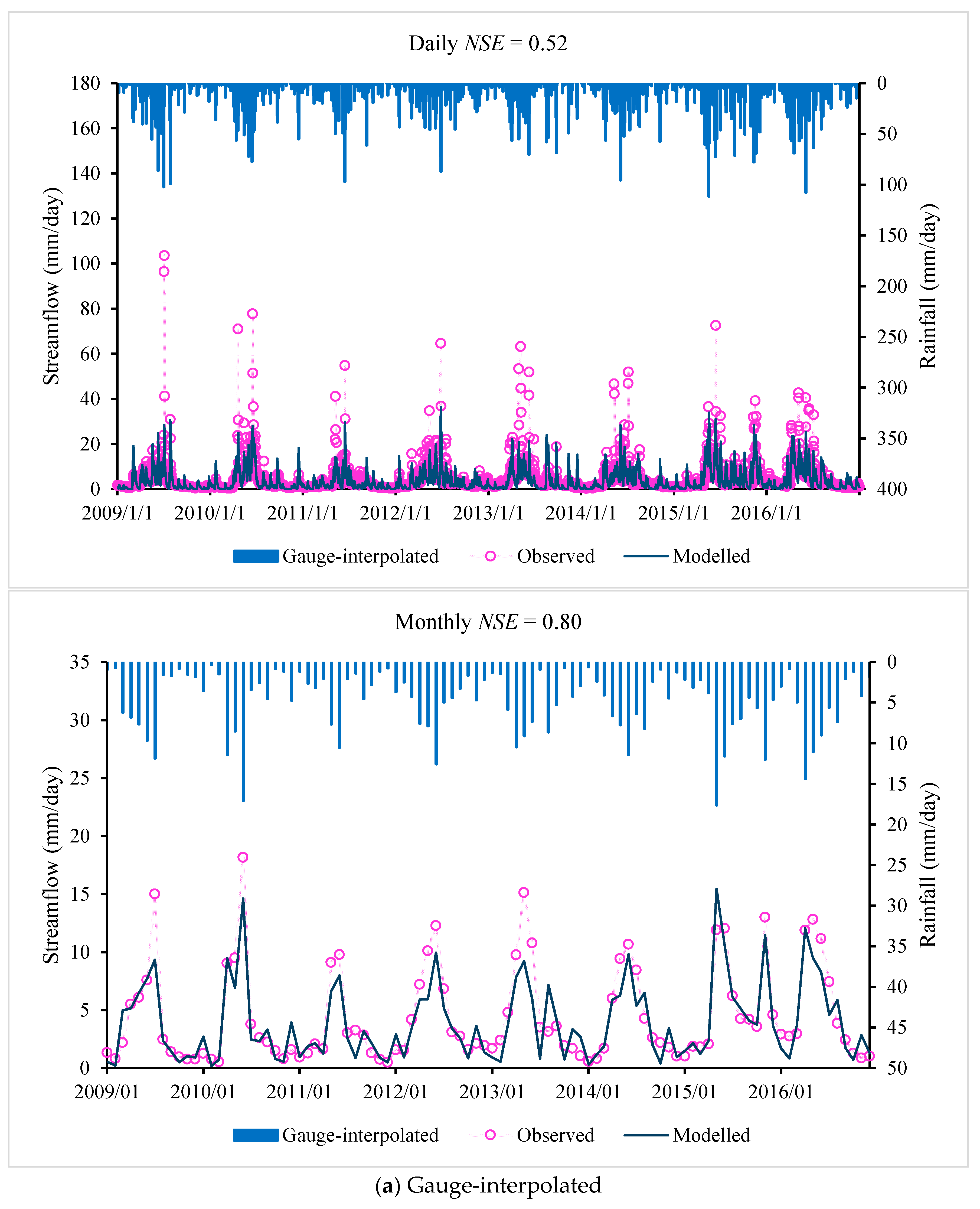
These results show that, among the three precipitation datasets considered here for the Lijiang River basin, the CMADS precipitation datasets have a higher accuracy and better applicability in calibrating and validating the rainfall–runoff models. The reason that the gauge-interpolated rainfall always provides the worst result in flow simulations is due to the meteorological stations available in the Lijiang river basin being too sparsely distributed to permit reliable interpolation.
3.2. Precipitation Detection
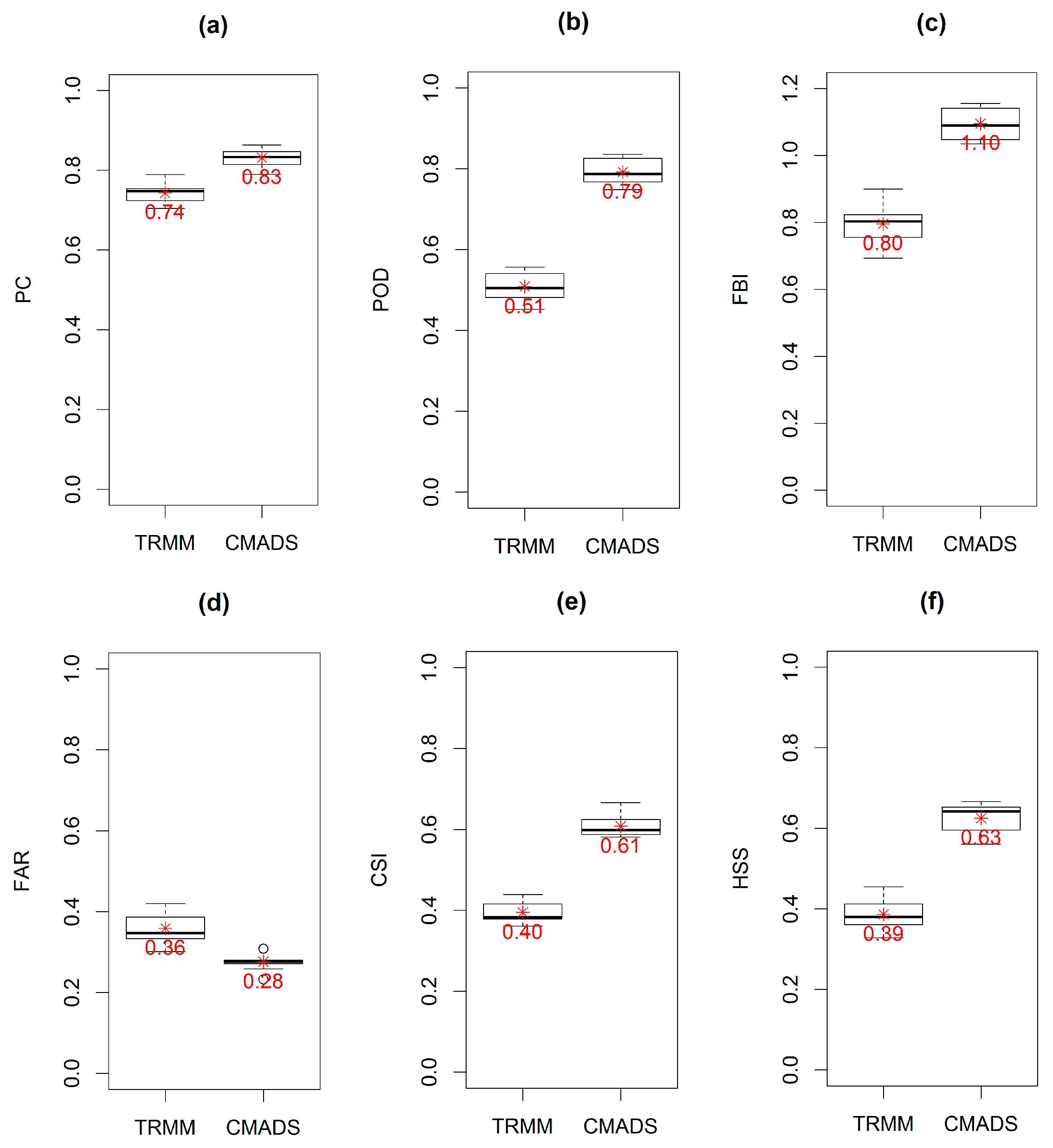
We examined the performance of TRMA-3B42V7 and CMADS using the six statistical measures (PC, POD, FBI, FAR, CSI and HSS) through the pixel-to-point comparison with the ground-based data. Following the studies of Dai [
67] and Vu et al. [
24], a minimum precipitation threshold of 1.0 mm per day was used for the precipitation and non-precipitation event for ground observation and satellite/reanalysis estimate. The contingency statistics of TRMA-3B42V7 and CMADS were evaluated each year through the precipitation datasets from 2008 to 2016.
Figure 5 shows the contingency statistics calculated for the TRMA-3B42V7 and CMADS.
For the statistics PC, POD and CSI, the CMADS scheme (with an average of 0.83, 0.79 and 0.61) shows higher values than TRMM (with an average of 0.74, 0.51 and 0.40). For the statistic FBI, CMADS gives a mean of 1.1 (ranging from 1.03 to 1.16) and is closer to the perfect score than the FBI of TRMM with a mean of 0.8 (ranging from 0.69 to 0.9). With respect to the FAR statistic, CMADS has a smaller FAR with an average of 0.28 (ranging from 0.23 to 0.31) than TRMM with an average of 0.36 (ranging from 0.30 to 0.42). Finally, the HSS statistic for CMADS has a larger value with a mean of 0.63 (ranging 0.56 to 0.67) than TRMM with a mean of 0.39 (ranging from 0.33 to 0.45). These results indicate that the CMADS scheme shows better performance than TRMA-3B42V7 for all the six contingency statistics. Overall, compared to TRMM data, CMADS show better agreement with the ground observation data in Lijiang river basin.
3.3. Uncertainty Analysis
All precipitation products are limited by quantitative inaccuracies and they can exhibit significant bias and errors in spatial and temporal variability. As the runoff-generation is highly sensitive to the spatial and temporal variability of precipitation data, the spatial and temporal variability of precipitation is one of the main source of uncertainty in rainfall–runoff modelling.
Parameter uncertainty is another source of uncertainty in rainfall-runoff modelling. The parameter uncertainty of each hydrologic model has been explored in this study. A GLUE uncertainty analysis is applied to assess parameter uncertainty of hydrologic models here.
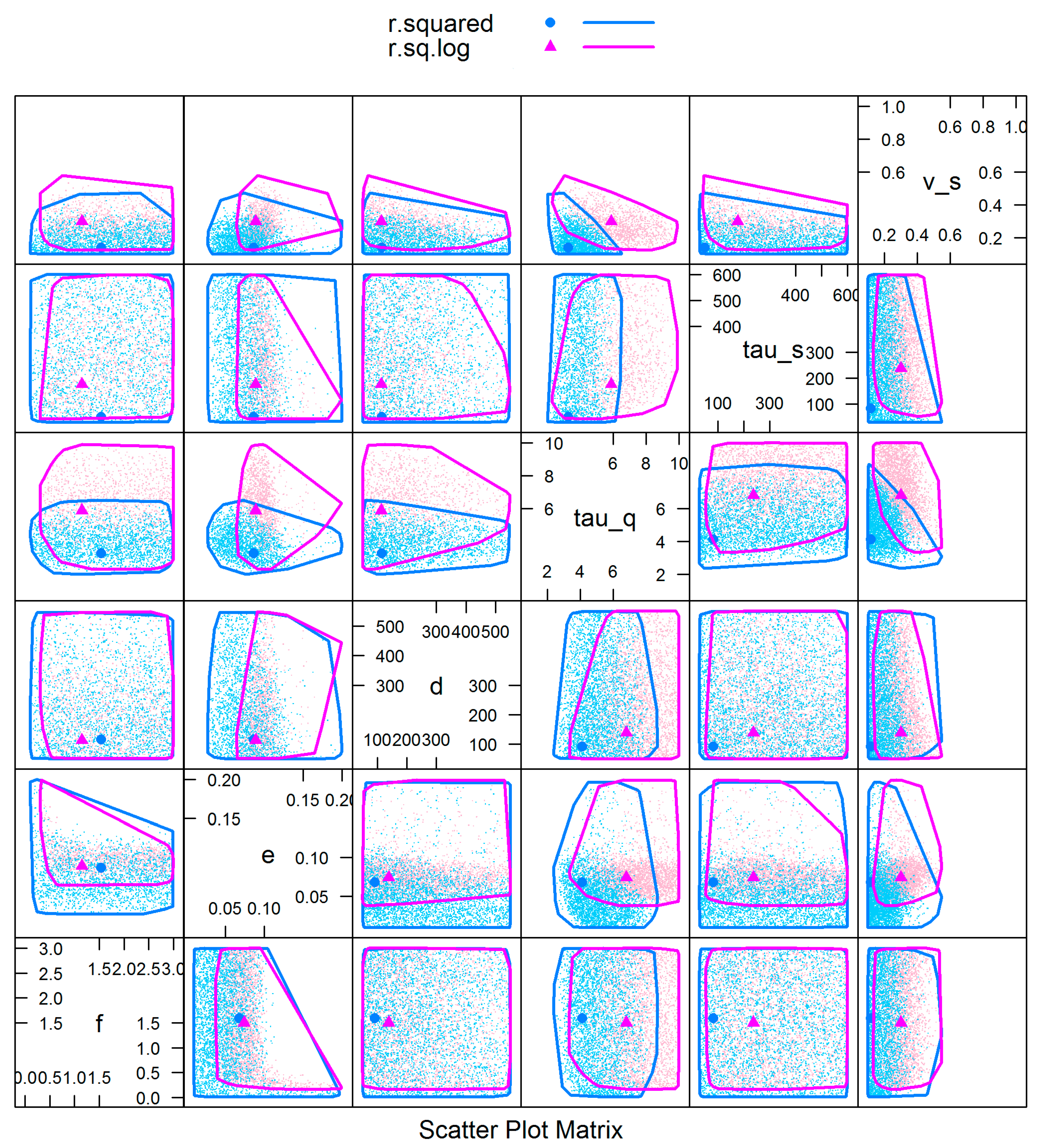
In the first case, for the IHACRES model, 100,000 samples are chosen from a uniform distribution for each parameter and the performance measures NSE and NSElog are used as the “likelihood” functions. Using a threshold value of NSE > 0.67 (or NSElog > 0.78) for the CMADS product, the GLUE algorithm finds 2000 (1416) behavioral solutions in 100,000 simulations with the IHACRES model. Using a threshold value of NSE > 0.56 (or NSElog > 0.69) for the TMPA-3B42V7 product, the GLUE algorithm finds 3180 (2819) behavioral solutions in 100,000 simulations with the IHACRES model.
The red (blue) dots and lines in
Figure 6 represent the distribution and boundary of behavioral parameters when using
NSElog (
NSE) as the likelihood function, with the calibrated parameter set for each rainfall dataset indicated. From the distribution of behavioral parameter sets, we see the parameters
d,
f and
tau_s have behavioral values distributed across the full parameter range, indicating these have the greatest uncertainty. In comparison, the distribution of
v_s for behavioral parameter sets is constricted to smaller values (<~0.5), particularly when using considering
NSE. The values of
tau_q are more constrained when considering
NSE, due to the focus
NSE gives to high flows compared to
NSElog. Generally, there is little interaction between most of the parameters. The main exception is the
e and
f parameters. The value of the
e parameter is constrained to <~0.1 providing
f > ~1, increasing rapidly for smaller values of
f. This indicates a highly non-linear interaction between these parameters. It should also be noted that the optimal value of the e parameter is considerably smaller than that found in Australia (0.166) found by Chapman (2001) [
68], due to the influence of other factors (e.g., atmospheric transmissivity).
A similar analysis is applied for the Sacramento model, where 100,000 samples are chosen obeying a uniform distribution, and
NSE and
NSElog are again defined as the likelihood functions. Using a threshold value of
NSE > 0.45 (or
NSElog > 0.53), the GLUE algorithm finds 929 (359) behavioral solutions in 100,000 simulations for the CMADS product with the Sacramento model. Using a threshold value of
NSE > 0.32 (or
NSElog > 0.43), the GLUE algorithm finds 1294 (140) behavioral solutions in 100,000 simulations for the TMPA-3B42V7 product with the Sacramento model. The pairwise correlation of behavioral parameters for the Sacramento model is shown in
Figure 7.
The meaning of the red (blue) dot and line in
Figure 7 is similar to that in
Figure 6. From the distribution of behavioral parameters, we can see the parameters
uztwm,
adimp and
lztwm show less uncertainties overall. When
NSE is selected as the likelihood function, the distribution of parameters
lzwm,
uztwm and
adimp are relatively low, while the distributions of parameters
lzpk and
lzsk are relatively high; when
NSElog is selected as the likelihood function, the distribution of the parameters
uztwm,
lztwm and
adimp is relatively low and the distribution of the parameter
pfree is relatively high, which indicates that these parameters may be more sensitive and less uncertain.
In the second case, model performance is considered satisfactory when
NSE is greater than 0.5 [
69,
70], with likelihood-function values > 0.5 defined as behavioral parameter sets. The behavioral parameter space may be used as further criteria for the evaluation of different precipitation products. The behavioral parameter space describes the number (and percentage) of behavioral solutions in 100,000 simulations, with 100,000 parameter sets generated by the same Monte Carlo random sampling method, with the same criteria of acceptability employed (i.e., the same threshold value and the objective function) for the different precipitation datasets. The statistics of the number and percentage of behavioral parameter sets for different precipitation schemes driving the IHACRES model are shown in
Table 9.
Using a threshold value of NSE > 0.5 (or NSElog > 0.5), the GLUE algorithm finds 5186 (12,095) behavioral solutions in 100,000 simulations for the CMADS precipitation product with the IHACRES model, while the GLUE algorithm achieves 1056 (9929) and 576 (9144) behavioral solutions in 100,000 simulations for the TMPA-3B42V7 and gauge-interpolated products with the IHACRES model. Therefore, the behavioral parameter space of the IHACRES model driven by the CMADS precipitation is larger than the behavioral parameter space driven by the other two precipitation inputs. The CMADS product gives a better performance than the TMPA-3B42V7 and gauge-interpolated products, because CMADS assimilated datasets are based on the large number of stations (nearly 40,000 regional automatic stations and 2421 national automatic stations in China), which gives it any priority in reflecting the actual processes of areal precipitation.
A similar analysis is applied for the Sacramento model as well. The statistics of the number and percentage of behavioral parameter sets for different precipitation schemes driving the Sacramento model are shown in
Table 10. For the Sacramento model, the behavioral parameter space is very sparse when using the GLUE method for the Lijiang River basin. Using a threshold value of
NSE > 0.5 (or
NSElog > 0.5), the GLUE algorithm finds 32 (60) behavioral solutions in 100,000 simulations for the CMADS precipitation dataset within the Sacramento model, while the GLUE algorithm achieves 0 (11) and 0 (5) behavioral solutions in 100,000 simulations for the TMPA-3B42V7 and gauge-interpolated products with the Sacramento model. Similar to their performance with the IHACRES model, the behavioral parameter space of the Sacramento model driven by the CMADS precipitation dataset is larger than the behavioral parameter space driven by the other two precipitation inputs. The CMADS product shows a better performance than the TMPA-3B42V7 and gauge-interpolated products, which, as mentioned before, is probably because the CMADS assimilated datasets are based on the strongly underconstrained large number of stations.
4. Discussion
Our work presents a comparative analysis for different precipitation datasets and their applicability for hydrologic modelling, including gauge-interpolated datasets, TMPA-3B42V7 and CMADS precipitation products. Two hydrologic models; IHACRES and Sacramento, are evaluated in the Lijiang River basin, as well as the accuracy of different precipitation datasets for hydrologic modelling.
The results show that the IHACRES and Sacramento models demonstrate a good and similar performance in the Lijiang River basin. Driven by the CMADS precipitation, the
NSE values of the IHACRES (Sacramento) model are 0.69 (0.68) and 0.70 (0.71) for the calibration and validation periods, respectively.
Figure 6 shows there are three sensitive parameters (
f,
e and
v_s) for the IHACRES model.
Figure 7 shows there are three sensitive parameters (
uztwm,
adimp and
lztwm) for the Sacramento model. The number of effective parameters is similar in both Sacramento model (with more parameters) and IHACRES model (with less parameters), consistent with sensitivity results in Shin et al. [
64].
The uncertainty analysis carried out for the IHACRES and Sacramento models show that the uncertainty in the model predictions is greater for the Sacramento model. To sum up, IHACRES and Sacramento perform similarly in terms of simulation performance and number of effective parameters, the latter model having far more insensitive parameters. What’s more, the IHACRES model has a reduced uncertainty compared with the Sacramento model. Based on these analyses, the authors conclude that IHACRES generally outperforms Sacramento in Lijiang river basin. It confirms previous findings (e.g., Orth et al. [
71]) that more parameters may lead to over-fitting without an improved performance of the hydrologic model.
Of the three precipitation datasets (gauge-interpolated product, TMPA-3B42V7 and CMADS products), the CMADS product gives the best performance in simulating the rainfall–runoff process in the Lijiang River basin. The overall performance (based on Daily
NSE values) of the CMADS product is 0.69 and 0.70 for the IHACRES and Sacramento models, respectively, with the overall performance of the TMPA-3B42V7 (0.56 and 0.56) and gauge-interpolated (0.57 and 0.52) products correspondingly much lower. From the analysis of
Figure 3 and
Figure 4, the hydrologic model driven by the CMADS product shows a superior skill in capturing the flow peaks because the CMADS reanalysis data are based on a large number of stations. However, these datasets overestimate the simulated flood peak and underestimate low flowrates, which is probably because the models are calibrated using the performance measure
NSE, being an objective function that puts more emphasis on high flowrates. The model calibrated using Nash–Sutcliffe efficiency on transformed streamflow
NSElog, which gives more emphasis to low flowrates, is presented in the
Supplementary Materials, as well as the model performance calibrated using
NSElog as an objective function. Similar conclusions can be reached with the models calibrated using the performance measure
NSElog as the objective function. The CMADS precipitation datasets perform best in all three precipitation datasets, followed by the TMPA-3B42V7 precipitation and then the gauge-interpolated product. Comparing the model performance using
NSElog and
NSE as the objective functions for calibration, the model calibrated using the performance measure
NSE performed better in simulating peak flows, while underestimating low flowrates. In contrast, the model calibrated using the performance measure
NSElog performs well in simulating low flowrates but underestimates the flood peak in the simulations.
The GLUE pairwise correlation of behavioral parameters (
Figure 5 and
Figure 6) give us an intuitional view of parameter uncertainties. From the distribution of behavioral parameters for the IHACRES model (
Figure 5), we see the parameters
d,
tau_s and
tau_q have the greatest uncertainties overall. Further analysis reveals that different precipitation products reshape the distribution of
tau_q greatly. The parameter
tau_q, which represents the time constant for quick flow store, is very sensitive to the precipitation input. For the Sacramento model (
Figure 6), the parameters
uztwm,
adimp and
lztwm show less uncertainties overall than other parameters.
The superiority of the CMADS product can also be found in the number of GLUE behavioral parameters (or their occupation percentage among all the uniformly distributed parameter sets), as well as their GLUE relative measurements coverage. From
Table 7 and
Table 8, we find the CMADS driven hydrologic models are responsible for more behavioral parameters than the hydrologic models driven by the other two precipitation datasets.
Although the two hydrologic models introduced here are widely used, the precipitation input data are basin-averaged precipitation. The comparison and applicability of different precipitation datasets maybe be affected by this “average” precipitation, since the spatial distribution and variability of different precipitation datasets may be weakened by the effect of spatial averaging. The improved accuracy of the CMADS precipitation dataset may be more obvious with the simulation of a distributed or semi-distributed model as the rainfall input. Moreover, different uncertainty-analysis methods may affect the efficiency of the uncertainty analysis, which thus requires further research.
5. Conclusions
Precipitation is a fundamental component of the global water cycle. Precipitation datasets range from conventional ground-based datasets to remote-sensing products and reanalysis datasets, such as the gauge-interpolated product, the TMPA-3B42V7 precipitation products and the CMADS datasets invoked here. The two hydrologic models (IHACRES and Sacramento) are introduced to evaluate their applicability in the basin, the impact of model complexity and the applicability of different precipitation datasets on the hydrologic modelling.
CMADS gives best results when used in IHACRES and Sacramento to simulate flow in the Lijiang River basin. The CMADS precipitation datasets (Daily
NSE = 0.69 for the IHACRES model; Daily
NSE = 0.70 for the Sacramento model) give improved applicability and accuracy compared with the gauge-interpolated datasets (Daily
NSE = 0.57 for the IHACRES model; Daily
NSE = 0.52 for the Sacramento model) and TMPA-3B42V7 datasets (Daily
NSE = 0.56 for the IHACRES model; Daily
NSE = 0.56 for the Sacramento model) in the Lijiang River basin. From the analysis of
Figure 3 and
Figure 4, we conclude that the CMADS precipitation-driven hydrologic models give better skill in capturing the streamflow peaks. Interpolation of gauge data performed worst, reflecting the impact of low gauge density
The precipitation detection ability of TRMA-3B42V7 and CMADS is also evaluated using six statistical measures (PC, POD, FBI, FAR, CSI and HSS) through a pixel-to-point comparison to the ground-based data. CMADS (with an average of 0.83, 0.79, 1.1, 0.28, 0.61 and 0.63) shows better performance and is closer to the perfect score than TRMM (with an average of 0.74, 0.51, 0.80, 0.36, 0.4 and 0.39).
Based on the analysis of
Table 7, for the IHACRES model and using
NSE as the likelihood function, the number and percentage of behavioral parameters for the CMADS, TMPA-3B42V7 and gauge-interpolated product are 5186 (5.19%), 1056 (1.06%) and 576 (0.58%). Using
NSElog as the likelihood function, the number and percentage of behavioral parameters for the corresponding precipitation datasets are 12,095 (12.1%), 9929 (9.93%) and 9144 (9.14%). Similar phenomena can be found with the same analysis of the Sacramento model in
Table 8 but the behavioral parameter sets for that model are very sparse. We conclude that the CMADS precipitation-driven hydrologic models are more accurate, as they are responsible for more behavioral parameters than the hydrologic models driven by the other two precipitation datasets. The TMPA-3B42V7 datasets show slightly better performance than the gauge-interpolated product in this case study, indicating that global datasets are particularly useful in poorly gauged areas.
The performance of the IHACRES model (DailyNSE = 0.69 driven by the CMADS product) and Sacramento model (DailyNSE = 0.70 driven by the CMADS product) give respectable results. While both models work well, IHACRES gives lower predictive uncertainty compared to Sacramento, which implies that the general applicability of the IHACRES model is preferable to the Sacramento model in the Lijiang River basin.