Correction and Informed Regionalization of Precipitation Data in a High Mountainous Region (Upper Indus Basin) and Its Effect on SWAT-Modelled Discharge
Abstract
1. Introduction
2. Study Area and Data
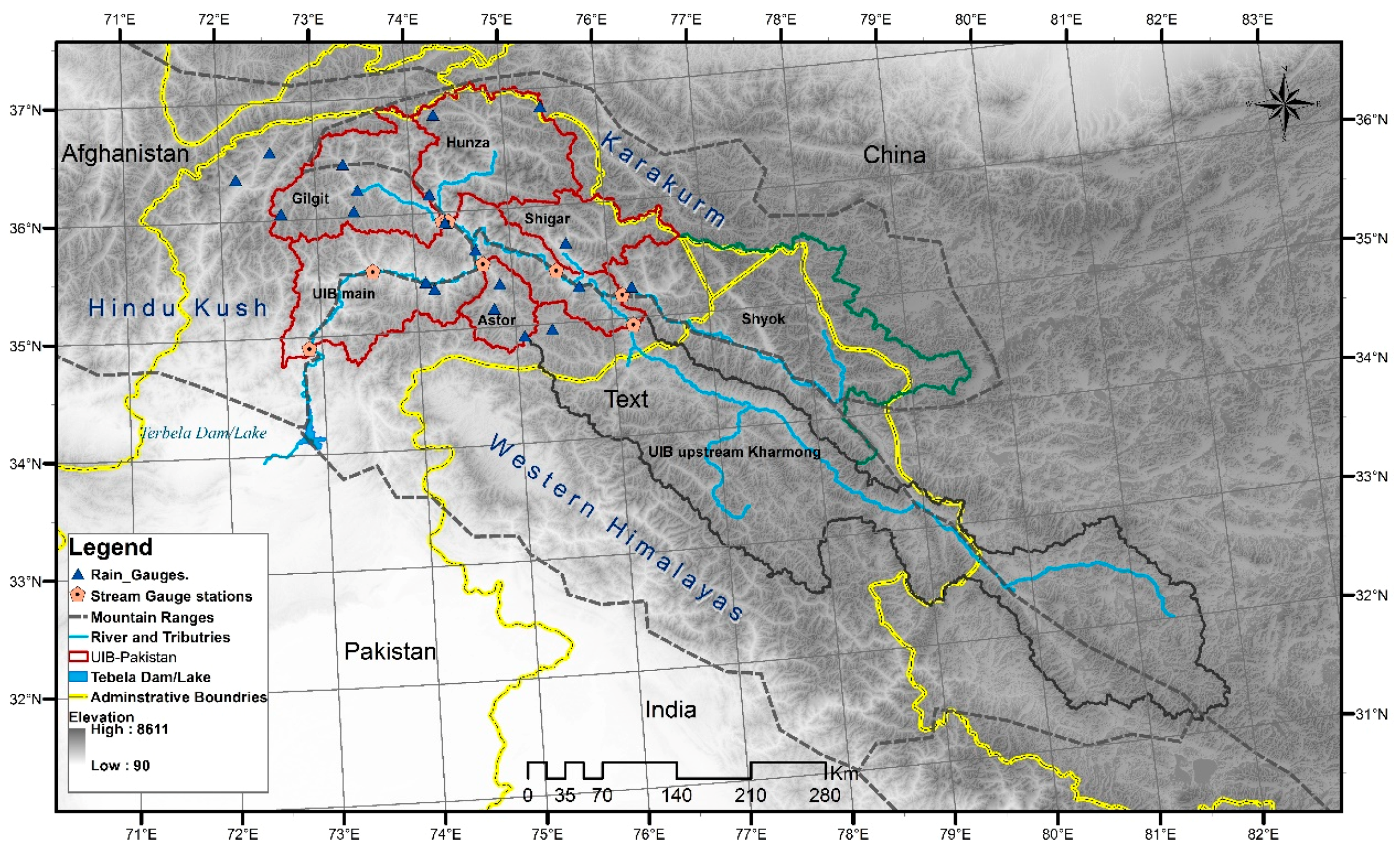
2.1. Study Area—The Upper Indus River Basin (UIB)
2.2. Observed Hydro-Climatic Data
2.2.1. Observed Precipitation Data
2.2.2. Observed Discharge Data
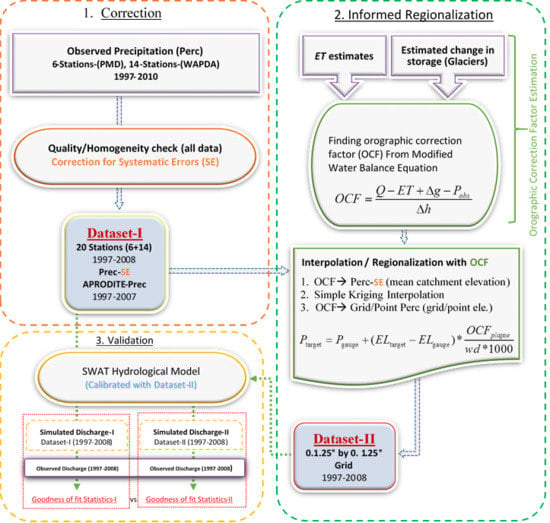
3. Methodology
3.1. Relevant Literature-Correction Methods
- an interpolation or regionalization of point rainfall measurements
- applying a “Doing Hydrology Backward (DHB)” (Kirchner’s methodology), estimating catchment-averaged precipitation rates from streamflow fluctuations, measured at the catchment outlet.
3.2. Method Used in the Present Study
3.2.1. Correction of Systematic Errors
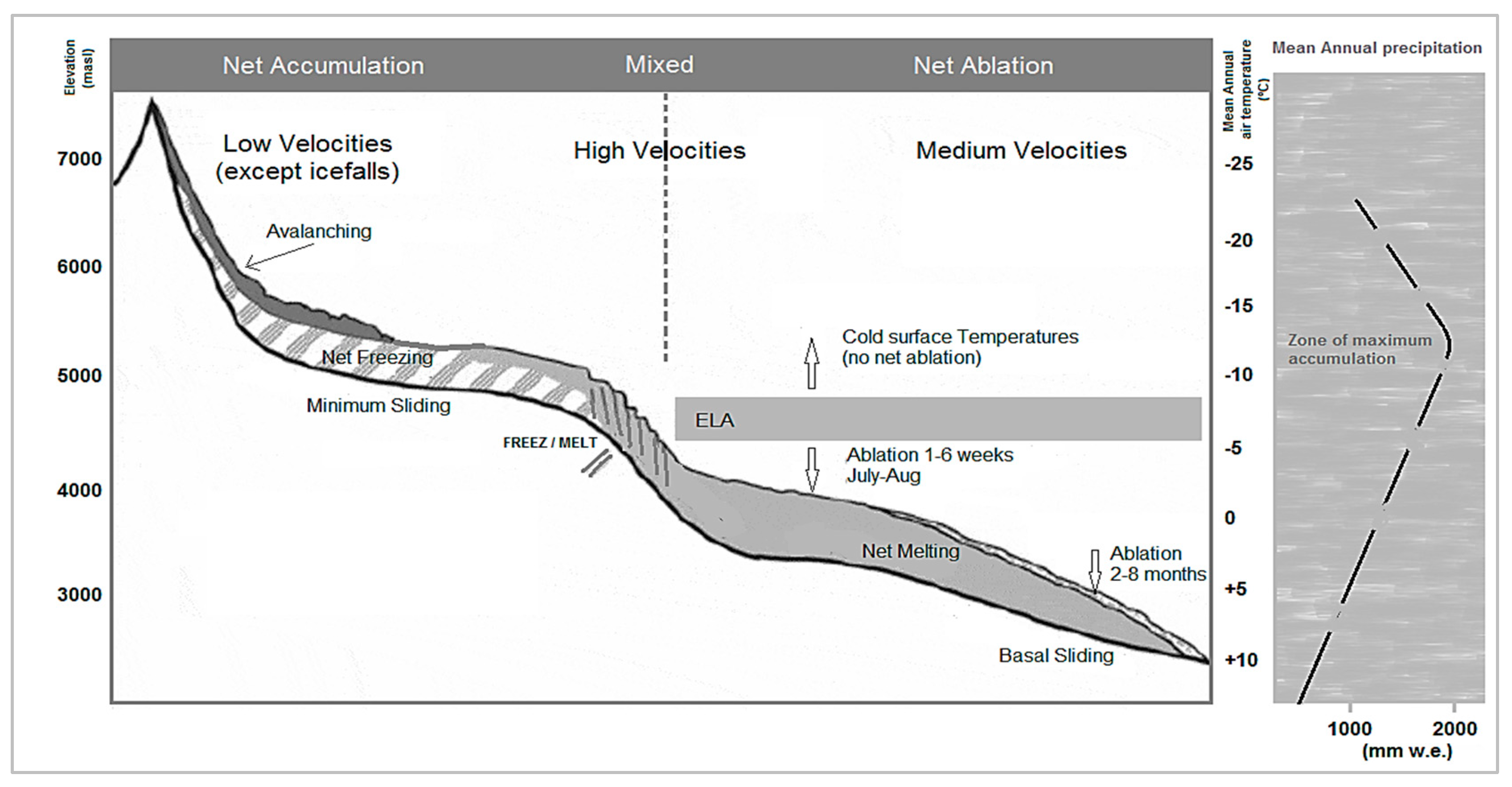
3.2.2. Estimating the “Orographic Correction Factor” (OCF) by Doing Hydrology Backward (DHB) plus Interpolation (Informed Regionalization (IR))
- (a)
- (b)
- The Gilgit watershed, though spanning over the northern end of the Hindukush range (bordering the western Karakoram) is assigned the same value of +0.09 mwe year−1, because, as reported by Reference [82], this watershed has more similarities with the climatic regime of the Karakoram region (Hunza basin), rather than the rest of the Hindukush area.
- (c)
- For the Shyok river basin, a snow cover change of +0.11 mwe year−1 is assumed based on the value given by Reference [83] for the east Karakorum.
- (d)
- For the region covered by the Astor basin and the parts of UIB downstream of Kharmong, except the aforementioned tributary catchments, the selection is not straight forward, as some of the above studies claim a constant/slight increase in snow cover area in this region (e.g., Reference [82]), while others suggest a negative mass balance. Therefore, for the current study, the glacier mass balance in this region is taken as neutral, with no increase or decrease.
- (e)
- For the parts of UIB, upstream of Kharmong, which have experienced a consistent decrease in snow/glacier cover, according to most of the literature, a value of −0.45 mwe year−1 is assigned, based on the mean mass balance value [83] for the Spiti-Lahaul region.
3.2.3. Regionalization Procedure—Step-Wise Interpolation
3.2.4. Validation of Estimates Precipitation by Means of the SWAT Hydrological Model
4. Results and Discussion
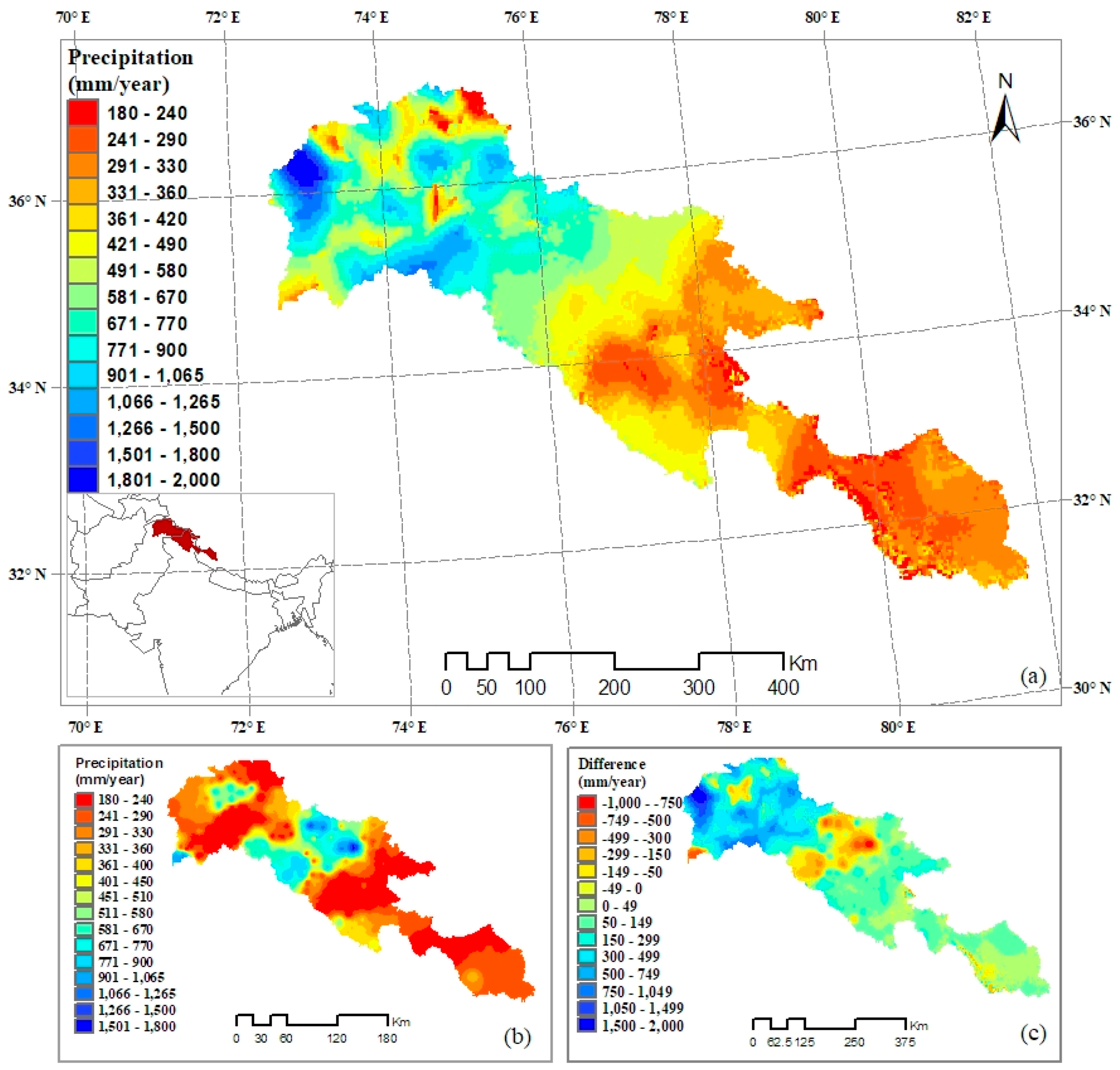
4.1. Construction of Orographically-Corrected Precipitation Datasets
4.2. True Areal Precipitation and OCF’s
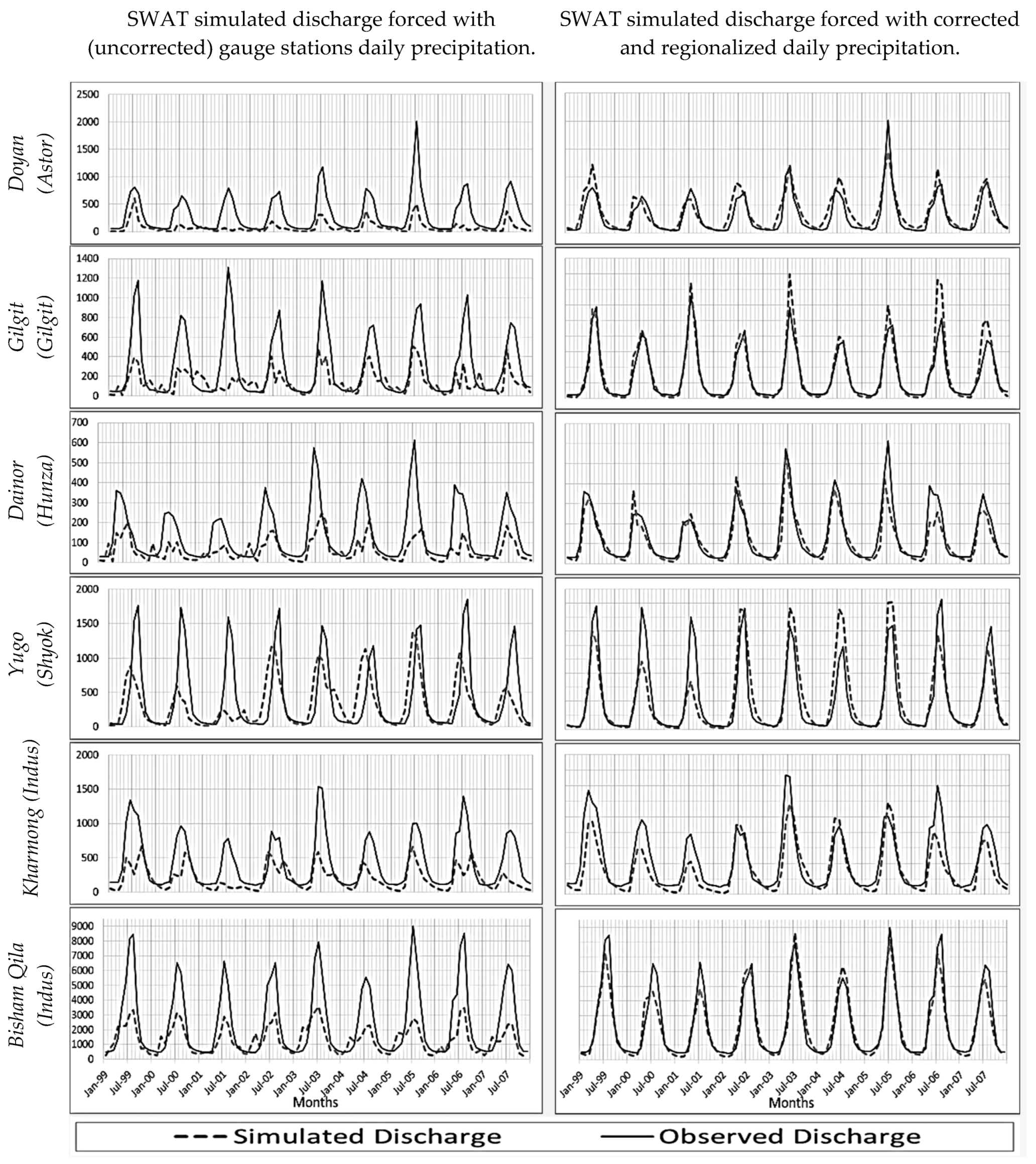
4.3. Validation of the Corrected Precipitation against SWAT-Simulated Discharge
4.4. Merits and Limitation of the Proposed Method and Regionalized Data
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Duncan, M.R.; Austin, B.; Fabry, F.; Austin, G.L. The effect of gauge sampling density on the accuracy of streamflow prediction for rural catchments. J. Hydrol. 1993, 142, 445–476. [Google Scholar] [CrossRef]
- Singh, P.; Jain, S.K.; Kumar, N. Estimation of Snow and Glacier-Melt Contribution to the Chenab River, Western Himalaya. Mt. Res. Dev. 1997, 17, 49. [Google Scholar] [CrossRef]
- Andréassian, V.; Perrin, C.; Michel, C.; Usart-Sanchez, I.; Lavabre, J. Impact of imperfect rainfall knowledge on the efficiency and the parameters of watershed models. J. Hydrol. 2001, 250, 206–223. [Google Scholar] [CrossRef]
- Kobold, M.; Sušelj, K. Precipitation forecasts and their uncertainty as input into hydrological models. Hydrol. Earth Syst. Sci. 2005, 9, 322–332. [Google Scholar] [CrossRef]
- Leander, R.; Buishand, T.A.; van den Hurk, B.J.J.M.; de Wit, M.J.M. Estimated changes in flood quantiles of the river Meuse from resampling of regional climate model output. J. Hydrol. 2008, 351, 331–343. [Google Scholar] [CrossRef]
- Rueland, D.; Larrat, V.; Guinot, V. A Comparison Oftwo Conceptual Models for the Simulation of Hydro-Climatic Variability Over 50 Years in a Large Sudano-Sahelian Catchment; International Association of Hydrological Sciences: Wallingford, UK, 2010. [Google Scholar]
- Moulin, L.; Gaume, E.; Obled, C. Uncertainties on mean areal precipitation: Assessment and impact on streamflow simulations. Hydrol. Earth Syst. Sci. 2009, 13, 99–114. [Google Scholar] [CrossRef]
- Liu, Y.B.; de Smedt, F. WetSpa Extension, A GIS-Based Hydrologic Model for Flood Prediction and Watershed Management: Documentation and User Manual; Vrije Universiteit Brussel: Brussel, Belgium, 2004. [Google Scholar]
- Obled, C.; Wendling, J.; Beven, K. The sensitivity of hydrological models to spatial rainfall patterns: An evaluation using observed data. J. Hydrol. 1994, 159, 305–333. [Google Scholar] [CrossRef]
- Rodda, J.C. Report on precipitation. Int. Assoc. Sci. Hydrol. Bull. 1971, 16, 37–47. [Google Scholar] [CrossRef]
- Yatagai, A.; Kamiguchi, K.; Arakawa, O.; Hamada, A.; Yasutomi, N.; Kitoh, A. APHRODITE: Constructing a Long-Term Daily Gridded Precipitation Dataset for Asia Based on a Dense Network of Rain Gauges. Bull. Am. Meteor. Soc. 2012, 93, 1401–1415. [Google Scholar] [CrossRef]
- Palazzi, E.; Filippi, L.; von Hardenberg, J. Insights into elevation-dependent warming in the Tibetan Plateau-Himalayas from CMIP5 model simulations. Clim. Dyn. 2017, 48, 3991–4008. [Google Scholar] [CrossRef]
- Wijngaard, R.R.; Lutz, A.F.; Nepal, S.; Khanal, S.; Pradhananga, S.; Shrestha, A.B.; Immerzeel, W.W. Future changes in hydro-climatic extremes in the Upper Indus, Ganges, and Brahmaputra River basins. PLoS ONE 2017, 12, e0190224. [Google Scholar] [CrossRef] [PubMed]
- Palazzi, E.; von Hardenberg, J.; Provenzale, A. Precipitation in the Hindu-Kush Karakoram Himalaya: Observations and future scenarios. J. Geophys. Res. Atmos. 2013, 118, 85–100. [Google Scholar] [CrossRef]
- Singh, P.; Kumar, N. Effect of orography on precipitation in the western Himalayan region. J. Hydrol. 1997, 199, 183–206. [Google Scholar] [CrossRef]
- Dhar, O.N.; Rakhecha, P.R. The effect of elevation on monsoon rainfall distribution in the central Himalayas. In Monsoon Dynamics; Lighthill, M.J., Pearce, R.P., Eds.; Cambridge University Press: New York, NY, USA, 1981; pp. 253–260. [Google Scholar]
- Dahri, Z.H.; Ludwig, F.; Moors, E.; Ahmad, B.; Khan, A.; Kabat, P. An appraisal of precipitation distribution in the high-altitude catchments of the Indus basin. Sci. Total Environ. 2016, 548–549, 289–306. [Google Scholar] [CrossRef] [PubMed]
- Pang, H.; Hou, S.; Kaspari, S.; Mayewski, P.A. Influence of regional precipitation patterns on stable isotopes in ice cores from the central Himalayas. Cryosphere 2014, 8, 289–301. [Google Scholar] [CrossRef]
- Hewitt, K. Glacier Change, Concentration, and Elevation Effects in the Karakoram Himalaya, Upper Indus Basin. Mt. Res. Dev. 2011, 31, 188–200. [Google Scholar] [CrossRef]
- Wake, C.P. Glaciochemical Investigations as a Tool for Determining the Spatial and Seasonal Variation of Snow Accumulation in the Central Karakoram, Northern Pakistan. Ann. Glaciol. 1989, 13, 279–284. [Google Scholar] [CrossRef]
- Valéry, A.; Andréassian, V.; Perrin, C. Regionalization of precipitation and air temperature over high-altitude catchments—Learning from outliers. Hydrol. Sci. J. 2010, 55, 928–940. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; Droogers, P.; de Jong, S.M.; Bierkens, M.F.P. Large-scale monitoring of snow cover and runoff simulation in Himalayan river basins using remote sensing. Remote Sens. Environ. 2009, 113, 40–49. [Google Scholar] [CrossRef]
- Lutz, A.F.; Immerzeel, W.W.; Kraaijenbrink, P.D.A.; Shrestha, A.B.; Bierkens, M.F.P. Climate Change Impacts on the Upper Indus Hydrology: Sources, Shifts and Extremes. PLoS ONE 2016, 11, e0165630. [Google Scholar] [CrossRef] [PubMed]
- Ali, K.F.; de Boer, D.H. Spatial patterns and variation of suspended sediment yield in the upper Indus River basin, northern Pakistan. J. Hydrol. 2007, 334, 368–387. [Google Scholar] [CrossRef]
- Internat. Centre for Integrated Mountain Development. The Status of Glaciers in the Hindu Kush-Himalayan Region; Bajracharya, S.R., Shrestha, B., Eds.; International Centre for Integrated Mountain Development: Kathmandu, Nepal, 2011. [Google Scholar]
- RGI Consortium. Randolph Glacier Inventory 5.0. A Dataset of Global Glacier Outlines: Version 5.0; GLIMS Technical Report; Global Land Ice Measurements from Space: Boulder, CO, USA, 2015. [Google Scholar] [CrossRef]
- Tahir, A.A.; Chevallier, P.; Arnaud, Y.; Ahmad, B. Snow cover dynamics and hydrological regime of the Hunza River basin, Karakoram Range, Northern Pakistan. Hydrol. Earth Syst. Sci. 2011, 15, 2275–2290. [Google Scholar] [CrossRef]
- Bookhagen, B.; Burbank, D.W. Topography, relief, and TRMM-derived rainfall variations along the Himalaya. Geophys. Res. Lett. 2006, 33, 21. [Google Scholar] [CrossRef]
- Ali, S.; Li, D.; Congbin, F.; Khan, F. Twenty first century climatic and hydrological changes over Upper Indus Basin of Himalayan region of Pakistan. Environ. Res. Lett. 2015, 10, 14007. [Google Scholar] [CrossRef]
- Hasson, S.U. Future Water Availability from Hindukush-Karakoram-Himalaya upper Indus Basin under Conflicting Climate Change Scenarios. Climate 2016, 4, 40. [Google Scholar] [CrossRef]
- Karim, A.; Veizer, J. Water balance of the Indus River Basin and moisture source in the Karakoram and western Himalayas: Implications from hydrogen and oxygen isotopes in river water. J. Geophys. Res. 2002, 107, 190. [Google Scholar] [CrossRef]
- Hewitt, K. Tributary glacier surges: An exceptional concentration at Panmah Glacier, Karakoram Himalaya. J. Glaciol. 2007, 53, 181–188. [Google Scholar] [CrossRef]
- Archer, D. Contrasting hydrological regimes in the upper Indus Basin. J. Hydrol. 2003, 274, 198–210. [Google Scholar] [CrossRef]
- Khan, F.; Pilz, J.; Amjad, M.; Wiberg, D.A. Climate variability and its impacts on water resources in the Upper Indus Basin under IPCC climate change scenarios. IJGW 2015, 8, 46. [Google Scholar] [CrossRef]
- Khan, F.; Pilz, J.; Ali, S. Improved hydrological projections and reservoir management in the Upper Indus Basin under the changing climate. Water Environ. J. 2017, 31, 235–244. [Google Scholar] [CrossRef]
- Kirchner, J.W. Catchments as simple dynamical systems: Catchment characterization, rainfall-runoff modeling, and doing hydrology backward. Water Resour. Res. 2009, 45, 2135. [Google Scholar] [CrossRef]
- Teuling, A.J.; Lehner, I.; Kirchner, J.W.; Seneviratne, S.I. Catchments as simple dynamical systems: Experience from a Swiss prealpine catchment. Water Resour. Res. 2010, 46, 305. [Google Scholar] [CrossRef]
- Creutin, J.D.; Delrieu, G.; Lebel, T. Rain Measurement by Raingage-Radar Combination: A Geostatistical Approach. J. Atmos. Ocean. Technol. 1988, 5, 102–115. [Google Scholar] [CrossRef]
- Beek, E.G.; Stein, A.; Janssen, L.L.F. Spatial variability and interpolation of daily precipitation amount. Stoch. Hydrol. Hydraul. 1992, 6, 304–320. [Google Scholar] [CrossRef]
- Kurtzman, D.; Kadmon, R. Mapping of temperature variables in Israel: A comparison of different interpolation methods. Clim. Res. 1999, 13, 33–43. [Google Scholar] [CrossRef]
- Shen, S.S.P.; Dzikowski, P.; Li, G.; Griffith, D. Interpolation of 1961–1997 Daily Temperature and Precipitation Data onto Alberta Polygons of Ecodistrict and Soil Landscapes of Canada. J. Appl. Meteor. 2001, 40, 2162–2177. [Google Scholar] [CrossRef]
- Kyriakidis, P.C.; Kim, J.; Miller, N.L. Geostatistical Mapping of Precipitation from Rain Gauge Data Using Atmospheric and Terrain Characteristics. J. Appl. Meteor. 2001, 40, 1855–1877. [Google Scholar] [CrossRef]
- Buytaert, W.; Celleri, R.; Willems, P.; Bièvre, B.D.; Wyseure, G. Spatial and temporal rainfall variability in mountainous areas: A case study from the south Ecuadorian Andes. J. Hydrol. 2006, 329, 413–421. [Google Scholar] [CrossRef]
- Stahl, K.; Moore, R.D.; Floyer, J.A.; Asplin, M.G.; McKendry, I.G. Comparison of approaches for spatial interpolation of daily air temperature in a large region with complex topography and highly variable station density. Agric. For. Meteorol. 2006, 139, 224–236. [Google Scholar] [CrossRef]
- Daly, C. Guidelines for assessing the suitability of spatial climate data sets. Int. J. Climatol. 2006, 26, 707–721. [Google Scholar] [CrossRef]
- Schuurmans, J.M.; Bierkens, M.F.P. Effect of spatial distribution of daily rainfall on interior catchment response of a distributed hydrological model. Hydrol. Earth Syst. Sci. 2007, 11, 677–693. [Google Scholar] [CrossRef]
- Carrera-Hernández, J.J.; Gaskin, S.J. Spatio temporal analysis of daily precipitation and temperature in the Basin of Mexico. J. Hydrol. 2007, 336, 231–249. [Google Scholar] [CrossRef]
- Caruso, C.; Quarta, F. Interpolation methods comparison. Comput. Math. Appl. 1998, 35, 109–126. [Google Scholar] [CrossRef]
- Lanza, L.G.; Ramírez, J.A.; Todini, E. Stochastic rainfall interpolation and downscaling. Hydrol. Earth Syst. Sci. 2001, 5, 139–143. [Google Scholar] [CrossRef]
- New, M.; Todd, M.; Hulme, M.; Jones, P. Precipitation measurements and trends in the twentieth century. Int. J. Climatol. 2001, 21, 1889–1922. [Google Scholar] [CrossRef]
- Xia, Y.; Winterhalter, M.; Fabian, P. A Model to Interpolate Monthly Mean Climatological Data at Bavarian Forest Climate Stations. Theor. Appl. Climatol. 1999, 64, 27–38. [Google Scholar] [CrossRef]
- Tabony, R.C. The estimation of missing climatological data. J. Climatol. 1983, 3, 297–314. [Google Scholar] [CrossRef]
- Wallis, J.R.; Lettenmaier, D.P.; Wood, E.F. A daily hydroclimatological data set for the continental United States. Water Resour. Res. 1991, 27, 1657–1663. [Google Scholar] [CrossRef]
- Luo, W.; Taylor, M.C.; Parker, S.R. A comparison of spatial interpolation methods to estimate continuous wind speed surfaces using irregularly distributed data from England and Wales. Int. J. Climatol. 2008, 28, 947–959. [Google Scholar] [CrossRef]
- Huth, R.; Nemesová, I. Estimation of Missing Daily Temperatures: Can a Weather Categorization Improve Its Accuracy? J. Clim. 1995, 8, 1901–1916. [Google Scholar] [CrossRef]
- DeGaetano, A.T.; Eggleston, K.L.; Knapp, W.W. A Method to Estimate Missing Daily Maximum and Minimum Temperature Observations. J. Appl. Meteor. 1995, 34, 371–380. [Google Scholar] [CrossRef]
- Cressie, N.A.C. Statistics for Spatial Data; John Wiley & Sons, Inc: Hoboken, NJ, USA, 1993. [Google Scholar]
- Goovaerts, P. Geostatistics for Natural Resources Evaluation; Oxford University Press: New York, NY, USA; Oxford, UK, 1997. [Google Scholar]
- Goovaerts, P. Geostatistical approaches for incorporating elevation into the spatial interpolation of rainfall. J. Hydrol. 2000, 228, 113–129. [Google Scholar] [CrossRef]
- Boer, E.P.J.; de Beurs, K.M.; Hartkamp, A.D. Kriging and thin plate splines for mapping climate variables. Int. J. Appl. Earth Observ. Geoinf. 2001, 3, 146–154. [Google Scholar] [CrossRef]
- Webster, R.; Oliver, M.A. Geostatistics for Environmental Scientists; John Wiley & Sons, Ltd.: Chichester, UK, 2007. [Google Scholar]
- Chiles, J.-P. Geostatistics. Modeling Spatial Uncertainty/Jean-Paul Chiles, 2nd ed.; Wiley-Blackwell: Oxford, UK, 2012. [Google Scholar]
- Bussières, N.; Hogg, W. The objective analysis of daily rainfall by distance weighting schemes on a Mesoscale grid. Atmos.-Ocean. 1989, 27, 521–541. [Google Scholar] [CrossRef]
- Eckstein, B.A. Evaluation of spline and weighted average interpolation algorithms. Comput. Geosci. 1989, 15, 79–94. [Google Scholar] [CrossRef]
- Hutchinson, M.F.; Gessler, P.E. Splines—More than just a smooth interpolator. Geoderma 1994, 62, 45–67. [Google Scholar] [CrossRef]
- Luo, Z.; Wahba, G.; Johnson, D.R. Spatial–Temporal Analysis of Temperature Using Smoothing Spline ANOVA. J. Clim. 1998, 11, 18–28. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Saz-Sánchez, M.A.; Cuadrat, J.M. Comparative analysis of interpolation methods in the middle Ebro Valley (Spain): Application to annual precipitation and temperature. Clim. Res. 2003, 24, 161–180. [Google Scholar] [CrossRef]
- Sluiter, R. Interpolation Methods for Climate Data—Literature Review. KNMI Intern Rapport; Intern Rapport; IR 2009-04: De Bilt, The Netherlands, 2009; Available online: https://www.snap.uaf.edu/attachments/Interpolation_methods_for_climate_data.pdf (accessed on 5 February 2018).
- Szentimrey, T.; Bihari, Z.; Szalai, S. Meteorological Interpolation Based on Surface Homogenized Data Basis (MISH); European Geosciences Union, General Assembly: Vienna, Austria, 2005; Available online: https://www.snap.uaf.edu/attachments/Interpolation_methods_for_climate_data.pdf (accessed on 5 February 2018).
- Krier, R.; Matgen, P.; Goergen, K.; Pfister, L.; Hoffmann, L.; Kirchner, J.W.; Uhlenbrook, S.; Savenije, H.H.G. Inferring catchment precipitation by doing hydrology backward: A test in 24 small and mesoscale catchments in Luxembourg. Water Resour. Res. 2012, 48, 225. [Google Scholar] [CrossRef]
- Weingartner, R.; Viviroli, D.; Schädler, B. Water resources in mountain regions: A methodological approach to assess the water balance in a highland-lowland-system. Hydrol. Process. 2007, 21, 578–585. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; Wanders, N.; Lutz, A.F.; Shea, J.M.; Bierkens, M.F.P. Reconciling high-altitude precipitation in the upper Indus basin with glacier mass balances and runoff. Hydrol. Earth Syst. Sci. 2015, 19, 4673–4687. [Google Scholar] [CrossRef]
- Isaaks, E.H.; Srivastava, R.M. Applied Geostatistics; OUP: New York, NY, USA, 1989. [Google Scholar]
- Schädler, B.; Weingartner, R. Ein detaillierter hydrologischer Blick auf die Wasserresourcen der Schweiz. Wasser Energ. Luft, Schweizerischer Wasserwirtschaftsverband 2002, 94, 189–197. [Google Scholar]
- Ranzi, R.; Bacchi, B.; Grossi, G. Runoff measurements and hydrological modelling for the estimation of rainfall volumes in an Alpine basin. Q. J. R. Meteorol. Soc. 2003, 129, 653–672. [Google Scholar] [CrossRef]
- Kling, H.; Nachtnebel, H.P.; Fürst, J. Mean Annual Precipitation from the Water Balance—Mean annual areal precipitation using water balance data. In Federal Ministry of Agriculture, Forestry, Environment and Water Management, Vienna, Hydrological Atlas Austria, 2nd delivery, Map 2.3; Austrian Art and Culture Publisher: Vienna, Austria, 2003; ISBN 3-85437-250-7. [Google Scholar]
- Valéry, A.; Andréassian, V.; Perrin, C. Inverting the hydrological cycle: When streamflow measurements help assess altitudinal precipitation gradients in mountain areas. IAHS Publ. 2009, 333, 281–286. [Google Scholar]
- Ma, Y.; Zhang, Y.; Yang, D.; Farhan, S.B. Precipitation bias variability versus various gauges under different climatic conditions over the Third Pole Environment (TPE) region. Int. J. Climatol. 2015, 35, 1201–1211. [Google Scholar] [CrossRef]
- Yang, D.; Goodison, B.E.; Ishida, S.; Benson, C.S. Adjustment of daily precipitation data at 10 climate stations in Alaska: Application of World Meteorological Organization intercomparison results. Water Resour. Res. 1998, 34, 241–256. [Google Scholar] [CrossRef]
- Mark, B.G.; Seltzer, G.O. Tropical glacier meltwater contribution to stream discharge: A case study in the Cordillera Blanca, Peru. J. Glaciol. 2003, 49, 271–281. [Google Scholar] [CrossRef]
- Archer, D.R.; Fowler, H.J. Spatial and temporal variations in precipitation in the Upper Indus Basin, global teleconnections and hydrological implications. Hydrol. Earth Syst. Sci. 2004, 8, 47–61. [Google Scholar] [CrossRef]
- Tahir, A.A.; Adamowski, J.F.; Chevallier, P.; Haq, A.U.; Terzago, S. Comparative assessment of spatiotemporal snow cover changes and hydrological behavior of the Gilgit, Astore and Hunza River basins (Hindukush–Karakoram–Himalaya region, Pakistan). Meteorol. Atmos. Phys. 2016, 128, 793–811. [Google Scholar] [CrossRef]
- Gardelle, J.; Berthier, E.; Arnaud, Y.; Kääb, A. Region-wide glacier mass balances over the Pamir-Karakoram-Himalaya during 1999–2011. Cryosphere 2013, 7, 1263–1286. [Google Scholar] [CrossRef]
- Kääb, A.; Berthier, E.; Nuth, C.; Gardelle, J.; Arnaud, Y. Contrasting patterns of early twenty-first-century glacier mass change in the Himalayas. Nature 2012, 488, 495–498. [Google Scholar] [CrossRef] [PubMed]
- Paul, F. Revealing glacier flow and surge dynamics from animated satellite image sequences: Examples from the Karakoram. Cryosphere 2015, 9, 2201–2214. [Google Scholar] [CrossRef]
- Rankl, M.; Kienholz, C.; Braun, M.H. Glacier changes in the Karakoram region mapped by multimission satellite imagery, links to GeoTIFF and ESRI shape file, supplement to: Rankl, Melanie; Kienholz, Christian; Braun, Matthias Holger (2014): Glacier changes in the Karakoram region mapped by multimission satellite imagery. Cryosphere 2014, 8, 977–989. [Google Scholar]
- Scherler, D.; Bookhagen, B.; Strecker, M.R. Spatially variable response of Himalayan glaciers to climate change affected by debris cover. Nat. Geosci. 2011, 4, 156–159. [Google Scholar] [CrossRef]
- Gurung, D.R. Snow-Cover Mapping and Monitoring in the Hindu Kush-Himalayas; International Centre for Integrated Mountain Development: Kathmandu, Nepal, 2011. [Google Scholar]
- ICIMOD-HKH Snow Cover-WebApp. Historic Changes in Snow Cover in the HKH Region. Available online: http://geoapps.icimod.org/HKHSnowCover/ (accessed on 4 April 2018).
- Zhang, Y.; Leuning, R.; Hutley, L.B.; Beringer, J.; McHugh, I.; Walker, J.P. Using long-term water balances to parameterize surface conductances and calculate evaporation at 0.05° spatial resolution. Water Resour. Res. 2010, 46, 333. [Google Scholar] [CrossRef]
- Pelgrum, H.; Miltenburg, I.; Cheema, M.; Klaasse, A.; Bastiaanssen, W. ET Look: A novel continental evapotranspiration algorithm. Remote Sens. Hydrol. 2010, 10875, 1087. [Google Scholar]
- Zeng, Z.; Piao, S.; Lin, X.; Yin, G.; Peng, S.; Ciais, P.; Myneni, R.B. Global evapotranspiration over the past three decades: Estimation based on the water balance equation combined with empirical models. Environ. Res. Lett. 2012, 7, 14026. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Cheema, M.J.M.; Immerzeel, W.W.; Miltenburg, I.J.; Pelgrum, H. Surface energy balance and actual evapotranspiration of the transboundary Indus Basin estimated from satellite measurements and the ETLook model. Water Resour. Res. 2012, 48, 227. [Google Scholar] [CrossRef]
- Cherif, I.; Alexandridis, T.K.; Jauch, E.; Chambel-Leitao, P.; Almeida, C. Improving remotely sensed actual evapotranspiration estimation with raster meteorological data. Int. J. Remote Sens. 2015, 36, 4606–4620. [Google Scholar] [CrossRef]
- Fekete, B.M.; Vörösmarty, C.J.; Grabs, W. High-resolution fields of global runoff combining observed river discharge and simulated water balances. Glob. Biogeochem. Cycles 2002, 16. [Google Scholar] [CrossRef]
- Bookhagen, B.; Burbank, D.W. Toward a complete Himalayan hydrological budget: Spatiotemporal distribution of snowmelt and rainfall and their impact on river discharge. J. Geophys. Res. 2010, 115, 39. [Google Scholar] [CrossRef]
- Garee, K.; Chen, X.; Bao, A.; Wang, Y.; Meng, F. Hydrological Modeling of the Upper Indus Basin: A Case Study from a High-Altitude Glacierized Catchment Hunza. Water 2017, 9, 17. [Google Scholar] [CrossRef]
- Esri. Average Annual Actual Evapotranspiration in mm/year. Built Using “MOD16 Global Evapotranspiration Product”. Available online: http://www.arcgis.com/home/item.html?id=31f7c3727abf42249a43fe8f25470af4 (accessed on 4 March 2018).
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large Area Hydrologic Modeling and Assessment Part I: Model Development. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Srinivasan, R.; Ramanarayanan, T.S.; Arnold, J.G.; Bednarz, S.T. Large Area Hydrologic Modeling and Assessment Part II: Model Application. J. Am. Water Resour. Assoc. 1998, 34, 91–101. [Google Scholar] [CrossRef]
- Lehner, B.; Verdin, K.; Jarvis, A. New Global Hydrography Derived from Spaceborne Elevation Data. Eos Trans. AGU 2008, 89, 93. [Google Scholar] [CrossRef]
- FAO-UNESCO. FAO-UNESCO Soil Map of the World, Version 3.6; FAO Geonetwork; Food and Agriculture Organization of the United Nations: Rome, Italy, 2007. [Google Scholar]
- USGS EROS Data Center. GLCC—Global Land Cover Characteristics Data Base, Version 2.0; USGS, Earth Resources Observation and Science (EROS) Center: Sioux Falls, SD, USA, 2002.
- Abbaspour, K.C.; Yang, J.; Maximov, I.; Siber, R.; Bogner, K.; Mieleitner, J.; Zobrist, J.; Srinivasan, R. Modelling hydrology and water quality in the pre-alpine/alpine Thur watershed using SWAT. J. Hydrol. 2007, 333, 413–430. [Google Scholar] [CrossRef]

| Description | S. No. | Station Name | Latitude (°N) | Longitude (°E) | Altitude (m) |
|---|---|---|---|---|---|
| High Altitude (2367–4440 m.a.s.l.) stations operated by Water and Power Development Authority, Pakistan (WAPDA) | 1 | Burzil | 34.916 | 75.90 | 4030 |
| 2 | Deosai | 35.09 | 75.54 | 4149 | |
| 3 | Hushe | 35.42 | 76.37 | 3075 | |
| 4 | Khot Pass | 36.52 | 72.58 | 3505 | |
| 5 | Khunjrab | 36.84 | 75.42 | 4440 | |
| 6 | Naltar | 36.17 | 74.18 | 2898 | |
| 7 | Ramma | 35.36 | 74.81 | 3179 | |
| 8 | Rattu | 35.15 | 74.8 | 2718 | |
| 9 | Shendoor | 36.09 | 72.55 | 3712 | |
| 10 | Shigar | 35.63 | 75.53 | 2367 | |
| 11 | Ushkore | 36.05 | 73.39 | 3051 | |
| 12 | Yasin | 36.45 | 73.3 | 3350 | |
| 13 | Zani | 36.33 | 72.17 | 3895 | |
| 14 | Ziarat | 36.77 | 74.46 | 3020 | |
| Low Altitude Stations (1250–2210 m.a.s.l) operated by Pakistan Meteorological Department (PMD) | 15 | Chillas | 35.42 | 74.10 | 1250 |
| 16 | Astore | 35.37 | 74.90 | 2168 | |
| 17 | Bunji | 35.67 | 74.63 | 1372 | |
| 18 | Gilgit | 35.92 | 74.33 | 1460 | |
| 19 | Gupis | 36.17 | 73.40 | 2156 | |
| 20 | Skardu | 35.3 | 75.68 | 2210 |
| S. No. | River/Tributary | Station | Area (km2) | Mean Discharge | Elevation (m.a.s.l) | Duration (Years) | |
|---|---|---|---|---|---|---|---|
| (m3/s) | mm/year | ||||||
| 1 | Astore River | Doyan | 3906 | 138 | 1115 | 1580 | 1999–2008 |
| 2 | Gilgit River | Gilgit | 12,778 | 303 | 748 | 1430 | 1999–2008 |
| 3 | Hunza River | Dainyor | 13,761 | 294 | 674 | 1420 | 1999–2008 |
| 4 | Shigar River | Shigar | 6934 | 200 | 937 | 2220 | 2001 |
| 5 | Indus River * | Kachura | 113,745 | 1151 | 319 | 2180 | 1999–2008 |
| 6 | Shyok River | Yugo | 32,935 | 410 | 393 | 2460 | 1999–2007 |
| 7 | Indus River | Kharmang | 70,882 | 460 | 205 | 2500 | 1999–2007 |
| 8 | Indus River | Besham Qila | 165,611 | 2425 | 462 | 600 | 1999–2008 |
| Variable | Snow | Mixed | Rain |
|---|---|---|---|
| ΔPw | 0.15 | 0.15 | 0.20 |
| ΔPe | 0.10 | 0.30 | 0.30 |
| ΔPt | 0.10 | 0.10 | 0.10 |
| CR | 100/1.13 | 100/1.05 | |
| Zone | Brun et al. (2017) | Kääb et al. (2015) | Gardelle et al. (2013) | Kääb et al. (2012) |
|---|---|---|---|---|
| * mwe year−1 | mwe year−1 | mwe year−1 | mwe year−1 | |
| (2003–2008) | (2000–2016) | (1999–2008 a/10 b) | (2003–2008) | |
| Karakoram | −0.09 ± 0.12 | −0.03 ± 0.14 | +0.11 ± 0.14 (east) b +0.09 ± 0.18 (west) a | −0.03 ± 0.04 |
| Hindu Kush | −0.42 ± 0.18 | −0.12 ± 0.14 | +0.12 ± 0.14 | −0.20 ± 0.06 |
| Spiti–Lahaul (Western Himalayas) | −0.42 ± 0.26 | −0.37 ± 0.15 | +0.45 ± 0.14 | −0.38 ± 0.06 |
| S. No. | Catchment | Area (km2) | Glacier Cover (%) | Elevation (m.a.s.l.) | 1 Δg mwe year−1 | Δg mm year−1 | 2ET mm year–1 |
|---|---|---|---|---|---|---|---|
| 1 | Astore River | 3906 | 13.5 | ~4200 | 0 | 0 | 139 |
| 2 | Gilgit River | 12,778 | 6.4 | ~4016 | +0.09 | 5.85 | 120 |
| 3 | Hunza River | 13,761 | 27.7 | ~4646 | +0.09 | 24.99 | 96 |
| 4 | Shigar River | 6934 | 30.4 | ~4900 | +0.09 | 27.27 | 30 |
| 7 | Indus Main ** | 24,260 | 6.9 | ~3150 | 0 | 0 | 197 |
| 5 | Shyok River | 32,928 | 23.6 | ~4993 | +0.11 | 25.96 | 40 |
| 6 | Kharmong * | 70,882 | 3.7 | ~4690 | −0.45 | −16.82 | 123 |
| 8 | Whole UIB | 165,611 | 11.7 | ~3676 | +0.07 | 7.87 | 137 |
| Catchment | Mean Discharge Qt mm year−1 | Change in Glacier Storage Δg mm year−1 | Actual Evapo-Transpiration ET mm year−1 | True Precipitation mm year−1 |
|---|---|---|---|---|
| Astore River | 1115 | 0 | 139 | 1254 |
| Gilgit River | 748 | 5.85 | 120 | 874 |
| Hunza River | 674 | 24.99 | 96 | 795 |
| Shigar River | 937 | 27.27 | 30 | 994 |
| Indus Main ** | 623 | 0 | 197 | 820 |
| Shyok River | 391 | 25.96 | 40 | 456 |
| Kharmong * | 205 | −16.82 | 123 | 312 |
| Whole UIB | 462 | 7.87 | 137 | 608 |
| Catchment | Mean annual Precipitation | OCFplapse c per 1000 m Elev. (Corrected Observed) | OCFmultiplicative a Raw Observed/APHRODITE | OCFmultiplicative b (Corrected–Observed) | ||
|---|---|---|---|---|---|---|
| Raw Observed/APHRODITE + | Corrected ++ Observed | True +++ (Estimated) | ||||
| (mm) | (mm) | (mm) | (mm/km) | (multipl) | (multipl) | |
| Astor | 581 | 788 | 1254 | 300 | 2.16 | 1.59 |
| Gilgit | 265 | 473 | 874 | 620 | 3.30 | 1.85 |
| Hunza | 360 | 493 | 795 | 320 | 2.21 | 1.61 |
| Shigar | 341 | 509 | 938 | 190 | 2.75 | 1.84 |
| Indus Main ** | 343 | 481 | 820 | 380 | 2.39 | 1.71 |
| Shyok | 140 | -- | 456 | -- | 3.25 | -- |
| Kharmong * | 221 | -- | 360 | -- | 1.63 | -- |
| UIB (whole) | 367 | 544 | 608 | -- | 1.66 | 1.12 |
| Goodness of Fit | SWAT-Simulated Discharge for Uncorrected Gauge Station Precipitation | SWAT-Simulated Discharge for Corrected and Regionalized Precipitation | |||||
|---|---|---|---|---|---|---|---|
| Indices | |||||||
| Gauge station (River) | R2 | NS | PBIAS | R2 | NS | PBIAS | |
| Doyan (Astor) | 0.45 | 0.07 | −54.68 | 0.77 | 0.76 | 12.40 | |
| Gilgit (Gilgit) | 0.60 | 0.03 | −72.87 | 0.77 | 0.76 | −12.80 | |
| Dainor (Hunza) | 0.39 | 0.19 | −49.47 | 0.88 | 0.86 | −0.50 | |
| Shigar (Shigar) | 0.11 | −0.43 | −40.28 | 0.75 | 0.73 | 2.30 | |
| Kachura (Indus) | 0.27 | −0.05 | −37.12 | 0.78 | 0.78 | 5.10 | |
| Shatyal (Indus) | 0.78 | 0.44 | −41.75 | 0.89 | 0.89 | 3.10 | |
| Yugo (Shyok) | 0.27 | 0.22 | −19.43 | 0.69 | 0.69 | −5.60 | |
| Kharmang (Indus) | 0.42 | 0.06 | −51.66 | 0.75 | 0.70 | 19.70 | |
| Bisham Qila (Indus) | 0.77 | 0.41 | −45.36 | 0.86 | 0.85 | 4.70 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, A.J.; Koch, M. Correction and Informed Regionalization of Precipitation Data in a High Mountainous Region (Upper Indus Basin) and Its Effect on SWAT-Modelled Discharge. Water 2018, 10, 1557. https://doi.org/10.3390/w10111557
Khan AJ, Koch M. Correction and Informed Regionalization of Precipitation Data in a High Mountainous Region (Upper Indus Basin) and Its Effect on SWAT-Modelled Discharge. Water. 2018; 10(11):1557. https://doi.org/10.3390/w10111557
Chicago/Turabian StyleKhan, Asim Jahangir, and Manfred Koch. 2018. "Correction and Informed Regionalization of Precipitation Data in a High Mountainous Region (Upper Indus Basin) and Its Effect on SWAT-Modelled Discharge" Water 10, no. 11: 1557. https://doi.org/10.3390/w10111557
APA StyleKhan, A. J., & Koch, M. (2018). Correction and Informed Regionalization of Precipitation Data in a High Mountainous Region (Upper Indus Basin) and Its Effect on SWAT-Modelled Discharge. Water, 10(11), 1557. https://doi.org/10.3390/w10111557