Migration of Gyrotactic Micro-Organisms in Water
Abstract
1. Introduction
2. Materials and Methods
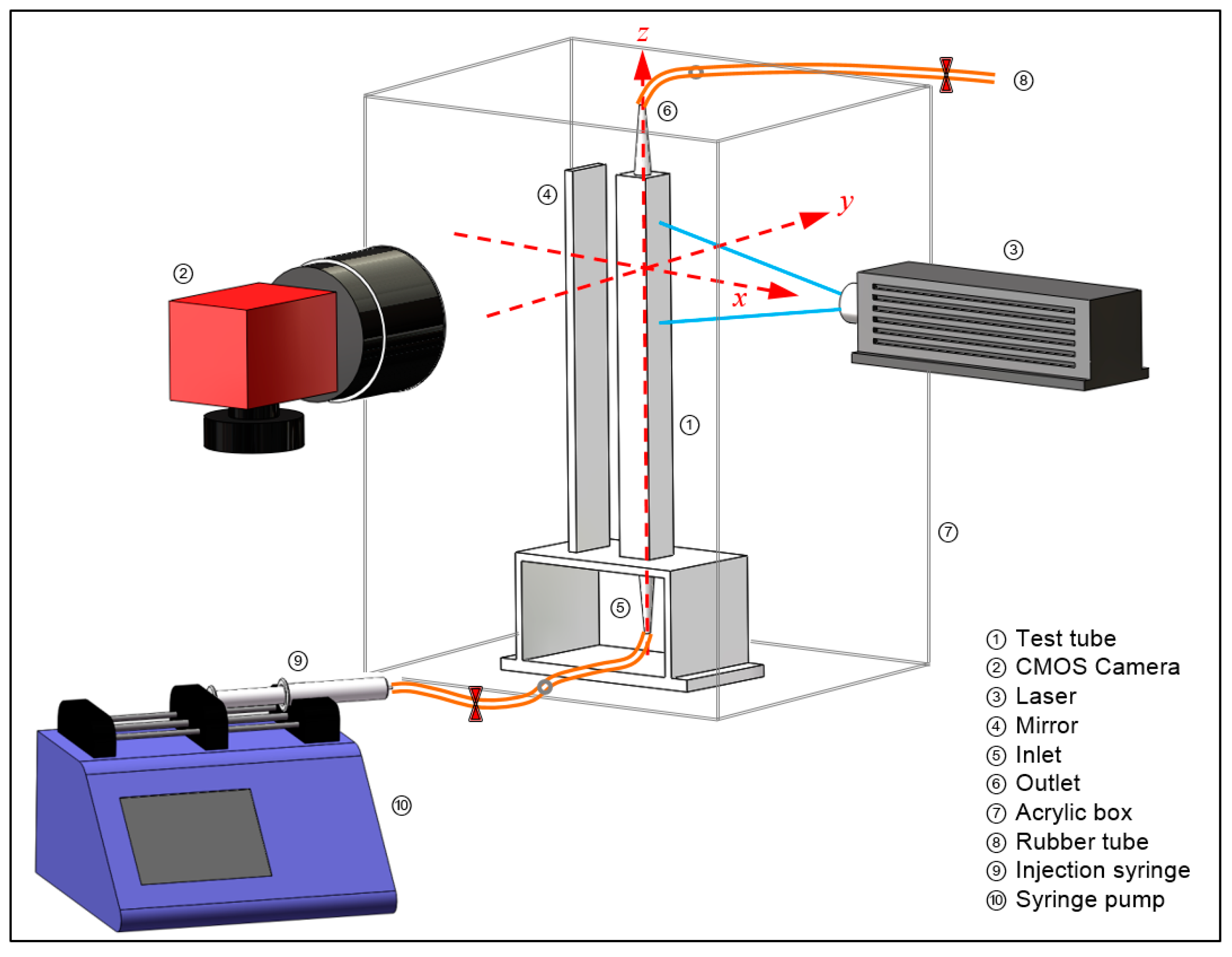
2.1. Experimental Setup
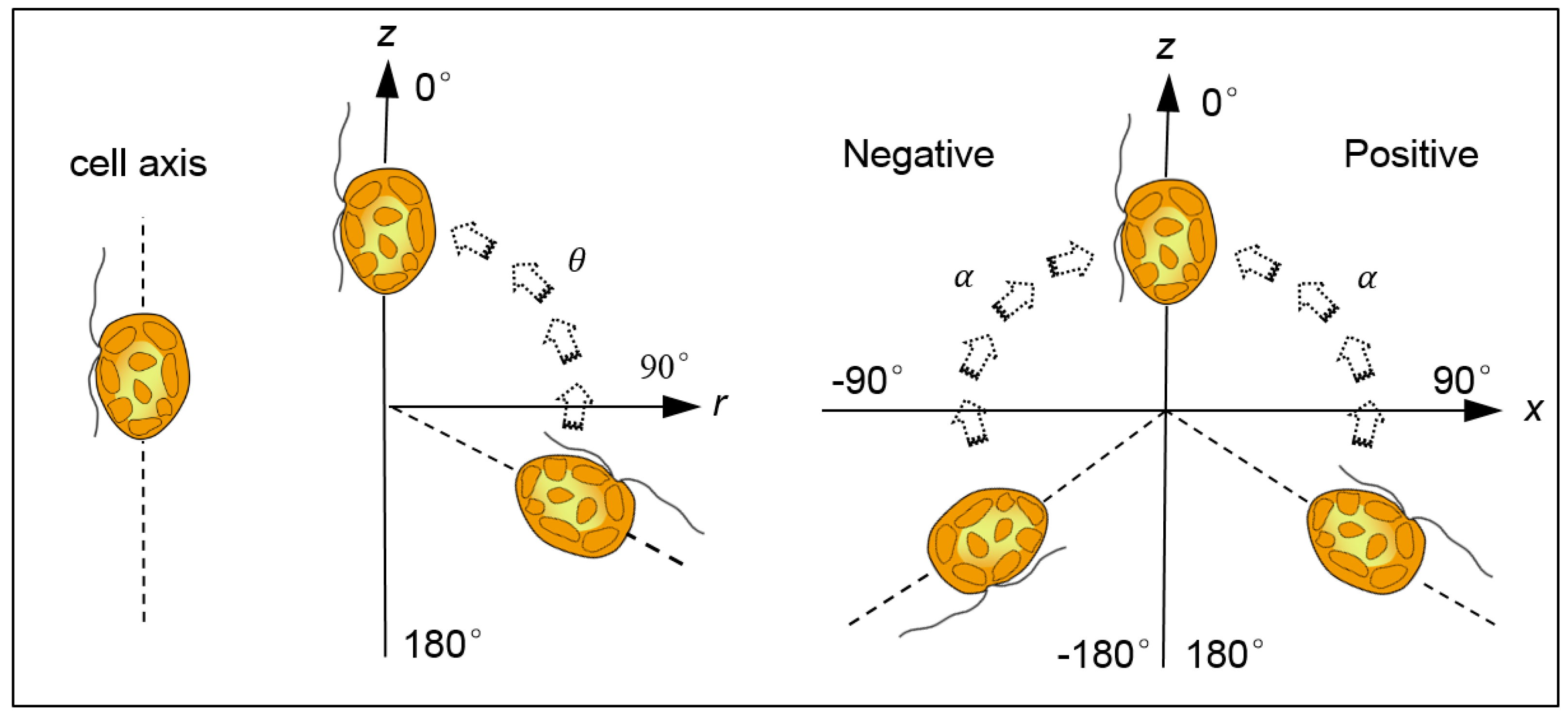
2.2. Image Processing and Analysis Methods
2.3. Fokker-Planck Model
3. Results
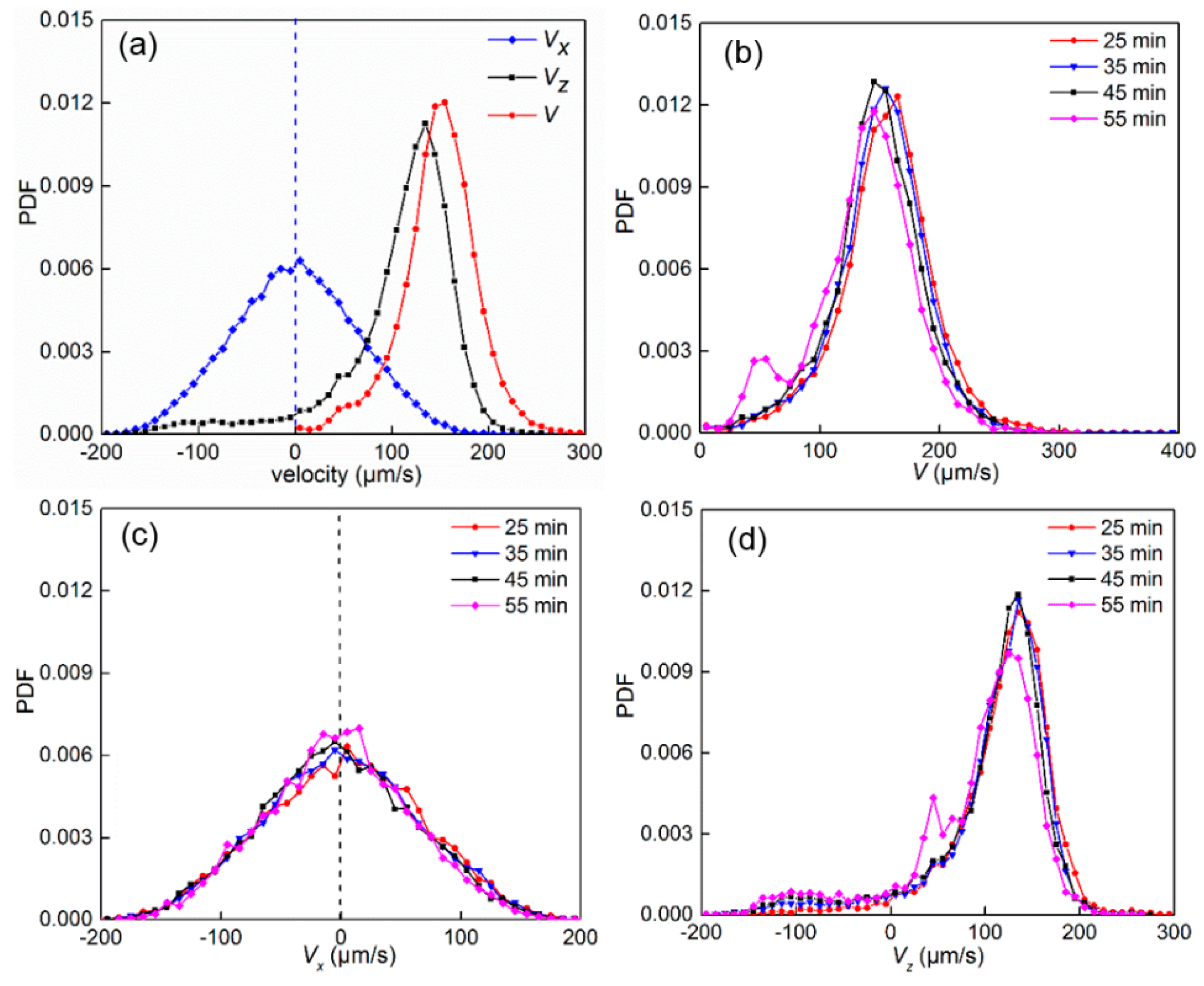
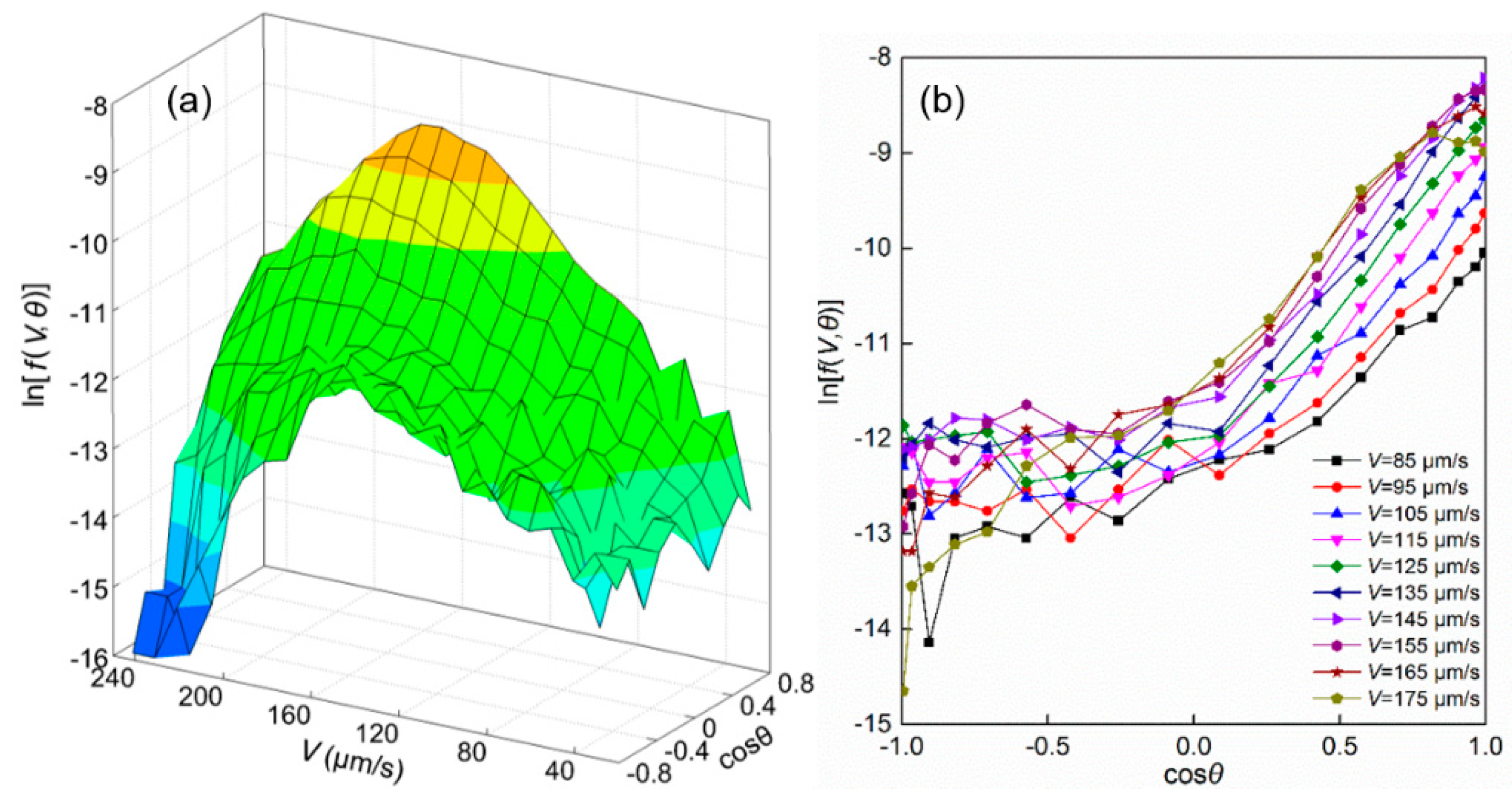
3.1. Swimming Velocity and Direction Distribution
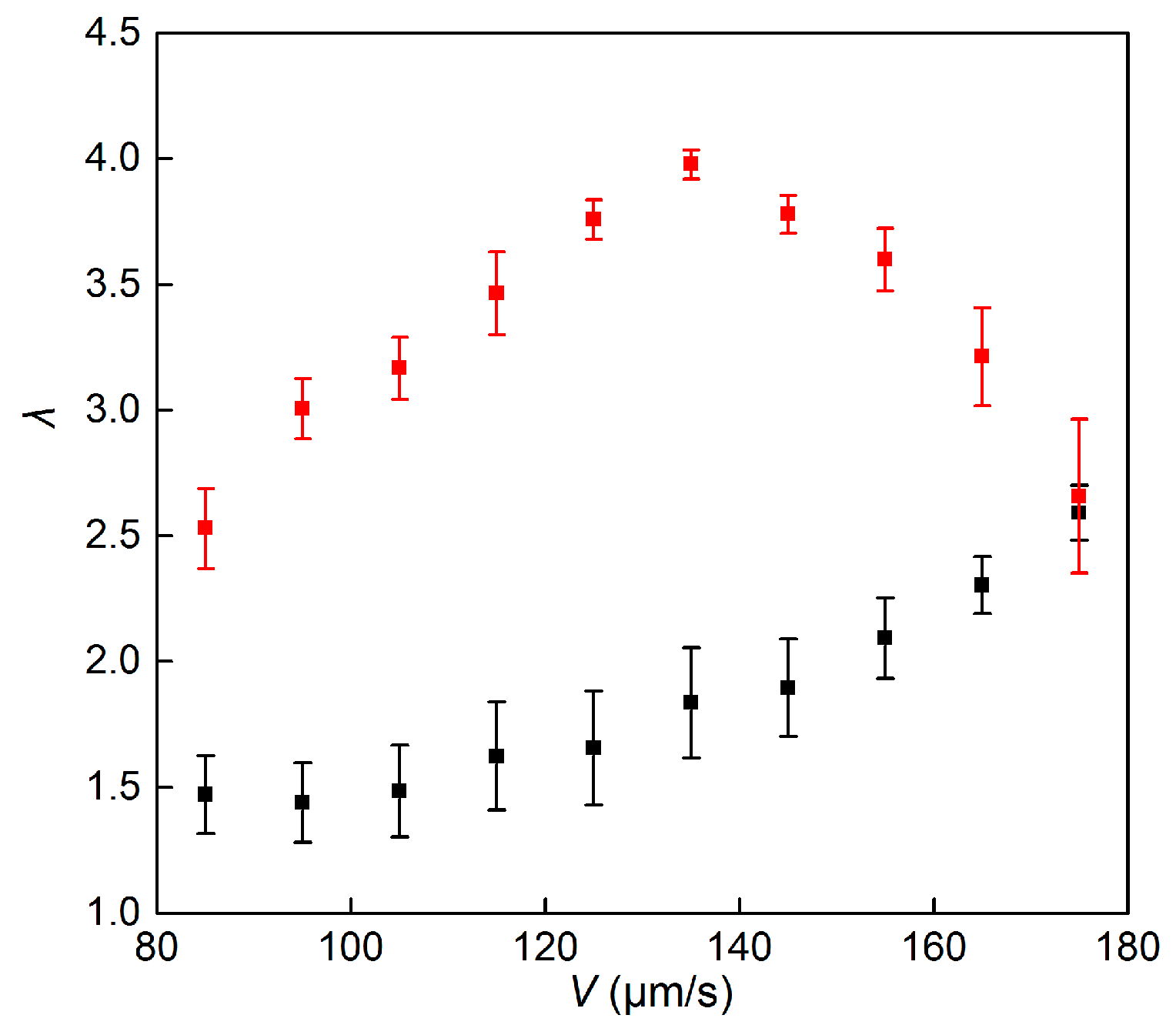
3.2. Relative Strength of Reorientation by Gravitational Torque to Rotational Diffusion
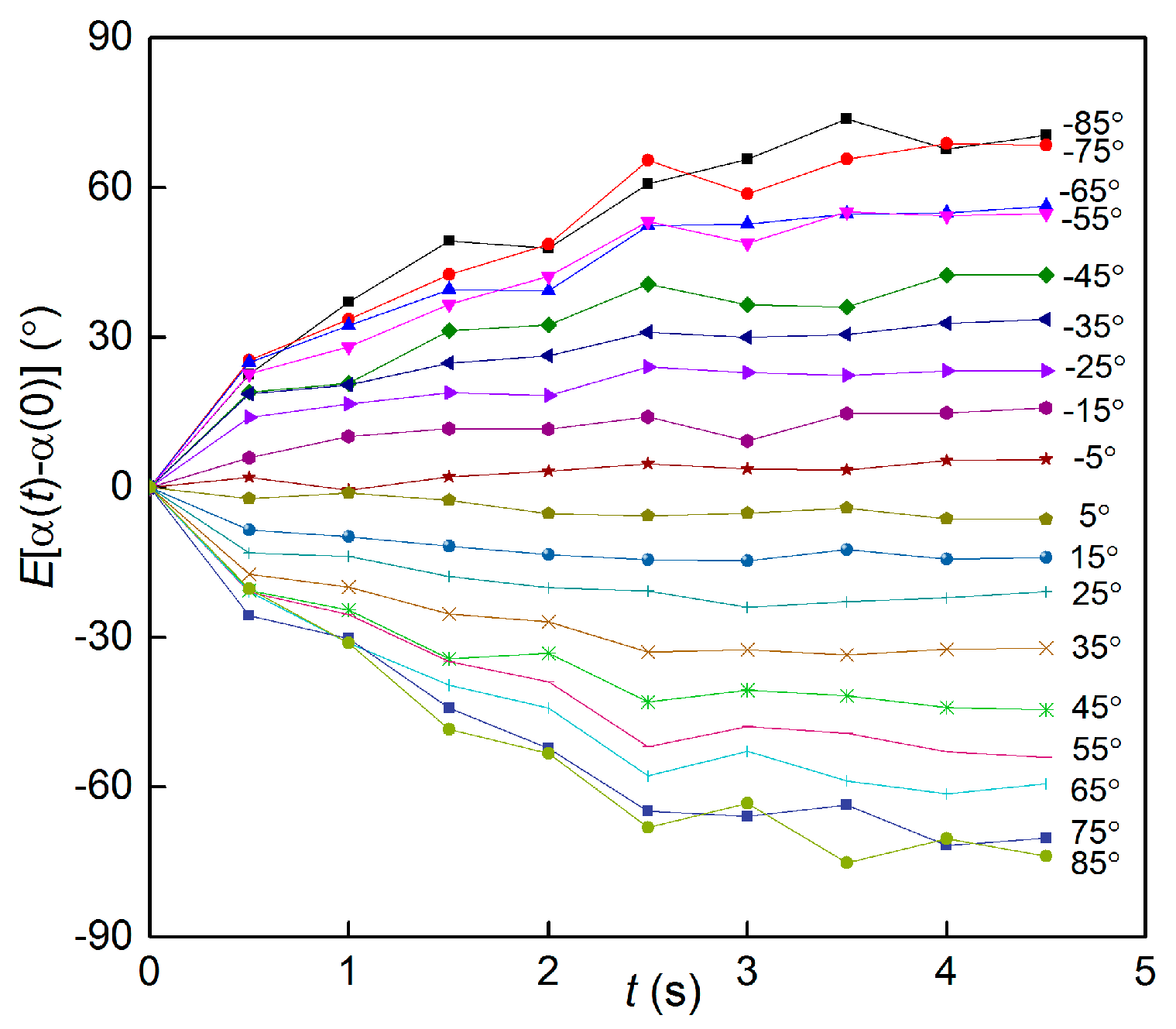
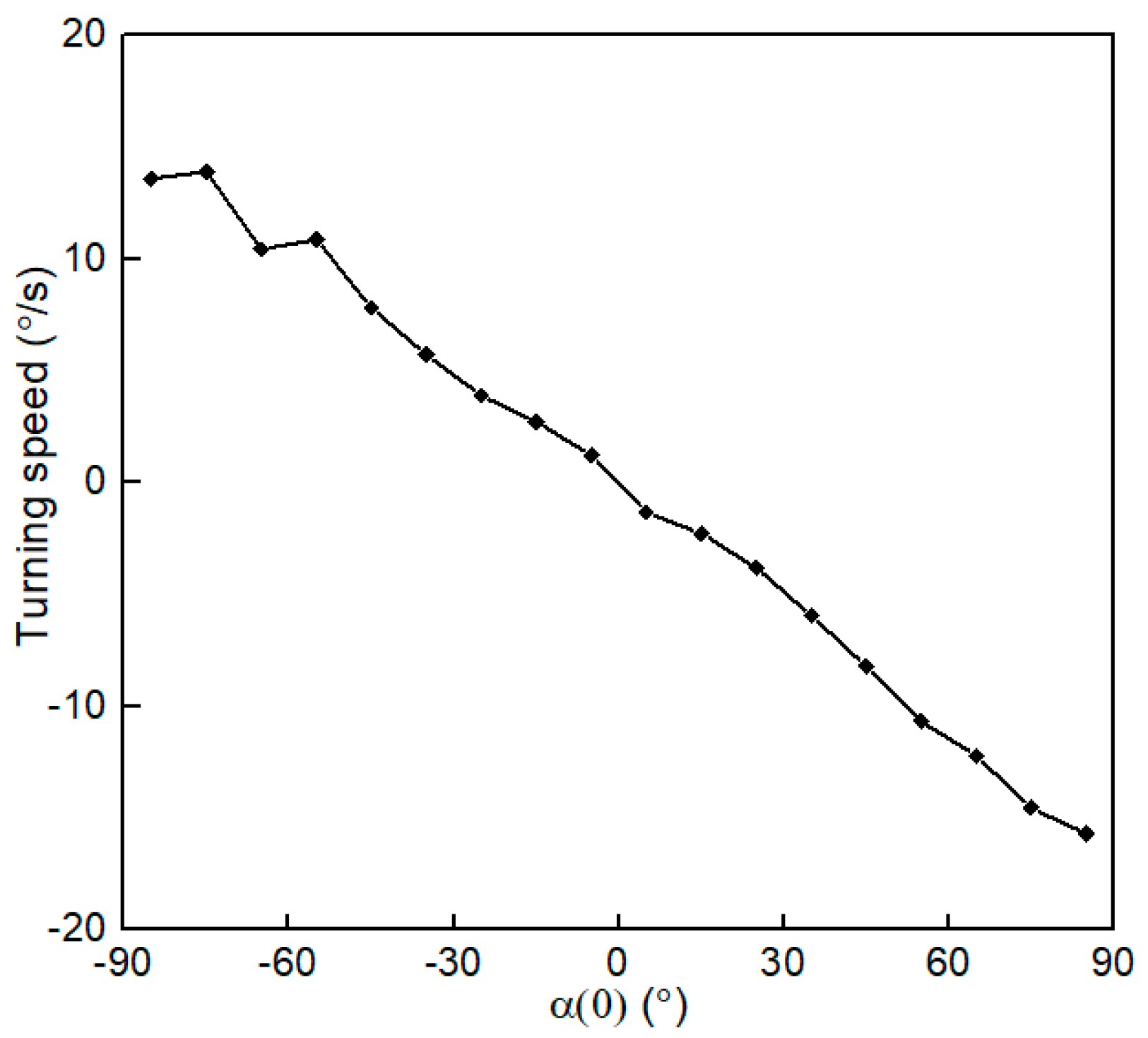
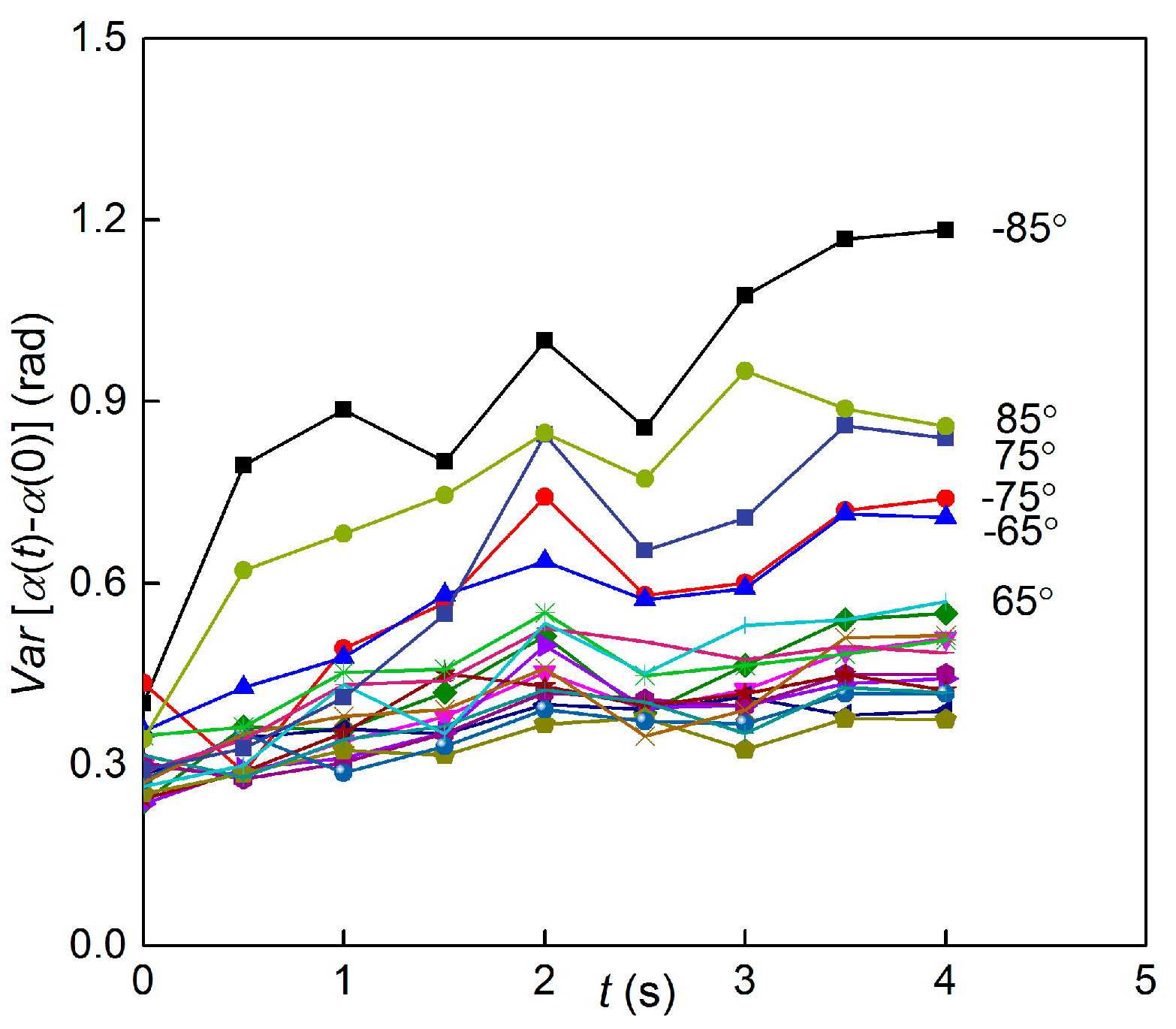
3.3. Time Scale of Reorientation by Gravitational Torque
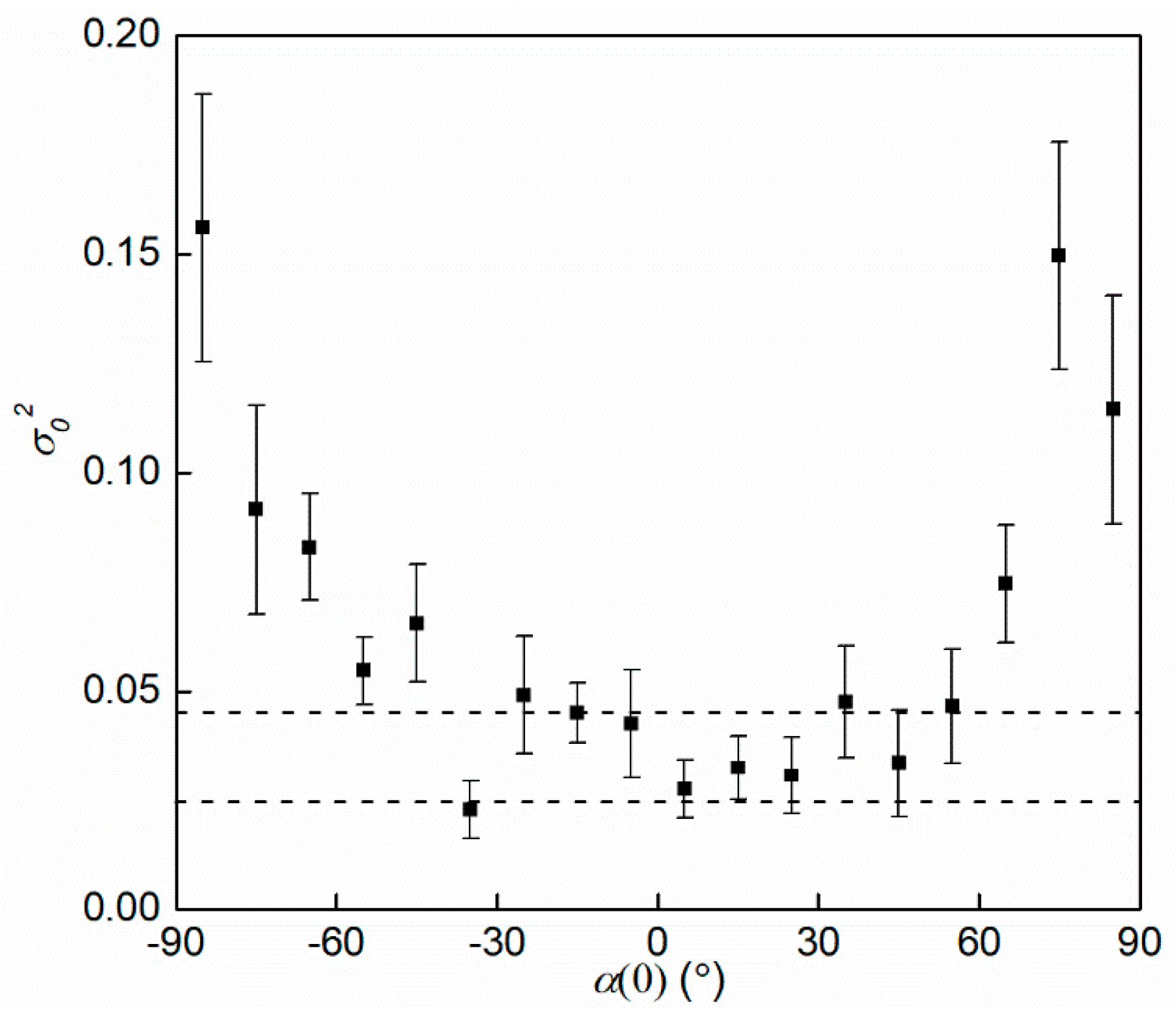
3.4. Rotational Diffusion Coefficient
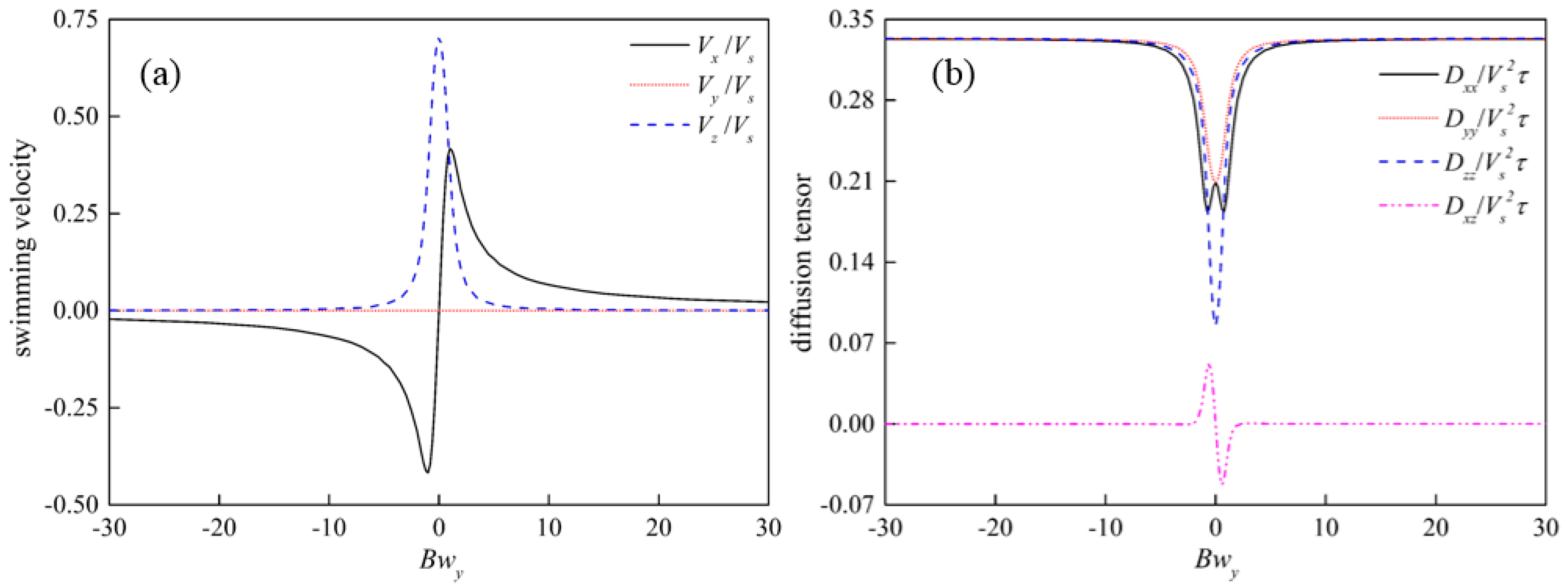
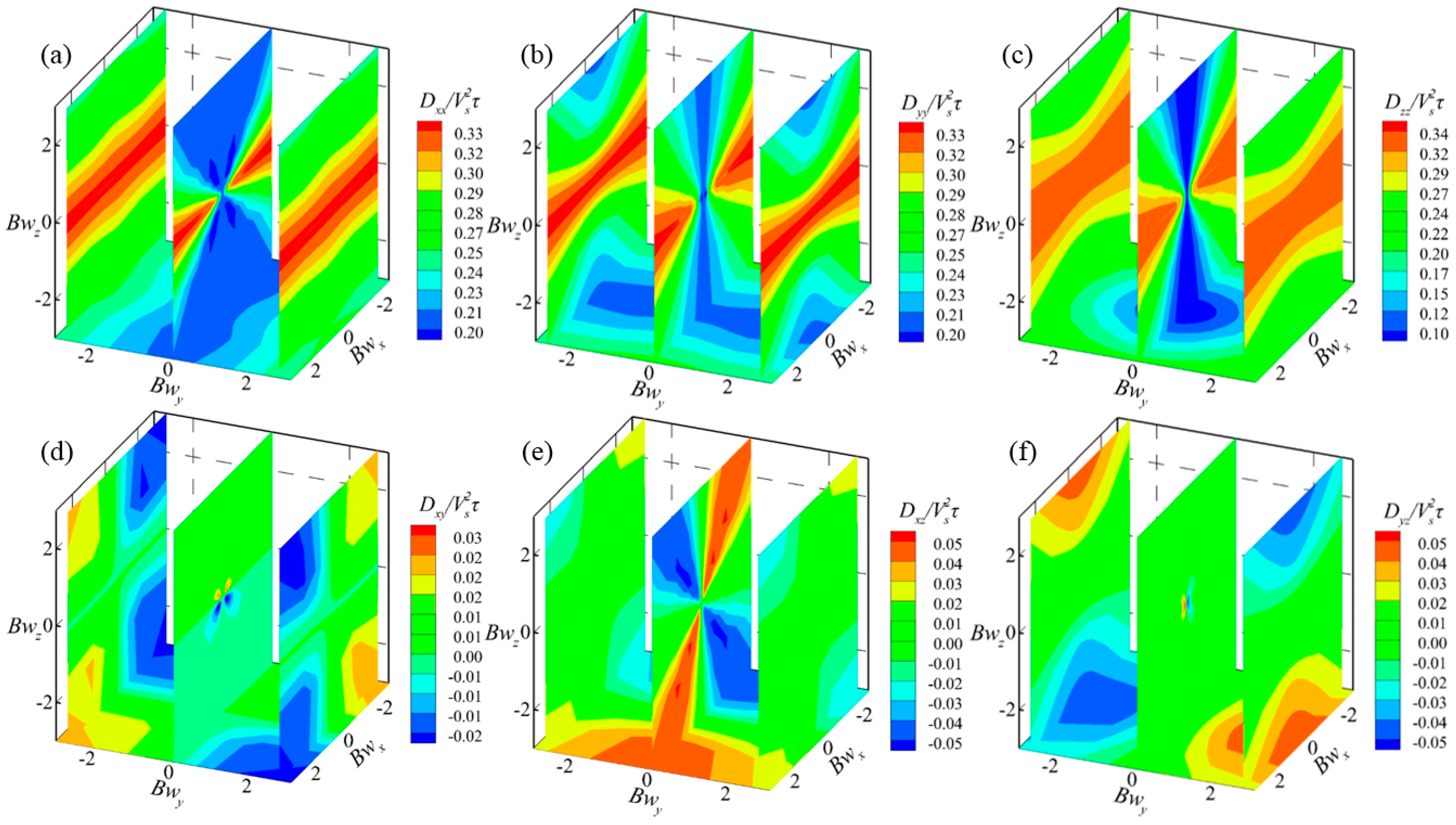
3.5. Swimming Characteristics of H. akashiwo in Vorticity Field
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pedley, T.J.; Kessler, J.O. Hydrodynamic phenomena in suspensions of swimming microorganism. Annu. Rev. Fluid Mech. 1992, 24, 313–358. [Google Scholar] [CrossRef]
- Pedley, T.J.; Kessler, J.O. A new continuum model for suspensions of gyrotactic micro-organisms. J. Fluid Mech. 1990, 212, 155–182. [Google Scholar] [CrossRef] [PubMed]
- Hwang, Y.; Pedley, T.J. Bioconvection under uniform shear: Linear stability analysis. J. Fluid Mech. 2014, 738, 522–562. [Google Scholar] [CrossRef]
- Hwang, Y.; Pedley, T.J. Stability of downflowing gyrotactic microorganism suspensions in a two-dimensional vertical channel. J. Fluid Mech. 2014, 749, 750–777. [Google Scholar] [CrossRef]
- Durham, W.M.; Climent, E.; Barry, M.; Lillo, F.D.; Boffetta, G.; Cencini, M.; Stocker, R. Turbulence drives microscale patches of motile phytoplankton. Nat. Commun. 2013, 4, 2148. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, R.E. Green Algae as model organisms for biological fluid dynamics. Annu. Rev. Fluid Mech. 2015, 47, 343–375. [Google Scholar] [CrossRef] [PubMed]
- Durham, W.M.; Kessler, J.O.; Stocker, R. Disruption of vertical motility by shear triggers formation of thin phytoplankton layers. Science 2009, 323, 1067–1070. [Google Scholar] [CrossRef] [PubMed]
- Bearon, R.N.; Grünbaum, D.; Cattolico, R.A. Effects of salinity structure on swimming behavior and harmful algal bloom formation in Heterosigma akashiwo, a toxic raphidophyte. Mar. Ecol. Prog. 2006, 306, 153–163. [Google Scholar] [CrossRef]
- Kempton, J.; Keppler, C.J.; Lewitus, A.; Shuler, A.; Wilde, S. A novel Heterosigma akashiwo (Raphidophyceae) bloom extending from a South Carolina bay to offshore waters. Harmful Algae 2008, 7, 235–400. [Google Scholar] [CrossRef]
- Durham, W.M.; Stocker, R. Thin phytoplankton layers: Characteristics, mechanisms, and consequences. Annu. Rev. Mar. Sci. 2012, 4, 177–207. [Google Scholar] [CrossRef] [PubMed]
- Bearon, R.N.; Grünbaum, D.; Cattolico, R.A. Relating cell-level swimming behaviors to vertical population distributions in Heterosigma akashiwo (Raphidophyceae), a harmful alga. Limnol. Oceanogr. 2004, 49, 607–613. [Google Scholar] [CrossRef]
- Harvey, E.L.; Menden-Deuer, S. Predator-induced fleeing behaviors in phytoplankton: A new mechanism for harmful algal bloom formation? PLoS ONE 2012, 7, e46438. [Google Scholar] [CrossRef] [PubMed]
- Hill, N.A.; Häder, D.P. A biased random walk model for the trajectories of swimming micro-organisms. J. Theor. Biol. 1997, 186, 503–526. [Google Scholar] [CrossRef] [PubMed]
- Zeng, L.; Pedley, T.J. Distribution of gyrotactic micro-organisms in complex three-dimensional flows. Part I. Horizontal shear flow past a vertical circular cylinder. J. Fluid Mech. 2018, 852, 358–397. [Google Scholar] [CrossRef]
- Sineshchekov, O.; Lebert, M.; Häder, D.P. Effects of light on gravitaxis and velocity in Chlamydomonas reinhardtii. J. Plant Physiol. 2000, 157, 247–254. [Google Scholar] [CrossRef]
- Martin, M.; Barzyk, A.; Bertin, E.; Peyla, P.; Rafai, S. Photofocusing: Light and flow of phototactic microswimmer suspension. Phys. Rev. E 2016, 93, 051101. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Zeng, L.; Wu, Y.H.; Gao, Y.H.; Zhao, Y.J. Swimming characteristics of gyrotactic microorganisms in low-Reynolds-number flow: Chlamydomonas reinhardtii. Energy Ecol. Environ. 2017, 2, 289–295. [Google Scholar] [CrossRef]
- Croze, O.A.; Bearon, R.N.; Bees, M.A. Gyrotactic swimmer dispersion in pipe flow: Testing the theory. J. Fluid Mech. 2017, 816, 481–506. [Google Scholar] [CrossRef]
- Keppler, C.J.; Hoguet, J.; Smith, K.; Ringwood, A.H.; Lewitus, A.J. Sublethal effects of the toxic alga Heterosigma akashiwo on the southeastern oyster (Crassostrea virginica). Harmful Algae 2005, 4, 275–285. [Google Scholar] [CrossRef]
- Rensel, J.E.J.; Haigh, N.; Tynan, T.J. Fraser river sockeye salmon marine survival decline and harmful blooms of Heterosigma akashiwo. Harmful Alage 2010, 10, 98–115. [Google Scholar] [CrossRef]
- Tobin, E.D.; Grünbaum, D.; Patterson, J.; Cattolico, R.A. Behavioral and physiological changes during benthic-pelagic transition in the harmful alga, Heterosigma akashiwo: Potential for rapid bloom formation. PLoS ONE 2013, 8, e76663. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Spivack, A.J.; Menden-Deuer, S. pH alters the swimming behaviors of the raphidophyte Heterosigma akashiwo: Implications for bloom formation in an acidified ocean. Harmful Algae 2013, 26, 1–11. [Google Scholar] [CrossRef]
- Strom, S.L.; Harvey, E.L.; Fredrickson, K.A.; Menden-Deuer, S. Broad salinity tolerance as a refuge from predation in the harmful raphidophyte alga Heterosigma akashiwo (raphidophyceae). J. Phycol. 2013, 49, 20–31. [Google Scholar] [CrossRef] [PubMed]
- Harvey, E.L.; Jeong, H.J.; Menden-Deuer, S. Avoidance and attraction: Chemical cues influence predator-prey interactions of planktonic protists. Limnol. Oceanogr. 2013, 58, 1176–1184. [Google Scholar] [CrossRef]
- Harvey, E.L.; Menden-Deuer, S.; Rynearson, T.A. Persistent intra-specific variation in genetic and behavioral traits in the raphidophyte, Heterosigma akashiwo. Front. Microbiol. 2015, 6, 1277. [Google Scholar] [CrossRef] [PubMed]
- Sengupta, A.; Carrara, F.; Stocker, R. Phytoplankton can actively diversify their migration strategy in response to turbulent cues. Nature 2017, 543, 555–558. [Google Scholar] [CrossRef] [PubMed]
- Häder, D.P.; Lebert, M. Real time computer-controlled tracking of motile microorganisms. Photochem. Photobiol. 1985, 42, 509–514. [Google Scholar] [CrossRef] [PubMed]
- Häder, D.P.; Vogel, K. Simultaneous tracking of flagellates in real time by image analysis. J. Math. Biol. 1991, 30, 63–72. [Google Scholar] [CrossRef]
- Vladimirov, V.A.; Denissenko, P.V.; Pedley, T.J.; Wu, M.; Moskalev, I.S. Algal motility measured by a laser-based tracking method. Mar. Freshw. Res. 2000, 51, 589–600. [Google Scholar] [CrossRef]
- Vladimirov, V.A.; Wu, M.S.C.; Pedley, T.J.; Denissenko, P.V.; Zakhidova, S.G. Measurement of cell velocity distributions in populations of motile algae. J. Exp. Biol. 2004, 207, 1203–1216. [Google Scholar] [CrossRef] [PubMed]
- Harvey, E.L.; Menden-Deuer, S. Avoidanve, movement, and mortality: The interactions between a protistan grazer and Heterosigma akashiwo, a harmful algal bloom species. Limnol. Oceanogr. 2011, 56, 371–378. [Google Scholar] [CrossRef]
- Leptos, K.C.; Guasto, J.S.; Gollub, J.P.; Pesci, A.I.; Goldstein, R.E. Dynamics of enhanced tracer diffusion in suspensions of swimming eukaryotic microorganisms. Phys. Rev. L 2009, 103, 198103. [Google Scholar] [CrossRef] [PubMed]
- Kessler, J.O. Hydrodynamic focusing of motile algal cells. Nature 1985, 313, 218–220. [Google Scholar] [CrossRef]
- Kessler, J.O. Individual and collective fluid dynamics of swimming cells. J. Fluid Mech. 1986, 173, 191–205. [Google Scholar] [CrossRef]
- Lillo, D.F.; Cencini, M.; Durham, W.M.; Barry, M.; Stocker, R.; Climent, E.; Boffetta, G. Turbulent fluid acceleration generates clusters of gyrotactic microorganisms. Phys. Rev. Lett. 2014, 112, 044502. [Google Scholar] [CrossRef] [PubMed]
- Ardekani, A.M.; Doostmohannadi, A.; Desai, N. Transport of particles, drops, and small organisms in density stratified fluids. Phys. Rev. F 2017, 2, 100503. [Google Scholar] [CrossRef]
- Lovecchio, S.; Zonta, F.; Marchioli, C.; Soldati, A. Thermal stratification hinders gyrotactic micro-organism rising in free-surface turbulence. Phys. Fluids 2017, 29, 053302. [Google Scholar] [CrossRef]
- Lovecchio, S.; Zonta, F.; Soldati, A. Influence of thermal stratification on the surfacing and clustering of floaters in free surface turbulence. Adv. Water Resour. 2014, 72, 22–31. [Google Scholar] [CrossRef]
- Zhan, C.; Sardina, G.; Lushi, E.; Brandt, L. Accumulation of motile elongated micro-organisms in turbulence. J. Fluid Mech. 2014, 739, 22–36. [Google Scholar] [CrossRef]
- Ardekani, M.N.; Sardina, G.; Brandt, L.; Karpboss, L.; Bearon, R.N.; Variano, E.A. Sedimentation of inertia-less prolate spheroids in homogenous isotropic turbulence with application to non-motile phytoplankton. J. Fluid Mech. 2017, 831, 655–674. [Google Scholar] [CrossRef]
- Mashayekhpour, M.; Marchioli, C.; Lovecchio, S.; Lay, E.N.; Soldati, A. Wind effect on gyrotactic micro-organism surfacing in free-surface turbulence. Adv. Water Resour. 2017. [Google Scholar] [CrossRef]
- Enriquez, R.M.; Taylor, J.R. Numerical simulations of the competition between wind-driven mixing and surface heating in triggering spring phytoplankton blooms. ICES J. Mar. Sci. 2015, 72, 1926. [Google Scholar] [CrossRef]
- Croze, O.A.; Sardina, G.; Ahmed, M.; Bees, M.A.; Brandt, L. Dispersion of swimming algae in laminar and turbulent channel flows: Consequences for photobioreactors. J. R. Soc. Interface 2013, 10, 20121041. [Google Scholar] [CrossRef] [PubMed]
- Hill, N.A.; Bees, M.A. Taylor dispersion of gyrotactic swimming micro-organisms in a linear flow. Phys. Fluids 2002, 14, 2598–2605. [Google Scholar] [CrossRef]
- Manela, A.; Frankel, I. Generalized Taylor dispersion in suspensions of gyrotactic swimming micro-organisms. J. Fluid Mech. 2003, 490, 99–127. [Google Scholar] [CrossRef]
- Bearon, R.N.; Hazel, A.L.; Thorn, G.J. The spatial distribution of gyrotactic swimming micro-organisms in laminar flow fields. J. Fluid Mech. 2011, 680, 602–635. [Google Scholar] [CrossRef]
- Bearon, R.N.; Bees, M.A.; Croze, O.A. Biased swimming cells do not disperse in pipes as tracers: A population model based on microscale behaviour. Phys. Fluids 2012, 24, 121902. [Google Scholar] [CrossRef]
- Pedley, T.J.; Kessler, J.O. The orientation of spheroidal microorganisms swimming in a flow field. Proc. R. Soc. Lond. 1987, 231, 47–70. [Google Scholar] [CrossRef]
- Fehchle, T. How dinoflagellates swim. Protist 2001, 152, 329–338. [Google Scholar] [CrossRef]
- Visser, A.W.; Kirboe, T. Plankton motility patterns and encounter rates. Oecologia 2006, 148, 538–546. [Google Scholar] [CrossRef] [PubMed]

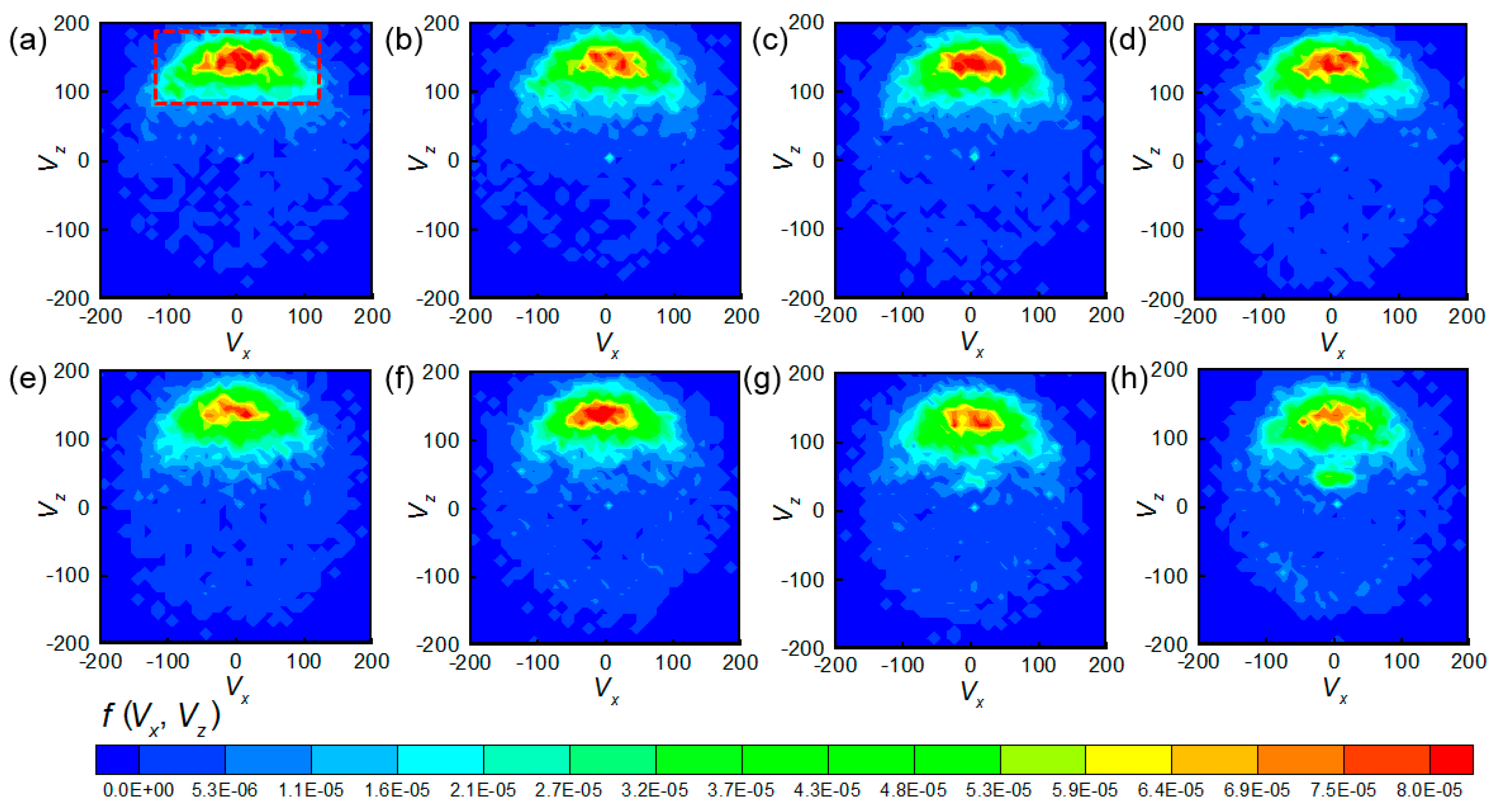
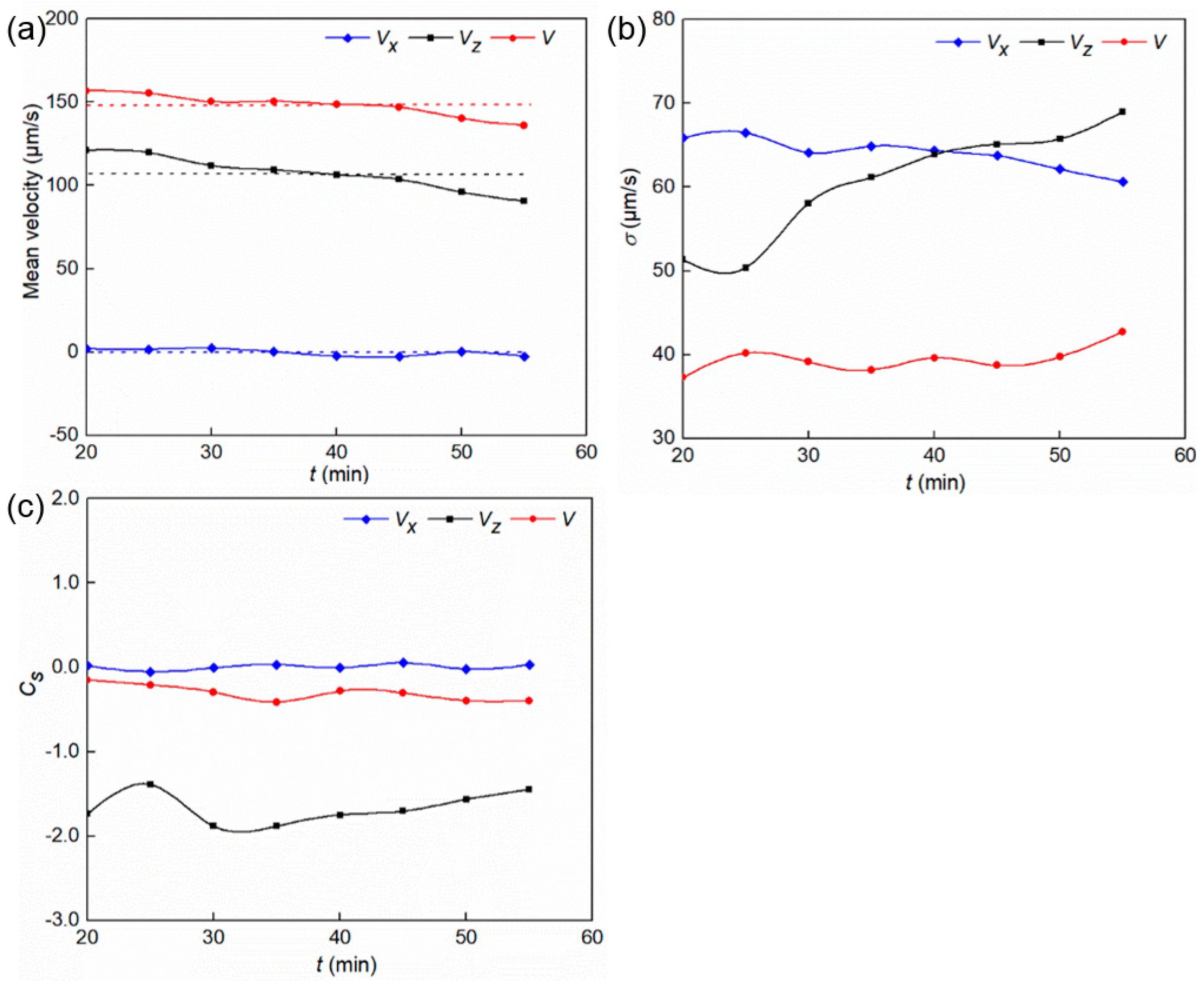

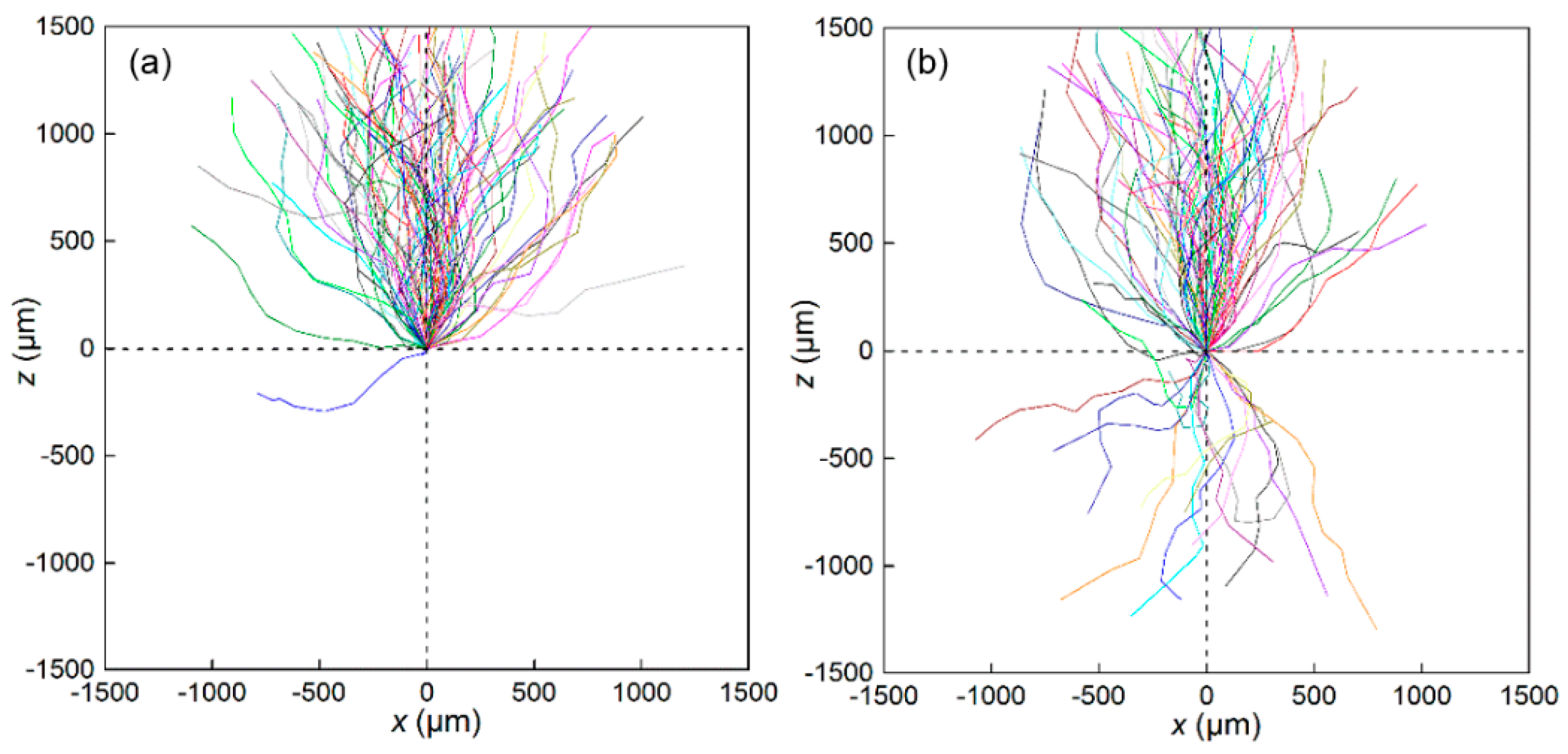
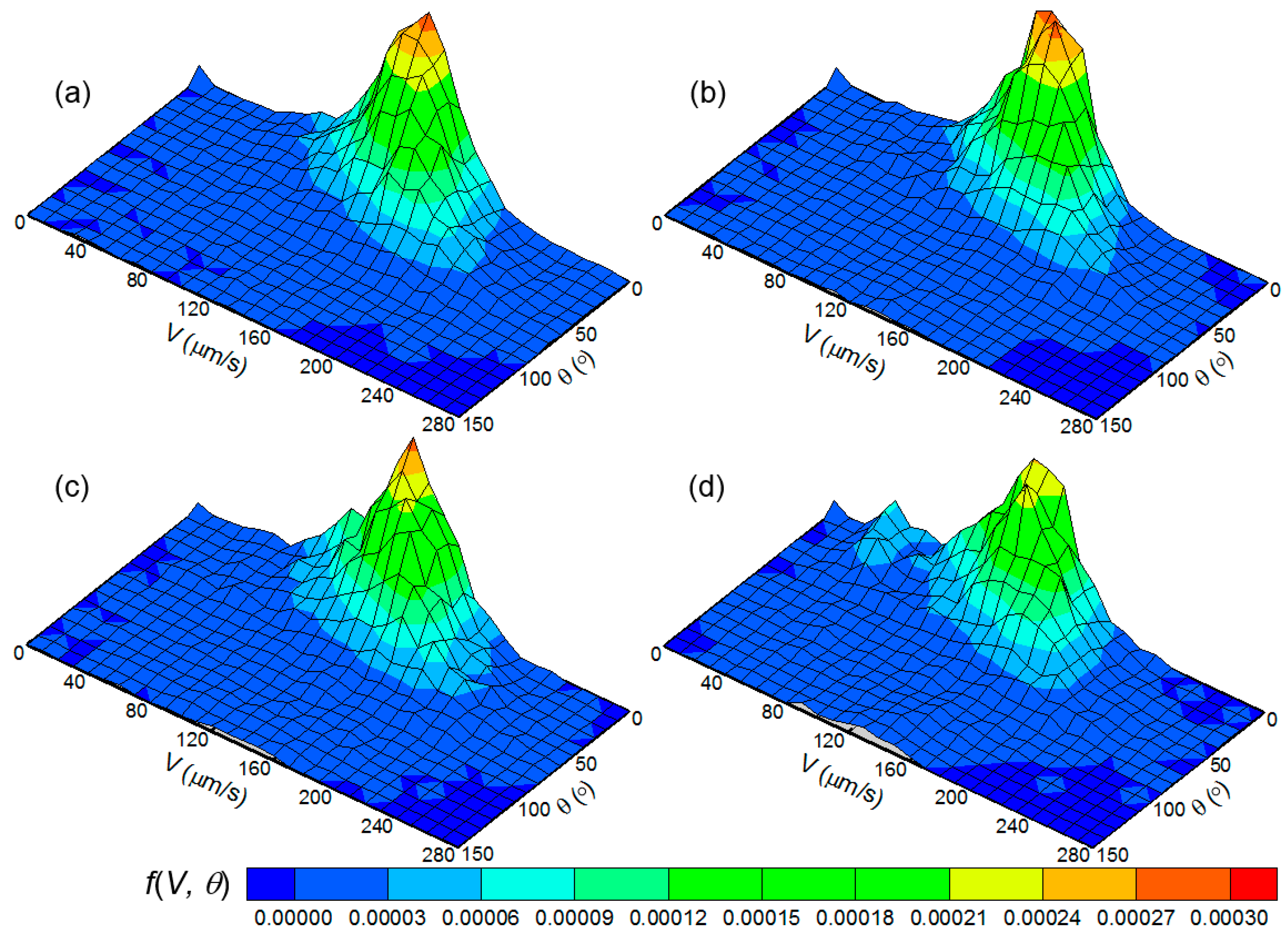

| Sets | 20 min | 25 min | 30 min | 35 min | 40 min | 45 min | 50 min | 55 min |
|---|---|---|---|---|---|---|---|---|
| 1 | N11 | N12 | N13 | N14 | N15 | N16 | N17 | N18 |
| 2 | N21 | N22 | N23 | N24 | N25 | N26 | N27 | N28 |
| 3 | N31 | N32 | N33 | N34 | N35 | N36 | N37 | N38 |
| Sum | N1 | N2 | N3 | N4 | N5 | N6 | N7 | N8 |
| Algae | V (μm s−1) | B (s) | Dr (rad2 s−1) | Paper |
|---|---|---|---|---|
| C. nivalis | 63 | 3.4 | 0.067 | [1,2] |
| C. nivalis | 55 | 2.7 | 0.084 | [13] |
| C. nivalis | 38 | 6 | 0.036 | [30] |
| D. salina | 62.7 ± 0.4 | 10.5 ± 1.3 | 0.23 ± 0.06 | [18] |
| H. akashiwo | - | 2 | - | [7] |
| H. akashiwo (CCMP3107) | - | 4.9 ± 1.5 | - | [26] |
| H. akashiwo (CCMP452↑ a) | 74.5 ± 42.4 | 19.3 ± 13.5 | - | [26] |
| H. akashiwo (CCMP452↓ b) | 73.8 ± 46.2 | −23.1 ± 10.2 | - | [26] |
| H. akashiwo (CCMP452) | 49–66 | - | - | [11] |
| H. akashiwo (CCAP934-1) | 88–119 | - | - | [11] |
| H. akashiwo | 20–145 | - | - | [12] |
| H. akashiwo (CCMP3107) | 25–58 | - | - | [23] |
| H. akashiwo | 85–135 | - | - | [24] |
| H. akashiwo (7 strains) | 33–115 | - | - | [25] |
| H. akashiwo (GY-H24) | 117–156 | 5.6 | 0.046 | Present work |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Wu, Y.; Zeng, L. Migration of Gyrotactic Micro-Organisms in Water. Water 2018, 10, 1455. https://doi.org/10.3390/w10101455
Chen X, Wu Y, Zeng L. Migration of Gyrotactic Micro-Organisms in Water. Water. 2018; 10(10):1455. https://doi.org/10.3390/w10101455
Chicago/Turabian StyleChen, Xiao, Yihong Wu, and Li Zeng. 2018. "Migration of Gyrotactic Micro-Organisms in Water" Water 10, no. 10: 1455. https://doi.org/10.3390/w10101455
APA StyleChen, X., Wu, Y., & Zeng, L. (2018). Migration of Gyrotactic Micro-Organisms in Water. Water, 10(10), 1455. https://doi.org/10.3390/w10101455




