1. Introduction
Large freshwater lakes play an important role in the earth’s ecosystems, not only because they contain 68% of the global fresh water reservoir, but also because of their economic, social and biological importance as they provide habitats for wildlife, irrigation for agriculture, energy, transport and most importantly water for drinking [
1]. The large areal extent of some of these lakes makes traditional water monitoring time and resource consuming, hence inefficient, yet continuous water quality monitoring of lakes is of great importance in detecting environmental changes [
2].
Lake Balaton, which covers an area of 596 km
, is the largest lake in Central Europe and one the most important natural and tourist attractions in Hungary and Central Europe. It provides recreational facilities, and is an aesthetics and cultural resort, which attracts the largest tourist industry in the country [
3]. There are several ongoing ecosystem monitoring programs at Lake Balaton. These programs aim to monitor important biological and ecological aspects of biodiversity and food web interactions in the lake. Examples for former monitoring programs for Lake Balaton can be found in [
4,
5].
The lake has gone through significant changes in the past decades, and only lately were these changes experienced as advantageous. In the 1970s, increased nutrient loads of anthropogenic origin, such as inadequate wastewater management and agricultural runoff, and abiotic factors resulted in degradation of water quality of Balaton. Anthropogenic impacts, i.e., intensification of agricultural activities and increase in the number of settlements along the shore, caused eutrophication of the lake. The eutrophication process was successfully stopped and reversed by introducing a combination of technological and management solutions [
6,
7]. Recent unpublished data suggests that the lake has recovered and returned to the pre-eutrophic conditions.
As a result of these past events, there is an increasing demand for continuous monitoring of biotic and abiotic changes of the lake. Advances in remote sensing technology allow for the use of satellites for monitoring water constituents. The European Space Agency’s (ESA) Ocean and Land Color Instrument (OLCI) onboard the Sentinel 3A and 3B satellites collects data of high spectral and spatial resolutions, and due to the frequent revisit time, they provide the possibility to monitor the water quality of Lake Balaton. In this work, we will study the water monitoring capabilities of Sentinel 3 (S3) for this lake, focusing on three important water quality parameters that affect the lake’s water color through scattering and/or absorption: Chlorophyll-a (Chl-a), Colored Dissolved Organic Matter (CDOM) and Total Suspended Matter (TSM).
Chl-a is a major photosynthetic pigment which occurs in phytoplankton, i.e., in the ubiquitous, microscopic, free-floating and suspended organisms found in the illuminated (euphotic) layer of the lakes. The amount of phytoplankton in the water collectively accounts for the trophic state of the lake. Although these organisms are the base of the aquatic food web, their excess could be harmful. Phytoplankton face a great number of abiotic and biotic limitations (light, temperature, other algae, herbivores, etc.), which influence the phytoplankton growth [
8]. Nutrient enrichment is very important, since it leads to the eutrophication of lakes, which can lead to alternate states [
9].
CDOM is the colored (optically active) fraction of the dissolved organic matter (DOM) of waters, consisting mostly of humic and fulvic acids. Although CDOM is considered as an indicator of DOM [
10,
11], its origin can vary, as the amount of CDOM is affected by external factors and diffuse sources from the catchment. CDOM in waters is autochtonous, i.e., coming from degradation of algae or macrophytes in the given water body, and/or allochtonous, i.e., coming from the catchment area.
TSM includes a wide range of particulate material for the given water column. The origin of TSM can be local, such as wind induced resuspension and/or distant, for instance from tributaries [
12]. TSM contains both organic and inorganic matter, and has a significant impact on the spatial and temporal aspects of the optical properties of the water bodies [
13].
Ocean color remote sensing methodology could potentially be a useful tool to track the variability and monitor these water quality parameters [
14,
15,
16]. In situ observations have documented that Lake Balaton shows a large spatial and temporal variation in the amount and the distribution of Chl-a, CDOM and TSM. This, and the fact that Lake Balaton is regularly monitored by field sampling and measurements, makes the lake particularly well suited for validating retrieval of water quality products for complex aquatic environments from the Copernicus S3 OLCI instrument. The computation of the standard Chl-a, CDOM and TSM maps from OLCI is generally performed by using a Neural Network (NN) method [
17,
18].
However, optical properties of local environments might show large deviations from the data used for training state-of-the-art models. This can lead to erroneous retrieval of water quality parameters [
19]. Therefore, it is often required to use a local model, adjusted to the given area. An alternative powerful regression approach, the Gaussian Process Regression (GPR) model, has lately been investigated for biophysical parameter retrieval from remotely sensed data. The GPR model has been shown to outperform some other parameteric and non-parameteric machine learning methods, such as NNs, in the estimation of these biophysical parameters [
20,
21,
22,
23,
24]. Hence, the GPR model can be an alternative candidate for estimating water quality parameters from data acquired by S3 OLCI in Lake Balaton.
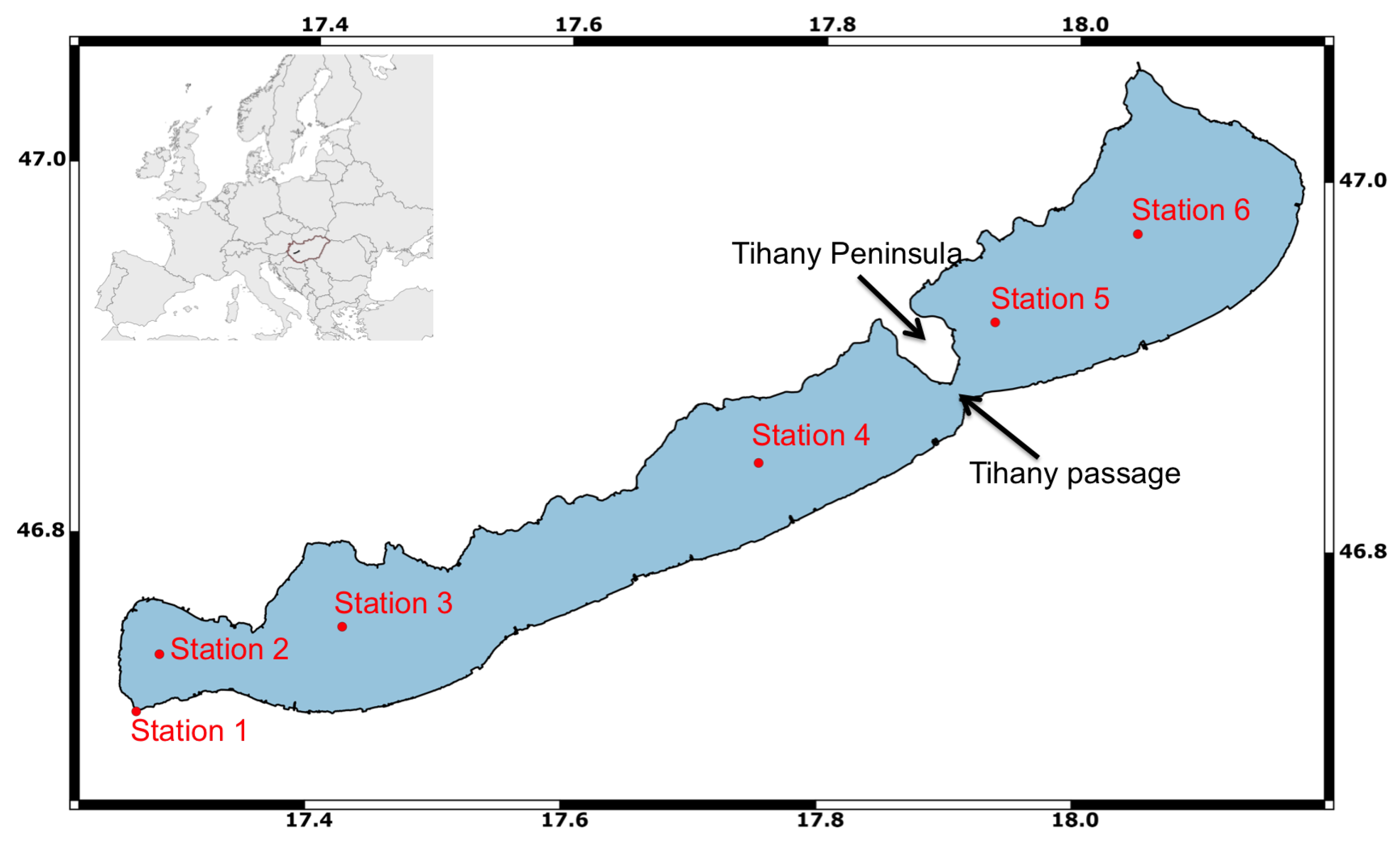
In this work, our primary objective is to investigate the quality of the global S3 OLCI complex water products for Lake Balaton. For this, we compare the OLCI Level 2 (L2) water quality products (Chl-a, CDOM and TSM) against in situ measurements collected at six fixed stations in the lake in 2017. Hence, the first part of the work is a preliminary study, which aims to investigate the possibility of using S3 OLCI L2 water quality products to monitor Lake Balaton, and at the same time evaluate the performance of S3 OLCI L2 products for this highly complex aquatic environment.
Our secondary objective is to investigate the performance of the Machine Learning GPR approach, tuned locally for Lake Balaton. The GPR model is noted to have several advantageous properties. In addition to it’s powerful regression strength, it also provides the possibility to access feature relevance, through feature ranking. As shown in [
24,
25], the regression strength and the efficiency of the model can be improved by using features selected by using ranking methods. In order to select the most suitable number and combination of spectral bands to be used in the GPR model for estimating Chl-a content of Lake Balaton, we applied the recently published Automatic Model Selection Algorithm (AMSA) [
25] to data from the lake, extended with synthesised data of the same Chl-a ranges.
Finally, we visually compare the estimates for S3 OLCI L2 Chl-a products with the locally trained GPR model. Note, we do not specifically aim to compare the estimates of the NN with the locally trained GPR model, since the NN was trained on a dataset which differs in optical properties and size from the matchup data we used to train the local GPR model. Hence, our contribution in this work is to test S3 OLCI L2 water quality products for the diverse Lake Balaton conditions, and to comparatively assess the value of using a locally tuned Machine Learning GPR model.
4. Discussion
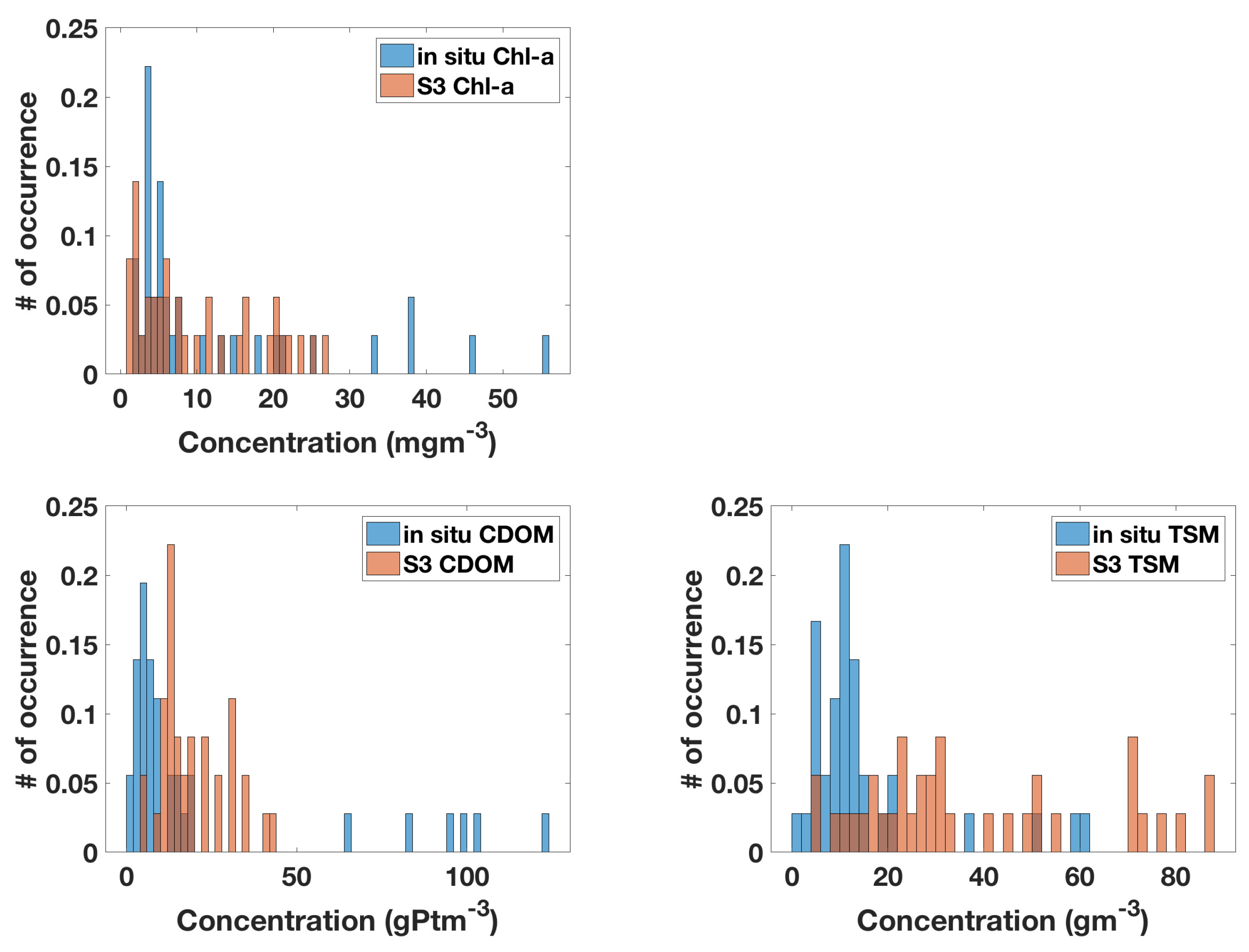
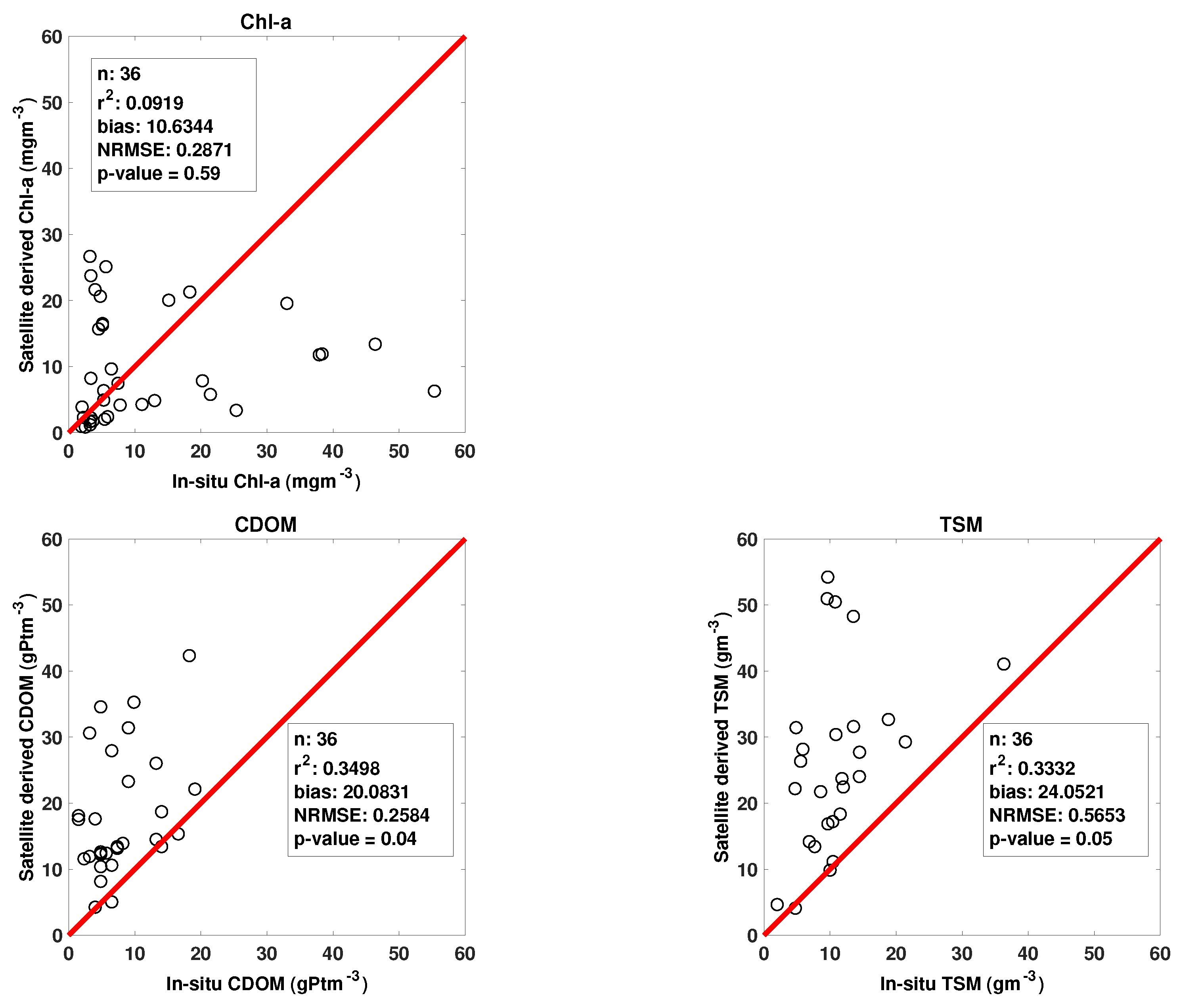
In this work, we studied the possibility of using S3 OLCI L2 products to monitor water quality parameters in Lake Balaton. For this, we first used in situ measurements of Chl-a, CDOM and TSM to evaluate the performance of the state-of-the-the-art complex water algorithm for S3 OLCI. The overall finding was that the correlation between in situ measurements and the S3 OLCI L2 products was low and not significant. It was the lowest value for Chl-a content, and somewhat higher for CDOM and TSM. Note, there are few published validation results for S3 OLCI L2 water quality parameters for complex waters, since S3 OLCI data only lately has become available. However, for the MEdium Resolution Imaging Spectrometer (MERIS), which had similar spectral and spatial resolution as S3 OLCI, similar validation results have been documented using NN algorithms to retrieve water quality parameters. This includes the over and underestimation of Chl-a concentration [
37], and large overestimation of TSM [
31].
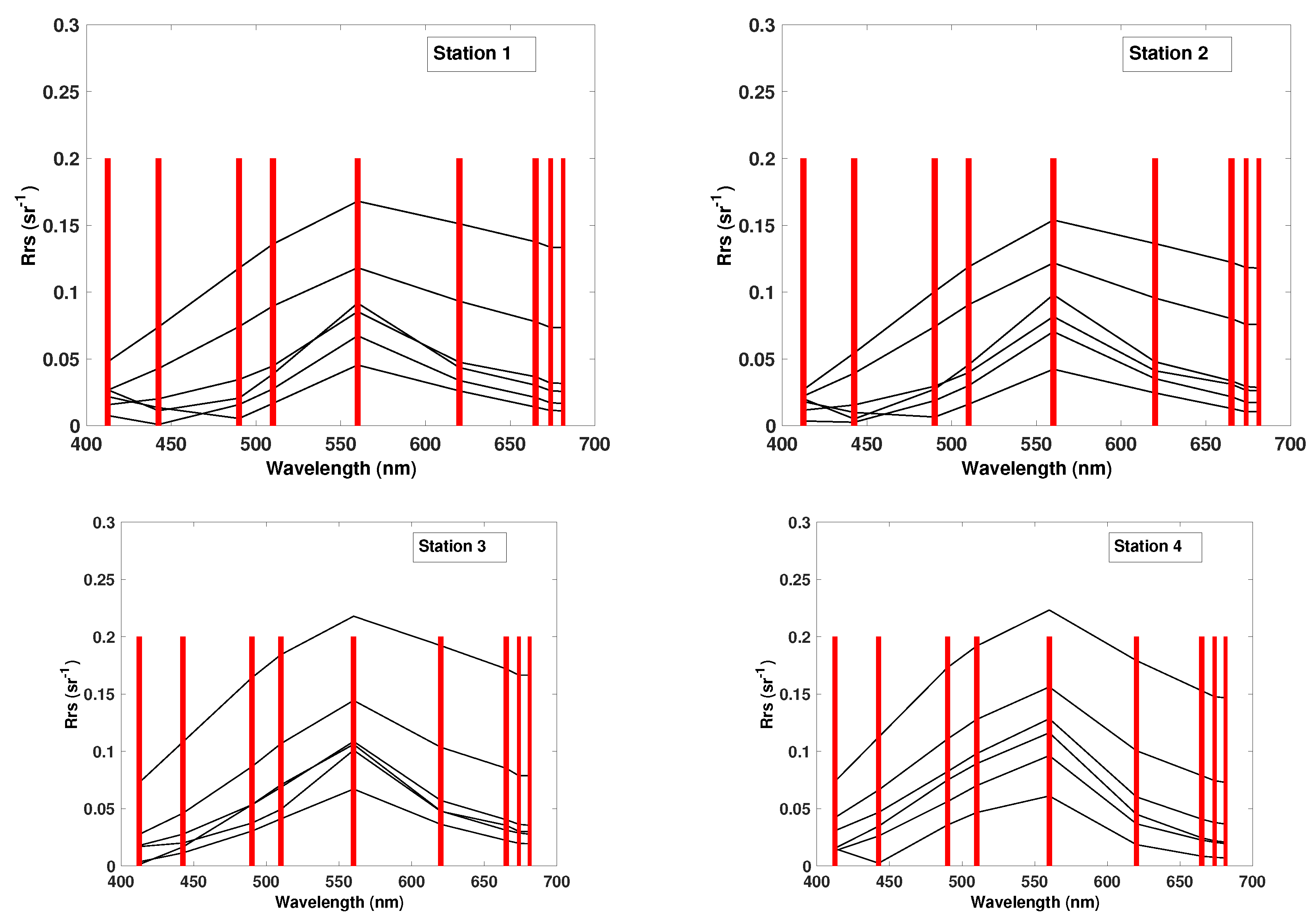
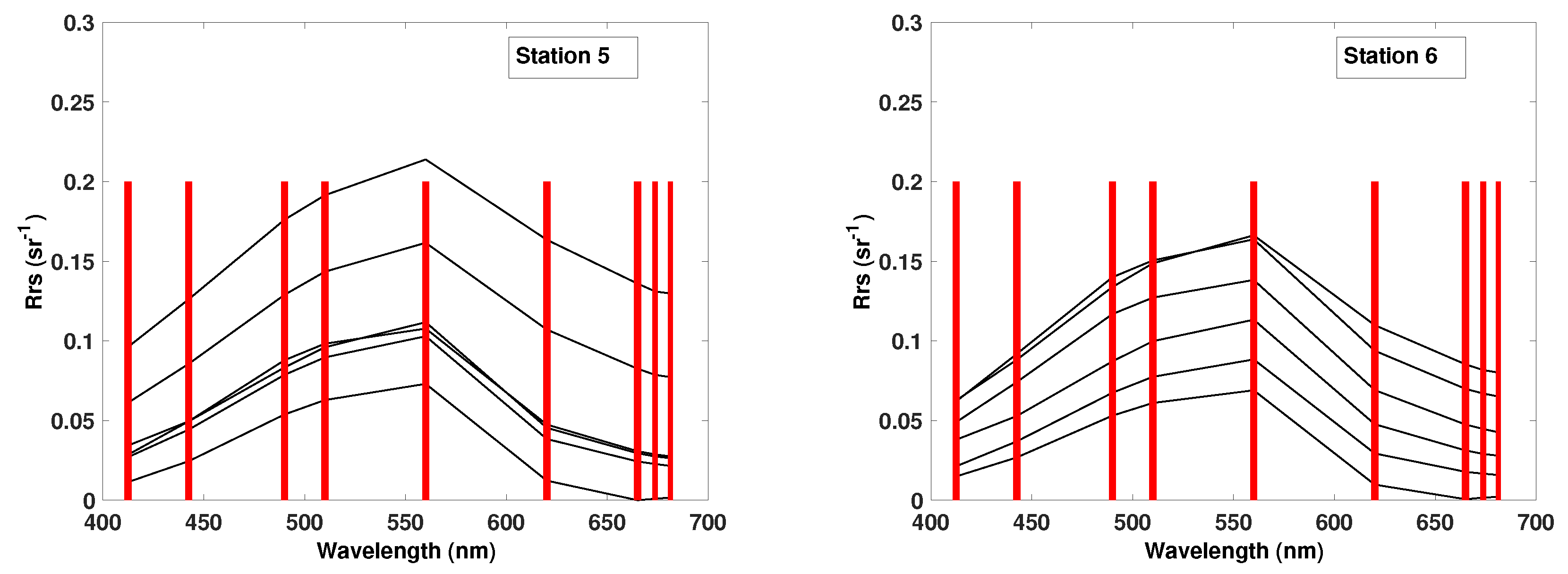
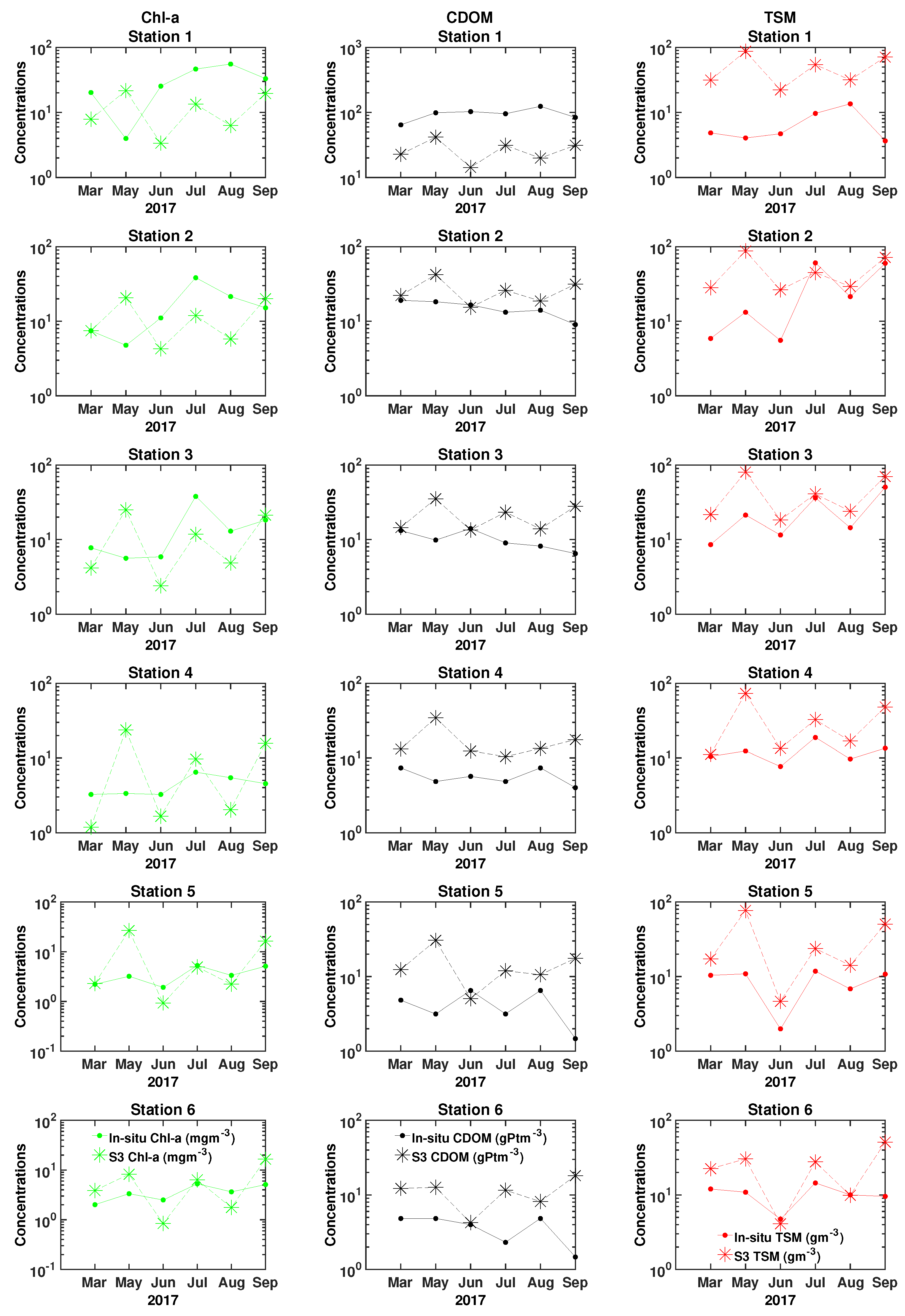
The station-wise study resulted in the best qualitative correspondence, i.e., lowest NRSME and bias, and highest correlation, for Chl-a and CDOM at stations representing oligotrophic waters (Stations 5 and 6). The range of the in situ measurements at these stations were between 2 and 5 mg m for Chl-a and 2–7 g Pt m for CDOM, which are the lowest of all stations. Here, the TSM concentrations were also in the lower ranges, in comparison to the other stations. The computed measures did not reveal any significant differences between the stations for TSM.
The monthly analyses showed that the S3 OLCI estimates were in quite good correspondence with the observations for Chl-a. CDOM and TSM estimates had less agreement with the in situ measurements. We found that May resulted in the poorest fit in terms the computed statistical measures. The in situ Chl-a ranges were lowest in May, but conversely, for this month the CDOM and TSM ranges were large.
These results might be related to inaccuracies in the atmospheric correction and water quality retrieval algorithms because of the lack of training data from Lake Balaton in the dataset used to establish the state-of-the-the-art models for complex waters [
38].
The above results motivated us to investigate the capabilities of a locally trained GPR model for monitoring the complex environment of Lake Balaton. The overall findings for the S3 OLCI products showed the poorest performance for Chl-a content retrieval, which is the most important water quality parameter. Therefore, we studied the possibility of improving Chl-a content estimation in Lake Balaton by using the alternative approach. We obtained a larger, more representative dataset suitable for evaluating a locally tuned model by extending the in situ measurements with a synthetic dataset for S3 OLCI, generated for complex waters.
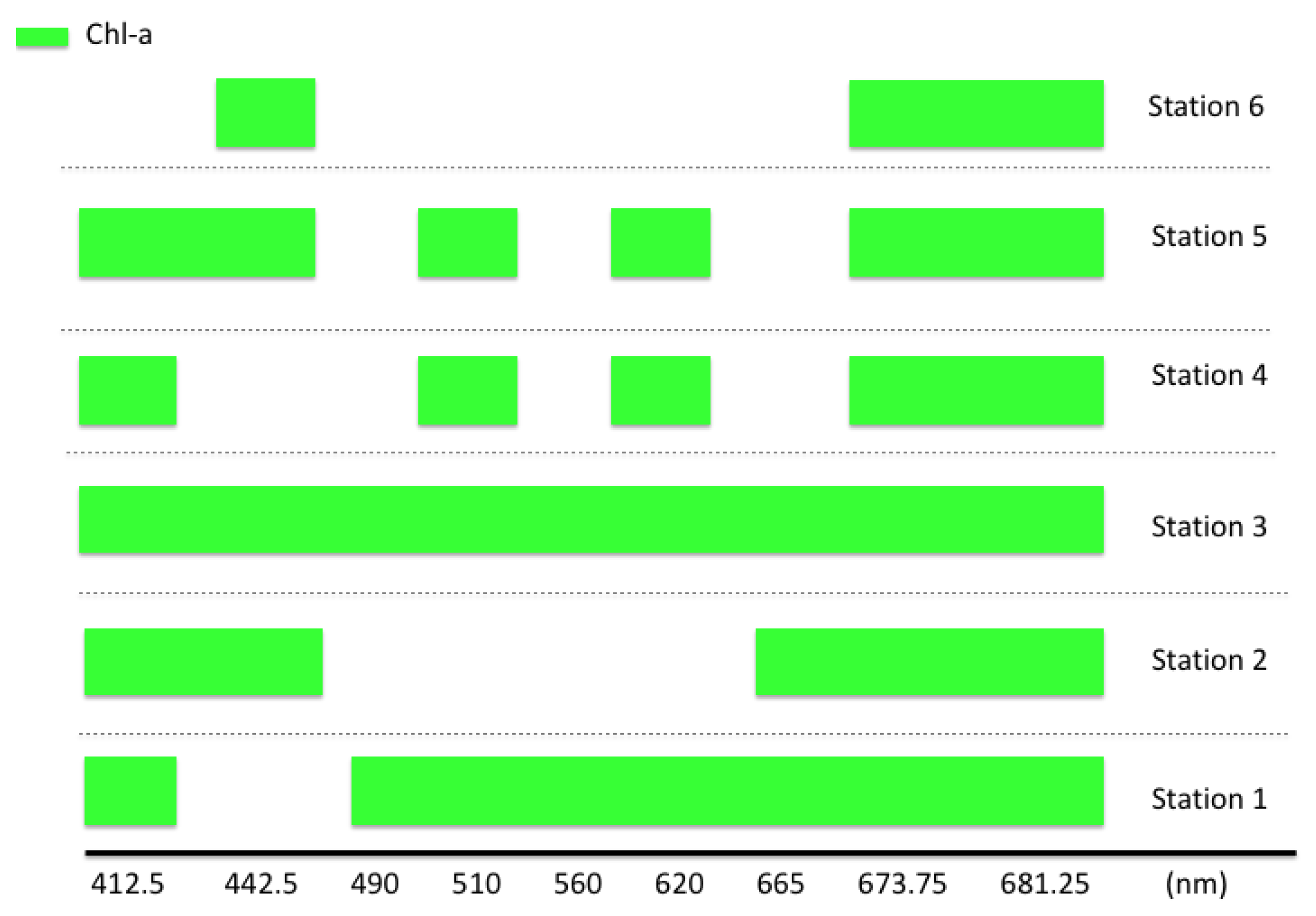
Using the AMSA approach to determine the most suitable number and combination of spectral bands to be used in the GPR model, we obtained significant improvements in regression strength. Even though the four feature ranking methods currently implemented in AMSA are-derived from different mathematical principles, the ranking showed high consistency. Our station-wise feature ranking experiment showed that the most relevant bands were highly dependent of the water properties and the water quality parameter in question. Our study suggested that for Chl-a estimation in Lake Balaton the bands 1, 4, 6, 8 and 9 are the most important in the GPR model. These bands have been previously shown to be sensitive to Chl-a in different datasets [
24]. Bands positioned in the red part of the electromagnetic spectrum, corresponding to the longer wavelengths, might be important due to the second absorption peak of the Chl-a molecule [
39]. Recent studies have presented the benefit of using S3 OLCI red bands to monitor Chl-a in optically complex environments [
40,
41]. Chl-a estimation can be improved by using models with these red bands. This is in good correspondence with our results. The station-wise analysis of AMSA showed that inclusion of red bands were necessary to obtain the ‘best’ GPR model for all cases. The 5-band model for Lake Balaton also was found to use these red bands as inputs to achieve improved Chl-a retrieval. The inclusion of additional blue-green bands has been shown to be advantageous, when the aquatic environment has large variation in Chl-a content [
42]. Our results also indicated that bands corresponding to lower relative wavelengths are also required to optimize the GPR model for the lake.
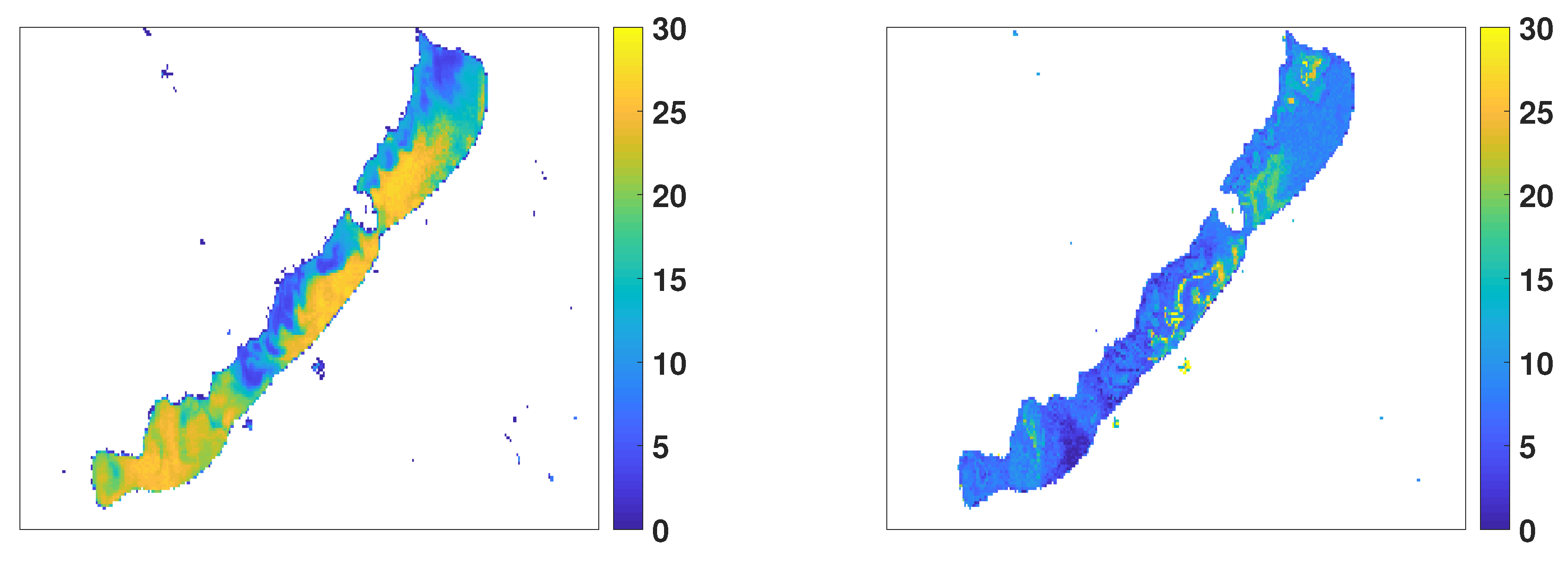
We visually compared the predictive power of the locally tuned 5-band GPR model with S3 OLCI L2 Chl-a products for Chl-a estimation. The Chl-a map produced by using S3 OLCI L2 NN algorithm seemed to show high sensitivity to the TSM content. The estimated Chl-a contents were significantly above the in situ measurements, indicating overestimation. This is in good agreement with the validation results, which showed that S3 OLCI assigns high values to Chl-a content below about 10 mg m. This is a surprising finding, since the state-of-the-the art NN was trained on samples containing values up to 30 mg m. A possible explanation for this overestimation is that complex optical properties of the lake results in sensitivity to other water constituents, such as TSM. This might lead to erroneous Chl-a content estimates. This also suggests the importance of using an alternative flexible approach for local, highly complex aquatic environment. The Chl-a map produced by the 5-band GPR model seemed to show better correspondence with the measured Chl-a content range for the particular month. The model could capture fine details and patches, which can be explained by the bathymetry and currents in the lake.
5. Conclusions
Our analysis showed that S3 OLCI provides the excellent possibility to monitor Lake Balaton, due to its spectral and spatial resolution and the good quality of the data. However, our validation results indicate the need of algorithm development for optically highly complex waters. We can conclude that based on the evaluation study of the alternative approach on the composite dataset, the GPR model seems to be able to improve the estimation of Chl-a concentration in Lake Balaton.
We believe that the development of an accurate, fast and robust water quality retrieval model for Lake Balaton would certainly be generally beneficial. This is due to the fact that Lake Balaton’s optical properties represent different kinds of aquatic environments: eutrophic, mesotrophic, oligotrophic, turbid and clear waters, and possible contribution of bottom reflectance. Hence, the lake represents a unique test site for the development of retrieval models for water quality parameters for optically complex waters.
For future work, we will collect in situ radiometric data, which might allow to further exploit the optical properties of Lake Balaton and understand eventual challenges with regard to the atmospheric correction algorithm. Furthermore, we will further test and validate the alternative model presented here on data originating from various other water bodies. This might allow us to understand the generalization capabilities of the 5-band GPR model.