A Simplified Infiltration Model for Predicting Cumulative Infiltration during Vertical Line Source Irrigation
Abstract
:1. Introduction
2. Materials and Methods
2.1. VLSI Modeling
2.1.1. Governing Equation
2.1.2. Modeled Scenarios
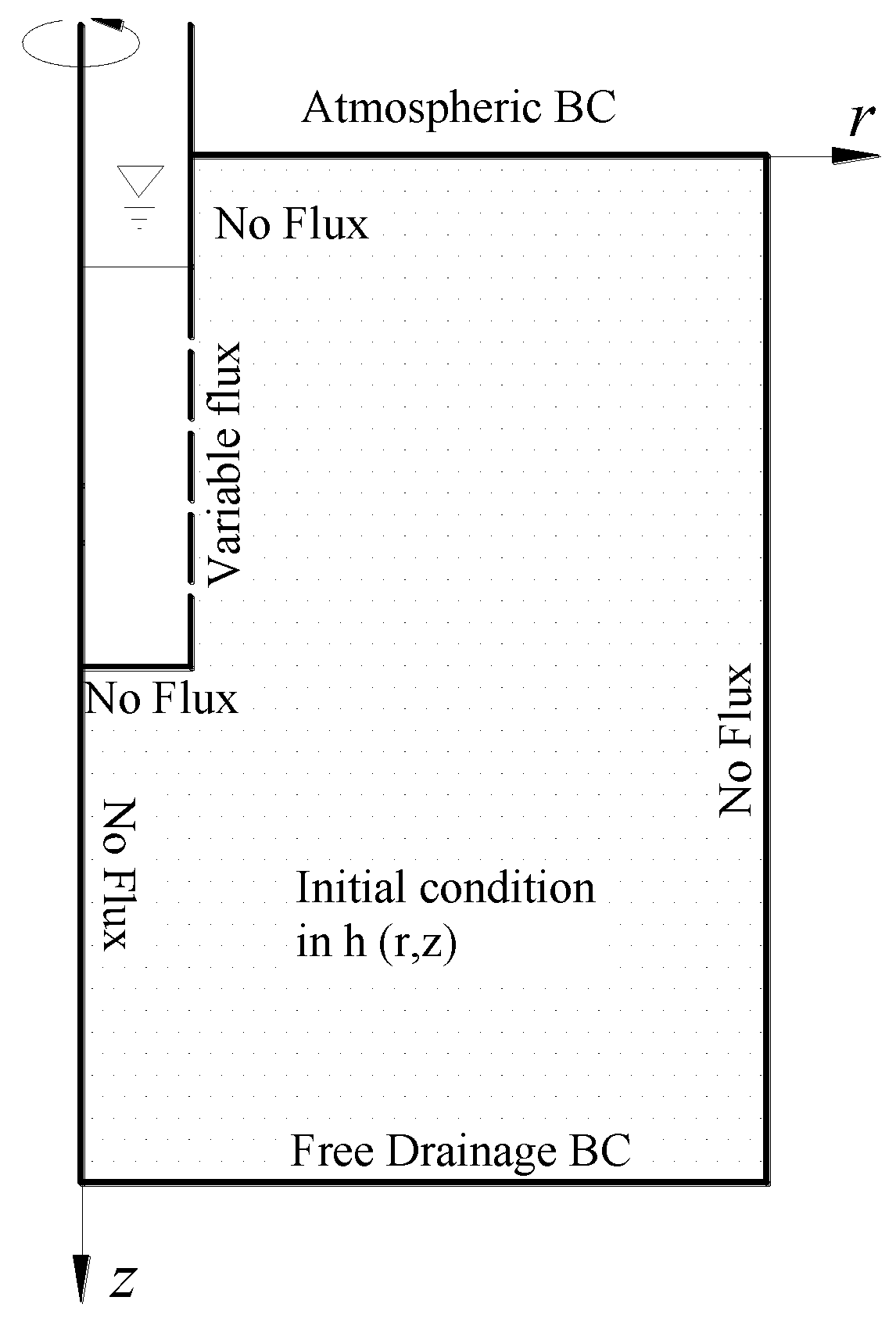
2.1.3. Initial and Boundary Conditions
2.2. Analytic Method
2.3. Error Analysis
3. Results and Discussion
3.1. Different Factors Affecting Cumulative Infiltration of Vertical Line Source Irrigation
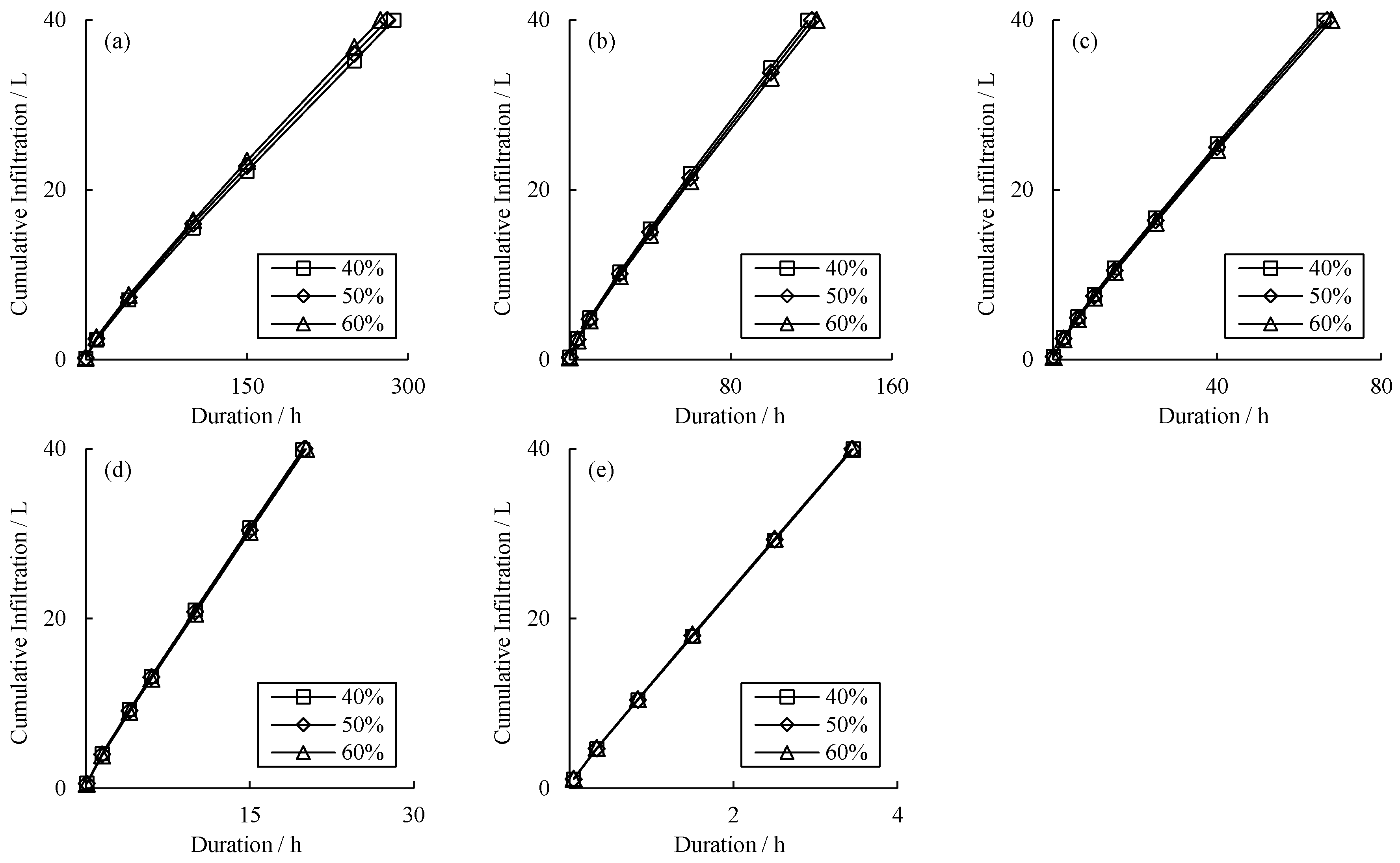
3.1.1. Effect of Initial SWC on Cumulative Infiltration
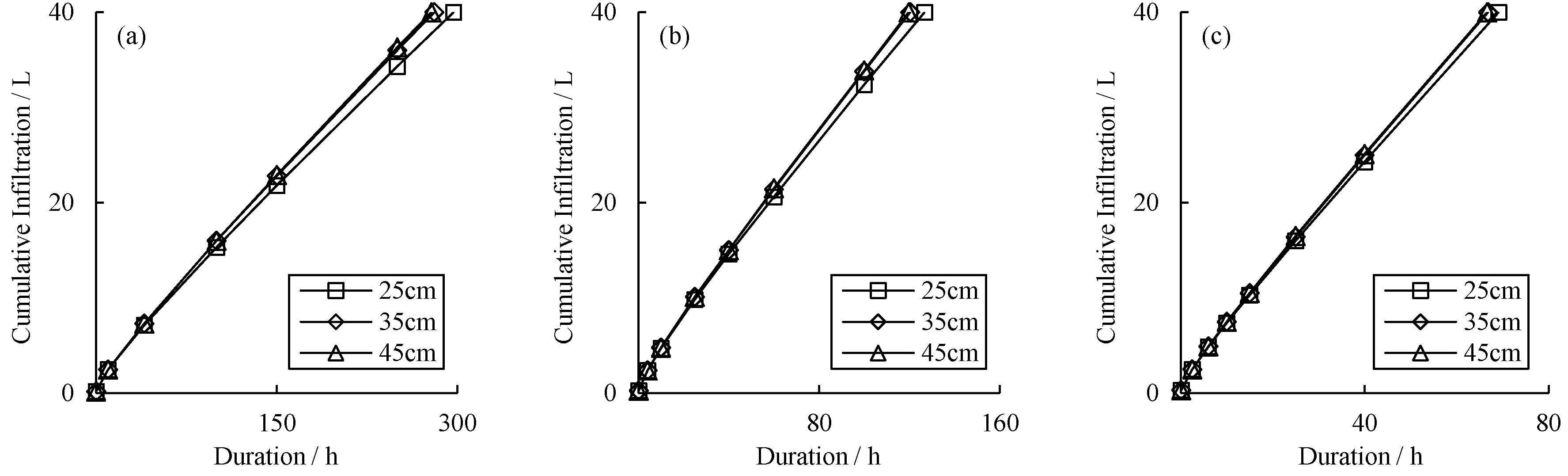
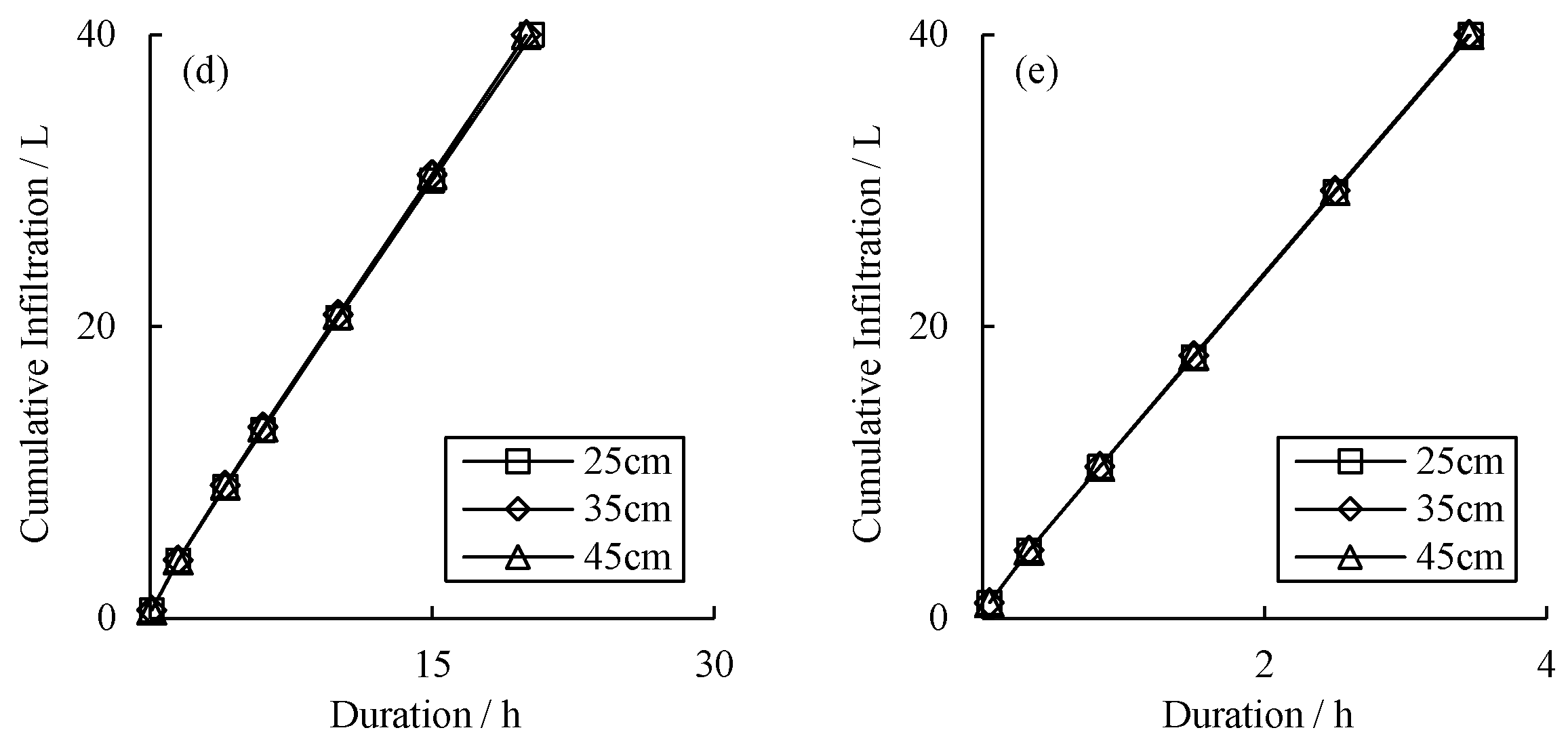
3.1.2. Effect of Tube Burial Depth on Cumulative Infiltration
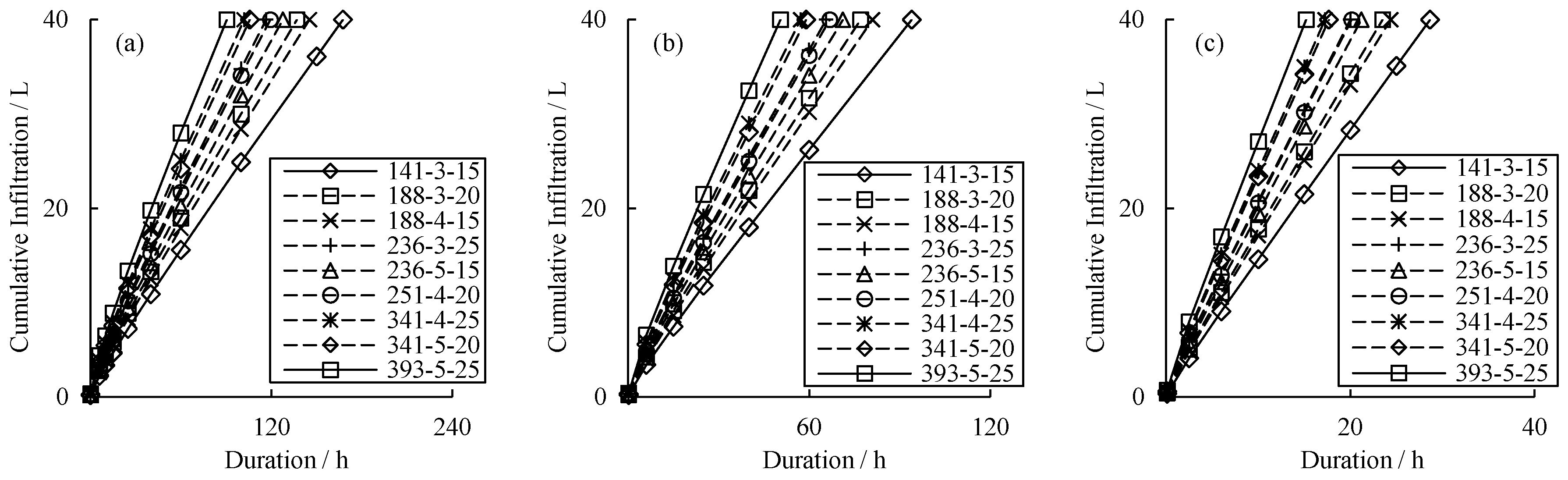
3.1.3. Effect of Tube Seepage Area on Cumulative Infiltration
3.2. Establishment of a Simplified Model
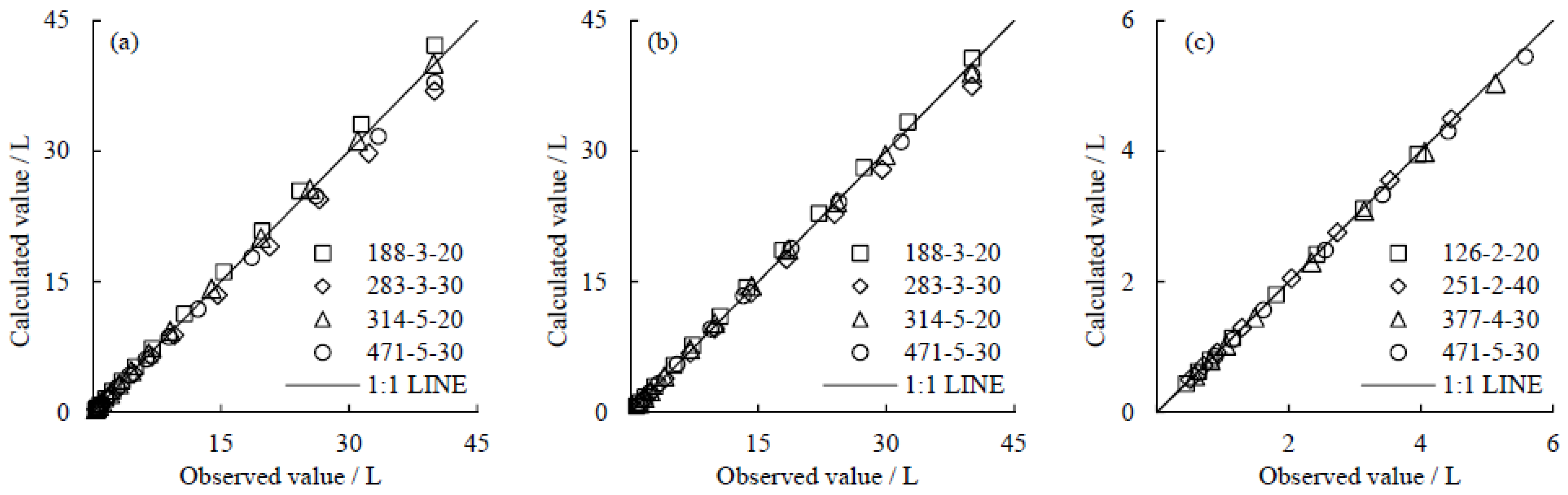
3.3. Evaluation of the Simplified Model
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Deng, X.P.; Shan, L.; Zhang, H.; Turner, N.C. Improving agricultural water use efficiency in arid and semiarid areas of China. Agric. Water Manag. 2006, 80, 23–40. [Google Scholar] [CrossRef]
- Du, S.; Kang, S.; Li, F.; Du, T. Water use efficiency is improved by alternate partial root-zone irrigation of apple in arid Northwest China. Agric. Water Manag. 2017, 179, 184–192. [Google Scholar] [CrossRef]
- Zeng, C.; Wang, Q.; Fan, J. Effect of initial water content on vertical line-source infiltration characteristics of soil. Trans. Chin. Soc. Agric. Eng. 2010, 26, 24–30. (In Chinese) [Google Scholar]
- Cheng, H.J.; Wang, Q.J.; Bai, Y.G.; Cai, J.S.; Zeng, C. Influence of line source length of vertical line source irrigation on wetted soil change characteristics. Trans. Chin. Soc. Agric. Eng. 2010, 26, 32–37. (In Chinese) [Google Scholar]
- Khatri, K.L.; Smith, R.J. Real-time prediction of soil infiltration characteristics for the management of furrow irrigation. Irrig. Sci. 2006, 25, 33–43. [Google Scholar] [CrossRef]
- Bamutaze, Y.; Tenywa, M.M.; Majaliwa, M.J.G.; Vanacker, V.; Bagoora, F.; Magunda, M.; Obandog, J.; Wasigeh, J.E. Infiltration characteristics of volcanic sloping soils on Mt. Elgon, Eastern Uganda. Catena 2010, 80, 122–130. [Google Scholar] [CrossRef]
- Bai, D.; He, J.; Guo, L.; Wang, X.; Liang, Z. Infiltration characteristics of vertical tube sub-irrigation as affected by various factors. Trans. Chin. Soc. Agric. Eng. 2016, 32, 101–105. (In Chinese) [Google Scholar]
- Li, Y.B.; Fan, Y.W.; Liu, Y.; Ma, X.Y. Influencing Factors and Simplified Model of Film Hole Irrigation. Water 2017, 9, 543. [Google Scholar] [CrossRef]
- El-Nesr, M.N.; Alazba, A.A.; Šimůnek, J. HYDRUS simulations of the effects of dual-drip subsurface irrigation and a physical barrier on water movement and solute transport in soils. Irrig. Sci. 2014, 32, 111–125. [Google Scholar] [CrossRef]
- Boštjan, N.; Kechavarzi, C.; Coulon, F.; Pintar, M. Numerical investigation of the influence of texture, surface drip emitter discharge rate and initial soil moisture condition on wetting pattern size. Irrig. Sci. 2014, 32, 421–436. [Google Scholar]
- Huang, M.; Barbour, S.L.; Elshorbagy, A.; Zettl, J.D.; Si, B.C. Infiltration and drainage processes in multi-layered coarse soils. Can. J. Soil Sci. 2011, 91, 185–197. [Google Scholar] [CrossRef]
- Khoshravesh-Miangoleh, M.; Kiani, R.A. Effect of magnetized water on infiltration capacity of different soil textures. Soil Use Manag. 2014, 30, 588–594. [Google Scholar] [CrossRef]
- Li, Z.; Wu, P.; Feng, H.; Zhao, X.; Huang, J.; Zhuang, W. Simulated experiment on effect of soil bulk density on soil infiltration capacity. Trans. Chin. Soc. Agric. Eng. 2009, 25, 40–45. (In Chinese) [Google Scholar]
- Yang, J.L.; Zhang, G.L. Water infiltration in urban soils and its effects on the quantity and quality of runoff. J. Soils Sediments 2011, 11, 751–761. [Google Scholar] [CrossRef]
- León, J.; Echeverría, M.T.; Martí, C.; Badía, D. Can ash control infiltration rate after burning? An example in burned calcareous and gypseous soils in the Ebro Basin (NE Spain). Catena 2015, 135, 377–382. [Google Scholar] [CrossRef]
- Liu, H.; Lei, T.W.; Zhao, J.; Yuan, C.P.; Fan, Y.T.; Qu, L.Q. Effects of rainfall intensity and antecedent soil water content on soil infiltrability under rainfall conditions using the run off-on-out method. J. Hydrol. 2011, 396, 24–32. [Google Scholar] [CrossRef]
- Stewart, R.D.; Rupp, D.E.; Najm, M.R.A.; Selker, J.S. Modeling effect of initial soil moisture on sorptivity and infiltration. Water Resour. Res. 2013, 49, 7037–7047. [Google Scholar] [CrossRef]
- Cheng, H. Experimental Studies on the Characteristics Soil of Water Moisture Movement and Growth Grapevine under Vertical Line Source Irrigation. Master’s Thesis, Xi’an University of Technology, Xi’an, China, 2010. (In Chinese). [Google Scholar]
- Patel, N.; Rajput, T.B.S. Effect of drip tape placement depth and irrigation level on yield of potato. Agric. Water Manag. 2007, 88, 209–223. [Google Scholar] [CrossRef]
- Šimůnek, J.; Genuchten, M.T.; Šejna, M. Development and applications of the HYDRUS and STANMOD software packages and related codes. Vadose Zone J. 2008, 7, 587–600. [Google Scholar] [CrossRef]
- Šimůnek, J.; Van Genuchten, M.T.; Šejna, M. Recent developments and applications of the HYDRUS computer software packages. Vadose Zone J. 2016, 15, 1–25. [Google Scholar] [CrossRef]
- Saito, H.; Simunek, J.; Scanlon, B.R.; Reedy, R.C. Numerical Analysis of Coupled Water, Vapor and Heat Transport in the Vadose Zone using HYDRUS. Vadose Zone J. 2006, 5, 784–800. [Google Scholar] [CrossRef]
- Skaggs, T.H.; Trout, T.J.; Šimůnek, J.; Shouse, P.J. Comparison of HYDRUS-2D Simulations of Drip Irrigation with Experimental Observations. J. Irrig. Drain. Eng. 2004, 130, 304–310. [Google Scholar] [CrossRef]
- Li, S.; Wang, Q. Simulation of Soil Water Distribution under Vertical Line Source Infiltration. Trans. Chin. Soc. Agric. Mach. 2011, 42, 51–57. (In Chinese) [Google Scholar]
- Šimůnek, J.; Van Genuchten, M.T.; Šejna, M. The HYDRUS Software Package for Simulating the Two-and Three-Dimensional Movement of Water, Heat, and Multiple Solutes in Variably Saturated Media; Technical Manual, Version 1.0; PC Progress: Prague, Czech Republic, 2006; p. 241. [Google Scholar]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Zhang, L.J.; Wang, Y.K.; Xin, X.G.; Li, H.Y. Appropriate surge spring root irrigation layout and irrigation norm of jujube on mountain land. J. Northwest A F Univ. 2010, 38, 211–217. (In Chinese) [Google Scholar]
- Carsel, R.F.; Parrish, R.S. Developing joint probability distributions of soil water retention characteristics. Water Resour. Res. 1988, 24, 755–769. [Google Scholar] [CrossRef]
- Jiang, P.; Lei, T.; Liu, X.; Yang, W.; Xin, L.; Wang, Q. Principles and experimental verification of capillary suction method for fast measurement of field capacity. Trans. Chin. Soc. Agric. Eng. 2006, 22, 1–5. (In Chinese) [Google Scholar]
- Rab, M.A.; Chandra, S.; Fisher, P.D.; Robinson, N.J.; Kitching, M.; Aumann, C.D.; Imhof, M. Modelling and prediction of soil water contents at field capacity and permanent wilting point of dryland cropping soils. Soil Res. 2011, 49, 389–407. [Google Scholar] [CrossRef]
- Philip, J.R. The Theory of Infiltration: 4. Sorptivity and Algebraic Infiltration Equations. Soil Sci. 1957, 84, 257–264. [Google Scholar] [CrossRef]
- Singh, D.K.; Rajput, T.B.S.; Singh, D.K.; Sikarwar, H.S.; Sahoo, R.N.; Ahmad, T. Simulation of soil wetting pattern with subsurface drip irrigation from line source. Agric. Water Manag. 2006, 83, 130–134. [Google Scholar] [CrossRef]
- Moriasi, D.; Arnold, J.; Van Liew, M.W.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
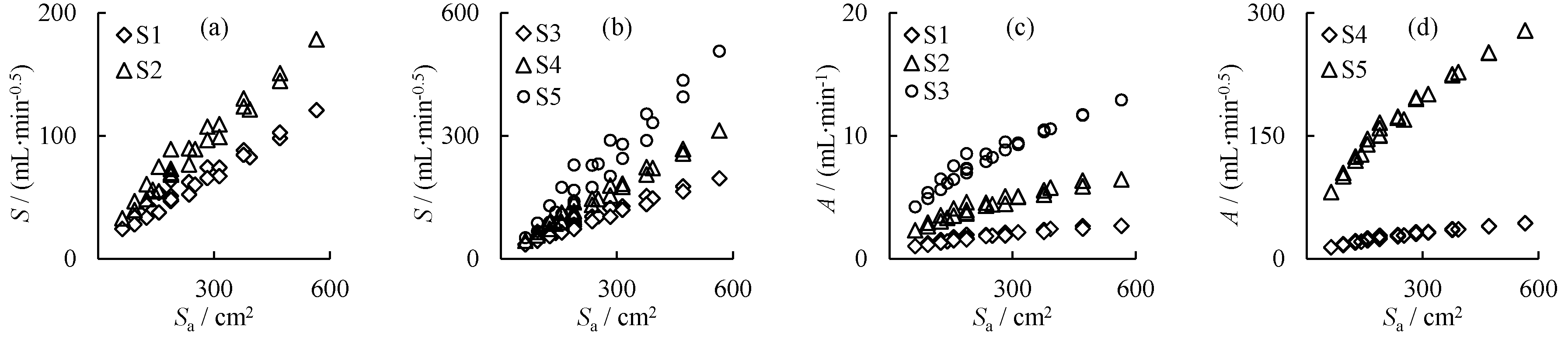


| Diameter (cm) | Length (cm) | Seepage Area (cm2) | Clay Loam | Silt Loam | Loam | Sandy Loam | Sand | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S | A | S | A | S | A | S | A | S | A | |||
| 2 | 10 | 63 | 24.21 | 1.02 | 33.09 | 2.33 | 34.96 | 4.22 | 43.87 | 13.91 | 51.39 | 81.17 |
| 15 | 94 | 33.89 | 1.28 | 46.95 | 2.95 | 50.36 | 5.38 | 66.19 | 17.75 | 87.34 | 104.66 | |
| 20 | 126 | 43.70 | 1.52 | 60.77 | 3.54 | 65.89 | 6.49 | 88.95 | 21.43 | 129.49 | 124.90 | |
| 25 | 157 | 53.60 | 1.75 | 74.86 | 4.10 | 81.67 | 7.56 | 112.62 | 24.95 | 174.12 | 146.14 | |
| 30 | 188 | 63.82 | 1.95 | 89.14 | 4.60 | 98.12 | 8.55 | 137.98 | 28.13 | 228.90 | 165.76 | |
| 3 | 10 | 94 | 28.07 | 1.14 | 39.53 | 2.66 | 43.95 | 4.90 | 57.65 | 16.66 | 66.96 | 100.63 |
| 15 | 141 | 39.47 | 1.41 | 56.12 | 3.33 | 63.46 | 6.15 | 85.62 | 21.06 | 114.16 | 127.13 | |
| 20 | 188 | 51.01 | 1.67 | 73.11 | 3.95 | 83.00 | 7.36 | 115.46 | 25.07 | 167.27 | 150.20 | |
| 25 | 236 | 62.39 | 1.92 | 89.91 | 4.57 | 102.92 | 8.51 | 146.47 | 28.85 | 228.08 | 173.34 | |
| 30 | 283 | 74.33 | 2.12 | 107.35 | 5.08 | 123.59 | 9.50 | 178.67 | 32.36 | 289.28 | 196.40 | |
| 4 | 10 | 126 | 33.48 | 1.30 | 48.43 | 3.05 | 55.15 | 5.64 | 73.43 | 19.52 | 89.46 | 119.63 |
| 15 | 188 | 46.93 | 1.60 | 68.44 | 3.75 | 79.03 | 6.98 | 108.75 | 24.20 | 139.57 | 150.41 | |
| 20 | 251 | 60.15 | 1.89 | 88.98 | 4.42 | 103.18 | 8.25 | 145.54 | 28.48 | 231.22 | 169.96 | |
| 25 | 314 | 74.13 | 2.14 | 109.39 | 5.05 | 127.80 | 9.43 | 183.33 | 32.61 | 279.36 | 200.83 | |
| 30 | 377 | 88.13 | 2.35 | 130.34 | 5.58 | 152.95 | 10.48 | 223.24 | 36.15 | 353.32 | 223.69 | |
| 5 | 10 | 157 | 37.62 | 1.51 | 54.85 | 3.51 | 64.42 | 6.45 | 89.28 | 22.39 | 108.58 | 139.51 |
| 15 | 236 | 52.31 | 1.84 | 76.76 | 4.31 | 91.62 | 7.91 | 131.77 | 27.26 | 174.43 | 171.80 | |
| 20 | 314 | 67.18 | 2.15 | 98.95 | 5.08 | 119.25 | 9.28 | 175.19 | 31.93 | 244.54 | 200.53 | |
| 25 | 393 | 82.48 | 2.44 | 121.37 | 5.80 | 147.27 | 10.57 | 221.34 | 36.03 | 331.86 | 227.52 | |
| 30 | 471 | 97.97 | 2.66 | 144.54 | 6.37 | 176.23 | 11.66 | 267.90 | 39.90 | 435.52 | 250.93 | |
| 6 | 10 | 188 | 48.13 | 1.57 | 69.93 | 3.69 | 73.04 | 7.28 | 105.56 | 25.17 | 132.16 | 159.15 |
| 15 | 283 | 65.59 | 1.90 | 96.68 | 4.48 | 102.91 | 8.86 | 154.40 | 30.38 | 201.64 | 194.72 | |
| 20 | 377 | 84.37 | 2.18 | 123.78 | 5.20 | 133.32 | 10.34 | 205.64 | 35.06 | 288.74 | 224.75 | |
| 25 | 471 | 102.50 | 2.45 | 150.73 | 5.90 | 164.26 | 11.72 | 256.96 | 39.65 | 394.96 | 251.61 | |
| 30 | 565 | 120.73 | 2.67 | 178.33 | 6.44 | 196.17 | 12.91 | 312.54 | 43.51 | 506.28 | 278.22 | |
| Soil Texture | a | b | c | d |
|---|---|---|---|---|
| Minqin sandy loam | 0.521 | 29.91 | 0.017 | 10.48 |
| Minqin aeolian sand | 1.181 | 21.38 | 0.183 | 62.65 |
| Soil | MAE (L) | RMSE (L) | PBIAS (%) | NSE |
|---|---|---|---|---|
| Sandy loam from Hexi Corridor | 0.480 | 0.908 | 0.444 | 0.995 |
| Aeolian sand from Hexi Corridor | 0.428 | 0.642 | 0.321 | 0.997 |
| Clay loam from Turpan Depression | 0.028 | 0.043 | 0.900 | 1.000 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, Y.; Huang, N.; Gong, J.; Shao, X.; Zhang, J.; Zhao, T. A Simplified Infiltration Model for Predicting Cumulative Infiltration during Vertical Line Source Irrigation. Water 2018, 10, 89. https://doi.org/10.3390/w10010089
Fan Y, Huang N, Gong J, Shao X, Zhang J, Zhao T. A Simplified Infiltration Model for Predicting Cumulative Infiltration during Vertical Line Source Irrigation. Water. 2018; 10(1):89. https://doi.org/10.3390/w10010089
Chicago/Turabian StyleFan, Yanwei, Ning Huang, Jiaguo Gong, Xiaoxia Shao, Jie Zhang, and Tong Zhao. 2018. "A Simplified Infiltration Model for Predicting Cumulative Infiltration during Vertical Line Source Irrigation" Water 10, no. 1: 89. https://doi.org/10.3390/w10010089
APA StyleFan, Y., Huang, N., Gong, J., Shao, X., Zhang, J., & Zhao, T. (2018). A Simplified Infiltration Model for Predicting Cumulative Infiltration during Vertical Line Source Irrigation. Water, 10(1), 89. https://doi.org/10.3390/w10010089






