Abstract
Identification of the key environmental indicators (KEIs) from a large number of environmental variables is important for environmental management in tidal flat reclamation areas. In this study, a modified principal component analysis approach (MPCA) has been developed for determining the KEIs. The MPCA accounts for the two important attributes of the environmental variables: pollution status and temporal variation, in addition to the commonly considered numerical divergence attribute. It also incorporates the distance correlation (dCor) to replace the Pearson’s correlation to measure the nonlinear interrelationship between the variables. The proposed method was applied to the Tiaozini sand shoal, a large-scale tidal flat reclamation region in China. Five KEIs were identified as dissolved inorganic nitrogen, Cd, petroleum in the water column, Hg, and total organic carbon in the sediment. The identified KEIs were shown to respond well to the biodiversity of phytoplankton. This demonstrated that the identified KEIs adequately represent the environmental condition in the coastal marine system. Therefore, the MPCA is a practicable method for extracting effective indicators that have key roles in the coastal and marine environment.
1. Introduction
Coastal tidal flats have often been reclaimed to moderate the conflict between population growth and land scarcity [1]. In China, about 1.12 million hectare (ha) of coastal flats has been reclaimed since 1979 [2], and the number will increase another 0.25 million ha by 2020 [3]. Numerous studies have noted that the reclamation has noticeable effects on the coastal marine environment [4,5,6,7]. To characterize the local environment with changes that are caused by reclamation and evaluate the environmental effect of reclamation activity, it is essential to identify the key environmental indicators (KEIs) from a large number of environmental variables. The KEIs also provide useful tools for tracking the environmental progress, supporting policy evaluation, and informing the public about coastal and marine governance.
Environmental issues often involve analysis of a wide range of variables simultaneously. Principal component analysis (PCA) can effectively reduce the dimension of a multivariate data set by using only the first few principal components (PCs) [8], while still preserving its structure to the extent possible [9]. Therefore, PCA has been commonly employed in environmental fields to identify the KEIs. For example, Pejman et al. used PCA to extract the most significant parameters contributing to water quality variations for all seasons in Haraz River Basin in India [10]. Yang and Yao et al. identified the soil organic matter as an indispensable enabling factor of soil quality from a total of 22 soil properties on the coast in the northern of Jiangsu province of China [11,12]. With the PCA method, Berger et al. selected five variables as the most key water quality variables, including electric conductivity, oxygen concentration, caffeine, silicate, and toxic units with respect to pesticides, and they were significantly correlated with the ecological quality in German streams [13]. Ouyang et al. extract the parameters that are most important in assessing seasonal variations of river water quality from 16 physical and chemical parameters in LSJR basin, USA [14]. In the coastal and marine region, González-Oreja and Sáiz-Salinas applied PCA to propose the dissolved oxygen from the data set of 30 abiotic variables as the key environmental factor controlling the distribution of benthos in the Bilbao and Plentzia estuary, Spain [15]. Performing PCA on the long-term data of physico-chemical and biological variables in the Nervión estuary, Borja et al. confirmed the redox potential, dissolved oxygen and metal concentrations of the sediments to be the critical controllers determining the local benthic structure [16]. Looi et al. extracted the seven major components out of 28 variables by 48 samples of the coastal water of the Straits of Malacca, Malaysia, with relation to the pollution contribution from minerals-related parameters, natural and anthropogenic sources [17]. Udayakumar et al. used PCA to locate the major parameter affecting the ecological health of the coastal water in the Mangalore coastal region in India [18]. On the basis of PCA, Iyer et al. constructed a statistical model to explain the relationships between the various physicochemical variables and the environmental conditions in the Cochin coast in south west India [19]. Wilbers et al. identified the four key factors to explain the presence of pollution in surface water from the dataset of 32 sampling locations in the Mekong Delta of Vietnam [20]. In the Kuwait Bay, AI-Mutairi et al. calculated three principal components responsible for water quality variations, in which the first component included DO and pH, the second including PO4, TSS, and NO3, and the last containing seawater temperature and turbidity [21]. The PCA also has been performed to compare the heavy metal composition among the coastal sediments and reduce the dimensionality of the original chemical variables into a few factors to identify the noteworthy elements in the contaminated areas [22,23]. Simeonov et al. defined the structure of the 15 analytes sediment data collected from the western coastline of the USA as four latent factors conditionally named “anthropogenic”, “organic”, “natural”, and “hot spots” [24]. Pereira et al.s’ work demonstrated the importance of organic matter content and the fine-grained fraction of sediments on the control of the bioavailable metals distribution in the Paraguaçu estuary, Brazil [25]. However, these previous attempts were conducted primarily based on the numerical divergence of a data set but with inadequate consideration of the other two important attributes: pollution status and temporal variation. In addition, the Pearson’s linear correlation was frequently used to detect the correlations of the environmental variables, whereas they are often inherently nonlinear in nature [26].
The objective of this study is to develop an approach to identify the KEIs accounting for all three important attributes of the environmental variables and their nonlinear interrelationships. To achieve this, a modified PCA method (MPCA) was proposed. The three attributes were taken as coordinates to construct a three-dimensional environmental characteristic space, and the distance correlation (dCor) was used to measure the nonlinear interrelationships between the variables. The MPCA was applied to determine the KEIs in the Tiaozini sand shoal, which is a large-scale tidal flat reclamation region in China. The identified KEIs were shown to successfully represent the local environmental characteristics. The approach provides a practicable tool to identify the KEIs for assessing the environment quality in coastal reclamation areas. The results can be used as part of a framework to assess the effects of coastal reclamation and relevant policies, as well as provide subsequent ecosystem services for protecting coastal and marine environments. The results can also be used to provide technological support for the establishment of coastal environmental monitoring and administration system for conservation and sustainable development of marine resources.
2. Methods and Materials
2.1. MPCA
Assume that A is an (m × n) matrix containing measurements of n environmental variables, each measured at m sampling sites. Firstly, A was normalized through the properties of data divergence, variables pollution status, and temporal variation to develop three matrixes D, P, and T.
- (i)
- Matrix of data divergence D = [dij](m×n)where, aij is the value of the jth variable measured at the ith sampling site; is the spatial average of the jth variable; σj is the spatial standard deviation of the jth variable; and, dij is the data divergence of aij, which indicates the spatial differentiation of the jth variable.
- (ii)
- Matrix of pollution status P = [pij](m×n)where, pij is the pollution index of aij; Sj is the environmental quality standard of the jth variable; pH is the power of hydrogen in water; pHju, pHjd are the upper and lower limits of pH standard value, respectively; and, DOf is the saturation concentration of dissolved oxygen in water. A pij greater than 1.0 indicates that the value of aij exceeds the environmental quality guidelines.
- (iii)
- Matrix of temporal variation T = [tij](m×n)where, tij is the temporal fluctuation intensity of aij; is the measurement at the kth monitoring; is the temporal average of aij; l is the total monitoring times. sgn is the sign function with a value of 1 if there is an overall increasing tendency of aij and −1 otherwise. The bigger the absolute value of tij, the larger the temporal variation of aij.
The spatial distribution, pollution status, and the temporal variation of an environmental variable are independent, and thus can be used to construct a three-dimensional characteristic space (C-Space). Mathematically, dij, pij, and tij are the projected lengths of aij on the respective coordinates of the C-Space (Figure 1). The measurement vector of any variable in the three-dimensional space can be written as:
where, vij is the measurement vector of the jth variable at the ith sampling site; , , and are the three coordinate vectors, respectively, in the C-Space. Thus, vij indicates the integrated environmental feature of the jth variable at the ith sampling site.
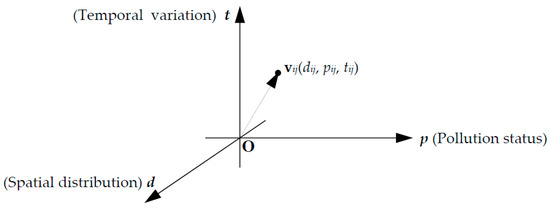
Figure 1.
Sketch of the C-Space and the vector of an arbitrary variable measurement.
In a normal PCA, the Pearson’s correlations for variables are calculated to indicate their paired linear dependences. However, in an environmental system, these dependences usually show a strong non-linear nature [26] and are difficult to effectively detect by the Pearson’s correlation. This study uses the distance correlation (dCor) instead to measure the relationships of the environmental variables. This method has been shown to have remarkable advantages in detecting non-linear or non-monotone relationships among random variables [27].
Firstly, defining the C-Space distance of the αth variable vα:
where, is the Euclidean norm; φkl is the C-Space distance between the kth and the lth sampling site of the αth variable vα.
Similarly:
where, ϕkl is the distance between the kth and the lth sampling site of the βth variable vβ.
The empirical distance covariance (dCov) of vα and vβ can be calculated as:
Then, the empirical distance correlation (dCor) is given as:
Based on the dCor among the environmental variables, the comprehensive matrix R can then be established as:
The eigenvalue problems of matrix R can be solved:
where, λ is the eigenvalue; I is the identity matrix. The eigenvectors of R are the principal components (PCs), and their orders are determined based on the magnitude of their corresponding eigenvalues. The eigenvector with the largest eigenvalue best represents A and is defined as the first PC. Similarly, the eigenvector with the second-largest eigenvalue best represents the residual left in A once the first eigenvector has been removed and is defined as the second PC. Each subsequent eigenvector is defined the same way. Typically, only the top several PCs are needed to achieve a high level of discriminating accuracy with an accumulated contribution rate greater than 75%. Herein, the contribution rate of the gth PC is computed as:
where, cg and λg are the contribution rate and eigenvalue of the gth PC, respectively.
The criteria proposed by Andrews et al. [28] is then employed to determine the most appropriate indicators from the remaining PCs to construct the KEIs of the environmental variables: (1) Only the variables with a factor loading (the corresponding element of the eigenvector) within 10% of the highest factor loading (using absolute values) are retained from each remaining PC; (2) If the variables are correlated (correlation coefficient of >0.60 and significant (two-tailed) at ϸ ≤ 0.01), the variable with the highest sum of correlation coefficients (absolute values) is retained for the KEIs; otherwise, all of the variables are retained. The variables contained in the KEIs are the most important contributors to the integrated environmental condition of spatial distribution, marine pollution, and temporal variation. The main steps of the MPCA are illustrated in Figure 2.
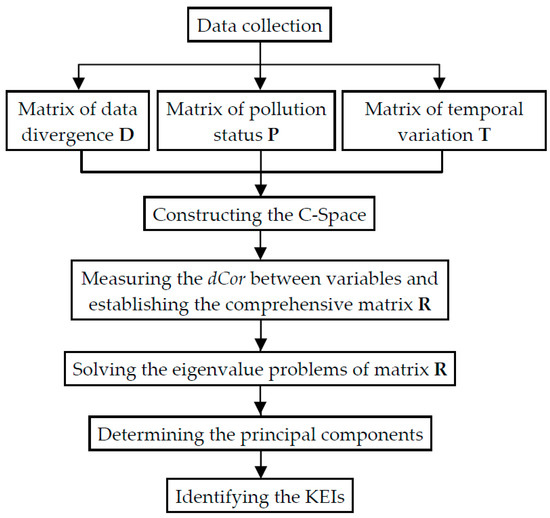
Figure 2.
Flow-chart of the main steps used to perform the modified principal component analysis approach (MPCA).
2.2. Application Area
The Tiaozini sand shoal is a roughly 52,882 ha large silt-muddy flat on the coast in the northern of Jiangsu province in China, embraced by the radiative sand ridge in the Yellow Sea with stable and relatively high-speed deposition in recent decades [29]. According to the Jiangsu Coastal Development Program (China’s National Development and Reform Commission (NDRC), 2009), the local government planned a large-scale reclamation project covering a 22,773.33 ha area in this flat to ease the mounting shortage of the agricultural land resource, named as Tiaozini Land Reclamation (Figure 3). The project was designed to be carried out over three phases to reclaim 6746.67 ha, 8446.67 ha, and 7579.99 ha of the land successively. Phase I was completed in July 2013 and the other two have not yet been started. In this study, the proposed MPCA was applied to identify the KEIs in the reclamation region using the environmental data collected before and after the Phase I project.
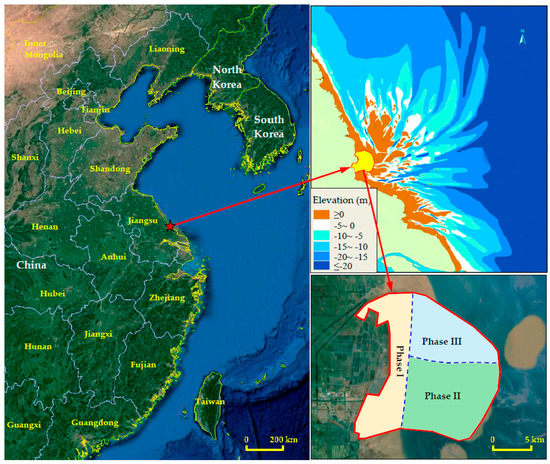
Figure 3.
Geographical location of the Tiaozini Land Reclamation (32°42′28.61′′ E to 32°52′56.25′′ E and 120°53′35.10′′ N to 121°04′51.13′′ N).
2.3. Field Sampling
We carried out the field sampling effort in September 2013, after the completion of the Phase I project. The marine monitoring system included 12 sampling sites (Figure 4). Eight water quality variables plus seven variables in the sediment compartment were measured at each site. pH, dissolved oxygen (DO), chemical oxygen demand (COD), dissolved inorganic nitrogen (DIN), soluble reactive phosphorus (SRP), petroleum (PETRO), as well as heavy metals Cd and Hg were measured in the water column. Sulphide, total organic carbon (TOC), PETRO, total Kjeldahl nitrogen (TKN), total phosphorus (TP), Cd, and Hg were measured in the sediment sample. We conducted the marine phytoplankton measurements synchronously. Historical monitoring data of the same variables in April 2010 were collected from an official report of “Marine environmental monitoring report for Tiaozini Reclamation Region” (Jiangsu Marine Environmental Monitoring and Forecasting Center, Jiangsu Marine fisheries research institute, 2010) in order to represent the environmental status of the area before reclamation.
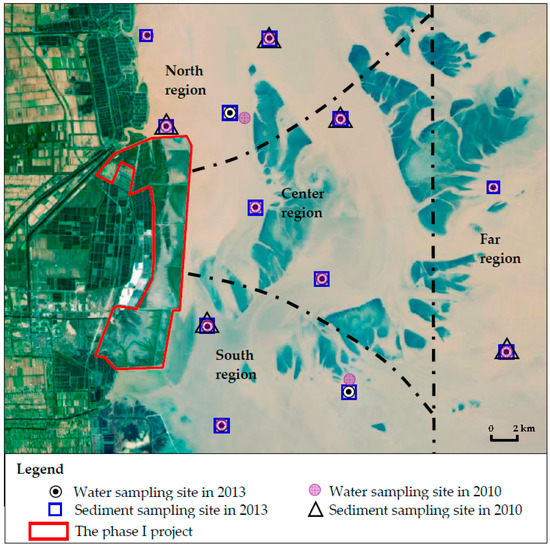
Figure 4.
Location of the sampling sites.
All the samples were collected, stored, and analyzed according to China’s national standard “Specification of Oceanographic Survey” (GB/T 12763-2007) and “Specification for Marine Monitoring” (GB 17378-2007) issued by the General Administration of Quality Supervision, Inspection and Quarantine and the Standardization Administration of China, as well as “Technical specification of marine biological quality monitoring” (HY/T 078-2005) issued by the State Oceanic Administration of China.
Descriptive statistics was conducted to describe the main characteristics of the coastal environment in the study area both pre- (Table 1) and post (Table 2) the Phase I project. The corresponding limits of each variable as per the environmental quality guidelines of China Sea Water Quality Standard (CSWQS GB 3097-1997) and China Marine Sediment Quality (CMSQ GB 18668-2002) are also listed in Table 1 and Table 2.

Table 1.
Descriptive statistics of measured variables of water and sediment samples pre-Phase I (April 2010).

Table 2.
Descriptive statistics of measured variables of water and sediment samples post-Phase I (September 2013).
Figure 5 compares the environmental variable measurements (mean value with spatial standard deviation) between pre- and post-Phase I project. Monitoring data indicated that the spatial and temporal variations in the concentrations of pH and DO were relatively stable. After the Phase I project, the concentrations of PETRO increased noticeably both in the water column and sediment, largely because of the oil spill of working vessels and oily wastewater discharge from working equipment during the land reclamation. The concentrations of all the other variables showed different degrees of decrease.
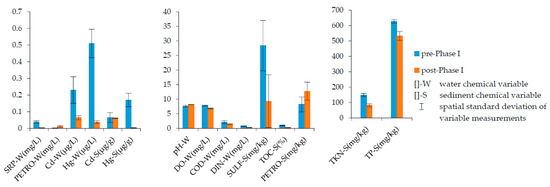
Figure 5.
Comparison of environmental variable measurements between pre- and post-Phase I project.
Figure 6 demonstrates the temporal variation in the Shannon-Wiener index, Rmargalef and Pielou index of phytoplankton (mean value with spatial standard deviation) before and after the Phase I project. The spatial distributions of the post-Phase I biodiversity indices were more symmetrical than those of the pre-Phase I. Overall, the Shannon-Wiener index and Rmargalef of phytoplankton increased, and the Pielou index reduced slightly post the land reclamation.
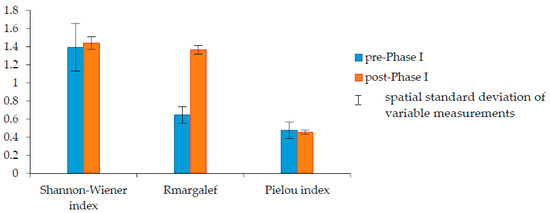
Figure 6.
Comparison of phytoplankton biodiversity between pre- and post-Phase I project.
3. Results
All the monitoring variables were taken as potential environmental indicators (PEIs). A pool of attributes consisting of 8 water variables (pH, DO, COD, DIN, SRP, PETRO, Cd, Hg) and seven sediment variables (Sulphide, TOC, PETRO, TKN, TP, Cd, Hg) were established. Due to the limited pre-reclamation sediment data (there were 12 sediment sampling sites in 2013 but only 5 in 2010), the temporal fluctuation intensity of the variables could not be calculated at every site. To deal with this issue, the study area was divided into four sub-regions: North, Center, South, and Far, each includes at least one sediment sampling site and several water sampling sites in both years (Figure 4). The spatial averages of each variable during pre- and post-Phase I periods were calculated in each sub-region. Then Equation (3) was used to obtain the sub-region’s overall temporal fluctuation intensity. Given that the temporal fluctuation intensity of a variable at any sampling site can be approximately represented by the overall value of the sub-region in which the site is located, the matrix T in the study area could be obtained. The matrix D and P were constructed using Equations (1) and (2), respectively, with the data set measured in September 2013 (Table 2) to highlight the spatial distribution and environmental quality of the variables post the Phase I reclamation and avoid overuse of the historical data. Thus, the measurement vectors in the C-Space could be built according to Equation (4).
The pollution status (p), temporal variation (t), and spatial variation (d) of all the PEIs are illustrated in the box charts shown in Figure 7. Both pollutant statuses and temporal fluctuation intensities show strong variations among the measured variables, while the spatial variations appear closer to each other. The variable measurements could meet the water and sediment quality objectives in general, except for DIN (p ranged from 0.51 to 1.81); at all of the sampling sites, PETRO in the water column significantly rose (t ranged from 0.44 to 0.68) and Hg in the sediment experienced a huge change (t ranged from −0.98 to −0.91) post the reclamation.
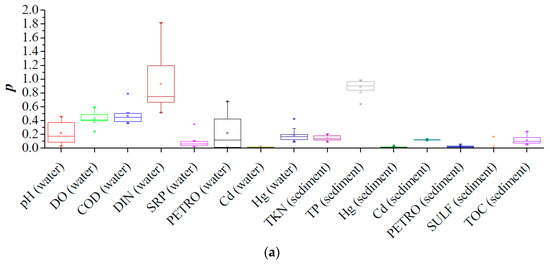
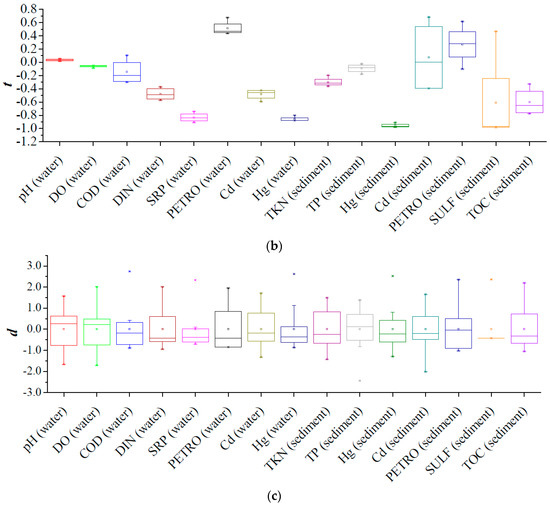
Figure 7.
The box charts of (a) pollution status; (b) temporal variation; and, (c) spatial variation of the variable measurements.
The distance correlations among the variables were calculated using Equations (5)–(8) and are shown in Table 3.

Table 3.
Distance correlations (dCor) among the measured variables across the reclamation area.
The Kaiser Meyer Olkin test (KMO) was first performed to measure the sampling adequacy for the appropriateness to proceed with a factor analysis. The KMO result was 0.884, confirming the sampling to be adequate for the PCA analysis. The MPCA was then conducted to select the representative quality indicators to construct the KEIs from the pool of PEIs.
The results presented in Table 4 show that the first four PCs accounted for 79.71% of the total characteristics of the coastal marine system, and the extraction rate of different variables ranged from 73.82% to 92.14%. Therefore, these PCs contained the primary information of the original data set. The order by which the PCs were interpreted was determined by the magnitude of their eigenvalues. The first PC explained 57.52% of the variance. The factor loadings of all the variables in the first PC were positive and showed relatively narrow differences. PC1 included six highly weighted variables of which the factor loadings were within 10% of the highest one: CdW (0.288), pHW (0.273), DOW (0.283), HgW (0.278), SulphideS (0.268), and TOCS (0.267). It also had the moderate loadings from DINW (0.251), CODW (0.250), TKNS (0.254), and TPS (0.252), which could be explained by nutrient condition in the water column and sediment. The highest loading from CdW was the result of significant correlation that existed among pHW, DOW, SRPW, CODW, HgW, TKNS, SulphideS, CdS and CdW (Table 3). Because all of the highly weighted variables comprised in this component were significantly correlated (dCor > 0.6 and ϸ < 0.01) with CdW except TOCs (see Table 3), PC1 could be identified as the “aqueous toxin and organic pollution component”.

Table 4.
MPCA results for selecting the key environmental indicators (KEIs) from the studied samples.
The second PC explained 9.14% of the variance with high factor loading from DINW (−0.479) and a moderate factor loading from pHW (−0.399), DOW (−0.325), SRPW (0.390), SulphideS (0.323), and TOCS (0.316). PC2 could be identified as the “eutrophication component” since it mainly explained variations in characters that are related to the marine eutrophication. In PC2, DINW correlated strongly with pHW (dCor = 0.918 and ϸ < 0.01) and DOW (dCor = 0.826 and ϸ < 0.01), and weakly with SRPW (dCor = 0.373 and ϸ > 0.05), SulphideS (dCor = 0.374 and ϸ > 0.05) and TOCS (dCor = 0.495 and ϸ > 0.05) (Table 3). The negative loading of DINW and DOW in PC 2 and their strongly interrelationship were perhaps due to nitration/denitrification in the coastal region. This also suggests that an increasing in DO concentration would favor the nitrogen process, thus increasing the DINW value.
The third and fourth PC explained 7.24% and 5.81% of the variance with high factor loading from PETROW (0.574) and HgS (0.517), respectively, and could be termed the “construction pollution component” as well as the “sedimentary toxin component”. The sum of correlation coefficients of PETROW (7.595) and HgS (8.129) were the lowest in the water and sediment variables, respectively (see Table 3). Except for CdS, the dCor of PETROW with any other measurement variables was less than 0.60. It was the same for HgS except for with TOCS. This showed that these two indicators were relatively independent among the measured variables.
In PC1, the six highly weighted variables could be divided into two significantly correlated groups: pHW-CdW-DOW-HgW of the water column and TOCS-SulphideS of the sediment compartment. CdW and TOCS were the ones with the highest sum of correlation coefficients (9.553 and 8.921, see Table 3) in each group, respectively. Both CdW and TOCS were retained in the KEIs due to their relatively weak correlation (dCor = 0.581 and ϸ > 0.01, see Table 3). Only one indicator was highly weighted in PC2 (DINW), PC3 (PETROW) and PC4 (HgS), respectively. Thus, the KEIs are comprised of CdW, DINW, PETROW, TOCS, and HgS.
4. Discussion
In the KEIs, CdW, and TOCS selected from PC1 were the most highly correlated in the water and sediment variables, respectively. CdW well correlated (dCor > 0.60) with the toxic pollutant indices SulphideS, CdS and HgW, as well as the eutrophication indices SRPW, DOW, CODW, and TKNS. The strongest correlations existed between CdW and SulphideS (0.822, ϸ < 0.01) and between CdW and SRPW (0.735, ϸ < 0.01) within the two groups, respectively. This is related to the precipitation of Cd sulfide [31] and good correlation between Cd and PO4 [32] in the seawater. Many studies indicated that Cd could act as either a toxin or a tracer nutrient in marine environments [33,34,35,36]. In agreement with the previous research, CdW held the largest factor loading (0.288) in PC1, thus playing a critical role in the coastal environment.
TOCS, also selected from PC1, is a direct measure of the organic matter content in the sediment. Table 3 shows that TOCS strongly correlated with SulphideS (0.805, ϸ < 0.01) and HgS (0.780, ϸ < 0.01), and thus could be considered as a major controlling factor for toxin matter enrichment in sediments. This agrees with previous studies such as [37,38,39,40,41]. In addition, TOCS correlated strongly with SRPW (0.724, ϸ < 0.01), but relatively weakly with TPS (0.484, ϸ > 0.05) in the study area. This is consistent with the findings of Hong et al. [42] on the relationship between the organic matter and phosphorus in the Southwest Yellow Sea. The distribution of TOCS had remarkable effects on the circulation process of phosphorus in the study area, and thus could be considered a sensitive geochemical indicator.
DINW, PETROW and HgS were the only high factor loading indicators in PC2, PC3 and PC4, respectively. As can be seen from Table 4, PC2 explained 9.14% of the total characteristics of which DINW made the most contribution (−0.479). DINW was also the only variable exceeding the CSWQS guideline during the monitoring period post Phase I reclamation (maximum value of the pollution status p was 1.81, see Figure 7a). According to the Bulletin of Marine Environmental Quality of Jiangsu Province [43,44,45,46], DINW is the main pollutant of seawater in the region. The nutrient contamination is one of the fundamental characteristics of the local marine water environment. Therefore, it is reasonable to identify DINW as the key indicator to represent eutrophication conditions in the reclamation area. PETROW and HgS were relatively independent among the PEIs. PETROW, with the highest factor loading (0.574) in PC3, increased sharply after the Phase I reclamation (see Figure 7b) largely due to the oil pollution of the construction equipment. Therefore, it could be reasonably chosen as the representative contaminant of the high-duty construction of reclamation. As the biggest contributor to PC4, HgS showed the highest absolute temporal fluctuation at all the sampling sites (|t| > 0.90, see Figure 7b). The relative independence and drastic change made it sensible to select HgS to be an important indicator in the region.
Because of the direct dependency and high sensitivity of phytoplankton communities on the environmental variables in the coastal marine system [47,48], the biodiversity of phytoplankton was used as the response data of the local environmental conditions impacted by reclamation. Figure 8 illustrates the comparison of the measurements of KEIs between pre- and post-Phase I project. After the reclamation, the concentrations of CdW, TOCS, DINW, and HgS significantly decreased; although the concentration of PETROW increased, it remained at a rather low level. These variations indicate that the local environmental condition after the reclamation favored the development of phytoplankton more than the pre-reclamation condition in the region. This is consistent with the performance of the biodiversity of phytoplankton (see Figure 6). To further evaluate the validity of the selected KEIs, multiple regression analysis was conducted using the KEIs as independent variables and the biodiversity indices as dependent variables. The multiple regressions yielded coefficients of determination (R2) of 0.996 for Rmargalef, 0.918 for the Shannon-Wiener index, and 0.938 for the Pielou index after the Phase I project, as well as 0.994 for Rmargalef, 0.912 for the Shannon-Wiener index, and 0.957 for the Pielou index before the Phase I project (Table 5). The results suggested that the identified KEIs were well representative of the coastal environmental system.
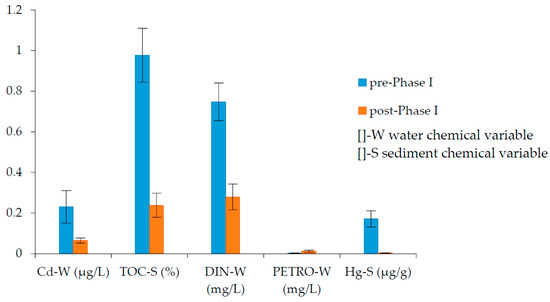
Figure 8.
Comparison of measurements of the KEIs between pre- and post Phase I project.

Table 5.
Multiple regressions of the KEIs on the phytoplankton biodiversity.
PCA has become a frequently used tool of identifying the KEIs in environmental applications due to its advantage of effective dimensionality reduction with minimal information loss. Many researchers had performed PCA to reduce the dimensionality of environmental variables to identify the key elements [17,22,23,24], locate the critical controllers in determining the local aquatic structure [15,16,49,50,51], as well as reveal the KEIs responsible for water quality variations [18,19,20,21,25]. In the normal PCA algorithm, the Pearson’s correlation was often used to measure the correlations of the environmental variables and construct the correlation coefficient matrix R for the subsequent factor analysis. However, the Pearson’s correlation is difficult to be applicable when the interrelationships of the variables are nonlinear. For example, we calculate the Pearson’s correlation coefficient of CdW with SulphideS, CdW with SRPW, CdW with pHW, CdW with DOW, TOCS with HgS, and TOCS with SulphideS in the C-space of the study region. The results indicate that the correlation coefficients are −0.329, 0.0975, −0.0191, −0.146, −0.208, and −0.406, respectively, and their significant values (two-tailed) are all larger than 0.05. The Pearson’s correlation can’t capture the strong nonlinear relationships among these variables. The errors should cause the information distortion of high loading factors in the subsequent factor analysis, and negatively affect the determining results of KEIs in the system. In this study, the adoption of the distance correlation (dCor) solves this problem effectively. The validation test of KEIs demonstrates that the proposed MPCA is a suitable method for identifying the KEIs in the coastal and marine environment. The method also can be extended to extract the key indicators to support environmental quality management in other regions across the world where the environmental systems present the non-linear or non-monotone characteristics.
5. Conclusions
A modified principal component analysis approach (MPCA) has been developed to identify the KEIs. In the MPCA algorithm, a characteristic space composed of three attribute dimensions of spatial distribution, pollution status, and temporal variation of environmental variables was constructed to embody their integrated environmental characteristics. The distance correlation (dCor) was introduced to detect the nonlinear relationships inherently existing between these variables. The MPCA was applied to identify the KEIs from the PEIs consisting of eight water plus seven sediment chemical variables in the Tiaozini large-scale tidal flat reclamation area. The identified KEIs in the reclamation area included DIN, Cd, and PETRO in the water column, and Hg, TOC in the sediment. Satisfactory responses of the KEIs to the biodiversity of phytoplankton both pre- and post-Phase I project indicate that the selected KEIs adequately represent the environmental condition of the reclamation region. Therefore, the proposed MPCA is suitable for extracting effective indicators that play key roles in the coastal and marine environment. The use of the KEIs can help policy makers and researchers to monitor the environmental changes in coastal reclamation area and make informative decisions on selecting management strategies for the sustainable development and utilization of seawater resources. Next, efforts should be devoted to using more cases to further test the validation of the MPCA in different coastal and marine systems. It will also be of interest to collect long time-serial data to analyze the complex interrelationships between the KEIs and marine plankton, and discuss the environmental behavior and ecological effects of the KEIs with specially designed numerical experiments in the study region.
Acknowledgments
This work was financially supported by the State Key Program of National Natural Science of China (Grant No. 51739002), the National Nature Science Foundation of China (Grant No. 51379060, 51379058, 51479064 and 51308183), Qing Lan Project, the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD), National Key Technology R&D Program (Grant No. 2012BAB03B04), and the China Scholarship Council (CSC).
Author Contributions
Kejian Chu and Zulin Hua conceived and designed the algorithm; Wenjuan Liu, Min Tan and Yongzhi Jia collected the data; Kejian Chu, Wenjuan Liu, Xiaodong Liu and Li Gu analyzed the data; Kejian Chu wrote the manuscript; Yuntong She revised and edited the manuscript.
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
References
- Yue, Q.; Zhao, M.; Yu, H.M.; Xu, W.; Ou, L. Total quantity control and intensive management system for reclamation in China. Ocean Coast. Manag. 2016, 120, 64–69. [Google Scholar] [CrossRef]
- Meng, W.Q.; Hua, B.B.; He, M.X.; Liu, B.Q.; Mo, X.Q.; Li, H.Y.; Wang, Z.L.; Zhang, Y. Temporal-spatial variations and driving factors analysis of coastal reclamation in China. Estuar. Coast. Shelf Sci. 2017, 191, 39–49. [Google Scholar] [CrossRef]
- Ma, Z.J.; Melville, D.S.; Liu, J.G.; Chen, Y.; Yang, H.Y.; Ren, W.W.; Zhang, Z.W.; Piersma, T.; Li, B. Rethinking China’s new great wall. Science 2014, 346, 912–914. [Google Scholar] [CrossRef] [PubMed]
- Protecting and Conserving the North-East Atlantic and it’s resources (OSPAR). Assessment of the Environmental Impact of Land Reclamation, Biodiversity Series; Publication Number 368/2008; OSPAR Commission: London, UK, 2008; pp. 13–14. [Google Scholar]
- Angus, T.L.L. China’s greatest leap forward and the ones left behind: The twofold problem causing the rise in land disputes: Land reclamation and environmental degradation. Tulane Environ. Law J. 2008, 21, 341–390. [Google Scholar]
- Humood, A.N. The role of environmental impact assessment in protecting coastal and marine environments in rapidly developing islands: The case of Bahrain, Arabian Gulf. Ocean Coast. Manag. 2015, 104, 159–169. [Google Scholar]
- Lai, S.; Loke, L.H.L.; Hilton, M.J.; Boumac, T.J.; Todd, P.A. The effects of urbanisation on coastal habitats and the potential for ecological engineering: A Singapore case study. Ocean Coast. Manag. 2015, 103, 78–85. [Google Scholar] [CrossRef]
- Magyar, N.; Hatvani, I.G.; Székely, I.K.; Herzig, A.; Dinkad, M.; Kovácsa, J. Application of multivariate statistical methods in determining spatial changes in water quality in the Austrian part of Neusiedler See. Ecol. Eng. 2013, 55, 82–92. [Google Scholar] [CrossRef]
- Pozo, C.; Ruíz-Femeniab, R.; Caballerob, J.; Guillén-Gosálbeza, J.; Jiméneza, L. On the use of Principal Component Analysis for reducing the number of environmental objectives in multi-objective optimization: Application to the design of chemical supply chains. Chem. Eng. Sci. 2012, 69, 146–158. [Google Scholar] [CrossRef]
- Pejman, A.H.; Nabi Bidhendi, G.R.; Karbassi, A.R.; Mehrdadi, N.; EsmaeiliBidhendi, M. Evaluation of spatial and seasonal variations in surface water quality using multivariate statistical techniques. Int. J. Environ. Sci. Technol. 2009, 6, 467–476. [Google Scholar] [CrossRef]
- Yang, J.S.; Yao, R.J. Evaluation of soil quality in reclaimed coastal regions in North Jiangsu Province. Chin. J. Eco-Agric. 2009, 17, 410–415. [Google Scholar] [CrossRef]
- Yao, R.J.; Yang, J.S.; Gao, P.; Zhang, J.B.; Jin, W.H. Determining minimum data set for soil quality assessment of typical salt-affected farmland in the coastal reclamation area. Soil Tillage Res. 2013, 128, 137–148. [Google Scholar] [CrossRef]
- Berger, E.; Haase, P.; Kuemmerlen, M.; Leps, M.; Schafer, R.B.; Sundermann, A. Water quality variables and pollution sources shaping stream macroinvertebrate communities. Sci. Total Environ. 2017, 587, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Ouyang, Y.; Nkedi-Kizza, P.; Wu, Q.T.; Shinde, D.; Huang, C.H. Assessment of seasonal variations in surface water quality. Water Res. 2006, 40, 3800–3810. [Google Scholar] [CrossRef] [PubMed]
- González-Oreja, J.A.; Sáiz-Salinas, J.I. Exploring the relationships between abiotic variables and benthic community structure in a polluted estuarine system. Water Res. 1998, 32, 3799–3807. [Google Scholar] [CrossRef]
- Borja, A.; Muxika, I.; Franco, J. Long-term recovery of soft-bottom benthos following urban and industrial sewage treatment in the Nervión estuary (southern Bay of Biscay). Mar. Ecol. Prog. Ser. 2006, 313, 43–55. [Google Scholar] [CrossRef]
- Looi, L.J.; Aris, A.Z.; Johari, W.L.W.; Yusoffc, F.M.; Hashim, Z. Baseline metals pollution profile of tropical estuaries and coastal waters of the Straits of Malacca. Mar. Pollut. Bull. 2013, 74, 471–476. [Google Scholar] [CrossRef] [PubMed]
- Udayakumar, P.; Abhilash, P.P.; Ouseph, P.P. Assessment of water quality using principal component analysis—A case study of the Mangalore coastal region, India. J. Environ. Sci. Eng. 2009, 51, 179–186. [Google Scholar] [PubMed]
- Iyer, C.S.; Sindhu, M.; Kulkarni, S.G.; Tambe, S.S.; Kulkarni, B.D. Statistical analysis of the physico-chemical data on the coastal water of Cochin. J. Environ. Monit. 2003, 5, 324–327. [Google Scholar] [CrossRef] [PubMed]
- Wilbers, G.J.; Becker, M.; Nga, L.T.; Sebesvari, Z.; Renaud, F.G. Spatial and temporal variability of surface water pollution in the Mekong Delta, Vietnam. Sci. Total Environ. 2014, 485–486, 653–665. [Google Scholar] [CrossRef] [PubMed]
- AI-Mutairi, N.; Abahussain, A.; EI-Battay, A. Spatial and temporal characterizations of water quality in Kuwait Bay. Mar. Pollut. Bull. 2014, 83, 127–131. [Google Scholar] [CrossRef] [PubMed]
- Fujita, M.; Ide, Y.; Sato, D.; Kench, P.S.; Kuwahara, Y.; Yokoki, H.; Kayanne, H. Heavy metal contamination of coastal lagoon sediments: Fongafale Islet, Funafuti Atoll, Tuvalu. Chemosphere 2014, 95, 628–634. [Google Scholar] [CrossRef] [PubMed]
- Zhuang, W.; Gao, X.L. Integrated Assessment of Heavy Metal Pollution in the Surface Sediments of the Laizhou Bay and the Coastal Waters of the Zhangzi Island, China: Comparison among Typical Marine Sediment Quality Indices. PLoS ONE 2014, 9, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Simeonov, V.; Stanimirova, I.; Tsakovski, S. Multivariate statistical interpretation of coastal sediment monitoring data. Fresenius J. Anal. Chem. 2001, 370, 719–722. [Google Scholar] [CrossRef] [PubMed]
- Pereira, T.D.; Moreira, I.T.A.; de Oliveira, O.M.C.; Rios, M.C.; Filho, W.A.C.S.; de Almeida, M.; de Carvalho, G.C. Distribution and ecotoxicology of bioavailable metals and As in surface sediments of Paraguacu estuary, Todosos Santos Bay, Brazil. Mar. Pollut. Bull. 2015, 9, 166–177. [Google Scholar] [CrossRef] [PubMed]
- Young, P.C.; Chotai, A.; Beven, K.J. Data-based mechanistic modelling and the simplification of environmental systems. In Environment Modelling: Finding Simplicity in Complexity, 2nd ed.; Wainwright, J., Mulligan, M., Eds.; Wiley: Chichester, UK, 2004; pp. 371–388. ISBN 0-471-49617-0. [Google Scholar]
- Szekely, G.; Rizzo, M. Measuring and testing independence by correlation distances. Ann. Stat. 2007, 35, 2769–2794. [Google Scholar] [CrossRef]
- Andrews, S.S.; Mitchell, J.P.; Mancinelli, R.; Karlen, K.L.; Hartz, T.K.; Horwath, W.R.; Pettygrove, G.S.; Scow, K.M.; Munk, D.S. On-farm assessment of soil quality in California’s central valley. Agron. J. 2002, 94, 12–23. [Google Scholar] [CrossRef]
- Ding, X.R.; Kang, Y.Y.; Ge, X.P.; Li, Q.; Zhang, T.T. Tidal flat evolution analysis using remote sensing on Tiaozini flat of the radial sand ridges. J. Hohai Univ. (Nat. Sci.) 2011, 39, 231–236. [Google Scholar]
- Persaud, D.; Jaagumagi, R.; Hayton, A. Guidelines for the Protection and Management of Aquatic Sediment Quality in Ontario; Ontario Ministry of the Environment and Energy: Toronto, ON, Canada, 1993; p. 3. Available online: http://www.itrcweb.org/contseds-bioavailability/References/guide_aquatic_sed93.pdf (accessed on 1 February 2011).
- Al-Farawati, R.; van den Berg, C.M.G. Metal-sulfide complexation in seawater. Mar. Chem. 1999, 63, 331–352. [Google Scholar] [CrossRef]
- De Baar, H.J.W.; Saager, P.M.; Notling, R.F.; van der Meer, J. Cadmium versus phosphate in the world ocean. Mar. Chem. 1994, 46, 261–281. [Google Scholar] [CrossRef]
- Lane, T.W.; Morel, F.M.M. A biological function for cadmium in marine diatoms. Proc. Natl. Acad. Sci. USA 2000, 97, 4627–4631. [Google Scholar] [CrossRef] [PubMed]
- Kremling, K.; Streu, P. The behaviour of dissolved Cd, Co, Zn, and Pb in North Atlantic near-surface waters (30°N/60°W–60°N/2°W). Deep Sea Res. Part I Oceanogr. Res. Pap. 2001, 48, 2541–2567. [Google Scholar] [CrossRef]
- Xu, Y.; Feng, L.; Jeffrey, P.D.; Shi, Y.G.; Morel, F.M.M. Structure and metal exchange in the cadmium carbonic anhydrase of marine diatoms. Nature 2008, 452, 56–61. [Google Scholar] [CrossRef] [PubMed]
- Janssen, D.J.; Conway, T.M.; John, S.G.; Christian, J.R.; Kramer, D.I.; Pedersen, T.M.; Cullen, J.T. Undocumented water column sink for cadmium in open ocean oxygen-deficient zones. Proc. Natl. Acad. Sci. USA 2014, 111, 6888–6893. [Google Scholar] [CrossRef] [PubMed]
- Yuan, H.M.; Song, J.M.; Li, X.G.; Li, N.; Duan, L.Q. Distribution and contamination of heavy metals in surface sediments of the South Yellow Sea. Mar. Pollut. Bull. 2012, 64, 2151–2159. [Google Scholar] [CrossRef] [PubMed]
- Huang, K.M.; Lin, S. The carbon-sulfide-iron relationship and sulfate reduction rate in the East China Sea continental shelf sediments. Geochem. J. 1995, 29, 301–315. [Google Scholar] [CrossRef]
- Gao, X.L.; Li, P.M. Concentration and fractionation of trace metals in surface sediments of intertidal Bohai Bay, China. Mar. Pollut. Bull. 2012, 64, 1529–1536. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.L.; Li, P.M.; Chen, C.T.A. Assessment of sediment quality in two important areas of mariculture in the Bohai Sea and the northern Yellow Sea based on acid-volatile sulfide and simultaneously extracted metal results. Mar. Pollut. Bull. 2013, 72, 281–288. [Google Scholar] [CrossRef] [PubMed]
- Sunderland, E.M.; Gobas, F.A.P.C.; Branfireun, B.A.; Heyes, A. Environmental controls on the speciation and distribution of mercury in coastal sediments. Mar. Chem. 2006, 102, 111–123. [Google Scholar] [CrossRef]
- Hong, Y.N.; Geng, J.J.; Qiao, S.; Zhang, Y.Z.; Ding, L.L.; Wang, X.R.; Ren, H.Q. Phosphorus fractions and matrix-bound phosphine in coastal surface sediments of the Southwest Yellow Sea. J. Hazard. Mater. 2010, 181, 556–564. [Google Scholar] [CrossRef] [PubMed]
- Bulletin of Marine Environmental Quality of Jiangsu Province. 2010. Available online: http://web.jsocean.cn:82/searchnews_details.html?action=2025 (accessed on 9 March 2011).
- Bulletin of Marine Environmental Quality of Jiangsu Province. 2011. Available online: http://web.jsocean.cn:82/searchnews_details.html?action=2026 (accessed on 18 January 2012).
- Bulletin of Marine Environmental Quality of Jiangsu Province. 2012. Available online: http://web.jsocean.cn:82/searchnews_details.html?action=2027 (accessed on 24 July 2013).
- Bulletin of Marine Environmental Quality of Jiangsu Province. 2013. Available online: http://web.jsocean.cn:82/searchnews_details.html?action=2028 (accessed on 11 April 2014).
- Suikkanen, S.; Laamanen, M.; Huttune, M. Long term changes in summer phytoplankton communities of the open northern Baltic Sea. Estuar. Coast. Shelf Sci. 2007, 71, 580–592. [Google Scholar] [CrossRef]
- Griffiths, J.R.; Hajdu, S.; Downing, A.S.; Hjerne, O.; Larsson, U.; Winder, M. Phytoplankton community interactions and environmental sensitivity in coastal and offshore habitats. OIKOS 2016, 125, 1134–1143. [Google Scholar] [CrossRef]
- Rodriguez-Villanueva, V.; Martinez-Lara, R.; Zamora, V.M. Polychaete community structure of the northwestern coast of Mexico: Patterns of abundance and distribution. Hydrobiologia 2003, 496, 385–399. [Google Scholar] [CrossRef]
- Silveira, C.B.; Vieira, R.P.; Cardoso, A.M.; Paranhos, R.; Albano, R.M.; Martins, O.B. Influence of salinity on bacterioplankton communities from the Brazilian rain forest to the coastal Atlantic ocean. PLoS ONE 2011, 6, e17789. [Google Scholar] [CrossRef] [PubMed]
- Lacharite, M.; Jorgensen, L.L.; Metaxas, A.; Lien, V.S.; Skjoldal, H.R. Delimiting oceanographic provinces to determine drivers of mesoscale patterns in benthic megafauna: A case study in the Barents Sea. Prog. Oceanogr. 2016, 146, 187–198. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).