Abstract
Cities depend on multiple heterogeneous, interconnected infrastructures to provide safe water to consumers. Given this complexity, efficient numerical techniques are needed to support optimal control and management of a water distribution network (WDN). This paper introduces a holistic analysis framework to support water utilities on the decision making process for an efficient supply management. The proposal is based on graph spectral techniques that take advantage of eigenvalues and eigenvectors properties of matrices that are associated with graphs. Instances of these matrices are the adjacency matrix and the Laplacian, among others. The interest for this application is to work on a graph that specifically represents a WDN. This is a complex network that is made by nodes corresponding to water sources and consumption points and links corresponding to pipes and valves. The aim is to face new challenges on urban water supply, ranging from computing approximations for network performance assessment to setting device positioning for efficient and automatic WDN division into district metered areas. It is consequently created a novel tool-set of graph spectral techniques adapted to improve main water management tasks and to simplify the identification of water losses through the definition of an optimal network partitioning. Two WDNs are used to analyze the proposed methodology. Firstly, the well-known network of C-Town is investigated for benchmarking of the proposed graph spectral framework. This allows for comparing the obtained results with others coming from previously proposed approaches in literature. The second case-study corresponds to an operational network. It shows the usefulness and optimality of the proposal to effectively manage a WDN.
1. Introduction
Starting from 19th Century, Water Distribution Networks (WDN) were designed using a traditional approach based on mathematical models to find their optimal system layout in terms of water demand and pressure level satisfaction in each node. Nowadays, new challenges come from network management of an old water system designed more than 50–70 years ago. For instance, significant water losses in the WDN can usually be spotted, raising some cases up to 70% [1]. The issue often leads to having nodal pressures that are lower than a minimum service level. On top of this, there is a bigger problem regarding WDNs delay in terms of management and innovations when compared to other network public services (electricity, transport, gas, etc.). This fact is noticeable nowadays when there still is a bias on a lack of development of urban water issues with respect to smart cities research [2,3]. It is necessary to propose new paradigms, creating a novel framework analysis in research and development for urban water management.
The complexity of WDN management depends on different peculiar aspects, such as network connectivity or asset location (e.g., pipes, pumps, valves). In addition, any WDN performance shows a strong dependency on the complex network geometry produced by traditional design criteria, i.e., placing looped pipes under every street. These complex geometries and topologies require innovative approaches for the analysis and management of a WDN with a densely layout of up to tens of thousands of nodes and hundreds of looped paths that can be considered as complex networks [4]. Recently, there have flourished algorithms and mathematical tools in graph and complex network theory to better analyse the behaviour and evolution of complex systems [5,6,7]. All of these tools are focused on how “structure affects function” [5] as key aspect for their development. Among the most important methodologies handling complex networks are the Graph Spectral Techniques (GSTs) [8]. GSTs analyze network topologies by exploiting the properties of some graph matrices, providing useful information about the global and local performance and evolution of network systems.
A number of GSTs have been applied to WDNs over the last years. These shown to be useful to define an optimal clustering layout through spectral clustering [9,10,11]. GSTs also supported approaching preliminary assessments of the global network robustness through graph matrices eigenvalues [12,13,14], providing surrogate robustness metrics. However, these studies only use some GSTs properties and do not provide an overall framework regarding the opportunities offered by the study of network eigenvalues and eigenvectors.
This paper proposes a GST tool-set based on two graph matrices and their relative spectra for supporting several applications on WDNs management. The aim is to present a complete outline on the capabilities provided by graph spectral techniques applied to WDNs and assemble them into a unique framework. The paper highlights how GST metrics and their algorithms aid to face some crucial tasks of WDN management by just using topological and geometric information. In literature exist several approaches enhancing graph theoretic approaches for WDN management with hydraulic information. There are addressed this way the problem of network failures quantified both with respect to physical connectivity and water supply service level [15,16,17,18], resilience analysis [19], ranking pipes [20], and vulnerability analysis [21]. However, there are a series of advantages of focusing the analysis only on the network topology. The GST tool-set provides a solution in the frequent case of not having available hydraulic information, fosters real-time response for WDN management, makes it easier to deal with large-scale WDNs, provides an initial solution to further applications (e.g., specific algorithms for sensor location), presents a surrogate solution for WDN management in all of the cases, even for disruption scenarios (such as single or multiple component removal), and can be easily extended to contain hydraulic information by weighting the graph, but using similar methodologies to those proposed in this paper.
This paper approaches several issues. Firstly, it is done a robustness analysis by computing the strength of the network connectivity using a number of spectral metrics. This is of high interest to assess the impact of any network perturbation (single or multiple component removal) resulting from random network failures or targeted attacks [22]. The paper also undertakes through GSTs a water network clustering to define the optimal dimension and shape of a District Meter Area (DMA) [23,24]. In addition, there are also tackled both the problem of an optimal sensor placement [25,26,27] and the identification of the most sensitive nodes to malicious attacks [28,29]. Besides providing a unique GST framework for urban water management, this work also presents novelty elements such as the application of spectral tools for several WDN tasks: approaching connectivity and continuity analysis, finding an optimal number of clusters for the water network partitioning, and selecting the most “influential” nodes for locating quality sensors and metering stations. The GST framework is especially useful for aiding the decision making process for real-time WDN management and in the frequent case of not having available hydraulic information.
Last but not least, another two important aspects supporting the use of graph spectral techniques are the following: (a) dealing with easy to implement metrics that can be efficiently solved by standard linear algebra methods; and (b) providing mathematical elegance to the proposed procedures, as they are supported by mathematical theorems. The outline of the paper is the following. First, it provides a brief survey of the principal graph spectral techniques, independently of the application field in which they are used. The main graph matrices and some important eigenvalues and their eigenvectors are defined and explained. In order to better show the meaning and efficiency of spectral tools, a simple Example Network is analyzed. Finally, the GST tool-set is tested on two case studies, a real small-size and an artificial medium-size water system. The conclusions section includes a comparison and analysis of the results.
2. Spectral Graph Theory
Spectral graph theory is a mathematical approach combining both linear algebra and graph theory [30] in order to exploit eigenvalue and eigenvector properties. This way, the main benefit of spectral graph theory is its simplicity, as any system can be successfully analyzed just through the spectrum of its associated graph matrix, M. Spectral graph parameters contain a lot of information on both local and global graph structure. The computational complexity to compute eigenvalues and eigenvectors of graph matrices is O(n3), where n is the number of vertices/nodes (it is usual to name the elements of a graph as vertices and edges and the elements of a network as nodes and links; we make this distinction throughout the paper.) in the associated graph/network. From the 1990s, graph spectra have been used for several important applications in many fields [31]; such as expanders and combinatorial optimization, complex networks and the internet topology, data mining, computer vision and pattern recognition, internet search, load balancing and multiprocessor interconnection networks, anti-virus protection, knowledge spread, statistical databases and social networks, quantum computing, bioinformatics, coding theory, control theory, and computer sciences.
2.1. Graph Matrices
The Adjacency matrix, A, and the Laplacian matrix, L, are widely used in graph analysis. Another matrices such as the Modularity matrix, the Similarity matrix, and the sign-less Laplacian are omitted from the current GST tool-set. Using them will make a wider GST mathematical framework but require a further investigation that falls out of the scope of this proposal. The following items synthetically describe a number of graph matrices that are related to A and L, whose properties are introduced and developed in this paper.
- Adjacency Matrix A: let G = (V, E) be an undirected graph with n-vertices set V and m-edges set E. A common way to represent a graph is to define its Adjacency matrix A, whose elements aij = aji = 1 if nodes i and j are directly connected and aij = aji = 0 otherwise. The degree of node i of A is defined as ;
- Weighted Adjacency Matrix W: it is possible to express the weighted Adjacency matrix W, in case to be available information about the connection strength between vertices of the graph G. Edge weights are expressed in terms of proximity and/or similarity between vertices. Thus, all of the weights are non-negative. That is, wij = wji ≥ 0 if i and j are connected, wij = wji = 0 otherwise. The degree of a node i of W is defined as ;
- Un-normalized Laplacian Matrix L: one of the main utilities of spectral graph theory is the Laplacian matrix [32] and both its un-normalized and normalized version [8]. Let Dk = diag(ki) be the diagonal matrix of the vertex connectivity degrees, the Laplacian matrix is defined as the difference between Dk and the Adjacency matrix A (or the weighted Adjacency matrix W if it is considered a weighted graph). The un-normalized Laplacian matrix is defined by L = Dk − A (L = Dk − W);
- Random Walk Normalized Laplacian Matrix Lrw: it is closely related to a random walk representation. Its definition comes from the Laplacian matrix L being multiplied by the inverse of the diagonal matrix of the vertex connectivity degrees, Dk. Then, [33].
It is worth to highlight that the above described Laplacian matrices are positive semi-definite and have n non-negative real-valued eigenvalues 0 = λ1 ≤ … ≤ λn. These properties are of main importance in the graph spectral theory.
2.2. Network Eigenvalues
This section provides a quick survey of some graph eigenvalues properties. It is not exhaustive. However, there are enounced the most important properties for further mathematical reference. These are about eigenvalues that are used in the paper regarding WDN applications.
- The Largest eigenvalue (Spectral radius or Index) λ1: it refers to the Adjacency graph matrix A and it plays an important role in modelling a moving substance propagation in a network. It takes into account not only immediate neighbours of vertices, but also the neighbours of the neighbours [34]. Spectral radius concept is often introduced by using the example of how a virus spread in a network. The smaller the Spectral radius the larger the robustness of a network against the spread of any virus in it. In this regard, the epidemic threshold is proportional to the Inverse of Spectral radius 1/λ1 [35]. This fact can be explained as the number of walks in a connected graph is proportional to λ1. The greater the number of walks of a network, the more intensive is the spread of the moving substance in it. The other way round, the higher the Spectral radius, the better is the communication into a network.
- The Spectral gap ∆λ: it represents the difference between the first and second eigenvalue of an Adjacency matrix, A. It is a measure of network connectivity strength. In particular, it quantifies the robustness of network connections and the presence of bottlenecks, articulation points, or bridges. This is of significant importance, as the removal of a bridge splits the network in two or more parts. The larger the Spectral gap the more robust is the network [36].
- The Multiplicity of zero eigenvalue m0: the multiplicity of the eigenvalue 0 of L is equal to the number of connected components A1, …, Ak in the graph; thus, the matrix L has as many eigenvalues 0 as connected components [37].
- The Eigengap λk+1 − λk: it is a spectral utility specifically designed for network clustering. A suitable number of clusters k may be chosen such that all eigenvalues λ1, …, λk of Laplacian matrix L are very small, but λk+1 is relatively large [38]. The more significant the difference for a-priori proposing the number of clusters the better is the further clustering configuration.
- The Second smallest eigenvalue (Algebraic connectivity) λ2: it refers to the Laplacian matrix. λ2 plays a special role in many graph theories related problems [39]. It quantifies the strength of network connections and its robustness to link failures. The larger the Algebraic connectivity is the more difficult to cut a graph into independent components. It is also related to the min-cut problem of a data set for spectral clustering [37].
A simple Example Network with n = 18 nodes and a varying number of links m (from 27 to 30) is illustrated in the Figure 1 by its different possible layouts. Example Network will be useful as an instance for spectral metrics computation. This will also show the possible applications for water distribution network management. The first Example Network layout, A), is composed by two separated network subregions. Layout B) comes from adding a single link to A) to obtain a connected network. An additional link is added to B) to obtain C). Table 1 and Figure 2 and Figure 3 show the spectral metrics computed on the previous described network layouts (Figure 1).
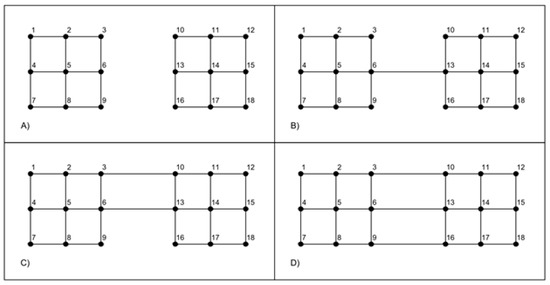
Figure 1.
Four layouts of the Example Network with the same number of nodes and a different number of links. A) two separated subregions; B) a single edge links the two subregions; C) two edges link the two subregions; D) three edges link the two subregions.

Table 1.
Spectral metrics for the four cases of the example network.
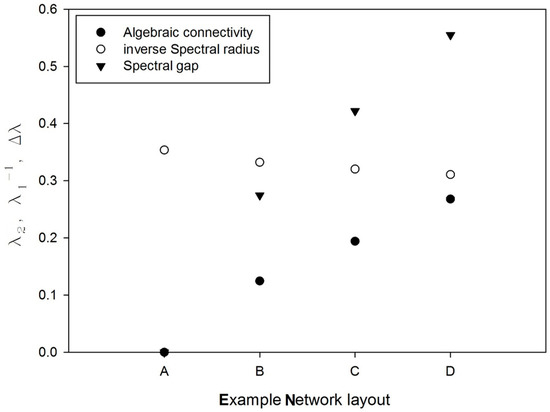
Figure 2.
Algebraic connectivity, Inverse Spectral radius and Spectral radius for the layout A, B, C, and D of Example Network.
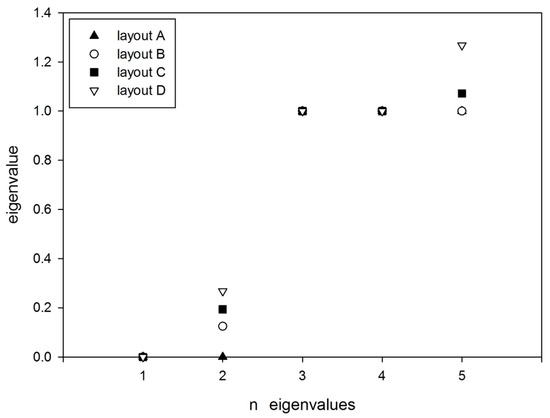
Figure 3.
First five eigenvalues for the cases A, B, C, and D of the Example Network.
Table 1 reports how the Spectral radius, the Spectral gap, and the Algebraic connectivity increase with the number of links between the subregions. The same result is also shown in Figure 1, where it is clear that the general connectivity and robustness increase from A) to D). Algebraic connectivity and Spectral gap start from zero for the separated layout A). Both measures significantly increase in the other layouts, A) to D). This show how these two metrics may be used as a measure of the network connectivity strength [40].
The measures for Spectral radius (Table 1) start from values greater than zero for layout A). Then, these values decrease as the number of connections increase. In this regard, Spectral radius can be used as a parameter to quantify the communication rate or the connectivity level of the network. It is also noticed how Spectral radius hardly varies for the four analyzed Example Network layouts. This result is explained as the measure ranges from the average node degree kmean and the maximum node degree of the network kmax [41] that in Example Network ranges between kmean = 2.67 to kmax = 4.00 (for layout A) and kmean = 3.00 to kmax = 4.00 (for layout D).
Figure 2 shows the top five eigenvalues λ1, …, λ5 of the Laplacian matrix for the four layout configurations of Example Network. It is noticeable that some eigenvalues are equal for all of the layouts. The first eigenvalue λ1 is always equal to zero because the graph Laplacian matrix is positive semi-definite [37].
In layout A) the Multiplicity of zero, m0, is equal to 2. Consequently, also the second eigenvalue λ2 (the Algebraic connectivity) is equal to zero (Table 1). This means that there are two separated subregions in the network, as the number of multiplicity of zero, m0, is equal to the number of the disconnected subregions. In all four layouts, the maximum eigengap occurs between the third eigenvalue λ3 and the second eigenvalue λ2. This indicates that, from a topological point of view, the optimal number of clusters to split the network is two. These results match with those naturally expected by the Example Network construction and also by its visualization. It also important to highlight that the value of the eigengap decreases as the number of links between the two A) regions increases. This suggests that the eigengap criterion works better when the clusters in the network can be well defined (not overlapping).
2.3. Network Eigenvectors
Graph eigenvectors contain a lot of information about the graph structure. The above described matrices are based on eigenvalue spectra and have been proposed into several applications [34,42,43]. It is worth highlighting that graph eigenvectors are not graph invariants since they depend on the labelling of graphs [30]. This characteristic can become into an advantage at some cases. This is shown in the following subsection where there are introduced the principal eigenvector, the Fiedler eigenvector, and problems that are related to simultaneous usage of several eigenvectors.
- Principal eigenvector: it corresponds to the largest A-eigenvalue, v1, of a connected graph. It gives the possibility to rank graph vertices by its coordinates with respect to the number of paths passing through them to connect two nodes in the network [44]. The number of paths can be seen as the “importance” (also called the centrality) of node i. In this regard, the eigenvector centrality attributes a score to each node equals to the corresponding coordinate of the principal eigenvector. Groups of highly interconnected nodes are more “important” for the communication in comparison to equally high connected nodes do not form groups, that is, whose neighbours are less connected than them (according to the social principle that “I am influential if I have influential friends”). An important Principal eigenvector application is on Web search engines as Google’s PageRank algorithm [45];
- The Fiedler eigenvector: it corresponds to the second smallest Laplacian (or normalized Laplacian) eigenvalue of a connected graph. Fiedler [39] first demonstrated that the eigenvector v2 associated to the second smallest eigenvalue λ2 provides an approximate solution to the graph bi-partitioning problem. This is approached according to the signs of the components of v2. A subgraph is encompassed by nodes with positive components in the Fiedler eigenvector. The other subgraph contains nodes that are related to negative Fiedler eigenvector components. The v2 values closer to 0 correspond to “better” splits. In this regard, if a number of clusters k ≥ 2 is needed, then it is useful to resort to the Recursive spectral bisection [46,47]. According to this, the Fiedler eigenvector is used to bi-divide the vertices of the graph by the sign of its coordinates and the process is iterated then for each defined sub-part until reach the targeted number k of clusters.
- Other Eigenvector: an alternative to obtain a good graph partitioning for k ≥ 2 clusters is related to the first k smallest eigenvector of the Laplacian matrix (or normalized Laplacian). The approach is based on solving the relaxed versions of the RCut problem (NCut problem) to define the so-called spectral clustering (normalized spectral clustering). It has been demonstrated in literature [33] that the normalized spectral clustering, based on the Random Walk Normalized Laplacian Matrix Lrw, shows a superior performance to other spectra alternatives to find a clustering configuration. The solution is simultaneously characterized by both a minimum number of cuts and a well-balanced clusters size. According to [33], the minimization of the NCut problem is equal to the minimization of the Rayleigh quotient.
The expression of Equation (1) is minimized by the smallest eigenvalue of the (D − A) matrix that is in correspondence to its smallest eigenvector. In this regard, the minimization of the NCut problem is related to the solution of the generalized eigenvalues system.
According to the expression of L = − A, and pre-multiplying by , the problem is reduced to the classical eigenvalues system.
Finally, the spectral clustering consists of the following steps:
- definition of Adjacency matrix A (or weighted Adjacency matrix W);
- computation of the Laplacian L;
- computation of the first k eigenvectors of normalized Laplacian Lrw matrix
- definition of the matrix Unxk containing the first k eigenvectors as columns; and,
- clustering the nodes of the network into clusters C1, …, Ck using the k-means algorithm applied to the rows of the Unxk matrix.
It is important to clarify that the boundary links, Nec, are those for which each of the connected nodes belong to different clusters Ck. An important aspect according of the spectral algorithm is to change the representation of the nodes from Euclidean space to points in the Unxk matrix. This new data space enhances important cluster-properties and the final configuration has an easier detection [37]. Successful applications for the water distribution networks can be found in [11,14].
Figure 4 and Figure 5 show the outcome from applying eigenvector techniques to Example Network. Regarding the Principal eigenvector, the eigenvector centrality v1,i is evaluated for layout D). Table 2 shows that the two most important nodes are the node 6 and the node 13 (marked in Table 2), as those nodes correspond the maximum value of the eigenvector. The connectivity degree for these nodes is ki = 4, and they are connected to other nodes with a connectivity degree ki = 4 (that is node 5 and node 13 are connected to node 6; node 14 and node 6 are connected to node 13). So, the two most important nodes, identified with the eigenvector centrality, are those nodes that have highly connected adjacent neighbour. These nodes 6 and 13 can consequently be considered “central” nodes for the communication of the network (from a topological point of view). Similar results are obtained also for the other Example Network layouts.
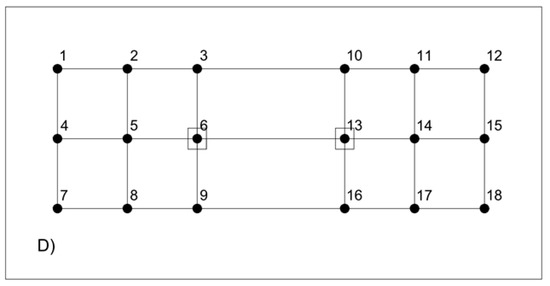
Figure 4.
Two most important nodes, computed by the eigenvector centrality, for the layout D of Example Network.
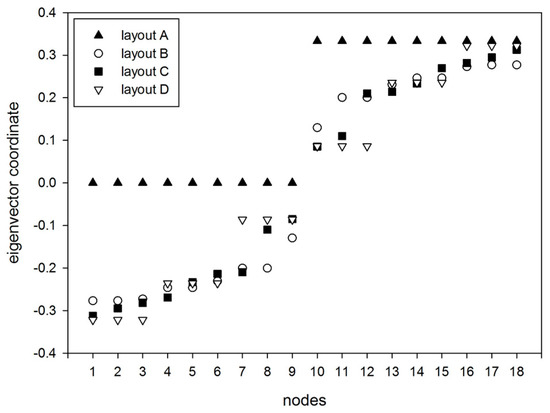
Figure 5.
Fiedler eigenvector coordinates for the layout A, B, C, and D.

Table 2.
Eigenvector centrality for all the nodes in Example Network, layout D.
Regarding the Fiedler eigenvector, the coordinates of v2 for the four layouts of Example Network are shown in Figure 5. The Fiedler eigenvector has a number of components (coordinates) equal to the number of nodes. It is clear that the coordinates have positive and negative values for the four layouts. In particular, it is possible to define two well separated groups. The first ranges from node 1 to node 9 (negative values), while the second is made by node 10 up to node 18 (positive values). By splitting the nodes of the network according to their coordinates for v2, it is possible to define a bisection of them.
Analysing layout A (two separated groups), it is straightforward to see how the two groups of coordinates are well defined, having a constant value for each group. In the other layouts, the difference between two groups is less clear, as the number of connected links increases. However, the bisection of the nodes of the network can still be defined for these networks because the sign is preserved. In all of the layouts, the two clusters are defined having the same number of nodes (Figure 5).
Regarding to the clustering problem via the NCut minimization problem, the optimal clustering layout for Example Network proposes to take two clusters (k = 2), in compliance with the eigengap property (Figure 3). The Fiedler bipartition, according to the second eigenvector of the Laplacian matrix, provides the same clustering configuration than NCut algorithm. This is an expected result, as only the second eigenvector is considered in the definition of the matrix Unxk for k = 2.
3. Case Study
All of the metrics and algorithms based on the Graph Spectral Techniques described above can be considered as an operational GST tool-set that is able to solve key management issues of water distribution networks. GSTs are tested on the real small-size water system of Parete (a town with 10,800 inhabitants located in a densely populated area near Caserta, Italy) and on the synthetic medium-size water system of C-Town [48]. The main characteristics of both WDNs are reported in Table 3.

Table 3.
Main characteristics of water distribution network of C-Town and Parete. The symbol in brackets “-” indicates that the parameter is dimensionless.
The Eigenvalues significance, explained in the previous section, is described for the two case studies. The Adjacency and the Laplacian matrices of these two networks are defined and the principal eigenvalues computed. It is important to note that the graphs are considered unweighted to better show the efficiency of the proposed management framework. This is based only on the topological knowledge of WDNs, as it is frequent to do not have available any hydraulic information about the network. Then, a novel GST tool-set is proposed that provides global and local network information key to develop operational algorithms and procedures to face complex tasks in WDNs management. It is however possible to attribute some weights to the network by taking into account the “strength” of the link between nodes [7]. In the WDNs case, the weights could represent background knowledge on geometric and hydraulic characteristics of the pipes (diameter, length, conductivity, flow, and velocity, among others).
Table 4 shows the network eigenvalues for the two case studies. The multiplicity of the 0-eigenvalue from the Adjacency matrix is, for both of the case studies, equal to m0 = 1. This means that in both WDNs, there is only one connected component. It is interesting to note that also for complex network models (made by thousands of components) it is still easy to check if any anomaly observed in the water supply is caused by the decomposition of the original network in several subregions (as it is the case of unexpected pipe disruptions or valve malfunctions).

Table 4.
Principal Eigenvalues of the Adjacency and Laplacian matrices of water distribution network of C-Town and Parete.
GSTs also provide support to compute a surrogate index for the topological WDNs robustness regarding the following two features: (a) The presence of “bottlenecks” or articulation points. These are subregions that are connected to others through a single link. Removing any node or link at the bottleneck causes network disconnection. Bottlenecks are computed through the value of the Spectral gap Δλ, as calculated on the Adjacency matrix; (b) The network “strength” to get split into subregions, computed through the value of the Algebraic connectivity λ2 calculated on the Laplacian matrix. The values of the Spectral gap and the Algebraic connectivity aid and simplify the assessment of robustness of a WDN, as it was preliminary proposed by [12,13,14]. In the current case studies, it is clear that the corresponding values of the two spectral measures are small and near to zero, Δλ = 0.0685 and λ2 = 0.0212 for Parete, while Δλ = 0.0303 and λ2 = 0.0006 for C-Town. These small values are justified by the fact that WDNs are sparser than other networks as Internet or social networks. This is due to both geographical embedding and economic constraints [7,11].
The larger Spectral gap for Parete than for C-Town suggests that Parete has a smaller number of bottlenecks. When considering the Algebraic connectivity, Parete shows greater tolerance to the efforts to be split into isolated parts with respect to C-Town. Comparing the two case studies, Parete evidently is more robust against node and link failure than C-Town (as we can expect from comparing a real utility network design as it has Parete to a synthetic WDN). The smaller value of the Spectral radius inverse shows that Parete have a more efficient layout than C-Town in terms of communication and degree connectivity. In this regard, the inverse of the Spectral radius can be used as a global measure of the reachability of network elements and the paths multiplicity. These first results obtained with spectral metrics support a preliminary visual analysis of the two WDNs, through which it is possible to observe a more cohesive shape (and so a more robust structure) for Parete than C-Town. These GSTs measures aid hydraulic experts to quantify several intuitive aspects of WDNs performance. In addition, GSTs make it possible to approach a structure analysis of large networks for which just a visual analysis does not provide enough information.
The three Eigenvectors techniques explained in the previous section are tested on Parete and C-Town WDNS. These are the Fiedler eigenvector, Ncut methods based on the other eigenvectors and the principal eigenvector. Through the Fielder Eigenvector and Ncut methods, it is possible to face the important and arduous task associated with permanent water network partitioning (WNP) [23]. WNP consists into define optimal discrete network areas, District Meter Area (DMA), aimed to improve the water network management (i.e., water budget, pressure management, or water losses localization). This should be done avoiding to negatively affect the hydraulic performance of the system that could be significantly deteriorated by shutting-off some pipes [23,49]. Choosing a suitable number of subregions and their respective layouts by a clustering algorithm is essential to design a WDN partition into DMAs. The definition of the number of clusters attempts to take into account some peculiarities of the system (i.e., water demand, pressure distribution, or elevation), which often are not available for the entire water network. A clustering method based on GSTs only considers network topological characteristics and is able to capture inherent cluster-properties of the system.
While the second smallest eigenvalue (Algebraic connectivity) is interpreted as a measure of the strength to split the network in sub-graphs, the eigengap λk+1 − λk could be interpreted as a measure of the surplus of the strength needed to split the network from k + 1 to k clusters. Once defining the maximum eigengap λk+1 − λk, it is clear that, from a topological point of view, it is better to split the network at most up to k clusters, since a greater surplus of strength is needed to split the network in k + 1 and more clusters. For this reason, the maximum eigengap can be used to define the optimal number of clusters from a topological and connectivity point of view. Figure 6 shows the first ten eigenvalues of the Laplacian matrix for the graph of C-Town and Parete. It is clear that the first largest eigengap for C-Town, occurs between the sixth and the fifth eigenvalue (λ6 − λ5 = 0.002), while for Parete occurs between the fifth and the fourth eigenvalue (λ5 − λ4 = 0.042). This metric suggests that, an optimal number of clusters on which subdivided the water distribution networks of C-Town and Parete is, respectively, k = 5 and k = 4.
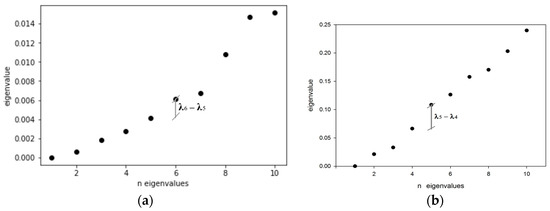
Figure 6.
First 10 eigenvalues for the two case studies: (a) C-Town network; and, (b) Parete network.
Once it is defined a suitable number of clusters for a WDN, it is necessary to set the optimal layout at each sub-region in which the WDN is subdivided (clustering phase) to approach a complete water network partitioning [23]. The clustering phase focuses on identify clusters shape, aiming both to balance the number of the nodes and to minimize the number of boundary pipes between clusters. Approaching an appropriate network clustering is essential. This constitutes the starting point for the subsequent division phase that consists on choosing the boundary pipes in which to insert gate valves and flow meters, as it is widely described in [50].
Spectral clustering offers a valid and powerful tool to exploit the properties of the Laplacian matrix spectrum. Figure 7 reports the Fiedler eigenvectors, v2, for C-Town and Parete WDNs. It is clear, as it was shown on Example Network, that the coordinates of the second eigenvector, v2, easily define an optimal bipartition layout for the network. These divide the network nodes according to the signs (positive or negative) for the corresponding value of the Fiedler eigenvector. It is worth highlighting that this procedure ensures the continuity of each defined cluster, as each node of a cluster is linked at least to another node of the same cluster.
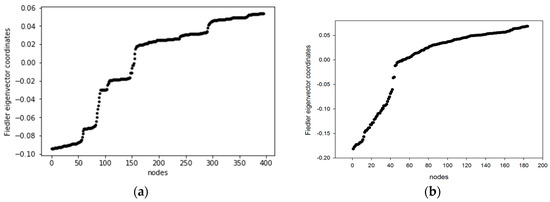
Figure 7.
Fiedler eigenvector v2 coordinates for the two case studies: (a) C-Town network; and, (b) Parete network.
In case of the optimal number of clusters (defined by the maximum value of the eigengap) is higher than two, then the first clustering configuration obtained as outcome of the Fiedler eigenvector v2, can be used as input for a recursive bisection process. That is, for each cluster, the Fiedler eigenvector v2 can be computed for the next clustering up to reach the targeted number of clusters. This network bisection can also represent a starting layout for other recursive algorithms that require an initial random choice of the clustering layout. Another GST based powerful tool for the optimal clustering layout of a water distribution network, is the Ncut spectral clustering [33], already explained in the Eigenvector techniques section, based on the use of other eigenvectors further than v2.
Figure 8 shows the optimal clustering layout through Ncut spectral clustering. The results are given for a number of k = 4 clusters for Parete and k = 5 clusters for C-Town, according to the optimal number of clusters defined through the eigengap for both of the case studies. It is worth to point out that the clusters are well balanced in terms of number of nodes (a standard deviation dst = 2.7% for Parete and dst = 8.1% for C-Town). The number of boundary pipes is small with respect to the total number of pipes (about Nec = 16 for Parete and Nec = 4 for C-Town, corresponding to 5.7% and 1%, respectively).
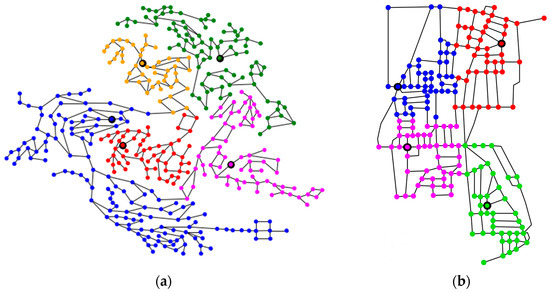
Figure 8.
Optimal clustering layout for the two case studies with different colors for each clusters and highlighting the most important nodes of each cluster according to the eigenvector centrality of the partitioned networks: (a) C-Town network (k = 5); and (b) Parete network (k = 4).
GSTs propose a solution for ranking WDN nodes and then select the most important points. The WDNs of Parete and C-Town are ranked according to the score attributed by the corresponding coordinates to the first eigenvector, v1, of the Adjacency matrix. Ranking WDN nodes is useful for locating optimal nodes in which locate devices (i.e., chlorine stations, pressure regulation valves, quality sensors, flow meters, etc.). The identification of the most important nodes can also contribute as initial guess for further development of specific device location algorithms. The applications range, for instance, from detecting accidental or intentional contamination to control pipe flows and node pressures. These challenging tasks can be approached through GSTs, even when no other information is available rather than the network topology. As it is explained in the previous section, the eigenvector centrality can spot the most “influential” nodes, according to the number of neighbours of the adjacent nodes. The idea behind the network centrality concept is to identify which points are traversed by the greatest number of connections. Central nodes are thus considered as essential nodes for network connectivity and have influence over large network areas. Figure 8 points out also the most important nodes based on the eigenvector centrality criterion. The results show the highest centrality node per each DMA of the C-Town and Parete partitioned WDNs. After WDNs clustering, the process is focus on every single Adjacency matrix related to water distribution sub-networks. The eigenvector centrality provides most the important nodes per cluster or DMA, from a topological and connectivity point of view.
4. Conclusions
This paper proposes a survey of the possibilities offered by graph spectral techniques. There is provided a complete tool-set of several metrics and algorithms, borrowed from graph spectral techniques (GSTs), and applied to water network operations and management. The tool-set is based on topological and geometric information of the water network layout. No hydraulic data (such as diameter, roughness, pressure, etc.) is required. This made the proposal particularly attractive, as it is a common situation that often face water utilities. Another advantage of the proposal lies on the huge GST tool-set applicability to any water distribution network. It also is straightforward its adaptation to deal with near real-time challenges, as avoiding any hydraulic simulation that often stall having a suitable speed on having network performance results
The application of the proposed GST tool-set has shown to provide useful metrics for continuity check, testing if there is any unconnected part of the water network. GSTs also made it possible to approach topological robustness analysis, aiding to develop water system design or to network resilience assessments. Another challenges in water management have been also addressed, such as partitioning the water distribution network into district metered areas through a spectral clustering process. Ranking nodes importance in a water distribution network is useful for approaching valve or sensor location. The most “influential” or important nodes have also been obtained thanks to the GST tool-set framework.
Further work will lead to investigate new opportunities coming from GSTs for water distribution management. These will be towards using meaningful weights on pipes and nodes. The aim will be to add partial or complete hydraulics knowledge to the purely topological based solutions provided by GSTs.
Acknowledgments
The authors have no funding to report.
Author Contributions
Each of the authors contributed to the design, analysis and writing of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Farley, M.; World Health Organization. Leakage Management and Control: A Best Practice Training Manual; World Health Organization: Geneva, Switzerland, 2001. [Google Scholar]
- Neirotti, P.; De Marco, A.; Cagliano, A.C.; Mangano, G.; Scorrano, F. Current trends in Smart City initiatives: Some stylised facts. Cities 2014, 38, 25–36. [Google Scholar] [CrossRef]
- Albino, V.; Berardi, U.; Dangelico, R.M. Smart Cities: Definitions, dimensions, performance, and initiatives. J. Urban Technol. 2015, 22, 3–21. [Google Scholar] [CrossRef]
- Mays, L.W. Water Distribution System Handbook; McGraw-Hill Education: New York, NY, USA, 1999; ISBN 978-0-07-134213-1. [Google Scholar]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
- Barabási, A.-L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef] [PubMed]
- Boccaletti, S.; Latora, V.; Moreno, Y.; Chavez, M.; Hwang, D.-U. Complex networks: Structure and dynamics. Phys. Rep. 2006, 424, 175–308. [Google Scholar] [CrossRef]
- Chung, F.R.K. Spectral Graph Theory; American Mathematical Society: Providence, RI, USA, 1996; ISBN 978-0-8218-0315-8. [Google Scholar]
- Herrera, M.; Canu, S.; Karatzoglou, A.; Pérez-García, R.; Izquierdo, J. An approach to water supply clusters by semi-supervised learning. In Proceedings of the 9th International Congress on Environmental Modelling and Software, Ottawa, ON, Canada, 1 July 2010. [Google Scholar]
- Gutiérrez-Pérez, J.A.; Herrera, M.; Pérez-García, R.; Ramos-Martínez, E. Application of graph-spectral methods in the vulnerability assessment of water supply networks. Math. Comput. Model. 2013, 57, 1853–1859. [Google Scholar] [CrossRef]
- Di Nardo, A.; Di Natale, M.; Giudicianni, C.; Greco, R.; Santonastaso, G.F. Complex network and fractal theory for the assessment of water distribution network resilience to pipe failures. Water Sci. Technol. Water Supply 2017, 17, ws2017124. [Google Scholar] [CrossRef]
- Yazdani, A.; Jeffrey, P. Robustness and vulnerability analysis of water distribution networks using graph theoretic and complex network principles. In Proceedings of the 2010 Water Distribution System Analysis, Tucson, Arizona, 12–15 September 2010; pp. 933–945. [Google Scholar] [CrossRef]
- Yazdani, A.; Jeffrey, P. Complex network analysis of water distribution systems. Chaos Interdiscip. J. Nonlinear Sci. 2011, 21, 016111. [Google Scholar] [CrossRef] [PubMed]
- Di Nardo, A.; Di Natale, M.; Giudicianni, C.; Musmarra, D.; Varela, J.M.R.; Santonastaso, G.F.; Simone, A.; Tzatchkov, V. Redundancy features of water distribution systems. Procedia Eng. 2017, 186, 412–419. [Google Scholar] [CrossRef]
- Diao, K.; Sweetapple, C.; Farmani, R.; Fu, G.; Ward, S.; Butler, D. Global resilience analysis of water distribution systems. Water Res. 2016, 106, 383–393. [Google Scholar] [CrossRef] [PubMed]
- Shuang, Q.; Zhang, M.; Yuan, Y. Performance and reliability analysis of water distribution systems under cascading failures and the identification of crucial pipes. PLoS ONE 2014, 9, e88445. [Google Scholar] [CrossRef] [PubMed]
- Torres, J.M.; Duenas-Osorio, L.; Li, Q.; Yazdani, A. Exploring topological effects on water distribution system performance using graph theory and statistical models. J. Water Resour. Plan. Manag. 2017, 143, 04016068. [Google Scholar] [CrossRef]
- Candelieri, A.; Soldi, D.; Archetti, F. Network analysis for resilience evaluation in water distribution networks. Environ. Eng. Manag. J. 2015, 14, 1261–1270. [Google Scholar]
- Soldi, D.; Candelieri, A.; Archetti, F. Resilience and vulnerability in urban water distribution networks through network theory and hydraulic simulation. Procedia Eng. 2015, 119, 1259–1268. [Google Scholar] [CrossRef]
- Candelieri, A.; Giordani, I.; Archetti, F. Supporting resilience management of water distribution networks through network analysis and hydraulic simulation. In Proceedings of the 2017 21st International Conference on Control Systems and Computer Science (CSCS), Bucharest, Romania, 29–31 May 2017; pp. 599–605. [Google Scholar]
- Agathokleous, A.; Christodoulou, C.; Christodoulou, S.E. Topological robustness and vulnerability assessment of water distribution networks. Water Resour. Manag. 2017, 31, 4007–4021. [Google Scholar] [CrossRef]
- Greco, R.; Di Nardo, A.; Santonastaso, G. Resilience and entropy as indices of robustness of water distribution networks. J. Hydroinform. 2012, 14, 761–771. [Google Scholar] [CrossRef]
- Di Nardo, A.; Di Natale, M.; Santonastaso, G.F.; Venticinque, S. An automated tool for smart water network partitioning. Water Resour. Manag. 2013, 27, 4493–4508. [Google Scholar] [CrossRef]
- Alvisi, S.; Franchini, M. A procedure for the design of district metered areas in water distribution systems. Procedia Eng. 2014, 70, 41–50. [Google Scholar] [CrossRef]
- Pérez, R.; Puig, V.; Pascual, J.; Peralta, A.; Landeros, E.; Jordanas, L. Pressure sensor distribution for leak detection in Barcelona water distribution network. Water Sci. Technol. Water Supply 2009, 9, 715–721. [Google Scholar] [CrossRef]
- Antunes, C.H.; Dolores, M. Sensor location in water distribution networks to detect contamination events—A multiobjective approach based on NSGA-II. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016; pp. 1093–1099. [Google Scholar]
- Tinelli, S.; Creaco, E.; Ciaponi, C. Sampling significant contamination events for optimal sensor placement in water distribution systems. J. Water Resour. Plan. Manag. 2017, 143, 04017058. [Google Scholar] [CrossRef]
- Gomes, R.; Marques, A.S.; Sousa, J. Decision support system to divide a large network into suitable District Metered Areas. Water Sci. Technol. 2012, 65, 1667–1675. [Google Scholar] [CrossRef] [PubMed]
- Di Nardo, A.; Di Natale, M.; Musmarra, D.; Santonastaso, G.F.; Tzatchkov, V.; Alcocer-Yamanaka, V.H. Dual-use value of network partitioning for water system management and protection from malicious contamination. J. Hydroinform. 2015, 17, 361–376. [Google Scholar] [CrossRef]
- Arsić, B.; Cvetković, D.; Simić, S.K.; Škarić, M. Graph spectral techniques in computer sciences. Appl. Anal. Discrete Math. 2012, 6, 1–30. [Google Scholar] [CrossRef]
- Cvetković, D.; Simić, S. Graph spectra in computer science. Linear Algebra Appl. 2011, 434, 1545–1562. [Google Scholar] [CrossRef]
- Mohar, B. The Laplacian spectrum of graphs. In Graph Theory, Combinatorics, and Applications; Wiley: Hoboken, NJ, USA, 1991; pp. 871–898. [Google Scholar]
- Shi, J.; Malik, J. Normalized cuts and image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 888–905. [Google Scholar] [CrossRef]
- Bonacich, P. Power and centrality: A family of measures. Am. J. Sociol. 1987, 92, 1170–1182. [Google Scholar] [CrossRef]
- Wang, Y.; Chakrabarti, D.; Wang, C.; Faloutsos, C. Epidemic spreading in real networks: An eigenvalue viewpoint. In Proceedings of the 2003 22nd International Symposium on Reliable Distributed Systems, Florence, Italy, 6–8 October 2003; pp. 25–34. [Google Scholar]
- Donetti, L.; Neri, F.; Muñoz, M.A. Optimal network topologies: Expanders, cages, Ramanujan graphs, entangled networks and all that. J. Stat. Mech. Theory Exp. 2006, 2006, P08007. [Google Scholar] [CrossRef]
- Von Luxburg, U. A tutorial on spectral clustering. Stat. Comput. 2007, 17, 395–416. [Google Scholar] [CrossRef]
- Mohar, B. Some applications of laplace eigenvalues of graphs. In Graph Symmetry; NATO ASI Series; Springer: Dordrecht, The Netherlands, 1997; pp. 225–275. ISBN 978-90-481-4885-1. [Google Scholar]
- Fiedler, M. Algebraic connectivity of graphs. Czechoslov. Math. J. 1973, 23, 298–305. [Google Scholar]
- Estrada, E. Network robustness to targeted attacks. The interplay of expansibility and degree distribution. Eur. Phys. J. B-Condens. Matter Complex Syst. 2006, 52, 563–574. [Google Scholar] [CrossRef]
- Cvetkovic, D.M.; Doob, M.; Sachs, H. Spectra of Graphs: Theory and Application; Academic Press: Berlin, Germany, 1980; ISBN 978-0-12-195150-4. [Google Scholar]
- Dorogovtsev, S.N.; Mendes, J.F.F. Evolution of Networks: From Biological Nets to the Internet and WWW; Oxford University Press: Oxford, MS, USA; New York, NY, USA, 2014; ISBN 978-0-19-968671-1. [Google Scholar]
- Wang, Z.; Thomas, R.J.; Scaglione, A. Generating random topology power grids. In Proceedings of the 41st Annual Hawaii International Conference on System Sciences (HICSS 2008), Waikoloa, HI, USA, 7–10 January 2008; p. 183. [Google Scholar]
- Wei, T.-H. Algebraic Foundations of Ranking Theory. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 1952. [Google Scholar]
- Brin, S.; Page, L. The anatomy of a large-scale hypertextual web search engine. In Proceedings of the Seventh International World-Wide Web Conference (WWW 1998), Brisbane, Australia, 14–18 April 1998. [Google Scholar]
- Barnard, S.T.; Simon, H.D. Fast multilevel implementation of recursive spectral bisection for partitioning unstructured problems. Concurr. Comput. Pract. Exp. 1994, 6, 101–117. [Google Scholar] [CrossRef]
- Pothen, A.; Simon, H.; Liou, K. Partitioning sparse matrices with eigenvectors of graphs. SIAM J. Matrix Anal. Appl. 1990, 11, 430–452. [Google Scholar] [CrossRef]
- Ostfeld, A.; Salomons, E.; Ormsbee, L.; Uber, J.G.; Bros, C.M.; Kalungi, P.; Burd, R.; Zazula-Coetzee, B.; Belrain, T.; Kang, D.; et al. Battle of the water calibration networks. J. Water Resour. Plan. Manag. 2012, 138, 523–532. [Google Scholar] [CrossRef]
- Herrera, M.; Abraham, E.; Stoianov, I. A graph-theoretic framework for assessing the resilience of sectorised water distribution networks. Water Resour. Manag. 2016, 30, 1685–1699. [Google Scholar] [CrossRef]
- Sela Perelman, L.; Allen, M.; Preis, A.; Iqbal, M.; Whittle, A.J. Automated sub-zoning of water distribution systems. Environ. Model. Softw. 2015, 65, 1–14. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).