Modelling Wetland Growing Season Rainfall Interception Losses Based on Maximum Canopy Storage Measurements
Abstract
:1. Introduction
2. Materials and Methods
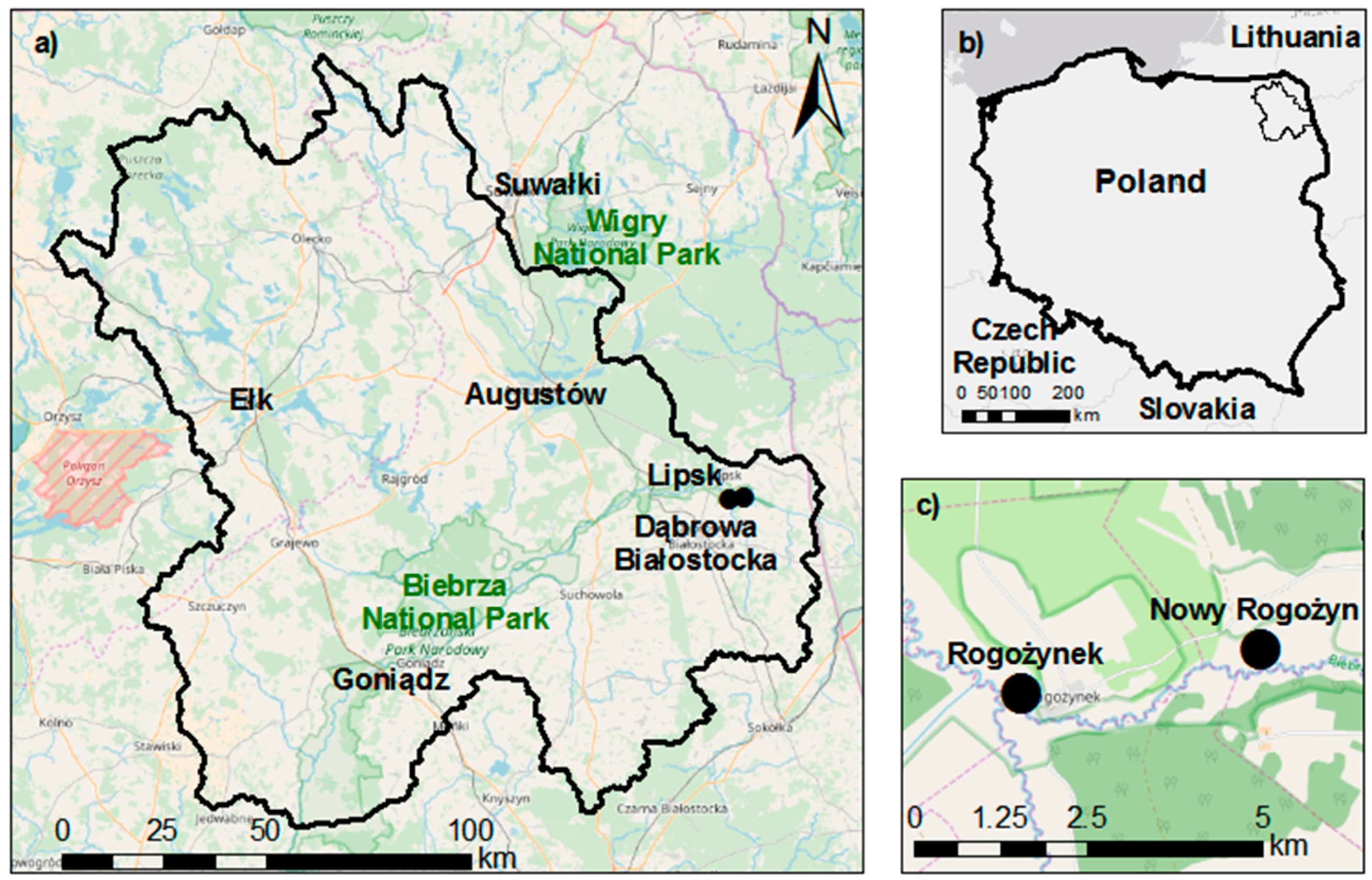
2.1. Study Site
2.2. Maximum Canopy Storage Field Measurements
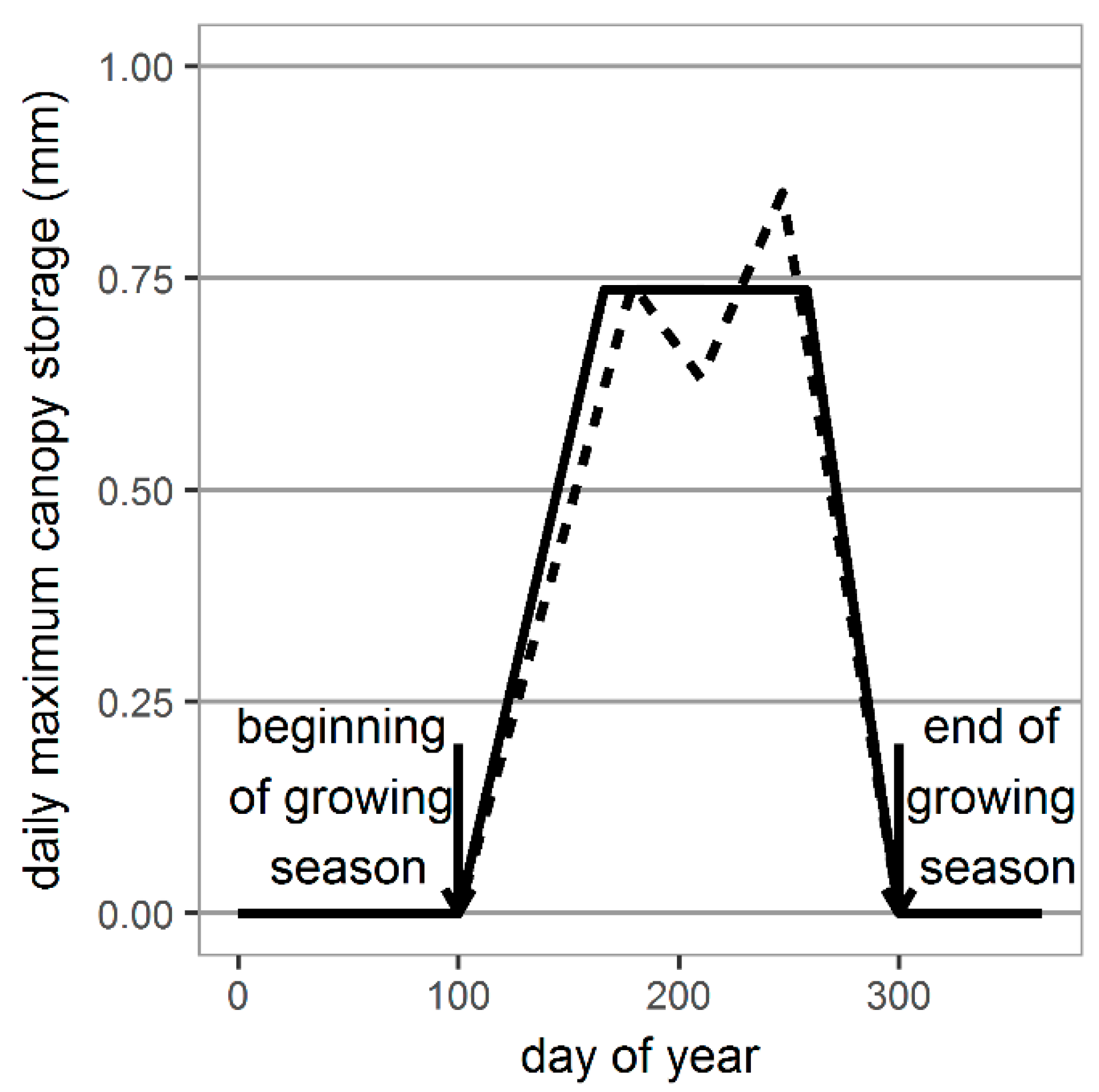
2.3. Generating Daily Values of Maximum Canopy Storage
2.4. Interception Losses Model
3. Results
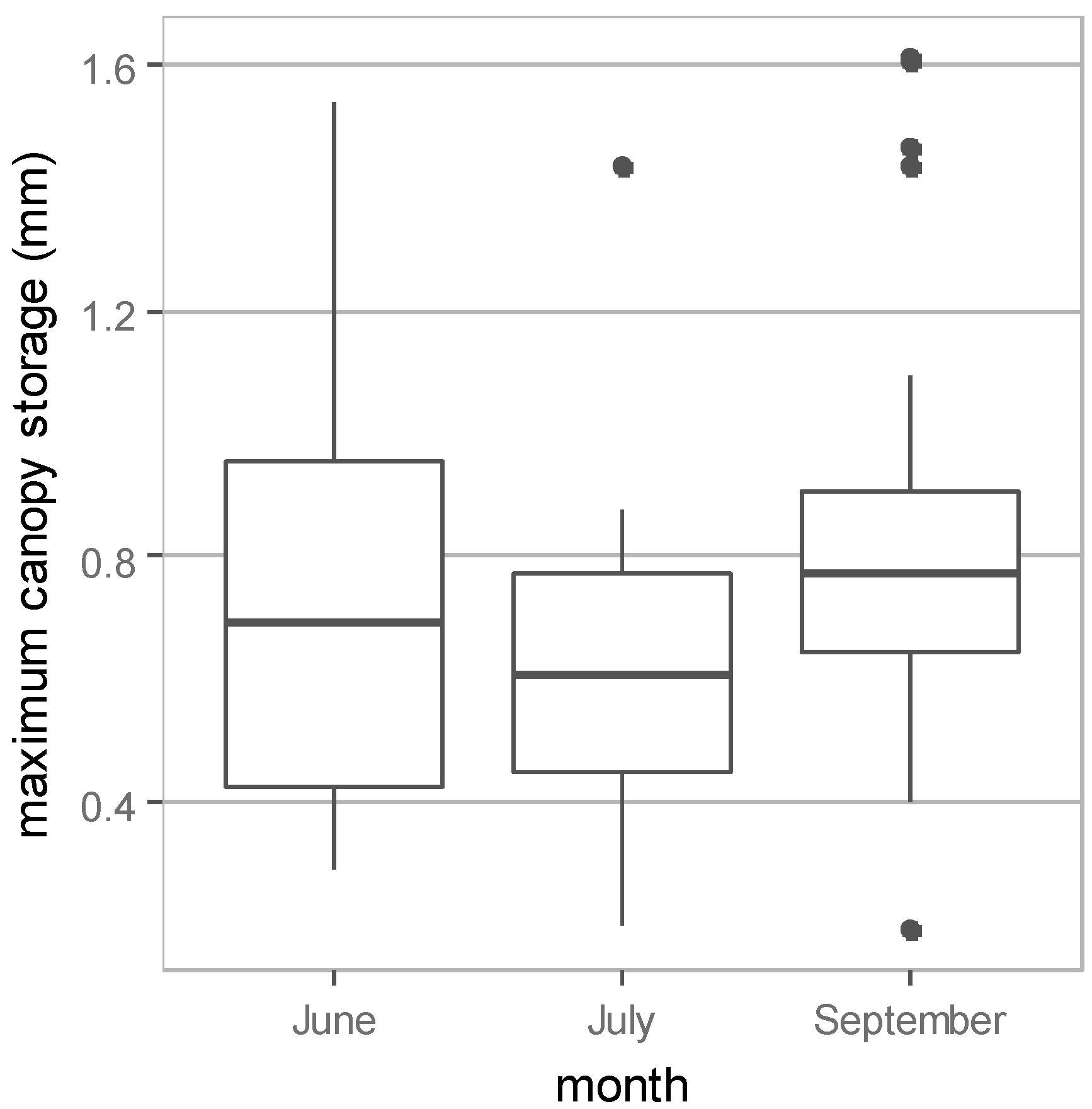
3.1. Field Measurement Results
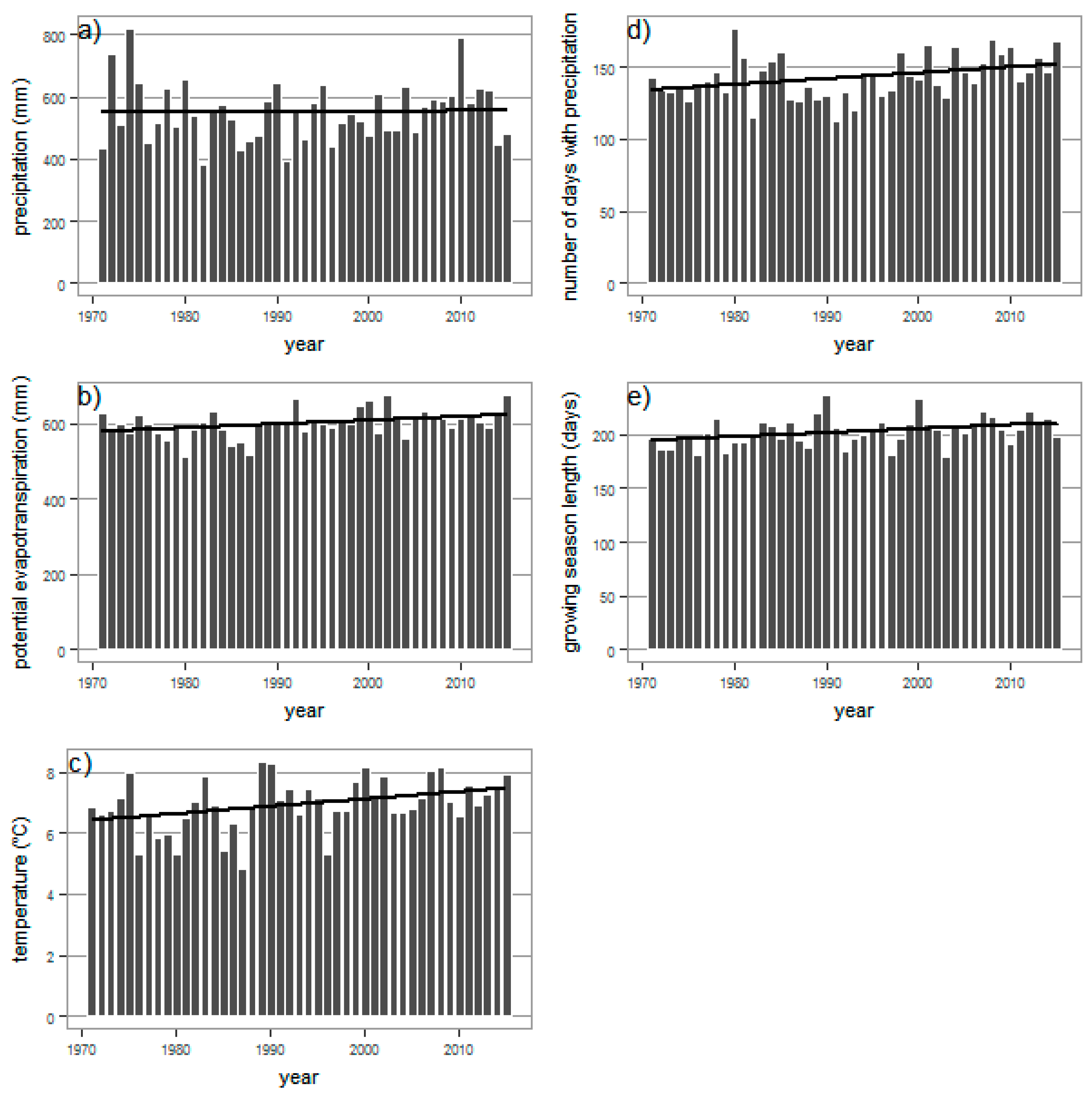
3.2. Meteorological Element Trends, 1971–2015
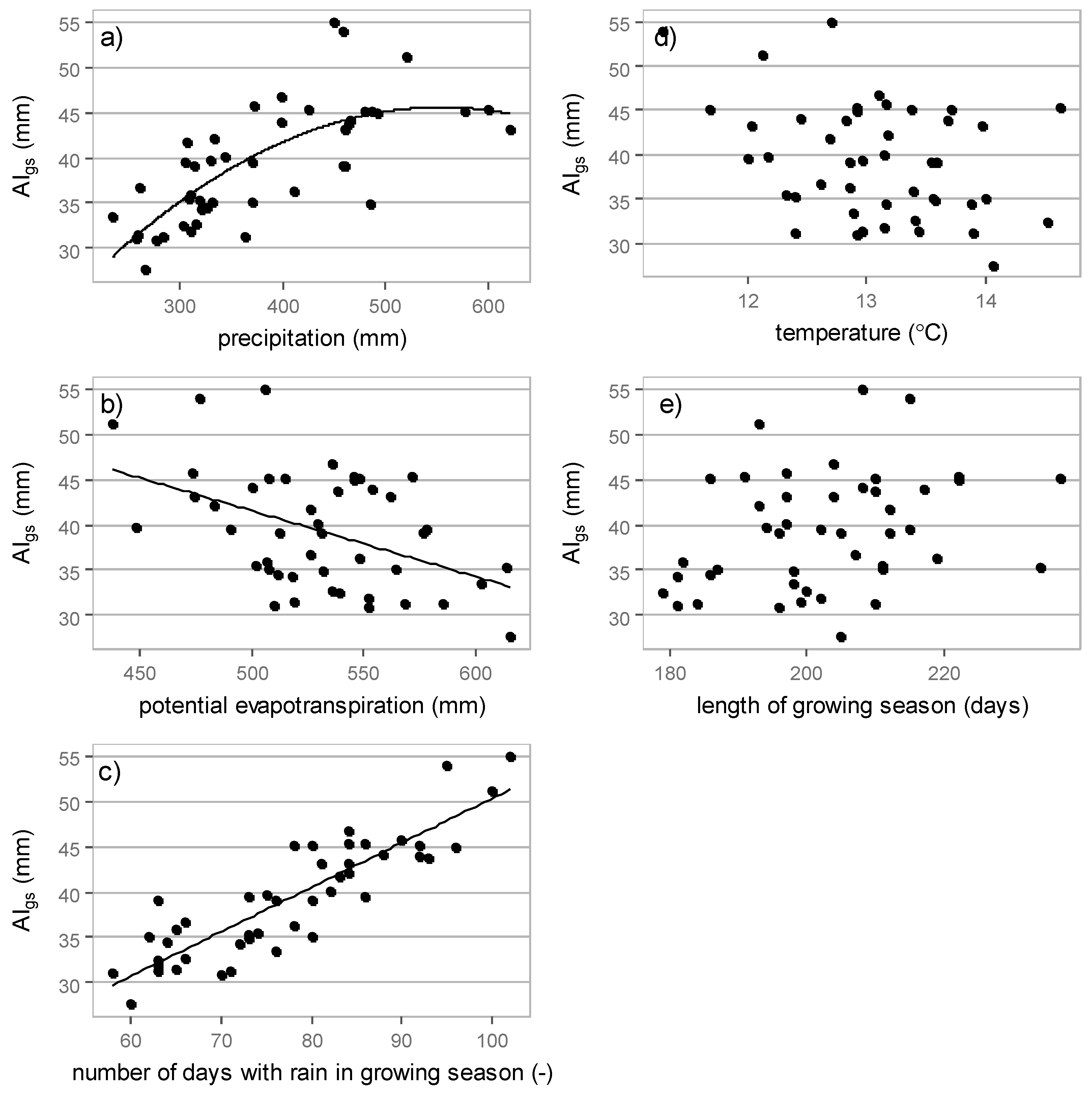
3.3. Relations between Interception Losses and Meteorological Elements
3.3.1. Growing Season Interception
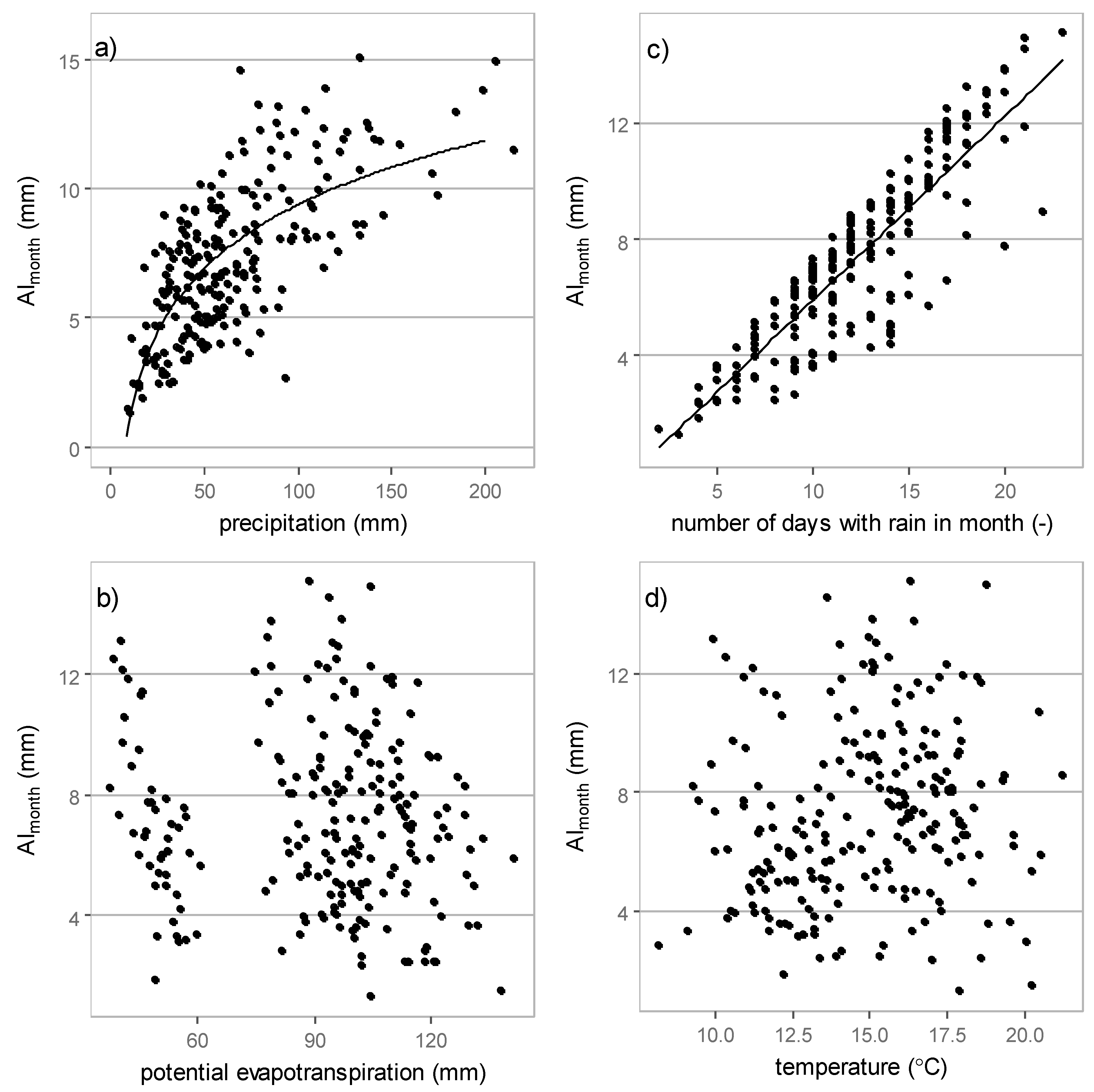
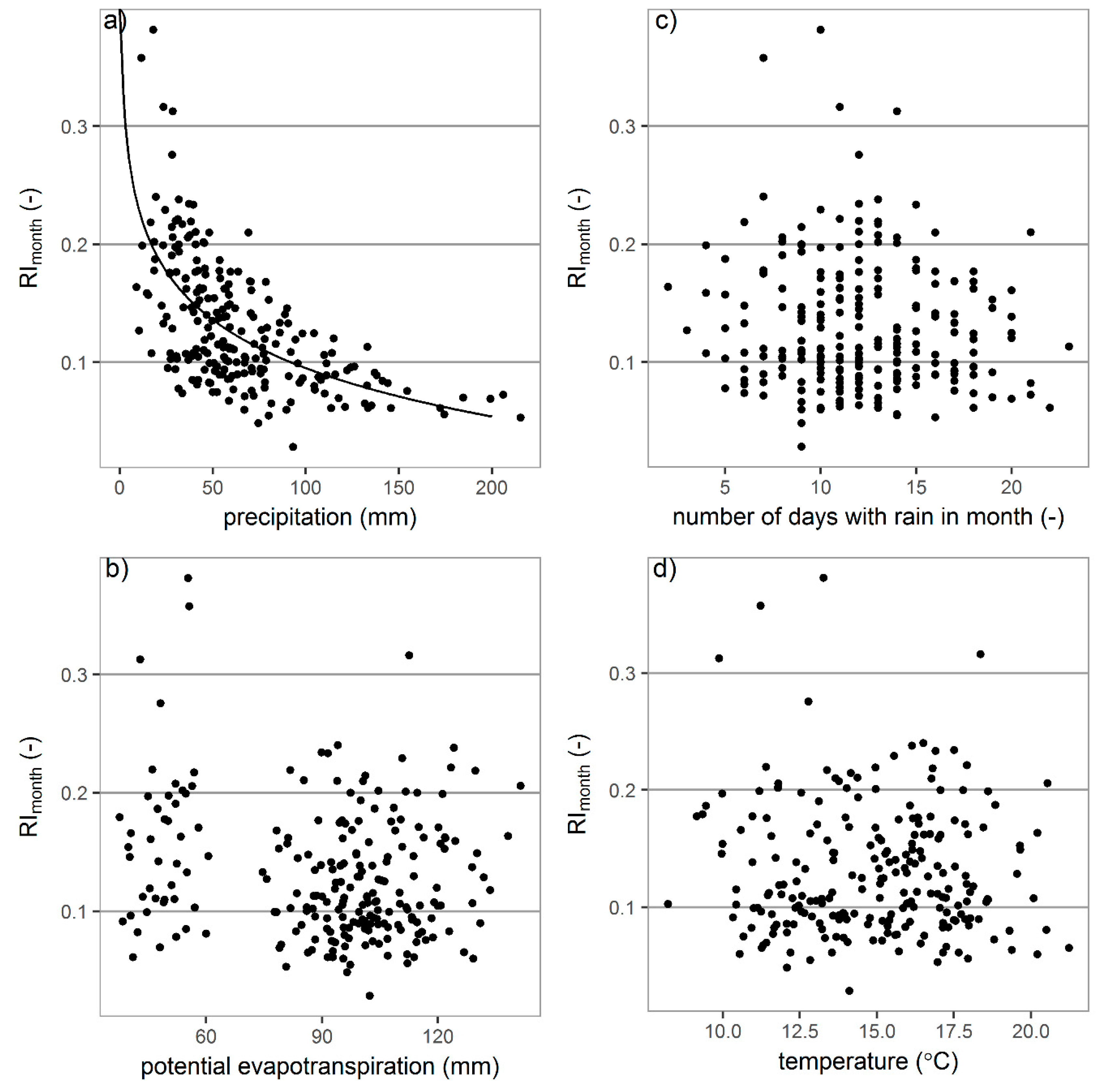
3.3.2. Monthly Interception
4. Discussion
4.1. Maximum Canopy Storage
4.2. Interception Losses
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wood, M.K.; Jones, T.L.; Vera-Cruz, M.T. Rainfall interception by selected plants in the Chihuahuan desert. J. Range Manag. 1998, 51, 91–96. [Google Scholar] [CrossRef]
- Van Dijk, A.; Bruijnzeel, L.A. Modelling rainfall interception by vegetation of variable density using an adapted analytical model. Part 1. Model description. J. Hydrol. 2001, 247, 230–238. [Google Scholar] [CrossRef]
- Muzylo, A.; Llorens, P.; Valente, F.; Keizer, J.J.; Domingo, F.; Gash, J.H.C. A review of rainfall interception modelling. J. Hydrol. 2009, 370, 191–206. [Google Scholar] [CrossRef]
- Campbell, C.L.; Madden, L.V. Introduction to Plant Disease Epidemiology; John Wiley & Sons: New York, NY, USA, 1990. [Google Scholar]
- Bradley, D.J.; Gilbert, G.S.; Parker, I.M. Susceptibility of clover species to fungal infection: The interaction of leaf surface traits and environment. Am. J. Bot. 2003, 90, 857–864. [Google Scholar] [CrossRef] [PubMed]
- Brueggemann, E.; Spindler, G. Wet and dry deposition of sulphur at the site melpitz in East Germany—In memorium dedicated to wolfgang rolle. Water Air Soil Pollut. 1999, 109, 81–99. [Google Scholar] [CrossRef]
- Wesely, M.L.; Sisterson, D.L.; Jastrow, J.D. Observations of the chemical-properties of dew on vegetation that affect the dry deposition of SO2. J. Geophys. Res. Atmos. 1990, 95, 7501–7514. [Google Scholar] [CrossRef]
- Brewer, C.A.; Smith, W.K. Patterns of leaf surface wetness for montane and subalpine plants. Plant Cell Environ. 1997, 20, 1–11. [Google Scholar] [CrossRef]
- Hanba, Y.T.; Moriya, A.; Kimura, K. Effect of leaf surface wetness and wettability on photosynthesis in bean and pea. Plant Cell Environ. 2004, 27, 413–421. [Google Scholar] [CrossRef]
- Savenije, H.H.G. The importance of interception and why we should delete the term evapotranspiration from our vocabulary. Hydrol. Process. 2004, 18, 1507–1511. [Google Scholar] [CrossRef]
- Grayson, R.B.; Moore, I.D.; McMahon, T.A. Physically based hydrologic modeling: 1. A terrain-based model for investigative purposes. Water Resour. Res. 1992, 28, 2639–2658. [Google Scholar] [CrossRef]
- Garrote, L.; Bras, R.L. A distributed model for real-time flood forecasting using digital elevation models. J. Hydrol. 1995, 167, 279–306. [Google Scholar] [CrossRef]
- Reggiani, P.; Rientjes, T.H.M. Flux parameterization in the representative elementary watershed approach: Application to a natural basin. Water Resour. Res. 2005, 41, 18. [Google Scholar] [CrossRef]
- Liu, Z.Y.; Todini, E. Towards a comprehensive physically-based rainfall-runoff model. Hydrol. Earth Syst. Sci. 2002, 6, 859–881. [Google Scholar] [CrossRef]
- Beven, K.; Kirkby, M.J. A physically based, variable contributing area model of basin hydrology/un modèle à base physique de zone d’appel variable de l’hydrologie du bassin versant. Hydrol. Sci. J. 1979, 24, 43–69. [Google Scholar] [CrossRef]
- Abbot, M.; Bathurst, J.; Cunge, J.; O’Connell, P.; Rasmussen, J. An introduction to the European hydrologic system-systeme hydologique Europeen, ”She”, 1: History and philosophy of a physically based, distributed modelling system. J. Hydrol. 1990, 87, 45–59. [Google Scholar] [CrossRef]
- Liu, Y.; De Smedt, F. Wetspa extension, a gis-based hydrologic model for flood prediction and watershed management. Vrije Universiteit Brussel Belgium 2004, 1, e108. [Google Scholar]
- Grah, R.F.; Wilson, C.C. Some components of rainfall interception. J. For. 1944, 42, 890–898. [Google Scholar]
- Wohlfahrt, G.; Bianchi, K.; Cernusca, A. Leaf and stem maximum water storage capacity of herbaceous plants in a mountain meadow. J. Hydrol. 2006, 319, 383–390. [Google Scholar] [CrossRef]
- Yu, K.L.; Pypker, T.G.; Keim, R.F.; Chen, N.; Yang, Y.B.; Guo, S.Q.; Li, W.J.; Wang, G. Canopy rainfall storage capacity as affected by sub-alpine grassland degradation in the Qinghai-Tibetan Plateau, China. Hydrol. Process. 2012, 26, 3114–3123. [Google Scholar] [CrossRef]
- Thurow, T.L.; Blackburn, W.H.; Warren, S.D.; Taylor, C.A. Rainfall interception by midgrass, shortgrass, and live oak mottes. J. Range Manag. 1987, 40, 455–460. [Google Scholar] [CrossRef]
- Jetten, V.G. Interception of tropical rain forest: Performance of a canopy water balance model. Hydrol. Process. 1996, 10, 671–685. [Google Scholar] [CrossRef]
- Germer, S.; Elsenbeer, H.; Moraes, J.M. Throughfall and temporal trends of rainfall redistribution in an open tropical rainforest, south-western Amazonia (Rondonia, Brazil). Hydrol. Earth Syst. Sci. 2006, 10, 383–393. [Google Scholar] [CrossRef]
- Czikowsky, M.J.; Fitzjarrald, D.R. Detecting rainfall interception in an Amazonian rain forest with eddy flux measurements. J. Hydrol. 2009, 377, 92–105. [Google Scholar] [CrossRef]
- Holder, C.D. Rainfall interception and fog precipitation in a tropical montane cloud forest of Guatemala. For. Ecol. Manag. 2004, 190, 373–384. [Google Scholar] [CrossRef]
- Aboal, J.R.; Jimenez, M.S.; Morales, D.; Hernandez, J.M. Rainfall interception in laurel forest in the Canary Islands. Agric. For. Meteorol. 1999, 97, 73–86. [Google Scholar] [CrossRef]
- Dykes, A.P. Rainfall interception from a lowland tropical rainforest in Brunei. J. Hydrol. 1997, 200, 260–279. [Google Scholar] [CrossRef]
- Grelle, A.; Lundberg, A.; Lindroth, A.; Moren, A.S.; Cienciala, E. Evaporation components of a boreal forest: Variations during the growing season. J. Hydrol. 1997, 197, 70–87. [Google Scholar] [CrossRef]
- Shachnovich, Y.; Berliner, P.R.; Bar, P. Rainfall interception and spatial distribution of throughfall in a pine forest planted in an arid zone. J. Hydrol. 2008, 349, 168–177. [Google Scholar] [CrossRef]
- Sraj, M.; Brilly, M.; Mikos, M. Rainfall interception by two deciduous mediterranean forests of contrasting stature in Slovenia. Agric. For. Meteorol. 2008, 148, 121–134. [Google Scholar] [CrossRef]
- Dunkerley, D.L.; Booth, T.L. Plant canopy interception of rainfall and its significance in a banded landscape, arid western New South Wales, Australia. Water Resour. Res. 1999, 35, 1581–1586. [Google Scholar] [CrossRef]
- Tromble, J.M. Interception of rainfall by tarbush. J. Range Manag. 1983, 36, 525–526. [Google Scholar] [CrossRef]
- Kołodziej, J.; Liniewicz, K.; Bednarek, H. Intercepcja opadów atmosferycznych w łanach zbóż. Acta Agrophys. 2005, 6, 381–391. (In Polish) [Google Scholar]
- Rutter, A.J.; Robins, P.C.; Morton, A.J.; Kershaw, K.A. Predictive model of rainfall interception in forests. 1. Derivation of model from observations in a plantation of corsican pine. Agric. Meteorol. 1972, 9, 367–384. [Google Scholar] [CrossRef]
- Berezowski, T.; Chormański, J.; Kleniewska, M.; Szporak-Wasilewska, S. Towards rainfall interception capacity estimation using ALS LiDAR data. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 735–738. [Google Scholar]
- Suliga, J.; Chormanski, J.; Szporak-Wasilewska, S.; Kleniewska, M.; Berezowski, T.; van Griensven, A.; Verbeiren, B. Derivation from the Landsat 7 NDVI and ground truth validation of LAI and interception storage capacity for wetland ecosystems in Biebrza Valley, Poland. In Proceedings of the SPIE Remote Sensing for Agriculture, Ecosystems, and Hydrology XVII, Toulouse, France, 22–24 September 2015. [Google Scholar]
- De Jong, S.M.; Jetten, V.G. Estimating spatial patterns of rainfall interception from remotely sensed vegetation indices and spectral mixture analysis. Int. J. Geogr. Inf. Sci. 2007, 21, 529–545. [Google Scholar] [CrossRef]
- Gomez, J.A.; Giraldez, J.V.; Fereres, E. Rainfall interception by olive trees in relation to leaf area. Agric. Water Manag. 2001, 49, 65–76. [Google Scholar] [CrossRef]
- Hoyningen-Huene, J.V. Die Interzeption des Niederschlages in Landwirtschaftlichen Pflanzenbeständen; Arbeitsbericht Deutscher Verband für Wasserwirtschaft und Kulturbau, DVWK: Braunschweig, Germany, 1981. [Google Scholar]
- Verbeiren, B.; Khanh Nguyen, H.; Wirion, C.; Batelaan, O. An earth observation based method to assess the influence of seasonal dynamics of canopy interception storage on the urban water balance. Belgeo 2016, 2016. [Google Scholar] [CrossRef]
- Wirion, C.; Ho, K.N.; Bauwens, W.; Verbeiren, B. Using remote sensing to describe urban surface properties for improved hydrological modelling. In Proceedings of the 10th International Urban Drainage Modeling Conference, Quebec, QC, Canada, 20–23 September 2015. [Google Scholar]
- Górniak, A. Klimat i termika wód powierzchniowych kotliny biebrzańskiej. In Kotlina Biebrzańska i Biebrzański Park Narodowy: Aktualny Stan, Zagrożenia i Potrzeby Czynnej Ochrony Środowiska; Ekonomia i Środowisko: Białystok, Poland, 2004. (In Polish) [Google Scholar]
- Kossowska-Cezak, U.; Olszewski, K.; Przybylska, G. Climate of the Biebrza Valley. Zesz. Probl. Postepow Nauk Rolniczych 1991, 372, 119–158. (In Polish) [Google Scholar]
- West, N.E.; Gifford, G.F. Rainfall interception by cool-desert shrubs. J. Range Manag. 1976, 29, 171–172. [Google Scholar] [CrossRef]
- Ignar, S.; Węglewska, A.; Szporak-Wasilewska, S.; Chormański, J. Spatial and temporal variability of the interception in the natural wetland valley, the lower Biebrza basin case study. Ann. Warsaw Univ. Life Sci.-SGGW Land Reclam. 2013, 45, 111–119. [Google Scholar] [CrossRef]
- Calder, I.R.; Hall, R.L.; Rosier, P.T.W.; Bastable, H.G.; Prasanna, K.T. Dependence of rainfall interception on drop size: 2. Experimental determination of the wetting functions and two-layer stochastic model parameters for five tropical tree species. J. Hydrol. 1996, 185, 379–388. [Google Scholar] [CrossRef]
- Szporak-Wasilewska, S.; Szatyłowicz, J.; Okruszko, T.; Ignar, S. Application of the surface energy balance system model (SEBS) for mapping evapotranspiration of extensively used river valley with wetland vegetation. Towards Horiz. 2013, 2020, 929–942. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop evapotranspiration—guidelines for computing crop water requirements—FAO irrigation and drainage paper 56. FAO Rome 1998, 300, D05109. [Google Scholar]
- Gash, J.H.C. Analytical model of rainfall interception by forests. Q. J. R. Meteorol. Soc. 1979, 105, 43–55. [Google Scholar] [CrossRef]
- Kępińska-Kasprzak, M.; Mager, P. Thermal growing season in Poland calculated by two different methods. Ann. Warsaw Univ. Life Sci. Land Reclam. 2015, 47, 261–273. [Google Scholar] [CrossRef]
- McLeod, A.I. Kendall Rank Correlation and Mann–Kendall Trend Test, Version 2.2; The R Foundation for Statistical Computing: Vienna, Austria, 2015. [Google Scholar]
- Monson, R.K.; Grant, M.C.; Jaeger, C.H.; Schoettle, A.W. Morphological causes for the retention of precipitation in the crowns of alpine plants. Environ. Exp. Bot. 1992, 32, 319–327. [Google Scholar] [CrossRef]
- Pypker, T.G.; Bond, B.J.; Link, T.E.; Marks, D.; Unsworth, M.H. The importance of canopy structure in controlling the interception loss of rainfall: Examples from a young and an old-growth douglas-fir forest. Agric. For. Meteorol. 2005, 130, 113–129. [Google Scholar] [CrossRef]
- Klaassen, W.; Bosveld, F.; de Water, E. Water storage and evaporation as constituents of rainfall interception. J. Hydrol. 1998, 212, 36–50. [Google Scholar] [CrossRef]
- Gash, J.; Wright, I.; Lloyd, C.R. Comparative estimates of interception loss from three coniferous forests in Great Britain. J. Hydrol. 1980, 48, 89–105. [Google Scholar] [CrossRef]
- Loustau, D.; Berbigier, P.; Granier, A. Interception loss, throughfall and stemflow in a maritime pine stand. II. An application of gash’s analytical model of interception. J. Hydrol. 1992, 138, 469–485. [Google Scholar] [CrossRef]
- Dunkerley, D. Measuring interception loss and canopy storage in dryland vegetation: A brief review and evaluation of available research strategies. Hydrol. Process. 2000, 14, 669–678. [Google Scholar] [CrossRef]
- Hormann, G.; Branding, A.; Clemen, T.; Herbst, M.; Hinrichs, A.; Thamm, F. Calculation and simulation of wind controlled canopy interception of a beech forest in northern Germany. Agric. For. Meteorol. 1996, 79, 131–148. [Google Scholar] [CrossRef]
- Levia, D.F.; Keim, R.F.; Carlyle-Moses, D.E.; Frost, E.E. Throughfall and stemflow in wooded ecosystems. In Forest Hydrology and Biogeochemistry: Synthesis of Past Research and Future Directions; Levia, D.F., CarlyleMoses, D., Tanaka, T., Eds.; Springer: Dordrecht, The Netherlands, 2011; Volume 216, pp. 425–443. [Google Scholar]
- Calder, I.R. Evaporation in the Uplands; John Wiley & Sons Ltd.: Chichester, UK, 1990. [Google Scholar]
- Kozłowski, R.; Jóźwiak, M. Transformacja opadów atmosferycznych w strefie drzew wybranych ekosystemów leśnych w górach świętokrzyskich = the transformation of precipitation in the tree canopy in selected forest ecosystems of poland’s świętokrzyskie mountains. Przegl. Geogr. 2017, 89, 133–153. (In Polish) [Google Scholar] [CrossRef]


| Date | Number of Samples | Maximum Canopy Storage | |||||
|---|---|---|---|---|---|---|---|
| mm H2O per Unit Area | g H2O per Sampling Area | ||||||
| Mean ± SD | min | max | Mean ± SD | min | max | ||
| 26–29 June | 28 | 0.74 ± 0.35 | 0.29 | 1.54 | 46.4 ± 21.9 | 17.9 | 96.2 |
| 28–30 July | 19 | 0.63 ± 0.27 | 0.20 | 1.44 | 39.5 ± 16.9 | 12.2 | 89.7 |
| 4–5 September | 21 | 0.85 ± 0.39 | 0.19 | 1.61 | 53.2 ± 24.4 | 12.1 | 100.6 |
| Meteorological Parameter | Annual Mean | Trend Slope | Growing Season Mean | Trend Slope | Annual M-K Tau |
|---|---|---|---|---|---|
| precipitation (mm) | 552 ** | +0.15 mm/year | 383 ** | −0.02 mm/year | 0.062 ** |
| potential evapotranspiration (mm) | 600 * | +1 mm/year | 530 * | +1.76 mm/year | 0.259 * |
| temperature (°C) | 6.9 * | +0.02 °C/year | 13.1 * | +0.02 °C/year | 0.259 * |
| number of days with precipitation (-) | 143 * | +0.4 day/year | 78 ** | +0.18 day/year | 0.274 * |
| growing season length (-) | 204 * | +0.37 day/year | 0.272 * |
| Meteorological Element | Absolute Interception (mm) | Relative Interception (-) |
|---|---|---|
| precipitation | 0.72 * | 0.75 * |
| potential evapotranspiration | 0.45 * | 0.05 ** |
| numbers of days with rain | 0.88 * | 0.13 ** |
| temperature | 0.36 * | 0.28 * |
| growing season length | 0.30 * | 0.08 ** |
| Meteorological Element | May | June | July | August | September | All Data | |
|---|---|---|---|---|---|---|---|
| precipitation | AI | 0.68 | 0.62 | 0.74 | 0.67 | 0.71 | 0.69 |
| RI | 0.60 | 0.77 | 0.70 | 0.65 | 0.59 | 0.62 | |
| potential evapotranspiration | AI | 0.40 | 0.59 | 0.73 | 0.64 | 0.69 | * |
| RI | * | * | * | 0.37 | * | * | |
| numbers of days with rain | AI | 0.92 | 0.98 | 0.97 | 0.98 | 0.97 | 0.88 |
| RI | * | * | * | * | * | * | |
| temperature | AI | * | 0.35 | 0.50 | 0.38 | 0.31 | * |
| RI | * | * | * | * | * | * | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ciężkowski, W.; Berezowski, T.; Kleniewska, M.; Szporak-Wasilewska, S.; Chormański, J. Modelling Wetland Growing Season Rainfall Interception Losses Based on Maximum Canopy Storage Measurements. Water 2018, 10, 41. https://doi.org/10.3390/w10010041
Ciężkowski W, Berezowski T, Kleniewska M, Szporak-Wasilewska S, Chormański J. Modelling Wetland Growing Season Rainfall Interception Losses Based on Maximum Canopy Storage Measurements. Water. 2018; 10(1):41. https://doi.org/10.3390/w10010041
Chicago/Turabian StyleCiężkowski, Wojciech, Tomasz Berezowski, Małgorzata Kleniewska, Sylwia Szporak-Wasilewska, and Jarosław Chormański. 2018. "Modelling Wetland Growing Season Rainfall Interception Losses Based on Maximum Canopy Storage Measurements" Water 10, no. 1: 41. https://doi.org/10.3390/w10010041
APA StyleCiężkowski, W., Berezowski, T., Kleniewska, M., Szporak-Wasilewska, S., & Chormański, J. (2018). Modelling Wetland Growing Season Rainfall Interception Losses Based on Maximum Canopy Storage Measurements. Water, 10(1), 41. https://doi.org/10.3390/w10010041





