Estimating Carbon Dioxide (CO2) Emissions from Reservoirs Using Artificial Neural Networks
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Collection
2.2. Input Variables and Data Processing
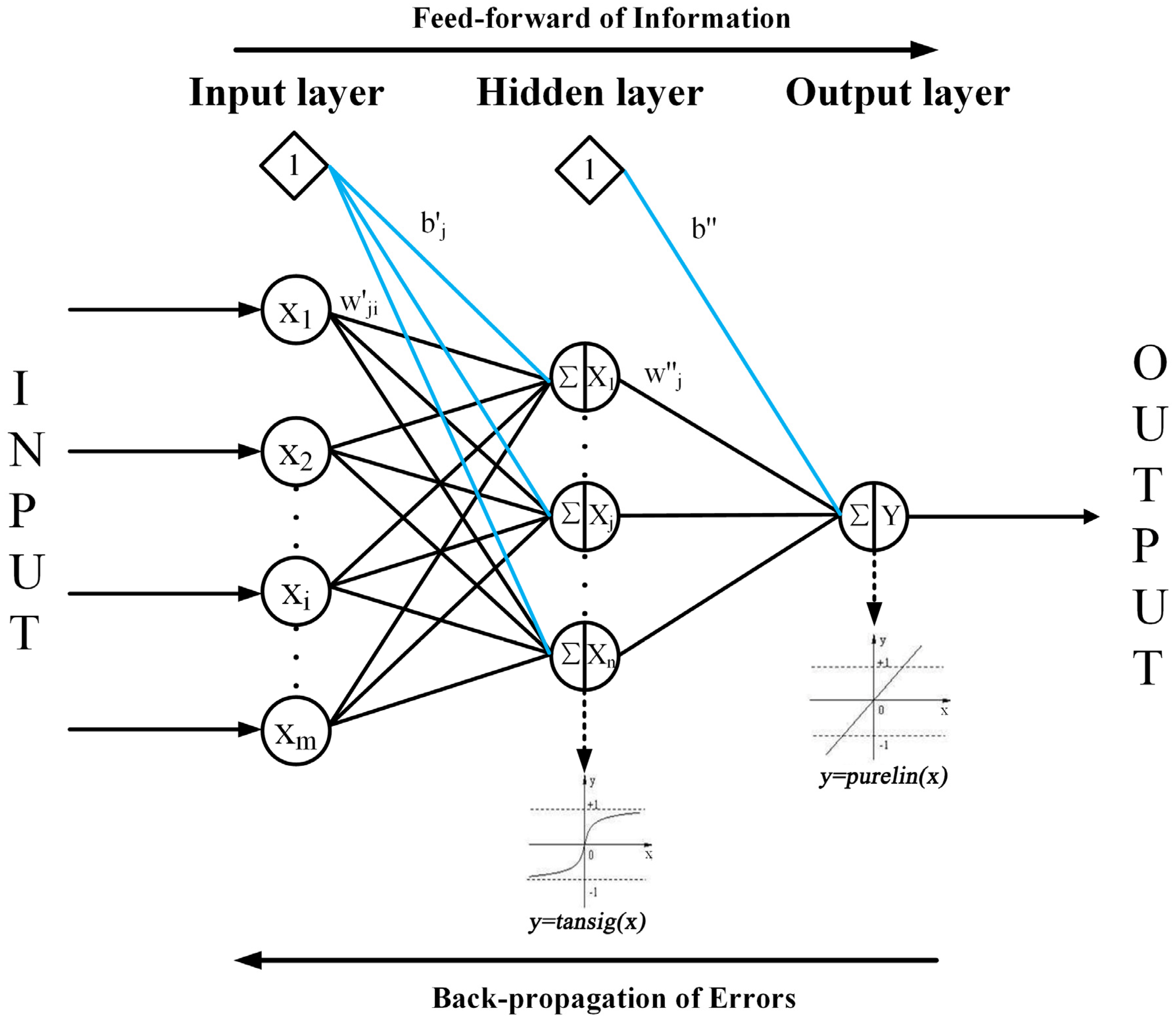
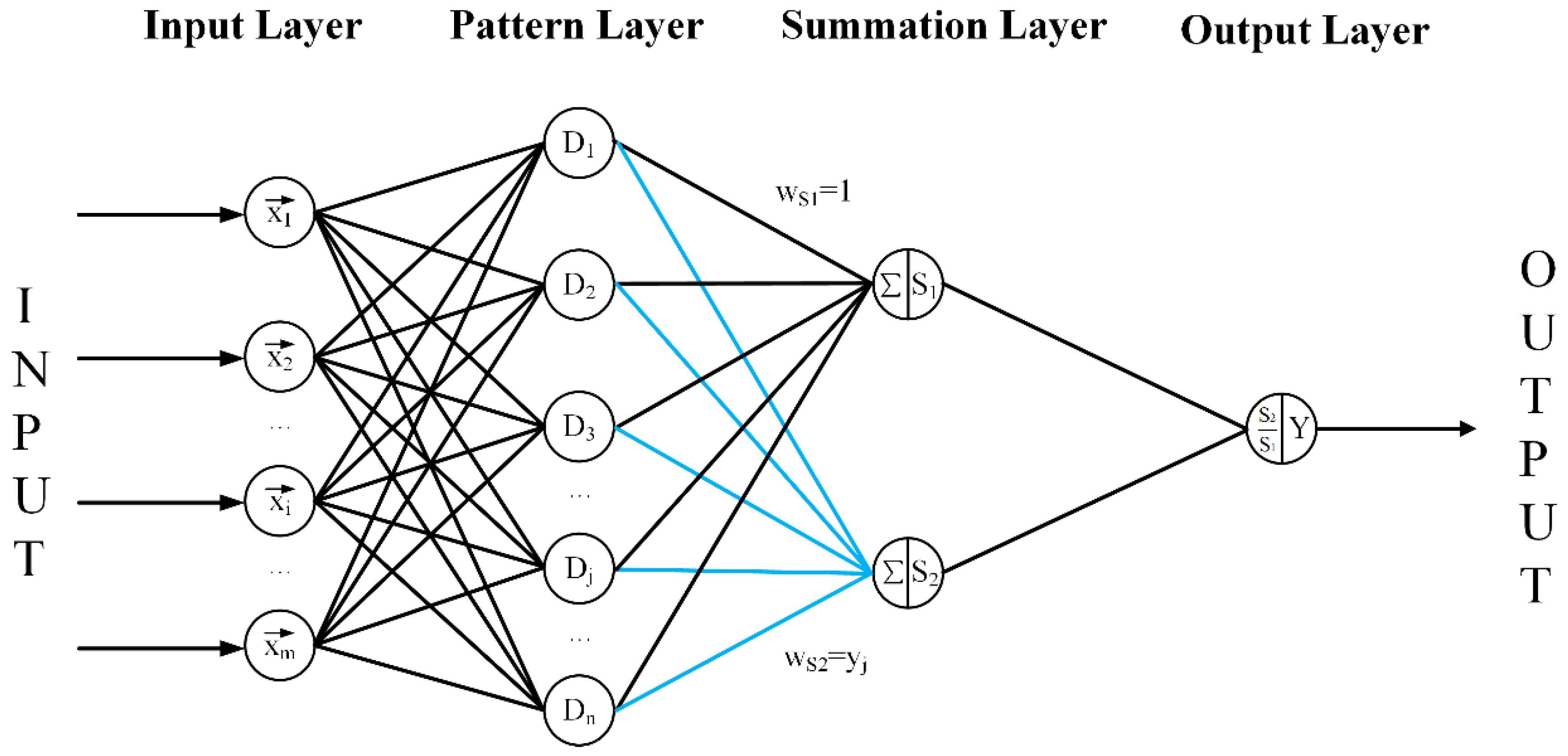
2.3. Artificial Neural Networks (ANNs)
2.3.1. Back Propagation Neural Networks (BPNNs)
2.3.2. General Regression Neural Networks (GRNNs)
2.4. Statistical Regression Models
2.5. Performance Metrics
3. Results
3.1. Alternative Input Variable Selection
3.2. Model Parameters Selection
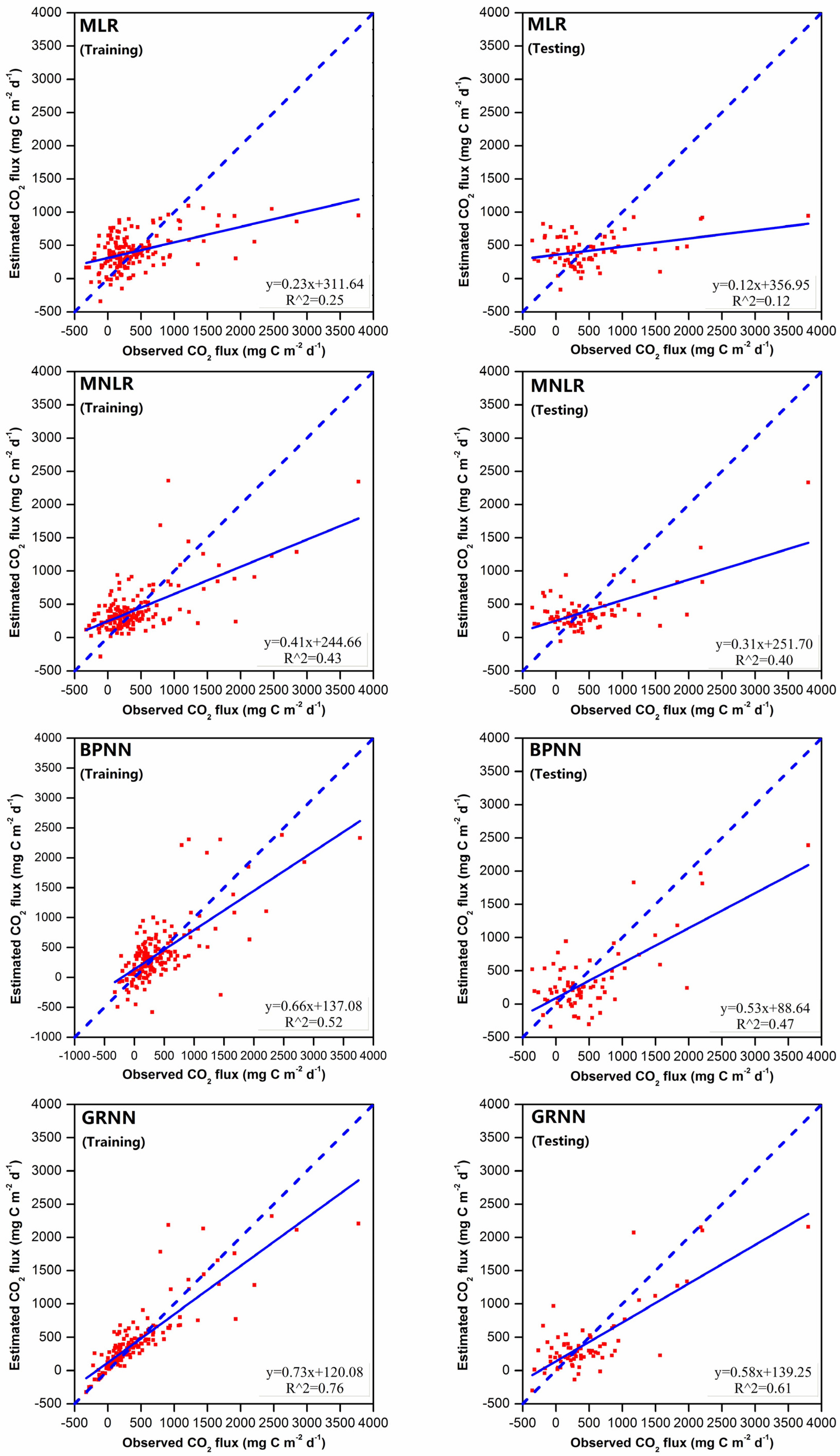
3.3. Model Performances
3.4. Sensitivity Analysis
4. Discussion
4.1. Comparison of Results Obtained by Models
4.2. Sensitivity Analysis
4.3. Application of Established Model
4.3.1. Estimation of the Global Magnitude of the CO2 Fluxes from Reservoirs
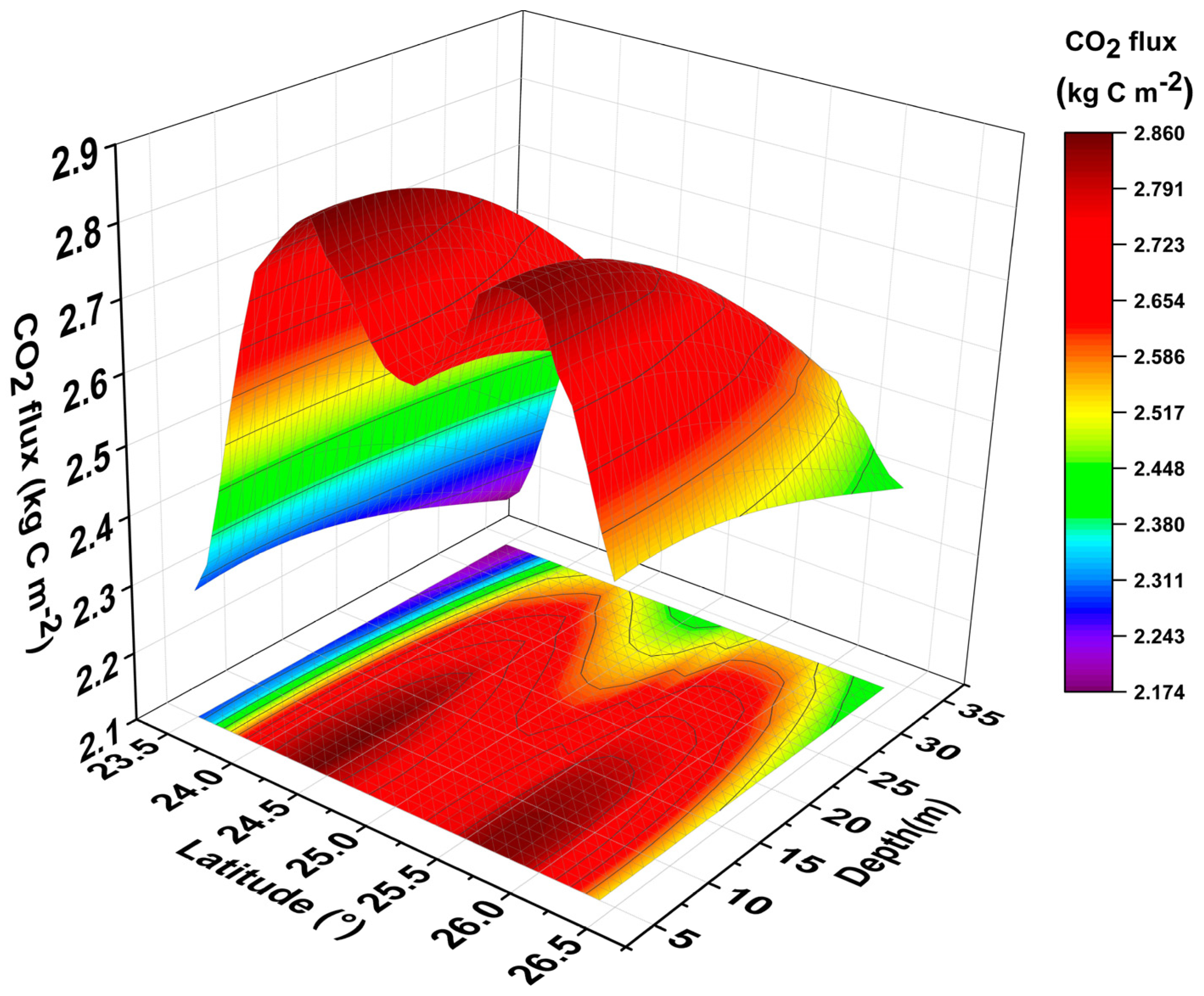
4.3.2. Estimations of CO2 Emissions from a Planned Reservoir
4.4. Future Research Directions
5. Conclusions
Supplementary Materials
Author Contributions
Conflicts of Interest
References
- Rudd, J.W.M.; Hecky, R.E. Are hydroelectric reservoirs significant sources of greenhouse gases? Ambio 1993, 22, 246–248. [Google Scholar]
- Tremblay, A.; Varfalvy, L.; Roehm, C.; Garneau, M. Greenhouse Gas Emissions-Fluxes and Processes: Hydroelectric Reservoirs and Natural Environments; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2005; ISBN 3-540-23455-1. [Google Scholar]
- Teodoru, C.R.; Bastien, J.; Bonneville, M.C.; del Giorgio, P.A.; Demarty, M.; Garneau, M.; Hélie, J.F.; Pelletier, L.; Prairie, Y.T.; Roulet, N.T. The net carbon footprint of a newly created boreal hydroelectric reservoir. Glob. Biogeochem. Cycles 2012, 26. [Google Scholar] [CrossRef]
- Demarty, M.; Bastien, J.; Tremblay, A.; Hesslein, R.H.; Gill, R. Greenhouse gas emissions from boreal reservoirs in Manitoba and Québec, Canada, measured with automated systems. Environ. Sci. Technol. 2009, 43, 8908–8915. [Google Scholar] [CrossRef] [PubMed]
- Roland, F.; Vidal, L.O.; Pacheco, F.S.; Barros, N.O.; Assireu, A.; Ometto, J.P.H.B.; Cimbleris, A.C.P.; Cole, J.J. Variability of carbon dioxide flux from tropical (Cerrado) hydroelectric reservoirs. Aquat. Sci. 2010, 72, 283–293. [Google Scholar] [CrossRef]
- Mosher, J.J.; Fortner, A.M.; Phillips, J.R.; Bevelhimer, M.S.; Stewart, A.J.; Troia, M.J. Spatial and temporal correlates of greenhouse gas diffusion from a hydropower reservoir in the Southern United States. Water 2015, 7, 5910–5927. [Google Scholar] [CrossRef]
- Bevelhimer, M.S.; Stewart, A.J.; Fortner, A.M.; Phillips, J.R.; Mosher, J.J. CO2 is dominant greenhouse gas emitted from six hydropower reservoirs in Southeastern United States during peak summer emissions. Water 2016, 8, 15. [Google Scholar] [CrossRef]
- St. Louis, V.L.; Kelly, C.A.; Duchemin, É.; Rudd, J.W.M.; Rosenberg, D.M. Reservoir surfaces as sources of greenhouse gases to the atmosphere: A global estimate. Bioscience 2000, 50, 766–775. [Google Scholar] [CrossRef]
- Saidi, H.; Koschorreck, M. CO2 emissions from German drinking water reservoirs. Sci. Total Environ. 2017, 581, 10–18. [Google Scholar] [CrossRef] [PubMed]
- Fearnside, P.M.; Pueyo, S. Greenhouse gas emissions from tropical dams. Nat. Clim. Chang. 2012, 2, 382–384. [Google Scholar] [CrossRef]
- Barros, N.; Cole, J.J.; Tranvik, L.J.; Prairie, Y.T.; Bastviken, D.; Huszar, V.L.M.; del Giorgio, P.; Roland, F. Carbon emission from hydroelectric reservoirs linked to reservoir age and latitude. Nat. Geosci. 2011, 4, 593–596. [Google Scholar] [CrossRef]
- Deemer, B.R.; Harrison, J.A.; Li, S.; Beaulieu, J.J.; Delsontro, T.; Barros, N.; Bezerra-Neto, J.F.; Powers, S.M.; dos Santos, M.A.; Vonk, J.A. Greenhouse gas emissions from reservoir water surfaces: A new global synthesis. Bioscience 2016, 66, 949–964. [Google Scholar] [CrossRef]
- Raymond, P.A.; Hartmann, J.; Lauerwald, R.; Sobek, S.; McDonald, C.; Hoover, M.; Butman, D.; Striegl, R.; Mayorga, E.; Humborg, C. Global carbon dioxide emissions from inland waters. Nature 2013, 503, 355–359. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Wu, B.F.; Zeng, Y. Spatial and temporal patterns of greenhouse gas emissions from three gorges reservoir of china. Biogeosciences 2013, 10, 1219–1230. [Google Scholar] [CrossRef]
- Teodoru, C.R.; Prairie, Y.T.; del Giorgio, P.A. Spatial heterogeneity of surface CO2 fluxes in a newly created eastmain-1 reservoir in Northern Quebec, Canada. Ecosystems 2011, 14, 28–46. [Google Scholar] [CrossRef]
- Hertwich, E.G. Addressing biogenic greenhouse gas emissions from hydropower in LCA. Environ. Sci. Technol. 2013, 47, 9604–9611. [Google Scholar] [CrossRef] [PubMed]
- Soumis, N.; Duchemin, É.; Canuel, R.; Lucotte, M. Greenhouse gas emissions from reservoirs of the Western United States. Glob. Biogeochem. Cycles 2004, 18. [Google Scholar] [CrossRef]
- Li, S.Y.; Zhang, Q.F.; Bush, R.T.; Sullivan, L.A. Methane and CO2 emissions from China’s hydroelectric reservoirs: A new quantitative synthesis. Environ. Sci. Pollut. Res. 2015, 22, 5325–5339. [Google Scholar] [CrossRef] [PubMed]
- Lehner, B.; Liermann, C.R.; Revenga, C.; Vörösmarty, C.; Fekete, B.; Crouzet, P.; Döll, P.; Endejan, M.; Frenken, K.; Magome, J.; et al. High-resolution mapping of the world’s reservoirs and dams for sustainable river-flow management. Front. Ecol. Environ. 2011, 9, 494–502. [Google Scholar] [CrossRef]
- Musenze, R.S.; Grinham, A.; Werner, U.; Gale, D.; Sturm, K.; Udy, J.; Yuan, Z.G. Assessing the spatial and temporal variability of diffusive methane and nitrous oxide emissions from subtropical freshwater reservoirs. Environ. Sci. Technol. 2014, 48, 14499–14507. [Google Scholar] [CrossRef] [PubMed]
- De Faria, F.A.M.; Jaramillo, P.; Sawakuchi, H.O.; Richey, J.E.; Barros, N. Estimating greenhouse gas emissions from future Amazonian hydroelectric reservoirs. Environ. Res. Lett. 2015, 10, 1–13. [Google Scholar] [CrossRef]
- Rosa, L.P.; dos Santos, M.A.; Gesteira, C.; Xavier, A.E. A model for the data extrapolation of greenhouse gas emissions in the Brazilian hydroelectric system. Environ. Res. Lett. 2016, 11. [Google Scholar] [CrossRef]
- Dogan, E.; Sengorur, B.; Koklu, R. Modeling biological oxygen demand of the Melen River in Turkey using an artificial neural network technique. J. Environ. Manag. 2009, 90, 1229–1235. [Google Scholar] [CrossRef] [PubMed]
- Lu, F.; Chen, Z.; Liu, W.Q.; Shao, H.B. Modeling chlorophyll-a concentrations using an artificial neural network for precisely eco-restoring lake basin. Ecol. Eng. 2016, 95, 422–429. [Google Scholar] [CrossRef]
- Antanasijević, D.; Pocajt, V.; Ristić, M.; Perić-Grujić, A. Modeling of energy consumption and related GHG (greenhouse gas) intensity and emissions in Europe using general regression neural networks. Energy 2015, 84, 816–824. [Google Scholar] [CrossRef]
- Antanasijević, D.Z.; Ristić, M.Đ.; Perić-Grujić, A.A.; Pocajt, V.V. Forecasting GHG emissions using an optimized artificial neural network model based on correlation and principal component analysis. Int. J. Greenh. Gas Control 2014, 20, 244–253. [Google Scholar] [CrossRef]
- Antonopoulos, V.Z.; Antonopoulos, A.V. Daily reference evapotranspiration estimates by artificial neural networks technique and empirical equations using limited input climate variables. Comput. Electron. Agric. 2017, 132, 86–96. [Google Scholar] [CrossRef]
- Vakili, M.; Sabbagh-Yazdi, S.R.; Khosrojerdi, S.; Kalhor, K. Evaluating the effect of particulate matter pollution on estimation of daily global solar radiation using artificial neural network modeling based on meteorological data. J. Clean. Prod. 2017, 141, 1275–1285. [Google Scholar] [CrossRef]
- Ding, W.F.; Zhang, J.S.; Leung, Y. Prediction of air pollutant concentration based on sparse response back-propagation training feedforward neural networks. Environ. Sci. Pollut. Res. 2016, 23, 19481–19494. [Google Scholar] [CrossRef] [PubMed]
- Salami, E.S.; Salari, M.; Ehteshami, M.; Bidokhti, N.T.; Ghadimi, H. Application of artificial neural networks and mathematical modeling for the prediction of water quality variables (case study: Southwest of Iran). Desalin. Water Treat. 2016, 57, 27073–27084. [Google Scholar] [CrossRef]
- Maier, H.R.; Jain, A.; Dandy, G.C.; Sudheer, K.P. Methods used for the development of neural networks for the prediction of water resource variables in river systems: Current status and future directions. Environ. Model. Softw. 2010, 25, 891–909. [Google Scholar] [CrossRef]
- Haberl, H.; Erb, K.H.; Krausmann, F.; Gaube, V.; Bondeau, A.; Plutzar, C.; Gingrich, S.; Lucht, W.; Fischer-Kowalski, M. Quantifying and mapping the human appropriation of net primary production in earth’s terrestrial ecosystems. Proc. Natl. Acad. Sci. USA 2007, 104, 12942–12947. [Google Scholar] [CrossRef] [PubMed]
- Antonopoulos, V.Z.; Gianniou, S.K.; Antonopoulos, A.V. Artificial neural networks and empirical equations to estimate daily evaporation: Application to Lake Vegoritis, Greece. Hydrol. Sci. J. 2016, 61, 2590–2599. [Google Scholar] [CrossRef]
- Nielsen, M.A. Neural Networks and Deep Learning; Determination Press: USA, 2015. Available online: http://neuralnetworksanddeeplearning.com/ (accessed on 29 December 2017).
- He, B.; Oki, T.; Sun, F.B.; Komori, D.; Kanae, S.; Wang, Y.; Kim, H.; Yamazaki, D. Estimating monthly total nitrogen concentration in streams by using artificial neural network. J. Environ. Manag. 2011, 92, 172–177. [Google Scholar] [CrossRef] [PubMed]
- Specht, D.F. A general regression neural network. IEEE Trans. Neural Netw. 1991, 2, 568–576. [Google Scholar] [CrossRef] [PubMed]
- Kisi, O. Pan evaporation modeling using least square support vector machine, multivariate adaptive regression splines and M5 model tree. J. Hydrol. 2015, 528, 312–320. [Google Scholar] [CrossRef]
- Sammen, S.S.H.; Mohamed, T.A.; Ghazali, A.H.; El-Shafie, A.H.; Sidek, L.M. Generalized regression neural network for prediction of peak outflow from dam breach. Water Resour. Manag. 2017, 31, 549–562. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; El-Shafie, A.; Jaafar, O.; Afan, H.A.; Sayl, K.N. Artificial intelligence based models for stream-flow forecasting: 2000–2015. J. Hydrol. 2015, 530, 829–844. [Google Scholar] [CrossRef]
- Zhao, D.Q.; Chen, J.N.; Wang, H.Z.; Tong, Q.Y.; Cao, S.B.; Sheng, Z. Gis-based urban rainfall-runoff modeling using an automatic catchment-discretization approach: A case study in Macau. Environ. Earth Sci. 2009, 59, 465–472. [Google Scholar] [CrossRef]
- Csábrági, A.; Molnár, S.; Tanos, P.; Kovács, J. Application of artificial neural networks to the forecasting of dissolved oxygen content in the hungarian section of the river danube. Ecol. Eng. 2017, 100, 63–72. [Google Scholar] [CrossRef]
- Firat, M.; Gungor, M. Generalized regression neural networks and feed forward neural networks for prediction of scour depth around bridge piers. Adv. Eng. Softw. 2009, 40, 731–737. [Google Scholar] [CrossRef]
- Safari, M.-J.-S.; Aksoy, H.; Mohammadi, M. Artificial neural network and regression models for flow velocity at sediment incipient deposition. J. Hydrol. 2016, 541, 1420–1429. [Google Scholar] [CrossRef]
- Stamenković, L.J.; Antanasijević, D.Z.; Ristić, M.Đ.; Perić-Grujić, A.A.; Pocajt, V.V. Modeling of methane emissions using artificial neural network approach. J. Serbian Chem. Soc. 2015, 80, 421–433. [Google Scholar] [CrossRef]
- Wang, L.; Kisi, O.; Zounemat-Kermani, M.; Salazar, G.A.; Zhu, Z.; Gong, W. Solar radiation prediction using different techniques: Model evaluation and comparison. Renew. Sustan. Enery Rev. 2016, 61, 384–397. [Google Scholar] [CrossRef]
- Wassermann, L. All of Nonparametric Statistics, 3rd ed.; Springer: New York, NY, USA, 2006; pp. 30–35. ISBN 978-0-387-30623-05. [Google Scholar]
- Prairie, Y.T.; Alm, J.; Beaulieu, J.; Barros, N.; Battin, T.; Cole, J.; Giorgio, P.D.; DelSontro, T.; Guérin, F.; Harby, A.; et al. Greenhouse gas emissions from freshwater reservoirs: What does the atmosphere see? Ecosystems 2017, 1–14. [Google Scholar] [CrossRef]
| Parameters | Unit | Min | Max | Mean | Median | SD | VC |
|---|---|---|---|---|---|---|---|
| Lat | ° | −42.93 | 68.00 | 31.96 | 38.17 | 26.36 | 0.83 |
| Age | yrs | 1.00 | 95.00 | 39.09 | 36.00 | 24.55 | 0.63 |
| Chl-a | μg L−1 | 0.20 | 137.50 | 12.03 | 4.13 | 24.78 | 1.96 |
| WT | °C | 6.30 | 35.00 | 17.88 | 17.40 | 5.52 | 0.30 |
| MD | m | 0.30 | 400.00 | 26.58 | 15.00 | 40.26 | 1.52 |
| RT | days | 1.25 | 13,140.00 | 665.75 | 180.00 | 1689.54 | 2.54 |
| DOC | mg L−1 | 1.25 | 30.00 | 4.79 | 3.82 | 4.01 | 0.84 |
| TP | μg L−1 | 1.40 | 500.00 | 62.61 | 29.00 | 96.89 | 1.55 |
| NPP0 | mg C m−2 d−1 | 151.90 | 3200.68 | 1529.21 | 1574.50 | 604.70 | 0.40 |
| CO2 flux | mg C m−2 d−1 | −356.00 | 3800.00 | 400.90 | 254.75 | 569.89 | 1.42 |
| Variables | n | Correlation | Sig. | Variables | n | Correlation | Sig. |
|---|---|---|---|---|---|---|---|
| Lat | 236 | −0.025 | 0.69 | RT | 98 | 0.055 | 0.59 |
| Age | 266 | −0.307 | 0.00 | DOC | 51 | 0.129 | 0.36 |
| Chl-a | 69 | −0.115 | 0.35 | TP | 47 | 0.005 | 0.98 |
| WT | 158 | −0.118 | 0.13 | NPP0 | 234 | 0.153 | 0.02 |
| MD | 217 | −0.151 | 0.02 |
| Statistical Parameters | Unit | Training Set | Testing Set |
|---|---|---|---|
| n | 76 | 175 | |
| Min | mg C m−2 d−1 | −325.90 | −356.00 |
| Max | mg C m−2 d−1 | 3776.00 | 3800.00 |
| Mean | mg C m−2 d−1 | 390.82 | 486.40 |
| Median | mg C m−2 d−1 | 243.29 | 312.03 |
| SD | mg C m−2 d−1 | 549.75 | 664.02 |
| Model | Training Data Set | Testing Data Set | ||||||
|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | R2 | NSE | RMSE | MAE | R2 | NSE | |
| MLR | 476.42 | 313.22 | 0.25 | 0.25 | 625.36 | 429.96 | 0.12 | 0.11 |
| MNLR | 417.26 | 282.00 | 0.43 | 0.42 | 529.53 | 391.46 | 0.40 | 0.36 |
| BPNN | 396.59 | 268.53 | 0.52 | 0.48 | 505.43 | 395.33 | 0.47 | 0.42 |
| GRNN | 272.50 | 147.62 | 0.76 | 0.75 | 418.48 | 295.34 | 0.61 | 0.60 |
| Model | RMSE (mg C m−2 d−1) | R2 | ||||||
|---|---|---|---|---|---|---|---|---|
| GRNN | BPNN | MNLR | MLR | GRNN | BPNN | MNLR | MLR | |
| All | 418.48 | 505.43 | 529.53 | 625.36 | 0.61 | 0.47 | 0.40 | 0.12 |
| Skip MD | 432.14 | 552.55 | 530.95 | 629.10 | 0.59 | 0.35 | 0.39 | 0.11 |
| Skip NPP0 | 463.63 | 567.08 | 532.26 | 635.25 | 0.52 | 0.38 | 0.38 | 0.09 |
| Skip Age | 462.65 | 519.62 | 535.68 | 633.44 | 0.57 | 0.45 | 0.39 | 0.10 |
| Skip Lat | 469.06 | 555.51 | 628.93 | 620.69 | 0.51 | 0.32 | 0.11 | 0.13 |
| Studies | Sample Size | Type of Dataset | Method | Area (105 km2) | CO2 (Tg C yr−1) | |
|---|---|---|---|---|---|---|
| This study | 251 | All reservoirs | Individual 1 | 4.47 | 40.03 3 | |
| Previous studies | Deemer et al. [12] | 229 | All reservoirs | Average 2 | 3.1 | 36.8 |
| Hertwich [16] | 142 | Hydroelectric | Average 2 | 3.3 | 76 | |
| Barros et al. [11] | 85 | Hydroelectric | Average 2 | 3.4 | 48 | |
| St. Louis et al. [8] | 19 | All reservoirs | Average 2 | 15.0 | 272.2 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Ye, X.; Huang, P. Estimating Carbon Dioxide (CO2) Emissions from Reservoirs Using Artificial Neural Networks. Water 2018, 10, 26. https://doi.org/10.3390/w10010026
Chen Z, Ye X, Huang P. Estimating Carbon Dioxide (CO2) Emissions from Reservoirs Using Artificial Neural Networks. Water. 2018; 10(1):26. https://doi.org/10.3390/w10010026
Chicago/Turabian StyleChen, Zhonghan, Xiaoqian Ye, and Ping Huang. 2018. "Estimating Carbon Dioxide (CO2) Emissions from Reservoirs Using Artificial Neural Networks" Water 10, no. 1: 26. https://doi.org/10.3390/w10010026
APA StyleChen, Z., Ye, X., & Huang, P. (2018). Estimating Carbon Dioxide (CO2) Emissions from Reservoirs Using Artificial Neural Networks. Water, 10(1), 26. https://doi.org/10.3390/w10010026




