1. Introduction
The granular fluid mixture involved in geophysical flow phenomena can be considered a complex particle suspension, since the entire system is composed of particles with different shapes and sizes that are dispersed and/or suspended in a Newtonian or non-Newtonian fluid [
1,
2]. Describing the complete behavior of these materials is particularly relevant considering the variety of natural phenomena in which they are involved such as, the rapid mass movement conveyed by a viscous interstitial fluid, the sediment transport in bodies of water, landslides, pyroclastic flows, debris, mud and hyper-concentrated flows [
3,
4,
5,
6,
7]. In particular, over the past 50 years, the risk of landslides, debris flow and debris avalanches has increased enormously worldwide, and the difficulty associated with describing the flow properties has recently motivated several experimental, numerical and theoretical studies. Even when using state-of-the-art technologies, it is still difficult to extract common features or a general trend for different flow configurations [
8]. Particularly, a lack of studies focused on the properties of the ‘post-failure’ material, i.e., the soil–water mixture that flows after the triggering phase, still exists. In fact, after starting, these materials are in a viscous-like regime, where they flow similarly to a fluid [
4,
5,
6,
7,
8,
9,
10].
The description of a geophysical granular flow (wet or dry) is not easy because of the uncertainty in the constitutive equations for the flowing materials. The flow behavior of these mixtures are usually described with reference to a critical solid concentration (i.e., the ratio of the volume of solids to the total volume) for which the transition between the colloidal regime and the hydrodynamics regime corresponds to a viscoplastic flow behavior [
5,
8]. Most flow models have been developed to describe the motion of dry granular flows and particle–fluid suspensions but these approaches do not provide a unique rheological formula for the solid–fluid composite [
4,
5,
7,
8,
11,
12,
13,
14]. For debris flow modelling, a first approach considers the flowing material as a non-Newtonian fluid with an empirical Bingham generalized rheology. This methodology appears to be a successful choice for pure mudflows but it is not suitable for the case of non-colloidal particles involved in the flowing mixture [
8,
15,
16], in which not only hydrodynamic interactions due to the fluid but also different types of particles interactions, such as frictional interactions (i.e., contact occurrence) or collisional interactions (i.e., intensely agitation) occur [
16,
17].
For the case of dry granular materials, the rheological behavior is controlled by frictional and collisional experience between the grains [
18]. On the contrary, in the case of a granular material immersed in a fluid, the viscous interaction between the grains and the surrounding fluid play a role, which has to be considered. The flow behavior of these complex granular–fluid mixtures has been considered to be controlled by the rheological properties of the ‘matrix’, i.e., a mixture of fine (colloidal) sediment and water in which the coarse particles are dispersed [
13]. Several studies have already demonstrated that the rheological behavior of these suspensions is strongly affected by the grain size distribution of the involved soil, the solid volumetric concentration, the interstitial fluid viscosity and the particles shape [
6,
7,
10]. In particular, the particle shape affects rheology by changing the nature of fluid–particle (e.g., it depends on particles orientation with respect to the flow) and particle–particle interactions (e.g., indeed the orbit of a rotating non-spherical particle encloses a greater volume for potential interactions than that of a spherical particle). Previous theoretical and experimental studies on the rheology of suspensions considering irregular particles is less extensive than for spherical particles. The current work investigates the suitability of the recent frictional approach [
16,
19,
20] for the study of the rheological behavior of granular fluid mixtures involved into fast flow-like natural phenomena with regards to their viscous flow regime considering not only spherical particles but also irregular grains.
To the scope, we considered the theory developed for the dry granular case (MiDi 2004) and then adapted for suspensions [
20]. Typically, the mechanical behavior of the viscous suspensions involved in fast flow-like phenomena is analyzed in reference to the response of the material subjected to a regime of shear stresses, and therefore, characterized by mathematical models that establish functional relationships between stress, strain and time for the case of dilute and viscous suspensions, in which the dynamics appear to be primarily controlled by hydrodynamic interactions [
21]. In the literature, the shear stress is typically measured as a function of the shear rate, thus imposing different values of the solid volumetric concentration [
18,
22,
23]. Other authors have measured the shear stress based on a nontrivial rheology, which is characterized by a viscosity that diverges when increasing the volume fraction and the development of normal stress effects [
8,
16,
22,
24,
25]. Under this methodology, the shear stress and the solid concentration during shear are measured by imposing different values of normal stress.
The information on dry granular flows has considerably improved during the past decade due to numerous studies based on the kinetic theory [
26] and frictional approaches [
12,
18,
23,
27,
28]. In this study, we will refer to the latter studies, in which the primary characteristics of dense granular flows are correctly predicted using a simple heuristic rheology based on a dimensional analysis, and the interpretation of the constitutive law is given in terms of the relevant time scales controlling the grain motion. These studies demonstrated that if we consider a homogeneous shear flow of granular material subjected to a shear rate
and a confining pressure
σ, then the strain tensor depends only on one parameter, i.e., the shear rate
, whereas the stress tensor depends on two parameters, i.e., the normal stress
σ and the shear stress
τ. These three quantities can define two dimensionless numbers: the friction coefficient
µ = τ/σ (i.e., the ratio between the shear stress and the normal stress) and the inertial number
(where
d is the particle diameter and
ρs is the particle density). Starting from a study on dry granular, Courrech et al. [
19] systematically studied avalanche durations for different particle sizes, different densities and different interstitial fluid viscosities in a rotating drum configuration. They determined the relevant time-scales controlling the flow and found the relevant dimensionless number characterizing the different flow regimes. Then, Cassar et el. [
16] demonstrated that the time-scale analysis provided by the study of Courrech et al. [
19] for intermittent avalanches could also be applied to describe the continuous flow properties and that the frictional approach [
12] could be extended to the case of immersed granular flows. Boyer et al. [
20] determined that if a local unique rheology exists, then there should be a unique relationship between a rescaled shear stress
µ and a rescaled shear rate
I. Hence, the flow behavior of granular-fluid flows can be described by the same constitutive law used for dry materials with a modified dimensionless inertial number, i.e., the viscous number
(where
ηf is the fluid viscosity), and the constitutive law for the granular-fluid mixture can be expressed as a function of
Iv:
where
Ф is particles volume concentration. Specifically the friction law of the dense suspensions
µ(
Iv) can be described as the superposition of the contact contribution
µc(
Iv) and the hydrodynamic contribution
µh(
Iv), as follows [
20]:
The contact contribution must provide two asymptotic behaviors: (i) the friction coefficient
µ tends to the minimum value
µ1 (static friction coefficient) when
Iv tends to 0 and (ii)
µ tends to the maximum value
µ2 (called dynamic friction coefficient) at larger shear rates. In this work the contact contribution
µc(
Iv) is similar to that reported for dry granular media [
16], where
I0 is a fitting constant:
On the other hand, since the shear and normal stress scale viscously and could be expressed by dimensionless effective viscosities (
ητ,
ησ) which are function of
Ф, the hydrodynamic contribution
µh(
Iv) results:
Hydrodynamic contribution does not saturate for large Iv, whereas it should recover Einstein’s viscosity at a vanishing volume fraction Ф.
Thus, Boyer et al. [
20] and Pellegrino et al. [
29] studied the flow behavior of viscous suspensions using an original pressure-imposed annular cell. Their studies demonstrated that the theoretical experimental approach recently developed to unify the suspension and granular flows under a common framework could be successfully applied to the case of viscous suspensions for spherical particles. Although the application of the kinetic theory for the analysis of wet and dry granular mixtures has produced promising developments for multiphase systems [
26], we decided to refer our analysis to the extension of the granular paradigm to viscous suspensions [
20].
In particular, the objective of the current study is to understand how the frictional approach may be suitable for the study of the rheological behavior of granular fluid mixtures involved in fast flow-like natural phenomena with regards to their viscous flow regime considering not only spherical particles but also irregular grains, and in cases where there are limitations. Therefore, we will refer to the experimental studies conducted by Schippa and Lamberti [
30]. In their experiments on the dynamics of granular fluid mixtures, they used a large original pressure-imposed rheometer to analyze several viscous suspensions composed of various combinations of granular and viscous fluids considering particles of different materials (glass, plastic and sand), particles of different shapes (spherical and irregular) and fluids with different viscosities (air, water and water–glycerin solution). These experiments produced a large amount of interesting and promising data [
10,
30] that have not been completely described so far.
In their study, Schippa and Lamberti [
30] preliminarily analyzed the experimental data using the indications derived from the works of Bagnold [
8] and Savage and Hutter [
24]. Based on their experimental results, Schippa and Lamberti [
30] described the rheological behavior of the mixtures in both the quasi static and dynamic regimes. In light of new theories that were recently developed regarding the flow behavior of viscous suspensions [
16,
19,
20], the goal of the present study is to reinterpret and review the experimental results of Schippa and Lamberti [
30] using the novel frictional approach provided by [
16] for immersed granular and then developed by [
20] for viscous suspensions of spheres. We carefully reconsider the experiments of Schippa and Lamberti [
30], and apply the frictional approach to a large set of data to test both the relevance of the proposed argument and the pertinence of a complete rheological description of viscous suspension behavior via a volume fraction law and a frictional law using an analytical model consistent with both frictional and hydrodynamic interactions.
In the development of this study, a comparison between the available two sets of experimental data referring to different experimental apparatus (i.e., [
20,
30]) and similar granular-fluid mixtures (i.e., suspension of spherical particles) is performed to explore any possible scale effects and limits of the experimental apparatus, which may affect the results. Moreover, to determine the effects due to irregularly shaped grains, we consider a representative set of data involving irregular grains viscous suspensions.
Although the application of the proposed theory appears to be closely linked to the specific flow configurations [
31,
32,
33,
34,
35], it could be used as a valuable tool for modeling the flowing phase of dense granular materials. In fact, when the friction between the grains becomes considerable or/and dominant, assuming a pressure-dependent yield stress and an effective viscosity based on the shear rate and the local pressure may be an adequate choice for the case of highly concentrated debris flow mixtures [
27,
36]. Thus, it is possible to consider the frictional nature of the analyzed materials while considering the influence of the interstitial fluid on the development of the flowing conditions.
In this sense and under these limitations, we provide a complete rheological description of the flow behavior of viscous suspensions with regular or irregular particles by means of an appropriate original volume fraction law to be used together with a friction law for shear stress. It leads to a new perspective: the possibility of using the simple constitutive model derived from the frictional approach, for the case of fully developed flow of a solid–fluid mixture with irregular particles as the case of debris flow phenomenon.
2. Large Scale Experimental Rheometer: Data-Set, Set up and Procedures
The experiments performed using a large-scale annular rheometer were considered [
30], and two representative sets of granular fluid mixtures were selected. The first involving plastic beads (i.e., regular grains) is taken into consideration, in order to investigate any experimental apparatus scale effects and any limitation related to the test procedures; the second, related to irregular plastic grains, is taken into account in order to analyze the effects of the particle shape on the rheological behavior of the viscous granular fluid.
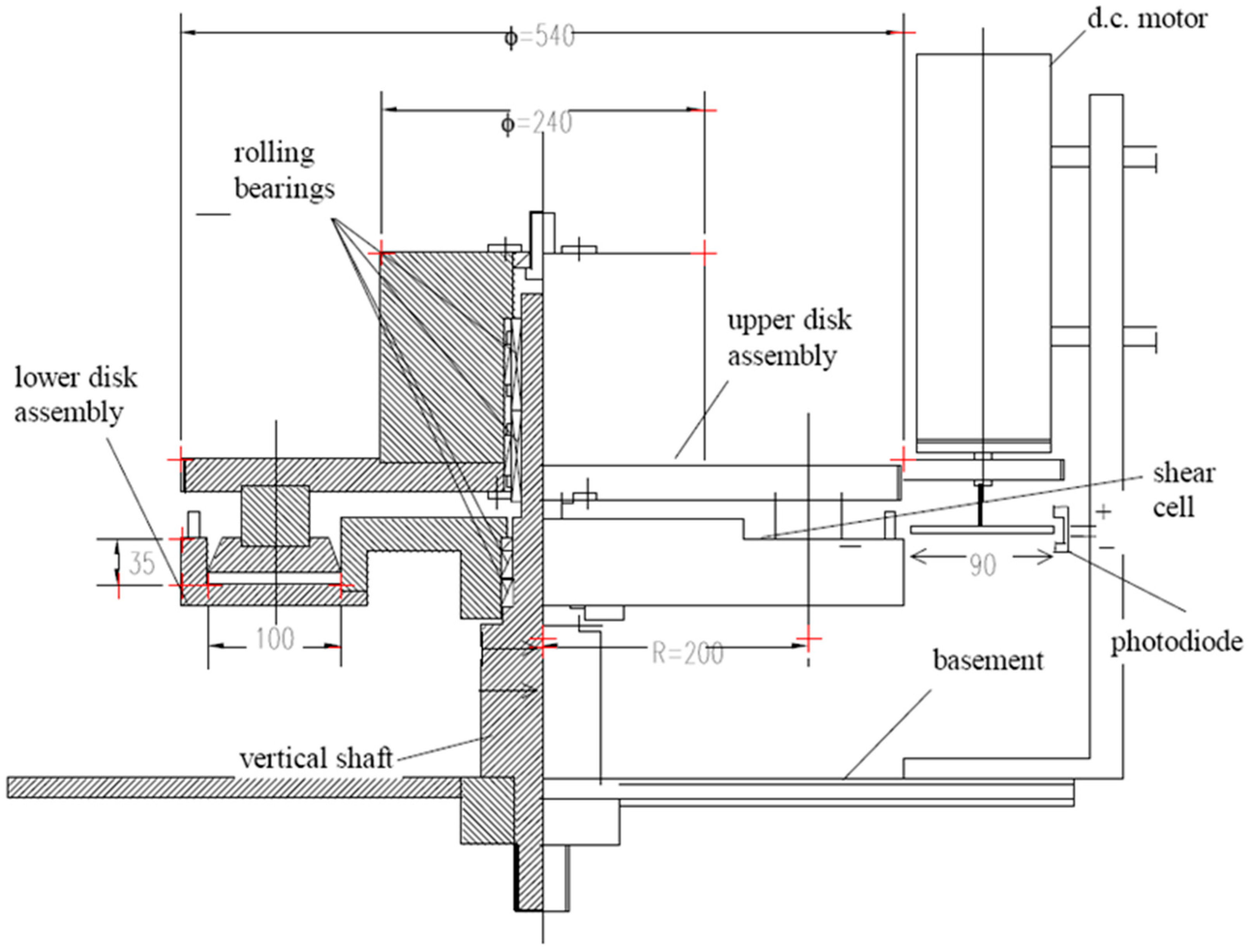
The apparatus consists of two concentric horizontal aluminum circular disk assemblies mounted on a vertical shaft fixed on the basement of the apparatus, as indicated in
Figure 1. The lower disk assembly is mounted on the shaft with two roller bearings that allow rotation but not vertical motion. The lower disk is restrained from rotating via a torque arm connected to a load cell. This lower part, which is referred to as the channel, has an annular trough 100 mm wide and 35 mm deep and a mean radius of 200 mm. The channel is closed by a heavy rotating upper disk assembly mounted on the same vertical shaft through two roller bearings that allow both rotation and vertical movements. In the lower part of the upper disk assembly, a horizontal plate is lodged in the cavity of the lower disk, forming the ceiling of the channel. The plate was machined to fit into the channel (i.e., the shear cell), thus avoiding contact with the side walls of the channel. The clearance is 0.4 mm, which prevents the used grains with diameters larger than 1 mm from entering the meatus between the vertical walls of the shear cell and the outer edge of the upper plate but allows liquids to pass through the gap. On the outer part of the top disk assembly, a cogged wheel is coupled to the gear of a DC variable speed servomotor to drive any angular velocity of the upper disk in the range of 0.0–10.0 s
−1. The vertical displacement of the upper disk is measured with respect to the channel bottom via a cable linear position transducer. The normal stress applied to the granular was obtained via a system of counterweights balancing the upper disk. The surfaces of the upper (i.e., the ceiling of the channel) and lower disks (i.e., the bottom of the channel) were roughened using a glued sand paper sheet with a roughness of approximately 1.2 mm.
Before starting a run, the shearing channel is filled with a known amount of granular material that is carefully mixed with the liquid (special attention is paid to removing any trapped air). After a few rotations to settle the material (the lower plate remaining at rest), the vertical position of the upper disk is measured. The counter weight that is needed to strictly balance the disk weight is determined, and a fixed pressure is generated by unloading the counterweight. Then, the disk is allowed to turn, and a run is performed according to one of the three following procedures: one or more assigned velocities of the upper disk are reached, and the corresponding upper disk displacements are measured; the velocity is increased until a desired displacement of the rotating disk is reached; the velocity of the upper disk is increased step-wise and subsequently decreased. During the test, several desired velocities were reached.
The channel was machined to yield a hard smooth sidewall to reduce any shear stress on the wall and avoid any degradation due to the shearing grains.
The stress transmitted to the lower disk, velocity and vertical displacement of the upper disk are monitored during the test, whereas the pre-assigned vertical pressure is held constant. Furthermore, two glass windows in the external sidewall of the channel (with an angular distance of 90° to the rotational axis) are incorporated to allow for visual observations and video recording of the shearing layer (see
Figure 2).
The torque
T, angular velocity
ω and displacement of the upper disk are monitored, and a video is recorded. The shear stress
τ and the shear rate
within the material can be calculated using the formulae as follows (being negligible the residual shear stress related to both the centrifugal effects and the vertical boundary conditions):
where
R0 and
Ri are the radii of the outer annulus and inner annulus, respectively;
Rm = (
R0 +
Ri)/2 is the mean radius and
δm is the measured depth of the channel during the shearing. Thus, different shearing conditions can be measured in a short time with an assigned vertical pressure and varying concentrations or a specific assigned concentration condition can be quickly reproduced.
The tests refer to plastic spheres with uniform diameters and irregular granules obtained via crushing and sieved plastic cylinders (see
Figure 3) immersed in a glycerin–water solution. Their physical characteristics are listed in
Table 1 and
Table 2.
According to any theories, granular concentration is an important state variable and should be experimentally determined with high accuracy. The actual concentration was measured from the displacement of the upper disk, whereas the displacement is conventionally set to 0 when the upper disk is in contact with the channel bed. The volume fraction concentration has been conveniently measured considering a residual volume related to the presence of the sandpaper glued on the ceiling and the roof of the channel [
21]. In their study on the effects of boundary conditions on the measurements in an annular shear cell, Orlando and Shen [
21] demonstrated that for high concentrated flows, the presence of the sandpaper boundary yields the lowest calculated solid volumetric concentration. Hence, we have re-analyzed the data and determined that the presence of the sandpaper induces a systematic error of approximately 1.5% in the measured volume fraction. The error has been properly considered into the conversion process of the acquired measurements.
The range of the significant parameters both imposed and measured during the tests are listed in
Table 3.
3. Experimental Results and Discussion
Using a frictional approach, the granular paradigm was applied to particles suspended in a fluid of viscosity ηf sheared at a constant particle pressure σ. If the Stokes number is small, then viscous forces are dominant at the particle scale, and the system is no longer governed by the inertial number I; hence, the dimensionless viscous number Iv should be used. Under this consideration, the rheology of viscous suspensions with spheres under imposed-pressure flow conditions could be described using constitutive laws expressed as two functions of Iv (see Equation (1)) τ = µ(Iv) and Φ(Iv), where µ(Iv) = τ/σ is the friction coefficient; and Φ is the solid volumetric concentration.
In the current study, we considered a set of data from Schippa and Lamberti [
30] experiments associated with a small Stokes number. According to [
19], three regimes can be characterized based on the value of the dimensionless Stokes number
St, density ratio
r =
ρs/
ρf (where
is fluid density) and Reynolds number defined as the ratio between the two
Re =
St/
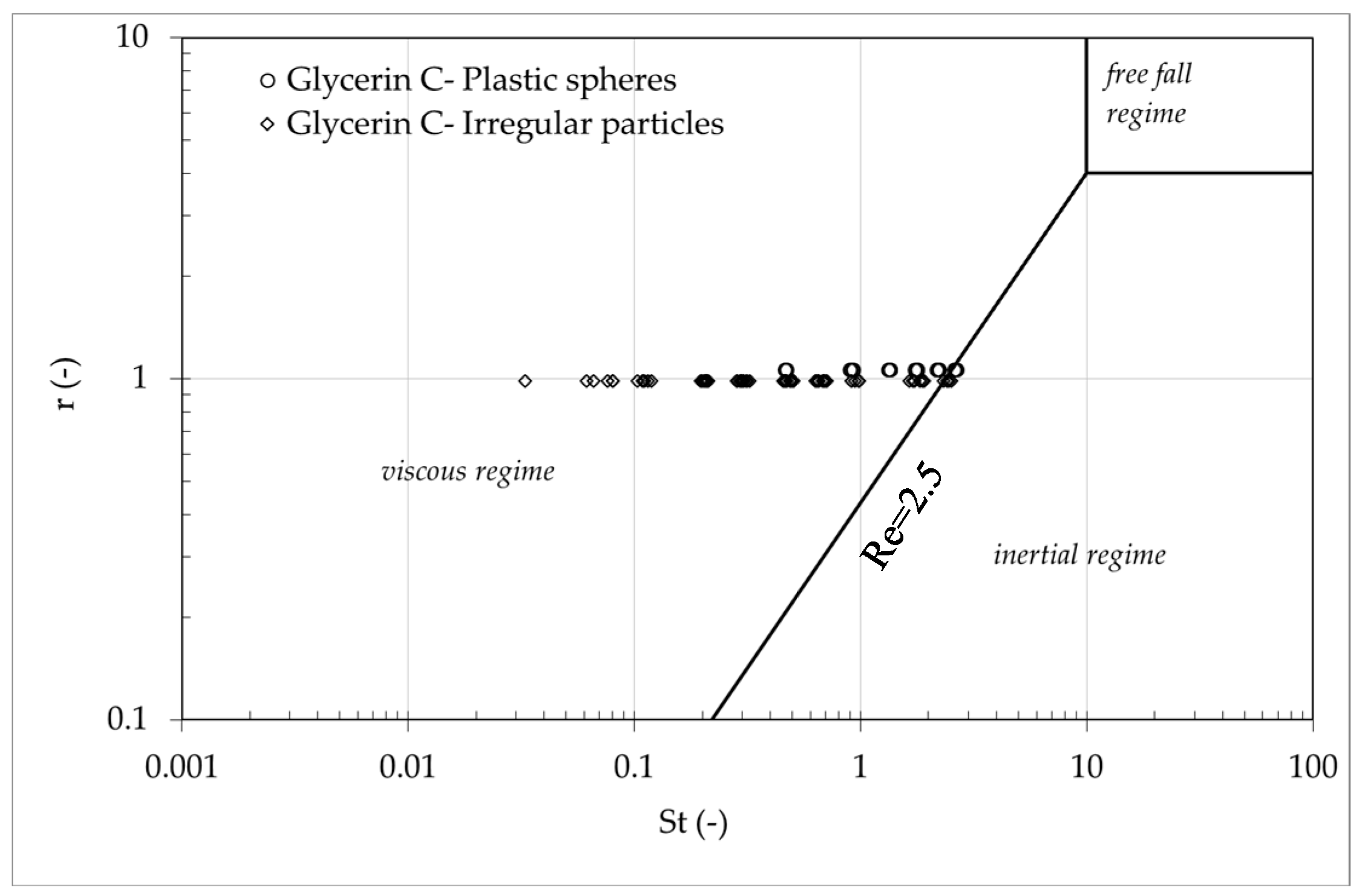
r: (i) a viscous regime, where the particle reaches the viscous limit velocity during its elementary motion; (ii) an inertial regime, where it reaches the inertial limit velocity; (iii) and a free-fall regime, where it follows an accelerated motion. In case of granular avalanches in fluid, Courrech du Pont et al. [
19] derived the boundaries for the three different regimes, and they are reported in
Figure 4, along with the experimental data herein considered (i.e., mixture composed by glycerin C and plastic spheres, as well as the mixture composed by glycerin C and irregular plastic particles) which actually refer to the viscous regime.
In the current study, we interpret the selected data available from Schippa and Lamberti [
30] based on both the relationship between the friction coefficient and the viscous number and the relationship between the solid volumetric concentration and the viscous number. We demonstrate that all of the data obtained for different particle sizes, materials and fluid viscosities collapse to a single curve,
µ(
Iv) and
Φ(
Iv), depending on the particle geometry, no matter of fluid viscosity. Then, we compare the re-interpreted results with the experimental evidence from Boyer et al. [
20] for both the immersed spherical particles and the immersed irregular particles to evaluate the consistency of the provided results. The data relative to the irregular particles are used to stress the effects of the grain shape and the relevance of the adopted theory [
16,
18,
20] for the case of non-spherical particles.
3.1. Limits of the Experimental Apparatus
With reference to the large scale rheometer tests performed by Schippa and Lamberti [
30], the correlation between the friction coefficient
μ and the viscous number
Iv is illustrated in
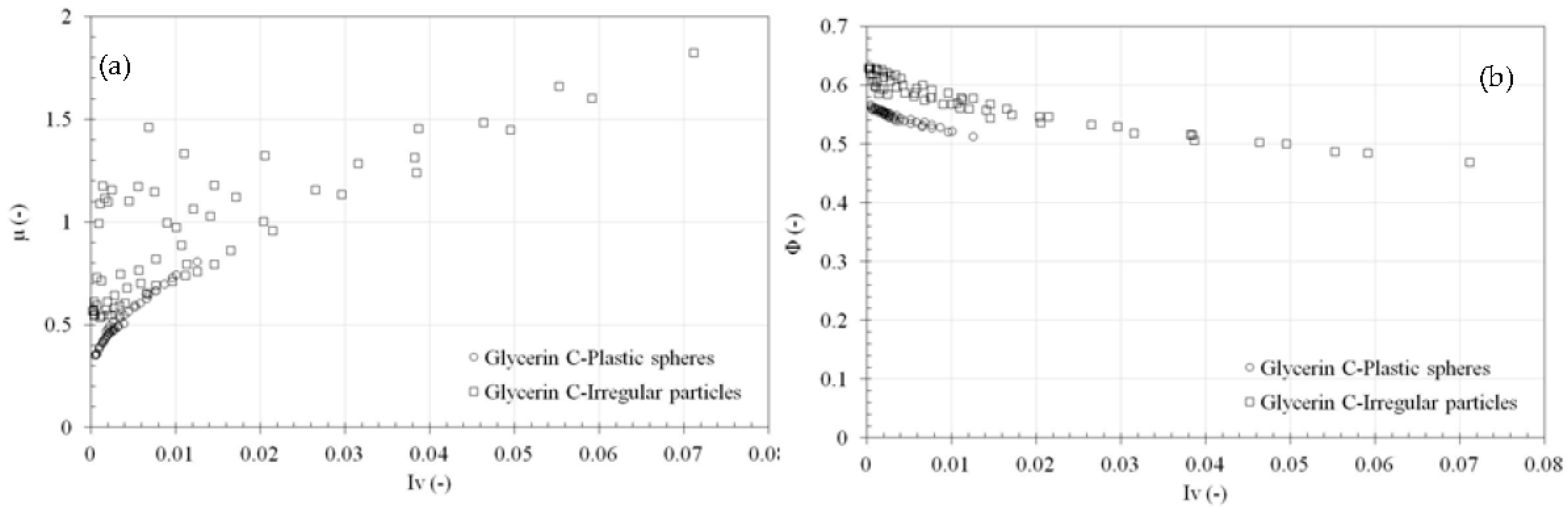
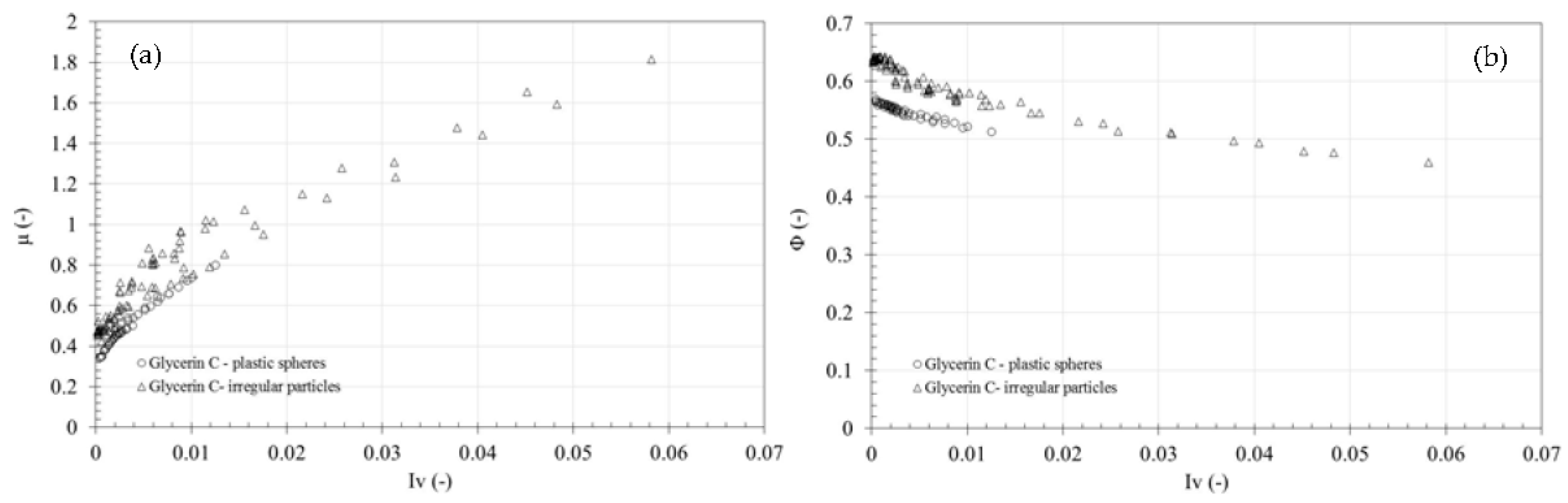
Figure 5 for both the glycerin C and plastic spheres mixture and the glycerine C and irregular plastic particles mixtures. The graph reports the entire set of data. For the spherical grains, the data show a consistent relationship between the friction coefficient
µ and the viscous number
Iv, whereas for the irregular grains, there is a relevant dispersion in the data. Similarly, the observed fluctuating trend is evident when the particle volume fraction
Φ is plotted versus the viscous number
Iv (right side in
Figure 5).
The scatter of data is likely due to the experimental problems related to both the test configuration at a low shear rate and to the irregular shape of the grains. Therefore, we thoroughly examined the data pertaining to the irregular plastic particle–glycerin C solution.
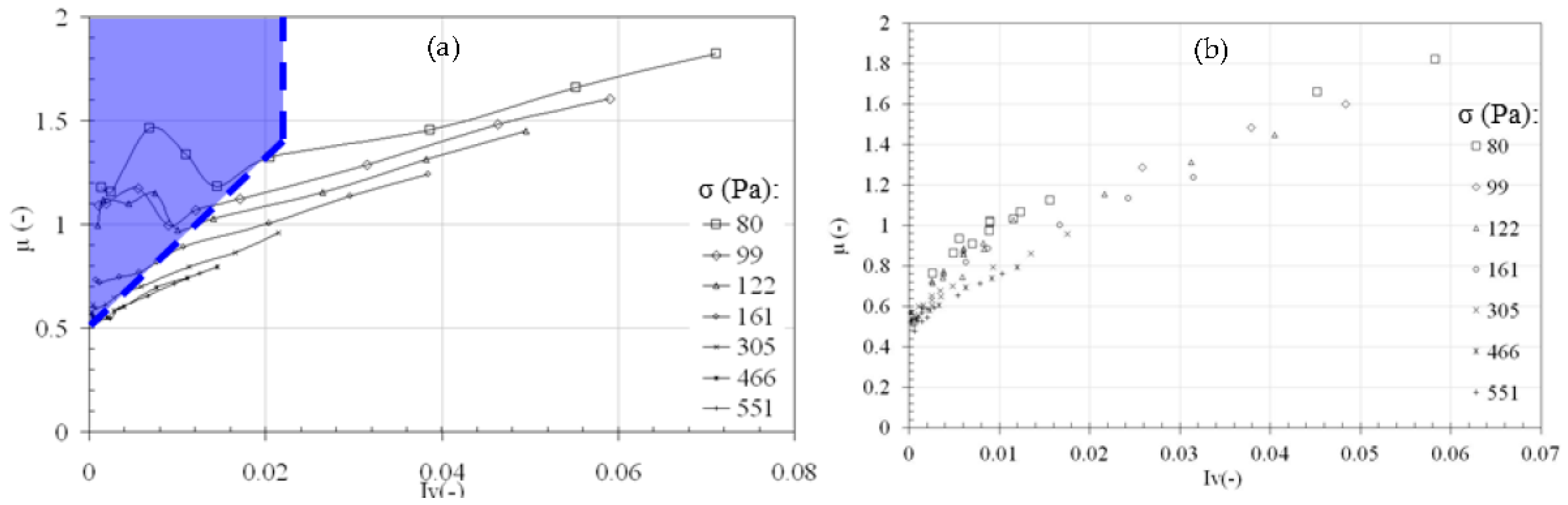
Figure 6 depicts the relationship between the friction coefficient and the viscous number of the tests for the irregular plastic particle–glycerin C solution. The data are grouped according to the imposed normal stress.
An irregular trend in the results can be appreciated: each curve related to any imposed normal stress, exhibits a peak corresponding to the lower shear rate values; on the contrary, for the higher values of the shear rate, the trends become stable. The measures corresponding to the lower shear rate values are highly scattered, and the lower the imposed vertical pressure is (i.e., less than 100 Pa), the more significant the scatter results. The fluctuations in the observed measurements may be due to critical problems related to the configuration of the experimental setup. In fact, according to the density ratio of the plastic irregular particle–glycerin solution analyzed in the current study, we may exclude any relevant effects related to the stratification.
In effects corresponding to the lower rotational speeds assigned to the upper disk (i.e., shear rates lower than 40 s
−1), irregular vertical movements of the upper disk were observed; upper disk vibrations were more significant under low normal pressures, i.e., smaller than 100–130 Pa. Based on visual observations using the lateral window mounted on the outer wall (see
Figure 2), at a low confining pressure, only a portion of the particles in contact with the upper disk surface is actually sheared (i.e., “partially shearing” condition). The vertical extension of the actual sheared layer increases with the increase of applied normal stress, up to the point at which the whole particle domain is sheared, and the “simple shearing” configuration is recovered.
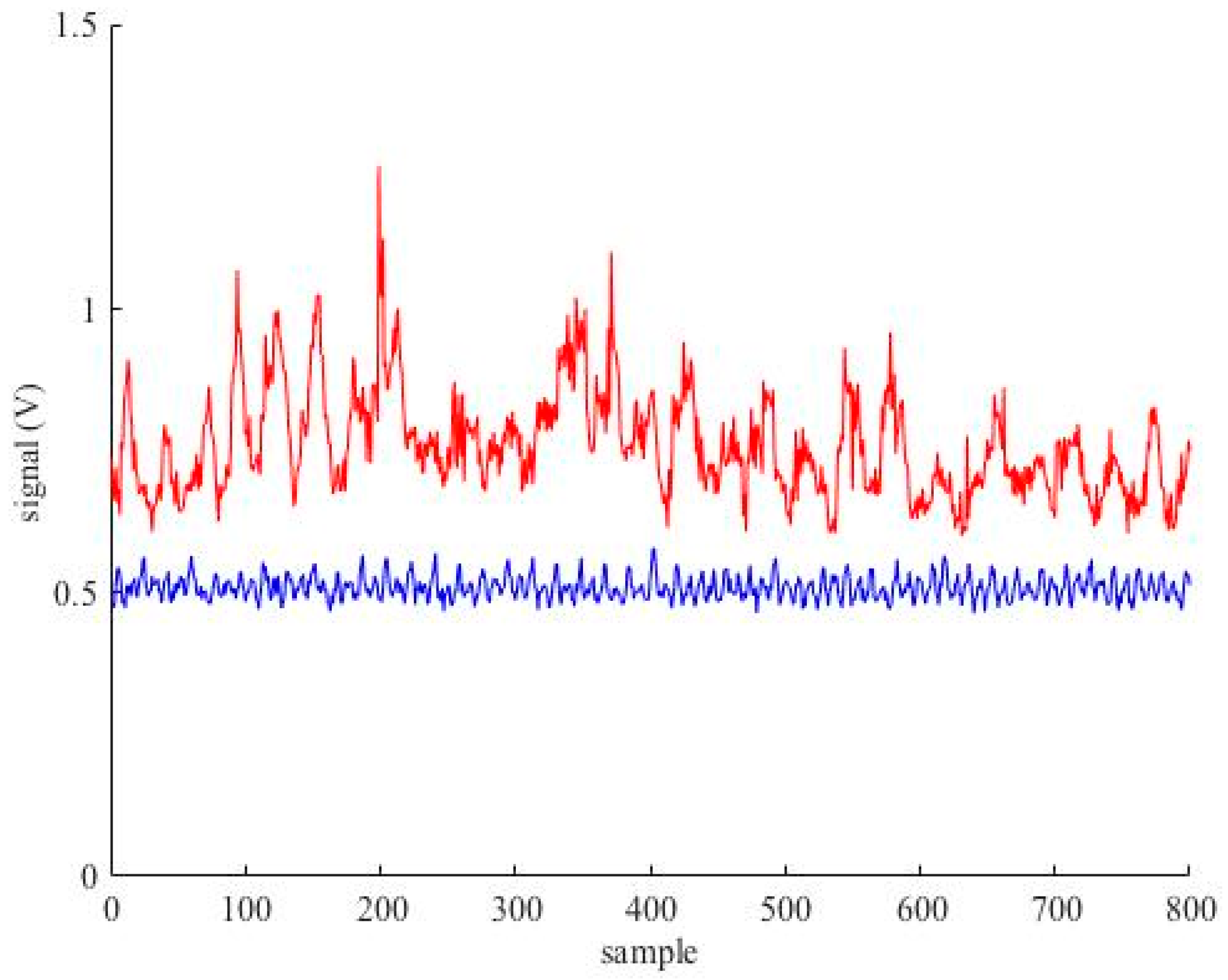
Figure 7 shows the signal registered by the load cell mounted on the lower plate of the annular rheometer (i.e., the signal associated with the shear force of the mixture), during representative runs corresponding to “simple shearing” and “partially shearing” condition. In case of partially shearing condition, it is evident the fluctuation in measured shear stress (with the shear rate being controlled).
Based on these considerations, we should consider only the data related to the tests that do not exhibit instability due to the combination of the lower rotational speed and the lower imposed normal stress, and the simple shearing configuration is applied.
Figure 8 illustrates the correlation between the friction coefficient
µ and the viscous number
Iv and the correlation between the particle volume fraction
Φ and the viscous number
Iv, respectively, for both the spherical and irregular particles. The graphs refer to the entire set of data for the plastic sphere–glycerin C solution and to the filtered set of data (i.e., simple shearing condition) for the irregular plastic particle–glycerin C solution. We can appreciate two different trends in both the cases of
µ(
Iv) and
Φ(
Iv) as a consequence of the different shape of the particle dispersed in the mixtures. It puts in evidence the effect of the grain shape on the rheological behavior of the dense granular flows, and it is discussed in details in the following sections. To this scope, we first analyze the case of the spherical particle, and then we consider the irregular grains.
3.2. Application of the Frictional Theory to Viscous Suspensions with Spheres
Based on several studies [
16,
19,
20], we described the flow behavior of the viscous suspensions using the same frictional argument used for dry granular [
12] by replacing the dimensionless parameter
I (i.e., the inertial number) with the dimensionless viscous number
Iv. Thus, the rheological behavior of the viscous suspensions can be completely expressed by two functions of
Iv:
τ = μ(Iv)⋅σ and
Ф = Ф(Iv) (see Equation (1)).
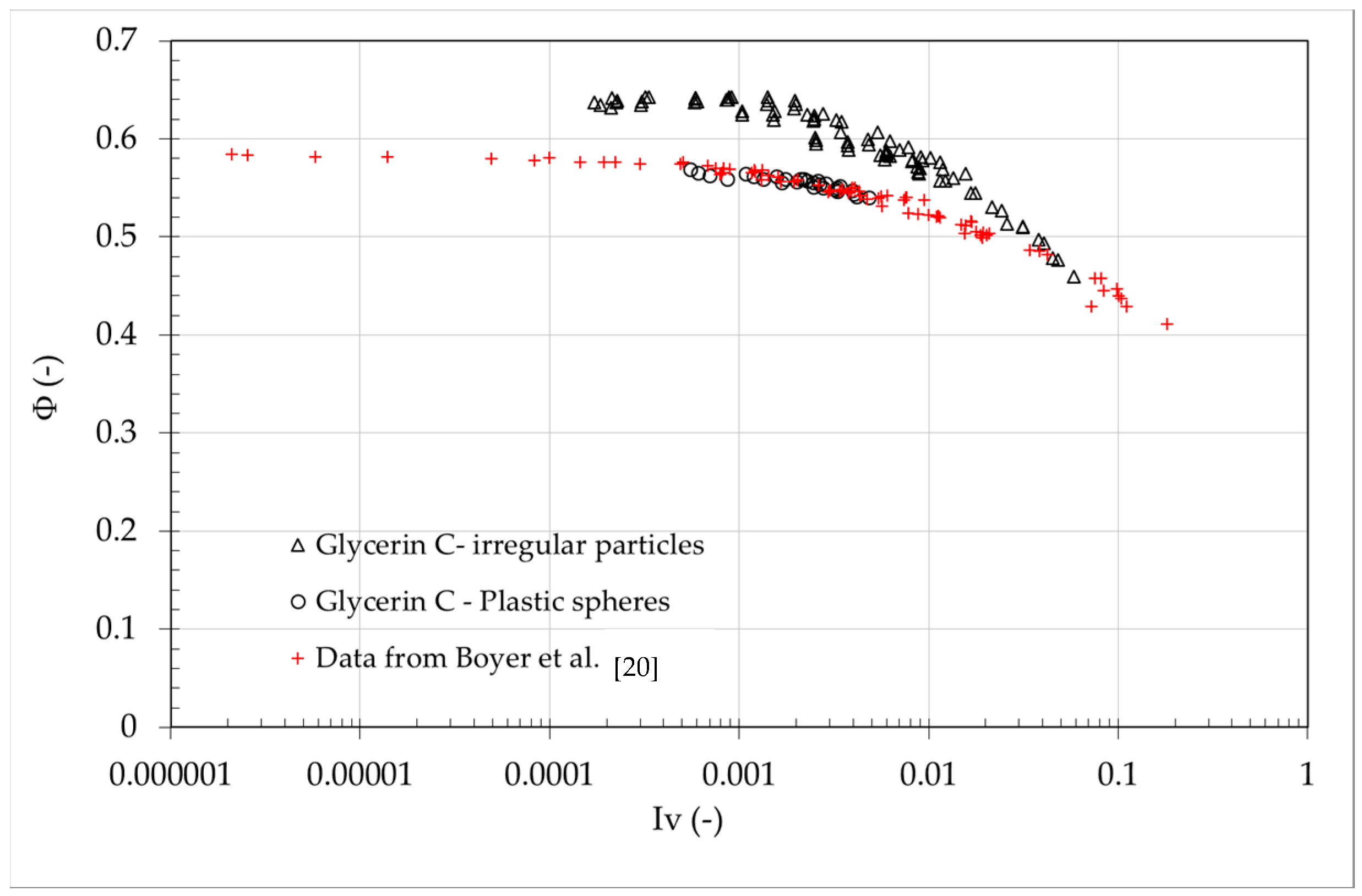
To test the relevance of the frictional approach, in
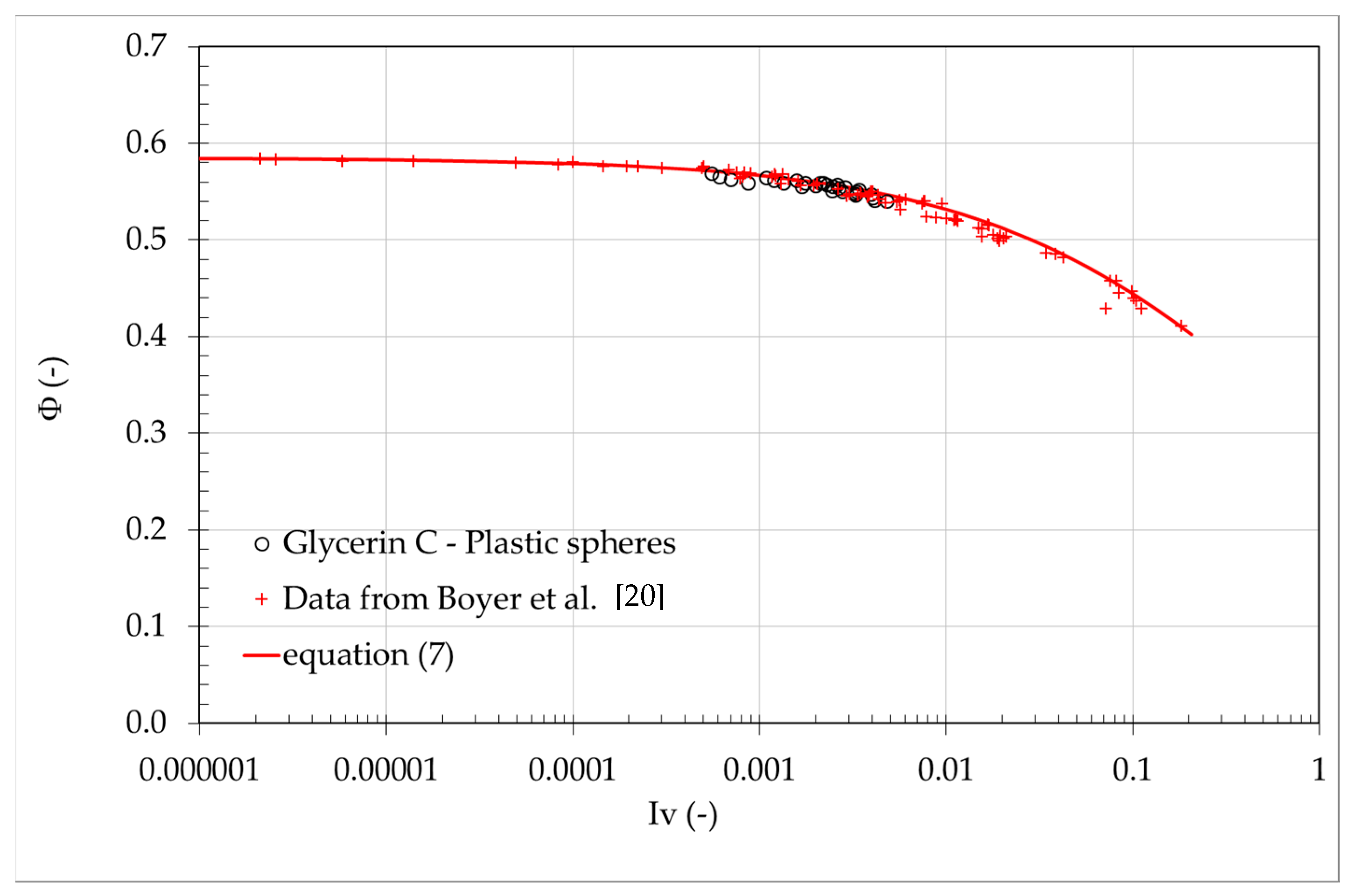
Figure 9 the volume fraction
Ф is plotted versus
Iv for the plastic spheres–glycerin C solution and a comparison of the viscous suspension data from Boyer et al. [
20]. In the latter experiments they used two combinations of regular particles and fluid: poly (methyl methacrylate) (PMMA) spheres having diameter
d = 1.1 mm in a Triton X-100/water/ zinc chloride mixture of viscosity
ηf = 3.1 Pa∙s; and polystyrene spheres (
d = 0.58 mm) in polyethylene glycol-ran-propylene glycol monobutylether
ηf = 2.15 Pa∙s. All of the experimental data derived for the different particle sizes and fluid viscosities collapse onto a single curve
Ф(
Iv). The volume fraction results a decreasing function of
Iv; this behavior is consistent with the increasing of shear rate which leads to the dilation of the mixture.
To estimate the maximum volume fraction during the shearing
Φm (i.e., the
Φ value for
Iv close to zero), the correlation between the solid concentration
Φ and the viscous number
Iv for the data of the plastic sphere–glycerin C solution is reported on a semi-logarithmic scale in
Figure 9.
Based on the experiments, the value of the maximum volume fraction during shearing is
Φm = 0.585, which is extremely close to the critical volume fraction reported for viscous suspensions [
20] and comparable with the maximum concentration that is actually reachable after vibration for plastic spheres [
24]. In previous studies [
16,
20], a consistent model was used to describe the evolution of the volume fraction
Φ as a function of
Iv. It was observed that an appropriate model should have an asymptotic form of (
Φm −
Φ)
α Iv1/2 at
Iv→0 and be positive for all values of
Iv. The function that satisfactorily models the experimental measurements can be given as follows:
This model (Equation (7)) was used for the entire range of the measured viscous numbers and fully captured the experimental observations, as illustrated in
Figure 9.
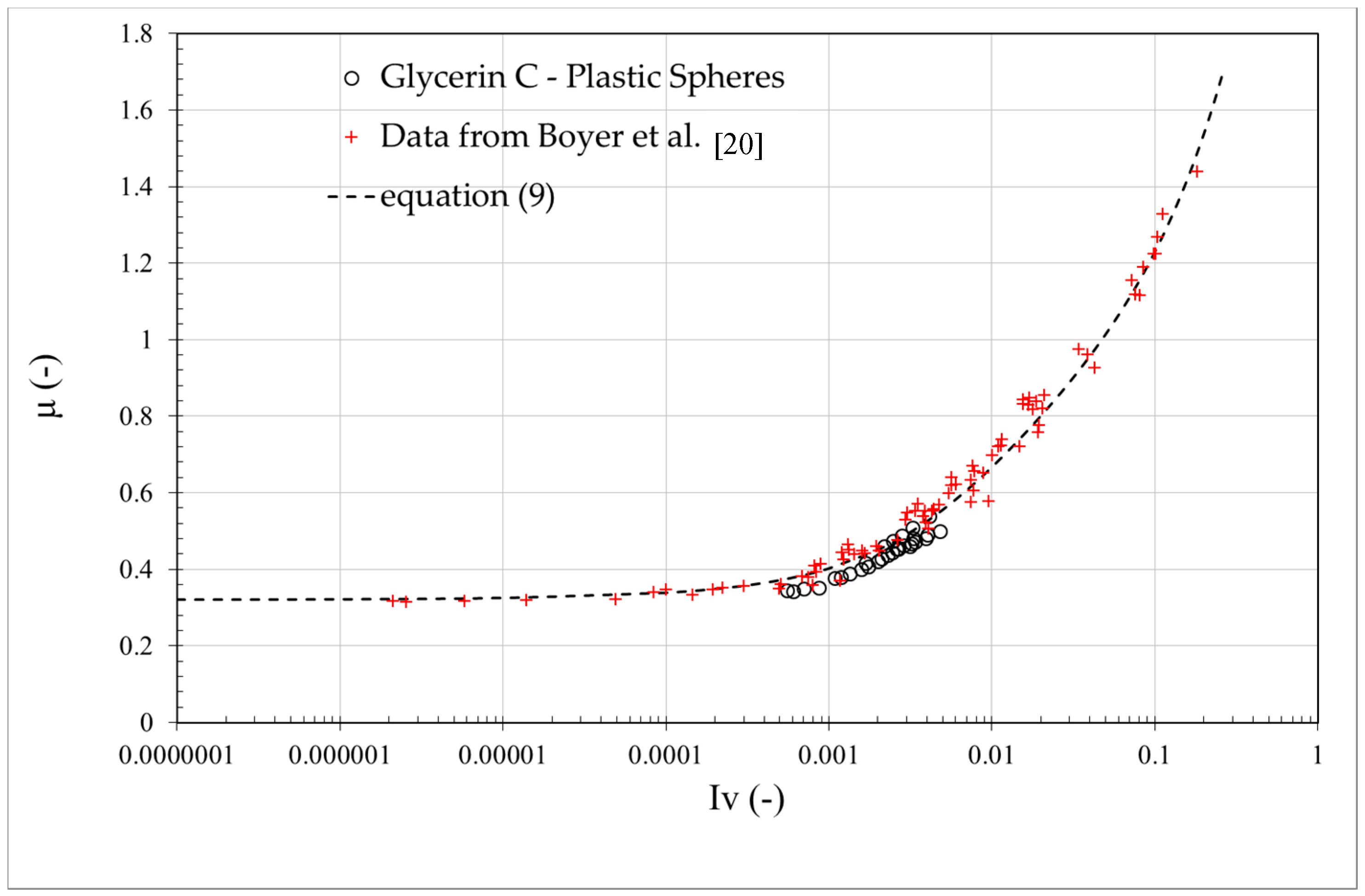
Figure 10 depicts the correlation between the friction coefficient
µ and the viscous number
Iv for the plastic spheres–glycerin C solution and a comparison of the viscous suspension data from Boyer et al. [
20]. Again, the pertinence of the viscous number
Iv was demonstrated by the collapse of all of the data to a single curve
μ(
Iv).
Referring to Equation (4), the friction law
µ(
Iv) for dense suspensions with spheres can be described as the addition of the contact contribution
µc(
Iv) and the hydrodynamic contribution
µh(
Iv) (see Equation (2)). For the case of suspensions of spheres, the hydrodynamic contribution
µh(
Iv) recovers Einstein’s viscosity at low volume fraction
Φ and represents non-saturating behaviour at large
Iv, as follow [
12,
16,
20]:
where
µ1,
µ2 and
I0 are constants; and
Φm is the value of the maximum concentration during the shear. In this condition, the friction law
µ(
Iv) of the dense suspensions with spheres can be described as follows considering Equations (2), (3) and (8):
The friction coefficient
µ tends to a finite value
µ1 = 0.32 as
Iv tends to zero (see
Figure 10) and then increases with an increasing
Iv. The value of
µ1 (i.e., the quasi-static value of the friction coefficient) is extremely close to values observed for both the dry granular materials (i.e.,
µ1 = 0.320−0.384, [
12,
18]) and the value measured by Boyer et al. [
20] for viscous suspensions (i.e.,
µ1 = 0.32 ± 0.03). As observed in a previous study [
16,
20], in contrast to the dry-granular rheology, the quasi-static friction coefficient
µ1 does not saturate at large values of
Iv. This behavior is consistent with the additional viscous contribution to the total stress
τ. The trend in the data considered in the current study is consistent with that reported by Boyer et al. [
20] irrespective of the mixture characteristics. The proposed approach demonstrates that the influence of the fluid can be entirely captured by the frictional relations, and the primary effect of the liquid can be predicted regardless of the bead diameters and the fluid viscosity, the data collapsed to a single curve, which can be described by a constitutive law.
The model (Equation (9)) was used for the entire range of the measured viscous numbers and fully captured the experimental observations. Thus, it is confirmed that the rheology of the viscous spheres suspensions under the imposed pressure flow conditions is well described by the constitutive laws of Equations (7) and (9). It has similar features to dry-granular rheology as long as the viscous number Iv is substituted by the inertial number I, and any scale effects due to the experimental apparatus or tested mixture has been observed.
3.3. Re-Interpretation of the Theory to Viscous Suspensions with Irregular-Shaped Particles
Based on previous considerations, we applied the frictional argument used for viscous suspensions with spheres to describe the flow behavior of viscous suspensions with no spherical particles to determine whether the proposed approach could be suitable for the study of viscous mixtures composed by irregular grains. Thus, we should express the results for irregular particles completely using two functions of
Iv:
τ =
µ(
Iv)·
σ and
Φ =
Φ(
Iv). A preliminary analysis on the irregular plastic particle–glycerin C solution, as reported in
Section 3.1, has already put in evidence the relevance of the shape of the particles in terms of
µ-vs.-
Iv relationship. In effect a significant scatter is clearly obtained from the data for viscous suspensions with spherical particles [
20,
30] as it is evident from
Figure 8. In fact, increasing the viscous number
Iv (
Iv > 0.005), the data relative to the irregular particles dramatically deviate from the spherical trend. Nevertheless, the friction coefficient and the viscous number correlate satisfactorily, and all of the experimental data derived for the irregular particles collapse onto a single curve
µ(
Iv). In case of irregular grains, corresponding to lower
Iv values (i.e., essentially a combination of higher normal stress and lower shear rate) the grains are in close contact each other and because of irregular shape they may partly or temporarily experience clogging configuration which leads to relatively higher shear stress and volume concentration, in comparison with shearing spheres. On the opposite, increasing viscous number
Iv (i.e., a combination of increasing shear rate and decreasing normal stress) dilatation is more effective, as it is evident from
Figure 8 and
Figure 11.
In order to verify if the frictional approach is relevant also for the case of irregular particles, we first validate the solid concentration relationship,
Φ =
Φ(
Iv). Again, the pertinence of the viscous number
Iv was demonstrated by the collapse of all of the data to a single curve
Φ(
Iv), as indicated in
Figure 11 for the plastic irregular particle-glycerin C solution. As expected, the volume fraction is a decreasing function of
Iv due to the dilatation of the mixture resulting from the increasing shear rate. From the correlation between the solid concentration
Φ and the viscous number
Iv in a semi-logarithmic chart, it is possible to determine the maximum volume fraction
Φm obtained during the shearing when
Iv tends to 0, as illustrated in
Figure 11. Based on the experiments, the value of the maximum volume fraction during shearing is
Φm = 0.66 for the case of irregular particles, whereas in the case of spherical particle
Φm = 0.585 according to Boyer et al. [
20]. As expected, once again we obtained a different
Φ(
Iv) curve as a function of the shape of the particles dispersed in the analyzed mixtures, as indicated in
Figure 11.
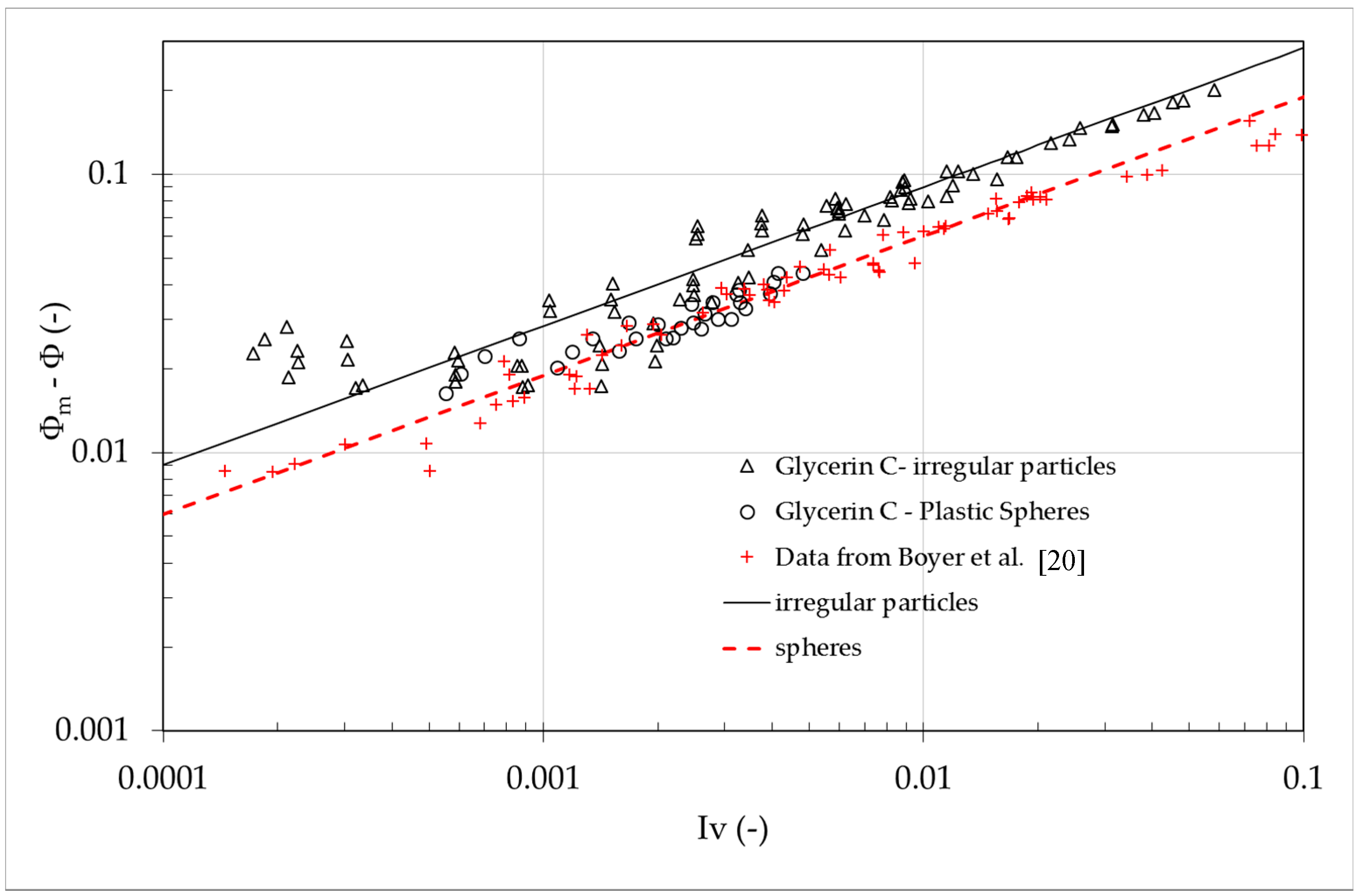
Figure 12 reports the relationship between the viscous number
Iv and the difference between the maximum volume fraction during the shearing
Φm and the measured solid concentration
Φ for the case of plastic irregular particle–glycerin C solution. In the same picture, are also reported the data for regular grains. It is evident the asymptotic behavior, for both spheres and irregular grains,
(Фm − Ф) = K·Iv1/2. Nevertheless, a different value for the constant
K should be considered in order to fit spherical and irregular particles, respectively.
A consistent model for volume fraction results in the asymptotic form
at vanishing
Iv and
Φ(
Iv) > 0 for any
Iv. Therefore the consistent general model for
Φ(
Iv) may be expressed as:
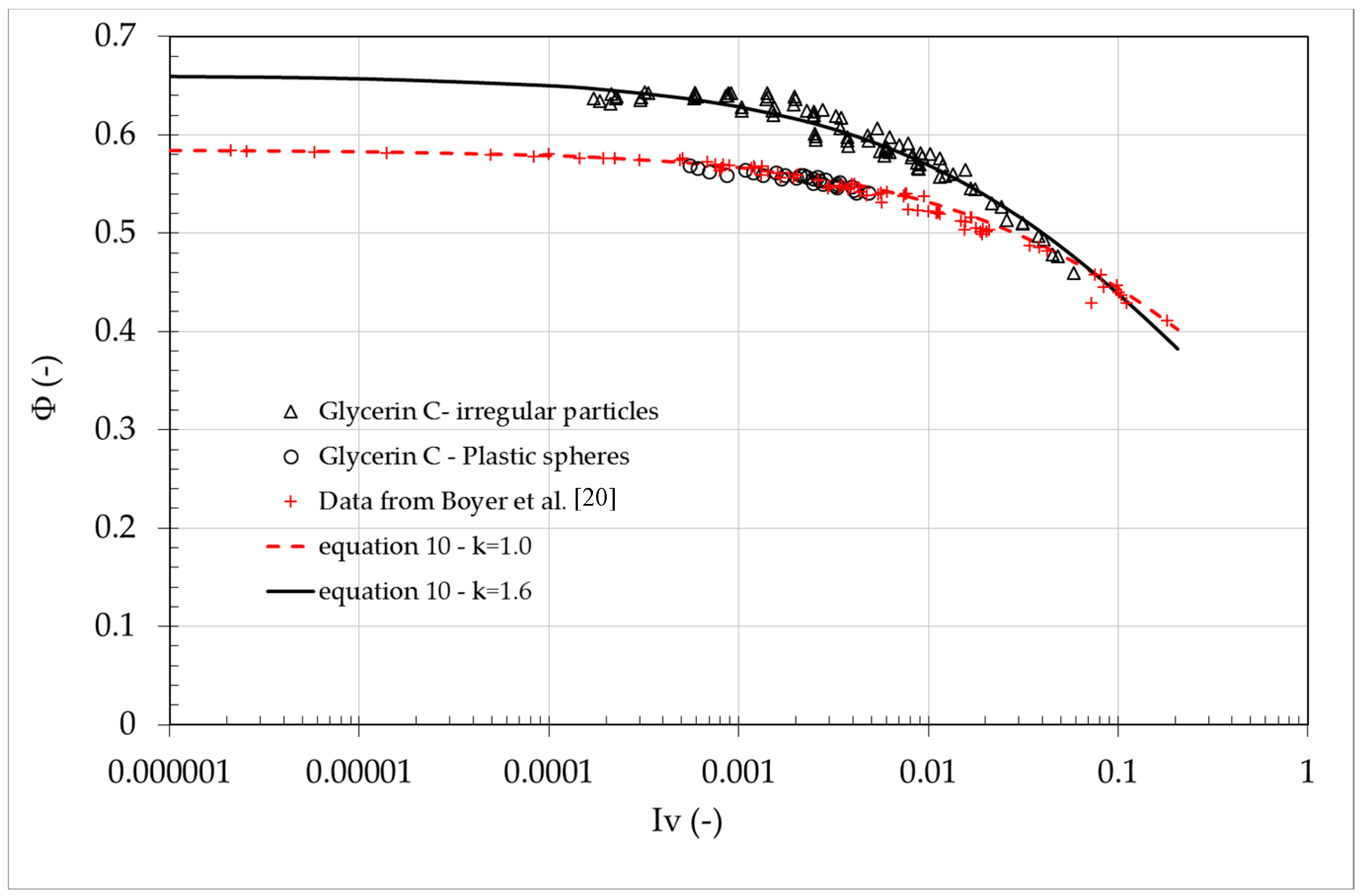
where
k is a fitting parameter depending on the shearing material. The Equation (10) represents a new general model which may be used also in case of spherical particles, assuming
k = 1 (cmp. Equation (7)).
Since Equation (10) satisfactorily models the current measurements, as depicted in
Figure 13, it was used for the entire range of the measured viscous numbers and fully captured the experimental observations both in case of regular and irregular particles. The trends of the experiments are similar, even though a scatter between the data for irregular particles sheared in a glycerin solution and the data for the spherical grains suspensions is observed, especially for relatively low viscous numbers (i.e.,
Iv < 0.01).
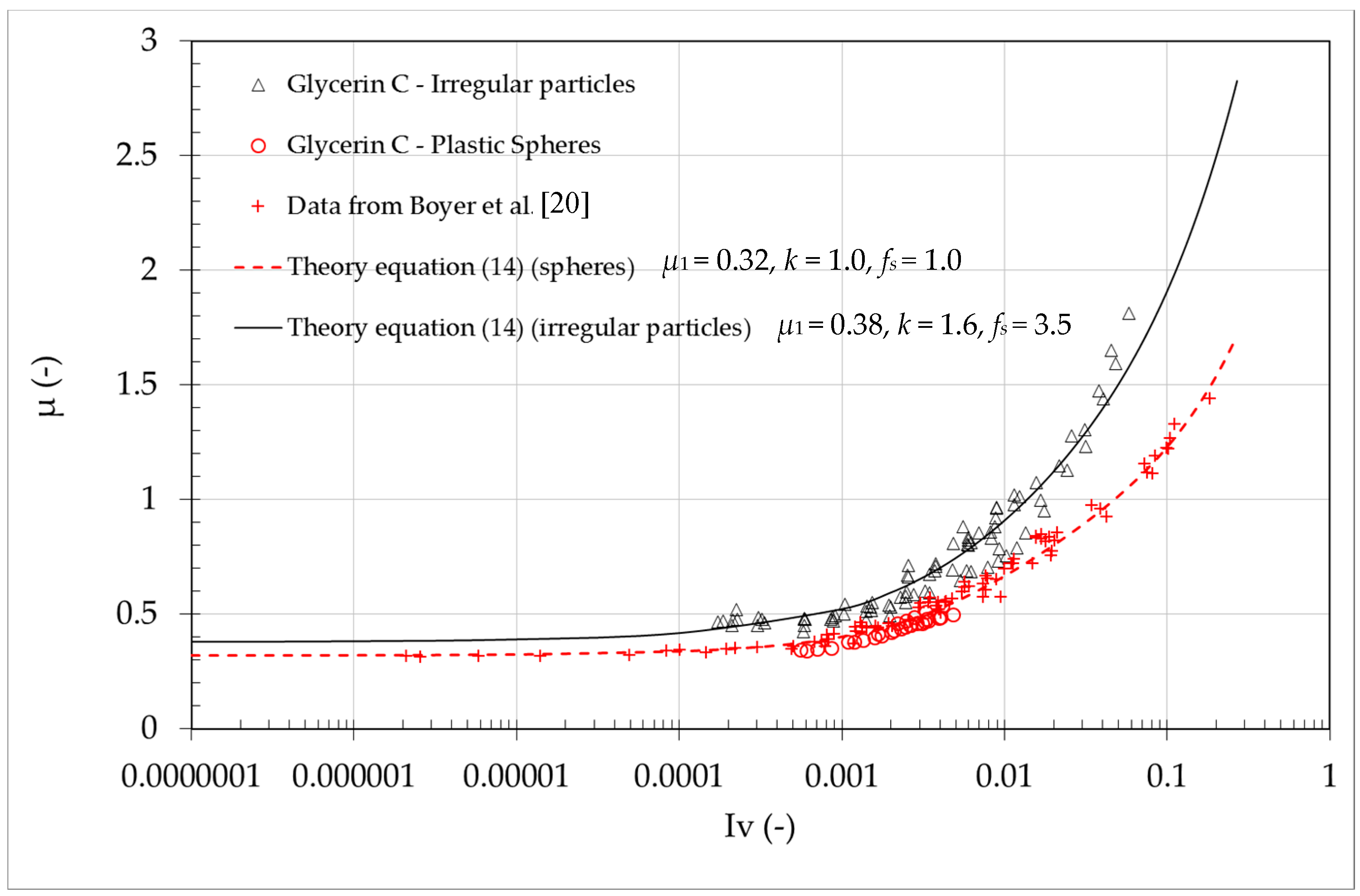
Additionally, the friction law of the dense suspensions µ(Iv) used for the plastic sphere–glycerin C solution and expressed by Equation (9) has been modified for the case of irregular particles. In this case, no variation is needed for the contact contribution µc(Iv) reported in Equation (3)
From
Figure 14 we extrapolated a limiting value of the friction coefficient
µ1 = 0.38 for dense suspensions with irregular shaped particles. The value is slightly higher than the value measured for spherical particles. For the hydrodynamic contribution
µh(
Iv), the asymptotic behavior of
Φ close to
Φm given by the power law
(Equation (10)) for irregular particles is considered. Starting from the definition of the viscous number,
Iv, we properly consider the effective shear viscosity as follow:
According to the theory, we assumed that the effective shear viscosity tends to Einstein’s viscosity at O(
Φ) as follow:
where
fs is a fitting parameter also accounting for granular shape. Identifying these two latter equations, and recovering Equation (4), we have:
Eventually the friction law of the dense suspensions with irregular particles
µ(
Iv) results:
Best fit is obtained using the following values of the characteristic parameters:
µ1 = 0.38,
µ2 = 0.7,
I0 = 0.05,
k = 1.6,
fs = 3.5, according to the experimental results (see
Figure 14)
This model (Equation (14)) was used for the entire range of the measured viscous numbers and fully captured the experimental observations for irregular particles suspensions, as illustrated in
Figure 14. For viscous suspensions with non-spherical grains, the shape plays a significant role, and the frictional rheology applied to the shearing spheres is no longer suitable. Thus, the granular paradigm extended to viscous grain suspensions could be applicable to the case of different-shaped particles as long as the characteristic parameters of the constitutive law are opportunely defined. In fact we propose a new interpretation of the original formulation accounting for the effects associated with the specific characteristics of the suspension.
Under this constraints a unified rheological model based on the granular theory is still possible in the viscous regime, and it provides a complete rheological description of the flow behavior.
In particular, referring to the collisional component of the friction law, the model accounts for the parameters µ1, µ2 and I0; whereas the parameters k and fs refer to the hydrodynamic component of the friction law.
The parameter µ2 (i.e., the asymptotic friction value at large shear rate) and the constant I0, according to the experimental results, do not depend neither on the characteristics of the suspension, nor on the grain shape, and they may be assumed in effect as a constant.
Therefore the fitting parameters reduce to µ1, k and fs. As far as the coefficient µ1 is concern, it may be experimentally derived, referring to vanishing shear rate condition. On the other hand, the parameters k and fs may be set up investigating the dilute limit of the suspension.
4. Conclusions
In the current study, we investigated the rheological behavior of viscous suspensions typically involved in debris flow phenomena with particular reference to the flow intermediate regime (known as the “dense” flow regime). The goal of the study was to consider the flow behavior of viscous suspensions accounting for spherical and irregular particle shapes. We referred to a recent approach proposed by Cassar et al. [
16] and Boyer et al. [
20] to unify the suspensions and granular rheology under a common framework. This approach is particularly attractive for a number of reasons. First, the mixture of water and granular material is treated as a single-phase flow with a simple but realistic rheology suggested by experiments on dry granular flow for modelling the resistance in the particle phase. In fact, describing the flow in terms of an effective friction coefficient works for both granular flows and suspensions, even though the interactions between the particles are quite different. Secondly, this approach also applies to the range of concentrations where both hydrodynamics and collisions are relevant, and the effective shear viscosity close to the jamming transition suggests it may be useful for studying jamming systems. Lastly, the description of the flow of immersed dense granular materials using a simple heuristic model that considers not only the hydrodynamic effects but also the frictional nature of the grains could be useful in engineering applications.
The frictional theory was applied to a significant set of experimental data derived from an extensive laboratory experiment performed by Schippa and Lamberti [
30] using an original pressure-imposed large rheometer for several mixtures involving both regular and irregular grains.
In effect, the shape of the particles likely plays a fundamental role in the flow dynamics, and the constitutive laws proposed by the frictional theory for the spheres [
15,
18] are no longer valid and must be modified in order to consider the effects of the particle shape.
Thus, we propose a new consistent general model (i.e., Equations (10) and (14)) for the volume fraction law and friction law which accounts for the particle shape.
The fitting parameters reduce just to the static friction angle µ1, and the two parameters, k and fs related to the grain shape. The latter relate to the volume fraction behaviour in case of significant shear rate and for vanishing grain volume concentration. As far as the coefficient µ1 is concerned, it may be experimentally derived referring to vanishing shear rate condition. On the other hand, the parameters k and fs may be set-up referring to the dilute limit of the suspension.
The discussed results suggest that this relatively simple theory based on a rheology for the particle and the fluid interaction, could be successfully applied to steady fully developed flows of saturated granular–liquid mixtures in the viscous regime. This theory was applied to idealized debris flow mixtures composed by viscous fluid and grains having different shapes to reproduce conditions which are typically present in the prototype. Despite some experimental limitations which have been conveniently investigated and considered, the frictional theory along with the new volume fraction law herein presented accounting for the particle shape, represents a suitable approach if the specific mixture characteristics are taken into account, and the fitting model parameters have been set according to experimental results.