Symmetry of Energy Divergence Anomalies Associated with the El Niño-Southern Oscillation
Abstract
:1. Introduction
2. Experiments
2.1. ENSO Events
2.2. Reanalysis Data
2.3. Vertically Integrated Energy Budget
2.4. Data Scaling
2.5. Symmetry and Asymmetry
3. Results
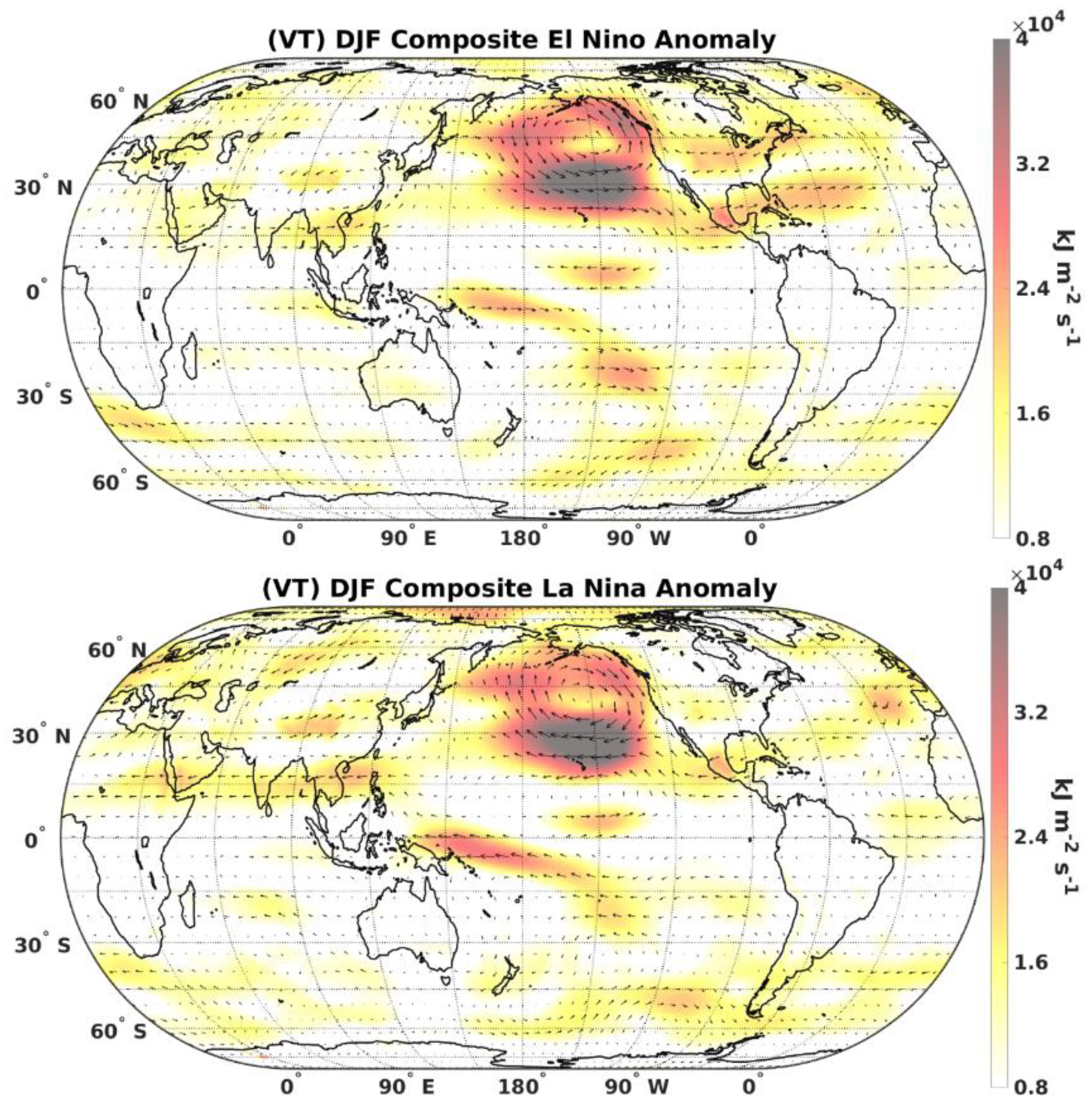
3.1. Sensible Heat Flux Divergence
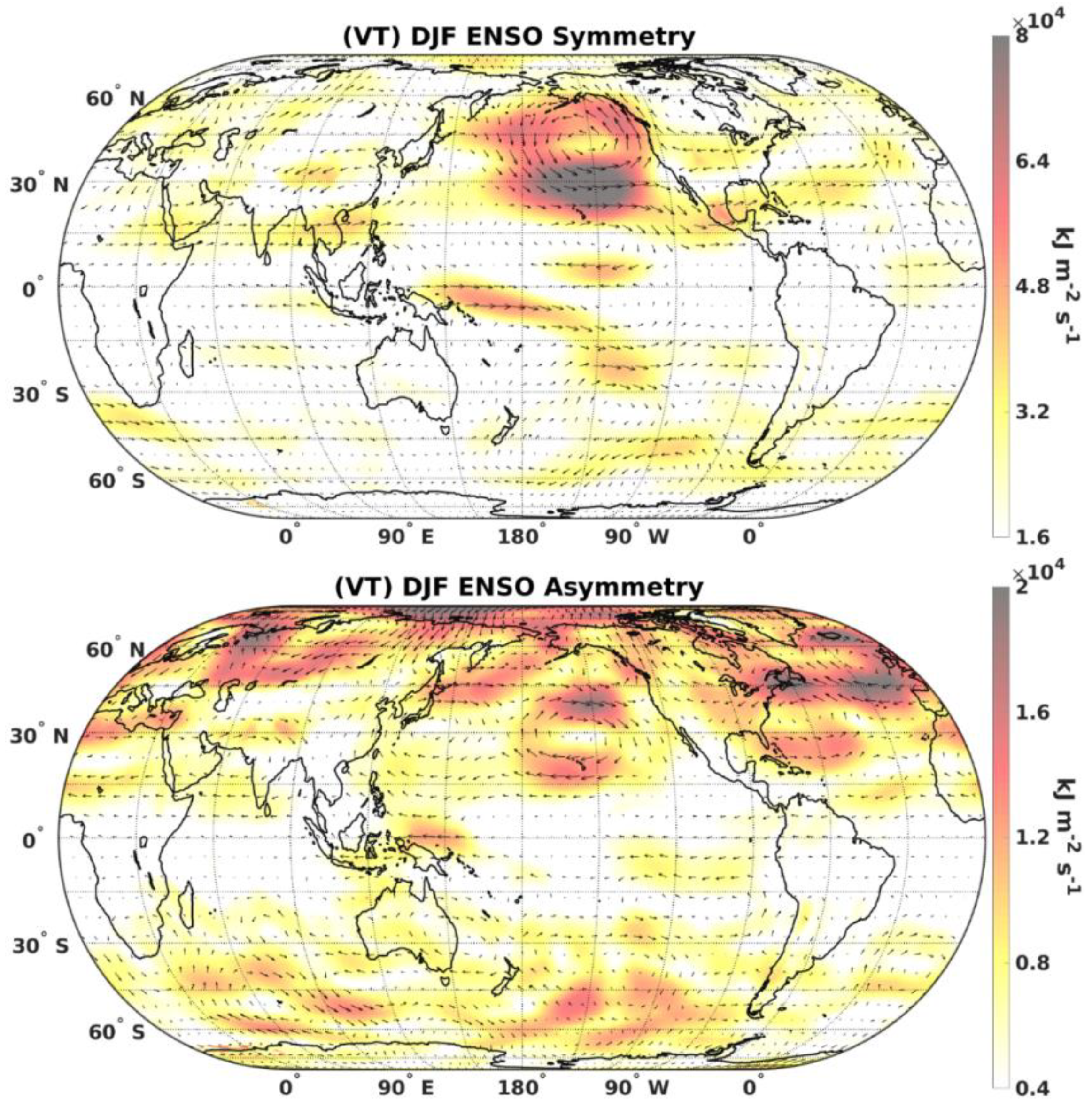
3.2. Symmetry and Asymmetry of Sensible Heat Flux Divergence
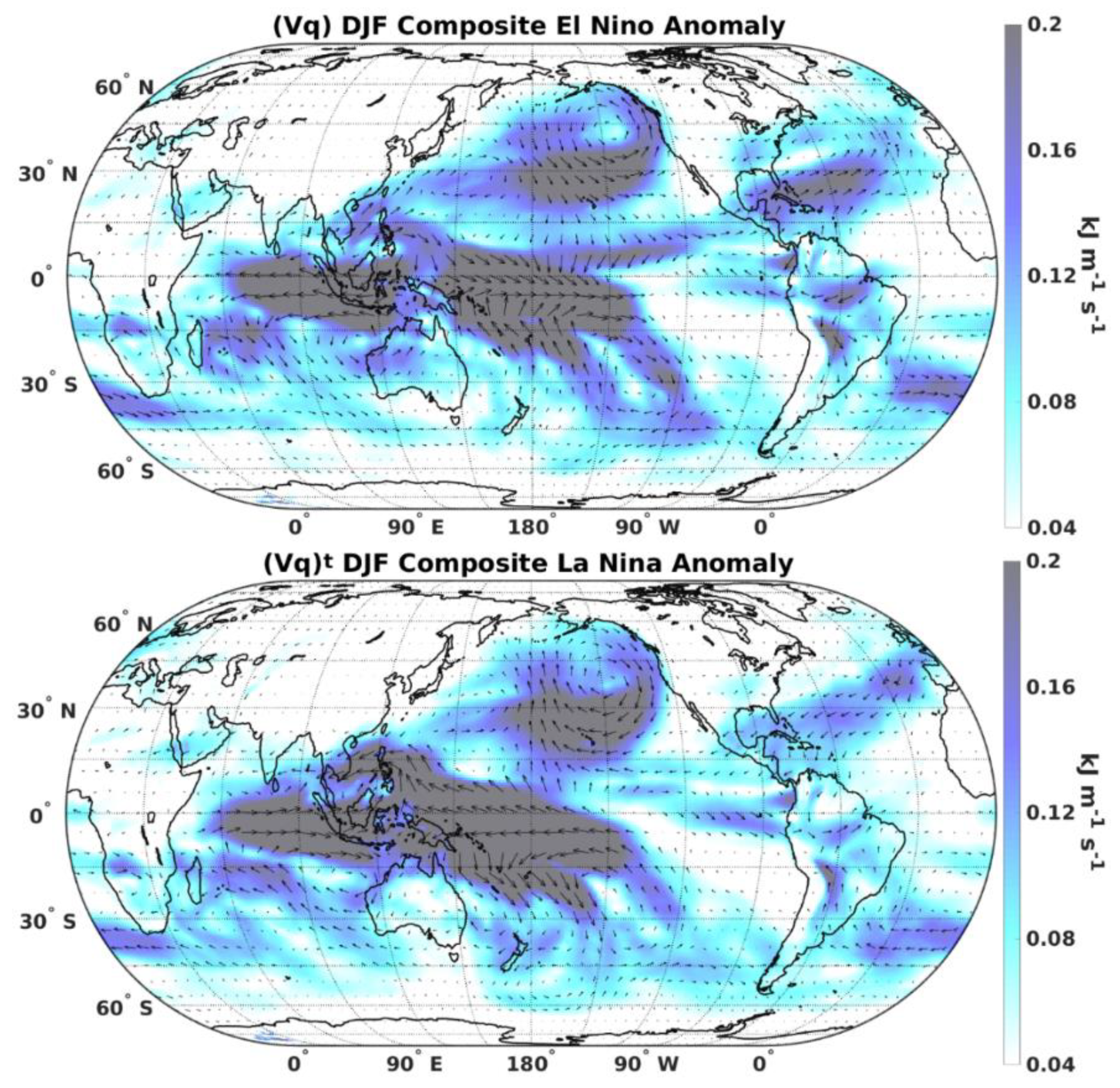
3.3. Latent Heat Flux Divergence
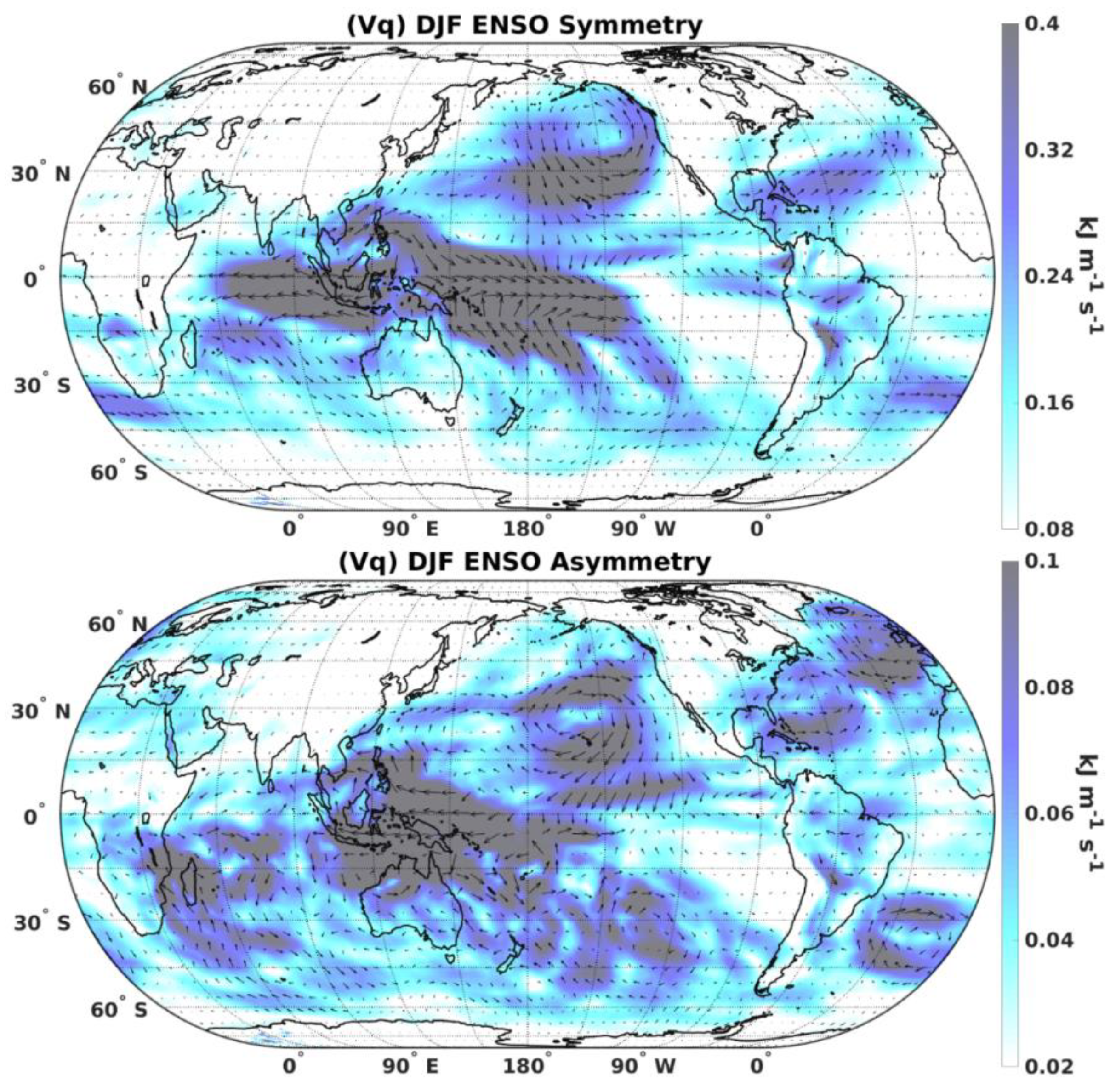
3.4. Symmetry and Asymmetry of Latent Heat Flux Divergence
4. Discussion
4.1. ENSO, PNA, and NAO Climate Variability
4.2. Eurasia and the Southern Hemisphere
4.3. Directions for Future Work
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Trenberth, K.E.; Branstator, G.W.; Karoly, D.; Kumar, A.; Lau, N.C.; Ropelewski, C. Progress during TOGA in understanding and modeling global teleconnections associated with tropical sea surface temperatures. J. Geophys. Res. Oceans 1998, 103, 14291–14324. [Google Scholar] [CrossRef] [Green Version]
- Collins, M.; An, S.I.; Cai, W.; Ganachaud, A.; Guilyardi, E.; Jin, F.F.; Jochum, M.; Lengaigne, M.; Power, S.; Timmermann, A.; et al. The impact of global warming on the tropical Pacific Ocean and El Niño. Nat. Geosci. 2010, 3, 391. [Google Scholar] [CrossRef]
- Barnston, A.G.; Glantz, M.H.; He, Y. Predictive skill of statistical and dynamical climate models in SST forecasts during the 1997–1998 El Niño episode and the 1998 La Niña onset. Bull. Am. Meteorol. Soc. 1999, 80, 217–244. [Google Scholar] [CrossRef]
- Okumura, Y.M.; Deser, C. Asymmetry in the duration of El Niño and La Niña. J. Clim. 2010, 23, 5826–5843. [Google Scholar] [CrossRef]
- Ropelewski, C.F.; Jones, P.D. An extension of the Tahiti–Darwin southern oscillation index. Mon. Weather Rev. 1987, 115, 2161–2165. [Google Scholar] [CrossRef]
- McPhaden, M.J.; Bahr, F.; Du Penhoat, Y.; Firing, E.; Hayes, S.P.; Niiler, P.P.; Richardson, P.L.; Toole, J.M. The response of the western equatorial Pacific Ocean to westerly wind bursts during November 1989 to January 1990. J. Geophys. Res. Oceans 1992, 97, 14289–14303. [Google Scholar] [CrossRef]
- Rasmusson, E.M.; Carpenter, T.H. Variations in tropical sea surface temperature and surface wind fields associated with the Southern Oscillation/El Niño. Mon. Weather Rev. 1982, 110, 354–384. [Google Scholar] [CrossRef]
- Cayan, D.R. Latent and sensible heat flux anomalies over the northern oceans: Driving the sea surface temperature. J. Phys. Oceanogr. 1992, 22, 859–881. [Google Scholar] [CrossRef]
- Ropelewski, C.F.; Halpert, M.S. North American precipitation and temperature patterns associated with the El Niño/Southern Oscillation (ENSO). Mon. Weather Rev. 1986, 114, 2352–2362. [Google Scholar] [CrossRef]
- Brönnimann, S. Impact of El Niño–southern oscillation on European climate. Rev. Geophys. 2007, 45. [Google Scholar] [CrossRef]
- Stechmann, S.N.; Ogrosky, H.R. The Walker circulation, diabatic heating, and outgoing longwave radiation. Geophys. Res. Lett. 2014, 41, 9097–9105. [Google Scholar] [CrossRef]
- Johnson, N.C.; Kosaka, Y. The impact of eastern equatorial Pacific convection on the diversity of boreal winter El Niño teleconnection patterns. Clim. Dyn. 2016, 47, 3737–3765. [Google Scholar] [CrossRef]
- Franzke, C.; Feldstein, S.B. The continuum and dynamics of Northern Hemisphere teleconnection patterns. J. Atmos. Sci. 2005, 62, 3250–3267. [Google Scholar] [CrossRef]
- Deser, C.; Simpson, I.R.; McKinnon, K.A.; Phillips, A.S. The Northern Hemisphere extratropical atmospheric circulation response to ENSO: How well do we know it and how do we evaluate models accordingly? J. Clim. 2017, 30, 5059–5082. [Google Scholar] [CrossRef]
- Straus, D.M.; Shukla, J. Does ENSO force the PNA? J. Clim. 2002, 15, 2340–2358. [Google Scholar] [CrossRef]
- Scaife, A.A.; Arribas, A.; Blockley, E.; Brookshaw, A.; Clark, R.T.; Dunstone, N.; Eade, R.; Fereday, D.; Folland, C.K.; Gordon, M.; et al. Skillful long-range prediction of European and North American winters. Geophys. Res. Lett. 2014, 41, 2514–2519. [Google Scholar] [CrossRef] [Green Version]
- Hurrell, J.W.; Deser, C. North Atlantic climate variability: The role of the North Atlantic Oscillation. J. Mar. Syst. 2010, 79, 231–244. [Google Scholar] [CrossRef]
- Capotondi, A.; Wittenberg, A.T.; Newman, M.; Di Lorenzo, E.; Yu, J.Y.; Braconnot, P.; Cole, J.; Dewitte, B.; Giese, B.; Guilyardi, E.; et al. Understanding ENSO diversity. Bull. Am. Meteorol. Soc. 2015, 96, 921–938. [Google Scholar] [CrossRef]
- Ropelewski, C.F.; Halpert, M.S. Precipitation patterns associated with the high index phase of the Southern Oscillation. J. Clim. 1989, 2, 268–284. [Google Scholar] [CrossRef]
- Halpert, M.S.; Ropelewski, C.F. Surface temperature patterns associated with the Southern Oscillation. J. Clim. 1992, 5, 577–593. [Google Scholar] [CrossRef]
- Freeman, E.; Woodruff, S.D.; Worley, S.J.; Lubker, S.J.; Kent, E.C.; Angel, W.E.; Berry, D.I.; Brohan, P.; Eastman, R.; Gates, L.; et al. ICOADS Release 3.0: A major update to the historical marine climate record. Int. J. Climatol. 2017, 37, 2211–2232. [Google Scholar] [CrossRef] [Green Version]
- Dai, A.; Wigley, T.M.L. Global patterns of ENSO-induced precipitation. Geophys. Res. Lett. 2000, 27, 1283–1286. [Google Scholar] [CrossRef] [Green Version]
- Mo, K.C. Interdecadal modulation of the impact of ENSO on precipitation and temperature over the United States. J. Clim. 2010, 23, 3639–3656. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, J.; Singh, V.P.; Xu, C.Y.; Deng, J. Influence of ENSO on precipitation in the East River basin, South China. J. Geophys. Res. Atmos. 2013, 118, 2207–2219. [Google Scholar] [CrossRef]
- Davey, M.K.; Brookshaw, A.; Ineson, S. The probability of the impact of ENSO on precipitation and near-surface temperature. Clim. Risk Manage. 2014, 1, 5–24. [Google Scholar] [CrossRef]
- Garreaud, R.; Battisti, D.S. Interannual (ENSO) and interdecadal (ENSO-like) variability in the Southern Hemisphere tropospheric circulation. J. Clim. 1999, 12, 2113–2123. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, D.P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Zhang, T.; Perlwitz, J.; Hoerling, M.P. What is responsible for the strong observed asymmetry in teleconnections between El Niño and La Niña? Geophys. Res. Lett. 2014, 41, 1019–1025. [Google Scholar] [CrossRef] [Green Version]
- Frauen, C.; Dommenget, D.; Tyrrell, N.; Rezny, M.; Wales, S. Analysis of the nonlinearity of El Niño–Southern Oscillation teleconnections. J. Clim. 2014, 27, 6225–6244. [Google Scholar] [CrossRef]
- Larkin, N.K.; Harrison, D.E. ENSO warm (El Niño) and cold (La Niña) event life cycles: Ocean surface anomaly patterns, their symmetries, asymmetries, and implications. J. Clim. 2002, 15, 1118–1140. [Google Scholar] [CrossRef]
- Hoerling, M.P.; Kumar, A.; Zhong, M. El Niño, La Niña, and the nonlinearity of their teleconnections. J. Clim. 1997, 10, 1769–1786. [Google Scholar] [CrossRef]
- Dogar, M.M.; Kucharski, F.; Azharuddin, S. Study of the global and regional climatic impacts of ENSO magnitude using SPEEDY AGCM. J. Earth Syst. Sci. 2017, 126, 30. [Google Scholar] [CrossRef]
- Kim, S.; Son, H.Y.; Kug, J.S. Relative roles of equatorial central Pacific and western North Pacific precipitation anomalies in ENSO teleconnection over the North Pacific. Clim. Dyn. 2017, 1–11. [Google Scholar] [CrossRef]
- Xie, S.P.; Zhou, Z.Q. Seasonal modulations of El Niño–related atmospheric variability: Indo–western Pacific Ocean feedback. J. Clim. 2017, 30, 3461–3472. [Google Scholar] [CrossRef]
- Shaw, T.A.; Pauluis, O. Tropical and subtropical meridional latent heat transports by disturbances to the zonal mean and their role in the general circulation. J. Atmos. Sci. 2012, 69, 1872–1889. [Google Scholar] [CrossRef]
- Piani, C.; Haerter, J.O.; Coppola, E. Statistical bias correction for daily precipitation in regional climate models over Europe. Theor. Appl. Climatol. 2010, 99, 187–192. [Google Scholar] [CrossRef]
- Simmons, A.J.; Willett, K.M.; Jones, P.D.; Thorne, P.W.; Dee, D.P. Low-frequency variations in surface atmospheric humidity, temperature, and precipitation: Inferences from reanalyses and monthly gridded observational data sets. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef] [Green Version]
- Atlaskin, E.; Vihma, T. Evaluation of NWP results for wintertime nocturnal boundary-layer temperatures over Europe and Finland. Q. J. R. Meteorol. Soc. 2012, 138, 1440–1451. [Google Scholar] [CrossRef] [Green Version]
- Shrestha, D.L.; Robertson, D.E.; Wang, Q.J.; Pagano, T.C.; Hapuarachchi, H.A.P. Evaluation of numerical weather prediction model precipitation forecasts for short-term streamflow forecasting purpose. Hydrol. Earth. Syst. Sci. 2013, 17, 1913–1931. [Google Scholar] [CrossRef] [Green Version]
- Yu, L.; Weller, R.A. Objectively analyzed air–sea heat fluxes for the global ice-free oceans (1981–2005). Bull. Am. Meteorol. Soc. 2007, 88, 527–540. [Google Scholar] [CrossRef]
- Newman, M.; Kiladis, G.N.; Weickmann, K.M.; Ralph, F.M.; Sardeshmukh, P.D. Relative contributions of synoptic and low-frequency eddies to time-mean atmospheric moisture transport, including the role of atmospheric rivers. J. Clim. 2012, 25, 7341–7361. [Google Scholar] [CrossRef]
- Lupo, A.R.; Smith, P.J.; Zwack, P. A diagnosis of the explosive development of two extratropical cyclones. Mon. Weather Rev. 1992, 120, 1490–1523. [Google Scholar] [CrossRef]
- Neiman, P.J.; May, P.T.; Shapiro, M.A. Radio acoustic sounding system (RASS) and wind profiler observations of lower-and midtropospheric weather systems. Mon. Weather Rev. 1992, 120, 2298–2313. [Google Scholar] [CrossRef]
- Yu, J.Y.; Kim, S.T. Identifying the types of major El Niño events since 1870. Int. J. Climatol. 2013, 33, 2105–2112. [Google Scholar] [CrossRef]
- Troup, A.J. The ‘southern oscillation’. Q. J. R. Meteorol. Soc. 1965, 91, 490–506. [Google Scholar] [CrossRef]
- Wolter, K.; Timlin, M.S. Measuring the strength of ENSO events: How does 1997/98 rank? Weather 1998, 53, 315–324. [Google Scholar] [CrossRef]
- Wolter, K.; Timlin, M.S. El Niño/Southern Oscillation behaviour since 1871 as diagnosed in an extended multivariate ENSO index (MEI. ext). Int. J. Climatol. 2011, 31, 1074–1087. [Google Scholar] [CrossRef]
- Kirtman, B.P.; Min, D.; Infanti, J.M.; Kinter, J.L., III; Paolino, D.A.; Zhang, Q.; Van Den Dool, H.; Saha, S.; Mendez, M.P.; Becker, E.; et al. The North American multimodel ensemble: Phase-1 seasonal-to-interannual prediction; phase-2 toward developing intraseasonal prediction. Bull. Am. Meteorol. Soc. 2014, 95, 585–601. [Google Scholar] [CrossRef]
- Huang, B.; Thorne, P.W.; Banzon, V.F.; Boyer, T.; Chepurin, G.; Lawrimore, J.H.; Menne, M.J.; Smith, T.M.; Vose, R.S.; Zhang, H.M. Extended reconstructed sea surface temperature, version 5 (ERSSTv5): Upgrades, validations, and intercomparisons. J. Clim. 2017, 30, 8179–8205. [Google Scholar] [CrossRef]
- Alexander, M.A.; Bladé, I.; Newman, M.; Lanzante, J.R.; Lau, N.C.; Scott, J.D. The atmospheric bridge: The influence of ENSO teleconnections on air–sea interaction over the global oceans. J. Clim. 2002, 15, 2205–2231. [Google Scholar] [CrossRef]
- Ji, X.; Neelin, J.D.; Mechoso, C.R. Baroclinic-to-barotropic pathway in El Niño–Southern Oscillation teleconnections from the viewpoint of a barotropic Rossby wave source. J. Atmos. Sci. 2016, 73, 4989–5002. [Google Scholar] [CrossRef]
- L’Heureux, M.L.; Tippett, M.K.; Barnston, A.G. Reply to “Comment on ‘Characterizing ENSO Coupled Variability and Its Impact on North American Seasonal Precipitation and Temperature’”. J. Clim. 2017, 30, 437–441. [Google Scholar] [CrossRef]
- European Centre for Medium-Range Weather Forecasts. 2009, updated monthly. ERA-Interim Project. Research Data Archive at the National Center for Atmospheric Research, Computational and Information Systems Laboratory. Available online: https://doi.org/10.5065/D6CR5RD9 (accessed on 1 July 2016).
- Kim, H.M.; Alexander, M.A. ENSO’s modulation of water vapor transport over the Pacific–North American region. J. Clim. 2015, 28, 3846–3856. [Google Scholar] [CrossRef]
- Simmons, A. ERA-Interim: New ECMWF reanalysis products from 1989 onwards. ECMWF Newslet. 2006, 110, 25–36. [Google Scholar]
- Reutter, P.; Škerlak, B.; Sprenger, M.; Wernli, H. Stratosphere–troposphere exchange (STE) in the vicinity of North Atlantic cyclones. Atmos. Chem. Phys. 2015, 15, 10939–10953. [Google Scholar] [CrossRef] [Green Version]
- Dessler, A.E.; Schoeberl, M.R.; Wang, T.; Davis, S.M.; Rosenlof, K.H.; Vernier, J.P. Variations of stratospheric water vapor over the past three decades. J. Geophys. Res. Atmos. 2014, 119. [Google Scholar] [CrossRef]
- Trenberth, K.E. Climate diagnostics from global analyses: Conservation of mass in ECMWF analyses. J. Clim. 1991, 4, 707–722. [Google Scholar] [CrossRef]
- Mayer, M.; Haimberger, L. Poleward atmospheric energy transports and their variability as evaluated from ECMWF reanalysis data. J. Clim. 2012, 25, 734–752. [Google Scholar] [CrossRef]
- Zhang, T.; Hoerling, M.P.; Perlwitz, J.; Sun, D.Z.; Murray, D. Physics of US surface temperature response to ENSO. J. Clim. 2011, 24, 4874–4887. [Google Scholar] [CrossRef]
- Capek, R. Which is the best projection for the world map. In Proceedings of the 20th international Cartographic Conference, Beijing, China, 6–10 August 2001; Volume 5, pp. 3084–3093. [Google Scholar]
- Kutta, E.; Hubbart, J.A.; Svoma, B.M.; Eichler, T.; Lupo, A.R. Symmetric and asymmetric components of anomalous tropospheric-mean horizontal fluxes of latent and sensible heat associated with ENSO events of variable magnitude. Atmos. Res. 2017, 198, 173–184. [Google Scholar] [CrossRef]
- Greenland, D.; Goodin, D.G.; Smith, R.C. (Eds.) Climate Variability and Ecosystem Response at Long-Term Ecological Research Sites; Oxford University Press: New York, NY, USA, 2003; p. 9. [Google Scholar]
- Wilks, D. Statistical Methods in the Atmospheric Sciences, 3rd ed.; Elsevier Inc.: Waltham, MA, USA, 2011. [Google Scholar]
- Meehl, G.A.; Teng, H. Multi-model changes in El Niño teleconnections over North America in a future warmer climate. Clim. Dyn. 2007, 29, 779–790. [Google Scholar] [CrossRef]
- Dunstone, N.; Smith, D.; Scaife, A.; Hermanson, L.; Eade, R.; Robinson, N.; Andrews, M.; Knight, J. Skillful predictions of the winter North Atlantic Oscillation one year ahead. Nat. Geosci. 2016, 9, 809–814. [Google Scholar] [CrossRef]
- Zhou, L.T.; Wu, R. Respective impacts of the East Asian winter monsoon and ENSO on winter rainfall in China. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
- Chen, W.; Lan, X.; Wang, L.; Ma, Y. The combined effects of the ENSO and the Arctic Oscillation on the winter climate anomalies in East Asia. Chin. Sci. Bull. 2013, 58, 1355–1362. [Google Scholar] [CrossRef] [Green Version]
- Mokhov, I.I.; Timazhev, A.V. November. Climatic anomalies in Eurasia from El Niño/La Niña effects. Dokl. Earth Sci. 2013, 453, 1141–1144. [Google Scholar] [CrossRef]
- Mujumdar, M.; Preethi, B.; Sabin, T.P.; Ashok, K.; Saeed, S.; Pai, D.S.; Krishnan, R. The Asian summer monsoon response to the La Niña event of 2010. Meteorol. Appl. 2012, 19, 216–225. [Google Scholar] [CrossRef] [Green Version]
- Gaughan, A.E.; Staub, C.G.; Hoell, A.; Weaver, A.; Waylen, P.R. Inter-and Intra-annual precipitation variability and associated relationships to ENSO and the IOD in southern Africa. Int. J. Climatol. 2016, 36, 1643–1656. [Google Scholar] [CrossRef]
- Stott, P. How climate change affects extreme weather events. Science 2016, 352, 1517–1518. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Deser, C.; Yu, J.Y.; DiNezio, P.; Clement, A. El Niño and southern oscillation (ENSO): A review. In Coral Reefs of the Eastern Tropical Pacific; Springer Science Publisher: New York, NY, USA, 2017; pp. 85–106. [Google Scholar]
- Guilyardi, E.; Wittenberg, A.; Balmaseda, M.; Cai, W.; Collins, M.; McPhaden, M.J.; Watanabe, M.; Yeh, S.W. Fourth CLIVAR workshop on the evaluation of ENSO processes in climate models: ENSO in a changing climate. Bull. Am. Meteorol. Soc. 2016, 97, 817–820. [Google Scholar] [CrossRef]
- Bellenger, H.; Guilyardi, É.; Leloup, J.; Lengaigne, M.; Vialard, J. ENSO representation in climate models: From CMIP3 to CMIP5. Clim. Dyn. 2014, 42, 1999–2018. [Google Scholar] [CrossRef]
| El Niño | DJF ONI | La Niña | DJF ONI |
|---|---|---|---|
| 1979–1980 | 0.6 °C | 1983–1984 | −0.6 °C |
| 1982–1983 | 2.2 °C | 1984–1985 | −1.0 °C |
| 1986–1987 | 1.2 °C | 1988–1989 | −1.7 °C |
| 1987–1988 | 0.8 °C | 1995–1996 | −0.9 °C |
| 1991–1992 | 1.7 °C | 1998–1999 | −1.5 °C |
| 1994–1995 | 1.0 °C | 1999–2000 | −1.7 °C |
| 1997–1998 | 2.2 °C | 2000–2001 | −0.7 °C |
| 2002–2003 | 0.9 °C | 2005–2006 | −0.8 °C |
| 2004–2005 | 0.6 °C | 2007–2008 | −1.6 °C |
| 2006–2007 | 0.7 °C | 2008–2009 | −0.8 °C |
| 2009–2010 | 1.5 °C | 2010–2011 | −1.4 °C |
| 2014–2015 | 0.6 °C | 2011–2012 | −0.8 °C |
| 2015–2016 | 2.5 °C |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kutta, E.; Hubbart, J.A.; Eichler, T.P.; Lupo, A.R. Symmetry of Energy Divergence Anomalies Associated with the El Niño-Southern Oscillation. Atmosphere 2018, 9, 342. https://doi.org/10.3390/atmos9090342
Kutta E, Hubbart JA, Eichler TP, Lupo AR. Symmetry of Energy Divergence Anomalies Associated with the El Niño-Southern Oscillation. Atmosphere. 2018; 9(9):342. https://doi.org/10.3390/atmos9090342
Chicago/Turabian StyleKutta, Evan, Jason A. Hubbart, Timothy P. Eichler, and Anthony R. Lupo. 2018. "Symmetry of Energy Divergence Anomalies Associated with the El Niño-Southern Oscillation" Atmosphere 9, no. 9: 342. https://doi.org/10.3390/atmos9090342
APA StyleKutta, E., Hubbart, J. A., Eichler, T. P., & Lupo, A. R. (2018). Symmetry of Energy Divergence Anomalies Associated with the El Niño-Southern Oscillation. Atmosphere, 9(9), 342. https://doi.org/10.3390/atmos9090342







