Characteristics of the Underestimation Error of Annual Maximum Rainfall Depth Due to Coarse Temporal Aggregation
Abstract
:1. Introduction
2. Case Study
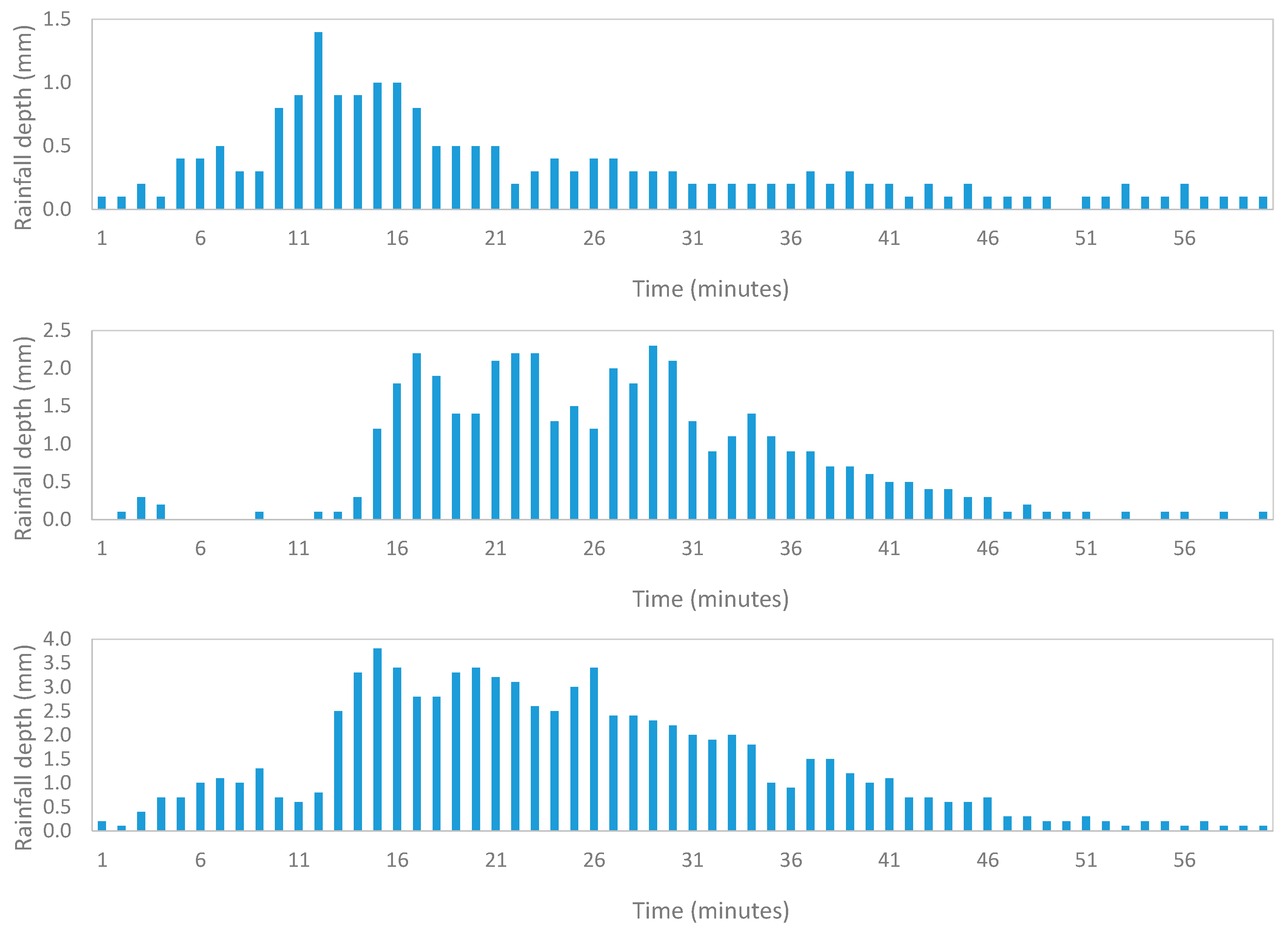
3. Methods
4. Results and Discussion
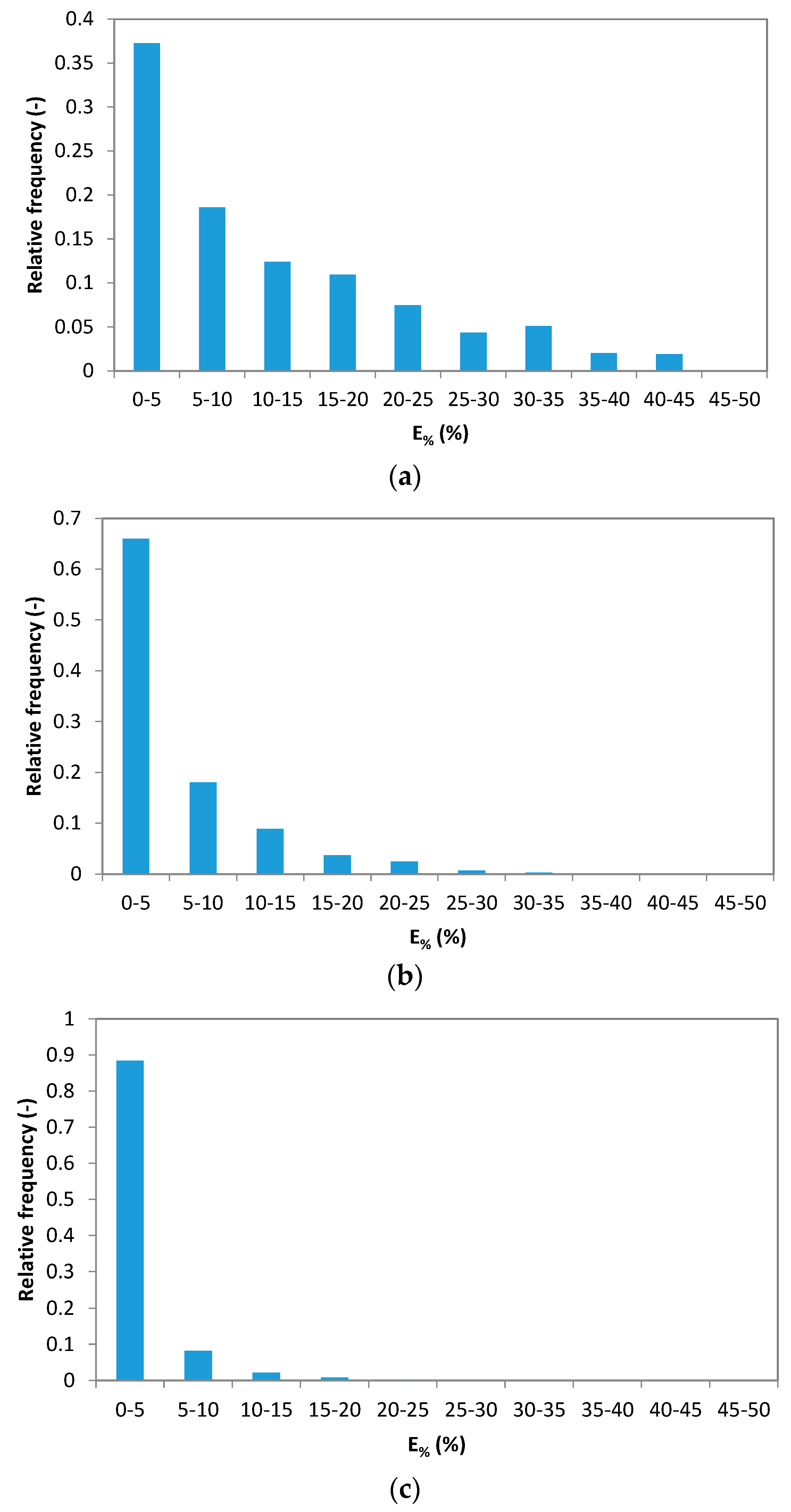
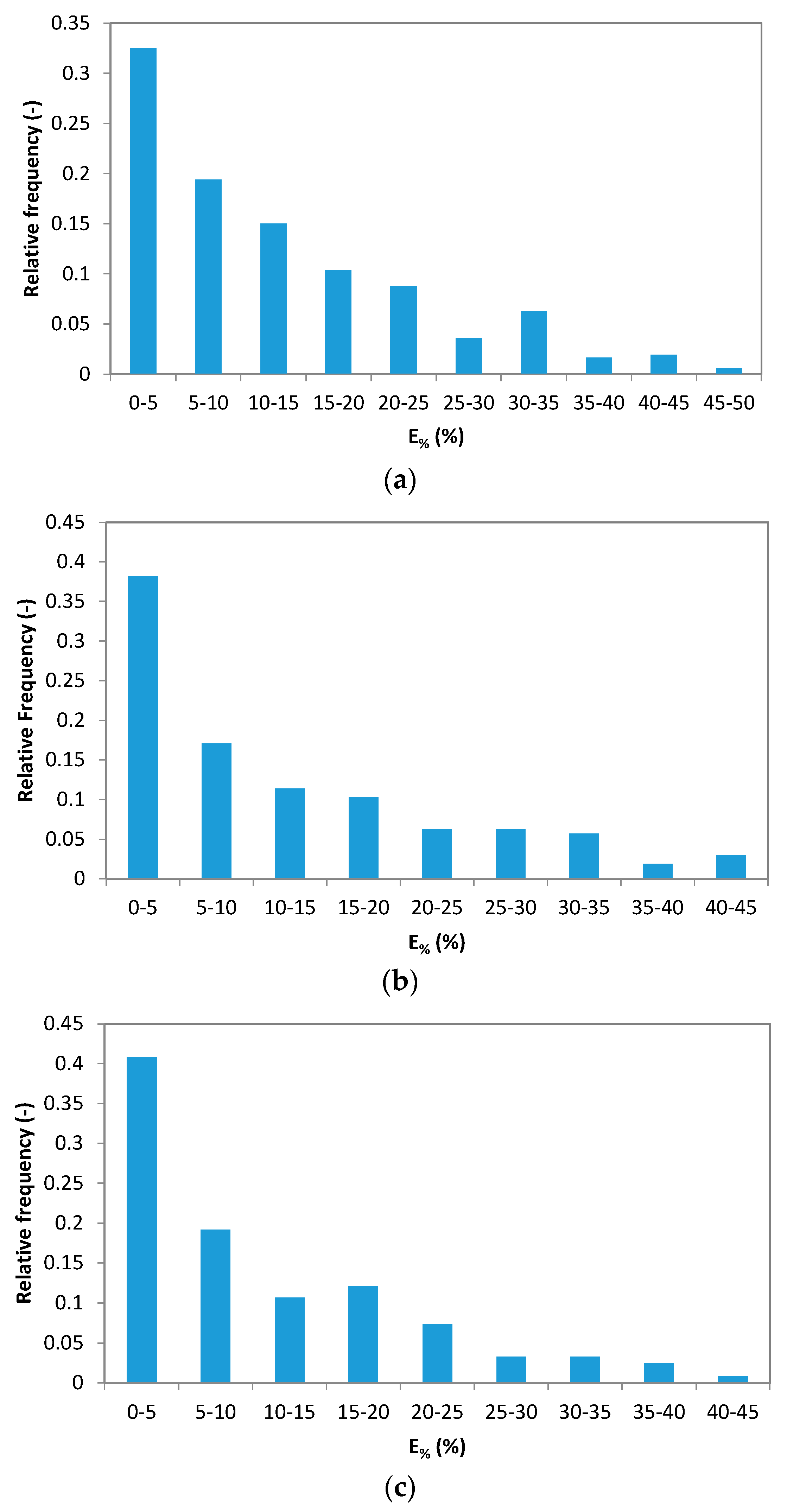
4.1. Single Error Analysis
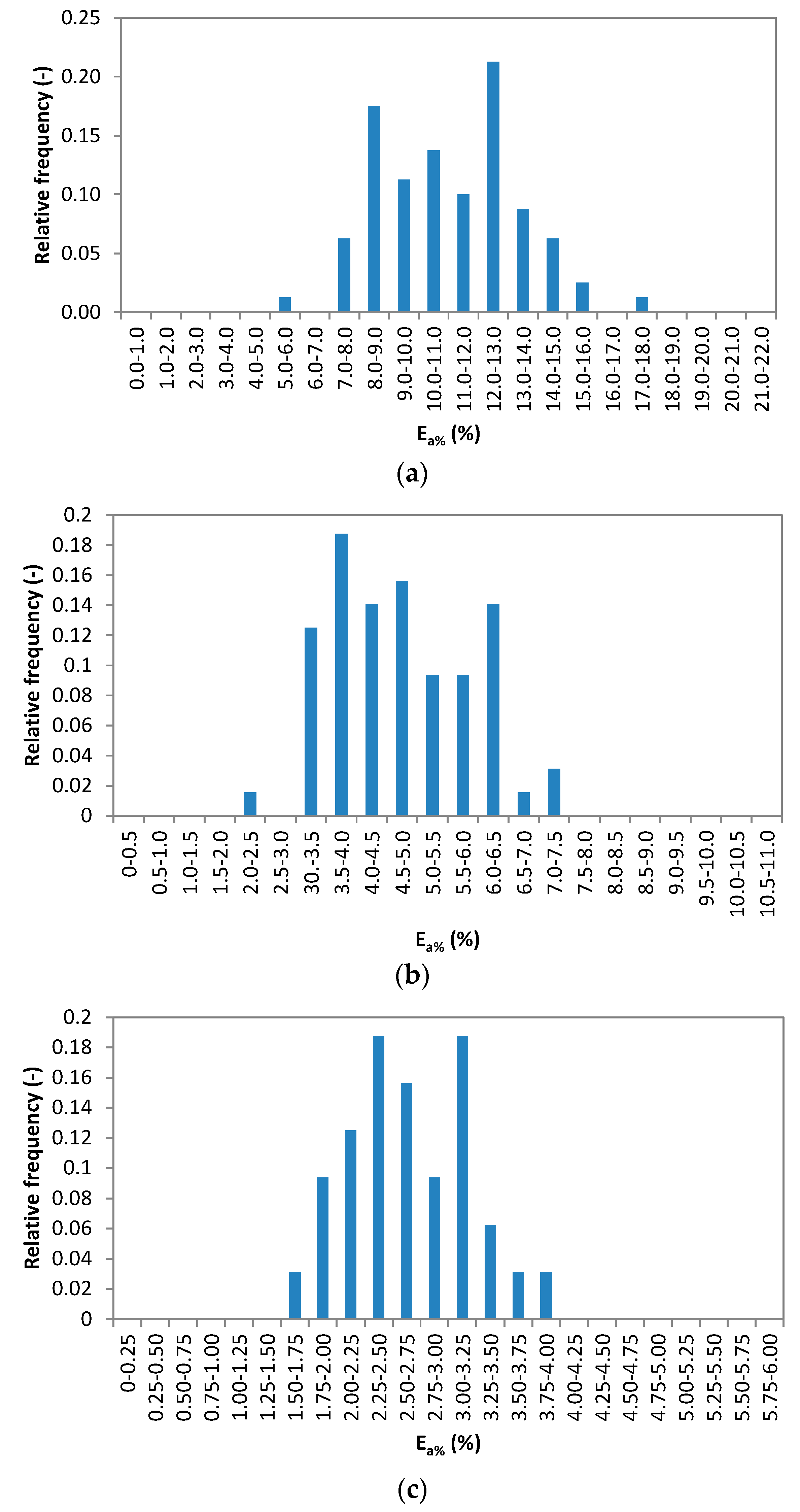
4.2. Average Error Analysis
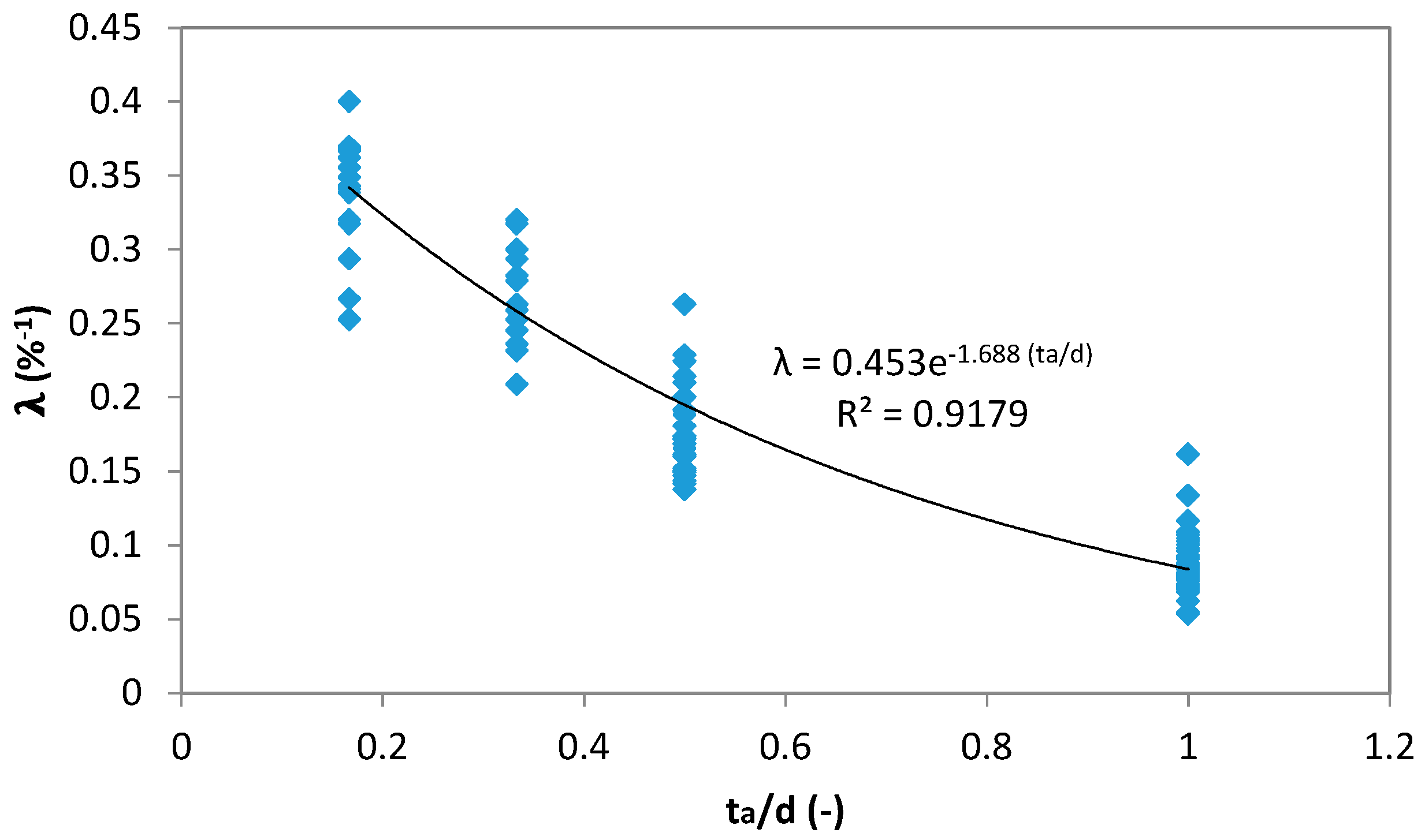
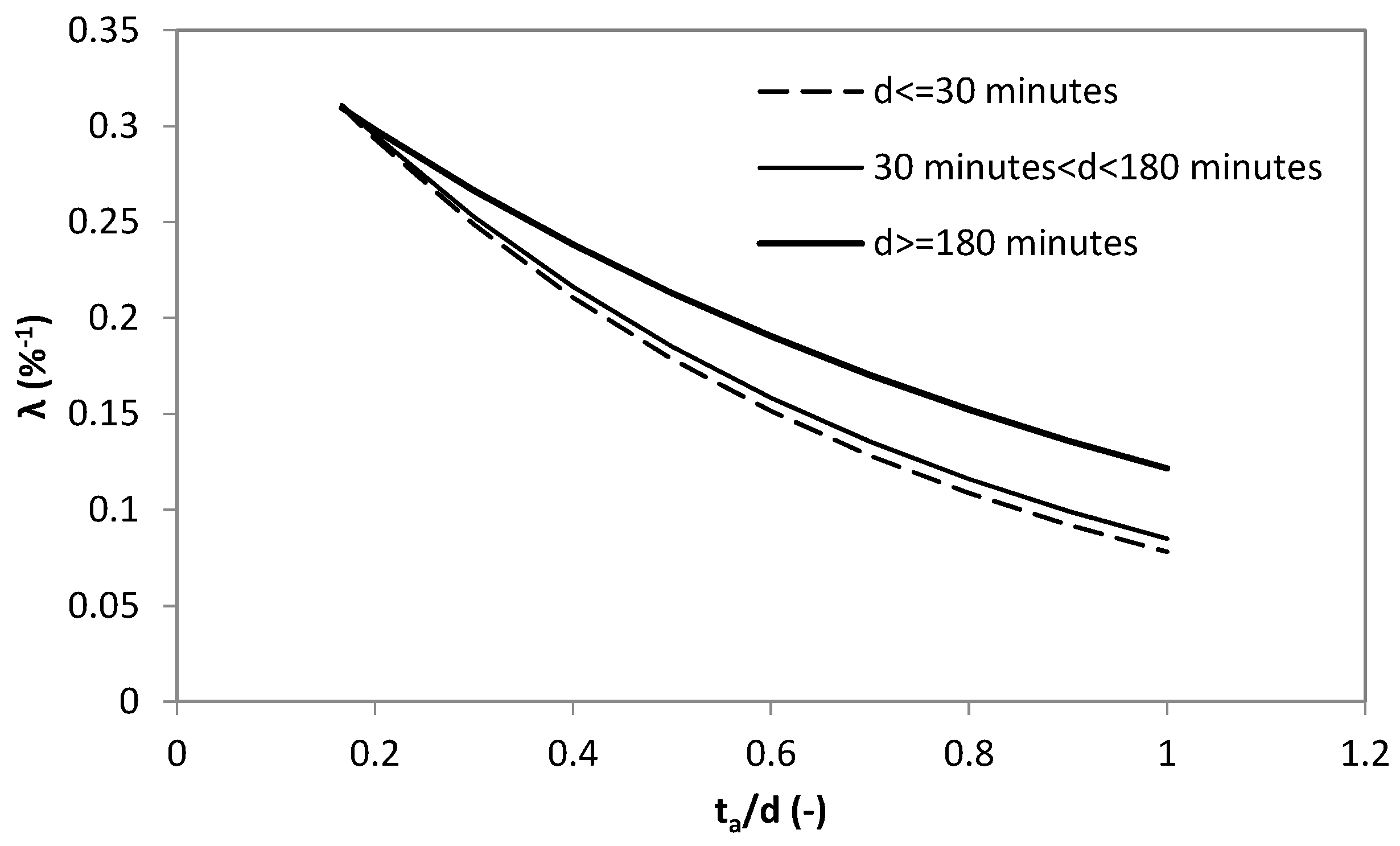
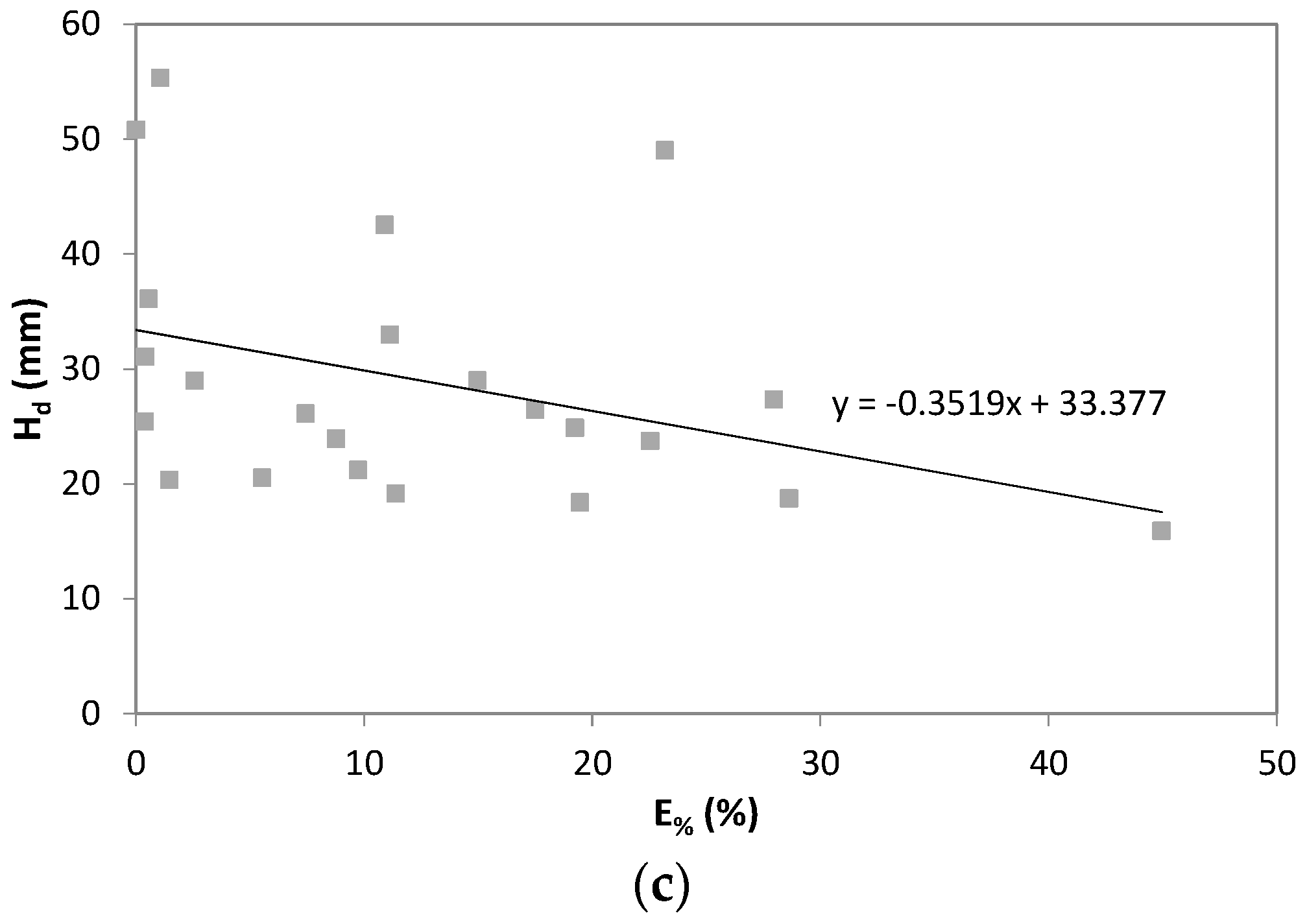
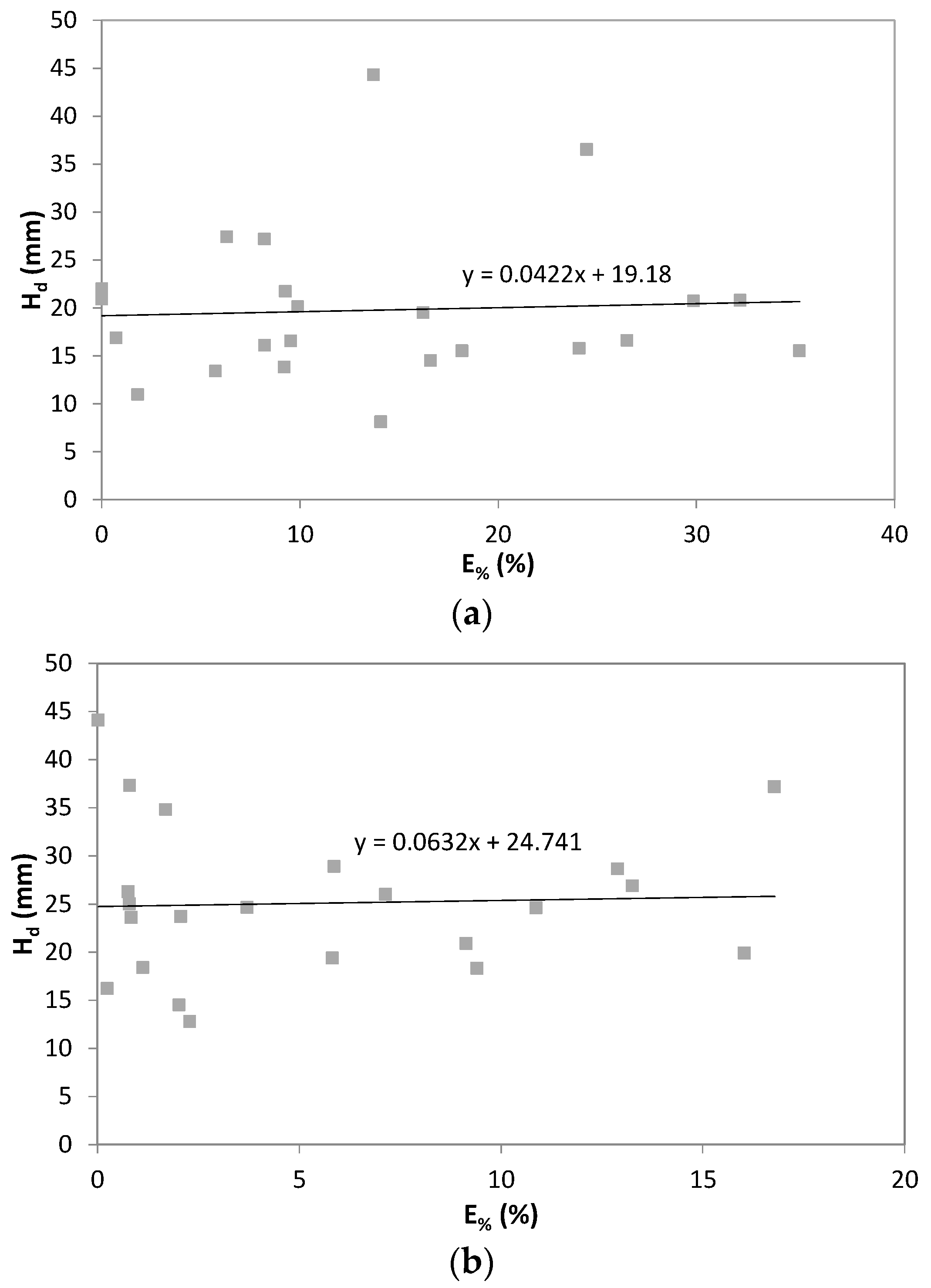
4.3. Correlation Hd-Error
4.4. Correction Procedure
- The λ parameter of the exponential distribution function (Equation (3) or Equation (4)) through the use of Equations (6)–(8) has to be quantified.
- A set of underestimation errors (i = 1, …, n), respecting the probability density function of point 1, has to be generated,
- Each generated value has to be combined with a specific uncorrected on the basis of the inverse correlation between these quantities.
- Each has to be corrected in accordance with the following equation.where and are the corrected and uncorrected values, respectively.
- In the case of the Montecarlo procedure, steps 2, 3, and 4 have to be repeated.
5. Conclusions
- -
- Annual maximum rainfall depth series derived from very old data inevitably involve many underestimated values due to the adoption of recording systems that only recently allow very small temporal aggregations.
- -
- The underestimated Hd values due to the coarse temporal aggregation of historical rainfall data may be minimized/eliminated through the use of deterministic or stochastic approaches.
- -
- In the deterministic approach, an average correction is identically applied to all Hd values characterized by the same ta and d.
- -
- In the stochastic approach, a more complex procedure can be adopted, which requires a thorough knowledge of the statistical characteristics of the underestimation error.
- -
- The single underestimation error follows an exponential distribution law characterized by a parameter linked to ta and d.
- -
- The average underestimation error follows a normal distribution law characterized by two parameters, which include the expected value and the standard deviation. This produces a reduced dispersion of the random variable in cases of greater practical interest.
- -
- The correlation between the single underestimation error and the corresponding maximum annual rainfall depth can be assumed inversely related with a probability of 78%.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Woolhiser, D.A.; Osborn, H.B. A stochastic model of dimensionless thunderstorm rainfall. Water Resour. Res. 1985, 21, 511–522. [Google Scholar] [CrossRef]
- Abdo, K.S.; Fiseha, B.M.; Rientjes, T.H.M.; Gieske, A.S.M.; Haile, A.T. Assessment of climate change impacts on the hydrology of Gilgel Abay catchment in Lake Tana basin, Ethiopia. Hydrol. Process. 2009, 23, 3661–3669. [Google Scholar] [CrossRef]
- Haile, A.T.; Rientjes, T.H.M.; Gieske, A.; Jetten, V.; Mekonnen, G. Satellite remote sensing and conceptual cloud modelling for convective rainfall simulation. Adv. Water Resour. 2011, 34, 26–37. [Google Scholar] [CrossRef]
- Zeng, N.; Shuttleworth, J.W.; Gash, J.H.C. Influence of temporal variability of rainfall on interception loss, Part I. Point analysis. J. Hydrol. 2000, 228, 228–241. [Google Scholar] [CrossRef]
- Melone, F.; Corradini, C.; Morbidelli, R.; Saltalippi, C.; Flammini, A. Comparison of theoretical and experimental soil moisture profiles under complex rainfall patterns. J. Hydrol. Eng. 2008, 13, 1170–1176. [Google Scholar] [CrossRef]
- Morbidelli, R.; Corradini, C.; Saltalippi, C.; Flammini, A.; Rossi, E. Infiltration-soil moisture redistribution under natural conditions: Experimental evidence as a guideline for realizing simulation models. Hydrol. Earth Syst. Sci. 2011, 15, 2937–2945. [Google Scholar] [CrossRef]
- Morbidelli, R.; Saltalippi, C.; Flammini, A.; Rossi, E.; Corradini, C. Soil water content vertical profiles under natural conditions: Matching of experiments and simulations by a conceptual model. Hydrol. Proc. 2014, 28, 4732–4742. [Google Scholar] [CrossRef]
- Milly, P.; Eagleson, P. Effect of storm scale on surface runoff volume. Water Resour. Res. 1988, 24, 620–624. [Google Scholar] [CrossRef]
- Govindaraju, R.S.; Morbidelli, R.; Corradini, C. Use of similarity profiles for computing surface runoff over small watersheds. J. Hydrol. Eng. 1999, 4, 100–107. [Google Scholar] [CrossRef]
- Zhang, G.P.; Fenicia, F.; Rientjes, T.H.M.; Reggiani, P.; Savenije, H.H.G. Modeling runoff generation in Geer river basin with improved model parameterization to the REW approach. Phys. Chem. Earth 2005, 30, 285–296. [Google Scholar] [CrossRef]
- Kusumastuti, D.I.; Struthers, I.; Sivapalan, M.; Reynolds, D.A. Threshold effects in catchment storm response and the occurrence and magnitude of flood events: Implications for flood frequency. Hydrol. Earth Syst. Sci. 2007, 11, 1515–1528. [Google Scholar] [CrossRef]
- De Vos, N.J.; Rientjes, T.H.M. Multi-objective training of artificial neural networks for rainfall-runoff modelling. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Morbidelli, R.; Saltalippi, C.; Flammini, A.; Corradini, C.; Brocca, L.; Govindaraju, R.S. An investigation of the effects of spatial heterogeneity of initial soil moisture content on surface runoff simulation at a small watershed scale. J. Hydrol. 2016, 539, 589–598. [Google Scholar] [CrossRef]
- Angel, J.R.; Palecki, M.A.; Hollinger, S.E. Storm precipitation in the United States, Part II: Soil erosion characteristics. J. Appl. Meteorol. 2005, 44, 947–959. [Google Scholar] [CrossRef]
- Camici, S.; Tarpanelli, A.; Brocca, L.; Melone, F.; Moramarco, T. Design soil moisture estimation by comparing continuous and storm-based rainfall-runoff modeling. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef] [Green Version]
- Faccini, F.; Paliaga, G.; Piana, P.; Sacchini, A.; Watkins, C. The Bisagno stream catchment (Genoa, Italy) and its major floods: Geomorphic and land use variations in the last three centuries. Geomorphology 2016, 273, 14–27. [Google Scholar] [CrossRef]
- Vormoor, K.; Lawrence, D.; Schlichting, L.; Wilson, D.; Wong, W.K. Evidence for changes in the magnitude and frequency of observed rainfall vs. snowmelt driven floods in Norway. J. Hydrol. 2016, 538, 33–48. [Google Scholar] [CrossRef]
- Masud, M.B.; Khaliq, M.N.; Wheater, H.S. Analysis of meteorological droughts for the Saskatchewan River Basin using univariate and bivariate approaches. J. Hydrol. 2015, 522, 452–466. [Google Scholar] [CrossRef]
- Mallya, G.; Mishra, V.; Niyogi, D.; Tripathi, S.; Govindaraju, R.S. Trends and variability of droughts over the Indian monsoon region. Weather Clim. Extr. 2016, 12, 43–68. [Google Scholar] [CrossRef]
- Haile, A.T.; Rientjes, T.H.M.; Habib, E.; Jetten, V.; Gebremichael, M. Rain event properties at the source of the Blue Nile River. Hydrol. Earth Syst. Sci. 2011, 15, 1023–1034. [Google Scholar] [CrossRef] [Green Version]
- Hershfield, D.M. Rainfall Frequency Atlas of the United States for Durations From 30 Minutes to 24 Hours and Return Periods from 1 to 100 Years; US Weather Bureau Technical Paper N. 40; U.S. Dept. of Commerce: Washington, DC, USA, 1961. Available online: https://www.lm.doe.gov/cercla/documents/fernald_docs/CAT/109669.pdf (accessed on 1 August 2018).
- Weiss, L.L. Ratio of true to fixed-interval maximum rainfall. J. Hydraul. Div. 1964, 90, 77–82. [Google Scholar]
- Young, C.B.; McEnroe, B.M. Sampling adjustment factors for rainfall recorded at fixed time intervals. J. Hydrol. Eng. 2003, 8, 294–296. [Google Scholar] [CrossRef]
- Yoo, C.; Jun, C.; Park, C. Effect of rainfall temporal distribution on the conversion factor to convert the fixed-interval into true-interval rainfall. J. Hydrol. Eng. 2015, 20. [Google Scholar] [CrossRef]
- Morbidelli, R.; Saltalippi, C.; Flammini, A.; Cifrodelli, M.; Picciafuoco, T.; Corradini, C.; Casas-Castillo, M.C.; Fowler, H.J.; Wilkinson, S.M. Effect of temporal aggregation on the estimate of annual maximum rainfall depths for the design of hydraulic infrastructure systems. J. Hydrol. 2017, 554, 710–720. [Google Scholar] [CrossRef]
- Miller, J.F.; Frederick, R.H.; Tracey, R.J. Precipitation-frequency atlas of the western United States. In NOAA Atlas 2; National Weather Service, National Oceanic and Atmospheric Administration, U.S. Dept. of Commerce: Washington, DC, USA, 1973. Available online: https://repository.library.noaa.gov/view/noaa/7303 (accessed on 1 August 2018).
- Frederick, R.H.; Myers, V.A.; Auciello, E.P. Five-to 60-min Precipitation Frequency for the Eastern and Central United States; NOAA Technical Memorandum NWS HYDRO-35; National Oceanic and Atmospheric Administration, National Weather Service: Silver Spring, MD, USA, 1977. Available online: https://repository.library.noaa.gov/view/noaa/6435 (accessed on 1 August 2018).
- Huff, F.A.; Angel, J.R. Rainfall Frequency Atlas of the Midwest. In Illinois State Water Survey Bulletin 71, Midwest Climate Center Research Rep. 92-03; Illinois State Water Survey: Champaign, IL, USA, 1992; Available online: https://www.ideals.illinois.edu/bitstream/handle/2142/94532/ISWSB-71.pdf?sequence=1 (accessed on 1 August 2018).
- Sivapalan, M.; Bloschl, G. Transformation of point rainfall to areal rainfall: Intensity-duration-frequency curves. J. Hydrol. 1998, 204, 150–167. [Google Scholar] [CrossRef]
- Willems, P. Compound intensity/duration/frequency-relationships of extreme precipitation for two seasons and two storm types. J. Hydrol. 2000, 233, 189–205. [Google Scholar] [CrossRef]
- Overeem, A.; Buishand, A.; Holleman, I. Rainfall depth-duration-frequency curves and their uncertainties. J. Hydrol. 2008, 348, 124–134. [Google Scholar] [CrossRef]
- De Michele, C.; Zenoni, E.; Pecora, S.; Rosso, R. Analytical derivation of rain intensity-duration-area-frequency relationships from event maxima. J. Hydrol. 2011, 399, 385–393. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Kozonis, D.; Manetas, A. A mathematical framework for studying rainfall intensity-duration-frequency relationships. J. Hydrol. 1998, 206, 118–135. [Google Scholar] [CrossRef]
- Morbidelli, R.; Saltalippi, C.; Flammini, A.; Corradini, C.; Wilkinson, S.M.; Fowler, H.J. Influence of temporal data aggregation on trend estimation for intense rainfall. Adv. Water Resour. 2018, in press. [Google Scholar]
- Burlando, P.; Rosso, R. Scaling and multiscaling models of depth-duration-frequency curves for storm precipitation. J. Hydrol. 1996, 187, 45–64. [Google Scholar] [CrossRef]
- Boni, G.; Parodi, A.; Rudari, R. Extreme rainfall events: Learning from raingauge time series. J. Hydrol. 2006, 327, 304–314. [Google Scholar] [CrossRef]
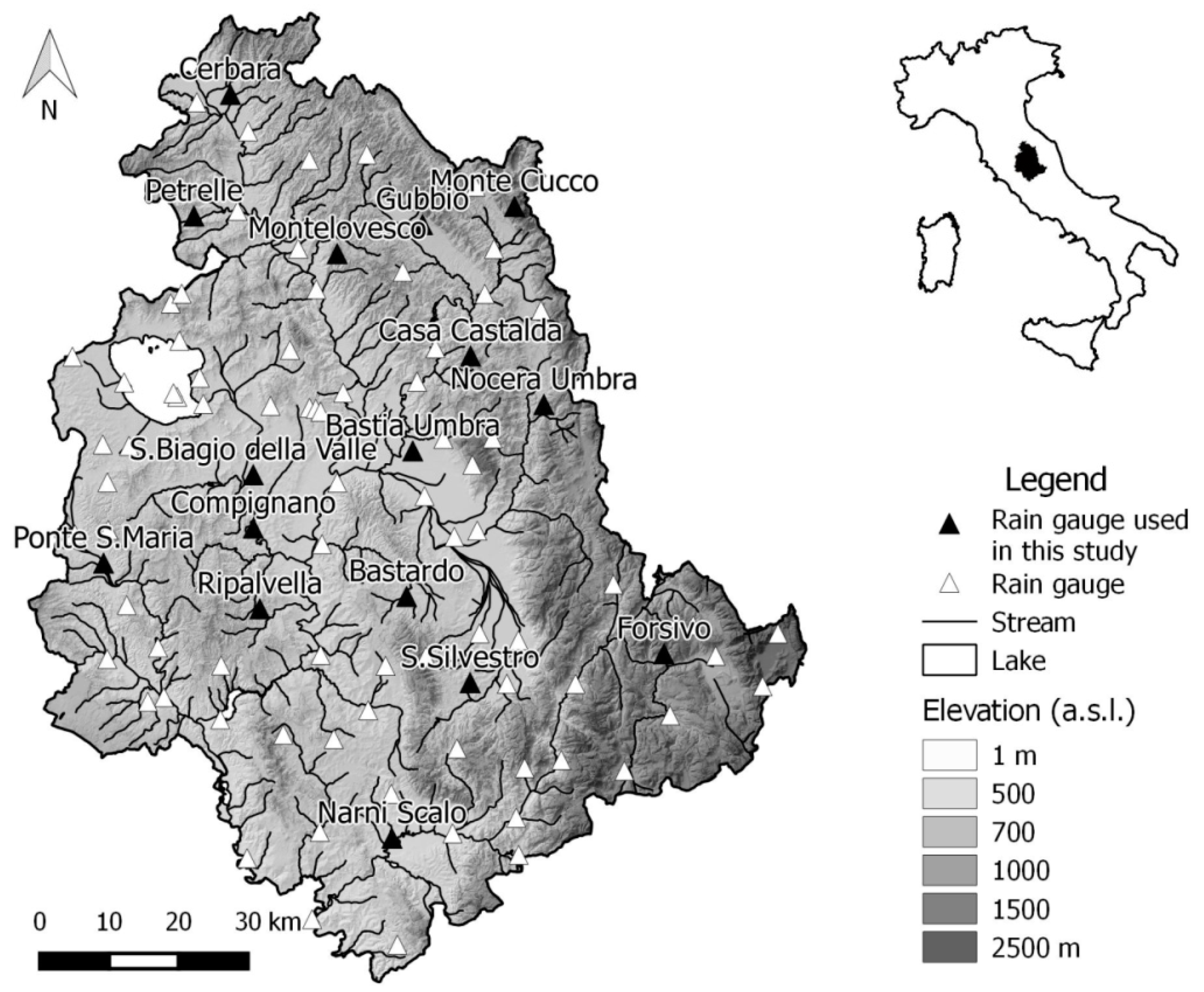

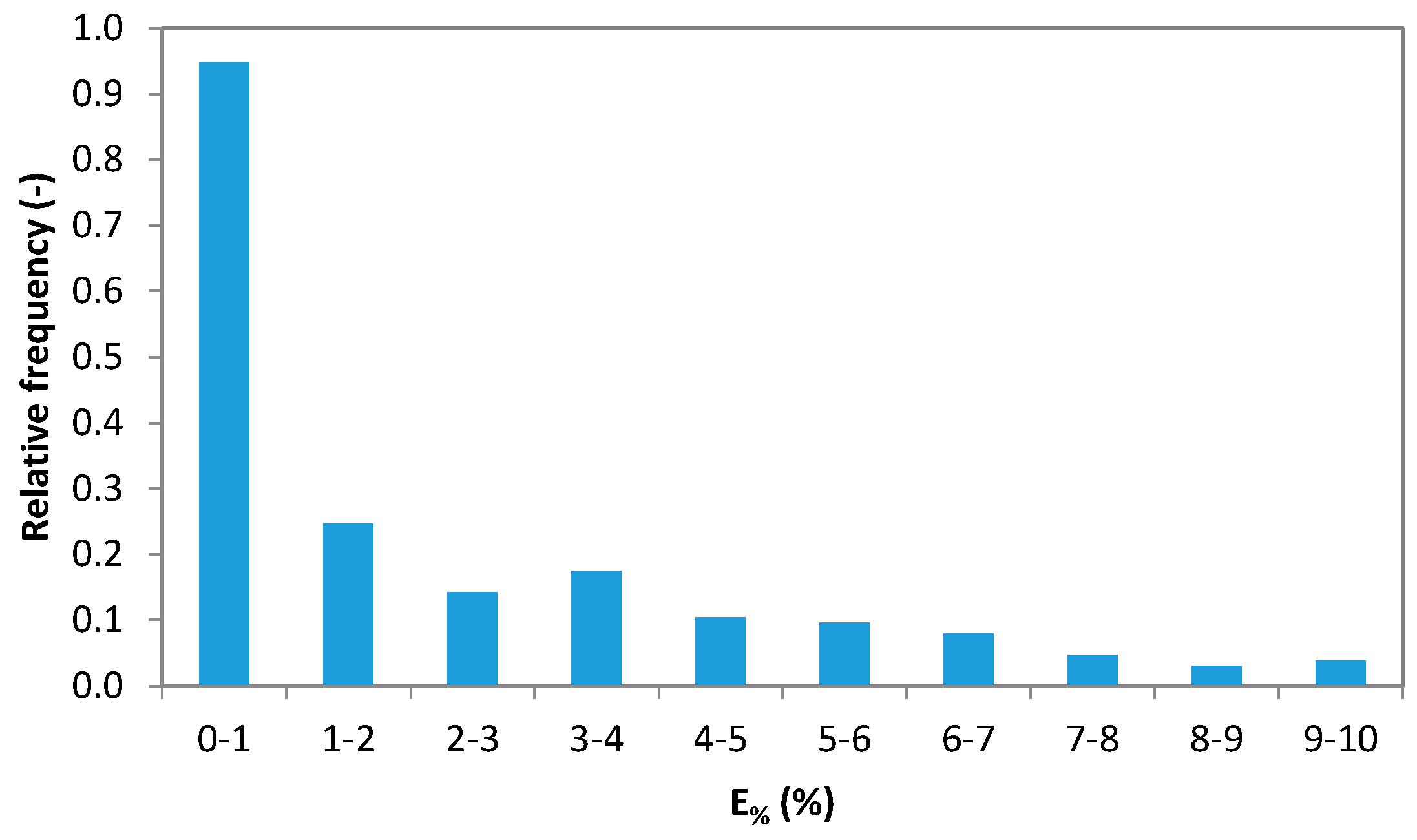

| Rain Gauge Station | Altitude (m a.s.l.) | Mean Annual Rainfall (mm) | UTM33 X (m) | UTM33 Y (m) |
|---|---|---|---|---|
| Bastardo | 331 | 803.8 | 300,489 | 4,748,742 |
| Bastia Umbra | 203 | 753.0 | 301,377 | 4,769,716 |
| Cerbara | 310 | 834.3 | 275,092 | 4,821,081 |
| Casa Castalda | 730 | 971.0 | 309,715 | 4,783,398 |
| Compignano | 240 | 756.8 | 278,394 | 4,758,593 |
| Forsivo | 963 | 867.0 | 337,588 | 4,740,488 |
| Gubbio | 471 | 946.5 | 302,789 | 4,802,329 |
| Monte Cucco | 1087 | 1344.4 | 316,046 | 4,804,934 |
| Montelovesco | 634 | 833.0 | 290,484 | 4,798,142 |
| Narni Scalo | 109 | 907.5 | 298,381 | 4,713,916 |
| Nocera Umbra | 534 | 937.6 | 320,281 | 4,776,405 |
| Petrelle | 342 | 897.7 | 269,830 | 4,803,553 |
| Ponte Santa Maria | 240 | 790.1 | 256,802 | 4,753,550 |
| Ripalvella | 453 | 879.1 | 279,329 | 4,746,964 |
| San Biagio della Valle | 257 | 707.2 | 278,380 | 4,766,281 |
| San Silvestro | 381 | 897.9 | 309,649 | 4,736,325 |
| “Observed” Rainfall Depth (mm) | “Generated” Rainfall Depth (mm) | |||||
|---|---|---|---|---|---|---|
| ta | ||||||
| 1 min | 10 min | 15 min | 30 min | 60 min | 180 min | 360 min |
| 0.2 | 1.6 | 1.8 | 2.2 | 2.6 | 7.0 | 8.0 |
| 0.2 | 0.2 | 0.4 | 0.4 | 3.2 | 1.0 | 0.0 |
| 0.0 | 0.4 | 0.0 | 1.2 | 1.2 | 0.0 | 0.0 |
| 0.2 | 0.0 | 0.4 | 2.0 | 0.8 | 0.0 | 0.0 |
| 0.2 | 0.0 | 0.0 | 1.2 | 0.2 | 0.0 | 0.0 |
| 0.4 | 0.0 | 1.2 | 0.0 | 0.0 | 0.0 | 0.0 |
| 0.0 | 0.2 | 0.6 | 0.8 | 0.0 | 0.0 | 0.0 |
| 0.2 | 1.0 | 1.4 | 0.0 | 0.0 | 0.0 | 0.0 |
| 0.2 | 0.2 | 1.2 | 0.0 | 0.0 | 0.0 | 0.0 |
| 0.0 | 0.6 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 0.2 | 1.2 | 0.0 | 0.2 | 0.0 | 0.0 | 0.0 |
| 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 0.0 | 0.2 | 0.4 | 0.0 | 0.0 | 0.0 | 0.0 |
| 0.0 | 0.0 | 0.4 | 0.0 | 0.0 | 0.0 | 0.0 |
| 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 0.0 | 0.2 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 0.0 | 0.2 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 0.0 … | 0.4 … | 0.0 … | 0.0 … | 0.0 … | 0.0 … | 0.0 … |
| d | ||||||
|---|---|---|---|---|---|---|
| Year | 30 min | 60 min | 180 min | 360 min | 720 min | 1440 min |
| 1992 | 31.39 | 3.99 | 0.02 | 1.76 | 0.01 | 0.03 |
| 1993 | 29.73 | 13.97 | 0.46 | 2.68 | 0.93 | 0.03 |
| 1994 | 5.10 | 1.67 | 0.00 | 0.02 | 0.00 | 0.12 |
| 1995 | 4.59 | 12.36 | 1.40 | 0.01 | 0.00 | 0.00 |
| 1996 | 8.46 | 0.61 | 0.00 | 0.81 | 0.00 | 0.05 |
| 1997 | 4.36 | 7.86 | 0.00 | 0.00 | 0.00 | 1.37 |
| 1998 | 4.44 | 0.00 | 2.84 | 0.60 | 1.06 | 0.02 |
| 1999 | 0.69 | 3.12 | 0.39 | 0.15 | 0.43 | 0.06 |
| 2000 | 22.12 | 4.10 | 0.00 | 1.29 | 0.24 | 0.00 |
| 2001 | 3.60 | 1.29 | 0.12 | 0.38 | 0.31 | 0.00 |
| 2002 | 11.33 | 2.25 | 0.04 | 0.00 | 0.00 | 0.00 |
| 2003 | 0.18 | 0.06 | 0.00 | 0.06 | 0.03 | 0.46 |
| 2004 | 24.48 | 7.43 | 0.23 | 0.32 | 0.03 | 2.69 |
| 2005 | 0.16 | 0.23 | 0.00 | 0.16 | 0.43 | 0.14 |
| 2006 | 31.65 | 0.34 | 0.28 | 0.00 | 0.59 | 0.61 |
| 2007 | 10.94 | 10.06 | 0.83 | 0.06 | 0.00 | 0.00 |
| 2008 | 1.22 | 5.13 | 0.74 | 0.00 | 0.02 | 0.06 |
| 2009 | 0.01 | 0.01 | 0.72 | 0.00 | 0.02 | 0.00 |
| 2010 | 48.74 | 2.89 | 0.00 | 0.21 | 0.11 | 0.19 |
| 2011 | 0.18 | 0.22 | 0.02 | 0.12 | 0.00 | 0.02 |
| 2012 | 5.51 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 2013 | 34.94 | 3.96 | 0.00 | 0.76 | 0.46 | 0.00 |
| 2014 | 4.21 | 0.00 | 0.52 | 0.00 | 0.00 | 0.00 |
| 2015 | 17.39 | 0.32 | 0.55 | 0.80 | 0.29 | 0.00 |
| Ea% | 12.73 | 3.41 | 0.38 | 0.42 | 0.21 | 0.24 |
| d | ||||||
|---|---|---|---|---|---|---|
| Year | 30 min | 60 min | 180 min | 360 min | 720 min | 1440 min |
| 1992 | 1.09 | 1.31 | 0.02 | 1.52 | 0.01 | 0.03 |
| 1993 | 0.77 | 0.37 | 0.46 | 1.61 | 0.43 | 0.01 |
| 1994 | 5.10 | 1.67 | 0.00 | 0.02 | 0.00 | 0.00 |
| 1995 | 4.59 | 5.02 | 0.09 | 0.01 | 0.00 | 0.00 |
| 1996 | 8.46 | 0.61 | 0.00 | 0.06 | 0.00 | 0.01 |
| 1997 | 4.36 | 2.43 | 0.00 | 0.00 | 0.00 | 1.18 |
| 1998 | 1.39 | 0.00 | 0.52 | 0.60 | 0.50 | 0.02 |
| 1999 | 0.69 | 2.27 | 0.39 | 0.15 | 0.11 | 0.06 |
| 2000 | 0.46 | 0.82 | 0.00 | 0.16 | 0.08 | 0.00 |
| 2001 | 3.60 | 0.72 | 0.12 | 0.12 | 0.06 | 0.00 |
| 2002 | 11.33 | 2.25 | 0.02 | 0.00 | 0.00 | 0.00 |
| 2003 | 0.18 | 0.06 | 0.00 | 0.03 | 0.03 | 0.46 |
| 2004 | 0.00 | 3.73 | 0.00 | 0.32 | 0.03 | 0.18 |
| 2005 | 0.16 | 0.23 | 0.00 | 0.16 | 0.09 | 0.14 |
| 2006 | 0.00 | 0.34 | 0.28 | 0.00 | 0.59 | 0.61 |
| 2007 | 10.94 | 4.10 | 0.09 | 0.03 | 0.00 | 0.00 |
| 2008 | 1.22 | 4.34 | 0.21 | 0.00 | 0.02 | 0.06 |
| 2009 | 0.00 | 0.00 | 0.00 | 0.00 | 0.02 | 0.00 |
| 2010 | 1.85 | 1.58 | 0.00 | 0.21 | 0.11 | 0.04 |
| 2011 | 0.18 | 0.13 | 0.02 | 0.05 | 0.00 | 0.02 |
| 2012 | 5.51 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 2013 | 21.08 | 3.96 | 0.00 | 0.25 | 0.15 | 0.00 |
| 2014 | 4.21 | 0.00 | 0.52 | 0.00 | 0.00 | 0.00 |
| 2015 | 6.35 | 0.32 | 0.55 | 0.40 | 0.29 | 0.00 |
| Ea% | 3.90 | 1.51 | 0.14 | 0.24 | 0.10 | 0.12 |
| ta/d (-) | μ (%) | σ (%) | cv (-) |
|---|---|---|---|
| 1.000 | 11.88 | 2.29 | 0.20 |
| 0.500 | 4.73 | 1.12 | 0.24 |
| 0.333 | 2.68 | 0.55 | 0.21 |
| 0.250 | 1.67 | 0.57 | 0.34 |
| 0.166 | 1.18 | 0.49 | 0.42 |
| 0.083 | 0.52 | 0.24 | 0.45 |
| 0.055 | 0.35 | 0.24 | 0.69 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morbidelli, R.; Saltalippi, C.; Flammini, A.; Picciafuoco, T.; Dari, J.; Corradini, C. Characteristics of the Underestimation Error of Annual Maximum Rainfall Depth Due to Coarse Temporal Aggregation. Atmosphere 2018, 9, 303. https://doi.org/10.3390/atmos9080303
Morbidelli R, Saltalippi C, Flammini A, Picciafuoco T, Dari J, Corradini C. Characteristics of the Underestimation Error of Annual Maximum Rainfall Depth Due to Coarse Temporal Aggregation. Atmosphere. 2018; 9(8):303. https://doi.org/10.3390/atmos9080303
Chicago/Turabian StyleMorbidelli, Renato, Carla Saltalippi, Alessia Flammini, Tommaso Picciafuoco, Jacopo Dari, and Corrado Corradini. 2018. "Characteristics of the Underestimation Error of Annual Maximum Rainfall Depth Due to Coarse Temporal Aggregation" Atmosphere 9, no. 8: 303. https://doi.org/10.3390/atmos9080303
APA StyleMorbidelli, R., Saltalippi, C., Flammini, A., Picciafuoco, T., Dari, J., & Corradini, C. (2018). Characteristics of the Underestimation Error of Annual Maximum Rainfall Depth Due to Coarse Temporal Aggregation. Atmosphere, 9(8), 303. https://doi.org/10.3390/atmos9080303









