Long-Term Rainfall Trends over the Tanzania Coast
Abstract
:1. Introduction
2. Data and Methods
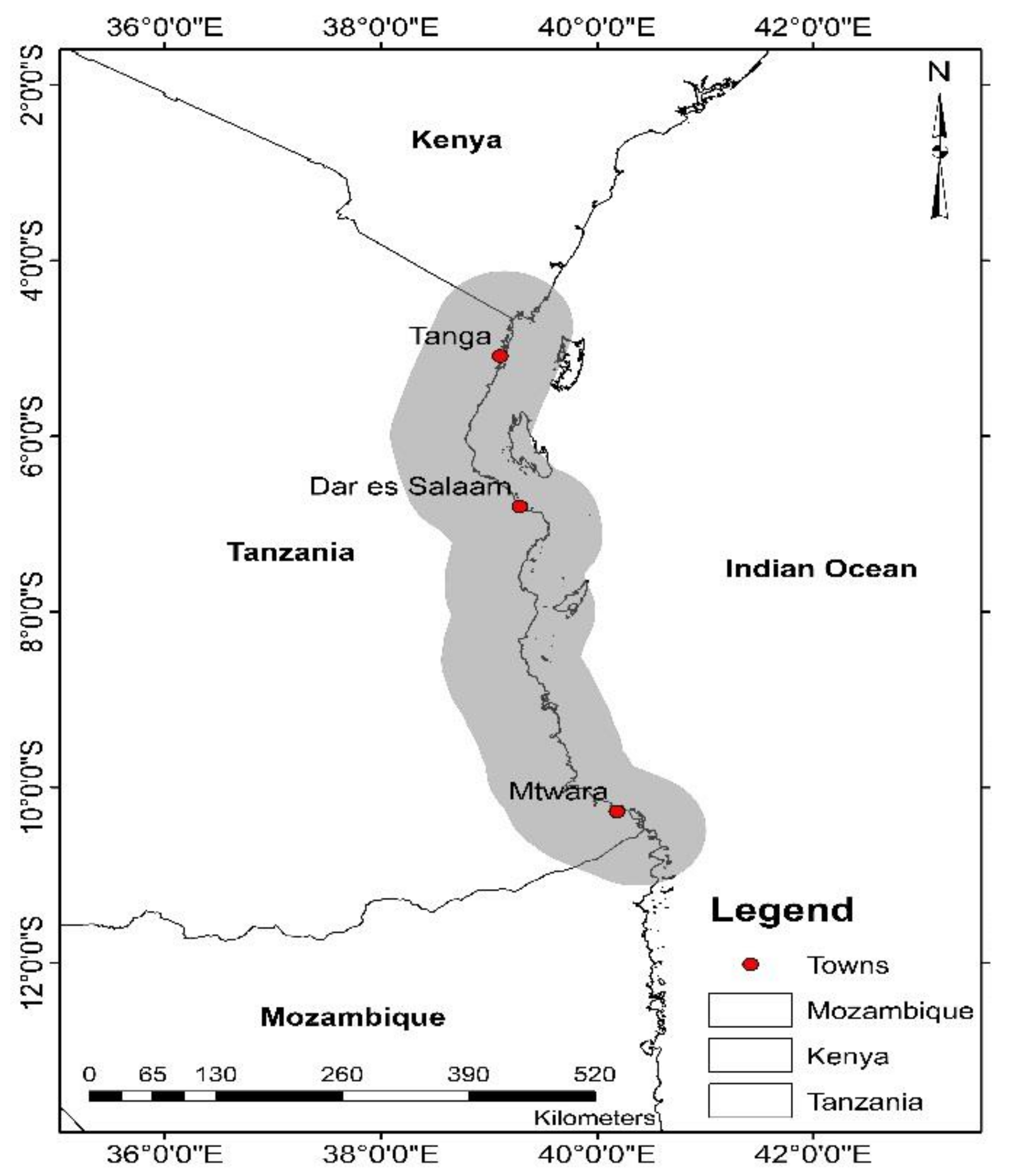
2.1. Description of the Study Area
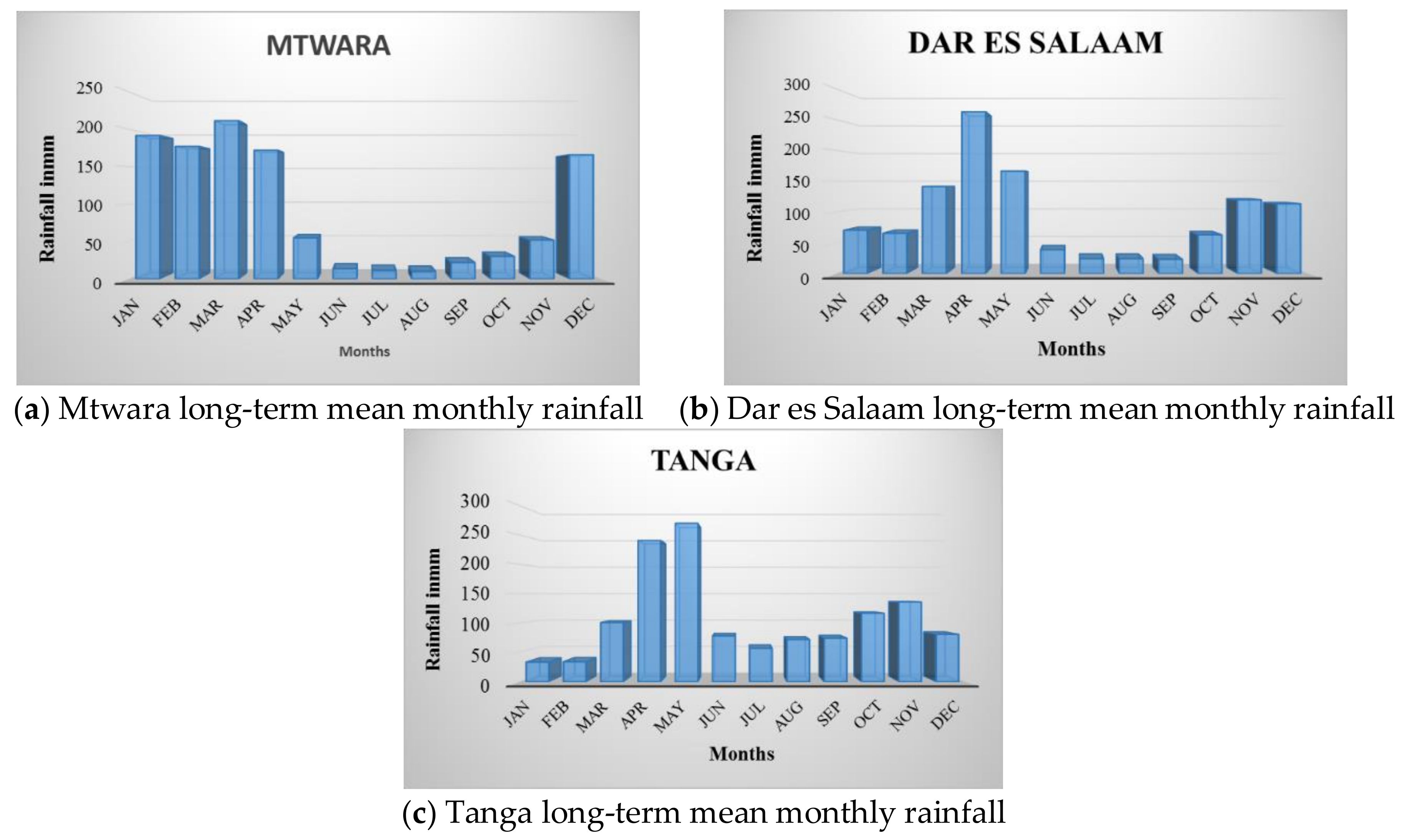
2.2. Rainfall Data
2.3. Reanalysis Products
2.4. Techniques for Trend Detection
2.4.1. The Mann-Kendall Test
2.4.2. The Sen’s Estimator of Slope
3. Results
3.1. Moving Average Rainfall
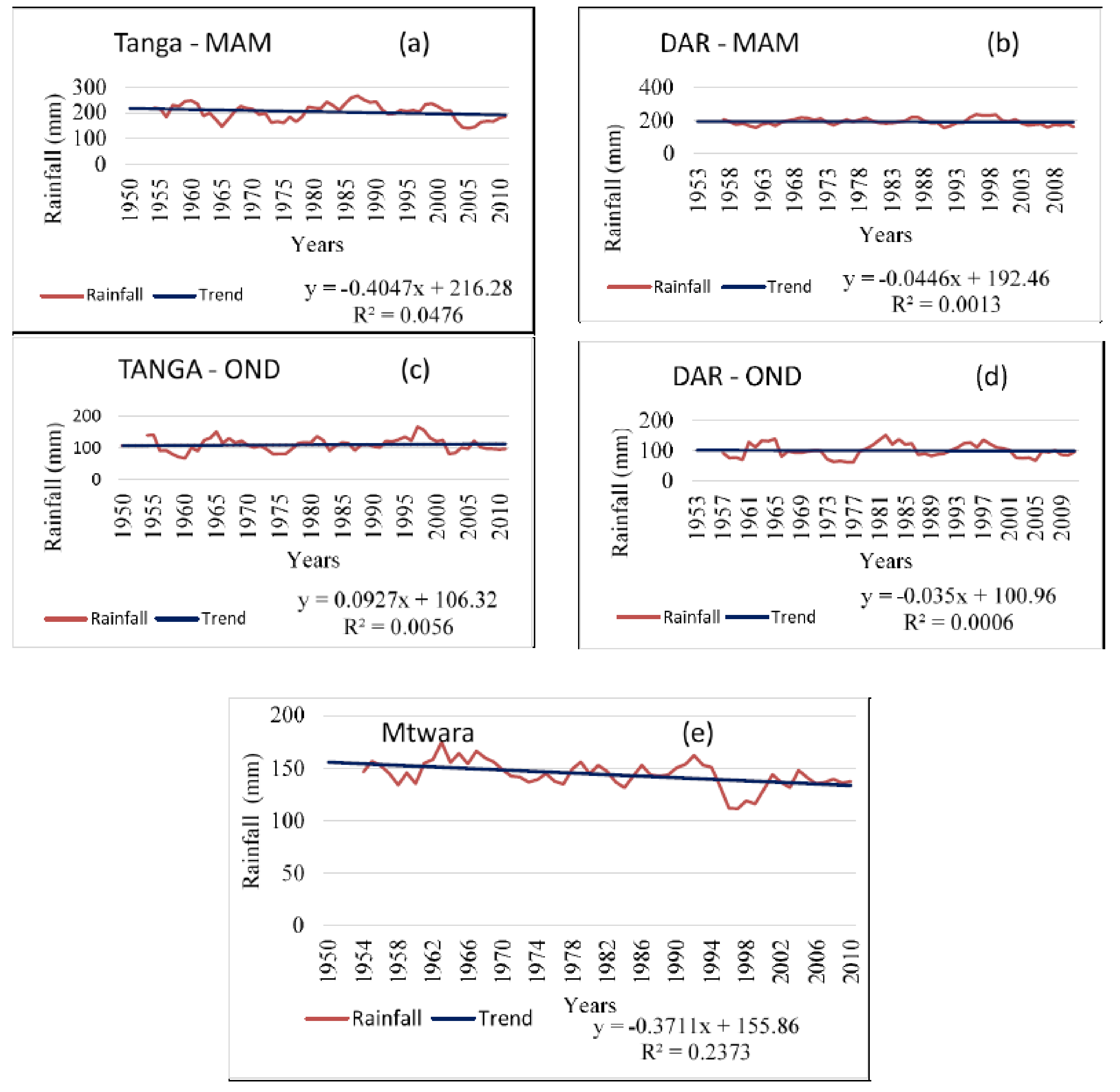
3.2. Monthly Rainfall Trends
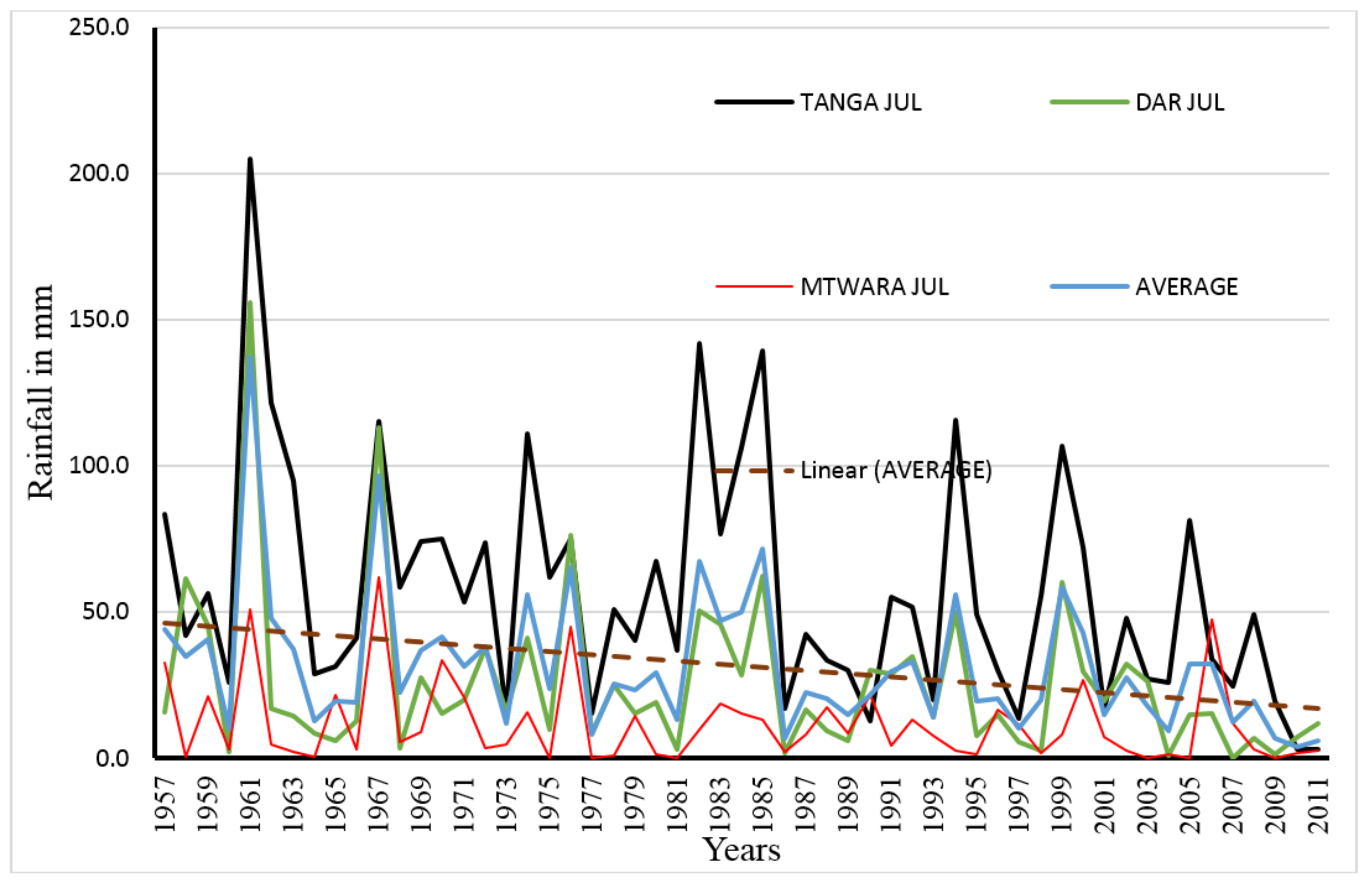
3.3. July Rainfall Pattern
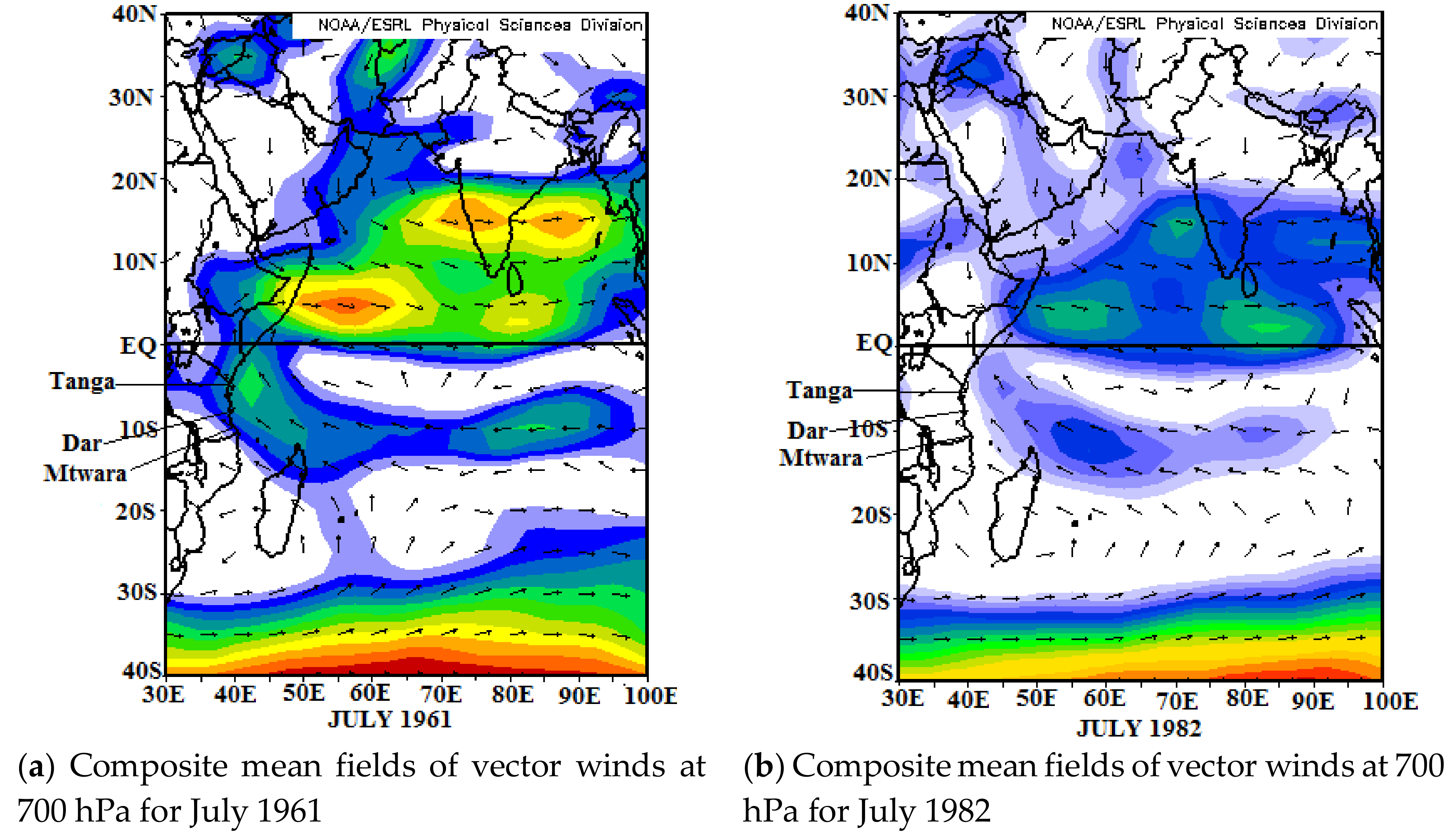
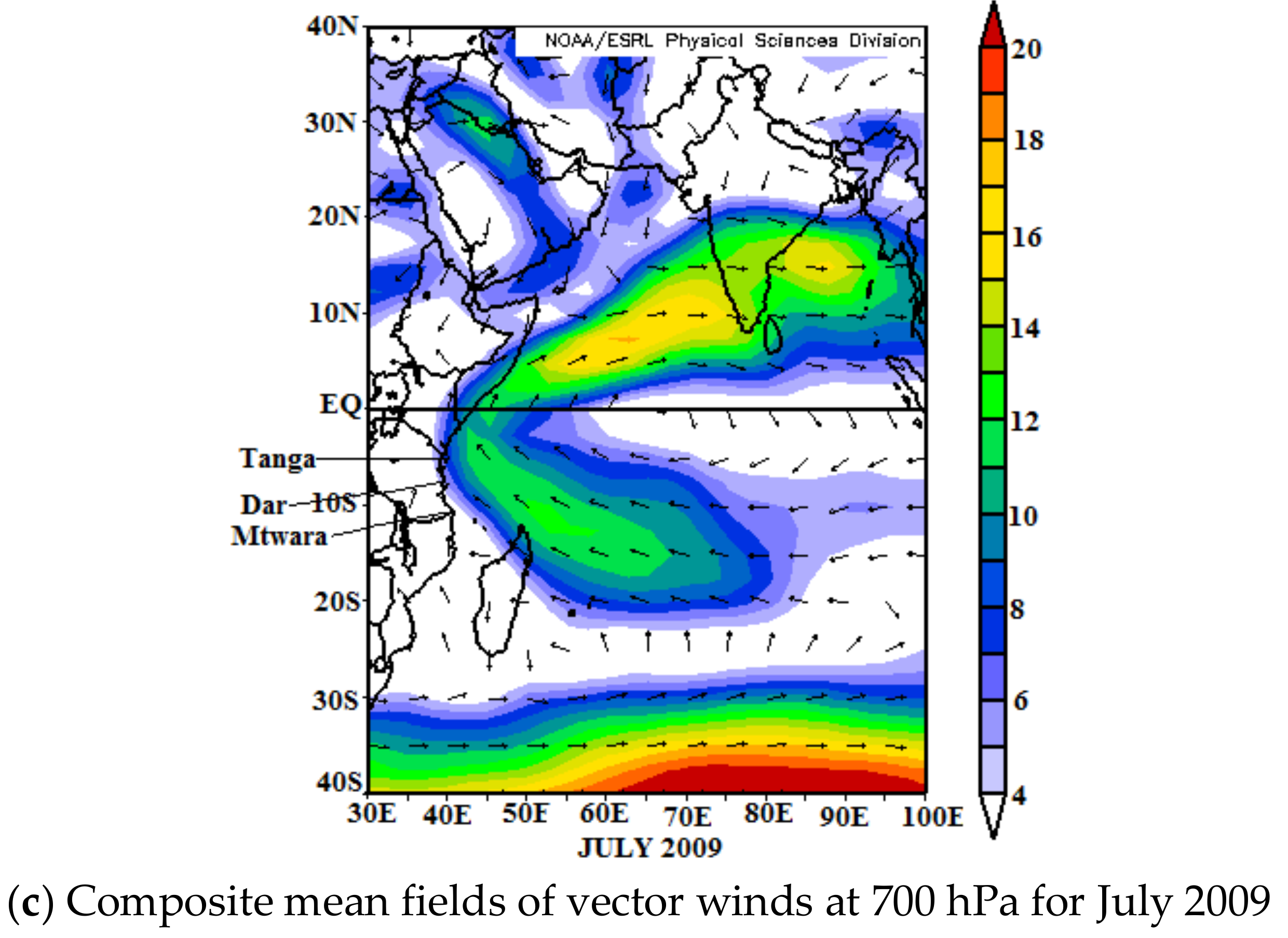
3.4. Relations between Vector Wind and July Rainfall
4. Discussion and Summary
Conflicts of Interest
References
- Moyo, M.; Simson, R.; Jacob, A.; de Mevius, F. Attaining Middle Income Statu—Tanzania Growth and structural transformation required to reach middle income status by 2025. In Proceedings of the Dar es Salaam, International Growth Centre, Tanzania, 31 March 2012. [Google Scholar]
- Kabanda, T.A.; Jury, M.R. Inter-annual variability of short rains over northern Tanzania. Clim. Res. 1999, 13, 231–241. [Google Scholar] [CrossRef]
- Mitchell, D. Tanzania’s Cashew Sector: Constraints and Challenges in a Global Environment (English); Africa Region Working Paper Series No. 70; World Bank: Washington, DC, USA, 2004. [Google Scholar]
- Zorita, E.; Tilya, F.F. Rainfall variability in northern Tanzania in the March–May season (long rains) and its links to large-scale climate forcing. Clim. Res. 2002, 20, 31–40. [Google Scholar] [CrossRef]
- Kabanda, T.A.; Jury, M.R. Synoptic evolution of composite wet spells over northern Tanzania. Clim. Res. 2000, 15, 239–248. [Google Scholar] [CrossRef]
- Kijazi, A.L.; Reason, C.J.C. Relationships between intraseasonal rainfall variability of coastal Tanzania and ENSO. Theor. Appl. Climatol. 2005, 82, 153–176. [Google Scholar] [CrossRef]
- Mapande, A.T.; Reason, C. Interannual rainfall variability over western Tanzania. Int. J. Climatol. 2005, 25, 1355–1368. [Google Scholar] [CrossRef]
- Zarenistanak, M.; Dhorde, A.G.; Kripalani, R.H. Trend analysis and change point detection of annual and seasonal precipitation and temperature series over southwest Iran. J. Earth Syst. Sci. 2014, 123, 281–295. [Google Scholar] [CrossRef]
- Longobardi, A.; Villani, P. Trend analysis of annual and seasonal rainfall time series in the Mediterranean area. Int. J. Climatol. 2010, 30, 1538–1546. [Google Scholar] [CrossRef]
- Haigh, M.J. Sustainable management of headwater resources: The Nairobi headwater declaration (2002) and beyond. Asian J. Water Environ. Pollut. 2004, 1, 17–28. [Google Scholar]
- Mosmann, V.; Castro, A.; Fraile, R.; Dessens, J.; Sanches, J.L. Detection of statistically significant trends in the summer precipitation of mainland Spain. Atmos. Res. 2004, 70, 43–53. [Google Scholar] [CrossRef]
- Partal, T.; Kahya, E. Trend analysis in Turkish precipitation data. Hydrol. Process. 2006, 20, 2011–2026. [Google Scholar] [CrossRef]
- Smadi, M.M.; Zghoul, A. A sudden change in rainfall characteristics in Amman, Jordan during the Mid 1950’s. Am. J. Environ. Sci. 2006, 2, 84–91. [Google Scholar] [CrossRef]
- Modarres, R.; da Silva, V. Rainfall trends in arid and semi-arid regions of Iran. J. Arid Environ. 2007, 70, 344–355. [Google Scholar] [CrossRef]
- Raziei, T. Investigation of annual precipitation trends in homogeneous precipitation subdivisions of Western Iran. In Proceedings of the BALWOIS 2008, Ohrid, Macedonia, 27–31 May 2008. [Google Scholar]
- Karpouzos, D.K.; Kavalieratou, S.; Babajimopoulos, C. Trend analysis of precipitation data in Pieria Region (Greece). Eur. Water 2010, 30, 31–40. [Google Scholar]
- Nenwiini, S.C.; Kabanda, T.A. Trends and variability assessment of rainfall in Vhembe South Africa. J. Hum. Ecol. 2013, 42, 171–176. [Google Scholar] [CrossRef]
- Nyenzi, B.S.; Kavishe, M.; Tibaijuka, P.F.; Kuluretera, V.; Nassib, I.R.; Tilya, F.F. A Study on Long Range Weather Forecasting in Tanzania; Research Report No. 1/97; Directorate of Meteorology Tanzania: Dodoma, Tanzania, 1997. [Google Scholar]
- Gamoyo, M.; Reason, C.; Obura, D. Rainfall variability over the East African coast. Theor. Appl. Climatol. 2015, 120, 311–322. [Google Scholar] [CrossRef]
- Sumner, G.N. The use of correlation linkages in the assessment of daily rainfall patterns. J. Hydrol. 1983, 66, 169–181. [Google Scholar] [CrossRef]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-year Reanalysis Project. Bull. Am. Meteor. Soc. 1996, 77, 437–471. [Google Scholar] [CrossRef]
- Smith, L. Trends in Russian Arctic river-ice formation and breakup. Phys. Geogr. 2000, 20, 46–56. [Google Scholar]
- Hirsch, R.M.; Alexander, R.B.; Smith, R.A. Selection of methods for the detection and estimation of trends in water quality. Water Resour. Res. 1991, 27, 803–813. [Google Scholar] [CrossRef]
- Burn, D.H.; Hag Elnur, M.A. Detection of hydrologic trends and variability. J. Hydrol. 2002, 255, 107–122. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Salmi, T.; Maatta, A.; Anttila, P.; Ruoho-Airola, T.; Amnell, T. Detecting Trends of Annual Values of Atmospheric Pollutants by the Mann–Kendall Test and Sen’s Slope Estimates-the Excel Template Application Makesens. In Air Quality No. 31; Finnish Meteorological Institute: Helsinki, Finland, 2002. [Google Scholar]
- Refat Nasher, N.M.; Uddin, M.N. Maximum and minimum temperature trends variation over northern and southern part of Bangladesh. J. Environ. Sci. Nat. Res. 2013, 6, 83–88. [Google Scholar]
- Sirois, A. A Brief and Biased Overview of Time Series Analysis or How to Find that Evasive Trend. In WMO Report No. 133: WMO/EMEP Workshop on Advanced Statistical Methods and Their Application to Air Quality Data Sets, Helsinki, Finland, 14–18 September 1998; WMO: Geneva, Switzerland, 1998. [Google Scholar]
- Martin, P.J.; Topper, C.P.; Bashiru, R.A.; Boma, F.; de Waal, D.; Harries, H.C.; Kasuga, L.J.; Katanila, N.; Kikoka, L.P.; Lamboll, R.; et al. Cashew nut production in Tanzania: Constraints and progress through integrated crop management. Crop Prot. 1997, 16, 5–14. [Google Scholar] [CrossRef]
- Makarau, A. Intra-Seasonal Oscillatory Modes of the Southern Africa Summer Circulation. Ph.D. Thesis, University of Cape Town, Kapstadt, South Africa, 1995. [Google Scholar]
- D’Abreton, P.C.; Tyson, P.O. Three-dimensional kinematic modelling of water vapour transport over southern Africa. Water SA 1996, 22, 297–306. [Google Scholar]
- Hewitson, B.C.; Tennant, W.; Walawege, R. Atmospheric Moisture Transport and Sources for Southern Africa; WRC Report No. 1012/1/04; Water Research Commission: Pretoria, South Africa, 2004. [Google Scholar]
- Kiangi, P.M.R. The Weather systems affecting eastern-southern Africa. In Seminar on Tropical Meteorology; WMO/TD-No. 277; WMO: Geneva, Switzerland, 1989. [Google Scholar]
| Time Series | First Year | Last Year | n | Test Z | Signific. | Q (mm/Year) |
|---|---|---|---|---|---|---|
| January | 1954 | 2011 | 58 | −3.21 | ** | −1.290 |
| February | 1954 | 2011 | 58 | −2.19 | * | −0.838 |
| March | 1954 | 2011 | 58 | 2.83 | ** | 0.955 |
| April | 1954 | 2011 | 58 | −3.21 | ** | −0.901 |
| May | 1954 | 2011 | 58 | 1.42 | 0.186 | |
| June | 1954 | 2011 | 58 | −0.59 | −0.024 | |
| July | 1954 | 2011 | 58 | −3.81 | *** | −0.142 |
| August | 1954 | 2011 | 58 | 1.62 | 0.061 | |
| September | 1954 | 2011 | 58 | −2.15 | * | −0.198 |
| October | 1954 | 2011 | 58 | 1.33 | 0.221 | |
| November | 1954 | 2011 | 58 | 1.74 | + | 0.370 |
| December | 1954 | 2011 | 58 | −2.58 | * | −1.096 |
| Time Series | First Year | Last Year | n | Test Z | Signific. | Q (mm/Year) |
|---|---|---|---|---|---|---|
| January | 1957 | 2011 | 55 | −2.70 | ** | −0.586 |
| February | 1957 | 2011 | 55 | −1.18 | −0.315 | |
| March | 1957 | 2011 | 55 | 1.36 | 0.410 | |
| April | 1957 | 2011 | 55 | −1.89 | + | −0.606 |
| May | 1957 | 2011 | 55 | 0.12 | 0.074 | |
| June | 1957 | 2011 | 55 | 1.95 | + | 0.263 |
| July | 1957 | 2011 | 55 | −4.75 | *** | −0.419 |
| August | 1957 | 2011 | 55 | −2.17 | * | −0.169 |
| September | 1957 | 2011 | 55 | −2.12 | * | −0.181 |
| October | 1957 | 2011 | 55 | 0.81 | 0.177 | |
| November | 1957 | 2011 | 55 | −1.10 | −0.428 | |
| December | 1957 | 2011 | 55 | −0.19 | −0.066 |
| Time Series | First Year | Last Year | n | Test Z | Signific. | Q (mm/Year) |
|---|---|---|---|---|---|---|
| January | 1954 | 2011 | 58 | 1.56 | 0.180 | |
| February | 1954 | 2011 | 58 | 0.42 | 0.049 | |
| March | 1954 | 2011 | 58 | −1.66 | + | −0.443 |
| April | 1954 | 2011 | 58 | −0.80 | −0.326 | |
| May | 1954 | 2011 | 58 | −1.95 | + | −0.962 |
| June | 1954 | 2011 | 58 | 1.19 | 0.211 | |
| July | 1954 | 2011 | 58 | −3.51 | *** | −0.518 |
| August | 1954 | 2011 | 58 | −0.98 | −0.120 | |
| September | 1954 | 2011 | 58 | −4.96 | *** | −0.956 |
| October | 1954 | 2011 | 58 | 1.10 | 0.330 | |
| November | 1954 | 2011 | 58 | −1.23 | −0.402 | |
| December | 1954 | 2011 | 58 | 0.71 | 0.155 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kabanda, T. Long-Term Rainfall Trends over the Tanzania Coast. Atmosphere 2018, 9, 155. https://doi.org/10.3390/atmos9040155
Kabanda T. Long-Term Rainfall Trends over the Tanzania Coast. Atmosphere. 2018; 9(4):155. https://doi.org/10.3390/atmos9040155
Chicago/Turabian StyleKabanda, Tibangayuka. 2018. "Long-Term Rainfall Trends over the Tanzania Coast" Atmosphere 9, no. 4: 155. https://doi.org/10.3390/atmos9040155
APA StyleKabanda, T. (2018). Long-Term Rainfall Trends over the Tanzania Coast. Atmosphere, 9(4), 155. https://doi.org/10.3390/atmos9040155





