Influence of Common Assumptions Regarding Aerosol Composition and Mixing State on Predicted CCN Concentration
Abstract
1. Introduction
2. Experiments
2.1. Site Description and Measurements
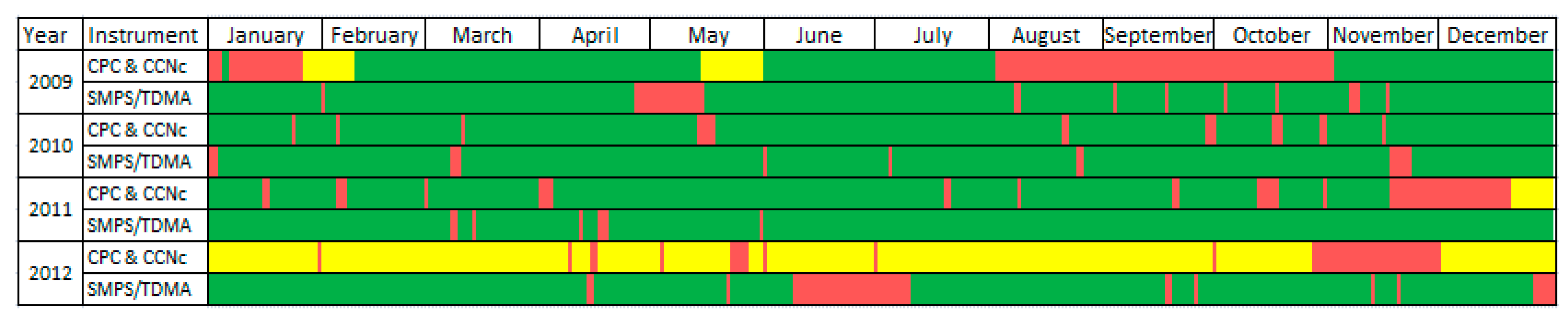
2.2. Screening and Time Interval Selection
- The total particle concentration (NCN) calculated by integrating the SMPS size distribution differed significantly from that directly measured with the CPC
- The NCCN measured with the CCNc exceeded the NCN measured by the CPC, possibly due to malfunction of the CCNc
- The sample flow entering the upstream (1st) DMA had an RH > 30%, or
- The sample flow entering the downstream (2nd) DMA had an RH < 85%.
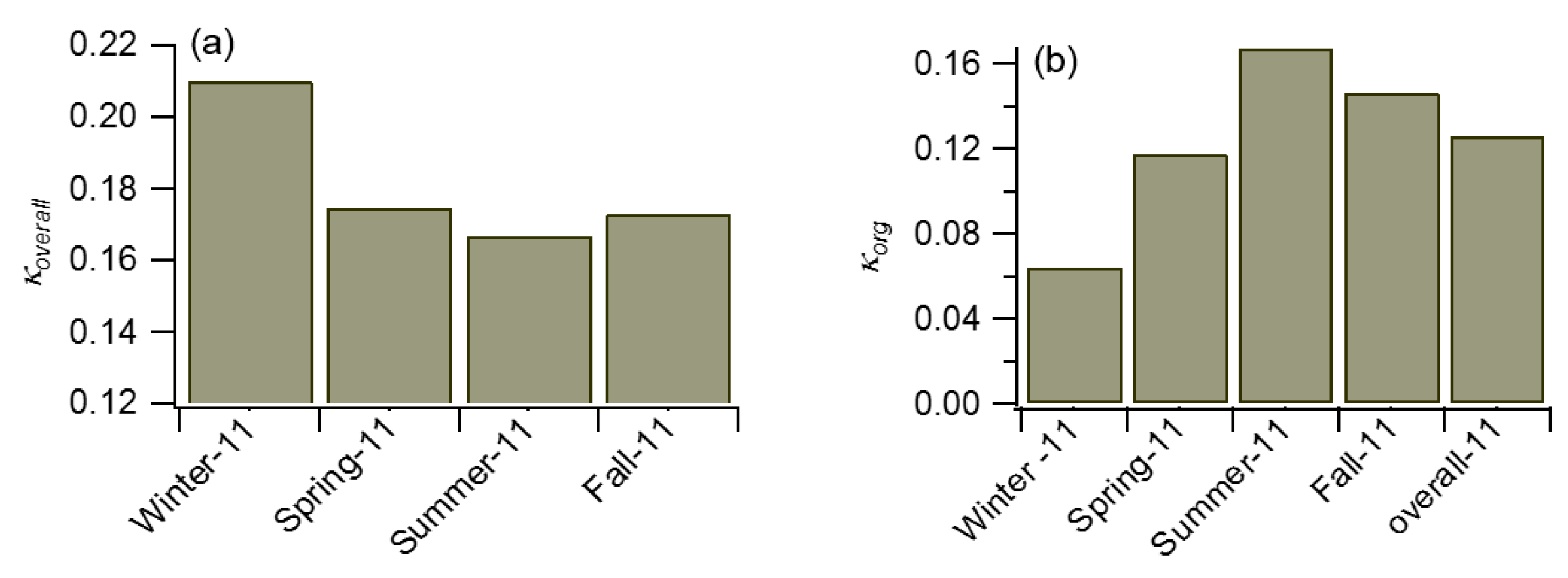
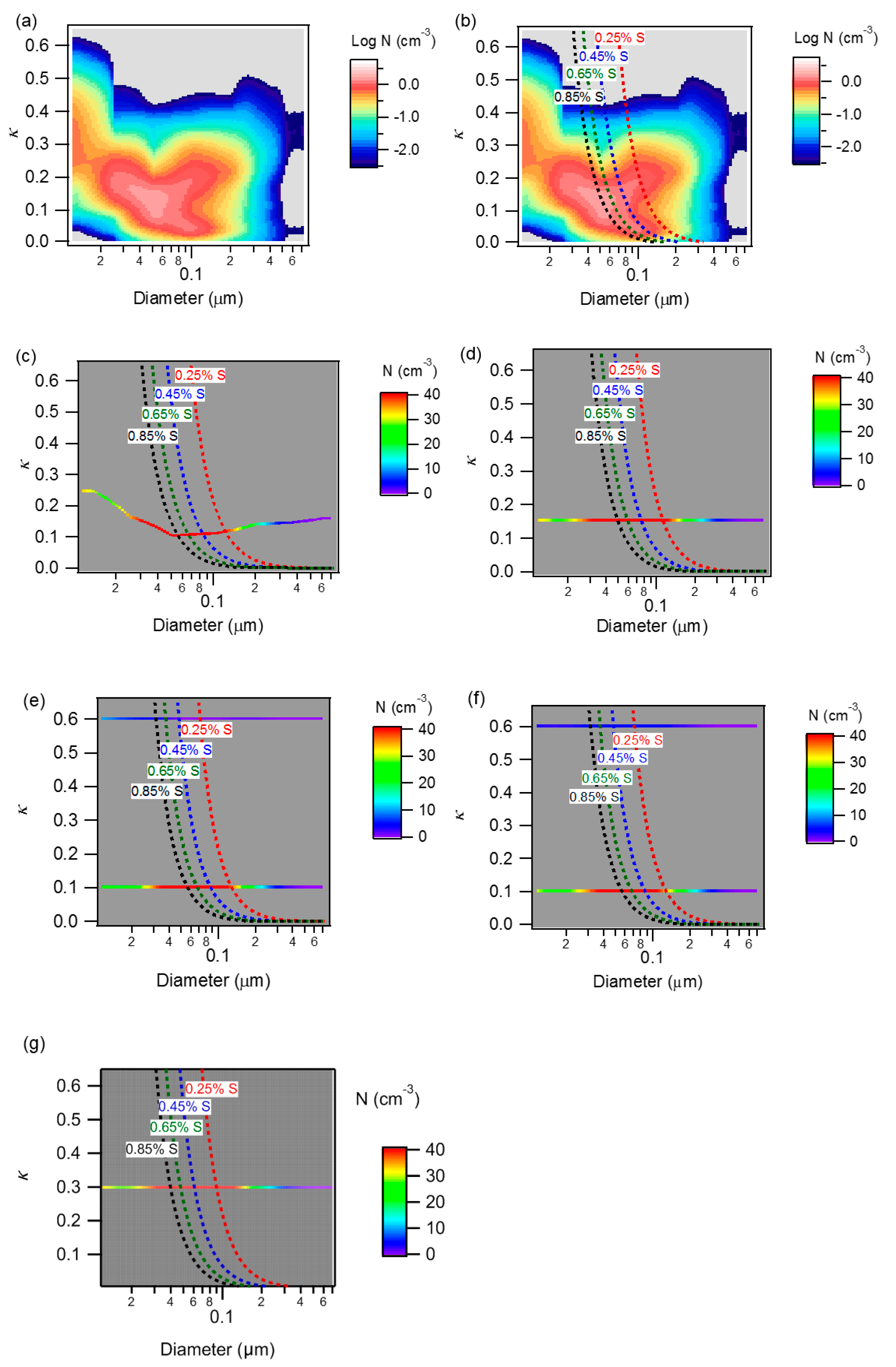
2.3. Use of Κ-Köhler Theory
2.4. Description of Models Used for Estimating NCCN
3. Results and Discussion
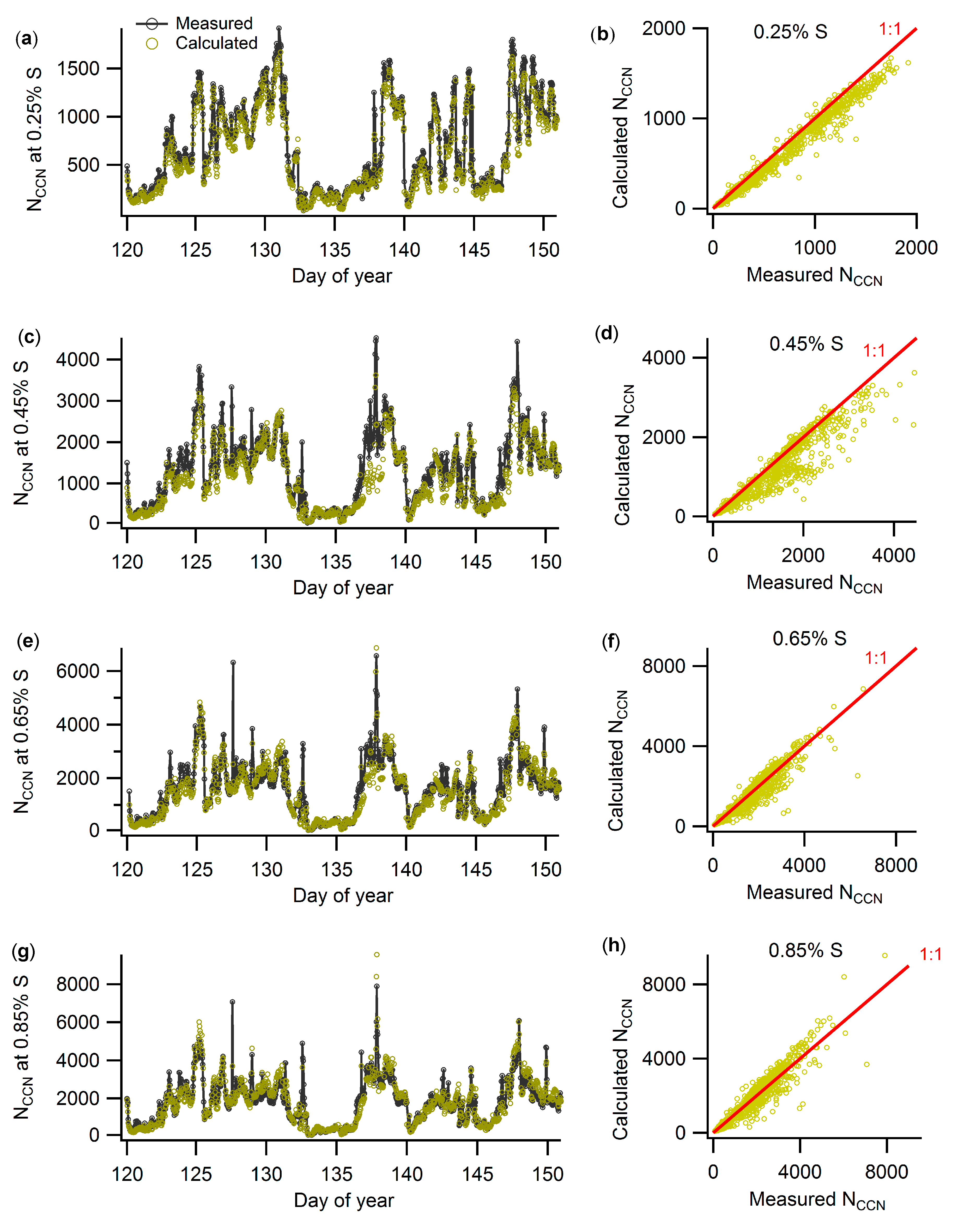
3.1. Comparison between Measured and Baseline NCCN Estimate
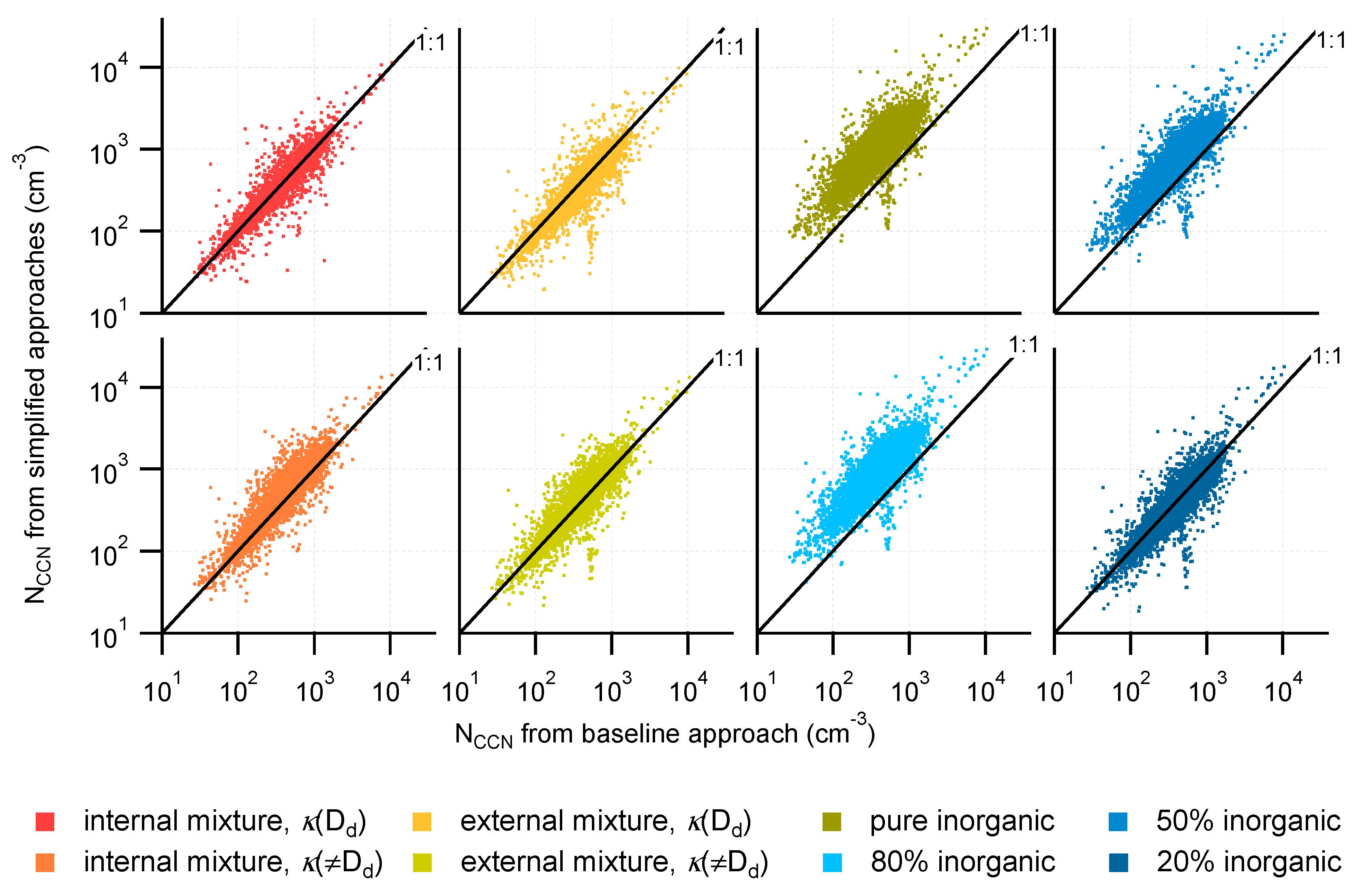
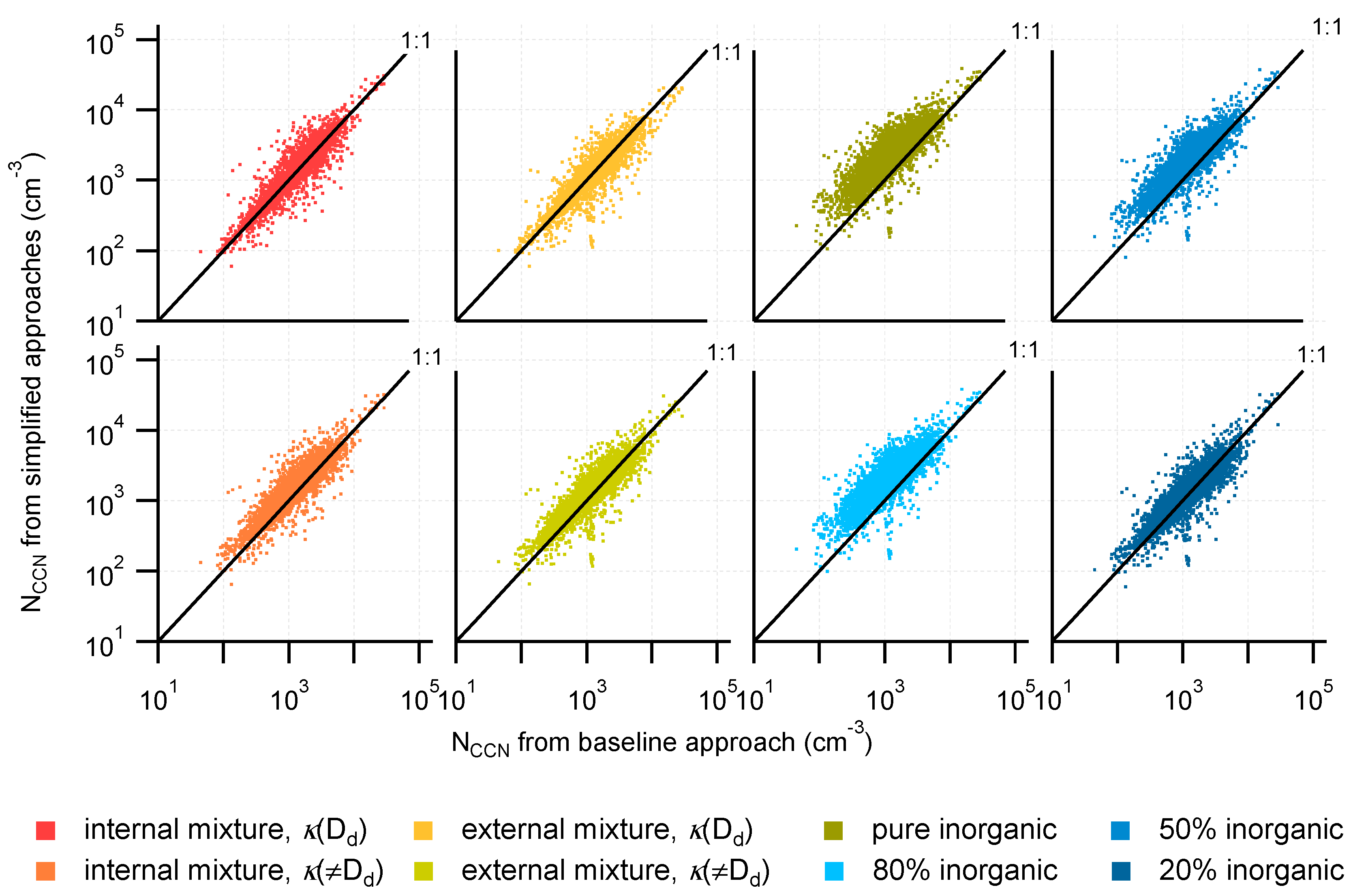
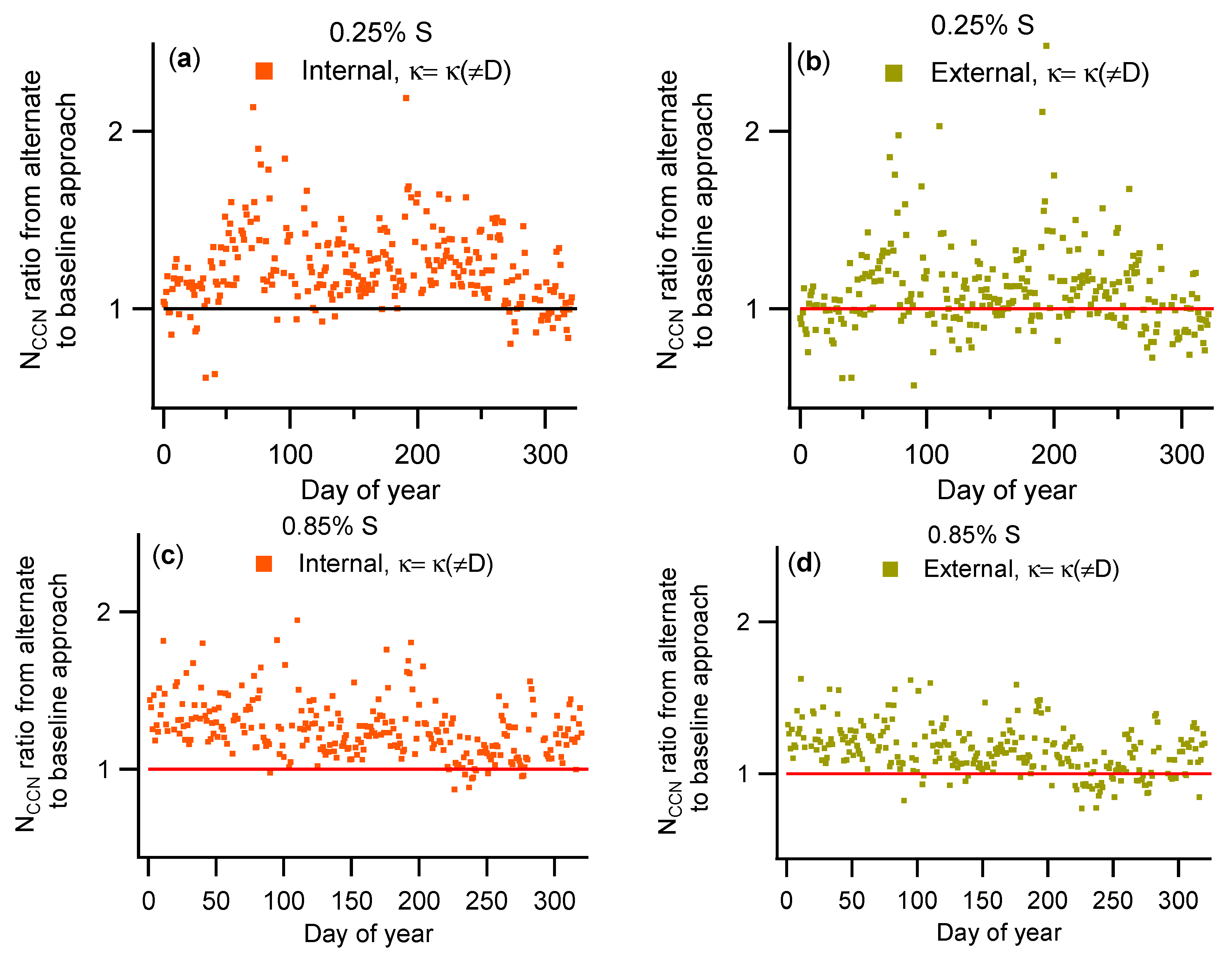
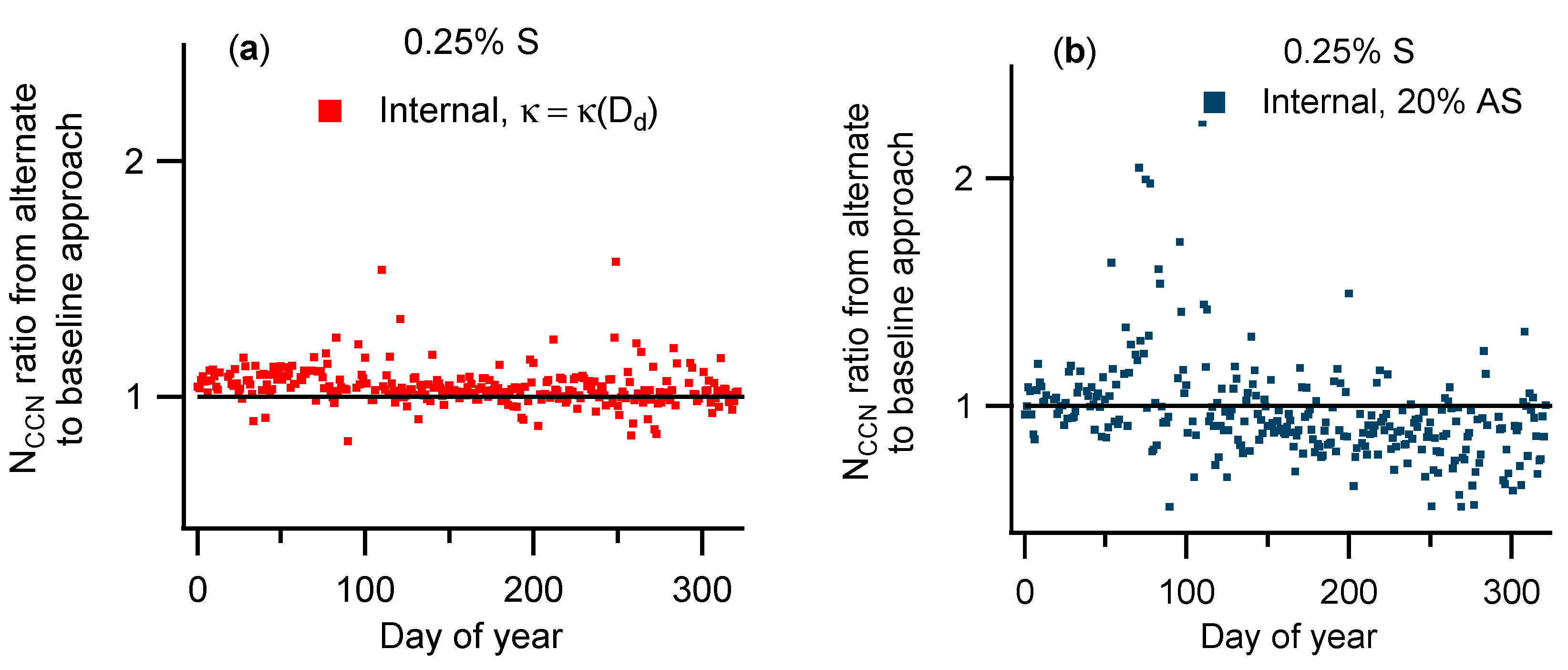
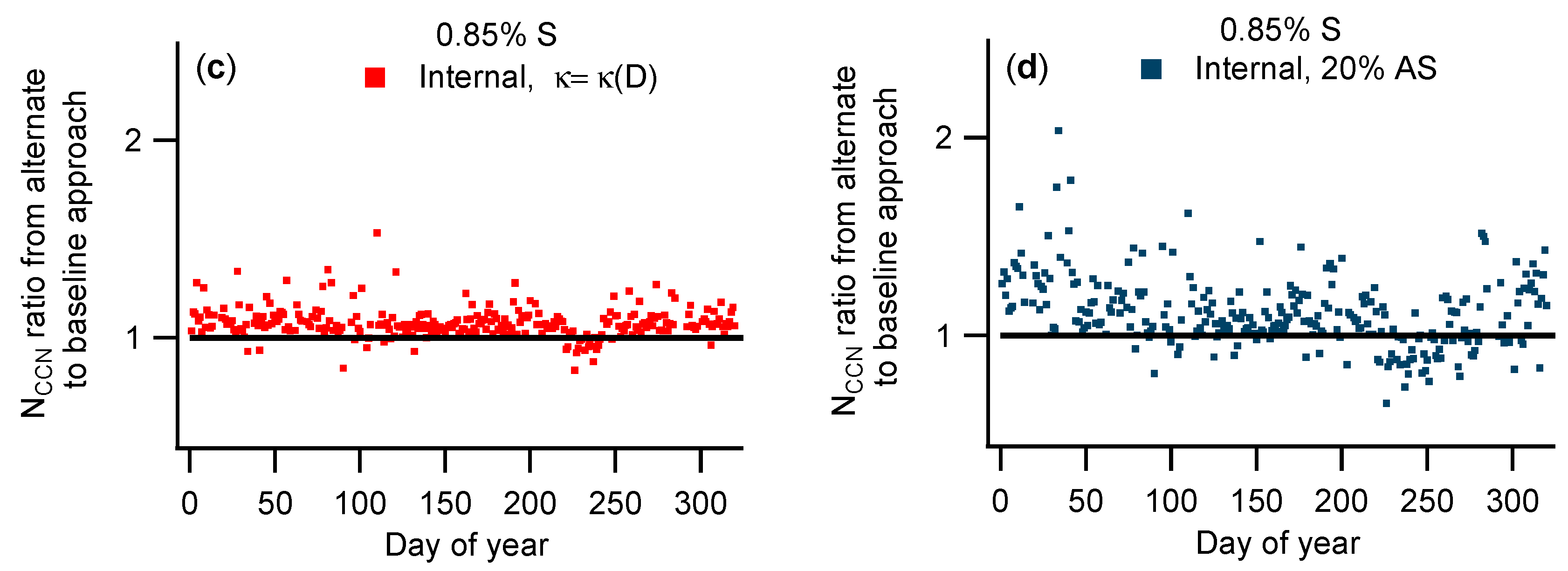
3.2. Comparison of NCCN Calculated from Different Approaches
4. Summary and Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Köhler, H. The nucleus in and the growth of hygroscopic droplets. Trans. Faraday Soc. 1936, 32, 1152–1161. [Google Scholar] [CrossRef]
- Hallquist, M.; Wenger, J.C.; Baltensperger, U.; Rudich, Y.; Simpson, D.; Claeys, M.; Dommen, J.; Donahue, N.M.; George, C.; Goldstein, A.H.; et al. The formation, properties and impact of secondary organic aerosol: Current and emerging issues. Atmos. Chem. Phys. 2009, 9, 5155–5236. [Google Scholar] [CrossRef]
- Pennington, M.R.; Bzdek, B.R.; Depalma, J.W.; Smith, J.N.; Kortelainen, A.-M.; Ruiz, L.H.; Petäjä, T.; Kulmala, M.; Worsnop, D.R.; Johnston, M.V. Identification and quantification of particle growth channels during new particle formation. Atmos. Chem. Phys. 2013, 13, 10215–10225. [Google Scholar] [CrossRef]
- Abbatt, J.; Broekhuizen, K.; Pradeepkumar, P. Cloud condensation nucleus activity of internally mixed ammonium sulfate/organic acid aerosol particles. Atmos. Environ. 2005, 39, 4767–4778. [Google Scholar] [CrossRef]
- Prenni, A.J.; Petters, M.D.; Kreidenweis, S.M.; Demott, P.J.; Ziemann, P.J. Cloud droplet activation of secondary organic aerosol. J. Geophys. Res. 2007, 112. [Google Scholar] [CrossRef]
- Bigg, E. Discrepancy between observation and prediction of concentrations of cloud condensation nuclei. Atmos. Res. 1986, 20, 81–86. [Google Scholar] [CrossRef]
- Chan, M.N.; Kreidenweis, S.M.; Chan, C.K. Measurements of the Hygroscopic and Deliquescence Properties of Organic Compounds of Different Solubilities in Water and Their Relationship with Cloud Condensation Nuclei Activities. Environ. Sci. Technol. 2008, 42, 3602–3608. [Google Scholar] [CrossRef] [PubMed]
- Raymond, T.M. Cloud activation of single-component organic aerosol particles. J. Geophys. Res. 2002, 107. [Google Scholar] [CrossRef]
- Raymond, T.M. Formation of cloud droplets by multicomponent organic particles. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Roberts, G.C. Sensitivity of CCN spectra on chemical and physical properties of aerosol: A case study from the Amazon Basin. J. Geophys. Res. 2002, 107. [Google Scholar] [CrossRef]
- Smith, J.N.; Dunn, M.J.; Vanreken, T.M.; Iida, K.; Stolzenburg, M.R.; Mcmurry, P.H.; Huey, L.G. Chemical composition of atmospheric nanoparticles formed from nucleation in Tecamac, Mexico: Evidence for an important role for organic species in nanoparticle growth. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Yli-Juuti, T.; Nieminen, T.; Hirsikko, A.; Aalto, P.P.; Asmi, E.; Hõrrak, U.; Manninen, H.E.; Patokoski, J.; Maso, M.D.; Petäjä, T.; et al. Growth rates of nucleation mode particles in Hyytiälä during 2003−2009: Variation with particle size, season, data analysis method and ambient conditions. Atmos. Chem. Phys. 2011, 11, 12865–12886. [Google Scholar] [CrossRef]
- Ruehl, C.R.; Davis, J.F.; Wilson, K.R. An interfacial mechanism for cloud droplet formation on organic aerosols. Science 2016, 351, 1447–1450. [Google Scholar] [CrossRef] [PubMed]
- Bilde, M.; Svenningsson, B. CCN activation of slightly soluble organics: The importance of small amounts of inorganic salt and particle phase. Tellus 2004, 56, 128–134. [Google Scholar] [CrossRef]
- Hartz, K.E.H.; Tischuk, J.E.; Chan, M.N.; Chan, C.K.; Donahue, N.M.; Pandis, S.N. Cloud condensation nuclei activation of limited solubility organic aerosol. Atmos. Environ. 2006, 40, 605–617. [Google Scholar] [CrossRef]
- Svenningsson, B.; Rissler, J.; Swietlicki, E.; Mircea, M.; Bilde, M.; Facchini, M.C.; Decesari, S.; Fuzzi, S.; Zhou, J.; Mønster, J.; Rosenørn, T. Hygroscopic growth and critical supersaturations for mixed aerosol particles of inorganic and organic compounds of atmospheric relevance. Atmos. Chem. Phys. 2006, 6, 1937–1952. [Google Scholar] [CrossRef]
- Petters, M.D.; Kreidenweis, S.M. A single parameter representation of hygroscopic growth and cloud condensation nucleus activity. Atmos. Chem. Phys. 2007, 7, 1961–1971. [Google Scholar] [CrossRef]
- Moore, R.H.; Bahreini, R.; Brock, C.A.; Froyd, K.D.; Cozic, J.; Holloway, J.S.; Middlebrook, A.M.; Murphy, D.M.; Nenes, A. Hygroscopicity and composition of Alaskan Arctic CCN during April 2008. Atmos. Chem. Phys. 2011, 11, 11807–11825. [Google Scholar] [CrossRef]
- Bougiatioti, A.; Fountoukis, C.; Kalivitis, N.; Pandis, S.N.; Nenes, A.; Mihalopoulos, N. Cloud condensation nuclei measurements in the marine boundary layer of the Eastern Mediterranean: CCN closure and droplet growth kinetics. Atmos. Chem. Phys. 2009, 9, 7053–7066. [Google Scholar] [CrossRef]
- Chang, R.Y.-W.; Slowik, J.G.; Shantz, N.C.; Vlasenko, A.; Liggio, J.; Sjostedt, S.J.; Leaitch, W.R.; Abbatt, J.P.D. The hygroscopicity parameter (κ) of ambient organic aerosol at a field site subject to biogenic and anthropogenic influences: Relationship to degree of aerosol oxidation. Atmos. Chem. Phys. 2010, 10, 5047–5064. [Google Scholar] [CrossRef]
- Chuang, P.Y.; Collins, D.R.; Pawlowska, H.; Snider, J.R.; Jonsson, H.H.; Brenguier, J.L.; Flagan, R.C.; Seinfeld, J.H. CCN measurements during ACE-2 and their relationship to cloud microphysical properties. Tellus 2000, 52, 843–867. [Google Scholar] [CrossRef]
- Covert, D.S.; Gras, J.L.; Wiedensohler, A.; Stratmann, F. Comparison of directly measured CCN with CCN modeled from the number-size distribution in the marine boundary layer during ACE 1 at Cape Grim, Tasmania. J. Geophys. Res. Atmos. 1998, 103, 16597–16608. [Google Scholar] [CrossRef]
- Furutani, H.; Dallosto, M.; Roberts, G.; Prather, K. Assessment of the relative importance of atmospheric aging on CCN activity derived from field observations. Atmos. Environ. 2008, 42, 3130–3142. [Google Scholar] [CrossRef]
- Gácita, M.S.; Longo, K.M.; Freire, J.L.M.; Freitas, S.R.; Martin, S.T. Impact of mixing state and hygroscopicity on CCN activity of biomass burning aerosol in Amazonia. Atmos. Chem. Phys. 2017, 17, 2373–2392. [Google Scholar] [CrossRef]
- Kammermann, L.; Gysel, M.; Weingartner, E.; Herich, H.; Cziczo, D.J.; Holst, T.; Svenningsson, B.; Arneth, A.; Baltensperger, U. Subarctic atmospheric aerosol composition: 3. Measured and modeled properties of cloud condensation nuclei. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef]
- Kuwata, M.; Kondo, Y.; Miyazaki, Y.; Komazaki, Y.; Kim, J.H.; Yum, S.S.; Tanimoto, H.; Matsueda, H. Cloud condensation nuclei activity at Jeju Island, Korea in spring 2005. Atmos. Chem. Phys. 2008, 8, 2933–2948. [Google Scholar] [CrossRef]
- Mircea, M.; Facchini, M.C.; Decesari, S.; Fuzzi, S.; Charlson, R.J. The influence of the organic aerosol component on CCN supersaturation spectra for different aerosol types. Tellus 2002, 54, 74–81. [Google Scholar] [CrossRef]
- Moore, R.H.; Cerully, K.; Bahreini, R.; Brock, C.A.; Middlebrook, A.M.; Nenes, A. Hygroscopicity and composition of California CCN during summer 2010. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Rissler, J.; Vestin, A.; Swietlicki, E.; Fisch, G.; Zhou, J.; Artaxo, P.; Andreae, M.O. Size distribution and hygroscopic properties of aerosol particles from dry-season biomass burning in Amazonia. Atmos. Chem. Phys. 2006, 6, 471–491. [Google Scholar] [CrossRef]
- Roberts, G.C.; Day, D.A.; Russell, L.M.; Dunlea, E.J.; Jimenez, J.L.; Tomlinson, J.M.; Collins, D.R.; Shinozuka, Y.; Clarke, A.D. Characterization of particle cloud droplet activity and composition in the free troposphere and the boundary layer during INTEX-B. Atmos. Chem. Phys. 2010, 10, 6627–6644. [Google Scholar] [CrossRef]
- Roberts, G.; Mauger, G.; Hadley, O.; Ramanathan, V. North American and Asian aerosols over the eastern Pacific Ocean and their role in regulating cloud condensation nuclei. J. Geophys. Res. 2006, 111. [Google Scholar] [CrossRef]
- Rose, D.; Nowak, A.; Achtert, P.; Wiedensohler, A.; Hu, M.; Shao, M.; Zhang, Y.; Andreae, M.O.; Pöschl, U. Cloud condensation nuclei in polluted air and biomass burning smoke near the mega-city Guangzhou, China—Part 1: Size-resolved measurements and implications for the modeling of aerosol particle hygroscopicity and CCN activity. Atmos. Chem. Phys. 2010, 10, 3365–3383. [Google Scholar] [CrossRef]
- Shantz, N.C.; Leaitch, W.R.; Phinney, L.; Mozurkewich, M.; Toom-Sauntry, D. The effect of organic compounds on the growth rate of cloud droplets in marine and forest settings. Atmos. Chem. Phys. 2008, 8, 5869–5887. [Google Scholar] [CrossRef]
- Wang, J.; Cubison, M.J.; Aiken, A.C.; Jimenez, J.L.; Collins, D.R. The importance of aerosol mixing state and size-resolved composition on CCN concentration and the variation of the importance with atmospheric aging of aerosols. Atmos. Chem. Phys. 2010, 10, 7267–7283. [Google Scholar] [CrossRef]
- Ervens, B.; Cubison, M.J.; Andrews, E.; Feingold, G.; Ogren, J.A.; Jimenez, J.L.; Quinn, P.K.; Bates, T.S.; Wang, J.; Zhang, Q.; et al. CCN predictions using simplified assumptions of organic aerosol composition and mixing state: A synthesis from six different locations. Atmos. Chem. Phys. 2010, 10, 4795–4807. [Google Scholar] [CrossRef]
- Broekhuizen, K.; Chang, R.-W.; Leaitch, W.R.; Li, S.-M.; Abbatt, J.P.D. Closure between measured and modeled cloud condensation nuclei (CCN) using size-resolved aerosol compositions in downtown Toronto. Atmos. Chem. Phys. 2006, 6, 2513–2524. [Google Scholar] [CrossRef]
- Cubison, M.J.; Ervens, B.; Feingold, G.; Docherty, K.S.; Ulbrich, I.M.; Shields, L.; Prather, K.; Hering, S.; Jimenez, J.L. The influence of chemical composition and mixing state of Los Angeles urban aerosol on CCN number and cloud properties. Atmos. Chem. Phys. 2008, 8, 5649–5667. [Google Scholar] [CrossRef]
- Lance, S.; Nenes, A.; Mazzoleni, C.; Dubey, M.K.; Gates, H.; Varutbangkul, V.; Rissman, T.A.; Murphy, S.M.; Sorooshian, A.; Flagan, R.C.; et al. Cloud condensation nuclei activity, closure, and droplet growth kinetics of Houston aerosol during the Gulf of Mexico Atmospheric Composition and Climate Study (GoMACCS). J. Geophys. Res. 2009, 114. [Google Scholar] [CrossRef]
- Padró, L.T.; Moore, R.H.; Zhang, X.; Rastogi, N.; Weber, R.J.; Nenes, A. Mixing state and compositional effects on CCN activity and droplet growth kinetics of size-resolved CCN in an urban environment. Atmos. Chem. Phys. 2012, 12, 10239–10255. [Google Scholar] [CrossRef]
- Zaveri, R.A.; Barnard, J.C.; Easter, R.C.; Riemer, N.; West, M. Particle-resolved simulation of aerosol size, composition, mixing state, and the associated optical and cloud condensation nuclei activation properties in an evolving urban plume. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef]
- Bhattu, D.; Tripathi, S.N. CCN closure study: Effects of aerosol chemical composition and mixing state. J. Geophys. Res. Atmos. 2015, 120, 766–783. [Google Scholar] [CrossRef]
- Gunthe, S.S.; King, S.M.; Rose, D.; Chen, Q.; Roldin, P.; Farmer, D.K.; Jimenez, J.L.; Artaxo, P.; Andreae, M.O.; Martin, S.T.; et al. Cloud condensation nuclei in pristine tropical rainforest air of Amazonia: Size-resolved measurements and modeling of atmospheric aerosol composition and CCN activity. Atmos. Chem. Phys. 2009, 9, 7551–7575. [Google Scholar] [CrossRef]
- Medina, J.; Nenes, A.; Sotiropoulou, R.-E.P.; Cottrell, L.D.; Ziemba, L.D.; Beckman, P.J.; Griffin, R.J. Cloud condensation nuclei closure during the International Consortium for Atmospheric Research on Transport and Transformation 2004 campaign: Effects of size-resolved composition. J. Geophys. Res. 2007, 112. [Google Scholar] [CrossRef]
- Stroud, C.A.; Nenes, A.; Jimenez, J.L.; Decarlo, P.F.; Huffman, J.A.; Bruintjes, R.; Nemitz, E.; Delia, A.E.; Toohey, D.W.; Guenther, A.B.; et al. Cloud Activating Properties of Aerosol Observed during CELTIC. J. Atmos. Sci. 2007, 64, 441–459. [Google Scholar] [CrossRef]
- Conant, W.C.; Vanreken, T.M.; Rissman, T.A.; Varutbangkul, V.; Jonsson, H.H.; Nenes, A.; Jimenez, J.L.; Delia, A.E.; Bahreini, R.; Roberts, G.C.; et al. Aerosol-cloud drop concentration closure in warm cumulus. J. Geophys. Res. Atmos. 2004, 109. [Google Scholar] [CrossRef]
- Dusek, U.; Frank, G.P.; Hildebrandt, L.; Curtius, J.; Schneider, J.; Walter, S.; Chand, D.; Drewnick, F.; Hings, S.; Jung, D.; et al. Size Matters More Than Chemistry for Cloud-Nucleating Ability of Aerosol Particles. Science 2006, 312, 1375–1378. [Google Scholar] [CrossRef] [PubMed]
- Cantrell, W.; Shaw, G.; Cass, G.R.; Chowdhury, Z.; Hughes, L.S.; Prather, K.A.; Guazzotti, S.A.; Coffee, K.R. Closure between aerosol particles and cloud condensation nuclei at Kaashidhoo Climate Observatory. J. Geophys. Res. Atmos. 2001, 106, 28711–28718. [Google Scholar] [CrossRef]
- Chang, R.-W.; Liu, P.; Leaitch, W.; Abbatt, J. Comparison between measured and predicted CCN concentrations at Egbert, Ontario: Focus on the organic aerosol fraction at a semi-rural site. Atmos. Environ. 2007, 41, 8172–8182. [Google Scholar] [CrossRef]
- Liu, P.S.K.; Leaitch, W.R.; Banic, C.M.; Li, S.-M.; Ngo, D.; Megaw, W.J. Aerosol observations at Chebogue Point during the 1993 North Atlantic Regional Experiment: Relationships among cloud condensation nuclei, size distribution, and chemistry. J. Geophys. Res. Atmos. 1996, 101, 28971–28990. [Google Scholar] [CrossRef]
- Rissler, J.; Swietlicki, E.; Zhou, J.; Roberts, G.; Andreae, M.O.; Gatti, L.V.; Artaxo, P. Physical properties of the sub-micrometer aerosol over the Amazon rain forest during the wet-to-dry season transition—Comparison of modeled and measured CCN concentrations. Atmos. Chem. Phys. 2004, 4, 2119–2143. [Google Scholar] [CrossRef]
- Vanreken, T.M. Toward aerosol/cloud condensation nuclei (CCN) closure during CRYSTAL-FACE. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Wang, J.; Lee, Y.-N.; Daum, P.H.; Jayne, J.; Alexander, M.L. Effects of aerosol organics on cloud condensation nucleus (CCN) concentration and first indirect aerosol effect. Atmos. Chem. Phys. 2008, 8, 6325–6339. [Google Scholar] [CrossRef]
- Ervens, B.; Cubison, M.; Andrews, E.; Feingold, G.; Ogren, J.A.; Jimenez, J.L.; Decarlo, P.; Nenes, A. Prediction of cloud condensation nucleus number concentration using measurements of aerosol size distributions and composition and light scattering enhancement due to humidity. J. Geophys. Res. 2007, 112. [Google Scholar] [CrossRef]
- Almeida, G.P.; Brito, J.; Morales, C.A.; Andrade, M.F.; Artaxo, P. Measured and modelled cloud condensation nuclei (CCN) concentration in São Paulo, Brazil: The importance of aerosol size-resolved chemical composition on CCN concentration prediction. Atmos. Chem. Phys. 2014, 14, 7559–7572. [Google Scholar] [CrossRef]
- Asa-Awuku, A.; Moore, R.H.; Nenes, A.; Bahreini, R.; Holloway, J.S.; Brock, C.A.; Middlebrook, A.M.; Ryerson, T.B.; Jimenez, J.L.; Decarlo, P.F.; et al. Airborne cloud condensation nuclei measurements during the 2006 Texas Air Quality Study. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- Che, H.C.; Zhang, X.Y.; Wang, Y.Q.; Zhang, L.; Shen, X.J.; Zhang, Y.M.; Ma, Q.L.; Sun, J.Y.; Zhang, Y.W.; Wang, T.T. Characterization and parameterization of aerosol cloud condensation nuclei activation under different pollution conditions. Sci. Rep. 2016, 6. [Google Scholar] [CrossRef] [PubMed]
- Mircea, M.; Facchini, M.C.; Decesari, S.; Cavalli, F.; Emblico, L.; Fuzzi, S.; Vestin, A.; Rissler, J.; Swietlicki, E.; Frank, G.; et al. Importance of the organic aerosol fraction for modeling aerosol hygroscopic growth and activation: A case study in the Amazon Basin. Atmos. Chem. Phys. 2005, 5, 3111–3126. [Google Scholar] [CrossRef]
- Quinn, P.K.; Bates, T.S.; Coffman, D.J.; Covert, D.S. Influence of particle size and chemistry on the cloud nucleating properties of aerosols. Atmos. Chem. Phys. 2008, 8, 1029–1042. [Google Scholar] [CrossRef]
- Mahish, M.; Collins, D. Analysis of a Multi-Year Record of Size-Resolved Hygroscopicity Measurements from a Rural Site in the U.S. Aerosol Air Qual. Res. 2017, 17, 1389–1400. [Google Scholar] [CrossRef]
- Collins, D. Tandem Differential Mobility Analyzer/Aerodynamic Particle Sizer (APS) Handbook; No. DOE/SC-ARM-TR-090; U.S. Department of Energy: Washington, DC, USA, 2010.
- Gasparini, R.; Li, R.; Collins, D.R. Integration of size distributions and size-resolved hygroscopicity measured during the Houston Supersite for compositional categorization of the aerosol. Atmos. Environ. 2004, 38, 3285–3303. [Google Scholar] [CrossRef]
- Roberts, G.; Nenes, A. A Continuous-Flow Streamwise Thermal-Gradient CCN Chamber for Atmospheric Measurements. Aerosol Sci. Technol. 2005, 39, 206–221. [Google Scholar] [CrossRef]
- Jefferson, A. Aerosol Observing System (AOS) Handbook; Technical Report ARM-TR-014; U.S. Department of Energy: Washington, DC, USA, 2011.
- Ng, N.L.; Herndon, S.C.; Trimborn, A.; Canagaratna, M.R.; Croteau, P.L.; Onasch, T.B. An Aerosol Chemical Speciation Monitor (ACSM) for Routine Monitoring of the Composition and Mass Concentrations of Ambient Aerosol. Aerosol Sci. Technol. 2011, 45, 780–794. [Google Scholar] [CrossRef]
- Bond, T.C.; Anderson, T.L.; Campbell, D. Calibration and intercomparison of filter-based measurements of visible light absorption by aerosols. Aerosol Sci. Technol. 1999, 30, 582–600. [Google Scholar] [CrossRef]
- Watson, T.B. Aerosol Chemical Speciation Monitor (ACSM) Instrument Handbook; No. DOE/SC-ARM-TR-196; U.S. Department of Energy: Washington, DC, USA, 2017.
- Yang, M.; Howell, S.G.; Zhuang, J.; Huebert, B.J. Attribution of aerosol light absorption to black carbon, brown carbon, and dust in China—Interpretations of atmospheric measurements during EAST-AIRE. Atmos. Chem. Phys. 2009, 9, 2035–2050. [Google Scholar] [CrossRef]
- Nakao, S.; Tang, P.; Tang, X.; Clark, C.H.; Qi, L.; Seo, E.; Asa-Awuku, A.; Cocker, D. Density and elemental ratios of secondary organic aerosol: Application of a density prediction method. Atmos. Environ. 2013, 68, 273–277. [Google Scholar] [CrossRef]
- Fast, J.; Zhang, Q.; Tilp, A.; Shippert, T.; Parworth, C.; Mei, F. Organic Aerosol Component (OACOMP) Value-Added Product; No. DOE/SC-ARM-TR-131; U.S. Department of Energy: Washington, DC, USA, 2013.


| Instrument | Measurement | Manufacturer/Model | Installation Date |
|---|---|---|---|
| Scanning Mobility Particle Sizer (SMPS; part of the “TDMA” system) | Size distribution from 0.012 to 0.74 µm dry diameter (Dd) | Fabricated, Texas A&M University, TX, U.S. | 2005 |
| Hygroscopic Tandem Differential Mobility Analyzer (HTDMA; part of the “TDMA” system) | Hygroscopic growth factor distributions of 0.013, 0.025, 0.05, 0.1, 0.2, 0.4, and 0.6µm Dd particles at 90% RH | Fabricated, Texas A&M University, TX, U.S. | 2005 |
| Cloud Condensation Nuclei counter (CCNc) | CCN concentration at a fixed set of supersaturations | CCN-100 Droplet Measurement Technologies, Longmont, CO, U.S. | 2009 |
| Condensation Particle Counter (CPC) | Concentration of Dd > 0.01 µm particles | Model 3010 TSI, Inc., Shoreview, MN, U.S. | 1996 |
| Aerosol Chemical Speciation Monitor (ACSM) | Sub 1-μm chemical composition (organics, sulfate, nitrate, ammonium, and chloride) | Aerodyne Research, Inc., Billerica, MA, U.S. | 2010 |
| Particle Soot Absorption Photometer (PSAP) | Sub 1-μm absorption coefficient (used to infer black carbon concentration) | Radiance Research, Seattle, WA, U.S. | 1992 |
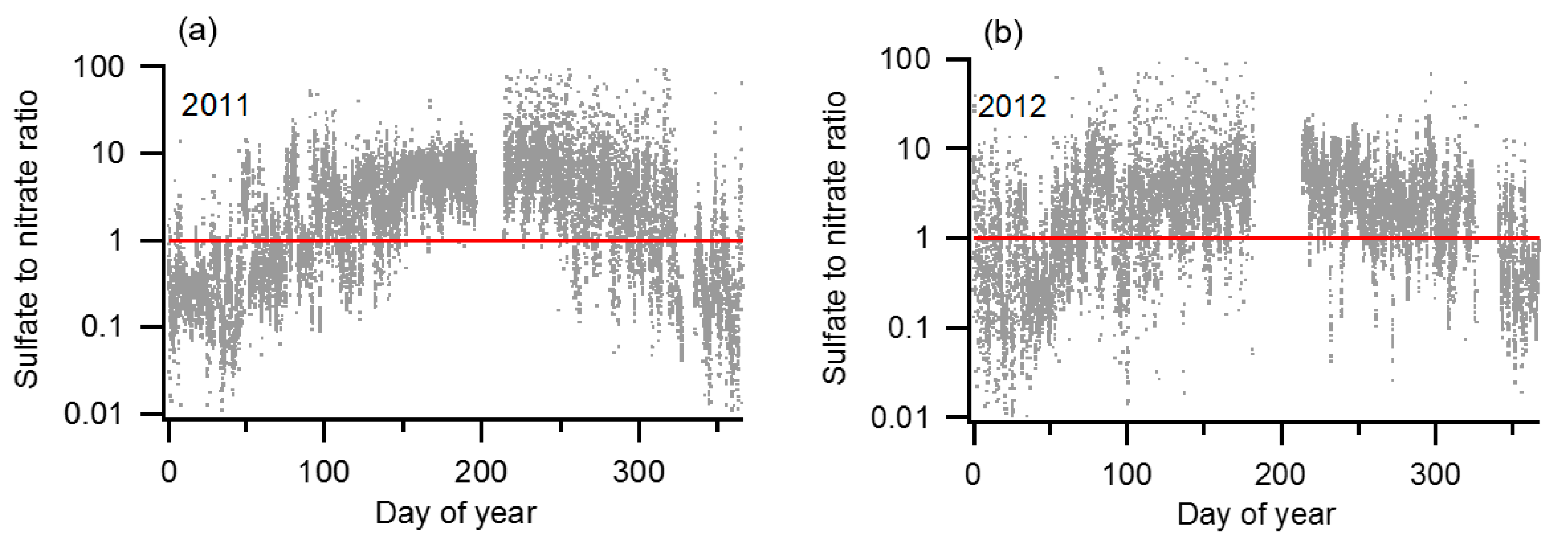
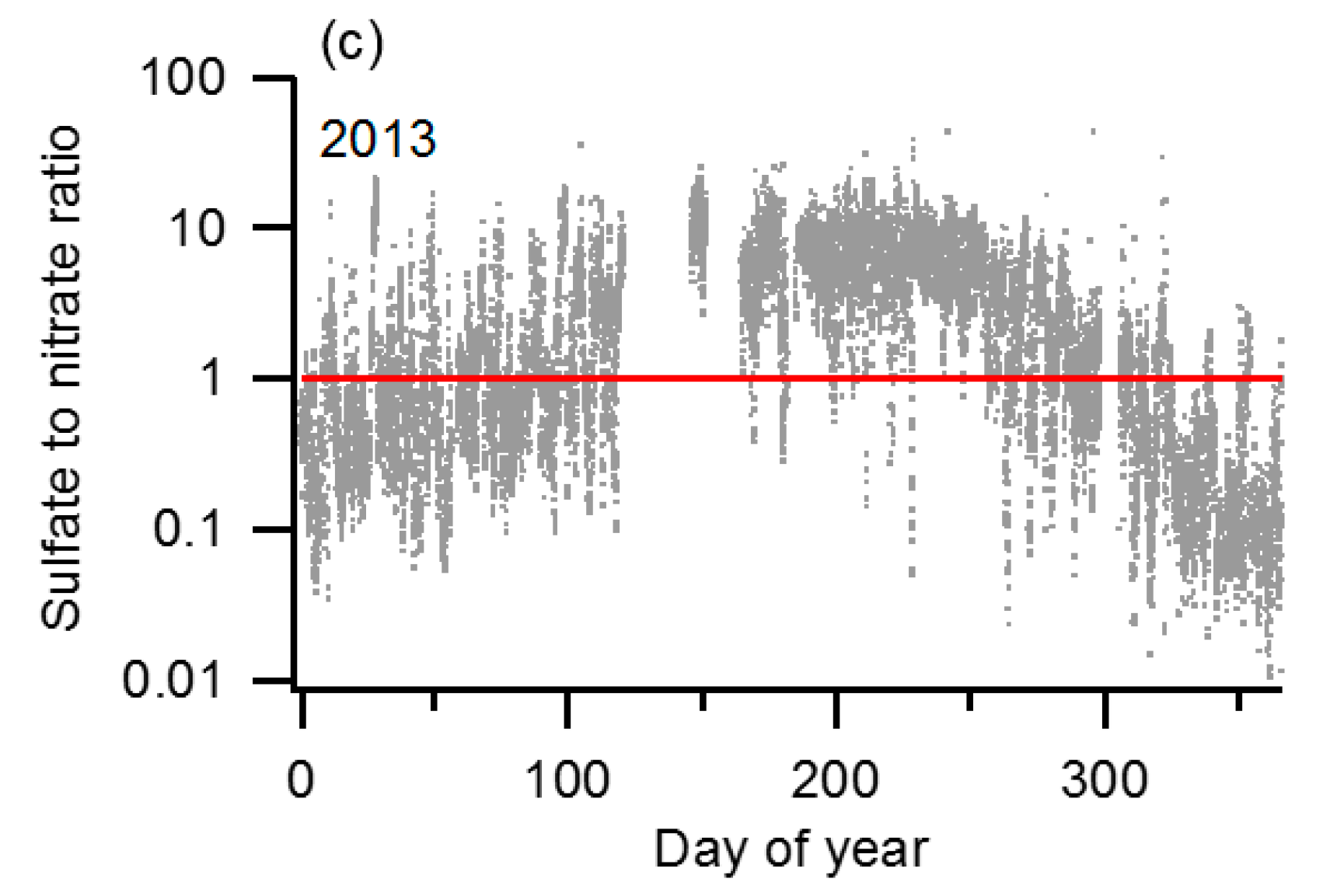
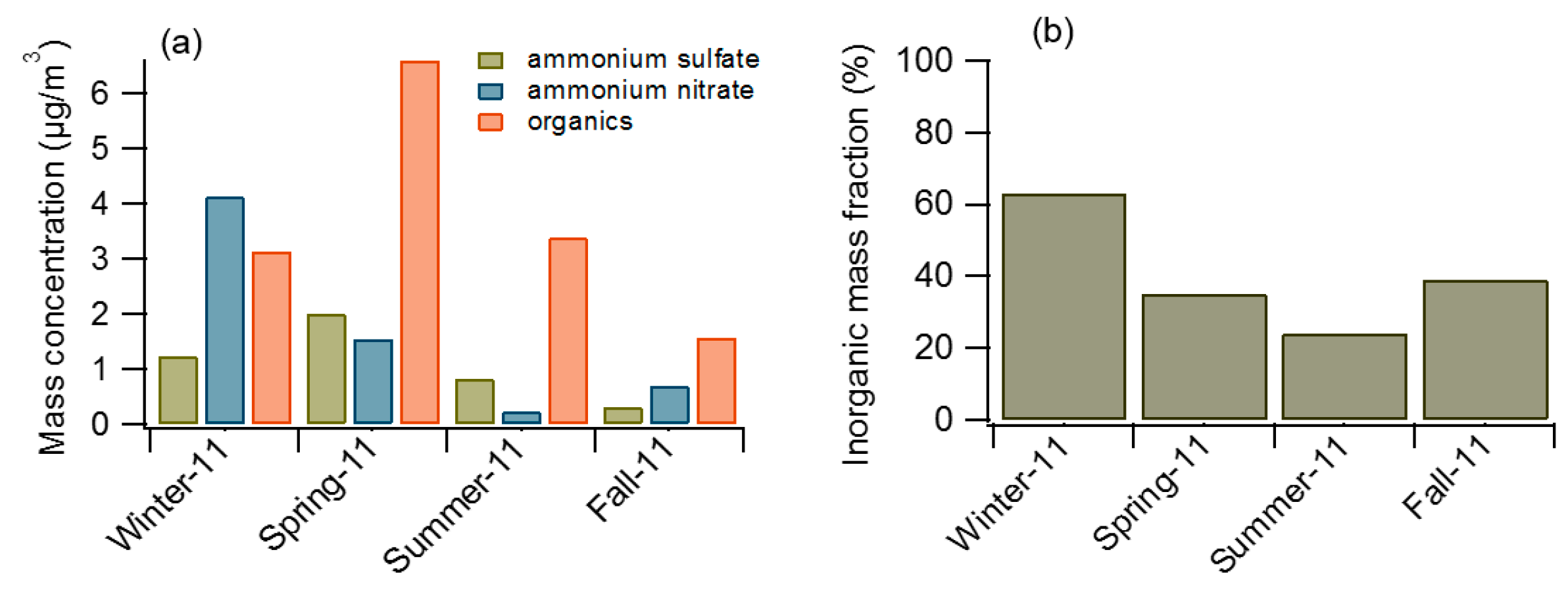
| Year | Mass Concentration Fraction (%) | ||
|---|---|---|---|
| Total Organics | Ammonium Sulfate | Ammonium Nitrate | |
| 2011 | 57 | 17 | 26 |
| 2012 | 56 | 18 | 26 |
| 2013 | 56 | 24 | 20 |
| Year/Month | NRMSE @ % S | |||
|---|---|---|---|---|
| 0.25 | 0.45 | 0.65 | 0.85 | |
| 2009 | 0.53 | 0.36 | 0.35 | 0.35 |
| 2010 | 0.22 | 0.29 | 0.27 | 0.25 |
| May 2011 | 0.17 | 0.22 | 0.21 | 0.21 |
| 2011 | 0.29 | 0.29 | 0.26 | 0.26 |
| 2012 | - | 0.33 | 0.38 | 0.36 |
| Model | Slope (m) @ % S | Correlation Coefficient (r2) @ % S | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.25 | 0.45 | 0.65 | 0.85 | 0.25 | 0.45 | 0.65 | 0.85 | ||
| Baseline | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| Internal, κ = κ(Dd) | 1.01 | 1.02 | 1.01 | 1.01 | 0.002 | 0.87 | 0.87 | 0.85 | 0.84 |
| Internal, κ = κ( Dd) | 1.21 | 1.18 | 1.13 | 1.10 | 0.095 | 0.82 | 0.81 | 0.80 | 0.80 |
| External, κ = κ(Dd) | 0.90 | 0.92 | 0.90 | 0.90 | 0.009 | 0.81 | 0.81 | 0.78 | 0.77 |
| External, κ = κ( Dd) | 1.06 | 1.07 | 1.02 | 1.00 | 0.061 | 0.80 | 0.80 | 0.79 | 0.77 |
| Internal, pure AS | 2.37 | 1.82 | 1.57 | 1.43 | 0.400 | 0.67 | 0.69 | 0.68 | 0.67 |
| Internal, 50% AS | 1.76 | 1.50 | 1.33 | 1.26 | 0.285 | 0.72 | 0.75 | 0.76 | 0.74 |
| Internal, 20% AS | 1.05 | 1.05 | 1.03 | 0.99 | 0.057 | 0.72 | 0.78 | 0.77 | 0.76 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahish, M.; Jefferson, A.; Collins, D.R. Influence of Common Assumptions Regarding Aerosol Composition and Mixing State on Predicted CCN Concentration. Atmosphere 2018, 9, 54. https://doi.org/10.3390/atmos9020054
Mahish M, Jefferson A, Collins DR. Influence of Common Assumptions Regarding Aerosol Composition and Mixing State on Predicted CCN Concentration. Atmosphere. 2018; 9(2):54. https://doi.org/10.3390/atmos9020054
Chicago/Turabian StyleMahish, Manasi, Anne Jefferson, and Don R. Collins. 2018. "Influence of Common Assumptions Regarding Aerosol Composition and Mixing State on Predicted CCN Concentration" Atmosphere 9, no. 2: 54. https://doi.org/10.3390/atmos9020054
APA StyleMahish, M., Jefferson, A., & Collins, D. R. (2018). Influence of Common Assumptions Regarding Aerosol Composition and Mixing State on Predicted CCN Concentration. Atmosphere, 9(2), 54. https://doi.org/10.3390/atmos9020054





