Assessing the Skill of Convection-Allowing Ensemble Forecasts of Precipitation by Optimization of Spatial-Temporal Neighborhoods
Abstract
1. Introduction
2. Case and Experimental Design
3. Methods
3.1. Probability Matched Mean (PMM) Method
- (1)
- The grid-point precipitation values of all the ensemble members (Nm) are sorted into a monotonically decreasing order, named sequence 1.
- (2)
- The forecast values are selected at every Nm interval from sequence 1 to obtain sequence 2, of which the grid-point number is the same as the total number of grid points in the study area. There are altogether Nm kinds of equal probability cases in sequence 2. The authors chose the ith case randomly, where i = 1, 2, 3, ···, Nm.
- (3)
- The forecast values in the EM field are ranked from highest to lowest to obtain sequence 3, with the location of each value stored along with its rank.
- (4)
- The largest precipitation value from sequence 2 is reassigned to the grid-point location of the corresponding largest EM value from sequence 3, and so on, until the lowest value from sequence 2 is reassigned to the last location of the minimum EM value from sequence 3. Finally, the PMM precipitation forecasting field is obtained. Here, sequence 3 plays a bridge role in providing the location of each value for the PMM sequence.
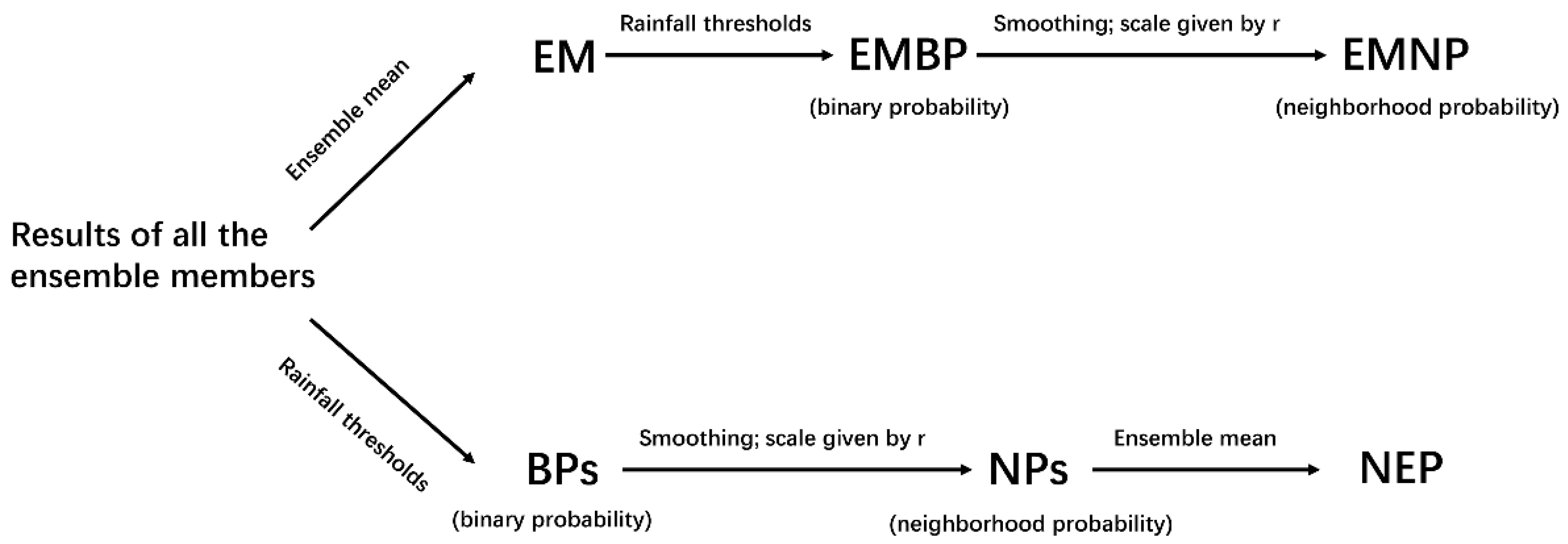
3.2. NP Method with Temporal Factors
3.3. FSS with Temporal Factors
4. The Deterministic Forecast Results
4.1. Domain Total Precipitation
4.2. Grid Coverage
5. The Probabilistic Forecast Results
5.1. The Results of Spatial Neighborhood
5.1.1. Distribution of Spatial Neighborhood Probability
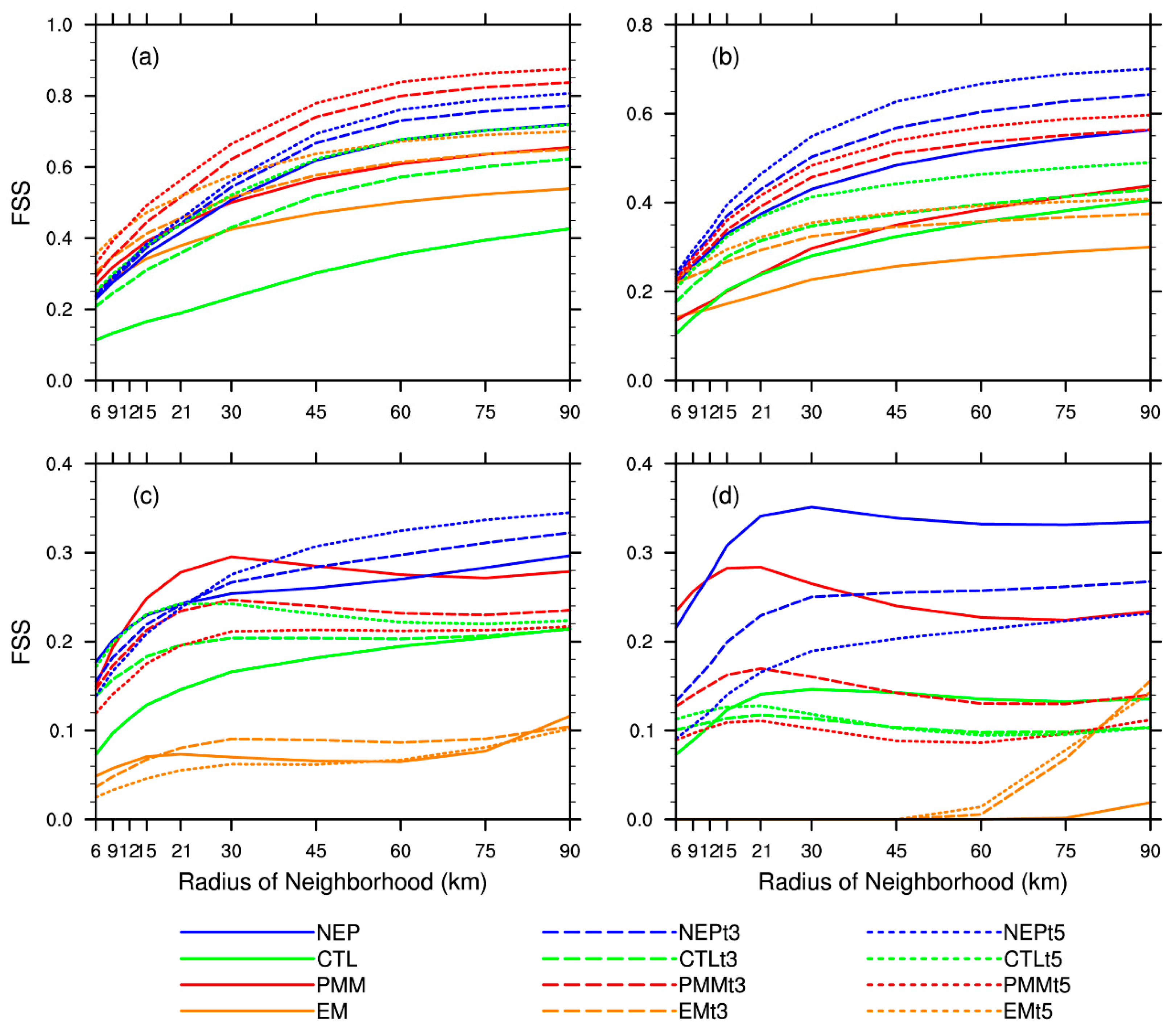
5.1.2. FSS of Spatial Neighborhood
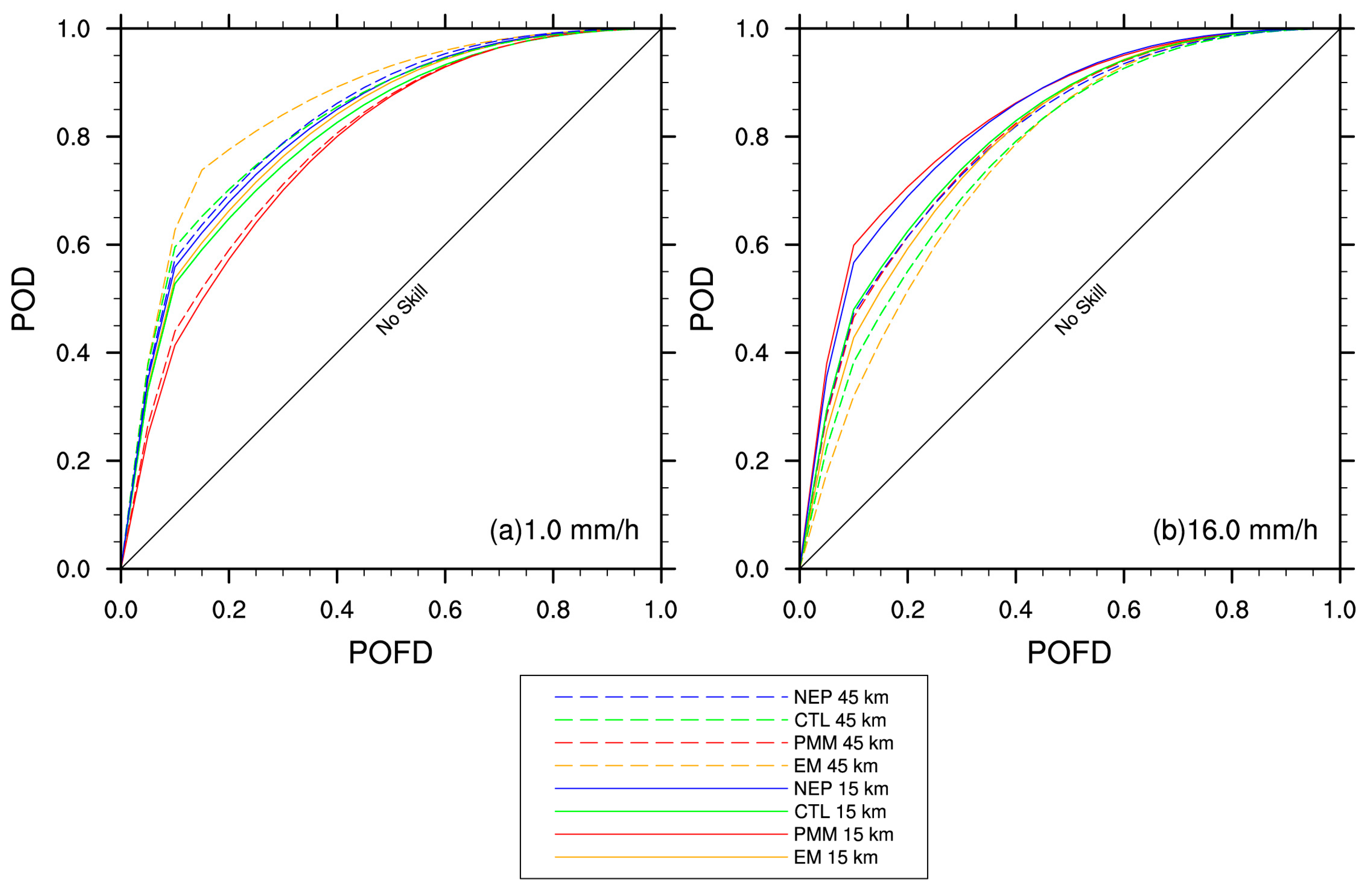
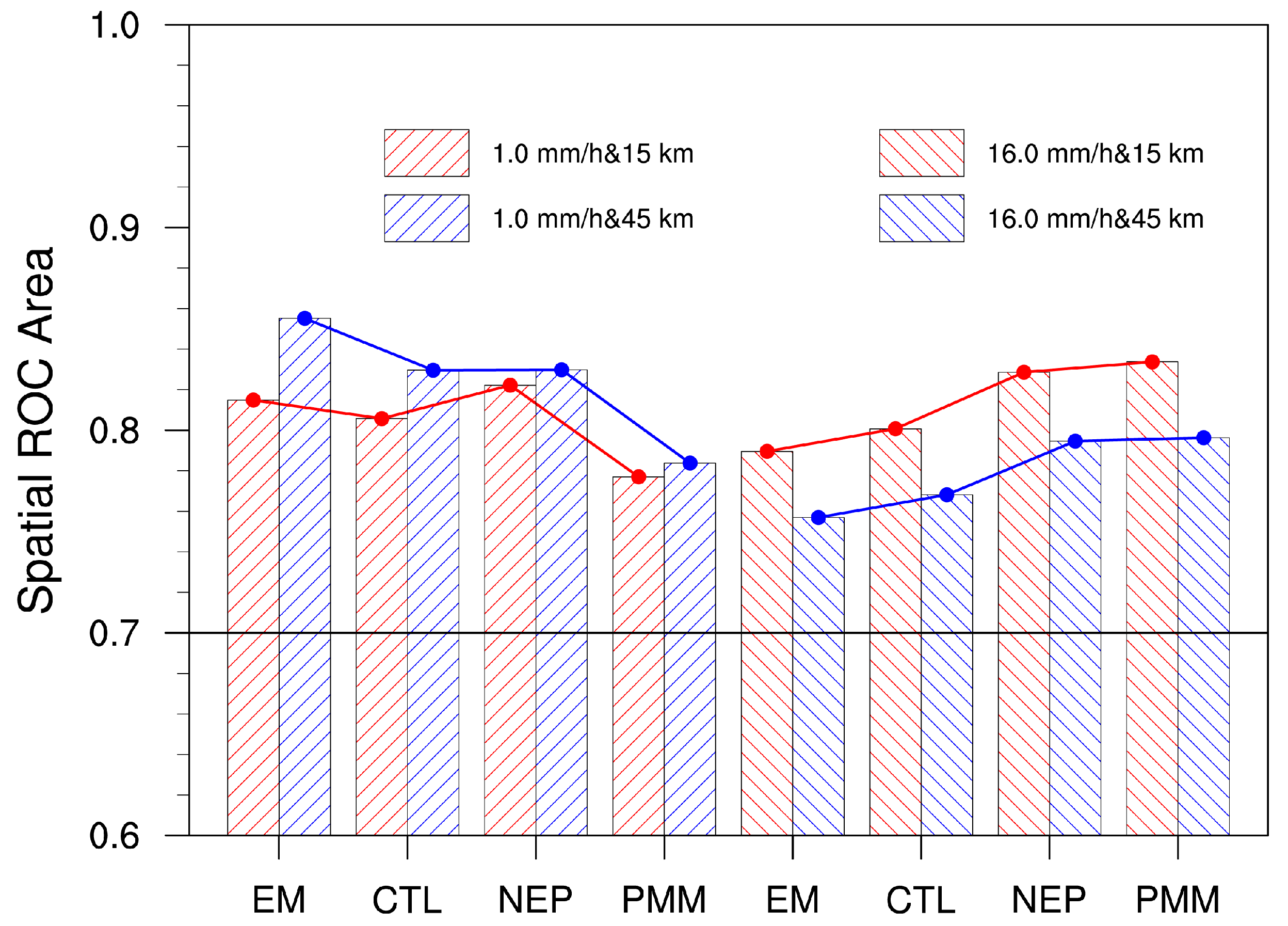
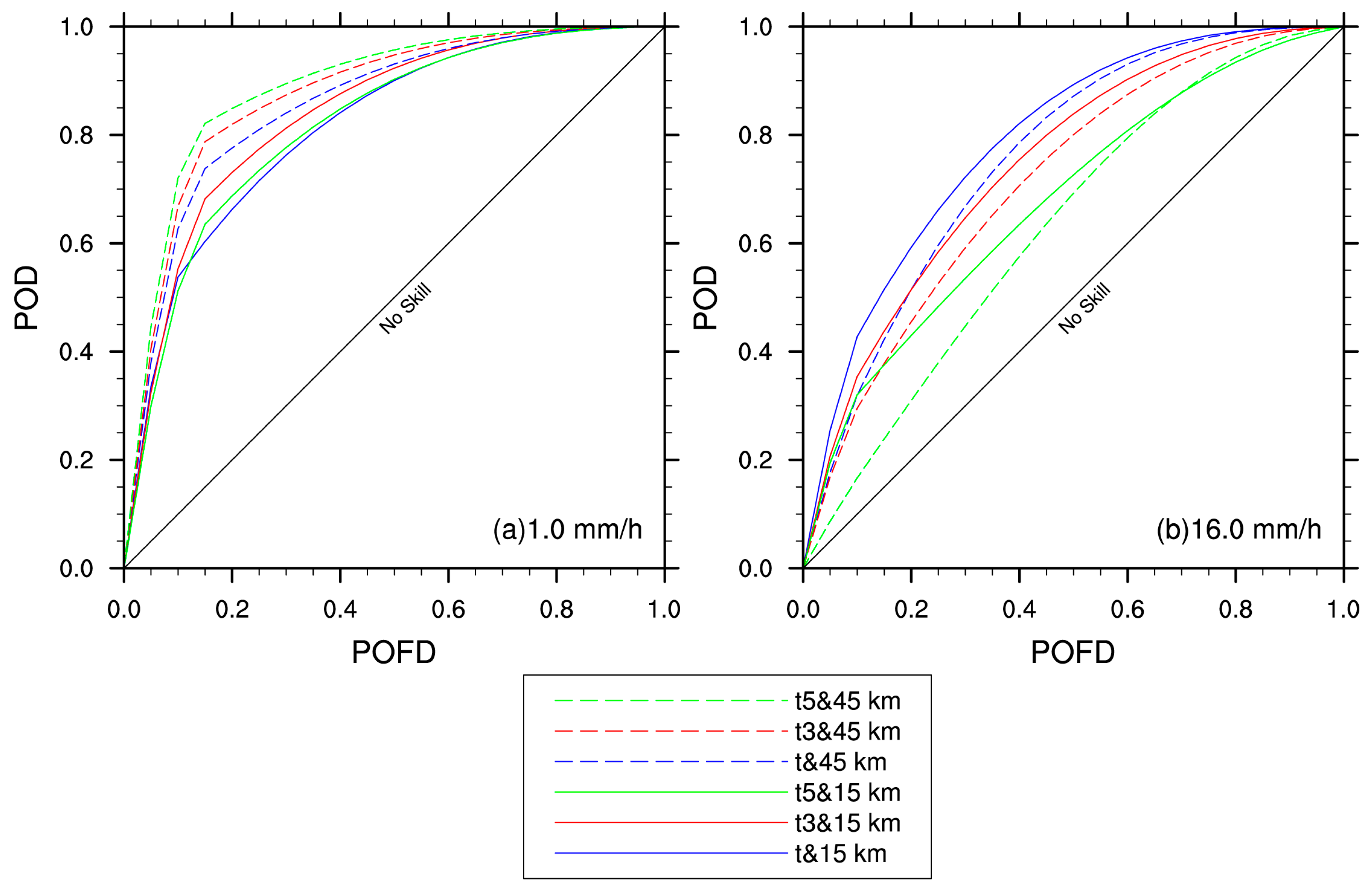
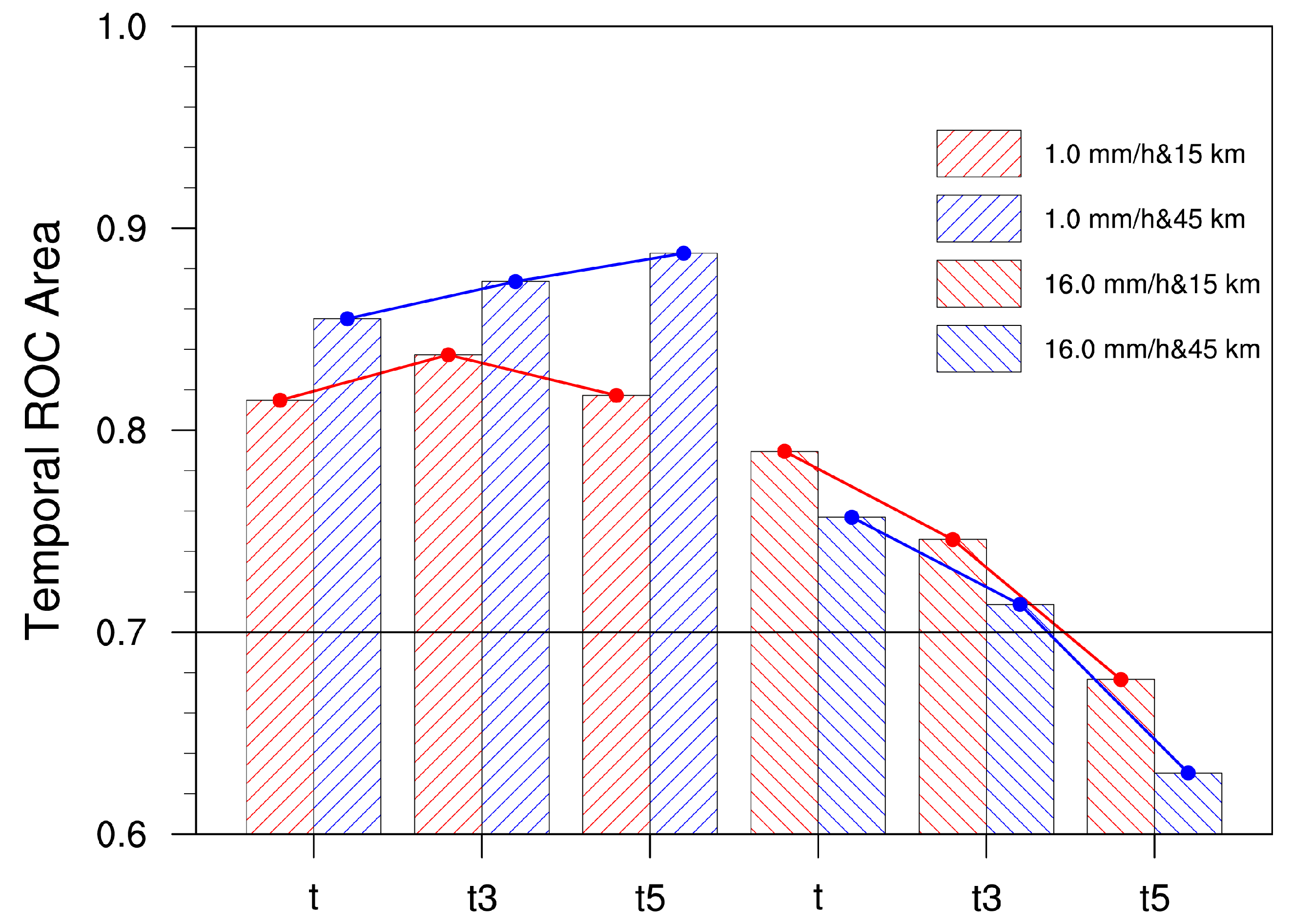
5.1.3. ROC Curves of Spatial Neighborhood
5.2. The Results of Temporal Neighborhood
5.2.1. FSS of Temporal Neighborhood Included
5.2.2. Distribution of Temporal Neighborhood Probability
5.2.3. ROC Curves of Temporal Neighborhood
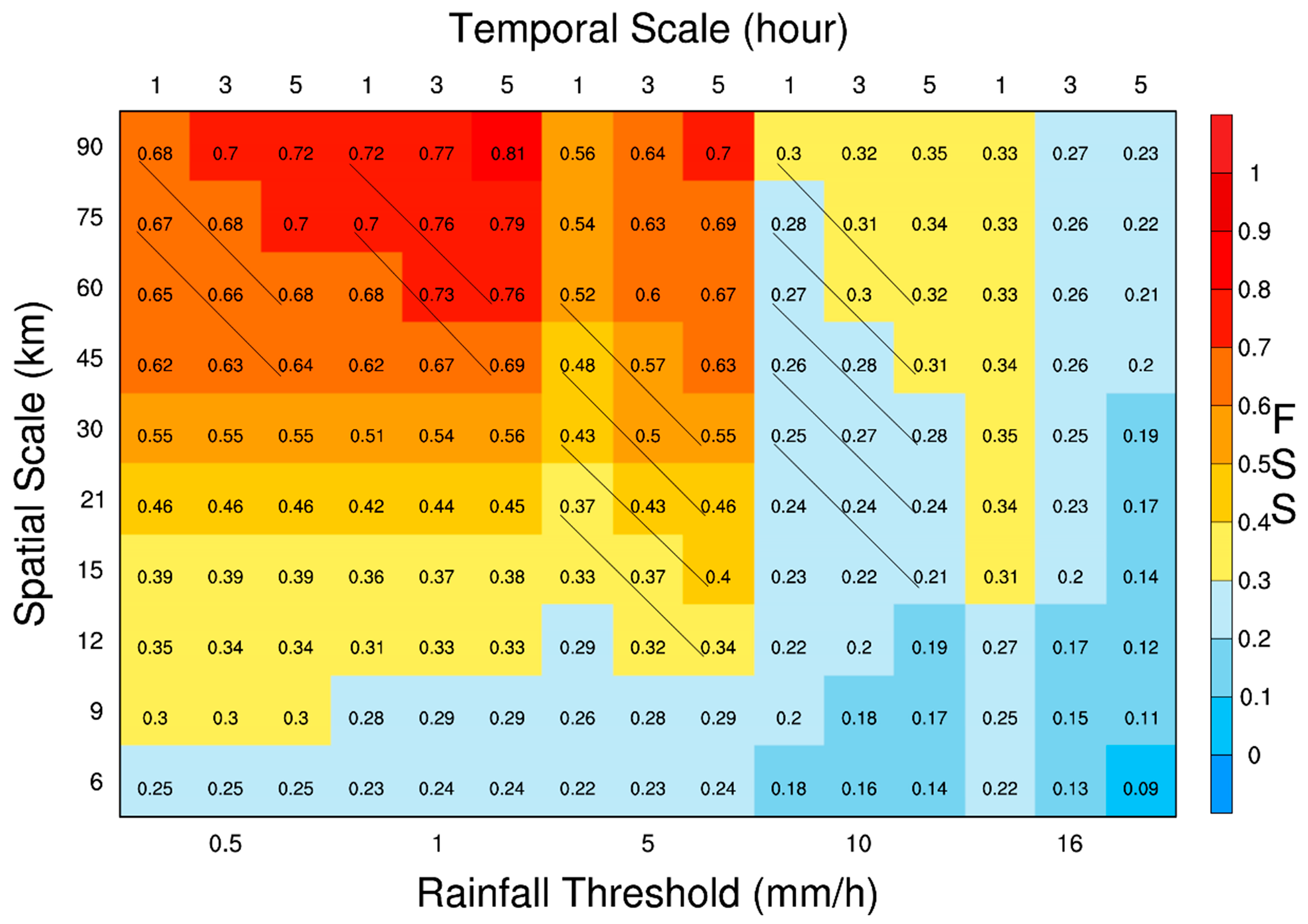
5.3. Comprehensive FSS of Spatial-Temporal Scales
6. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Tennant, W. Improving initial condition perturbations for MOGREPS-UK. Q. J. R. Meteorol. Soc. 2015, 141, 2324–2336. [Google Scholar] [CrossRef]
- Bentzien, S.; Friederichs, P. Generating and calibrating probabilistic quantitative precipitation forecasts from the high-resolution NWP model COSMO-DE. Weather Forecast. 2012, 27, 988–1002. [Google Scholar] [CrossRef]
- Kühnlein, C.; Keil, C.; Craig, G.C.; Gebhardt, C. The impact of downscaled initial condition perturbations on convective-scale ensemble forecasts of precipitation. Q. J. R. Meteorol. Soc. 2014, 140, 1552–1562. [Google Scholar] [CrossRef]
- Schwartz, C.S.; Romine, G.S.; Weisman, M.L.; Sobash, R.A.; Fossell, K.R.; Manning, K.W.; Trier, S.B. A Real-Time Convection-Allowing Ensemble Prediction System Initialized by Mesoscale Ensemble Kalman Filter Analyses. Weather Forecast. 2015, 30, 1158–1181. [Google Scholar] [CrossRef]
- Schwartz, C.S.; Romine, G.S.; Sobash, R.A.; Fossell, K.R.; Weisman, M.L. NCAR’s Experimental Real-Time Convection-Allowing Ensemble Prediction System. Weather Forecast. 2015, 30, 1645–1654. [Google Scholar] [CrossRef]
- Xue, M.; Kong, F.; Weber, D.; Thomas, K.W.; Wang, Y.; Brewster, K.; Droegemeier, K.K.; Kain, J.S.; Weiss, S.J.; Bright, D.R.; et al. CAPS Realtime Storm-scale Ensemble and High-resolution Forecasts as Part of the NOAA Hazardous Weather Testbed 2007 Spring Experiment. In Proceedings of the 22th Conference on Weather Analysis and Forecasting, 18th Conference on Numerical Weather Prediction, Park City, UT, USA, 25–29 June 2007. [Google Scholar]
- Kong, F.; Xue, M.; Thomas, K.W.; Droegemeier, K.K.; Wang, Y.H.; Brewster, K.; Gao, J.D. Real-time storm-scale ensemble forecast experiment—Analysis of 2008 spring experiment data. In Proceedings of the 24th Conference on Several Local Storms, Savannah, GA, USA, 27–31 October 2008. [Google Scholar]
- Kong, F.; Xue, M.; Thomas, K.W.; Wang, Y.H.; Brewster, K.; Gao, J.D.; Droegemeier, K.K. A realtime storm-scale ensemble forecast system: 2009 spring experiment. In Proceedings of the 23th Conference on Weather Analysis and Forecasting, 19th Conference on Numerical Weather Prediction, Omaha, NE, USA, 1–5 June 2009. [Google Scholar]
- Xue, M.; Kong, F.; Thomas, K.W.; Wang, Y.H.; Brewster, K.; Gao, J.D.; Wang, X.G.; Weiss, S. CAPS Realtime Storm Scale Ensemble and High Resolution Forecasts for the NOAA Hazardous Weather Testbed 2010 Spring Experiment. In Proceedings of the 25th Conference on Several Local Storms, Denver, CO, USA, 11–14 October 2010. [Google Scholar]
- Clark, A.J.; Weiss, S.J.; Kain, J.S.; Jirak, I.L.; Coniglio, M.; Melick, C.J. An Overview of the 2010 Hazardous Weather Testbed Experimental Forecast Program Spring Experiment. Bull. Am. Meteorol. Soc. 2012, 93, 55–74. [Google Scholar] [CrossRef]
- Li, X.; He, H.; Chen, C.; Miao, Z.; Bai, S. A Convection-allowing ensemble forecast based on the breeding growth method and associated optimization of precipitation forecast. J. Meteorol. Res. 2017, 31, 955–964. [Google Scholar] [CrossRef]
- Zhuang, X.R.; Min, J.Z.; Wang, S.Z.; Zhou, K.; Cai, Y.C. A blending method for storm-scale ensemble forecast and its application to Beijing extreme precipitation event on July 21, 2012. Chin. J. Atmos. Sci. 2017, 41, 30–42. [Google Scholar] [CrossRef]
- Cai, Y.C.; Min, J.Z.; Zhuang, X.R. Comparison of different stochastic physics perturbation schemes on a storm-scale ensemble forecast in a heavy rain event. Plateau Meteorol. 2017, 36, 407–423. [Google Scholar] [CrossRef]
- Baldwin, M.E.; Kain, J.S. Sensitivity of Several Performance Measures to Displacement Error, Bias, and Event Frequency. Weather Forecast. 2006, 21, 636–648. [Google Scholar] [CrossRef]
- Schwartz, C.S.; Kain, J.S.; Weiss, S.J.; Xue, M.; Bright, D.R.; Kong, F.Y.; Thomas, K.W.; Levit, J.J.; Coniglio, M.C.; Wandishin, M.S. Toward Improved Convection-Allowing Ensembles: Model Physics Sensitivities and Optimizing Probabilistic Guidance with Small Ensemble Membership. Weather Forecast. 2010, 25, 263–280. [Google Scholar] [CrossRef]
- Mittermaier, M.P.; Roberts, N.M. Intercomparison of Spatial Forecast Verification Methods: Identifying Skillful Spatial Scales Using the Fractions Skill Score. Weather Forecast. 2010, 25, 343–354. [Google Scholar] [CrossRef]
- Ebert, E.E. Fuzzy verification of high-resolution gridded forecasts: A review and proposed framework. Meteorol. Appl. 2008, 15, 51–64. [Google Scholar] [CrossRef]
- Roberts, N.M.; Lean, H.W. Scale-Selective Verification of Rainfall Accumulations from High-Resolution Forecasts of Convective Events. Mon. Weather Rev. 2008, 136, 78–97. [Google Scholar] [CrossRef]
- Weusthoff, T.; Ament, F.; Arpagaus, M.; Rotach, M.W. Assessing the Benefits of Convection-Permitting Models by Neighborhood Verification: Examples from MAP D-PHASE. Mon. Weather Rev. 2010, 138, 3418–3433. [Google Scholar] [CrossRef]
- Clark, A.J.; Kain, J.S.; Stensrud, D.J.; Xue, M.; Kong, F.Y.; Coniglio, M.C.; Thomas, K.W.; Wang, Y.H.; Brewster, K.; Gao, J.D.; et al. Probabilistic Precipitation Forecast Skill as a Function of Ensemble Size and Spatial Scale in a Convection-Allowing Ensemble. Mon. Weather Rev. 2011, 139, 1410–1418. [Google Scholar] [CrossRef]
- Pan, L.J.; Zhang, H.F.; Chen, X.T.; Wang, J.P.; Chen, F.J. Neighborhood-based precipitation forecasting capability analysis of high-resolution models. J. Trop. Meteorol. 2015, 31, 632–642. [Google Scholar] [CrossRef]
- Kong, F.Y.; Droegemeier, K.K.; Hickmon, N.L. Multiresolution Ensemble Forecasts of an Observed Tornadic Thunderstorm System. Part I: Comparsion of Coarse- and Fine-Grid Experiments. Mon. Weather Rev. 2006, 134, 807–833. [Google Scholar] [CrossRef]
- Clark, A.J.; Gallus, W.A.; Xue, M.; Kong, F.Y. A comparison of precipitation forecast skill between small convection-allowing and large convection-parameterizing ensembles. Weather Forecast. 2009, 24, 1121–1140. [Google Scholar] [CrossRef]
- Ebert, E.E. Ability of a Poor Man’s Ensemble to Predict the Probability and Distribution of Precipitation. Mon. Weather Rev. 2001, 129, 2461–2480. [Google Scholar] [CrossRef]
- Berenguer, M.; Surcel, M.; Zawadzki, I.; Xue, M.; Kong, F.Y. The Diurnal Cycle of Precipitation from Continental Radar Mosaics and Numerical Weather Prediction Models. Part II: Intercomparison among Numerical Models and with Nowcasting. Mon. Weather Rev. 2012, 140, 2689–2705. [Google Scholar] [CrossRef]
- Schwartz, C.S.; Romine, G.S.; Smith, K.R.; Weisman, M.L. Characterizing and Optimizing Precipitation Forecasts from a Convection-Permitting Ensemble Initialized by a Mesoscale Ensemble Kalman Filter. Weather Forecast. 2014, 29, 1295–1318. [Google Scholar] [CrossRef]
- Ebert, E.E. Neighborhood Verification: A Strategy for Rewarding Close Forecasts. Weather Forecast. 2009, 24, 1498–1510. [Google Scholar] [CrossRef]
- Schwartz, C.S.; Kain, J.S.; Weiss, S.J.; Xue, M.; Bright, D.R.; Kong, F.Y.; Thomas, K.W.; Levit, J.J.; Coniglio, M.C. Next-Day Convection-Allowing WRF Model Guidance: A Second Look at 2-km versus 4-km Grid Spacing. Mon. Weather Rev. 2009, 137, 3351–3372. [Google Scholar] [CrossRef]
- Stensrud, D.J.; Yussouf, N. Reliable Probabilistic Quantitative Precipitation Forecasts from a Short-Range Ensemble Forecasting System. Weather Forecast. 2007, 22, 3–17. [Google Scholar] [CrossRef]
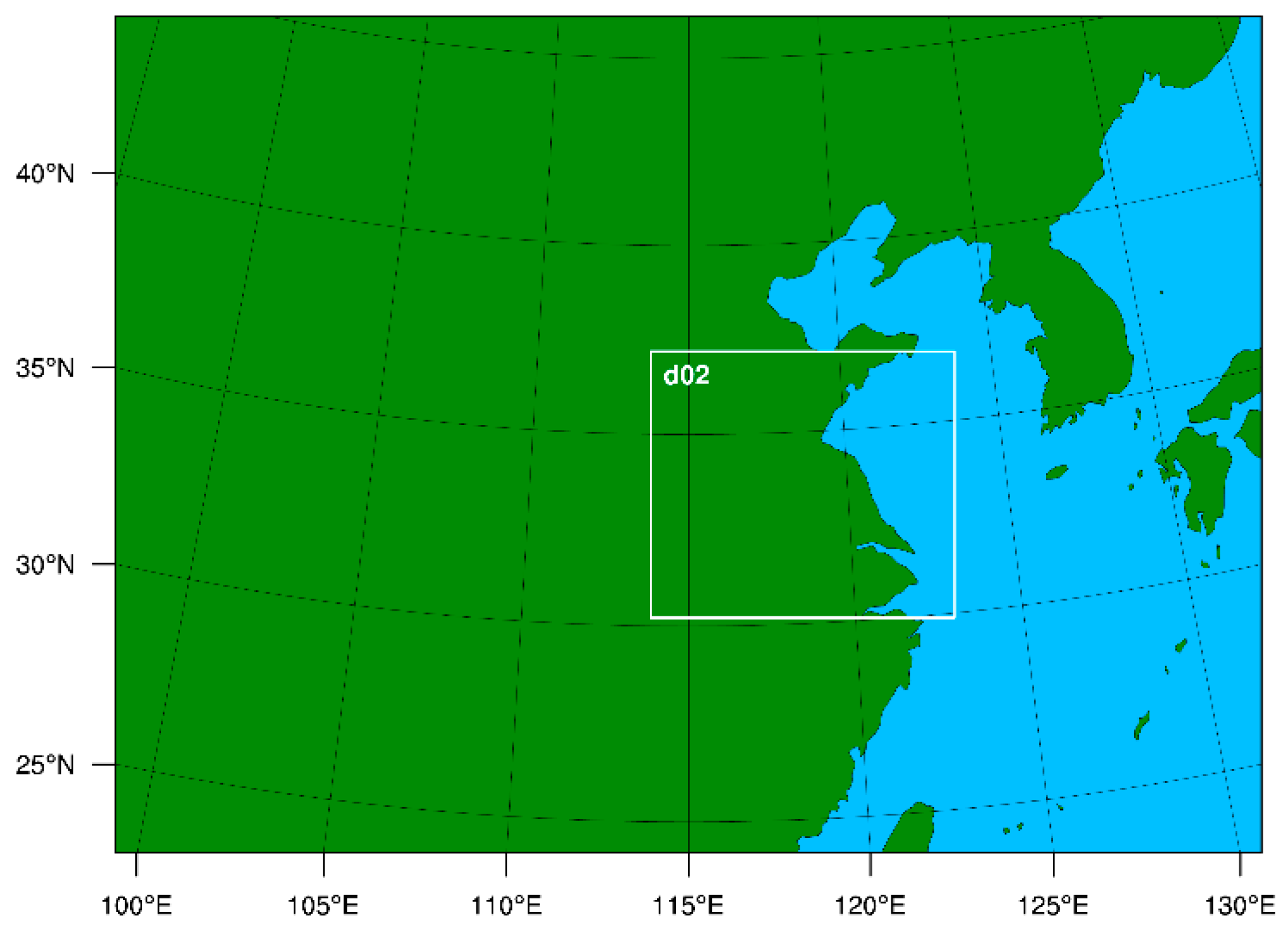
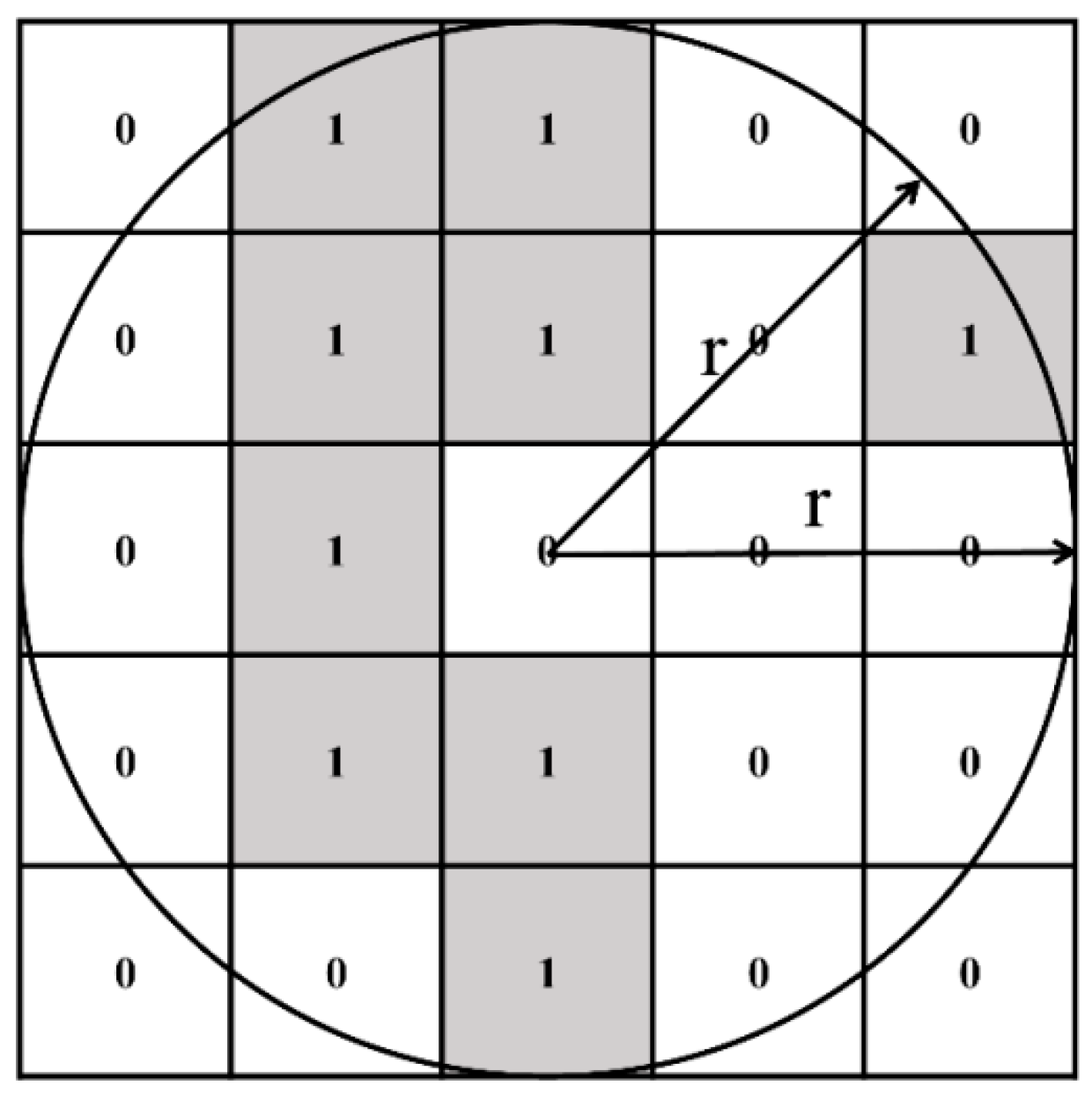
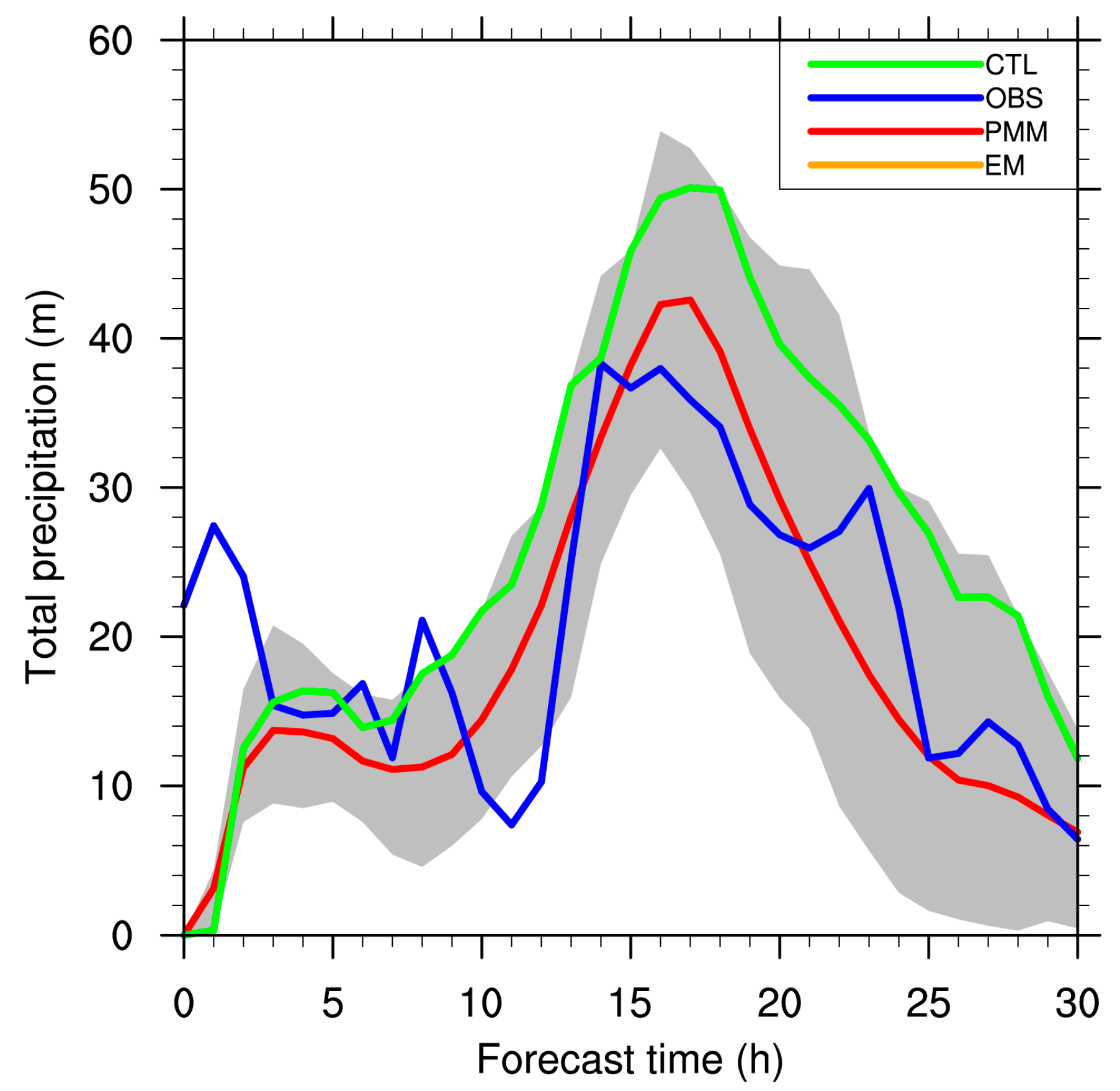
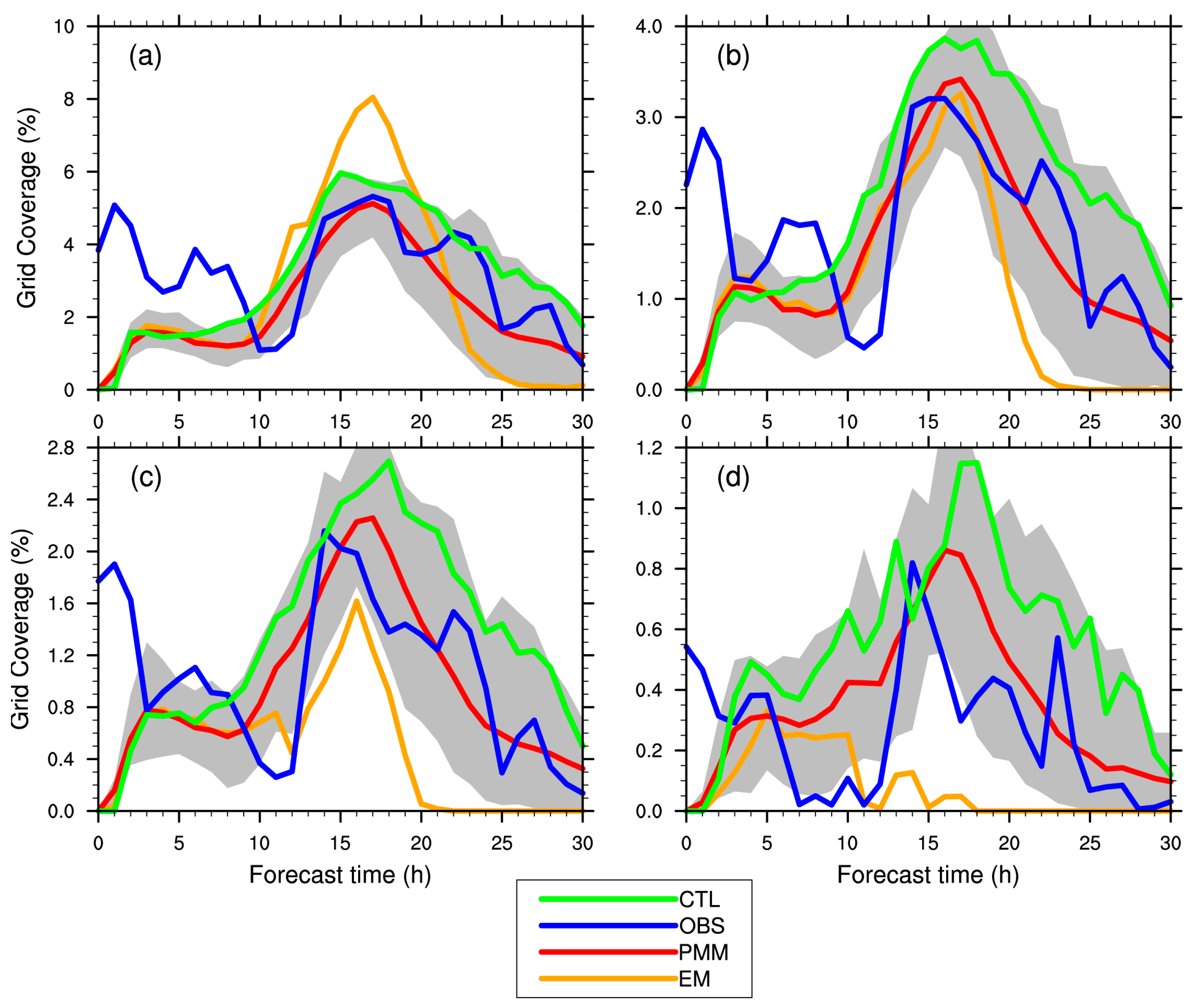



| Physical Parameterization | Outer Domain (d01) | Inner Domain (d02) |
|---|---|---|
| Cumulus | Grell-Freitas scheme | None |
| Microphysics | Morrison double-moment scheme | |
| Longwave radiation | Rapid Radiative Transfer Model scheme (RRTM) | |
| Shortwave radiation | Dudhia scheme | |
| Planetary boundary layer | Yonsei University scheme | |
| Land surface | Noah land surface model | |
| Observed | ||||
| Yes | No | |||
| Forecast | Yes | a | b | a + b |
| No | c | d | c + d | |
| a + c | b + d | |||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, S.; Chen, C.; He, H.; Wu, D.; Zhang, C. Assessing the Skill of Convection-Allowing Ensemble Forecasts of Precipitation by Optimization of Spatial-Temporal Neighborhoods. Atmosphere 2018, 9, 43. https://doi.org/10.3390/atmos9020043
Ma S, Chen C, He H, Wu D, Zhang C. Assessing the Skill of Convection-Allowing Ensemble Forecasts of Precipitation by Optimization of Spatial-Temporal Neighborhoods. Atmosphere. 2018; 9(2):43. https://doi.org/10.3390/atmos9020043
Chicago/Turabian StyleMa, Shenjia, Chaohui Chen, Hongrang He, Dan Wu, and Chenxi Zhang. 2018. "Assessing the Skill of Convection-Allowing Ensemble Forecasts of Precipitation by Optimization of Spatial-Temporal Neighborhoods" Atmosphere 9, no. 2: 43. https://doi.org/10.3390/atmos9020043
APA StyleMa, S., Chen, C., He, H., Wu, D., & Zhang, C. (2018). Assessing the Skill of Convection-Allowing Ensemble Forecasts of Precipitation by Optimization of Spatial-Temporal Neighborhoods. Atmosphere, 9(2), 43. https://doi.org/10.3390/atmos9020043




