An Analysis of Dynamic Instability on TC-Like Vortex Using the Regularization-Based Eigenmode Linear Superposition Method
Abstract
1. Introduction
2. Introduction of the Basic Equations and Method
2.1. Basic Equations and Numerical Methods for the Stability Analysis
2.2. Regularization Method
3. Numerical Model and Application of Regularization Method
3.1. Basic State Votex and Its Stability
3.2. Application of the Regularization Method
3.2.1. Determination of the Regularization Parameter
3.2.2. Distribution of the Mode Coefficients
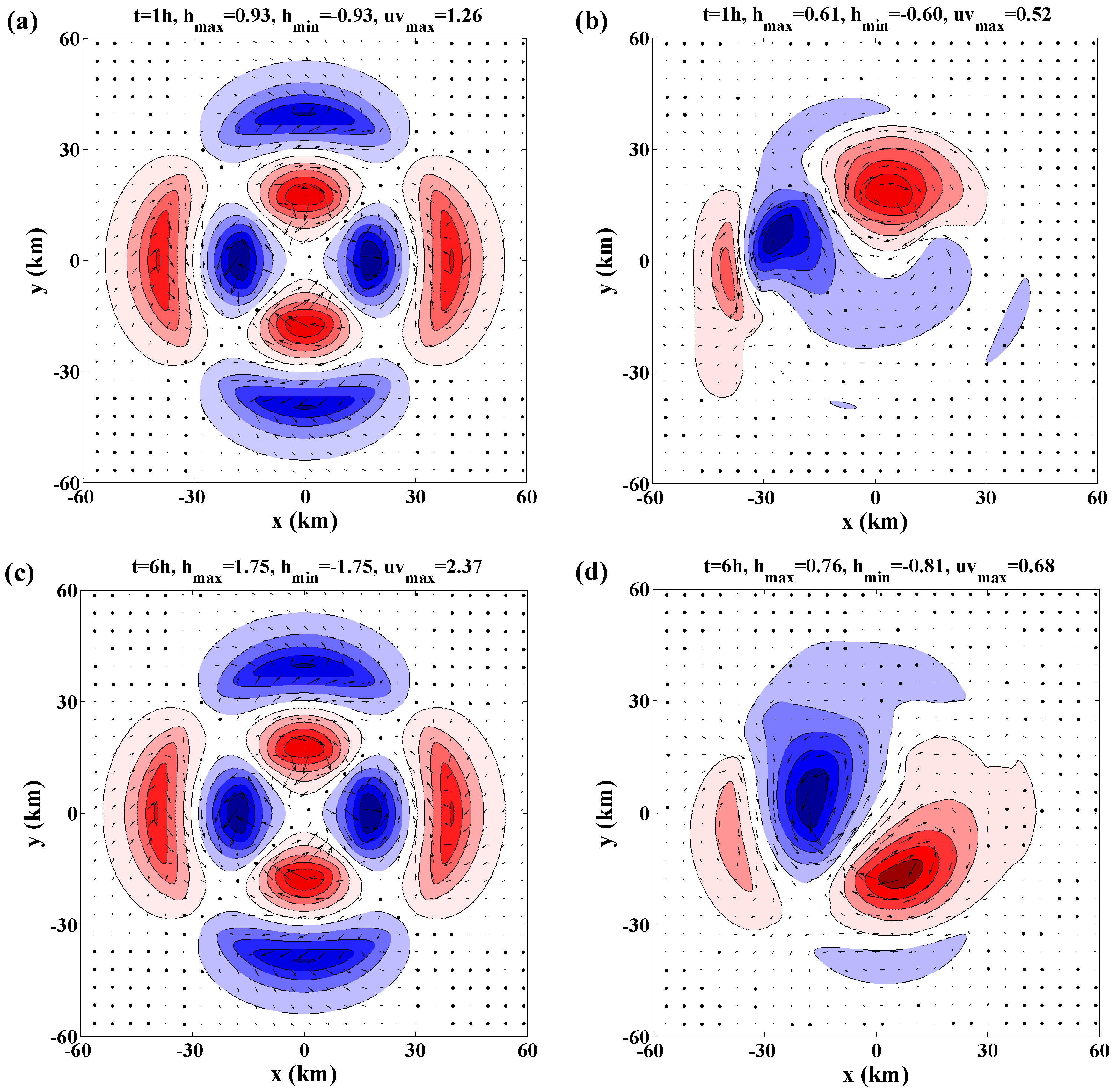
3.2.3. The Results of the Mode Linear Superposition
4. The Application of Mode Analysis in TC Dynamics
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Montgomery, M.T.; Kallenbach, R.J. A theory for vortex Rossby-waves and its application to spiral bands and intensity changes in hurricanes. Q. J. R. Meteorol. Soc. 1997, 123, 435–465. [Google Scholar] [CrossRef]
- Schubert, W.H.; Montgomery, M.T.; Taft, R.K.; Guinn, T.A.; Fulton, S.R.; Kossin, J.P.; Edwards, J.P. Polygonal eyewalls, asymmetric eye contraction, and potential vorticity mixing in hurricanes. J. Atmos. Sci. 1999, 56, 1197–1223. [Google Scholar] [CrossRef]
- Wang, Y. Vortex Rossby waves in a numerically simulated tropical cyclone. Part I: Overall structure, potential vorticity, and kinetic energy budgets. J. Atmos. Sci. 2002, 59, 1213–1238. [Google Scholar] [CrossRef]
- Wang, Y. Vortex Rossby waves in a numerically simulated tropical cyclone. Part II: The role in tropical cyclone structure and intensity changes. J. Atmos. Sci. 2002, 59, 1239–1262. [Google Scholar] [CrossRef]
- Schecter, D.A.; Montgomery, M.T. Damping and pumping of a vortex Rossby wave in a monotonic cyclone: Critical layer stirring versus inertia-buoyancy wave emission. Phys. Fluids 2004, 16, 1334–1348. [Google Scholar] [CrossRef]
- Schecter, D.A.; Montgomery, M.T. Conditions that inhibit the spontaneous radiation of spiral inertia–gravity waves from an intense mesoscale cyclone. J. Atmos. Sci. 2006, 63, 435–456. [Google Scholar] [CrossRef]
- Schecter, D.A. The spontaneous imbalance of an atmospheric vortex at high Rossby number. J. Atmos. Sci. 2008, 65, 2498–2521. [Google Scholar] [CrossRef]
- Montgomery, M.T.; Nicholls, M.E.; Cram, T.A.; Saunders, A. A vortical hot tower route to tropical cyclogenesis. J. Atmos. Sci. 2006, 63, 355–386. [Google Scholar] [CrossRef]
- Nguyen, S.; Smith, R.; Montgomery, M.T. Tropical-cyclone intensification and predictability in three dimensions. Q. J. R. Meteorol. Soc. 2008, 134, 563–582. [Google Scholar]
- Moller, J.; Montgomery, M.T. Vortex Rossby waves and hurricane intensification in a barotropic model. J. Atmos. Sci. 1999, 56, 1674–1687. [Google Scholar] [CrossRef]
- Moller, J.; Montgomery, M. Tropical cyclone evolution via potential vorticity anomalies in a three-dimensional balance model. J. Atmos. Sci. 2000, 57, 3366–3387. [Google Scholar] [CrossRef]
- Nolan, D.S.; Montgomery, M.T. Nonhydrostatic, three-dimensional perturbations to balanced, hurricane-like vortices. Part I: Linearized formulation, stability, and evolution. J. Atmos. Sci. 2002, 59, 2989–3020. [Google Scholar] [CrossRef]
- Kossin, J.P.; Eastin, M.D. Two distinct regimes in the kinematic and thermodynamic of the hurricane eye and eyewall. J. Atmos. Sci. 2001, 58, 1079–1090. [Google Scholar] [CrossRef]
- Menelaou, K.; Yau, M.K.; Martinez, Y. On the dynamics of the secondary eyewall genesis in Hurricane Wilma (2005). Geophys. Res. Lett. 2012, 39, L04801. [Google Scholar] [CrossRef]
- Montgomery, M.T.; Shapiro, L.J. Generalized CharneyStern and Fjørtoft theorems for rapidly rotating vortices. J. Atmos. Sci. 1995, 52, 1829–1833. [Google Scholar] [CrossRef]
- Rozoff, C.M.; Kossin, J.P.; Schubert, W.H.; Mulero, P.J. Internal control of hurricane intensity: The dual nature of potential vorticity mixing. J. Atmos. Sci. 2009, 66, 133–147. [Google Scholar] [CrossRef]
- Hendricks, E.A.; Schubert, W.H.; Taft, R.K.; Wang, H.; Kossin, J.P. Life cycles of hurricane-like vorticity rings. J. Atmos. Sci. 2009, 66, 705–722. [Google Scholar] [CrossRef]
- Schecter, D.A.; Dubin, D.H.E.; Cass, A.C.; Driscoll, C.F.; Lansky, I.M.; O’Neil, T.M. Inviscid damping of asymmetries on a two-dimensional vortex. Phys. Fluids 2000, 12, 2397. [Google Scholar] [CrossRef]
- Montgomery, M.T.; Lu, C. Free waves on barotropic vortices. Part I: Eigenmode structure. J. Atmos. Sci. 1997, 54, 1868–1885. [Google Scholar] [CrossRef]
- Zhong, W.; Zhang, D.L. An Eigenfrequency Analysis of Mixed Rossby–Gravity Waves on Barotropic Vortices. J. Atmos. Sci. 2014, 71, 2186–2203. [Google Scholar] [CrossRef]
- Martinez, Y.H.; Brunet, G.; Yau, M.K. On the dynamics of 2D hurricane-like vortex symmetrization. J. Atmos. Sci. 2010, 67, 3559–3580. [Google Scholar] [CrossRef]
- Menelaou, K.; Yau, M.K.; Martinez, Y. Impact of asymmetric dynamical processes on the structure and intensity change of two-dimensional hurricane-like annular vortices. J. Atmos. Sci. 2013, 70, 559–582. [Google Scholar] [CrossRef]
- Flatau, M.; Stevens, D.E. Barotropic and inertial insta-bilities in the hurricane outflow layer. Geophys. Astrophys. Fluid Dyn. 1989, 47, 1–18. [Google Scholar] [CrossRef]
- Nolan, D.S.; Montgomery, M.T.; Grasso, L.D. The wavenumber-one instability and trochoidal motion of TC-like vortices. J. Atmos. Sci. 2001, 58, 3243–3270. [Google Scholar] [CrossRef]
- Tikhonov, A.; Arsenin, V. Solutions to Ill-Posed Problems; V. H. Winston & Sons: Washington, DC, USA, 1977; p. 491. [Google Scholar]
- Shen, Y.Z.; Xu, H. Spectral decomposition formula of regularization solution for ill-posed equation. J. Geod. Geodyn. 2002, 22, 10–14. (In Chinese) [Google Scholar] [CrossRef]
- Zhou, J.W.; Ou, J.K. On alteration of quasi-stable points and some problems concerning free net adjustment. Acta Geod. Cartogr. Sin. 1984, 13, 161–170. (In Chinese) [Google Scholar]
- Tikhonov, A.N. On the solution of incorrectly posed problem and the method of regularization. Sov. Math. 1963, 4, 1035–1038. [Google Scholar]
- Phillips, D.L. A technique for the numerical solution of certain integral equations of the first kind. J. Assoc. Comput. Mach. 1962, 9, 84–97. [Google Scholar] [CrossRef]
- Golub, G.H.; Heath, M.; Wahba, G. Generalized cross-validation as a method for choosing a good ridge parameter. Technometrios 1979, 21, 215–223. [Google Scholar] [CrossRef]
- Hansen, P.C.; O’Leary, D.P. The use of the L-curve in the regularization of discrete ill-posed problems. SIAM J. Sci. Comput. 1993, 14, 1487–1503. [Google Scholar] [CrossRef]
- Nolan, D.S.; Montgomery, M.T. The algebraic growth of wavenumber one disturbances in hurricane-like vorticies. J. Atmos. Sci. 2000, 57, 3514–3538. [Google Scholar] [CrossRef]
- Zhong, W.; Zhang, D.L.; Lu, H.C. A theory for mixed vortex Rossby-gravity waves in tropical cyclones. J. Atmos. Sci. 2009, 66, 3366–3381. [Google Scholar] [CrossRef]
- Zhong, W.; Lu, H.C.; Zhang, D.L. Mesoscale barotropic instability of vortex Rossby waves in tropical cyclones. Adv. Atmos. Sci. 2010, 27, 243–252. [Google Scholar] [CrossRef]
- Kossin, J.P.; Schubert, W.H. Mesovortices, polygonal flow patterns, and rapid pressure falls in hurricane-like vortices. J. Atmos. Sci. 2001, 58, 2196–2209. [Google Scholar] [CrossRef]
- Hendricks, E.A. Tropical Cyclone Evolution via Internal Asymmetric Dynamics. Ph.D. Thesis, Colorado State University, Fort Collins, CO, USA, 2008; 150p. [Google Scholar]
- Hendricks, E.A.; Schubert, R.K.; Chen, Y.H. Hurricane eyewall evolution in a forced shallow-water model. J. Atmos. Sci. 2014, 71, 1623–1643. [Google Scholar] [CrossRef]
- Liu, S.; Zhong, W.; Lu, H.C.; Liu, J.C. The contribution of structure and evolution of potential vorticity tower to the intensity change of Hurricane Wilma (2005). Chin. J. Geophys. 2015, 58, 1513–1525. (In Chinese) [Google Scholar] [CrossRef]
- Boyd, J.P. Chebyshev and Fourier Spectral Methods; Courier Corporation Press: Mineola, NY, USA, 2001; 689p. [Google Scholar]
- Lonfat, M.; Chen, S.S.; Mark, F.D. Precipitation distribution in tropical cyclones using the Tropical Rainfall Measuring Mission (TRMM) microwave imager: A global perspective. Mon. Weather Rev. 2004, 132, 1645–1660. [Google Scholar] [CrossRef]
- Yang, L.; Fei, J.-F.; Huang, X.-G. Asymmetric distribution of convection in tropical cyclones over the Western North Pacific Ocean. Adv. Atmos. Sci. 2016, 33, 1306–1321. [Google Scholar] [CrossRef]
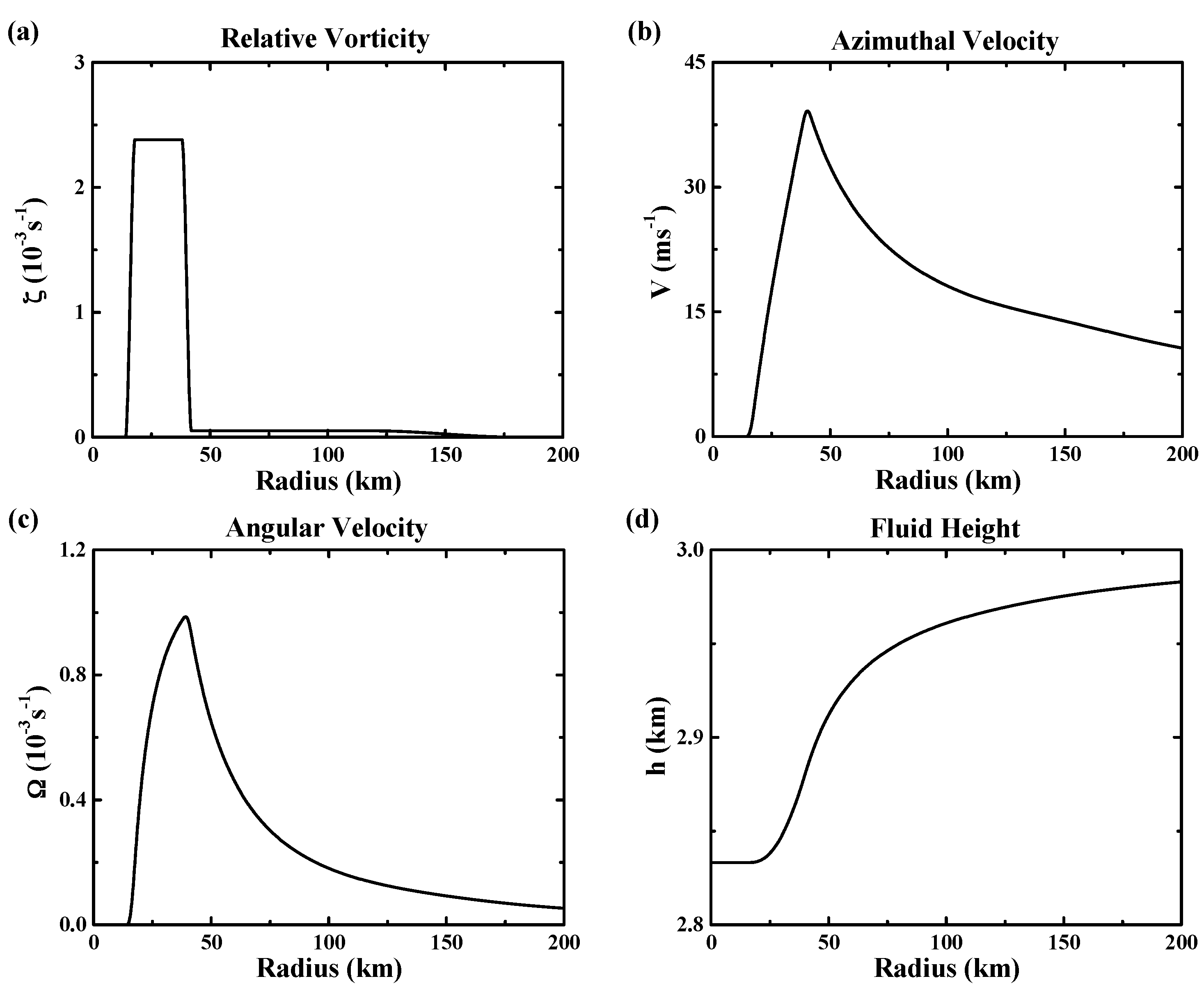
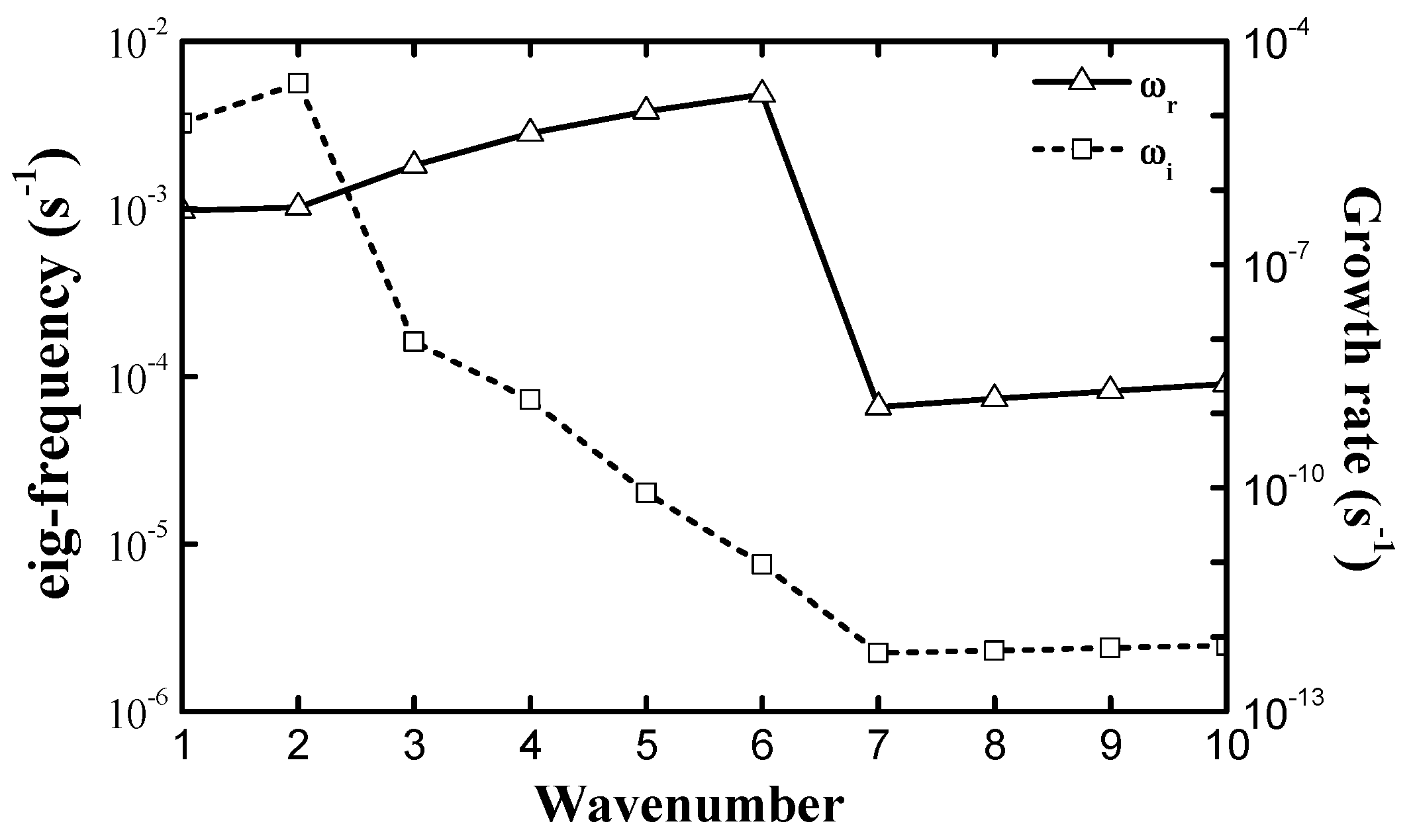
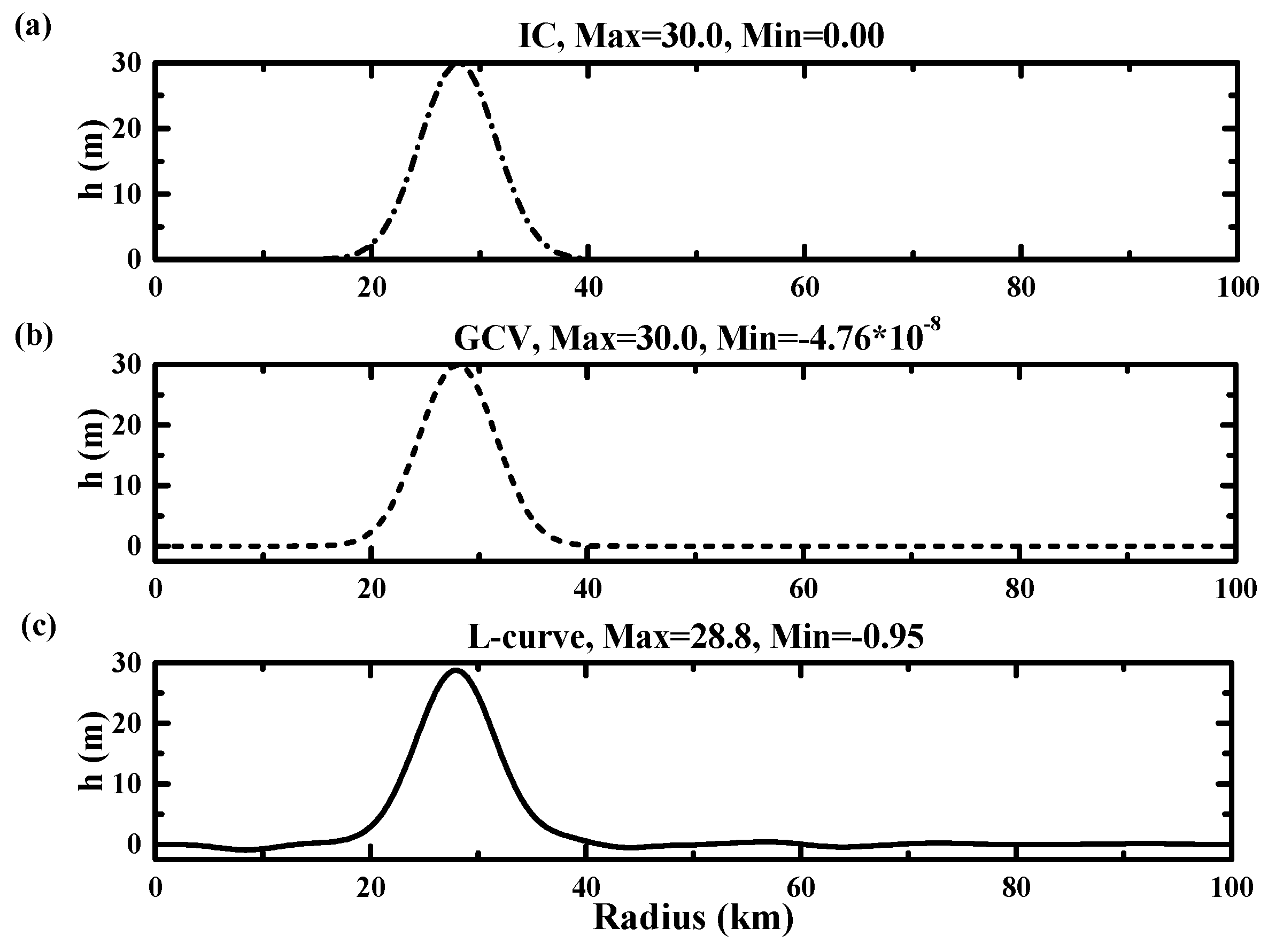

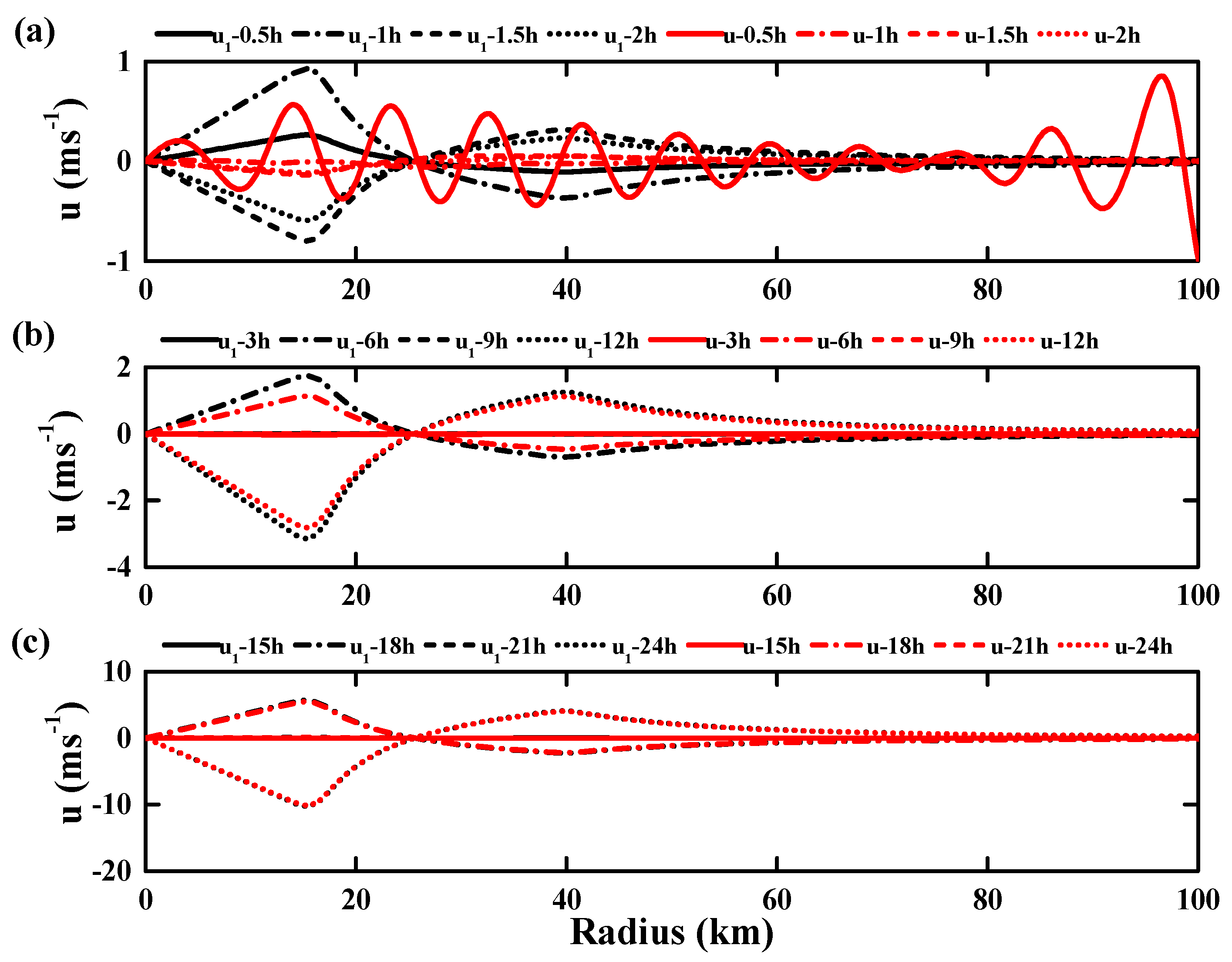

| Parameter | ζ1 (s−1) | ζ2 | ζ3 | r1 (km) | r2 | r3 | r4 | r5 | r6 |
|---|---|---|---|---|---|---|---|---|---|
| value | 0.0 | 1.68 × 10−3 | 1.0 × 10−4 | 14 | 18 | 38 | 42 | 120 | 180 |
© 2018 by the authors. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Zhong, W.; Liu, Y.; Xiang, J. An Analysis of Dynamic Instability on TC-Like Vortex Using the Regularization-Based Eigenmode Linear Superposition Method. Atmosphere 2018, 9, 26. https://doi.org/10.3390/atmos9010026
Liu S, Zhong W, Liu Y, Xiang J. An Analysis of Dynamic Instability on TC-Like Vortex Using the Regularization-Based Eigenmode Linear Superposition Method. Atmosphere. 2018; 9(1):26. https://doi.org/10.3390/atmos9010026
Chicago/Turabian StyleLiu, Shuang, Wei Zhong, Yudi Liu, and Jie Xiang. 2018. "An Analysis of Dynamic Instability on TC-Like Vortex Using the Regularization-Based Eigenmode Linear Superposition Method" Atmosphere 9, no. 1: 26. https://doi.org/10.3390/atmos9010026
APA StyleLiu, S., Zhong, W., Liu, Y., & Xiang, J. (2018). An Analysis of Dynamic Instability on TC-Like Vortex Using the Regularization-Based Eigenmode Linear Superposition Method. Atmosphere, 9(1), 26. https://doi.org/10.3390/atmos9010026




