Abstract
The Three Gorges Dam (TGD) is one of the largest hydroelectric projects in the world. Monitoring the spatiotemporal distribution of extreme precipitation offers valuable information for adaptation and mitigation strategies and reservoir management schemes. This study examined variations in extreme precipitation over the Three Gorges Reservoir area (TGRA) in China to investigate the potential role of climate warming and Three Gorges Reservoir (TGR). The trends in extreme precipitation over the TGRA were investigated using the iterative-based Mann–Kendall (MK) test and Sen’s slope estimator, based on weather station daily data series and TRMM (Tropical Rainfall Measuring Mission) data series. The mean and density distribution of extreme precipitation indices between pre-dam and post-dam, pre-1985 and post-1985, and near and distant reservoir area were assessed by the Mann–Whitney test and the Kolmogorov–Smirnov test. The ratio of extreme precipitation to non-extreme precipitation became larger. The precipitation was characterized by increases in heavy precipitation as well as decreases in light and moderate rain. Comparing extreme precipitation indices between pre-1985 (cooling) and post-1985 (warming) indicated extreme precipitation has changed to become heavier. Under climate warming, the precipitation amount corresponding to more than the 95th percentile increased at the rate of 6.48%/°C. Results from comparing extreme precipitation for the pre- and post-dam, near reservoir area (NRA) and away from the reservoir area (ARA) imply an insignificant role of the TGR on rainfall extremes over the TGRA. Moreover, the impoundment of TGR did not exert detectable impacts on the surface relative humidity (RH) and water vapor pressure (WP).
1. Introduction
Rainfall extremes could have many negative effects on the environment and the human population. The frequent occurrence of rainfall extremes produces multiple disasters, including urban flooding, server soil erosion, landslides and debris flows [1]. Moreover, rainfall extremes affect the ecological process of the terrestrial ecosystem [2,3]. The spatial patterns of extreme precipitation trends exhibit heterogeneous characteristics, especially at a smaller scale, due to factors including warming, water vapor trends and topography differences [4,5].
Rainfall extremes have been reported to become more frequent under warming conditions [6,7]. Due to global warming, the atmospheric water-holding capacity would increase at the rate of 7%/°C (described by the Clausius–Clapeyron (CC) relationship) [8]. A higher atmospheric water content increases the possibility of extreme precipitation occurrences. Westra et al. (2013) found that global extreme precipitation changed in proportion to changes in global mean temperature at a rate between 5.9%/°C and 7.7%/°C [7]. Apart from global warming, other anthropogenic factors such as dam construction (hereafter interchanged with reservoirs) will affect extreme precipitation variation [9,10]. Reservoir impoundment would increase the water surface area while the intense moisture-heat exchange in the reservoirs might alter the precipitation pattern. Moreover, dams provide the means for irrigation, so dams trigger regional land use and land cover changes which then could affect the regional climate (temperature and precipitation) [11]. Over the past six decades, the number of dams and reservoirs has increased significantly, and the total area of reservoirs reached 507,102 km2 [12]. Approximately 50,000 large dams (higher than 15 m) were in operation worldwide [13].
The notion that large reservoirs could be expected to alter natural precipitation patterns surrounding dams is nothing new [14]. Hossain et al. (2010) and Yigzaw et al. (2012) show that extreme precipitation (99th percentile) showed a 4% increase per year after dam construction [9,10]. Pizarro et al. (2013) compared the intensity of extreme precipitation located near water bodies to those away from water bodies, revealing higher precipitation intensity at locations closer to water bodies [15].
Recently, many efforts have been made to investigate physical factors to determine how large reservoirs change extreme precipitation patterns. Artificial reservoirs can influence regional convective patterns and associated thunderstorms [16]. A newly formed reservoir can widen open water bodies and enhance the moisture supply for precipitation, hence serving as a feeder for precipitation [17]. Eltahir (1989) concluded that it is highly likely that the open water evaporation from the Bahr River has a significant effect on the climate of the nearby dry regions [18]. Gangoiti et al. (2011) demonstrated that terrestrial evaporation (including from lakes and reservoirs) can play an important role in creating extreme precipitation events [19]. Apart from local evaporative feeder mechanisms triggered by reservoirs, dams can be considered enhancers of convective available potential energy (CAPE), which in turn might induce more precipitation [20]. Degu et al. (2011) found a higher possibility of storm intensification in impounded basins of reservoirs in the Mediterranean and arid climates of the United States [21]. This phenomenon is due to the increasing correlation observed between CAPE and extreme precipitation events. Some dams serve for irrigation, which enhances atmospheric water moisture content through evaporation and transpiration. The added water vapor will result in strong spatial gradients of CAPE, which in turn enhance the likelihood of the formation of convective precipitation [17]. Degu et al. (2011) found a higher possibility of storm intensification in impounded basins of reservoirs in the Mediterranean and arid climate zones of the United States compared to humid climate zones [21].
The Three Gorges Dam (TGD) is the largest hydroelectric dam project in the world [22]. The Three Gorges Reservoir (TGR) has a length of 660 km and 1084 km2 of water surface area, representing a significant land use and evaporation changes that are expected to result in changes in the regional weather and climate patterns [23]. Recently, some climate disaster events appearing near the TGR area urged the public to pay attention to the impact of the TGR on the climatic system. After the TGR began operating, some studies were conducted to investigate the variation characteristic of precipitation [24,25,26,27] and air temperature [28,29]. A numerical model simulated precipitation changes under control and land use change triggered by the TGD and indicated no significant change in precipitation [23]. Wu et al. (2006) detected the influences of the TGD on the precipitation around the vicinity of the TGD using satellite rainfall data during 1998 and 2006 [30]. They concluded that the precipitation amount had increased in the northern part of the TGR and decreased near the TGD. Later, another study proved that this precipitation change characteristic was just part of the natural inter-annual oscillation based on observations before and after 1980 [24]. The TGD began to impound water in 2003. However, the aforementioned study [24] only included a four-year precipitation dataset after impoundment. Annual mean precipitation in the TGRA has been followed closely, while the study of precipitation pattern and heavy precipitation variation was limited. Zhao et al. (2010) examined extreme precipitation changes in the Three Gorges Reservoir Region from 1958 to 2007 [25], and found the changes might have become more frequent after 1980. However, in the Zhao et al. (2010) study, they did not analyze the roles of climate warming and the TGR on extreme precipitation changes. Li et al. (2014) investigated the changes in hourly rainfall during 2009 and 2011 [27]. They found that more intense and longer-duration precipitation was observed in the northern TGR. Due to a lack of high-resolution rainfall data before 2009, this study cannot compare intense rainfall variation with that before the TGD presence.
On the whole, the previous studies paid more attention to annual precipitation changes in the TGRA. Although a few studies involved extreme precipitation, they only presented the long-term change trends in the extreme precipitation. Little evidence is available on what factors affect extreme precipitation in the TGRA. The possible factors influencing changes in extreme precipitation are analyzed based on the longer daily precipitation data series in this study. The roles of climate warming and ENSO (El Niño–Southern Oscillation) on extreme precipitation are discussed. In addition, we attempt to determine whether the impoundment of the TGR changes the extreme precipitation near the TGR.
2. Study Area
The TGR is 660 km long and has an average width of 1.1 km. When the water level reaches 175 m, the TGR has a total area of 1084 km2 and a water storage capacity of 39.3 billion m3. The reservoir began to store water in 2003. The extent of the impact the reservoir can have on the local climate remains controversial. García (1994) found an increase in foggy and rainy days after the operation of dams in Spain and concluded that changes occur only on a local scale of no more than 12 km from the water body [31]. The systematic changes triggered by dams and impounded reservoirs can result in increased local moisture availability and significantly affect mesoscale circulation, which is around 100 km [21,32]. Fu and Zhu (1984) pointed out that the extent affected by the Xinanjiang reservoir is 50–60 km on average [33]. In this study, the region 0–40 km away from the TGR was deemed as the zone of influence of the TGR in the precipitation aspect. To compare the reservoir’s effects on extreme precipitation, the study area was extended from the TGR to around 100 km away. The area 0–100 km away from the TGR was defined as the Three Gorges Reservoir area (TGRA) (Figure 1). The TGRA was categorized into two subareas, including the near reservoir area (NRA) and the area away from the reservoir area (ARA) (Figure 1). The NRA was the area 0–40 km away from the TGR, while the ARA was 40–100 km away from the TGR.
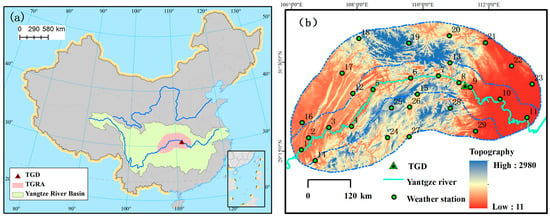
Figure 1.
Location of the Three Gorges Reservoir area (a); the topography of Three Gorges Reservoir area and the location of weather stations (b). Further weather station information is provided in supplemental Table 1.
The mountainous area is mainly in the middle region of the TGRA (Figure 1). The elevation ranges from 11 m to 2980 m. The TGRA is in the transition zone between two monsoon systems: the Asian southeastern summer monsoon and the Indian southwestern monsoon [24]. This climatic feature, combined with local irregular terrain, has shaped the TGR’s complicated rainfall regime.
The means of annual precipitation are between 820 and 1420 mm. More than 75% of precipitation is concentrated between June and September. The mean annual evapotranspiration varies between 563.34 mm and 962 mm [34]. The FAO aridity index (AI, i.e., precipitation/evapotranspiration) is about 1.45. TGRA (Three Gorges Reservoir Area) is classified as a humid zone according to the FAO aridity index, i.e., higher than 0.75 [35].
3. Data Source and Selected Precipitation Indices
There were 29 national weather stations within the TGRA, from which daily rainfall data was selected for this study. The NRA encompassed 15 stations. The remaining stations were in the ARA. The location and distribution of 29 rain gauge stations over the TGRA are shown in Figure 1. Supplemental Table S1 lists the detailed information of these stations including ID, name, latitude, longitude, and altitude.
The selected stations did not have uniform starting years to collect precipitation data. Since investigation on long-term trends in extreme precipitation would be based on a longer dataset, the research period was deemed to be 1959–2013.
To understand extreme precipitation changes over the TGRA, four rainfall indices were selected for the period spanning 1959–2013. The four rainfall indices include annual maximum consecutive 5-day precipitation amount (Mx5), extreme precipitation (P95) and the extreme to non-extreme precipitation ratio (E–NE) (Table 1). The Mx5 and P95 can be deemed as the magnitude of extreme precipitation. The E–NE can be utilized to analyze the change in fraction of extreme precipitation. These three indices are related to the wetness conditions. According to the daily precipitation amounts, this study categorized the remaining daily precipitation as eight different percentile intensities (P025, P25, P35, …, P85), excluding extreme precipitation (P95). The 25th, 35th, …, 95th percentiles of precipitation were calculated based on daily rainfall from 1971 to 2000 (the reference period) at each weather station. This means that different weather stations have various percentiles of precipitation.

Table 1.
Extreme climate indices used in this study.
Apart from weather station data series, satellite rainfall datasets were also applied to explore spatial precipitation patterns. The new Version 7 (V7) of the TRMM 3B42 product for the period 1998 and 2014 was used in this study, which considered ground observed rain information to remove the bias of satellite retrievals [37]. Recently, TRMM data were widely used to examine extreme precipitation events due to their relatively high-resolution characteristic [38]. The TRMM rain data and in situ rain gauge data had good agreement for all rain intensity categories except light rain (<1 mm day−1) [26]. Due to the aforementioned validation, TRMM was used in this data directly without further validation. The spatial resolution of TRMM data is 0.25° × 0.25°.
Global and local temperature data sets were used. The global air temperature was from the GISS Surface Temperature Analysis (GISTEMP) (Available online: https://data.giss.nasa.gov/gistemp/). Local temperature was from the 29 national climate stations. Annual temperature changes were estimated based on daily mean temperature at 29 national weather stations.
The ENSO cycle is represented by three ENSO indices, e.g., the multivariate ENSO index (MEI), Southern Oscillation Index (SOI) and sea surface temperature (SST). In this study, SOI values were selected to denote ENSO (Climate Research Unit of the University of East Anglia https://crudata.uea.ac.uk/cru/data/soi/). The daily relative humidity (RH) data sets were from the 29 national weather stations. Daily actual water vapor pressure (WP) was calculated from daily relative humidity and temperature data.
4. Methodology
4.1. Statistical Analysis
4.1.1. Mann–Kendall
The Mann–Kendall and Sen’s estimators are widely used to estimate trends in the climate and hydrological parameters [39,40,41]. The Mann–Kendall test is based on the assumption that the detected data are independent and identically distributed. However, some datasets cannot satisfy the assumption. The iterative-based Mann–Kendall (MK) method was adopted to detect trends in extreme precipitation at the 0.05 significance level in this study [42]. This method can remove serial correlation of detected datasets.
The MK method was also used to detect trends in the varying time data sets in addition to the fixed time span (from 1959 to 2013). The starting years were from 1959 to 1997, while the ending years were from 1975 to 2013 in this study. The minimum time span was 15 years, such as from 1959 to 1975, from 1960 to 1976 or from 1997 to 2013. The maximum time span was 54 years (from 1959 to 2013). The MK method used in the varying timing data sets is called as the moving-MK method. Sen’s slope, the number of stations showing significant positive and negative trends in P95, E–NE and Mx5 during different time spans, was estimated.
4.1.2. Field Significance Test
When analyzing a number of weather stations, a simultaneous evaluation of multiple hypothesis tests is performed and therefore the problem of test multiplicity or field significance arises [43]. For example, for a spatial field with N = 29 independent weather stations (locations), α = 0.05 is the significant level forf each local test. How many locations’ null hypotheses are rejected causes the whole region’s null hypothesis to be rejected. Field significance can be defined as the collective significance of a group of hypothesis tests [44]. Consequently, this study estimated the minimum number of locally significant trends to conclude that all changes were not caused by random variability. The resampling technique was performed to detect the field significance of the number of stations with statistical trends [7,45]. The detailed resampling technique can be found in Westra et al. (2013) [7].
4.1.3. Mann–Whitney Test and Kolmogorov–Smirnov Test
The statistical significance of changes in the mean and distribution from two different datasets was tested using the two-sided Mann–Whitney test [46] and Kolmogorov–Smirnov [47] test, respectively, at a 0.05 significance level. The null hypothesis for the Mann–Whitney test is that the two series from two periods or two locations have equal medians or means. The Kolmogorov–Smirnov test compares two datasets under the null hypothesis that they were drawn from the same but unspecified distribution.
4.2. Experimental Design
4.2.1. Role of Climate Warming on Extreme Precipitation
It is well documented that increasing atmospheric temperature has caused extreme precipitation to become more and more frequent [6,7,48]. The change point years in air temperature at 29 weather stations were detected using Pettitt [49] (Table 2). Abrupt changes at 21 stations (72% of 29 stations) were detected between 1982 and 1987. The MK method was used to detect trends in the temperature from 1959 to the change point year and from the change point year to 2013 at each station (Table 2). The decreasing trends before change points and increasing trends after change points were predominant. Pooling air temperature for the whole TGRA exhibited a decreasing trend before 1985, then a sharp increase after 1985 (Figure 2). The year 1985 was deemed as the change point over the TGRA. The cooling trends before 1985 were likely to be connected partly to the decrease in solar irradiance and the change in the Arctic Oscillation [50]. The change in the Arctic Oscillation controls cold air intrusions into north China. Solar irradiance exhibited a dimming to a brightening transition in the 1990s. Regarding the global temperature, it maintained a slowly increasing trend before 1985, while it showed a faster increasing trend after 1985. Based on the above analysis, the entire time series was divided into two periods (1959–1985 and 1986–2013) to investigate the effects of climatic change on rainfall extremes in the TGRA. The climate was warmer during the period from 1986 to 2013 compared to 1959–1985.

Table 2.
Abrupt change year of air temperature at 29 stations.
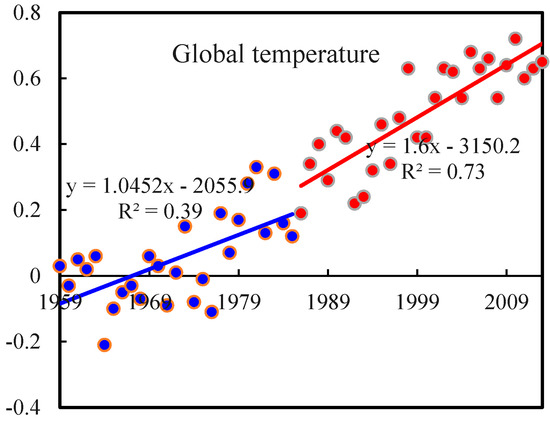
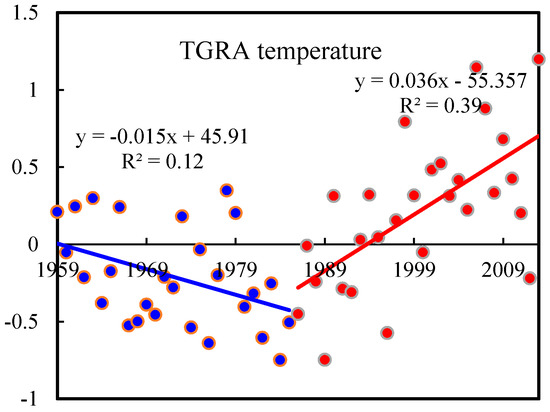
Figure 2.
Global and TGRA air temperature changes for the period 1959 to 2013.
The moving-MK method was used in the P95, E–NE and Mx5. This part concentrated on the changing differences between the two periods (1959–1985 and 1986–2013). The Mann–Whitney and Kolmogorov–Smirnov tests were applied to detect the mean and distribution changes in three extreme precipitation indices between the two periods. Finally, the method provided by the literature [51,52] to examine changes in precipitation characteristics () in association with changes in global temperature () was used. The authors calculated the precipitation amount difference (∆P) for nine precipitation intensities (P025, P25, P35, …, P95) at 29 stations and global temperature differences () between any two (different) years within 1959–2013. The ∆P/∆T ratios were represented as the response rate of the different precipitation intensities to global warming.
4.2.2. Role of ENSO on Extreme Precipitation
Based on the lag effects of El Niño–Southern Oscillation (ENSO) on extreme precipitation, the average Southern Oscillation Index (SOI) values from last November to March was calculated to assess the relationship between ENSO and extreme precipitation [6]. For the non-normalized SOI value, the values of the SOI below −7 often indicate El Niño episodes, while the values of the SOI above +7 are typical of La Niña episodes. In this study, the normalized SOI was used [53]. SOI values below −1 indicate El Niño years, while SOI values above +1 are typical of La Niña years. We classified the whole research period into two types based on SOI values, e.g., class I years with SOI < 0, class II years with SOI > 0. The hypothesis is ENSO has effects on extreme precipitation. Based on the hypothesis, the extreme precipitation during class I years and class II years present different characteristics. The statistical differences in extreme precipitation between class I years and class II years were tested by the Mann–Whitney test and the Kolmogorov–Smirnov test.
4.2.3. Role of the TGR on Extreme Precipitation
According to previous study conclusions [16,17,20,21], impounded reservoirs have larger effects on precipitation near a reservoir than those away from a reservoir. The hypothesis was extreme precipitation over the near the reservoir (NRA) was more likely to be affected by the TGR rather than the away from the reservoir area (ARA) in this study.
To show a clearer picture on the impact of dams on extreme precipitation, paired analyses were performed as a function of pre-dam and post-dam measurements and at locations near the reservoir area (NRA) and away from the reservoir area (ARA). Daily precipitation from both ground weather stations and TRMM was used. Since the TGR began to impound water in 2003, the period from 2003 to 2013 was deemed as the post-dam period. To keep the same number of comparison years, the period from 1992 to 2002 was deemed as the pre-dam period when using weather stations as the data source. Among 29 stations, 15 stations (No.1–No.15 in Figure 1b) were in the NRA, while the remaining stations (No.16–No.29 in Figure 1b) were in the ARA. The statistical differences in extreme precipitation between pre-dam and post-dam or between areas of NRA and ARA were tested by the Mann–Whitney test and the Kolmogorov–Smirnov test.
5. Results and Discussion
5.1. Long-Term Trends in Extreme Precipitation Indices
The trends of P95, E–NE and Mx5 for the period of 1959–2013 were evaluated (Figure 3). During this period, nineteen of a total 29 weather stations showed increasing trends in P95 with a median increase of 1.78 mm/year. Among them, only two stations exhibited statistically significant (p-value < 0.05) increasing trends. There were no stations showing a significant decreasing trend. The median slope in stations with declining trends in P95 was −0.61 mm/year (Figure 3). Obviously, increasing trends in P95 were more pronounced during the period of 1959–2013. Whether trends in P95 showing significant positive and negative trends occurred due to random chance was tested by resampling methodology. Figure 4 demonstrates that the number of stations showing significant both increasing and decreasing trends were inside a 95% distribution area generated by 1000 bootstrap trials (Figure 4). Therefore, the significant increasing and decreasing trends of annual P95 day in the TGRA were not field significant.
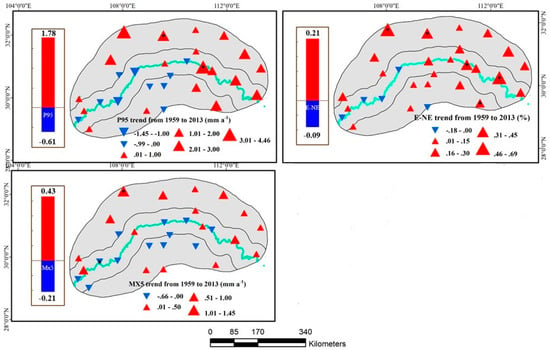
Figure 3.
Changes in P95, (E–NE, Mx5 for the period of 1959–2013. Red upward and blue downward triangles indicate increasing and decreasing tendencies, respectively. The triangle size represents the magnitude of these positive and negative trends. The black spot in the triangles represents significant trends at a 5% significance level. The red bar is the median slope of upward trend stations, while the blue bar is the median slope of downward trend stations.
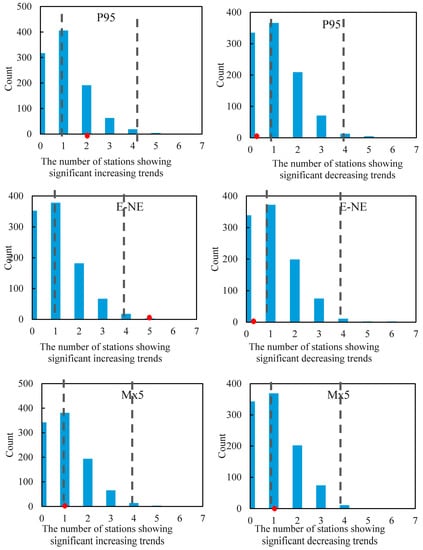
Figure 4.
The field significant test for statistically significant increasing and decreasing trends. The bar chart represents the distribution of stations with a statistically significant trend after implementing the MK (Mann–Kendall) test on 1000 bootstrap extreme precipitation indices. The area between vertical black dashed lines represents 95% of the distribution. The red filled circle represents the number of stations with a statistically significant trend.
During the period from 1959 to 2013, the E–NE exhibited increasing trends at 24 stations, five stations more than that in P95. Only five of a total 29 climatic stations showed decreasing trends in the E–NE, with a median decrease of –0.09%/year, while the E–NE significantly increased (p-value < 0.05) at five climatic stations during the years 1959–2013, i.e., three stations more than P95. The median slope with increasing trends in E–NE was reached at 0.21% (Figure 3). The result indicated that precipitation intensities had changed and the contribution from extreme precipitation had increased. Similarly, the distribution of the number of stations showing significant decreasing and increasing trends was generated using the resampling technique. The number of stations showing increasing trends was outside the 95% distribution, while the number of stations showing decreasing trends was inside this distribution (Figure 4). Thus, positive trends in the E–NE were field significant.
There were 12 stations showing decreasing trends in Mx5, among which only one station had a statistically significant (p-value < 0.05) trend for the period of 1959 to 2013. Similarly, only one station exhibited a significant increase during the period of 1959–2013 (Figure 3). The median slope at stations with positive trends was 0.43 mm/year, while the median slope with negative trends was 0.21 mm/year. According to change spatial distributions of P95, E–NE and Mx5, stations with decreasing trends were mainly located along the Yangtze River and the southern area of the Yangtze River. Obviously, the trends in Mx5 were not field significant (Figure 4).
There were more stations presenting increasing trends in extreme precipitation indices compared with those showing decreasing trends. These results are in line with trends of the worldwide average [6,7] and the whole of China except for the northeastern and northern parts [54].
To investigate precipitation intensity changes, trends in precipitation amount changes in different precipitation intensities (P025, P25, P35, …, P95) were detected using the MK method. The median changes ((slope × 54 years)/mean) × 100% for nine intensities at 29 stations were calculated. Figure 5 gives the median changes at 29 stations for every intensity. P95 showed a positive trend with a 21.9% median increase while P25 had a slight increase. However, all other percentile precipitation amounts showed a decreasing trend. This result supported the previous findings that the frequency or intensity of heavy precipitation events must increase at the expense of moderate and/or light precipitation events [55,56], which was confirmed by the increase in the E–NE. Analysis of daily precipitation data over Asia implied a remarkable shift of precipitation rate from light to heavy rain [57]. This kind of precipitation structure was referred to as the “it never rains, but it pours” model of change [58]. Previous studies found that light rain showed an overwhelming decreasing trend over Asia [57] and China [59].
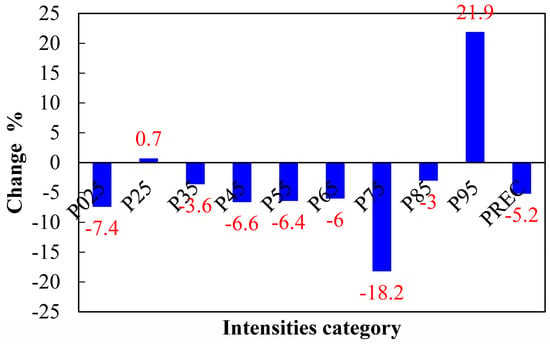
Figure 5.
Median changes (%) of precipitation amount for nine precipitation intensities among 29 stations during the period of 1959–2013.
5.2. Role of Climate Warming and ENSO on Extreme Precipitation Events
Changes in P95, E–NE and Mx5 were evaluated by the moving-MK test during a time varying period with start year from 1959 to 1997 and end year from 1975 to 2013. To compare changes in extreme precipitation, the mean of Sen’s slope (Figure 6) and the number of stations with significant increasing and decreasing trends (Figure 7) in three extreme precipitation indices between pre-1985 and post-1985 were calculated.
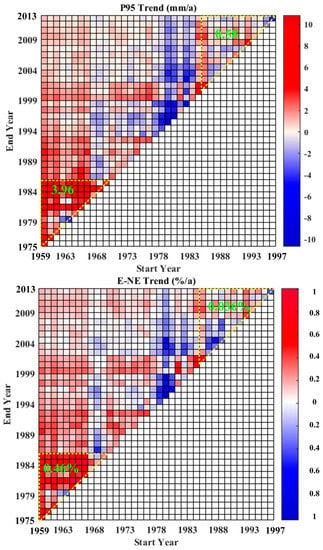
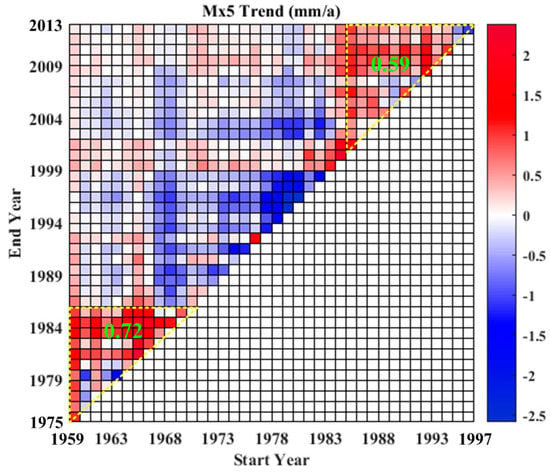
Figure 6.
Median Sen’s slopes in P95, E–NE and Mx5 among 29 stations during different time spans for periods with different starting years (1959–1997) and ending years (1975–2013). Median Sen’s slopes within the downward yellow triangle were from 1959 to 1985, while median Sen’s slopes within the upward yellow triangle were from 1986 to 2013. (/a = per annual).
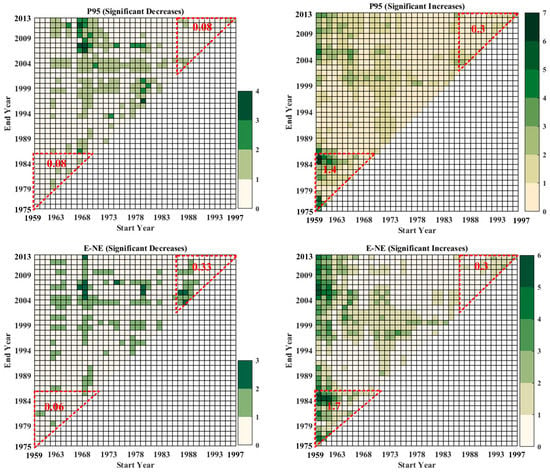
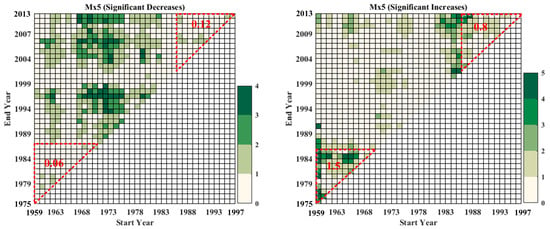
Figure 7.
Number of stations with significant decreasing (left panel) and increasing (right panel) trends in P95, E–NE and Mx5 during different time spans for periods with different starting years (1959–1997) and ending years (1975–2013). Number of stations within downward red triangles were from 1959 to 1985, while number of stations within upward red triangles were from 1986 to 2013.
Figure 6 and Figure 7 show the increasing trend in P95 was predominant during the period from 1959 to 2013. The decreasing trend was concentrated between 1975 and 1982. Mean Sen’s slope from 1959 to 1985 was higher than that from 1986 to 2013, 3.96 mm/year and 0.58 mm/year, respectively. The mean number of stations with significant increasing trends from 1959 to 1985 was also more than that from 1986 to 2013. The E–NE showed similar change characteristics as P95. Mean Sen’s slope from 1959 to 1985 was 0.46%, higher than that from 1986 to 2013, which was 0.036%. Interestingly, there were more stations with significant positive trends during the warming period (post-1985) than those during the cooling period (pre-1985). The Mx5 exhibited a similar positive slope with 0.72 mm/year from 1959 to 1985 and 0.59 mm/year from 1986 to 2013. Both global and local temperatures showed sharply increasing trends from 1986 to 2013 compared to those from 1959 to 1985. It is noteworthy that increasing air temperature did not make consecutive dry days become longer in duration.
Negative trends were predominant for the period 1959 to 1985, in terms of local surface temperature, and then trends reversed after 1985. Global air temperature maintained an increasing trend for the period from 1959 to 1985, though the trend magnitude was less than that post-1985. Extreme precipitation during both pre-1985 and post- 1985 showed increasing trends. However, the upward trends in extreme precipitation before 1985 would be obviously more pronounced based on the Sen’s slope and number of stations with significant positive trends. It is interesting to note that extreme indices showed an increasing trend at more stations during the cooling period compared to those during the warming period.
In addition to trend detection, the mean and distributions for all four indices were calculated and compared based on the Mann–Whitney and Kolmogorov–Smirnov tests for the pre-1985 and post-1985 periods (Table 3 and Figure 8). No significant change in mean (Table 3) and distribution for Mx5 for the two periods was observed (Figure 8). However, it was noticed that mean and distribution of P95 and E–NE changed significantly (p-value < 0.05) from the pre-1985 to post-1985 periods. The mean in P95 increased from 308.6 mm during the pre-1985 period to 321.9 mm during the post-1985 period. The E–NE during post-1985 became 0.41 compared to 0.37 during pre-1985. Extreme precipitation during post-1985 was found to be heavier.

Table 3.
Statistical difference tests in the mean in the extreme rainfall indices (P95/mm, E–NE (fraction) and MX5/mm) between pre-1985 and post-1985 periods.
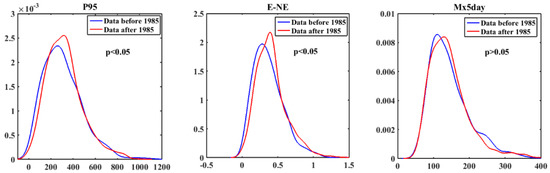
Figure 8.
Density distributions for P95, E-NE and Mx5, respectively, for the pre-1985 (blue) and post-1985 (red) periods. Statistical significance was estimated using the Kolmogorov–Smirnov test for distributions of the extreme precipitation indices.
Due to climatic system complexity, it is difficult to separate the contributions of the effects of global and local temperature on the changes in the extreme precipitation. It is confirmed that the warming climate had effects on the extreme precipitation variations. Based on the above analysis, extreme precipitation (P95 and E–NE) has changed significantly in the mean and distribution from the cooling to warming environment. Lü et al. (2017) found the global temperature played more roles in affecting extreme precipitation (daily maximum precipitation) than local temperatures in the Yangtze River Basin [60]. Figure 9 plotted the changes in the precipitation amount for nine precipitation intensities responding to per 1 °C increase in global surface temperature from 1959 to 2013 (). The ratios for middle and light precipitation intensities were negative except for P25. However, ratio for P95 was 6.48%/°C. Considering the 0.7 °C increase in the global surface temperature from 1959 to 2013, P95 would increase by 4.5%. This is in line with the 7%/°C increase rate in the atmosphere’s moisture-holding capacity estimated by the Clausius–Clapeyron equation. Westra et al. (2014) found that extreme rainfall intensity is likely to increase at a rate equal to or above the atmosphere’s capacity to hold moisture, leading to increases of 7% or more per 1 °C [61]. Considering the fact that higher temperature can hold more moisture in the atmosphere, we need to confirm whether water moisture pressure and RH during post-1985 period are higher than these during pre-1985 period. Interestingly, RH and WP during pre-1985 period were higher (Table 4). RH and WP were calculated from local meteorological data at surface weather stations. The precipitable water source did not originate from the local moisture, but from ocean transported by the East Asian monsoon [62,63]. Thus, the lower WP in the surface might not trigger weaker extreme precipitation.
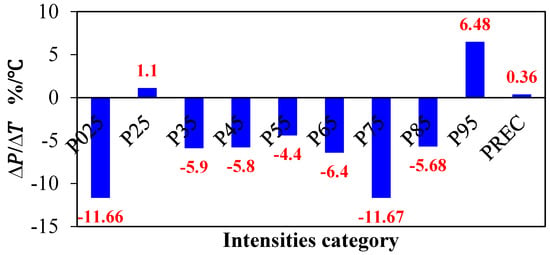
Figure 9.
Changes in precipitation amount for nine precipitation intensities and PREC per one-degree Celsius increase in global surface temperature (%/°C).

Table 4.
Statistical difference tests for the mean and distribution in the RH (%) and WP (hPa) between pre-1985 and post-1985 periods.
The effects of ENSO on extreme precipitation were investigated (Table 5 and Figure 10). Extreme precipitation did not show a statistical significant difference between class I years with SOI < 0 and class II years with SOI > 0, though extreme precipitation (P95 and E-NE) appeared to be heavier during class II years with SOI < 0.

Table 5.
Statistical difference tests for the mean in the extreme rainfall indices (P95/mm, E–NE (fraction), MX5/mm) in between class I years with SOI < 0 and class II years with SOI > 0.
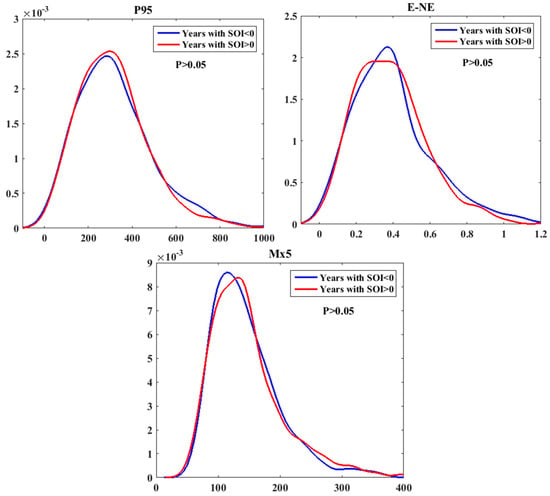
Figure 10.
Density distributions for P95, E-NE and Mx5, respectively, for the class I years (blue) and class II years (red) periods. Statistical significance was estimated using the Kolmogorov–Smirnov test for distributions of the extreme precipitation indices.
5.3. Role of TGR on Extreme Precipitation
Table 6 and Table 7 present the means and their statistical difference in P95, E–NE and Mx5 from weather stations. The density distributions and their statistical difference in P95, E–NE and Mx5 are shown in Figure 11. First, extreme precipitation indices at NRA stations during pre-dam and post-dam were compared. There were few distinctions in means and distributions in P95 between pre-dam and post-dam. The E–NE during post-dam was slightly higher than those during pre-dam, but it was not significant. Regarding distribution, E–NE showed significant differences between the pre-dam period and the post-dam period. A significant increase was observed in Mx5, from 131.1 mm to 141.2 mm. Meanwhile, Mx5 also exhibited significant difference in the distribution aspect. Based on the above analysis, a conclusion that extreme precipitation at the NRA has become much heavier after the TGD construction.

Table 6.
Statistical difference tests for the mean in the extreme rainfall indices (P95/mm, E–NE (fraction) and Mx5/mm) from weather stations for the different periods. (ARA: reservoir area and the NRA: near reservoir area).

Table 7.
Statistical difference tests for the mean in the extreme rainfall indices (P95/mm, E–NE (fraction) and Mx5/mm) from weather stations for the different locations.
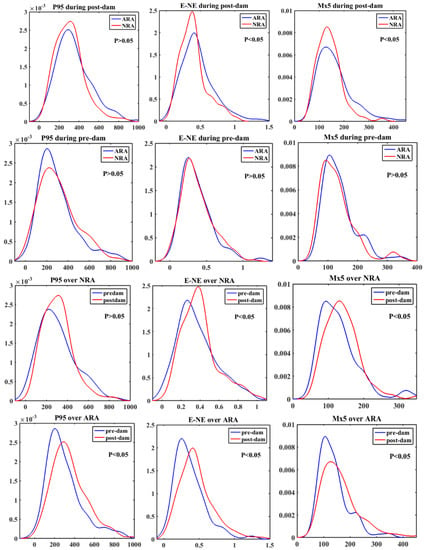
Figure 11.
Density distributions for P95, E–NE and Mx5, respectively, for the pre- and post- dam periods, over the ARA (reservoir area) and the NRA (near reservoir area). Statistical significance was estimated using the Kolmogorov–Smirnov test for distributions of the extreme precipitation indices.
However, whether these extreme precipitation changes were due to natural climatic systems or the TGD construction factors was not assured. Therefore, extreme precipitation changes at the ARA between pre-dam and post-dam periods were compared. Table 6 suggests the means in extreme precipitation indices (including P95, E–NE and Mx5) during the post-dam period were higher than these during the pre-dam period. The distributions also showed significant differences between the pre-dam and post-dam periods. Extreme precipitation, both at ARA and NRA locations, became heavier after the TGD construction compared with those during the pre-dam period, making it difficult to reach a conclusion that increasing extreme precipitation was linked to the TGD impounding.
Differences in extreme precipitation indices at the ARA and NRA locations after dam construction were compared. The interesting results are shown in Table 7. The means of extreme precipitation (P95, E–NE and Mx5) at the ARA locations were higher than those at the NRA locations (p < 0.05). Moreover, the distributions of E–NE and Mx5 appeared to show significant distinction. These findings were different from the hypothesis that the reservoir will increase extreme precipitation frequency or intensity near the TGR. To examine whether this extreme precipitation pattern existed during the pre-dam period, the extreme precipitation between the areas of NRA and ARA locations during this period was compared (Table 7). However, the extreme precipitation did not show large differences between areas of NRA and ARA.
It is highly likely that that the TGR did not show detectable effects on extreme precipitation around the TGR compared to natural precipitation variations. Most studies suggested that dams and their impounded reservoirs modify extreme precipitation patterns [9,10,20,21]. These conclusions were based on the facts that adjacent land use and land cover have been changed due to dams. More land might be brought under irrigation, for example. Irrigation makes more surface water available for evaporation and transpiration, which consequently can trigger the formation of convective storm systems under the right set of supporting conditions [32]. However, the TGD is constructed for flood protection, hydropower and navigation. It is not used for irrigation purposes. Furthermore, the TGD is located within a humid climate zone, which leads to less effects of the TGR on local climate. Degu et al. (2011) reported that large dams influenced local climate mostly in Mediterranean, and semi–arid climates, while for humid climates the influence is less apparent [21]. The phenomenon that higher rainfall intensities at locations closer to inland water bodies was accentuated in dryer climates [15].
Additional to data from weather stations, TRMM precipitation data were also included. Due to high resolution TRMM rainfall data (0.25° × 0.25°) being available after 1998, the years from 1998 to 2003 were deemed as the pre-dam period, while the years from 2004 to 2014 were referred to as the post-dam period. It should be noted that the dividing period for TRMM is different from that for weather stations (from 1992 to 2002 and from 2003 to 2013). Figure 12 gives spatial distribution of mean for P95, E–NE, Mx5 from TRMM data during pre-dam and post-dam periods, and their differences between pre-dam and post-dam periods. Table 8 and Table 9 give the mean extreme precipitation indices (P95, E–NE, Mx5) from TRMM data and statistical differences in the mean (p-mw) and distribution (p-ks) estimated by the Mann–Whitney and Kolmogorov–Smirnov tests.
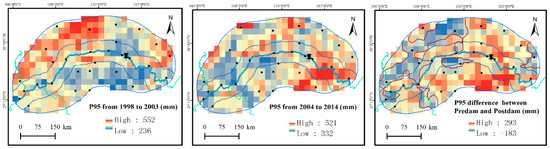
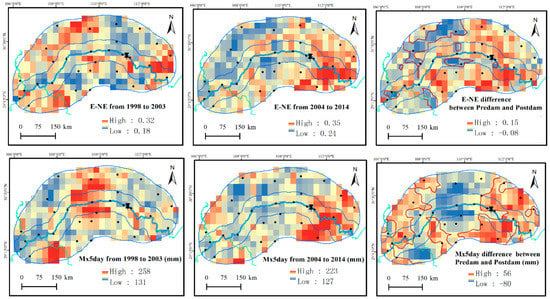
Figure 12.
Spatial distribution of mean P95, E–NE, Mx5 from TRMM data for pre-dam and post-dam period, their difference between pre-dam and post-dam period.

Table 8.
Statistical difference tests for the mean and distribution in the extreme rainfall indices (P95/mm, E–NE (fraction) and Mx5/mm) from TRMM data for the different periods.

Table 9.
Statistical difference tests for the mean and distribution in the extreme rainfall indices (P95/mm, E–NE (fraction) and Mx5/mm) from TRMM data for the different locations.
Regarding extreme precipitation indices over the NRA during the post-dam period, they were significantly different in the mean and distribution compared with that during the pre-dam period. When comparing extreme precipitation indices over the ARA, similar results could be obtained. It was observed that there was a minimal difference in extreme precipitation indices for the NRA and the ARA. The P95 for the ARA was 411 mm, while for the NAR it was 405 mm, for instance. Therefore, it was difficult to reach a conclusion that the reservoir could exert some effects on extreme precipitation.
Although TGR did not show detectable effects on extreme precipitation around the TGR, we need to know whether other meteorological elements, i.e., WP and RH, in collection with precipitation, were changed due to TGR impoundment. Firstly, RH at the same region (ARA or NRA) was compared between the pre-dam and the post-dam periods (Table 10). The means of RH at both the ARA and the NRA locations during the pre-dam period were higher than those during the post-dam period (p < 0.05). WP at both the ARA and the NRA locations presented similar changes with RH. Then, RH at the same period (pre-dam or post-dam) was compared between the ARA and the NRA locations (Table 11). It is interesting to note RH at the ARA locations was larger than that at the NRA locations after TGR impoundment. These results mean that the impoundment of TGR did not affect RH and WP. In other words, the effects of TGR on RH and WP could be undetected or much smaller than other factors.

Table 10.
Statistical difference tests for the mean and distribution in the RH (%) and WP (hPa) at the same locations for the different periods.

Table 11.
Statistical difference tests for the mean and distribution in the RH (%) and WP (hPa) at the same locations for the different locations.
6. Conclusions
Three extreme precipitation indices were used, including annual precipitation amounts corresponding to more than the 95th percentile of precipitation (P95), the ratio of extreme to non-extreme precipitation (E–NE) and maximum consecutive 5-day precipitation amounts (Mx5), in this study. During the period from 1959 to 2013, increasing trends in P95, E–NE and Mx5 were predominant, while only the E–NE was field significant. The heavy precipitation accounted for larger proportion through comparing the trend of precipitation amount from different precipitation intensities. Thus, an increasing trend in the top high percentile precipitation was at the expense of the declining trends in light and middle precipitation.
ENSO did not show detectable associations with extreme precipitation. To detect the effect of climate warming on extreme precipitation, the whole period was divided into two sub-periods, including the cooling period (pre-1985) and warming period (post-1985) based on atmospheric temperature variations. Increasing trends in P95, E–NE and Mx5 during the pre-1985 period were more pronounced than those during the warming period (post-1985), though these three indices showed upward trends during both periods. The P95 and E–NE have changed significantly in the mean and distribution aspects from the pre-1985 to post-1985 periods. Extreme precipitation became heavier during post-1985. Due to climate warming, P95 increased at the rate of 6.48%/°C. However, climate warming did not trigger increases in RH and WP from surface weather stations.
Through comparing extreme precipitation indices over the NRA, Mx5 show significant differences between the pre-dam and post-dam years. However, over the ARA, there are three extreme precipitation indices (P95, E–NE and Mx5) exhibiting significant differences between pre-dam and post-dam construction. During the pre-dam period, extreme precipitation over the NRA and the ARA did not show a large difference. During the post-dam period, extreme precipitation over the NRA was smaller than that over the ARA. These results are contrary to the hypothesis that the impounding reservoir has larger effects on precipitation near the reservoir than that away from reservoir. Moreover, the results from TRMM precipitation analysis did not show an effect of the TGR on extreme precipitation. Therefore, the variation of extreme precipitation over the TGRA is related more to the natural climate system. Furthermore, the impoundment of TGR did not affect RH and WP.
Supplementary Materials
The following are available online at www.mdpi.com/2073-4433/9/1/24/s1, Table S1: General Information for 29 Meteorological stations.
Acknowledgments
The work was supported by the National Natural Science Foundation of China (No. 41401633, No. 41471340 and No. 91544102).
Author Contributions
Mingquan Lü and Shengjun Wu proposed the idea; Mingquan Lü wrote the paper; Jilong Chen and Jun Liu provided important suggestions for data analysis and paper writing; Yi Jiang and Xunlai Chen performed the analysis.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhang, D.L.; Lin, Y.; Zhao, P.; Yu, X.; Wang, S.; Kang, H.; Ding, Y. The Beijing extreme rainfall of 21 July 2012: “Right results” but for wrong reasons. Geophys. Res. Lett. 2013, 40, 1426–1431. [Google Scholar] [CrossRef]
- Chen, Z.M.; Xu, Y.H.; Zhou, X.H.; Tang, J.W.; Kuzyakov, Y.; Yu, H.Y.; Fan, J.L.; Ding, W.X. Extreme rainfall and snowfall alter responses of soil respiration to nitrogen fertilization: A 3-year field experiment. Glob. Chang. Biol. 2017. [Google Scholar] [CrossRef] [PubMed]
- Sun, G.; Wang, Z.; Zhu-Barker, X.; Zhang, N.; Wu, N.; Liu, L.; Lei, Y. Biotic and abiotic controls in determining exceedingly variable responses of ecosystem functions to extreme seasonal precipitation in a mesophytic alpine grassland. Agric. For. Meteorol. 2016, 228, 180–190. [Google Scholar] [CrossRef]
- Re, M.; Barros, V.R. Extreme rainfalls in SE South America. Clim. Chang. 2009, 96, 119–136. [Google Scholar] [CrossRef]
- Choi, W.; Tareghian, R.; Choi, J.; Hwang, C.S. Geographically heterogeneous temporal trends of extreme precipitation in Wisconsin, USA during 1950–2006. Int. J. Climatol. 2014, 34, 2841–2852. [Google Scholar] [CrossRef]
- Min, S.-K.; Zhang, X.; Zwiers, F.W.; Hegerl, G.C. Human contribution to more-intense precipitation extremes. Nature 2011, 470, 378–381. [Google Scholar] [CrossRef] [PubMed]
- Westra, S.; Alexander, L.V.; Zwiers, F.W. Global increasing trends in annual maximum daily precipitation. J. Clim. 2013, 26, 3904–3918. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Dai, A.; Rasmussen, R.M.; Parsons, D.B. The changing character of precipitation. Bull. Am. Meteorol. Soc. 2003, 84, 1205–1217. [Google Scholar] [CrossRef]
- Hossain, F.; Jeyachandran, I.; Pielke, R., Sr. Dam safety effects due to human alteration of extreme precipitation. Water Resour. Res. 2010, 46, W03301. [Google Scholar] [CrossRef]
- Yigzaw, W.; Hossain, F.; Kalyanapu, A. Impact of artificial reservoir size and land use/land cover patterns on probable maximum precipitation and flood: Case of Folsom Dam on the American River. J. Hydrol. Eng. 2012, 18, 1180–1190. [Google Scholar] [CrossRef]
- Deng, X.; Zhao, C.; Yan, H. Systematic modeling of impacts of land use and land cover changes on regional climate: A review. Adv. Meteorol. 2013, 11. [Google Scholar] [CrossRef]
- Lehner, B.; Liermann, C.R.; Revenga, C.; Vörösmarty, C.; Fekete, B.; Crouzet, P.; Döll, P.; Endejan, M.; Frenken, K.; Magome, J.; et al. High-resolution mapping of the world’s reservoirs and dams for sustainable river-flow management. Front. Ecol. Environ. 2011, 9, 494–502. [Google Scholar] [CrossRef]
- Berga, L.J.; Buil, M.; Bofill, E. Dams and reservoirs, societies and environment in the 21st century. In Proceedings of the International Symposium on Dams in Societies of the 21st Century, Barcelona, Spain, 18 June 2006; Taylor and Francis Group: London, UK, 2006. [Google Scholar]
- Eltahir, E.A.B.; Bras, R.L. Precipitation recycling. Rev. Geophys. 1996, 34, 367–378. [Google Scholar] [CrossRef]
- Pizarro, R.; Garcia-Chevesich, P.; Valdes, R.; Dominguez, F.; Hossain, F.; Ffolliott, P.; Olivare, C.; Morales, C.; Balocchi, F.; Bro, P. Inland water bodies in Chile can locally increase rainfall intensity. J. Hydrol. 2013, 481, 56–63. [Google Scholar] [CrossRef]
- Haberlie, A.M.; Ashley, W.S.; Fultz, A.J.; Eagan, S.M. The effect of reservoirs on the climatology of warm-season thunderstorms in Southeast Texas, USA. Int. J. Climatol. 2016, 36, 1808–1820. [Google Scholar] [CrossRef]
- Woldemichael, A.T.; Hossain, F.; Pielke, R., Sr. Impacts of postdam land use/land cover changes on modification of extreme precipitation in contrasting hydroclimate and terrain features. J. Hydrometeorol. 2014, 15, 777–800. [Google Scholar] [CrossRef]
- Eltahir, E.A.B. A feedback mechanism in annual rainfall, Central Sudan. J. Hydrol. 1989, 110, 323–334. [Google Scholar] [CrossRef]
- Gangoiti, G.; Gómez-Domenech, I.; Sáez de Cámara, E. Origin of the water vapor responsible for the European extreme rainfalls of August 2002: 2. A new methodology to evaluate evaporative moisture sources, applied to the August 11–13 central European rainfall episode. J. Geophys. Res. Atmos. 2011, 116, D21103. [Google Scholar] [CrossRef]
- Hossain, F.; Jeyachandran, I.; Pielke, R. Have large dams altered extreme precipitation patterns? Eos Trans. Am. Geophys. Union 2009, 90, 453–454. [Google Scholar] [CrossRef]
- Degu, A.M.; Hossain, F.; Niyogi, D.; Pielke, R., Sr.; Shepherd, J.M.; Voisin, N.; Chronis, T. The influence of large dams on surrounding climate and precipitation patterns. Geophys. Res. Lett. 2011, 38, L04405. [Google Scholar] [CrossRef]
- Xu, X.; Tan, Y.; Yang, G. Environmental impact assessments of the Three Gorges Project in China: Issues and interventions. Earth-Sci. Rev. 2013, 124, 115–125. [Google Scholar] [CrossRef]
- Miller, N.L.; Jin, J.; Tsang, C.F. Local climate sensitivity of the Three Gorges Dam. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Xiao, C.; Yu, R.C.; Fu, Y.F. Precipitation characteristics in the Three Gorges Dam Vicinity. Int. J. Climatol. 2010, 30, 2021–2024. [Google Scholar] [CrossRef]
- Zhao, F.; Deng, H.; Zhao, X.Y. Rainfall regime in Three Gorges area in China and the control factors. Int. J. Climatol. 2010, 30, 1396–1406. [Google Scholar]
- Zhao, F.; Shepherd, M. Precipitation Changes near Three Gorges Dam, China. Part I: A spatiotemporal validation analysis. J. Hydrometeorol. 2012, 13, 735–745. [Google Scholar] [CrossRef]
- Li, Z.; Yang, D.; Hong, Y.; Zhang, J.; Qi, Y. Characterizing spatiotemporal variations of hourly rainfall by gauge and radar in the mountainous three gorges region. J. Appl. Meteorol. Clim. 2014, 53, 873–889. [Google Scholar] [CrossRef]
- Deng, H.; Zhao, F.; Zhao, X.Y. Changes of extreme temperature events in Three Gorges area, China. Environ. Earth Sci. 2012, 66, 1783–1790. [Google Scholar] [CrossRef]
- Song, Z.; Liang, S.; Feng, L.; He, T.; Song, X.P.; Zhang, L. Temperature changes in Three Gorges Reservoir Area and linkage with Three Gorges Project. J. Geophys. Res. Atmos. 2017. [Google Scholar] [CrossRef]
- Wu, L.; Zhang, Q.; Jiang, Z. Three Gorges Dam affects regional precipitation. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- García, J. El impacto climatico de los embalses cantábricos. Ser. Geogr. 1994, 4, 33–42. [Google Scholar]
- Degu, A.M.; Hossain, F. Investigating the mesoscale impact of artificial reservoirs on frequency of rain during growing season. Water Resour. Res. 2012, 48, W05510. [Google Scholar] [CrossRef]
- Fu, B.; Zhu, C. The effects of Xinanjiang reservoir on precipitation. Geojournal 1984, 8, 229–234. [Google Scholar] [CrossRef]
- Lv, M.; Chen, J.; Mirza, Z.A.; Chen, C.; Wen, Z.; Jiang, Y. Spatial distribution and temporal variation of reference evapotranspiration in the three gorges reservoir area during 1960–2013. Int. J. Climatol. 2016, 36, 4497–4511. [Google Scholar] [CrossRef]
- FAO (Food and Agriculture Organization of the United Nations). World Map of Desertification; Food and Agricultural Organization (FAO): Rome, Italy, 1977. [Google Scholar]
- Ali, H.; Mishra, V.; Pai, D.S. Observed and projected urban extreme rainfall events in India. J. Geophys. Res. Atmos. 2014, 119, 12621–12641. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Pombo, S.; de Oliveira, R.P. Evaluation of extreme precipitation estimates from TRMM in Angola. J. Hydrol. 2015, 523, 663–679. [Google Scholar] [CrossRef]
- Mann, H.B. Non-parametric tests again trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Griffin: London, UK, 1975. [Google Scholar]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Wang, X.L.; Swail, V.R. Changes of extreme wave heights in Northern Hemisphere oceans and related atmospheric circulation regimes. J. Clim. 2001, 14, 2204–2221. [Google Scholar] [CrossRef]
- Wilks, D.S. On “field significance” and the false discovery rate. J. Appl. Meteorol. Climatol. 2006, 45, 1181–1189. [Google Scholar] [CrossRef]
- Douglas, E.M.; Vogela, R.M.; Kroll, C.N. Trends in floods and low flows in the United States: Impact of spatial correlation. J. Hydrol. 2000, 240, 90–105. [Google Scholar] [CrossRef]
- Wilks, D.S. Resampling hypothesis tests for autocorrelated fields. J. Clim. 1997, 10, 65–82. [Google Scholar] [CrossRef]
- Mann, H.B.; Whitney, D.R. On a test of whether one of two random variables is stochastically larger than the other. Ann. Math. Stat. 1947, 18, 50–60. [Google Scholar] [CrossRef]
- Massey, F.J., Jr. The Kolmogorov–Smirnov test for goodness of fit. J. Am. Stat. Assoc. 1951, 46, 68–78. [Google Scholar] [CrossRef]
- Pall, P.; Allen, M.; Stone, D. Testing the Clausius–Clapeyron constraint on changes in extreme precipitation under CO2 warming. Clim. Dyn. 2007, 28, 351–363. [Google Scholar] [CrossRef]
- Pettitt, A.N. A non-parametric approach to the change-point problem. Appl. Stat. 1979, 28, 126–135. [Google Scholar] [CrossRef]
- Qi, L.; Wang, Y. Changes in the observed trends in extreme temperatures over china around 1990. J. Clim. 2012, 25, 5208–5222. [Google Scholar] [CrossRef]
- Liu, S.C.; Fu, C.; Shiu, C.-J.; Chen, J.-P.; Wu, F. Temperature dependence of global precipitation extremes. Geophys. Res. Lett. 2009, 36, L17702. [Google Scholar] [CrossRef]
- Shiu, C.-J.; Liu, S.C.; Fu, C.; Dai, A.; Sun, Y. How much do precipitation extremes change in a warming climate? Geophys. Res. Lett. 2012, 39, L17707. [Google Scholar] [CrossRef]
- Ropelewski, C.F.; Jones, P.D. An extension of the Tahiti-Darwin Southern Oscillation Index. Mon. Weather Rev. 1987, 115, 2161–2165. [Google Scholar] [CrossRef]
- Zhou, B.; Xu, Y.; Wu, J.; Dong, S.; Shi, Y. Changes in temperature and precipitation extreme indices over China: Analysis of a high-resolution grid dataset. Int. J. Climatol. 2016, 36, 1051–1066. [Google Scholar] [CrossRef]
- Giorgi, F.; Im, E.-S.; Coppola, E.; Diffenbaugh, N.S.; Gao, X.J.; Mariotti, L.; Shi, Y. Higher hydroclimatic intensity with global warming. J. Clim. 2011, 24, 5309–5324. [Google Scholar] [CrossRef]
- Trenberth, K.E. Changes in precipitation with climate change. Clim. Res. 2011, 41, 123–138. [Google Scholar] [CrossRef]
- Qian, Y.; Gong, D.; Fan, J.; Leung, L.R.; Bennartz, R.; Chen, D.; Wang, W. Heavy pollution suppresses light rain in China: Observations and modeling. J. Geophys. Res. Atmos. 2010, 114, D00K02. [Google Scholar] [CrossRef]
- Rajah, K.; O’Leary, T.; Turner, A.; Petrakis, G.; Leonard, M.; Westra, S. Changes to the temporal distribution of daily precipitation. Geophys. Res. Lett. 2014, 41, 8887–8894. [Google Scholar] [CrossRef]
- Liu, B.; Xu, M.; Henderson, M. Where have all the showers gone? Regional declines in light precipitation events in China, 1960–2000. Int. J. Climatol. 2011, 31, 1177–1191. [Google Scholar] [CrossRef]
- Lü, M.; Wu, S.; Chen, J.; Chen, C.; Wen, Z.; Huang, Y. Changes in extreme precipitation in the Yangtze River basin and its association with global mean temperature and ENSO. Int. J. Climatol. 2017. [Google Scholar] [CrossRef]
- Westra, S.; Fowler, H.J.; Evans, J.P.; Alexander, V.; Berg, P.; Johnson, F.; Kendon, E.J.; Lenderink, G.; Roberts, N.M. Future changes to the intensity and frequency of short duration extreme rainfall. Rev. Geophys. 2014, 52, 522–555. [Google Scholar] [CrossRef]
- Wei, J.; Knoche, H.R.; Kunstmann, H. Contribution of transpiration and evaporation to precipitation: An ET-Tagging study for the Poyang Lake region in Southeast China. J. Geophys. Res. Atmos. 2015, 120, 6845–6864. [Google Scholar] [CrossRef]
- Wu, S.; Yin, Y.; Zheng, D.; Yang, Q. Moisture conditions and climate trends in China during the period 1971–2000. Int. J. Climatol. 2006, 26, 193–206. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).