Impacts of Climate Change on Rainfall Erosivity in the Huai Luang Watershed, Thailand
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
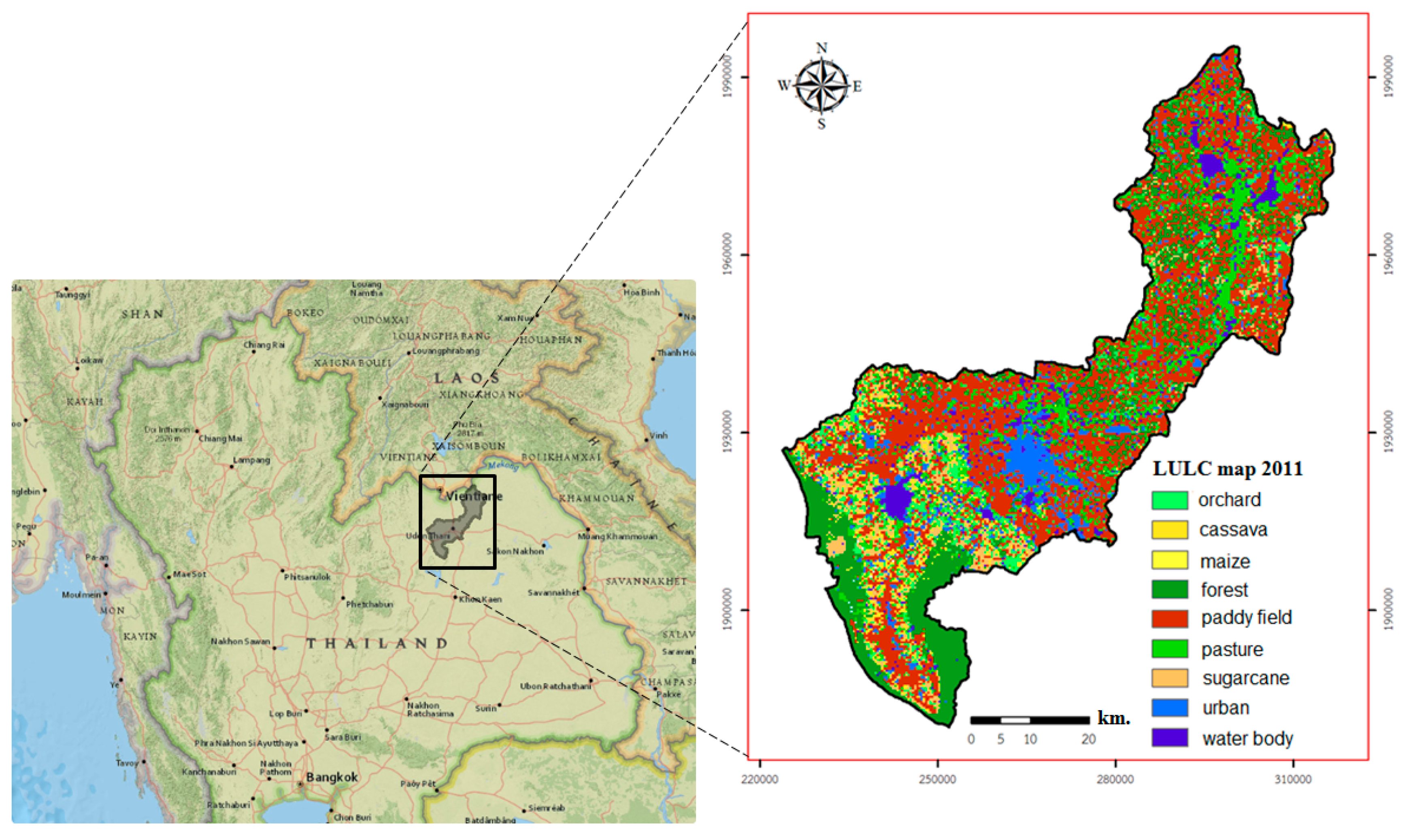
2.1.1. Study Area
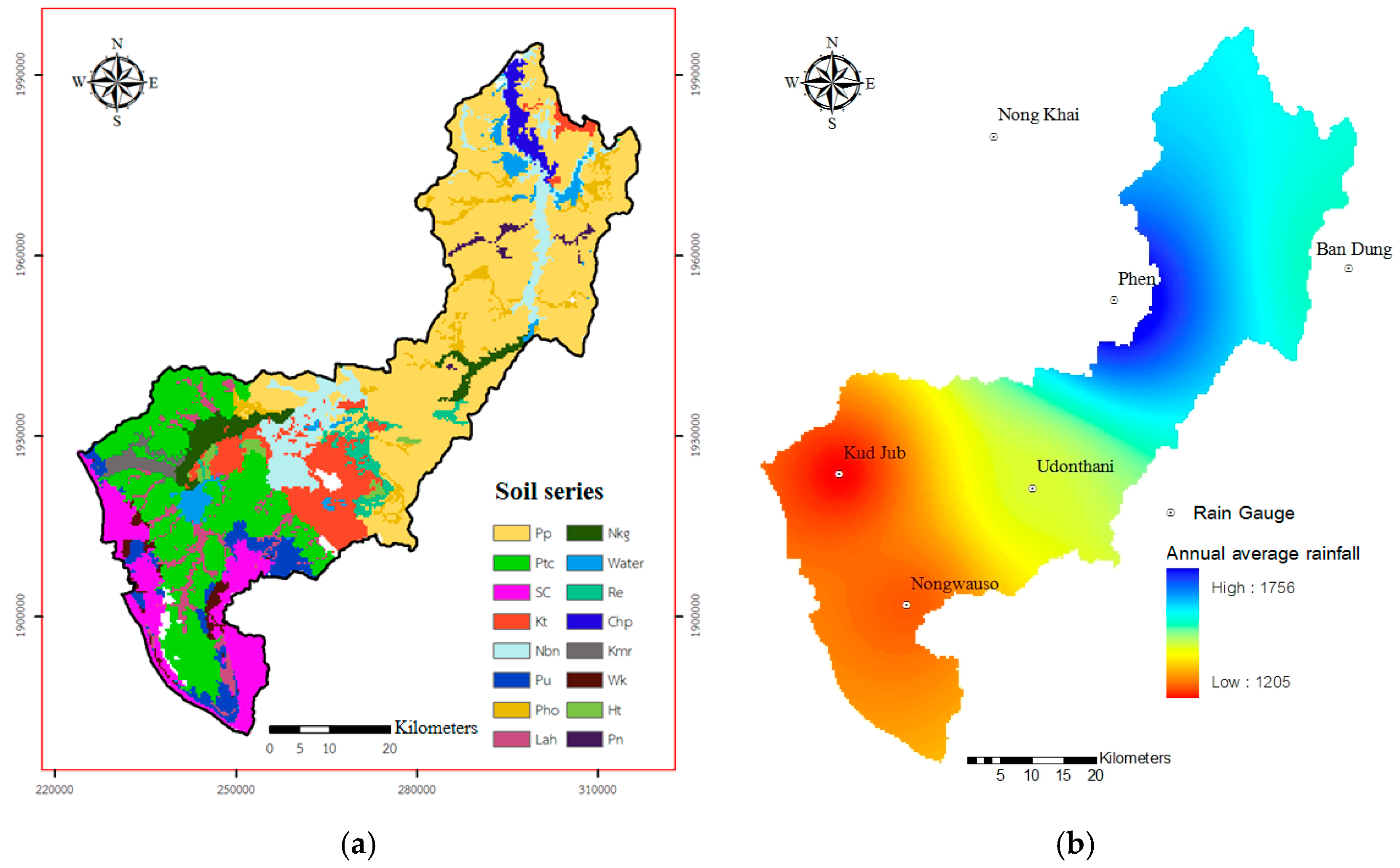
2.1.2. Soil Series
2.1.3. Climate
2.2. Data and Methods
2.2.1. Observed Precipitation
2.2.2. Estimation of Rainfall Erosivity
2.2.3. General Circulation Models (GCMs)
3. Results and Discussion
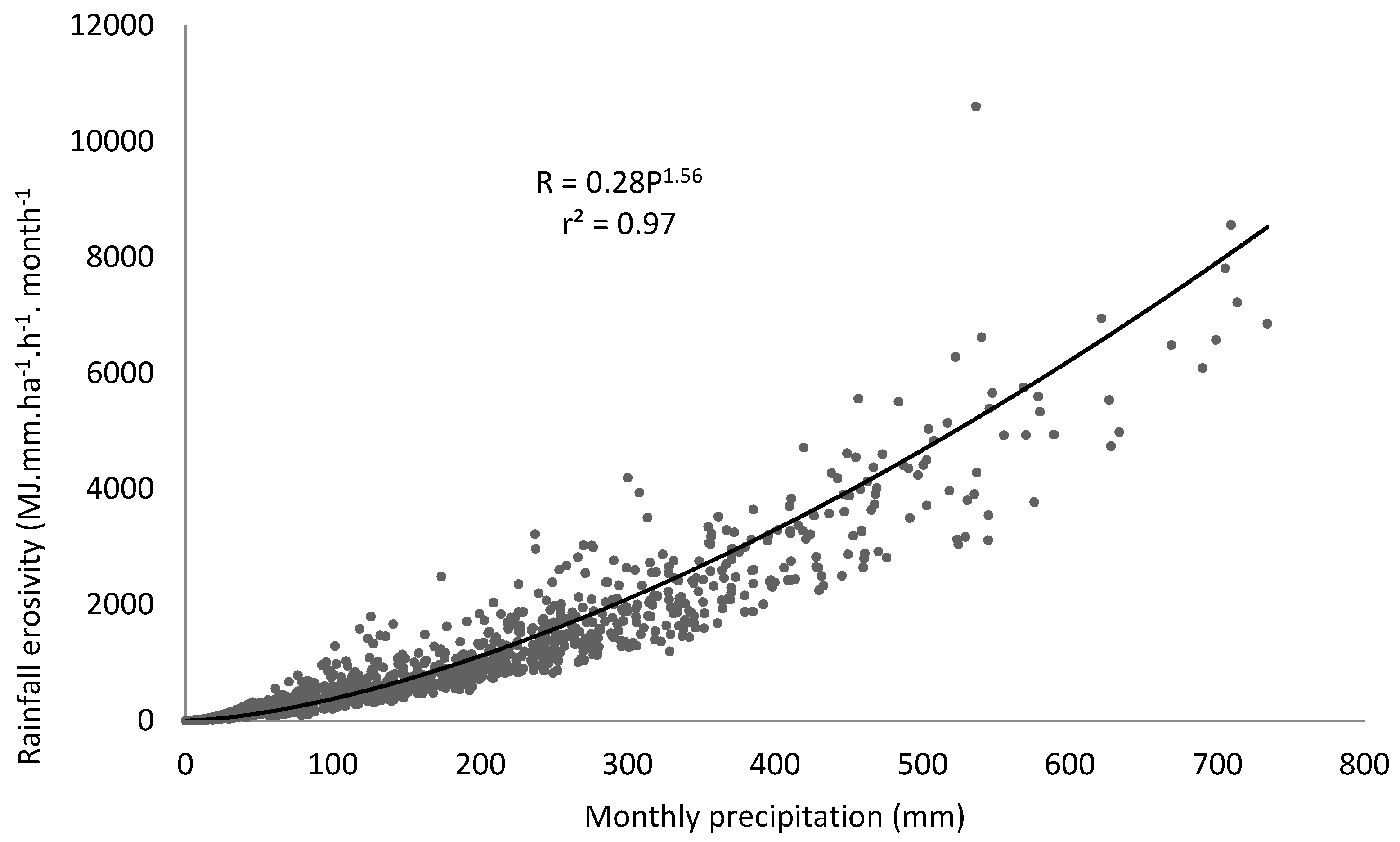
3.1. Estimation of Rainfall Erosivity (R-Factor) Using Observed Precipitation
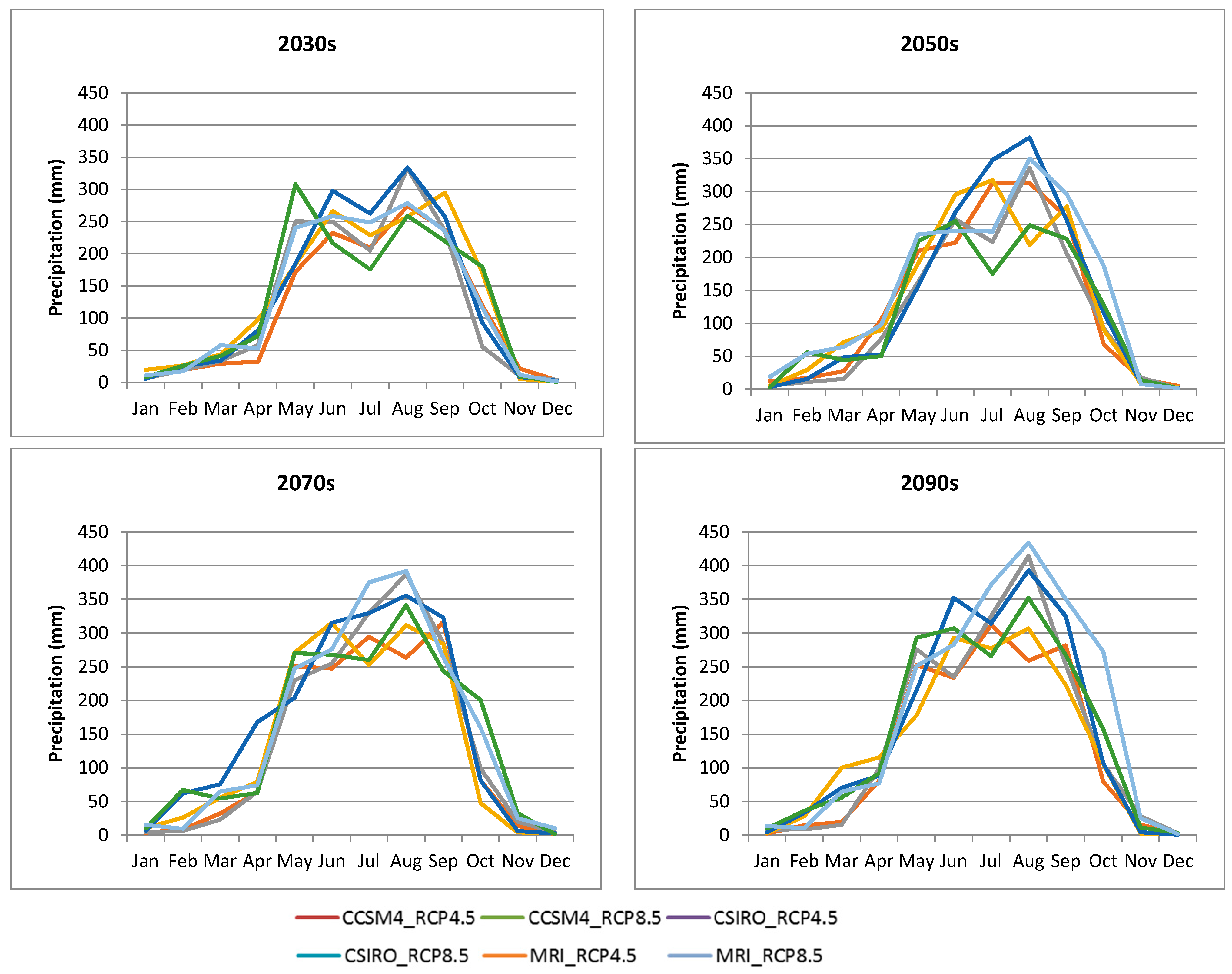
3.2. Impact of Climate Change on Precipitation
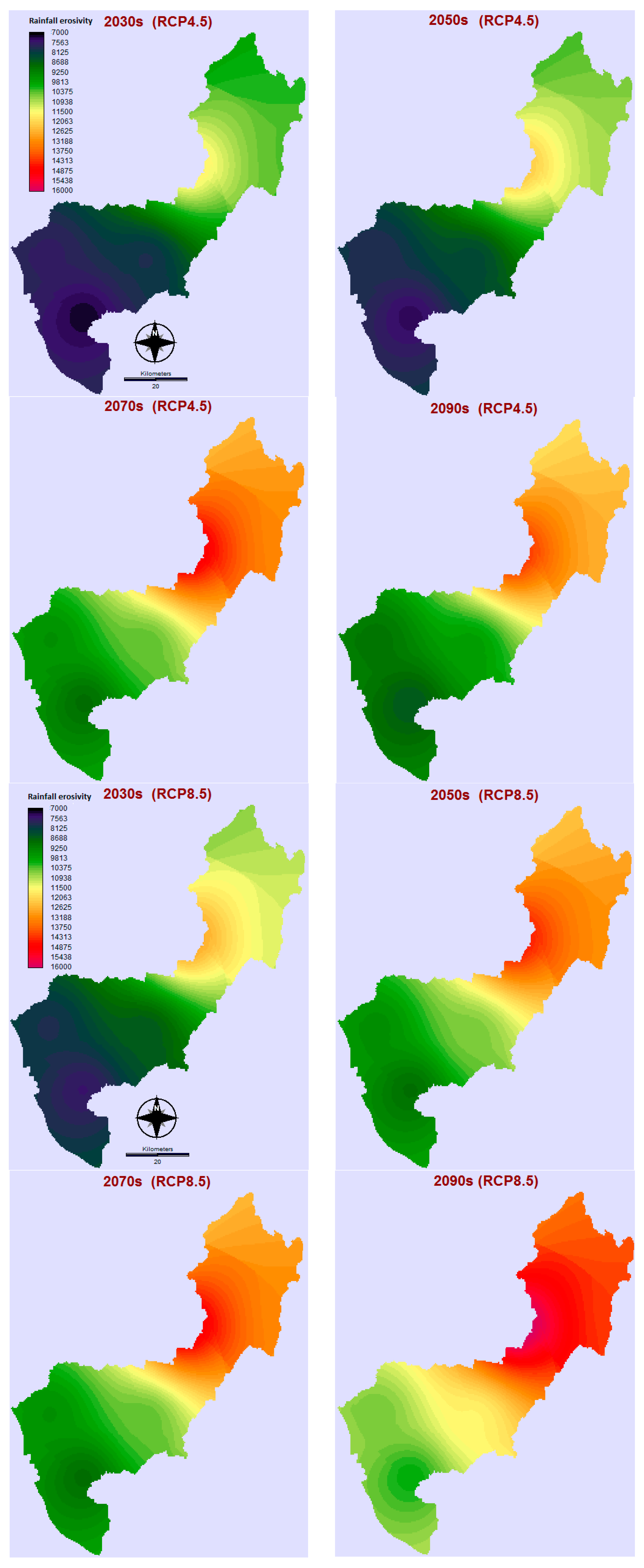
3.3. Impact of Climate Change on Rainfall Erosivity
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Renard, K.G.; Foster, G.A.; Weesies, G.A.; McCool, D.K.; Yoder, D.C. Predicting Soil Erosion by Water: A Guide to Conservation Planning with the Revised Universal Soil Loss Equation (RUSLE). In USDA Agriculture Handbook; Agricultural Research Service: Washington, DC, USA, 1997; No. 703; pp. 400–404. [Google Scholar]
- Wischmeier, W.H.; Smith, D.D. Predicting Rainfall Erosion Losses. In USDA Agricultural Handbook; Agricultural Research Service: Washington, DC, USA, 1978; No. 537; p. 58. [Google Scholar]
- Cohen, M.J.; Shepherd, K.D.; Walsh, M.G. Empirical formulation of the Universal Soil Loss Equation for erosion risk assessment in a tropical watershed. Geodermal 2005, 124, 235–252. [Google Scholar] [CrossRef]
- Diodato, N. Estimating RUSLE’s rainfall factor in the part of Italy with a Mediterranean rainfall regime. Hydrol. Earth Syst. Sci. 2004, 8, 103–107. [Google Scholar] [CrossRef]
- Diodato, N.; Bellochi, G. Estimating monthly (R)USLE climate input in a Mediterranean region using limited data. J. Hydrol. 2007, 345, 224–236. [Google Scholar] [CrossRef]
- Angulo-Martínez, M.; Beguería, S. Estimating rainfall erosivity from daily precipitation records: A comparison among methods using data from the Ebro Basin (NE Spain). J. Hydrol. 2009, 379, 111–121. [Google Scholar] [CrossRef]
- Hernando, D.; Romana, M.G. Estimating the rainfall erosivity factor from monthly precipitation data in the Madrid Region (Spain). J. Hydrol. Hydromech. 2015, 63, 55–62. [Google Scholar] [CrossRef]
- Fournier, F. Climate Erosion; Presses Universitaires de France: Paris, France, 1960. [Google Scholar]
- Arnoldous, H.M.J. An approximation of the rainfall factor in the USLE. In Assessment of Erosion; De Boodt, M., Gabriels, D., Eds.; Wiley: Chichester, UK, 1980; pp. 127–132. [Google Scholar]
- Plangoen, P.; Babel, M.S. Projected Rainfall Erosivity Changes under Future Climate in the Upper Nan Watershed, Thailand. J. Earth Sci. Clim. Chang. 2014, 5. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change (IPCC). The physical science basis. In Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Solomon, S., Qin, D., Manning, M., Chen, Z., Marquis, M., Averyt, K.B., Tignor, M., Miller, H.L., Eds.; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Neal, M.R.; Nearing, M.A.; Vining, R.C.; Southworth, J.; Pfeifer, R.A. Climate change impacts on soil erosion in Midwest United States with changes in crop management. CATENA 2005, 61, 165–184. [Google Scholar] [CrossRef]
- Nearing, A.M. Potential changes in rainfall erosivity in the U.S. with climate change during the 21st century. J. Soil Water Conserv. 2001, 56, 229–232. [Google Scholar]
- Zhang, X.C. A comparison of explicit and implicit spatial downscaling of GCM output for soil erosion and crop production assessments. Clim. Chang. 2007, 84, 337–363. [Google Scholar] [CrossRef]
- Zhang, X.C.; Liu, W.Z. Simulating potential response of hydrology, soil erosion, and crop productivity to climate change in Changwu tableland region on the Loess Plateau of China. Agric. For. Meteorol. 2005, 131, 127–142. [Google Scholar] [CrossRef]
- Favis-Mortlock, D.T.; Guerra, A.J.T. The implications of general circulation model estimates of rainfall for future erosion: A case study from Brazil. CATENA 1999, 37, 329–354. [Google Scholar] [CrossRef]
- Mullan, D.; Favis-Mortlock, D.; Fealy, R. Addressing key limitations associated withmodelling soil erosion under the impacts of future climate change. Agric. For. Meteorol. 2012, 156, 18–30. [Google Scholar] [CrossRef]
- Mullan, D. Soil erosion under the impacts of future climate change: Assessing the statistical significance of future changes and the potential on-site and off-site problems. CATENA 2013, 109, 234–246. [Google Scholar] [CrossRef]
- Plangoen, P.; Babel, M.S.; Clemente, R.S.; Shrestha, S.; Tripathi, N. Simulating the Impacts of Future Land Use and Climate Change on Soil Erosion and Deposition in the Mae Nam Nan Sub-Catchment. Sustainability 2013, 5, 3244–3274. [Google Scholar] [CrossRef]
- Zhang, Y.-G.; Nearing, M.A.; Zhang, X.-C.; Xie, Y.; Wei, H. Projected rainfall erosivity changes under climate change from multi model and multi scenario projections in Northeast China. J. Hydrol. 2010, 384, 97–106. [Google Scholar] [CrossRef]
- Shiono, P.; Ogawa, S.; Miyamoto, T.; Kameyama, K. Expected impacts of climate change on rainfall erosivity of farmlands in Japan. Ecol. Eng. 2013, 61, 678–689. [Google Scholar] [CrossRef]
- Hoomehr, S.; Schwartza, J.S.; Yoder, D. Potential changes in rainfall erosivity under GCM climate change scenarios for the southern Appalachian region, USA. CATENA 2016, 136, 141–151. [Google Scholar] [CrossRef]
- Panagos, P.; Borrelli, P.; Meusburger, K.; Yu, B.; Klik, A.; Lim, K.J.; Yang, J.E.; Ni, J.; Miao, C.; Chattopadhyay, N.; et al. Global rainfall erosivity assessment based on high-temporal resolution rainfall records. Sci. Rep. 2017, 7. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.C.; Nearing, M.A. Impact of climate change on soil erosion, runoff and wheat productivity in central Oklahoma. CATENA 2005, 61, 185–195. [Google Scholar] [CrossRef]
- Park, S.; Jin, C.; Choi, C. Predicting soil erosion under land-cover area and climate changes using the revised universal soil loss equation. In Remote Sensing for Agriculture, Ecosystems, and Hydrology Xiii. Proceedings of SPIE; Neale, C.M.U., Maltese, A., Richter, K., Eds.; Spie-Int Soc Optical Engineering: Bellingham, WA, USA, 2011. [Google Scholar]
- Mondal, A.; Khare, D.; Kundu, S.; Meena, P.K.; Mishra, P.K.; Shukla, R. Impact of climatechange on future soil erosion in different slope, land use, and soil-type conditions in a part of the Narmada River Basin, India. J. Hydrol. Eng. 2015, 20. [Google Scholar] [CrossRef]
- Clemente, R.S.; Prasher, S.O.; Barrington, S.F. PESTFADE—A new pesticide fate and transport model: Model development and verification. Trans. ASAE 1993, 36, 357–367. [Google Scholar] [CrossRef]
- Panagos, P.; Meusburger, K.; Ballabio, C.; Borrelli, P.; Beguería, S.; Klik, A.; Rymszewicz, A.; Michaelides, S.; Olsen, P.; Tadić, M.P.; et al. Reply to the comment on “Rainfall erosivity in Europe” by Auerswald et al. Sci. Total Environ. 2015, 532, 853–857. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, P.T.S.; Wendland, E.; Nearing, M.A. Rainfall erosivity in Brazil: A review. Catena 2013, 100, 139–147. [Google Scholar] [CrossRef]
- Prasannakumar, V.; Vijith, H.; Abinod, S.; Geetha, N. Estimation of soil erosion risk within a small mountainous sub-watershed in Kerala, India, using Revised Universal Soil Loss Equation (RUSLE) and geo-information technology. Geosci. Front. 2012, 3, 209–215. [Google Scholar] [CrossRef]
- Land Development Department (LDD). Group of Soil Series for Economic Crops of Thailand; Office of Soil Survey and Land use Planning, Ministry of Agriculture and Cooperatives: Bangkok, Thailand, 2005. (In Thai)
- Southeast Asia START Regional Center (SEA START). Southeast Asia Regional Vulnerability to Changing Water Resource and Extreme Hydrological Events due to Climate Change; Technical Report No. 15; Southeast Asia START Regional Centre: Bangkok, Thailand, 2006. [Google Scholar]
- Land Development Department (LDD). Soil Series Map Scale 1:25,000; Land Development Department. Ministry of Agriculture and Cooperatives: Bangkok, Thailand, 2007.
- Land Development Department (LDD). Soil Erosion in Thailand; Ministry of Agriculture and Cooperatives: Bangkok, Thailand, 2002. (In Thai)
- Foster, G.R.; Toy, T.E.; Renard, K.G. Comparison of the USLE, RUSLE1.06c, and RUSLE2 for application to highly disturbed lands. In Proceedings of the 1st Interagency Conference on Research in the Watersheds, Benson, AZ, USA, 27–30 October 2003. [Google Scholar]
- Brown, L.C.; Foster, G.R. Storm erosivity using idealized intensity distributions. Trans. ASAE 1987, 30, 379–386. [Google Scholar] [CrossRef]
- McSweeney, C.F.; Jones, R.G.; Lee, R.W.; Rowell, D.P. Selecting CMIP5 GCMs for downscaling over multiple regions. Clim. Dyn. 2015, 44, 3237–3260. [Google Scholar] [CrossRef]
- Fowler, H.J.; Blenkinsop, S.; Tebald, C. Linking climate change modelling to impacts studies: Recent advances in downscaling techniques for hydrological modeling. Int. J. Climatol. 2007, 27, 1547–1578. [Google Scholar] [CrossRef]
- Gudmundsson, L.; Bremnes, J.B.; Haugen, J.E.; Engen-Skaugen, T. Technical Note: Downscaling RCM precipitation to the station scale using statistical transformations—A comparison of methods. Hydrol. Earth Syst. Sci. 2012, 16, 3383–3390. [Google Scholar] [CrossRef]


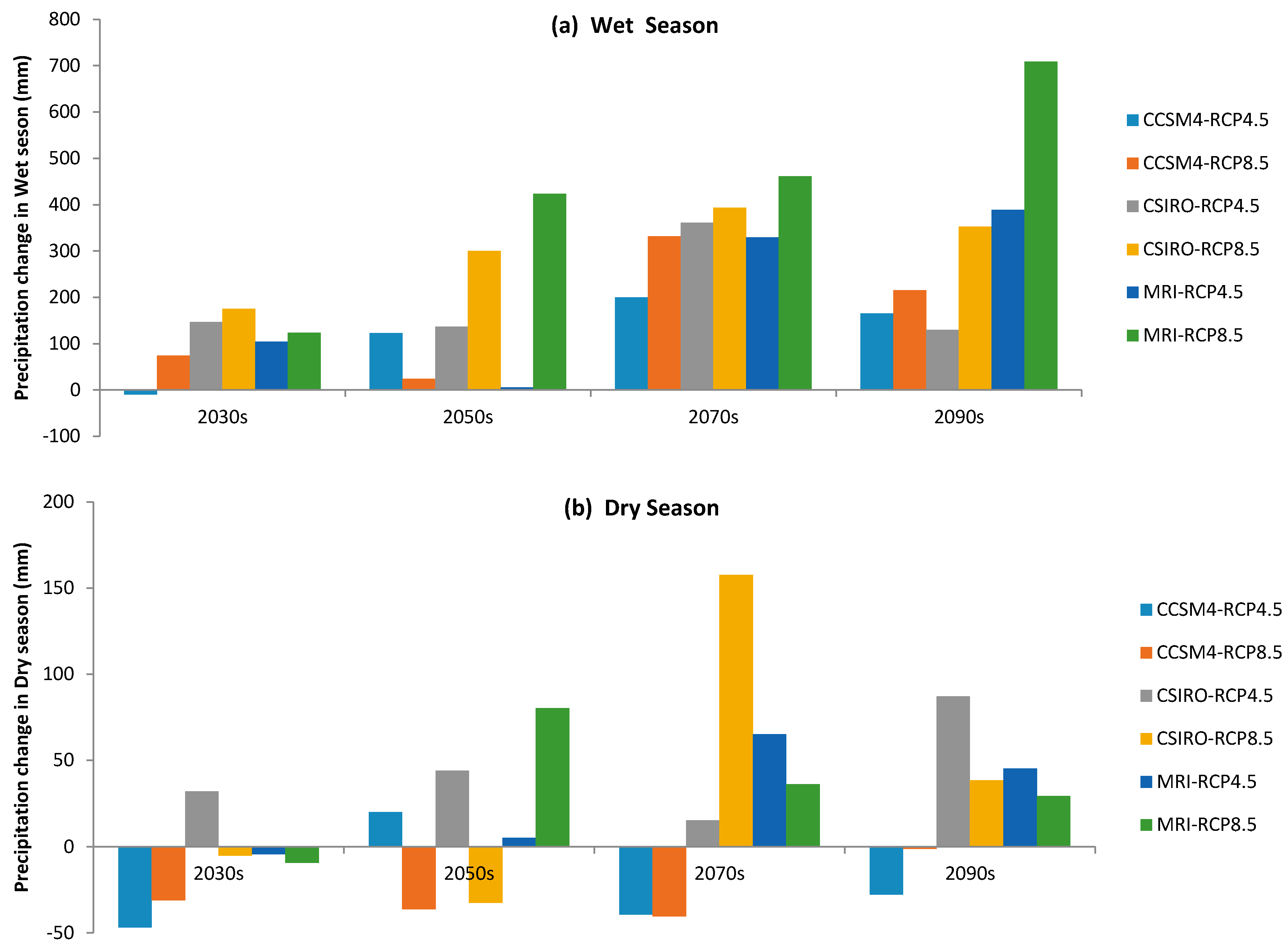

| Authors | Study area and Location | Climate Models | Climate Scenarios | Baseline Period | Projected Period | Projected Change in Precipitation (%) | Projected Change in Rainfall Erosivity (%) |
|---|---|---|---|---|---|---|---|
| Zhang et al., 2010 [20] | Northeast of China | CGCM3.1 (T47) CGCM3.1 (T63) CSIRO-MK3.0 UKMO-HadCM3 UKMO-HadGEM1 ECHAM5/MPI-OM | A2, A1B, B1 | 1960–1999 | 2030–2059 2070–2099 | +13.33 +21.33 | +54.33 +73.66 |
| Shiono et al., 2013 [21] | Hokkaido Island, Japan | RCM20 | A2 | 1995–2009 | 2031–2050 2081–2100 | +30 +8 | +26 +23 |
| Plangoen et al., 2014 [10] | Upper Nan Watershed, Thailand | PRECIS: ECHAM4, GFDLR-30, HadCM3 and CCSM3 | A2,B2,A1B, B1 | 1971–2000 | 2011–2040 | +2.14 | +5.02 |
| 2041–2070 | +5.19 | +10.32 | |||||
| 2071–2099 | +7.00 | +14.20 | |||||
| Hoomehr et al., 2016 [22] | Southern Appalachian region, USA | CCSM | A1FI, A1B, B1 | 1959–2000 | 2010–2099 | +3 to +12 | +7 to +19 |
| Panagos et al., 2017 [23] | EUROPE | HadGEM2 | RCP4.5 | 2010s | 2050s | - | −23.9 to 78.2 |
| Year | Author(s) | Country/Region | Erosion Models | Climate Models | Climate Scenarios |
|---|---|---|---|---|---|
| 2010 | Zhang et al. [20] | Northeast China | RUSLE | CGCM3.1 (T47),CGCM3.1 (T63), CSIRO-MK3.0, UKMO-Hadcm3, UKMO-HadGEM1, ECHAM5/MPI-OM | A2, A1B, B1 |
| 2011 | Park et al. [25] | All land areas of Korea | RUSLE | Mesoscale Model Version 5 | A1B |
| 2013 | Plangoen et al. [19] | Mae Nam Nan sub-catchment, Thailand | RUSLE | CCSM3 HadCM3 PRECIS RCM | A2, A1B, B1 |
| 2015 | Mondal et al. [26] | Narmada River Basin, India | USLE | HADCM3 | A2 |
| Model Center | Model Name | Resolution (⁰) | Scenario | Timescale | Temporal Resolution |
|---|---|---|---|---|---|
| National Center for Atmospheric Research | CCSM4 | 1.25 × 0.94 | Historical, RCP 4.5 and RCP 8.5 | Daily | 1982–2005 2021–2040 (2030s) 2041–2060 (2050s) 2061–2080 (2070s) 2081–2100 (2090s) |
| Commonwealth Scientific and Industrial Research Organization in collaboration with Queensland Climate Change Centre of Excellence | CSIRO-MK3.6.0 | 1.875 × 1.875 | Historical, RCP 4.5 and RCP 8.5 | Daily | 1982–2005 2021–2040 (2030s) 2041–2060 (2050s) 2061–2080 (2070s) 2081–2100 (2090s) |
| Meteorological Research Institute, Japan | MRI-CGCM3 | 1.1 × 1.1 | Historical, RCP 4.5 and RCP 8.5 | Daily | 1982–2005 2021–2040 (2030s) 2041–2060 (2050s) 2061–2080 (2070s) 2081–2100 (2090s) |
| Station Name | Longitude (Eastings) | Latitude (Northings) | Annual Average Rainfall | R-Factor Model (MJ mm ha−1 h−1 year−1) |
|---|---|---|---|---|
| Udon Thani | 102.48.00 | 17.23.00 | 1417.3 | R = 0.23P1.58 |
| r2 = 0.98 | ||||
| Phen | 102.55.00 | 17.39.00 | 1786.3 | R = 0.25P1.58 |
| r2 = 0.98 | ||||
| Ban Dung | 103.15.42 | 17.41.53 | 1504.7 | R = 0.36P1.52 |
| r2 = 0.97 | ||||
| Kud Jub | 102.37.00 | 17.13.00 | 1205.0 | R = 0.51P1.45 |
| r2 = 0.96 | ||||
| Nong Wau So | 102.37.00 | 17.13.00 | 1248.3 | R = 0.49P1.46 |
| r2 = 0.95 | ||||
| Nong Khai | 102.44.00 | 17.52.00 | 1582.8 | R = 0.23P1.59 |
| r2 = 0.98 | ||||
| All 6 stations data | R = 0.28P1.56 | |||
| r2 = 0.97 | ||||
| Code | 354201 | 354001 | 354005 | 354008 | 354009 | 352201 | All 6 Stations |
|---|---|---|---|---|---|---|---|
| Station | Udon Thani | Phen | Ban Dung | Kud Jub | Nong Wau So | Nong Khai | Average |
| Jan | 11 | 19 | 16 | 13 | 4 | 24 | 15 |
| Feb | 84 | 82 | 105 | 107 | 64 | 53 | 83 |
| Mar | 258 | 194 | 200 | 176 | 133 | 138 | 183 |
| Apr | 416 | 644 | 501 | 341 | 579 | 391 | 479 |
| May | 1104 | 1632 | 1205 | 1026 | 784 | 1198 | 1158 |
| Jun | 1419 | 2228 | 1827 | 1195 | 958 | 1608 | 1539 |
| Jul | 1397 | 1746 | 1740 | 1092 | 1155 | 1732 | 1477 |
| Aug | 1754 | 2767 | 2538 | 1540 | 1734 | 1901 | 2039 |
| Sept | 1411 | 1975 | 1702 | 1447 | 1258 | 1456 | 1542 |
| Oct | 341 | 480 | 175 | 294 | 379 | 423 | 349 |
| Nov | 18 | 31 | 24 | 32 | 24 | 29 | 26 |
| Dec | 7 | 24 | 4 | 0 | 4 | 13 | 9 |
| Annual * | 8220 | 11,824 | 10,036 | 7261 | 7077 | 8967 | 8898 |
| GCM | Scenario | 2030s | 2050s | 2070s | 2090s | ||||
|---|---|---|---|---|---|---|---|---|---|
| Rainfall (mm) | Change (%) | Rainfall (mm) | Change (%) | Rainfall (mm) | Change (%) | Rainfall (mm) | Change (%) | ||
| CCSM4 | RCP4.5 | 1360.4 | −4.0 | 1560.0 | 10.1 | 1577.9 | 11.3 | 1554.8 | 9.7 |
| RCP8.5 | 1460.7 | 3.1 | 1405.5 | −0.8 | 1708.7 | 20.6 | 1631.8 | 15.1 | |
| CSIRO-MK3 | RCP4.5 | 1595.9 | 12.6 | 1598.2 | 12.8 | 1793.5 | 26.5 | 1634.6 | 15.3 |
| RCP8.5 | 1587.1 | 12.0 | 1684.9 | 18.9 | 1968.8 | 38.9 | 1808.5 | 27.6 | |
| MRI-CGCM3 | RCP4.5 | 1517.5 | 7.1 | 1428.1 | 0.8 | 1812.4 | 27.9 | 1851.5 | 30.6 |
| RCP8.5 | 1531.6 | 8.1 | 2066.9 | 45.8 | 1914.6 | 35.1 | 2155.4 | 52.1 | |
| Average | 1282.1 | 6.4 | 1623.9 | 14.6 | 1795.9 | 26.7 | 1772.7 | 25.0 | |
| Climate Models | GHGES | Annual Rainfall Erosivity (MJ mm ha−1 h−1 year−1) | Mean Change (%) | Stdev. | ||
|---|---|---|---|---|---|---|
| Min | Max | Mean | ||||
| Base line | 6530 | 11,363 | 8302 | 0.00 | 1343 | |
| 2030s | ||||||
| CCSM4 | RCP4.5 | 6539 | 10,705 | 8114 | −2.26 | 1266 |
| RCP8.5 | 7204 | 12,344 | 9280 | 11.78 | 1513 | |
| CSIRO-MK3.6.0 | RCP4.5 | 7974 | 12,790 | 9858 | 18.74 | 1401 |
| RCP8.5 | 8074 | 13,108 | 10,109 | 21.77 | 1490 | |
| MRI-CGCM3 | RCP4.5 | 7113 | 11,224 | 8893 | 7.12 | 1126 |
| RCP8.5 | 7377 | 12,248 | 9359 | 12.73 | 1405 | |
| Average | 7380 | 12,070 | 9269 | 12 | 1367 | |
| 2050s | ||||||
| CCSM4 | RCP4.5 | 8031 | 13,350 | 10,074 | 21.34 | 1538 |
| RCP8.5 | 6998 | 11,757 | 8866 | 6.79 | 1446 | |
| CSIRO-MK3.6.0 | RCP4.5 | 7845 | 12,616 | 9808 | 18.14 | 1433 |
| RCP8.5 | 8678 | 14,089 | 11,025 | 32.80 | 1592 | |
| MRI-CGCM3 | RCP4.5 | 6293 | 10,442 | 8088 | −2.58 | 1126 |
| RCP8.5 | 11,210 | 17,233 | 14,009 | 68.74 | 1665 | |
| Average | 8176 | 13,248 | 10,312 | 24 | 1467 | |
| 2070s | ||||||
| CCSM4 | RCP4.5 | 8160 | 13,302 | 10,217 | 23.07 | 1530 |
| RCP8.5 | 8943 | 14,786 | 11,449 | 37.91 | 1685 | |
| CSIRO-MK3.6.0 | RCP4.5 | 9561 | 16,445 | 12,506 | 50.64 | 1954 |
| RCP8.5 | 10,966 | 17,034 | 13,376 | 61.12 | 1844 | |
| MRI-CGCM3 | RCP4.5 | 9060 | 14,618 | 11,390 | 37.20 | 1540 |
| RCP8.5 | 9757 | 15,313 | 12,187 | 46.80 | 1598 | |
| Average | 9408 | 15,250 | 11,854 | 43 | 1692 | |
| 2090s | ||||||
| CCSM4 | RCP4.5 | 8025 | 13,281 | 10,110 | 21.78 | 1608 |
| RCP8.5 | 8513 | 14,084 | 10,729 | 29.23 | 1570 | |
| CSIRO-MK3.6.0 | RCP4.5 | 7869 | 12,976 | 10,045 | 20.99 | 1485 |
| RCP8.5 | 9552 | 15,407 | 12,042 | 45.05 | 1745 | |
| MRI-CGCM3 | RCP4.5 | 9764 | 15,894 | 12,272 | 47.82 | 1736 |
| RCP8.5 | 12,247 | 19,086 | 15,159 | 82.59 | 1843 | |
| Average | 9328 | 15,121 | 11,726 | 41 | 1665 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Plangoen, P.; Udmale, P. Impacts of Climate Change on Rainfall Erosivity in the Huai Luang Watershed, Thailand. Atmosphere 2017, 8, 143. https://doi.org/10.3390/atmos8080143
Plangoen P, Udmale P. Impacts of Climate Change on Rainfall Erosivity in the Huai Luang Watershed, Thailand. Atmosphere. 2017; 8(8):143. https://doi.org/10.3390/atmos8080143
Chicago/Turabian StylePlangoen, Pheerawat, and Parmeshwar Udmale. 2017. "Impacts of Climate Change on Rainfall Erosivity in the Huai Luang Watershed, Thailand" Atmosphere 8, no. 8: 143. https://doi.org/10.3390/atmos8080143





