Analysis of Precipitation Extremes in the Qinghai-Tibetan Plateau, China: Spatio-Temporal Characteristics and Topography Effects
Abstract
:1. Introduction
2. Experiments
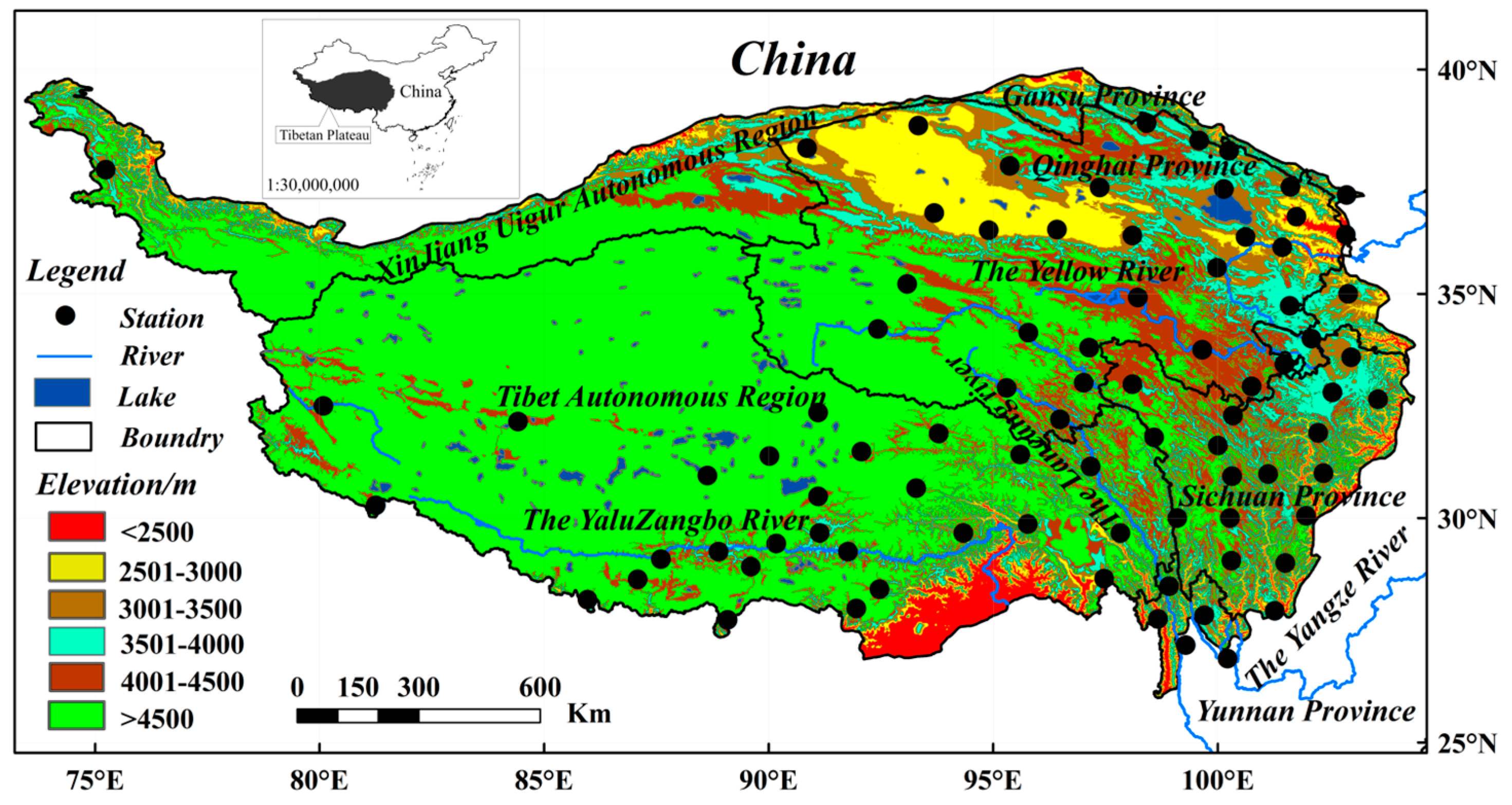
2.1. Study Area
2.2. Data Source
2.3. Data Quality and Homogeneity Test
2.4. Indices of Extreme Precipitation
2.5. Statistic Analysis
3. Results
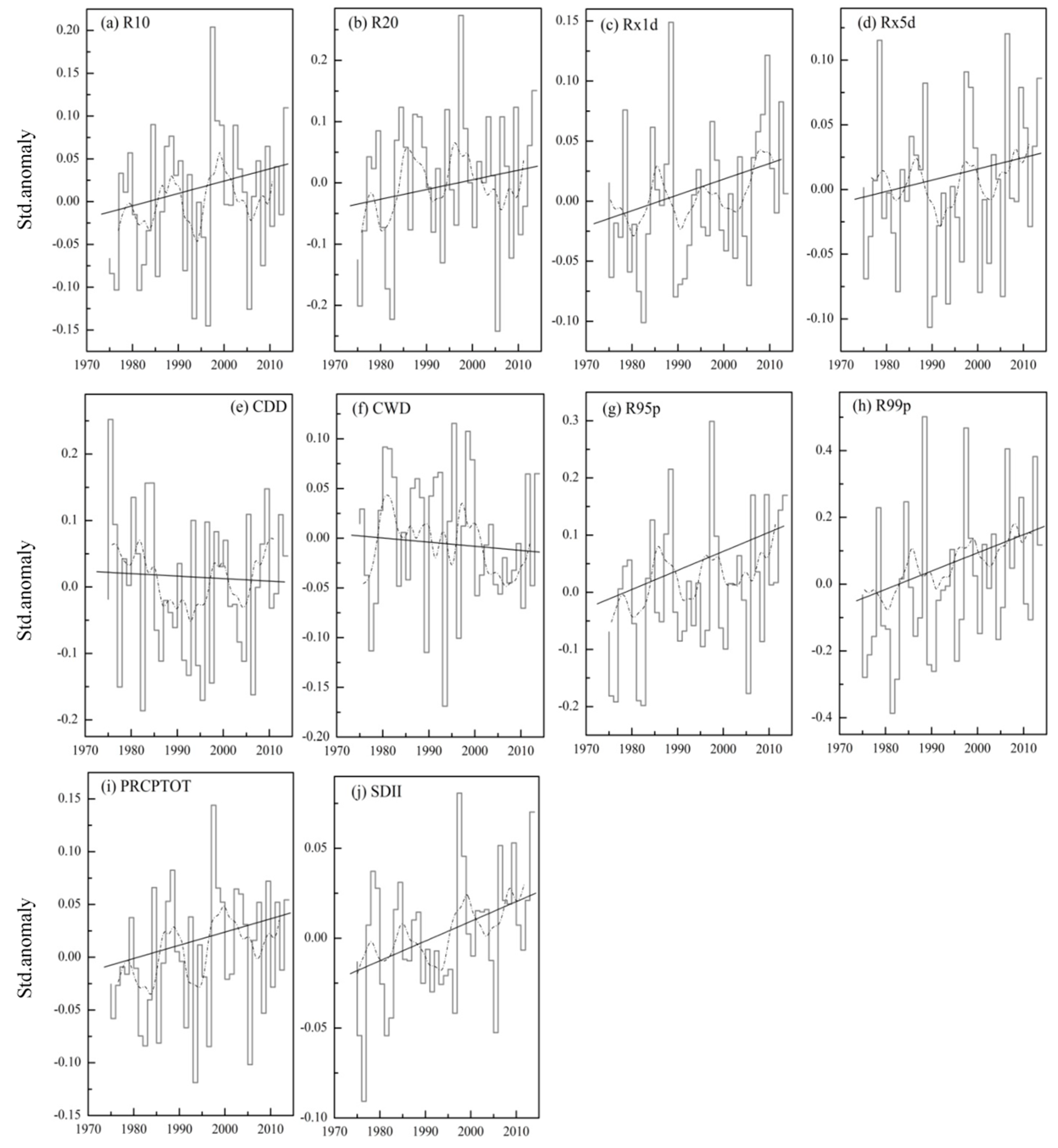
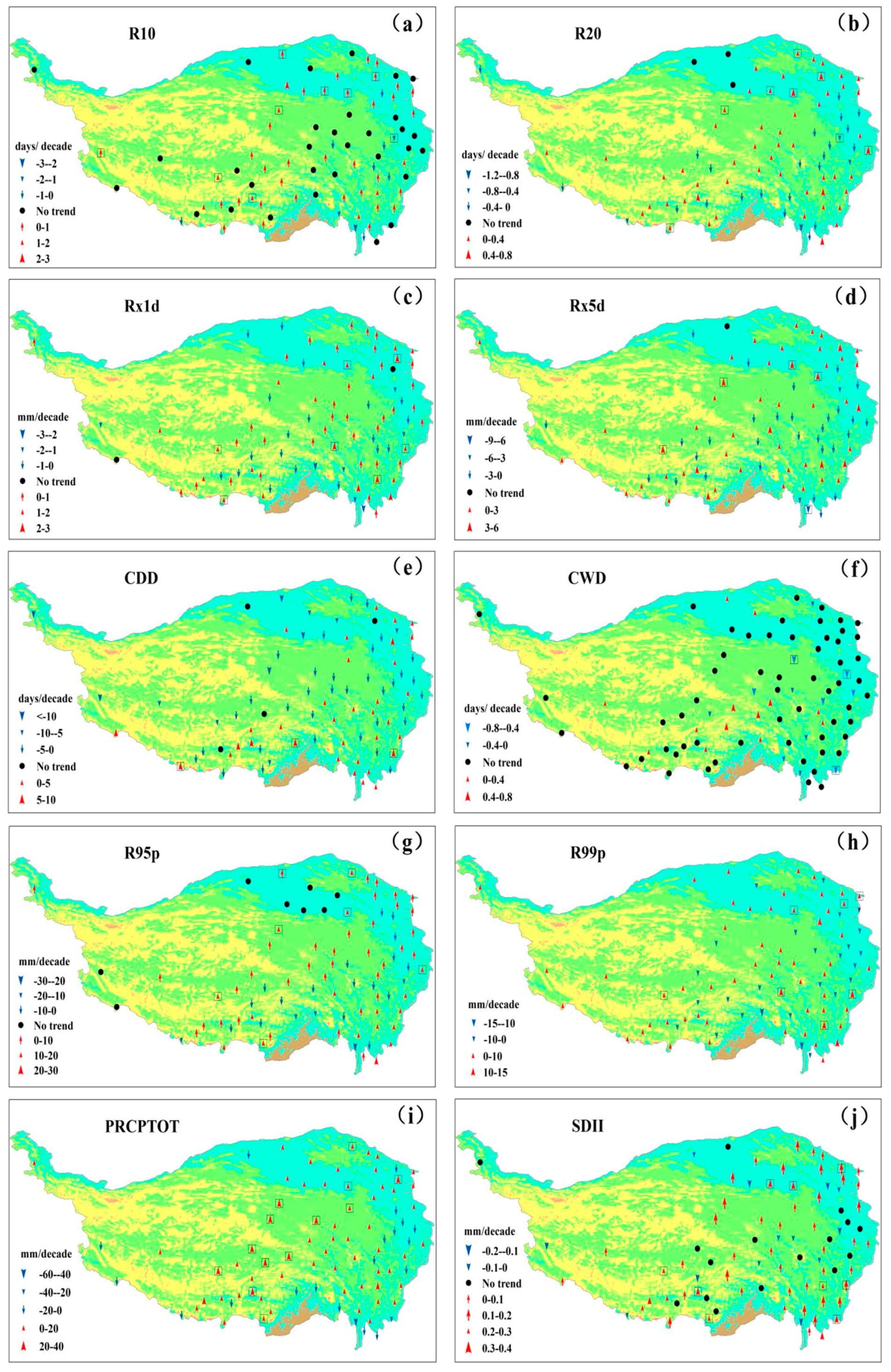
3.1. Spatiotemporal Variability and Trends of Extreme Precipitation
3.1.1. Threshold Indices
3.1.2. Absolute Indices
3.1.3. Duration Indices
3.1.4. Percentile-Based Indices
3.1.5. Other Indices
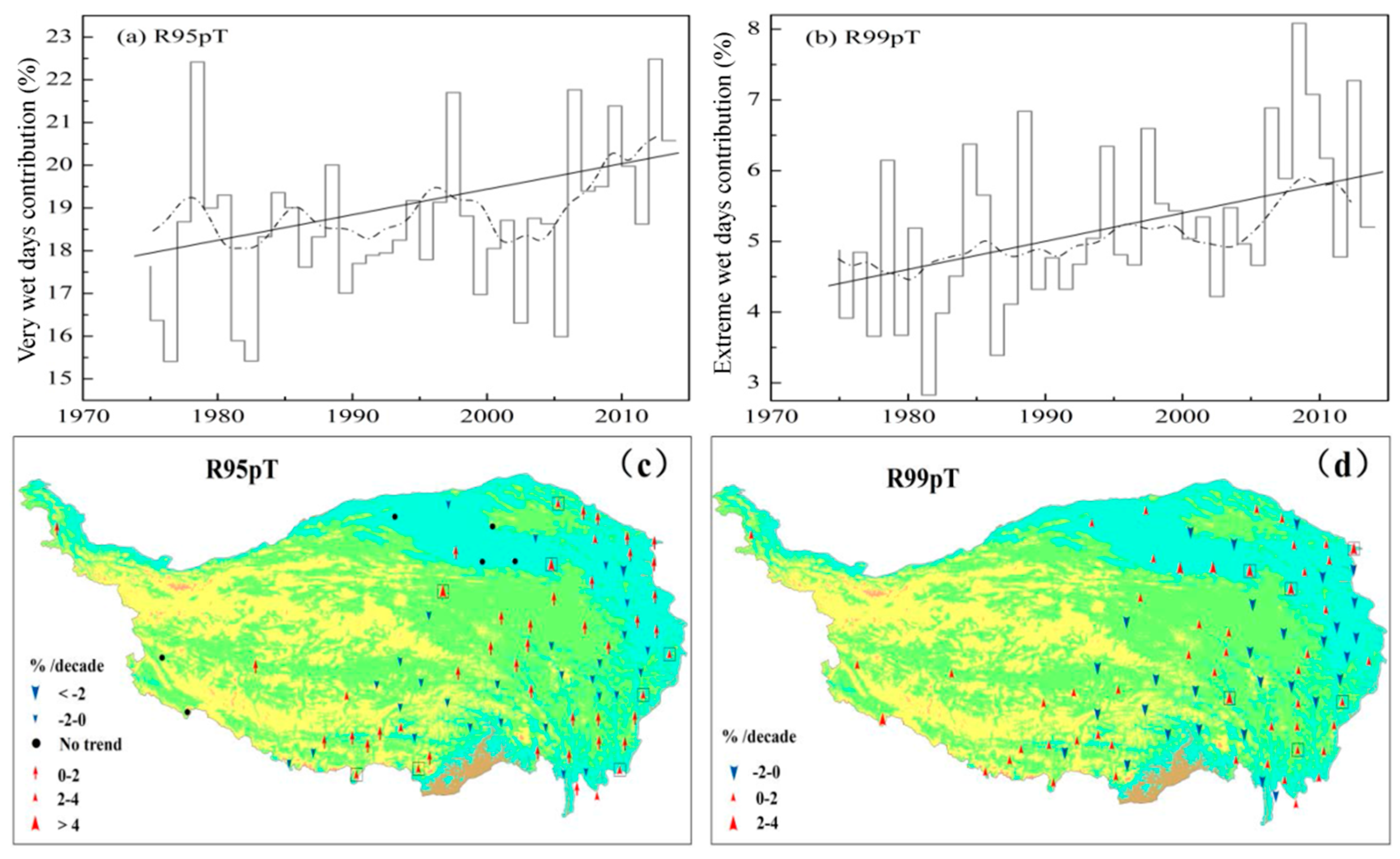
3.2. Contribution of Extreme Precipitation to Total Precipitation
3.3. Relationship between Precipitation Extremes and Topography
4. Discussion
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Katz, R.W.; Brown, B.G. Extreme events in a changing climate: Variability is more important than averages. Clim. Chang. 1992, 3, 289–302. [Google Scholar] [CrossRef]
- Salinger, M.J.; Griffiths, G.M. Trends in New Zealand daily temperature and rainfall extremes. Int. J. Climatol. 2001, 21, 1437–1452. [Google Scholar] [CrossRef]
- López-Moreno, J.I.; Vicente-Serrano, S.M.; Angulo-Martínez, M.; Beguería, S.; Kenawy, A. Trends in daily precipitation on the northeastern Iberian Peninsula, 1955–2006. Int. J. Climatol. 2010, 30, 1026–1041. [Google Scholar] [CrossRef]
- Bennett, K.E.; Walsh, J.E. Spatial and temporal changes in indices of extreme precipitation and temperature for Alaska. Int. J. Climatol. 2015, 35, 1434–1452. [Google Scholar] [CrossRef]
- Ji, Y.; Zhou, G.; Wang, S.; Wang, L. Increase in flood and drought disasters during 1500–2000 in Southwest China. Nat. Hazards 2015. [Google Scholar] [CrossRef]
- Liu, M.; Xu, X.; Sun, Y.A.; Wang, K.; Liu, W.; Zhang, X. Is southwestern China experiencing more frequent precipitation extremes? Environ. Res. Lett. 2014, 9, 064002. [Google Scholar] [CrossRef]
- Gao, Y.; Feng, Q.; Wei, L.; Lu, A.; Wang, Y.; Yang, J.; Cheng, A.; Wang, Y.; Su, Y.; Liu, L.; et al. Changes of daily climate extremes in Loess Plateau during 1960–2013. Quatern. Int. 2015, 37, 15–21. [Google Scholar]
- Alexander, L.V.; Zhang, X.; Peterson, T.C.; Caesar, J.; Gleason, B.; Klein Tank, A.; Haylock, M.; Collins, D.; Trewin, B.; Rahimzadeh, F.; et al. Global observed changes in daily climate extremes of temperature and precipitation. J. Geophys. Res. 2006, 111, D05109. [Google Scholar] [CrossRef]
- Groisman, P.Y.; Knight, R.W.; Easterling, D.R.; Karl, T.R.; Hegerl, G.C.; Razuvaev, V.N. Trends in Intense Precipitation in the Climate Record. J. Clim. 2005. [Google Scholar] [CrossRef]
- Peterson, T.C.; Zhang, X.B.; Brunt-India, M.; Vázquez-Aguirre, J.L. Changes in North American extremes derived from daily weather data. J. Geophys. Res. Atmos. 2008, 113, D07113. [Google Scholar] [CrossRef]
- You, Q.; Kang, S.; Aguilar, E.; Pepin, N.; Fludel, W.-A.; Yan, Y.; Xu, Y.; Zhang, Y.; Huang, J. Changes in daily climate extremes in China and their connection to the large scale atmospheric circulation during 1961–2003. Clim. Dynam. 2010, 36, 2399–2417. [Google Scholar] [CrossRef]
- Li, Y.G.; He, D.; Hua, J.M.; Cao, J. Variability of extreme precipitation over Yunnan Province, China 1960–2012. Int. J. Climatol. 2015, 35, 245–258. [Google Scholar] [CrossRef]
- Choi, G.; Collins, D.; Ren, G.; Trewin, B.; Baldi, M.; Fukuda, Y.; Afzaal, M.; Pianmana, T.; Gomboluudev, P.; Huong, P.; et al. Changes in means and extreme events of temperature and precipitation in the Asia-Pacific Network region, 1955–2007. Int. J. Climatol. 2009, 29, 1906–1925. [Google Scholar] [CrossRef]
- Moberg, A.; Jones, P.D.; Lister, D.; Walther, A.; Brunet, M.; Jacobeit, J.; Alexander, L.V.; Della-Marta, P.M.; Luterbacher, J.; Yiou, P.; et al. Indices for daily temperature and precipitation extremes in Europe analyzed for the period 1901–2000. J. Geophys. Res. 2006, 111, D22106. [Google Scholar] [CrossRef]
- Ye, D.; Gao, Y. The Meteorology of the Qinghai-Xizang (Tibet) Plateau; Science Press: Beijing, China, 1979; pp. 1–278. (In Chinese) [Google Scholar]
- Hsu, H.H.; Liu, X. Relationship between the Tibetan Plateau heating and East Asian summer monsoon rainfall. Geophys. Res. Lett. 2003. [Google Scholar] [CrossRef]
- Kang, S.; Xu, Y.; You, Q.; Fl¨ugel, W.A.; Pepin, N.; Yao, T. Review of climate and cryospheric change in the Tibetan Plateau. Environ. Res. Lett. 2010, 5, 015101. [Google Scholar] [CrossRef] [Green Version]
- Chen, B.; Xu, X.; Yang, S.; Zhang, W. On the origin and destination of atmospheric moisture and air mass over the Tibetan Plateau. Theor. Appl. Climatol. 2012, 110, 423–435. [Google Scholar] [CrossRef]
- Xu, X.; Lu, C.; Shi, X.; Gao, S. World water tower: An atmospheric perspective. Geophys. Res. Lett. 2008. [Google Scholar] [CrossRef]
- Shen, M.; Piao, S.; Cong, N.; Zhang, G.; Jassens, I.A. Precipitation impacts on vegetation spring phenology on the Tibetan Plateau. Glob. Chang. Biol. 2015. [Google Scholar] [CrossRef] [PubMed]
- Tao, S.; Ding, Y. Observational evidence of the influence of the Qinghai-Xizang (Tibet) Plateau on the occurrence of heavy rain and severe convective storms in China. Bull. Am. Meterol. Soc. 1981, 62, 23–30. [Google Scholar] [CrossRef]
- Wang, B.; Bao, Q.; Hoskins, B.; Wu, G.; Liu, Y. Tibetan Plateau warming and precipitation change in East Asia. Geophys. Res. Lett. 2008, 35, L14702. [Google Scholar] [CrossRef]
- IPCC Climate Change. The Physical Science Basis. In Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Huang, M.; Peng, G.B.; Leslie, L.M.; Shao, X.M.; Sha, W.Y. Seasonal and regional temperature changes in China over the 50 year period 1951–2000. Meteorol. Atmos. Phys. 2005, 89, 105–115. [Google Scholar] [CrossRef]
- Xu, Z.X.; Gong, T.L.; Li, J.Y. Decadal trend of climate in the Tibetan Plateau-regional temperature and precipitation. Hydrol. Process. 2008, 22, 3056–3065. [Google Scholar] [CrossRef]
- You, Q.; Kang, S.; Aguilar, E.; Yan, Y. Changes in daily climate extremes in the eastern and central Tibetan Plateau during 1961–2005. J. Geophys. Res. 2008, 113, D07101. [Google Scholar] [CrossRef]
- Li, Z.X.; He, Y.; Wang, P.; Theakstone, W.H.; An, W.; Wang, X.; Lu, A.; Zhang, W.; Cao, W. Changes of daily climate extremes in southwestern China during 1961–2008. Glob. Planet. Chang. 2012, 80, 255–272. [Google Scholar]
- Wang, S.; Zhang, M.; Wang, B.; Sun, M.; Li, X. Recent changes in daily extremes of temperature and precipitation over the western Tibetan Plateau, 1973–2011. Quatern. Int. 2013, 313, 110–117. [Google Scholar] [CrossRef]
- Zhang, K.; Pan, S.; Cao, L.; Wang, Y.; Zhao, Y.; Zhang, W. Spatial distribution and temporal trends in precipitation extremes over the Hengduan Mountains region, China, from 1961 to 2012. Quatern. Int. 2014, 349, 346–356. [Google Scholar] [CrossRef]
- Maussion, F.; Scherer, D.; Mölg, T.; Collier, E.; Curio, J.; Finkelnburg, R. Precipitation Seasonality and Variability over the Tibetan Plateau as Resolved by the High Asia Reanalysis. J. Clim. 2014, 27, 1910–1927. [Google Scholar] [CrossRef]
- You, Q.; Fraedrich, K.; Ren, G.; Ye, B.; Meng, X.; Kang, S. Inconsistencies of precipitation in the eastern and central Tibetan Plateau between surface adjusted data and reanalysis. Theor. Appl. Climatol. 2012, 109, 485–496. [Google Scholar] [CrossRef]
- Long, Q.; Chen, Q.; Gui, K.; Zhang, Y. A Case Study of a Heavy Rain over the Southeastern Tibetan Plateau. Atmosphere 2016, 7, 118. [Google Scholar] [CrossRef]
- Li, Z.; He, Y.; Theakstone, W.H.; Wang, X.; Zhang, W.; Cao, W.; Du, J.; Xin, H.; Chang, L. Altitude dependency of trends of daily climate extremes in southwestern China, 1961–2008. J. Geogr. Sci. 2012, 22, 416–430. [Google Scholar] [CrossRef]
- Ji, Z.; Kang, S.; Cong, Z.; Zhang, Q.; Yao, T. Simulation of carbonaceous aerosols over the Third Pole and adjacent regions: Distribution, transportation, deposition, and climatic effects. Clim. Dynam. 2015, 45, 2831–2846. [Google Scholar] [CrossRef]
- Qiu, J. Environment: Riding on the roof of the world. Nature 2007, 449, 398–402. [Google Scholar] [CrossRef] [PubMed]
- Wan, W.; Xiao, P.; Feng, X.; Li, H.; Ma, R.; Duan, H.; Zhao, L. Monitoring lake changes of Qinghai-Tibetan Plateau over the past 30 years using satellite remote sensing data. Chin. Sci. Bull. 2014, 59. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhang, Y.; Liu, L.; Liu, F.; Zhang, H. Recent changes in wetlands on the Tibetan Plateau: A review. J. Geogr. Sci. 2015, 25, 879–896. [Google Scholar] [CrossRef]
- Wan, G.; Yang, M.; Liu, Z.; Wang, X.; Liang, X. The Precipitation Variations in the Qinghai-Xizang (Tibetan) Plateau during 1961–2015. Atmosphere 2017, 8, 80. [Google Scholar] [CrossRef]
- WMO. Calculation of Monthly and Annual 30-Year Standard Normals; WCDP-No.10, WMO-TD/No. 34; World Meteorological Organization: Geneva, Switzerland, 1989; p. 11. [Google Scholar]
- Zhang, X.; Feng, Y. RClimDex (1.0) User Manual. Available online: http://etccdi.pacificclimate.org/software.shtml (accessed on 10 September 2004).
- Aguilar, E.; Auer, I.; Brunet, M.; Peterson, T.C.; Wieringa, J. Guidance on metadata and homogenization. Wmo. Td. 2003, 1186, 53. [Google Scholar]
- Wang, X.L.; Feng, Y. RHtestsV4 User Manual. Available online: http://etccdi.pacificclimate.org/software.shtml (accessed on 20 July 2013).
- Xu, L.; Shi, Z.; Wang, Y.; Zhang, S.; Chu, X.; Yu, P.; Wang, Y. Spatiotemporal variation and driving forces of reference evapotranspiration in Jing River Basin, northwest China. Hydrol. Process. 2015, 23, 4846–4862. [Google Scholar] [CrossRef]
- Shi, Z.; Shan, N.; Xu, L.; Yang, X.; Gao, J.; Guo, H.; Dong, L. Spatiotemporal variation of temperature, precipitation and wind trends in a desertification prone region of China from 1960 to 2013. Int. J. Climatol. 2016. [Google Scholar] [CrossRef]
- Wei, W.; Shi, Z.; Yang, X.; Wei, Z.; Liu, Y.; Zhang, Z.; Ge, G.; Zhang, X.; Guo, H.; Zhang, K.; et al. Recent Trends of Extreme Precipitation and Their Teleconnection with Atmospheric Circulation in the Beijing-Tianjin Sand Source Region, China, 1960–2014. Atmosphere 2017, 8, 83. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric Tests against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Measures; Charles Griffin: London, UK, 1975. [Google Scholar]
- Dinpashoh, Y.; Jhajharia, D.; Fakheri-Fard, A.; Singh, V.P.; Kahya, E. Trends in reference crop evapotranspiration over Iran. J. Hydrol. 2011, 399, 422–433. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Von Storch, H. Misuses of Statistical Analysis in Climate Research Analysis of Climate Variability; Springer: Berlin/Heidelberg, Germany, 1999; pp. 11–26. [Google Scholar]
- Yue, S.; Pilon, P.; Phinney, B.; Cavadias, G. The influence of autocorrelation on the ability to detecttrend in hydrological series. Hydrol. Process. 2002, 16, 1807–1829. [Google Scholar] [CrossRef]
- Han, H.; Gao, T.; Yi, H.; Yang, M.; Yan, X.; Ren, G.; Yang, J. Extraction of Relief Amplitude Based on Change Point Method: A Case Study on the Tibetan Plateau. Sci. Geogr. Sin. 2012, 1, 101–104. (In Chinese) [Google Scholar]
- Liu, H.; Duan, K. Effects of North Atlantic Oscillation on summer precipitation over the Tibetan Plateau. J. Glaciol. Geocryol. 2012, 2, 311–318. (In Chinese) [Google Scholar]
- Liu, X.; Yin, Z. Spatial and temporal variation of summer precipitation over the eastern Tibetan Plateau and the North Atlantic Oscillation. J. Clim. 2001, 14, 2896–2909. [Google Scholar] [CrossRef]
- Dong, W.; Lin, Y.; Wright, J.S.; Ming, Y.; Xie, Y.; Wang, B.; Luo, Y.; Huang, W.; Huang, J.; Wang, L.; et al. Summer rainfall over the southwestern Tibetan Plateau controlled by deep convection over the Indian subcontinent. Nat. Commun. 2016, 7, 10925. [Google Scholar] [CrossRef] [PubMed]
- New, M.; Hewitson, B.; Stephenson, D.B.; Tsiga, A.; Kruger, A.; Manhique, A.; Gomez, B.; Coelho, C.A.S.; Masisi, D.N.; Kululanga, E.; et al. Evidence of trends in daily climate extremes over southern and west Africa. J. Geophys. Res. Atmos. 2006, 111, D14102. [Google Scholar] [CrossRef]
- Vincent, L.A.; Mekis, E. Changes in daily and extreme temperature and precipitation indices for Canada over the 20th century. Atmos. Ocean 2006, 44, 177–193. [Google Scholar] [CrossRef]
- Rahimzadeh, F.; Asgari, A.; Fattahi, E. Variability of extreme temperature and precipitation in Iran during Recent decades. Int. J. Climatol. 2009, 29, 329–343. [Google Scholar] [CrossRef]
- Sanchez-Moreno, J.F.; Mannaerts, C.M.; Jetten, V. Influence of topography on rainfall variability in Santiago Island, Cape Verde. Int. J. Climatol. 2014, 34, 1081–1097. [Google Scholar] [CrossRef]
- Konrad, C.E., II. Relationships between precipitation event types and topography in the southern Blue Ridge mountains of the southeastern USA. Int. J. Climatol. 1996, 16, 49–62. [Google Scholar] [CrossRef]
- Hession, S.L.; Moore, N. A spatial regression analysis of the influence of topography on monthly rainfall in East Africa. Int. J. Climtol. 2011, 31, 1440–1456. [Google Scholar] [CrossRef]
- Tian, L.; Yao, T.; Li, Z.; MacClune, K.; Wu, G.; Xu, B.; Li, Y.; Lu, A.; Shen, Y. Recent rapid warming trend revealed from the isotopic record in Muztagata ice core, eastern Pamirs. J. Geophys. Res. 2006, 111, D13103. [Google Scholar] [CrossRef]
| Type | Name | Definition | Units |
|---|---|---|---|
| Threshold | Number of heavy precipitation days (R10) | Annual count of days when RR ≥ 10 mm | days |
| Number of very heavy precipitation days (R20) | Annual count of days when RR ≥ 20 mm | days | |
| Absolute | Maximum one-day precipitation amount (R×1d) | Monthly maximum one-day precipitation | mm |
| Maximum five-day precipitation amount (R×5d) | Monthly maximum consecutive five-day precipitation | mm | |
| Duration | Consecutive dry days (CDD) | Maximum number of consecutive days with RR < 1 mm | days |
| Consecutive wet days (CWD) | Maximum number of consecutive days with RR ≥ 1 mm | days | |
| Percentile | Very wet day precipitation (R95p) | Annual total precipitation when RR > 95th percentile of 1975–2014 daily precipitation | mm |
| Extremely wet day precipitation (R99p) | Annual total precipitation when RR > 99th percentile of 1975–2014 daily precipitation | mm | |
| Other | Annual total wet-day precipitation (PRCPTOT) | Annual total precipitation from wet days (RR ≥ 1 mm) | mm |
| Simple daily intensity index (SDII) | Average precipitation on wet days | mm day−1 |
| Index | Units | Trend Magnitudes | Increasing | No Trend | Decreasing |
|---|---|---|---|---|---|
| R10 | days per decade | 0.27 ± 0.07 (−0.12, 0.41) | 42 (50.6%, 9.6%) | 31 (37.3%) | 10 (12%, 1.2%) |
| R20 | days per decade | 0.07 ± 0.03 (0.01, 0.13) | 54 (65.1%, 8.4%) | 6 (7.2%) | 23 (27.7%, 1.2%) |
| R×1d | mm per decade | 0.45 ± 0.12 (0.21, 0.68) | 55 (66.3%, 8.4%) | 2 (2.4%) | 26 (31.3%, 0.0%) |
| R×5d | mm per decade | 0.50 ± 0.24 (0.03, 0.97) | 49 (59.0%, 4.8%) | 1 (1.2%) | 33 (39.8%, 1.2%) |
| CDD | days per decade | −0.87 ± 0.51 (−1.89, 0.16) | 34 (41.0%, 3.6%) | 4 (4.8%) | 45 (54.2%, 0.0%) |
| CWD | days per decade | −0.02 ± 0.03 (−0.07, 0.03) | 13 (15.7%, 0.0%) | 58 (69.9%) | 12 (14.5%, 3.6%) |
| R95p | mm per decade | 3.24 ± 0.88 (1.49, 4.99) | 54 (65.0%, 8.4%) | 7 (8.4%) | 22 (26.5%, 0.0%) |
| R99p | mm per decade | 1.96 ± 0.53 (0.91, 3.01) | 57 (68.7%, 8.4%) | 0 (0.0%) | 26 (31.3%, 0.0%) |
| PRCPTOT | mm per decade | 6.98 ± 1.60 (3.80, 10.16) | 62 (74.7%, 15.6%) | 0 (0.0%) | 21 (25.3%, 0.0%) |
| SDII | (mm day−1) per decade | 0.08 ± 0.01 (0.05, 0.11) | 54 (65.1%, 10.8%) | 1 (19.3%) | 13 (15.7%, 0.0%) |
| Indices | R10 | R20 | R×1d | R×5d | CDD | CWD | R95P | R99P | PRCPTOT | SDII |
|---|---|---|---|---|---|---|---|---|---|---|
| Coefficient | 0.079 | 0.110 | 0.090 | 0.077 | −0.116 | 0.112 | 0.068 | 0.126 | 0.362 * | −0.056 |
| Precipitation Extremes | <2500 | 2501–3000 | 3001–3500 | 3501–4000 | 4001–4500 | >4501 |
|---|---|---|---|---|---|---|
| Number of Stations | 9 | 19 | 17 | 18 | 14 | 6 |
| R10 | −0.30 | 0.45 | 0.24 | 0.22 | 0.24 | 0.78 |
| R20 | −0.01 | 0.05 | 0.07 | 0.06 | 0.14 | 0.09 |
| R×1d | 0.35 | 0.11 | 0.81 | 0.45 | 0.37 | 0.82 |
| R×5d | −1.22 | 0.41 | 0.94 | 0.84 | 0.37 | 1.44 |
| R95P | 3.85 | 2.29 | 3.26 | 2.83 | 3.63 | 5.99 |
| R99P | 2.53 | 0.82 | 2.65 | 2.20 | 1.75 | 2.54 |
| CDD | 0.56 | −0.86 | −1.10 | 0.46 | −1.79 | −3.86 |
| CWD | −0.16 | −0.52 | −0.07 | 0.06 | 0.01 | −0.05 |
| PRCPTOT | −9.42 | 4.40 | 4.26 | 10.57 | 11.38 | 26.39 |
| SDII | 0.12 | 0.07 | 0.09 | 0.08 | 0.05 | 0.10 |
| Precipitation Extremes | Flat | Mesa | Hill | Low Rolling Mountain |
|---|---|---|---|---|
| Number of Stations | 29 | 21 | 17 | 16 |
| R10 | 0.47 | 0.14 | 0.33 | −0.01 |
| R20 | 0.11 | 0.03 | 0.13 | −0.04 |
| R×1d | 0.58 | 0.26 | 0.62 | 0.27 |
| R×5d | 0.37 | 0.77 | 1.25 | −0.40 |
| R95p | 4.02 | 2.83 | 5.62 | −0.01 |
| R99p | 2.67 | 0.92 | 2.25 | 1.72 |
| CDD | −1.69 | −0.36 | −1.23 | 0.48 |
| CWD | −0.36 | −0.07 | 0.09 | −0.07 |
| PRCPTOT | 9.51 | 6.22 | 12.40 | −2.38 |
| SDII | 0.10 | 0.06 | 0.08 | 0.07 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ge, G.; Shi, Z.; Yang, X.; Hao, Y.; Guo, H.; Kossi, F.; Xin, Z.; Wei, W.; Zhang, Z.; Zhang, X.; et al. Analysis of Precipitation Extremes in the Qinghai-Tibetan Plateau, China: Spatio-Temporal Characteristics and Topography Effects. Atmosphere 2017, 8, 127. https://doi.org/10.3390/atmos8070127
Ge G, Shi Z, Yang X, Hao Y, Guo H, Kossi F, Xin Z, Wei W, Zhang Z, Zhang X, et al. Analysis of Precipitation Extremes in the Qinghai-Tibetan Plateau, China: Spatio-Temporal Characteristics and Topography Effects. Atmosphere. 2017; 8(7):127. https://doi.org/10.3390/atmos8070127
Chicago/Turabian StyleGe, Genbatu, Zhongjie Shi, Xiaohui Yang, Yuguang Hao, Hao Guo, Fandjinou Kossi, Zhiming Xin, Wei Wei, Zhiyong Zhang, Xiao Zhang, and et al. 2017. "Analysis of Precipitation Extremes in the Qinghai-Tibetan Plateau, China: Spatio-Temporal Characteristics and Topography Effects" Atmosphere 8, no. 7: 127. https://doi.org/10.3390/atmos8070127
APA StyleGe, G., Shi, Z., Yang, X., Hao, Y., Guo, H., Kossi, F., Xin, Z., Wei, W., Zhang, Z., Zhang, X., Liu, Y., & Liu, J. (2017). Analysis of Precipitation Extremes in the Qinghai-Tibetan Plateau, China: Spatio-Temporal Characteristics and Topography Effects. Atmosphere, 8(7), 127. https://doi.org/10.3390/atmos8070127





