A Diagnosis of Some Dynamical Processes Underlying a Higher-Latitude Typhoon Using the Multiscale Window Transform
Abstract
:1. Introduction
2. Data and Methodology
2.1. Data
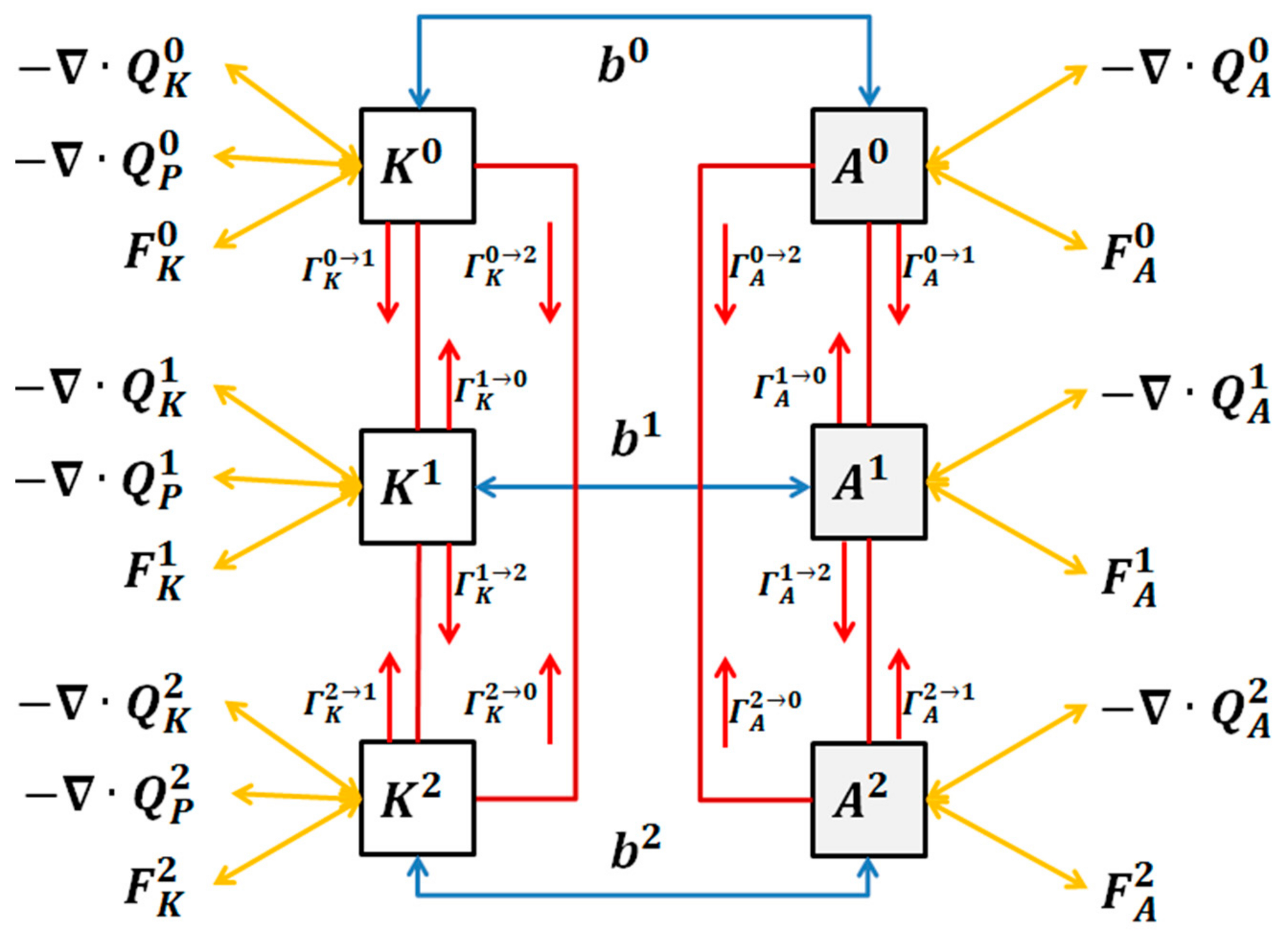
2.2. Multiscale Window Transform (MWT) and Localized Multiscale Energy and Vorticity Analysis (MS-EVA)
3. Result
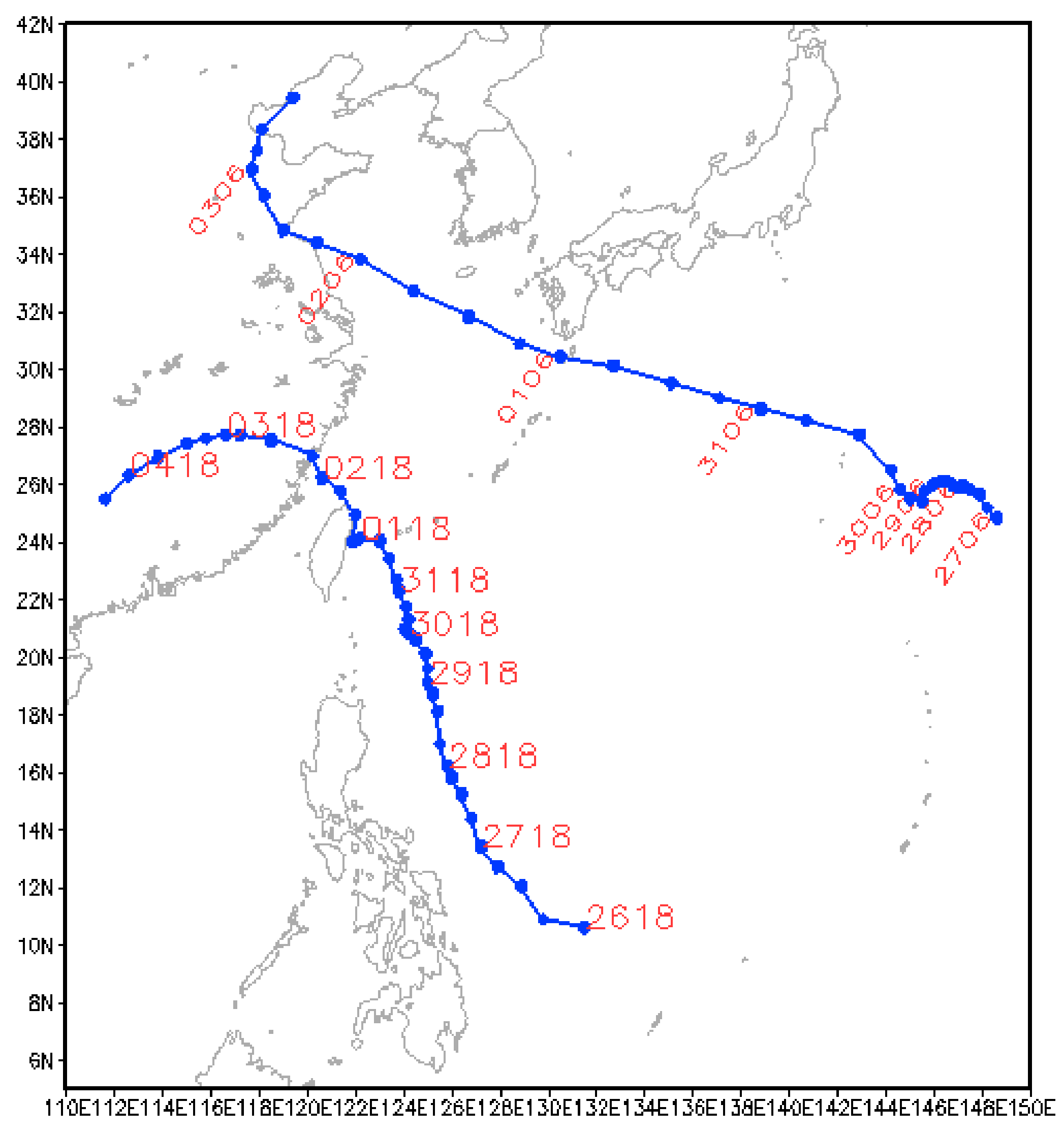
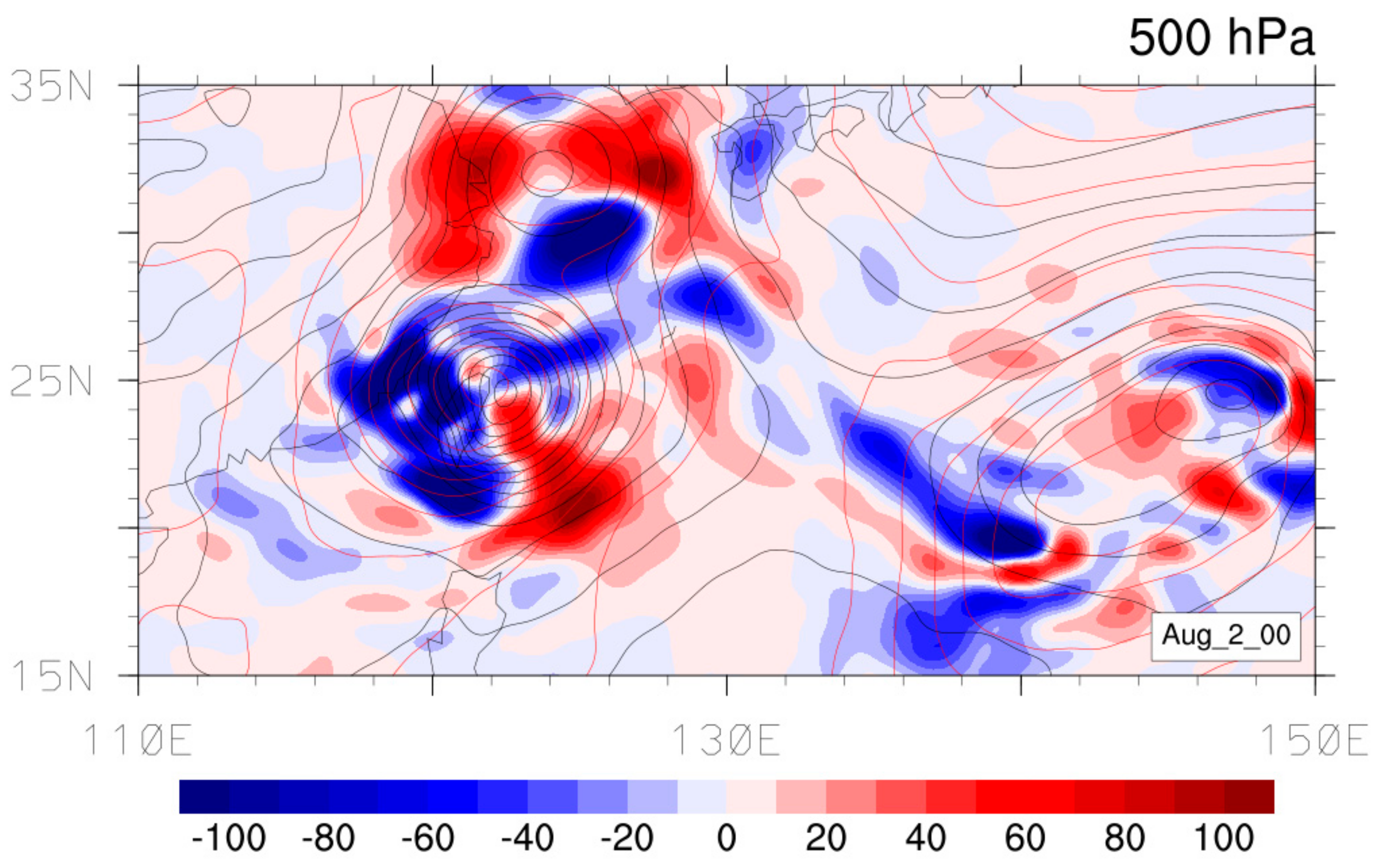
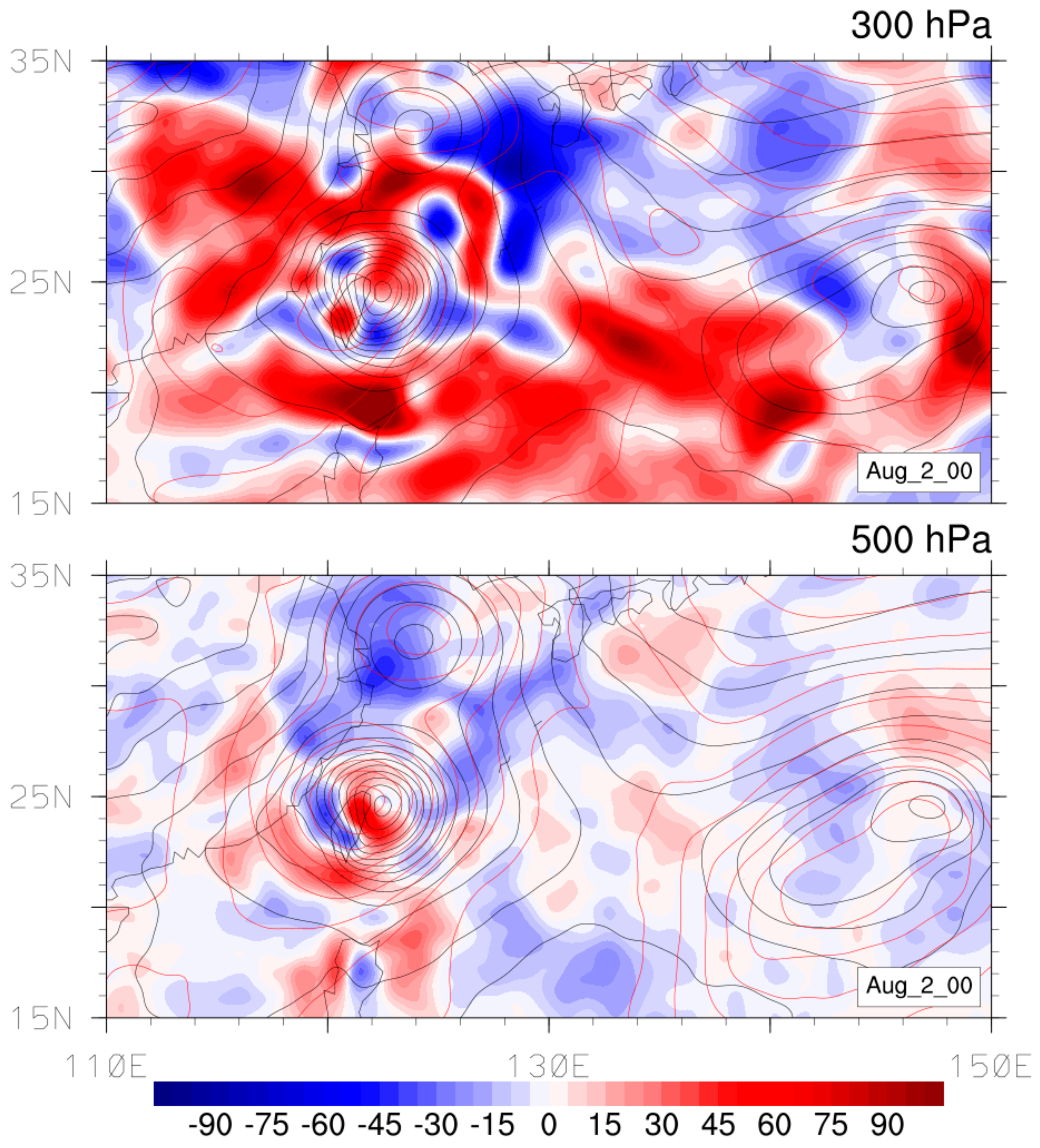
3.1. General Circulation Analyses
3.1.1. MS-EVA Setup
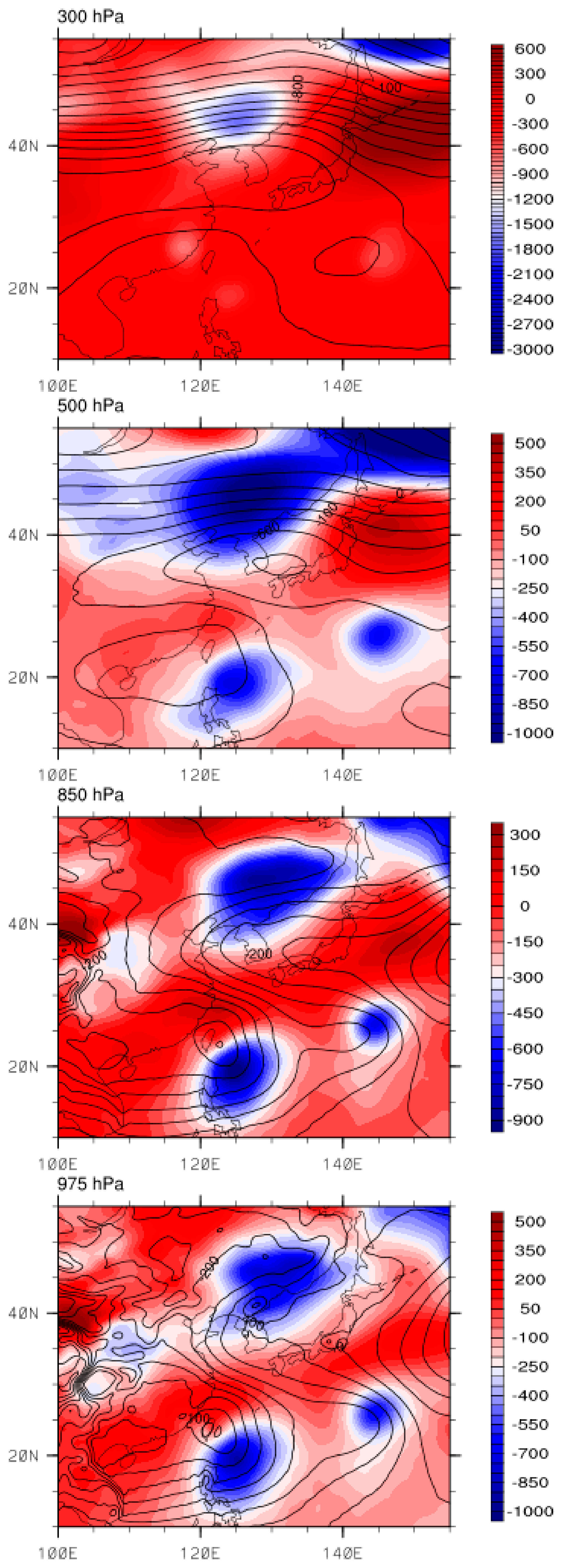
3.1.2. Circulation Analysis
3.2. Multiscale Energy Transfer Analyses
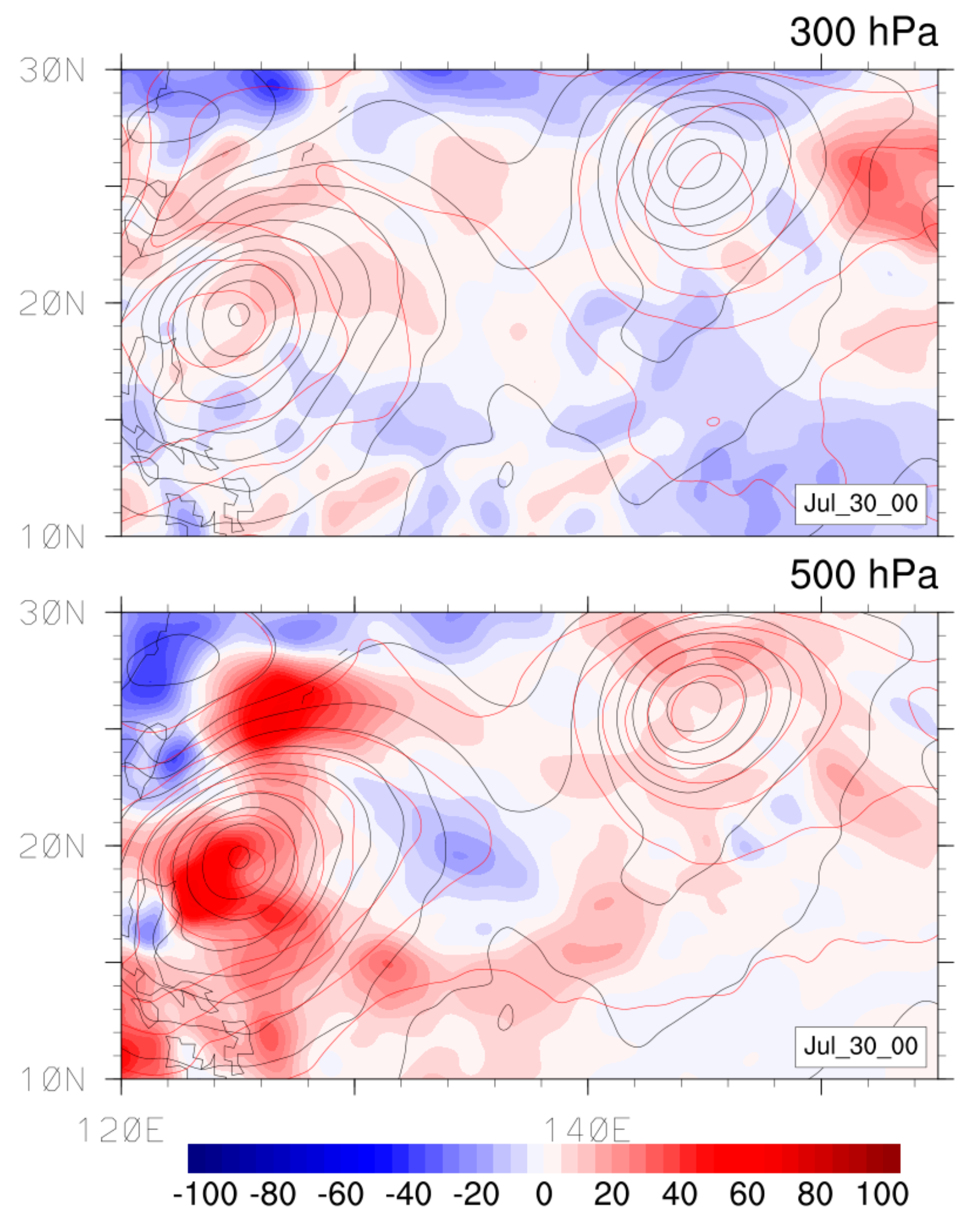
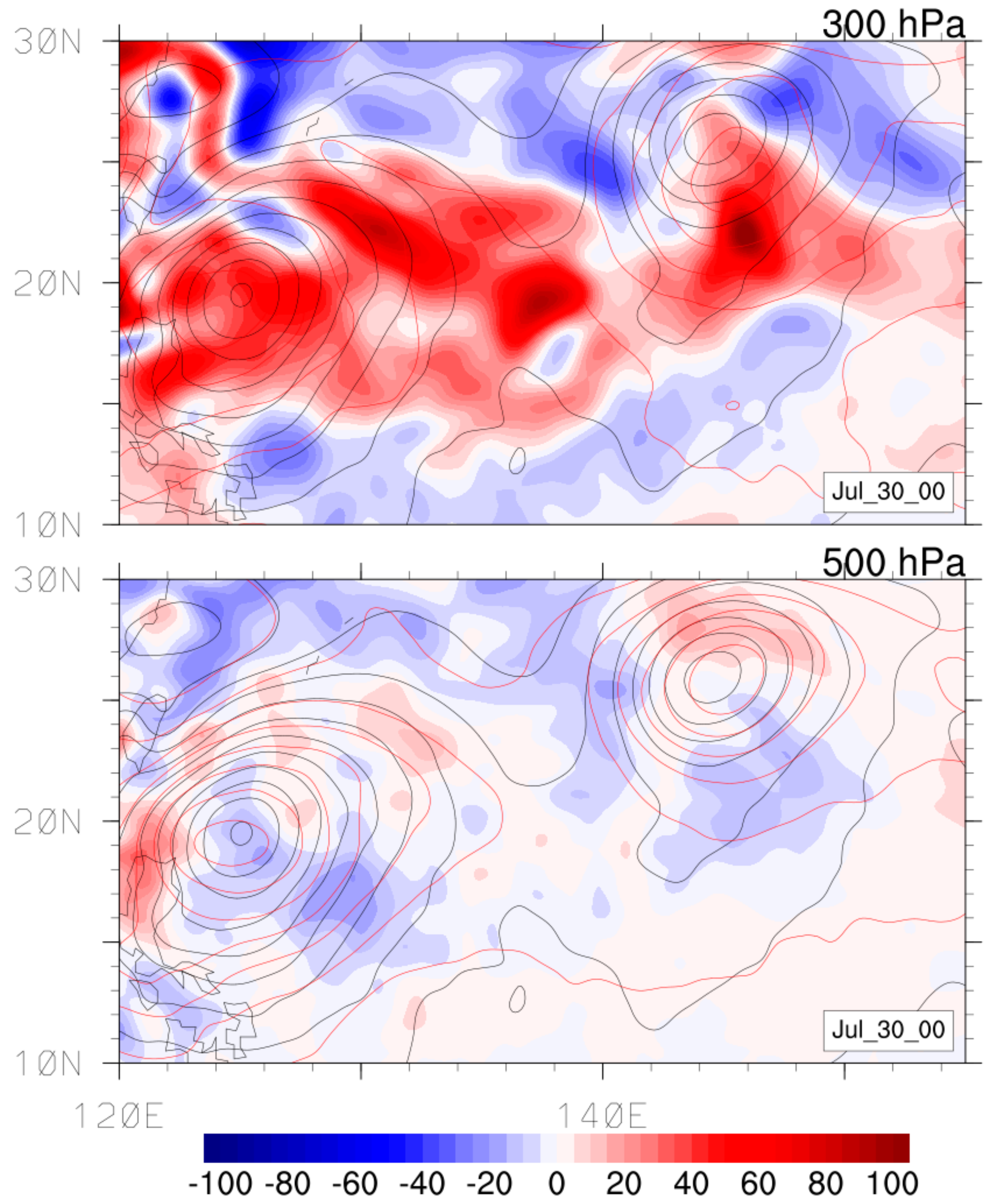
3.2.1. Formation Stage
Kinetic Energy Transfer
Available Potential Energy Transfer
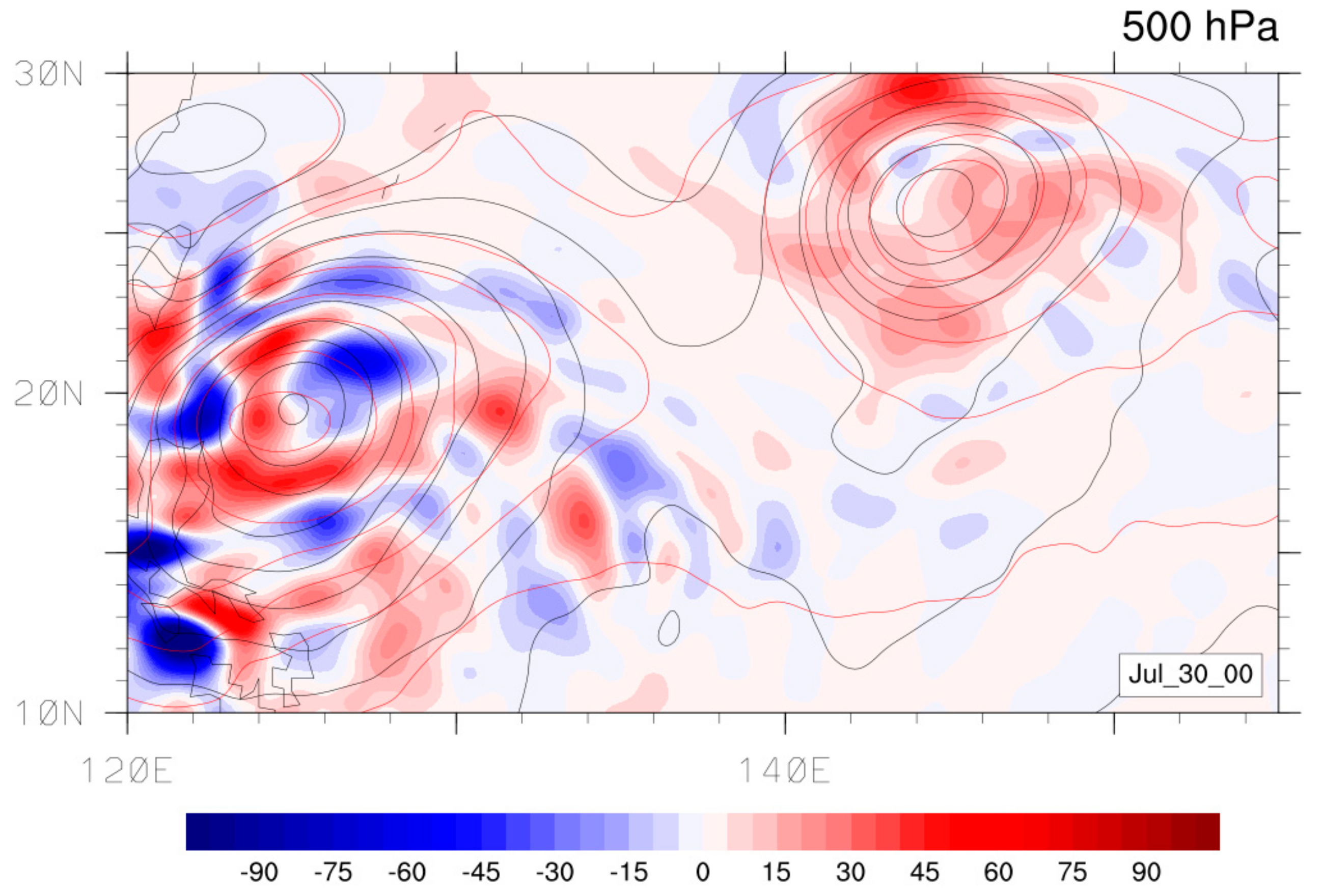
3.2.2. Intensification and Decay
Kinetic Energy Transfer
Available Potential Energy Transfer
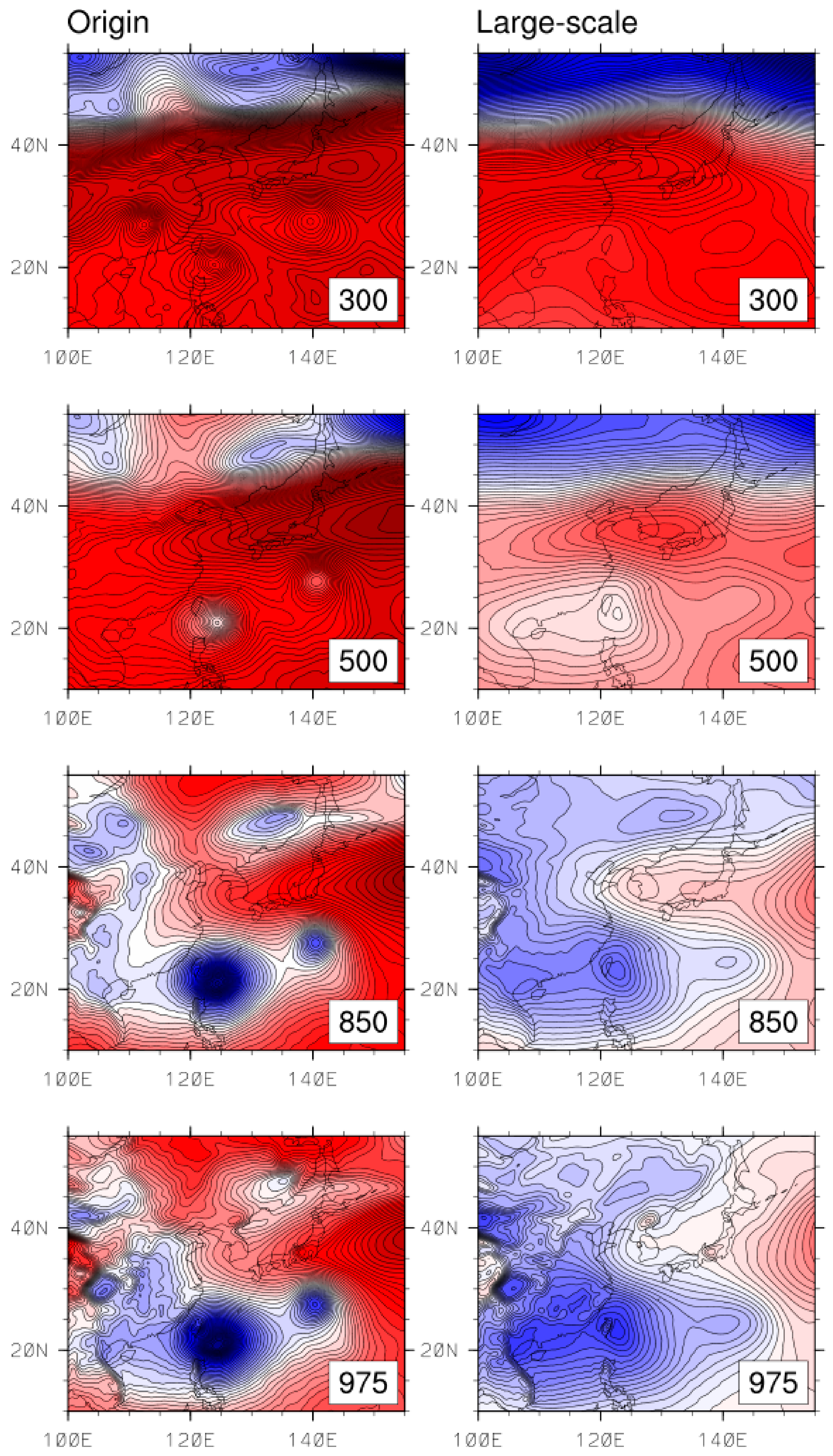
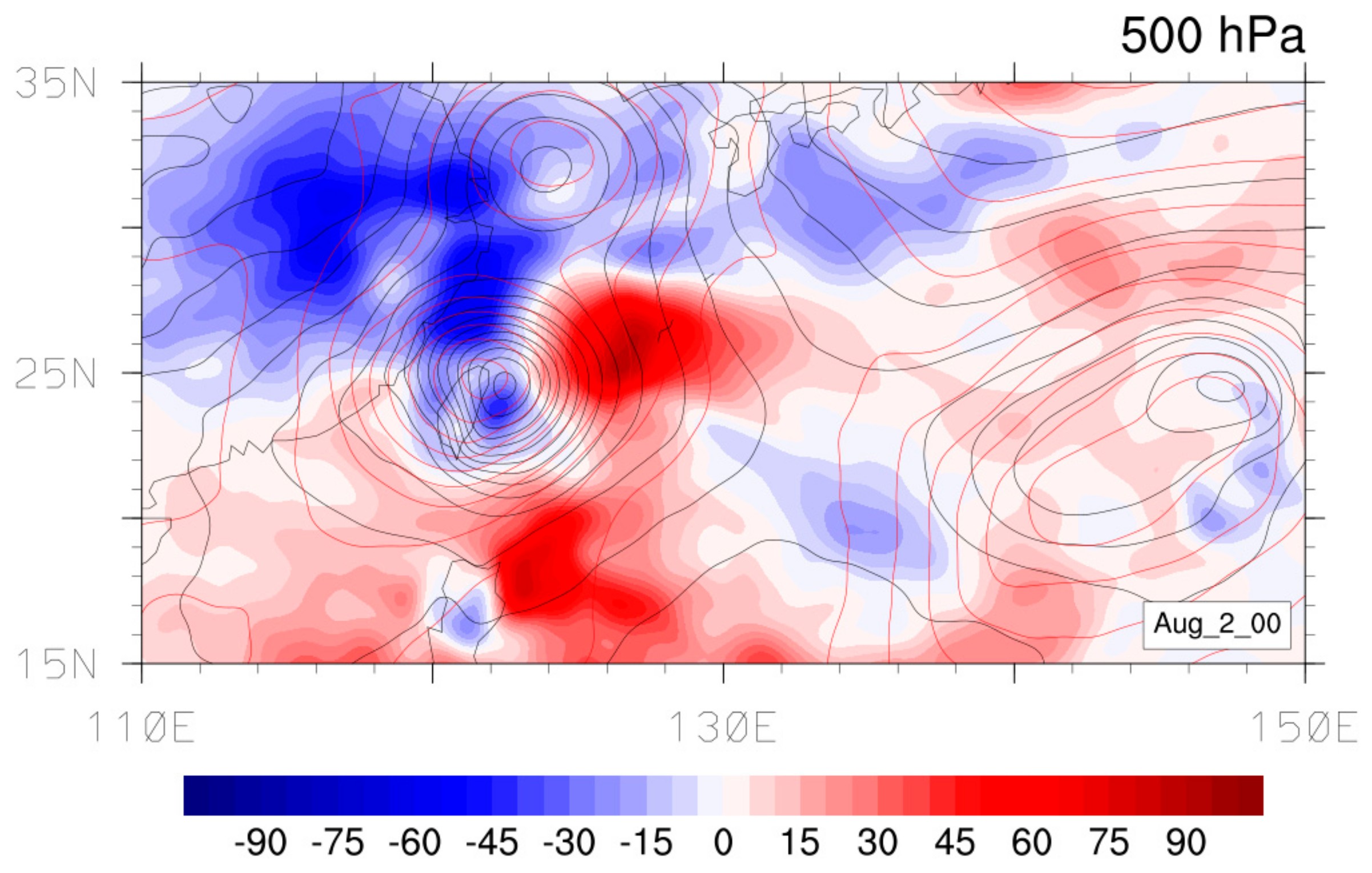
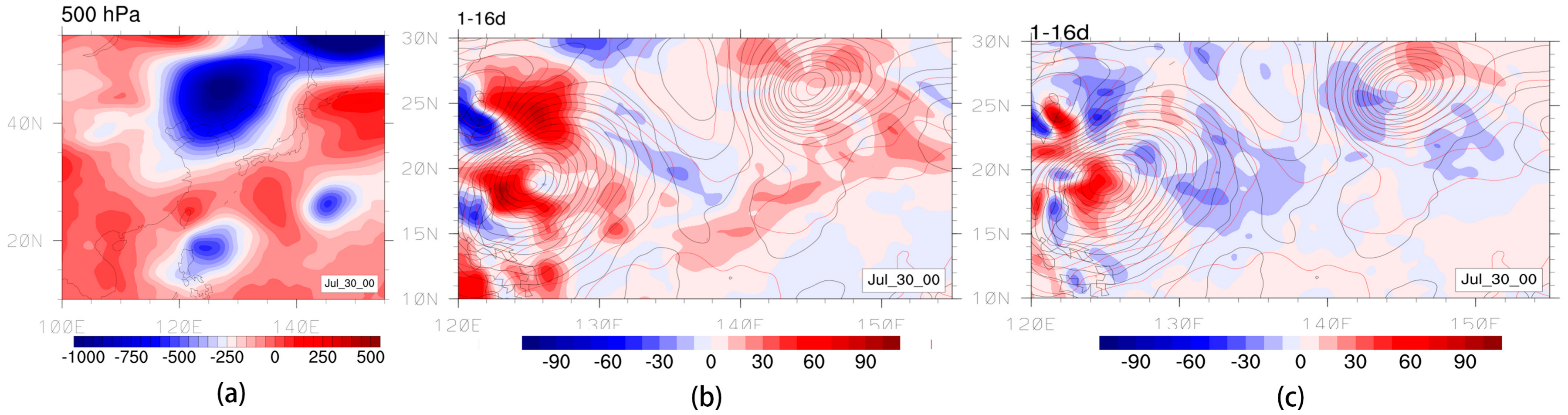
3.3. Sensitivity Study
4. Conclusions and Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cheung, K.K.W. Large-scale environmental parameters associated with tropical cyclone formations in the western North Pacific. J. Clim. 2010, 17, 466–484. [Google Scholar] [CrossRef]
- Mcbride, J.L.; Keenan, T.D. Climatology of tropical cyclone genesis in the Australian region. Inter. J. Clim. 1982, 2, 13–33. [Google Scholar] [CrossRef]
- Montgomery, M.T.; Farrell, B.F. Tropical cyclone formation. J. Atmos. Sci. 1993, 50, 285–308. [Google Scholar] [CrossRef]
- Sadler, J.C. A role of the tropical upper tropospheric trough in early season typhoon development. Mon. Weather Rev. 1974, 104, 57. [Google Scholar] [CrossRef]
- Landsea, C.W. A climatology of intense (or major) Atlantic hurricanes. Mon. Weather Rev. 1993, 121, 1703. [Google Scholar] [CrossRef]
- Molinari, J.; Vollaro, D.; Skubis, S.; Dickinson, M. Origins and mechanisms of eastern Pacific tropical cyclogenesis: A case study. Mon. Weather Rev. 2010, 128, 2000. [Google Scholar] [CrossRef]
- Gray, W.M. Global view of the origin of tropical disturbances and storms. Mon. Weather Rev. 1968, 96, 87. [Google Scholar] [CrossRef]
- Ritchie, E.A.; Holland, G.J. Large-scale patterns associated with tropical cyclogenesis in the western Pacific. Mon. Weather Rev. 1999, 127, 2027–2043. [Google Scholar] [CrossRef]
- Qiu, W.Y.; Wu, L.G. Influence of north-west Pacific monsoon depression on tropical cyclogenesis. J. Meteorol. Sci. 2015, 35, 237–247. (In Chinese) [Google Scholar]
- Li, X.Y.; Wu, L.G.; Zong, H.J. Analysis of influence of monsoon gyres on tropical cyclogenesis over the western North Pacific. Trans. Atmos. Sci. 2014, 37, 653–664. (In Chinese) [Google Scholar]
- Zong, H.J.; Wu, L.G. Re-examination of tropical cyclone formation in monsoon troughs over the western North Pacific. Adv. Atmos. Sci. 2015, 32, 924–934. [Google Scholar] [CrossRef]
- Zhang, W.L.; Zhang, D.L.; Wang, A.S.; Cui, X.P. An investigation of the genesis of typhoon Durian (2001) from a monsoon trough. Acta Meteorol. Sin. 2008, 67, 811–827. (In Chinese) [Google Scholar]
- Zhu, C.W.; Nakazawa, T.; Li, J.P. Modulation of tropical depression/cyclone over the Indian-Western Pacific oceans by Madden-Julian oscillation. J. Meteorol. Sci. 2004, 62, 42–50. (In Chinese) [Google Scholar]
- Maloney, E.D.; Hartmann, D.L. Modulation of hurricane activity in the gulf of Mexico by the Madden-Julian oscillation. Science 2000, 287, 2002–2004. [Google Scholar] [CrossRef] [PubMed]
- Maloney, E.D.; Hartmann, D.L. The Madden-Julian oscillation, barotropic dynamics, and North Pacific tropical cyclone formation. Part I: Observations. J. Atmos. Sci. 2001, 58, 2545–2558. [Google Scholar] [CrossRef]
- Sun, Z.; Mao, J.Y.; Wu, G.X. Influences of intraseasonal oscillations on the clustering of tropical cyclone activities over the western North Pacific during boreal summer. J. Meteorol. Sci. 2009, 33, 950–958. (In Chinese) [Google Scholar]
- Ooyama, K.V. Conceptual evolution of the theory and modeling of the tropical cyclone. J. Meteorol. Soc. Jpn. Ser. II 1982, 60, 369–380. [Google Scholar] [CrossRef]
- Papin, P. Using the Rossby radius of deformation as a forecasting tool for tropical cyclogenesis. In Proceedings of the National Conference on Undergraduate Research, Ithaca, NY, USA, 31 March–2 April 2011. [Google Scholar]
- Duan, J.J.; Wu, L.G. Kinetic energy budget analysis of tropical cyclogenesis precursors in the monsoon trough. J. Meteorol. Sci. 2016, 36, 141–148. (In Chinese) [Google Scholar]
- Liang, X.S. Canonical transfer and multiscale energetics for primitive and quasi-geostrophic atmospheres. J. Atmos. Sci. 2016, 73. [Google Scholar] [CrossRef]
- Liang, X.S.; Anderson, D.G.M. Multiscale window transform. Siam J. Multiscale Model. Simul. 2007, 6, 437–467. [Google Scholar] [CrossRef]
- Liang, X.S.; Robinson, A.R. Localized multi-scale energy and vorticity analysis: II. Finite-amplitude instability theory and validation. Dyn. Atmos. Oceans 2007, 44, 51–76. [Google Scholar] [CrossRef]
- Pedlosky, J. Geophysical Fluid Dynamics, 2nd ed.; Springer: New York, NY, USA, 1987; 710p. [Google Scholar]
- Tao, Y.W. Analysis of the August 2012 atmospheric circulation and weather. Meteorol. Mon. 2012, 28, 1429–1435. (In Chinese) [Google Scholar]
- Zhou, N.F. Analysis of the July 2012 atmospheric circulation and weather. Meteorol. Mon. 2012, 38, 1307–1312. (In Chinese) [Google Scholar]
- Zhang, D.L.; Bao, N. Oceanic cyclogenesis as induced by a mesoscale convective system moving offshore. Part ii: Genesis and thermodynamic transformation. Mon. Weather Rev. 1996, 124, 2206. [Google Scholar] [CrossRef]
- Emanuel, K.A. An air-sea interaction theory for tropical cyclones. Part I: Steady-state maintenance. J. Atmos. Sci. 1986, 43, 585–605. [Google Scholar] [CrossRef]
- Emanuel, K.A. The theory of hurricanes. Ann. Rev. Fluid Mech. 2003, 23, 179–196. [Google Scholar] [CrossRef]
- Rotunno, R.; Emanuel, K.A. An air–sea interaction theory for tropical cyclones. Part II: Evolutionary study using a nonhydrostatic axisymmetric numerical model. J. Atmos. Sci. 1987, 44, 542–561. [Google Scholar] [CrossRef]
- Fujiwhara, S. On the growth and decay of vortical systems. Q. J. R. Meteorol. Soc. 1923, 49, 75–104. [Google Scholar] [CrossRef]
- Fujiwhara, S. The natural tendency towards symmetry of motion and its application as a principle in meteorology. Q. J. R. Meteorol. Soc. 1921, 47, 287–292. [Google Scholar] [CrossRef]
- Guinn, T.A.; Schubert, W.H. Hurricane spiral bands. J. Atmos. Sci. 1993, 50, 3380. [Google Scholar] [CrossRef]
- Ma, J.W.; Liang, X.S. Dynamical processes underlying the wintertime Atlantic blockings. J. Atmos. Sci. 2017, in press. [Google Scholar]
- Xu, F.; Liang, X.S. On the generation and maintenance of the 2012–2013 sudden stratospheric warming. J. Atmos. Sci. 2017, in press. [Google Scholar]
| Kinetic Energy (KE) | Available Potential Energy (APE) | ||
|---|---|---|---|
| Time rate of change of KE | Time rate of change of APE | ||
| Flux of KE | Flux of APE | ||
| Canonical KE transfer | Canonical APE transfer | ||
| Rate of buoyancy conversion | Rate of inverse buoyancy conversion | ||
| Pressure flux | Source/Sink (usually negligible) | ||
| Dissipation | Diffusion | ||
| Parameter | Value |
|---|---|
| Window bounds () | 2, 7, 8 (64 d, 32 d, 1 d) |
| Horizontal Grid | 801 × 561 |
| Vertical Levels | 975 hPa, 950 hPa, 925 hPa, 900 hPa, 875 hPa, 850 hPa, 825 hPa, 800 hPa, 750 hPa, 700 hPa, 650 hPa, 600 hPa, 550 hPa, 500 hPa, 450 hPa, 400 hPa, 350 hPa, 300 hPa, 250 hPa, 225 hPa, 200 hPa, 175 hPa, 150 hPa, 125 hPa, 100 hPa, 70 hPa, 50 hPa, 30 hPa, 20 hPa, 10 hPa |
| Spatial Resolution | 0.125° |
| Time Interval | 6 h |
| Case | Remark | ||
|---|---|---|---|
| Case 1 | 7 (1 day) | 2 (32 days) | Standard Run |
| Case 2 | 6 (2 days) | 2 (32 days) | |
| Case 3 | 7 (1 day) | 3 (16 days) | |
| Case 4 | 6 (2 days) | 3 (16 days) |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Liang, X.S. A Diagnosis of Some Dynamical Processes Underlying a Higher-Latitude Typhoon Using the Multiscale Window Transform. Atmosphere 2017, 8, 118. https://doi.org/10.3390/atmos8070118
Wang L, Liang XS. A Diagnosis of Some Dynamical Processes Underlying a Higher-Latitude Typhoon Using the Multiscale Window Transform. Atmosphere. 2017; 8(7):118. https://doi.org/10.3390/atmos8070118
Chicago/Turabian StyleWang, Lan, and X. San Liang. 2017. "A Diagnosis of Some Dynamical Processes Underlying a Higher-Latitude Typhoon Using the Multiscale Window Transform" Atmosphere 8, no. 7: 118. https://doi.org/10.3390/atmos8070118
APA StyleWang, L., & Liang, X. S. (2017). A Diagnosis of Some Dynamical Processes Underlying a Higher-Latitude Typhoon Using the Multiscale Window Transform. Atmosphere, 8(7), 118. https://doi.org/10.3390/atmos8070118





