Effects of Boundary Layer Height on the Model of Ground-Level PM2.5 Concentrations from AOD: Comparison of Stable and Convective Boundary Layer Heights from Different Methods
Abstract
:1. Introduction
2. Materials
2.1. Radiosonde Data
2.2. Ground-Based PM2.5 Concentration Data
2.3. AERONET AOD Data
2.4. BLH Data From NCEP
3. Methodology
3.1. The Method Used to Estimate the BLH
3.2. The Method of Estimating PM2.5
4. Results and Discussion
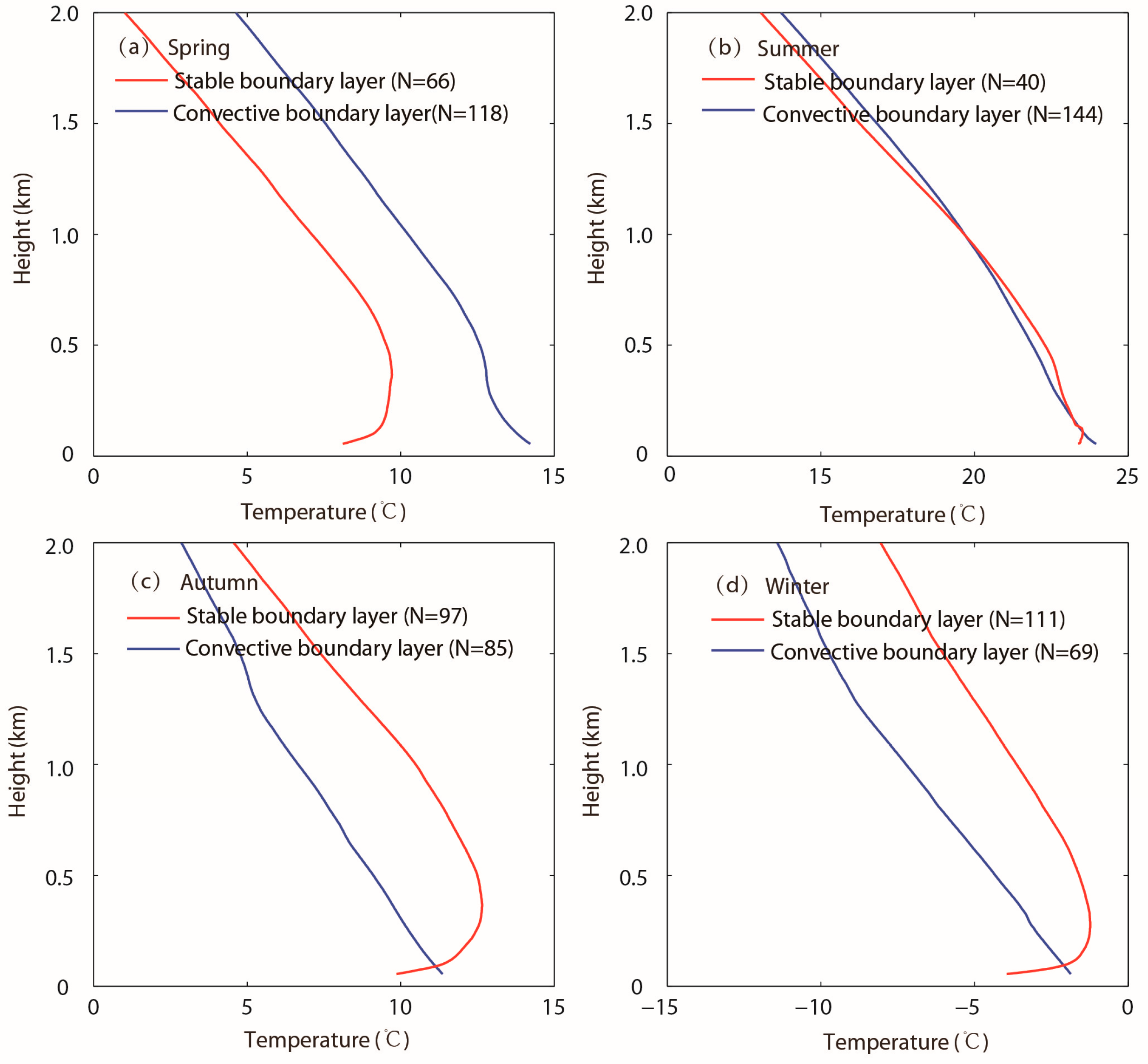
4.1. Seasonal Difference of Stable and Convective Boundary Layer
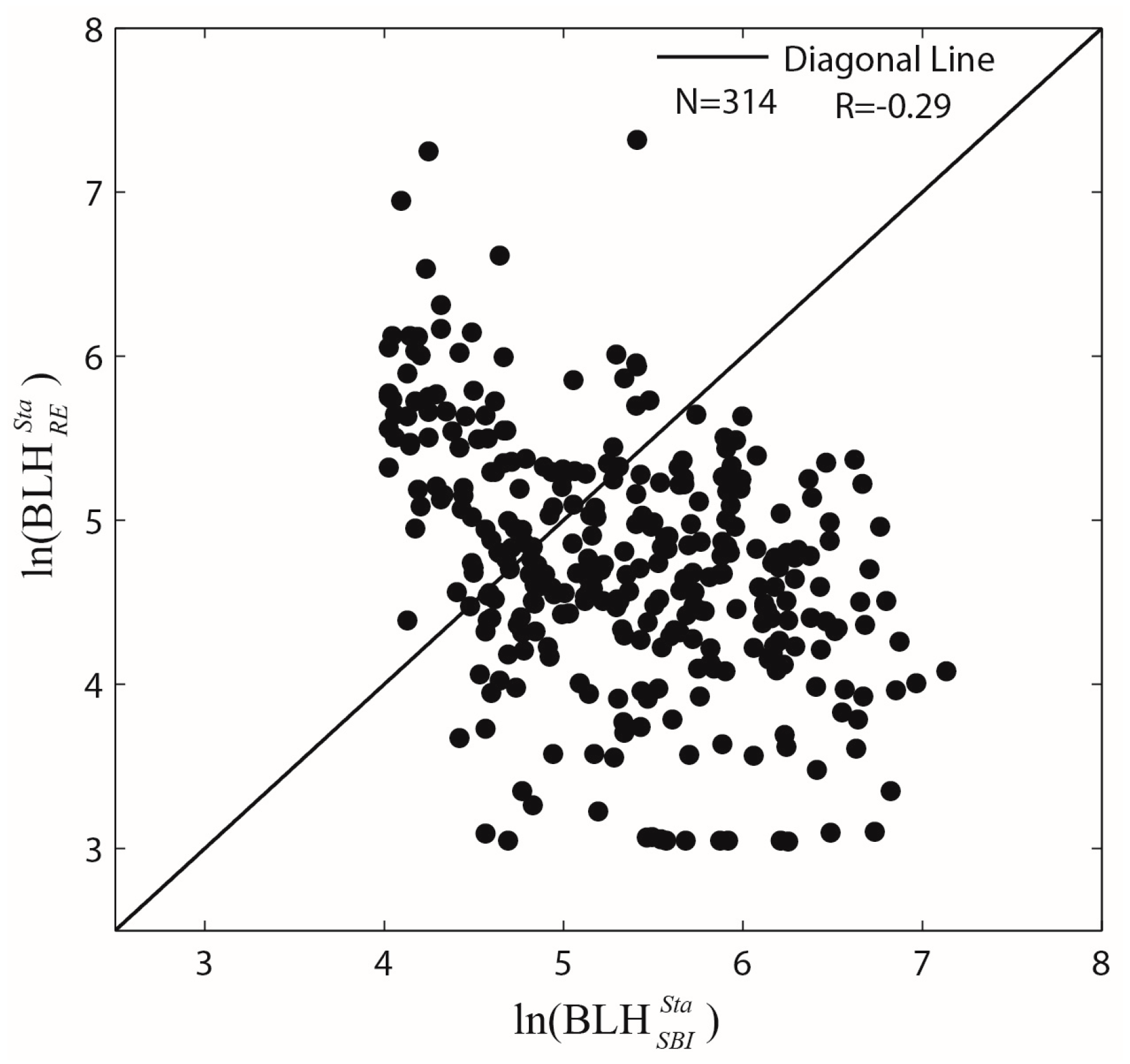
4.2. Statistical Comparison among Different BLH Methods
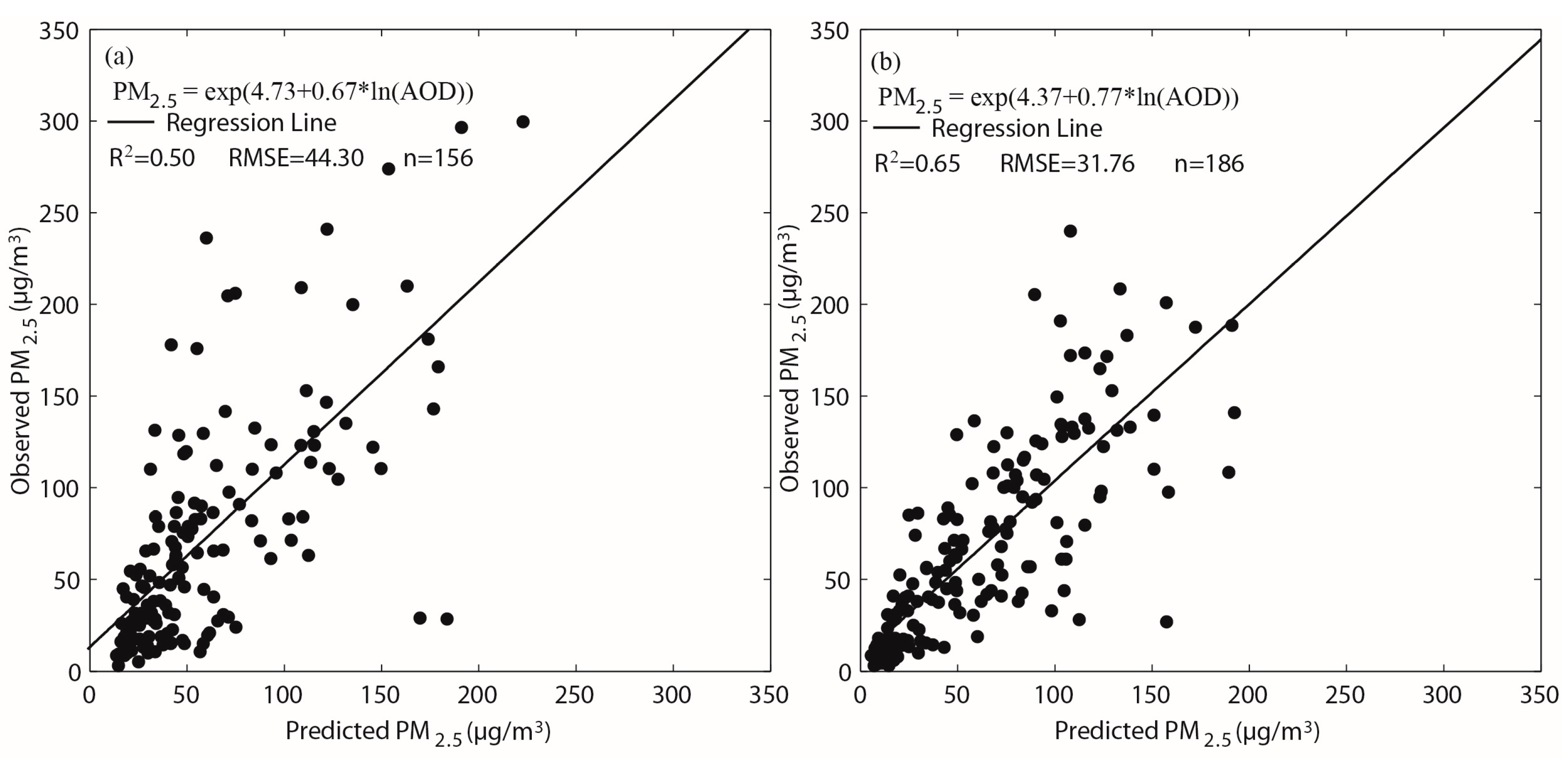
4.3. Performances of Simple Lognormal Models
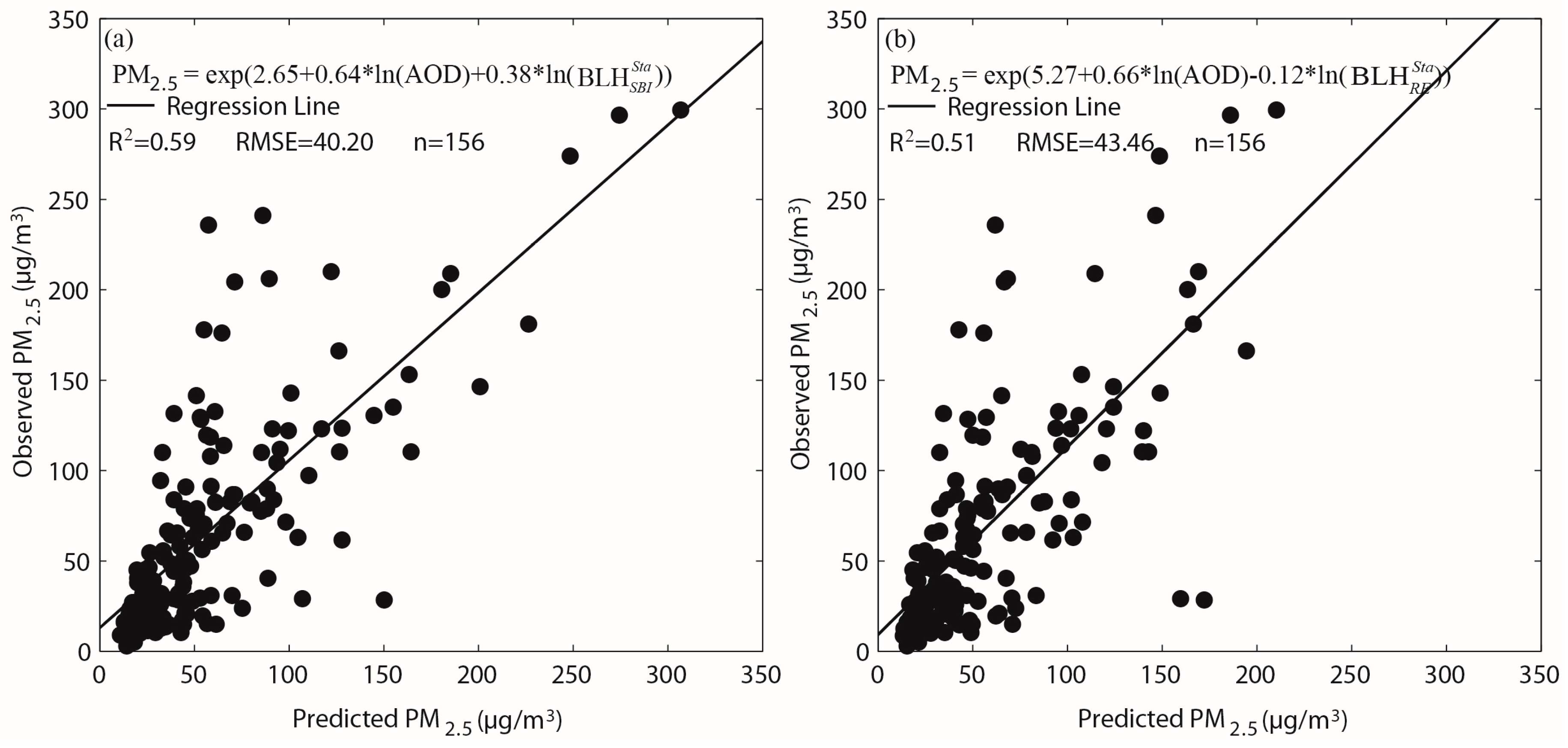
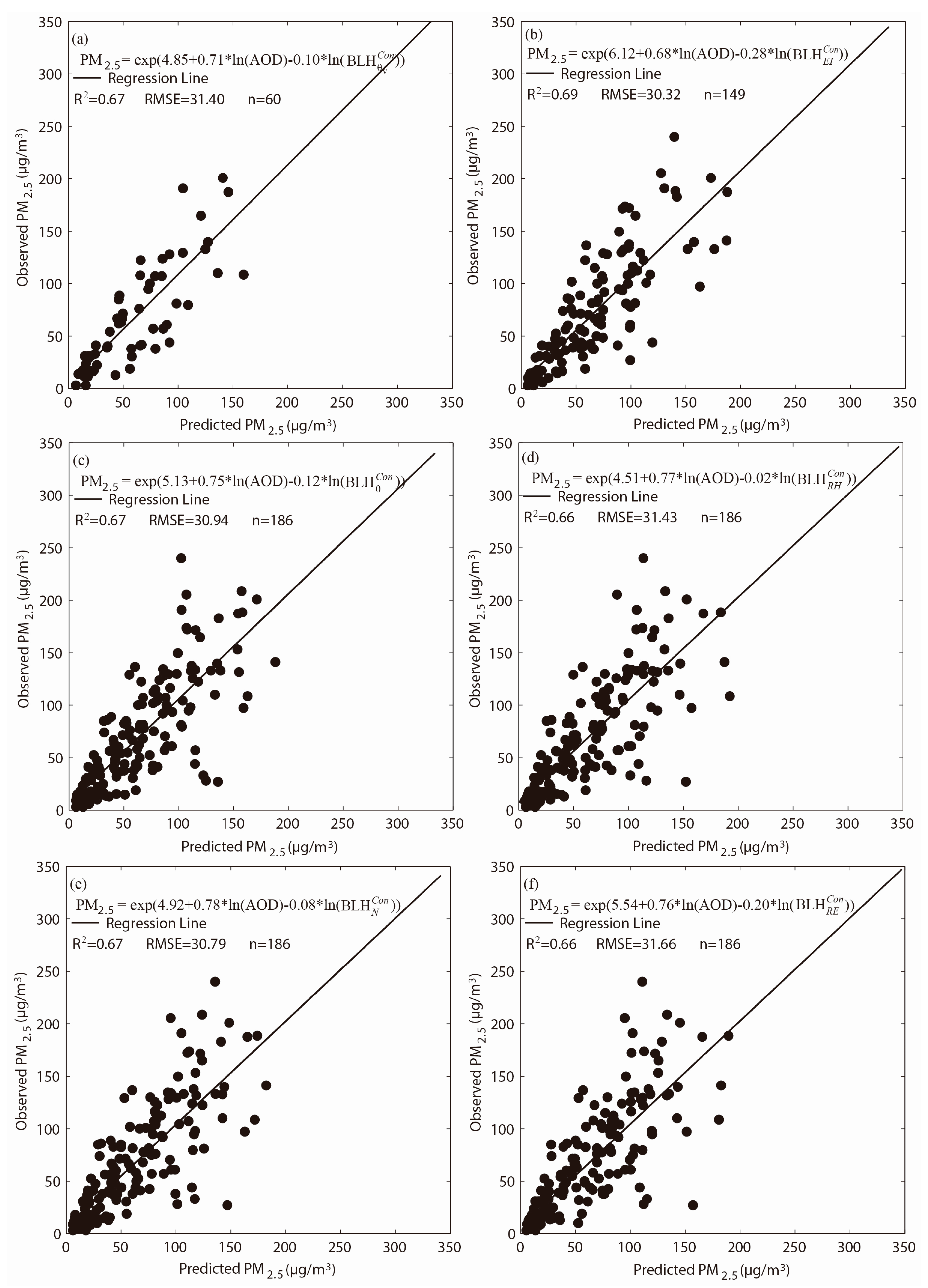
4.4. Ability of Different Blhs to Estimate Surface PM2.5 Concentrations
4.5. Optimal Model to Estimate Surface PM2.5 Concentrations
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Pope, C.A.; Burnett, R.T.; Thun, M.J.; Calle, E.E.; Krewski, D.; Ito, K.; Thurston, G.D. Lung cancer, cardiopulmonary mortality, and long-term exposure to fine particulate air pollution. JAMA 2002, 287, 1132–1141. [Google Scholar] [CrossRef] [PubMed]
- Kappos, A.D.; Bruckmann, P.; Eikmann, T.; Englert, N.; Heinrich, U.; Hoppe, P.; Koch, E.; Krause, G.H.; Kreyling, W.G.; Rauchfuss, K.; et al. Health effects of particles in ambient air. Int. J. Hyg. Environ. Health 2004, 207, 399–407. [Google Scholar] [CrossRef] [PubMed]
- Miller, K.A.; Siscovick, D.S.; Sheppard, L.; Sullivan, J.H.; Anderson, G.L.; Kaufman, J.D. Long-term exposure to air pollution and incidence of cardiovascular events in women. N. Engl. J. Med. 2007, 356, 447–458. [Google Scholar] [CrossRef] [PubMed]
- Sacks, J.D.; Stanek, L.W.; Luben, T.J.; Johns, D.O.; Buckley, B.J.; Brown, J.S.; Ross, M. Review particulate matter–induced health effects: Who is susceptible? Environ. Health Perspect. 2011, 119, 446–454. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Christopher, S.A. Intercomparison between satellite-derived aerosol optical thickness and PM2.5 mass: Implications for air quality studies. Geophys. Res. Lett. 2003, 30, 267–283. [Google Scholar] [CrossRef]
- Van Donkelaar, A.; Martin, R.V.; Park, R.J. Estimating ground-level PM2.5 using aerosol optical depth determined from satellite remote sensing. J. Geophys. Res. Atoms. 2006, 111, 5049–5066. [Google Scholar]
- Hoff, R.M.; Christopher, S.A. Remote sensing of particulate pollution from space: Have we reached the promised land? J. Air Waste Manag. Assoc. 2009, 59, 642–644. [Google Scholar]
- Tian, J.; Chen, D. A semi-empirical model for predicting hourly ground-level fine particulate matter (PM2.5) concentration in southern Ontario from satellite remote sensing and ground-based meteorological measurements. Remote Sens. Environ. 2010, 14, 221–229. [Google Scholar] [CrossRef]
- Li, C.; Hsu, N.C.; Tsay, S.C. A study on the potential applications of satellite data in air quality monitoring and forecasting. Atmos. Environ. 2011, 45, 3663–3675. [Google Scholar] [CrossRef]
- Tao, J.H.; Zhang, M.G.; Chen, L.F.; Wang, Z.F.; Su, L.; Ge, C.; Han, X.; Zou, M.M. A method to estimate concentrations of surface-level particulate matter using satellite-based aerosol optical thickness. Sci. China Earth Sci. 2013, 56, 1422–1433. [Google Scholar] [CrossRef]
- Koelemeijer, R.; Homan, C.; Matthijsen, J. Comparison of spatial and temporal variations of aerosol optical thickness and particulate matter over Europe. Atmos. Environ. 2006, 40, 5304–5315. [Google Scholar] [CrossRef]
- You, W.; Zang, Z.L.; Pan, X.B.; Zhang, L.F.; Chen, D. Estimating PM2.5 in Xi'an, China using aerosol optical depth: A comparison between the MODIS and MISR retrieval models. Sci. Total Environ. 2015, 505, 1156–1165. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Franklin, M.; Kahn, R.; Koutrakis, P. Using aerosol optical thickness to predict ground-level PM2.5, concentrations in the St. Louis area: A comparison between MISR and MODIS. Remote Sens. Environ. 2007, 107, 33–44. [Google Scholar] [CrossRef]
- Gupta, P.; Christopher, S.A. Particulate matter air quality assessment using integrated surface, satellite, and meteorological products: Multiple regression approach. J. Geophys. Res. 2009, 114. [Google Scholar] [CrossRef]
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1998; p. 666. [Google Scholar]
- Garratt, J.R. The Atmospheric Boundary Layer; Cambridge University Press: Cambridge, UK, 1992; p. 335. [Google Scholar]
- Seibert, P.; Beyrich, F.; Gryning, S.E.; Joffre, S.; Rasmussen, A.; Tercier, P. Review and intercomparison of operational methods for the determination of the mixing height. Atmos. Environ. 2000, 34, 1001–1027. [Google Scholar] [CrossRef]
- Seidel, D.J.; Ao, C.O.; Li, K. Estimating climatological planetary boundary layer heights from radiosonde observations: Comparison of methods and uncertainty analysis. J. Geophys. Res. 2010, 115, D16113. [Google Scholar] [CrossRef]
- Bradley, R.S.; Keimig, F.T.; Diaz, H.F. Recent changes in the North American Arctic boundary layer in winter. J. Geophys. Res. 1993, 98, 8851–8858. [Google Scholar] [CrossRef]
- Wang, X.Y.; Wang, K.C. Homogenized variability of radiosonde-derived atmospheric boundary layer height over the global land surface from 1973 to 2014. J. Clim. 2016, 29, 6893–6908. [Google Scholar] [CrossRef]
- Basha, G.; Ratnam, M.V. Identification of atmospheric boundary layer height over a tropical station using high resolution radiosonde refractivity profiles: Comparison with GPS radio occultation measurements. J. Geophys. Res. 2009, 114, D16101. [Google Scholar] [CrossRef]
- Ferrero, L.; Riccio, A.; Perrone, M.; Sangiorgi, G.; Ferrini, B.S.; Bolzacchini, E. Mixing height determination by tethered balloon-based particle soundings and modeling simulations. Atmos. Res. 2011, 102, 145–156. [Google Scholar] [CrossRef]
- Durre, I.; Vose, R.S.; Wuertz, D.B. Overview of the integrated global radiosonde archive. J. Clim. 2006, 19, 53–68. [Google Scholar] [CrossRef]
- Durre, I.; Yin, X. Enhanced radiosonde data for studies of vertical structure. Bull. Am. Meteorol. Soc. 2008, 89, 1257–1262. [Google Scholar] [CrossRef]
- Li, W. Technical Assessment Report of L-Band Upper Air Sounding System; China Meteorological Press: Beijing, China, 2009; p. 95. [Google Scholar]
- Seidel, D J; Zhang, Y.; Beljaars, A.; Golaz, J.; Jacobson, A.R.; Medeiros, B. Climatology of the planetary boundary layer over the continental United States and Europe. J. Geophys. Res. Atoms. 2012, 117, 127–135. [Google Scholar] [CrossRef]
- Holben, B.N.; Eck, T.F.; Slutsker, I.; Tanré, D.; Buis, J.P.; Setzer, A.; Vermote, E.; Reagan, J.A.; Kaufman, Y.J.; Nakajima, T.; et al. AERONET—A federated instrument network and data archive for aerosol characterization. Remote Sens. Environ. 1998, 66, 1–16. [Google Scholar] [CrossRef]
- Holben, B.N.; Tanré, D.; Smirnov, A.; Eck, T.F.; Slutsker, I.; Abuhassan, N.; Newcomb, W.W.; Schafer, J.S.; Chatenet, B.; Lavenu, F.; et al. An emerging ground-based aerosol climatology: Aerosol optical depth from AERONET. J. Geophys. Res. 2001, 106, 12067–12097. [Google Scholar] [CrossRef]
- Tripathi, S.N.; Dey, S.; Chandel, A.; Srivastava, S.; Singh, R.P.; Holben, B.N. Comparison of MODIS and AERONET derived aerosol optical depth over the Ganga Basin, India. Ann. Geophys. 2005, 23, 1093–1101. [Google Scholar] [CrossRef]
- Ge, J.M.; Su, J.; Fu, Q.; Ackerman, T.P.; Huang, J.P. Dust aerosol forward scattering effects on ground-based aerosol optical depth retrievals. J. Quant. Spectrosc. Radiat. Transf. 2011, 112, 310–319. [Google Scholar] [CrossRef]
- Xia, X.A.; Chen, H.B.; Wang, P.C. Validation of MODIS aerosol retrievals and evaluation of potential cloud contamination in East Asia. J. Environ. Sci. 2004, 16, 832–837. [Google Scholar]
- Li, X. Validation of Aerosol Optical Thickness Product over China with MODIS Data Operated at NSMC. J. Appl. Meteorol. Sci. 2009, 20, 147–156. [Google Scholar]
- Qi, Y.L.; Ge, J.M.; Huang, J.P. Spatial and temporal distribution of MODIS and MISR aerosol optical depth over northern China and comparison with AERONET. Chin. Sci. Bull. 2013, 58, 2497–2506. [Google Scholar] [CrossRef]
- Munchak, L.A.; Levy, R.C.; Mattoo, S.; Remer, L.A. MODIS 3 km aerosol product: Applications over land in an urban/suburban region. Atmos. Meas. Tech. 2013, 6, 1747–1759. [Google Scholar] [CrossRef]
- Schaap, M.; Apituley, A.; Timmermans, R.M.A.; Koelemeijer, R.B.A.; Leeuw, G.D. Exploring the relation between aerosol optical depth and PM2.5 at Cabauw, the Netherlands. Atmos. Chem. Phys. 2008, 9, 909–925. [Google Scholar] [CrossRef]
- Tao, R; Che, H.Z.; Chen, Q.L.; Tao, J; Wang, Y.Q.; Sun, J.Y.; Wang, H.; Zhang, X.Y. Study of aerosol optical properties based on ground measurements over Sichuan Basin, China. Aerosol. Air. Qual. Res. 2014, 14, 905–915. [Google Scholar] [CrossRef]
- You, W.; Zang, Z.L.; Zhang, L.F.; Li, Z.J.; Chen, D.; Zhang, G. Estimating ground-level PM10 concentration in northwestern China using geographically weighted regression based on satellite AOD combined with CALIPSO and MODIS fire count. Remote Sens. Environ. 2015, 168, 276–285. [Google Scholar] [CrossRef]
- Hong, S.Y. Nonlocal boundary layer vertical diffusion in a medium-range forecast model. Mon. Weather. Rev. 1996, 124, 2322. [Google Scholar] [CrossRef]
- Han, J; Witek, M.L.; Teixeira, J.; Sun, R.Y.; Pan, H.L.; Fletcher, J.K.; Bretherton, C.S. Implementation in the NCEP GFS of a Hybrid Eddy-Diffusivity Mass-Flux (EDMF) Boundary Layer Parameterization with Dissipative Heating and Modified Stable Boundary Layer Mixing. Weather Forecast. 2016, 31, 341–352. [Google Scholar] [CrossRef]
- National Centers for Environmental Prediction Climate Forecast System. Available online: http://cfs.ncep.noaa.gov/ (accessed on 29 January 2013).
- Holzworth, G.C. Estimates of mean maximum mixing depths in the contiguous United States. Mon. Weather Rev. 1964, 92, 235–242. [Google Scholar] [CrossRef]
- Oke, T.R. Boundary Layer Climates, 2nd ed.; Halsted Press: New York, NY, USA, 1988; p. 435. [Google Scholar]
- Sorbjan, Z. Structure of the Atmospheric Boundary Layer; Prentice Hall: Englewood Cliffs, NJ, USA, 1989; p. 317. [Google Scholar]
- Ao, C.O.; Waliser, D.E.; Chan, S.K.; Li, J.L.; Tian, B.J.; Xie, F.Q.; Mannucci, A.J. Planetary boundary layer heights from GPS radio occultation refractivity and humidity profiles. J. Geophys. Res. Atoms. 2012, 117, D16117. [Google Scholar] [CrossRef]
- Sokolovskiy, S.; Kuo, Y.H.; Rocken, C.; Schreiner, W.S.; Hunt, D.; Anthes, R.A. Monitoring the atmospheric boundary layer by GPS radio occultation signals recorded in the open-loop mode. Geophys. Res. Lett. 2006, 33, L12813. [Google Scholar] [CrossRef]
- Xie, F.; Wu, D.L.; Ao, C.O.; Mannucci, A.J.; Kursinski, E.R. Advances and limitations of atmospheric boundary layer observations with GPS occultation over southeast Pacific Ocean. Atmos. Chem. Phys. 2012, 12, 903–918. [Google Scholar] [CrossRef]
- Wang, X.Y.; Wang, K.C. Estimation of atmospheric mixing layer height from radiosonde data. Atmos. Meas. Tech. 2014, 7, 1701–1709. [Google Scholar] [CrossRef]
- Song, W.Z.; Jia, H.F.; Huang, J.F.; Zhang, Y.Y. A satellite-based geographically weighted regression model for regional PM2.5 estimation over the Pearl River Delta region in China. Remote Sens. Environ. 2014, 154, 1–7. [Google Scholar] [CrossRef]
- Lazar, A.; Vintzileos, A.; Doblas-Reyes, F.J.; Rogel, P.; Delecluse, P. Seasonal forecast of tropical climate with coupled ocean–atmosphere general circulation models: On the respective role of the atmosphere and the ocean components in the drift of the surface temperature error. Tellus A 2005, 57, 387–397. [Google Scholar] [CrossRef]
- Zhao, T.; Guo, W.; Fu, C. Calibrating and evaluating reanalysis surface temperature error by topographic correction. J. Clim. 2008, 21, 1440–1446. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, M.; Sun, M.; Wang, B.; Huang, X.Y.; Wang, Q.; Feng, F. Comparison of surface air temperature derived from NCEP/DOE R2, ERA-interim, and observations in the arid northwestern China: A consideration of altitude errors. Theor. Appl. Climatol. 2015, 119, 99–111. [Google Scholar] [CrossRef]
- Li, J.; Chen, H.B.; Li, Z.Q.; Wang, P.C.; Cribb, M.; Fan, X.H. Low-level temperature inversions and their effect on aerosol condensation nuclei concentrations under different large-scale synoptic circulations. Adv. Atmos. Sci. 2015, 32, 898–908. [Google Scholar] [CrossRef]
- Malek, E.; Davis, T.; Martin, R.S.; Silva, P.J. Meteorological and environmental aspects of one of the worst national air pollution episodes (January, 2004) in Logan, Cache Valley, Utah, USA. Atmos. Res. 2006, 79, 108–122. [Google Scholar] [CrossRef]
- Silva, P.J.; Vawdrey, E.L.; Corbett, M.; Erupe, M. Fine particle concentrations and composition during wintertime inversions in Logan, Utah, USA. Atmos. Environ. 2007, 41, 5410–5422. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, Y.S.; Zhang, C.C. Vertical observations and analysis of PM2.5, O3, and NOx at Beijing and Tianjin from tower during summer and autumn 2006. Adv. Atmos. Sci. 2010, 27, 123–136. [Google Scholar] [CrossRef]
- Chu, D.A.; Tsai, T.C.; Chen, J.P.; Chang, S.C.; Jeng, Y.J.; Chang, W.L.; Lin, M.H. Interpreting aerosol lidar profiles to better estimate surface PM 2.5, for columnar AOD measurements. Atmos. Environ. 2013, 79, 172–187. [Google Scholar] [CrossRef]
- Liu, S.; Min, H.S.S.; He, L.Y.; Niu, Y.W.; Bruegemann, B.; Gnauk, T.; Herrmann, H. Size distribution and source analysis of ionic compositions of aerosols in polluted periods at Xinken in Pearl River Delta (PRD) of China. Atmos. Environ. 2008, 42, 6284–6295. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Z. Estimation of PM2.5 from fine-mode aerosol optical depth. J. Remote Sens. 2013, 17, 929–943. [Google Scholar]
- Lin, C.; Li, Y.; Yuan, Z.; Lau, A.K.H.; Li, C.C.; Fung, J.C.H. Using Satellite Remote Sensing Data to Estimate the High-Resolution Distribution of Ground-Level PM2.5. Remote Sens. Environ. 2015, 156, 117–128. [Google Scholar] [CrossRef]
- Chenge, Y.; Brutsaert, W. Flux-profile relationships for wind speed and temperature in the stable atmospheric boundary layer. Bound. Layer Meteorol. 2005, 114, 519–538. [Google Scholar] [CrossRef]
- Kelley, N.D.; Jonkman, B.J. The Stable Atmospheric Boundary Layer: A Challenge for Wind Turbine Operations. Proceedings of AGU Fall Meeting, San Francisco, CA, USA, 15–19 December 2008. [Google Scholar]
- Mahrt, L. Characteristics of submeso winds in the stable boundary layer. Bound. Layer Meteorol. 2009, 130, 1–14. [Google Scholar] [CrossRef]
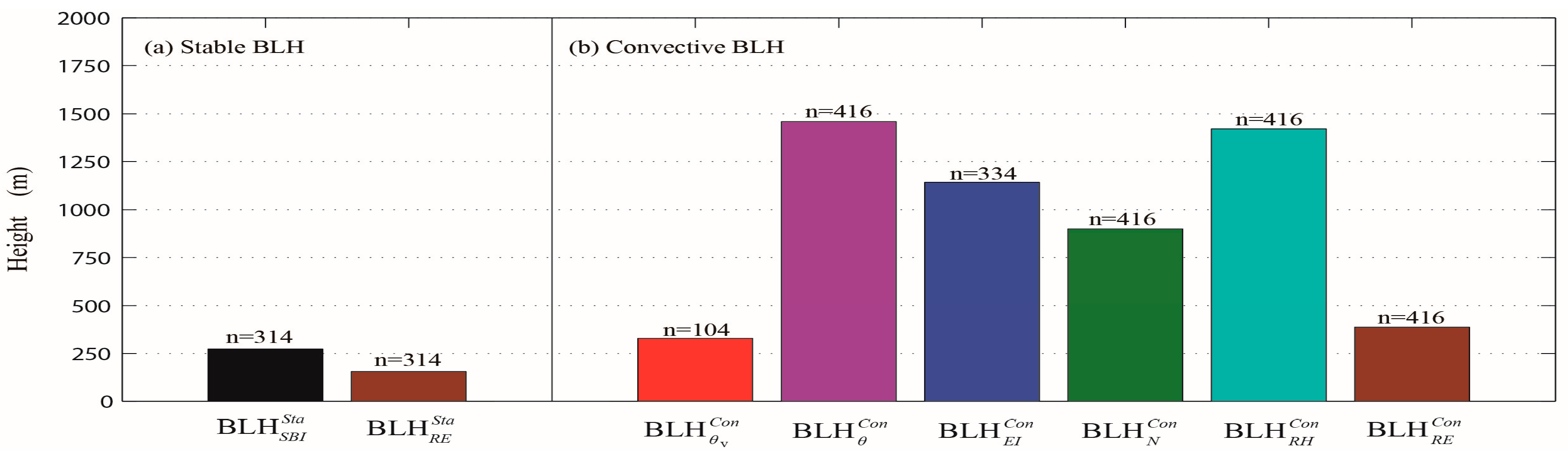

| Source | Abbreviation | Method | Types of boundary layer | |
|---|---|---|---|---|
| Stable | Convective | |||
| Radiosonde | Height of the top of a surface-based temperature inversion | √ | ||
| Height of the virtual potential temperature (θv) equaling the surface value. | √ | |||
| Height of the maximum vertical gradient of potential temperature (θ) | √ | |||
| Height of the base of an elevated temperature inversion | √ | |||
| Height of the minimum vertical gradient of relative humidity (RH) | √ | |||
| Height of the minimum vertical gradient of refractivity (N) | √ | |||
| Reanalysis | Height of PBL from NCEP reanalysis | √ | ||
| Height of PBL from NCEP reanalysis | √ | |||
| Season | Stable Boundary Layer | Convective Boundary Layer |
|---|---|---|
| Spring | 66 (35.87%) | 118 (64.13%) |
| Summer | 40 (21.74%) | 144 (78.26%) |
| Autumn | 97 (53.30%) | 85 (46.70%) |
| Winter | 111 (61.67%) | 69 (38.33%) |
| Total | 314(43.01%) | 416(56.99%) |
| M-III-Sta | Independent Variable | R2 | RMSE |
|---|---|---|---|
| 1 | AOD (0.67 **) | 0.50 | 44.30 |
| 2 | AOD (0.52 **),RHsur (0.02 **) | 0.62 | 38.73 |
| 3 | AOD (0.53 **), RHsur (0.01 **), (0.28 **) | 0.65 | 37.02 |
| 4 | AOD (0.53 **), RHsur (0.01 **), (0.23 **),Tsur(−0.01 *) | 0.68 | 35.44 |
| M-III-Con | Independent Variable | R2 | RMSE |
|---|---|---|---|
| 1 | AOD (0.77 **) | 0.65 | 31.76 |
| 2 | AOD (0.68 **),(−0.28 **) | 0.69 | 30.32 |
| 3 | AOD (0.67 **),(−0.19 **),WSsur (−0.22 **) | 0.70 | 29.89 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zang, Z.; Wang, W.; Cheng, X.; Yang, B.; Pan, X.; You, W. Effects of Boundary Layer Height on the Model of Ground-Level PM2.5 Concentrations from AOD: Comparison of Stable and Convective Boundary Layer Heights from Different Methods. Atmosphere 2017, 8, 104. https://doi.org/10.3390/atmos8060104
Zang Z, Wang W, Cheng X, Yang B, Pan X, You W. Effects of Boundary Layer Height on the Model of Ground-Level PM2.5 Concentrations from AOD: Comparison of Stable and Convective Boundary Layer Heights from Different Methods. Atmosphere. 2017; 8(6):104. https://doi.org/10.3390/atmos8060104
Chicago/Turabian StyleZang, Zengliang, Weiqi Wang, Xinghong Cheng, Bin Yang, Xiaobin Pan, and Wei You. 2017. "Effects of Boundary Layer Height on the Model of Ground-Level PM2.5 Concentrations from AOD: Comparison of Stable and Convective Boundary Layer Heights from Different Methods" Atmosphere 8, no. 6: 104. https://doi.org/10.3390/atmos8060104
APA StyleZang, Z., Wang, W., Cheng, X., Yang, B., Pan, X., & You, W. (2017). Effects of Boundary Layer Height on the Model of Ground-Level PM2.5 Concentrations from AOD: Comparison of Stable and Convective Boundary Layer Heights from Different Methods. Atmosphere, 8(6), 104. https://doi.org/10.3390/atmos8060104








