Feasibility Study of Rain Rate Monitoring from Polarimetric GNSS Propagation Parameters
Abstract
:1. Introduction
2. Methods
2.1. Shapes of Raindrops
2.2. Raindrop Size Distribution
2.3. Calculation Models of Phase Shift Parameters
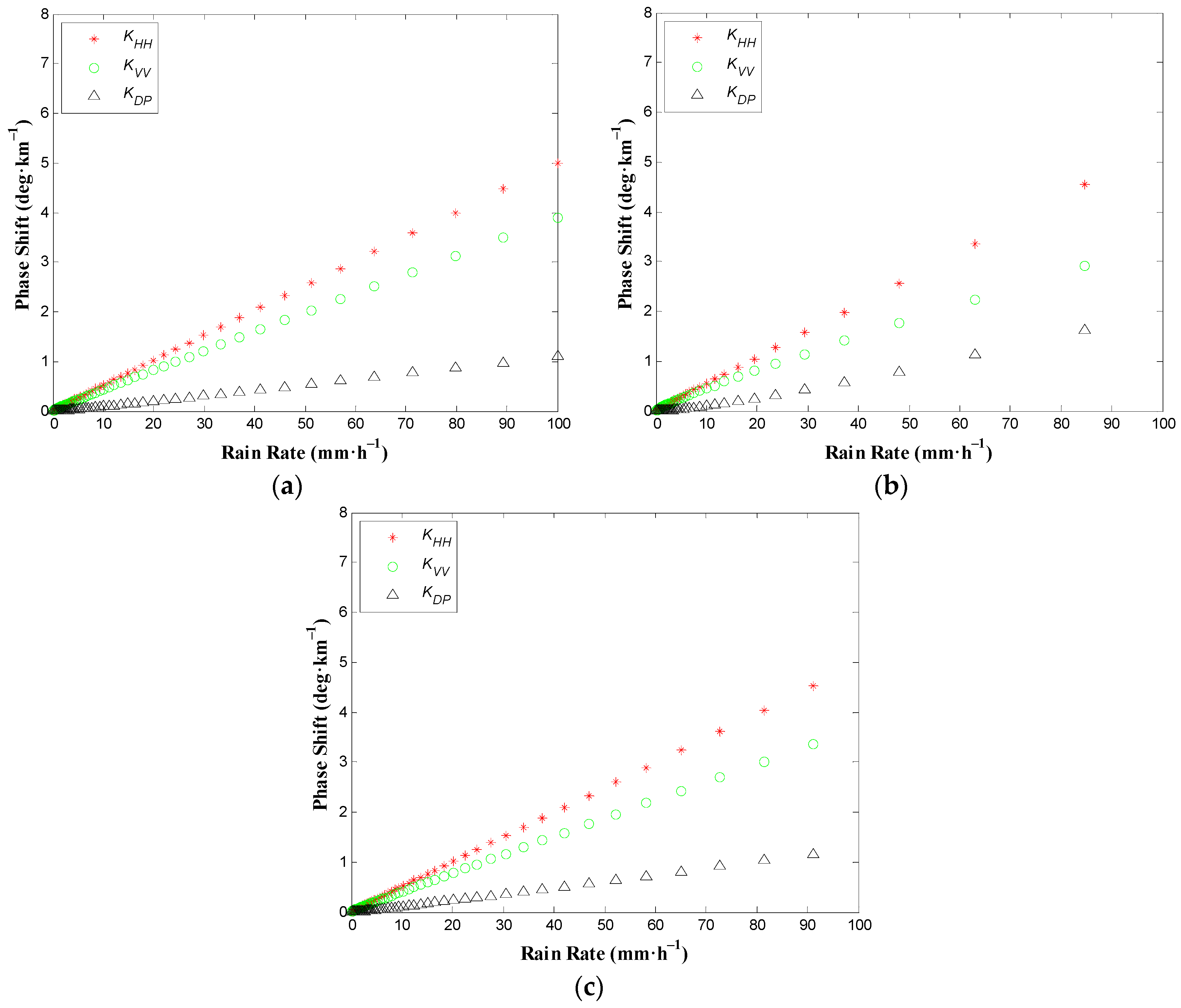
3. Simulation Analysis and Discussion
3.1. Numerical Simulations Based on Simulated Raindrop Size Distribution
3.2. Sensitivity Analysis of Phase Shift with Respect to Shape of Raindrops
3.3. Sensitivity Analysis of Phase Shift with Respect to Frequency
3.4. Sensitivity Analysis of Phase Shift with Respect to Elevation Angle
3.5. Simulation Calculation of Phase Shift under Real Rainfall
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Jin, S.G.; Cardellach, E.; Xie, F.Q. GNSS Remote Sensing: Theory, Methods and Applications; Springer: Berlin, Germany, 2014; pp. 17–240. [Google Scholar]
- Bevis, M.; Businger, S.; Herring, T.A.; Rocken, C.; Anthes, R.A.; Ware, R.H. GPS meteorology: Remote sensing of atmospheric water vapor using the Global Positioning System. J. Geophys. Res. 1992, 97, 15787–15801. [Google Scholar] [CrossRef]
- Wang, H.; He, J.; Wei, M.; Zhang, Z. Synthesis analysis of one severe convection precipitation event in Jiangsu using ground-based GPS technology. Atmosphere 2015, 6, 908–927. [Google Scholar] [CrossRef]
- Ware, R.; Rocken, C.; Solheim, F.; Exner, M.; Schreiner, W.; Anthes, R.; Businger, S. GPS sounding of the atmosphere from low Earth orbit: Preliminary results. Bull. Am. Meteorol. Soc. 1996, 77, 19–40. [Google Scholar] [CrossRef]
- Mannucci, A.J.; Wilson, B.D.; Yuan, D.N.; Ho, C.H.; Lindqwister, U.J.; Runge, T.F. A global mapping technique for GPS-derived ionospheric total electron content measurements. Radio Sci. 1998, 33, 565–582. [Google Scholar] [CrossRef]
- Hu, X.; Wu, X.C.; Gong, X.Y.; Xiao, C.Y.; Zhang, X.X.; Fu, Y.; Yang, G.L. An introduction of mountain-based GPS radio occultation experiments in China. Adv. Space Res. 2008, 42, 1723–1729. [Google Scholar] [CrossRef]
- Armatys, M.; Komjathy, A.; Axelrad, P.; Katzberg, S.J. A comparison of GPS and scatterometry sensing of ocean wind speed and direction. In Proceedings of the 2000 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Honolulu, HI, USA, 24–28 July 2000; pp. 2861–2863.
- Rius, A.; Nogues-Correig, O.; Ribo, S.; Cardellach, E.; Oliveras, S.; Valencia, E.; Park, H.; Tarongi, J.M.; Camps, A.; van der Marel, H.; et al. Altimetry with GNSS-R interferometry: First proof of concept experiment. GPS Solut. 2012, 16, 231–241. [Google Scholar] [CrossRef]
- Najibi, N.; Jin, S. Physical reflectivity and polarization characteristics for snow and ice-covered surfaces interacting with GPS signals. Remote Sens. 2013, 5, 4006–4030. [Google Scholar] [CrossRef]
- Cardellach, E.; Rius, A.; Cerezo, F. Polarimetric GNSS Radio-Occultations for heavy rain detection. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Honolulu, HI, USA, 25–30 July 2010; pp. 3841–3844.
- Cardellach, E.; Tomás, S.; Oliveras, S.; Padullés, R.; Rius, A.; de la Torre-Juarez, M.; Joseph Turk, F.; Ao, C.O.; Kursinski, E.R.; Schreiner, B.; et al. Sensitivity of PAZ LEO polarimetric GNSS radio-occultation experiment to precipitation events. IEEE Trans. Geosci. Remote Sens. 2015, 53, 190–206. [Google Scholar] [CrossRef]
- Padullés, R.; Cardellach, E.; de la Torre Juárez, M.; Tomás, S.; Turk, F.J.; Oliveras, S.; Rius, A. Atmospheric polarimetric effects on GNSS radio occultations: The ROHP-PAZ field campaign. Atmos. Chem. Phys. 2016, 16, 635–649. [Google Scholar] [CrossRef]
- Yan, W.; An, H.; Fu, Y.; Han, Y.; Wang, X.; Ai, W. A method for estimating rain rate from polarimetric GNSS measurements: Preliminary analysis. Atmos. Res. 2014, 149, 70–76. [Google Scholar] [CrossRef]
- Thombre, S.; Hurskainen, H.; Nurmi, J. Wideband, high gain, high linearity, low noise amplifier for GNSS frequencies with compensation for low frequency instability. In Proceedings of the 2010 5th Advanced Satellite Multimedia Systems Conference and the 11th Signal Processing for Space Communications Workshop, Cagliari, Italy, 13–15 September 2010; pp. 349–354.
- International Telecommunications Union (ITU). Recommendation ITU-R P.838-3 Specific Attenuation Model for Rain for Use in Prediction Methods; ITU: Geneva, Switzerland, 2003. [Google Scholar]
- Oguchi, T. Electromagnetic Wave Propagation and Scattering in Rain and Other Hydrometeors. Proc. IEEE 1983, 71, 1029–1079. [Google Scholar] [CrossRef]
- Goddard, J.W.; Cherry, S.M. The ability of dual-polarization radar (copolar linear) to predict rainfall rate and microwave attenuation. Radio Sci. 1984, 19, 201–208. [Google Scholar] [CrossRef]
- Notaroš, B.M.; Bringi, V.N.; Kleinkort, C.; Kennedy, P.; Huang, G.-J.; Thurai, M.; Newman, A.J.; Bang, W.; Lee, G. Accurate characterization of winter precipitation using multi-angle snowflake camera, visual hull, advanced scattering methods and polarimetric radar. Atmosphere 2016, 7, 81. [Google Scholar] [CrossRef]
- Gorgucci, E.; Baldini, L. An examination of the validity of the mean raindrop-shape model for dual-polarization radar rainfall retrievals. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2752–2761. [Google Scholar] [CrossRef]
- Pruppacher, H.R.; Beard, K.V. A wind tunnel investigation of the internal circulation and shape of water drops falling at terminal velocity in air. Q. J. R. Meteorol. Soc. 1970, 96, 247–256. [Google Scholar] [CrossRef]
- Beard, K.V.; Chuang, C. A new model for the equilibrium shape of raindrops. J. Atmos. Sci. 1987, 44, 1509–1524. [Google Scholar] [CrossRef]
- Brandes, E.A.; Zhang, G.; Vivekanandan, J. Experiments in rainfall estimation with a polarimetric radar in a subtropical environment. J. Appl. Meteorol. 2002, 41, 674–685. [Google Scholar] [CrossRef]
- Thurai, M.; Huang, G.J.; Bringi, V.N.; Randeu, W.L.; Schönhuber, M. Drop shapes, model comparisons, and calculations of polarimetric radar parameters in rain. J. Atmos. Ocean. Technol. 2007, 24, 1019–1032. [Google Scholar] [CrossRef]
- Bahrami, M.; Mohassel, J.R.; Taheri, M.M. An exact solution of coherent wave propagation in rain medium with realistic raindrop shapes. Prog. Electromagn. Res. 2008, 79, 107–118. [Google Scholar] [CrossRef]
- An, H.; Yan, W.; Huang, Y.; Ai, W.; Wang, Y.; Zhao, X.; Huang, X. GNSS Measurement of Rain Rate by Polarimetric Phase Shift: Theoretical Analysis. Atmosphere 2016, 7, 101. [Google Scholar] [CrossRef]
- Laws, J.O.; Parsons, D.A. The relation of raindrop-size to intensity. Trans. Am. Geophys. Union 1943, 24, 452–460. [Google Scholar] [CrossRef]
- Olsen, R.L.; Rogers, D.V.; Hodge, D.B. The aRb relation in the calculation of rain attenuation. IEEE Trans. Antennas Propag. 1978, 26, 318–329. [Google Scholar] [CrossRef]
- Ulbrich, C.W. Natural variations in the analytical form of the raindrop-size distribution. J. Clim. Appl. Meteorol. 1983, 22, 1764–1775. [Google Scholar] [CrossRef]
- Chandrasekar, V.; Bringi, V.N. Simulation of radar reflectivity and surface measurements of rainfall. J. Atmos. Ocean. Technol. 1987, 4, 464–478. [Google Scholar] [CrossRef]
- Bringi, V.N.; Chandrasekar, V.; Hubbert, J.; Gorgucci, E.; Randeu, W.L.; Schoenhuber, M. Raindrop size distribution in different climatic regimes from disdrometer and dual-polarized radar analysis. J. Atmos. Sci. 2003, 60, 354–365. [Google Scholar] [CrossRef]
- Atlas, D.; Ulbrich, C.W. Path- and area-integrated rainfall measurement by microwave attenuation in the 13 cm band. J. Appl. Meteorol. 1977, 16, 1322–1331. [Google Scholar] [CrossRef]
- Gunn, R.; Kinzer, G.D. The terminal velocity of fall for water droplets in stagnant air. J. Meteorol. 1949, 6, 243–248. [Google Scholar] [CrossRef]
- Montopoli, M.; Botta, G.; Marzano, F.S. Modeling polarimetric microwave propagation parameters from globally distributed raindrop size distribution measurements. In Proceedings of the 3rd European Conference on Antennas and Propagation (EuCAP 2009), Berlin, Germany, 23–27 March 2009.
- Mishchenko, M.I.; Travis, L. Capabilities and limitations of a current FORTRAN implementation of the T-matrix method for randomly oriented, rotationally symmetric scatterers. J. Quant. Spectrosc. Radiat. Transf. 1998, 60, 309–324. [Google Scholar] [CrossRef]
- Duffo, N.; Vall llossera, M.; Camps, A.; Corbella, I.; Torres, F. Polarimetric emission of rain events: Simulation and experimental results at X-Band. Remote Sens. 2009, 1, 107–121. [Google Scholar] [CrossRef]
- Ray, P.S. Broadband complex refractive indices of ice and water. Appl. Opt. 1972, 11, 1836–1844. [Google Scholar] [CrossRef] [PubMed]
- Bringi, V.N.; Huang, G.J.; Chandrasekar, V.; Gorgucci, E. A methodology for estimating the parameters of a gamma raindrop size distribution model from polarimetric radar data: Application to a squall-line event from the TRMM/Brazil campaign. J. Atmos. Ocean. Technol. 2002, 19, 633–645. [Google Scholar] [CrossRef]
- Gorgucci, E.; Scarchilli, G.; Chandrasekar, V. Specific differential phase estimation in the presence of nonuniform rainfall medium along the path. J. Atmos. Ocean. Technol. 1999, 16, 1690–1697. [Google Scholar] [CrossRef]
- Ajaji, G.O. Characteristics of rain induced attenuation and phase shift at cm and mm waves using a tropical raindrop size distribution model. Int. J. Infrared Millim. Waves 1985, 6, 771–806. [Google Scholar] [CrossRef]
- Xie, Y.; Chen, Z.; Dai, J.; Hu, P. Analysis on raindrop spectrum in four types of precipitation in Shanghai. J. Meteorol. Sci. 2015, 35, 353–361. [Google Scholar]
- Xiong, F.; Zhou, Y. Study of Moment Methods in Estimating Three Parameters of Gamma Raindrop Size Distribution. Meteorology 2016, 42, 777–789. [Google Scholar]
- Hajj, G.A.; Kursinski, E.R.; Romans, L.J.; Bertiger, W.I.; Leroy, S.S. A technical description of atmospheric sounding by GPS occultation. J. Atmos. Sol. Terr. Phys. 2002, 64, 451–469. [Google Scholar] [CrossRef]
- García, J.G.; Mercader, P.I.; Muravchik, C.H. Use of GPS carrier phase double differences. Latin Am. Appl. Res. 2005, 35, 115–120. [Google Scholar]
- Bai, W.H.; Sun, Y.Q.; Du, Q.F.; Yang, G.L.; Yang, Z.D.; Zhang, P.; Bi, Y.M.; Wang, X.Y.; Cheng, C.; Han, Y. An introduction to the FY3 GNOS instrument and mountain-top tests. Atmos. Meas. Tech. 2014, 7, 1817–1823. [Google Scholar] [CrossRef]
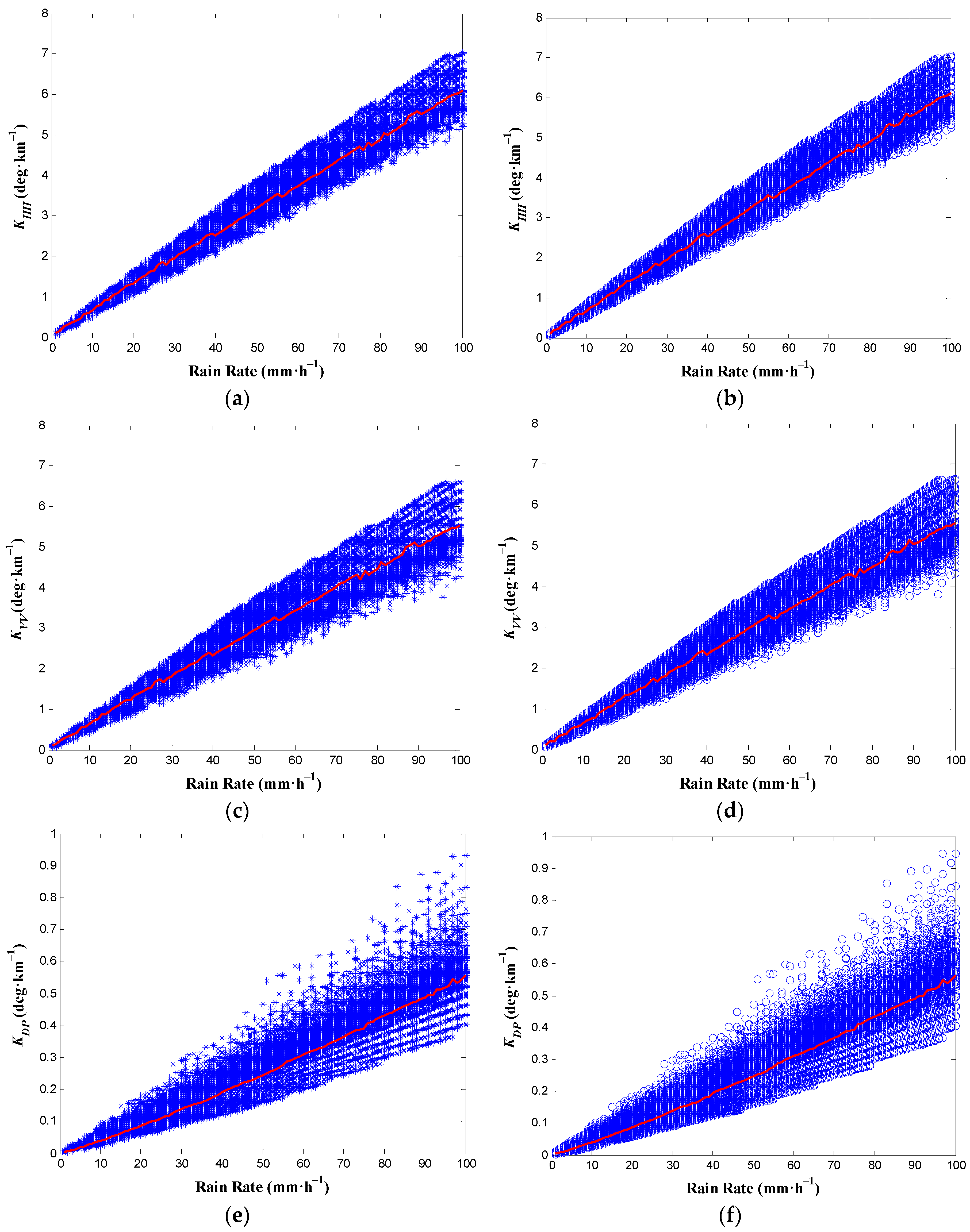
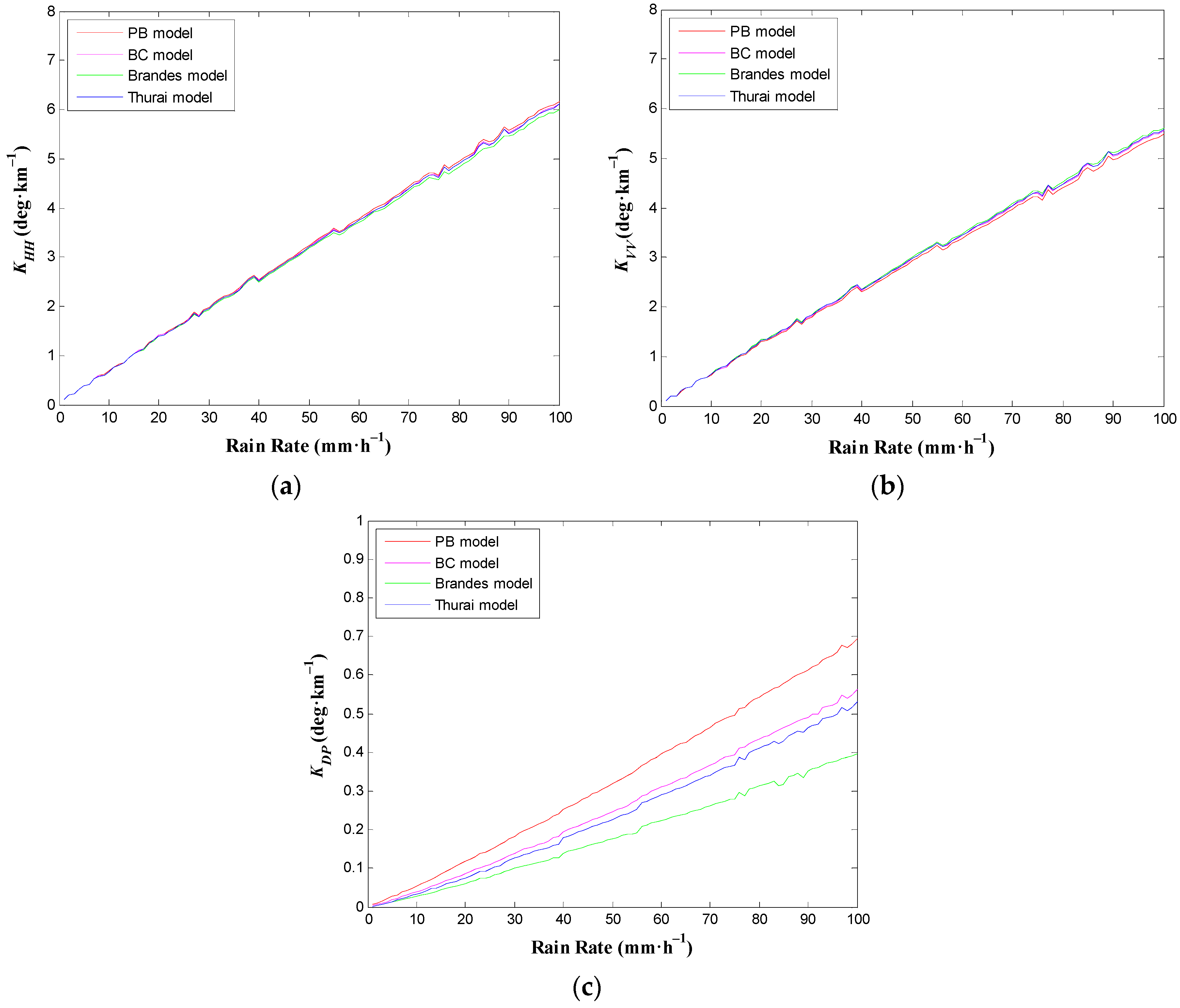
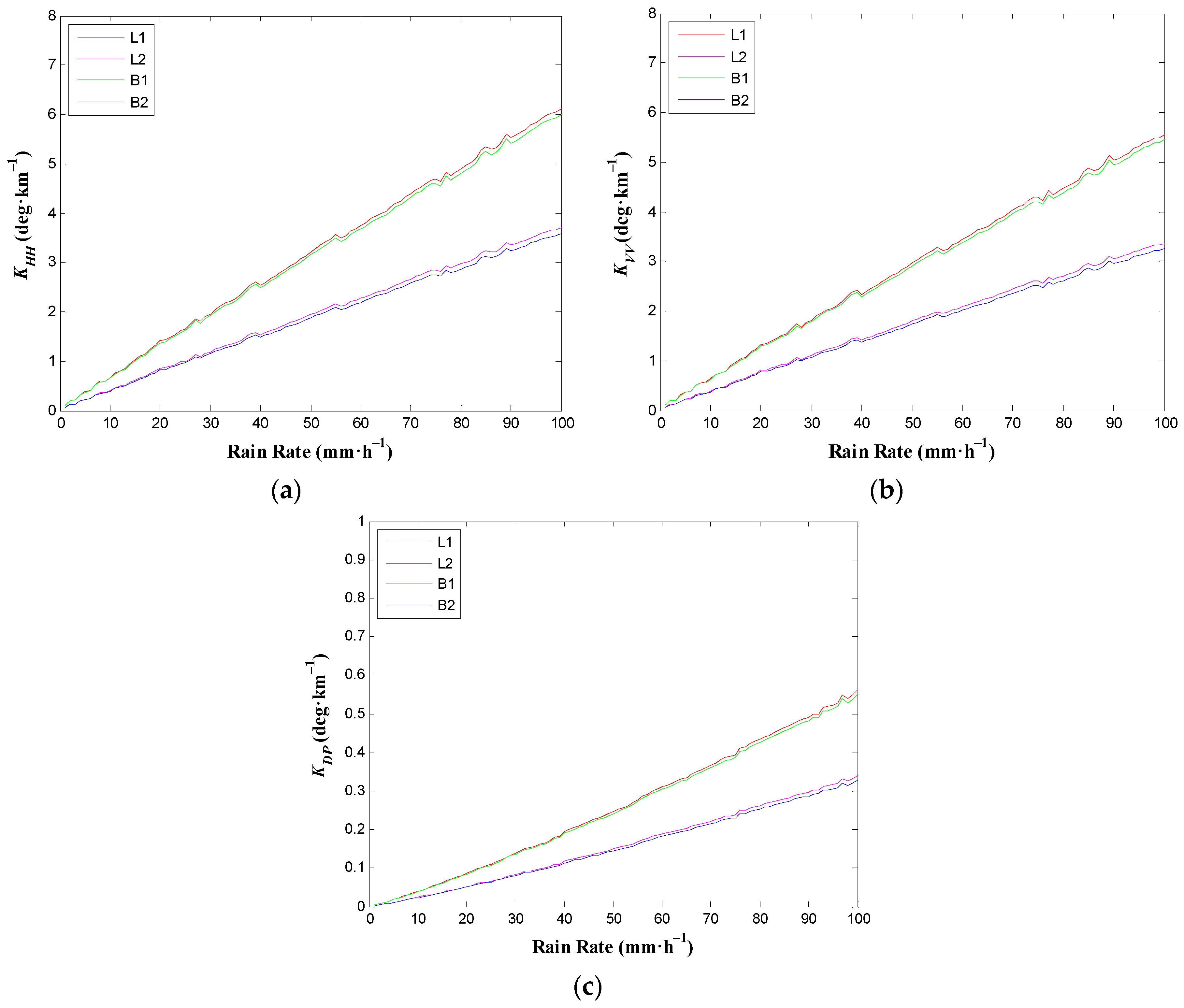
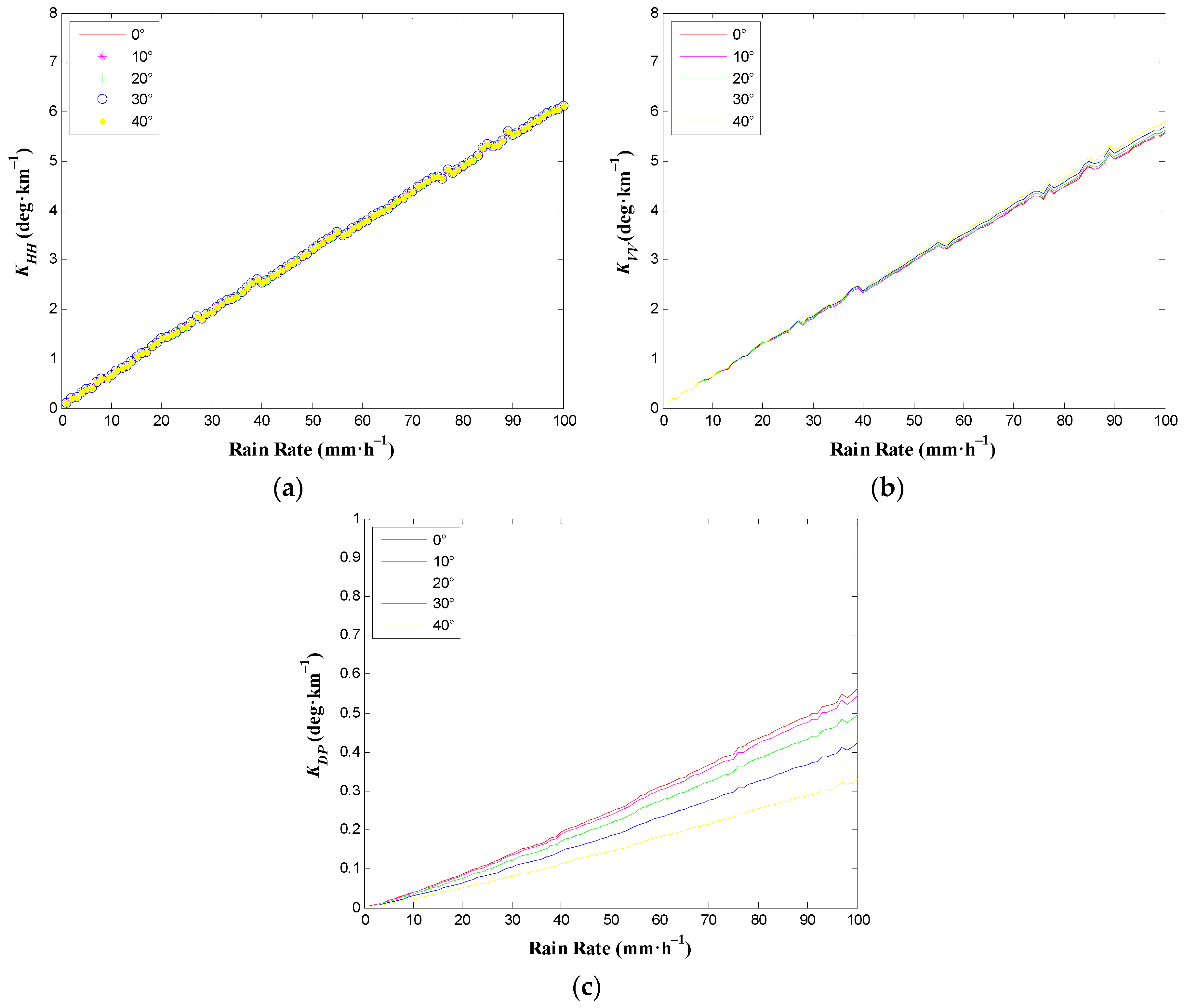
| Model | Expressions |
|---|---|
| PB model: | |
| BC model: | |
| Brandes model: | |
| Thurai model: |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
An, H.; Yan, W.; Huang, Y.; Zhao, X.; Wang, Y.; Ai, W. Feasibility Study of Rain Rate Monitoring from Polarimetric GNSS Propagation Parameters. Atmosphere 2016, 7, 159. https://doi.org/10.3390/atmos7120159
An H, Yan W, Huang Y, Zhao X, Wang Y, Ai W. Feasibility Study of Rain Rate Monitoring from Polarimetric GNSS Propagation Parameters. Atmosphere. 2016; 7(12):159. https://doi.org/10.3390/atmos7120159
Chicago/Turabian StyleAn, Hao, Wei Yan, Yunxian Huang, Xianbin Zhao, Yingqiang Wang, and Weihua Ai. 2016. "Feasibility Study of Rain Rate Monitoring from Polarimetric GNSS Propagation Parameters" Atmosphere 7, no. 12: 159. https://doi.org/10.3390/atmos7120159
APA StyleAn, H., Yan, W., Huang, Y., Zhao, X., Wang, Y., & Ai, W. (2016). Feasibility Study of Rain Rate Monitoring from Polarimetric GNSS Propagation Parameters. Atmosphere, 7(12), 159. https://doi.org/10.3390/atmos7120159





