Comprehensive Evaluation of High-Resolution Satellite-Based Precipitation Products over China
Abstract
:1. Introduction
2. Study Area and Dataset
2.1. Study Area

2.2. Satellite-Based Precipitation Dataset
| Name | Temporal Resolution | Spatial Resolution | Domain | Corrected by Gauges | References |
|---|---|---|---|---|---|
| GSMaP-MVK | 1 h | 0.1° | 60°S–60°N | No | [57,58] |
| GSMaP-Gauge | 1 h | 0.1° | 60°S–60°N | Yes | [44,57,58] |
| CMORPH | 1 day | 0.25° | 60°S–60°N | No | [5] |
| CMORPH-CRT | 1 day | 0.25° | 60°S–60°N | Yes | [65] |
| PERSIANN | 3 h | 0.25° | 60°S–60°N | No | [3,4] |
| PRESIANN-CDR | 1 day | 0.25° | 60°S–60°N | Yes | [3,4,64] |
2.3. Ground Reference Data
2.4. Statistical Evaluation Metrics
3. Results and Discussion
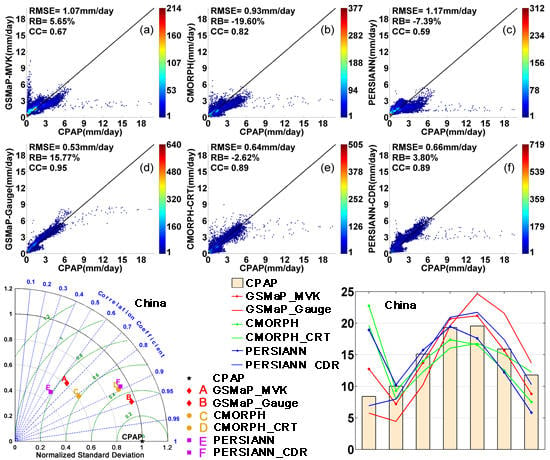
3.1. Four Year Daily Mean Precipitation
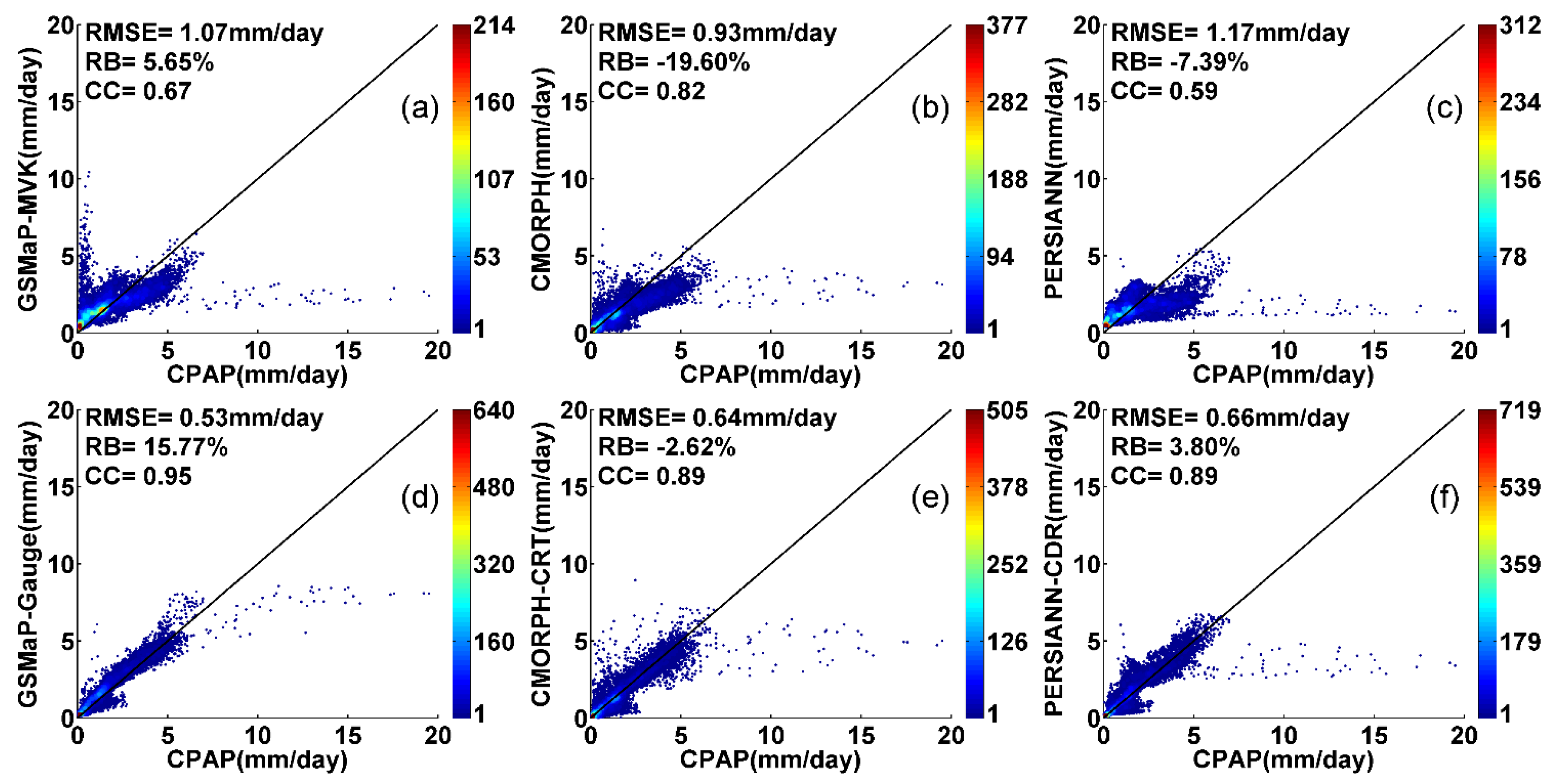
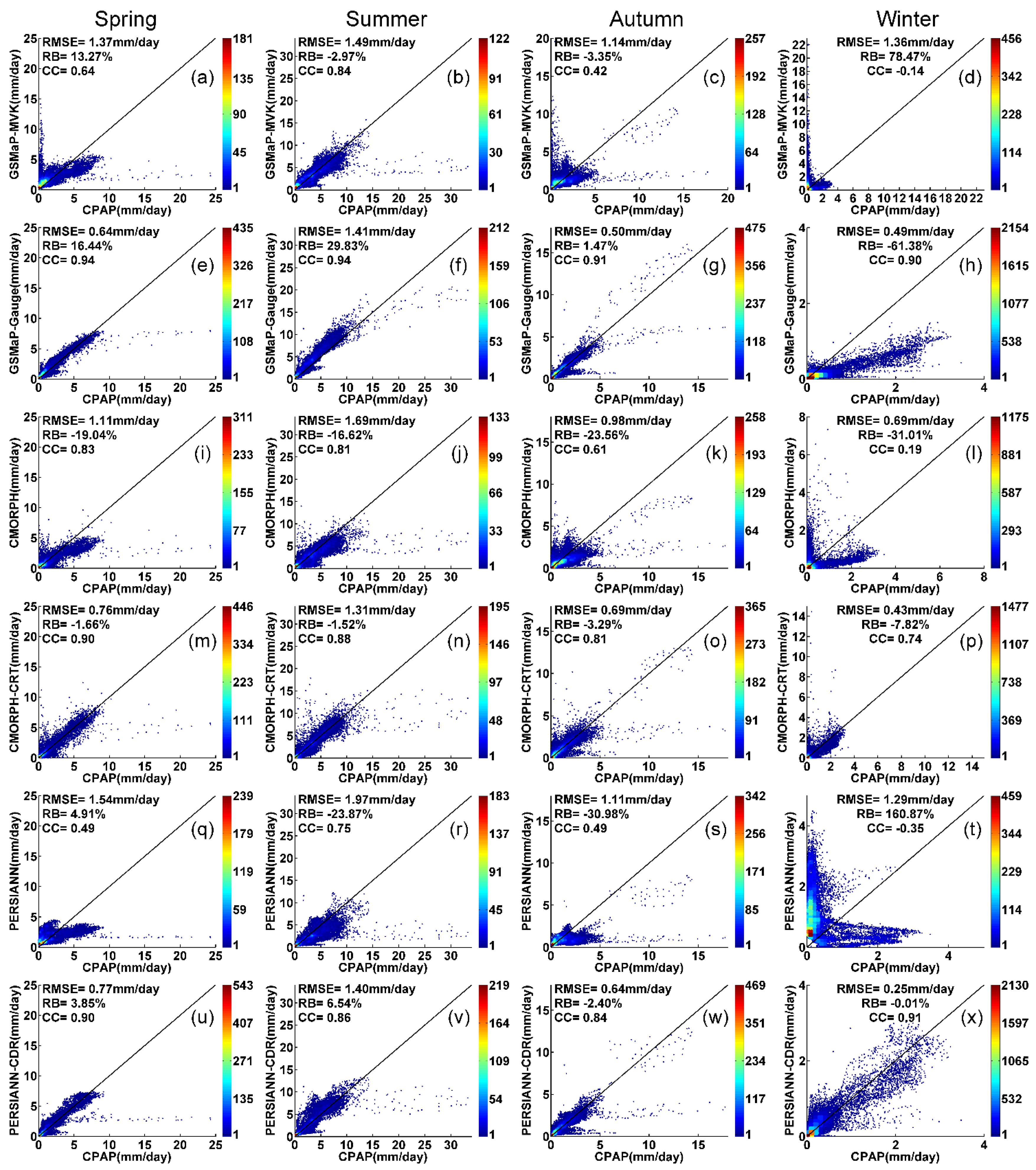
3.2. Seasonal Daily Mean Precipitation
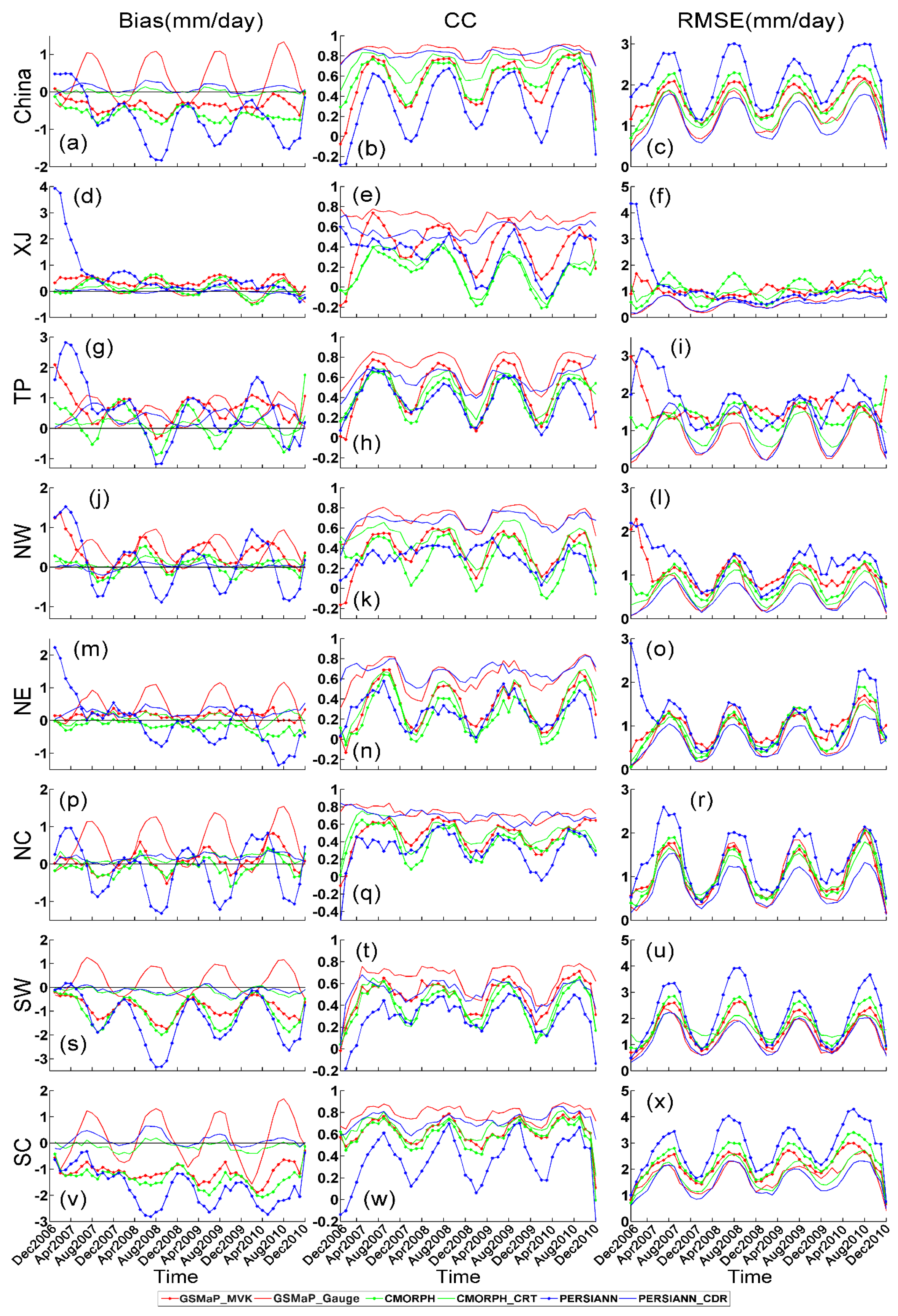
3.3. Time Series Monthly Precipitation
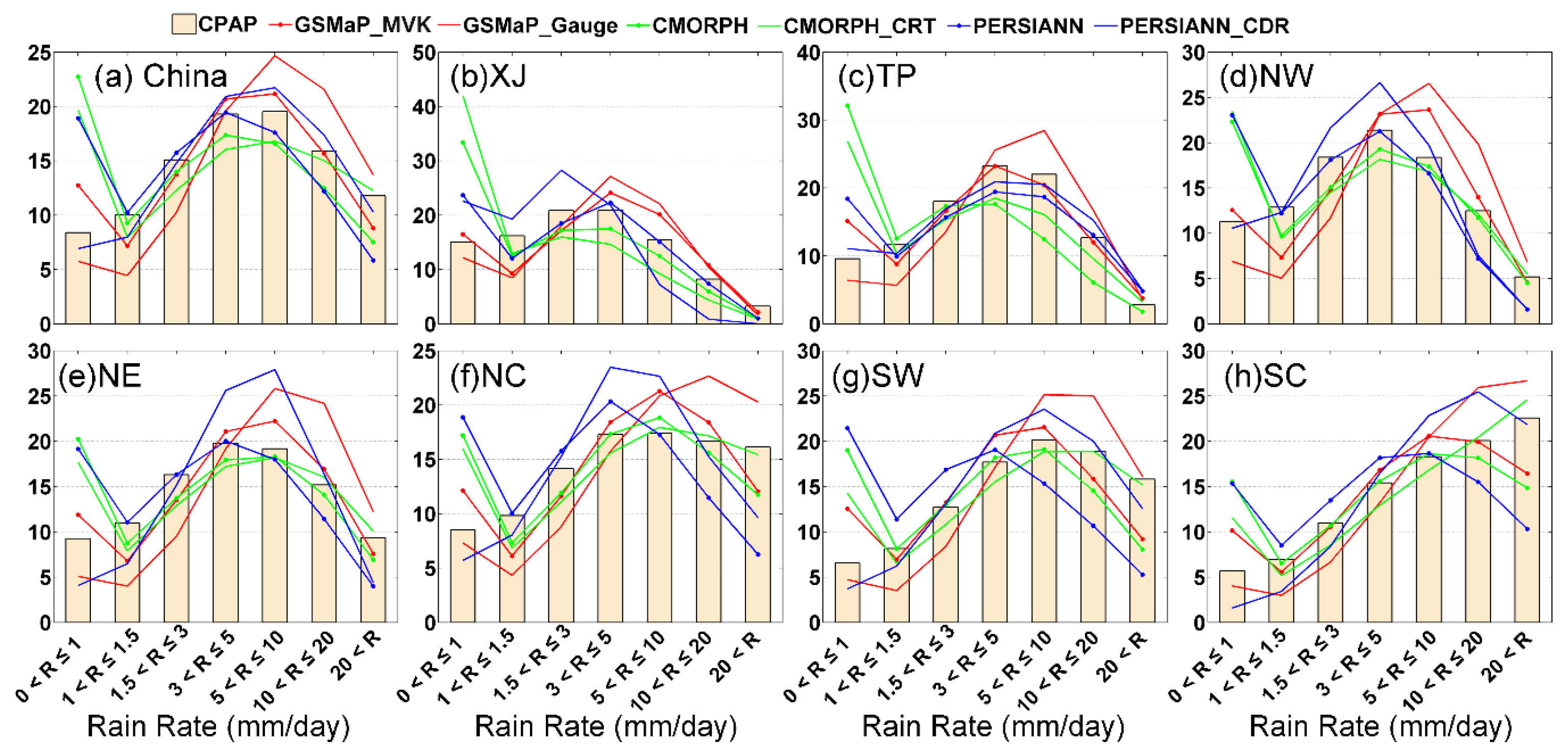
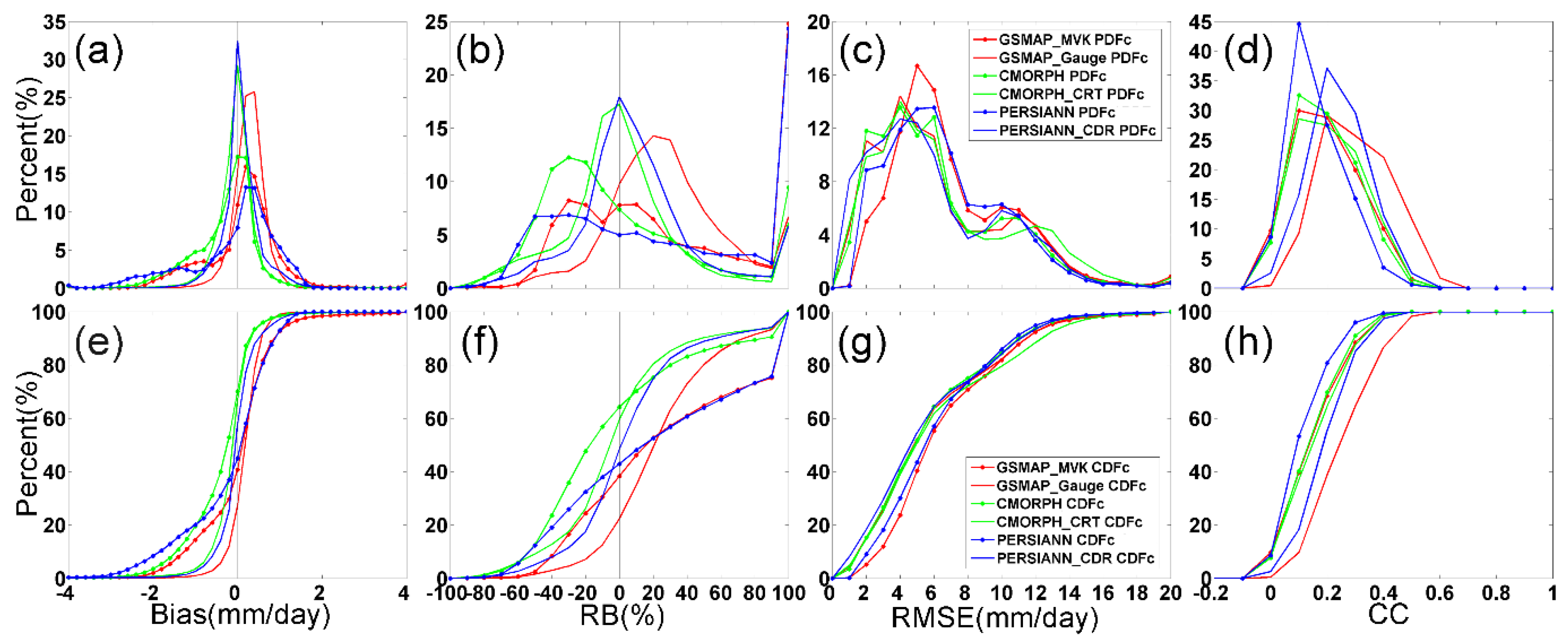
3.4. Probability Distribution by Occurrence
| Index | R (mm/Day) |
|---|---|
| 1 | 0 < R ≤ 1 |
| 2 | 1 < R ≤ 1.5 |
| 3 | 1.5 < R ≤ 3 |
| 4 | 3 < R ≤ 5 |
| 5 | 5 < R ≤ 10 |
| 6 | 10 < R ≤ 20 |
| 7 | R > 20 |
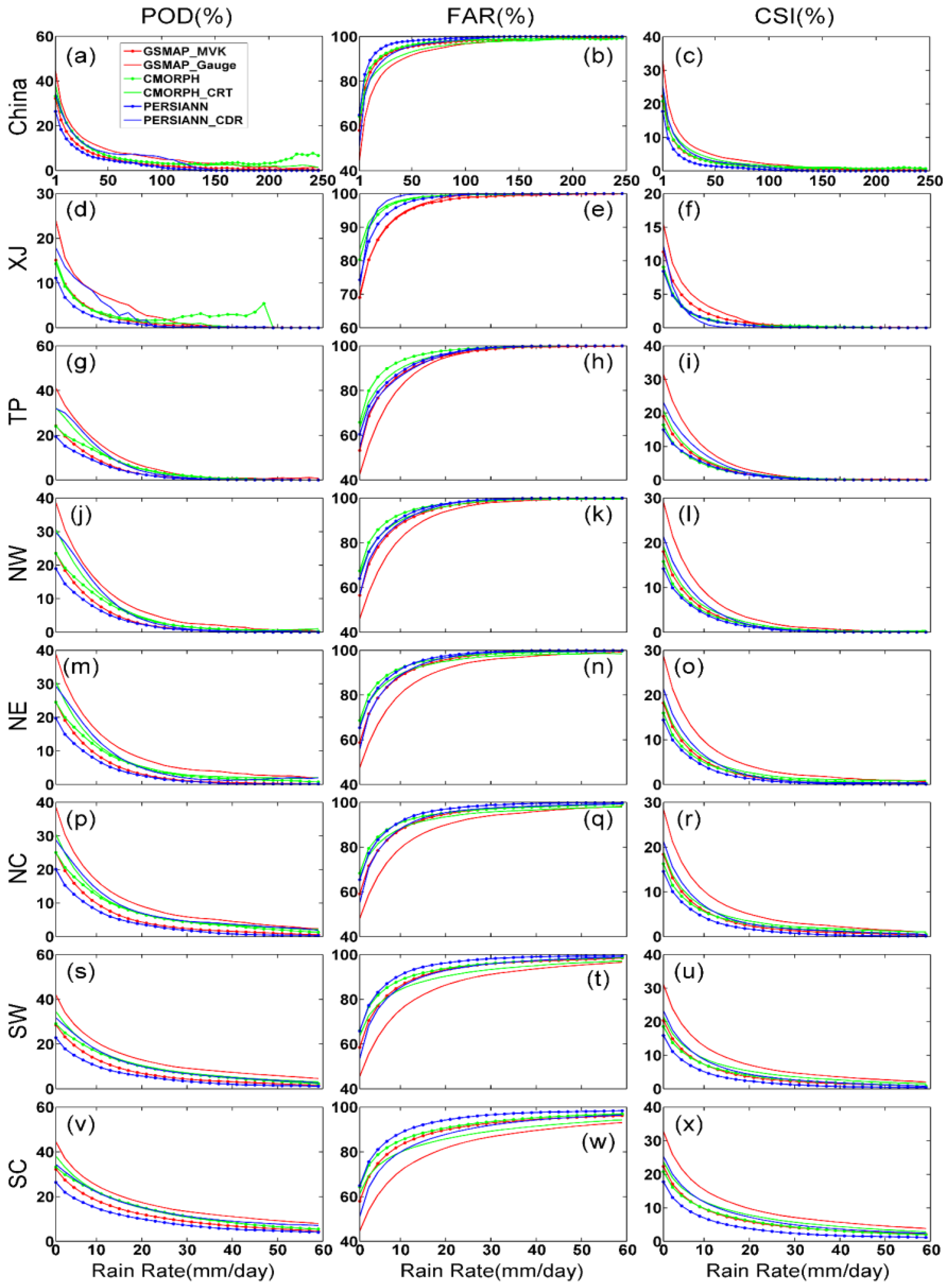
3.5. Contingency Statistics
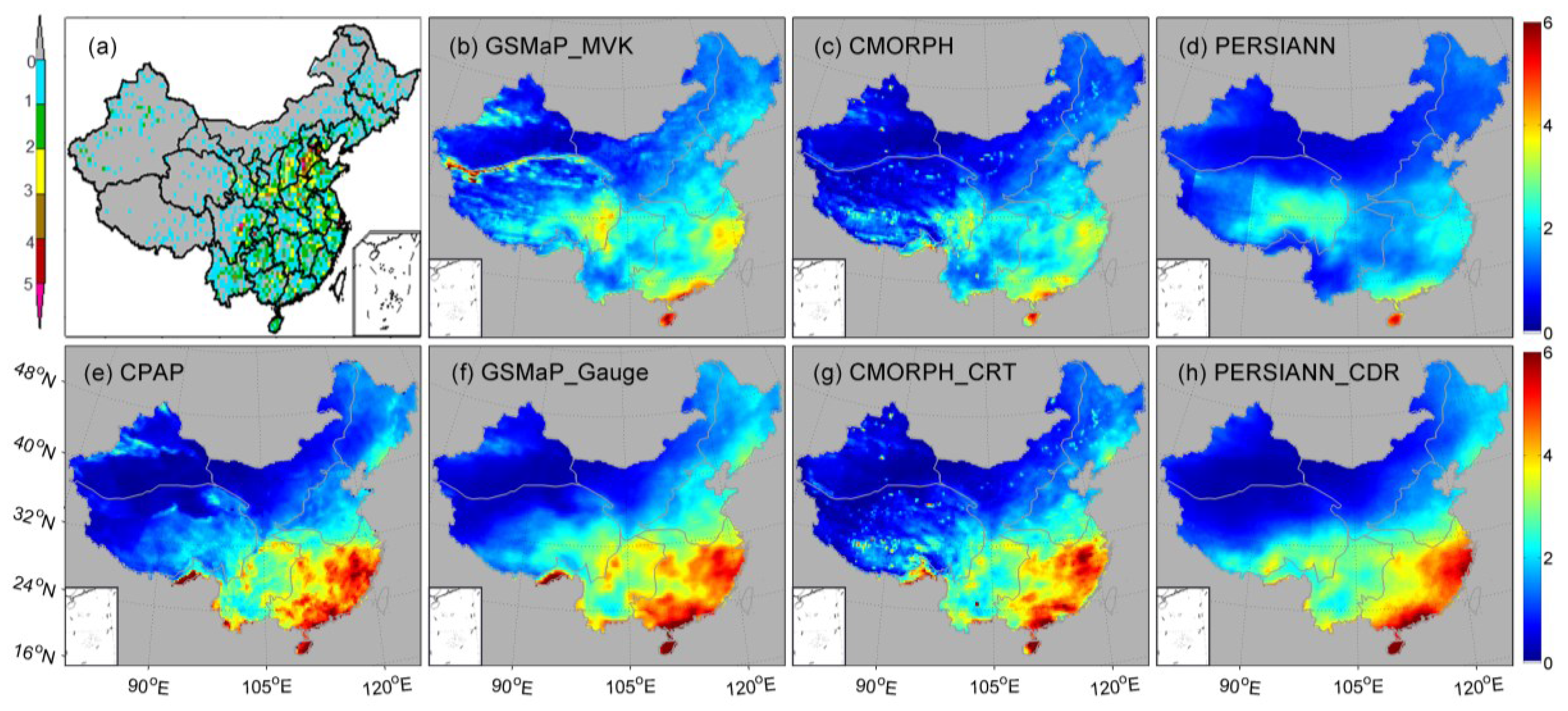
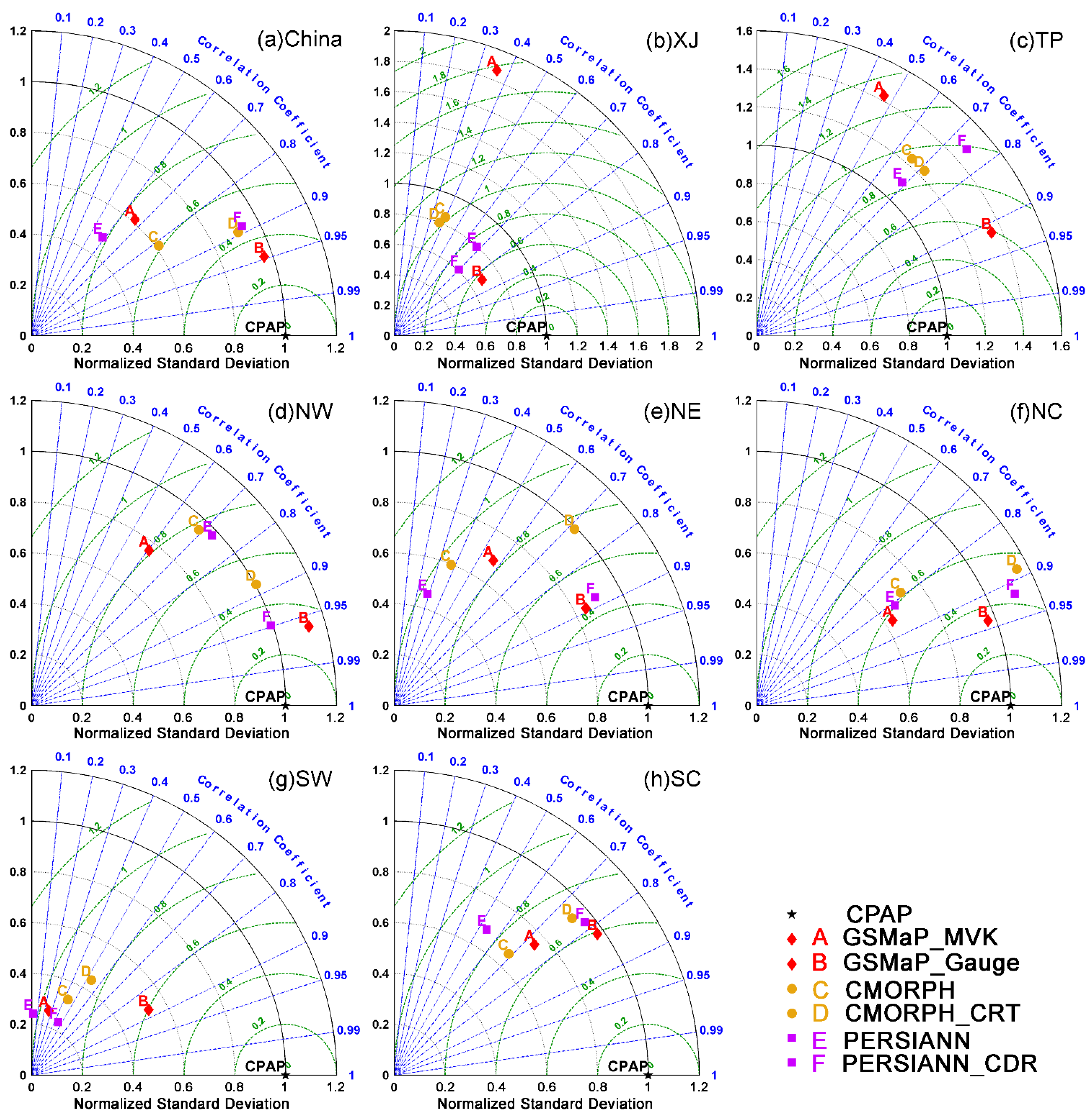
3.6. Spatial Analysis
4. Summary and Conclusions
- (1)
- Generally, the bias-correction procedures successfully reduce errors for all the three groups of satellite-based precipitation products. Specifically, regional overestimation or underestimation of precipitation, season-dependent errors and snow surface induced errors are reduced. However, the bias-correction procedure in GSMaP_Gauge may be not helpful in reducing errors in a mean sense.
- (2)
- For the four-year mean daily precipitation, all the six satellite products are capable of capturing the overall spatial pattern of precipitation. GSMaP_Gauge produces better fractional coverage with the highest CC (0.95) and lowest RMSE (0.53 mm/day), but also has a relatively high RB (15.77%) over China, while CMORPH_CRT exhibits amounts closer to CPAP. Among the satellite-based precipitation products without bias-adjustment, CMORPH demonstrates the best performance with the highest CC (0.82), and lowest RMSE (0.93 mm/day), but also a relatively higher RB (−19.60%). CMORPH_CRT fails to remove the highlighted overestimation speckles which appear in CMORPH without bias-correction. GSMaP_MVK displays relatively poor performance in XJ, TP and NW with relatively low CCs and shows large overestimation along the northern hillside of Tibetan Plateau. Therefore, it should be used cautiously in mountainous regions. CMORPH and GSMaP perform poorly over ice/snow covered surfaces, while PERSIANN displays a distinct overestimation over TP.
- (3)
- All the bias-corrected products provide improvements over their corresponding satellite-only counterparts. Among the bias-corrected products, GSMaP_Gauge shows the highest CC (0.90–0.94) but also a relatively high RB (−61.38%–16.44%) and RMSE (0.49–1.41 mm/day) for the seasonal four-year daily mean precipitation (Figure 4 and Figure 5, Table A1). Similar to the other precipitation products, it exhibits the worst performance in winter. PERSIANN_CDR shows the closest performance to CPAP in winter among all satellite-based products.
- (4)
- Season-dependent variations of error are present, and in particular, larger error values are observed during the monsoon season (April to October) for satellite-only precipitation products. These season-dependent variations are reduced by bias-adjustment procedures (Figure 7). GSMaP_MVK and CMORPH show underestimations for the entire study period. After bias-correction, GSMaP_Gauge consistently displays the highest CC (>0.7), but displays a relatively higher overestimation in warm seasons and a slight underestimation in cold seasons. This may be evidence for over-correction in the gauge-adjustment algorithm which could be improved in the future.
- (5)
- All the satellite-only precipitation products greatly overdetect the occurrence of rain rates less than 1 mm/day over dry regions (e.g., XJ, TP and NW) (Figure 8) and underdetect heavy rain events (>20 mm/day) over eastern China in wet climates. The bias-corrected products show decreased overdetection of light precipitation events. However, the bias-correction in PERSIANN and GSMaP tend to overcorrect the overdetection of light rain events and underdetection of heavy rain events. Moreover, gauge adjustment in CMORPH_CRT has little effect in reducing the light rain overdetection, but manifests detection patterns close to those of CPAP when the rain rate is over 1 mm/day.
- (6)
- Satellite-based precipitation products display low PODs for rain rates less than 60 mm/day. GSMaP_Gauge outperforms other two bias-corrected precipitation products with a maximum POD (~50%), maximum CSI (about 35%), and minimum FAR (~40%) for the rainfall rates less than 100 mm/day.
- (7)
- The underestimation by all satellite-based products is primarily distributed over southern and southeastern China while the overestimation is dominant over northern and western China. These satellite-based products exhibit better performance over the south and southeastern parts of China than over the north and northwestern parts of China in terms of Bias and RB (Figure 10 and Figure 11).
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix
| Index | Time | Type | XJ | TP | NW | NE | NC | SW | SC |
|---|---|---|---|---|---|---|---|---|---|
| RB (%) | 4 Years | GSMaP_MVK | 108.20 | 67.70 | 56.89 | 9.36 | 2.47 | −30.87 | −29.03 |
| GSMaP_Gauge | 5.29 | 27.07 | 40.91 | 26.21 | 29.15 | 7.58 | 5.26 | ||
| CMORPH | 3.15 | −4.26 | 13.34 | −13.69 | −6.37 | −35.64 | −33.81 | ||
| CMORPH_CRT | −12.85 | −2.62 | 6.47 | 2.77 | 8.83 | −8.13 | −3.07 | ||
| PERSIANN | 96.01 | 68.72 | 25.03 | 0.48 | −11.59 | −47.17 | −43.71 | ||
| PERSIANN_CDR | −13.16 | 19.90 | 3.39 | 16.73 | 8.93 | −6.32 | 1.73 | ||
| Spring | GSMaP_MVK | 101.82 | 169.02 | 106.82 | 20.28 | 21.22 | −29.12 | −33.00 | |
| GSMaP_Gauge | −1.24 | 53.84 | 59.97 | 23.28 | 37.16 | 7.82 | 3.41 | ||
| CMORPH | −13.32 | 24.99 | 35.17 | −27.82 | 0.38 | −26.75 | −36.12 | ||
| CMORPH_CRT | −10.75 | 0.29 | 9.15 | −2.24 | 12.37 | −4.52 | −1.79 | ||
| PERSIANN | 83.05 | 205.60 | 79.08 | −6.55 | 26.49 | −37.56 | −46.57 | ||
| PERSIANN_CDR | −22.11 | 30.12 | 7.29 | 22.10 | 10.94 | −6.69 | 1.46 | ||
| Summer | GSMaP_MVK | 77.97 | −1.26 | 25.44 | 1.02 | 0.23 | −22.21 | −11.79 | |
| GSMaP_Gauge | 51.72 | 30.71 | 50.47 | 34.75 | 37.02 | 18.94 | 24.32 | ||
| CMORPH | 40.65 | −34.16 | 16.06 | −5.76 | −0.27 | −34.92 | −19.81 | ||
| CMORPH_CRT | −14.13 | −5.71 | 7.96 | 4.33 | 4.77 | −7.88 | 1.08 | ||
| PERSIANN | 27.40 | −0.85 | −23.24 | −25.13 | −31.06 | −42.94 | −28.08 | ||
| PERSIANN_CDR | −4.39 | 21.35 | 3.53 | 10.33 | 5.77 | −2.27 | 6.61 | ||
| Autumn | GSMaP_MVK | 74.95 | 58.70 | 27.50 | 36.27 | −16.21 | −49.94 | −40.69 | |
| GSMaP_Gauge | −28.51 | 0.52 | 18.95 | 20.97 | 14.57 | −6.35 | 1.42 | ||
| CMORPH | −15.13 | 20.12 | −10.29 | −5.73 | −27.83 | −48.42 | −41.95 | ||
| CMORPH_CRT | −14.31 | 0.49 | 5.52 | 22.71 | 6.08 | −13.90 | −4.87 | ||
| PERSIANN | 12.16 | −1.91 | 0.82 | 32.39 | −19.07 | −70.86 | −59.89 | ||
| PERSIANN_CDR | −22.92 | 5.25 | 4.29 | 30.01 | 7.99 | −15.47 | −3.85 | ||
| Winter | GSMaP_MVK | 315.48 | 1228.02 | 552.85 | −20.10 | 20.21 | −49.54 | −72.91 | |
| GSMaP_Gauge | −66.16 | 2.01 | −66.26 | −68.28 | −51.06 | −69.72 | −65.58 | ||
| CMORPH | −50.69 | 332.97 | 22.97 | −87.49 | −32.69 | −20.63 | −74.32 | ||
| CMORPH_CRT | −9.47 | 27.54 | −26.91 | −66.78 | 55.74 | 1.88 | −22.07 | ||
| PERSIANN | 583.45 | 1582.36 | 753.58 | 308.40 | 99.73 | −21.53 | −76.66 | ||
| PERSIANN_CDR | −0.36 | 51.13 | −27.01 | 36.68 | 44.09 | −7.17 | −9.60 | ||
| RMSE (mm/day) | 4 Years | GSMaP_MVK | 0.95 | 1.17 | 0.59 | 0.39 | 0.30 | 1.58 | 1.28 |
| GSMaP_Gauge | 0.26 | 0.49 | 0.37 | 0.42 | 0.58 | 0.79 | 0.55 | ||
| CMORPH | 0.48 | 0.61 | 0.36 | 0.46 | 0.35 | 1.63 | 1.47 | ||
| CMORPH_CRT | 0.48 | 0.57 | 0.22 | 0.34 | 0.33 | 1.17 | 0.60 | ||
| PERSIANN | 0.57 | 0.93 | 0.38 | 0.43 | 0.38 | 1.99 | 1.87 | ||
| PERSIANN_CDR | 0.34 | 0.68 | 0.14 | 0.32 | 0.28 | 1.22 | 0.57 | ||
| Spring | GSMaP_MVK | 0.87 | 1.69 | 0.69 | 0.43 | 0.43 | 1.61 | 1.98 | |
| GSMaP_Gauge | 0.37 | 0.56 | 0.39 | 0.35 | 0.59 | 1.05 | 0.63 | ||
| CMORPH | 0.65 | 0.61 | 0.49 | 0.62 | 0.42 | 1.51 | 2.08 | ||
| CMORPH_CRT | 0.72 | 0.52 | 0.28 | 0.53 | 0.39 | 1.26 | 0.89 | ||
| PERSIANN | 0.70 | 1.64 | 0.69 | 0.30 | 0.65 | 1.86 | 2.67 | ||
| PERSIANN_CDR | 0.46 | 0.53 | 0.21 | 0.35 | 0.29 | 1.40 | 0.81 | ||
| Summer | GSMaP_MVK | 0.73 | 1.12 | 0.77 | 0.78 | 0.72 | 3.03 | 1.39 | |
| GSMaP_Gauge | 0.59 | 1.24 | 1.03 | 1.28 | 1.71 | 1.92 | 1.95 | ||
| CMORPH | 0.81 | 1.51 | 0.74 | 0.91 | 0.85 | 3.33 | 1.82 | ||
| CMORPH_CRT | 0.62 | 1.43 | 0.48 | 0.65 | 0.75 | 2.31 | 1.31 | ||
| PERSIANN | 0.51 | 1.20 | 0.84 | 1.27 | 1.55 | 4.02 | 2.45 | ||
| PERSIANN_CDR | 0.49 | 1.68 | 0.34 | 0.62 | 0.64 | 2.54 | 1.27 | ||
| Autumn | GSMaP_MVK | 1.27 | 1.32 | 0.49 | 0.42 | 0.35 | 1.74 | 1.19 | |
| GSMaP_Gauge | 0.41 | 0.51 | 0.20 | 0.25 | 0.27 | 0.71 | 0.57 | ||
| CMORPH | 0.67 | 0.89 | 0.53 | 0.36 | 0.47 | 1.73 | 1.26 | ||
| CMORPH_CRT | 0.63 | 0.67 | 0.33 | 0.40 | 0.34 | 1.15 | 0.59 | ||
| PERSIANN | 0.43 | 0.58 | 0.46 | 0.45 | 0.44 | 2.25 | 1.68 | ||
| PERSIANN_CDR | 0.45 | 0.66 | 0.20 | 0.31 | 0.27 | 1.11 | 0.59 | ||
| Winter | GSMaP_MVK | 1.71 | 2.02 | 1.01 | 0.35 | 0.37 | 0.44 | 1.31 | |
| GSMaP_Gauge | 0.29 | 0.09 | 0.09 | 0.19 | 0.28 | 0.41 | 1.16 | ||
| CMORPH | 0.37 | 0.66 | 0.22 | 0.27 | 0.34 | 0.76 | 1.32 | ||
| CMORPH_CRT | 0.44 | 0.21 | 0.13 | 0.29 | 0.37 | 0.76 | 0.65 | ||
| PERSIANN | 1.29 | 1.84 | 0.99 | 0.87 | 0.49 | 0.44 | 1.45 | ||
| PERSIANN_CDR | 0.24 | 0.17 | 0.07 | 0.17 | 0.21 | 0.26 | 0.44 | ||
| CC | 4 Years | GSMaP_MVK | 0.37 | 0.43 | 0.60 | 0.56 | 0.85 | 0.23 | 0.74 |
| GSMaP_Gauge | 0.84 | 0.92 | 0.96 | 0.89 | 0.94 | 0.85 | 0.82 | ||
| CMORPH | 0.39 | 0.67 | 0.69 | 0.38 | 0.79 | 0.35 | 0.69 | ||
| CMORPH_CRT | 0.37 | 0.72 | 0.88 | 0.71 | 0.89 | 0.47 | 0.76 | ||
| PERSIANN | 0.68 | 0.70 | 0.73 | 0.29 | 0.81 | −0.01 | 0.52 | ||
| PERSIANN_CDR | 0.70 | 0.75 | 0.95 | 0.88 | 0.92 | 0.37 | 0.78 | ||
| Spring | GSMaP_MVK | 0.54 | 0.30 | 0.70 | 0.57 | 0.90 | 0.42 | 0.70 | |
| GSMaP_Gauge | 0.79 | 0.87 | 0.94 | 0.84 | 0.95 | 0.76 | 0.94 | ||
| CMORPH | 0.20 | 0.56 | 0.43 | 0.13 | 0.76 | 0.51 | 0.74 | ||
| CMORPH_CRT | 0.23 | 0.71 | 0.72 | 0.36 | 0.89 | 0.60 | 0.85 | ||
| PERSIANN | 0.25 | 0.49 | 0.61 | 0.64 | 0.66 | 0.21 | 0.42 | ||
| PERSIANN_CDR | 0.62 | 0.79 | 0.87 | 0.82 | 0.93 | 0.46 | 0.88 | ||
| Summer | GSMaP_MVK | 0.80 | 0.82 | 0.81 | 0.65 | 0.78 | 0.30 | 0.75 | |
| GSMaP_Gauge | 0.80 | 0.92 | 0.94 | 0.88 | 0.91 | 0.85 | 0.82 | ||
| CMORPH | 0.55 | 0.70 | 0.80 | 0.51 | 0.70 | 0.44 | 0.67 | ||
| CMORPH_CRT | 0.55 | 0.69 | 0.90 | 0.81 | 0.82 | 0.56 | 0.67 | ||
| PERSIANN | 0.73 | 0.77 | 0.73 | 0.47 | 0.76 | 0.10 | 0.56 | ||
| PERSIANN_CDR | 0.73 | 0.74 | 0.95 | 0.87 | 0.88 | 0.36 | 0.73 | ||
| Autumn | GSMaP_MVK | 0.23 | 0.21 | 0.48 | 0.62 | 0.53 | 0.33 | 0.90 | |
| GSMaP_Gauge | 0.80 | 0.73 | 0.96 | 0.88 | 0.81 | 0.84 | 0.94 | ||
| CMORPH | 0.15 | 0.39 | 0.36 | 0.40 | 0.50 | 0.28 | 0.88 | ||
| CMORPH_CRT | 0.26 | 0.54 | 0.77 | 0.64 | 0.59 | 0.36 | 0.90 | ||
| PERSIANN | 0.63 | 0.55 | 0.44 | 0.34 | 0.16 | 0.13 | 0.86 | ||
| PERSIANN_CDR | 0.62 | 0.57 | 0.91 | 0.87 | 0.68 | 0.43 | 0.90 | ||
| Winter | GSMaP_MVK | −0.13 | −0.06 | −0.31 | −0.28 | 0.10 | 0.14 | 0.54 | |
| GSMaP_Gauge | 0.50 | 0.49 | 0.53 | 0.67 | 0.92 | 0.45 | 0.81 | ||
| CMORPH | −0.26 | 0.04 | −0.06 | −0.29 | 0.33 | 0.08 | 0.59 | ||
| CMORPH_CRT | −0.19 | 0.13 | 0.21 | −0.23 | 0.66 | 0.13 | 0.69 | ||
| PERSIANN | 0.53 | 0.04 | 0.38 | 0.06 | 0.30 | −0.16 | −0.20 | ||
| PERSIANN_CDR | 0.56 | 0.40 | 0.65 | 0.76 | 0.94 | 0.34 | 0.80 |
References
- Behrangi, A.; Khakbaz, B.; Jaw, T.C.; AghaKouchak, A.; Hsu, K.L.; Sorooshian, S. Hydrologic evaluation of satellite precipitation products over a mid-size basin. J. Hydrol. 2011, 397, 225–237. [Google Scholar] [CrossRef]
- Zawadzki, I.; Desrochers, C.; Torlaschi, E.; Bellon, A. A radar-raingauge comparison. In Proceedings of the 23rd Conference on Radar Meteorology, Snowmass, CO, USA, 22–26 September 1986; American Meteorological Society: Snowmass, CO, USA; pp. 121–124.
- Hsu, K.L.; Gao, X.G.; Sorooshian, S.; Gupta, H.V. Precipitation estimation from remotely sensed information using artificial neural networks. J. Appl. Meteorol. 1997, 36, 1176–1190. [Google Scholar] [CrossRef]
- Sorooshian, S.; Hsu, K.-L.; Gao, X.; Gupta, H.V.; Imam, B.; Braithwaite, D. Evaluation of persiann system satellite-based estimates of tropical rainfall. Bull. Am. Meteorol. Soc. 2000, 81, 2035–2046. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P.P. Cmorph: A method that produces global precipitation estimates from passive microwave and infrared data at high spatial and temporal resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Ushio, T.; Sasashige, K.; Kubota, T.; Shige, S.; Okamoto, K.; Aonashi, K.; Inoue, T.; Takahashi, N.; Iguchi, T.; Kachi, M.; et al. A kalman filter approach to the global satellite mapping of precipitation (gsmap) from combined passive microwave and infrared radiometric data. J. Meteorol. Soc. Jpn. 2009, 87, 137–151. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Bolvin, D.T.; Gu, G.J.; Nelkin, E.J.; Bowman, K.P.; Hong, Y.; Stocker, E.F.; Wolff, D.B. The trmm multisatellite precipitation analysis (tmpa): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Casella, D.; Dietrich, S.; di Paola, F.; Formenton, M.; Mugnai, A.; Porcù, F.; Sanò, P. Pm-gcd—A combined ir-mw satellite technique for frequent retrieval of heavy precipitation. Nat. Hazards Earth Syst. Sci. 2012, 12, 231–240. [Google Scholar] [CrossRef]
- Milewski, A.; Elkadiri, R.; Durham, M. Assessment and comparison of tmpa satellite precipitation products in varying climatic and topographic regimes in morocco. Remote Sens. 2015, 7, 5697–5717. [Google Scholar] [CrossRef]
- Casella, D.; Panegrossi, G.; Sano, P.; Dietrich, S.; Mugnai, A.; Smith, E.; Tripoli, G.J.; Formenton, M.; di Paola, F.; Leung, W.-Y.H. Transitioning from crd to cdrd in bayesian retrieval of rainfall from satellite passive microwave measurements: Part 2. Overcoming database profile selection ambiguity by consideration of meteorological control on microphysics. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4650–4671. [Google Scholar] [CrossRef]
- Di Paola, F.; Casella, D.; Dietrich, S.; Mugnai, A.; Ricciardelli, E.; Romano, F.; Sanò, P. Combined mw-ir precipitation evolving technique (pet) of convective rain fields. Nat. Hazards Earth Syst. Sci. 2012, 12, 3557–3570. [Google Scholar] [CrossRef]
- Mugnai, A.; Smith, E.A.; Tripoli, G.J.; Bizzarri, B.; Casella, D.; Dietrich, S.; di Paola, F.; Panegrossi, G.; Sanò, P. Cdrd and pnpr satellite passive microwave precipitation retrieval algorithms: Eurotrmm/eurainsat origins and h-saf operations. Nat. Hazards Earth Syst. Sci. 2013, 13, 887–912. [Google Scholar] [CrossRef]
- Ricciardelli, E.; Cimini, D.; di Paola, F.; Romano, F.; Viggiano, M. A statistical approach for rain intensity differentiation using meteosat second generation–spinning enhanced visible and infrared imager observations. Hydrol. Earth Syst. Sci. 2014, 18, 2559–2576. [Google Scholar] [CrossRef]
- Chen, S.; Liu, H.; You, Y.; Mullens, E.; Hu, J.; Yuan, Y.; Huang, M.; He, L.; Luo, Y.; Zeng, X.; et al. Evaluation of high-resolution precipitation estimates from satellites during july 2012 beijing flood event using dense rain gauge observations. PLoS ONE 2014, 9, e89681. [Google Scholar] [CrossRef] [PubMed]
- Yong, B.; Chen, B.; Gourley, J.J.; Ren, L.; Hong, Y.; Chen, X.; Wang, W.; Chen, S.; Gong, L. Intercomparison of the version-6 and version-7 tmpa precipitation products over high and low latitudes basins with independent gauge networks: Is the newer version better in both real-time and post-real-time analysis for water resources and hydrologic extremes? J. Hydrol. 2014, 508, 77–87. [Google Scholar]
- Xue, X.; Hong, Y.; Limaye, A.S.; Gourley, J.J.; Huffman, G.J.; Khan, S.I.; Dorji, C.; Chen, S. Statistical and hydrological evaluation of trmm-based multi-satellite precipitation analysis over the wangchu basin of bhutan: Are the latest satellite precipitation products 3b42v7 ready for use in ungauged basins? J. Hydrol. 2013, 499, 91–99. [Google Scholar] [CrossRef]
- Stisen, S.; Sandholt, I. Evaluation of remote-sensing-based rainfall products through predictive capability in hydrological runoff modelling. Hydrol. Process. 2010, 24, 879–891. [Google Scholar] [CrossRef]
- Puca, S.; Porcu, F.; Rinollo, A.; Vulpiani, G.; Baguis, P.; Balabanova, S.; Campione, E.; Ertürk, A.; Gabellani, S.; Iwanski, R. The validation service of the hydrological saf geostationary and polar satellite precipitation products. Nat. Hazards Earth Syst. Sci. 2014, 14, 871–889. [Google Scholar] [CrossRef]
- Di Paola, F.; Ricciardelli, E.; Cimini, D.; Romano, F.; Viggiano, M.; Cuomo, V. Analysis of catania flash flood case study by using combined microwave and infrared technique. J. Hydrometeorol. 2014, 15, 1989–1998. [Google Scholar] [CrossRef]
- Dietrich, S.; Casella, D.; di Paola, F.; Formenton, M.; Mugnai, A.; Sanò, P. Lightning-based propagation of convective rain fields. Nat. Hazards Earth Syst. Sci. 2011, 11, 1571–1581. [Google Scholar] [CrossRef]
- Su, F.G.; Hong, Y.; Lettenmaier, D.P. Evaluation of trmm multisatellite precipitation analysis (tmpa) and its utility in hydrologic prediction in the la plata basin. J. Hydrometeorol. 2008, 9, 622–640. [Google Scholar] [CrossRef]
- Turk, F.J.; Arkin, P.; Ebert, E.E.; Sapiano, M.R.P. Evaluating high-resolution precipitation products. Bull. Am. Meteorol. Soc. 2008, 89, 1911–1916. [Google Scholar] [CrossRef]
- Hong, Y.; Hsu, K.L.; Moradkhani, H.; Sorooshian, S. Uncertainty quantification of satellite precipitation estimation and monte carlo assessment of the error propagation into hydrologic response. Water Resour. Res. 2006, 42, W08421. [Google Scholar] [CrossRef]
- Maggioni, V.; Reichle, R.H.; Anagnostou, E.N. The efficiency of assimilating satellite soil moisture retrievals in a land data assimilation system using different rainfall error models. J. Hydrometeorol. 2012, 14, 368–374. [Google Scholar] [CrossRef]
- Stephens, G.L.; Kummerow, C.D. The remote sensing of clouds and precipitation from space: A review. J. Atmos. Sci. 2007, 64, 3742–3765. [Google Scholar] [CrossRef]
- Falck, A.S.; Maggioni, V.; Tomasella, J.; Vila, D.A.; Diniz, F.L.R. Propagation of satellite precipitation uncertainties through a distributed hydrologic model: A case study in the tocantins-araguaia basin in brazil. J. Hydrol. 2015, 527, 943–957. [Google Scholar] [CrossRef]
- Maggioni, V.; Vergara, H.J.; Anagnostou, E.N.; Gourley, J.J.; Hong, Y.; Stampoulis, D. Investigating the applicability of error correction ensembles of satellite rainfall products in river flow simulations. J. Hydrometeorol. 2013, 14, 1194–1211. [Google Scholar] [CrossRef]
- Hong, Y.; Adler, R.F. Towards an early-warning system for global landslides triggered by rainfall and earthquake. Int. J. Remote Sens. 2007, 28, 3713–3719. [Google Scholar] [CrossRef]
- Sapiano, M.R.P.; Arkin, P.A. An intercomparison and validation of high-resolution satellite precipitation estimates with 3-hourly gauge data. J. Hydrometeorol. 2009, 10, 149–166. [Google Scholar] [CrossRef]
- Wei, C.C.; Roan, J. Retrievals for the rainfall rate over land using special sensor microwave imager data during tropical cyclones: Comparisons of scattering index, regression, and support vector regression. J. Hydrometeorol. 2012, 13, 1567–1578. [Google Scholar] [CrossRef]
- Habib, E.; Haile, A.T.; Tian, Y.; Joyce, R.J. Evaluation of the high-resolution cmorph satellite rainfall product using dense rain gauge observations and radar-based estimates. J. Hydrometeorol. 2012, 13, 1784–1798. [Google Scholar] [CrossRef]
- Bitew, M.M.; Gebremichael, M. Evaluation through independent measurements: Complex terrain and humid tropical region in ethiopia. In Satellite Rainfall Applications for Surface Hydrology; Springer Netherlands: Berlin, Germany, 2010; pp. 205–214. [Google Scholar]
- Romilly, T.G.; Gebremichael, M. Evaluation of satellite rainfall estimates over ethiopian river basins. Hydrol. Earth Syst. Sci. 2011, 15, 1505–1514. [Google Scholar] [CrossRef]
- Hsu, K.-L.; Sorooshian, S. Satellite-based precipitation measurement using persiann system. In Hydrological Modelling and the Water Cycle; Sorooshian, S., Hsu, K.-L., Coppola, E., Tomassetti, B., Verdecchia, M., Visconti, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 63, pp. 27–48. [Google Scholar]
- Ebert, E.E.; Janowiak, J.E.; Kidd, C. Comparison of near-real-time precipitation estimates from satellite observations and numerical models. Bull. Am. Meteorol. Soc. 2007, 88, 47–64. [Google Scholar] [CrossRef]
- Hirpa, F.A.; Gebremichael, M.; Hopson, T. Evaluation of high-resolution satellite precipitation products over very complex terrain in ethiopia. J. Appl. Meteorol. Climatol. 2010, 49, 1044–1051. [Google Scholar] [CrossRef]
- Yamamoto, M.; Ueno, K.I.; Nakamura, K. Comparison of satellite precipitation products with rain gauge data for the khumb region, nepal himalayas. J. Meteorol. Soc. Jpn. 2011, 89, 597–610. [Google Scholar] [CrossRef]
- Kubota, T.; Ushio, T.; Shige, S.; Kida, S.; Kachi, M.; Okamoto, K. Verification of high-resolution satellite-based rainfall estimates around japan using a gauge-calibrated ground-radar dataset. J. Meteorol. Soc. Jpn. 2009, 87A, 203–222. [Google Scholar] [CrossRef]
- Ngo-Duc, T.; Matsumoto, J.; Kamimera, H.; Bui, H.-H. Monthly adjustment of global satellite mapping of precipitation (gsmap) data over the vugia–thubon river basin in central vietnam using an artificial neural network. Hydrol. Res. Lett. 2013, 7, 85–90. [Google Scholar] [CrossRef]
- Shrestha, M.; Takara, K.; Kubota, T.; Bajracharya, S. Verification of gsmap rainfall estimates over the central himalayas. J. Jpn. Soc. Civ. Eng. 2011, 67, I_37–I_42. [Google Scholar] [CrossRef]
- Taniguchi, A.; Shige, S.; Yamamoto, M.K.; Mega, T.; Kida, S.; Kubota, T.; Kachi, M.; Ushio, T.; Aonashi, K. Improvement of high-resolution satellite rainfall product for typhoon morakot (2009) over taiwan. J. Hydrometeorol. 2013, 14, 1859–1871. [Google Scholar] [CrossRef]
- Tian, Y.D.; Peters-Lidard, C.D.; Adler, R.F.; Kubota, T.; Ushio, T. Evaluation of gsmap precipitation estimates over the contiguous united states. J. Hydrometeorol. 2010, 11, 566–574. [Google Scholar] [CrossRef]
- Veerakachen, W.; Raksapatcharawong, M.; Seto, S. Performance evaluation of global satellite mapping of precipitation (gsmap) products over the chaophraya river basin, thailand. Hydrol. Res. Lett. 2014, 8, 39–44. [Google Scholar] [CrossRef]
- Mega, T.; Ushio, T.; Kubota, T.; Kachi, M.; Aonashi, K.; Shige, S. Gauge adjusted global satellite mapping of precipitation (gsmap_gauge). In Proceedings of the 2014 XXXIth URSI General Assembly and Scientific Symposium (URSI GASS), Beijing, China, 16–23 August 2014; pp. 1–4.
- Shen, Y.; Xiong, A.Y.; Wang, Y.; Xie, P.P. Performance of high-resolution satellite precipitation products over china. J. Geophys. Res. 2010, 115, D02114. [Google Scholar] [CrossRef]
- Zhou, T.J.; Yu, R.C.; Chen, H.M.; Dai, A.; Pan, Y. Summer precipitation frequency, intensity, and diurnal cycle over china: A comparison of satellite data with rain gauge observations. J. Clim. 2008, 21, 3997–4010. [Google Scholar] [CrossRef]
- Gao, Y.C.; Liu, M.F. Evaluation of high-resolution satellite precipitation products using rain gauge observations over the tibetan plateau. Hydrol. Earth Syst. Sci. 2013, 17, 837–849. [Google Scholar] [CrossRef]
- Li, Z.; Yang, D.W.; Hong, Y. Multi-scale evaluation of high-resolution multi-sensor blended global precipitation products over the yangtze river. J. Hydrol. 2013, 500, 157–169. [Google Scholar] [CrossRef]
- Yin, Z.Y.; Zhang, X.Q.; Liu, X.D.; Colella, M.; Chen, X.L. An assessment of the biases of satellite rainfall estimates over the tibetan plateau and correction methods based on topographic analysis. J. Hydrometeorol. 2008, 9, 301–326. [Google Scholar] [CrossRef]
- Guo, H.; Chen, S.; Bao, A.M.; Hu, J.J.; Gebregiorgis, A.S.; Xue, X.W.; Zhang, X.H. Inter-comparison of high-resolution satellite precipitation products over central asia. Remote Sens. 2015, 7, 7181–7211. [Google Scholar] [CrossRef]
- Tang, Z.Y.; Wang, Z.H.; Zheng, C.Y.; Fang, J.Y. Biodiversity in china’s mountains. Front. Ecol. Environ. 2006, 4, 347–352. [Google Scholar] [CrossRef]
- Qian, W.; Lin, X. Regional trends in recent precipitation indices in china. Meteorol. Atmos. Phys. 2005, 90, 193–207. [Google Scholar] [CrossRef]
- Chen, S.; Hong, Y.; Cao, Q.; Gourley, J.J.; Kirstetter, P.E.; Yong, B.; Tian, Y.D.; Zhang, Z.X.; Shen, Y.; Hu, J.J.; et al. Similarity and difference of the two successive v6 and v7 trmm multisatellite precipitation analysis performance over china. J. Geophys. Res. 2013, 118, 13060–13074. [Google Scholar] [CrossRef]
- Bothe, O.; Fraedrich, K.; Zhu, X.H. Precipitation climate of central asia and the large-scale atmospheric circulation. Theor. Appl. Climatol. 2012, 108, 345–354. [Google Scholar] [CrossRef]
- Carr, L.E.; Elsberry, R.L. Monsoonal interactions leading to sudden tropical cyclone track changes. Mon. Weather Rev. 1995, 123, 265–289. [Google Scholar] [CrossRef]
- Aonashi, K.; Awaka, J.; Hirose, M.; Kozu, T.; Kubota, T.; Liu, G.S.; Shige, S.; Kida, S.; Seto, S.; Takahashi, N.; et al. Gsmap passive microwave precipitation retrieval algorithm: Algorithm description and validation. J. Meteorol. Soc. Jpn. 2009, 87A, 119–136. [Google Scholar] [CrossRef]
- Kubota, T.; Shige, S.; Hashizurne, H.; Aonashi, K.; Takahashi, N.; Seto, S.; Hirose, M.; Takayabu, Y.N.; Ushio, T.; Nakagawa, K.; et al. Global precipitation map using satellite-borne microwave radiometers by the gsmap project: Production and validation. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2259–2275. [Google Scholar] [CrossRef]
- Okamoto, K.; Ushio, T.; Iguchi, T.; Takahashi, N.; Iwanami, K. The global satellite mapping of precipitation (gsmap) project. In Proceedings of the 2005 IEEE International Geoscience and Remote Sensing Symposium, IGARSS ’05, Seoul, Korea, 25–29 July 2005; pp. 3414–3416.
- Shige, S.; Yamamoto, T.; Tsukiyama, T.; Kida, S.; Ashiwake, H.; Kubota, T.; Seto, S.; Aonashi, K.; Okamoto, K. The gsmap precipitation retrieval algorithm for microwave sounders-part i: Over-ocean algorithm. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3084–3097. [Google Scholar] [CrossRef]
- Seto, S.; Takahashi, N.; Iguchi, T. Rain/no-rain classification methods for microwave radiometer observations over land using statistical information for brightness temperatures under no-rain conditions. J. Appl. Meteorol. 2005, 44, 1243–1259. [Google Scholar] [CrossRef]
- Takahashi, N.; Awaka, J. Introduction of a melting layer model to a rain retrieval algorithm for microwave radiometers. In Proceedings of the 2005 IEEE International Geoscience and Remote Sensing Symposium, IGARSS ’05, Seoul, Korea, 25–29 July 2005; pp. 3404–3409.
- Xie, P.P.; Yatagai, A.; Chen, M.Y.; Hayasaka, T.; Fukushima, Y.; Liu, C.M.; Yang, S. A gauge-based analysis of daily precipitation over east asia. J. Hydrometeorol. 2007, 8, 607–626. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Xie, P. Integrated Multi-Satellite Retrievals for GPM (IMERG) Technical Documentation. Available online: http://pmm.nasa.gov/sites/default/files/document_files/IMERG_ATBD_V4.4.pdf (accessed on 4 February 2015).
- Ashouri, H.; Hsu, K.-L.; Sorooshian, S.; Braithwaite, D.K.; Knapp, K.R.; Cecil, L.D.; Nelson, B.R.; Prat, O.P. Persiann-cdr: Daily precipitation climate data record from multisatellite observations for hydrological and climate studies. Bull. Am. Meteorol. Soc. 2015, 96, 69–83. [Google Scholar] [CrossRef]
- Xie, P.; Yoo, S.-H.; Joyce, R.; Yarosh, Y. Bias-Corrected Cmorph: A 13-Year Analysis of High-Resolution Global Precipitation. Available online: http://ftp.cpc.ncep.noaa.gov/precip/CMORPH_V1.0/REF/EGU_1104_Xie_bias-CMORPH.pdf (accessed on 28 October 2014).
- Chen, M.Y.; Shi, W.; Xie, P.P.; Silva, V.B.S.; Kousky, V.E.; Higgins, R.W.; Janowiak, J.E. Assessing objective techniques for gauge-based analyses of global daily precipitation. J. Geophys. Res. 2008, 113, D04110. [Google Scholar] [CrossRef]
- Shen, Y.; Feng, M.; Zhang, H.; Gao, F. Interpolation methods of china daily precipitation data. J. Appl. Meteorol. Sci. 2010, 21, 279–286. [Google Scholar]
- China Meteorological Data Sharing Service System. Available online: http://cdc.nmic.cn/sksj.do?method=ssrjscp (accessed on 10 January 2015).
- Xie, P.P. Personal Communication; NOAA Federal: Washington, DC, USA, 2014. [Google Scholar]
- Chen, S.; Hong, Y.; Cao, Q.; Kirstetter, P.-E.; Gourley, J.J.; Qi, Y.; Zhang, J.; Howard, K.; Hu, J.; Wang, J. Performance evaluation of radar and satellite rainfalls for typhoon morakot over taiwan: Are remote-sensing products ready for gauge denial scenario of extreme events? J. Hydrol. 2013, 506, 4–13. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Story, G.J.; Forecaster, H.; Center, W.G.R.F. Determining WSR-88D Precipitation Algorithm Performance Using the Stage III Precipitation Processing System; West Gulf River Forecast Center: Fort Worth, TX, USA, 2001. [Google Scholar]
- Surussavadee, C.; Staelin, D.H. Correcting microwave precipitation retrievals for near-surface evaporation. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Honolulu, HI, USA, 25–30 July 2010; pp. 1312–1315.
- Kamal-Heikman, S.; Derry, L.A.; Stedinger, J.R.; Duncan, C.C. A simple predictive tool for lower brahmaputra river basin monsoon flooding. Earth Interact. 2007, 11, 1–11. [Google Scholar] [CrossRef]
- Grody, N.C.; Weng, F. Microwave emission and scattering from deserts: Theory compared with satellite measurements. IEEE Trans. Geosci. Remote Sens. 2008, 46, 361–375. [Google Scholar] [CrossRef]
- Tian, Y.; Peters-Lidard, C.D.; Choudhury, B.J.; Garcia, M. Multitemporal analysis of trmm-based satellite precipitation products for land data assimilation applications. J. Hydrometeorol. 2007, 8, 1165–1183. [Google Scholar] [CrossRef]
- Fu, Y.F.; Liu, G.S. Possible misidentification of rain type by trmm pr over tibetan plateau. J. Appl. Meteorol. Climatol. 2007, 46, 667–672. [Google Scholar] [CrossRef]
- Liu, M.; Xu, X.; Sun, A.Y.; Wang, K.; Yue, Y.; Tong, X.; Liu, W. Evaluation of high-resolution satellite rainfall products using rain gauge data over complex terrain in southwest china. Theor. Appl. Climatol. 2014, 1–17. [Google Scholar] [CrossRef]
- Negri, A.J.; Adler, R.F. An intercomparlson of three satellite infrared rainfall techniques over Japan and surrounding waters. J. Appl. Meteorol. 1993, 32, 357–373. [Google Scholar] [CrossRef]
- Tuttle, J.D.; Carbone, R.E.; Arkin, P.A. Comparison of ground-based radar and geosynchronous satellite climatologies of warm-season precipitation over the united states. J. Appl. Meteorol. Climatol. 2008, 47, 3264–3270. [Google Scholar] [CrossRef]
- Ferraro, R.R.; Smith, E.A.; Berg, W.; Huffman, G.J. A screening methodology for passive microwave precipitation retrieval algorithms. J. Atmos. Sci. 1998, 55, 1583–1600. [Google Scholar] [CrossRef]
- Grody, N.C. Classification of snow cover and precipitation using the special sensor microwave imager. J. Geophys. Res. 1991, 96, 7423–7435. [Google Scholar] [CrossRef]
- Chen, S.; Hong, Y.; Cao, Q.; Tian, Y.D.; Hu, J.J.; Zhang, X.H.; Li, W.Y.; Carr, N.; Shen, X.Y.; Qiao, L. Intercomparison of precipitation estimates from wsr-88d radar and trmm measurement over continental united states. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4444–4456. [Google Scholar] [CrossRef]
- Kidd, C.; Bauer, P.; Turk, J.; Huffman, G.J.; Joyce, R.; Hsu, K.L.; Braithwaite, D. Intercomparison of high-resolution precipitation products over northwest europe. J. Hydrometeorol. 2012, 13, 67–83. [Google Scholar] [CrossRef]
- Sohn, B.J.; Han, H.-J.; Seo, E.-K. Validation of satellite-based high-resolution rainfall products over the korean peninsula using data from a dense rain gauge network. J. Appl. Meteorol. Climatol. 2010, 49, 701–714. [Google Scholar] [CrossRef]
- Tesfagiorgis, K.; Mahani, S.E.; Khanbilvardi, R. Bias correction of satellite rainfall estimation using a radar-gauge product. Hydrol. Earth Syst. Sci. 2010, 7, 8913–8945. [Google Scholar] [CrossRef]
- Andermann, C.; Longuevergne, L.; Bonnet, S.; Crave, A.; Davy, P.; Gloaguen, R. Impact of transient groundwater storage on the discharge of himalayan rivers. Nat. Geosci. 2012, 5, 127–132. [Google Scholar] [CrossRef]
- Shige, S.; Kida, S.; Ashiwake, H.; Kubota, T.; Aonashi, K. Improvement of tmi rain retrievals in mountainous areas. J. Appl. Meteorol. Climatol. 2013, 52, 242–254. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, H.; Chen, S.; Bao, A.; Hu, J.; Yang, B.; Stepanian, P.M. Comprehensive Evaluation of High-Resolution Satellite-Based Precipitation Products over China. Atmosphere 2016, 7, 6. https://doi.org/10.3390/atmos7010006
Guo H, Chen S, Bao A, Hu J, Yang B, Stepanian PM. Comprehensive Evaluation of High-Resolution Satellite-Based Precipitation Products over China. Atmosphere. 2016; 7(1):6. https://doi.org/10.3390/atmos7010006
Chicago/Turabian StyleGuo, Hao, Sheng Chen, Anming Bao, Junjun Hu, Banghui Yang, and Phillip M. Stepanian. 2016. "Comprehensive Evaluation of High-Resolution Satellite-Based Precipitation Products over China" Atmosphere 7, no. 1: 6. https://doi.org/10.3390/atmos7010006
APA StyleGuo, H., Chen, S., Bao, A., Hu, J., Yang, B., & Stepanian, P. M. (2016). Comprehensive Evaluation of High-Resolution Satellite-Based Precipitation Products over China. Atmosphere, 7(1), 6. https://doi.org/10.3390/atmos7010006