Precipitation Sensitivity to the Mean Radius of Drop Spectra: Comparison of Single- and Double-Moment Bulk Microphysical Schemes

Abstract

In this study, two bulk microphysical schemes were compared across mean radius values of the entire drop spectra. A cloud-resolving mesoscale model was used to analyze surface precipitation characteristics. The model included the following microphysical categories: water vapour, cloud droplets, raindrops, ice crystals, snow, graupel, frozen raindrops and hail. Two bulk schemes were used: a single-moment scheme in which the mean radius was specified as a parameter and a double-moment scheme in which the mean radius of drops was calculated diagnostically with a fixed value for the cloud droplet number concentration. Experiments were conducted out for three values of the mean radius (in the single-moment scheme) and two cloud droplet number concentrations (in the double-moment scheme). There were large differences in the surface precipitation for the two schemes, the simulated precipitation generated by the double-moment scheme had a higher sensitivity. The single-moment scheme generated an unrealistic collection rate of cloud droplets by raindrops and hail as well as unrealistic evaporation of rain and melting of solid hydrometeors; these processes led to inaccurate timing and amounts of surface precipitation.

1. Introduction

Storm clouds typically generate hazardous weather phenomena, such as surface hail, intense rainfall, strong winds, lightning, downbursts and tornadoes. These events can cause sudden floods and hail damage resulting in agricultural and property losses, as well as loss of life. Numerical models are often used to understand storms characteristics. Apart from theoretically studying storms, numerical models can help predict storms, prevent damage and alert people to imminent danger. Therefore, the level of complexity of numerical models can be a very important factor in improving the study and prediction of storms.

The complexity of numerical models relates to their dimensionality (1-D, 2-D and 3-D models) and the descriptiveness of the microphysical parameterizations. The microphysical complexity of numerical models refers to the choice of microphysical scheme, the number of microphysical categories used and the type of size distribution. Numerical models of convective storms can use explicit bin schemes [1,2,3], bulk schemes [4,5,6,7,8,9] or hybrid bulk-bin microphysical schemes [10,11]. Bulk microphysical schemes are more commonly used due to their lower computational time and memory requirements. These schemes assume a particular size distribution function for each microphysical category and predict one or more variables (mixing ratio, number concentration, cross section, radar reflectivity, etc.) proportional or equal to the corresponding moment of the size distribution function. Therefore, depending on the number of moments—single-moment [12,13,14,15,16,17], double-moment [18,19,20,21,22] and triple-moment [23,24,25,26]—bulk microphysical schemes can be distinguished.

Many studies compare microphysical bulk schemes with different numbers of moments. The most common comparisons are between single-moment and double-moment schemes [19,27,28,29,30]. In their study, van Weverberg et al. [29] compared single- and double-moment schemes by focusing on the climate simulations of intense precipitation. Morrison et al. [27] investigated stratiform precipitation in a simulated squall line by comparing single-moment and double-moment bulk schemes. The results showed that the storm structures generated by both schemes were similar, but there were differences in the surface precipitation in the convective and stratiform regions caused by the different evaporation rates of the raindrops in the various storm regions. The different evaporation rates of raindrops were a function of the distribution parameters (the intercept and slope parameters) generated by the two schemes. In the convective region, the intercept parameter is greater in the double-moment scheme than its fixed value in the single-moment scheme due to the significantly greater collision-coalescence process. In the stratiform region, larger mean sizes of raindrops (smaller slope parameters) lead to a reduced evaporation rate generated by the double-moment scheme compared with the single-moment scheme. Lim and Hong [30] developed the double-moment bulk microphysical scheme by upgrading the single-moment scheme of the Weather Research and Forecasting model (WRF). The authors added the prognostic concentration of cloud droplets, raindrops and cloud condensation nuclei (CCN). There are substantial differences between the two schemes. The double-moment scheme simulated a higher raindrop number concentration in convective regions (compared with the low concentration in stratiform regions) because of the enhanced melting of solid ice elements. Low values of the rain number concentration is the result of stronger evaporation in stratiform regions. In the single-moment scheme, the boundary between these regions is unclear. Additionally, the raindrop number concentration is uniformly distributed with low values and weak radar reflectivity. The authors concluded that the advantage of the double-moment scheme lies in its ability to predict cloud water and rain number concentrations with explicit CCN representations. Baba and Takahashi [31] examined the impact of the double-moment scheme on stratiform precipitation in a mid-latitude squall line. For this purpose, the authors used a full double moment scheme, a full single-moment scheme and various partial double-moment schemes. They noted that the single-moment scheme produced stronger rain (higher rain rates) than the double-moment scheme. Additionally, the single-moment scheme simulated a nearly constant vertical profile of the melting rate toward the surface because of the prescribed value of the intercept parameter of graupel. In the double-moment scheme, the melting profile of heavy ice precipitation penetrated below 0 °C (i.e., melting depends on the size of ice elements).

In the literature, there is a lack of sensitivity studies comparing the various microphysical schemes by changing the values of the mean drop radius (for the distribution in which the radius is a parameter) or examining the impacts of different values on simulated surface precipitation. In the case of Khrgian-Mazin distributed drops, Ćurić et al. [8] varied the mean drop radius (from 10–50 μm in 10 μm steps) and compared the results with those of the conventional approach (monodisperse distribution for cloud droplets and the Marshall-Palmer distribution of raindrops) of the single-moment bulk scheme. We assume that the drops (cloud droplets and raindrops) are described by a unified Khrgian-Mazin size distribution with a division between cloud droplet and raindrop spectra [22]. A unified size distribution of the overall drops prevents an unnatural gap (discontinuity) at the limit of the two spectra. Our sensitivity study compares two microphysical bulk schemes (single moment and double moment) by varying the mean radius of the entire drop spectra (in the single-moment scheme), which is analogous to changing the corresponding cloud droplet number concentration (in the double-moment scheme). We focused on surface precipitation produced by a simulated storm.

This paper is organized as follows. The model description and model setup used in this sensitivity study are described in Section 2. The model results and discussion are provided in Section 3. A summary and conclusions are presented in Section 4.

2. Description of the Cloud Model

2.1. General Model Characteristics

A cloud-resolving mesoscale model was used [21] with the option to choose the number of moments of the size distribution function describing any of the microphysical categories. The cloud model calculates time-dependent, non-hydrostatic and fully compressible equations. The prognostic variables of the model are: the three Cartesian velocity components, perturbation potential temperature and pressure and eight microphysics categories (water vapour, cloud droplets, raindrops, ice crystals, snow, graupel, frozen raindrops and hail) represented by one (mixing ratio; the single-moment scheme) or two moments (mixing ratio and number concentration; the double-moment scheme) of the size distribution function. The cloud droplet number concentration was fixed in the given experiment in the double-moment bulk microphysical scheme. However, the double-moment bulk microphysical scheme has a disadvantage because it does not predict the cloud droplet number concentration as a result of absence of the aerosol particles. Our future efforts are directed towards the representation of the aerosol particles in the cloud model. Therefore, one (in the single-moment scheme) or two moments (in the double-moment scheme) of the size distribution function were solved at every grid point and at each time step.

The model area was 80 × 80 × 15 km. We used a horizontal grid spacing of 1000 m and a vertical grid spacing of 500 m. The experiments were terminated after 120 min. The short time step for integrating acoustic wave terms was 1 s. The large time step for the other terms was 6 s. The wave-radiating open boundary condition was used for the lateral boundaries. The turbulence was treated using a 1.5-order turbulent kinetic energy formulation. The effect of the Coriolis force was ignored in our simulations. The cloud simulations were performed over a flat terrain.

Cloud droplets were generated by condensation using a saturation adjustment scheme derived from Tao et al. [32]. Melting of ice crystals is an additional source for cloud droplets. Raindrops were formed by the autoconversion of cloud droplets in agreement with Meyers et al. [19], as well as the melting of solid precipitating categories (snow, graupel, frozen raindrops and hail), or the shedding of excess water from the hailstones in a wet growth regime of hail. Furthermore, raindrops grow mainly by the accretion of cloud droplets, or by collision with ice crystals and snow at temperatures higher than 0 °C. Additionally, collisions between cloud droplets and solid precipitating categories are sources for rain at temperatures higher than 0 °C. A collision-induced breakup of raindrops is not considered. Ice crystals are initiated by the depositional nucleation and homogeneous freezing of cloud droplets below −40 °C. The nucleation of ice crystals via the depositional process begins when water vapour is supersaturated with respect to the ice surface at temperatures below 0 °C. The number concentration of the ice crystals is equivalent to the concentration of active natural ice nuclei in the given temperature, in accordance with Fletcher [33].

Snow can be produced through the autoconversion of ice crystals and the Bergeron-Findeisen process. Graupel is formed by the autoconversion mechanism of snow in agreement with Swann [34]. Frozen raindrops are generated by the immersion freezing of raindrops and by interactions of raindrops with ice crystals and snow. Hailstones are initiated through an autoconversion process of graupel and frozen raindrops. Once formed, hail continues to grow primarily through interactions with cloud droplets, as well as via collisions with raindrops, ice crystals and snow. The interactions of hail with hailstone embryos (graupel and frozen raindrops) are ignored. Hail mass content decreases through melting and sublimation processes. The some production terms are given in more detail [21].

2.2. Initial State of the Atmosphere

The base state was horizontally homogeneous and it was obtained from a single sounding of which the skewed-T/log p thermodynamic diagram is presented in Figure 1. The wind direction strongly changed (from southeast to northwest) from the surface to 1 km above ground level. The prevailing wind was in a northwest direction. The wind speed increased from the ground (approximately 7 m·s⁻¹) with altitude to approximately 17 m·s⁻¹ at 9 km above ground level. There was a large moisture content under approximately 3 km above ground level. The water vapour mixing ratio reaches a maximum value (approximately 13 g·kg⁻¹) at a level of 900 mb. These environment characteristics are typical for the evolution of severe storms over the region of Western Serbia [35].

Figure 1. Initial sounding of temperature (solid line) and dew point (dashed line) plotted on a skew T/log p diagram (Belgrade, June 13, 1982). Coordinate lines denote pressure (hPa) and temperature (°C). Height values and wind barbs are shown on the right-hand side of the figure.

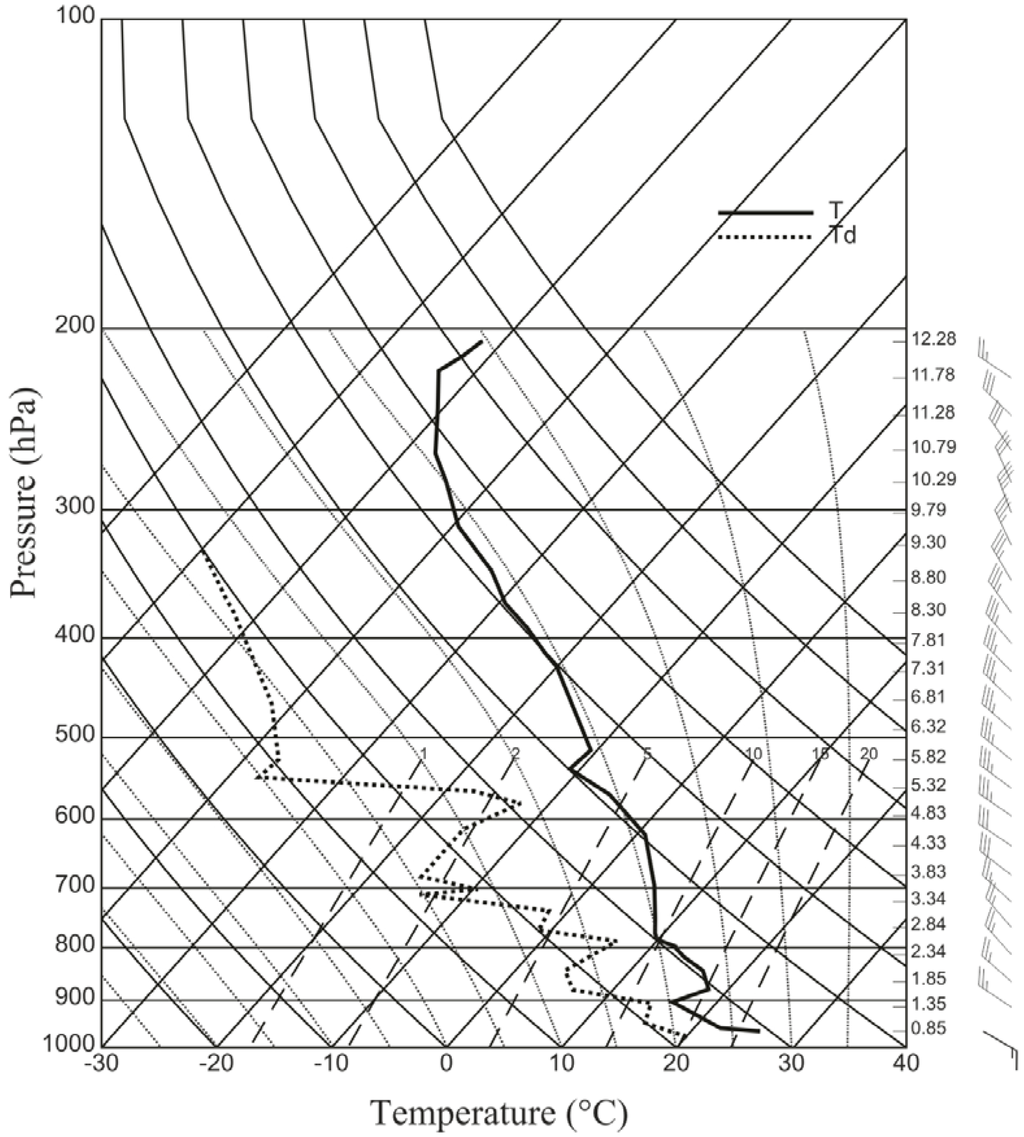
Figure 1. Initial sounding of temperature (solid line) and dew point (dashed line) plotted on a skew T/log p diagram (Belgrade, June 13, 1982). Coordinate lines denote pressure (hPa) and temperature (°C). Height values and wind barbs are shown on the right-hand side of the figure.

For cloud initiation, we used an ellipsoidal warm bubble with a maximum temperature perturbation of 2.0 K in its centre. The bubble has a horizontal radius of 10 km and a vertical radius of 1.5 km. The coordinates of the thermal bubble centre are (x, y, z) = (16, 64, 1.65) km.

2.3. Model Versions

We used two versions of a cloud model that depended on the number of moments used as prognostic quantities. In general, the n-th order moment of the size distribution function of the microphysical category X is defined similarly to Ochou et al. [36] as

$$m_n={\displaystyle \underset{D_{X,min}}{\overset{D_{X,max}}{\int }}{D}^{n}N(D)dD}$$

(1)

where N(D) is the size distribution function of the microphysical category X; D_X,min and D_X,max are the minimum and maximum diameters, respectively, of category X. These boundaries are presented in Table 1. In particular, substituting n = 0 into Equation (1) yields:

$$m_0={\displaystyle \underset{D_{X,min}}{\overset{D_{X,max}}{\int }}N(D)dD}=n_X$$

(2)

Therefore, we note that the zeroth moment m₀ of the size distribution function represents the number concentration n_X of the microphysical category X. Additionally, substituting n = 3 into Equation (1) and using the definition of the liquid water content:

$$w_X=\rho q_X={\displaystyle \underset{D_{X,min}}{\overset{D_{X,max}}{\int }}\frac{\pi }{6}{\rho }_X{D}^{3}N(D)dD}$$

(3)

we obtain

$$q_X=\frac{\pi }{6}\frac{{\rho }_X}{\rho }{\displaystyle \underset{D_{X,min}}{\overset{D_{X,max}}{\int }}{D}^{3}N(D)dD}=\frac{\pi }{6}\frac{{\rho }_X}{\rho }{m}_3$$

(4)

where ρ is the air density; q_X and ρ_X are the mixing ratio and density of any microphysical category X, respectively. The densities of water (ρ_r), snow (ρ_s), graupel (ρ_g) and hail (frozen raindrops; ρ_h = ρ_f) are 1000 kg·m⁻³, 100 kg·m⁻³, 400 kg·m⁻³ and 917 kg·m⁻³, respectively.

Thus, the mixing ratio q_X is proportional to the third moment of the size distribution function N(D). The particle shape of any microphysical category was assumed to be spherical.

Table 1. Maximum and minimum diameters of the microphysical categories [22].

Hydrometeors	DX,min (mm)	DX,max (mm)
Cloud droplets	0.0	0.2
Raindrops	0.2	10.0
Ice crystals	0.0	1.0
Snow	0.0	5.0
Graupel	0.0	5.0
Frozen raindrops	0.0	5.0
Hail	5.0	50.0

Table 1. Maximum and minimum diameters of the microphysical categories [22].

Hydrometeors	DX,min (mm)	DX,max (mm)
Cloud droplets	0.0	0.2
Raindrops	0.2	10.0
Ice crystals	0.0	1.0
Snow	0.0	5.0
Graupel	0.0	5.0
Frozen raindrops	0.0	5.0
Hail	5.0	50.0

The assumed size distribution function of the entire drop spectra (cloud droplets and raindrops) is the unified Khrgian-Mazin size distribution defined as [22,37]:

$$N(D)=\frac{A{D}^2}{4}\text{exp}\left(-\frac{BD}{2}\right)$$

(5)

where A and B are parameters of the size distribution (5):

$$A=1.452\frac{\rho Q}{{\rho }_w{R}_M^6},\hspace{0.17em}\hspace{0.17em}B=\frac{3}{R_M}$$

(6)

R_M is the mean radius of the entire drop spectra:

$$R_M={\left(\frac{3\rho \left(q_c+q_r\right)}{4\pi {\rho }_w\left(n_c+n_r\right)}\right)}^{\frac{1}{3}}$$

(7)

here Q = q_c + q_r is the total mixing ratio of the drops (cloud droplets and raindrops); q_c (n_c) and q_r (n_r) are the mixing ratios (number concentration) of the cloud water and rain, respectively. The cloud ice was distributed in accordance with Hu and He [5]. The solid precipitating elements (snow, graupel, frozen raindrops and hail) were assumed by the exponential size distribution function [12]:

$$N(D)=N_{0X} \text{exp}(-{\lambda }_{X}D)$$

(8)

where N_0X is the intercept parameter and λ_X is the slope parameter calculated iteratively as

$${\lambda }_X={\left\{\frac{\pi }{6}\frac{{\rho }_X}{\rho }\frac{N_{0X}}{q_X}\left[\Gamma \left(4;{\lambda }_X{D}_{X,max}\right)-\Gamma \left(4;{\lambda }_X{D}_{X,min}\right)\right]\right\}}^{0.25}$$

(9)

where ρ_X and q_X are the density and mixing ratio, respectively, of the microphysical category X. Γ(4; λ_XD_X,max) and Γ(4; λ_XD_X,min) are the incomplete gamma functions calculated by the algorithm of Abramowitz and Stegun [38]. This cloud model can be used for numerical weather prediction, although the slope parameter is calculated iteratively (due to the large computing time). In the single-moment scheme, the values of the intercept parameters N_0X are fixed and are presented in Table 2. The values of the intercept parameters for snow (N_0s), graupel (N_0g) and hail (N_0h) are proposed by Gunn and Marshall [39], Murakami [6] and Federer and Waldvogel [40], respectively. The intercept parameter for frozen raindrops (N_0f) takes the same value as the corresponding parameter for hail (Table 2). In the case with the double-moment version, this parameter is calculated diagnostically as

$$N_{0X}=\frac{{\lambda }_X{n}_X}{\text{exp}(-{\lambda }_X{D}_{X,min})-\text{exp}(-{\lambda }_X{D}_{X,max})}$$

(10)

Therefore, differences in the values of the slope parameter depend on whether the parameter N_0X is calculated (in the double-moment scheme) or prescribed (in the single-moment scheme).

Table 2. The values of the intercept parameters N_0X (in m⁻⁴) for solid precipitating elements.

Hydrometeors	N0X (m−4)
Snow	3 × 106
Graupel	1.1 × 106
Frozen raindrops	4 × 104
Hail	4 × 104

Table 2. The values of the intercept parameters N_0X (in m⁻⁴) for solid precipitating elements.

Hydrometeors	N0X (m−4)
Snow	3 × 106
Graupel	1.1 × 106
Frozen raindrops	4 × 104
Hail	4 × 104

2.4. Experiment Design

We tested two versions of the model: the first model version uses the double-moment bulk microphysical scheme (mixing ratio and number concentration), while the second version is characterized by one moment of the size distribution function (only the mixing ratio). Three values of R_M were tested in the experiments using the single-moment scheme. In the case of the double-moment bulk microphysical scheme, the radius R_M is diagnostically calculated by Equation (7). Typical orders of magnitude of q_c, q_r and n_r are 10⁻³ kg·kg⁻¹ [19,22], 10⁻³ kg·kg⁻¹ and 10–10⁴ m⁻³ [19,21], respectively. The values of the cloud droplet number concentration depend on the concentration of the active cloud condensation nuclei (CCN). The CCN concentration strongly varies by region (continental vs. maritime, urban vs. rural environment, etc.). Typical values of the cloud droplet number concentration range from a few tens per cubic centimeter (10⁷–10⁸ m⁻³; for maritime clouds) to a few hundred per cubic centimeter (10⁸–10⁹ m⁻³; for continental clouds; [37,41]). Therefore, an abundance of cloud droplets (compared with raindrops) causes the cloud droplet number concentration to greatly affect the radius R_M. Hence, larger values of the radius R_M (smaller n_c) are usually characteristics of maritime clouds; in contrast, smaller values of R_M (higher n_c) correspond to continental clouds.

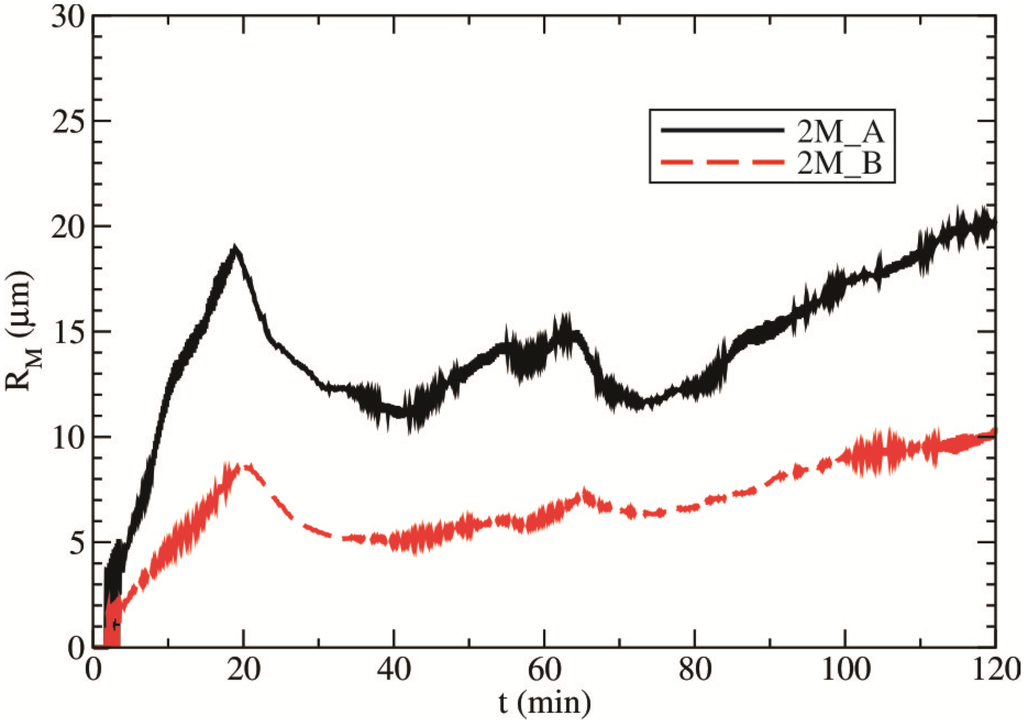
Figure 2. The evolution of the mean radius of the entire drop spectra R_M (in μm) for n_c = 60 cm⁻³ (experiment 2M_A) and n_c = 600 cm⁻³ (experiment 2M_B). The mean values of the radius R_M are presented (within the cloud volume).

Figure 2. The evolution of the mean radius of the entire drop spectra R_M (in μm) for n_c = 60 cm⁻³ (experiment 2M_A) and n_c = 600 cm⁻³ (experiment 2M_B). The mean values of the radius R_M are presented (within the cloud volume).

The double-moment scheme was tested for two amounts of the number concentration of cloud droplets that represent typical maritime clouds (n_c = 60 cm⁻³) and continental clouds (n_c = 600 cm⁻³). The diagnostically calculated values of a given radius R_M (within the cloud volume) as a function of time are shown in Figure 2. These values correspond to the mean values of this radius. The mean values of the radius R_M are averaged over all grid points within the cloud volume. Experiment 2M_A corresponds to the cloud droplet number concentration of 60 cm⁻³, whereas experiment 2M_B relates to a typical continental concentration of 600 cm⁻³. Note that the cloud developed in experiment 2M_A is characterized by a mean drop radius of approximately 15–20 μm. In the second scenario, a higher cloud droplet number concentration leads to smaller cloud droplets; therefore, the value of the given radius is approximately 5–10 μm during much of the cloud’s lifetime. Observing the values of the radius R_M in Figure 2, it can be concluded that experiment 1M_10 corresponds to experiment 2M_A and that experiment 1M_20 corresponds to experiment 2M_B. Taking into consideration the values obtained by the double-moment bulk microphysical scheme, the sensitivity experiments performed by the single-moment scheme have been tested for three values of the radius R_M (from 10–30 μm at a step of 10 μm). Therefore, we have three experiments (1M_10, 1M_20 and 1M_30) that depend on the value of R_M.

3. Model Results and Discussion

3.1. Model Results

The evolution of the surface precipitation is shown in Figure 3. The amounts and timing of the occurrence of (a) rain and (b) hail accumulations over the model area are discussed. The evolution is presented for the double-moment bulk microphysical scheme (experiments 2M_A and 2M_B) and for the single-moment scheme (experiments 1M_10, 1M_20 and 1M_30). The single-moment scheme generally allows more rain to reach the ground than the double-moment scheme in the late stage of the cloud (Figure 3a). Additionally, the regularity between the amounts of surface precipitation and changes in the values of the mean drop radius was not observed in Figure 3a for the single-moment experiments. In contrast, in the experiments with the double-moment scheme, an increase in the cloud droplet number concentration (analogous to the decrease in the mean drop radius) leads to a large reduction in the rain accumulation on the ground. Therefore, the case with the 10-fold higher concentration of cloud droplets (2M_B) results in an approximately two-fold smaller amount of rain at the surface compared with test 2M_A.

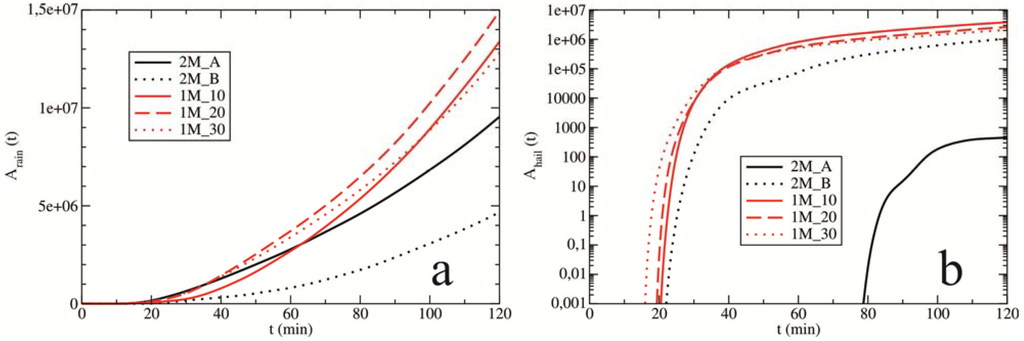
Figure 3. (a) Rain and (b) hail accumulation (in tonnes) on the ground over time. The evolutions are presented for experiments designed by the double-moment scheme (2M_A and 2M_B) and single-moment scheme (1M_10, 1M_20 and 1M_30).

Figure 3. (a) Rain and (b) hail accumulation (in tonnes) on the ground over time. The evolutions are presented for experiments designed by the double-moment scheme (2M_A and 2M_B) and single-moment scheme (1M_10, 1M_20 and 1M_30).

Considering the amounts of hail on the ground (Figure 3b), the single-moment scheme simulates a larger amount of surface hail than the alternative scheme (especially for experiment 2M_A). The most obvious difference between the sensitivity tests created by the single-moment scheme and the double-moment scheme is for the case with n_c = 60 cm⁻³. An increase in the cloud droplet number concentration by a factor of 10 leads to an approximately 2500-fold increase in the amount of surface hail in experiment 2M_B. Additionally, the appearance of hailstones at the surface (in experiments 1M_10, 1M_20 and 1M_30) occurs much earlier than in experiment 2M_A. Experiment 2M_B is characterized by a much earlier appearance of surface hail, which is similar to the single-moment experiments. Examining the evolution of the surface hail (amounts and timing), the double-moment scheme is more sensitive to the increasing cloud droplet number concentration (or mean radius of the drop spectra) compared with the single-moment scheme. Therefore, experiments created by the single-moment scheme show slight sensitivity when changing the mean radius of the drop spectra R_M.

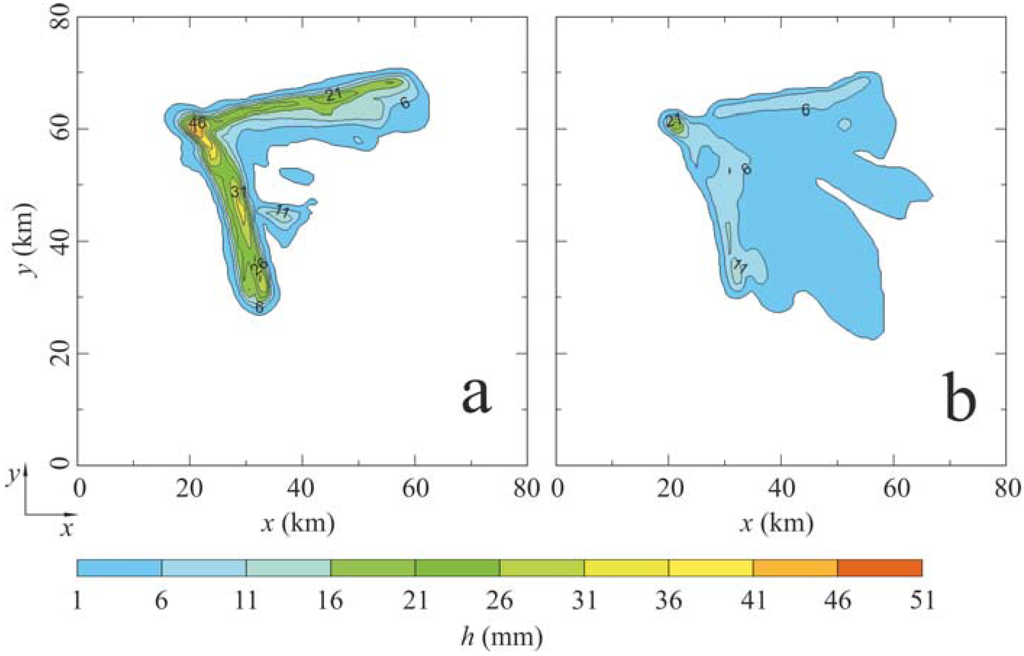
Figure 4. The horizontal distribution of the total surface precipitation of the double-moment scheme at t = 120 min for experiment (a) 2M_A and (b) 2M_B. Isohyets are drawn at 5 mm; the base isohyet is 1 mm. The height of accumulated precipitation on the ground h (in mm) is represented using a scale at the bottom of the figure.

Figure 4. The horizontal distribution of the total surface precipitation of the double-moment scheme at t = 120 min for experiment (a) 2M_A and (b) 2M_B. Isohyets are drawn at 5 mm; the base isohyet is 1 mm. The height of accumulated precipitation on the ground h (in mm) is represented using a scale at the bottom of the figure.

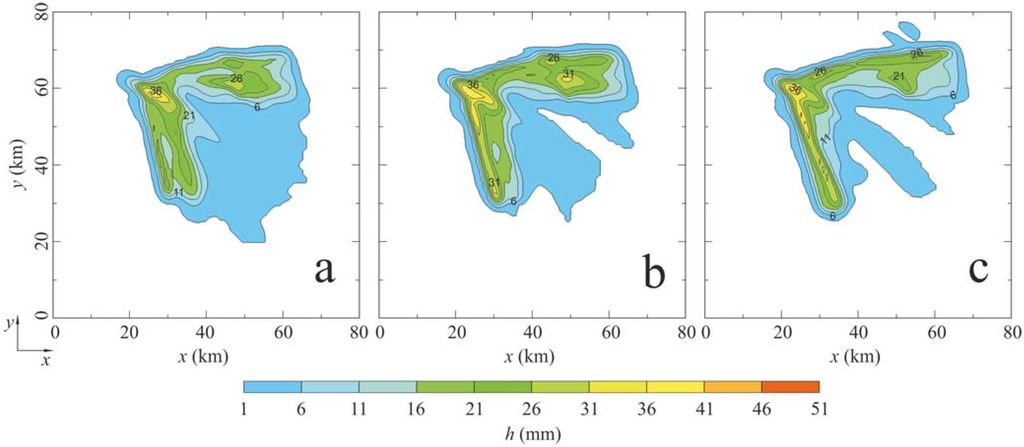
Figure 5. As in Figure 4 but for the single-moment scheme for experiment (a) 1M_10; (b) 1M_20 and (c) 1M_30.

Figure 5. As in Figure 4 but for the single-moment scheme for experiment (a) 1M_10; (b) 1M_20 and (c) 1M_30.

Figure 4 depicts a horizontal distribution of the overall surface precipitation (in mm) for the double-moment scheme at the end of the time integration. Note that experiment 2M_A generates narrow bands of intense rainfall, while these rainbands disappear and the precipitation field is more uniform in experiment 2M_B. Similarly, Figure 5 shows the total precipitation field for the single-moment scheme. In this case, the precipitation field is characterized by slightly wider rainbands that spread over a large horizontal area. The horizontal distribution of the surface precipitation is less sensitive to a change in the parameter R_M than the results displayed in Figure 4. Similarly, Ćurić et al. [8] concluded that the single-moment bulk scheme with the Khrgian-Mazin distribution produces more cumulative rainfall over a large area than other cases.

3.2. Discussion

3.2.1. Rain

We analyzed the mass contribution of production term P to the microphysics fields by integrating the term within the cloud volume V at current time step ∆t:

$$M={\displaystyle \underset{V}{\int }\rho P\text{Δ}tdV}$$

(11)

The corresponding cumulative sum of the mass contribution (11) can be written as

$$\mathrm{\Sigma }dM={\displaystyle \sum _{t=0}^{i\cdot \text{Δ}t}M\left(t\right)}={\displaystyle \sum _{t=0}^{i\cdot \text{Δ}t}{\displaystyle \underset{V}{\int }\rho P\left(t\right)\text{Δ}tdV}}$$

(12)

where i (i = 1, ..., n) is the time steps counter and n (n = 1200) is the total number of time steps. A comparison of the mass contributions between the two schemes is possible because the expressions for the mass transfer P are identical in both schemes. The only difference is that the double-moment scheme calculates the conversion rates for the number concentration, which leads to different parameters of the size distribution (diagnostically calculated; Equations (7), (9) and (10)) compared with the single-moment scheme (prescribed R_M, N_0X; diagnostically defined λ_X by Equation (9)). Furthermore, these parameters directly affect the mass transfers. These diagnostically defined parameters are the functions of the corresponding mixing ratios (and number concentrations in the double-moment scheme), i.e., the mixing ratios indirectly affect the mass transfers.

Initially, raindrops are formed by random collisions of cloud droplets which present autoconversion. In Figure 6, the autoconversion mass contribution to the raindrop production as a function of time for all experiments is depicted. All sensitivity tests well simulated this microphysical process by varying the mean radius of the drop spectra (experiments with the single-moment scheme) or analogously by changing the values of the cloud droplet number concentration (tests 2M_A and 2M_B). Namely, when the mean cloud droplet size is large, droplets are more likely to quickly transform into raindrops, which is analogous to a smaller concentrations of cloud droplets. Conversely, a higher cloud droplet number concentration leads to a slower transition of cloud droplets to raindrops for a given cloud water mixing ratio.

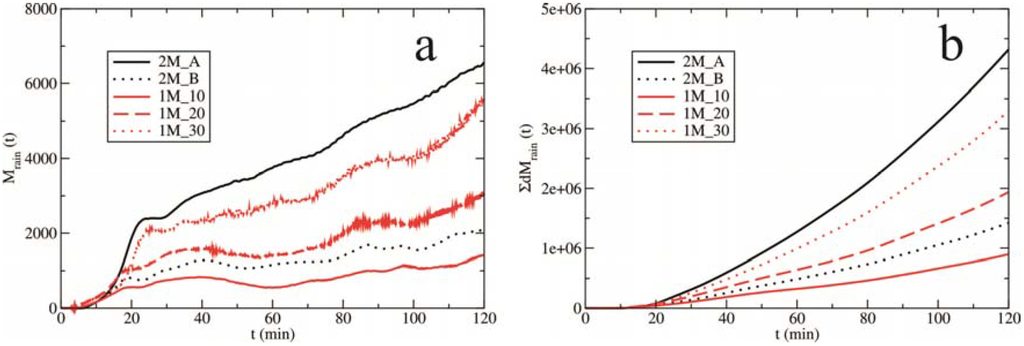
Figure 6. The mass contribution, M (in tonnes), to rain by the autoconversion of cloud droplets (a) as a function of time and (b) their corresponding cumulative sums. The evolutions are presented for all experiments.

Figure 6. The mass contribution, M (in tonnes), to rain by the autoconversion of cloud droplets (a) as a function of time and (b) their corresponding cumulative sums. The evolutions are presented for all experiments.

Raindrops (formed by the autoconversion of cloud droplets or by the melting of solid precipitating elements) can further grow by collecting cloud droplets. Figure 7 presents the mass contribution to rain by the accretion of cloud droplets over time. Similar dependences were observed for experiments 2M_A, 2M_B and 1M_20. A very small mass contribution to rain can be observed in 1M_10. The overall mass contribution (expressed by the cumulative sum) is only ~2 t, whereas the total mass contributions in other sensitivity experiments are over 10⁵ t. Figure 8 presents the mean values of (a) the cloud water mixing ratio (q_c) and (b) the rainwater mixing ratio (q_r) as a function of time for all sensitivity experiments. The values of the cloud water mixing ratio are generally higher for the double-moment experiments (especially for experiment 2M_B) compared with the single-moment experiments. Differences are most obvious in the early stage of a cloud’s life. Higher values of q_c for the experiment 2M_B (Figure 8a) are the result of the reduced autoconversion of cloud droplets to rain (Figure 6). In all experiments, as the cloud droplet number concentration increases (or as the mean radius decreases), there is more cloud water available due to the reduced autoconversion. Rainwater mixing ratios have approximately the same values, particularly in the later stages of a cloud's life (for all experiments).

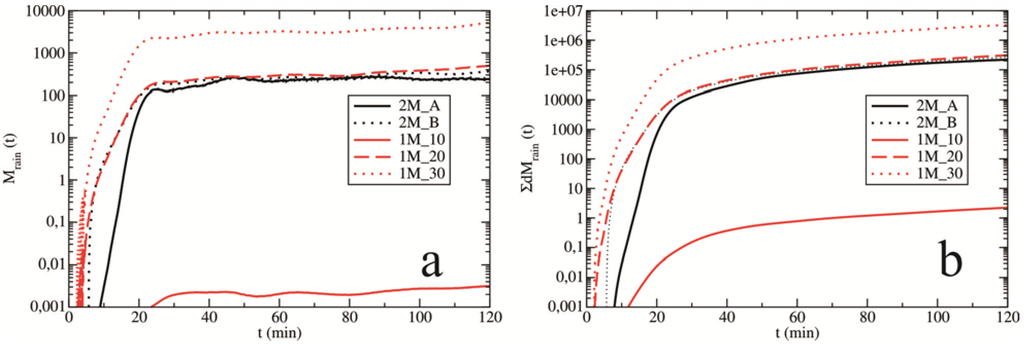
Figure 7. The mass contribution, M (in tonnes), to rain by the accretion of cloud droplets (a) as a function of time and (b) their corresponding cumulative sums. The evolutions are presented for all experiments.

Figure 7. The mass contribution, M (in tonnes), to rain by the accretion of cloud droplets (a) as a function of time and (b) their corresponding cumulative sums. The evolutions are presented for all experiments.

Figure 8. The mean values of (a) the cloud water mixing ratio and (b) the rainwater mixing ratio (in g·kg⁻¹) as a function of time. The evolutions are presented for all experiments.

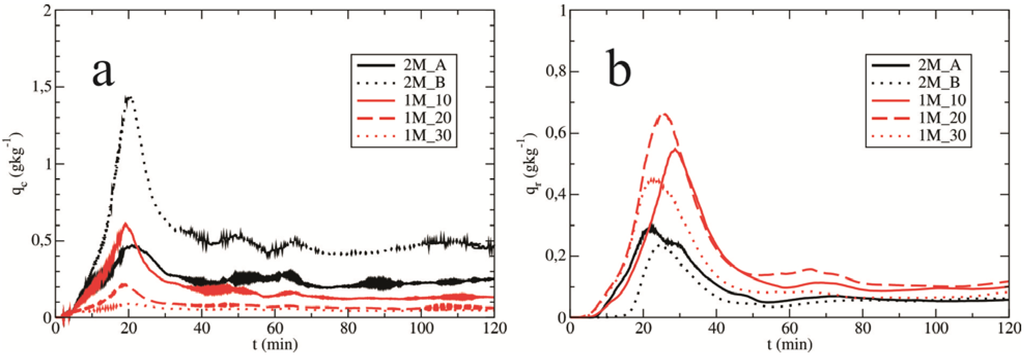
Figure 8. The mean values of (a) the cloud water mixing ratio and (b) the rainwater mixing ratio (in g·kg⁻¹) as a function of time. The evolutions are presented for all experiments.

Figure 9 shows the maximum values of the rain number concentrations prognostically calculated in the double-moment scheme (2M_A and 2M_B) and diagnostically defined in the single-moment model (1M_10, 1M_20 and 1M_30) with the unified Khrgian-Mazin size distribution:

$$n_r=\frac{A}{B^3}\left[\text{Γ}\left(3;\frac{B{D}_{r,max}}{2}\right)-\text{Γ}\left(3;\frac{B{D}_{r,min}}{2}\right)\right]$$

(13)

Figure 9. The maximum concentration of raindrops n_r (in m⁻³) as a function of time for all experiments.

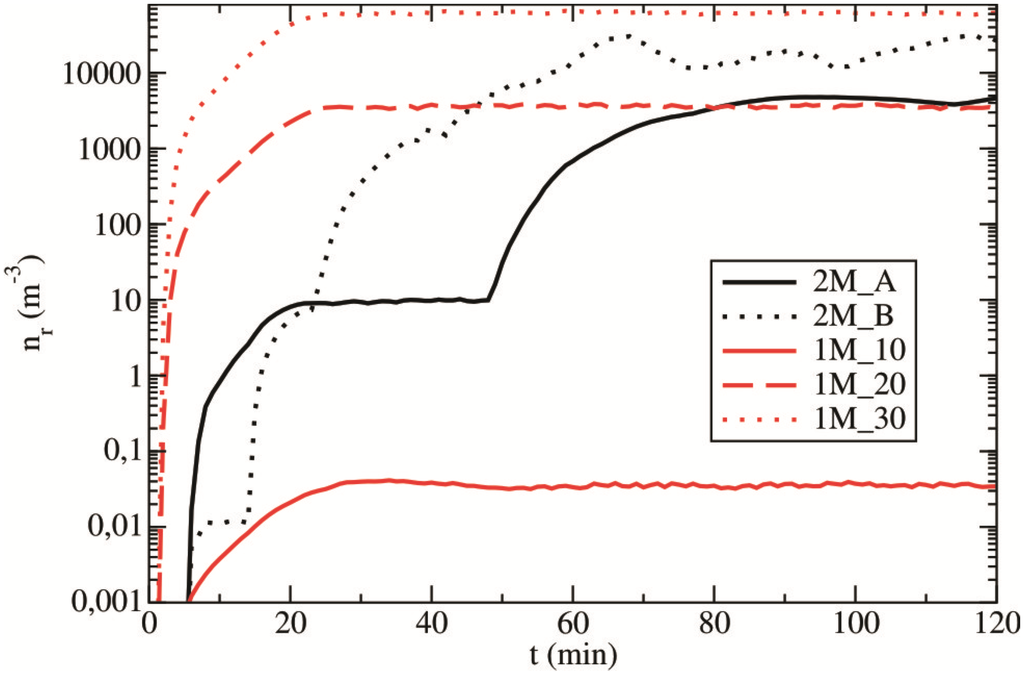
Figure 9. The maximum concentration of raindrops n_r (in m⁻³) as a function of time for all experiments.

In Figure 9, test 1M_10 is characterized by an unrealistic and very low concentration of raindrops [41,42]. The maximum concentrations of rain do not exceed 0.04 m⁻³. We use the maximum raindrop number concentration to examine the mass contribution to rain in a precipitating zone (characterized by the maximum raindrop number concentration). Very low concentrations of raindrops significantly reduced the collection of cloud droplets (Figure 7) leading to a small mass contribution to the further development of the rain field. Other sensitivity tests generated substantially higher rain concentrations, while experiment 1M_30 overestimates the concentration of raindrops by ~60,000 m⁻³ [42,43]. Niu et al. [42] used an observed dataset of raindrops with raindrop number concentration that do not exceed 1500 m⁻³. Tang et al. [43] calculated the total rain concentration from datasets (obtained with a Persivel disdrometer) for three climatic regions and two rain types (convective and stratiform rain). The authors concluded that the total rain concentration does not exceed 700 m⁻³ for convective precipitation. Additionally, experiment 2M_B is characterized by higher values of raindrop number concentration (up to 30,000 m⁻³). In their numerical study, Meyers et al. [19] reported a value of 30 L⁻¹ (30,000 m⁻³) for the maximum raindrop concentration. The increased concentration of raindrops is the result of a faster rate of change for the rain concentration by the melting of increased mass content of solid precipitating elements (see Figure 10).

Figure 10. The mass contribution, M (in tonnes), to rain caused by the melting of solid precipitating elements (graupel, frozen raindrops and hail) (a) as a function of time and (b) their corresponding cumulative sums. The evolutions are presented for all experiments.

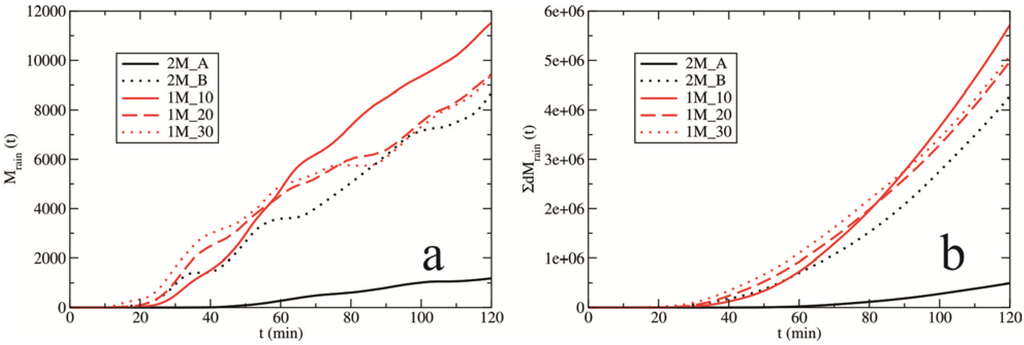
Figure 10. The mass contribution, M (in tonnes), to rain caused by the melting of solid precipitating elements (graupel, frozen raindrops and hail) (a) as a function of time and (b) their corresponding cumulative sums. The evolutions are presented for all experiments.

In addition to these processes, rain development is significantly influenced by the melting of precipitation. Figure 10 demonstrates the overall mass contribution to the raindrop production by melting hailstone embryos and grains of hail as a function of time. Note that melting in the tests generated by the single-moment scheme prevails over the corresponding contributions in the cases with the double-moment scheme. Additionally, experiment 1M_10 presents the most intense melting and rapid transfer to raindrops, which are distributed over a very small rainfall concentration (see Figure 9). Figure 11 presents the mean values of (a) graupel; (b) frozen raindrops and (c) hail mixing ratio as a function of time for all experiments. The cause-and-effect relationship between the mixing ratios depicted in Figure 11 and the change in the mean radius of drops for the single-moment experiments is not obvious (especially in Figure 11c). A higher cloud droplet number concentration (smaller R_M) leads to larger mass amounts of ice categories (graupel, frozen raindrops and hail) due to pronounced riming for the double-moment experiments. A sudden increase in mixing ratios (Figure 11) is a result of strong riming in the early stage of the cloud's life; after approximately 30 min, a rapid decrease is associated with strong melting of ice elements to rain. In all experiments except 2M_A (see Figure 10), larger amounts of rain created by the melting of solid precipitating elements is a consequence of the greater mass content (see Figure 11), i.e., the stronger formation and growth of these elements, as seen later. Analogously, in experiment 2M_A, the small contribution to the rain field of the melting (Figure 10) is a consequence of a very low mass content of the ice precipitating categories (see Figure 11). A sudden increase in the rainwater mixing ratio (see Figure 8b) is associated with strong melting of ice precipitating elements in the early stage of the cloud’s life (Figure 10) as simulated by the single-moment scheme.

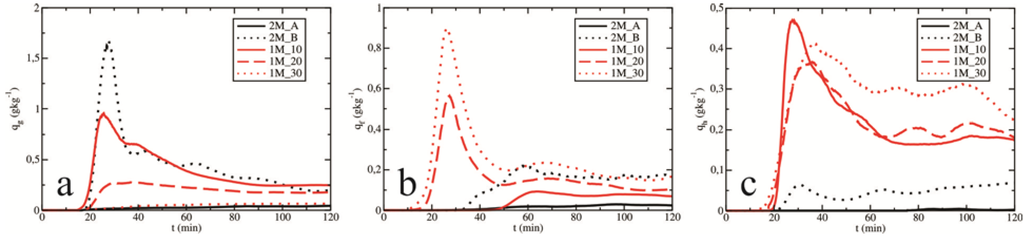
Figure 11. The mean values of (a) graupel; (b) frozen raindrops and (c) hail mixing ratio (in g·kg⁻¹) as a function of time. The evolutions are presented for all experiments.

Figure 11. The mean values of (a) graupel; (b) frozen raindrops and (c) hail mixing ratio (in g·kg⁻¹) as a function of time. The evolutions are presented for all experiments.

Figure 12. The mass contribution, M (in tonnes), to water vapour caused by the evaporation of raindrops (a) as a function of time and (b) their corresponding cumulative sums. The evolutions are presented for all experiments.

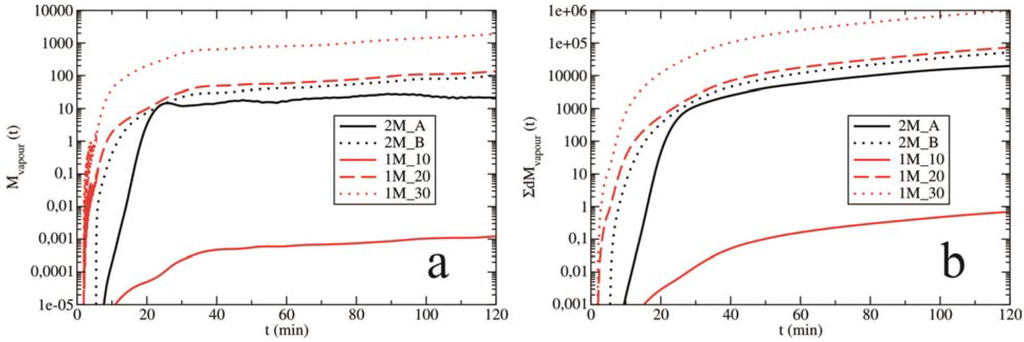
Figure 12. The mass contribution, M (in tonnes), to water vapour caused by the evaporation of raindrops (a) as a function of time and (b) their corresponding cumulative sums. The evolutions are presented for all experiments.

The rain reduction is caused by the interaction of raindrops with solid precipitating elements, by immersion freezing and by evaporation of raindrops. Figure 12 presents the mass contribution of raindrop evaporation for all analyzed experiments. Our results show that this process is one of the most dominant factors of rain reduction and is strongly dependent on the drop size. The evaporation rate depends on the evaporative surface, which is proportional to the diameter squared. Therefore, a larger raindrop evaporates faster and produces a larger amount of water vapour compared with a smaller drop under the same ambient conditions (air temperature and relative humidity). However, large raindrops have a higher terminal velocity and a shorter fall time. Hence, the evaporation is negligible compared with the case of smaller raindrops. Therefore, the population of smaller raindrops will quickly evaporate below the cloud base compared with the population of larger raindrops. In contrast, for a single-moment scheme (Figure 12), a larger radius R_M (larger raindrops) leads to a stronger decline of rain via evaporation. In the double-moment scheme, increasing the cloud droplet number concentration (2M_B) leads to greater evaporation of raindrops. A higher cloud droplet number concentration causes a slower autoconversion of cloud droplets to raindrops (Figure 6) which are more numerous compared with experiment 2M_A in much of the cloud’s lifetime (see Figure 9). Therefore, experiment 2M_B is characterized by a population of smaller and more numerous raindrops (in the precipitating zone) that evaporate quickly below the cloud base (Figure 12); the result is a reduced amount of surface precipitation (see Figure 3a and Figure 4b). Similarly, van Weverberg et al. [29] noted that the double-moment scheme simulated reduced evaporation due to the presence of larger raindrops compared with the single-moment scheme. The single-moment scheme produces more rain (Figure 4) due to stronger melting of ice precipitating elements compared with the double-moment scheme (Figure 10).

Figure 13. The mass contribution, M (in tonnes), to hail caused by the initial production terms (a) as a function of time and (b) their corresponding cumulative sums. The evolutions are presented for all experiments.

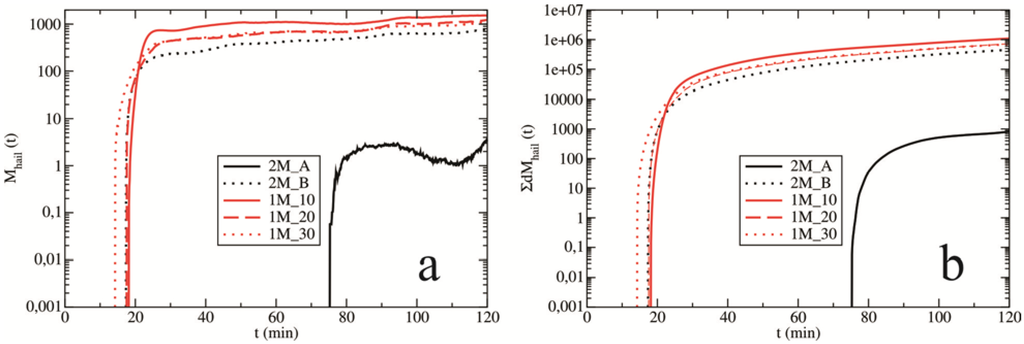
Figure 13. The mass contribution, M (in tonnes), to hail caused by the initial production terms (a) as a function of time and (b) their corresponding cumulative sums. The evolutions are presented for all experiments.

3.2.2. Hail

Hailstones are initially formed by the autoconversion mechanisms of graupel and frozen raindrops. The total contribution of the two processes to hail formation is shown in Figure 13. Figure 13 depicts (a) the current mass contribution to the hail field and (b) the corresponding cumulative sums for all experiments. The mass contribution had a low sensitivity following the experiments simulated by the single-moment scheme. Additionally, the values of the mass contribution are generally greater than those produced by the double-moment scheme. Figure 14 presents the mean values of the slope parameter λ (derived from Equation (9)) for (a) graupel; (b) frozen raindrops and (c) hail over time. The values of the slope parameter were averaged over all grid points for which hailstones were present. The autoconversion of graupel (P_gauth) and frozen raindrops (P_fauth) to hail are inversely proportional to 1/λ_g⁴ and 1/λ_f⁴ [5,21]. The values of the slope parameters λ_g and λ_f (for the single-moment scheme) lie between the corresponding values for the double-moment scheme over most of the time integration. Based on these values, it was expected that the autoconversion rates for the single-moment scheme would lie between the corresponding rates for the double-moment scheme, but this did not occur (Figure 13). The slope parameter for category X (in the single-moment scheme) is proportional to the mixing ratio, whereas in the double-moment scheme the slope parameter is influenced by two microphysical fields: the mixing ratio and the number concentration. Thus, the mass contributions caused by the autoconversion of hailstone embryos to hail (see Figure 13) for the single-moment scheme are higher than those of the double-moment scheme, particularly for experiment 2M_A. In the case of 2M_B, a larger content of available cloud water (smaller P_raut; see Figure 6) leads to stronger riming of hailstone embryos and rapid transitions to hail via autoconversion.

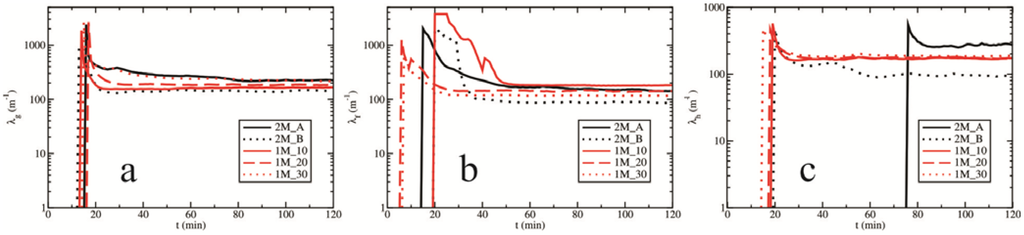
Figure 14. The mean values of the slope parameter λ (in m⁻¹) of (a) graupel; (b) frozen raindrops and (c) hail over time for all experiments.

Figure 14. The mean values of the slope parameter λ (in m⁻¹) of (a) graupel; (b) frozen raindrops and (c) hail over time for all experiments.

Figure 15. The mass contribution, M (in tonnes), caused by the production terms for the growth of hail (a) as a function of time and (b) their corresponding cumulative sums. The evolutions are presented for all experiments.

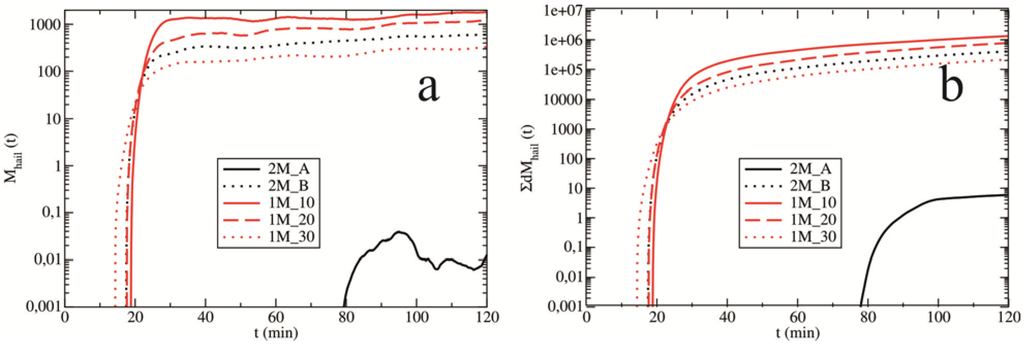
Figure 15. The mass contribution, M (in tonnes), caused by the production terms for the growth of hail (a) as a function of time and (b) their corresponding cumulative sums. The evolutions are presented for all experiments.

Figure 16. The mean diameter of hailstones D_h (in mm) as a function of time for all experiments. The mean values of the hail diameters are presented.

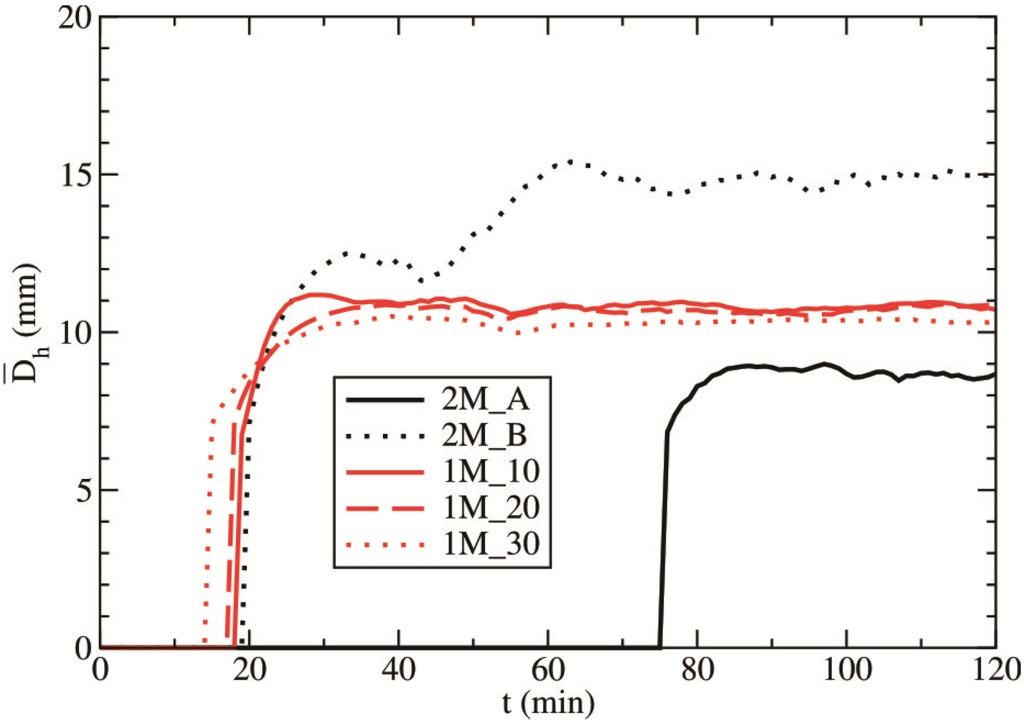
Figure 16. The mean diameter of hailstones D_h (in mm) as a function of time for all experiments. The mean values of the hail diameters are presented.

Furthermore, hail grows by colliding with cloud droplets, ice crystals, raindrops and snow. The total mass contribution of these processes to the hail field is depicted in Figure 15. Compared with the initial formation of hailstones depicted in Figure 13, we noted a similar behaviour of this contribution over time. The prevailing process for hail growth is the accretion of cloud droplets – D_hacw (in the dry growth of hail; [22]). Similar to the autoconversion (P_gauth and P_fauth) above, D_hacw = f (1/λ_h) [21]. Considering only the values of the slope parameter for hail (Figure 14c), it can be concluded that experiment 2M_B should be characterized by the strongest growth of hailstones (due to the lowest values of the slope parameter) compared with the single-moment scheme; however, this outcome was not apparent (Figure 15). This inconsistency was analyzed using the mean diameter of hail depicted in Figure 16. Figure 16 presents the mean diameter of hailstones over time. The mean diameter of hailstones D_h can be defined as

$${\overline{D}}_h=\frac{{\displaystyle \underset{D_{h,min}}{\overset{D_{h,max}}{\int }}DN(D)dD}}{{\displaystyle \underset{D_{h,min}}{\overset{D_{h,max}}{\int }}N(D)dD}}$$

(14)

Therefore, substituting the size distribution function (8) into Equation (14), we obtained the mean diameter of hail

$${\overline{D}}_h=\frac{1}{{\lambda }_h}\frac{\text{Γ}\left(2;{\lambda }_h{D}_{h,max}\right)-\text{Γ}\left(2;{\lambda }_h{D}_{h,min}\right)}{\text{exp}\left(-{\lambda }_h{D}_{h,min}\right)-\text{exp}\left(-{\lambda }_h{D}_{h,max}\right)}$$

(15)

as a function of the slope parameter of hail—λ_h. We used the mean values of the slope parameter (Figure 14) for calculating the hail diameter presented in Equation (15). Experiments 1M_10, 1M_20 and 1M_30 generated the mean diameter of hail, which takes the value of approximately 1 cm, whereas test 2M_B presents the values as approximately 1.5 cm. Hailstones with a smaller mean size (in the single-moment scheme) should fall more slowly; thus, they slowly collect other elements. This finding contradicts the collection rates of the microphysical elements by hailstones (Figure 15). Because of the lack of the single-moment scheme, calculating the mean diameter is only possible by using the mixing ratio, which has an indirect impact on the collection processes and precipitation amounts at the surface. Note that varying the mean radius of the drops–R_M–leads to nearly unchanged values of the mean diameters of the hailstones (Figure 16). In contrast, the double-moment scheme allows wide variability in the mean diameters of the microphysical categories because it calculates the mean diameters as a function of the mixing ratio and number concentration. In the double-moment case, the mean diameters evolve more realistically in contrast to the single-moment scheme [19]. The small increase in hail is well simulated in test 2M_A. The higher values of the slope parameter (i.e., smaller diameters of the hailstones; see Figure 14c and Figure 16) lead to slower hailstone growth. However, a smaller frequency of the collisions between hailstones and cloud droplets (low concentration of cloud droplets) and a smaller mass content of the available cloud water (Figure 8a) for the growth of hail (due to larger P_raut; see Figure 6) lead to a small mean hail size (~0.8–0.9 cm). A lower average dimension of hail (Figure 16) leads to a slower fall velocity and a smaller cross-sectional area. Therefore, the growth of hail is slower (2M_A; see Figure 15). With higher cloud droplet number concentrations, a greater frequency of collisions with cloud droplets and a larger mass content of available cloud water (due to slower P_raut) leads to an increase in hail production (Figure 15) and larger hailstones (2M_B; see Figure 16).

Figure 17 shows the total reduction of hail due to sublimation and melting. The hail reduction (in experiment 2M_A) is a consequence of the low hail content and smaller mean size of hail grains (see Figure 16) that are significantly melting. Other sensitivity experiments show similar and significantly stronger melting and sublimation. When analyzing the mean diameter of hail (Figure 16), it was expected that the sensitivity tests generated by the single-moment scheme would show a significantly stronger hail reduction compared with test 2M_B; however, this outcome did not occur. Namely, the smaller mean diameters of hail grains (~1 cm) should lead to enhanced melting of hailstones compared with test 2M_B (~1.5 cm). The single-moment scheme does not simulate a wider range of mean hail diameters for various values of R_M (see Figure 16); therefore, the consequence is an unrealistic description of the microphysical processes. Finally, in the double-moment scheme, as the cloud droplet concentration increases, more hail reaches the ground (Figure 3b) because of the enhanced autoconversion of hailstone embryos (Figure 13) and the stronger growth of hail (Figure 15).

Figure 17. The mass contribution, M (in tonnes) caused by the sink of hail (a) as a function of time and (b) their corresponding cumulative sums. The evolutions are presented for all experiments.

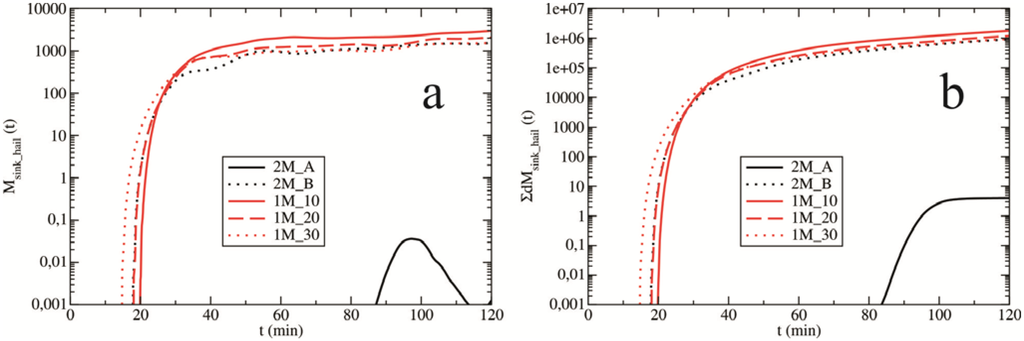
Figure 17. The mass contribution, M (in tonnes) caused by the sink of hail (a) as a function of time and (b) their corresponding cumulative sums. The evolutions are presented for all experiments.

4. Conclusions

In this sensitivity study, we simulated the surface precipitation for different bulk microphysical schemes (double-moment and single-moment schemes). We compared whether the single-moment bulk microphysical scheme agrees with the alternative double-moment scheme when changing the values of the mean radius of the liquid drops that were specified as a parameter in the given experiment. In the alternative double-moment scheme, the mean radius is calculated diagnostically, whereas the cloud droplet number concentration is prescribed. The model results for three values of the mean drop radius (in the single-moment scheme) and two concentrations of cloud droplets (in the double-moment scheme) were compared.

The main conclusions in this sensitivity study are as follows:

• The single-moment bulk microphysical scheme generates more surface rain than the double-moment scheme, particularly in the later stage of the cloud’s life. The cloud droplet number concentration increase (analogous to a decrease in the mean drop radius) leads to a large reduction in the accumulation of surface rain in the double-moment scheme. The single-moment scheme yields significantly more hail than the double-moment scheme.
• The double-moment scheme shows a much higher sensitivity of the amount and spatial distribution of the surface precipitation to the changing concentration of cloud droplets (or mean radius of the entire drop spectra) compared with the single-moment scheme.
• The diagnostic rain concentration defined by the single-moment scheme may be unrealistic, i.e., underestimated or overestimated. In the case of very low rain concentrations, the accretion of cloud droplets (one of the primary processes in rain development) is insignificant. Nonetheless, the melting of precipitating ice is enormous, leading to a population of giant raindrops that is inconsistent with the observations. In the case with the single-moment scheme, large raindrops evaporate much faster compared with the population of smaller drops. Therefore, this scheme does not accurately simulate the evaporation of raindrops.
• In the sensitivity experiments generated by the double-moment scheme, there is a positive correlation between the increase in the cloud droplet number concentration and the size of the hail grains, consequently leading to an increase in hail production. Additionally, a higher cloud droplet number concentration leads to a greater mass of hail via pronounced riming. This cause-and-effect relationship is not observed in the single-moment experiments.
• The mean diameter of the hail, which is diagnostically determined by the single-moment scheme, is not consistent with the microphysical processes, such as the accretion rates, melting and sublimation of hailstones. Changing the mean radius of the drops has little impact on the mean diameters of the hailstones. An incorrect determination of the mean diameter of the hailstones by the single-moment scheme leads to an unrealistic description of microphysical processes.
• We strongly recommend using the double-moment bulk microphysical scheme with the unified Khrgian-Mazin size distribution for the entire drop spectrum. The prescribed value for the cloud droplet number concentration (or the mean radius of drops in the single-moment scheme) depends on the type of simulated cloud (maritime or continental). Therefore, the values of 60 and 600 cm⁻³ are recommended for the prescribed values of the cloud droplet number concentration in maritime and continental cases, respectively. Hence, the measurement of the cloud droplet number concentration can be very useful and substantial for numerical prediction of storms and theoretical considerations. If a cloud is simulated using the single-moment scheme, then a mean radius of 20 or 30 µm is appropriate for maritime convective clouds. Higher values of the mean radius of drops (e.g., 40 or 50 μm) are not observed [41]; therefore, these values are not recommended for simulating convective clouds with the single-moment scheme. The typical value of 10 µm for continental clouds [41] is not recommended due to the unrealistically small raindrop number concentration. Hence, we suggest using slightly higher values for the mean radius of drops (e.g., 15 μm).