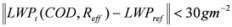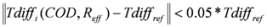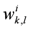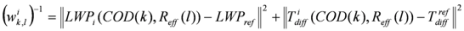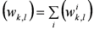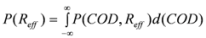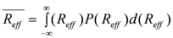Next Article in Journal / Special Issue
Initial Assessment of the Spectrometer for Sky-Scanning, Sun-Tracking Atmospheric Research (4STAR)-Based Aerosol Retrieval: Sensitivity Study
Previous Article in Journal / Special Issue
A Polarized Atmospheric Radiative Transfer Model for Calculations of Spectra of the Stokes Parameters of Shortwave Radiation Based on the Line-by-Line and Monte Carlo Methods
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Atmosphere
Volume 3
Issue 4
10.3390/atmos3040468
atmosphere-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Development of a Ground Based Remote Sensing Approach for Direct Evaluation of Aerosol-Cloud Interaction

by
Bomidi Lakshmi Madhavan
1,*,
Yuzhe He
2,
Yonghua Wu
2,
Barry Gross
2,
Fred Moshary
2 and
Samir Ahmed
2
1
Particle and Aerosol Research Lab, Department of Chemical Engineering, Indian Institute of Technology Bombay, Mumbai 400-076, India
2
NOAA-CREST, The City College of the City University of New York, New York, NY 10031, USA
*
Author to whom correspondence should be addressed.
Atmosphere 2012, 3(4), 468-494; https://doi.org/10.3390/atmos3040468
Submission received: 13 June 2012 / Revised: 27 August 2012 / Accepted: 21 September 2012 / Published: 17 October 2012
(This article belongs to the Special Issue Advances in Studies of Atmospheric Aerosol and Clouds Using Remote Sensing Techniques)
Browse Figures
Versions Notes

Abstract

:
The possible interaction and modification of cloud properties due to aerosols is one of the most poorly understood mechanisms within climate studies, resulting in the most significant uncertainty as regards radiation budgeting. In this study, we explore direct ground based remote sensing methods to assess the Aerosol-Cloud Indirect Effect directly, as space-borne retrievals are not directly suitable for simultaneous aerosol/cloud retrievals. To illustrate some of these difficulties, a statistical assessment of existing multispectral imagers on geostationary (e.g., GOES)/Moderate Resolution Imaging Spectroradiometer (MODIS) satellite retrievals of the Cloud Droplet Effective Radius (Reff) showed significant biases especially at larger solar zenith angles, further motivating the use of ground based remote sensing approaches. In particular, we discuss the potential of using a combined Microwave Radiometer (MWR)—Multi-Filter Rotating Shadowband Radiometer (MFRSR) system for real-time monitoring of Cloud Optical Depth (COD) and Cloud Droplet Effective Radius (Reff), which are combined with aerosol vertical properties from an aerosol lidar. An iterative approach combining the simultaneous observations from MFRSR and MWR are used to retrieve the COD and Reff for thick cloud cases and are extensively validated using the DoE Southern Great Plains (SGP) retrievals as well as regression based parameterized model retrievals. In addition, we account for uncertainties in background aerosol, surface albedo and the combined measurement uncertainties from the MWR and MFRSR in order to provide realistic uncertainty estimates, which is found to be ~10% for the parameter range of interest in Aerosol-Cloud Interactions. Finally, we analyze a particular case of possible aerosol-cloud interaction described in the literature at the SGP site and demonstrate that aerosol properties obtained at the surface can lead to inconclusive results in comparison to lidar-derived aerosol properties near the cloud base.

1. Introduction

One of the outstanding issues regarding the earth’s energy balance and subsequent climate budget are the indirect effects that aerosols have on cloud radiative properties. In particular, Twomey [1] increased aerosol loading results in higher concentration of cloud condensation nuclei that ultimately lead to increased cloud droplet number concentration and smaller effective cloud droplets, which have to be compared, however, for constant liquid water paths. Unlike direct cloud effects on the climate, the aerosol-cloud indirect interactions are very hard to measure directly from satellites, since simultaneous aerosol loadings (especially below cloud base) and cloud properties such as COD and/or Reff are not possible and therefore efforts at quantifying these effects are limited to statistical trends studied over large domains. However, because of the difficulties of more direct approaches, extensive satellite studies of aerosol-cloud indirect effect have been pursued and supported by significant improvement in multispectral satellite sensors onboard polar orbiting satellites.
For example, regional measurements and resultant cloud products from MODIS (MODerate resolution Imaging Spectroradiometer) were used [2] together with aerosol properties estimated from the MODIS (e.g., aerosol optical depth product) to ascertain statistical relationships between appropriate aerosol and cloud parameters which include Cloud Top Temperature and Pressure, Cloud Droplet Number Concentration (CDNC), Total Cloud Fraction, Water Path, Cloud Droplet Effective Radius (Reff), Cloud Optical Thickness (COD), Cloud Condensation Nuclei (CCN) and Aerosol Optical Thickness (AOT). In this study, it was found that on average large regions are laden with fluctuating correlations between cloud and aerosol metrics, which average to zero as might be expected. However, with appropriate binning of the data by Liquid Water Path (LWP) and with ancillary data provided by ISCCP (International Satellite Cloud Climatology Project) to ascertain regions of dominant cloud type (stratus or convective clouds), an inverse relationship between the size of the water droplet (effective radius) and column cloud droplet number concentration, cloud optical thickness (reflectivity) and cloud fraction emerged. These relationships were connected to the aerosol properties through an observed inverse correlation between aerosols and droplet radii in support of the general Aerosol Indirect Effect (AIE).
However, the story is not so clear-cut. For example, both modeling and observation studies have suggested possible correlations between AOT and LWP [3,4]. Nevertheless, the analysis of the data showed significant differences between low AOT (ta < 0.1) and higher AOT (ta > 0.1). In particular, for low AOT, a strong positive correlation was observed, but for high AOT, a strong negative correlation between aerosols and water path was observed. Further studies showed even more complex behavior. To remove some of the inherent difficulties in simultaneous cloud/aerosol retrieval, aircraft measurements of large scale marine stratocumulus decks showed significant correlation between CDNC and accumulation mode number concentration (AMNC) below cloud base [5] reporting a regression result of 0.72 ± 0.04 with an R2 of 0.90. This result indicates that a satellite remote sensing approach to quantifying CDNC should be a reasonable proxy for aerosol signatures (at least for relatively clean maritime conditions) in exploring aerosol-cloud interaction. To utilize this observation, Han et al. [6], studied the correlations between LWP and CDNC for warm water clouds (cloud-top temperature > 273 K, optical thickness 1 < tc < 15). These results, however, revealed three distinct relationships between cloud liquid water path with aerosol changes: increasing, approximately constant, or decreasing as column CDNC increases, each occurring with nearly equal probability. The negative correlation may result from the mechanism that an increase of CDNC with subsequent reduction in cloud droplet size can enhance evaporation just below cloud base. In this scenario, the cloud decouples from the boundary layer in warmer locations, decreasing the supply of water to the cloud from the surface, thereby reducing the cloud liquid water.
While such statistical studies have provided some useful information, poor temporal statistics make it particularly difficult to establish underlying causal mechanisms. One possible approach maybe the use of suitable multispectral imagers on geostationary platforms (e.g., GOES) for simultaneous cloud/aerosol retrieval. One clear advantage is that characterization of the cloud diurnal cycle is potentially feasible with geostationary satellite instruments. In particular, the availability of additional spectral channels at 1.6, 3.9, and 12 or 13.3 μm in addition to the original VIS (0.65 μm) and IR (10.8 μm) channels have led to the operational retrieval of optical depth, effective radius and LWP and motivates the possibility of following the cloud through its lifecycle as it is transported in polluted areas [7]. However, even in this case, a large number of issues degrading the observations can be expected. For example, the poor spatial resolution of the satellite observations ~4 km are significantly above the optimal length scales attributed to the aerosol/cloud processed under investigation. In particular, extensive investigations [8,9] based on the analysis of ground based/in situ observations on the appropriate scales indicate the need for spatial sampling of the processes <1 km. Based on realistic advection velocities of 5 m∙s−1, temporal sampling averaging should be constrained to ~3 min which is reachable with our MFRSR/MWR/lidar approach.
In addition, an equally difficult issue is to retrieve the true aerosol loading near the cloud base. In particular, it is quite evident that column measurements of aerosol optical depth do not provide the vertical information needed to quantify the pollution level at the cloud base. Furthermore, the relationship between optical depth and particle number depends on the microphysical distribution models and does not discriminate between aerosol types below cloud base that impact cloud micro-physics and aerosol particles located higher than cloud top that only interact with the radiative transfer above clouds. Therefore, it is clearly important to develop short-term measurements with high temporal resolution to eliminate many of the previously cited ambiguities. In particular, under such an approach, simultaneous measurements of clouds and aerosol loading below cloud base along with important vertical updraft data are achievable. Most importantly, within the measurement cycle, the exact nature of the cloud within the cloud lifecycle including general meso-scale processes is less important for these short-term measurements.
Various efforts have been made to develop retrieval algorithms to infer COD and Reff from ground based passive radiometric measurements. In one approach, a Microwave Radiometer (MWR) is combined with Millimeter-wavelength Cloud Radar (MMCR) to infer droplet diameters. In this case, the radar reflectivity and the MWR LWP provide the information to retrieve Reff [10]. However, the cost of the MMCR can be quite substantial. On the other hand, significant success in combining COD from the Multi-filter Rotating Shadowband Radiometer (MFRSR) together with LWP from MWR is a reasonable cost-effective solution [11,12,13]. One drawback in this method is obviously the limitation that observations must be made during daytime. However, significant aerosol-cloud interaction signals should exist during daytime especially under conditions of strong convective heating which enhances vertical uptake [14].
In particular, a number of studies have made the attempt to explore Aerosol-Cloud Interaction at the SGP site using the available instrument suites. For example, the MMCR/MWR technique was applied [15] to explore a number of potential cases together with a Raman lidar, which was used to estimate aerosol CCN below the cloud. This study did in fact find a number of cases showing reasonable Aerosol Indirect Effects. In particular, the Aerosol Cloud Index (ACI) was defined [16,17] as
Atmosphere 03 00468 i001
which represents the relative change in mean cloud droplet effective radius (Reff) for a relative change in aerosol extinction (α) for clouds having the same LWP. Values of ACI ~0.1 were found for multiple cases over the multiyear datasets which are reasonable for considering the upper theoretical limit of ACI < 1/3.
However, one of the main purposes is to avoid the use of the MMCR and explore the potential of the MFRSR/MWR retrieval. For example, Kim et al. [18] used this approach to explore potential aerosol-cloud modifications. Unlike the Feingold study however, they did not make use of the lidar extinction being content to use surface Nephelometer measurements instead. This approach seems to be sufficient if the cloud base is sufficiently low to the surface, which in fact holds for most examples considered. However, it was noted in their study that some examples did not satisfy this requirement and that the poor results on these days are inferred to decoupling between the surface and aloft aerosols.
Due to lack of current long-term data at the NYC CCNY site, we limit our present study to testing and demonstrating this approach using the multi-year measurements performed at the SGP site of the Atmospheric Radiation Measurement (ARM) Program. In addition, we make use of the filtering accomplished by previous studies to identify optimal cases. The present study is organized as follows: In Section 2, we provide a detailed assessment of satellite based retrievals in comparison to existing ground retrievals pertaining to overcast clouds and highlight the need for utilizing ground based remote sensing for effective cloud retrievals. In Section 3, we describe the details of ground-based instruments used for cloud property and provide assessments when possible to illustrate the performance of these instruments. In Section 4, we describe our retrieval algorithm and make quantitative comparisons with the other algorithms. Section 5 mainly focuses on validating our retrieval approach with the comparison of algorithms described in the previous section. In Section 6, a thorough sensitivity analysis is performed focusing on cloud droplet effective radius retrieval errors resulting from both uncertainties in the ambient environment (including surface albedo) as well as those from the measurements themselves. In Section 7, we re-examine a previously studied aerosol-cloud interaction case at SGP site to highlight the importance of using upper atmosphere aerosol measurements. Finally, section 8 provides a thorough discussion followed by our conclusions in Section 9.

2. Assessment of Satellite-Based Remote Sensing for Cloud Property Retrievals

2.1. Background

Optical depth retrievals from satellite radiances are particularly sensitive to assumptions regarding particle phase and single scattering properties as well as instrument calibration [19]. For thick cloud cases, uncertainties in satellite optical depth retrievals are further magnified because of the asymptotic relationship between reflectance and optical depth [12] whereas small differences in reflectance equate to very large differences in optical depth as they tend to become large. This uncertainty likely contributes to much of the scatter in our comparisons. Due to horizontal transport of photons, bias in visible optical depth retrievals from satellite radiances are known to occur when the scale of the satellite retrieval is less than a radiative smoothing scale that depends on cloud geometry [20]. The cloud retrievals from VISST algorithm (GOES) have been compared with active and passive radiometric measurements at surface sites, primarily ARM SGP central facility in Oklahoma [21,22]. Another possible source of bias in optical depth is caused by sub-pixel variability of optical depth. A satellite radiometer measures pixel mean radiance and from this quantity derives an optical depth that equates to an approximation of the logarithmic mean of the optical depth within the pixel. The exact relationship in any given instance between pixel-mean radiance and the desired pixel-mean optical depth depends on the variability of the cloud field within the pixel but would result in the satellite measured COD being biased low (discussed in Section 2.3) [23].

2.2. Comparisons between Different Satellite Retrievals

To obtain cloud property measurements (COD and Reff) from satellites, the need for multi-wavelength imager measurements is critical. Over the past 10 years, significant improvements in multispectral satellite sensors onboard polar and geostationary orbiting satellites and the radiative transfer modeling of clouds have provided a mechanism for the retrieval of relevant cloud microphysical properties as well as estimates of aerosol column properties.
In order to improve the climatology of satellite-derived cloud properties over the ARM SGP domain (32N–42N, 91W–105W), the Visible Infrared Solar-infrared Split Window Technique (VISST algorithm), developed by Minnis et al. [24], is used. Although the latest version of the VISST algorithms is fairly complex, the essence of the VISST relies mainly on the thermal (12.0 µm and 10.8 µm) channels to determine cloud temperature and phase, the visible (0.65 µm) reflectance to retrieve COD, and the solar-infrared (3.9 µm) radiance to derive cloud particle size. To visualize this VISST algorithm performance, we show in Figure 1, the TOA reflectance measurement space as a function of COD and Reff. Clearly, the retrieval sensitivity for the cloud effective radius is nearly independent of the visible COD retrieval. Therefore, a reasonably accurate calibration of the 3.9 mm should result in quite good retrievals of the Reff as long as the cloud parameterization is reasonably accurate.
Atmosphere 03 00468 g001 1024
Figure 1. Reflectance sensitivity plot for Visible Infrared Solar-infrared Split Window Technique (VISST) channels assuming water phase cloud.
Figure 1. Reflectance sensitivity plot for Visible Infrared Solar-infrared Split Window Technique (VISST) channels assuming water phase cloud.
Atmosphere 03 00468 g001
The GOES radiances are calibrated with collocated measurements from the TRMM (Tropical Rainfall Measuring Mission Visible Infrared Scanner) [25]. Based on various size distributions of water droplets and hexagonal ice crystal columns, radiances are modeled in VISST to simulate liquid and ice clouds, respectively [26]. The resultant VISST algorithm provides cloud optical depth, phase, effective particle size, ice or liquid water path, effective radiating temperature, and effective cloud height (determined from the effective cloud temperature using a vertical profile of temperature for a particular location). The pixel level data from GOES-WEST (G10/G11) & GOES-EAST (G12/G13) over ARM SGP domain were obtained in netcdf format from the archives of the ARM site.
In a fairly similar multispectral approach, the MODIS (Moderate Resolution Imaging Spectroradiometer) Level 2, Collection 5 retrievals [27] are provided at 1 km × 1 km spatial resolution at nadir by combining infrared and visible techniques to determine physical and radiative properties. Using the MODIS visible (0.645 mm) and near-infrared (1.64, 2.13, and 3.75 mm) spectral bands, the daytime shortwave cloud retrieval algorithm over land surfaces will provide the cloud optical thickness and effective particle radius. To retrieve cloud optical thickness and effective particle radius, a radiative transfer model is first used to compute the reflected intensity field (radiance). This radiance, Iλ(0,−m,f), is normalized in terms of the incident solar flux, F0(λ), such that the reflection function, Rλ(t,Reff;m,m0,f), is given by,
Atmosphere 03 00468 i002
where t is the total optical thickness of the atmosphere (or cloud), Reff the effective particle radius as defined in Hansen and Travis [28]. The differences in reflected solar radiation between the 0.645 mm and 1.64 mm bands contain information regarding cloud particle phase due to distinct differences in bulk absorption characteristics between water and ice at the longer wavelength. If the cloud is composed of ice, or if the surface is snow covered, then reflectance of the cloud at both 1.64 mm and 2.13 mm bands will show a decrease in reflectance, but the reduction is more significant with the former band. Details of retrieval technique are described in King et al. [29].
Inter-comparison of cloud retrievals from MODIS and GOES in Figure 2 demonstrate fairly good linear correlation for both COD (r2 ~ 0.92) and Reff (r2 ~ 0.86). Here, we use both 10 km and 20 km spatial domains centering the Central Facility at Lamont, Oklahoma. Simultaneous matchups are reported when GOES observations are averaged ±1 h around the MODIS over-flight over the four-year data period (2007–2010). Minnis et al. [30] reported that MODIS tends to throw out a large percentage of small clouds, but the average CODs only differed by ~2.0 in non-polar regions. In summary, due to the very similar structure of the algorithms, strong agreement is expected.
Atmosphere 03 00468 g002 1024
Figure 2. Comparison plots of Moderate Resolution Imaging Spectroradiometer (MODIS) and Geostationary Operational Environmental Satellites (GOES) derived Cloud Optical Depth (COD) and Cloud Droplet Effective Radius (REFF) with 10 km (a,b) and 20 km (c,d) averaging centering ARM SGP site Lamont (Oklahoma) for the data covering 2007–2010.
Figure 2. Comparison plots of Moderate Resolution Imaging Spectroradiometer (MODIS) and Geostationary Operational Environmental Satellites (GOES) derived Cloud Optical Depth (COD) and Cloud Droplet Effective Radius (REFF) with 10 km (a,b) and 20 km (c,d) averaging centering ARM SGP site Lamont (Oklahoma) for the data covering 2007–2010.
Atmosphere 03 00468 g002

2.3. Preliminary Comparisons between GOES-VISST and Ground Based Techniques

While the satellite comparisons themselves are consistent with no appreciable bias observed, it is important to assess the validation performance against independent approaches making use of entirely different methodologies. To do this, we make use of the extensive ground based retrievals from the SGP site [12], which we will refer to in this study as based on the Min method, which will be explained in much greater detail in Section 4. Since the VISST algorithm has gone through different versions, we concentrate on the latest version (V4). The pixel level datasets are given at 4 km resolution that is commensurate with the MFRSR FOV. However, to ensure some extra homogeneity in the observation scenes, we look at 20 km regions. The resultant data within the 20 km domain consists of 20 pixels. At the same time, the ground products provide data every 20 s. Using a 30-min interval, this leads to 90 ground measurements. With these caveats in mind, we use the following matchup protocol between the ground based and GOES VISST algorithm.
  • Only those cases where number of water phase cloud pixels (out of 20) in the 5 × 5 box (20-km resolution) is greater than 15 are used and no ice phase clouds are detected.
  • The variability (standard deviation) of the COD <50% of the mean COD.
  • The ground-based retrievals are acceptable only if all 90 measurements are cloud flagged.
These severe constraints were applied to the VISST V4 retrievals from 1 July 2011 to 22 November 2011 and the comparisons of both the COD (left column) and Reff (right column) are illustrated in Figure 3. The upper row was restricted to observations where the solar zenith angle, θsun < 50 degrees while the bottom row was filtered in the range 50 degrees < θsun < 70 degrees.
Atmosphere 03 00468 g003 1024
Figure 3. Comparison of VISST GOES cloud products against ground based retrievals—columns are respectively for COD and Reff. The upper row is filtered for solar zenith angle qsun < 50 degrees while the bottom row was filtered in the range 50 degrees < θsun < 70 degrees. The horizontal and vertical error bars represent the standard deviations in ground and GOES retrievals respectively corresponding to both COD and Reff.
Figure 3. Comparison of VISST GOES cloud products against ground based retrievals—columns are respectively for COD and Reff. The upper row is filtered for solar zenith angle qsun < 50 degrees while the bottom row was filtered in the range 50 degrees < θsun < 70 degrees. The horizontal and vertical error bars represent the standard deviations in ground and GOES retrievals respectively corresponding to both COD and Reff.
Atmosphere 03 00468 g003
The most important observation is that although the COD retrievals are fairly robust over all solar zenith angles especially for COD < 50, the effective radius shows very strong bias and poor correlation to ground retrievals when θsun > 50 degrees. Specifically, GOES retrieved Reff is larger than ground retrieved Reff. To understand this, we note that as the solar zenith angle increases, the ‘effective’ cloud optical depth also becomes larger. For this reason, photons incident on a water cloud will be more likely to be reflected back to satellite from an upper part of the cloud without penetrating into a lower part of the cloud. On the other hand, photons transmitted through the cloud encounter the entire vertical profile regardless of the cloud optical depth. Since many researchers [31,32,33,34,35,36] have reported that cloud droplet effective radius increases from cloud base to cloud top, the GOES retrieved Reff based on reflection geometry is biased high. These difficulties make it even more important that ground approaches are explored.

3. Ground-Based Instrumentation and Data Processing

In the present study, we focus on the measurements from the ground-based radiometers, namely, the Multi-Filter Rotating Shadowband Radiometer (MFRSR, Model: MFR-7, Yankees Environmental Systems Inc.) and the profiling Microwave Radiometer (MWR, Model: MP-3000A, Radiometrics) for cloud retrievals. It should be pointed out that the MP-3000A at CCNY is an advanced radiometric system in comparison to the existing dual channel MWR at the ARM site.
The MFRSR is a seven channel radiometer with six passbands of 10 nm FWHM (Full Width Half Maximum) centered at 415, 500, 615, 670, 870 and 940 nm and an unfiltered Si broadband (300–1,100 nm) channels. It uses an automated shadowbanding technique to measure the total-horizontal (global), diffuse-horizontal and direct-normal spectral irradiances through a single optical path [12,37,38]. The global and diffuse components are measured directly and the direct-normal component is computed from the difference of the two measured components. On a clear day, most of the solar radiation received by a horizontal surface will be direct-normal irradiance, while on a cloudy day most will be diffuse-horizontal irradiance. Observations of atmospheric irradiance (direct, diffuse and global) under overcast skies by MFRSR therefore provide the potential capability to infer cloud transmittance or the COD.
At CCNY, we use an automated MFRSR data processing algorithm developed at NASA GISS by Alexandrov et al. [39] with cloud screening procedure [40] being used for aerosol retrieval as well as calibration. In our application, the calibration is crucial since the cloud properties are determined radiatively from a diffuse transmission, which can only be obtained from the diffuse irradiance if calibrated. In the GISS method the calibration independent direct to diffuse ratio was used in the regression analysis to enhance the stability of regression and decrease the noise in the retrieved calibration coefficients when compared to traditional Langley technique. Since, this method does not require stable aerosol loading over long time periods; it takes care of data for which Langley regression fails. Thus, more observational data is included in the determination of the calibration coefficients. The most notable aspect about this MFRSR processing algorithm is that both calibration and retrieval procedures are not separated, while the traditional retrievals [41,42,43] require prior determination of calibration constants (through a calibration procedure) and applied to the data. In this approach, contributions due to different physical parameters (such as aerosol extinction, gaseous absorption) into total optical depths are separated first and then calibration is applied independently. Thus, calibration errors in one parameter do not affect the accuracy of the other retrievals.
To improve the consistency over long time periods, the NASA GISS algorithm is applied simultaneously to a set of daily datasets covering at least a month (or a maximum of 4 months) of measurements through a sequential set of procedures: first, all days are cloud screened, then all 870 nm records are calibrated using compatibility between the direct and diffuse measurements. This approach allows for stabilization of the daily calibration constants at each step using a robust smoothing technique. Internal coefficients are instantaneous, derived for each day (using direct to diffuse ratio and size-regression methods) independently from other days, while the external coefficients result from averaging (smoothing) and/or interpolation of time series of internal coefficients over a long period (default ~4 months). These external coefficients are the ones ultimately used to compute the top-of-atmosphere (TOA) irradiance. In our cloud retrieval algorithm, the measured irradiance is divided by a nominal TOA irradiance value to obtain the diffuse transmittance. Here, I0 is directly related to the calibration constant, C = exp(−c), where c is the external calibration coefficient making the calibration coefficient of the MFRSR a critical parameter.
The resultant atmospheric transmittances are therefore calculated under cloudy conditions as the ratio of calibrated diffuse irradiance to the TOA irradiance value. However, in order to obtain simultaneously both the COD and Reff of the prevailing thick clouds, we require an additional measurement which can give the total liquid water content in the cloud layer, termed as liquid water path, in the zenith direction which is the main function of the MWR. In particular, both column integrated precipitable water vapor (PWV) and cloud liquid water path (LWP) are defined as,
Atmosphere 03 00468 i003
and Atmosphere 03 00468 i004
where ρwt is the density of liquid water (~106 g∙m−3), ρv(z) is the vertical distribution of water vapor density (expressed in g∙m−3) and w(z) is the vertical distribution of cloud liquid water content (expressed in g∙m−3). Here we express PWV in cm and LWP in g∙m−2. Using the above relations, the cloud droplet effective radius (Reff), an important property governing the cloud radiative transfer [28], is defined as the ratio of third to second moments of the size distribution of the cloud droplet number concentration. For a spatially homogeneous cloud,
Atmosphere 03 00468 i005
where N(r) is the size distribution of the cloud droplets and r (= Reff) is the cloud droplet radius. In case of vertically inhomogeneous clouds,
Atmosphere 03 00468 i006
The double integrals are taken over droplet radius and over the depth of the cloud. Evaluating the definition of Reff in terms of measured LWP and tc (or COD),
Atmosphere 03 00468 i007
Atmosphere 03 00468 i008
where Qe(r) is the extinction efficiency for a cloud droplet of radius (r). For λ = 415 nm and for modified gamma size distribution with width p = 7 [44], the weighted extinction efficiency can be approximated by,
Atmosphere 03 00468 i009
which is only a slight correction to Q415nm (r) ≈ 2, yielding the simple and often used result
Atmosphere 03 00468 i010
The profiling Microwave Radiometer (MWR) at CCNY contains two radio frequency (RF) subsystems sharing the same antenna and antenna pointing system in the same cabinet. The water vapor profiling subsystem utilizes sky brightness temperature observations at selected frequencies between 22 and 30 GHz (21 channels). The temperature profiling subsystem utilizes sky brightness temperature observations at selected frequencies between 51 and 59 GHz (14 channels). The profiler nominally views in zenith direction and makes use of atmospheric radiation measurements in the RF domain and provides high resolution vertical profiles of temperature, humidity, water vapor and low resolution profiles of liquid density at 58 altitude levels, starting with 50 m steps from the surface up to 500 m, then 100 m steps to 2 km, and 250 m steps from 2 to 10 km. In addition, surface relative humidity, temperature and barometric pressure measured by the radiometer are used in the determination of profiles. An internally mounted and vertically pointed Infrared Thermometer (IRT) indicates the presence of cloud and measures cloud base temperature, if clouds are present. Knowing cloud base temperature yields the vapor density at cloud base (at saturation) and when combined with the retrieved temperature profile, yields cloud base altitude. These physical measurements are important constraints for profile retrieval. Neural networks (site specific) derived using the Stuttgart Neural Network Simulator and long-term record of radiosonde profiles are provided by Radiometrics. A standard back-propagation algorithm was used for training and a standard feed-forward network is used for profile determination. Although the number of independent measurements (eigen values) are less than the 58 retrieved layers, the finer resolution provides better displays and easier processing in subsequent data processing steps.
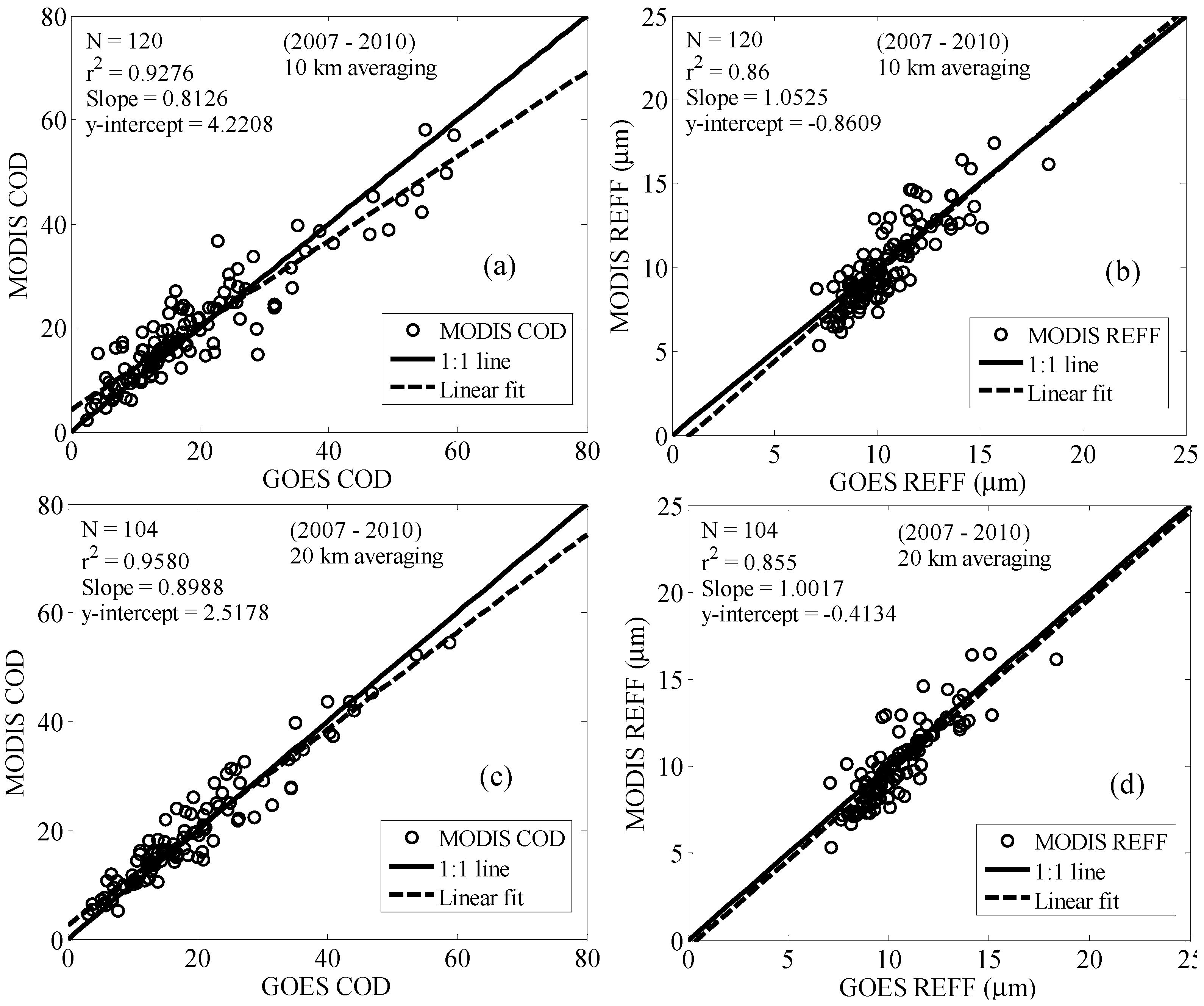
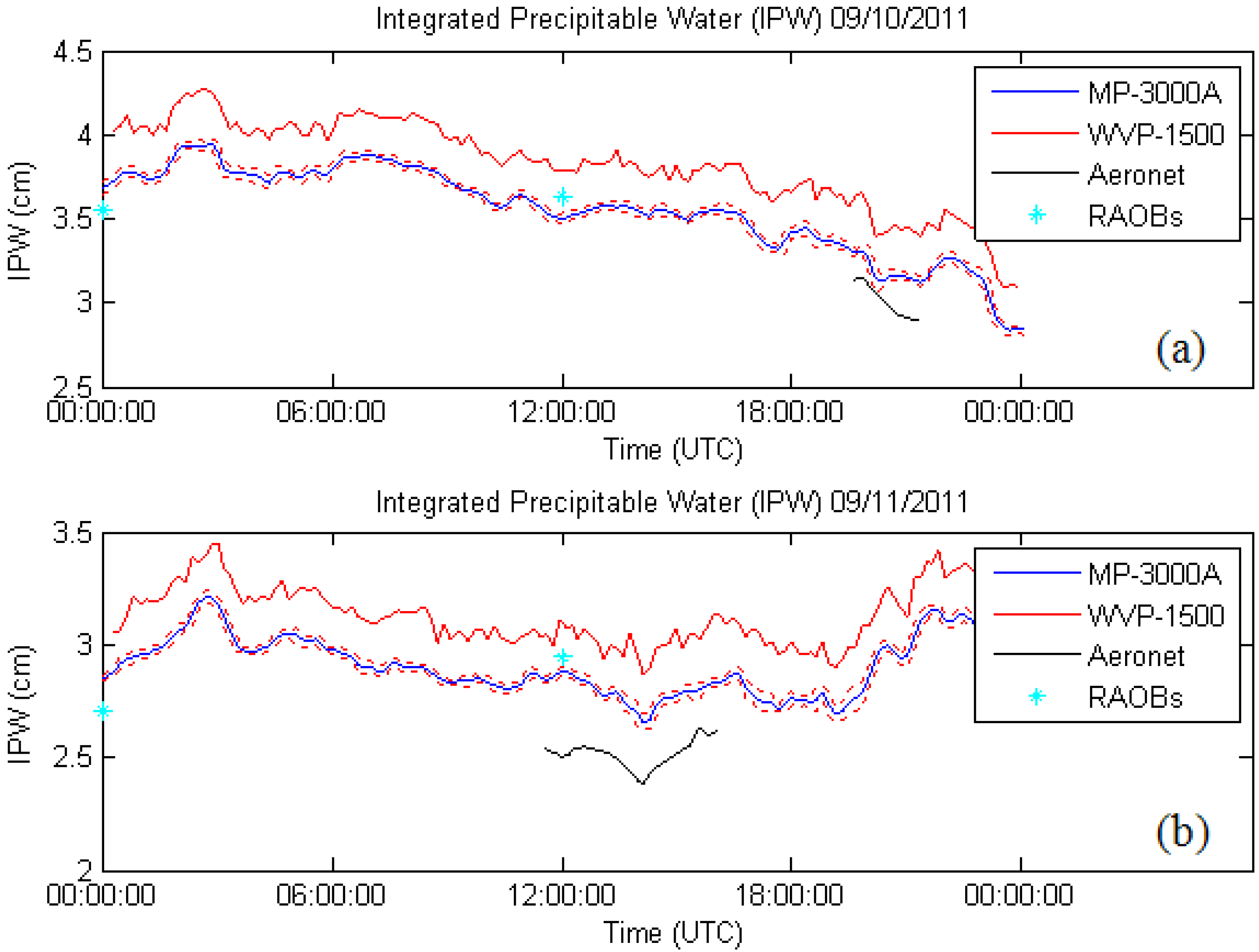
In our application, we are interested mainly in the LWP but validation of this parameter is very difficult in the absence of aircraft measurements. On the other hand, direct channel calibration for our system can be tested. To do this, we have made some cross validations against the two instruments against existing radiosondes and AERONET at the Brookhaven National Laboratory (BNL) as part of an overall calibration exercise. The results are given in Figure 4 for the 2 days when all measurements are available. For both days, the MP-3000A was a better match against the AERONET retrievals than with the WVP-1500. In addition, there is clear improvement (especially for day 2) in the comparisons against the Radiosonde launches. This comparison illustrates the general consistency in the calibration of the radiometers. However, we do note a near constant bias between the two systems, which is likely due to differences in the algorithm training datasets used by the different systems.
Atmosphere 03 00468 g004 1024
Figure 4. Inter-comparison of column Integrated precipitable water (IPW) from MP-3000A, WVP-1500 (microwave radiometers), AERONET and Radiosondes (RAOBs) for (a) 10 September 2011, and (b) 11 September 2011. Red lines with which blue line is flanked represents the interval of confidence for the MP-3000A dataset based solely on temporal fluctuations of retrieval.
Figure 4. Inter-comparison of column Integrated precipitable water (IPW) from MP-3000A, WVP-1500 (microwave radiometers), AERONET and Radiosondes (RAOBs) for (a) 10 September 2011, and (b) 11 September 2011. Red lines with which blue line is flanked represents the interval of confidence for the MP-3000A dataset based solely on temporal fluctuations of retrieval.
Atmosphere 03 00468 g004

4. Development of an Iterative Algorithm for Retrieval of Optically Thick Cloud Properties

Of the various ground based cloud retrieval techniques, the most extensively used and referenced approach for measurements from the MFRSR-MWR system is the Non-linear Least Squares (NLSQ) retrieval algorithm of Min and Harrison [12] hereafter referred as MIN, which is based on the parameterization of cloud droplet scattering properties at 415 nm on the effective radius and LWP using Mie theory. MIN uses an adjoint formulation of the radiative transfer [45] to maintain accuracy and improve its execution speed. In this approach, traditional Langley regression of the direct-normal irradiance taken on clear stable days are used to extrapolate the MFRSR's response to the TOA [37], and this calibration is applied to the total-horizontal irradiance. Harrison and Michalsky [37] have indicated that the standard deviation of the traditional Langley analysis inferred extra-terrestrial response from a single retrieval at a difficult site to be approximately 5%. The MIN method is applied to measurements of atmospheric transmittance at 415 nm band because this band is completely insensitive to absorption by ozone and by permanent atmospheric gases, and the surface albedo is low and stable for natural surfaces (except for snow-covered surfaces). Moreover, for this wavelength, both the asymmetry parameter and the single scattering albedo (close to unity) show little dependence on droplet size.
In another approach, Matamoros et al. [13] builds a parameterized regression based inversion of a plane parallel radiative transfer (RT) model hereafter referred as PAR based on the assumption of a fixed rural background aerosol mode for SGP ARM site. The parameterization based on regression fitting from the RT simulations is given by
Atmosphere 03 00468 i011
where P1 = −0.4330 × AOD + 3.6659,
     P2 = −0.7686 × AOD + 2.0895, and
     P3 = −0.1986 × AOD − 5.7936
Here µ0 is the cosine of the solar zenith angle, T is the atmospheric transmittance, rg is the surface albedo at 415 nm, tc and re respectively are the visible COD and cloud droplet effective radii (Reff). The linear dependence of P1, P2 and P3 with AOD agrees for AOD ranging from 0 to 0.2. Also, this method points out that AOD has an effect in the retrieval of cloud properties, but was unable to prove that introducing AOD improves the agreement between the retrieved properties and the true (and unknown) values of COD and Reff. Of course, this approach can be extended to more regional realistic aerosol models for different locations as needed.
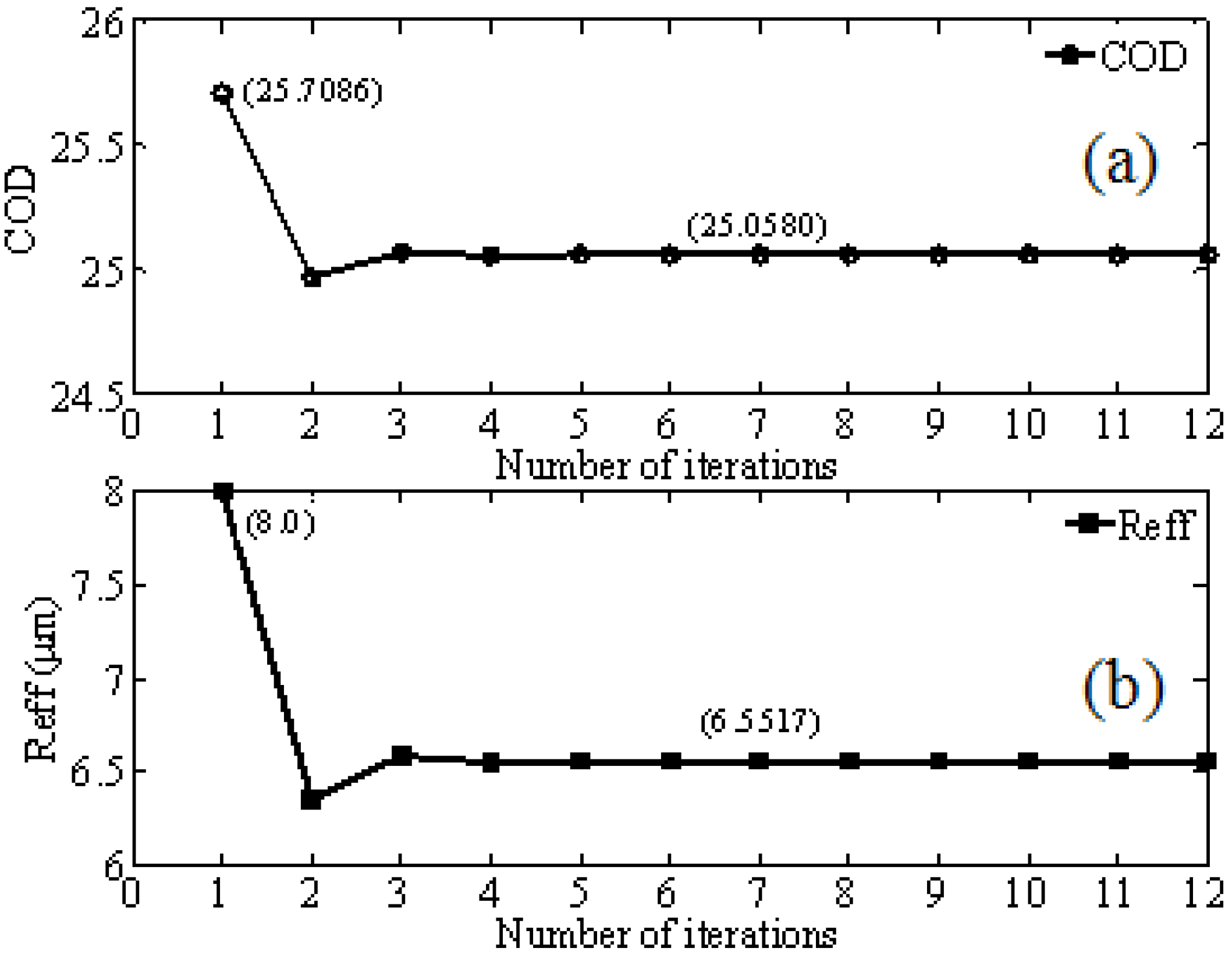
In our analysis, we closely follow the MIN algorithm but instead of a NLSQ optimization, we develop an iterative inversion approach. This iteration approach forms the basis of our retrieval algorithm, hereafter referred to as RET. Initially, Reff is fixed at 8 mm and the first estimation of COD from the Look-Up-Table (LUT) is obtained. Then Q415nm(Reff) is estimated from Equation (9) assuming again Reff = 8 mm. Subsequently, by introducing the MWR measured value of LWP (i.e., LWPmeas), Equation (10) is used to obtain better estimation of effective radius (Reff), which will again obtain a better estimate of COD using the LUT. This iteration procedure continues until stable values of COD and Reff (i.e., convergence of LWPtheory to LWPmeas occurs) are obtained for each of the atmospheric transmittance measurement (as shown in Figure 5).
Atmosphere 03 00468 g005 1024
Figure 5. Convergence of iterative retrieval algorithm for (a) COD and (b) Reff.
Figure 5. Convergence of iterative retrieval algorithm for (a) COD and (b) Reff.
Atmosphere 03 00468 g005
The schematic of our LUT based iterative approach for cloud optical properties of thick cloud is illustrated in Figure 6. To implement efficiently, initial 2D LUT’s are developed for the LWP and diffuse transmittance and interpolation is used when readjusting Reff during the retrieval. By comparing with the results of the MIN approach obtained from the SGP database, we can assess our local algorithm.
Atmosphere 03 00468 g006 1024
Figure 6. Schematic illustration of the algorithm flow for the LUT based iterative approach for retrieving cloud optical properties of thick water clouds. Here cloud liquid water path (LWPmeas) represents the real-time instantaneous liquid water path measurement from MWR and the order (or number) of iteration is denoted by “n” as subscript to the variable terms.
Figure 6. Schematic illustration of the algorithm flow for the LUT based iterative approach for retrieving cloud optical properties of thick water clouds. Here cloud liquid water path (LWPmeas) represents the real-time instantaneous liquid water path measurement from MWR and the order (or number) of iteration is denoted by “n” as subscript to the variable terms.
Atmosphere 03 00468 g006
As discussed earlier, we require real-time measurements of atmospheric transmittance (for 415 nm wavelength) as a function of cosine of solar zenith angle (m0) from the MFRSR, the LWP from the MWR as well an estimate of aerosol loading and surface albedo. The Santa Barbara DISORT Atmospheric Radiative Transfer (SBDART, version 2.4) [44] model, which is based on the DISORT algorithm (Discrete Ordinate Radiative Transfer) to account for multiple scattering within layered media [46] is used for computing the radiation fluxes at the surface and at the TOA. Within SBDART, atmospheric transmittance is defined as the ratio of downwelling irradiance at the surface to that at the TOA for a narrow wavelength band corresponding to the MFRSR 415 nm channel. In a preliminary analysis, we define a site-specific (average) aerosol model based on the long-term climatological record of AERONET Level 2 datasets. The aerosol climatology parameters include aerosol optical depth (AOD), single scattering albedo (SSA) and asymmetry parameter (g) spectrally covering the shortwave region. Also, the climatological surface albedo value is chosen from the ASRVN (AERONET Surface Reflectance Validation Network) data record. SBDART treats atmosphere as a plane parallel system, so vertical inhomogenities of the atmosphere and the aerosol distribution can be taken into account. Given the fixed aerosol model, surface albedo, atmospheric model (US62 Standard Atmosphere), a LUT for the inverse of the atmospheric transmittance (T−1) can be computed by varying the COD, Reff and m0 together in the radiative transfer code. From the LUT, as expected, the linearity of the relationship between COD and T−1 is observed and their slope is dependent on m0, while the intercept is almost independent.

5. Inter-Comparison of Ground-Based Cloud Property Retrieval Approaches at the ARM SGP Site

At SGP ARM site, the Microwave Water Radiometer (MWR, Model WVR-1100) measures column-integrated amounts of water vapor and liquid water. This MWR receives microwave radiation from the sky at dual frequencies (23.8 GHz and 31.4 GHz), which allow simultaneous determination of total water vapor and liquid water burdens along the selected path. In the present study, we have taken care to exclude LWPs recorded during precipitation from our analysis. Various studies have reported uncertainties in LWP retrievals to be around 20–30 g∙m−2 [47,48,49,50].
Atmosphere 03 00468 g007 1024
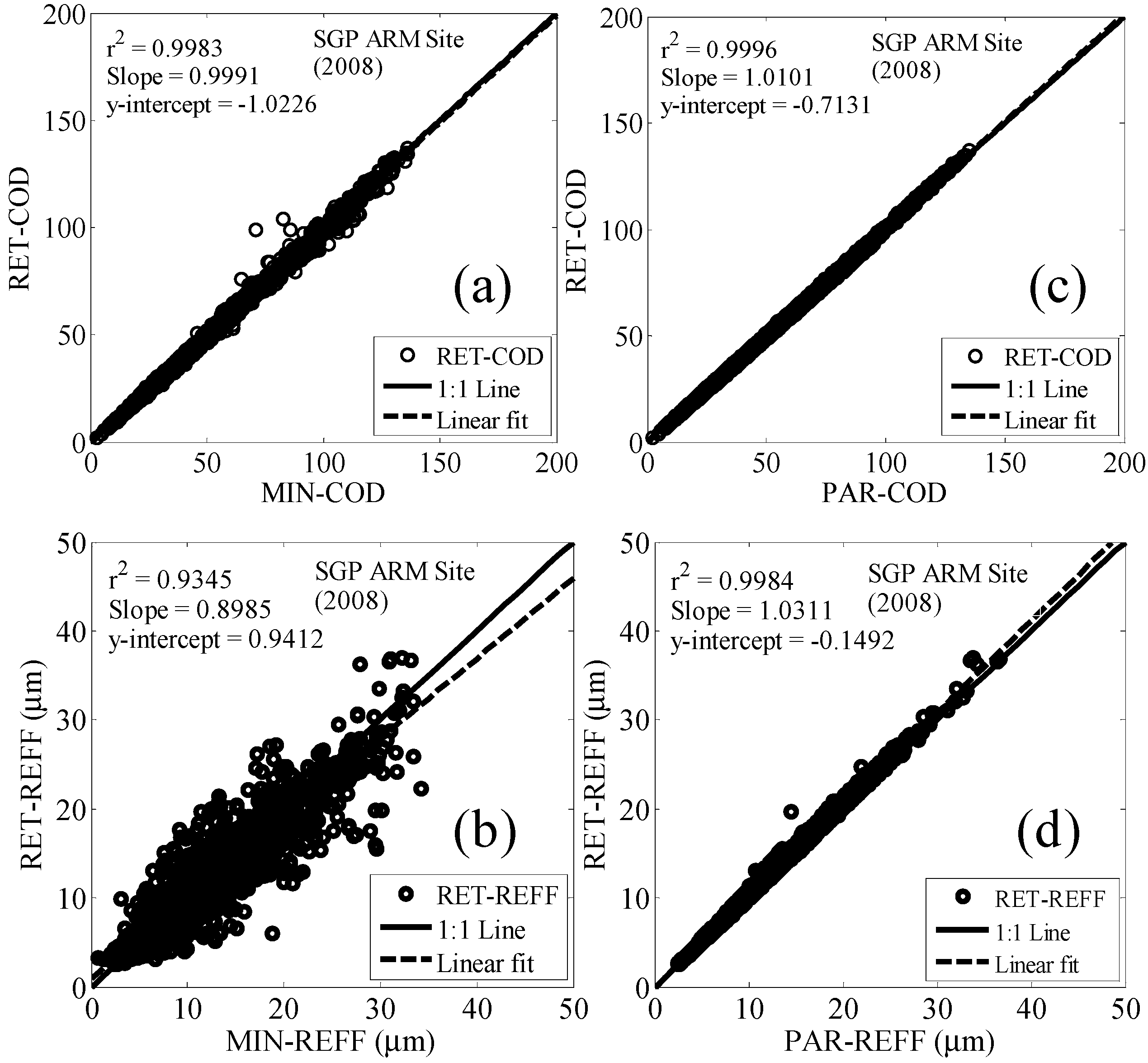
Figure 7. Scatter plot between retrieved instantaneous COD and REFF using RET approach compared to those of MIN (a,b) and PAR (c,d) retrievals.
Figure 7. Scatter plot between retrieved instantaneous COD and REFF using RET approach compared to those of MIN (a,b) and PAR (c,d) retrievals.
Atmosphere 03 00468 g007
Existing cloud optical properties from MFRSR are obtained using the MIN algorithm which are stored within the SGP Value Added Product (VAP) called MFRSRCLDOD [51]. To apply our algorithm, we use the atmospheric transmittance as a function of cosine of solar zenith angles for thick cloud cases along with instantaneous LWP measurements from MWR, which are available in the VAP. Cloud retrievals from our approach (RET) are compared with MIN retrievals and parameterization (PAR) scheme are shown as scatter plots in Figure 7 for the period from April to September 2008. COD retrievals from our approach show excellent correlation (r2 ~ 0.99) and consistency with those obtained from both the methods and this is maintained over large datasets. However, we note that there is a spread or discrepancy in the retrieved Reff from RET approach which we will see is mainly due to the difference in LWP measurements used by the MIN algorithm.
Atmosphere 03 00468 g008 1024
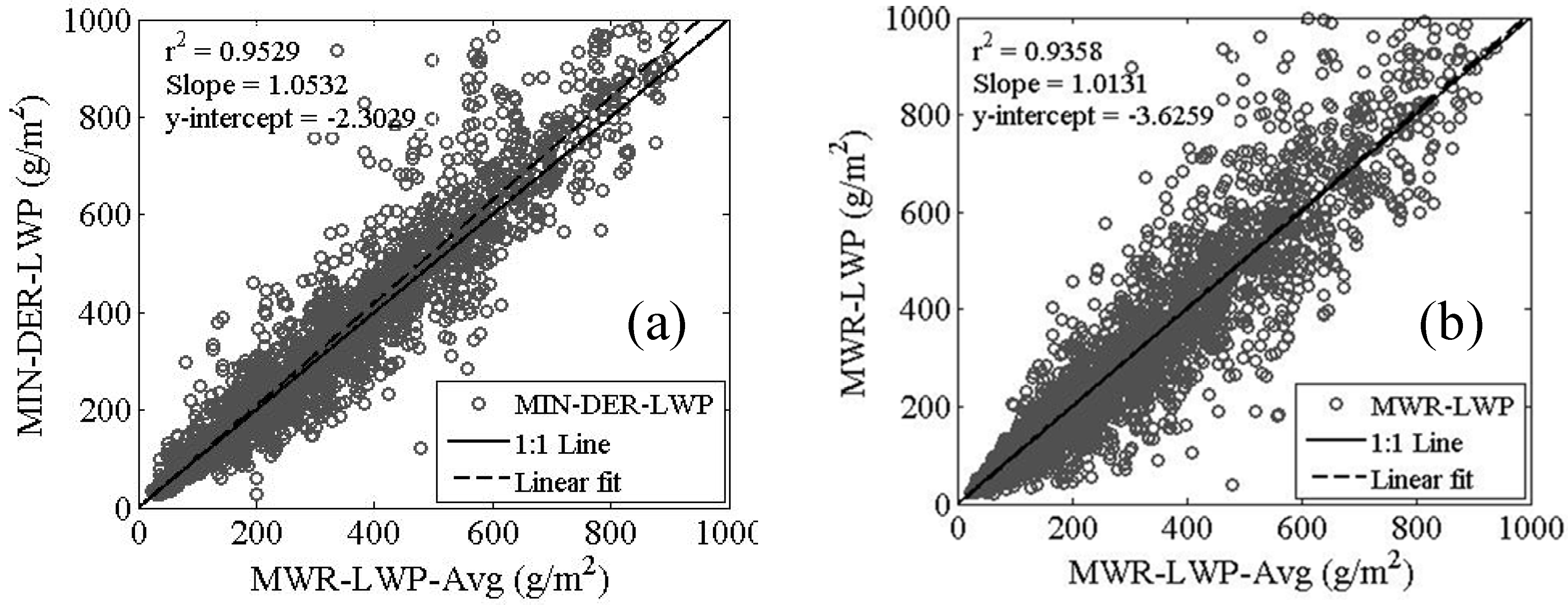
Figure 8. Regression plots between LWP derived in different ways (a) Closure comparison between averaged measured and derived LWP, and (b) Averaged versus Instantaneous LWP.
Figure 8. Regression plots between LWP derived in different ways (a) Closure comparison between averaged measured and derived LWP, and (b) Averaged versus Instantaneous LWP.
Atmosphere 03 00468 g008
In understanding the Reff discrepancy, we note that the MIN retrievals are based on an internal estimation of 5 min averaged LWP and the details of that averaging are not accessible. Therefore, when we perform an averaging procedure, it may not be identical to the approach that MIN uses. To test this, we perform in Figure 8(a) a closure study where the MIN retrieval products are used to “derive” the LWP (MIN-DER) which are compared to the averaged LWP. The discrepancy is of the same order of magnitude of the errors in Reff observed illustrating that there is ambiguity in how the average was calculated. The sensitivity is further demonstrated where the instantaneous LWP is compared to the averaged LWP demonstrating comparably higher variability (Figure 8(b)). The point we wish to emphasize is that the effective radius errors, which are clearly driven by the LWP uncertainties, are not only due to instantaneous radiometric errors in LWP but also due to the in atmospheric variability of LWP within a given averaging window. However, in our study we do not plan on exploring this averaging ambiguity in assessing error since literature estimates of the LPW error were available and this value was the one that was ultimately used in our improved sensitivity analysis (Section 6). On the other hand, in our comparisons against PAR, maximum relative fractional differences are less than 5% and 8% for COD and Reff respectively were obtained when compared with the MIN retrievals at ARM SGP site. Here, no ambiguity in the actual LWP occurs since this parameter is identically provided in both algorithms.

6. Sensitivity Analysis of Cloud Droplet Effective Radius Retrievals

To assess the realistic errors in cloud droplet effective radius retrievals that can occur, a rigorous sensitivity analysis is performed focusing on errors that may result due to incorrect atmosphere/aerosol assumptions below the cloud as well as imprecise surface albedo. Other variables such as geometric cloud base and cloud extent are less important and will not be considered here. Also, it is not possible to analyze all mechanisms individually since the inversion of each variable taken separately is not stable. Hence, we adopt the following approach for performing the sensitivity analysis of retrieved Reff:
  • (1) Fix the “reference” state (mean atmosphere, mean surface) along with a reference cloud (CODref, Reffref) to provide the algorithm with reference values for LWPref and Tdiffref.
  • (2) Given the reference state, we now perform the retrieval sequentially for each atmosphere state, i.
  • (3) The retrieval looks for the solution set which simultaneously satisfies
    (LWP error) Atmosphere 03 00468 i012
    and Atmosphere 03 00468 i013
  • (4) The above inequalities define a set of COD and Reff cells in the inversion domain which are possible solutions. However, all such solutions should not be weighted equally since some of the solution cells fit the measurement better than others.
  • (5) For each cell in the set, COD(k,l) and Reff(k,l), we assign a weight Atmosphere 03 00468 i019 which measures the discrepancy between the reference measurement (LWPref, Tdiffref) and the model (for the ith atmosphere) evaluated at the cell (k,l). In other words, we weight the cell by the reciprocal distance the cell model is from the reference measurement in "measurement" space given by
    Atmosphere 03 00468 i014
  • (6) This process is performed sequentially for all atmosphere cases and the cumulative weights (summed over i) result in the 2D distribution of the admissible (COD, Reff) retrieval:
    Atmosphere 03 00468 i015
  • (7) Exactly, the same procedure is repeated for the surface albedo variability, which results in another 2D distribution function for this process.
  • (8) In order to combine the uncertainty from 2 separate processes each taken independently, the result is just the 2D convolution of the individual 2D probability density functions (PDFs) of each process taken separately and can be implemented using a suitable 2D convolution function.
  • (9) Once the combined PDF is generated, the final error associated with either parameter is the marginal distribution given by,
    Atmosphere 03 00468 i016
  • (10) Finally, given the 1D marginal distributions, the mean and standard deviation can be obtained directly from the appropriate numerical integrals over the 1D distributions
    Atmosphere 03 00468 i017
    Atmosphere 03 00468 i018
In performing this sensitivity analysis, we fix the “reference” state of cloud properties corresponding to those values which are most likely be influenced by aerosols within the aerosol-cloud interaction. Based on the cases considered by Feingold et al. [15], the LWP measurements seem to be constrained to a reasonably low values around 120 g·m−2 with Reff~6 mm. Using the approximate relationship of LWP = (2/3) ´ (Reff ´ COD), a representative COD ~30 can be obtained.
Once the “reference’ cloud state is determined, the variability of the atmosphere and surface albedo needs to be estimated. For the surface, we make use of the MODIS land surface product MODASRVN (accessed through Level 1 and Atmosphere Archive and Distribution System, http://ladsweb.nascom.nasa.gov/data/search.html), which provides the best estimate of the surface albedo since it routinely ingests AERONET aerosol properties allowing for the most accurate surface estimate from satellite that can be made. Since the surface albedo is only retrieved at the MODIS land surface channels, an extrapolation is performed on the spectral albedo retrievals to the 415 nm channel. In this analysis, we consider the surface albedo retrievals over the period 2007–2008. The atmospheric variability, on the other hand, comes from the microphysical aerosol retrievals of AERONET. In SBDART, the actual bimodal size distribution is not completely ingested but is approximated using the SSA (ω0), asymmetry parameter (g) and AOD (ta). While this approximation may miss some fine properties, the main variability is mostly determined by these parameters.
To demonstrate the sensitivity analysis, we apply the uncertainty approach for ARM SGP site datasets with “reference” state of CODref = 30 and Reffref = 6 mm. Figure 9 shows both the 2D distributions (Figure 9(a,c)) and corresponding 1D distributions integrated over the CODs (Figure 9(b,d)) for prevailing atmospheric variability and surface albedo. The convolved variability of both the processes (Figure 9(e,f)), which is broader than the individual processes alone, resulted in a stable standard deviation of ±0.47 mm from the “reference” state Reff of 6 mm.
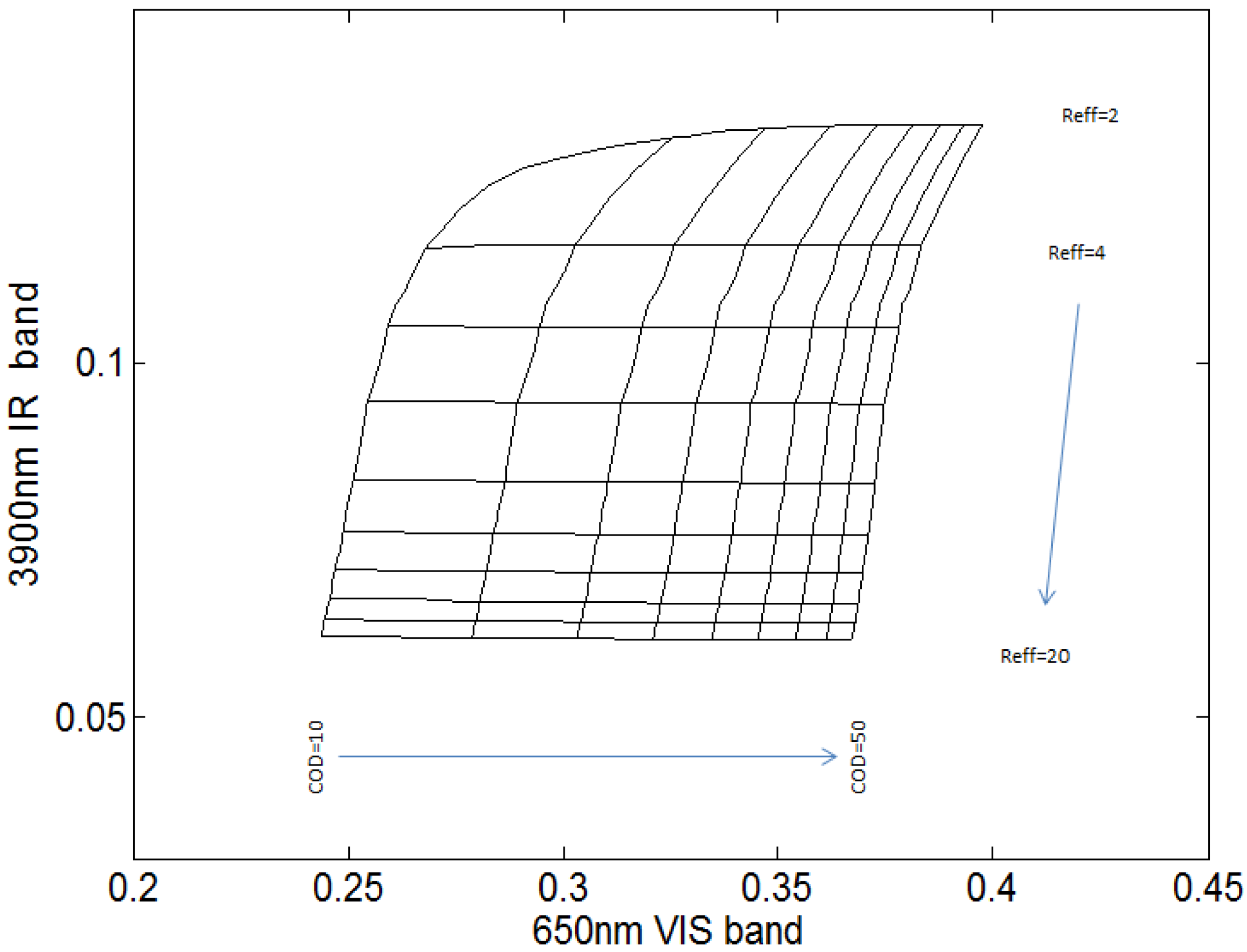
One interesting feature of the joint distribution is that there is a general overbias in the individual COD retrievals along with a subsequent underbias in the effective radius. The reason for this can be seen by looking at the dual channel radiometric plot of Figure 1. In particular, we note that the density of the COD retrieval contours increases in the direction of increasing COD. Since the COD parameter is sensitive mainly to the transmission alone, for a given VIS signal uncertainty distribution, the inversions will be distributed unevenly such that higher COD retrievals will occur with greater frequency than lower COD cases. On the other hand, the Reff parameter is inversely correlated to COD through the LWP. Therefore, an unbiased uncertainty on the LWP measurement will result in underestimating bias in the Reff parameter. However, this bias effect is significantly reduced during the convolution of the individual sources of variability.
In the above analysis, the conservative estimate of LWP is taken as 30 g∙m−2 because it roughly represents the detection limit of LWP with dual frequency radiometers [15,50] already existing at SGP site. One of the biggest sources of error in all dual frequency MWR retrieval models is that the variations in the vertical absorption profile are neglected despite the liquid water absorption profile being sensitive to temperature profile. As already indicated in Figure 4, retrieval of water vapor is significantly improved a multispectral radiometer which can better estimate the temperature profile. It has been suggested that LWP retrievals can be similarly improved with a high frequency 50 GHz channel [52]. Bosisio and Mallet [52] have demonstrated that the LWP retrievals with new inverse model can be improved by 10 g·m−2 by choosing three frequencies—two frequencies sensitive to water presence in the 20 to 30 GHz band [53,54] and one frequency around 50 GHz sensitive to the vertical profile of temperature [55,56]. However, Lohnert and Crewell [57] pointed out that when the 50.8 GHz channel is combined with lower two channels, the algorithm accuracy depends very much on the cloud model used. Therefore, though some improvement may be expected with the MP-3000A system, we limit our analysis to the conservative estimate.
Atmosphere 03 00468 g009 1024
Figure 9. 2D distributions (left panel) and respective 1D distributions integrated over the CODs (right panel) for atmospheric variability (a,b), surface albedo variability (c,d), and convolved variability (e,f) of both variable parameters.
Figure 9. 2D distributions (left panel) and respective 1D distributions integrated over the CODs (right panel) for atmospheric variability (a,b), surface albedo variability (c,d), and convolved variability (e,f) of both variable parameters.
Atmosphere 03 00468 g009
Instrument Radiometric uncertainties due to the sensor, data acquisitions, etc. are significantly smaller and are not considered in the error budgets. Based on the considerations by Feingold et al. [15], dynamic changes in the cloud droplet effective radii are around 30% making these measurements quite challenging. On the other hand, ground-based methods make some global assumptions including the requirements of single layer clouds and horizontal homogeneity (i.e., no broken clouds). The lack of broken clouds can be seen by imposing a buffer of one hour to the times when the lidar captures broken portion while coincident GOES data can assist in identifying single layer cases. Only when all these assets are combined, we can quantitatively explore the changes in Aerosol Cloud Index (ACI).

7. SGP Case Study for Aerosol-Cloud Interaction

To explore the aerosol-cloud interaction and illustrate the need for a complete measurement testbed we focus on an interesting case from those considered in Kim et al. [18]. In their study, while in most cases considered, a weak correlation was observed, the case of 13 April 2000 tends to show small anti-correlation. In their analysis, the surface extinction was obtained from a ground based Nephelometer, which seemed to show a slight increase in cloud droplet radius with increase in extinction in opposition to the assumed aerosol cloud trend. One possible explanation advanced in their study was that the surface aerosols were strongly decoupled from aerosols at the cloud base on this day.
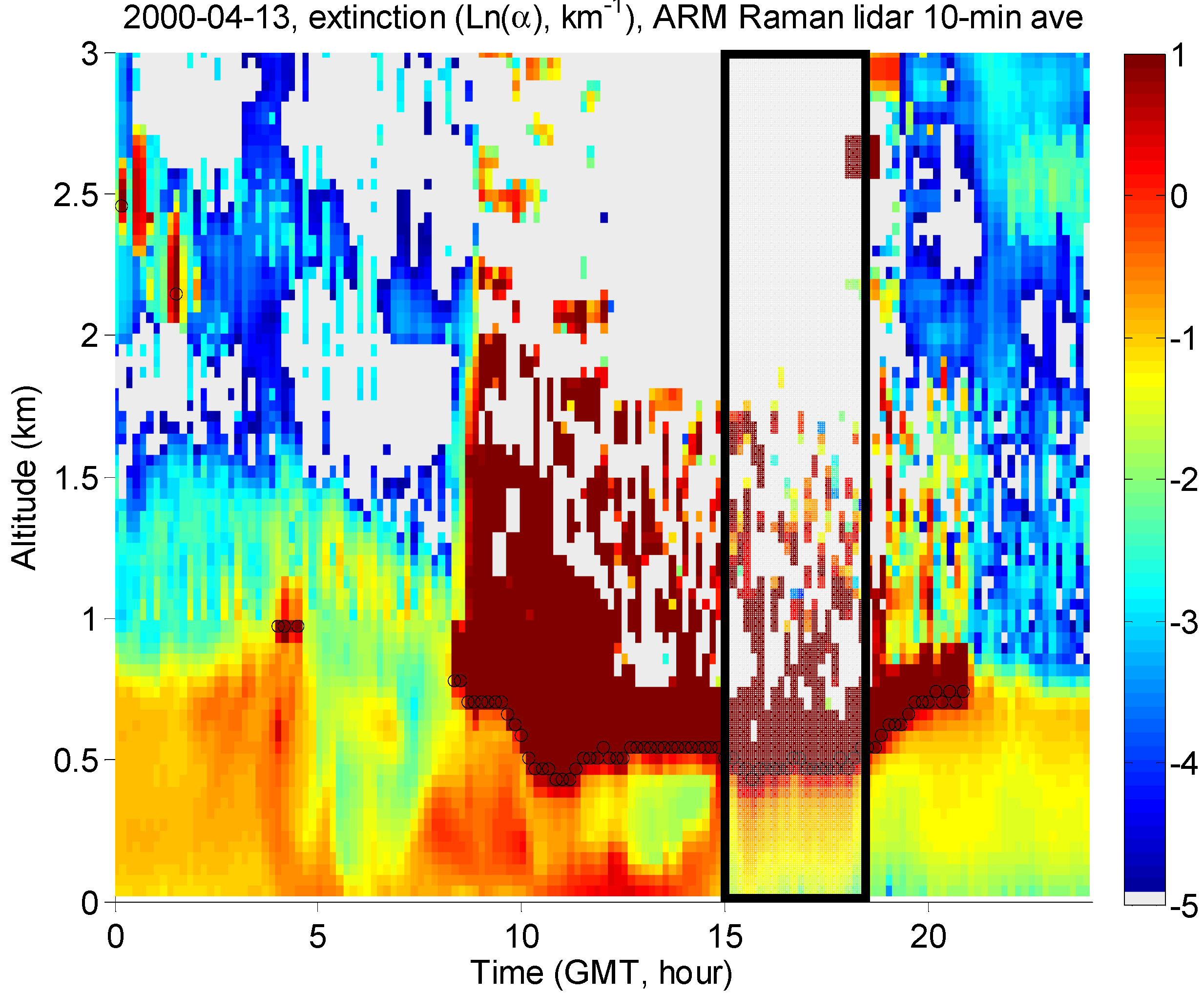
To assess this issue, we plot, in Figure 10, the Raman lidar derived extinction profile was shown for 13 April 2000. In particular, the period from 1500 to 1800 UTC time shows excellent horizontal homogeneity making the surface retrievals most reliable. However, although the aerosol convective mixing has begun to occur during this period, the Raman lidar extinction profiles seem to indicate that the vertical distribution of extinction is not uniform with smaller extinction at the surface, which may in part be due to aerosol extinction enhancement due to hygroscopic growth. In making this assessment, it is useful to point out that the SGP Raman Lidar has developed a sophisticated approach to extend the aerosol extinction measurement below the low channel overlap threshold greatly minimizing overlap issues [58]. In particular, analysis of near extinction data against Nephelometer measurements illustrates the near surface Raman Lidar returns to be realistic and errors should be significantly less than the dramatic differences observed between the surface and aloft aerosols.
Atmosphere 03 00468 g010 1024
Figure 10. Raman Lidar derived extinction profile and marked cloud boundary for 13 April 2000 at ARM SGP site.
Figure 10. Raman Lidar derived extinction profile and marked cloud boundary for 13 April 2000 at ARM SGP site.
Atmosphere 03 00468 g010
In Figure 11, we show on log scale the relationship between the effective radius and aerosol extinction where we consider both the surface extinction (lidar ground bin = 30 m) as well as the extinction 150 m below the cloud base. In this case, we selected only those points whose LWP was constrained between 90 < LWP < 120. This resulted in COD ranges 20 < COD < 30. Here the cloud base was determined using a simple threshold of 1 m−1 and is displayed as black circles in Figure 10.
Atmosphere 03 00468 g011 1024
Figure 11. Log-Log plot of Raman lidar extinction below cloud against the cloud droplet effective radius. “zb-150m” (blue circles) indicates the upper air atmospheric column layer which was used in the comparison (i.e., 150 m below the cloud base altitude denoted by zb), while 'zsurf' refers to the atmospheric layer closest to the surface (~30 m).
Figure 11. Log-Log plot of Raman lidar extinction below cloud against the cloud droplet effective radius. “zb-150m” (blue circles) indicates the upper air atmospheric column layer which was used in the comparison (i.e., 150 m below the cloud base altitude denoted by zb), while 'zsurf' refers to the atmospheric layer closest to the surface (~30 m).
Atmosphere 03 00468 g011
In this case, we see that the surface results are at best uncorrelated with no trend but a general trend is seen when considering the aerosol 150 m below cloud base (i.e., zb-150 m layer) although the statistical significance is not as high as we might expect. It is clear that the aloft extinction is on average significantly larger than the near surface which should be attributed to hygroscopic enhancement due to high RH in the vicinity of the cloud. However, local inhomogeneous concentration effects must also be a factor since the overall data clusters shape has been substantially modified. Overall, we believe that the most robust approach to account for the aerosol loading for ACI estimation is to make extinction measurements nearer to cloud base than to rely on surface measurements.
In summary, we see that the surface measurements can be less than optimal in looking for aerosol-cloud interactions and that profile measurements near the cloud base can be used to better probe these interactions under suitable conditions. Based on the regression slope, an IE exponent (or ACI) of 0.23 is obtained which is realistic if not on the high side in comparison to other cases seen [15]. McComiskey and Feingold [8] summarized results from seven different in situ airborne studies made for determining the ACI. In five of these studies observed values of ACI were comparable to ours (>0.20), whereas two other studies evidently showed lower values (~0.1). ACI values obtained from in situ ground based data were highest when compared with those obtained either from combined ground-based and satellite data, or from the data relying solely on satellite retrievals [59]. Clearly, the error budget we estimate is of the order of dynamic range making it hard to state that this is a clear observation of aerosol-cloud interaction but in comparison to the surface, we believe a clearer trend is detected and therefore any robust testbed should attempt measurements nearer to cloud base.

8. Discussion

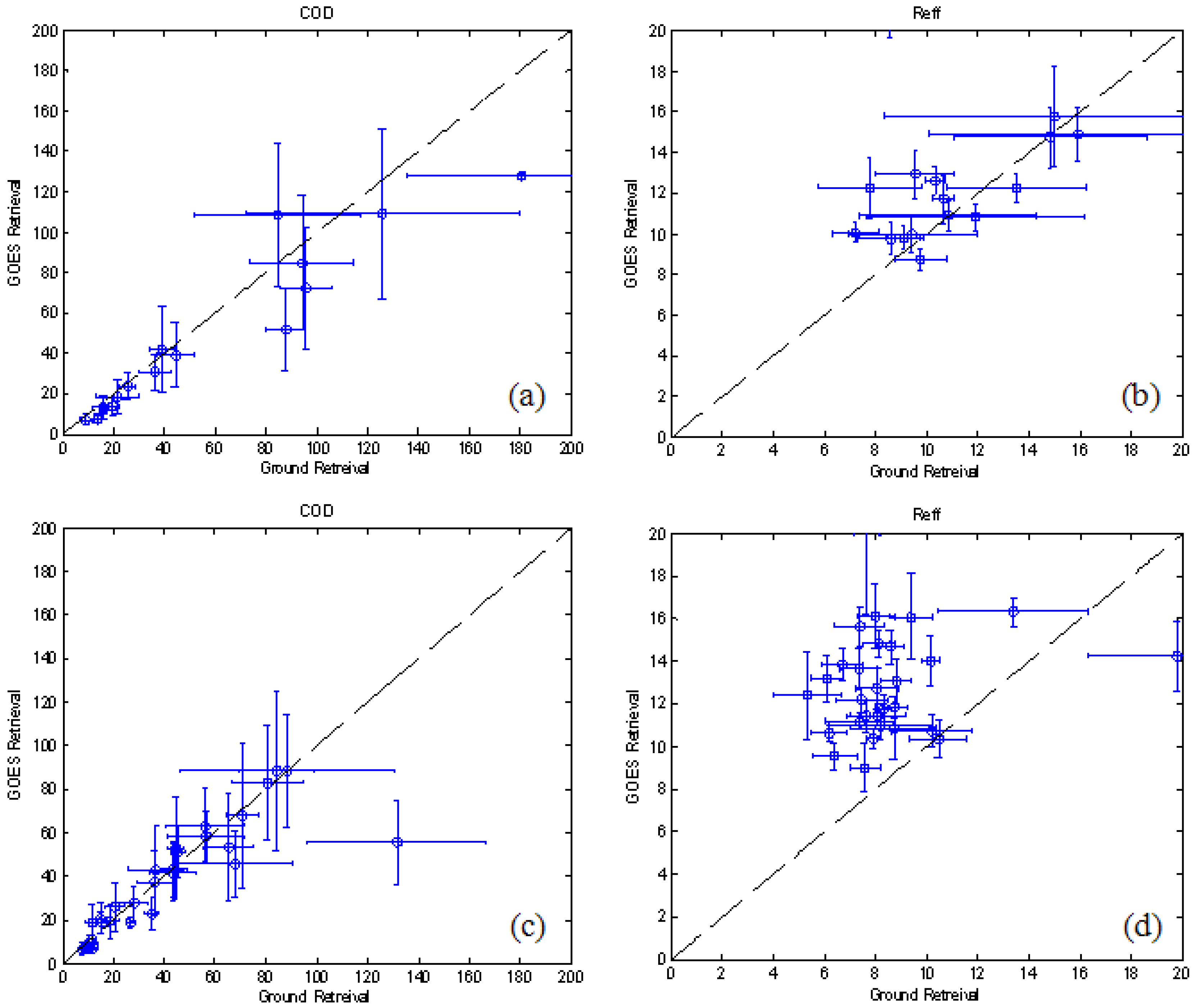
The present study is focused on exploring the direct ground based remote sensing methods for detection and quantification of aerosol-cloud interaction. As discussed in detail, even though sophisticated multispectral imagers onboard polar (e.g., MODIS) and geostationary (e.g., GOES) satellites are available, the inability to simultaneously retrieve aerosols and cloud properties makes such techniques extremely difficult. Furthermore, we found that the performance of the GOES-VISST algorithm retrievals when compared to ground based retrievals [12] resulted in a very strong bias and poor correlation of effective radius (Reff) for θsun > 50 degrees. The fact that cross-validations between MODIS and GOES were unbiased (Figure 4(b and d)) indicates that these issues are persistent across all platforms. This can be qualitatively explained by noting that for large observing angles, the effective optical depth increases and the photons interact mainly with the cloud top, which is usually has a higher Reff than the column averaged value. Motivated by these prevailing difficulties, this paper emphasizes the need for exploiting the capability of surface remote sensing which is crucial in avoiding the ambiguity of mesoscale phenomenon on aerosol/cloud interaction by suitable simultaneous probing of the interactions on short time scales (<1 min).
In this context, we studied existing retrieval approaches [12,13] that have been applied to the MFRSR-MWR combined system and developed a simple LUT based iteration approach adaptable under different atmospheric backgrounds for real-time monitoring of cloud retrievals. While the COD retrievals from our approach showed consistency with excellent correlation (r2 ~ 0.99), the spread or inconsistency in the retrieved Reff was commensurate with LWP errors that can occur due to an inability to synchronize our LWP averaging procedure to those used internally by the Min and Harrison [12] approach.
Once the consistency of our algorithm was demonstrated, a detailed sensitivity analysis for cloud droplet effective radius retrieval was carried out and illustrated using “reference” background conditions from the ARM SGP site to quantify the errors due to incorrect atmosphere/aerosol assumptions below the cloud layer, imprecise surface albedo as well as LWP and diffuse transmission uncertainties. In particular, we find that the convolved variability of both processes (atmosphere and surface albedo) was sufficiently small (~8%) to resolve possible ACI index trends.
Unlike many studies that attempt to use the aerosol loading at the surface [8], we investigated the difficulties that may result when the cloud layer is sufficiently high. In particular, we re-explore an interesting case at SGP site following Kim et al. [18], wherein the existing Nephelometer measurements showed slightly positive correlations in contradiction to expected ACI trends. In particular, using Raman lidar extinction as proxy for aerosol concentration, we found that while the effective radius and surface extinction were basically uncorrelated with no trend, a general trend was observed by considering the aerosol extinction 150 m below cloud base. In this case, the regression slope resulted in an ACI ~0.23, which is realistic and comparable to other cases [59].

9. Conclusions

In the present study, we have highlighted the capability of surface remote sensing as a crucial method in avoiding the ambiguity of statistically-based satellite aerosol/cloud interaction studies. Our overall goal is to describe the instrumentation and algorithms needed to provide simultaneous aerosol and cloud measurements at time resolutions suitable to isolate aerosol/cloud interactions that modify the cloud droplets. Due to the fairly small dynamic range that can be expected for the ACI index, a more thorough sensitivity study to account for realistic errors from both the measurements themselves and the variability of the environment were accounted for and it was shown that these errors which were ~8% were sufficiently small to resolve realistic ACI coefficients. A demonstration of the algorithm together with the retrieval uncertainty was given for a case where surface measurements alone did not result in any observable ACI. In particular, we emphasized the potential improvement that may occur if aloft aerosol measurements were used based on Raman Lidar measurements of aerosol extinction. In this case, a realistic ACI value (~0.23) was found although systemic deviations from the trend line were observed which makes the above result less than certain.
Although hardly conclusive, we believe the use of aloft aerosol measurements from lidar is important in obtaining better ACI measurements when cloud heights are sufficiently high. In such cases, the surface aerosols are expected to be quantitatively less representative of actual particles forming CCN nuclei.

Acknowledgements

This work is partially supported by the NOAA CREST Cooperative Center under contract NOAA #NA17AE1625. The statements, findings, conclusions, and recommendations presented in this manuscript are those of the authors and do not necessarily reflect the views of the National Oceanic and Atmospheric Administration or the Department of Commerce.

References

  1. Twomey, S. Influence of pollution on shortwave albedo of clouds. J. Atmos. Sci. 1977, 34, 1149–1152. [Google Scholar] [CrossRef]
  2. Chmura, N.; Menon, S. Analyzing Aerosol-Cloud Interactions Using MODIS Data. In Proceedings ofGCEP End-of-Summer Workshop, Washington, DC, USA, 15–17 August 2004.
  3. Storelvmo, T.; Kristjansson, J.E.; Myhre, G.; Johnsrud, M.; Stordal, F. Combined observational and modeling based study of the aerosol indirect effect. Atmos. Chem. Phys. 2006, 6, 3583–3601. [Google Scholar] [CrossRef]
  4. Myhre, G.; Stordal, F.; Johnsrud, M.; Kaufman, Y.J.; Rosenfeld, D.; Storelvmo, T.; Kristjansson, J.E.; Berntsen, T.K.; Myhre, A.; Isaksen, I.S.A. Aerosol-cloud interaction inferred from MODIS satellite data and Global aerosol models. Atmos. Chem. Phys. 2007, 7, 3081–3101. [Google Scholar] [CrossRef] [Green Version]
  5. Hegg, D.A.; Covert, D.S.; Jonsson, H.H.; Woods, R.K. A simple relationship between cloud drop number concentration and precursor aerosol concentration for the regions of Earth’s large marine stratocumulus decks. Atmos. Chem. Phys. 2012, 12, 1229–1238. [Google Scholar] [CrossRef]
  6. Han, Q.Y.; Rossow, W.B.; Zeng, J.; Welch, R. Three different behaviors of liquid water path of water clouds in aerosol-cloud interactions. J. Atmos. Sci. 2002, 59, 726–735. [Google Scholar] [CrossRef]
  7. Palikonda, R.; Phan, D.; Khaiyer, M.M.; Nordeen, M.L.; Ayers, J.K.; Spangenberg, D.A.; Doelling, D.R.; Yi, Y.; Minnis, P.; Nguyen, L.; et al. NASA-Langley Web-Based Operational Real-Time Cloud Retrieval Products from Geostationary Satellites. In Proceeding of 14th Conference on Satellite Meteorology and Oceanography, AMS, Atlanta, GA, USA, 29 January–2 February 2006.
  8. McComiskey, A.; Feingold, G. Quantifying error in the radiative forcing of the first aerosol indirect effect. Geophys. Res. Lett. 2008. [Google Scholar] [CrossRef]
  9. McComiskey, A.; Feingold, G. The scale problem in quantifying aerosol indirect effects. Atmos. Chem. Phys. 2012, 12, 1031–1049. [Google Scholar] [CrossRef]
  10. Frisch, A.S.; Feingold, G.; Fairall, C.W.; Uttal, T.; Snider, J.B. On cloud radar and microwave radiometer measurements of stratus cloud liquid water profiles. J. Geophys. Res.-Atmos. 1998, 103, 23195–23197. [Google Scholar] [CrossRef]
  11. Leontyeva, E.; Stamnes, K. Estimations of cloud optical-thickness from ground-based measurements of incoming solar-radiation in the Arctic. J. Climate 1994, 7, 566–578. [Google Scholar] [CrossRef]
  12. Min, Q.L.; Harrison, L.C. Cloud properties derived from surface MFRSR measurements and comparison with GOES results at the ARM SGP site. Geophys. Res. Lett. 1996, 23, 1641–1644. [Google Scholar] [CrossRef]
  13. Matamoros, S.; Gonzalez, J.A.; Calbo, J. A simple method to retrieve cloud properties from atmospheric transmittance and liquid water column measurements. J. Appl. Meteorol. Clim. 2011, 50, 283–295. [Google Scholar] [CrossRef]
  14. Han, J.Y.; Baik, J.J. Theoretical studies of convectively forced mesoscale flows in three dimensions. Part I: Uniform basic-state flow. J. Atmos. Sci. 2009, 66, 947–965. [Google Scholar] [CrossRef]
  15. Feingold, G.; Eberhard, W.L.; Veron, D.E.; Previdi, M. First measurements of the Twomey indirect effect using Ground-based remote sensors. Geophys. Res. Lett. 2003. [Google Scholar] [CrossRef]
  16. Feingold, G.; Remer, L.A.; Ramaprasad, J.; Kaufman, Y.J. Analysis of smoke impact on clouds in Brazilian biomass burning regions: An extension of Twomey’s approach. J. Geophys. Res.-Atmos. 2001, 106, 22907–22922. [Google Scholar]
  17. McComiskey, A.; Feingold, G.; Frisch, A.S.; Turner, D.D.; Miller, M.A.; Chiu, J.C.; Min, Q.L.; Ogren, J.A. An assessment of aerosol-cloud interactions in marine stratus clouds based on surface remote sensing. J. Geophys. Res.-Atmos. 2009. [Google Scholar] [CrossRef]
  18. Kim, B.G.; Schwartz, S.E.; Miller, M.A.; Min, Q.L. Effective radius of cloud droplets by ground-based remote sensing: Relationship to aerosol. J. Geophys. Res. Atmos. 2003. [Google Scholar] [CrossRef]
  19. Pincus, R.; Szczodrak, M.; Gu, J.J.; Austin, P. Uncertainty in-cloud optical depth estimates made from satellite radiance measurements. J. Climate 1995, 8, 1453–1462. [Google Scholar] [CrossRef]
  20. Davis, A.; Marshak, A.; Cahalan, R.; Wiscombe, W. The landsat scale break in stratocumulus as a three-dimensional radiative transfer effect: Implications for cloud remote sensing. J. Atmos. Sci. 1997, 54, 241–260. [Google Scholar] [CrossRef]
  21. Mace, G.G.; Ackerman, T.P.; Minnis, P.; Young, D.F. Cirrus layer microphysical properties derived from surface-based Millimeter radar and infrared interferometer data. J. Geophys. Res.-Atmos. 1998, 103, 23207–23216. [Google Scholar] [CrossRef]
  22. Dong, X.Q.; Ackerman, T.P.; Clothiaux, E.E.; Pilewskie, P.; Han, Y. Microphysical and radiative properties of boundary layer stratiform clouds deduced from Ground-based measurements. J. Geophys. Res.-Atmos. 1997, 102, 23829–23843. [Google Scholar] [CrossRef]
  23. Cahalan, R.F.; Ridgway, W.; Wiscombe, W.J.; Bell, T.L.; Snider, J.B. The albedo of fractal stratocumulus clouds. J. Atmos. Sci. 1994, 51, 2434–2455. [Google Scholar] [CrossRef]
  24. Minnis, P.; Kratz, D.P.; Coakley, J.A.J.; King, M.D.; Garber, D.P.; Heck, P.W.; Mayor, S.; Young, D.F.; Arduini, R.F. Cloud Optical Property Retrieval (Subsystem 4.3). Clouds and the Earth’s Radiant Energy System (Ceres) Algorithm Theoretical Basis Document. Available online: http://science.larc.nasa.gov/ceres/ATBD/pdf/ceres-atbd2.2-s4.3.pdf (accessed on 21 May 2011).
  25. Minnis, P.; Young, D.F.; Sun-Mack, S.; Heck, P.W.; Doelling, D.R.; Trepte, Q.Z. CERES cloud property retrievals from imagers on TRMM, Terra, and Aqua. Proc. SPIE 2003, 5235. [Google Scholar] [CrossRef]
  26. Minnis, P.; Garber, D.P.; Young, D.F.; Arduini, R.F. Parameterizations of reflectance and effective emittance for satellite remote sensing of cloud properties. J. Atmos. Sci. 1998, 55, 3313–3339. [Google Scholar] [CrossRef]
  27. Platnick, S.; King, M.D.; Ackerman, S.A.; Menzel, W.P.; Baum, B.A.; Riedi, J.C.; Frey, R.A. The MODIS cloud products: Algorithms and examples from TERRA. IEEE Trans. Geosci. Remote Sens. 2003, 41, 459–473. [Google Scholar] [CrossRef]
  28. Hansen, J.E.; Travis, L.D. Light-scattering in planetary atmospheres. Space Sci. Rev. 1974, 16, 527–610. [Google Scholar] [CrossRef]
  29. King, M.D.; Tsay, S.-C.; Platnick, S.E.; Wang, M.; Liou, K.N. Cloud Retrieval Algorithms for Modis: Optical Thickness, Effective Particle Radius, and Thermodynamics Phase. Available online: http://modis.gsfc.nasa.gov/data/atbd/atbd_mod05.pdf (accessed on 21 May 2011).
  30. Minnis, P.; Sun-Mack, S.; Young, D.F.; Heck, P.W.; Garber, D.P.; Chen, Y.; Spangenberg, D.A.; Arduini, R.F.; Trepte, Q.Z.; Smith, W.L.; et al. CERES edition-2 cloud property retrievals using TRMM VIRS and TERRA and AQUA MODIS data-part I: Algorithms. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4374–4400. [Google Scholar]
  31. Curry, J.A. Interactions among turbulence, radiation and microphysics in arctic stratus clouds. J. Atmos. Sci. 1986, 43, 90–106. [Google Scholar] [CrossRef]
  32. Garrett, T.J.; Hobbs, P.V. Long-range transport of continental aerosols over the Atlantic-ocean and their effects on cloud structures. J. Atmos. Sci. 1995, 52, 2977–2984. [Google Scholar] [CrossRef]
  33. Nicholls, S.; Leighton, J. An observational study of the structure of stratiform cloud sheets. 1. Structure. Q. J. Roy. Meteor. Soc. 1986, 112, 431–460. [Google Scholar] [CrossRef]
  34. Noonkester, V.R. Droplet spectra observed in marine stratus cloud layers. J. Atmos. Sci. 1984, 41, 829–845. [Google Scholar] [CrossRef]
  35. Slingo, A.; Nicholls, S.; Schmetz, J. Aircraft observation of marine stratocumulus during JASIN. Q. J. R. Meteorol. Soc. 1982, 108, 833–856. [Google Scholar] [CrossRef]
  36. Stephens, G.L.; Platt, C.M.R. Aircraft observations of the radiative and microphysical properties of stratocumulus and cumulus cloud fields. J. Clim. Appl. Meteorol. 1987, 26, 1243–1269. [Google Scholar] [CrossRef]
  37. Harrison, L.; Michalsky, J. Objective algorithms for the retrieval of optical depths from ground-based measurements. Appl. Opt. 1994, 33, 5126–5132. [Google Scholar] [CrossRef]
  38. Harrison, L.; Michalsky, J.; Berndt, J. Automated multifilter rotating shadow-band radiometer: An instrument for optical depth and radiation measurements. Appl. Optics 1994, 33, 5118–5125. [Google Scholar] [CrossRef]
  39. Alexandrov, M.D.; Lacis, A.A.; Carlson, B.E.; Cairns, B. Remote sensing of atmospheric aerosols and trace gases by means of Multifilter Rotating Shadowband Radiometer. Part I: Retrieval algorithm. J. Atmos. Sci. 2002, 59, 524–543. [Google Scholar] [CrossRef]
  40. Alexandrov, M.D.; Marshak, A.; Cairns, B.; Lacis, A.A.; Carlson, B.E. Automated cloud screening algorithm for MFRSR data. Geophys. Res. Lett. 2004, 31, L04118. [Google Scholar]
  41. Holben, B.N.; Eck, T.F.; Slutsker, I.; Tanre, D.; Buis, J.P.; Setzer, A.; Vermote, E.; Reagan, J.A.; Kaufman, Y.J.; Nakajima, T.; et al. AERONET—A federated instrument network and data archive for aerosol characterization. Remote Sens. Environ. 1998, 66, 1–16. [Google Scholar] [CrossRef]
  42. Schmid, B.; Matzler, C.; Heimo, A.; Kampfer, N. Retrieval of optical depth and particle size distribution of tropospheric and stratospheric aerosols by means of sun photometry. IEEE Trans. Geosci. Remote Sens. 1997, 35, 172–182. [Google Scholar] [CrossRef]
  43. Schmid, B.; Spyak, P.R.; Biggar, S.F.; Wehrli, C.; Sekler, J.; Ingold, T.; Matzler, C.; Kampfer, N. Evaluation of the applicability of solar and lamp radiometric calibrations of a precision sun photometer operating between 300 and 1025 nm. Appl. Opt. 1998, 37, 3923–3941. [Google Scholar]
  44. Ricchiazzi, P.; Yang, S.R.; Gautier, C.; Sowle, D. SBDART: A research and teaching software tool for plane-parallell radiative transfer in the Earth’s atmosphere. Bull. Am. Meteorol. Soc. 1998, 79, 2101–2114. [Google Scholar] [CrossRef]
  45. Min, Q.L.; Harrison, L.C. An adjoint formulation of the radiative transfer method. J. Geophys. Res.-Atmos. 1996, 101, 1635–1640. [Google Scholar] [CrossRef]
  46. Stamnes, K.; Tsay, S.C.; Wiscombe, W.; Jayaweera, K. Numerically stable algorithm for discrete-ordinate-method radiative-transfer in multiple-scattering and emitting layered media. Appl. Opt. 1988, 27, 2502–2509. [Google Scholar] [CrossRef]
  47. Liljegren, J.C.; Lesht, B.M. Measurements of Integrated Water Vapor and Cloud Liquid Water from Microwave Radiometer at the DOE ARM Cloud and Radiation Testbed in the Southern Great Plains. In Proceeding of 1996 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Lincoln, NE, USA, 26–30 May 1996.
  48. Westwater, E.R.; Han, Y.; Shupe, M.D.; Matrosov, S.Y. Analysis of integrated cloud liquid and precipitable water vapor retrievals from microwave radiometers during the surface heat budget of the Arctic ocean project. J. Geophys. Res.-Atmos. 2001, 106, 32019–32030. [Google Scholar] [CrossRef]
  49. Marchand, R.; Ackerman, T.; Westwater, E.R.; Clough, S.A.; Cady-Pereira, K.; Liljegren, J.C. An assessment of microwave absorption models and retrievals of cloud liquid water using clear-sky data. J. Geophys. Res.-Atmos. 2003. [Google Scholar] [CrossRef]
  50. Crewell, S.; Lohnert, U. Accuracy of cloud liquid water path from ground-based microwave radiometry—2. Sensor accuracy and synergy. Radio Sci. 2003. [Google Scholar] [CrossRef]
  51. Turner, D.D.; Lo, C.H.; Min, Q. Cloud Optical Properties from the Multi-Filter Shadowband Radiometer (MFRSRCLDOD): An ARM Value Added Product. Available online: http://www.arm.gov/publications/tech_reports/doe-sc-arm-tr-047.pdf (accessed on 15 July 2011).
  52. Bosisio, A.V.; Mallet, C. Influence of cloud temperature on brightness temperature and consequences for water retrieval. Radio Sci. 1998, 33, 929–939. [Google Scholar] [CrossRef]
  53. Westwater, E.R. The accuracy of water vapor and cloud liquid determination by dual-frequency ground-based microwave radiometry. Radio Sci. 1978, 13, 677–685. [Google Scholar] [CrossRef]
  54. Westwater, E.R.; Snider, J.B.; Falls, M.J. Ground-based radiometric observations of atmospheric emission and attenuation at 20.6, 31.65, and 90.0 GHz—A comparison of measurements and theory. IEEE T Antenn. Propag. 1990, 38, 1569–1580. [Google Scholar]
  55. Schiavon, G.; Solimini, D.; Westwater, E.R. Performance analysis of a multifrequency radiometer for predicting atmospheric propagation parameters. Radio Sci. 1993, 28, 63–76. [Google Scholar] [CrossRef]
  56. Basili, P.; Ciotti, P.; Fionda, E. Comparison Of Algorithms For Retrieval Of Water Vapor, Cloud Liquid And Atmospheric Attenuation By Microwave Radiometry. In Proceedings of Proceedings of the 1994 Progress in Electromagnetics Research Symposium, Noordwijk, The Netherlands, 11–15 July 1994; pp. 571–574.
  57. Lohnert, U.; Crewell, S. Accuracy of cloud liquid water path from ground-based microwave radiometry—1. Dependency on cloud model statistics. Radio Sci. 2003. [Google Scholar] [CrossRef]
  58. Ferrare, R.; Turner, D.; Clayton, M.; Schmid, B.; Redemann, J.; Covert, D.; Elleman, R.; Ogren, J.; Andrews, E.; Goldsmith, J.E.M.; et al. Evaluation of daytime measurements of aerosols and water vapor made by an operational Raman lidar over the Southern Great Plains. J. Geophys. Res. Atmos. 2006. [Google Scholar] [CrossRef]
  59. Lihavainen, H.; Kerminen, V.M.; Remer, L.A. Aerosol-cloud interaction determined by both in situ and satellite data over a Northern high-latitude site. Atmos. Chem. Phys. 2010, 10, 10987–10995. [Google Scholar] [CrossRef]

Share and Cite

MDPI and ACS Style

Madhavan, B.L.; He, Y.; Wu, Y.; Gross, B.; Moshary, F.; Ahmed, S. Development of a Ground Based Remote Sensing Approach for Direct Evaluation of Aerosol-Cloud Interaction. Atmosphere 2012, 3, 468-494. https://doi.org/10.3390/atmos3040468

AMA Style

Madhavan BL, He Y, Wu Y, Gross B, Moshary F, Ahmed S. Development of a Ground Based Remote Sensing Approach for Direct Evaluation of Aerosol-Cloud Interaction. Atmosphere. 2012; 3(4):468-494. https://doi.org/10.3390/atmos3040468

Chicago/Turabian Style

Madhavan, Bomidi Lakshmi, Yuzhe He, Yonghua Wu, Barry Gross, Fred Moshary, and Samir Ahmed. 2012. "Development of a Ground Based Remote Sensing Approach for Direct Evaluation of Aerosol-Cloud Interaction" Atmosphere 3, no. 4: 468-494. https://doi.org/10.3390/atmos3040468

Article Metrics

Back to TopTop