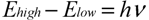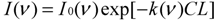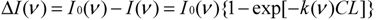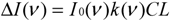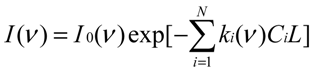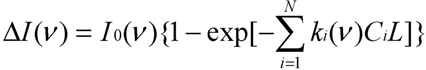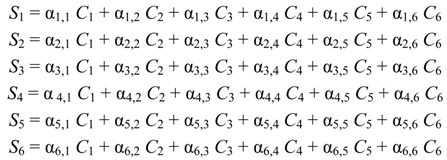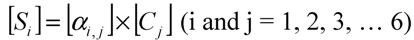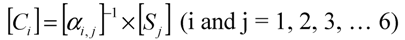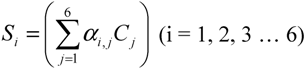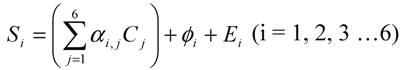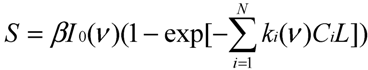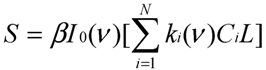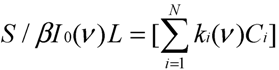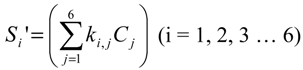Estimation of the Interference in Multi-Gas Measurements Using Infrared Photoacoustic Analyzers

Abstract

Two methods were described to estimate interference in the measurements of infrared (IR) photoacoustic multi-gas analyzer (PAMGA). One is IR spectroscopic analysis (IRSA) and the other is mathematical simulation. An Innova 1412 analyzer (AirTech Instruments, Ballerup, Denmark) with two different filter configurations was used to provide examples that demonstrate the two methods. The filter configuration in Example #1 consists of methane (CH₄), methanol (MeOH), ethanol (EtOH), nitrous oxide (N₂O), carbon dioxide (CO₂), and water vapor (H₂O), and in Example #2 of ammonia (NH₃), MeOH, EtOH, N₂O, CO₂, and H₂O. The interferences of NH₃ as a non-target gas in Example #1 were measured to validate the two methods. The interferences of H₂O and NH₃ as target gases in Example #2 were also measured to evaluate the analyzer’s internal cross compensation algorithm. Both simulation and experimental results showed that the interference between the target gases could be eliminated by the internal cross compensation algorithm. But the interferences of non-target gases on target gases could not be addressed by the internal cross compensation, while they could be assessed by the IRSA and mathematical simulation methods. If the IR spectrum of a non-target gas overlaps with that of target gas A at filter A, it could affect not only gas A (primary interference), but also other target gases by secondary interference (because the IR spectrum of gas A overlaps with gas B at filter B and thus affects gas B measurements). The IRSA and mathematical simulation methods can be used to estimate the interference in IR PAMGA measurements prior to purchase or calibration of the unit.

1. Introduction

Agriculture is an important source of air emissions, including greenhouse gases, volatile organic compounds, and ammonia (NH₃) [1,2,3]. Some of these emissions have been regulated by federal, state, and local agencies [4,5,6]. Measurements of air emissions from agriculture are needed to identify the emission sources, estimate the emission rates, compare the emission changes between different operational conditions, and evaluate the effectiveness of emission mitigation. The infrared (IR) photoacoustic multi-gas analyzer (PAMGA) (e.g., Innova 1412, AirTech Instruments, Ballerup, Denmark) has been widely used in the agricultural air emission studies ([7,8,9,10,11,12] and references therein). A National Air Emissions Monitoring Study (NAEMS) was conducted in recent past to monitor air emissions at 24 sites in nine states throughout the US [13,14,15] and IR PAMGA was also used at most of the NAEMS sites. A PAMGA (Innova 1312) was evaluated by the US Environmental Protection Agency [16] and was considered a certified analyzer for detecting ethanol from automotive exhaust in California [17]. Because the IR PAMGA adopts an IR spectroscopic method to measure multiple gases, interference due to overlap of the gas IR spectra that would most likely occur is a major concern for data accuracy. Therefore, there is a need for IR PAMGA users to better understand the interference in the IR PAMGA measurements and to determine if the IR PAMGA can be properly used. For this purpose, two methods, IR spectroscopic analysis (IRSA) and mathematical simulation, were introduced in the present study to investigate the interference in IR PAMGA measurements. Due to the complexity of the interference in the IR spectroscopic measurements, not all interference issues could be addressed by the proposed two methods. The objective of this study was to explore the proper use of the IR PAMGA in agriculture air quality studies including (1) configuring the filters based on the application of the IR PAMGA; (2) estimating the interference of non-target gases in the monitoring environment before conducting actual field experiments to determine if a particular IR PAMGA can be used in the application; (3) simulating the interference when new non-target gases were discovered after the actual field experiments were conducted to evaluate the IR PAMGA data; and (4) experimentally evaluating the analyzer’s internal cross compensation algorithm.

2. Analysis of the Interference in IR PAMGA Measurements

It is well known that interference exists in IR spectroscopic measurements and causes large uncertainties in observational data if it is not treated properly. Therefore, understanding of IR PAMGA interference is a critical step to ensure accurate air emission monitoring when using such instrumentation.

The principle of the IR PAMGA and IR photoacoustic technology were described in detail by Christensen [18,19] and also can be found in articles on the manufacturer’s website [20]. For readers not familiar with IR spectra, some discussion of basic IR spectral formulae will be provided before discussing the complexities of interference in IR PAMGA measurements.

2.1. IR Spectra of Gas Molecules

Each gas molecule has its own set of characteristic quantum energies. When a molecule absorbs external energy (such as photons in light), it transits from a lower to a higher energy level. When the molecule returns back to its lower energy level, it either emits a photon or releases heat or both. During the transition from one energy level to another, the difference between the higher energy level E_high and the lower level E_low of the molecule must be equal to the photon energy (hν) for energy conservation:

(1)

where ν is the wavenumber of the photon in cm⁻¹ and h is Planck’s constant. Most gas molecules absorb and emit photons in the IR region (ν = 10–14,000 cm⁻¹), in which the mid-IR region (670–4,000 cm⁻¹) is widely used in the IR detection of gas molecules. When an IR monochromatic light with single wavenumber enters a chamber that contains a single gas absorbing the light at the same wavenumber, the light intensity decreases after passing through the chamber. The change in light intensity before and after the chamber obeys Beer’s law (e.g., [21]):

(2)

or

(2a)

where I₀ and I are the light intensity before and after passing through the gas chamber at wavenumber ν, ΔI is the absorbed light intensity, L is the length of the chamber along the optical path in meters (m), C is the gas concentration in ppm, and k is the gas absorption coefficients at wavenumber ν in ppm⁻¹∙m⁻¹. I₀, I, ΔI, and k are functions of the wavenumber.

The gas concentration inside the chamber can be determined from Equations (2) or (2a) based on the change in light intensity, when the absorption coefficient k(ν) and optical length L are known. The absorption coefficients of many molecules have been determined in previous work and can be found in many databases (e.g., [22,23]). If the photon energy does not match the energy difference between the higher and lower energy levels, the molecule does not absorb the light at this wavenumber, i.e., the absorption coefficient k(ν) is zero, and therefore the light intensity remains unchanged, i.e., I(ν) = I₀(ν) or ΔI(ν) = 0. When a light covering a wide IR spectral range passes through a chamber with a single gas inside, the changes in light intensity will be the function of the wavenumber, which is referred to as the IR spectrum of the gas.

When the gas absorption is small (i.e., k(ν)CL << 1), the absorbed light intensity is linearly proportional to the gas concentration C:

(2b)

Simplification from Equation (2a) to (2b) is reasonable as long as the gas concentrations are in the linear measurement range because the IR gas analyzers provide a linear response to the gas concentrations. When an IR light intensity is modulated at an “audio” frequency, the heat released by the molecule when transiting from a higher to a lower energy level produces a sound signal at the same frequency inside the chamber that can be detected by microphones. Intensity of the microphone signal is proportional to the absorbed light intensity ΔI(ν) [18]. The change in microphone signal with the light wavenumber is referred to as the IR photoacoustic spectrum of the gas.

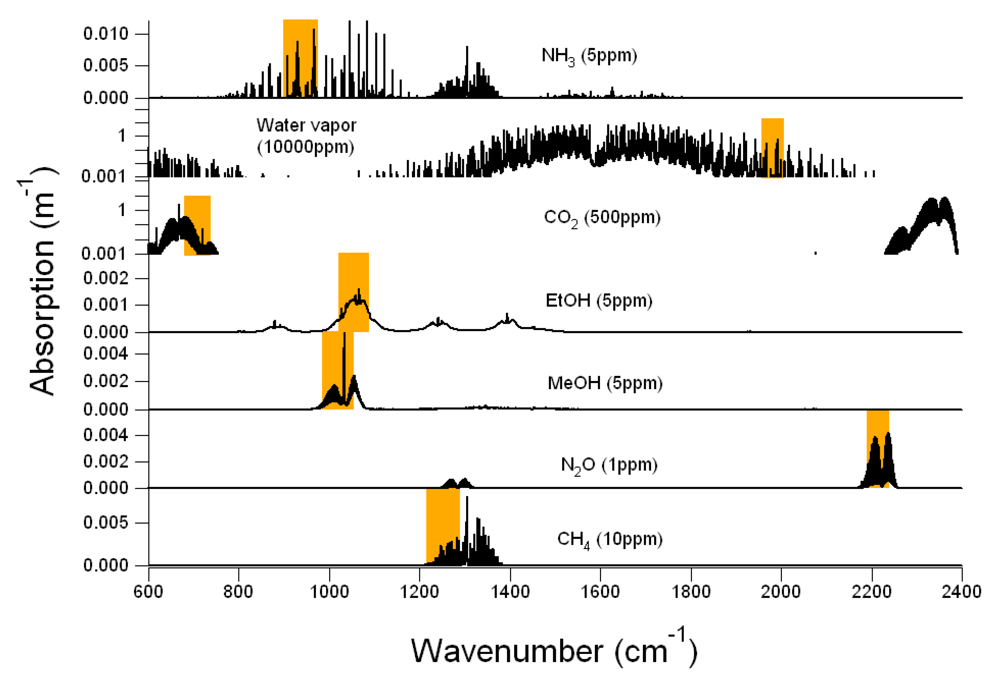
Figure 1 shows the IR absorption spectra of CH₄, CO₂, MeOH, EtOH, N₂O, NH₃ and H₂O in the IR region of 600–2,400 cm⁻¹. The IR spectral data of these molecules were obtained from the IR spectral library of the Pacific Northwest National Laboratory [23] in 0.1 cm⁻¹ resolution. Each gas molecule has its characteristic spectrum in terms of wavenumber region, absorption intensity, and structure (Figure 1), by which the gas can be identified and quantitatively detected. However, because every gas molecule has a set of characteristic IR spectra, the IR spectra of several gas molecules may overlap in a particular IR spectral region and therefore these gas molecules absorb light at the same wavenumber. Overlaps of the gas IR spectra can be seen in Figure 1.

Figure 1. Example of infrared (IR) absorption spectra of CH₄, CO₂, MeOH, EtOH, N₂O, NH₃ and H₂O (black solid lines). Locations and bandpass of filters corresponding to each gas are shown in orange rectangles on each plot. In Example #1, CH₄, CO₂, MeOH, EtOH, N₂O and H₂O are target gases and NH₃ is the non-target gas. In Example #2, CO₂, MeOH, EtOH, N₂O, NH₃ and H₂O are target gases and CH₄ is the non-target gas.

Figure 1. Example of infrared (IR) absorption spectra of CH₄, CO₂, MeOH, EtOH, N₂O, NH₃ and H₂O (black solid lines). Locations and bandpass of filters corresponding to each gas are shown in orange rectangles on each plot. In Example #1, CH₄, CO₂, MeOH, EtOH, N₂O and H₂O are target gases and NH₃ is the non-target gas. In Example #2, CO₂, MeOH, EtOH, N₂O, NH₃ and H₂O are target gases and CH₄ is the non-target gas.

If there are multiple gases inside the chamber and some of them absorb light at the same wavenumber ν, the transmitted light intensity becomes:

(3)

where N is the number of gas molecules that absorb light at wavenumber ν. The absorbed light intensity becomes:

(3a)

(

When the gas absorption is small (k(ν)CL << 1), the absorbed light intensity is:

(3b)

It is almost impossible to derive gas concentrations from Equations (3)–(3b) at a single IR wavenumber because the change in IR light intensity is due to absorption by several gases, but it may be possible to do so in multiple IR regions. For example, the Innova 1412 (AirTech Instruments, Ballerup, Denmark), an IR PAMGA, uses up to six filters to select IR light in up to six spectral regions to detect up to six gases sequentially. Because there are multiple gases in the monitoring environment in this case, overlaps of gas IR spectra may cause interference in gas detection and therefore may introduce measurement errors if the interference is not properly treated.

2.2. Estimation of the Interference by IR Spectroscopic Analysis (IRSA)

Because the IR PAMGA employs an IR spectroscopic technique to measure multiple gases, interference between the gases is likely to occur due to the overlaps of IR spectra. In order to reduce the interference, the first step is to properly configure the filters in IR PAMGA based on the IR absorption of all gases of interest in the monitoring environment. In the present study, two filter configurations were used as examples and are listed in Table 1, which includes channels, filter names, target gases, central, starting, and ending wavenumbers of the bandpass filters. In Example #1, six filters were selected to monitor target gases of MeOH, EtOH, N₂O, CO₂, CH₄ and H₂O in channels A, B, C, D, E, and W, respectively. In Example #2, the target gases were MeOH, EtOH, N₂O, CO₂, NH₃ and H₂O in channels A, B, C, D, E, and W, respectively. The IR absorption spectra of these gases are shown in Figure 1 (black thick lines) together with the locations and bandpass of the corresponding filters (orange rectangles). Filter names and their paired target gases are presented in Table 1. Concentrations of the target gases in Figure 1 were 10 ppm for CH₄, 5 ppm for MeOH, EtOH, and NH₃, 1 ppm for N₂O, 500 ppm for CO₂, and 10,000 ppm for H₂O. Because of the wide range in agricultural air emissions from very low (ppb level) in open sources to extremely high (thousands ppm level) in the enclosed animal housing, the vertical scale of the IR spectra in Figure 1 would change with the real concentrations, but the locations and bandpass of filters would not. According to Table 1 and Figure 1, the six gas/filter combinations in Example #1 corresponded to the six plots from the second to the seventh in Figure 1, and the six gas/filter combinations in Example #2 to those from the first to the sixth in Figure 1. The vertical-axis is a log scale for CO₂ and H₂O and linear for other gases.

First, the selected filters must be located in the absorption regions of their target gases, away from the strong absorption for high concentration gases, and close to the central peak for low concentration gases. Figure 1 shows that the H₂O filter was located at the far wings of a water vapor absorption band to avoid saturation caused by strong absorption near the band center. The CO₂ filter was located at a weak absorption band to avoid saturation as well. For other target gases, the filters were located near the band center to achieve stronger absorption.

Table 1. Filter configurations and filter/target gas combinations in Example #1 and #2.

Channel in Example #1	Channel in Example #2	Filter Name	Target Gas	Filter Center (cm−1)		FilterBandpass (cm−1)
A	A	UA 0936	MeOH	1,020	989–1,053
B	B	UA 0974	EtOH	1,061	1,027–1,096
C	C	UA 0985	N2O	2,215	2,193–2,237
D	D	UA 0982	CO2	710	683–737
E	-	UA 0969	CH4	1,254	1,220–1,289
-	E	UA 0976	NH3	941	908–974
W	W	SB 0527	H2O	1,985	1,965–2,205

Table 1. Filter configurations and filter/target gas combinations in Example #1 and #2.

Channel in Example #1	Channel in Example #2	Filter Name	Target Gas	Filter Center (cm−1)		FilterBandpass (cm−1)
A	A	UA 0936	MeOH	1,020	989–1,053
B	B	UA 0974	EtOH	1,061	1,027–1,096
C	C	UA 0985	N2O	2,215	2,193–2,237
D	D	UA 0982	CO2	710	683–737
E	-	UA 0969	CH4	1,254	1,220–1,289
-	E	UA 0976	NH3	941	908–974
W	W	SB 0527	H2O	1,985	1,965–2,205

Secondly, the selected filters should be located at the spectral regions where overlaps between the IR spectra are as few as possible because spectra overlaps would cause interference in multiple gas measurements. The overlaps between the gas IR spectra can be easily identified by aligning the IR spectra of all gases in one graph. Figure 1 shows the NH₃ interference at the MeOH and EtOH filters, the MeOH interference at the EtOH filter, and the EtOH interference at the MeOH filter. By contrast, the CH₄ interference on other gases is not likely to occur because the CH₄ absorption band is located far away from other filters. Because the IR spectra of water vapor cover a wide spectral range, water vapor interferes with most gases unless the air sample is dry. Therefore, a H₂O filter must be included in the filter configuration when the PAMGA is used in atmospheric applications. In Table 1, the H₂O filter was installed in channel W for both Examples #1 and #2. Although Figure 1 only represents the IR spectra of the selected filter configuration at the selected concentrations of their target gases, the procedure to examine the overlaps of gas IR spectra can be applied to any filter configuration at any gas concentration. Since it is not practical to produce graphs similar to Figure 1 for every filter configuration and every gas concentration in one presentation, users of the IR PAMGA can make similar graphs for the filter configurations and gas concentrations of interest to perform the IRSA. To study the interference between multiple gases at variable concentrations, gas absorption coefficients are more frequently used as described below.

In order to quantitatively compare the absorption of the selected gases at an IR PAMGA filter, absorption coefficients measured at the standard ambient pressure and temperature of 101.3 kPa and 25 °C by the PNNL [23] were used to derive the total absorption of the gases at that particular bandpass. The total absorption (m⁻¹) of a gas at a filter bandpass was an integration of individual absorption coefficients from the PNNL database over the entire filter bandpass and then multiplied by the gas concentration. 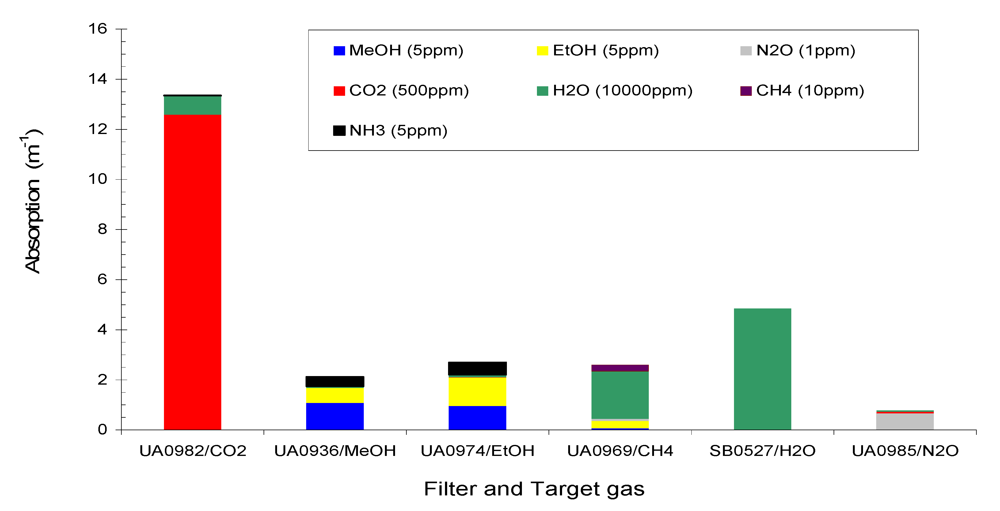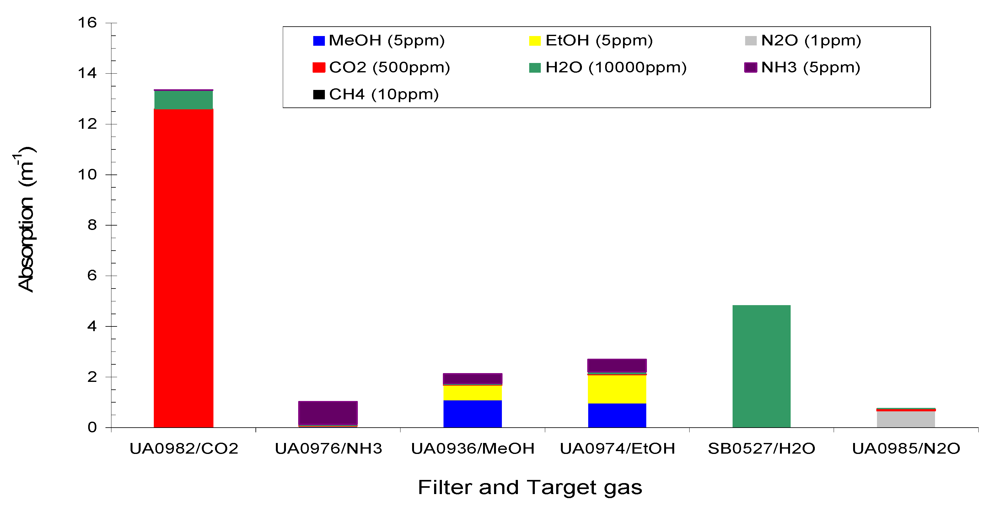Figure 2 shows the total absorption of the six target gases CH₄ (10 ppm), MeOH (5 ppm), EtOH (5 ppm), N₂O (1 ppm), CO₂ (500 ppm), H₂O (10,000 ppm) and a non-target gas NH₃ (5 ppm) at the six filters of Example #1. 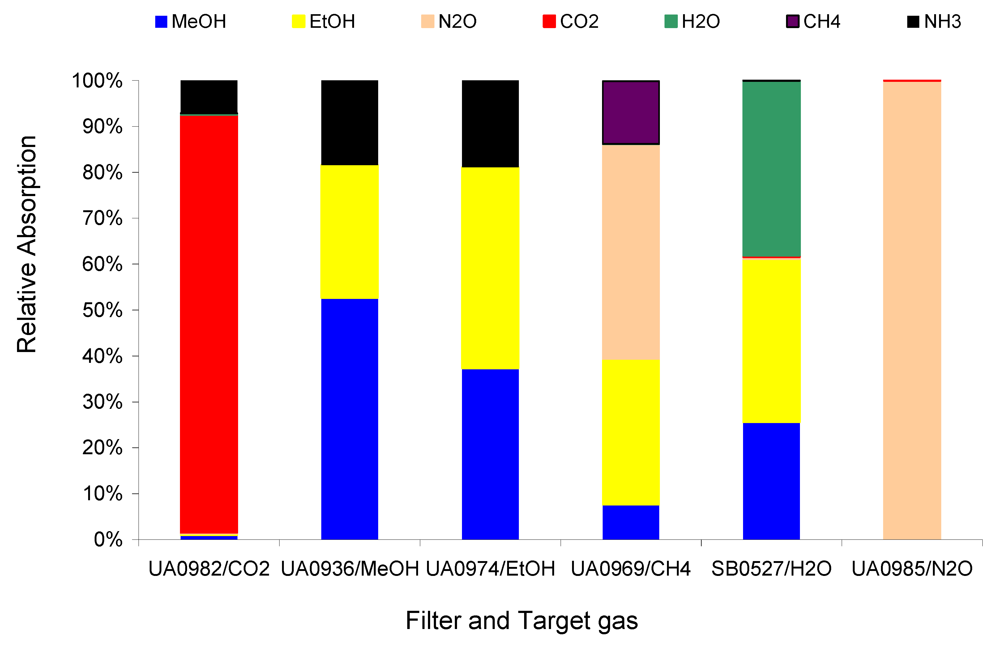Figure 3 shows the total absorption of the six target gases NH₃ (5 ppm), MeOH (5 ppm), EtOH (5 ppm), N₂O (1 ppm), CO₂ (500 ppm), H₂O (10,000 ppm), and a non-target gas CH₄ (10 ppm) at the six filters of the Example #2. It is seen in Figure 2 and Figure 3 that (1) total absorption at a given filter consisted of contributions from several gases due to the overlaps of IR spectra at that filter; (2) one gas contributed to several filters, and (3) non-target gases made contributions to several filters. Therefore, interference between the gases in IR PAMGA measurements would most likely occur. In order to separate the contributions of multiple gases in multiple filters and reduce the interference, mathematical algorithms are needed. The algebraic matrix method may be a good choice for this purpose because it can mathematically solve this kind of problem. Before introducing the algebraic matrix, we will continue to discuss the interference in IR PAMGA measurements based on gas IR spectra.

Figure 2. Absorption of Example #1 target gases (CH₄ = 10 ppm, CO₂ = 500 ppm, MeOH = 5 ppm, EtOH = 5 ppm, N₂O = 1 ppm, and H₂O = 10,000 ppm) and non-target gas (NH₃ = 5 ppm) at each filter.

Figure 2. Absorption of Example #1 target gases (CH₄ = 10 ppm, CO₂ = 500 ppm, MeOH = 5 ppm, EtOH = 5 ppm, N₂O = 1 ppm, and H₂O = 10,000 ppm) and non-target gas (NH₃ = 5 ppm) at each filter.

Figure 3. Absorption of Example #2 target gases (NH₃ = 5 ppm, CO₂ = 500 ppm, MeOH = 5 ppm, EtOH = 5 ppm, N₂O = 1 ppm, and H₂O = 10,000 ppm) and non-target gas (CH₄ = 10 ppm) at each filter.

Figure 3. Absorption of Example #2 target gases (NH₃ = 5 ppm, CO₂ = 500 ppm, MeOH = 5 ppm, EtOH = 5 ppm, N₂O = 1 ppm, and H₂O = 10,000 ppm) and non-target gas (CH₄ = 10 ppm) at each filter.

Figures 2 and 3 were produced for selected filter configurations and gas concentrations to show the possible interference between these gases. Similar plots can be made for different filter configurations at various gas concentrations after the total absorption at each filter are computed from the PNNL IR spectral database. Because gas concentrations vary in the real world, it is impossible to make graphs for every gas concentration to perform the IRSA. It would be better to have a single plot or table for a given filter configuration which can be used for IRSA at variable gas concentrations. For this purpose, total absorptions of these gases at a concentration of 1 ppm are provided in Table 2. 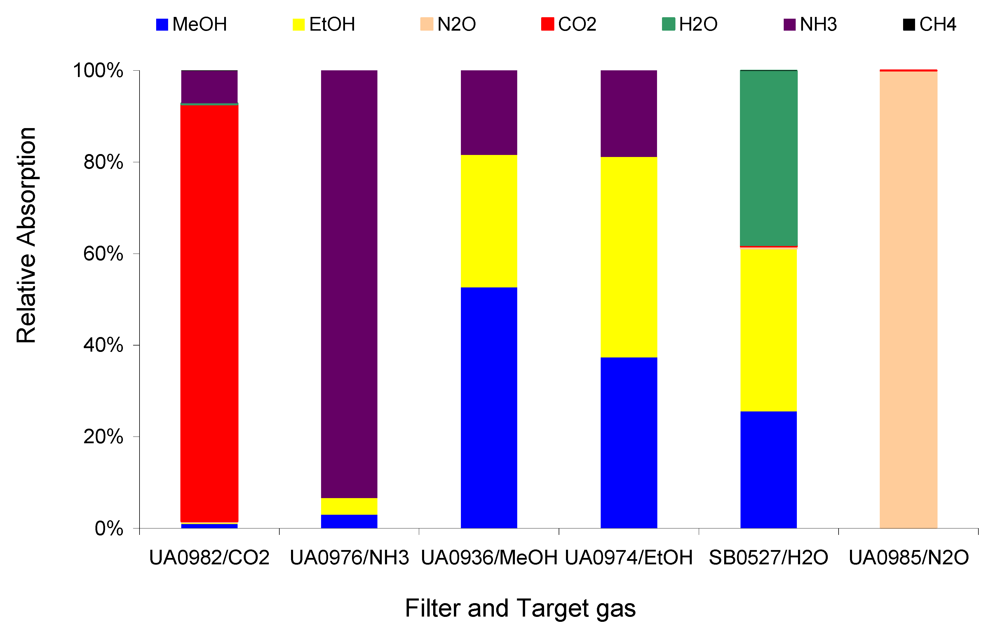Figure 4 compares the relative absorptions of the 1 ppm target gases CH₄, MeOH, EtOH, N₂O, CO₂, and H₂O in Example #1 with the introduction of 1 ppm non-target gas NH₃. Figure 5 shows the comparison between 1 ppm target gases NH₃, MeOH, EtOH, N₂O, CO₂, and H₂O in Example #2 with the introduction of 1 ppm non-target gas CH₄. Figure 4 depicts the strong interference of the non-target gas NH₃ on the target gases MeOH and EtOH, less interference on CH₄ and CO₂, and much less interference on N₂O. The relative absorption shown in Figure 4 and Figure 5 indicate the relative interference of the non-target on the target gases. The relative interference of 1 ppm non-target gas NH₃ on 1 ppm target gases MeOH, EtOH, N₂O, CO₂, and CH₄ are 349, 432, 0, 78, and 11 ppb per ppm NH₃, respectively, which were derived from Table 2. These relative interference values can be used to determine the interference of a non-target gas at any concentration, e.g., 10 ppm NH₃ could cause about 3.5, 4.3, 0, 0.8, and 0.1 ppm interference, respectively, in the measurements of MeOH, EtOH, N₂O, CO₂, and CH₄. Either the relative absorption in Figure 4 or the calculated relative interference in Table 2 can inform the user of how the non-target gas would directly affect the measurements of the target gases if the non-target gas exists. Obviously, the Example #1 cannot be used in applications where NH₃ appears to be at elevated concentrations.

As another example, the IRSA was applied to Figure 5. The relative interference of 1 ppm non-target gas CH₄ on 1 ppm target gases NH₃, MeOH, EtOH, N₂O, and CO₂ in Example #2 were hardly observed in Figure 5 but can be derived from Table 2. They were 11, 12, 21, 4, and 362 ppt per ppm CH₄, respectively, therefore can be neglected when the CH₄ concentration is low. When CH₄ was as high as 1,000 ppm, the errors caused directly by CH₄ would be 11, 12, 21, 4, and 362 ppb, respectively, in the NH₃, MeOH, EtOH, N₂O and CO₂ measurements. So, the CH₄ interference in Example #2 was still negligible even if the CH₄ was up to thousands of ppm, while the target gases were at a few ppm.

Figure 4. Relative absorption of 1 ppm non-target NH₃ and 1 ppm target gases at each filter in Example #1.

Figure 4. Relative absorption of 1 ppm non-target NH₃ and 1 ppm target gases at each filter in Example #1.

Figure 5. Relative absorption of 1 ppm non-target CH₄ and 1ppm target gases at each filter in Example #2.

Figure 5. Relative absorption of 1 ppm non-target CH₄ and 1ppm target gases at each filter in Example #2.

Table 2. Total absorption of 1 ppm gas at each filter, NH₃ relative interferenceon target gases in Examples #1, and CH₄ relative interference on target gases in Example #2.

Filter	Total Absorption of 1 ppm Gas (m−1)							NH3 RIF*ppbper ppm	CH4 RIF *pptper pm
	MeOH	EtOH	N2O	CO2	CH4	H2O	NH3
MeOH	2.2 × 10−1	1.2 × 10−1	5.0 × 10−6	1.5 × 10−5	2.6 × 10−6	5.2 × 10−6	7.6 × 10−2	349	12
EtOH	1.9 × 10−1	2.3 × 10−1	1.3 × 10−5	3.2 × 10−5	4.7 × 10−6	9.8 × 10−6	9.8 × 10−2	432	21
N2O	3.9 × 10−4	5.4 × 10−4	6.6 × 10−1	1.4 × 10−4	2.5 × 10−6	4.0 × 10−6	2.6 × 10−6	4 × 10−3	4
CO2	2.7 × 10−4	9.3 × 10−5	4.9 × 10−5	2.5 × 10−2	9.1 × 10−6	7.6 × 10−5	2.0 × 10−3	78	362
CH4	1.4 × 10−2	5.8 × 10−2	8.5 × 10−2	8.0 × 10−6	2.5 × 10−2	1.9 × 10−4	2.9 × 10−4	11	-
H2O	3.2 × 10−4	4.5 × 10−4	5.6 × 10−6	4.3 × 10−6	7.3 × 10−7	4.8 × 10−4	3.8 × 10−9	8 × 10−3	1517
NH3	5.8 × 10−3	6.9 × 10−3	2.2 × 10−5	1.1 × 10−5	1.9 × 10−6	6.0 × 10−6	1.8 × 10−1	-	11

* RIF: Relative Interference.

Table 2. Total absorption of 1 ppm gas at each filter, NH₃ relative interferenceon target gases in Examples #1, and CH₄ relative interference on target gases in Example #2.

Filter	Total Absorption of 1 ppm Gas (m−1)							NH3 RIF*ppbper ppm	CH4 RIF *pptper pm
	MeOH	EtOH	N2O	CO2	CH4	H2O	NH3
MeOH	2.2 × 10−1	1.2 × 10−1	5.0 × 10−6	1.5 × 10−5	2.6 × 10−6	5.2 × 10−6	7.6 × 10−2	349	12
EtOH	1.9 × 10−1	2.3 × 10−1	1.3 × 10−5	3.2 × 10−5	4.7 × 10−6	9.8 × 10−6	9.8 × 10−2	432	21
N2O	3.9 × 10−4	5.4 × 10−4	6.6 × 10−1	1.4 × 10−4	2.5 × 10−6	4.0 × 10−6	2.6 × 10−6	4 × 10−3	4
CO2	2.7 × 10−4	9.3 × 10−5	4.9 × 10−5	2.5 × 10−2	9.1 × 10−6	7.6 × 10−5	2.0 × 10−3	78	362
CH4	1.4 × 10−2	5.8 × 10−2	8.5 × 10−2	8.0 × 10−6	2.5 × 10−2	1.9 × 10−4	2.9 × 10−4	11	-
H2O	3.2 × 10−4	4.5 × 10−4	5.6 × 10−6	4.3 × 10−6	7.3 × 10−7	4.8 × 10−4	3.8 × 10−9	8 × 10−3	1517
NH3	5.8 × 10−3	6.9 × 10−3	2.2 × 10−5	1.1 × 10−5	1.9 × 10−6	6.0 × 10−6	1.8 × 10−1	-	11

* RIF: Relative Interference.

2.3. Experimental Tests on the Interference

In order to validate the IRSA method, experimental tests were conducted at California Analytical Instruments, Inc (CAI) using an Innova 1412 analyzer with two configurations as shown in Table 1. First, the analyzer was fully calibrated by CAI because it is a manufacturer authorized calibration facility. The NH₃ interferences as a non-target gas in Example #1 (because the NH₃ filter was not installed) are shown in Figure 6 and as a target gas in Example #2 (because the NH₃ filter was installed) are shown in Figure 7.

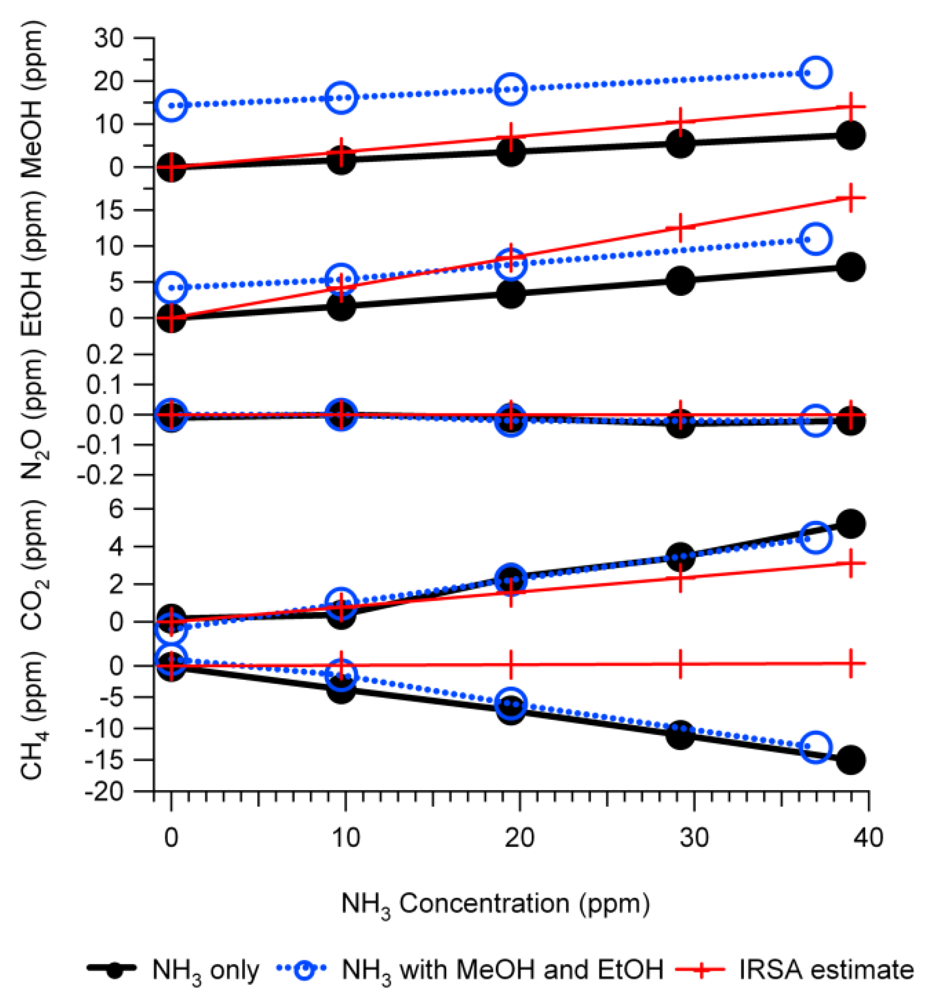
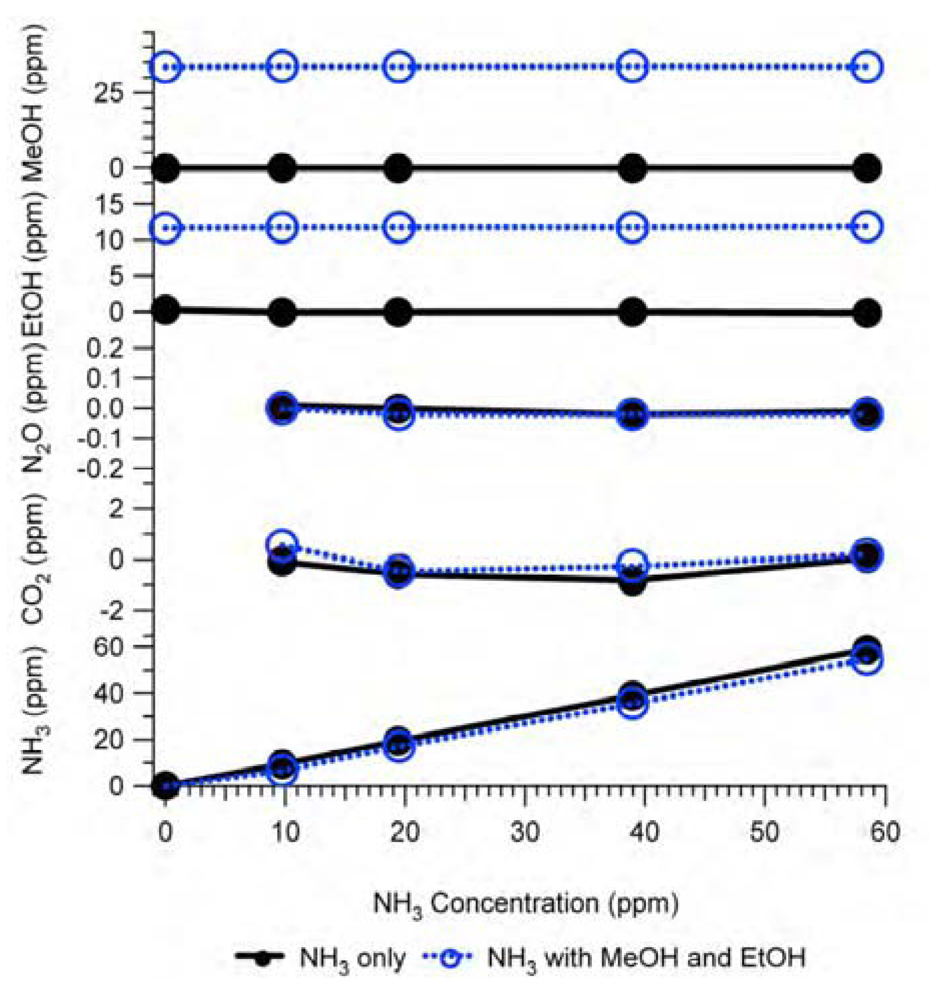
Figure 6. Interference of NH₃ in Example #1 as a non-target gas. Black solid lines with closed circles are experimental responses to NH₃ only (NH₃ = variable, other gases = 0 ppm), blue dash lines with open circles are experimental responses to NH₃ in the presence of MeOH (12.8 ppm) and EtOH (4.5 ppm), and red thin-lines with crosses are estimation by the IRSA method for the NH₃ only test. All gas mixtures were in N₂ balance and not humidified.

Figure 6. Interference of NH₃ in Example #1 as a non-target gas. Black solid lines with closed circles are experimental responses to NH₃ only (NH₃ = variable, other gases = 0 ppm), blue dash lines with open circles are experimental responses to NH₃ in the presence of MeOH (12.8 ppm) and EtOH (4.5 ppm), and red thin-lines with crosses are estimation by the IRSA method for the NH₃ only test. All gas mixtures were in N₂ balance and not humidified.

Figure 7. Interference of NH₃ in Example #2 as a target gas. Black solid lines with closed circles are experimental responses to NH₃ only (NH₃ = variable and other gases = 0 ppm) and blue dash lines with open circles are experimental responses to NH₃ in the presence of MeOH (35.2 ppm) and EtOH (12.2 ppm). All gas mixtures were in N₂ balance and not humidified. Analytical results of the interference of NH₃ as a target gas were not available because the IRSA method is used to estimate the interference of non-target gases.

Figure 7. Interference of NH₃ in Example #2 as a target gas. Black solid lines with closed circles are experimental responses to NH₃ only (NH₃ = variable and other gases = 0 ppm) and blue dash lines with open circles are experimental responses to NH₃ in the presence of MeOH (35.2 ppm) and EtOH (12.2 ppm). All gas mixtures were in N₂ balance and not humidified. Analytical results of the interference of NH₃ as a target gas were not available because the IRSA method is used to estimate the interference of non-target gases.

There are two tests shown in Figure 6: (1) the non-target gas NH₃ only was fed to the analyzer in various concentrations while all target gas concentrations were zero and (2) the non-target gas NH₃ was mixed with MeOH (12.8 ppm) and EtOH (4.5 ppm) in various concentrations before the mixture was fed to the analyzer while the other gas concentrations were zero. Experiment (1) was titled the “NH₃ only test” and experiment (2) the “tri-gas test”, which was the simplest case of a multi-gas test. In both experiments, the sample gases were obtained from standard gas cylinders in N₂ balance and were not humidified (H₂O = 0 ppm). The analyzer’s internal cross compensation algorithm was used in both experiments. The interference of non-target gas NH₃ on target gases MeOH, EtOH, N₂O, CO₂, and CH₄ were calculated based on the relative interference given in Table 2 at various NH₃ concentrations in the absence of other gases (NH₃ only test). The IRSA results are also shown in Figure 6. The experimental results in Figure 6 indicate that the NH₃ interference as non-target gas on the IR PAMGA measurements seem independent of the target gas concentrations because the line slopes in each graph are very close between the NH₃ only and tri-gas tests. Figure 6 reveals that the interference of non-target gases cannot be addressed by the analyzer’s internal cross compensation algorithm.

Comparisons between the experimental results and IRSA results in Figure 6 show a good agreement for N₂O and an overestimation for MeOH and EtOH. However, the negative interference of the non-target gas NH₃ on the target gas CH₄ measurements in Figure 6 was not predicted by the IRSA method. Because there was no direct overlapping spectra between NH₃ and CH₄ at the CH₄ filter, NH₃ did not directly interfere with CH₄ (primary interference), but NH₃ had a secondary interference on CH₄, i.e., NH₃ had a primary interference on EtOH at the EtOH filter and in turn EtOH had a primary interference on CH₄ at the CH₄ filter. The similar secondary inference of NH₃ on CH₄ via MeOH also happened due to the same procedure. It may be difficult to understand the negative interference of NH₃ on CH₄ as shown in Figure 6, but an explanation is provided below based on gas IR spectra as shown in Figure 1. The non-target gas NH₃ in Example #1 absorbed light at both MeOH and EtOH filters (Figures 1, 2, and 4) contributing a positive artifact in both MeOH and EtOH measurements. This positive artifact was then transferred to the CH₄ filter because MeOH and EtOH absorbed light at the CH₄ filter. In order to compensate for these positive artifacts at the CH₄ filter, the analyzer erroneously deduced a negative concentration of CH₄ through the internal cross compensation procedure. Because the IRSA method did not involve any cross compensation, it could not predict the secondary interference. Therefore, an algebraic matrix calculation is needed to estimate both primary and secondary interference, which will be discussed in Section 2.4.

The “NH₃ only” and “tri-gas” experiments were also conducted using the Example #2 analyzer, except that the NH₃ was a target gas because the NH₃ filter was installed in Example #2, and the results are shown in Figure 7. Figure 7 reveals that the interference of the target gas NH₃ on MeOH and EtOH was eliminated by the analyzer’s built-in cross compensation algorithm. No IRSA was performed for the NH₃ interference as a target gas because the IRSA method can only estimate the interference of non-target gases. Again, in order to simulate the interference of both target gas and non-target gas, an algebraic matrix is needed as described in Section 2.4.

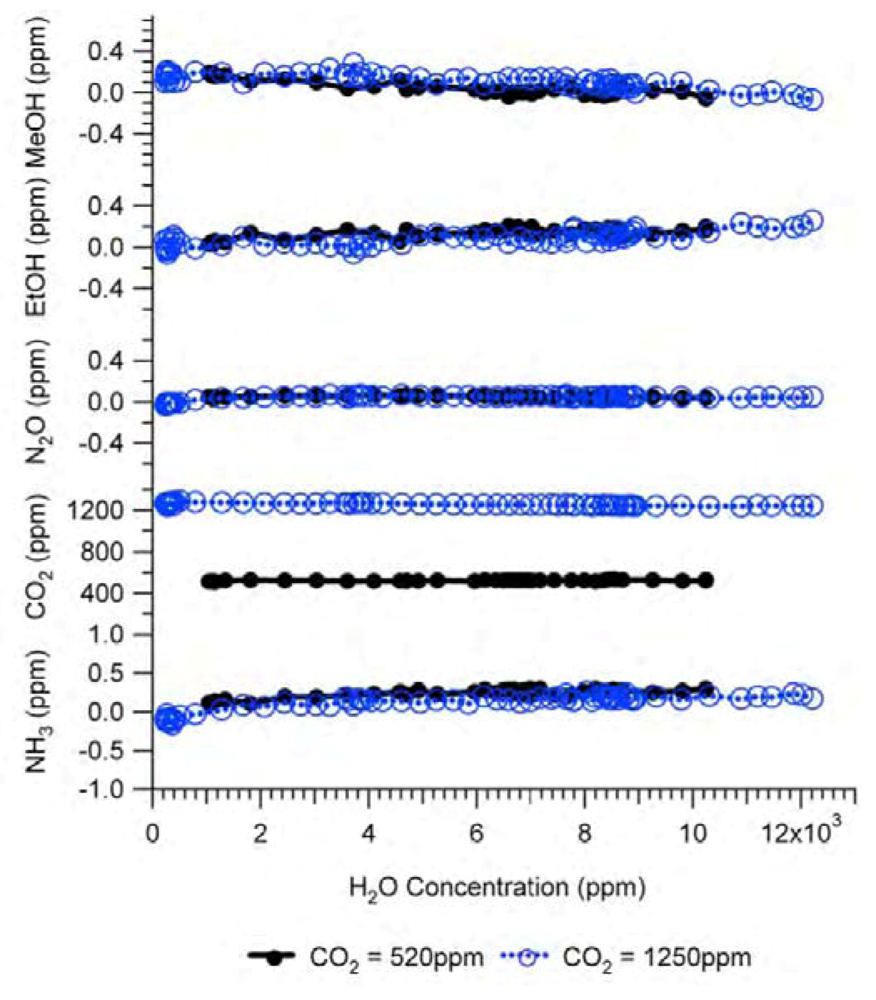
Because the IR spectrum of water vapor covers a wide spectral range and overlaps with that of many other gases, water vapor is a very important gas in terms of interference with other gas measurements. Therefore, water vapor must be measured as a target gas. This means that a H₂O filter must be included in the filter configuration. The interference of water vapor as a target gas in Example #2 was experimentally tested and the results are shown in Figure 8. The CO₂ gas at a constant concentration was humidified before entering the IR PAMGA using Nafion tubing over a heated water bath. The concentration of water vapor was adjusted by changing the water bath temperature. Two concentrations of CO₂ at 520 ppm and 1,250 ppm in ultra-zero air were used respectively in the tests, while all other gases were 0 ppm. Figure 8 reveals that the interference of water vapor as a target gas was also eliminated by the analyzer’s internal across compensation algorithm because changes in the measured concentrations of other target gases were almost independent of the water vapor concentrations.

Figure 8. Interference of H₂O in Example #2 as a target gas. Black solid lines with closed circles are experimental responses to 520 ppm CO₂ and blue dashed lines with open circles are experimental responses to 1,250 ppm CO₂. All other gases were 0 ppm. Analytical results of the interference of H₂O as a target gas were not available because the IRSA method is used to estimate the interference of non-target gases.

Figure 8. Interference of H₂O in Example #2 as a target gas. Black solid lines with closed circles are experimental responses to 520 ppm CO₂ and blue dashed lines with open circles are experimental responses to 1,250 ppm CO₂. All other gases were 0 ppm. Analytical results of the interference of H₂O as a target gas were not available because the IRSA method is used to estimate the interference of non-target gases.

2.4. Mathematical Simulation of the Interference

As discussed in Section 2.3 the internal cross compensation method of IR PAMGA can eliminate the interference between target gases but cannot address the interference of non-target gases. The IRSA method can be used to estimate the primary interference of non-target gases but cannot predict the secondary interference. Therefore, another approach is needed to address all of these issues. Because the interference in IR PAMGA occurred between multi-gases cross multiple filters, an algebraic matrix calculation would be a good method to solve the problem.

Assuming that six filters were installed in the IR PAMGA to measure six target gases including H₂O, S_i represents the microphone signal in μV from filter i (i = 1, 2, …, 6), C_j is the concentration in ppm of target gas j (j = 1, 2, …, 6), and α_i,j is the contribution of target gas j to the microphone signal S_i. The α_i,j is referred to as sensitivity coefficient in μV/ppm. Because of the overlaps of gas IR spectra, α_i≠j may not be zero, the target gas j would contribute to microphone signal S_i (i ≠ j) and cause interference on the measurement of the target gas i. In theory, the microphone signal S_i of IR PAMGA can be expressed as functions of the target gas concentrations C_j:

(4)

These linear algebraic Equations can also be expressed with an algebraic matrix Equation:

(4a)

or simply

(4b)

where both [S_i] and [C_i] are a 1 × 6 matrix and [α_i,j] a 6 × 6 matrix, respectively. Equation (4b) can be solved using an algebraic matrix Equation.

(4c)

where matrix [α_i,j]⁻¹ is the inverse of the matrix [α_i,j]. Because the method to calculate Equation (4c) can be found in any textbook of linear algebraic theory, it is not described here. In addition, there are many software packages with built-in programs to solve such linear algebra problems, so it is straightforward to calculate the variables [C_i] when microphone signals [S_i] and sensitivity coefficients [α_i,j] are known. The sensitivity coefficients [α_i,j] can be obtained by calibrating the IR PAMGA. Although six filters were assumed to derive Equations (4a)–(4c), the Equations can be applied to any number of filters in the PAMGA.

In order to introduce the interference of non-target gases, Equation (4) can also be expressed as:

(5)

In the real monitoring environments, there may be other gases as well as random electronic noise that, in addition to the target gases, contribute to the microphone signals. Considering all these factors, Equation (5) becomes

(5a)

where, φ_i is the total contribution of all non-target gases to the microphone signal S_i and E_i is the electronic noise (zero offset) at filter i. It is obvious that, for the same microphone signals S_i (i = 1, 2, 3,…6), the solutions C_j would be different between Equations (5) and (5a) if non-target gases and electronic noise exist (φ_i≠0 and E_i≠0). The differences in solution C_j between Equations (5) and (5b) are errors caused by non-target gas interference φ_i and noise E_i. In general, when the interference and electronic noise increase, the difference in solution between Equations (5a) and (5) also increases and therefore the uncertainty of the IR PAMGA measurements increases. There are several ways to reduce measurement errors. One is to decrease the electronic noise E_i by increasing the measurement interval. As mentioned in previous sections, properly configuring the filters in IR PAMGA based on the presence of all possible gases and their IR absorption properties is a key procedure to reduce the contribution of the non-target gas interference φ_i.

When the sensitivity coefficients α_i,j are available after calibration, the interference between the target gases can be simulated by solving Equation (5). It is also possible to evaluate the interference of non-target gases on IR PAMGA measurements by solving Equation (5a) when the non-target gases have also been calibrated. In some cases, when the calibrated sensitivity coefficients are not available, a simulation of the interference may be needed to assess its effect in the IR PAMGA measurements. Next we will discuss this possibility. Because the microphone signal of a single gas is proportional to the absorbed light intensity [18], it can be expressed as:

(6)

where β is a factor that includes the combined effects of temperature, pressure, thermal property of gases in the gas chamber, and geometry of the gas chamber, etc. [18]. Using Equation (3a), Equation (6) can be expressed as:

(6a)

Or using Equation (3b) when gas absorption is low, Equation (6) becomes:

(6b)

or:

(6c)

Now, it can be seen that Equation (6c) is similar to the algebraic matrix Equation (5). Defining S_i' = S_i/βI₀L (m⁻¹) as simulation signal, the simulation signals at the six filters in IR PAMGA are:

(7)

Equation (7) is also an algebraic matrix Equation similar to Equation (5). Thus, variables C_j can be solved from Equations (7) only if the simulation signals are known because absorption coefficients can be computed from available databases [23]. For mathematical simulation purposes, we may be able to use gas absorption coefficients k_i,_j instead of sensitivity coefficients α_i,_j, using the simulation signal S_i' instead of the microphone signal S_i to simulate the interference in IR PAMGA.

If we only consider the interference of one non-target gas without electronic noise (E_i = 0), then Equation (5a) becomes:

(7a)

where k_iⁿ and Cⁿ are the absorption coefficient at filter i and the concentration of the non-target gas, respectively. From Equations (7) and (7a), the interference of the non-target gas in IR PAMGA measurements can be mathematically estimated based on the selected filters and the IR absorption coefficients of all gases in the monitoring environment without calibrating the analyzer. This method might prove beneficial for IR PAMGA users when planning a new filter configuration for their analyzers. The procedure to simulate the interference using Equations (7) and (7a) is described below:

• Use initial concentrations of the target gas C_i^I and their absorption coefficients k_i,_j to calculate initial simulation signals S_i^I using Equation (7), where superscript “I” represent initial values.
• Add non-target gas absorption k_iⁿCⁿ in Equation (7a).
• Subtract k_iⁿCⁿ from the initial signals S_i^I to produce disturbed signals S_i^d, where superscript “d” represents disturbed values.
• Solve Equation (7) again using k_i,_j and S_i^d to obtain disturbed target gas concentrations C_i^d.
• The differences in target gas concentrations between initial C_i^I and disturbed C_i^d values reveal the interference of the non-target gas in IR PAMGA measurements.

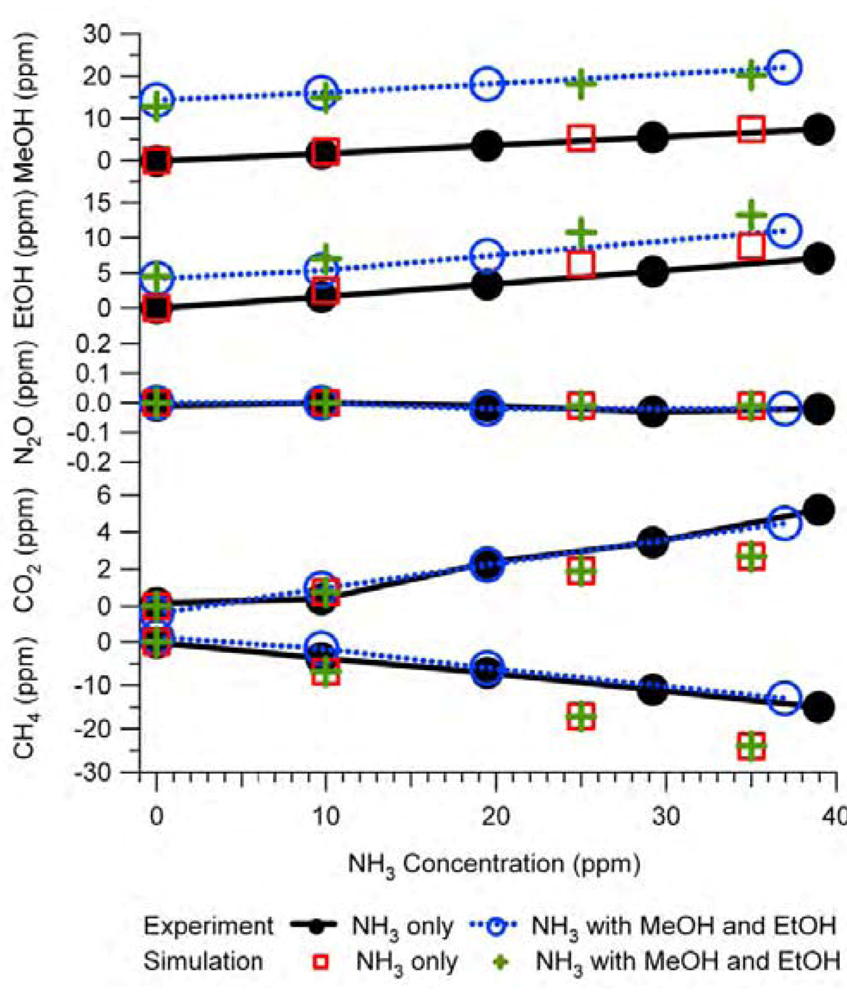
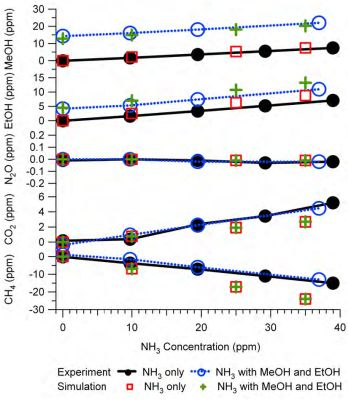
Figure 9 is an example of the simulation results and their comparison with the experimental tests. The experiments were the same as those described in Figure 6, therefore Figure 9 is similar to Figure 6 except that the NH₃ interference on IR PAMGA measurements was assessed by the mathematical simulation using Equations (7) and (7a) instead of the IRSA method. The NH₃ interference on target gases is almost independent of the target gas concentrations because the changes in interference with the NH₃ concentrations (line slopes) were very similar between the NH₃ only (NH₃ = variable and other gases = 0 ppm) and the tri-gas (MeOH = 12.8 ppm, EtOH = 4.5 ppm, NH₃ = variable, and other gases = 0 ppm) tests. Actually, the simulation was also conducted for multiple target gases at various concentrations in addition to the tri-gas (MeOH, EtOH and NH₃) in Figure 9 and the conclusion remained the same (not shown in any Figures because no experimental comparison was made). Table 3 compares the NH₃ relative interference (ppb per ppm NH₃) on target gases in Example #1 as a non-target gas. The relative interferences in Table 3 were obtained by IRSA, mathematical simulation, and experiments, respectively.

Table 3. Comparison of NH₃ relative interference on target gases in Example #1 as a non-target gas (ppb per ppm NH₃).

Target Gas	IRSA	Mathematical Simulation	Experiment (NH3 Only)	Experiment (Tri-Gas)
MeOH	349	212	182 ± 10	215 ± 42
EtOH	432	250	174 ± 8	172 ± 58
N2O	0.004	−0.4	0 ± 0.3	0 ± 0.4
CO2	78	76	103 ± 42	122 ± 28
CH4	11	−686	−377 ± 9	−302 ± 145

Table 3. Comparison of NH₃ relative interference on target gases in Example #1 as a non-target gas (ppb per ppm NH₃).

Target Gas	IRSA	Mathematical Simulation	Experiment (NH3 Only)	Experiment (Tri-Gas)
MeOH	349	212	182 ± 10	215 ± 42
EtOH	432	250	174 ± 8	172 ± 58
N2O	0.004	−0.4	0 ± 0.3	0 ± 0.4
CO2	78	76	103 ± 42	122 ± 28
CH4	11	−686	−377 ± 9	−302 ± 145

Figure 9. Interference of NH₃ on target gases in Example #1 as a non-target gas. Black solid lines with closed circles are experimental responses to NH₃ only (NH₃ = variable, other gases = 0 ppm), blue dash lines with open circles are experimental responses to NH₃ in the presence of MeOH (12.8 ppm) and EtOH (4.5 ppm), red squares are results of mathematical simulation for the NH₃ only test, and green crosses are simulation for the tri-gas test. All gas mixtures were in N₂ balance and not humidified.

Figure 9. Interference of NH₃ on target gases in Example #1 as a non-target gas. Black solid lines with closed circles are experimental responses to NH₃ only (NH₃ = variable, other gases = 0 ppm), blue dash lines with open circles are experimental responses to NH₃ in the presence of MeOH (12.8 ppm) and EtOH (4.5 ppm), red squares are results of mathematical simulation for the NH₃ only test, and green crosses are simulation for the tri-gas test. All gas mixtures were in N₂ balance and not humidified.

The agreement between predictions and experiments for MeOH and EtOH were improved significantly by the mathematical simulation in comparison with the IRSA results (Figures 6 and 9 and Table 3). The NH₃ relative interferences on N₂O and CO₂ predicted by both IRSA and mathematical simulation were similar. They agreed well with experiments for N₂O (almost zero), but the prediction was lower than the experimental results for CO₂. The negative effect of the NH₃ interference on CH₄ measurements was successfully predicted by the mathematical simulation, which was due to the secondary interference but could not be predicted by the IRSA method (Figures 6 and 9 and Table 3). The difference between measurements and simulations might be due to the zero offset E_i in the IR PAMGA which was ignored in the simplified Equation (7a). The rectangle simplification of the filter bandpass shape may result in some difference in calculating the absorption coefficients and therefore cause simulating errors in Equations (7) and (7a). The dependence of microphone signals on temperature and pressure was ignored when the sensitivity coefficients α_i,_j in Equations (5) and (5a) were replaced with gas IR absorption coefficients k_i,_j in Equations (7) and (7a) and the simulation signal S_i' was used, which might cause some simulation errors. The simulation accuracy could be improved if all target and non-target gases were calibrated and the calibration data were used in the mathematical simulation. But the calibration data of non-target gases were usually not available because the manufacturers rarely provided this information. This is one of the reasons why the gas absorption coefficients were used in this study instead of the calibration data to simulate the interference. Although both IRSA and mathematical simulation methods are not ready yet for use to correct the errors caused by the interference of non-target gases because of their accuracy, they still can be used to select filters, simulate the interference of non-target gases, and therefore would be helpful for properly using the IR PANGA. A significant advantage is that the two methods can be performed prior to the instrument calibration, which would be very convenient for IR PAMGA users.

The simulations of CH₄ interference in the Example #2 measurements as a non-target gas were also conducted at various target gas concentrations. It was predicted by the IRSA that the CH₄ interferences in the Example #2 measurements were nearly zero at all 6 filters because the absorption of CH₄ at any of these filters was almost zero. The mathematical simulation using Equations (7) and (7a) came to the same conclusion.

3. Discussion and Conclusions

Two methods, IRSA and mathematical simulation, were introduced to estimate the interference in IR PAMGA measurements. The methods were also validated by experimental results. An Innova 1412 analyzer with two filter configurations was used as an example to demonstrate the IRSA and mathematical simulation methods. The filter configurations were (1) six filters for CH₄, MeOH, EtOH, N₂O, CO₂, and H₂O in Example #1, and (2) six filters for NH₃, MeOH, EtOH, N₂O, CO₂, and H₂O in Example #2.

The internal cross compensation algorithm of IR PAMGA can eliminate the interference between target gases but cannot address the interference of non-target gases. The possibilities of interference in IR PAMGA measurements can be visualized by graphing and aligning the IR absorption spectra of all target gases, the locations of their corresponding bandpass filters, and the IR spectra of all possible non-target gases. The IRSA method is useful in configuring the filters and predicting the interference for IR PAMGA. Basically, if the IR spectrum of a non-target gas overlaps with that of a target gas in that filter, interference would occur. For example, the filter configuration of Example #1 restricted its use to monitoring environments where NH₃ was not present, because NH₃ absorbed light at several filters of Example #1 but was not a target gas. The filter configuration of the Example #2 allowed its use in the presence of non-target gas CH₄ because CH₄ hardly absorbed light at any filters. The IRSA was able to estimate the primary interference due to the direct spectra overlapping but could not predict the secondary interference that resulted from overlaps of multiple gas IR spectra.

Mathematical simulation using absorption coefficients and simulation signals in Equations (7) and (7a) instead of sensitivity coefficients and the microphone signals in Equations (5) and (5a) made it possible to evaluate the interference in PAMGA measurements prior to purchase and calibration of the analyzers. Although both IRSA and mathematical simulation methods can predict the interference, the simulation method is more accurate because the algebraic matrix calculation involves cross compensation. The simulation results agreed with the experimental results better than the IRSA method (Figures 6 and 8). The mathematical simulation also predicted the secondary interference due to the overlapping IR spectra of multiple gases (see the negative effects of NH₃ interference on CH₄ measurements in Figure 9) while the IRSA method did not.

The mathematical simulation might be more accurate should the calibrated sensitivity coefficients be used to solve Equations (5) and (5a) rather than using absorption coefficients to solve Equations (7) and (7a). Although the Innova 1412 calibration data can be downloaded from the analyzer or provided by the manufacturer, the calibration data (such as the span conversion factor, the humidity gain factor, and the concentration offset factor) cannot be directly used in Equations (5) and (5a) because the relationship between sensitivity coefficients and the calibration data could not be determined. The raw calibration data were internally converted to the factors of span conversion, humidity gain, and offset for the built-in cross compensation algorithm. This is one of the reasons why absorption coefficients and simulation signals were used to simulate the interference in the present study.

Although an Innova 1412 analyzer with two filter configurations was used in this paper as an example to demonstrate the IRSA and mathematical simulation methods, the two methods can be applied to any filter configurations of Innova 1412 and other types of IR PAMGA (such as Innova 1312 and its older versions) to assess interferences. It may be possible to perform post measurement adjustment to correct the errors caused by non-target gas interferences using the algebraic matrix calculation which would be the ultimate goal for IR PAMGA users. To reach this goal, a wider range of mathematical theory, more experimental tests, and closer collaboration with instrument manufacturers are needed. The IRSA and mathematical simulation methods are very important approaches to this goal.