Analysis of Global and Key PM2.5 Dynamic Mode Decomposition Based on the Koopman Method
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
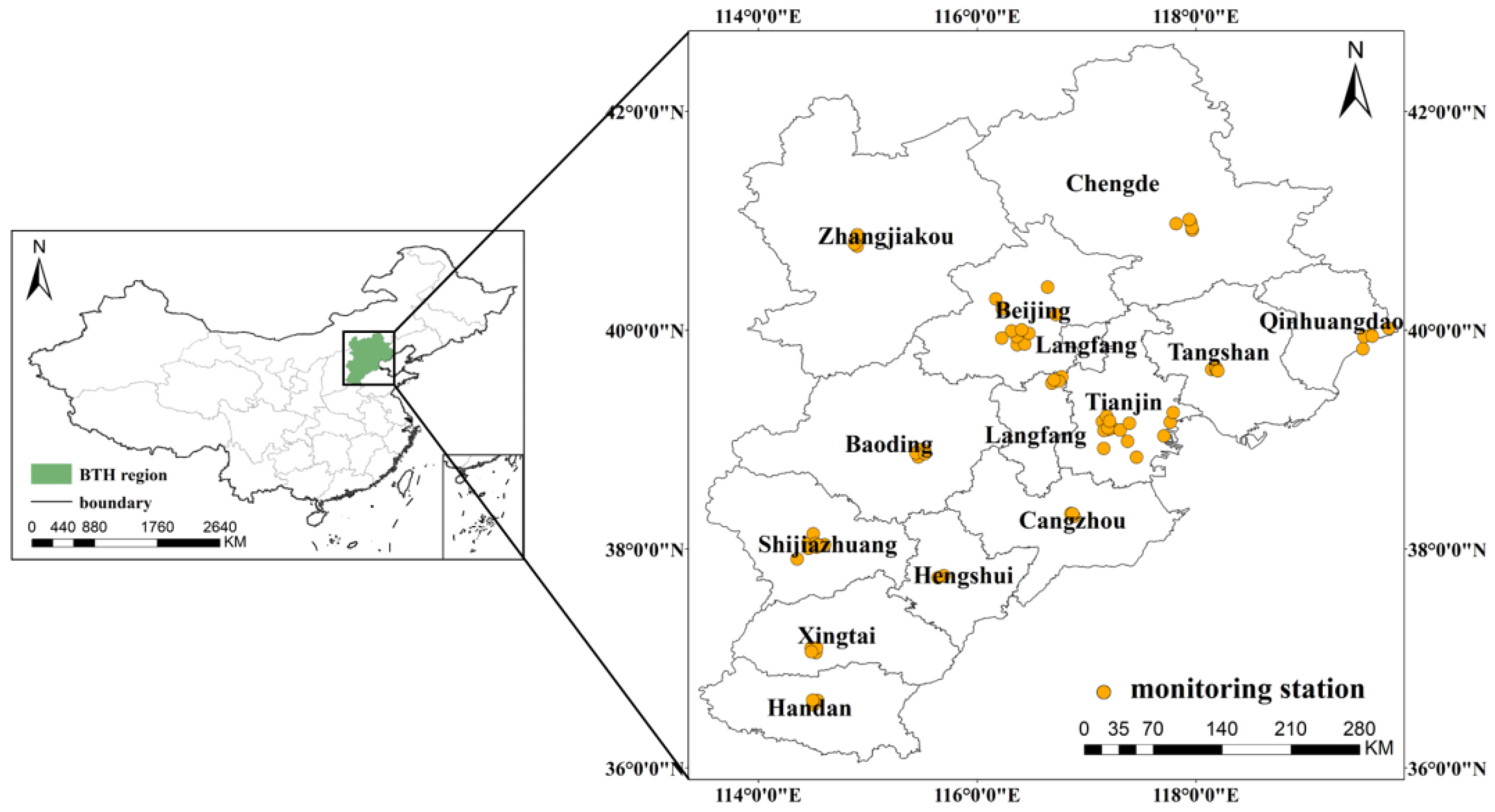
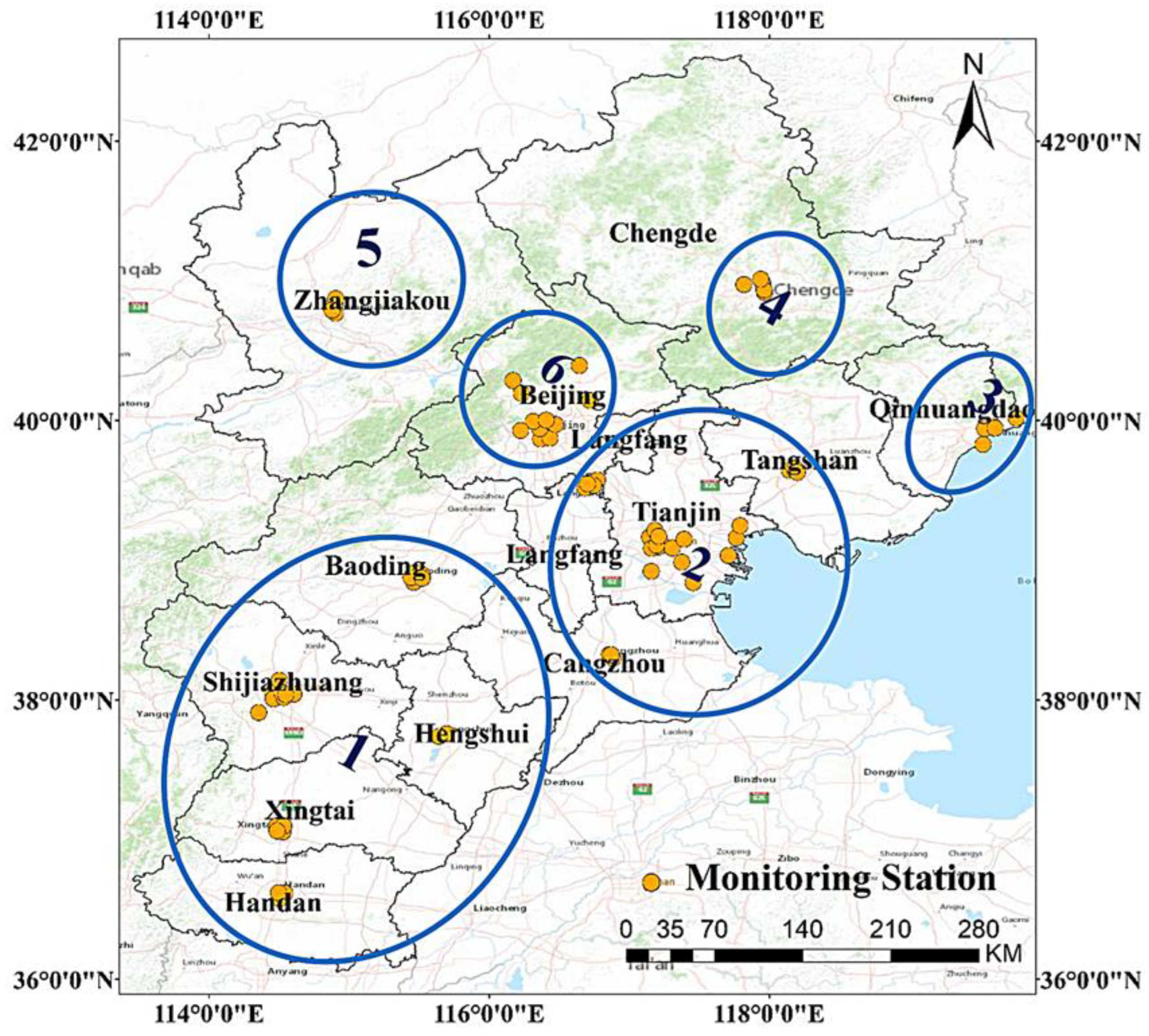
2.1.1. Study Area
2.1.2. Data Sources
2.2. Koopman Operator
2.2.1. Definition of Koopman Operator
2.2.2. Spectral Analysis of Koopman Operators
2.2.3. Hankel-DMD Algorithm
3. Results
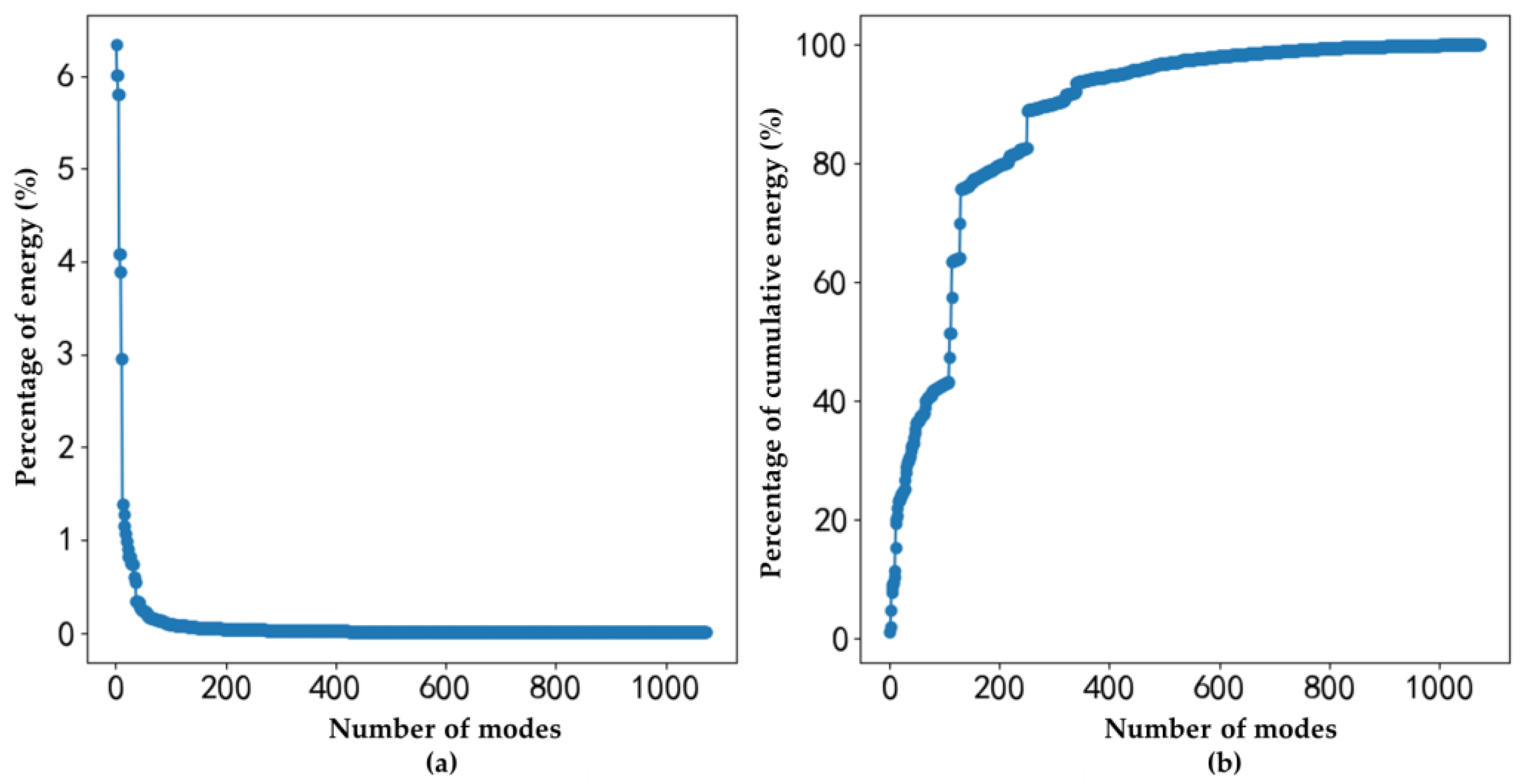
3.1. Analysis of PM2.5 Concentrations Mode Characteristics
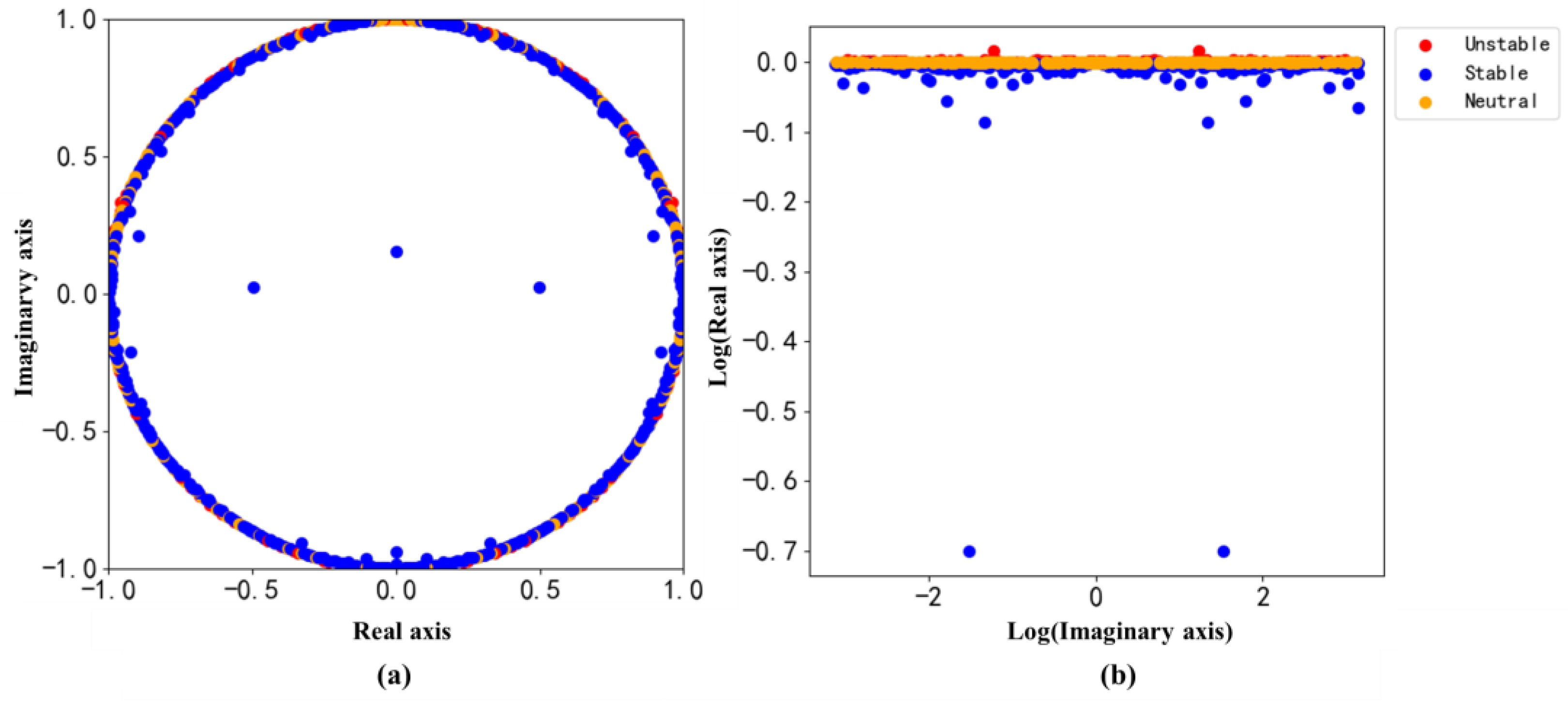
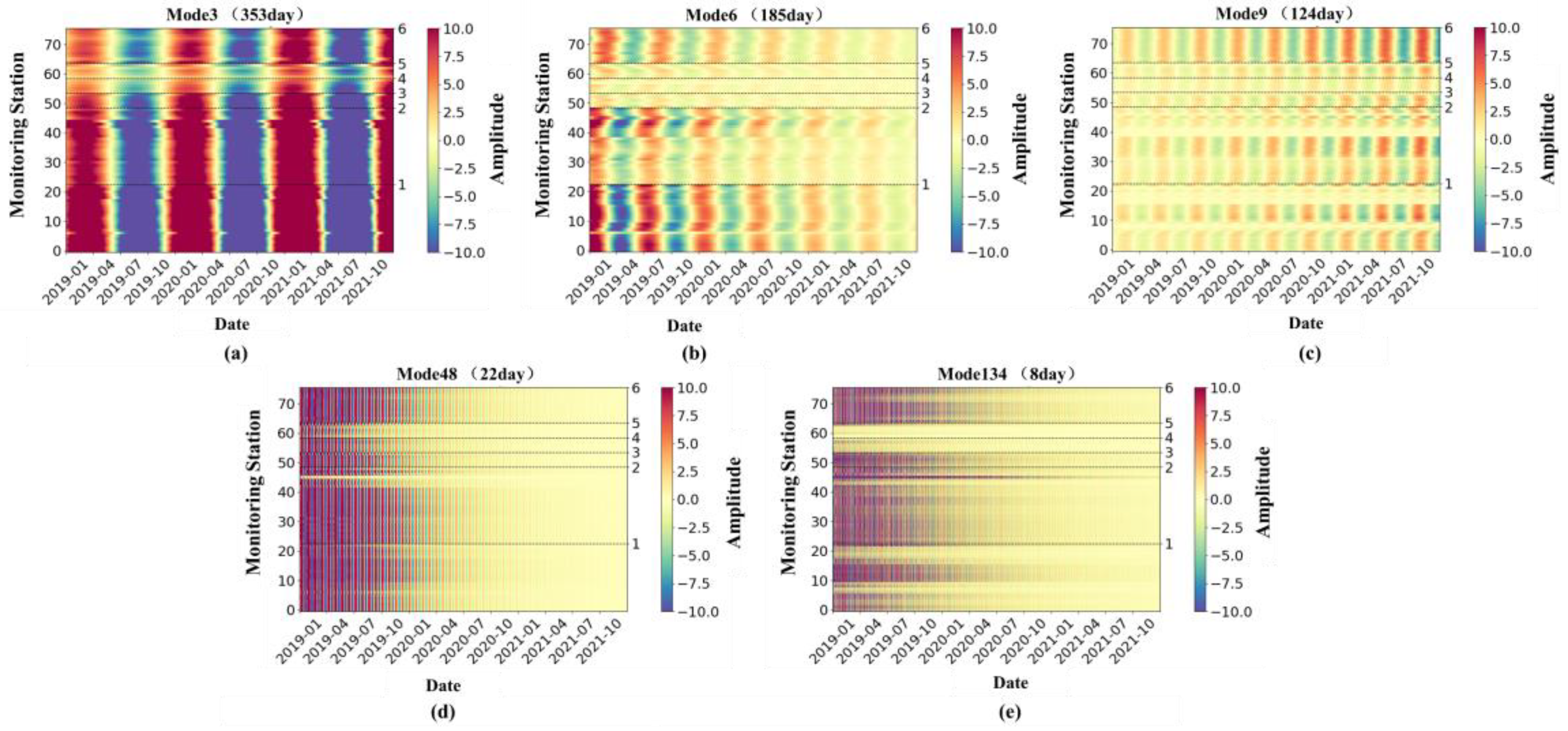
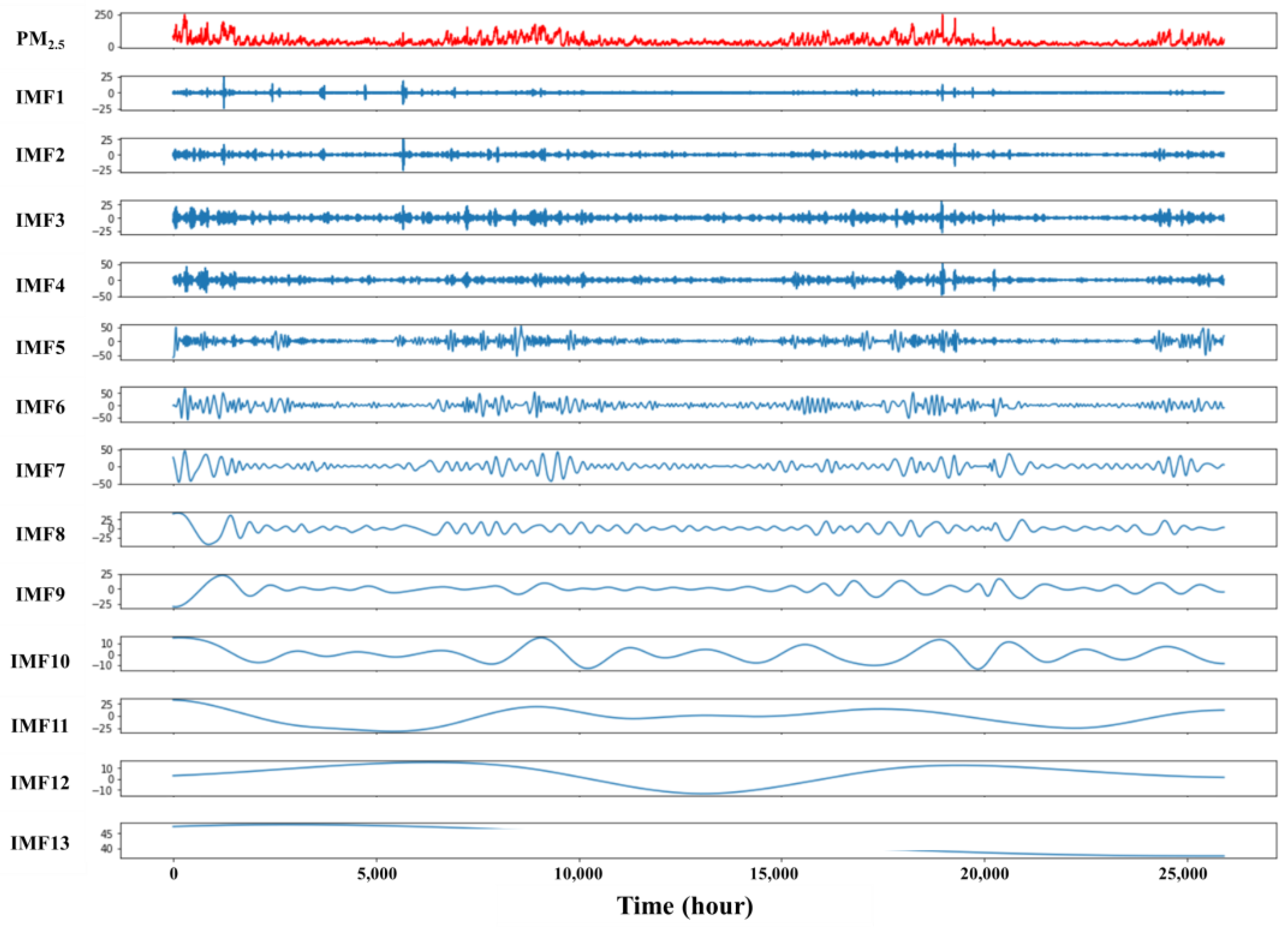
3.1.1. Mode Decomposition of Hourly PM2.5 Concentrations
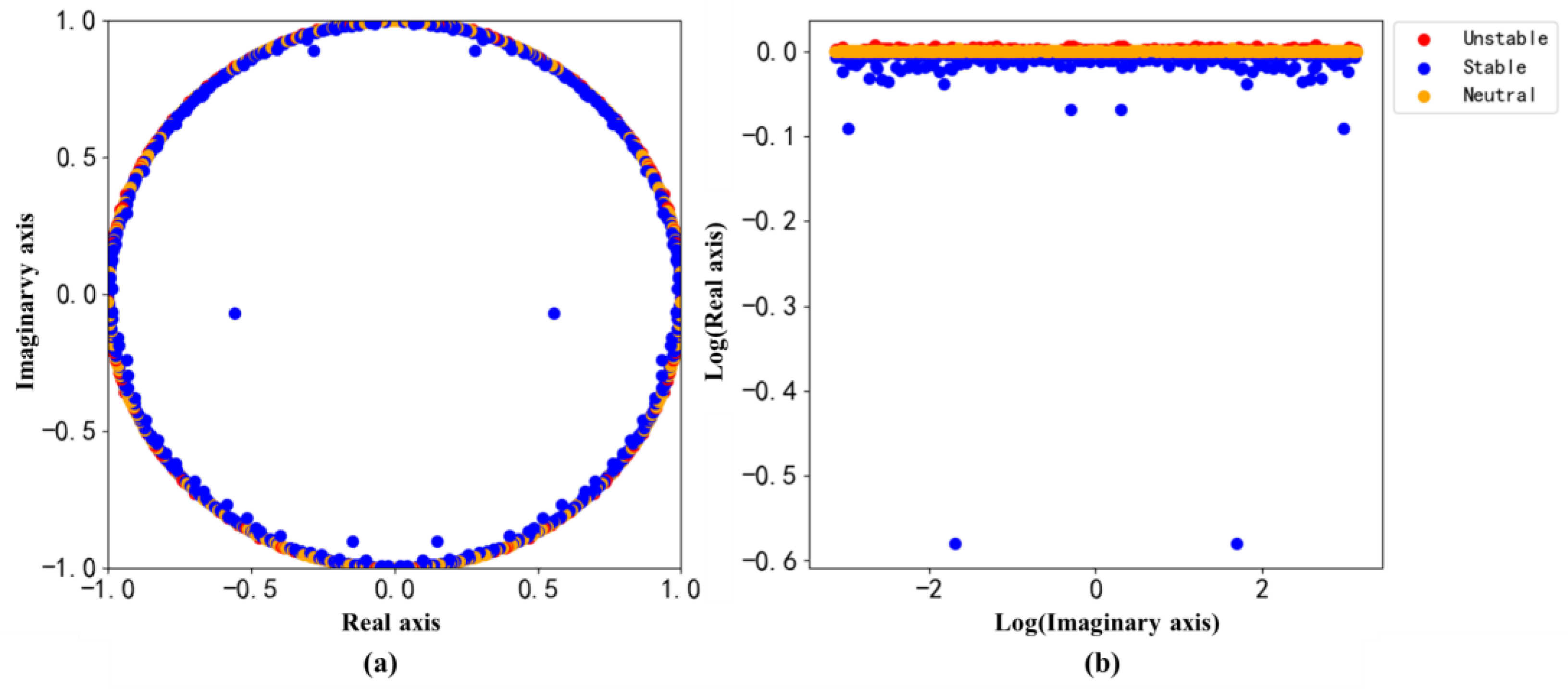
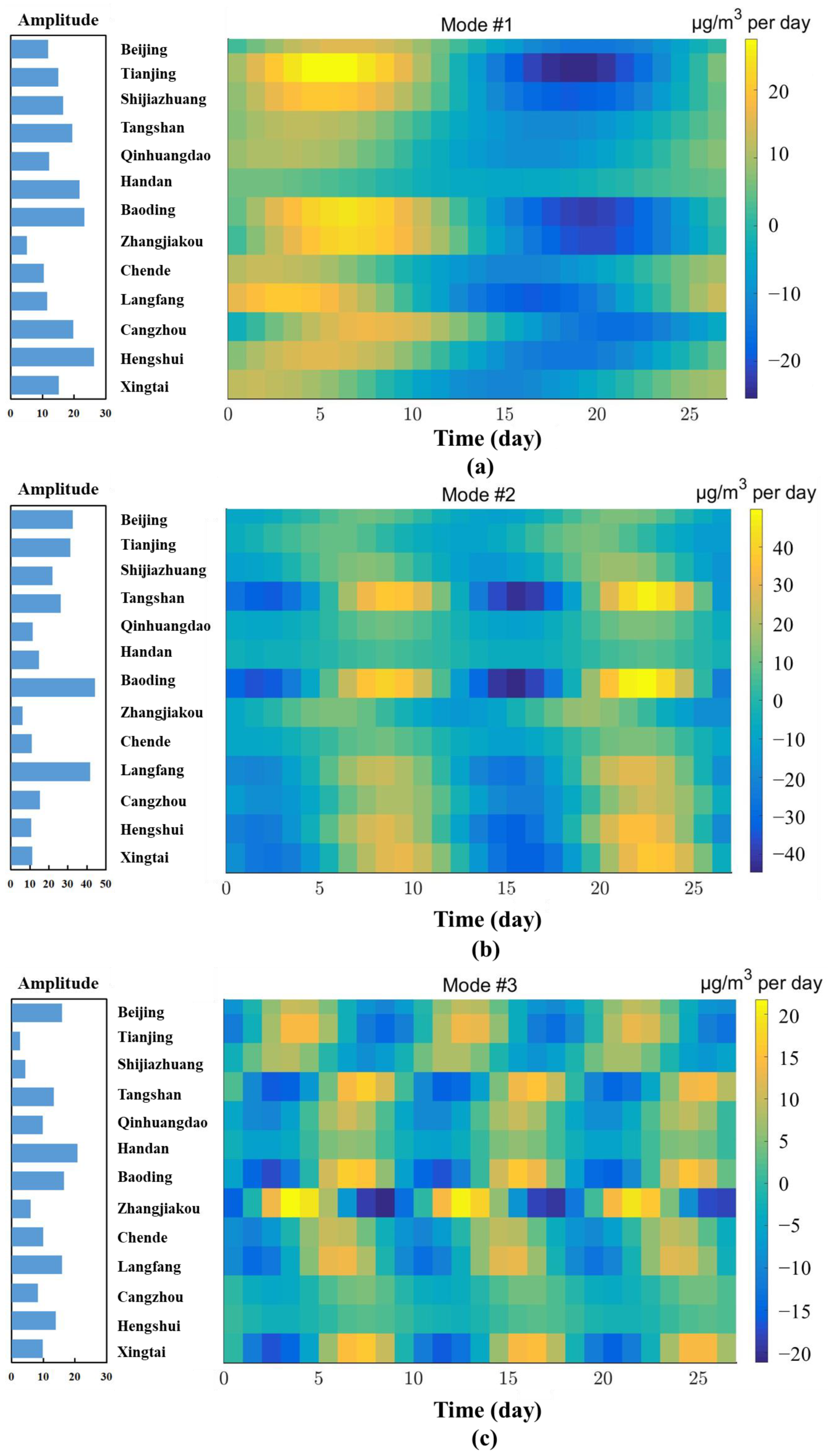
3.1.2. Mode Decomposition of Daily PM2.5 Concentrations
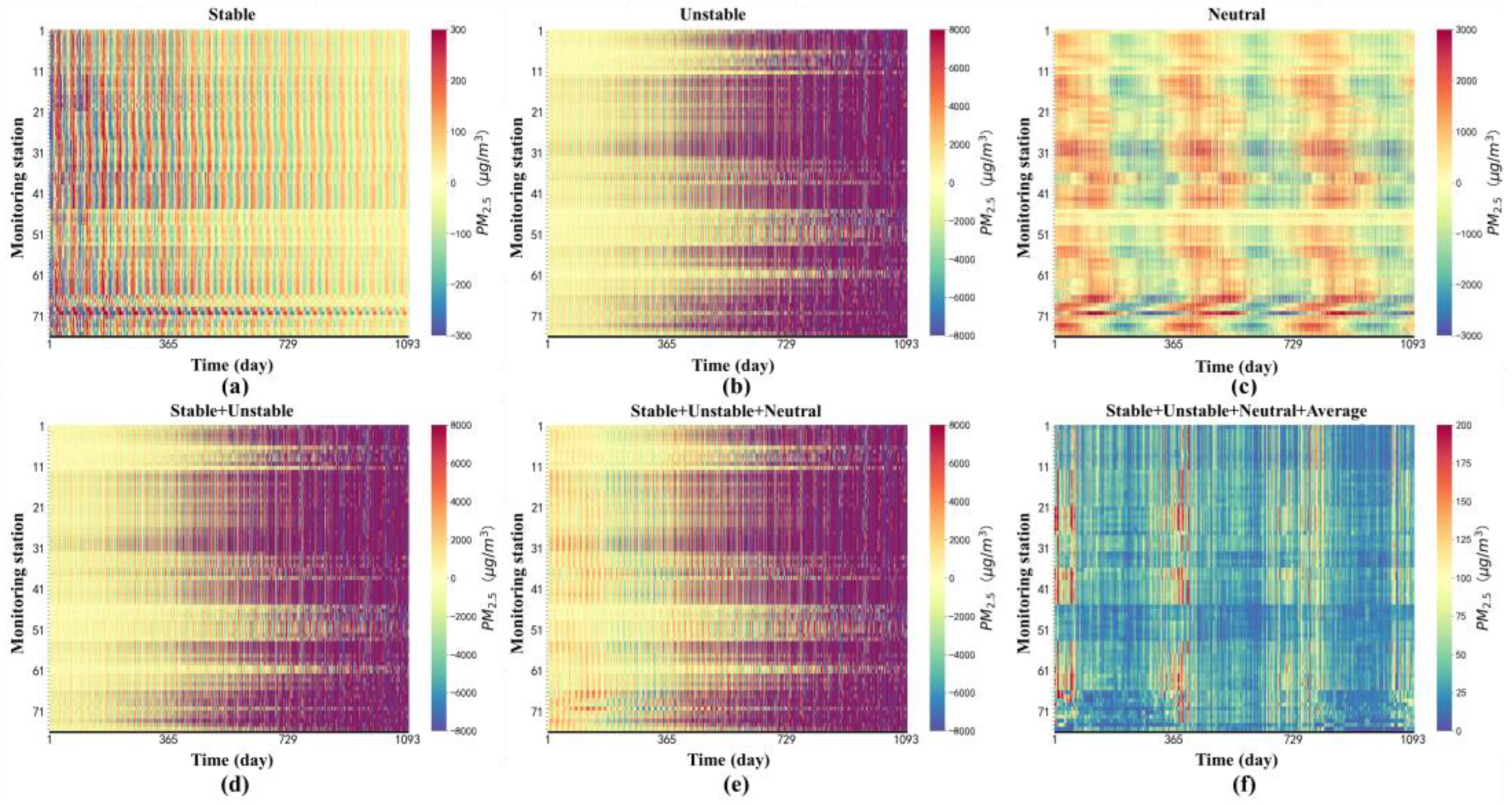
3.2. Reconstructing the Dynamic Process of PM2.5
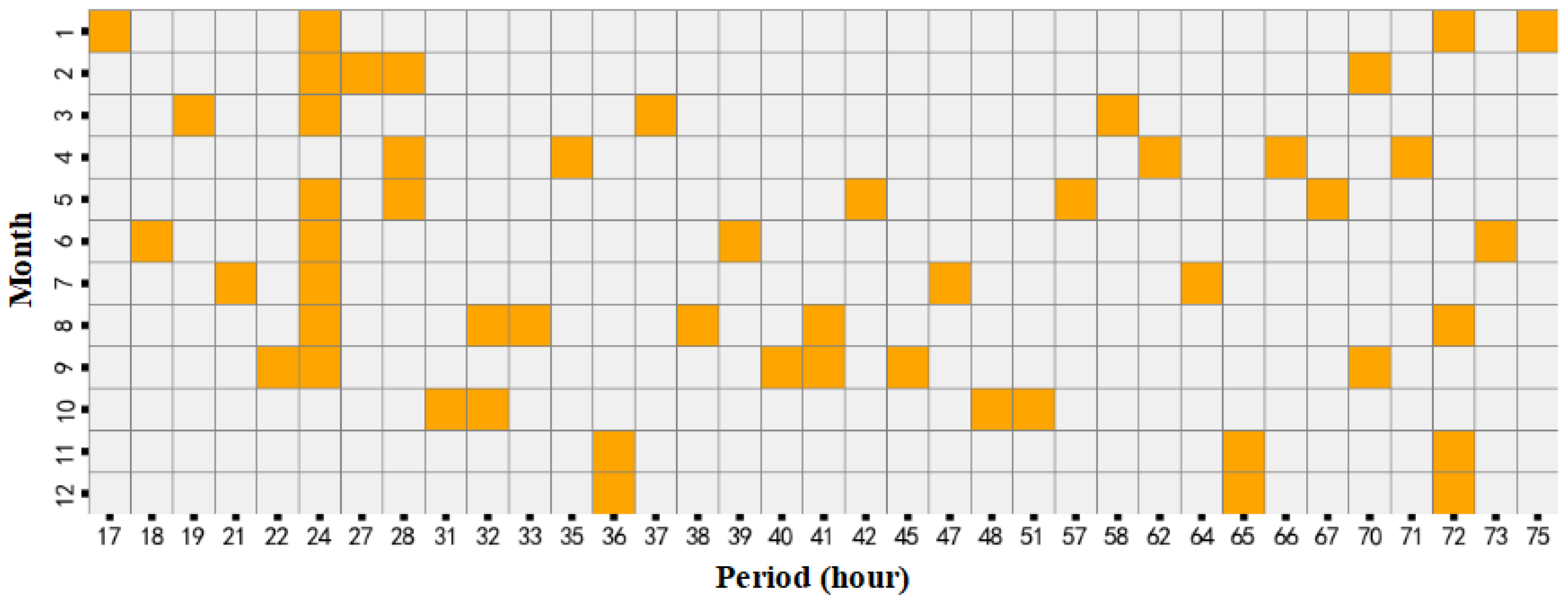
3.3. Analysis of PM2.5 Concentration Mode Characteristics during Special Events
3.4. Comparison of the Koopman Method with Other Mode Decomposition Methods
3.4.1. It Avoids Mode Mixing Compared to EMD
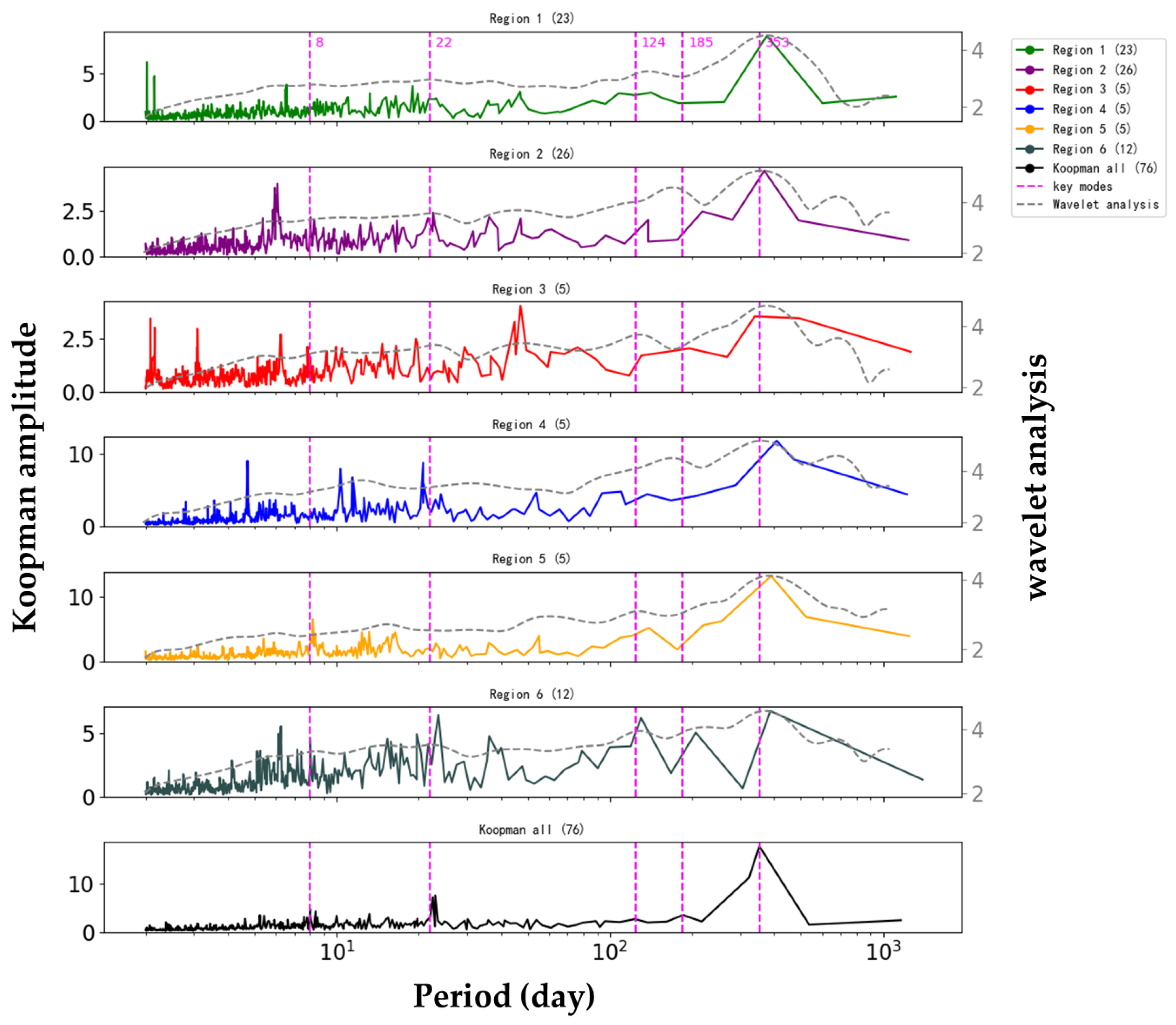
3.4.2. It Identifies the Key Mode Compared to Wavelet Analysis
4. Discussion
5. Conclusions
- (1)
- The KMD method effectively captures the key modes of PM2.5, identifying high-frequency dominant cycles of 24 h along with low-frequency cycles on annual, semi-annual, seasonal, and monthly scales. These modes include growth, decay, and persistent sub-modes, which offer substantial interpretability and enable accurate reconstruction of the dynamic processes, with a reconstruction error MAPE of only 0.6%. Furthermore, phase difference analysis using the Koopman method elucidates the sequence, specific locations, and spatiotemporal variations in pollution across thirteen distinct cities within the BTH region.
- (2)
- Compared with the EMD method, the Koopman approach clearly separates each dynamic feature of PM2.5 concentration, effectively distinguishing between high-frequency and low-frequency modes, and avoiding mode mixing phenomena.
- (3)
- Compared with wavelet analysis, the Koopman method focuses more on the global features of the system and can accurately identify the key dynamic modes of complex systems.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cohen, A.J.; Brauer, M.; Burnett, R.; Anderson, H.R.; Frostad, J.; Estep, K.; Balakrishnan, K.; Brunekreef, B.; Dandona, L.; Dandona, R. Estimates and 25-year trends of the global burden of disease attributable to ambient air pollution: An analysis of data from the Global Burden of Diseases Study 2015. Lancet 2017, 389, 1907–1918. [Google Scholar] [CrossRef]
- Yu, B.; Huang, C.; Liu, Z.; Wang, H.; Wang, L. A chaotic analysis on air pollution index change over past 10 years in Lanzhou, northwest China. Stoch. Environ. Res. Risk Assess. 2011, 25, 643–653. [Google Scholar] [CrossRef]
- Wang, F.; Chen, D.; Cheng, S.; Li, J.; Li, M.; Ren, Z. Identification of regional atmospheric PM10 transport pathways using HYSPLIT, MM5-CMAQ and synoptic pressure pattern analysis. Environ. Model. Softw. 2010, 25, 927–934. [Google Scholar] [CrossRef]
- Kiesewetter, G.; Schoepp, W.; Heyes, C.; Amann, M. Modelling PM2.5 impact indicators in Europe: Health effects and legal compliance. Environ. Model. Softw. 2015, 74, 201–211. [Google Scholar] [CrossRef]
- Lauret, P.; Heymes, F.; Aprin, L.; Johannet, A. Atmospheric dispersion modeling using artificial neural network based cellular automata. Environ. Model. Softw. 2016, 85, 56–69. [Google Scholar] [CrossRef]
- Sousa, S.; Martins, F.G.; Alvim-Ferraz, M.C.; Pereira, M.C. Multiple linear regression and artificial neural networks based on principal components to predict ozone concentrations. Environ. Model. Softw. 2007, 22, 97–103. [Google Scholar] [CrossRef]
- Qiao, W.; Tian, W.; Tian, Y.; Yang, Q.; Wang, Y.; Zhang, J. The forecasting of PM2.5 using a hybrid model based on wavelet transform and an improved deep learning algorithm. IEEE Access 2019, 7, 142814–142825. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, H.; Zhao, G.; Lian, J. Constructing a PM2.5 concentration prediction model by combining auto-encoder with Bi-LSTM neural networks. Environ. Model. Softw. 2020, 124, 104600. [Google Scholar] [CrossRef]
- Teng, M.; Li, S.; Xing, J.; Song, G.; Yang, J.; Dong, J.; Zeng, X.; Qin, Y. 24-Hour prediction of PM2.5 concentrations by combining empirical mode decomposition and bidirectional long short-term memory neural network. Sci. Total Environ. 2022, 821, 153276. [Google Scholar] [CrossRef]
- Guo, Y.; Quan, J.; Pan, Y.; Pu, W.; Feng, J.; Zhao, X.; Yuan, T. Multi-time scale variations of the PM2.5 in Beijing and its key mechanisms during 2008 to 2017. China Environ. Sci. 2022, 42, 1013–1021. [Google Scholar]
- Zaini, N.; Ean, L.W.; Ahmed, A.N.; Malek, M.A.; Chow, M.F. PM2.5 forecasting for an urban area based on deep learning and decomposition method. Sci. Rep. 2022, 12, 17565. [Google Scholar] [CrossRef]
- Qin, S.; Liu, F.; Wang, J.; Sun, B. Analysis and forecasting of the particulate matter (PM) concentration levels over four major cities of China using hybrid models. Atmos. Environ. 2014, 98, 665–675. [Google Scholar] [CrossRef]
- Avila, A.M.; Mezić, I. Data-driven analysis and forecasting of highway traffic dynamics. Nat. Commun. 2020, 11, 2090. [Google Scholar] [CrossRef]
- Manzoor, W.A.; Rawashdeh, S.; Mohammadi, A. Vehicular applications of koopman operator theory—A survey. IEEE Access 2023, 11, 25917–25931. [Google Scholar] [CrossRef]
- Kim, S.; Kim, M.; Lee, S.; Lee, Y.J. Discovering spatiotemporal patterns of COVID-19 pandemic in South Korea. Sci. Rep. 2021, 11, 24470. [Google Scholar] [CrossRef]
- Huynh, P.K.; Setty, A.R.; Le, T.B.; Le, T.Q. A noise-robust Koopman spectral analysis of an intermittent dynamics method for complex systems: A case study in pathophysiological processes of obstructive sleep apnea. IISE Trans. Healthc. Syst. Eng. 2023, 13, 101–116. [Google Scholar] [CrossRef]
- Schmid, P.J. Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 2010, 656, 5–28. [Google Scholar] [CrossRef]
- Mezić, I. Analysis of fluid flows via spectral properties of the Koopman operator. Annu. Rev. Fluid Mech. 2013, 45, 357–378. [Google Scholar] [CrossRef]
- Bruder, D.; Gillespie, B.; Remy, C.D.; Vasudevan, R. Modeling and control of soft robots using the koopman operator and model predictive control. arXiv 2019, arXiv:1902.02827. [Google Scholar]
- Bruder, D.; Fu, X.; Gillespie, R.B.; Remy, C.D.; Vasudevan, R. Data-driven control of soft robots using Koopman operator theory. IEEE Trans. Robot. 2020, 37, 948–961. [Google Scholar] [CrossRef]
- Folkestad, C.; Pastor, D.; Burdick, J.W. Episodic Koopman learning of nonlinear robot dynamics with application to fast multirotor landing. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 9216–9222. [Google Scholar]
- Ling, E.; Zheng, L.; Ratliff, L.J.; Coogan, S. Koopman operator applications in signalized traffic systems. IEEE Trans. Intell. Transp. Syst. 2020, 23, 3214–3225. [Google Scholar] [CrossRef]
- Colbrook, M.J.; Mezić, I.; Stepanenko, A. Limits and powers of Koopman learning. arXiv 2024, arXiv:2407.06312. [Google Scholar]
- Deng, C.; Qin, C.; Li, Z.; Li, K. Spatiotemporal variations of PM2.5 pollution and its dynamic relationships with meteorological conditions in Beijing-Tianjin-Hebei region. Chemosphere 2022, 301, 134640. [Google Scholar] [CrossRef] [PubMed]
- Cao, J.; Qiu, X.; Peng, L.; Gao, J.; Wang, F.; Yan, X. Impacts of the differences in PM2.5 air quality improvement on regional transport and health risk in Beijing–Tianjin–Hebei region during 2013–2017. Chemosphere 2022, 297, 134179. [Google Scholar] [CrossRef] [PubMed]
- Alsahli, M.M.; Al-Harbi, M. Allocating optimum sites for air quality monitoring stations using GIS suitability analysis. Urban Clim. 2018, 24, 875–886. [Google Scholar] [CrossRef]
- Liu, J.; He, C.; Si, Y.; Li, B.; Wu, Q.; Ni, J.; Xu, C. Toward Better and Healthier Air Quality: Global PM2.5 and O3 Pollution Status and Risk Assessment Based on the New WHO Air Quality Guidelines for 2021. Glob. Chall. 2024, 8, 2300258. [Google Scholar] [CrossRef]
- Cao, K.X.; Tang, M.M.; Ge, J.H.; Li, Z.K.; Wang, X.Y.; Li, G.X.; Wei, X.T. Comparison of methods to interpolate missing PM2.5 values: Based on air surveillance data of Beijing. J. Environ. Occup. Med. 2020, 37, 299–305. [Google Scholar]
- Ukhurebor, K.E.; Azi, S.O.; Aigbe, U.O.; Onyancha, R.B.; Emegha, J.O. Analyzing the uncertainties between reanalysis meteorological data and ground measured meteorological data. Measurement 2020, 165, 108110. [Google Scholar] [CrossRef]
- Koopman, B.O. Hamiltonian systems and transformation in Hilbert space. Proc. Natl. Acad. Sci. USA 1931, 17, 315–318. [Google Scholar] [CrossRef]
- Koopman, B.O.; Neumann, J.V. Dynamical systems of continuous spectra. Proc. Natl. Acad. Sci. USA 1932, 18, 255–263. [Google Scholar] [CrossRef]
- Mezić, I. Spectrum of the Koopman operator, spectral expansions in functional spaces, and state-space geometry. J. Nonlinear Sci. 2020, 30, 2091–2145. [Google Scholar] [CrossRef]
- Azencot, O.; Erichson, N.B.; Lin, V.; Mahoney, M. Forecasting sequential data using consistent koopman autoencoders. In Proceedings of the International Conference on Machine Learning, Vienna, Austria, 13–18 July 2020; pp. 475–485. [Google Scholar]
- Lusch, B.; Kutz, J.N.; Brunton, S.L. Deep learning for universal linear embeddings of nonlinear dynamics. Nat. Commun. 2018, 9, 4950. [Google Scholar] [CrossRef] [PubMed]
- Jovanović, M.R.; Schmid, P.J.; Nichols, J.W. Sparsity-promoting dynamic mode decomposition. Phys. Fluids 2014, 26, 024103. [Google Scholar] [CrossRef]
- Brunton, S.L.; Brunton, B.W.; Proctor, J.L.; Kaiser, E.; Kutz, J.N. Chaos as an intermittently forced linear system. Nat. Commun. 2017, 8, 19. [Google Scholar] [CrossRef]
- Takens, F. Detecting Strange Attractors in Turbulence. In Dynamical Systems and Turbulence, Warwick 1980: Proceedings of a Symposium Held at the University of Warwick 1979/80; Springer: Berlin/Heidelberg, Germany, 2006; pp. 366–381. [Google Scholar]
- Mezić, I.; Banaszuk, A. Comparison of systems with complex behavior. Phys. D Nonlinear Phenom. 2004, 197, 101–133. [Google Scholar] [CrossRef]
- Zareba, M.; Weglinska, E.; Danek, T. Air pollution seasons in urban moderate climate areas through big data analytics. Sci. Rep. 2024, 14, 3058. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Wang, H.; Zhang, S. Quantifying prediction and intervention measures for PM2.5 by a PDE model. J. Clean. Prod. 2020, 268, 122131. [Google Scholar] [CrossRef]
- Huang, N.E.; Wu, M.-L.C.; Long, S.R.; Shen, S.S.; Qu, W.; Gloersen, P.; Fan, K.L. A confidence limit for the empirical mode decomposition and Hilbert spectral analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2003, 459, 2317–2345. [Google Scholar] [CrossRef]
- Guo, T.; Zhang, T.; Lim, E.; Lopez-Benitez, M.; Ma, F.; Yu, L. A review of wavelet analysis and its applications: Challenges and opportunities. IEEE Access 2022, 10, 58869–58903. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Shelton, S.; Liyanage, G.; Jayasekara, S.; Pushpawela, B.; Rathnayake, U.; Jayasundara, A.; Jayasooriya, L.D. Seasonal variability of air pollutants and their relationships to meteorological parameters in an urban environment. Adv. Meteorol. 2022, 2022, 5628911. [Google Scholar] [CrossRef]
- Liu, Z.; Ji, D.; Wang, L. PM2.5 concentration prediction based on EEMD-ALSTM. Sci. Rep. 2024, 14, 12636. [Google Scholar]
- Kimothi, S.; Chilkoti, S.; Rawat, V.; Thapliyal, A.; Gautam, A.S.; Gautam, S. Micro- to macro-scaling analysis of PM2.5 in sensitive environment of Himalaya, India. Geol. J. 2023, 58, 4360–4378. [Google Scholar] [CrossRef]
- Mohtar, A.A.A.; Latif, M.T.; Baharudin, N.H.; Ahamad, F.; Chung, J.X.; Othman, M.; Juneng, L. Variation of major air pollutants in different seasonal conditions in an urban environment in Malaysia. Geosci. Lett. 2018, 5, 21. [Google Scholar] [CrossRef]
- Yuan, E.; Yang, G. SA–EMD–LSTM: A novel hybrid method for long-term prediction of classroom PM2.5 concentration. Expert Syst. Appl. 2023, 230, 120670. [Google Scholar] [CrossRef]
- Liu, R.; Shao, M.; Wang, Q.G. Multi-timescale variation characteristics of PM2.5 in different regions of China during 2014–2022. Sci. Total Environ. 2024, 920, 171008. [Google Scholar] [CrossRef]
- Chen, X.; Yin, L.; Fan, Y.; Song, L.; Ji, T.; Liu, Y.; Tian, J.; Zheng, W. Temporal evolution characteristics of PM2.5 concentration based on continuous wavelet transform. Sci. Total Environ. 2020, 699, 134244. [Google Scholar] [CrossRef]
- Fattah, M.A.; Morshed, S.R.; Kafy, A.-A.; Rahaman, Z.A.; Rahman, M.T. Wavelet coherence analysis of PM2.5 variability in response to meteorological changes in South Asian cities. Atmos. Pollut. Res. 2023, 14, 101737. [Google Scholar] [CrossRef]
- Sun, W.; Li, Z. Hourly PM2.5 concentration forecasting based on mode decomposition-recombination technique and ensemble learning approach in severe haze episodes of China. J. Clean. Prod. 2020, 263, 121442. [Google Scholar] [CrossRef]
- Huang, G.; Li, X.; Zhang, B.; Ren, J. PM2.5 concentration forecasting at surface monitoring sites using GRU neural network based on empirical mode decomposition. Sci. Total Environ. 2021, 768, 144516. [Google Scholar] [CrossRef]


| Mode | Period (Hourly) | Amplitude |
|---|---|---|
| 1 | 735.67 | 19.503 |
| 6 | 123.35 | 18.457 |
| 4 | 178.32 | 18.355 |
| 2 | 364.82 | 15.459 |
| 3 | 248.46 | 13.915 |
| 31 | 23.888 | 13.469 |
| 5 | 156.72 | 9.942 |
| 11 | 71.268 | 9.3099 |
| 30 | 24.313 | 8.5047 |
| 14 | 52.681 | 8.4439 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Y.; Liu, D.; Wang, B.; Zhang, F. Analysis of Global and Key PM2.5 Dynamic Mode Decomposition Based on the Koopman Method. Atmosphere 2024, 15, 1091. https://doi.org/10.3390/atmos15091091
Yu Y, Liu D, Wang B, Zhang F. Analysis of Global and Key PM2.5 Dynamic Mode Decomposition Based on the Koopman Method. Atmosphere. 2024; 15(9):1091. https://doi.org/10.3390/atmos15091091
Chicago/Turabian StyleYu, Yuhan, Dantong Liu, Bin Wang, and Feng Zhang. 2024. "Analysis of Global and Key PM2.5 Dynamic Mode Decomposition Based on the Koopman Method" Atmosphere 15, no. 9: 1091. https://doi.org/10.3390/atmos15091091
APA StyleYu, Y., Liu, D., Wang, B., & Zhang, F. (2024). Analysis of Global and Key PM2.5 Dynamic Mode Decomposition Based on the Koopman Method. Atmosphere, 15(9), 1091. https://doi.org/10.3390/atmos15091091







