Abstract
Methane is the second largest contributor to global surface air temperature rise. Reducing atmospheric methane will mitigate climate change and improve air quality. Since the main sink of methane is the hydroxyl radical (OH) in the atmosphere, increasing OH concentration will accelerate the methane oxidation process and reduce methane concentration. Because the primary source of OH is the reaction between water vapor and ozone, scientists have proposed a water vapor enhancement strategy to raise OH concentrations in the atmosphere and remove methane. We use a two-box model to evaluate interactions between OH and methane and a radiative kernel method to calculate radiative responses to water vapor content growth. This proves that increasing OH concentration does have a positive effect on methane reduction. If the concentration of OH is increased by 10% from its current value and maintained for 50 (100) years, 45 Tg yr−1 (67.5 Tg yr−1) more methane will be oxidized by OH, and the cumulative effects of the oxidation are equivalent to a 120.5 Gt (219.6 Gt) reduction in CO2 and will lower the global surface air temperature by 0.054 °C (0.099 °C). Our study also provides insights into a mixed picture of global and regional radiative responses to the growth of water vapor content. The reduced radiative forcing by methane removal cannot overpower the increased radiative forcing by water vapor from the global average point of view. However, due to OH’s greater sensitivity to water vapor and weaker radiative response at higher latitudes, this perspective may be reversed if abrupt CH4 emissions from permafrost thaw occur.
1. Introduction
1.1. Importance of Methane Mitigation for Climate
Methane (CH4) is a short-lived forcer that has an important warming effect on the climate. Although its lifetime is only about a decade, its global warming potential (GWP-20, integrated over 20 years after emissions) is more than 80 times stronger than that of carbon dioxide (CO2) [1]. The change in methane concentration from the pre-industry level in the atmosphere contributed 0.54 [0.43 to 0.65] W m−2 growth of the global effective radiative forcing, and this change increases the global surface air temperature relative to 1750 by 0.28 [0.19 to 0.39] °C, which is the second contributor to global warming just following CO2 [1]. The response of global surface air temperature to methane is even larger than that of CO2 due to one year’s current anthropogenic emissions (including long-lived and short-lived gases) in the 10-year timeframe after the emission [2].
The current global mean atmospheric methane abundance is 1925 ppb (nmol mol−1), with an increase of approximately 10 ppb per year over the past five years [3]. The primary natural emission sources are wetlands, while agriculture and waste contribute the most as anthropogenic sources, followed by fossil fuel sectors [4]. The main sink of methane is tropospheric OH (hydroxyl radical), which accounts for about 90% of atmospheric methane loss [4,5]. Other losses are from stratospheric, tropospheric Cl, and soil uptake [6,7]. The imbalance between total global methane emissions and total sinks still reached 21 Tg yr−1 during 2008–2017 [4]. Increased greenhouse gas concentrations would raise atmospheric temperatures, which would in turn enhance the decomposition process in wetlands and landfills, increasing methane emissions and forming positive feedback on the climate [8]. The increased emissions from wetlands can contribute to 0.03 ± 0.01 W m−2 growth of the global effective radiative forcing per degree of temperature rise [9,10,11].
Due to its powerful climate warming effect and the induced positive feedback, it is noted that methane mitigation is crucial to limit global warming to under 1.5 °C [12,13] and it can even help preserve Arctic summer sea ice [14]. Reaching this temperature target of the Paris Agreement would be hindered if methane continues to follow the path of its rapid growth over the past few years [15]. The mitigation of methane is much more efficient than that of other greenhouse gases to achieve the temperature target. Lowering one ppb of methane in the atmosphere is equivalent to a reduction of 0.27 ± 0.05 GtC [16]. If 95 Mt yr−1 methane reduction is added to the Nationally Determined Contributions, the global mean temperature will further be cooled by 0.015 to 0.075 °C in 2040 [17]. Implementing mitigation measures for short-lived climate forcers can contribute to achieving net-zero carbon emission by 2050, which was pledged by many countries, and also achieving many of the United Nations Sustainable Development Goals, particularly through methane reduction [18].
Unlike the effects of surface warming caused by the removal of NOx, SO2, or aerosols [19,20], methane mitigation is not only an effective way to reduce global warming pressure but also improves air quality as methane mitigation reduces ozone production [21]. It is a “win-win” approach and benefits both short-term climate warming reduction and improvements in human health (air quality) [1,22].
To mitigate the strong warming effect of methane, nano-porous zeolites were proposed to trap CH4 in the air and then oxidize it to CO2 by oxygen in an industrial array [23]. Using photocatalysis to oxidize CH4 to CO2 during natural convective air flows in a solar chimney was also suggested by other scientists [24]. However, this paper focuses only on the natural main oxidant and principal sink (OH, hydroxyl radical) effects on methane concentration in the atmosphere.
1.2. Relationship between Methane, Atmospheric OH, and Water Vapor
1.2.1. Relationship between Methane and Atmospheric OH
Since OH in the atmosphere is the main sink of methane, increasing the abundance of OH can result in a reduction in the tropospheric concentration of methane. It is estimated that a 4% decrease in global mean OH concentration can contribute to 22 Tg yr−1 methane increase [25]. A linearly fitted equation is given to express the relationship between OH concentration and methane build-up and states that a 10% variation in OH concentration can cause a 40 Tg yr−1 change in methane [26]. Another paper states that a 1.6 ± 0.2 percent decrease in tropospheric OH concentration during the pandemic has led to a global methane imbalance of 7.5 ± 0.8 Tg yr−1 due to a lower methane–OH reaction [27]. Methane lifetime also strongly correlates with OH concentration and decreases with increased OH concentration [28,29].
1.2.2. Relationship between Atmospheric OH and Water Vapor
The reaction involving water vapor and tropospheric ozone is the primary source of OH in the troposphere, the productivity of which can be enhanced by increasing water vapor concentration, temperature, and incoming solar radiation [1]. Warmer and wetter climate conditions can reduce methane lifetime and are beneficial for methane removal. The lifetime of CH4 could be reduced by 4.7 ± 1.7% per degree of atmospheric temperature rise due to the combined effect of the higher oxidation rate and higher water vapor concentration, which is equivalent to 0.03 ± 0.01 W m−2 global radiative forcing reduction [30]. However, the impact of atmospheric temperature on the productivity of OH is still under debate; it may have a weak impact [31] or even a negative impact [32]. But an agreement on the positive impact of the increased water vapor has been reached by scientists [31,32,33,34]. A 1% increase in global mass-weighted mean water vapor was found to lead to a 2.237% growth of OH concentration in the total atmosphere, and this coefficient (defined as ) can reach up to 5.507 in the Arctic region [35].
Hydroxyl (OH) in the Earth’s atmosphere serves as the primary sink for methane and can be enhanced by increasing the concentration of water vapor. A strategy has been suggested to reduce methane concentration in the atmosphere by the enhancement of atmospheric water vapor and then increasing OH sources [36]. Since the atmospheric vapor pressure deficit (the difference between saturated water vapor pressure and actual water vapor pressure) is increasing, which means that relative humidity is decreasing [37], the water vapor enhancement strategy may be feasible. However, the greenhouse gas effects of water vapor, which absorbs shortwave solar radiation and reflects longwave radiation back to Earth, cannot be ignored. It should be noted that the greenhouse effects of water vapor from anthropogenic sources are not considered in the IPCC report due to the negligible flux of anthropogenic water vapor (compared with the total amount of water vapor in the atmosphere) and the short lifetime of water vapor [38,39]. However, in the water vapor enhancement strategy, a large continuous flux of water vapor and a high concentration of water vapor are required to maintain a higher OH reaction and production rate. Thus, the balance between radiative forcing reduced by methane and increased by water vapor needs to be quantitatively assessed. The feasibility of removing atmospheric methane by increasing water vapor will be discussed from the perspective of radiative forcing changes in this paper.
2. Effects of OH on Methane Concentration
The oxidation of methane by OH is not a simple one-step reaction, the oxidation reaction sequence starts from R1, and the intermediate products are CH3O2, CH3O, CH2O and CHO. CO is generated in this reaction sequence from R2 and oxidized by R3. In the presence of NOx, the final product of CO oxidation is CO2 and O3 [40].
Since the most important roles in the hydroxyl oxidation cycle are methane and carbon monoxide [41], their basic mass balance equations for the oxidation reaction sequence are [28,42,43]
where [] indicates the concentrations in the atmosphere, is the emission rate (or source for OH), is the reaction rate, and represents other sinks for OH (for example, CH2O, Isoprene [44]). The one-box model is defined by these equations.
Because CH4 and CO concentrations in the Northern Hemisphere are higher than in the Southern Hemisphere, a two-box model was proposed to deal with species transport due to the concentration gradient between the two hemispheres [45,46]. This two-box model contains six coupled ordinary differential equations for three compounds (CH4, CO, and OH) in two hemispheres and can be written as
where is the timescale (usually 1 year); the subscripts and are Northern and Southern Hemisphere, respectively; and is positive (negative) if the reaction is a source (sink) for . Although the two-box model is criticized for ignoring spatial variations in species concentrations and emissions [47], it can provide comparable results to sophisticated models [44].
The two-box model is solved with MATLAB, and the initial concentrations of each compound and reaction rate coefficients are given in Table 1. It is noted that the spatial distribution of OH is under discussion. The Northern Hemispheric OH concentration is low [48], roughly equal [49], or high [34] compared to the Southern Hemisphere. We divided the OH parameters equally into two hemispheres in this work.

Table 1.
Initial concentrations and emission rates of each compound.
To quantify the impact of OH variation on methane, we first increase the OH source from the initial condition (Table 1) by 1.2 times and compare methane concentrations with the results of unperturbed ones from [46]. The solid lines in Figure 1 show the variation in methane concentrations from the unperturbed condition at different methane emission levels (1–1.5 times the initial emission rate). When a larger OH source (1.2 times the initial OH production rate) is imposed into the hydroxyl oxidation cycle, methane concentrations gradually decrease over time, although slowly in the early years due to the existing imbalanced CH4 budget (the CH4 budget needs to be reversed first), as can be seen from the dashed lines.
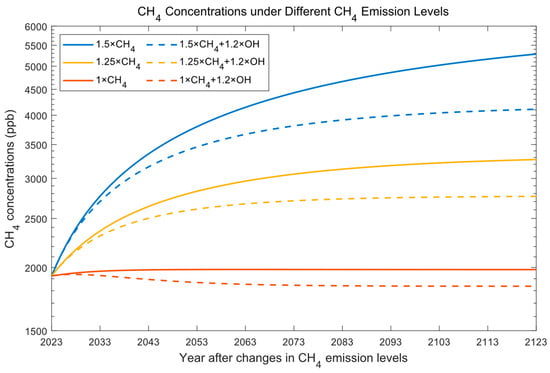
Figure 1.
CH4 concentrations vary with time.
As CH4 concentrations change over time (Figure 1), it is difficult to assess the impact of OH when different percentages of OH source rises are applied to the atmosphere. Therefore, we will compare the mean results over 50 and 100 years after a larger OH source is imposed in the following analyses. The variations in 50 (100)-year-averaged CH4 concentrations due to increased OH sources are shown in Figure 2. The dash lines are the 50-year-averaged variations, and the solid lines are the 100-year-averaged variations. If methane emissions are maintained at a higher (lower) level for a longer (short) time, CH4 concentrations will be higher (lower) at the start (OH source increase rate = 0 in Figure 2). CH4 concentrations will decline faster when they are higher when the reaction rate is maintained (Equation (1)).
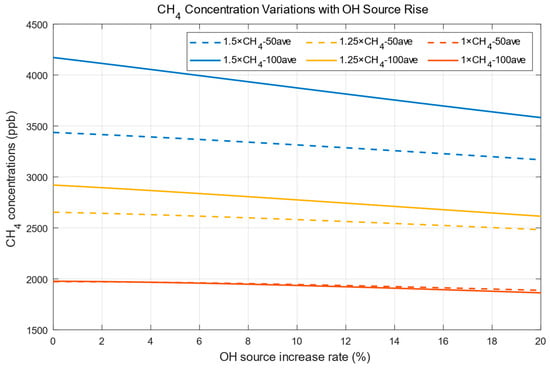
Figure 2.
CH4 concentration variations with OH source rise.
The 50 (100)-year-averaged variations in OH concentrations induced by increased OH sources can be seen in Figure 3. OH concentrations will increase when larger OH sources are put into the atmosphere despite different CH4 emission levels, but the change rate of OH concentrations are impacted by the CH4 emission levels. Higher levels of methane emissions will increase methane abundance, consume more OH, and suppress OH concentration, and vice versa [55]. This reduction (promotion) effect on the OH concentration is stronger with the higher (lower) methane emission level and longer suppression time. This is why the 100-year-averaged OH concentration is higher than the 50-year-averaged OH concentration (promotion effect) when methane emissions are at the current level. The reason is the same for the results of 1.5 times the initial emission level. The 50 (100)-year-averaged OH concentrations are calculated from .
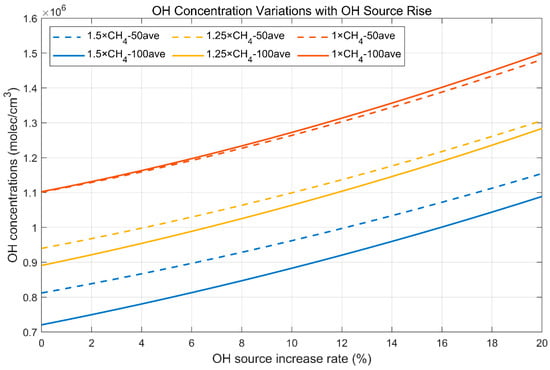
Figure 3.
OH concentration variations with OH source rise.
Methane concentrations will decrease as OH concentrations increase, as shown in Figure 4. Larger increases in OH concentration will induce more reductions in CH4 concentrations. As stated in Equation (1), higher CH4 concentration induced by higher CH4 emission levels will result in a faster rate of total CH4 loss when OH concentration growth rates are the same. Reductions in CH4 concentrations will be larger (smaller) with a longer time frame at higher (lower) emission levels. This is consistent with the explanations given in Figure 2. Average reductions in CH4 concentrations over 50 (100) years are calculated from . The OH concentration growth rate is obtained by from Figure 3. Since the denominators (OH source increase rate = 0 in Figure 3) are different, the final OH concentration growth rates are different, although the same amount of OH sources is imposed. If OH concentrations are raised by 10% from their original value and maintained for 50 years, 45 Tg yr−1 (15.9 ppb yr−1), 115.5 Tg yr−1 (40.7 ppb yr−1), and 186.6 Tg yr−1 (65.8 ppb yr−1), more methane will be oxidized by OH at the current, 1.25 times the current, and 1.5 times the current methane emissions levels. The reductions are 67.5 Tg yr−1 (23.8 ppb yr−1), 215.5 Tg yr−1 (76.0 ppb yr−1), and 398.5 Tg yr−1 (140.5 ppb yr−1) for 100 years at their respective methane emissions levels. Our results are comparable with those studies stated in the Introduction. To convert Tg to ppb, the number should be multiplied by
where is the conversion factor from ppb to Tg, is the molecular weight of air (28.97 kg kmol−1), is the molecular weight of species (kg kmol−1), and is the total mass of the atmosphere, [38].
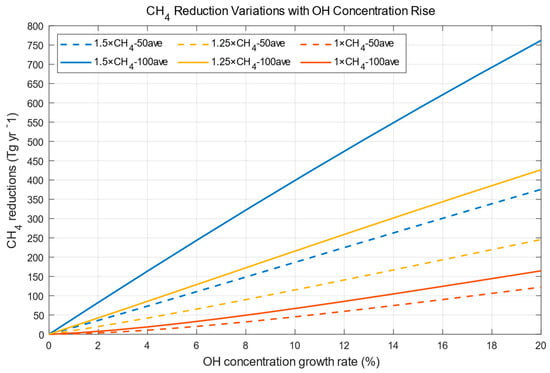
Figure 4.
CH4 reduction variations with OH concentration rise.
Appropriate metrics need to be applied to assess the impacts of CH4 concentration reductions. Although the 100-year global warming potential (GWP-100) is widely used in climate-related papers, it is not suitable for this work. The GWP is the time-integrated radiative forcing induced by 1 kg “pulse” emission [38], while in this work, the CH4 concentration is progressively reduced every year when we raise the OH concentration (from Figure 1), and these reductions are averaged over 50 (100) years (in Figure 4). These years-averaged concentration reductions are named “steps” at the rate of ppb (kg) yr−1 [1]. Here, we use the metric called combined Global Temperature change Potential (CGTP, in units of years) for the “step” concentration reductions, which is recommended by the 6th IPCC Report [1,56]. This metric gives an instrument for weighting the “step” concentration reductions (in kg yr−1) of short-lived greenhouse gases with the change in cumulative CO2 emissions (in kg). The recommended values for CGTP to calculate cumulative CO2 equivalent emissions over 50 and 100 years are 2823 and 3531, respectively [1]. This is also why we average the reductions in CH4 concentrations over the same time frames in Figure 2, Figure 3 and Figure 4. Another metric called transient climate response to cumulative CO2 (TCRE) is used to convert cumulative CO2 into global surface air temperature change. The recommended value for TCRE is 0.45 °C per 1000 Gt cumulative CO2 [1]. The cumulative CO2 equivalent reductions and corresponding temperature reductions are calculated by
where is the conversion factor from mass of CH4 to CO2, is the molecular weight of species , and are the average CH4 concentration reductions from Figure 4 (in Tg yr−1), and and are the equivalent cumulative CO2 (shown from the left axis of Figure 5) for 50 and 100 years (in Gt) (1 Gt (gigatons) = 103 Tg (teragrams) = 1012 kg), respectively. Since the water vapor enhancement strategy only accelerates oxidation from CH4 to CO2 and does not completely eliminate CH4 (from the source), the oxidation production CO2 should be subtracted in Equations (8) and (9). is the global surface air temperature reduction due to CH4 concentration reduction (shown on the right axis of Figure 5). From Figure 5, cumulative CO2 equivalent reductions are greater at a higher level of CH4 emissions and over a longer time frame. If OH concentrations are raised by 10% from their original value and maintained for 50 years, the equivalent cumulative CO2 reductions are 120.5 Gt, 307.8 Gt, and 501.6 Gt at the current, 1.25 times the current, and 1.5 times the current methane emissions levels. The equivalent cumulative CO2 reductions are 219.6 Gt, 702.4 Gt, and 1296.3 Gt for 100 years. The corresponding decreases in global surface air temperature are , , and for 50-year equivalent cumulative CO2 reductions. For 100-year equivalent cumulative CO2 reductions, they are , , and .
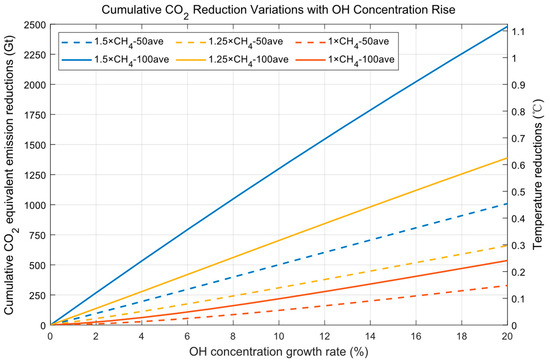
Figure 5.
Cumulative CO2 reduction variations with OH concentration rise.
3. Greenhouse Effects of Water Vapor
To evaluate radiative forcing in response to water vapor perturbations, a kernel method was proposed [57,58] and used by many scientists [59,60,61,62]. The basic radiative kernel equations are
where is the net TOA (top of the atmosphere) radiative flux as a function of water vapor content , air temperature , cloud properties , and surface albedo . indicates different levels (altitudes) in the atmospheric column. and are the average results. The factor is called the water vapor response kernel, which provides TOA radiative flux responses to the perturbations of water vapor . is absorbed incoming solar radiation and is the longwave radiation emitted from Earth.
The water vapor response kernel that constrains the interaction between radiative flux and water vapor variation is essential for assessing the greenhouse effects of water vapor. Radiation absorbed by water vapor is almost proportional to , as stated in many papers [57,59,63,64]. It has been observed that the dominant amount of radiation absorbed by water vapor matches the logarithmic relationship in the 0–560 cm−1 and 1250–1850 cm−1 bands, but in the 800–1250 cm−1 bands, the absorbed longwave radiation is proportional to [65]. Based on this theory, TOA radiative flux responses to water vapor perturbations in this work are calculated from linear and logarithmic aspects, respectively.
where is the linear water vapor kernel, is the logarithmic water vapor kernel, is the response of TOA radiative flux to perturbation of from , and and are the arbitrary states of water vapor content in the climate. It is noted that is independent of state and [57]. A hybrid kernel combining linear and logarithmic kernels is recommended to calculate the total radiative response flux [65] and adopted in the following analysis.
To calculate the water vapor kernel, we impose a one percent increase in water vapor into the atmosphere () and obtain . These original raw 4-D data (longitude, latitude, altitude, and time) of and calculated with CESM 1.1.2 are from [66]. All-sky annual mean linear water vapor kernels are given in Figure 6a,b. All-sky annual mean logarithmic water vapor kernels are given in Figure 7a,b. The all-sky global mean linear kernel is , and the all-sky global mean logarithmic kernel is . For example, if a 10% increase in water vapor content is imposed, the linear response of the radiative flux is , and is the logarithmic response.
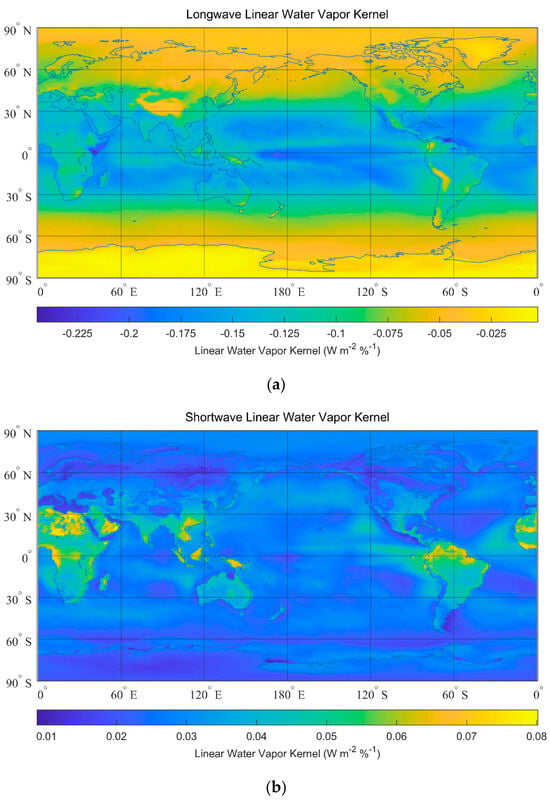
Figure 6.
All-sky linear water vapor kernels. (a) All-sky longwave linear water vapor kernels (global mean: ). (b) All-sky shortwave linear water vapor kernels (global mean: ).
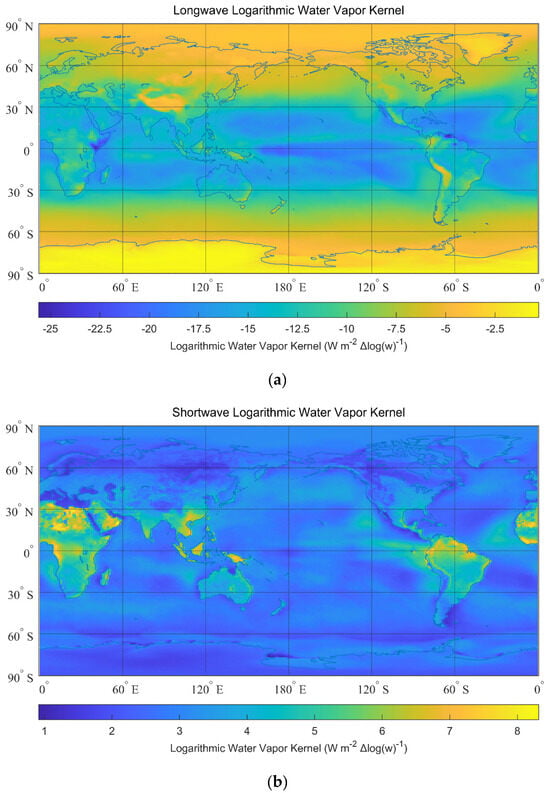
Figure 7.
All-sky logarithmic water vapor kernels. (a) All-sky longwave logarithmic water vapor kernels (global mean: ). (b) All-sky shortwave logarithmic water vapor kernels (global mean: ).
From Figure 6 and Figure 7, the strongest responses to the increase in water vapor content in tropical zones are comparable to existing papers [59,61,67,68,69,70]. The higher sensitivity of radiative responses to water vapor in the wetter tropic areas is mainly due to a higher net increase in vapor content at the same fractional growth rate. There are detailed explanations in existing papers [67,69], so they are not the focus of our study. Since the radiative response to a 10% increase in water vapor content is roughly the same magnitude as the increase in water vapor due to 1 K perturbation [71], the results from our calculation are comparable to the five-year observation-based results, in which the annual global mean values are to for longwave (shortwave) radiative responses to water vapor [60]. Radiative kernels in different regions are given in Table 2.

Table 2.
Radiative kernels in different regions.
4. Comparison of Radiative Forcing Due to Methane and Water Vapor Variations
We can now compare global mean radiative forcing, which is reduced due to methane removal, and radiative forcing, which is due increased due to higher water vapor content, when the same increase in OH concentration is required, as shown in Figure 8.
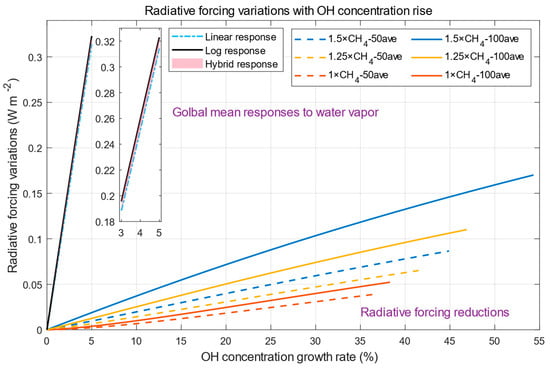
Figure 8.
Radiative forcing variations with a rise in OH concentration.
The comparison is discussed from two different perspectives. From the global mean perspective, the responses to water vapor are present in the left part of this figure. We choose 2.237 as the sensitivity of OH concentration to water vapor indicated in Section 1, which means that increasing OH by one percent requires only 1/2.237 percent growth of water vapor (and corresponding radiative responses to water vapor). Linear radiative responses to increases in water vapor required by increases in OH concentrations are presented by the blue dash-dot line, logarithmic responses are presented by the solid black line, and the pink area indicates the hybrid response zone.
Reductions in TOA radiative forcing due to reductions in CH4 concentrations can be assessed by [1,72]
where is a change in net downward radiative flux due to changes in greenhouse gases accounting for stratospheric temperature adjustments, is pre-industrial CH4 concentration, 731.41 ppb, and is atmospheric N2O concentration, 331 ppb [73]. , , . Only the changes in are taken into account, and is assumed not changed when the reductions in radiative forcing are calculated from Equation (15).
From Figure 8, the global mean radiative forcing increases from water vapor will exceed radiative forcing reductions due to methane removal (lower part of this figure) when the same rate of increase in OH concentration is required. From this perspective, removing atmospheric methane only by increasing water vapor content in the atmosphere may not be a good method. It should be noted that effective radiative forcing (ERF) may also be the parameter for comparison. ERF is an extended concept from SARF and is a change in net downward radiative flux due to changes in greenhouse gases accounting for adjustments not only in stratospheric temperature (SARF) but also in tropospheric temperature, clouds, and atmospheric circulation [1]. As the sum of adjustments is negatively proportional to SARF [74], the radiative benefits of methane reductions will be further below the penalty.
From the regional perspective, it may be noted that the radiative response to water vapor is not homogeneous, which is relatively low in some regions in Figure 6 and Figure 7 (e.g., high latitudes). As described in the Introduction, the sensitivity of OH concentration to water vapor in high-latitude regions can reach 5.507. This means increasing OH concentration in these regions by water vapor is more efficient with smaller negative impacts. But CH4 emissions from these high latitudes make up a small portion of today’s global CH4 emissions budget [1]. However, if an abrupt change in CH4 emissions from permafrost thaw occurs, as predicted by many scientists [75,76,77], increasing OH concentration by water vapor may be a good choice in this region.
5. Discussion
First, to maintain the OH concentration at a relatively high level, a continuously larger OH source is required. This means that a steady source of water vapor is needed, and the vapor concentration must be kept at a certain level in the atmosphere to produce enough OH. Because water vapor has a residence time of about ten days and the flux of anthropogenic vapor is less than natural evaporation [38], the greenhouse effect of water vapor from anthropogenic sources is not considered in the IPCC reports. But in the strategy this study is assessing, a steady and relatively large water vapor flux is needed; this is the reason for the consideration of its greenhouse effect.
Second, this work separated the effects of water vapor on methane reduction into three static parts, namely water–OH, CH4–OH, and water–CH4 relationships. A more sophisticated method needs to be applied to simulate the dynamic interactions among them, especially for minimizing the error in the water vapor content affected by condensation and precipitation. Another error may come from the interannual variability in water vapor response kernels [60]. This means that short-term (several years) observations and calculations of radiative responses to water vapor in this work may not accurately represent long-term (century) responses [64].
Third, from the perspective of atmospheric pressure levels (altitude), the strongest radiative forcing responses (longwave plus shortwave) to water vapor are between 700 hPa to 200 hPa, the responses between 1000 hPa (surface) to 700 hPa are relatively weak (please see the references) [59,64,66], while the highest OH concentrations are just below 700 hPa near the Equator [29,53]. This means that the water vapor enhancement implemented near the surface may have a better effective potential and lower environmental penalty than what is implemented in the high altitude. Since a validated method is required to weigh radiative forcing responses to methane and water vapor changes at different pressure levels, more detailed research could be conducted to identify the most appropriate zones for the water vapor enhancement strategy.
Last but not least, there are other limitations in this work. For example, there are many other factors considering the complexity of atmospheric chemistry that will complicate the application of this finding to the real world. We will investigate these areas in our future work and hope this work is merely a starting point that can inspire other future works in the field.
6. Conclusions
Methane is the second largest contributor to global surface air temperature rise relative to 1750, just following CO2. Methane concentrations in the atmosphere have continued to increase in recent decades. Reducing atmospheric methane will slow down climate change and improve air quality and is a vital way to meet the temperature limit set by the Paris Agreement.
Since the main sink of methane is OH in the atmosphere, increasing OH concentration will accelerate the methane oxidation process and reduce methane concentration. While the primary source of OH is the reaction between water vapor and ozone, a water vapor enhancement strategy was proposed to raise the OH concentration in the atmosphere and remove methane. We use a two-box model to evaluate the interaction between OH and methane and a radiative kernel method to calculate radiative responses to the growth of water vapor content in the atmosphere.
Using the two-box model proves that increasing the OH concentration does have a positive effect on methane reduction. If the concentration of OH is increased by 10% from its current value and maintained for 50 (100) years, 45 Tg yr−1 (67.5 Tg yr−1) more methane will be oxidized by OH; the cumulative effects of the oxidation are equivalent to a 120.5 Gt (219.6 Gt) reduction in CO2 and will lower the global surface air temperature by 0.054 °C (0.099 °C).
Our study also provides insights into a mixed picture of global and regional radiative responses to water vapor content growth. From the global average point of view, the increased radiative forcing due to higher water vapor content will exceed the reduced radiative forcing due to methane removal. Removing atmospheric methane only by increasing water vapor in the atmosphere may not be feasible for now. However, due to OH’s greater sensitivity to water vapor and weaker radiative response in high-latitude areas, this method may become feasible to address possible abrupt changes in CH4 emissions from permafrost thaw in the future.
Author Contributions
Y.L.: Writing—Original draft, Writing—Review and Editing, Investigation X.Y.: Methodology, Investigation. L.Z.: Methodology, Investigation. T.M.: Supervision, Reviewing and Editing. W.L.: Funding acquisition, Supervision, Reviewing and Editing. R.d.R.: Reviewing and Editing. All authors have read and agreed to the published version of the manuscript.
Funding
The present study was supported by the China Scholarship Council (File No. 202106950036), the European Commission H2020 Marie S Curie Research and Innovation Staff Exchange (RISE) award (Grant No. 871998), and the National Key Research and Development Plan (Key Special Project of Inter−governmental National Scientific and Technological Innovation Cooperation, Grant No. 2019YFE0197500).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The two-box model can be found from Turner et al. (2017) [64] and the data can be accessed via Github https://github.com/alexjturner/BoxModel_PNAS_20161223 (accessed on 1 June 2023). A revised two-box model can be found from Nguyen et al. (2020) [43], and the data can be accessed via Github https://github.com/Newton-Climate/OHMethane (accessed on 1 June 2023). The 4-D data for radiative kernels are from Pendergrass et al. (2018) [49] and can be accessed via Github https://github.com/apendergrass/cam5-kernels (accessed on 1 June 2023) and via Zenodo https://zenodo.org/record/997902 (accessed on 1 June 2023).
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Abernethy, S.; O’Connor, F.M.; Jones, C.D.; Jackson, R.B. Methane removal and the proportional reductions in surface temperature and ozone. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2021, 379, 20210104. [Google Scholar] [CrossRef]
- Shahabadi, M.B.; Huang, Y. Logarithmic radiative effect of water vapor and spectral kernels. J. Geophys. Res. Atmos. 2014, 119, 6000–6008. [Google Scholar] [CrossRef]
- Collins, W.J.; Webber, C.P.; Cox, P.M.; Huntingford, C.; Lowe, J.; Sitch, S.; E Chadburn, S.; Comyn-Platt, E.; Harper, A.B.; Hayman, G.; et al. Increased importance of methane reduction for a 1.5 degree target. Environ. Res. Lett. 2018, 13, 054003. [Google Scholar] [CrossRef]
- Collins, W.J.; Frame, D.J.; Fuglestvedt, J.S.; Shine, K.P. Stable climate metrics for emissions of short and long-lived species—Combining steps and pulses. Environ. Res. Lett. 2020, 15, 024018. [Google Scholar] [CrossRef]
- Dang, R.; Liao, H. Radiative Forcing and Health Impact of Aerosols and Ozone in China as the Consequence of Clean Air Actions over 2012–2017. Geophys. Res. Lett. 2019, 46, 12511–12519. [Google Scholar] [CrossRef]
- Dean, J.F.; Middelburg, J.J.; Röckmann, T.; Aerts, R.; Blauw, L.G.; Egger, M.; Jetten, M.S.M.; de Jong, A.E.E.; Meisel, O.H.; Rasigraf, O.; et al. Methane Feedbacks to the Global Climate System in a Warmer World. Rev. Geophys. 2018, 56, 207–250. [Google Scholar] [CrossRef]
- Dentener, F.; Stevenson, D.; Cofala, J.; Mechler, R.; Amann, M.; Bergamaschi, P.; Raes, F.; Derwent, R. The impact of air pollutant and methane emission controls on tropospheric ozone and radiative forcing: CTM calculations for the period 1990–2030. Atmos. Chem. Phys. 2005, 5, 1731–1755. [Google Scholar] [CrossRef]
- Dessler, A.E.; Zhang, Z.; Yang, P. Water-vapor climate feedback inferred from climate fluctuations, 2003–2008. Geophys. Res. Lett. 2008, 35, L20704. [Google Scholar] [CrossRef]
- Etminan, M.; Myhre, G.; Highwood, E.J.; Shine, K.P. Radiative forcing of carbon dioxide, methane, and nitrous oxide: A significant revision of the methane radiative forcing. Geophys. Res. Lett. 2016, 43, 12614–12623. [Google Scholar] [CrossRef]
- Feldl, N.; Bordoni, S.; Merlis, T.M. Coupled High-Latitude Climate Feedbacks and Their Impact on Atmospheric Heat Transport. J. Clim. 2017, 30, 189–201. [Google Scholar] [CrossRef]
- Gedney, N.; Huntingford, C.; Comyn-Platt, E.; Wiltshire, A. Significant feedbacks of wetland methane release on climate change and the causes of their uncertainty. Environ. Res. Lett. 2019, 14, 084027. [Google Scholar] [CrossRef]
- Gordon, N.D.; Jonko, A.K.; Forster, P.M.; Shell, K.M. An observationally based constraint on the water-vapor feedback. J. Geophys. Res. Atmos. 2013, 118, 12435–12443. [Google Scholar] [CrossRef]
- Haines, A.; Amann, M.; Borgford-Parnell, N.; Leonard, S.; Kuylenstierna, J.; Shindell, D. Short-lived climate pollutant mitigation and the Sustainable Development Goals. Nat. Clim. Chang. 2017, 7, 863–869. [Google Scholar] [CrossRef]
- Harmsen, M.; Fricko, O.; Hilaire, J.; van Vuuren, D.P.; Drouet, L.; Durand-Lasserve, O.; Fujimori, S.; Keramidas, K.; Klimont, Z.; Luderer, G.; et al. Taking some heat off the NDCs? The limited potential of additional short-lived climate forcers’ mitigation. Clim. Chang. 2020, 163, 1443–1461. [Google Scholar] [CrossRef]
- Heimann, I.; Griffiths, P.T.; Warwick, N.J.; Abraham, N.L.; Archibald, A.T.; Pyle, J.A. Methane Emissions in a Chemistry-Climate Model: Feedbacks and Climate Response. J. Adv. Model. Earth Syst. 2020, 12, e2019MS002019. [Google Scholar] [CrossRef]
- Heinze, C.; Eyring, V.; Friedlingstein, P.; Jones, C.; Balkanski, Y.; Collins, W.; Fichefet, T.; Gao, S.; Hall, A.; Ivanova, D.; et al. ESD Reviews: Climate feedbacks in the Earth system and prospects for their evaluation. Earth Syst. Dyn. 2019, 10, 379–452. [Google Scholar] [CrossRef]
- Held, I.M.; Soden, B.J. Water Vapor Feedback and Global Warming. Annu. Rev. Energy Environ. 2000, 25, 441–475. [Google Scholar] [CrossRef]
- Holmes, C.D.; Prather, M.J.; Søvde, O.A.; Myhre, G. Future methane, hydroxyl, and their uncertainties: Key climate and emission parameters for future predictions. Atmos. Chem. Phys. 2013, 13, 285–302. [Google Scholar] [CrossRef]
- Holmes, C.D. Methane Feedback on Atmospheric Chemistry: Methods, Models, and Mechanisms. J. Adv. Model. Earth Syst. 2018, 10, 1087–1099. [Google Scholar] [CrossRef]
- Huang, Y.; Ramaswamy, V.; Soden, B. An investigation of the sensitivity of the clear-sky outgoing longwave radiation to atmospheric temperature and water vapor. J. Geophys. Res. Atmos. 2007, 112, D05104. [Google Scholar] [CrossRef]
- Huang, Y.; Xia, Y.; Tan, X. On the pattern of CO2 radiative forcing and poleward energy transport. J. Geophys. Res. Atmos. 2017, 122, 10578–10593. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- IPCC. Summary for Policymakers. In Global Warming of 1.5 °C. An IPCC Special Report on the Impacts of Global Warming of 1.5 °C above Pre-Industrial Levels and Related Global Greenhouse Gas Emission Pathways, in the Context of Strengthening the Global Response to the Threat of Climate Change, Sustainable Development, and Efforts to Eradicate Poverty; Masson-Delmotte, V., Zhai, P., Pörtner, H.-O., Roberts, D., Skea, J., Shukla, P.R., Pirani, A., Moufouma-Okia, W., Péan, C., Pidcock, R., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2018; pp. 3–24. [Google Scholar]
- IPCC. Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M.I., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2021; p. 2391. [Google Scholar]
- Isaksen, I.S.A.; Gauss, M.; Myhre, G.; Anthony, K.M.W.; Ruppel, C. Strong atmospheric chemistry feedback to climate warming from Arctic methane emissions. Glob. Biogeochem. Cycles 2011, 25, GB2002. [Google Scholar] [CrossRef]
- Burkholder, J.B.; Sander, S.P.; Abbatt, J.; Barker, J.R.; Cappa, C.; Crounse, J.D.; Dibble, T.S.; Huie, R.E.; Kolb, C.E.; Kurylo, M.J.; et al. Chemical Kinetics and Photochemical Data for Use in Atmospheric Studies, Evaluation No. 19; Jet Propulsion Laboratory: Pasadena, CA, USA, 2019. [Google Scholar]
- Jackson, R.B.; Solomon, E.I.; Canadell, J.G.; Cargnello, M.; Field, C.B. Methane removal and atmospheric restoration. Nat. Sustain. 2019, 2, 436–438. [Google Scholar] [CrossRef]
- Koffi, E.N.; Bergamaschi, P.; Alkama, R.; Cescatti, A. An observation-constrained assessment of the climate sensitivity and future trajectories of wetland methane emissions. Sci. Adv. 2020, 6, eaay4444. [Google Scholar] [CrossRef]
- Kramer, R.J.; Matus, A.V.; Soden, B.J.; L’Ecuyer, T.S. Observation-Based Radiative Kernels From CloudSat/CALIPSO. J. Geophys. Res. Atmos. 2019, 124, 5431–5444. [Google Scholar] [CrossRef]
- Lan, X.; Thoning, K.W.; Dlugokencky, E.J. Trends in Globally-Averaged CH4, N2O, and SF6 Determined from NOAA Global Monitoring Laboratory Measurements (No. Version 2023-04). 2023. Available online: https://gml.noaa.gov/ccgg/trends_doi.html (accessed on 1 June 2023).
- Lelieveld, J.; Gromov, S.; Pozzer, A.; Taraborrelli, D. Global tropospheric hydroxyl distribution, budget and reactivity. Atmos. Chem. Phys. 2016, 16, 12477–12493. [Google Scholar] [CrossRef]
- Li, M.; Karu, E.; Brenninkmeijer, C.; Fischer, H.; Lelieveld, J.; Williams, J. Tropospheric OH and stratospheric OH and Cl concentrations determined from CH4, CH3Cl, and SF6 measurements. NPJ Clim. Atmospheric Sci. 2018, 1, 29. [Google Scholar] [CrossRef]
- Liu, R.; Su, H.; Liou, K.-N.; Jiang, J.H.; Gu, Y.; Liu, S.C.; Shiu, C. An Assessment of Tropospheric Water Vapor Feedback Using Radiative Kernels. J. Geophys. Res. Atmos. 2018, 123, 1499–1509. [Google Scholar] [CrossRef]
- López-Comí, L.; Morgenstern, O.; Zeng, G.; Masters, S.L.; Querel, R.R.; Nedoluha, G.E. Assessing the sensitivity of the hydroxyl radical to model biases in composition and temperature using a single-column photochemical model for Lauder, New Zealand. Atmos. Chem. Phys. 2016, 16, 14599–14619. [Google Scholar] [CrossRef]
- Lund, M.T.; Aamaas, B.; Stjern, C.W.; Klimont, Z.; Berntsen, T.K.; Samset, B.H. A continued role of short-lived climate forcers under the Shared Socioeconomic Pathways. Earth Syst. Dyn. 2020, 11, 977–993. [Google Scholar] [CrossRef]
- Maycock, A.C.; Smith, C.J.; Rap, A.; Rutherford, O. On the Structure of Instantaneous Radiative Forcing Kernels for Greenhouse Gases. J. Atmospheric Sci. 2021, 78, 949–965. [Google Scholar] [CrossRef]
- Meinshausen, M.; Nicholls, Z.R.J.; Lewis, J.; Gidden, M.J.; Vogel, E.; Freund, M.; Beyerle, U.; Gessner, C.; Nauels, A.; Bauer, N.; et al. The shared socio-economic pathway (SSP) greenhouse gas concentrations and their extensions to 2500. Geosci. Model Dev. 2020, 13, 3571–3605. [Google Scholar] [CrossRef]
- Miner, K.R.; Turetsky, M.R.; Malina, E.; Bartsch, A.; Tamminen, J.; McGuire, A.D.; Fix, A.; Sweeney, C.; Elder, C.D.; Miller, C.E. Permafrost carbon emissions in a changing Arctic. Nat. Rev. Earth Environ. 2022, 3, 55–67. [Google Scholar] [CrossRef]
- Monks, S.A.; Arnold, S.R.; Emmons, L.K.; Law, K.S.; Turquety, S.; Duncan, B.N.; Flemming, J.; Huijnen, V.; Tilmes, S.; Langner, J.; et al. Multi-model study of chemical and physical controls on transport of anthropogenic and biomass burning pollution to the Arctic. Atmos. Chem. Phys. 2015, 15, 3575–3603. [Google Scholar] [CrossRef]
- Montzka, S.A.; Spivakovsky, C.M.; Butler, J.H.; Elkins, J.W.; Lock, L.T.; Mondeel, D.J. New Observational Constraints for Atmospheric Hydroxyl on Global and Hemispheric Scales. Science 2000, 288, 500–503. [Google Scholar] [CrossRef]
- Naik, V.; Voulgarakis, A.; Fiore, A.M.; Horowitz, L.W.; Lamarque, J.-F.; Lin, M.; Prather, M.J.; Young, P.J.; Bergmann, D.; Cameron-Smith, P.J.; et al. Preindustrial to present-day changes in tropospheric hydroxyl radical and methane lifetime from the Atmospheric Chemistry and Climate Model Intercomparison Project (ACCMIP). Atmos. Chem. Phys. 2013, 13, 5277–5298. [Google Scholar] [CrossRef]
- Naus, S.; Montzka, S.A.; Pandey, S.; Basu, S.; Dlugokencky, E.J.; Krol, M. Constraints and biases in a tropospheric two-box model of OH. Atmos. Chem. Phys. 2019, 19, 407–424. [Google Scholar] [CrossRef]
- Nguyen, N.H.; Turner, A.J.; Yin, Y.; Prather, M.J.; Frankenberg, C. Effects of Chemical Feedbacks on Decadal Methane Emissions Estimates. Geophys. Res. Lett. 2020, 47, e2019GL085706. [Google Scholar] [CrossRef]
- Nicely, J.M.; Salawitch, R.J.; Canty, T.; Anderson, D.C.; Arnold, S.R.; Chipperfield, M.P.; Emmons, L.K.; Flemming, J.; Huijnen, V.; Kinnison, D.E.; et al. Quantifying the causes of differences in tropospheric OH within global models. J. Geophys. Res. Atmos. 2017, 122, 1983–2007. [Google Scholar] [CrossRef]
- Nicely, J.M.; Canty, T.P.; Manyin, M.; Oman, L.D.; Salawitch, R.J.; Steenrod, S.D.; Strahan, S.E.; Strode, S.A. Changes in Global Tropospheric OH Expected as a Result of Climate Change Over the Last Several Decades. J. Geophys. Res. Atmos. 2018, 123, 10774–10795. [Google Scholar] [CrossRef]
- Nisbet, E.G.; Fisher, R.E.; Lowry, D.; France, J.L.; Allen, G.; Bakkaloglu, S.; Broderick, T.J.; Cain, M.; Coleman, M.; Fernandez, J.; et al. Methane Mitigation: Methods to Reduce Emissions, on the Path to the Paris Agreement. Rev. Geophys. 2020, 58, e2019RG000675. [Google Scholar] [CrossRef]
- Ocko, I.B.; Sun, T.; Shindell, D.; Oppenheimer, M.; Hristov, A.N.; Pacala, S.W.; Mauzerall, D.L.; Xu, Y.; Hamburg, S.P. Acting rapidly to deploy readily available methane mitigation measures by sector can immediately slow global warming. Environ. Res. Lett. 2021, 16, 054042. [Google Scholar] [CrossRef]
- Patra, P.K.; Krol, M.C.; Montzka, S.A.; Arnold, T.; Atlas, E.L.; Lintner, B.R.; Stephens, B.B.; Xiang, B.; Elkins, J.W.; Fraser, P.J.; et al. Observational evidence for interhemispheric hydroxyl-radical parity. Nature 2014, 513, 219–223. [Google Scholar] [CrossRef]
- Pendergrass, A.G.; Conley, A.; Vitt, F.M. Surface and top-of-atmosphere radiative feedback kernels for CESM-CAM5. Earth Syst. Sci. Data 2018, 10, 317–324. [Google Scholar] [CrossRef]
- Peng, S.; Lin, X.; Thompson, R.L.; Xi, Y.; Liu, G.; Hauglustaine, D.; Lan, X.; Poulter, B.; Ramonet, M.; Saunois, M.; et al. Wetland emission and atmospheric sink changes explain methane growth in 2020. Nature 2022, 612, 477–482. [Google Scholar] [CrossRef]
- Prather, M.J. Time scales in atmospheric chemistry: Theory, GWPs for CH4 and CO, and runaway growth. Geophys. Res. Lett. 1996, 23, 2597–2600. [Google Scholar] [CrossRef]
- Prather, M.J. Lifetimes and time scales in atmospheric chemistry. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2007, 365, 1705–1726. [Google Scholar] [CrossRef]
- Prather, M.J.; Holmes, C.D.; Hsu, J. Reactive greenhouse gas scenarios: Systematic exploration of uncertainties and the role of atmospheric chemistry. Geophys. Res. Lett. 2012, 39, L09803. [Google Scholar] [CrossRef]
- Saunois, M.; Stavert, A.R.; Poulter, B.; Bousquet, P.; Canadell, J.G.; Jackson, R.B.; Raymond, P.A.; Dlugokencky, E.J.; Houweling, S.; Patra, P.K.; et al. The Global Methane Budget 2000–2017. Earth Syst. Sci. Data 2020, 12, 1561–1623. [Google Scholar] [CrossRef]
- Shell, K.M.; Kiehl, J.T.; Shields, C.A. Using the Radiative Kernel Technique to Calculate Climate Feedbacks in NCAR’s Community Atmospheric Model. J. Clim. 2008, 21, 2269–2282. [Google Scholar] [CrossRef]
- Sherwood, S.C.; Dixit, V.; Salomez, C. The global warming potential of near-surface emitted water vapour. Environ. Res. Lett. 2018, 13, 104006. [Google Scholar] [CrossRef]
- Smith, C.J.; Kramer, R.J.; Myhre, G.; Forster, P.M.; Soden, B.J.; Andrews, T.; Boucher, O.; Faluvegi, G.; Fläschner, D.; Hodnebrog, Ø.; et al. Understanding Rapid Adjustments to Diverse Forcing Agents. Geophys. Res. Lett. 2018, 45, 12023–12031. [Google Scholar] [CrossRef] [PubMed]
- Soden, B.J.; Held, I.M.; Colman, R.; Shell, K.M.; Kiehl, J.T.; Shields, C.A. Quantifying Climate Feedbacks Using Radiative Kernels. J. Clim. 2008, 21, 3504–3520. [Google Scholar] [CrossRef]
- Stevenson, D.S.; Zhao, A.; Naik, V.; O’Connor, F.M.; Tilmes, S.; Zeng, G.; Murray, L.T.; Collins, W.J.; Griffiths, P.T.; Shim, S.; et al. Trends in global tropospheric hydroxyl radical and methane lifetime since 1850 from AerChemMIP. Atmos. Chem. Phys. 2020, 20, 12905–12920. [Google Scholar] [CrossRef]
- Sun, T.; Ocko, I.B.; Hamburg, S.P. The value of early methane mitigation in preserving Arctic summer sea ice. Environ. Res. Lett. 2022, 17, 044001. [Google Scholar] [CrossRef]
- Thorsen, T.J.; Kato, S.; Loeb, N.G.; Rose, F.G. Observation-Based Decomposition of Radiative Perturbations and Radiative Kernels. J. Clim. 2018, 31, 10039–10058. [Google Scholar] [CrossRef]
- Tian, H.Q.; Xu, R.T.; Canadell, J.G.; Thompson, R.L.; Winiwarter, W.; Suntharalingam, P.; Davidson, E.A.; Ciais, P.; Jackson, R.B.; Janssens-Maenhout, G.; et al. A comprehensive quantification of global nitrous oxide sources and sinks. Nature 2020, 586, 248–256. [Google Scholar] [CrossRef]
- Turetsky, M.R.; Abbott, B.W.; Jones, M.C.; Anthony, K.W.; Olefeldt, D.; Schuur, E.A.G.; Grosse, G.; Kuhry, P.; Hugelius, G.; Koven, C.; et al. Carbon release through abrupt permafrost thaw. Nat. Geosci. 2020, 13, 138–143. [Google Scholar] [CrossRef]
- Turner, A.J.; Frankenberg, C.; Wennberg, P.O.; Jacob, D.J. Ambiguity in the causes for decadal trends in atmospheric methane and hydroxyl. Proc. Natl. Acad. Sci. USA 2017, 114, 5367–5372. [Google Scholar] [CrossRef]
- Turner, A.J.; Frankenberg, C.; Kort, E.A. Interpreting contemporary trends in atmospheric methane. Proc. Natl. Acad. Sci. USA 2019, 116, 2805–2813. [Google Scholar] [CrossRef]
- Anthony, K.W.; von Deimling, T.S.; Nitze, I.; Frolking, S.; Emond, A.; Daanen, R.; Anthony, P.; Lindgren, P.; Jones, B.; Grosse, G. 21st-century modeled permafrost carbon emissions accelerated by abrupt thaw beneath lakes. Nat. Commun. 2018, 9, 3262. [Google Scholar] [CrossRef]
- Wang, X.; Jacob, D.J.; Eastham, S.D.; Sulprizio, M.P.; Zhu, L.; Chen, Q.; Alexander, B.; Sherwen, T.; Evans, M.J.; Lee, B.H.; et al. The role of chlorine in global tropospheric chemistry. Atmos. Chem. Phys. 2019, 19, 3981–4003. [Google Scholar] [CrossRef]
- Wang, Y.; Ming, T.; Li, W.; Yuan, Q.; de Richter, R.; Davies, P.; Caillol, S. Atmospheric removal of methane by enhancing the natural hydroxyl radical sink. Greenh. Gases Sci. Technol. 2022, 12, 784–795. [Google Scholar] [CrossRef]
- Wuebbles, D.J.; Tamaresis, J.S. The Role of Methane in the Global Environment. In Atmospheric Methane: Sources, Sinks, and Role in Global Change; Khalil, M.A.K., Ed.; Springer: Berlin/Heidelberg, Germany, 1993; pp. 469–513. [Google Scholar]
- Xiong, H.; Ming, T.; Wu, Y.; Li, W.; Mu, L.; de Richter, R.; Yan, S.; Yuan, Y.; Peng, C. Numerical analysis of a negative emission technology of methane to mitigate climate change. Sol. Energy 2023, 255, 416–424. [Google Scholar] [CrossRef]
- Yin, Y.; Chevallier, F.; Ciais, P.; Broquet, G.; Fortems-Cheiney, A.; Pison, I.; Saunois, M. Decadal trends in global CO emissions as seen by MOPITT. Atmos. Chem. Phys. 2015, 15, 13433–13451. [Google Scholar] [CrossRef]
- Yin, Y.; Chevallier, F.; Ciais, P.; Bousquet, P.; Saunois, M.; Zheng, B.; Worden, J.; Bloom, A.A.; Parker, R.J.; Jacob, D.J.; et al. Accelerating methane growth rate from 2010 to 2017: Leading contributions from the tropics and East Asia. Atmos. Chem. Phys. 2021, 21, 12631–12647. [Google Scholar] [CrossRef]
- Yuan, W.; Zheng, Y.; Piao, S.; Ciais, P.; Lombardozzi, D.; Wang, Y.; Ryu, Y.; Chen, G.; Dong, W.; Hu, Z.; et al. Increased atmospheric vapor pressure deficit reduces global vegetation growth. Sci. Adv. 2019, 5, eaax1396. [Google Scholar] [CrossRef] [PubMed]
- Zelinka, M.D.; Hartmann, D.L. Climate Feedbacks and Their Implications for Poleward Energy Flux Changes in a Warming Climate. J. Clim. 2012, 25, 608–624. [Google Scholar] [CrossRef]
- Zhang, Z.; Zimmermann, N.E.; Stenke, A.; Li, X.; Hodson, E.L.; Zhu, G.; Huang, C.; Poulter, B. Emerging role of wetland methane emissions in driving 21st century climate change. Proc. Natl. Acad. Sci. USA 2017, 114, 9647–9652. [Google Scholar] [CrossRef]
- Zhao, Y.; Saunois, M.; Bousquet, P.; Lin, X.; Berchet, A.; Hegglin, M.I.; Canadell, J.G.; Jackson, R.B.; Dlugokencky, E.J.; Langenfelds, R.L.; et al. Influences of hydroxyl radicals (OH) on top-down estimates of the global and regional methane budgets. Atmos. Chem. Phys. 2020, 20, 9525–9546. [Google Scholar] [CrossRef]
- Zhao, Y.; Saunois, M.; Bousquet, P.; Lin, X.; Berchet, A.; Hegglin, M.I.; Canadell, J.G.; Jackson, R.B.; Deushi, M.; Jöckel, P.; et al. On the role of trend and variability in the hydroxyl radical (OH) in the global methane budget. Atmos. Chem. Phys. 2020, 20, 13011–13022. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).