Exploring the Origin of the Two-Week Predictability Limit: A Revisit of Lorenz’s Predictability Studies in the 1960s
Abstract
1. Introduction
2. A Review of the Studies in the 1960s for New Insights
- (1)
- Three approaches for atmospheric predictability (Lorenz 1969b [31]);
- (2)
- Atmospheric predictability as indicated by numerical experiments (Charney et al. 1966 [16]);
- (3)
- Atmospheric predictability as revealed by naturally occurring analogues (Lorenz 1969c [32]);
- (4)
- The predictability of a flow which possesses many scales of motion (Lorenz 1969d [18]).
- (a)
- A dynamical approach using atmospheric general circulation models;
- (b)
- An empirical approach based on natural “analogues”, defined below;
- (c)
- A dynamical-empirical approach that applied a system of 21, linear, 2nd-order ordinary differential equations (ODEs) with coefficients estimated using an atmospheric kinetic energy spectrum.
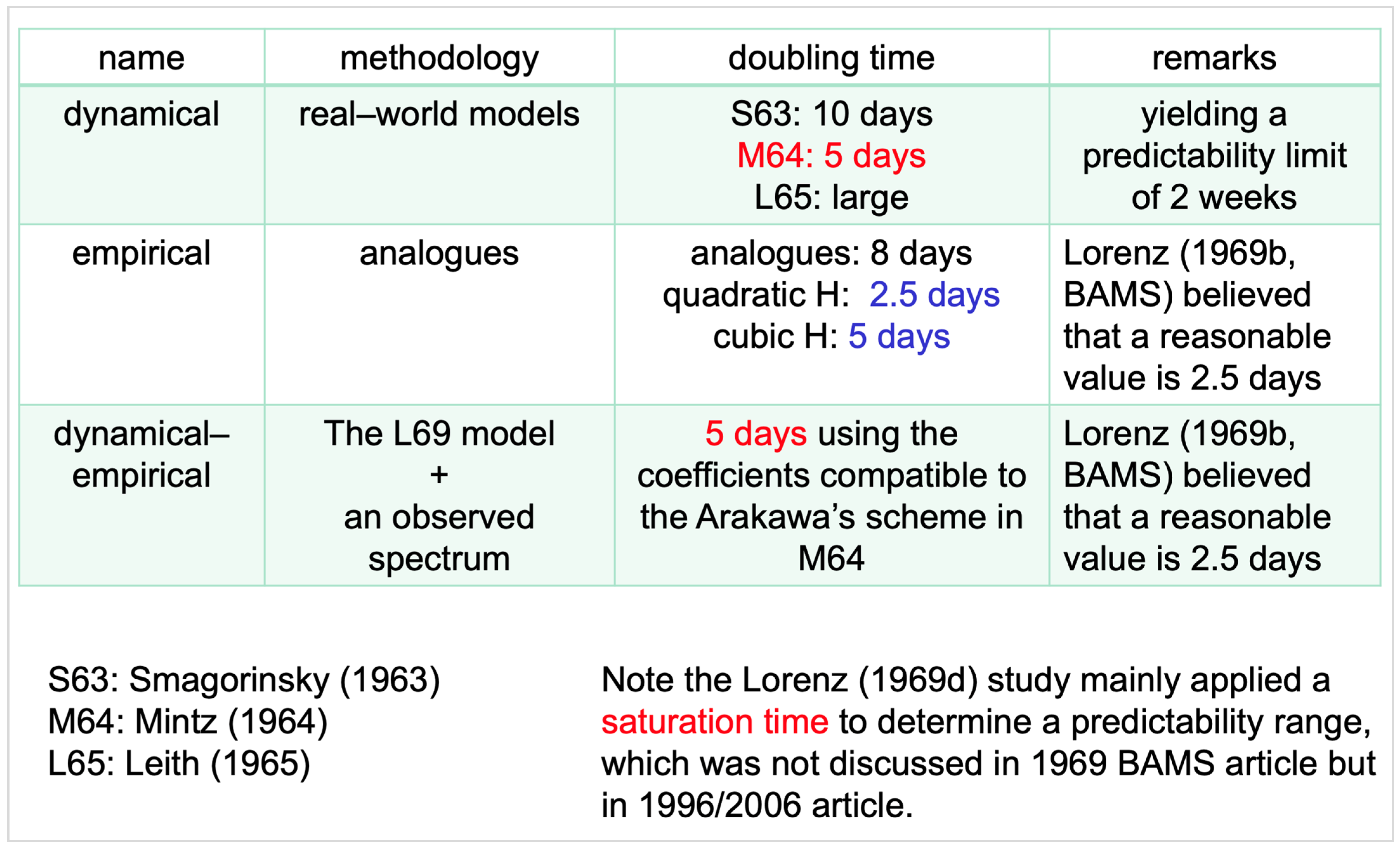
2.1. The Doubling Time of 5 Days and Its Extrapolation for Two-Week Predictability
“We may summarize our results in the statement that, based on the most realistic of the general circulation models available, the limit of deterministic predictability for the atmosphere is about two weeks in the winter and somewhat longer in the summer.”
“the limit of deterministic predictability, i.e., the limit of predictability of synoptic-scale motions, is about 2–3 weeks.”
“This statement first appeared in the aforementioned report of the NAS/NRC Panel on International Meteorological Cooperation, “The Feasibility of a Global Observation and Analysis Experiment.” It is based on numerical experiments conducted by the Panel with the use of various general circulation models, particularly the model developed at UCLA by Mintz and Arakawa.”
“It showed, for the first time using a realistic model of the atmosphere, the existence of a deterministic predictability limit the order of weeks. The report specifically says that the limit is two weeks, which became a matter of controversy later. To me, there is no reason that it is a fixed number. It should depend on many factors, such as the part of the time/space spectrum, climate and weather regimes, region of the globe and height in the vertical, season, etc.”
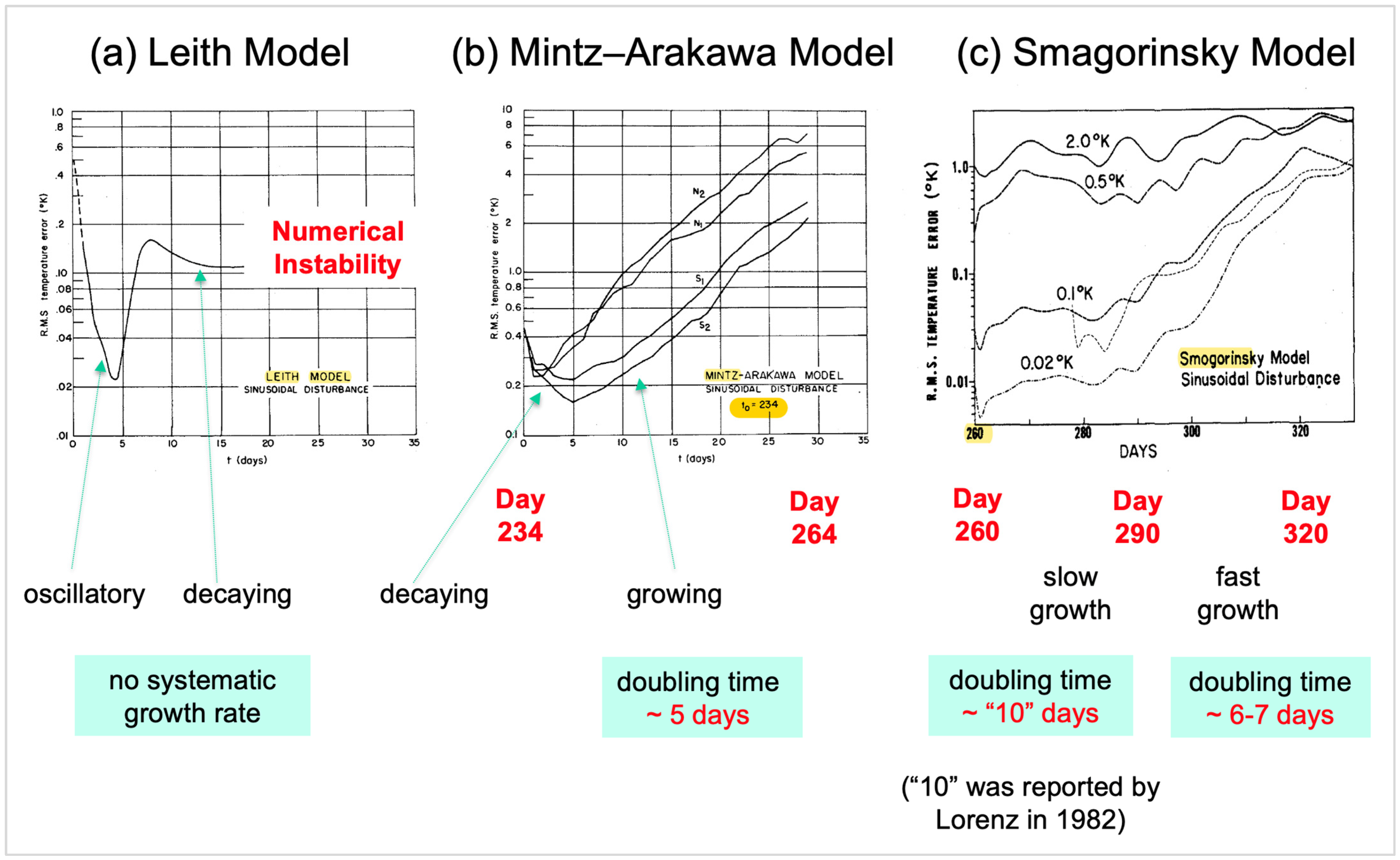
2.2. A Revisit of the Dynamical Approach in Charney et al. (1966)
“we note that all predictability in the Northern Hemisphere is lost at 26 days for the wave perturbation, 19 days for the random perturbation, and 29 days for the localized perturbation.”
“The smaller error disturbances, of amplitude 0.1°K and 0.02°K, show a slow but continuous growth until after about 30 days, when the doubling time reaches the value of 6 or 7 days. An examination of the actual flow patterns revealed that the motion was primarily periodic, with a small aperiodic component. ...... After about 30 days the vacillating regime changed to a more aperiodic behavior, and at that time the error grew more rapidly with a doubling time of 6 or 7 days. This behavior does not resemble very well the usual condition of the atmosphere in which strong instabilities appear always to exist.”
- Two different growth rates appeared for the first and second 30-day periods.
- An initial smaller growth rate during the first 30-day period was associated with quasi-period flow, but “suggested” that such a flow cannot represent the usual condition of the atmosphere. An estimated doubling time of 10 days was later reported by Lorenz (1982) [50].
- A larger growth rate, with a doubling time of six–seven days, was determined during the 2nd 30-day period, when numerical results of the Smagorinsky model displayed a more aperiodic response, indicating the early influence of Lorenz’s chaos study.
2.3. Error Doubling Times Estimated Using the Empirical Approach in Lorenz (1969c) [32]
“Analogues are two states of the atmosphere that exhibit resemblance to each other. Either state in a pair of analogues can be considered equivalent to the other state plus a small superposed ‘error.”
2.4. Major Findings within the Dynamical-Empirical Approach Using the Lorenz 1969 Model
- It consists of 21, linear, 2nd-order ordinary differential equations (ODEs), derived from a two-dimensional PDE that conserves vorticity.
- Coefficients for 21 ODEs were obtained based mode–mode interactions and an atmospheric kinetic energy spectrum.
- The PDE lacks baroclinic and dissipative processes and thus the 1969 model is not a turbulence model.
- The assumptions of “homogeneity” and “isotropy” in Lorenz (1969d) [18] do not permit variations in climatological properties from one location to another location.
- An eigenvalue analysis of the matrix for the 1969 system as well as relevant systems produces a large condition number, indicating ill-condition (Shen et al., 2022a) [17].
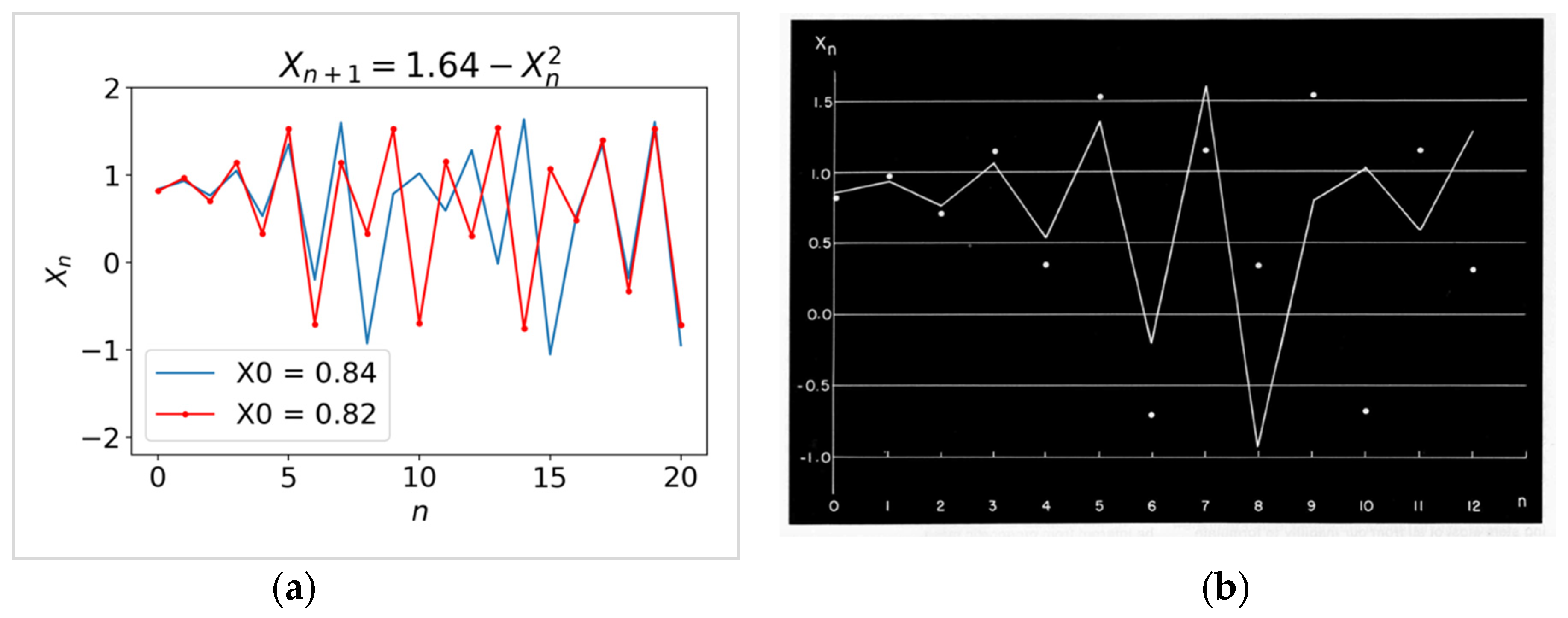
2.5. A Revisit of the Lorenz 1969 Model and Its Relationship to a Chaotic Map
“(Because of numerous assumptions entering the computations these results should not be regarded as the final word.)”
“We then conclude that the atmosphere possesses an intrinsic range of predictability of perhaps three weeks. ...... However, if the hoped-for improvements are some day realized, still further improvements will not appreciably increase the range of predictability.
Although we feel that the evidence favoring our conclusions is substantial, we must be quick to note that they are based upon a number of assumptions which cannot be rigorously defended. We are a long way from incorporating the true atmospheric equations into our procedure. We are therefore somewhat reluctant to name a maximum range of predictability without including a safety factor.”
2.6. Impact of a Spectral Gap on Extending Predictability Horizons
2.7. Smagorinsky’s Comments on the Analysis of Lorenz (1969b) [31]
“With this reservation in mind we conclude from these experiments that the deterministic limit of synoptic scale predictability is at least 3 weeks.”
- While the Lorenz 1969 model produced a doubling time of two–three days, the model lacked baroclinic instability.
- Within Lorenz’s analogue approach, the historical record is too short to be able to sufficiently close analogues which only differ by a measure of small error. To overcome deficiencies with large initial errors, Lorenz applied the so-called quadratic hypothesis in order to obtain a doubling time of less than three days.
3. Lorenz’s Updated Perspective and Recent Predictability Studies
“We must recognize, then, that some weather elements are predictable more than a month in advance, at least in the sense that most weather situations—even some that might well appear several years from now-are almost certain not to appear a month or two from now.
Among the most prominent features with some extended-range predictability are those associated with the El Nino-Southern Oscillation (ENSO) phenomenon.”
3.1. Recent Advances using PDE-based and AI-powered Systems
3.2. A View of Distinct Predictability Using a Generalized Lorenz Model
3.3. Proposed Future Research Directions
- Enhancing numerical methods by implementing variable time steps.
- Fusing AI with ensemble forecasting to refine predictive accuracy.
- Measuring the the sensitivity dependence on initial conditions (SDIC)—i.e. the butterfly effect—and chaotic behaviors in AI-driven systems.
- Improving spatial and/or temporal resolution through AI-powered downscaling.
- Expanding the functionality of AI models by integrating non-forecast variables.
- Discovering multiscale processes via singular value analysis of query, key, and value matrices.
- Crafting conceptual models to deepen the understanding of predictability.
- Reevaluating the boundaries of predictability horizons.
- Evaluating how the temporal extent of reanalysis data affects the precision of climate projections.
- Investigating AI-based model hallucinations and their linkage to sensitive dependence on initial conditions.
4. Concluding Remarks
“Much like Moore’s Law in the realm of computing, the predictability limit hypothesis, specifically the two-week predictability limit, is an empirical association based on practical modeling and idealized chaotic modeling from the 1960s. It stands as a limited set of observed findings and as a reasonable extrapolation from early modeling results during the 1960s, rather than constituting fundamental physics.”
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- National Academies of Sciences, Engineering, and Medicine. Earth System Predictability Research and Development: Proceedings of a Workshop in Brief; The National Academies Press: Washington, DC, USA, 2020. [Google Scholar] [CrossRef]
- National Research Council. When Weather Matters: Science and Services to Meet Critical Societal Needs; The National Academies Press: Washington, DC, USA, 2010. [Google Scholar] [CrossRef]
- National Academies of Sciences, Engineering, and Medicine. Next Generation Earth System Prediction: Strategies for Subseasonal to Seasonal Forecasts; The National Academies Press: Washington, DC, USA, 2016. [Google Scholar] [CrossRef]
- Sonechkin, D.M.; Samrov, V.P.; Zimin, N.E. The Model Averaged with Respect to Planetary Wave Phases Reveals the Ability to Overcome the Weekly Predictability Limit. Mon. Weather Rev. 1995, 123, 2461–2473. [Google Scholar] [CrossRef][Green Version]
- Mukougawa, H.; Sakai, H.; Hirooka, T. High Sensitivity to the Initial Condition for the Prediction of Stratospheric Sudden Warming. Geophys. Res. Lett. 2005, 32, L17806. [Google Scholar] [CrossRef]
- Shen, B.-W.; Tao, W.-K.; Wu, M.-L. African Easterly Waves in 30-day High-resolution Global Simulations: A Case Study during the 2006 NAMMA Period. Geophys. Res. Lett. 2010, 37, L18803. [Google Scholar] [CrossRef]
- Shen, B.-W.; Tao, W.-K.; Green, B. Coupling Advanced Modeling and Visualization to Improve High-Impact Tropical Weather Prediction (CAMVis). IEEE Comput. Sci. Eng. (CiSE) 2011, 13, 56–67. [Google Scholar] [CrossRef]
- Shen, B.-W. On the Predictability of 30-day Global Mesoscale Simulations of Multiple African Easterly Waves during Summer 2006: A View with a Generalized Lorenz Model. Geosciences 2019, 9, 281. [Google Scholar] [CrossRef]
- Krishnamurthy, V.; Sharma, A. Predictability at intraseasonal time scale. Geophys. Res. Lett. 2017, 44, 8530–8537. [Google Scholar] [CrossRef]
- Krishnamurthy, V. Predictability of weather and climate. Earth Space Sci. 2019, 6, 1043–1056. [Google Scholar] [CrossRef] [PubMed]
- Judt, F. Insights into Atmospheric Predictability through Global Convection-Permitting Model Simulations. J. Atmos. Sci. 2018, 75, 1477–1497. [Google Scholar] [CrossRef]
- Judt, F. Atmospheric predictability of the tropics, middle latitudes, and polar regions explored through global storm-resolving simulations. J. Atmos. Sci. 2020, 77, 257–276. [Google Scholar] [CrossRef]
- Shen, B.-W.; Pielke, R.A., Sr.; Zeng, X.; Zeng, X. 2023b: Lorenz’s View on the Predictability Limit. Encyclopedia 2023, 3, 887–899. [Google Scholar] [CrossRef]
- Lorenz, E.N. The Essence of Chaos; University of Washington Press: Seattle, WA, USA, 1993; 227p. [Google Scholar]
- Reeves, R.W. Edward Lorenz Revisiting the Limits of Predictability and Their Implications: An Interview from 2007. Bull. Am. Meteorol. Soc. 2014, 95, 681–687. [Google Scholar] [CrossRef]
- Charney, J.G.; Fleagle, R.G.; Lally, V.E.; Riehl, H.; Wark, D.Q. The feasibility of a global observation and analysis experiment. Bull. Am. Meteorol. Soc. 1966, 47, 200–220. [Google Scholar]
- Shen, B.-W.; Pielke, R.A., Sr.; Zeng, X. One Saddle Point and Two Types of Sensitivities within the Lorenz 1963 and 1969 Models. Atmosphere 2022, 13, 753. [Google Scholar] [CrossRef]
- Lorenz, E.N. The predictability of a flow which possesses many scales of motion. Tellus 1969, 21, 19. [Google Scholar]
- Vallis, G. Atmospheric and Oceanic Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2006; 745p. [Google Scholar]
- Lloveras, D.J.; Tierney, L.H.; Durran, D. Mesoscale Predictability in Moist Midlatitude Cyclones Is Not Sensitive to the Slope of the Background Kinetic Energy Spectrum. J. Atmos. Sci. 2022, 79, 119–139. [Google Scholar] [CrossRef]
- Owens, R.G.; Hewson, T.D. ECMWF Forecast User Guide; ECMWF: Reading, UK, 2018. [Google Scholar] [CrossRef]
- Lin, S.-J.; Shen, B.-W.; Putman, W.P.; Chern, J.-D. Application of the high-resolution finite-volume NASA/NCAR Climate Model for Medium-Range Weather Prediction Experiments. In Proceedings of the EGS-AGU-EUG Joint Assembly, Nice, France, 6–11 April 2003. [Google Scholar]
- Lorenz, E.N. Predictability—A problem partly solved. In Proceedings of the Seminar on Predictability, Reading, UK, 4–8 September 1995; ECMWF: Reading, UK, 1996; Volume 1. [Google Scholar]
- Lorenz, E.N. Predictability—A problem partly solved. In Predictability of Weather and Climate; Palmer, T., Hagedorn, R., Eds.; Cambridge University Press: Cambridge, UK, 2006; pp. 40–58. [Google Scholar]
- Shen, B.-W. Revisiting Lorenz’s Error Growth Models: Insights and Application. Encyclopedia 2024. [Google Scholar] [CrossRef]
- Pegion, K.; DelSole, T.; Becker, E.; Cicerone, T. 2019: Assessing the fidelity of predictability estimates. Clim. Dyn. 2019, 53, 7251–7265. [Google Scholar] [CrossRef]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Gleick, J. Chaos: Making a New Science; Penguin: New York, NY, USA, 1987; 360p. [Google Scholar]
- Stewart, I. Does God Play Dice? Blackwell Publishing Ltd.: Hoboken, NJ, USA, 1989; 401p. [Google Scholar]
- Lorenz, E.N. Studies of Atmospheric Predictability. [Part 1] [Part 2] [Part 3] [Part 4] Final Report, February, Statistical Forecasting Project; Air Force Research Laboratories, Office of Aerospace Research, USAF: Bedford, MA, USA, 1969; 145p. [Google Scholar]
- Lorenz, E.N. Three approaches to atmospheric predictability. Bull. Am. Meteorol. Soc. 1969, 50, 345–351. [Google Scholar]
- Lorenz, E.N. Atmospheric predictability as revealed by naturally occurring analogues. J. Atmos. Sci. 1969, 26, 636–646. [Google Scholar] [CrossRef]
- Lorenz, E.N. How much better can weather prediction become? MIT Technol. Rev. 1969, 39–49. [Google Scholar]
- Lorenz, E.N. The nature of the global circulation of the atmosphere: A present view. The Global Circulation of the Atmosphere, London, Roy. Meteor. Soc. 1969, 3–23. [Google Scholar]
- GARP. GARP topics. Bull. Am. Meteorol. Soc. 1969, 50, 136–141. [Google Scholar]
- Smagorinsky, J. Problems and promises of deterministic extended range forecasting. Bull. Am. Meteorol. Soc. 1969, 50, 286–312. [Google Scholar] [CrossRef]
- Lorenz, E.N. Progress Report on Atmospheric Predictability. Never Printed. 1970. [Google Scholar]
- Lorenz, E. Limits of Meteorological Predictability. Prepared for the American Meteorological Society, February. Unpublished. 1972. [Google Scholar]
- Lorenz, E.N. Estimates of atmospheric predictability at medium range. In Predictability of Fluid Motions; Holloway, G., West, B., Eds.; American Institute of Physics: New York, NY, USA, 1984; pp. 133–139. [Google Scholar]
- Lorenz, E.N. The growth of errors in prediction. In Turbulence and Predictability in Geophysical Fluid Dynamics and Climate Dynamics; Società Italiana di Fisica: Bologna, Italy, 1985; pp. 243–265. [Google Scholar]
- Rotunno, R.; Snyder, C. A generalization of Lorenz’s model for the predictability of flows with many scales of motion. J. Atmos. Sci. 2008, 65, 1063–1076. [Google Scholar] [CrossRef]
- Durran, D.R.; Gingrich, M. 2014: Atmospheric predictability: Why atmospheric butterflies are not of practical importance. J. Atmos. Sci. 2014, 71, 2476–2478. [Google Scholar] [CrossRef]
- Palmer, T.N.; Doring, A.; Seregin, G. The real butterfly effect. Nonlinearity 2014, 27, R123–R141. [Google Scholar] [CrossRef]
- Sun, Y.Q.; Zhang, F. A New Theoretical Framework for Understanding Multiscale Atmospheric Predictability. J. Atmos. Sci. 2020. [Google Scholar] [CrossRef]
- Shen, B.-W.; Pielke, R.A., Sr.; Zeng, X.; Cui, J.; Faghih-Naini, S.; Paxson, W.; Atlas, R. Three Kinds of Butterfly Effects Within Lorenz Models. Encyclopedia 2022, 2, 1250–1259. [Google Scholar] [CrossRef]
- Leith, C.E. Numerical Simulation of the Earth’s Atmosphere. Methods in Computational Physics; Academic Press: New York, NY, USA, 1965; Volume 4, pp. 1–28. [Google Scholar]
- Mintz, Y. Very long-term global integration of the primitive equations of atmospheric motion. In WMO-IUGG Symposium on Research and Development Aspects of Long-Range Forecasting; Tech. Note No. 66; World Meteorological Organization: Geneva, Switzerland, 1964; pp. 141–155. [Google Scholar]
- Smagorinsky, J. General circulation experiments with the primitive equations. I. The basic experiment. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Lewis, J. Roots of ensemble forecasting. Mon. Weather. Rev. 2005, 133, 1865–1885. [Google Scholar] [CrossRef]
- Lorenz, E.N. Atmospheric predictability experiments with a large numerical model. Tellus 1982, 34, 505–513. [Google Scholar] [CrossRef]
- Shen, B.-W.; Pielke Sr., R.A.; Zeng, X.; Baik, J.-J.; Faghih-Naini, S.; Cui, J.; Atlas, R. Is Weather Chaotic? Coexistence of Chaos and Order within a Generalized Lorenz Model. Bull. Am. Meteorol. Soc. 2021, 2, E148–E158. [Google Scholar] [CrossRef]
- Shen, B.-W.; Pielke Sr., R.A.; Zeng, X.; Cui, J.; Faghih-Naini, S.; Paxson, W.; Kesarkar, A.; Zeng, X.; Atlas, R. The Dual Nature of Chaos and Order in the Atmosphere. Atmosphere 2022, 13, 1892. [Google Scholar] [CrossRef]
- Lorenz, E.N. A study of the predictability of a 28-variable atmospheric model. Tellu 1965, 17, 321–333. [Google Scholar] [CrossRef]
- Lorenz, E.N. Some aspects of atmospheric predictability. European Centre for Medium Range Weather Forecasts, Seminar 1981. In Proceedings of the Problems and Prospects in Long and Medium Range Weather Forecasting, Reading, UK, 14–18 September 1984; pp. 1–20, (BWS: This study was presented in 1981 and cited as 1982 by Lorenz in his web site. However, it was published in 1984.). [Google Scholar]
- Shen, B.-W.; Pielke, R.A., Sr.; Zeng, X. 50th Anniversary of the Metaphorical Butterfly Effect since Lorenz (1972): Special Issue on Multistability, Multiscale Predictability, and Sensitivity in Numerical Models. Atmosphere 2023, 14, 1279. [Google Scholar] [CrossRef]
- Saiki, Y.; Yorke, J.A. Can the Flap of a Butterfly’s Wings Shift a Tornado into Texas—Without Chaos? Atmosphere 2023, 14, 821. [Google Scholar] [CrossRef]
- Leith, C.E. Atmospheric predictability and two-dimensional turbulence. J. Atmos. Sci. 1971, 28, 145–161. [Google Scholar] [CrossRef]
- Orszag, S.A. Fluid Dynamics; Balian, R., Peuble, J.L., Eds.; Gordon and Breach: London, UK, 1977. [Google Scholar]
- Aurell, E.; Boffetta, G.; Crisanti, A.; Paladin, G.; Vulpiani, A. Predictability in systems with many characteristic times: The case of turbulence. Phys. Rev. E 1996, 53, 2337–2349. [Google Scholar] [CrossRef]
- Li, T.Y.; Yorke, J.A. Period Three Implies Chaos. Am. Math. Mon. 1975, 82, 985–992. [Google Scholar] [CrossRef]
- Lorenz, E.N. The problem of deducing the climate from the governing equations. Tellus 1964, 16, 1–11. [Google Scholar] [CrossRef]
- May, R.M. Simple mathematical models with very complicated dynamics. Nature 1976, 261, 459–467. [Google Scholar] [CrossRef] [PubMed]
- Shen, B.-W. A Review of Lorenz’s Models from 1960 to 2008. Int. J. Bifurc. Chaos 2023, 33, 2330024. [Google Scholar] [CrossRef]
- Stewart, I. Seventeen Equations That Changed the World; Profile Book: London, UK, 2013; 342p. [Google Scholar]
- Lorenz, E.N. Climate is what you expect. [Prepared for publication by NCAR; unknown if actually printed. Possibly related to presentation at NCAR colloquium, Applications of statistics to modeling the Earth’s climate system, November 1994]. 1997. [Google Scholar]
- Magnusson, L.; Källén, E. Factors Influencing Skill Improvements in the ECMWF Forecasting System. Mon. Weather. Rev. 2013, 141, 3142–3153. [Google Scholar] [CrossRef]
- Zagar, N.; Szunyogh, I. Comments on “What Is the Predictability Limit of Midlatitude Weather?”. J. Atmospheric Sci. 2020, 77, 781–785. [Google Scholar] [CrossRef]
- Liu, H.-L.; Sassi, F.; Garcia, R.R. Error Growth in a Whole Atmosphere Climate Model. J. Atmos. Sci. 2009, 66, 173–186. [Google Scholar] [CrossRef]
- Mukougawa, H.; Hirooka, T. Predictability of stratospheric sudden warming: A case study for 1998/99 winter. Mon. Weather Rev. 2004, 132, 1764–1776. [Google Scholar] [CrossRef]
- Mishra, A.K.; Dwivedi, S.; Di Sante, F. Performance of the RegCM-MITgcm Coupled Regional Model in Simulating the Indian Summer Monsoon Rainfall. Pure Appl. Geophys. 2021, 178, 603–617. [Google Scholar] [CrossRef]
- Weyn, J.A.; Durran, D.R.; Caruana, R. Can Machines Learn to Predict Weather? Using Deep Learning to Predict Gridded 500-hPa Geopotential Height from Historical Weather Data. J. Adv. Model. Earth Syst. 2019, 11, 2680–2693. [Google Scholar] [CrossRef]
- Weyn, J.A.; Durran, D.R.; Caruana, R. Improving data-driven global weather prediction using deep convolutional neural networks on a cubed sphere. J. Adv. Model. Earth Syst. 2020, 12, e2020MS002109. [Google Scholar] [CrossRef]
- Weyn, J.; Durran, D.; Caruana, R.; Cresswell-Clay, N. Sub-seasonal forecasting with a large ensemble of deeplearning weather prediction models. J. Adv. Model. Earth Syst. 2021, 13, e2021MS002502. [Google Scholar] [CrossRef]
- Rasp, S.; Thuerey, N. Data-driven medium-range weather prediction with a Resnet pretrained on climate simulations: A new model for WeatherBench. J. Adv. Model. Earth Syst. 2021, 13, e2020MS002405. [Google Scholar] [CrossRef]
- Pathak, J.; Subramanian, S.; Harrington, P.; Raja, S.; Chattopadhyay, A.; Mardani, M.; Kurth, T.; Hall, D.; Li, Z.; Azizzadenesheli, K.; et al. Fourcastnet: A Global Data-Driven High-Resolution Weather Model Using Adaptive Fourier Neural Operators. arXiv 2022, arXiv:2202.11214. [Google Scholar]
- Bi, K.; Xie, L.; Zhang, H.; Chen, X.; Gu, X.; Tian, Q. Accurate medium-range global weather forecasting with 3D neural networks. Nature 2023, 619, 533–538. [Google Scholar] [CrossRef]
- Bonev, B.; Kurth, T.; Hundt, C.; Pathak, J.; Baust, M.; Kashinath, K.; Anandkumar, A. Spherical Fourier Neural Operators: Learning Stable Dynamics on the Sphere. arXiv 2023, arXiv:2306.03838. [Google Scholar]
- Chen, K.; Han, T.; Gong, J.; Bai, L.; Ling, F.; Luo, J.J.; Chen, X.; Ma, L.; Zhang, T.; Su, R.; et al. FengWu: Pushing The Skillful Global Medium-Range Weather Forecast Beyond 10 Days Lead. arXiv 2023, arXiv:2304.02948. [Google Scholar]
- Chen, L.; Zhong, X.; Zhang, F.; Cheng, Y.; Xu, Y.; Qi, Y.; Li, H. FuXi: A cascade machine learning forecasting system for15-day global weather forecast. NPJ Clim. Atmos. Sci. 2023, 6, 190. [Google Scholar] [CrossRef]
- Nguyen, T.; Brandstetter, J.; Kapoor, A.; Gupta, J.K.; Grover, A. Climax: A Foundation Model for Weather and Climate. arXiv 2023, arXiv:2301.10343. [Google Scholar]
- Lam, R.; Sanchez-Gonzalez, A.; Willson, M.; Wirnsberger, P.; Fortunato, M.; Alet, F.; Ravuri, S.; Ewalds, T.; Eaton-Rosen, Z.; Hu, W.; et al. Learning skillful medium-range global weather forecasting. Science 2023, 382, 1416–1421. [Google Scholar] [CrossRef]
- Selz, T.; Craig, G.C. Can artificial intelligence-based weather prediction models simulate the butterfly effect? Geophys. Res. Lett. 2023, 50, e2023GL105747. [Google Scholar] [CrossRef]
- Watt-Meyer, O.; Dresdner, G.; McGibbon, J.; Clark, S.K.; Henn, B.; Duncan, J.; Brenowitz, N.D.; Kashinath, K.; Pritchard, M.S.; Bonev, B.; et al. ACE: A fast, skillful learned global atmospheric model for climate prediction. arXiv 2023, arXiv:2310.02074v1. [Google Scholar] [CrossRef]
- Bach, E.; Krishnamurthy, V.; Mote, S.; Shukla, J.; Sharma, A.S.; Kalnay, E.; Ghil, M. Improved subseasonal prediction of South Asian monsoon rainfall using data-driven forecasts of oscillatory modes. Proc. Natl. Acad. Sci. USA 2024, 121, e2312573121. [Google Scholar] [CrossRef] [PubMed]
- Bouallègue, Z.B.; Clare, M.C.A.; Magnusson, L.; Gascón, E.; Maier-Gerber, M.; Janoušek, M.; Rodwell, M.; Pinault, F.; Dramsch, J.S.; Lang, S.T.K.; et al. The rise of data-driven weather forecasting: A first statistical assessment of machine learning-based weather forecasts in an operational-like context. Bull. Am. Meteorol. Soc. 2024, 105, E864–E883. [Google Scholar] [CrossRef]
- Li, H.; Chen, L.; Zhong, X.; Wu, J.; Chen, D.; Xie, S.P.; Chao, Q.; Lin, C.; Hu, Z.; Lu, B.; et al. A machine learning model that outperforms conventional global subseasonal forecast models. Phys. Sci. 2024. under review. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Horányi, A.; Muñoz Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I.; et al. ERA5 hourly data on single levels from 1979 to present. Copernic. Clim. Change Serv. (C3S) Clim. Data Store (CDS) 2018, 10. [Google Scholar]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 Global Reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Eyring, V.; Bony, S.; Meehl, G.A.; Senior, C.A.; Stevens, B.; Stouffer, R.J.; Taylor, K.E. Overview of the coupled model intercomparison project phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev. 2016, 9, 1937–1958. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. “Attention Is All You Need”. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2017; Volume 30, Available online: https://proceedings.neurips.cc/paper/2017/file/3f5ee243547dee91fbd053c1c4a845aa-Paper.pdf (accessed on 1 May 2024).
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale. arXiv 2020, arXiv:2010.11929. [Google Scholar] [CrossRef]
- Bodnar, C.; Bruinsma, W.P.; Lucic, A.; Stanley, M.; Brandstetter, J.; Garvan, P.; Riechert, M.; Weyn, J.; Dong, H.; Vaughan, A.; et al. Aurora: A Foundation Model of the Atmosphere. arXiv 2024, arXiv:2405.13063. [Google Scholar] [CrossRef]
- Kochkov, D.; Yuval, J.; Langmore, I.; Norgaard, P.; Smith, J.; Mooers, G.; Lottes, J.; Rasp, S.; Düben, P.; Klöwer, M.; et al. Neural General Circulation Models for Weather and Climate. arXiv 2024, arXiv:2311.07222. [Google Scholar] [CrossRef]
- Lang, S.; Alexe, M.; Chantry, M.; Dramsch, J.; Pinault, F.; Raoult, B.; Clare, M.C.; Lessig, C.; Maier-Gerber, M.; Magnusson, L.; et al. AIFS—ECMWF’S Data-Driven Forecasting System. arXiv 2024, arXiv:2406.01465. [Google Scholar] [CrossRef]
- Mardani, M.; Brenowitz, N.; Cohen, Y.; Pathak, J.; Chen, C.Y.; Liu, C.C.; Vahdat, A.; Kashinath, K.; Kautz, J.; Pritchard, M. Residual Diffusion Modeling for Km-scale Atmospheric Downscaling. arXiv 2023, arXiv:2309.15214. [Google Scholar] [CrossRef]
- Price, I.; Sanchez-Gonzalez, A.; Alet, F.; Ewalds, T.; El-Kadi, A.; Stott, J.; Mohamed, S.; Battaglia, P.; Lam, R.; Willson, M. 2024: GenCast: Diffusion-based ensemble forecasting for medium-range weather. arXiv 2023, arXiv:2312.15796. [Google Scholar] [CrossRef]
- Vonich, P.T.; Hakim, G.J. Predictability Limit of the 2021 Pacific Northwest Heatwave from Deep-Learning Sensitivity Analysis. arXiv 2024, arXiv:2406.05019. [Google Scholar] [CrossRef]
- Wu, Y.; Xue, W. Data-Driven Weather Forecasting and Climate Modeling from the Perspective of Development. Atmosphere 2024, 15, 689. [Google Scholar] [CrossRef]
- Shen, B.-W. Aggregated negative feedback in a generalized Lorenz model. Int. J. Bifurc. Chaos 2019, 29, 1950037. [Google Scholar] [CrossRef]
- Shen, B.-W.; Reyes, T.; Faghih-Naini, S. Coexistence of Chaotic and Non-Chaotic Orbits in a New Nine-Dimensional Lorenz Model. In 11th Chaotic Modeling and Simulation International Conference; CHAOS 2018; Skiadas, C., Lubashevsky, I., Eds.; Springer Proceedings in Complexity; Springer: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Zeng, X. Atmospheric Instability and Its Associated Oscillations in the Tropics. Atmosphere 2023, 14, 433. [Google Scholar] [CrossRef]
- Shen, B.-W.; Pielke, R.A., Sr.; Zeng, X. Special Issue Theme Topic: “Revisiting Butterfly Effect, Multiscale Dynamics, and Predictability Using Ai-Enhanced Modeling Framework (AEMF) and Chaos Theory”. 2024. Available online: https://www.mdpi.com/topics/B9N0115Q3E (accessed on 1 May 2024).
- Atlas, R.; Reale, O.; Shen, B.; Lin, S.; Chern, J.; Putman, W.; Lee, T.; Yeh, K.; Bosilovich, M.; Radakovich, J. Hurricane forecasting with the high-resolution NASA finite-volume General Circulation Model. Geophys. Res. Lett. 2005, 32, L03801. [Google Scholar] [CrossRef]
- Shen, B.-W.; Atlas, R.; Oreale, O.; Lin, S.-J.; Chern, J.-D.; Chang, J.; Henze, C.; Li, J.-L. Hurricane Forecasts with a Global Mesoscale-Resolving Model: Preliminary Results with Hurricane Katrina (2005). Geophys. Res. Lett. 2006, 33, L13813. [Google Scholar] [CrossRef]
- Shen, B.-W.; Atlas, R.; Chern, J.-D.; Reale, O.; Lin, S.-J.; Lee, T.; Chang, J. The 0.125 degree Finite Volume General Mesoscale Circulation Model: Preliminary simulations of mesoscale vortices. Geophys. Res. Lett. 2006, 33, L05801. [Google Scholar] [CrossRef]
- Paxson, W.; Shen, B.-W. A KdV-SIR Equation and Its Analytical Solutions for Solitary Epidemic Waves. Int. J. Bifurc. Chaos 2022, 32, 2250199. [Google Scholar] [CrossRef]
- Reynolds, C.A.; Webster, P.J.; Kalnay, E. Random error growth in NMC’s global forecasts. Mon. Weather Rev. 1994, 122, 1281–1305. [Google Scholar] [CrossRef]
- Kalnay, E. Atmospheric Modeling, Data Assimilation and Predictability; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar] [CrossRef]
- Shen, B.-W.; Pielke, R.A., Sr.; Zeng, X.; Baik, J.-J.; Faghih-Naini, S.; Cui, J.; Atlas, R.; Reyes, T.A. Is Weather Chaotic? Coexisting Chaotic and Non-Chaotic Attractors within Lorenz Models. In Proceedings of the 13th Chaos International Conference CHAOS 2020, Florence, Italy, 9–12 June 2020; Skiadas, C.H., Dimotikalis, Y., Eds.; Springer Proceedings in Complexity. Springer: Cham, Switzerland, 2021. [Google Scholar]


| Contents | References | |
|---|---|---|
| Lorenz’s View |
| Shen et al. (2023b, 2022a [13,17]) |
| Predictability Limit Hypothesis |
| Concluding remarks in this study |
| Term | Remarks | |
|---|---|---|
| Doubling time | The doubling time (or e-folding time) represents the time for a specific mode with a growth rate to increase by a factor of 2 (or ). | Charney et al. (1966) [16] |
| Saturation time | Saturation time is defined as the time for the perturbation (e.g., root-mean square error) to become saturated (i.e., reaching a time-independent constant). | Lorenz (1969d) [18] |
| Turnover time ( | Turnover time represents the time for a parcel with velocity to move a distance of , with being the velocity associated with wavenumber . The turnover time is further used to indicate the time that an error at one wavenumber spreads to another wavenumber, a movement within the spectral space. | Vallis (2006) [19]; Lloveras et al. (2022) [20] |
| Lyapunov exponent | A global Lyapunov exponent represents the long-term average of local growth rates that vary with time. Its reciprocal indicates the time scale for error growth. | Shen et al. (2022a) [17] |
| Anomaly correlation coefficients (ACC) | The maximum time duration associated ACC when 0.6 is defined as the predictability limit. | This definition has been used by operational centers for several decades (e.g., Owens and Hewson 2018 [21]; Lin, Shen et al., 2003 [22]). |
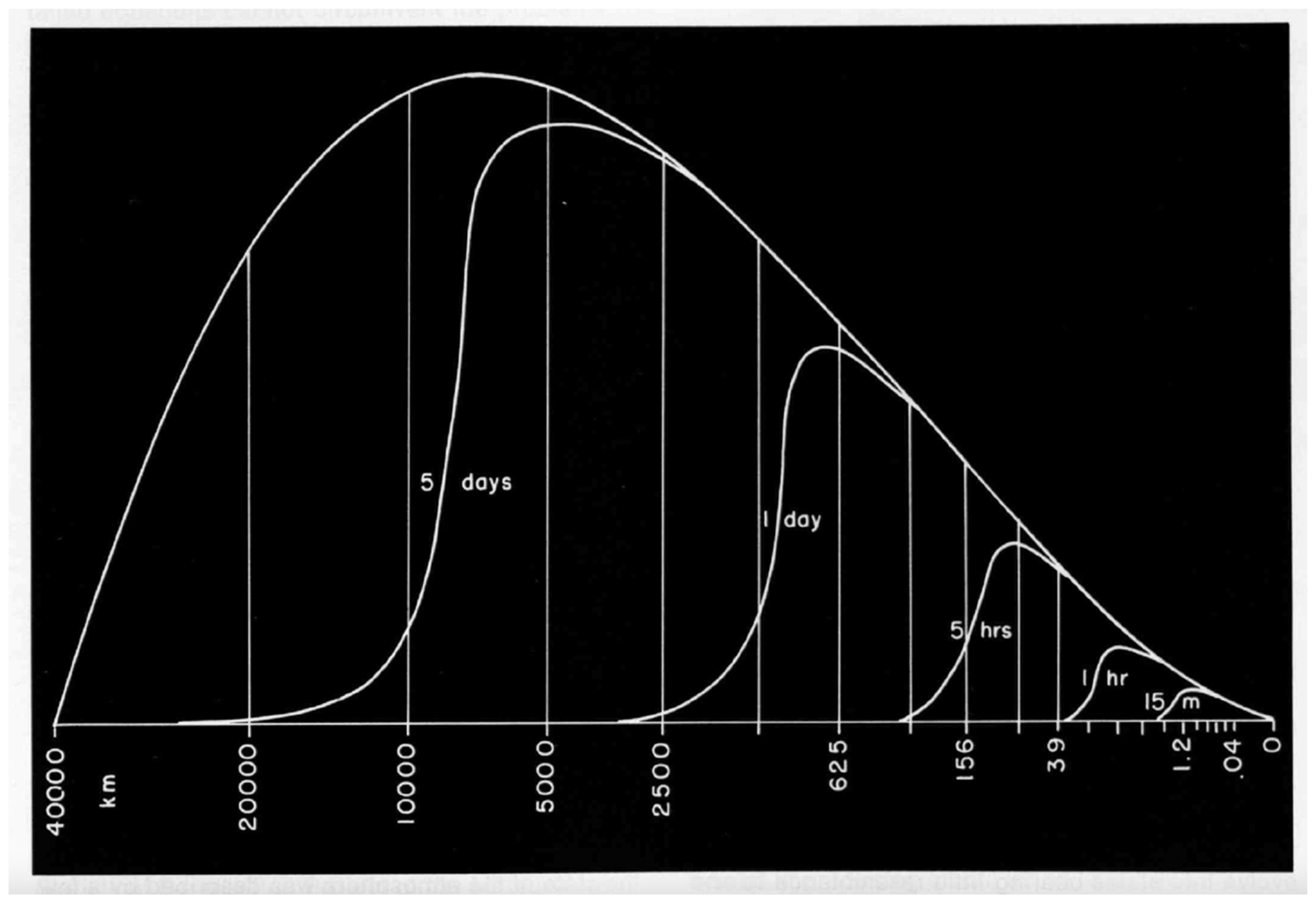
| n | k | λ | tn |
|---|---|---|---|
| 21 | 220 | 38 m | 2.9 min |
| 20 | 219 | 76 | 3.1 |
| 19 | 218 | 153 | 4.0 |
| 18 | 217 | 305 | 5.7 |
| 17 | 216 | 610 | 8.4 |
| 16 | 215 | 1221 | 13.0 |
| 15 | 214 | 2441 | 20.3 |
| 14 | 213 | 4883 | 32.1 |
| 13 | 212 | 9766 | 51.1 |
| 12 | 211 | 19,531 | 1.3 h |
| 11 | 1024 | 39 km | 2.2 |
| 10 | 512 | 78 | 3.6 |
| 9 | 256 | 156 | 5.8 |
| 8 | 128 | 312 | 9.5 |
| 7 | 64 | 625 | 15.7 |
| 6 | 32 | 1250 | 1.1 day |
| 5 | 16 | 2500 | 1.8 |
| 4 | 8 | 5000 | 3.2 |
| 3 | 4 | 10,000 | 5.6 |
| 2 | 2 | 20,000 | 10.1 |
| 1 | 1 | 40,000 | 16.8 |
| Study | Model’s Name | AI Technology | Data | Simulation Length | Evaluation Metric | Remark |
|---|---|---|---|---|---|---|
| Weyn et al. (2020) [72] | Deep Learning Weather Prediction (DLWP) | CNN | ERA5, 1979–2018, 2° | up to 7 days | RMSE, ACC | |
| Weyn et al. (2021) [73] | CNN | ERA5, 1979–2018, 1.4° | up to 6 weeks | RMSE, ACC, Continuous Ranked Probability Score (CRPS) | ||
| Rasp and Thuerey (2021) [74] | WeatherBench ResNet | Residual Neural Network (ResNet) | ERA5, 1979–2018; CMIP6, climate model simulations | up to 5 days | RMSE, ACC | |
| Bi et al. (2023) [76] | Pangu-Weather | (modified) Vision Transformer | ERA5, 1979–2017, 2.5° | up to 7 days | RMSE, ACC | |
| Selz and Craig (2023) [82] | the same | the same | the same | up to 72 h | RMSE, ACC | study butterfly effect |
| Bouallègue et al. (2024) [85] | the same | the same | the same | up to 10 days | the same | in an operational-like context |
| Lam et al. (2023) [81] | GraphCast | Graph Neural Network (GNN) | ERA5, 1979–2018, 2.5° | up to 14 days | RMSE, ACC | developed by Google |
| Pathak et al. (2022); Bonev et al. (2023) [75,77] | FourCast Net | Vision Transformer with Fourier Neural Operators | ERA5, 1979–2018, 2.5° | up to 1 or 2 weeks | ACC | manuscript posted; sponsored by Nvidia |
| Watt-Meyer et al. (2023) [83] | ACE | the same | the same FVGFS | 10 years | RMSE, time-mean RMSE | ACE stands for AI2 Climate Emulator |
| Nguyen et al. (2023) [80] | CimaX | Vision Transformer | CMIP6, 1850-current, various; ERA5, 1979–2018, 2.5° | up to 1 month | RMSE, ACC | sponsored by Microsoft |
| Chen, Zhong, et al. (2023) [79] | FuXi | modified Vision Transformer | ERA5, 1979–2018, 2.5° | up to 15 days | RMSE, ACC, CRPS | |
| Li et al. (2024) [86] | FuXi-S2S | Enhanced FuXi base model with other modules | ERA5, 1950–2021, 1.5° | up to 42 days | TCC, RPSS, BSS, COR | manuscript posted 14 February 2024 |
| Chen, Han, et al. (2023) [78] | FengWu | a cross-modal fusion transformer | ERA5, 1979–2018, 2.5° | up to 14 days | RMSE, ACC | |
| Bach et al. (2024) [84] | hybrid dynamical and data-driven methods | EOF, Neural network architecture, Ensemble Oscillation Correction (EnOC) | ERA5, 1979–2018, 2.5°; IMD rainfall, 1901–2016 | up to 46 days | RMSE, ACC, Bivariate Correlation Coefficient |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, B.-W.; Pielke, R.A., Sr.; Zeng, X.; Zeng, X. Exploring the Origin of the Two-Week Predictability Limit: A Revisit of Lorenz’s Predictability Studies in the 1960s. Atmosphere 2024, 15, 837. https://doi.org/10.3390/atmos15070837
Shen B-W, Pielke RA Sr., Zeng X, Zeng X. Exploring the Origin of the Two-Week Predictability Limit: A Revisit of Lorenz’s Predictability Studies in the 1960s. Atmosphere. 2024; 15(7):837. https://doi.org/10.3390/atmos15070837
Chicago/Turabian StyleShen, Bo-Wen, Roger A. Pielke, Sr., Xubin Zeng, and Xiping Zeng. 2024. "Exploring the Origin of the Two-Week Predictability Limit: A Revisit of Lorenz’s Predictability Studies in the 1960s" Atmosphere 15, no. 7: 837. https://doi.org/10.3390/atmos15070837
APA StyleShen, B.-W., Pielke, R. A., Sr., Zeng, X., & Zeng, X. (2024). Exploring the Origin of the Two-Week Predictability Limit: A Revisit of Lorenz’s Predictability Studies in the 1960s. Atmosphere, 15(7), 837. https://doi.org/10.3390/atmos15070837








