Abstract
The Qinghai-Tibetan Plateau (QTP) is the largest permafrost-covered area in the world, and it is critical to understand accurately and dynamically the cyclical changes in atmospheric aerosols in the region. However, due to the scarcity of researchers in this field and the complexity of analyzing the spatial and temporal dynamics of aerosols, there is a gap in research in this area, which we hope to fill. In this study, we constructed a new fusion algorithm based on the V5.2 algorithm and the second-generation deep blue algorithm through the introduced weight factor of light and dark image elements. We used the algorithm to analyze the spatial and temporal changes in aerosols from 2009–2019. Seasonal changes and the spatial distribution of aerosol optical depth (AOD) were analyzed in comparison with the trend of weight factor, which proved the stability of the fusion algorithm. Spatially, the AOD values in the northeastern bare lands and southeastern woodland decreased most significantly, and combined with the seasonal pattern of change, the AOD values in this region were higher in the spring and fall. In these 11 years, the AOD values in the spring and fall decreased the most, and the aerosol in which the AOD decreases occurred should be the cooling-type sulfate aerosol. In order to verify the accuracy of the algorithm, we compared the AOD values obtained by the algorithm at different time intervals with the measured AOD values of several AERONET stations, in which the MAE, RMSE, and R between the AOD values obtained by the algorithm and the measured averages of the 12 nearest AERONET stations in the QTP area were 0.309, 0.094, and 0.910, respectively. In addition, this study also compares the AOD results obtained from the fusion algorithm when dynamically weighted and mean-weighted, and the results show that the error value is smaller in the dynamic weighting approach in this study.
1. Introduction
The Qinghai-Tibetan Plateau (QTP) is not only the largest mid-latitude plateau in the world, but also the largest permafrost-covered area in the world [1,2]. Drastic changes in global climate and eco-thermal systems have led to ecosystem imbalances such as increased temperatures, precipitation, lake swamps, reduced forest cover, and permafrost degradation in the QTP region [3,4,5,6,7]. All these imbalances are inextricably linked to changes in the atmospheric environment [8], and it is therefore essential to accurately grasp the cyclical dynamics of the atmospheric environment, which is crucial for the global ecological balance and the protection of the climate environment. Aerosols, as common energy carriers in the atmosphere, can be used as a quantitative and intuitive characterization of atmospheric environmental changes [9,10].
Aerosols are composed of liquid or solid particles of 10−3–102 μm in size and usually come from the natural environment, such as forest fires, dust storms, volcanic eruptions, etc., but they can also be produced by humans, such as automobile exhaust, coal combustion, and factory emissions [11,12,13]. Depending on the physical form and chemical composition, aerosols can be in the form of haze, dust, sulfate-based aerosols, organic aerosols, nitrate aerosols, black carbon aerosols, bioaerosols, trace element aerosols, and many other forms. Among them, those that have a greater impact on the temperature are mainly black carbon aerosols of the absorbing warming type and sulfate aerosols of the scattering cooling type [14,15]. Although the overall proportion of aerosols in the atmosphere is not high, they have an important influence on the climate system and physical and chemical cycles because of their special properties [16]. Firstly, aerosols scatter and reflect sunlight and have radiative and optical properties that can alter the heat balance between the atmosphere and the Earth, thereby affecting temperature and climate change [17,18,19]. Secondly, some types of aerosols are the condensation nuclei of clouds, causing water vapor to condense into cloud droplets [20]. Due to the presence of condensation-active aerosols, the size and number of clouds will increase accordingly, which in turn affects the nature and formation of clouds themselves. These changes will have an impact on the amount of cloud radiation, precipitation, and climate balance [21,22,23]. In addition, aerosols have distinct spatial and temporal properties [20], and these can have a direct impact on the cyclical variability of the climate. Based on these important properties of aerosols, there is a need for precise quantification of aerosols.
Aerosol optical depth (AOD) is a measure of the reduction of light by aerosol particles, and is usually defined as the integral of the extinction coefficient of aerosols in an atmospheric column [24]. AOD is not only an important reference between regional air quality and atmospheric physical action, but also an important parameter for aerosol quantification of atmospheric loading and radiation. Currently, AOD monitoring can be divided into two categories: ground-based remote sensing and satellite remote sensing. Multi-band solar photometer remote sensing is one of the most widely used methods in ground-based remote sensing research, which is used in the aerosol robotic network (AERONET) aerosol station, where multi-band solar photometers are used to measure the brightness of visible and near-infrared radiation to obtain the optical properties of aerosols [25]. The AOD obtained from AERONET stations has a high accuracy and can usually be verified against results obtained by other methods. However, due to the limitation of the spatial distribution of ground observation stations, the data observed on the ground are insufficient and suffer from the problem of uneven spatial distribution [26]. Satellite remote sensing can effectively make up for this shortcoming; especially in areas where ground observation stations cannot be deployed under poor geographical conditions, the advantages of satellite remote sensing are more obvious. With the continuous development of satellite remote sensing technology, a variety of sensors have been used to study aerosol properties. The main principle of satellite remote sensing inversion of AOD is based on the radiation information received by the sensor, which is a combination of reflections from the surface and scattering from the Earth’s atmosphere [27]. In general, aerosols affect the radiance information received by satellites in two ways: when aerosols reflect light directly, the radiance increases; and when aerosols radiate in the direction of the lower atmosphere, the radiance decreases. Assuming that the Earth is a Lambertian body, and ignoring the effects of gas absorption, the reflectance at the top of the atmosphere (the apparent reflectance) is approximately equal to the ratio of reflected radiation to incident radiation above the atmosphere. The AOD can be calculated by modeling the function of atmospheric aerosol and measuring the apparent reflectance of the satellite sensor [27]. Therefore, the use of satellite remote sensing to determine AOD must be concerned with both the apparent reflectance and the aerosol’s own properties. Due to the variations in geography and aerosol composition across the globe, several methods have been developed over the decades to invert the AOD, each with its own characteristics and differing applicability.
In 1977, Kondratyev et al. simulated AOD under clear-sky conditions overland by selecting light and dark pixels in close spatial proximity and assuming that the optical properties of the atmosphere are constant. This method is known as the high-contrast surface method [28]. The light and dark pixels selected by this method are not limited to high albedo deserts or low albedo densely vegetated areas, but can be inverted over bright surfaces, which is mostly applied to the inversion of AOD in urban areas, and has high accuracy for areas with large differences between light and dark pixels [29]. However, it is not sufficiently usable because it is difficult to determine the surface reflectance of bright and dark pixels [30].
In 1988, Tanre et al., after considering the problems of the high contrast surface method, utilized atmospheric transmittance as a function of the structure of different images of the same area to determine the aerosol content, which is known as the structure function method [31]. This method is simple to express, takes advantage of the short-term constancy of surface reflectance, and has a high inversion accuracy in urban and desert areas [32]. However, this method makes it difficult to obtain the surface reflectance of the clean-day image [33] and is not well suited in densely vegetated areas because it ignores the scattering effects of multiple ground-air interactions, which are highly constrained by the pixel spacing [34,35].
In order to better invert AOD in densely vegetated areas, Kaufman et al., in 1997, proposed the dark target (DT) method, also known as the traditional dark target (DT) method [36]. This method is mainly based on the consideration that the surface reflectance in the densely vegetated area, i.e., the dark pixel area, is low, while the apparent reflectance received by the sensor is mainly from the atmosphere, and it is easy to differentiate the reflectance contributions from the atmosphere and the surface [37]. Additionally, there is a linear relationship between the short-wave infrared band (2.1 μm), the red band (0.66 μm), and the blue band (0.47 μm) of the dark image element, in which the apparent emissivity of the short-wave infrared band, which is minimally affected by the atmosphere, is approximately equal to the surface reflectivity, which makes it possible to differentiate between the surface reflectivities of the red and the blue bands, thus realizing the inversion of the AOD [36]. However, this method requires a priori knowledge and known high-precision surface reflectance and is not applicable to image elements with high reflectance (>0.15) [38]. Later, in order to improve the accuracy of the traditional DT method, some improvements were made by Kaufman et al. and Martins et al. during 1997–2002 [39,40,41]. In the following years, the DT method has been applied in many studies [42,43,44,45,46]. The results of some of these studies show that the DT method still has some shortcomings in the range of surface reflectance and empirical relationships, and the limitations and errors of surface reflectance still exist, which makes it more limited in arid, permafrost, glacier, and desert regions [45,46]. In order to further improve the applicability and accuracy of the DT method, Levy et al. proposed the well-known V5.2 algorithm, also known as the extended DT method, in 2007 [47]. This algorithm improves the reflectance range at the 2.12 μm band from 0–0.15 to 0–0.25 by utilizing the reflectance ratio relationship between the mid-infrared channel and the visible light, which can be used for the inversion of the AOD in semi-arid and arid regions with high reflectance. The improved vegetation index enhances the accuracy of the AOD inversion by improving the precision of the surface reflectance in the red and blue light bands. In 2020, Chen et al. successfully applied the V5.2 algorithm in the study of MODIS [48]. The V5.2 method is widely applied in MODIS aerosol products, of which the inversion accuracy is higher and the applicability is better. Among the MODIS aerosol products, the MO/YD04 L2 daily product and the MO/YD04 L3 every-8-days product are the ones with higher inversion accuracy and better applicability. The MO/YD04 series products are well suited to be used in the study of large study areas and long-period dynamical monitoring because of their advantages of wide range and validity. Although the V5.2 algorithm improves the reflectivity range and has certain advantages in wide-area research and periodic operations, the algorithm principle is consistent with the DT method, so it is more suitable for dark image areas covered by dense vegetation and there is still a certain degree of inversion error when it is applied in deserts, cities, glaciers, and other areas with high surface reflectivity.
In order to improve the accuracy of AOD inversion in regions of high albedo, scientists have proposed a methodology for building a library of surface reflectance to invert AOD. This method first assumes that the surface reflectance is constant over successive cycles or on the same date in different years. After that, cloud interference is eliminated by periodic near-minimum probing, and finally, pure pixels are obtained by atmospheric correction and then the surface reflectance of each pixel is determined one by one, and a surface reflectance library is constructed in this way. The most commonly used of the various methods based on surface reflectance libraries is the deep blue (DB) algorithm proposed by Hsu et al. in 2006 [49]. This algorithm is a method for inverting the AOD by building a surface reflectance library for the deep blue band (0.41 μm) under the assumption of a constant surface reflectance over the same period, utilizing the more pronounced aerosol feedback in the deep blue band [49,50]. This method was initially applied to AOD inversion in semi-arid and arid regions by Hsu et al. [49], where a triple-band inversion of (red) 0.67 μm, (blue) 0.49 μm, and (dark blue) 0.41 μm is used when the value of AOD is relatively large, whereas a double-band inversion of (blue) 0.49 μm, and (dark blue) 0.41 μm is used when the AOD is small band inversion. In this method, the accuracy of the inversion is lower at the urban-vegetation interface because only a static dark blue band surface reflectance library is used in the algorithm. Based on the problems of the DB algorithm, Hsu et al. made refinements to the DB algorithm’s surface reflectance library and the method for determining cloud detection. An improved DB algorithm (second-generation DB algorithm) was proposed in 2013 [51], which improved the applicability of aerosol inversion in areas covered by snow, ice, and clouds in addition to deserts and cities. The second-generation DB algorithm has better inversion accuracy in high surface albedo regions, and similar to the V5.2 algorithm, it also has good advantages for wide-area studies and periodic operations and has been better applied in MODIS aerosol products. Compared with the V5.2 algorithm, the second-generation DB algorithm is more suitable for aerosol inversion in high-brightness areas with high surface reflectivity.
In addition to the V5.2 algorithm and the second-generation DB algorithm, which have strong operational advantages, some common algorithms based on physics and mathematical principles have emerged in recent years, such as the MISR-based multi-angle algorithm (2004, 2011, 2021) [52,53,54], polarization algorithm (2000, 2001) [55,56], cloud top AOD method (2009) [57], bright image element method (2006) [58], constructing look-up table method (2019) [59], etc. Among them, the MISR-based multi-angle algorithm possesses the flexibility of image element angle selection, but it requires a specific sequence of image synthesis to ensure its inversion accuracy and is slow. The polarization algorithm, on the other hand, is based on the radiative properties of aerosols, needs to solve for a larger number of parameter factors, and requires a specified sensor, which is less efficient. The cloud top AOD algorithm is mainly applied to the aerosol inversion algorithm in the region with more clouds, and the algorithm has a strong directivity. The bright image element method mainly combines other data platforms with the advantages of MODIS multi-temporal observation, taking the clearest image in the observation time as the representative image, which requires specific types of remote sensing images. The method of constructing a look-up table is to build a table after checking the AOD under different combinations with meteorological factors, inverting the AOD according to the spectra of the alteration plate. The efficiency is relatively low [59]. It can be seen that these methods do not meet the requirements of wide-area periodic operations.
The study area of this paper is selected in the QTP region. The region is characterized by an obvious geographic breadth, spanning several provinces in China, with a land area of about 2.57 million km2, accounting for 26.8% of the total land area of China [60,61]. In addition, the region is characterized by a diversity of natural environments, ranging from plateau vegetation and mountain meadows with low surface albedo to deserts and snow and ice with high surface albedo [62,63,64,65]. Therefore, the V5.2 algorithm and the second-generation DB algorithm can meet the aerosol regional characteristics and operational dynamic monitoring in the QTP region. However, because these two algorithms are most suitable for low surface reflectivity and high surface reflectivity regions, respectively, it is necessary to integrate the two algorithms reasonably to be able to invert the performance of more accurate AOD.
In summary, this study introduces the dynamic weight factor by combining the year-to-year changes of light and dark features in QTP during 2009–2019, fuses the V5.2 algorithm and the second-generation DB algorithm with the introduced dynamic weight factor, and inverts the temporal and spatial changes of AOD during 2009–2019 through the fused algorithm. We hope to fill the gap in this research area in the QTP region. In order to ensure the stability and reliability of the fusion algorithm, we not only analyze the fusion algorithm in depth in terms of seasonal variations, but also validate and discuss the inversion results of the AOD by using the measured data from several AERONET stations. In order to ensure the reasonableness of the algorithm, we also compared the AOD results obtained by the dynamic weighting approach with the mean weighting approach. In this case, the dynamic weighting approach refers to the use of the fusion algorithm to invert the AOD when the weight factor is set as a year-by-year variable, and the mean weighting approach refers to the use of the fusion algorithm to invert the AOD when the weight factor is set as a mean constant.
2. Materials and Methods
2.1. Study Area
The QTP is located in the central part of Asia and the southwestern part of China, with an average altitude of about 4000 m amsl and an average altitude difference of 1000–2000 m. It ranges from approximately 73°19°–104°47′ E to 26°00′–39°47′ N and encompasses China’s longest river (Yangtze River), its largest freshwater lake (Qinghai Lake), and its tallest mountain (Mount Everest). The region is relatively thin on oxygen and is vulnerable to the southwest monsoon from the Indian Ocean region. The region is rich in geomorphic attributes, combining multiple features: tropical and boreal, glacier and river, grassland and desert [3]. In recent years, the dynamic monitoring of anthropogenic aerosols in urbanized areas has been a research hotspot, but due to the limitations of objective factors such as workforce, material, and financial resources, the research on the dynamic monitoring of aerosols in QTP areas, which are dominated by natural factors, has been seldom involved.
Figure 1 shows the study area of this experiment, which was mapped based on the latest 2021 version of the administrative area extent of the QTP and combined with the MODIS global land cover MCD12Q1 data from the National Aeronautics and Space Administration (NASA) website (https://ladsweb.modaps.eosdis.nasa.gov/ (accessed on 1 May 2023)), which is slightly changed from the 2015 version of the administrative area extent of the QTP [60]. The extent of the current study area is from 67°42′ to 104°47′ E longitude and from 26°00′ to 39°47′ N latitude (about 4000 km wide from east to west and 300–1500 km long from north to south). The study area was divided into nine land cover types: agricultural land, woodland, grasslands, shrubbery, lake wetland, urban land, desert, bare ground, and glacier. In addition, the red triangles in Figure 1 indicate the 12 AERONET stations that are closest to the QTP area and the 6 AERONET stations that are geomorphologically similar to the QTP area but at some distance. The observation times of these stations for the period 2009–2019 and the geographic information of each station are shown in Table 1.
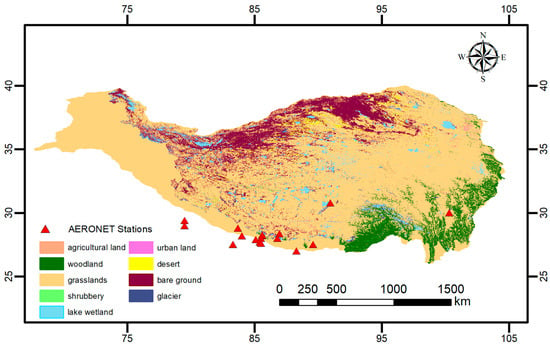
Figure 1.
Geographic location and nine land cover classifications of the QTP in this experimental study area. In addition, the red triangles indicate AERONET stations in and near the QTP area.

Table 1.
Observation times for the 18 AERONET stations during the period 2009–2019 and geographic information for each station. Stations closest to the QTP area are numbered 1–12, and those with similar geomorphic settings to the QTP area but at some distance are numbered 13–18.
2.2. Data Sources
Three main types of data were used in this study, with the first being the experimental data for the aerosol fusion algorithm. Due to the large spatial area and long time period of dynamic monitoring in the QTP region, we chose MODIS aerosol L2 products MOD04 (Terra) and MOY04 (Aqua) with medium resolution from 2009–2019. The products have a spatial resolution of 10 km and are downloaded from the official National Aeronautics and Space Administration (NASA) website (https://ladsweb.modaps.eosdis.nasa.gov/ (accessed on 1 May 2023)).
The second type of data used in the study is the MCD12Q1v006 data (MCD12Q1v006 is version 6 of the MCD12Q1 data, derived from supervised classification of MODIS and Aqua and Terra reflectance data. Supervised categorization is followed by additional post-processing, combining auxiliary information and a priori knowledge to further refine specific categories [66,67].) for the period of 2009–2020 for land cover classification, analyzing light and dark pixels and setting thresholds for the fusion algorithm, which has a spatial resolution of 500 m. (Downloaded from the official NASA website, https://ladsweb.modaps.eosdis.nasa.gov/ (accessed on 1 May 2023)).
The third type of data used in the study is the measured data used to validate the aerosol inversion results, i.e., the AODs of 2009–2019 Level 2.0 products from 18 AERONET stations near the QTP area shown in Table 1 (the L2.0 products were quality-controlled and cloud-screened compared to the L1.0 and L1.5 products), with the data wavelengths centered at 1020, 870, 675, 500, 440, 380, and 340 nm. In particular, for individual stations lacking Level 2.0 products, we supplemented the missing parts with Level 1.5 products. (Downloaded from the global automated aerosol remote sensing observing network AERONET jointly established by LOA-PHOTONS (CNRS) and NASA, https://aeronet.gsfc.nasa.gov/ (accessed on 1 May 2023)).
2.3. Principle Method of Satellite Inversion of AOD
It is assumed that the longitudinal absorption of the atmosphere is homogeneous and that the Earth’s surface is a homogeneous Lambertian body. Since the electromagnetic radiation information received by the satellite-borne sensors is a combination of the scattered radiation from the aerosol particles in the atmosphere and the reflected radiation from the Earth’s surface, the electromagnetic radiation, i.e., the apparent reflectivity, received by the sensors can be expressed as the following equation [27]:
where the apparent reflectance received by the sensor is ρφ(α,β,γ), the azimuthal angle of scattered radiation from the sun’s rays is γ, the angle of incidence (observation zenith angle) is α, the angle of observation (solar zenith angle) is β, the downward radiative flux with normalized surface reflectance is μφ(α), the total transmittance upward is θφ(β), the atmospheric backscattering ratio is τφ, the radiative reflectance of the path is εφ(α,β,γ), and the surface reflectance is δφ(α,β,γ).
If only single scattering is considered, εφ(α,β,γ) can be expressed in terms of the aerosol single scattering phase function σφ(α,β,γ), the relationship between the AOD, Aod, and the single scattering albedo, ϵ, [27]:
where the path radiation for molecular scattering is εθ(α,β,γ), the cosine of the angle of incidence α is ω0, and the cosine of the angle of observation β is ω. Equation (3) can be obtained by substituting Equation (2) into Equation (1) [27]:
According to Equation (3), the satellite-observed apparent reflectance is a function of both surface reflectance and AOD, and once one of these variables has been determined, it is possible to invert the other unknown quantity. Therefore, there are different algorithms for inverting AOD for feature types with different surface reflectance. The most commonly used algorithm for feature types with low surface reflectance is the V5.2 algorithm [47], while the most commonly used algorithm for feature types with high surface reflectance is the second-generation DB algorithm [51].
2.4. Principles of the V5.2 Algorithm
The V5.2 algorithm is more effective for AOD inversion in dark pixel regions with low surface reflectance such as mountain shadows, dense vegetation, swamps, and water bodies on land. The algorithm adds scattering angle and vegetation index and transforms the original reflectance ratio of visible and mid-infrared channels (VIS/SWIR) from a constant to a variable function [47], which can remove the effects of surface non-homogeneity and elevation difference. In this method, the surface reflectance relationship between the red (0.66 μm) and blue (0.47 μm) light bands and the surface reflectance band in the shortwave infrared (2.12 μm) is shown in Equations (4) and (5), and the scattering angle is calculated as shown in Equation (6):
where δ0.66 is the surface reflectance in the red band, δ0.47 is the surface reflectance in the blue band, and δ2.12 is the surface reflectance in the short-wave infrared band. β0 is the relative azimuth angle between the satellite and the sun, α0 is the zenith angle of the sun, and α1 is the zenith observation angle.
In addition, the radiation received in MODIS bands 7 and 5 are εN7 and εN5, respectively. Yint is the intercept (, ), Slope is the offset (, ), and NDVIswir is the vegetation index ().
When NDVIswir < 0.2, the vegetation coverage is low [68], where NDVIswir < 0.25, . When 0.25 ≤ NDVIswir ≤ 0.75, . When NDVIswir > 0.6, it indicates that the vegetation coverage rate is higher [68]. When NDVIswir > 0.75, . By substituting Equation (6) into Equations (4) and (5), Equations (7) and (8) can be obtained:
After substituting the relevant values of Yint, Slope, and NDVIswir, Equations (9)–(11) can be obtained:
When NDVIswir < 0.25:
When 0.25 ≤ NDVIswir ≤ 0.75:
When NDVIswir > 0.75:
2.5. Principle of the Second-Generation DB Algorithm
The second-generation DB algorithm [51], which is different from the V5.2 algorithm, is more effective in inverting AOD in high albedo regions such as cities, arid, deserts, icebergs, and snow bodies. The method utilizes a surface reflectance library built from MODIS or Sea WIFS images combined with a triple band of (red) 0.67 μm, (blue) 0.49 μm, and (deep blue) 0.41 μm, or a dual band of (blue) 0.49 μm and (deep blue) 0.41 μm, to invert the AOD. Assuming that the surface reflectivity of the same period is constant, according to the characteristics of the deep blue band, the reflectivity at the surface is poor while the reflectivity in the atmosphere is strong. The core method of the second-generation DB algorithm for inversion of AOD is shown in Equation (12):
where the relative azimuth angle is γφ, the solar zenith angle is αs, the zenith observation angle is βv, the atmospheric hemispheric albedo is ϵs, the upward and downward atmospheric transmissivities are μφ(α) and θφ(β), respectively, the scattering value for a clear day is δr(αs,βv,γφ), the aerosol albedo is δα(αs,βv,γφ), and the apparent reflectivity is δt(αs,βv,γφ).
2.6. The Technical Process and Validation Method of the Fusion Algorithm in this Study
Through the principle of V5.2 algorithm and the second-generation DB algorithm, it can be seen that the principle and common point of both algorithms focus on how to accurately determine the surface reflectance, while the difference lies in the applicability of the difference between high and low reflectance. Considering the wide geographical area and rich feature types of the QTP region, if we distinguish the light and dark pixels one by one and then apply the V5.2 algorithm and the second-generation DB algorithm in several small areas, it is not only a huge workload, but is also prone to cause a large error in the long-period dynamic monitoring. Therefore, the best way is to classify the light and dark pixels according to different feature types, setting the total weight of the light and dark pixels to 1. When the weight of the dark pixels is KR, the weight of the light pixels is 1 − KR. Then, it can be regarded as the trust ratio of AOD obtained by the inversion of the V5.2 algorithm is KR, while the trust ratio of AOD obtained by the inversion of the second-generation DB algorithm is 1 − KR and the trust ratio of the two algorithms is 1. Meanwhile, because the present study is a dynamic monitoring, the value of AOD obtained by the two algorithms is a variable, and the value of the weight KR will also be a variable based on the actual change of the feature type every year. At this point, if the product of several variables is then fused in a curve-varying manner, it will easily lead to the instability of the fusion algorithm. Based on the consideration of the above problems, the fusion algorithm proposed in this study first classifies light and dark pixels for feature types with different reflectance, and then linearly fuses the V5.2 algorithm and the second-generation DB algorithm by introducing a weight factor of light and dark pixels between 2009–2019.
Combined with the overall idea of the fusion algorithm, the technical flow chart of this experiment is shown in Figure 2, and the four colored modules, from top to bottom, represent the four different steps of the experimental technical flow.
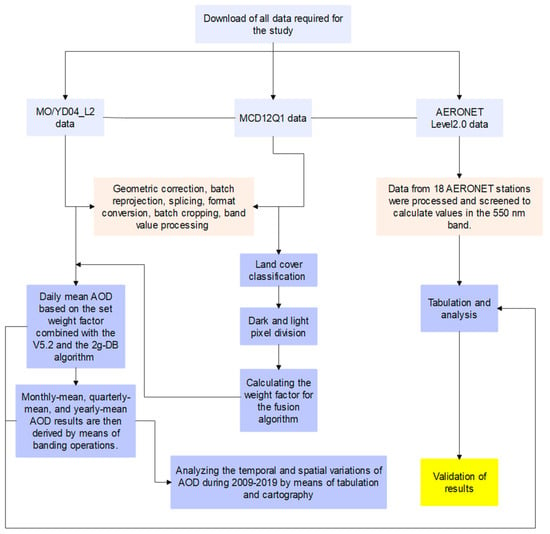
Figure 2.
Technical flowchart of this experiment.
1. The data required for the study was downloaded, including MO/YD04_L2 data for aerosol experiments, MCD12Q1 data for the setting of darkness and brightness weight factors for surface classification, and AERONET Level 2.0 data for aerosol validation.
2. The data was pre-processed, including geometric correction, batch reprojection, splicing, format conversion, batch cropping, band value processing, etc. for MO/YD04_L2 and MCD12Q1 data. The pre-processing of the AERONET Level 2.0 data is mainly to process and filter the measured AOD data from the 18 AERONET stations shown in Table 1 and to calculate the values in the 550 nm band.
3. Each of the data was post-processed, with post-processing of the MCD12Q1 data mainly based on the 17 categories of features defined by the International Geosphere-Biosphere Programme (IGBP), including 11 categories of natural vegetation, 3 categories of land use and land mosaics, and 3 categories of non-vegetated land, and 9 land-cover reclassifications were carried out by combining with the actual feature environment of the QTP region. The distribution of features is shown in Figure 1. The reclassification rules are shown in Table 2, which compares the nine reclassified features in this study with the 17 reclassified features in the IGBP.

Table 2.
Comparison of the 9 reclassified features in this study with the 17 classified features in the IGBP.
The reclassified features are classified as agricultural land, woodland, grasslands, shrubbery, lake wetland, urban land, desert, bare ground, and glacier. Then, the five feature types of agricultural land, woodland, grasslands, shrubbery, and lake wetland are classified as dark image element coverage areas based on the difference in surface reflectance, and the four feature types of urban land, desert, bare ground, and glacier are classified as bright image element coverage area, and finally, the year-by-year percentage is calculated based on the trend of bright and dark image elements from 2009–2019, and the normalized value is set as the weight factor of the fusion algorithm. For the post-processing of MO/YD04_L2 data, the daily mean AOD is fused according to the set weight factor combined with the inversion principle of the V5.2 algorithm and the second-generation DB algorithm, and the specific fusion algorithm is shown in Equation (13) as:
where FA is the AOD of the fusion algorithm, DTA and DBA are the AOD of the MOD04 product V5.2 algorithm and the second-generation DB algorithm, respectively, and KR is the weight factor of the dark image elements in the fusion algorithm from year to year (since we obtained KR from the data of MCD12Q1 for each year, we assume here that the weight factor is constant for each day, month, and quarter of the same year). The monthly, quarterly, and yearly average AOD are then fused by means of band math operations. Finally, the temporal and spatial changes of AOD during 2009–2019 are analyzed by tabulation and graphing.
The post-processing of AERONET Level 2.0 data is mainly for tabulation analysis and supplementation of missing data.
4. Validation analysis of the AOD results calculated by the fusion algorithm when the weight factors are taken as year-by-year variables was performed using the processed AERONET Level2.0 data. Since AERONET data, as shown in Table 1, are missing a large amount of data from many stations almost every year during 2009–2019, we analyzed the data for validation according to the total number of months of observation for each station according to the following three scenarios:
(a). When the total number of observed months is greater than 20, the complete and consecutive 20-month average data are evenly selected as the sample of the validation dataset and named as 1–20 data point sets for storage;
(b). When the total number of observed months is between 15 and 20 months, the missing data are supplemented by the mean values of the monthly data of the same cycle from the two nearest stations, and the supplemented 20 monthly average data are taken as the sample of the validation dataset and named as 1–20 data point sets for storage;
(c). When the total number of observed months is less than 15 months, the 20 complete and consecutive daily data are uniformly selected as samples of the validation dataset and named as 1–20 data point sets for storage.
After that, the AOD results calculated by the fusion algorithm when the weight factors changed year by year were used as the experimental dataset samples, and the experimental dataset samples were stored with monthly average data or daily data of the same period as the validation dataset samples, and the data of the validation samples and experimental samples were normalized. The validation method mainly includes MAE (mean absolute error), RMSE (root mean square error), and R (correlation coefficient).
In addition, in order to ensure the rationality of the fusion algorithm in this experiment, we also added an experimental group of six stations with more complete observation months inside and outside the QTP (station numbers: 1, 2, 6, 14, 15, 16), i.e., with the sample of the AERONET validation dataset remaining unchanged, we used the AOD results obtained by the fusion algorithm when the weight factor takes the mean constant during the period of 2009–2019 as the sample of the experimental dataset, and the same validation method is used to analyze the MAE, RMSE, and R between the two. Finally, the results of dynamic weighted analysis in the fusion algorithm and the average weighted analysis are compared. The reason for the newly added experimental group here to select stations with a more complete number of months of observation is that the difference between the weight factor when taken as an annual variable and an annual constant can only be better captured if the observation period is two years or more.
3. Results
3.1. Results of Feature Reclassification and Fusion Algorithm Thresholding during 2009–2020
Figure 3 shows the histogram of the dynamic trend of the nine features reclassified by combining the actual feature status of the IGBP and QTP regions for the period 2009–2020, during which four features, namely agricultural land, grasslands, urban land, and bare ground, are in a decreasing trend, while five features, namely woodland, shrubbery, lake wetland, desert, and glacier, are in an increasing trend. The largest proportion of dark image elements is in grassland areas, and the largest proportion of light image elements is in bare ground areas.
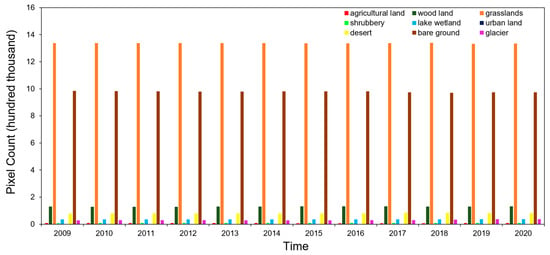
Figure 3.
Trends in the dynamics of the nine reclassified features between 2009–2020, with different colored bars representing different feature types.
Figure 4 is a scatter plot of the year-to-year changes in the dark image element weight factor of the fusion algorithm during 2009–2020, from which it can be seen that during this 12-year period, except for 2019 and 2020, the dark image element weight factor showed a slight upward trend as a whole, with a slight increase in the dark image elements, and the dark image feature types that increased were woodland, shrubbery, and lake wetland, which indicates that the medium and high level vegetation is influenced by the increase of precipitation and temperature to a certain extent, and the increase of standing water is conducive to the development of lakes and wetlands. The curve variation of the specific weight factor is:
where KR is the dark image element weight factor of the fusion algorithm and XT is the year value during 2009–2020.
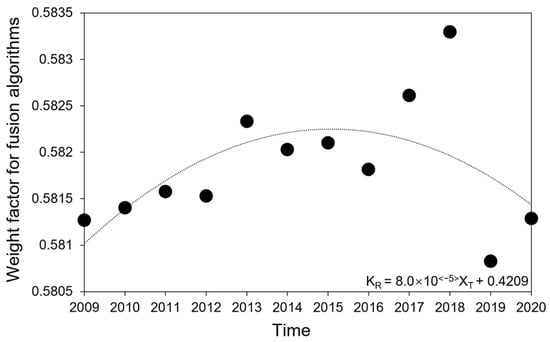
Figure 4.
Year-to-year changes in the fusion algorithm’s dark image element weight factor between 2009–2020, with quadratic trend lines added.
3.2. Multiscale Temporal and Spatial Variation of AOD during 2009–2019
Figure 5 shows the variation of daily mean AOD obtained through the fusion algorithm processing from 2009 to 2019, and the year-by-year daily mean values show an overall decreasing trend. Although the peak of the aerosol daily mean content exceeds 1 on individual dates in more years, the overall daily mean aerosol values from 2009–2019 are concentrated in the range interval of 0.2–0.5, which indicates an overall low aerosol content in the QTP region.
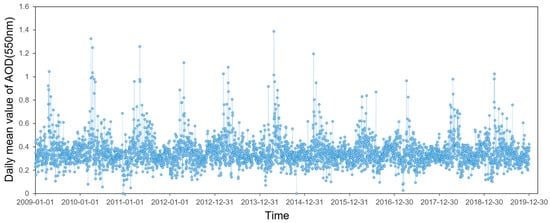
Figure 5.
Variation of daily mean AOD in the 550 nm band during 2009–2019 obtained by fusion algorithm processing.
Figure 6 shows the spatial year-to-year changes in AOD resolved by the fusion algorithm between 2009 and 2019, with three fluctuating increases in 2011, 2016, and 2018, but with an overall slow decreasing trend. The central zone was more stable, with spatial decreases concentrated in bare ground in the northeast and woodland areas in the southeast, while spatial increases were concentrated in edge areas in the southwest.
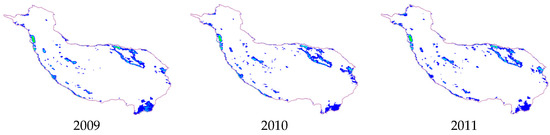
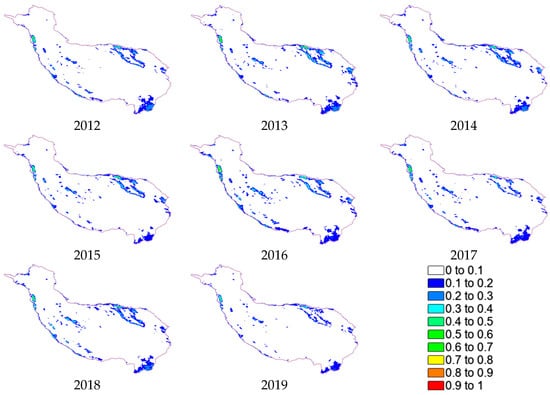
Figure 6.
The annual mean AOD content for each year from 2009 to 2019 was divided into ten classes based on spatial distribution.
Figure 7 shows the monthly variations of AOD, illustrated for example in the middle of 2009–2019 (2014), with monthly peaks of AOD occurring essentially in April and November of each year and the lowest monthly peaks occurring in February, the coldest month of the year. In particular, the woodland areas in the southeast and the fringes in the southwest have low aerosol levels during May-September, while temperatures are high during this cycle, and the western AOD gradually increases in October-November when aerosols spread from east to west due to westerly winds and cooling.
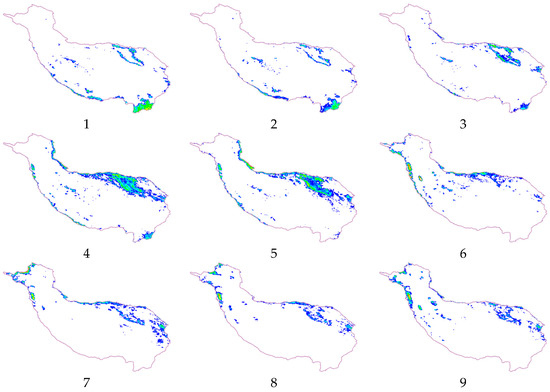
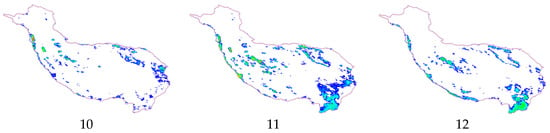
Figure 7.
The monthly mean AOD content for each month between 2009 and 2019 was divided into ten classes based on spatial distribution (illustrated by the example of 2014, the numbers 1–12 in the figure correspond to January–December 2014, and the legend is the same as Figure 6).
Figure 8 shows the spatial variation of seasonal AOD in the QTP area from 2009 to 2019. The four seasons in the QTP area are winter (December, January, February), spring (March, April, May), summer (June, July, August), and autumn (September, October, November), and the quarterly variations are expressed in the form of 2009–2014–2019 years. In terms of seasonal variation of AOD, autumn has the highest AOD throughout the year and summer has the lowest AOD throughout the year. AOD was significantly higher in spring and autumn than in winter and summer. Spatially, the AOD in spring is concentrated in the bare ground area in the northeast, whereas the AOD in autumn, except for the woodland area in the southeast, shows a homogeneous dispersion under the influence of autumn winds.
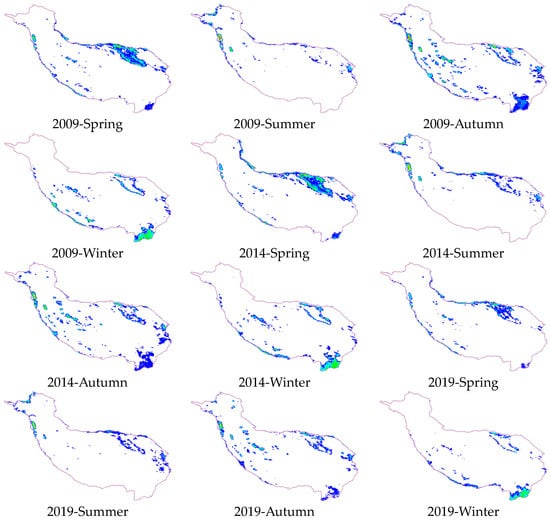
Figure 8.
The AOD mean content for the four seasons between 2009 and 2019 was divided into ten classes based on the spatial distribution (as illustrated for 2009, 2014, and 2019 with the same legend as Figure 6).
3.3. Comparison of AOD Values Inverted by Fusion Algorithms with AOD Values from the AERONET Observatory
The blue diamonds in Figure 9 and Figure 10 represent the experimental sample data and the orange squares represent the validation sample data. Figure 9 shows the validation comparison of the AOD results obtained by the fusion algorithm of this study with the measured results from 18 AERONET stations near the QTP area when the weight factor is a year-by-year variable. The results show that the overall errors of the 12 AERONET stations (station numbers: 1–12) that are closer to the QTP area are smaller and the correlation is better. The overall errors of the 6 AERONET stations that are geographically close to the QTP area but at a certain distance from the QTP area increase with distance, but the correlation does not change significantly. Figure 10 shows the validation comparison of the AOD results obtained by the fusion algorithm of this study with the measured results of six AERONET stations with more complete months of observation (station numbers: 1, 2, 6, 14, 15, 16) inside and outside the QTP when the weight factor is a mean constant. Comparing Figure 9 and Figure 10, the validation results for the same stations show that the fusion algorithm yields smaller AOD error values and better correlation when the weight factor is a year-by-year variable.
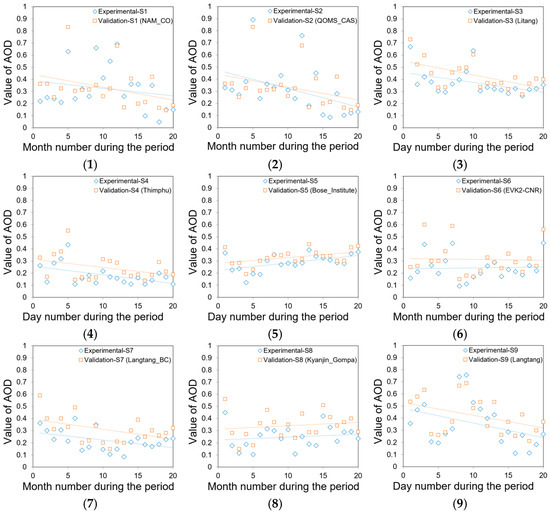
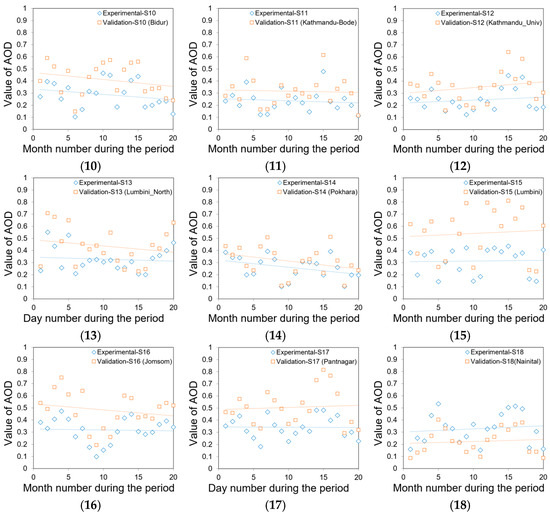
Figure 9.
Comparison of the AOD values inverted by the fusion algorithm for the period 2009–2019 with the measured results from each of the 18 AERONET stations near the QTP area when the weight factor is a year-by-year variable. The comparison groups of the 18 stations correspond to the numbers (1)–(18), respectively. Trend changes were added for all experimental and validation samples. The horizontal axis indicates the number of months or days in the period.
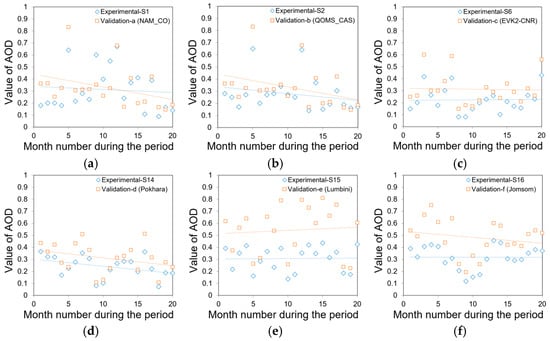
Figure 10.
When the weight factor is a mean constant, the AOD values inverted by the fusion algorithm for the period 2009–2019 are compared with the measured results from each of the 6 AERONET stations with relatively complete months of observation inside and outside of the QTP (station numbers: 1, 2, 6, 14, 15, 16). The comparison groups for the 6 sites correspond to (a–f), respectively. The horizontal axis indicates the number of months in the period.
Table 3 shows the MAE, RMSE, and R between the AOD values obtained by the fusion algorithm in this study and the measured AOD values from 18 AERONET stations around the QTP area when the weight factor is a year-to-year variable. The mean values of MAE, RMSE, and R for the 18 sets of validation results are 0.328, 0.113, and 0.913, respectively. Among them, the mean values of MAE, RMSE, and R for the first 12 sets of validation results closer to the QTP region were 0.309, 0.094, and 0.910, respectively, and the mean values of MAE, RMSE, and R for the last 6 sets of validation results farther from the QTP region were 0.365, 0.152, and 0.919, respectively. The results in Table 3 show that the overall error value is small when the AERONET station is close to the QTP area, and the overall error value increases as the station distance increases, but the correlation coefficients do not change much due to the geographic proximity.

Table 3.
MAE, RMSE, and R between the AOD inverted by the fusion algorithm and the AOD based on measurements at the 18 AERONET stations when the weight factor is a year-by-year variable.
Table 4 shows the MAE, RMSE, and R between the AOD values obtained by the fusion algorithm in this study and the measured AOD values of the 6 AERONET stations with more complete months of observation inside and outside the QTP when the weight factor is a mean constant. The mean values of MAE, RMSE, and R for these 6 groups of validation results are 0.350, 0.151, and 0.882, respectively. In Table 3, when the weight factor is a year-by-year variable, the mean values of MAE, RMSE, and R for these 6 groups of validation results are 0.339, 0.134, and 0.912, respectively. Both from the comparison of the results of each group and from the comparison of the overall results of the 6 groups, it can be seen that the fusion algorithm obtains a better correlation of the AOD and a smaller error when the weighting factor is a year-by-year variable.

Table 4.
MAE, RMSE, and R between the AOD inverted by the fusion algorithm and the AOD based on measurements at the 6 AERONET stations when the weight factor is a mean constant.
4. Discussion
Because the weight factor quoted in Figure 4 is the key to the validity of the fusion algorithm in this study, we first analyzed the trend of Figure 3 and Figure 4 in the context of the actual situation. It can be seen from Figure 4 that during the period of 2009–2019, the weight factor of the dark image element has shown a total of four decreases (2011–2012, 2013–2014, 2015–2016, 2018–2019) and a total of four increases (2009–2011, 2012–2013, 2014–2015, 2016–2018). The changes of decline and rise are more frequent and the number of changes is equal, so when the least squares method is used to reflect the trend of its curve, it changes to show a convex curve. This indicates that the energy transition between light and dark features in the QTP region was frequent during the 11 years due to multiple climatic and environmental factors. The highest peak in the trend of the curve in Figure 4 occurs in 2015, while the lowest peak occurs in 2019, and because the middle node of the 2009–2019 period is 2014, the overall weight factor shows an upward trend during this 11-year period. This overall upward trend is also reflected when we parse it as a linear change. Combined with Figure 3, this upward trend is most visually represented by the increase in the features of woodland, grasslands, shrubbery, and lake wetlands during the period 2009–2018. Among them, the increase in vegetation generally requires an appropriate increase in precipitation and temperature. However, by 2019, while the increase in precipitation and temperature continued [3], the weight factor of the dark image elements showed a minimum, and from Figure 3, it appears that during this year, agricultural land, grasslands, and shrubbery, which are low vegetation, are significantly decreasing, while lake wetland, desert, and bare ground are increasing continuously. Therefore, we can judge that the cause of the minimum value of the dark image element weight factor in 2019 is that the precipitation and temperature in 2019 had the highest peak value during the period of 2009–2019, and the excessively high precipitation and excessively high temperature have led to the death and abatement of a large number of low vegetation, in which a part of the dead low vegetation and the remaining water on the ground are transformed into lake wetland, while the other part of the dead low vegetation are transformed into desert and bare ground.
To further validate this judgment, we added the calculation of the weight factor and the analysis of the feature changes in the same area in 2020, which showed that the weight factor in 2020 was 0.5813, which was close enough to that of 2019 (0.5808), and the interconversion of several low vegetation and lake wetlands was consistent with that of 2019, which suggests that the trend of change derived from Figure 4 model is reliable. In addition, although the weight factor shows a general upward trend over the 2009–2019 period, the magnitude of its change is relatively small, so is it necessary to analyze the dynamics of this relatively small year-to-year change? We think it is totally necessary. Firstly, in the vast QTP area, this relatively small year-to-year fluctuation will affect the inter-transformation between multiple features. After that, combining the results in Table 3 and Table 4, we can also see that, compared with setting the weight factor as a mean constant, the results obtained by setting the weight factor as a year-by-year variable have a better correlation and smaller error, which can better reflect the change rule of AOD in the long-term dynamic monitoring.
In addition, before analyzing the validation results in Table 3 in detail, we need to explain the selection of the 18 AERONET stations in this study because there are fewer AERONET stations within the QTP area, and in order to make sure that the results of this experiment are adequately validated, we need as many AERONET stations as possible to provide sample data for the validation. When selecting AERONET stations, we mainly consider two conditions: one is that the geomorphologic environment is as similar as possible to the QTP area, and the other is that it is as close as possible to the QTP area in terms of distance. Because the eastern, western, and northern parts of QTP not only have large differences in geomorphological environment with the QTP area but also have very few AERONET stations and are far away from the QTP area, these areas cannot meet the above two conditions. On the other hand, in the highland area in the southern part of QTP, not only is the geomorphological environment very similar to that of the QTP area, but there is also a large number of AERONET stations in close proximity, so we chose the 18 AERONET stations in the southern part of QTP.
The results in Table 3 show that when the weight factor is a year-by-year variable, the overall error of the AOD computed by the fusion algorithm is relatively small for the first 12 groups of validation results that are closer to the QTP region, while the overall error is relatively large for the last 6 groups of validation results that are farther away from the QTP region. This is because, although the latter 6 groups of stations are geographically similar to the QTP region, (13) Lumbini_North, (15) Lumbini, (16) Jomsom, and (17) Pantnagar, among the latter 6 groups of stations, are closer to the populated areas of Nepal and India and are affected by the southwest monsoon winds of the Indian Ocean; therefore, the values of AOD are larger. Although the AOD values of the last 6 groups of stations are larger, resulting in larger error values, the overall correlation is not much different from the results of the first 12 groups, or even slightly better than that of the first 12 groups. This is not only due to the higher stability of the fusion algorithm in geographically similar areas, but also due to the high correlation of (14) Pokhara (R:0.964) in the last 6 groups of stations, which increases the overall value. The main reason for the high correlation of (14) Pokhara is that, among the 18 AERONET stations, (14) Pokhara has 111 months of observation during 2010–2019, which is the most continuous and complete observation data, and can accurately reflect the trend of the AOD on the annual and monthly scales, so the correlation of this station is the best. It is also worth noting that, while the correlation validation results are around 0.9 for most of the stations, there is a low correlation result here at Station (1), NAM_CO (R:0.752). Combined with the geographic location of this station, we believe that the possible reason for this is that the NAM_CO station is located in the central region of the QTP, and as can be seen in Figure 6, Figure 7 and Figure 8, the AOD values in this region have been extremely low during the period 2009.1–2019.12, which has an impact on the stations in this region in terms of capturing the changes in the AOD in the QTP region.
Meanwhile, as can be seen from Table 3, the mean values of MAE, RMSE, and R for the 18 groups of validation results are 0.328, 0.113, and 0.913, respectively. Among them, the mean values of MAE, RMSE, and R for the first 12 groups of validation results, which are nearer to the QTP region, are 0.309, 0.094, and 0.910, respectively. In order to validate the accuracy of the fusion algorithm, we need to compare the results with those of previous results of similar methods in the same region, but due to the scarcity of literature on the monitoring of long-period AOD dynamics in the QTP region, it is difficult to search for articles in the same study area to compare and analyze the results. Therefore, we first chose to compare the results with the DB algorithm or DT method in other study regions of the world. Among them, the results of Filonchyk et al. (2020) are RMSE 0.098–0.297 [69], the results of Zhang et al. (2016) are RMSE 0.123–0.150 [70], the results of Bilal et al. (2015) are RMSE 0.150–0.360 R 0.68–0.92 [71], and the results of Shi et al. (2013) are RMSE 0.24 [72]. In comparison with these results, the experimental results obtained in this study are better. However, the reliability of the fusion algorithm proposed in this study needs to be further explored because of the different study regions to be considered. In the absence of QTP regional results, we try to focus on selecting the experimental results of other approximation algorithms in the Chinese region for comparative analysis, which are R 0.698 and 0.688 for the results of Xie et al. (2019) [73], R 0.92 with an error value of 0.46 for the results of He et al. (2021) [74], R 0.747–0.905 with MAE of 0.067–0.18 and RMSE 0.067–0.302 for Filonchyk et al. (2019) [75], R 0.87 with RMSE of 0.29 and MAE of 0.23 for Qin et al. (2018) [76], and R 0.82–0.88 with MAE of 0.15–0.17 and RMSE of 0.17–0.27 for the results of Jiang et al. (2022) [77]. Compared with these results, the MAE, RMSE, and R values of this study are close enough to the values of the results of other studies, which also indicates that the fusion algorithm used in this study is reliable and the AOD results obtained by inversion through this fusion algorithm have high accuracy.
From Figure 5, the daily mean AOD is low, indicating that the main body of aerosols in the region is more from nature, except for factories and urban areas in the east. From Figure 6, the annual spatial change shows a phenomenon of stratification from northeast to southwest around the 45-degree line, in which the trend of the northeastern bare land and southeastern forested area, where the aerosols are spatially distributed the most, decreases year by year. This indicates that when the AOD increases in this region, it can inhibit the rise of air temperature to a certain extent, which in turn protects the stability of permafrost in this region. From this, we can judge that the composition of aerosols in the region is mainly composed of cooling sulfate aerosols, supplemented by warming black carbon aerosols. Combined with the temporal changes, the sulfate aerosol content of the cooling category mainly decreased from 2009 to 2019, while the black carbon aerosol content of the warming category mainly increased.
From the monthly scale change of AOD in Figure 7, the AOD in April and November is in the peak period of each year, and these two months are the period when the zero-curtain effect of permafrost is generated in the QTP area; especially, the zero-curtain effect in April lasts for a longer period of time and with the highest stability [3]. Therefore, we analyze the stability of the fusion algorithm in this paper in conjunction with the spring changes of AOD from 2009 to 2019. As can be seen in Figure 8, the AOD in the QTP region has higher values in the spring and fall and exhibits spatial zonal concentration. Among them, the distribution of AOD in spring was mainly concentrated in the bare land and desert in the northwest, grassland in the western edge, and woodland area in the southeast, and the bare land and desert area in the northwest had the highest content of AOD among these three areas. Looking at the changes in AOD from spring 2009 to 2014, there is a trend of increasing AOD in the northwest, while there is a small decrease in the western edge and southeastern regions and a small trend of increasing AOD in the three regions combined. Looking again at the change in AOD from spring 2014–2019, there is a significant trend of decreasing AOD in the northwest and southeast, while there is a small increase in AOD in the western edge and a significant trend of decreasing AOD in all three regions combined. During the period 2009–2014–2019, the change in spring AOD showed a trend of a small increase followed by a significant decrease, with an overall decreasing trend during this 11-year period. This is consistent with the trend of KR values in Figure 4 over the 2009–2014–2019 period. This can also indicate that the fusion algorithm in this study has high stability.
In summary, we not only analyzed the stability and reliability of the fusion algorithm in this study on monthly and daily scales from different time periods using multiple AERONET stations, but also analyzed the stability of the algorithm by examining the temporal and spatial variations of the AOD on seasonal scales in the QTP region from 2009 to 2019.
5. Conclusions
In this study, we fused the V5.2 algorithm and the second-generation DB algorithm by introducing the dynamic bright and dark pixel weight factor, and dynamically resolved the temporal and spatial changes of the AOD in the QTP region during the period 2009–2019 by the fusion algorithm in terms of days, months, seasons, and years, and made a judgment of the changes of the different types of aerosols in the QTP region and the AOD in this cycle as a whole. Overall, the AOD in this cycle shows a slowly decreasing trend, and the inhibiting effect on warming is weakening. The decreasing aerosols in this cycle are mainly cooling sulfate aerosols, while warming black carbon aerosols may continue to increase. The spatial decrease is mainly concentrated in the bare land in the northeast and the forested area in the southeast, while the spatial increase is mainly concentrated in the fringe area in the southwest, and this spatial decrease has resulted in the amplification of feature types such as woodland and desert. To ensure the reliability and stability of the fusion algorithm, we compared the AOD values obtained by the fusion algorithm with the measured AOD values of 18 AERONET stations for validation. The mean values of MAE, RMSE, and R for the 18 groups of validation results were 0.328, 0.113, and 0.913, respectively. The mean values of MAE, RMSE, and R for the first 12 groups of validation results that were closer to the QTP region were 0.309, 0.094, and 0.910, respectively, and the mean values of MAE, RMSE, and R of the last 6 groups of validation results that are farther away from the QTP region were 0.365, 0.152, and 0.919, respectively. Compared with previous studies using the DB algorithm and the DT method, the fusion algorithm proposed in this study has less error and higher correlation. Also, compared with previous studies with similar algorithms in the Chinese region, the values of MAE, RMSE, and R in this study are close enough to the values of the results of other studies, which indicates that the fusion algorithm used in this study is reliable and stable. Meanwhile, we analyzed the seasonal variation and spatial distribution of AOD in comparison with the trend of the weight factor, which further proved the stability of the fusion algorithm. In addition, this study also compares the AOD results obtained by the fusion algorithm when dynamically weighted and mean-weighted, and the results show that the dynamic weighting approach in this study has higher accuracy. Due to time constraints, the use of this algorithm to analyze the role of feedback between the atmosphere and climate relationships in permafrost regions will be studied in depth as the next phase of our research.
Author Contributions
Conceptualization, Z.Z.; methodology, Z.Z. and H.T.; software, Z.Z.; validation, Z.Z. and H.T.; formal analysis, Z.Z.; investigation, Z.Z.; resources, Z.Z. and H.T.; data curation, Z.Z.; writing—original draft preparation, Z.Z.; writing—review and editing, Z.Z. and H.T.; visualization, Z.Z.; supervision, Z.Z. and H.T.; project administration, Z.Z. and H.T.; funding acquisition, Z.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: [link1: https://ladsweb.modaps.eosdis.nasa.gov/, accessed on 1 May 2023; link2: https://aeronet.gsfc.nasa.gov/, accessed on 1 May 2023].
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zou, D.; Zhao, L.; Sheng, Y.; Chen, J.; Hu, G.; Wu, T.; Wu, J.; Xie, C.; Wu, X.; Pang, Q.; et al. A new map of permafrost distribution on the Tibetan Plateau. Cryosphere 2017, 11, 2527–2542. [Google Scholar] [CrossRef]
- Nan, Z.; Li, S.; Cheng, G. Prediction of permafrost distribution on the Qinghai-Tibet Plateau in the next 50 and 100 years. Sci. China Ser. D-Earth Sci. 2005, 48, 797–804. [Google Scholar] [CrossRef]
- Zhao, Z.; Tonooka, H. Analysis of Permafrost Distribution and Change in the Mid-East Qinghai–Tibetan Plateau during 2012–2021 Using the New TLZ Model. Remote Sens. 2022, 14, 6350. [Google Scholar] [CrossRef]
- Chen, H.; Zhu, Q.; Peng, C.; Wu, N.; Wang, Y.; Fang, X.; Gao, Y.; Zhu, D.; Yang, G.; Tian, J.; et al. The impacts of climate change and human activities on biogeochemical cycles on the Qinghai-Tibetan Plateau. Glob. Change Biol. 2013, 19, 2940–2955. [Google Scholar] [CrossRef] [PubMed]
- Sun, Q.; Liu, W.; Gao, Y.; Li, J.; Yang, C. Spatiotemporal Variation and Climate Influence Factors of Vegetation Ecological Quality in the Sanjiangyuan National Park. Sustainability 2020, 12, 6634. [Google Scholar] [CrossRef]
- Wang, G.; Li, Y.; Wu, Q.; Wang, Y. Impacts of permafrost changes on alpine ecosystem in Qinghai-Tibet Plateau. Sci. China Ser. D 2006, 49, 1156–1169. [Google Scholar] [CrossRef]
- Beck, I.; Ludwig, R.; Bernier, M.; Lévesque, E.; Boike, J. Assessing Permafrost Degradation and Land Cover Changes (1986–2009) using Remote Sensing Data over Umiujaq, Sub-Arctic Québec. Permafr. Periglac. Process. 2015, 26, 129–141. [Google Scholar] [CrossRef]
- Sun, A.; Yu, Z.; Zhou, J.; Acharya, K.; Ju, Q.; Xing, R.; Huang, D.; Wen, L. Quantified hydrological responses to permafrost degradation in the headwaters of the Yellow River (HWYR) in High Asia. Sci. Total Environ. 2020, 712, 135632. [Google Scholar] [CrossRef] [PubMed]
- McNeill, V.F. Atmospheric aerosols: Clouds, chemistry, and climate. Annu. Rev. Chem. Biomol. Eng. 2017, 8, 427–444. [Google Scholar] [CrossRef]
- Jacobson, M.C.; Hansson, H.C.; Noone, K.J.; Charlson, R.J. Organic atmospheric aerosols: Review and state of the science. Rev. Geophys. 2000, 38, 267–294. [Google Scholar] [CrossRef]
- Krieger, U.K.; Marcolli, C.; Reid, J.P. Exploring the complexity of aerosol particle properties and processes using single particle techniques. Chem. Soc. Rev. 2012, 41, 6631–6662. [Google Scholar] [CrossRef] [PubMed]
- Schulze, F.; Gao, X.; Virzonis, D.; Damiati, S.; Schneider, M.R.; Kodzius, R. Air Quality Effects on Human Health and Approaches for Its Assessment through Microfluidic Chips. Genes 2017, 8, 244. [Google Scholar] [CrossRef] [PubMed]
- Warneck, P.; Williams, J. The Atmospheric Aerosol. In The Atmospheric Chemist’s Companion; Springer: Dordrecht, The Netherlands, 2012; pp. 127–187. [Google Scholar] [CrossRef]
- Andreae, M.O.; Gelencsér, A. Black carbon or brown carbon? The nature of light-absorbing carbonaceous aerosols. Atmos. Chem. Phys. 2006, 6, 3131–3148. [Google Scholar] [CrossRef]
- Bond, T.C.; Doherty, S.J.; Fahey, D.W.; Forster, P.M.; Berntsen, T.; DeAngelo, B.J.; Flanner, M.G.; Ghan, S.; Kärcher, B.; Koch, D.; et al. Bounding the role of black carbon in the climate system: A scientific assessment. J. Geophys. Res. Atmos. 2013, 118, 5380–5552. [Google Scholar] [CrossRef]
- He, J.; Zha, Y.; Zhang, J.; Gao, J.; Li, Y.; Chen, X. Retrieval of aerosol optical thickness from HJ-1 CCD data based on MODIS-derived surface reflectance. Int. J. Remote Sens. 2015, 36, 882–898. [Google Scholar] [CrossRef]
- Ramanathan, V.; Crutzen, P.J.; Lelieveld, J.; Mitra, A.P.; Althausen, D.; Anderson, J.; Andreae, M.O.; Cantrell, W.; Cass, G.R.; Chung, C.E.; et al. Indian Ocean Experiment: An integrated analysis of the climate forcing and effects of the great Indo-Asian haze. J. Geophys. Res. Atmos. 2001, 106, 28371–28398. [Google Scholar] [CrossRef]
- Andreae, M.O.; Crutzen, P.J. Atmospheric aerosols: Biogeochemical sources and role in atmospheric chemistry. Science 1997, 276, 1052–1058. [Google Scholar] [CrossRef]
- Boucher, O.; Anderson, T.L. General circulation model assessment of the sensitivity of direct climate forcing by anthropogenic sulfate aerosols to aerosol size and chemistry. J. Geophys. Res. Atmos. 1995, 100, 26117–26134. [Google Scholar] [CrossRef]
- Li, Z.; Xu, H.; Li, K.; Li, D.; Xie, Y.; Li, L.; Zhang, Y.; Gu, X.; Zhao, W.; Tian, Q.; et al. Comprehensive Study of Optical, Physical, Chemical, and Radiative Properties of Total Columnar Atmospheric Aerosols over China: An Overview of Sun–Sky Radiometer Observation Network (SONET) Measurements. Bull. Am. Meteorol. Soc. 2018, 99, 739–755. [Google Scholar] [CrossRef]
- Sokolik, I.; Toon, O. Direct radiative forcing by anthropogenic airborne mineral aerosols. Nature 1996, 381, 681–683. [Google Scholar] [CrossRef]
- Maynard, R.L. Particulate air pollution. Urban Atmos. Its Eff. 2000, 1, 163–193. [Google Scholar] [CrossRef]
- Bérubé, K.A.; Jones, T.P.; Williamson, B.J.; Winters, C.; Morgan, A.J.; Richards, R.J. Physicochemical characterisation of diesel exhaust particles: Factors for assessing biological activity. Atmos. Environ. 1999, 33, 1599–1614. [Google Scholar] [CrossRef]
- Zhang, S.; Wu, J.; Fan, W.; Yang, Q.; Zhao, D. Review of aerosol optical depth retrieval using visibility data. Earth-Sci. Rev. 2020, 200, 102986. [Google Scholar] [CrossRef]
- Holben, B.N.; Eck, T.F.; Slutsker, I.; Tanré, D.; Buis, J.P.; Setzer, A.; Vermote, E.; Reagan, J.A.; Kaufman, Y.J.; Nakajima, T.; et al. AERONET—A federated instrument network and data archive for aerosol characterization. Remote Sens. Environ. 1998, 66, 1–16. [Google Scholar] [CrossRef]
- Chen, X.; Ding, J.; Wang, J.; Ge, X.; Raxidin, M.; Liang, J.; Chen, X.; Zhang, Z.; Cao, X.; Ding, Y. Retrieval of Fine-Resolution Aerosol Optical Depth (AOD) in Semiarid Urban Areas Using Landsat Data: A Case Study in Urumqi, NW China. Remote Sens. 2020, 12, 467. [Google Scholar] [CrossRef]
- Tang, Y.; Deng, R.; Liu, Y.; Xiong, L. Research Review of Remote Sensing for Atmospheric Aerosol Retrieval. Remote Sens. Technol. Appl. 2018, 333, 25–34. [Google Scholar] [CrossRef]
- Kondratev, K.I.; Buznikov, A.A.; Vasilev, O.B.; Smoktii, O.I. Influence of the atmosphere on the albedo in aerospace photography of the earth in visible light. Akad. Nauk SSSR Fiz. Atmos. i Okeana 1977, 13, 471–487. Available online: https://ui.adsabs.harvard.edu/abs/1977FizAO..13..471K/abstract (accessed on 4 July 2023).
- Isakov, V.Y.; Feind, R.E.; Vasilyev, O.B.; Welch, R.M. Retrieval of aerosol spectral optical thickness from AVIRIS data. Int. J. Remote Sens. 1996, 17, 2165–2184. [Google Scholar] [CrossRef]
- Kondratyev, K.Y.; Buznikov, A.A.; Vasilyev, O.B.; Smoktiy, O.I. Influence of the atmosphere on the spectral brightness and contrast of natural formations with spectrophotometric measurements of earth from space. Akad. Nauk SSSR Fiz. Atmos. i Okeana 1975, 11, 348–361. Available online: https://ui.adsabs.harvard.edu/abs/1975FizAO......348K/abstract (accessed on 4 July 2023).
- Tanré, D.; Deschamps, P.Y.; Devaux, C.; Herman, M. Estimation of Saharan aerosol optical thickness from blurring effects in Thematic Mapper data. J. Geophys. Res. Atmos. 1988, 93, 15955–15964. [Google Scholar] [CrossRef]
- Tanré, D.; Devaux, C.; Herman, M.; Santer, R.; Gac, J.Y. Radiative properties of desert aerosols by optical ground-based measurements at solar wavelengths. J. Geophys. Res. Atmos. 1988, 93, 14223–14231. [Google Scholar] [CrossRef]
- de Almeida Castanho, A.D.; Vanderlei Martins, J.; Artaxo, P. MODIS aerosol optical depth retrievals with high spatial resolution over an urban area using the critical reflectance. J. Geophys. Res. Atmos. 2008, 113, D02201. [Google Scholar] [CrossRef]
- Dubovik, O.; Herman, M.; Holdak, A.; Lapyonok, T.; Tanré, D.; Deuzé, J.L.; Ducos, F.; Sinyuk, A.; Lopatin, A. Statistically optimized inversion algorithm for enhanced retrieval of aerosol properties from spectral multi-angle polarimetric satellite observations. Atmos. Meas. Tech. 2011, 4, 975–1018. [Google Scholar] [CrossRef]
- Fougnie, B.; Chimot, J.; Vázquez-Navarro, M.; Marbach, T.; Bojkov, B. Aerosol retrieval from space-how does geometry of acquisition impact our ability to characterize aerosol properties. J. Quant. Spectrosc. Radiat. Transf. 2020, 256, 107304. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Tanré, D.; Remer, L.A.; Vermote, E.F.; Chu, A.; Holben, B.N. Operational remote sensing of tropospheric aerosol over land from EOS moderate resolution imaging spectroradiometer. J. Geophys. Res. Atmos. 1997, 102, 17051–17067. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Sendra, C. Algorithm for automatic atmospheric corrections to visible and near-IR satellite imagery. Int. J. Remote Sens. 1988, 9, 1357–1381. [Google Scholar] [CrossRef]
- Wang, Q.; Li, S.; Yang, J.; Zhou, D.; Song, G. A high-precision aerosol retrieval algorithm for FY-3D MERSI-II images. Environ. Int. 2023, 173, 107841. [Google Scholar] [CrossRef] [PubMed]
- Kaufman, Y.J.; Wald, A.E.; Remer, L.A.; Gao, B.; Li, R.; Flynn, F. The MODIS 2.1-/spl mu/m channel-correlation with visible reflectance for use in remote sensing of aerosol. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1286–1298. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Tanré, D. Algorithm for remote sensing of tropospheric aerosol from MODIS. NASA MODIS Algorithm Theor. Basis Doc. Goddard Space Flight Cent. 1998, 85, 3–68. [Google Scholar]
- Martins, J.V.; Tanré, D.; Remer, L.; Kaufman, Y.; Mattoo, S.; Levy, R. MODIS cloud screening for remote sensing of aerosols over oceans using spatial variability. Geophys. Res. Lett. 2002, 29, MOD4-1–MOD4-4. [Google Scholar] [CrossRef]
- Mi, W.; Li, Z.; Xia, X.; Holben, B.; Levy, R.; Zhao, F.; Chen, H.; Cribb, M. Evaluation of the moderate resolution imaging spectroradiometer aerosol products at two aerosol robotic network stations in China. J. Geophys. Res. Atmos. 2007, 112, D22S08. [Google Scholar] [CrossRef]
- Ge, B.; Li, Z.; Liu, L.; Yang, L.; Chen, X.; Hou, W.; Zhang, Y.; Li, D.; Li, L.; Qie, L. A dark target method for Himawari-8/AHI aerosol retrieval: Application and validation. IEEE Trans. Geosci. Remote Sens. 2018, 57, 381–394. [Google Scholar] [CrossRef]
- Levy, R.C.; Remer, L.A.; Kleidman, R.G.; Mattoo, S.; Ichoku, C.; Kahn, R.; Eck, T.F. Global evaluation of the Collection 5 MODIS dark-target aerosol products over land. Atmos. Chem. Phys. 2010, 10, 10399–10420. [Google Scholar] [CrossRef]
- Picon, A.; Oo, M.M.; Hernandez, E.; Jerg, M.; Gross, B.M.; Moshary, F.; Ahmed, S.A. Improved MODIS aerosol retrieval using modified VIS/MIR surface albedo ratio over urban scenes. In Proceedings of the Remote Sensing of Clouds and the Atmosphere XIII, SPIE, Boston, MA, USA, 7–11 July 2008; Volume 7107, pp. 246–257. [Google Scholar] [CrossRef]
- Wei, J.; Huang, B.; Sun, L.; Zhang, Z.; Wang, L.; Bilal, M. A simple and universal aerosol retrieval algorithm for Landsat series images over complex surfaces. J. Geophys. Res. Atmos. 2017, 122, 13338–13355. [Google Scholar] [CrossRef]
- Levy, R.C.; Remer, L.A.; Mattoo, S.; Vermote, E.F.; Kaufman, Y.J. Second-generation operational algorithm: Retrieval of aerosol properties over land from inversion of Moderate Resolution Imaging Spectroradiometer spectral reflectance. J. Geophys. Res. Atmos. 2007, 112, D13211. [Google Scholar] [CrossRef]
- Chen, L.; Wang, R.; Wei, G.; Han, J.; Zha, Y. A surface reflectance correction model to improve the retrieval of MISR aerosol optical depth supported by MODIS data. Adv. Space Res. 2021, 67, 858–867. [Google Scholar] [CrossRef]
- Hsu, N.C.; Tsay, S.C.; King, M.D.; Herman, J.R. Deep blue retrievals of Asian aerosol properties during ACE-Asia. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3180–3195. [Google Scholar] [CrossRef]
- Hsu, N.C.; Tsay, S.C.; King, M.D.; Herman, J.R. Aerosol properties over bright-reflecting source regions. IEEE Trans. Geosci. Remote Sens. 2004, 42, 557–569. [Google Scholar] [CrossRef]
- Hsu, N.C.; Jeong, M.J.; Bettenhausen, C.; Sayer, A.M.; Hansell, R.; Seftor, C.S.; Huang, J.; Tsay, S.C. Enhanced Deep Blue aerosol retrieval algorithm: The second generation. J. Geophys. Res. Atmos. 2013, 118, 9296–9315. [Google Scholar] [CrossRef]
- Diner, D.J.; Martonchik, J.V.; Kahn, R.A.; Pinty, B.; Gobron, N.; Nelson, D.L.; Holben, B.N. Using angular and spectral shape similarity constraints to improve MISR aerosol and surface retrievals over land. Remote Sens. Environ. 2005, 94, 155–171. [Google Scholar] [CrossRef]
- Lyapustin, A.; Wang, Y.; Laszlo, I.; Kahn, R.; Korkin, S.; Remer, L.; Levy, R.; Reid, J.S. Multiangle implementation of atmospheric correction (MAIAC): 2. Aerosol algorithm. J. Geophys. Res. Atmos. 2011, 116, D03211. [Google Scholar] [CrossRef]
- Si, Y.; Lu, Q.; Zhang, X.; Hu, X.; Wang, F.; Li, L.; Gu, S. A review of advances in the retrieval of aerosol properties by remote sensing multi-angle technology. Atmos. Environ. 2021, 244, 117928. [Google Scholar] [CrossRef]
- Deuzé, J.L.; Goloub, P.; Herman, M.; Marchand, A.; Perry, G.; Susana, S.; Tanré, D. Estimate of the aerosol properties over the ocean with POLDER. J. Geophys. Res. Atmos. 2000, 105, 15329–15346. [Google Scholar] [CrossRef]
- Deuzé, J.L.; Bréon, F.M.; Devaux, C.; Goloub, P.; Herman, M.; Lafrance, B.; Maignan, F.; Marchand, A.; Nadal, F.; Perry, G.; et al. Remote sensing of aerosols over land surfaces from POLDER-ADEOS-1 polarized measurements. J. Geophys. Res. Atmos. 2001, 106, 4913–4926. [Google Scholar] [CrossRef]
- Waquet, F.; Riedi, J.; Labonnote, L.C.; Goloub, P.; Cairns, B.; Deuzé, J.L.; Tanré, D. Aerosol remote sensing over clouds using A-Train observations. J. Atmos. Sci. 2009, 66, 2468–2480. [Google Scholar] [CrossRef]
- Liang, S.; Zhong, B.; Fang, H. Improved estimation of aerosol optical depth from MODIS imagery over land surfaces. Remote Sens. Environ. 2006, 104, 416–425. [Google Scholar] [CrossRef]
- Mao, Q.; Zhang, H.; Chen, Q.; Huang, C.; Yuan, Y. Satellite-based assessment of direct aerosol radiative forcing using a look-up table established through AERONET observations. Infrared Phys. Technol. 2019, 102, 103017. [Google Scholar] [CrossRef]
- Wang, Z.; Fan, H.; Wang, D.; Xing, T.; Wang, D.; Guo, Q.; Xiu, L. Spatial Pattern of Highway Transport Dominance in Qinghai–Tibet Plateau at the County Scale. ISPRS Int. J. Geo-Inf. 2021, 10, 304. [Google Scholar] [CrossRef]
- Ran, Q.; Hao, Y.; Xia, A.; Liu, W.; Hu, R.; Cui, X.; Xue, K.; Song, X.; Xu, C.; Ding, B.; et al. Quantitative Assessment of the Impact of Physical and Anthropogenic Factors on Vegetation Spatial-Temporal Variation in Northern Tibet. Remote Sens. 2019, 11, 1183. [Google Scholar] [CrossRef]
- Li, X.; Long, D.; Huang, Q.; Han, P.; Zhao, F.; Wada, Y. High-temporal-resolution water level and storage change data sets for lakes on the Tibetan Plateau during 2000–2017 using multiple altimetric missions and Landsat-derived lake shoreline positions. Earth Syst. Sci. Data 2019, 11, 1603–1627. [Google Scholar] [CrossRef]
- Li, H.; Liu, L.; Shan, B.; Xu, Z.; Niu, Q.; Cheng, L.; Liu, X.; Xu, Z. Spatiotemporal Variation of Drought and Associated Multi-Scale Response to Climate Change over the Yarlung Zangbo River Basin of Qinghai–Tibet Plateau, China. Remote Sens. 2019, 11, 1596. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, L.; Li, X.; Zhou, J.; Hu, Z. An integration of gauge, satellite, and reanalysis precipitation datasets for the largest river basin of the Tibetan Plateau. Earth Syst. Sci. Data 2020, 12, 1789–1803. [Google Scholar] [CrossRef]
- Hao, J.; Wu, T.; Wu, X.; Hu, G.; Zou, D.; Zhu, X.; Zhao, L.; Li, R.; Xie, C.; Ni, J.; et al. Investigation of a Small Landslide in the Qinghai-Tibet Plateau by InSAR and Absolute Deformation Model. Remote Sens. 2019, 11, 2126. [Google Scholar] [CrossRef]
- Li, Y.; Liang, Y.; Wei, T.; Chen, P.; Ji, X.; Liu, X. Spatiotemporal dynamics of rainfall interception and effective precipitation in the Loess Plateau after large-scale afforestation. Land Degrad. Dev. 2023, 34, 5004–5016. [Google Scholar] [CrossRef]
- Pan, X.; Wang, Z.; Gao, Y.; Dang, X.; Han, Y. Detailed and automated classification of land use/land cover using machine learning algorithms in Google Earth Engine. Geocarto Int. 2022, 37, 5415–5432. [Google Scholar] [CrossRef]
- Miura, T.; Huete, A.R.; Van Leeuwen, W.J.D.; Didanet, K. Vegetation detection through smoke-filled AVIRIS images: An assessment using MODIS band passes. J. Geophys. Res. Atmos. 1998, 103, 32001–32011. [Google Scholar] [CrossRef]
- Filonchyk, M.; Hurynovich, V. Validation of MODIS Aerosol Products with AERONET Measurements of Different Land Cover Types in Areas over Eastern Europe and China. J. Geovis. Spat. Anal. 2020, 4, 10. [Google Scholar] [CrossRef]
- Zhang, H.; Kondragunta, S.; Laszlo, I.; Liu, H.; Remer, L.A.; Huang, J.; Superczynski, S.; Ciren, P. An enhanced VIIRS aerosol optical thickness (AOT) retrieval algorithm over land using a global surface reflectance ratio database. J. Geophys. Res. Atmos. 2016, 121, 10,717–10,738. [Google Scholar] [CrossRef]
- Bilal, M.; Nichol, J.E. Evaluation of MODIS aerosol retrieval algorithms over the Beijing-Tianjin-Hebei region during low to very high pollution events. J. Geophys. Res. Atmos. 2015, 120, 7941–7957. [Google Scholar] [CrossRef]
- Shi, Y.; Zhang, J.; Reid, J.S.; Hyer, E.J.; Hsu, N.C. Critical evaluation of the MODIS Deep Blue aerosol optical depth product for data assimilation over North Africa. Atmos. Meas. Tech. 2013, 6, 949–969. [Google Scholar] [CrossRef]
- Xie, G.; Wang, M.; Pan, J.; Zhu, Y. Spatio-temporal variations and trends of MODIS C6. 1 Dark Target and Deep Blue merged aerosol optical depth over China during 2000–2017. Atmos. Environ. 2019, 214, 116846. [Google Scholar] [CrossRef]
- He, L.; Wang, L.; Li, Z.; Jiang, D.; Sun, L.; Liu, D.; Liu, L.; Yao, R.; Zhou, Z.; Wei, J. VIIRS Environmental Data Record and Deep Blue aerosol products: Validation, comparison, and spatiotemporal variations from 2013 to 2018 in China. Atmos. Environ. 2021, 250, 118265. [Google Scholar] [CrossRef]
- Filonchyk, M.; Yan, H.; Zhang, Z.; Yang, S.; Li, W.; Li, Y. Combined use of satellite and surface observations to study aerosol optical depth in different regions of China. Sci. Rep. 2019, 9, 6174. [Google Scholar] [CrossRef]
- Qin, W.; Wang, L.; Lin, A.; Zhang, M.; Bilal, M. Improving the Estimation of Daily Aerosol Optical Depth and Aerosol Radiative Effect Using an Optimized Artificial Neural Network. Remote Sens. 2018, 10, 1022. [Google Scholar] [CrossRef]
- Jiang, D.; Wang, L.; Yi, X.; Su, X.; Zhang, M. Comprehensive evaluation of multisource aerosol optical depth gridded products over China. Atmos. Environ. 2022, 278, 119088. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).