Abstract
The quanta-to-energy ratio plays a crucial role in converting energy units to quantum units in the context of photosynthetically active radiation (PAR). Despite its widespread use, the effects of atmospheric particles and solar zenith angle (SZA) on the quanta-to-energy ratio remain unclear. In this study, both simulation and observation data revealed that the principal wavelength, which can be transformed into the quanta-to-energy ratio using a constant, exhibits a slow initial growth, followed by a rapid increase beyond 60° solar zenith angles and a subsequent dramatic decrease after reaching its maximum value. The measured quanta-to-energy ratio demonstrates a variable range of less than 3% for SZA under 70° in a cloudless atmosphere, with significant changes only occurring at zenith angles above 80°. Simulation data indicate that ozone, wind speed, surface-level pressure, surface air temperature, and relative humidity have negligible effects on the quanta-to-energy ratio. The Ångstrom exponent exerts a minor influence on the quanta-to-energy ratio by affecting diffuse radiation. Visibility, however, is found to have a substantial impact on the quanta-to-energy ratio. As a result, two relationships are established, linking the principal wavelength to visibility and the diffuse fraction of PAR. The principal wavelength serves as an effective measure of solar spectrum variability, remaining unaffected by radiation energy. This implies that atmospheric parameters which do not alter the solar spectrum will not influence the principal wavelength. The strong correlations between the principal wavelength, visibility, and the diffuse fraction of PAR suggest a broader range of applications for the principal wavelength in various research domains, opening up new avenues for exploration and potential contributions to numerous fields.
1. Introduction
The quanta-to-energy ratio serves as a crucial parameter for converting photosynthetically active radiation (PAR) from energy units (irradiance, W m−2) to quantum units ( μmol m−2 s−1) [1,2,3]. This conversion facilitates precise and comprehensive modeling of vegetation photosynthesis [1,4,5,6,7] and ecosystem-atmosphere CO2 exchange [8,9], particularly for forests ecosystems [10,11]. The quanta-to-energy ratio can be defined using the following Equation:
where is the global downwelling irradiance reaching the underlying surface at a specific wavelength (), Planck’s constant , the velocity of light in vacuum , Avogadro constant , and are the lower and upper limits of the wavelength region under consideration and generally correspond to 400 nm and 700 nm, respectively [9,12,13,14]. The , referred to as the principal wavelength, serves as a novel metric that enables a qualitative assessment of variations in the spectral distribution of global PAR energy or quanta [3].
The concept of the quanta-to-energy ratio was first introduced by McCree in 1972 [12], who initially proposed a value of 4.57 μmol W−1 s−1 for this parameter at the Earth’s surface [12]. Subsequent studies by Morel and Smith [15] and Morel [16] expanded upon this idea, providing quanta-to-energy values for various locations. Morel and Smith [15] highlighted that the quanta-to-energy ratio for sea surfaces generally ranges around 4.6 ± 1% μmol W−1 s−1, emphasizing the potential variations across different environments. Notably, many research studies have adopted a constant value for the quanta-to-energy ratio, typically using either 4.6 or 4.57 μmol W−1 s−1, as illustrated in Table 1. The quanta-to-energy ratio has been widely employed across various observational studies and models, showcasing its significance in understanding the dynamics of PAR.

Table 1.
Published quanta-to-energy ratios of PAR.
Akitsu et al. [24] conducted a comprehensive analysis of the quanta-to-energy ratio reaching land surfaces, utilizing an extensive dataset from observational studies. Their research revealed that for solar zenith angles (SZA) less than 78°, the quanta-to-energy ratio may exhibit a 3% variability around McCree’s constant value due to changes in dew point temperature and clearness index. This finding suggests that McCree’s value remains a valid approximation for sea surfaces under low SZA conditions. The change in the quanta-energy ratio in seawater is significantly more complicated than that on the sea surface due to the absorption and scattering process of attenuation material in the ocean [3]. Reinart et al. [14] investigated the profiles of the quanta-to-energy ratio for both oceanic and coastal water types, revealing that this ratio is influenced by factors such as water depth and transparency. Consequently, the quanta-to-energy ratio may deviate by up to 24% from its value in the air. The relationship between the principal wavelength and the quanta-to-energy ratio is characterized by a single constant parameter, . Wang et al. [3] provided an exponential function relationship of the principal wavelength in Case I seawater, along with a semi-empirical function linking the deviation of the principal wavelength to chlorophyll-a concentration. A lack of large-scale observations and less attention to the quanta-to-energy ratio in seawater has led to the common practice of inputting a constant value of 4.57 µmol W−1 s−1 into the geochemical model. This constant value may significantly impact the accuracy and reliability of model simulation outcomes, underscoring the importance of further research in this area to improve our understanding and modeling capabilities.
There remain two key areas of inquiry regarding the quanta-to-energy ratio that warrant further investigation. Firstly, it is essential to characterize the variation of the quanta-to-energy ratio across a broad range of SZA, spanning from 0° to 90°. This will enable a more comprehensive understanding of the ratio’s behavior under diverse illumination conditions. Secondly, the spectral variability of global irradiance is influenced by the combination of radiation spectra from various sources, including the solar disk, clouds, and the atmosphere. Consequently, the quanta-to-energy ratio is inherently connected to the spectral composition of incident diffuse and direct beam irradiance within the 400–700 nm wavelength range. To address this complex interplay, it is crucial to explore how global irradiance can be effectively represented by diffuse and direct beam irradiance components. This study will primarily focus on these two research questions, aiming to advance our understanding of the quanta-to-energy ratio and its implications for energy balance and ecosystem processes in the context of complex spectral radiation dynamics. By addressing these knowledge gaps, we can improve the accuracy of geochemical models and our ability to predict and address the impacts of environmental changes on the Earth’s climate system.
The primary focus of this article revolves around the investigation of alterations in the quanta-to-energy ratio as it reaches terrestrial surfaces. Several works in the literature indicate that the quanta-to-energy at the surface is virtually insensitive to changes in both cloudiness and fine-mode aerosols [1,13]. Consequently, a representative value of 4.56 μmol W−1 s−1 can be employed across a wide range of cloud conditions with minimal error. However, Akitsu et al. [24] reported a dependence of the quanta-to-energy ratio on water vapor pressure, SZA, and clearness index. Notably, their findings revealed a more complex fluctuation in this ratio at high SZA compared to low SZA. Building upon this research, the present study examines the variations in the quanta-to-energy ratio at high SZA under a cloudless maritime atmosphere. By employing a substantial dataset and model outputs, we aim to investigate the potential applications of these findings. The paper is structured into five sections. Section 2 outlines the data sources used and provides an overview of the selected model. Section 3 summarizes the key features of the quanta-to-energy ratio at high SZA and explores its dependence on various factors such as SZA, visibility, Ångström exponent, ozone concentration, wind speed, surface-level pressure, air temperature, and relative humidity. Finally, Section 4 presents the main conclusions of the study and discusses potential applications of the findings in advancing our understanding of the dynamics and implications of the quanta-to-energy ratio.
2. Materials and Methods
2.1. Time-Series Measurements of the Spectral Irradiance of Photosynthetically Active Radiation (PAR)
The values of PAR and the quanta-to-energy ratio at Stations 1 and 2 are determined by time-series analysis of spectral irradiance measurements conducted by the Polar Oceanography and Global Ocean Change laboratory (POGOC) in northern Liaodong Bay during the boreal winter of 2012 (Figure 1). The optical instrument PRR-800, manufactured by Biospherical Instruments Inc. (BSI, San Diego CA, USA), was employed to measure surface downwelling irradiance () at 18 specific wavelengths (313, 380, 412, 443, 490, 510, 520, 532, 555, 565, 589, 625, 665, 683, 710, 765, 780, and 875 nm) [3,25,26,27]. Station 3 was conducted by the Remote Sensing Ocean Optics (ORSOO) laboratory under a clear sky in a river near Orcas Island on 20 June 1998 (Figure 1). A Tethered Spectral Radiometer Buoy (TSRB), manufactured by Satlantic Inc. (Halifax, NS, Canada), was utilized to record continuous measurements of downwelling irradiance just above the sea surface at 412, 443, 490, 555, 670, 684, and 700 nm [28]. To compensate for the data gap at low solar zenith angles, this study incorporates National Renewable Energy Laboratory (NREL) observation data recorded under cloudless skies over 20 days in 1987/1988 (Stations 4 and 5, as outlined in Table 2). Detailed information on the instruments used can be found in the Spectral Solar Radiation Database Documentation (https://www.nrel.gov/grid/solar-resource/spectral-solar.html, accessed on 31 January 2024). The NREL measurements include global-horizontal and diffuse-horizontal spectral irradiance (, and ) between 300 and 900 nm, enabling an investigation into the fluctuations of the quanta-to-energy ratio.
Figure 1.
The locations of solar radiation records. The circled numerals in the figure denote the respective station identification numbers.

Table 2.
Solar radiation records under cloudless atmospheric conditions.
Stations 1, 2, and 3 continuously monitored solar radiation, with a minimum observed solar zenith angle (SZA) of 40° and a maximum of 90°. Due to the high-frequency observations, Stations 1 and 2 obtained 65,534 and 73,001 samples, respectively. Station 3 collected 42,065 samples. At Stations 4 and 5, solar radiation was monitored hourly, with a minimum observed SZA of 4° and a maximum of 90°. The modest fluctuations evident in the diurnal time series suggest that solar radiation was not impacted by the presence of broken clouds (Figure 2A–C). The variability observed in PAR indicates that the dataset encompasses a wide range of cloudless sky conditions, spanning from low to high SZA, highlighting the diversity of the atmospheric conditions represented in the study.
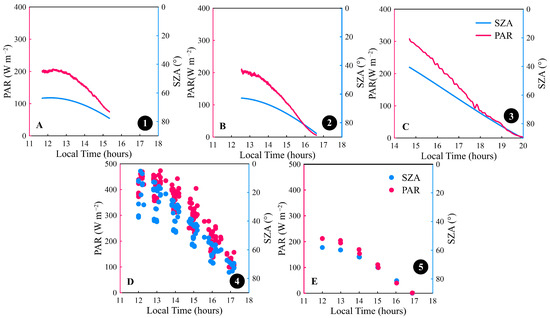
Figure 2.
(A–C) Diurnal time series of global irradiance of photosynthetically active radiation (PAR, red line) and coincident variation in solar zenith angle (blue line) for three consecutive measurements (Stations 1–3). The discrete observation data obtained at Stations 4 and 5 are also displayed in panels (D,E) in the same way (red dots for PAR and blue dots for solar zenith angle).
2.2. Principal Wavelength
The quanta-to-energy ratio can be simplified using the concept of the principal wavelength, as proposed by Wang et al. [3]. This simplification is possible due to the existence of a constant factor, μmol W−1 s−1nm−1 (Equation (1)). The principal wavelength serves as a representation of changes in the solar spectrum and offers a more robust explanation for solar spectral fluctuations compared to the quanta-to-energy ratio. Consequently, the subsequent sections of this study will primarily focus on the fluctuations of the principal wavelength across all observation stations.
2.3. Radiative Transfer Model
The SPCTRAL2 model, developed by Bird and Riordan [29], was initially employed to simulate incident downward radiation at the Earth’s surface. Subsequently, Gregg and Carder [30] applied this model to determine the downward irradiance entering the ocean. Bird and Hulstrom [31] the relevance of SPCTRAL2 to high SZA regions, such as the Arctic Ocean. Building on this work, Campbell and Aarup [32] pioneered the use of SPCTRAL2 to simulate PAR fluctuations at high SZA. The simplicity of the model, along with its minimal input requirements, has contributed to its widespread adoption and utility in various studies.
The SPCTRAL2 model attributes the attenuation of solar radiation in the visible and near-infrared spectral regions of the atmosphere to five distinct processes: Rayleigh scattering by mixed gases, absorption by mixed gases (predominantly oxygen), ozone absorption, aerosol absorption and scattering, and water vapor absorption. In this model, the global solar radiation () reaching the underlying surface is partitioned into two components: direct solar radiation () and diffuse solar radiation (). Direct solar radiation represents the portion of solar radiation that directly reaches the surface following atmospheric absorption. Conversely, diffuse solar radiation denotes the portion of solar radiation deviating from the beam direction due to scattering. The mathematical expressions for these radiation components can be represented as follows:
where the subscripts ‘g’, ‘d’, and ‘s’ denote global, direct, and diffuse radiation, respectively. is the extraterrestrial irradiance at the mean Earth–Sun distance for a given wavelength , while D serves as a correction factor accounting for variations in the Earth–Sun distance. The transmittance functions of the atmosphere at wavelength λ are denoted by , , , , and , which represent molecular (Rayleigh) scattering, aerosol attenuation, water vapor absorption, ozone absorption, and uniformly mixed gas absorption, respectively. The SZA is indicated by θ. In the SPCTRAL2 model, diffuse irradiance is further subdivided into three components: the Rayleigh scattering component ; the aerosol scattering component , and the component that accounts for multiple reflections of irradiance between the ground and the air . The detailed calculation formulas for these components can be found in the work of Bird and Riordan [29].
2.4. Simulated Sky-Radiances
To assess the model’s performance, this study compares the downwelling irradiance under different SZA at Stations 1 and 2 with simulated downwelling irradiance under identical atmospheric conditions and SZA. Simultaneous observations of various meteorological elements, such as surface air temperature (SAT), sea level pressure (SLP), wind speed, and humidity, were conducted at a nearby meteorological station, providing reliable parameters for the model. Table 3 presents the input parameters for the model at different SZAs for Stations 1 and 2. Additionally, the underlying surface albedo is required for the model. In situ observations were conducted using a features spectrometer manufactured by Analytical Spectral Devices Inc. (Boulder, CO, USA) to obtain ice–albedo data for Station 2, as depicted in Figure 3.

Table 3.
List of environmental variables incorporated into SPCTRAL2. The surface air temperature (SAT), humidity (H), and sea level pressure (SLP) data were obtained from a meteorological station in proximity to the optical observation station. Visibility (V) data were sourced from observations made by the meteorological bureau. Ozone concentration and Ångström exponent (AE) values were derived from the MODIS M3 aerosol product.
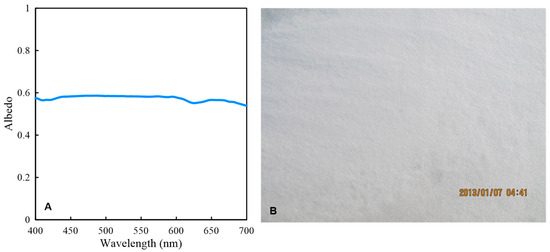
Figure 3.
Underlying surface albedo measurements at Station 2 (A), a location characterized by snow-covered sea ice (B).
Figure 4 provides a comparison between the downwelling irradiance obtained from the SPCTRAL2 simulation and the corresponding observational data. The relative inaccuracies between the two datasets are presented in Table 4. The observed and simulated solar radiation spectra exhibit a high degree of consistency, with a steady inaccuracy ranging from 2% to 3%. The highest inaccuracy is observed in Case 2C6, with a value of 7.08%. Overall, the SPCTRAL2 model demonstrates sufficient accuracy to meet the requirements of this study.
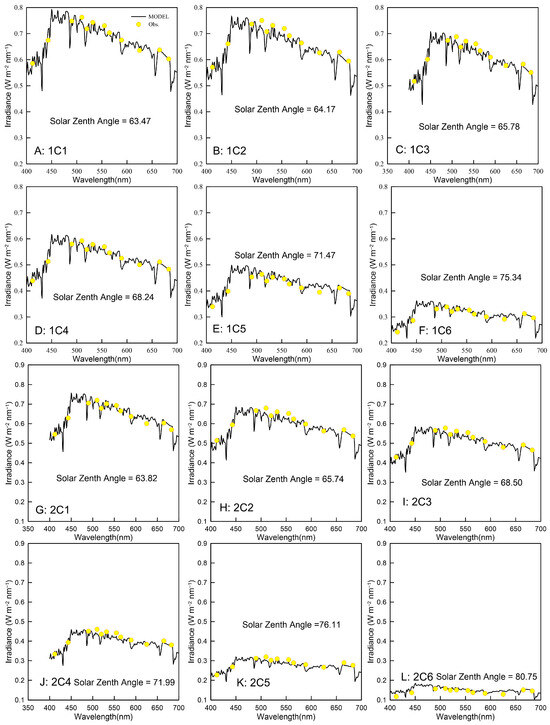
Figure 4.
Comparison of the simulated downwelling irradiance (black solid line) with the observation value at specific wavelengths (yellow dots). The requisite environmental variables utilized for the simulation process are enumerated in Table 3, with panels (A–L) corresponding to 1C1 to 2C6 in the table, respectively. The solar zenith angle during each observation is indicated within the individual plots.

Table 4.
The relative inaccuracies of the simulated downwelling irradiance when compared to the corresponding observed values.
3. Results and Discussion
3.1. Influence of the Solar Zenith Angle on the Principal Wavelength
Under clear sky conditions, the principal wavelength initially exhibits an implicit increase, followed by a subsequent decrease as the solar zenith angle increases (Figure 5A). The variation in principal wavelength is minimal when the solar zenith angle is below 60°, ranging from 543.97 nm (the quanta-to-energy ratio = 4.57 μmol W−1 s−1) at an SZA of 2.5° to 546.07 nm at 60° (the quanta-to-energy ratio = 4.58 μmol W−1 s−1) at Station 2 (Figure 5B). The principal wavelength reaches its maximum value of 551.95 nm (the quanta-to-energy ratio = 4.64 μmol W−1 s−1) when the SZA approaches 78°. Beyond this point, the principal wavelength rapidly declines, reaching 536.34 nm (the quanta-to-energy ratio = 4.51 μmol W−1 s−1) at an SZA of 87.43°, which corresponds to a decrease of approximately 1.5% compared to smaller SZAs. A similar pattern of fluctuation is observed at Stations 3 and 5 (Figure 5A). The equipment at station 3 is situated on the seawater surface. The principal wavelength at Station 3, located on the sea surface, is higher than that at Station 2 under high SZA conditions due to the influence of sea waves.
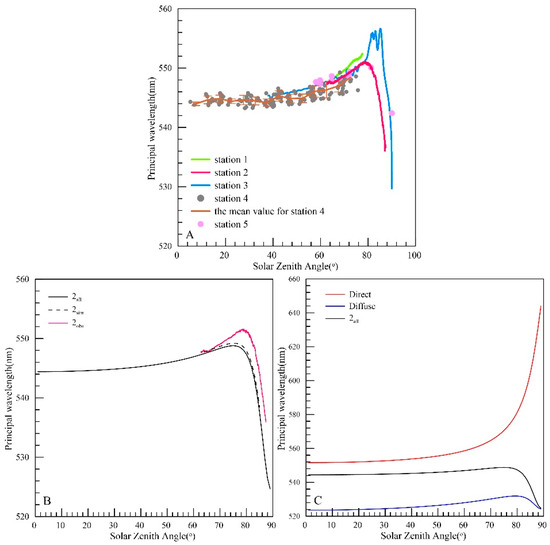
Figure 5.
Variation in the principal wavelength with increasing solar zenith angles (SZA). Panel (A) shows the observation principal wavelength for each of the five stations. Panel (B) is the comparison of the observation principal wavelength (red line) with the simulated value at Station 2 using the observed time series of atmospheric parameters (dashed line). The solid line represents the simulated output under the same atmospheric conditions of 1C1 with an SZA range of 0–90°. Panel (C) depicts the fluctuation of principal wavelength derived from global irradiance (black line), diffuse irradiance (blue line), and direct irradiance (red line) simulated by SPCTRAL2 as simulated by SPCTRAL2 in the identical meteorological conditions as 1C1 in Table 3.
Both the simulated principal wavelength obtained from the SPCTRAL2 model and the observed values exhibit consistent trends (Figure 5B). However, at high SZAs, the observed principal wavelength is greater than the simulated values. Rayleigh scattering can be employed to elucidate the fluctuation of the principal wavelength at low SZAs. Deirmendjian and Sekera [33] demonstrated that in a clean, clear atmosphere, Rayleigh scattering leads to a shift in the maximum spectral irradiance within the PAR region towards longer wavelengths as the solar zenith angle increases, resulting in the depletion of blue radiation. Nonetheless, this phenomenon cannot fully account for the abrupt decrease in principal wavelength observed at higher SZA. To address this, the definition formula of the principal wavelength was modified, and a relationship with the diffuse fraction of PAR (f) was established, yielding the following Equation:
where and are the principal wavelengths computed from global irradiance, diffuse irradiance, and direct irradiance, respectively.
Taking Station 2 as an example in Figure 5C, is observed to be greater than , while lies between the two, which may also be deduced from Equation (5). As the SZA increases, exhibits an increasing trend, whereas initially grows and subsequently drops. According to Equation (5), varies as a function of the diffuse fraction (f). When f is small, is more strongly influenced by . For instance, at a 30° SZA, the fraction of diffuse irradiance is 0.28, and the computed value of is 544.85 nm, which is closer to the value of of 552.69 nm. As the SZA increases, so does the diffuse irradiance fraction, reaching 0.56 at a 75° SZA. Concurrently, the value of 548.79 nm is found to be closer to the value of 531.35 nm. Upon further increase in SZA, f reaches 0.89 at an 85° SZA. The computed value at this moment is 537.73 nm, which is more closely aligned with = 529.18 nm. The rapid drop in principal wavelength can be attributed to the substantial increase in the diffuse fraction of PAR.
Under cloudless conditions, the principal wavelength typically exhibits minimal fluctuation, remaining close to 544.05 nm (the quanta-to-energy ratio = 4.57 μmol W−1 s−1) for SZAs below 70°. By excluding observation values at SZAs larger than 70°, a linear relationship between the principal wavelength and relative air mass is established, as shown in Figure 6. The principal wavelength gradually increases with increasing SZA until it reaches its maximum value, after which it rapidly declines. Observational data reveal that the principal wavelength can deviate by up to 1.5% (relative to 544.05 nm) at an SZA of 87.43°. Notably, the simulated principal wavelength decreases significantly by 3.5% at an SZA of 89°. Due to a lack of observational data, it is not possible to establish a connection between the principal wavelength and relative air mass at high SZAs. It is important to note that when utilizing the quanta-to-energy ratio at high SZAs, such as in polar regions, careful attention must be given to its dependence on SZA variations.
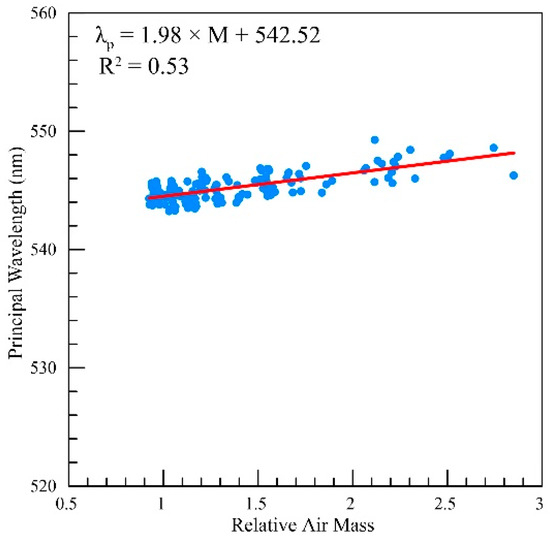
Figure 6.
The linear relationship between the principal wavelength and relative air mass. The blue dots represent the observation value of the principal wavelength at Station 4, while the red solid line denotes the relationship obtained through linear regression analysis. The linear regression equation, displayed in the upper left corner, exhibits a coefficient of determination (R2) of 0.53.
3.2. Effects of Atmospheric Absorption and Scattering on the Principal Wavelength
The preceding analysis examined the influence of solar zenith angle on the principal wavelength. As the solar zenith angle increases, the relative air mass undergoes significant changes, affecting the solar spectrum. In a cloudless sky, atmospheric components such as aerosols, ozone, and water vapor absorb and scatter light, considerably altering the solar spectrum. This section will explore the effects of these factors on the principal wavelength associated with global irradiance, diffuse irradiance, and direct radiation, as well as the diffuse fraction of PAR. The discussion will primarily focus on understanding the relationships and interactions between these variables and their respective impacts on the principal wavelength.
3.2.1. Visibility
Visibility is utilized in the model to calculate the aerosol extinction coefficient. Figure 7 depicts the effect of varying visibility on the principal wavelength. In this paper, we determine the principal wavelengths ( and ) related to global irradiance, diffuse irradiance, and direct radiation, as well as the diffuse fraction of PAR. To evaluate their variability, the standard deviation (SD) of and was calculated across a visibility range of 5–25 km, as shown in Table 5.
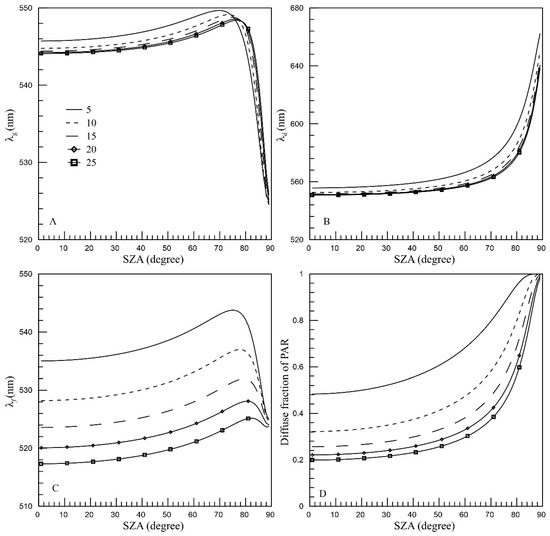
Figure 7.
The variation in (A), (B) and (C) as simulated by SPCTRAL2 with increasing SZA under a visibility range of 5–25 km. Panel (D) illustrates the diffusion fraction of PAR as a function of SZA for visibilities ranging from 5 to 25 km. In the figure, solid lines represent a visibility of 5 km, dotted lines indicate a visibility of 10 km, dashed lines correspond to a visibility of 15 km, diamond-marked solid lines represent a visibility of 20 km, and square-marked solid lines indicate a visibility of 25 km.

Table 5.
The standard deviation of and as simulated by the SPCTRAL2 model across a visibility range of 5–25 km.
Figure 7 reveals consistent profiles for and under different visibility conditions. At lower SZAs, and all decrease with increasing visibility. The SD for ranges from 7 to 8 nm at SZAs less than 80° and then declines significantly as the SZA increases (Table 5). The SD for is less than 4 nm for SZAs under 60° but rises as the SZA increases. The mean SD for is 0.78 nm for SZAs less than 60°, followed by a double-peak profile at SZAs of 60° and 80°. This trend is attributed to the increasing fraction of diffuse radiation in PAR as the SZA increases. Additionally, the SZA at which reaches its maximum value and increases considerably with increasing visibility.
3.2.2. Ångstrom Exponent (AE)
The Ångstrom exponential (AE) serves as an indicator of aerosol particle size [34,35]. Table 6 presents the simulated principal wavelengths ( and ) related to global irradiance, diffuse irradiance, and direct radiation under various AE. Figure 8 depicts the profiles of principal wavelengths at different AE values.

Table 6.
The standard deviation of and as simulated by the SPCTRAL2 model across a Ångstrom exponential range of 0.2–1.0.
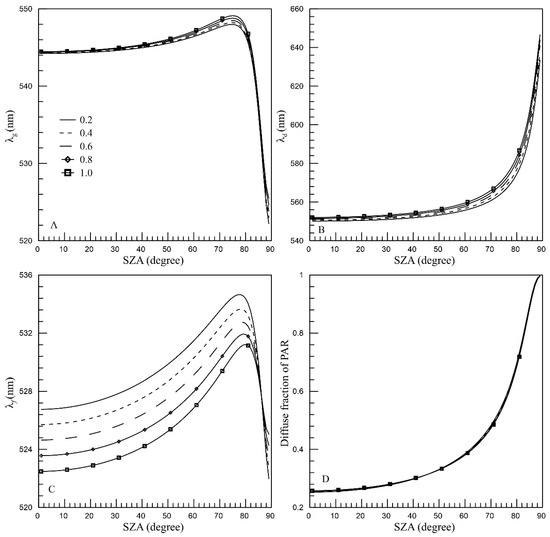
Figure 8.
The variation in (A), (B) and (C) as simulated by SPCTRAL2 with increasing SZA under a Ångstrom exponential range of 0.2–1.0. Panel (D) illustrates the diffusion fraction of PAR as a function of SZA. Solid lines represent an AE of 0.2; dotted lines indicate an AE of 0.4; dashed lines correspond to an AE of 0.6; diamond-marked solid lines represent an AE of 0.8; and square-marked solid lines indicate an AE of 1.0.
It can be observed that increases considerably with increasing AE. However, its SD is only 0.15 nm at a low SZA, such as 60°, which is approximately one-fifth of the SD affected by visibility, as seen in Table 5. While for direct irradiance also increases slightly with increasing AE, its influence is significantly less than that of visibility. On the other hand, for diffuse irradiance exhibits a substantial decrease as AE increases, with a more pronounced reduction compared to direct and global radiation. Notably, the SD of remains relatively constant across the entire SZA range. Moreover, the SZA at which reaches its maximum value and remains unchanged with varying AE. These properties might be attributed to the wavelength-independent nature of the AE.
3.2.3. Ozone, Wind Speed, SLP, SAT, and Relative Humidity
In this study, the effects of various parameters, including total column ozone, wind speed, surface-level pressure, surface air temperature, and relative humidity, on the principal wavelength are investigated (Figure 9). The ranges of these parameters are presented in Table 7. Here, we specifically demonstrate the variation of the principal wavelength with SZA under different total column ozone conditions.
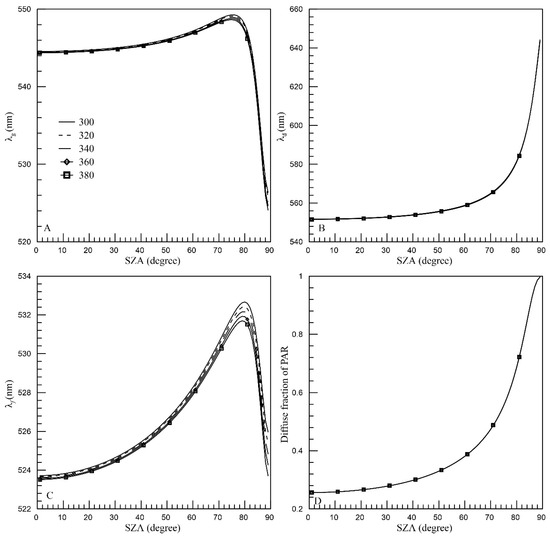
Figure 9.
The variation in (A), (B) and (C) as simulated by SPCTRAL2 with increasing SZA under an ozone concentration range of 300~380 Dobson units. Panel (D) illustrates the diffusion fraction of PAR as a function of SZA. Solid lines represent an ozone concentration of 300 Dobson units; dotted lines indicate an ozone concentration of 320 Dobson units; dashed lines correspond to an ozone concentration of 340 Dobson units; diamond-marked solid lines represent an ozone concentration of 360 Dobson units; and square-marked solid lines indicate an ozone concentration of 380 Dobson units.

Table 7.
The values of atmospheric parameters incorporated into the SPCTRALS2 model.
The results indicate that, among these parameters, only the total column ozone has a notable impact on the principal wavelength. However, this influence is considerably less substantial than that of aerosols. It can be inferred that the principal wavelength is not significantly affected by ozone, wind speed, surface-level pressure, surface air temperature, or relative humidity. This suggests that these factors play a relatively minor role in determining the principal wavelength under varying atmospheric conditions.
The preceding analysis reveals that visibility exerts the most significant influence on the principal wavelength, with aerosol Ångstrom Exponent (AE) having a secondary impact, while ozone, wind speed, surface-level pressure (SLP), surface air temperature (SAT), and relative humidity exhibit minimal effects. An increase in visibility results in a reduction of the principal wavelength, irrespective of whether it pertains to global irradiance, direct irradiance, or diffuse irradiance. AE has a limited effect on and , affecting only the value of . When comparing the effects of AE and visibility on , it is observed that the impact of AE remains constant with changing SZA, whereas the impact of visibility sharply decreases after 80°. At low SZA, visibility has an impact that is approximately four times greater than AE. Based on the SPECTRAL2 output, two relationships between the principal wavelength for global irradiance at 20° SZA and visibility, as well as the diffuse fraction of PAR, can be established, as shown in Figure 10. The inaccuracy in these relationships is attributed to AE.
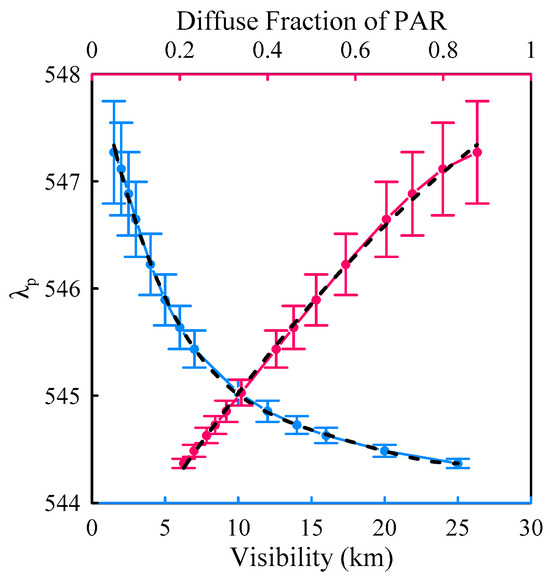
Figure 10.
The polynomial fitting relationships of the principal wavelength for global irradiance at an SZA of 20° with visibility (blue) and the diffuse fraction of PAR (red).
To validate the relationship between the diffuse fraction and principal wavelength, observed principal wavelength data are employed. Due to varying observation times, the on-site measured principal wavelength must be adjusted to a fixed SZA for consistency. In this case, the relationship between the principal wavelength and relative air mass, as depicted in Figure 6, is utilized to adjust the observed data to an SZA of 20°. Upon comparison, it is found that the model-fitting results align well with the observed data, as shown in Figure 10. This close agreement between the model and observations demonstrates the reliability and accuracy of the established relationship between the diffuse fraction and principal wavelength under different atmospheric conditions.
3.3. Prospective Applications of the Principal Wavelength
The principal wavelength, which effectively measures solar spectrum variability and remains unaffected by radiation energy, possesses unique characteristics that offer several potential applications in various research areas. By capitalizing on its distinct attributes, the principal wavelength could contribute significantly to fields such as atmospheric studies, remote sensing, and ecosystem research.
One potential application of the principal wavelength lies in the realm of visibility measurements and satellite-based visibility inversion. The strong correlation between the principal wavelength and visibility suggests its utility in this context, offering valuable insights into atmospheric aerosol particle size variations. This could have significant implications for urbanization studies and investigations of atmospheric pollutant diffusion.
Another area where the principal wavelength could prove useful is in the estimation of the diffuse fraction of PAR in observations. Given that the determination of f often poses challenges and requires stable platforms, the relationship between the principal wavelength and f offers a viable alternative. This method can be applied to satellite remote sensing, aiding in oceanic observation research and large-scale ecosystem studies.
The true potential of the principal wavelength likely extends beyond the discussed applications, as it not only inherits the research direction of the quanta-to-energy ratio but also opens up new avenues for exploration. By combining the principal wavelength with satellite remote sensing data, its application areas could be broadened to encompass forest systems, climate change at large scales, ecosystems, and more. Further research is required to fully harness the potential of the principal wavelength in these diverse domains.
4. Conclusions
The quanta-to-energy ratio is frequently employed as it facilitates the conversion between energy and quanta units. In some applications, the quanta-to-energy ratio of the underlying surface is often substituted with the constant value of 4.57 µmol W−1 s−1. Several studies have examined the factors influencing the quantum energy ratio, including the clearness index, SZA, and water vapor pressure. However, since its inception in 1974, the quanta-to-energy ratio has not been extensively explored, and its broader applications remain understudied. In the present work, observational data under a cloudless atmosphere and SPCTRAL2 model outputs are primarily utilized to investigate the variation in the quanta-to-energy ratio from a 0° to 90° SZA. The effects of various factors, such as aerosols, ozone, relative humidity, surface air temperature, surface-level pressure, and surface wind speed, on the quanta-to-energy ratio were studied using model simulations. Building on these findings, the potential applications of the quantum energy ratio will be further investigated, paving the way for its wider use in relevant fields.
The principal wavelength serves as a simplified representation of the quanta-to-energy ratio calculation using a single constant. Compared to the quanta-to-energy ratio, the principal wavelength offers a clearer physical interpretation and can elucidate variations in the solar spectrum, making it more intuitive and easier to comprehend [3]. Consequently, this study emphasizes the examination of the principal wavelength fluctuations under cloudless atmospheric conditions, with the aim of shedding light on the underlying factors contributing to these variations.
Both simulation and observation data revealed that the principal wavelength exhibits a gradual increase at SZAs from 0° to 90°, followed by a rapid rise beyond 60° and a subsequent sharp decline after reaching its maximum value. The Rayleigh scattering theory can account for the observed relationship between the principal wavelength and relative air mass at SZAs below 70°. This study attributes the decrease in principal wavelength to an increase in the diffuse fraction of PAR. Under cloudless meteorological conditions, the variability in the measured quanta-to-energy ratio remains within 3% for SZAs less than 70°. A significant change in the quanta-to-energy ratio is only observed at SZAs greater than 80°. Simulation results indicate that the quanta-to-energy ratio inaccuracy may approach 3% solely under the condition of an SZA of 89°, underscoring the negligible influence of the quanta-to-energy ratio on the solar radiation spectrum at lower SZAs.
Under cloudless meteorological conditions, the model simulations indicate that ozone, wind speed, surface-level pressure, surface air temperature, and relative humidity have negligible effects on the quanta-to-energy ratio. The Ångstrom exponent exerts a minor influence on the quanta-to-energy ratio by affecting diffuse radiation. On the other hand, visibility is found to have a substantial impact on the quanta-to-energy ratio. Consequently, two relationships are established, linking the principal wavelength to visibility and the diffuse fraction of PAR. Visibility can be measured through visual methods, transmissometers, and scatterometers. The diffuse fraction is typically calculated by shielding direct solar radiation. However, obtaining visibility and diffuse radiation from ship-based observations can be challenging due to the ship’s motion. The strong correlations identified in this study demonstrate that by measuring the solar radiation spectrum under cloudless atmospheric conditions at sea, it is possible to estimate visibility and the diffuse fraction of PAR, thus overcoming the limitations imposed by ship-based measurements.
Despite previous studies examining the quanta-to-energy ratio under various atmospheric conditions, their primary focus has been limited to treating it as a mere conversion factor. In contrast, the principal wavelength serves as a measure of solar spectrum variability and remains unaffected by radiation energy. This unique characteristic implies that atmospheric parameters that do not alter the solar radiation spectrum will not influence the principal wavelength. Consequently, its potential applications extend beyond that of a conversion constant, suggesting broader prospects for its future use in understanding and modeling solar radiation under different atmospheric conditions.
Author Contributions
W.W. contributed to the data acquisition, data analysis, research design, and manuscript writing. S.C., J.H. and R.D. checked the paper and proposed amendments. L.C. helped in the analysis of data and revised the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Scientific Research Foundation of the Third Institute of Oceanography, MNR (No. 2024023), the Special Fund for Marine Services and High-Quality Development of Fisheries in Fujian Province (FJHY-YYKJ-2024-1-12), the National Natural Science Foundation of China (No. 42130406), the Global Change and Air–Sea Interaction II (No. GASI-01-SIND-STwin and GASI-01-NPAC-STsum).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Stations 1~2 are available from the corresponding author on reasonable request. Sites 3~5 generated during and/or analysis during the current study are available in the National Renewable Energy Laboratory (https://www.nrel.gov/grid/solar-resource/, accessed on 31 January 2024).
Acknowledgments
Thank Jinping Zhao for providing the original data of Station 1 and Station 2. Thank Qiuli Shao for the preliminary analysis of the observed data and POGOC Polar Group for their assistance in field observation.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Yamashita, M.; Yoshimura, M. Estimation of Global and Diffuse Photosynthetic Photon Flux Density under Various Sky Conditions Using Ground-Based Whole-Sky Images. Remote Sens. 2019, 11, 932. [Google Scholar] [CrossRef]
- Li, R.; Zhao, L.; Ding, Y.; Wang, S.; Ji, G.; Xiao, Y.; Liu, G.; Sun, L. Monthly Ratios of PAR to Global Solar Radiation Measured at Northern Tibetan Plateau, China. Sol. Energy 2010, 84, 964–973. [Google Scholar] [CrossRef]
- Wang, W.; Zheng, J.; Jing, C.; Zhao, J. Relationship of the Quanta-to-Energy Ratio of Photosynthetically Active Radiation with Chlorophyll-a in Case I Seawater. J. Mar. Sci. Eng. 2022, 10, 2005. [Google Scholar] [CrossRef]
- Emmanuel, D.; Phillipe, D.; Malik, C. Radiative Transfer Code: Application to the Calculation of PAR. Proc. Indian. Acad. Sci. Earth Planet. Sci. 2000, 109, 407–413. [Google Scholar] [CrossRef]
- Akitsu, T.K.; Nasahara, K.N.; Ijima, O.; Hirose, Y.; Ide, R.; Takagi, K.; Kume, A. The Variability and Seasonality in the Ratio of Photosynthetically Active Radiation to Solar Radiation: A Simple Empirical Model of the Ratio. Int. J. Appl. Earth Obs. Geoinf. 2022, 108, 102724. [Google Scholar] [CrossRef]
- Zhou, H.; Yue, X.; Lei, Y.; Zhang, T.; Tian, C.; Ma, Y.; Cao, Y. Responses of Gross Primary Productivity to Diffuse Radiation at Global FLUXNET Sites. Atmos. Environ. 2021, 244, 117905. [Google Scholar] [CrossRef]
- Wang, W.; Jing, C.; Guo, X. Observation and Simulation of the Diffuse Attenuation Coefficient of Downwelling Irradiance in the Polar Ocean. Sci. China Earth Sci. 2023, 66, 1535–1546. [Google Scholar] [CrossRef]
- Noriega Gardea, M.M.A.; Corral Martínez, L.F.; Anguiano Morales, M.; Trujillo Schiaffino, G.; Salas Peimbert, D.P. Modelling Photosynthetically Active Radiation: A Review. Atmósfera 2020, 34, 357–370. [Google Scholar] [CrossRef]
- Osborne, B.A.; Kirk, J.T.O. Light and Photosynthesis in Aquatic Ecosystems. J. Appl. Ecol. 1995, 32, 448. [Google Scholar] [CrossRef]
- Jacovides, C.P.; Tymvios, F.S.; Asimakopoulos, D.N.; Theofilou, K.M.; Pashiardes, S. Global Photosynthetically Active Radiation and Its Relationship with Global Solar Radiation in the Eastern Mediterranean Basin. Theor. Appl. Climatol. 2003, 74, 227–233. [Google Scholar] [CrossRef]
- Niu, Z.; Wang, L.; Niu, Y.; Hu, B.; Zhang, M.; Qin, W. Spatiotemporal Variations of Photosynthetically Active Radiation and the Influencing Factors in China from 1961 to 2016. Theor. Appl. Clim. 2019, 137, 2049–2067. [Google Scholar] [CrossRef]
- McCree, K.J. Test of Current Definitions of Photosynthetically Active Radiation against Leaf Photosynthesis Data. Agric. Meteorol. 1972, 10, 443–453. [Google Scholar] [CrossRef]
- Dye, D.G. Spectral Composition and Quanta-to-Energy Ratio of Diffuse Photosynthetically Active Radiation under Diverse Cloud Conditions. J. Geophys. Res. D Atmos. 2004, 109, 1–12. [Google Scholar] [CrossRef]
- Reinart, A.; Arst, H.; Blanco-Sequeiros, A.; Herlevi, A. Relation between Underwater Irradiance and Quantum Irradiance in Dependence on Water Transparency at Different Depths in the Water Bodies. J. Geophys. Res. Ocean. 1998, 103, 7749–7752. [Google Scholar] [CrossRef]
- Morel, A.; Smith, R.C. Relation between Total Quanta and Total Energy for Aquatic Photosynthesis. Limnol. Oceanogr. 1974, 19, 591–600. [Google Scholar] [CrossRef]
- Morel, A. Available, Usable, and Stored Radiant Energy in Relation to Marine Photosynthesis. Deep-Sea Res. 1978, 25, 673–688. [Google Scholar] [CrossRef]
- Aguiar, L.J.G.; Fischer, G.R.; Ladle, R.J.; Malhado, A.C.M.; Justino, F.B.; Aguiar, R.G.; da Costa, J.M.N. Modeling the Photosynthetically Active Radiation in South West Amazonia under All Sky Conditions. Theor. Appl. Climatol. 2012, 108, 631–640. [Google Scholar] [CrossRef]
- Tsubo, M.; Walker, S. Relationships between Photosynthetically Active Radiation and Clearness Index at Bloemfontein, South Africa. Theor. Appl. Climatol. 2005, 80, 17–25. [Google Scholar] [CrossRef]
- Udo, S.O.; Aro, T.O. Global PAR Related to Global Solar Radiation for Central Nigeria. Agric. For. Meteorol. 1999, 97. [Google Scholar] [CrossRef]
- Meek, D.W.; Hatfield, J.L.; Howell, T.A.; Idso, S.B.; Reginato, R.J. Generalized Relationship between Photosynthetically Active Radiation and Solar Radiation. Agron. J. 1984, 76, 939–945. [Google Scholar] [CrossRef]
- Ge, S.; Smith, R.G.; Jacovides, C.P.; Kramer, M.G.; Carruthers, R.I. Dynamics of Photosynthetic Photon Flux Density (PPFD) and Estimates in Coastal Northern California. Theor. Appl. Climatol. 2011, 105, 107–118. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, Y.; Zhoub, Y. Measuring and Modelling Photosynthetically Active Radiation in Tibet Plateau during April-October. Agric. For. Meteorol. 2000, 102, 207–212. [Google Scholar] [CrossRef]
- Bai, J. Observations and Estimations of PAR and Solar Visible Radiation in North China. J. Atmos. Chem. 2012, 69, 231–252. [Google Scholar] [CrossRef]
- Akitsu, T.; Kume, A.; Hirose, Y.; Ijima, O.; Nasahara, K.N. On the Stability of Radiometric Ratios of Photosynthetically Active Radiation to Global Solar Radiation in Tsukuba, Japan. Agric. For. Meteorol. 2015, 209, 59–68. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, W.; Cooper, L. Calculation of Photosynthetically Available Radiation Using Multispectral Data in the Arctic. Chin. J. Polar Res. 2010, 22, 91–103. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, W.; Kang, S.-H.; Yang, E.-J.; Kim, T.-W. Optical Properties in Waters around the Mendeleev Ridge Related to the Physical Features of Water Masses. Deep. Sea Res. Part. II Top. Stud. Oceanogr. 2015, 120, 43–51. [Google Scholar] [CrossRef]
- Wang, W.; Zhao, J. Variation of Diffuse Attenuation Coefficient of Downwelling Irradiance in the Arctic Ocean. Acta Oceanol. Sin. 2014, 33, 53–62. [Google Scholar] [CrossRef]
- Du, K.P.; Xie, D.H.; Lee, Z.P.; He, M.X. A Semi-Analytical Data Processing Method for the Satlantic Hyper-TSRB. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Anchorage, AK, USA, 20–24 September 2004; Volume 5. [Google Scholar]
- Bird, R.E.; Riordan, C. Simple Solar Spectral Model for Direct and Diffuse Irradiance on Horizontal and Tilted Planes at the Earth’s Surface for Cloudless Atmospheres. J. Clim. Appl. Meteorol. 1986, 25, 87–97. [Google Scholar] [CrossRef]
- Gregg, W.W.; Carder, K.L. A Simple Spectral Solar Irradiance Model for Cloudless Maritime Atmospheres. Limnol. Oceanogr. 1990, 35, 1657–1675. [Google Scholar] [CrossRef]
- Bird, R.E.; Hulstrom, R.L. A Simplified Clear Sky Modal for Direct and Diffuse Insolation on Horizontal Surfaces; Solar Energy Research Institution: Golden, CO, USA, 1981. [Google Scholar]
- Campbell, J.W.; Aarup, T. Photosynthetically Available Radiation at High Latitudes. Limnol. Oceanogr. 1989, 34, 1490–1499. [Google Scholar] [CrossRef]
- Deirmendjian, D.; Sekera, Z. Global Radiation Resulting from Multiple Scattering in a Rayleigh Atmosphere. Tellus 1954, 6, 382–398. [Google Scholar] [CrossRef]
- Wang, W.; Zhu, D.; Jing, C.; Guo, X.; Chen, L. Spatial Distribution and Temporal Variation of Aerosol Optical Depth in the Western Pacific Ocean. Dyn. Atmos. Ocean. 2022, 99, 101303. [Google Scholar] [CrossRef]
- Wang, W.; Jing, C.; Zhu, D.; Guo, X. Features and Sources of Aerosol Properties over the Western Pacific Ocean Based on Shipborne Measurements. Meteorol. Atmos. Phys. 2023, 135, 24. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).