Abstract
The concern with the well-being of users in buildings has become increasingly essential, covering aspects related to health, energy efficiency, and productivity. The thermal environment evaluation in buildings has become more frequent due to the time people spend inside them. In this context, this study aimed to analyze thermal comfort in classrooms at a Brazilian University. During the autumn, 50 measurements were performed, resulting in 519 valid responses. The results of the linear regression analysis revealed that the thermal comfort range for females was 20.39–22.19 °C, while for males it was 19.47–22.56 °C. Through discriminant analysis, participants were classified based on their thermal sensation vote (TSV), predicted mean vote (PMV), and thermal preference votes (PREF), achieving a success rate of 76.1% for females and 81.6% for males in forming the groups, which demonstrates the effectiveness of discriminant functions in predicting thermal comfort for both groups. These results highlight the importance of considering gender differences in the search for thermal comfort conditions and providing guidelines that promote the well-being of occupants and the conscious use of energy. This implies adjusting the thermal conditions according to the specific needs of males and females in classrooms, always seeking to provide a suitable environment for activities, and considering energy efficiency and users’ productivity.
1. Introduction
Over the years, engineers and architects have become aware of the need to design more energy-efficient buildings. This implies reducing energy consumption and providing comfort indoors [1]. Considering that people spend about 90% of their time indoors, it is essential to ensure comfortable thermal conditions [2]. Several strategies are implemented to achieve this thermal comfort, including heating, ventilation, and air-conditioning systems [3], the application of thermal comfort and sustainability standards, and the inclusion of adaptability to individuals. These aspects are usually addressed in field research involving personal, environmental, interpersonal, and non-thermal factors [4]. To perform this analysis, it is important to include subjective responses from rating scales to describe individuals’ acceptability, comfort, and thermal sensation [5]. It is worth noting that due to the COVID-19 pandemic, the interest in ensuring healthier environments has become even more evident [6].
In this context, educational environments play a relevant role in people’s lives. They should value the well-being and performance of students throughout their academic stages, which require concentration and critical thinking [7]. However, environmental conditions can have an impact on these aspects. Educational levels range from kindergartens to universities [8], and research has focused on analyzing the relationship between thermal comfort and student satisfaction and productivity. Over the years, studies have been carried out in educational buildings, such as kindergartens in Slovenia and Korea [9,10], secondary schools in Portugal and Indonesia [11,12], elementary schools in Australia and Costa Rica [13,14], and universities in Ecuador, Malaysia, and Japan [15,16].
In addition to these studies, several statistical techniques have been used to investigate thermal comfort in classrooms. These approaches range from using factor analysis to examine whether the surrounding environment can influence math performance [17] to applying Bayesian statistical methods to improve building energy efficiency [18]. Logistic regression has also been used to identify acceptable air temperature limits in buildings with heating, ventilation, and air-conditioning (HVAC) systems [19]. Griffiths analysis was applied to measure the sensitivity of individuals to different temperatures [20] and clustering analysis to understand people’s predominant perception of the thermal environment [21].
Techniques such as linear regression [22] and discriminant analysis [23] have disclosed interactions between variables and categorized elements into independent groups. Lai and Chen [24] used linear regression to predict the distribution of thermal comfort based on subjective evaluations of thermal sensations. Maykot, Rupp, and Ghisi [25] determined thermal comfort temperatures for men and women in air-conditioned and mixed-mode offices. Gobo et al. [26] developed a thermal comfort model suitable for subtropical climates. Wu et al. [27] created an adaptive comfort model to evaluate the conditions of naturally ventilated residential buildings in China. In the study by Talukdar et al. [28], linear regression was applied to relate evaluations of thermal sensations to the operative internal temperature to estimate the neutral temperature. Singh and Chani [29] investigated naturally ventilated apartments to determine the corresponding temperatures and comfort range.
Niza and Broday [30] used discriminant analysis to categorize individuals based on their thermal sensations, obtaining an accuracy of over 96%. In addition, Wu, Li, and Qi [31] investigated the possibility of identifying an individual’s state of thermal comfort in the environment using electroencephalography (EEG) signals, achieving a discrimination rate of approximately 87.9%. Shan et al. [32] evaluated energy consumption in residential buildings based on thermophysical properties, achieving a classification rate of up to 97.9%. Gładyszewska-Fiedoruk and Sulewska [33] classified mental states in different thermal conditions using patterns of electroencephalogram (EEG) neural signals, optimizing the experience of individuals in buildings, where they achieved a classification rate of over 95% for both task and rest conditions. Neale, Kummert, and Bernier [34] used linear discriminant analysis to apply machine learning classification to predict building characteristics from electricity smart meter data.
In this context, the central aim of this research is to comprehensively investigate thermal comfort conditions in university classrooms, focusing on analyzing the differences in preferences and perceptions of thermal comfort between the female and male genders. The focus was on determining the thermal comfort temperatures for each gender based on the subjective responses collected from the participants and investigating how the participants distinguish themselves into groups based on thermal sensation votes (TSVs), predicted mean votes (PMVs), and thermal preference votes (PREF) using discriminant analysis. Although studies have been carried out at various levels of education to understand thermal comfort and its implications in classrooms, there is a lack of specific research into how thermal comfort preferences and perceptions may vary in university institutions. Most of the research has focused on younger age groups, such as kindergarten and elementary school, and little attention has been paid to higher education. Thus, the gap to be filled is understanding the differentiated thermal preferences of university students and how this can influence their satisfaction, academic performance, and well-being.
2. Materials and Methods
2.1. Research Information and Procedures for Obtaining the Variables
This research was conducted in the same environment and using the same database as the previous study by Bueno et al. [35]. A cluster analysis assessed the relationship between thermal dissatisfaction and productivity in university classrooms in southern Brazil. This region has a humid temperate climate (Cfb), moderately hot summers, mild winters, and predominantly rainy weather [36,37].
The campus in question houses several buildings for classrooms, laboratories, a university restaurant, and spaces for sports activities. The facilities are built with masonry materials and ceramic blocks [38], with an average area of approximately 65 m2 and a capacity for 42 students, as illustrated in Figure 1. All the analyzed classrooms have natural ventilation and similar dimensions.

Figure 1.
Classroom analyzed in the research.
Data collection was performed using 50 measurements, from 23 March to 14 June 2022, during the autumn. This period was chosen to collect data because this was the first semester in the university where presential classes took place since the COVID-19 pandemic started. During this period, 519 valid responses were obtained by employing questionnaires, which included information about environmental variables, personal variables, and thermal preferences. Measurements were taken during three periods of the day (morning, afternoon, and evening), and the number of participations was counted, not the total number of individuals.
Bueno et al. [35] collected the environmental variables using a device similar to the BABUC-A microclimate station manufactured by Brüel and Kjaer, as shown in Figure 2.
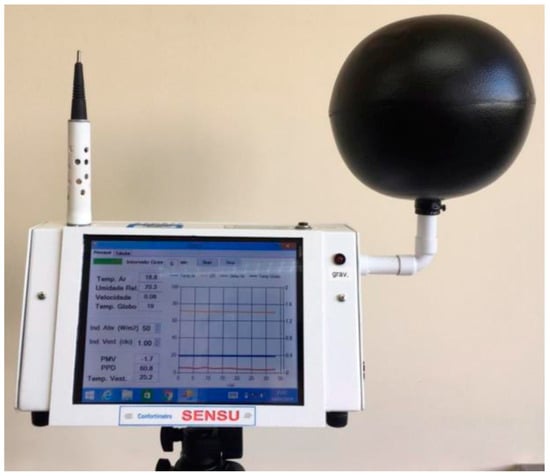
Figure 2.
Microclimatic station [39].
The microclimate station has built-in measurement sensors, ensuring high accuracy and resolution to guarantee reliable and detailed measurements. This enables real-time monitoring and access to data that have been recorded and stored over a period. The following values were obtained for the expanded uncertainties (coverage factor = 2, 95% probability) of the measured variables: dry and wet bulb temperature = ±0.2 °C; relative humidity RH = ±1%; globe temperature = ±0.03 °C.
Personal variables were obtained through a questionnaire that requested participants fill in information such as age, weight (in kg), height (in cm), gender (female/male), clothing used, the thermal sensation votes (TSVs) following the seven-point scale of ISO 7730 [40] (+3 hot, +2 warm, +1 slightly warm, 0 neutral, −1 slightly cool, −2 cool, −3 cold), and the thermal preference (PREF) described in ISO 10,551 [41] (+3 much warmer, +2 warmer, +1 a little warm, 0 neither warmer nor cooler, −1 slightly cooler, −2 cooler, −3 much cooler).
Clothing insulation was calculated for all participants according to ISO 9920 [42] and ASHRAE 55 [43]. For ambient temperature conditions, a minimum air velocity of 0.1 m/s was considered, as used by Wang et al. [44] and Fernández-Hernández et al. [45]. The metabolic rate adopted was 1.2 met, as established by ISO 8996 [46] for sedentary activities, corresponding to the activity performed by students in the classroom.
To obtain the PMV, calculations were performed using the thermal comfort tool developed by the Center for the Built Environment [47] of the University of Berkeley. To organize and tabulate the data obtained from the equipment, questionnaires and thermal comfort tools, MS Excel® spreadsheets were used. After obtaining the PMV and the data from the questionnaires, the statistical analysis was performed using the IBM SPSS Statistics software, version 23.
2.2. Development of Linear Regression Analysis in SPSS
For each completed measurement, the operative temperature (Top) was calculated as the simple average between the air temperature (ta) and mean radiant temperature (trm) following the method performed by Mičko et al. [48]. The mean PMV, TSV, and PREF were calculated for each gender, resulting in 95 mean values. Thus, it was possible to perform a simple linear regression analysis to obtain equations relating TSV and Top for males and females. This equation makes it feasible to obtain the comfort temperature for each gender. Furthermore, obtaining a comfort temperature range equivalent to a thermal comfort zone for each group becomes interesting. By replacing the TSV value of the equation with −0.5 and +0.5, it is possible to obtain, respectively, the lower and upper limits of a temperature range that meets category B, as presented in ISO 7730 [40]. In this category, the extremes of the comfort zone are about 10% of people feeling thermally dissatisfied, or 90% of people are thermally satisfied.
2.3. Development of Discriminant Analysis in SPSS
Canonical discriminant functions were developed to perform a statistical discriminant analysis to investigate how subjects discriminate against each other based on their thermal sensation, reality, and preference votes. In this study, the dependent variable was the thermal sensation votes (TSVs) reported by the participating students. After averaging the TSVs for each measurement, the non-integer values were categorized according to the seven-point scale of ISO 7730 [40], depicted in Figure 3. Therefore, five groups were formed for females and four for males to perform the discriminant analysis.
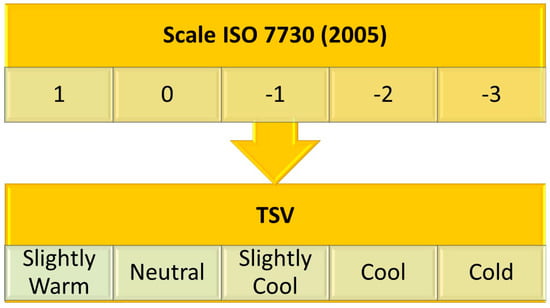
Figure 3.
Classification of TSVs into groups.
The measurements corresponded to students classified as slightly warm to group 1, neutral to group 0, slightly cool to group −1, cool to group −2, and cool to group −3. Next, Wilks’ Lambda test was used to test the hypotheses that the group means are equal or that there is a difference between them. The hypotheses tested were as follows:
H0:
equality of the group means.
H1:
at least one group mean is different.
Another test performed is Box’s M, which investigated whether the covariance matrices of the groups and their variables were homogeneous. The hypotheses tested were:
H0:
the matrices are homogeneous.
H1:
the matrices are not homogeneous.
The eigenvalues obtained provided information about the distinct groups within the discriminant functions. The more distant from one the eigenvalues are, the greater the variation between the groups, which explains the formation of the canonical discriminant functions [30]. According to Iacobucci et al. [49], the eigenvalues represent the variance present in the linear combination of the weights of the eigenvectors. Thus, the eigenvalues reflect the real factors in each discriminant function, contributing to their ability to distinguish between groups with significant similarities [50].
The relevance of these discriminant functions was evaluated using chi-square tests, which determine the separation of the observations into groups. All discriminant functions were tested together, revealing that the first function is always the most important for discrimination. Each independent variable (average predicted votes and thermal preference) has unstandardized coefficients used to formulate the discriminant functions. These coefficients helped to identify the coordinates of the centroids of the groups based on their averages, validating their characteristics and allowing the creation of canonical discriminant graphs to visualize the distance between the groups. In addition, a structural matrix was developed to understand how the variables influenced the formation of the discriminant function.
3. Results
3.1. Initial Measurement Results
Firstly, Table 1 shows the average values obtained throughout the 50 measurements regarding the environmental variables and the average PMV, TSV, and PREF.

Table 1.
Values of the variables per measurement.
3.2. Linear Regression Analysis
Excel spreadsheets were used to facilitate data entry in SPSS, so it was possible to start the linear regression analysis between the operative temperature (Top) and the thermal sensation votes (TSVs), obtaining the comfort temperature for female and male students in this classroom. Table 2 presents the means and standard deviations (SDs) for the variables that comprise this linear regression.

Table 2.
Descriptive statistics for genders.
In Table 3, there is a summary of the linear regression model, presenting the quality of the model developed along with the R-value that represents the multiple correlation coefficient and the R square that characterizes the percentage of variation in one variable over the other, in this case being the operative temperature (Top) on the thermal sensation votes (TSVs). The Durbin–Watson test has verified the existence of autocorrelation in the residuals (the difference between the predicted value and the observed value). Thus, this obtained value should vary between 0 and 4; the closer to 0, the greater the autocorrelation [51]. In the ANOVA, the F test verified how the fit of the regression model occurs, being for the female gender (F = 18.605, p < 0.05) and male gender (F = 28.058, p < 0.05), confirming that the model fits the data well. In the part that refers to the coefficients, the first row of values provides the intercept of the graph (B = constant). The second row presents the value of the angular coefficient that refers to the slope of the line induced by the variable that appears in the table, which is the TSVs. The t-test investigates two hypotheses:

Table 3.
Model summary, ANOVA, and coefficients.
H0:
coefficient of the constant is equal to zero (B = 0).
H1:
coefficient of the constant is different from zero (B ≠ 0).
The p-value for this test is less than 0.05, so the alternative hypothesis is accepted, proving that the coefficients are non-zero and have a weight on the straight-line equation.
Briefly, Table 4 shows the results of the linear regression analysis between TSV and Top employing the equations obtained; the value of comfort temperature is obtained when the person is in thermal neutrality (zero is inserted in the equation). A comfort temperature of 21.29 °C for female and 21.02 °C for male was found; furthermore, a comfort temperature range (thermal comfort zone) was obtained according to category B of ISO 7730 [40], replacing the TSV of the equation by −0.5 and +0.5, being the lower and upper limits for this temperature range.

Table 4.
Results of the linear regression analysis.
The comfort temperature range for females and males varies between 1.8 °C and 3.09 °C, respectively. For both cases, the values of the coefficient of determination were closer. Furthermore, it is important to note that the identified comfort temperature ranges apply specifically to the inhabitants of that region, considering its climatic conditions, or to areas with similar characteristics. This is related to the concept of “adaptive comfort”, where people gradually adjust to environmental conditions over time. Figure 4 shows the histogram that proves the normality of the data, following a normal distribution for both groups; thus, this distribution shows the good adequacy of the data in modeling the probability distribution of the comfort temperature. In the histogram, the female group is represented by purple and the male group by blue.
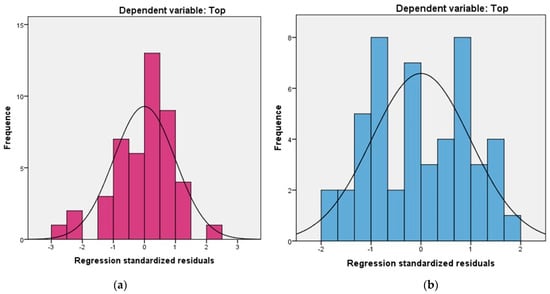
Figure 4.
(a) Representation of data normality by histogram for females; (b) representation of the normality of the data by histogram for males.
Figure 5 shows the relationship between operative temperature (Top) and thermal sensation votes (TSVs), showing a coefficient of determination (R2) of 0.297 for the female group and 0.374 for the male group; thus, Pearson’s correlation is considered weak due to the coefficient being R2 < 0.3 [52] and moderate for R2 ≥ 0.3 [53].

Figure 5.
(a) Linear regression analysis between TSV and Top for females; (b) linear regression analysis between TSV and Top for males.
3.3. Discriminant Analysis
At first, the data referring to TSV, PREF, and PMV for both genders were organized in Excel and then submitted to SPSS to obtain the descriptive statistics of these variables, with their respective means and standard deviations (Table 5).

Table 5.
Descriptive statistics.
For this discriminant analysis, the independent variables were the traditional PMV model and the students’ thermal preference for classrooms; thus, it was possible to form the discriminant functions responsible for classifying the observations, of each gender, into groups that represent the thermal sensation votes. Table 6 shows the number of observations in each group for both genders.

Table 6.
Number of observations of the groups.
Table 7 contains the Wilks’ Lambda tests, where all p-values were less than 0.05, meaning that the variables accepted the alternative hypothesis (H1) and indicated that at least one group means is different.

Table 7.
Test for equality of means.
In Table 8, the results of Box’s M test are presented. For the female group, the p-value was not significant (p > 0.05), showing that the covariance matrices are homogeneous; thus, H0 is accepted. The male group’s p-value was significant (p < 0.05), indicating that the covariance matrices are not homogeneous. Thus, H1 is accepted. The homogeneity assumption of the covariance matrices was met only for the female group. Still, this did not occur for the male group, but it is important to note that the sample sizes may influence this occurrence.

Table 8.
Box’s M test.
The eigenvalues corresponding to the female (98.8% and 1.2%) and male (93.4% and 6.6%) groups are contained in Table 9, in which the first discriminant function is the one that collaborates to express the differences that exist between the groups.

Table 9.
Eigenvalues.
The results of the function tests are contained in Table 10, in which the first discriminant function will always be significant due to the Chi-square value, which is responsible for the separations into groups. For both genders, the second discriminant function presented values higher than the acceptable significance level of 0.05, being 0.630 for females and 0.206 for males, showing that these variables are not statistically significant for discrimination into groups.

Table 10.
Wilks lambda and chi-square.
3.4. Discriminant Functions
For male and female genders, the discriminant functions of the independent variables (PMV and PREF) were elaborated on and are shown in Table 11. From these, the students in the classrooms were classified according to their group thermal sensations, and these results helped to gain a better view of how the groups are formed.

Table 11.
Discriminant functions.
In Table 12, the structure matrix contains all the variables that comprise the discriminant functions; those accompanied by asterisks are the most important and describe the highest correlations.

Table 12.
Structure matrix.
The coordinates of the centroids of each group (female and male) of thermal sensation symbolize the levels of the remoteness of the groups and the particularities of their components (individuals) (Table 13).

Table 13.
Centroids of the groups.
Figure 6 comprises the centroids of each group in the canonical discriminant functions. It is reproduced through scatter plots that make it possible to observe how the data behaved (1 slightly warm, 0 neutral, −1 slightly cool, −2 cool, −3 cold).
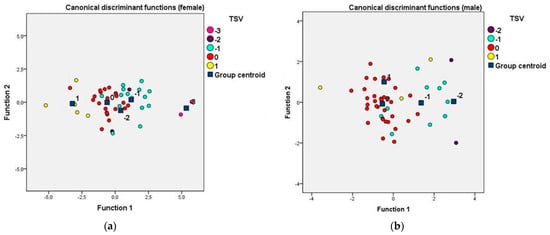
Figure 6.
(a) Centroids of the female group with the canonical discriminant functions.; (b) centroids of the male group with the canonical discriminant functions.
In the results, the success rate of the classification of the individuals was provided and calculated automatically by the software: 76.1% for the female group and 81.6% for the male group. These values showed a high probability of being correct in the classification and the effectiveness in forming canonical discriminant functions that verify the existence of differences in the thermal comfort of people based on their gender and thermal preference.
4. Discussion
4.1. General Aspects of the Research
This research assessed thermal comfort conditions in university classrooms, exploring statistical techniques to understand and anticipate these conditions. To achieve this goal, linear regression analysis was used to estimate the ideal comfort temperatures. In addition, it was possible to understand how different variables influence the participants’ perception of thermal comfort by developing discriminant functions.
According to Maroco [54], linear regression seeks to model the relationship between variables employing a straight line; this relationship can be of functional dependence and be used to predict the value of a variable. This research analyzed the relationship between the operative temperature and the thermal sensation votes under their magnitudes. From the modeling, equations were obtained that allowed us to calculate and predict the optimal comfort temperature for both genders in classrooms according to the comfort range established by ISO 7730 [40].
With the canonical discriminant functions, it was verified that thermal preference was the most prominent independent variable in forming these functions, representing the existing differences between the observations of the groups concerning the thermal sensation votes (dependent variable). Moreover, the thermal reality calculated by the PMVs did not significantly contribute to the formation of the functions, demonstrating that the users of the classrooms were thermally dissatisfied and preferred that the conditions of the environment be optimized. The accuracy of these functions was significant according to their thermal characteristics, and these discriminations can be used later for a more rigorous analysis.
In line with the purpose of this research, Torriani et al. [55] state that there are diverse thermal comfort expectations in educational environments, especially considering that adaptive capacities are less pronounced at earlier educational stages, such as elementary and high school. Therefore, it is understood that the more advanced a person’s educational stage, the greater their adaptive capacity in terms of clothing selection, window operations, and other actions. In addition, it is worth noting that temperature and comfort preference variations will also change throughout the different educational stages.
In this research, the environment under analysis is naturally ventilated. Faheem, Bhandari, and Tadepalli [56] emphasize that the same applies to Tiruchirappalli, India. They point out that implementing adaptive controls is essential to improve the internal environment. Additionally, Singh et al. [57] point out that significant energy consumption in buildings has become a global concern, mainly due to global warming and climate change. In this sense, specific adaptive comfort guidelines have become viable options in projects seeking to reduce energy consumption without jeopardizing occupants’ thermal comfort and indoor environmental quality (IEQ). This results in the planning of buildings focused on occupants and sustainability.
Another essential aspect is the provision of guidance to indoor users to promote well-being and the conscious use of energy. This type of measure was not commonly applied in the past, as evidenced by the research conducted by Run, Cévaër, and Dubé [58] in France. This research investigated a university building constructed in the late 1960s when energy issues were not considered particularly relevant. However, today the scenario differs substantially due to the advent of solutions that allow for the modernization of the building and its systems. In addition, simulations and even renovations have been introduced. However, such actions do not automatically guarantee an improvement in IEQ. Jain et al. [59] also highlight the importance of considering, at the planning stage, the continuous purpose of the building over time, including the maintenance and operation of building systems. According to Verma et al. [60], these aspects could be enriched by analyzing occupant behavior and measuring and simulating factors related to IEQ. These elements can promote individuals’ well-being, comfort, and health.
4.2. Specific Aspects of the Research
Based on the results obtained, it was found that this study did not reveal statistically significant differences between the female and male genders. This lack of differentiation can be attributed to the comfort temperature range, which varies between 1.8 °C and 3.09 °C for females and males, respectively. It is important to note that this variation results from various factors, such as local conditions, climate, and even the type of environment investigated. This phenomenon is similar to that observed in the study conducted by Yang et al. [61], which indicated that women tend to feel less comfortable in cold temperatures due to their lower metabolic rate and skin temperature. At the same time, men report less comfort in hot environments.
As for the linear regression analysis, the coefficients of determination (R2) were 0.297 for the female group and 0.374 for the male group. As Talukdar et al. [28] pointed out, the literature suggests that these relatively low values are due to the more prominent discomfort tendencies in naturally ventilated environments. Additionally, the p-value was considered significant (p < 0.001). In agreement with this study, Maykot, Rupp, and Ghisi [25] also carried out research in southern Brazil, specifically in Florianópolis, which shares similar climatic characteristics to the city of Ponta Grossa, both classified as temperate climates according to the Köppen–Geiger climate classification [62]. For these conditions, in the autumn, comfort temperatures were estimated at 24.8 °C for women and 25.2 °C for men, higher than the approximate values of 21.29 °C for the female group and 21.02 °C for the male group found in the present study. This discrepancy can be attributed to differences in climatic patterns, cooling methodologies, or even the method of obtaining the comfort temperature.
Only three variables were used to develop the canonical discriminant functions: TSV (dependent variable), PMV, and PREF (independent variables). This approach resulted in a classification success rate of 76.1% for the female group and 81.6% for the male group in the discriminant functions. Neale, Kummert, and Bernier [34] emphasize that the accuracy of classification in discriminant analysis is directly related to the variables used in the development of the model; therefore, the greater the number of variables used in the model, the greater the power of discrimination between groups. As a point of comparison, the accuracy rates in the studies by Wu, Li, and Qi [31] and Gladyszewska-Fiedoruk and Sulewska [33] were 87.9% and 88.52%, respectively. These results are similar to the findings of this study, demonstrating the effectiveness of the discriminant functions developed.
Based on the analyses carried out, evidence was found indicating the existence of an ideal temperature range for thermal comfort. The discriminant functions revealed that thermal preference was the most relevant variable in forming these functions, representing the differences between the groups regarding thermal sensation votes. On the other hand, the thermal reality calculated by the PMV did not significantly contribute to the formation of these functions.
4.3. Study Limitations
We identified some limitations of this study that may have influenced the results obtained. One of them concerns the limited number of observations per group, which may have impacted the analysis and, consequently, the accuracy of the results. It would be beneficial to perform a more significant number of measurements to obtain a more solid analysis and a better approximation of reality. On the other hand, data collection was restricted to autumn only, which may have limited the understanding of user behavior throughout the year. It is recommended to expand the measurements to the other seasons to obtain a more comprehensive view and increase the accuracy of the results.
Another limitation highlighted by Soto-Muñoz et al. [63] was also found in this research, which is the decrease in the number of responses throughout the questionnaire application. The researchers relied on the availability of the volunteer participants; however, a change in engagement was observed throughout the study. Furthermore, Parkinson et al. [64] pointed out that a binary approach to addressing gender is not comprehensive enough as gender is not limited to male and female categories. Future research should include other gender identities in the questionnaires to avoid possible errors arising from name-based gender estimation.
According to Hair, Anderson, and Black [65], discriminant analysis is sensitive to the ratio between the number of predictor variables and the sample size, recommending a ratio of 20 observations per predictor variable. This study used two predictor variables: thermal preference (PREF) and the PMV, so having at least 40 observations would be desirable.
4.4. Future Trends
Among the main future research trends is the application of machine learning (ML) to optimize the performance of comfort predictions and the combination of parameters [62,66]. In addition, it is essential to analyze the relationship between students’ economic vulnerability and its impacts on comfort temperature [67] and to investigate the implications of building orientations on occupants’ indoor conditions [68]. Another relevant point is the development of dynamic and complex models that connect occupants to the thermal environment to understand their productivity [63].
It is also necessary to investigate the impact of shading strategies and morphology on optimizing energy efficiency [69] and assessing climate change’s implications. Another essential aspect is the attention paid to energy consumption during the design phase [70]. In this way, possible problems can be mitigated even before construction begins, leading to various financial, sustainable, and thermal benefits. In addition, it is important to include new parameters that influence people’s perception of the environment, such as air quality, noise levels, and lighting. Therefore, studies that address and combine these parameters are becoming increasingly pertinent, and it is also important to incorporate physiological considerations [71] and even atmospheric pressure, which is rarely considered [72].
Similarly, it is essential to perform predictive analyses relating learning variables with environmental variables to discover favorable classroom conditions [73]. Furthermore, it is necessary to investigate how indoor environmental quality (IEQ) refers to class size, thermoregulatory indicators, and the thermophysical properties of building materials in educational buildings [74].
Since the onset of the COVID-19 pandemic, other needs must be prioritized in the built environment. Thapa et al. [75] report that in addition to the impacts on the economy, health, and lifestyle, overall comfort has been reduced, affecting the psychological well-being of individuals. In this sense, Rus et al. [76] highlight the importance of adapting the IEQ of educational buildings to medical protocols, providing better conditions of comfort and safety, reducing energy consumption, and improving learning ability, concentration, and performance. Finally, it is crucial to establish connections between thermal comfort and the Sustainable Development Goals (SDGs) to make spaces safer, more sustainable, inclusive, and resilient [77], contributing to people’s well-being and mitigating the challenges affecting both natural ecosystems and society in general [63].
5. Conclusions
Promoting thermal comfort can bring numerous advantages to building occupants, especially regarding productivity, energy efficiency, health, and well-being. A linear regression analysis revealed that the comfort temperature for people in thermal neutrality resulted in approximately 21.3 °C for women and 21 °C for men. In addition, a thermal comfort range was obtained based on ISO 7730 category B. By replacing the TSVs (thermal sensation votes) in the equation by −0.5 and +0.5, a comfortable temperature range was obtained between 20.39 °C and 22.19 °C for women and between 19.47 °C and 22.56 °C for men, so that the comfort temperature range varies from 1.8 °C to 3.09 °C for females and males, respectively, with no statistically significant differences. It is crucial to mention that these comfort temperature ranges are specific to the region’s inhabitants, considering their unique climatic conditions or areas with similar characteristics. In short, this is related to the concept of “adaptive comfort”, in which people gradually adapt to their environment over time.
Through discriminant analysis, it was found that the first canonical function was the most relevant in discriminating between the groups. The structure matrix revealed that the PREF variable had the highest correlation and was the most influential factor in determining the first discriminant function. However, the PMVs did not contribute significantly to the discriminant functions. The classification results showed a high success rate of 76.1% for the female group and 81.6% for the male group, indicating the relevance of the discriminant functions and how gender and thermal preference influence thermal comfort. Given the predictive capabilities of the equations formed, these findings may facilitate further studies in similar educational settings.
The measurements obtained 46 and 49 observations for the female and male groups, respectively. However, it is essential to note that variations in group size can impact the estimation of the discriminant functions and the classification of the observations. The groups showed significant variations, with most observations classified as neutral concerning thermal sensation. In some cases, extremes occurred on the TSV scale, where responses were considered “hot” and “cold” in the questionnaire. In summary, understanding and meeting the thermal needs of occupants is fundamental to creating healthy, productive, and efficient indoor environments. The application of the results of this study can contribute to the design of more sustainable and comfortable buildings, promoting the well-being and quality of life of those that use them.
In a broader context, the findings in this research may have implications for the physical conditions of the learning environment and student satisfaction, academic performance, and general well-being. A thermally comfortable environment impacts how students perceive their learning experience and can positively influence their engagement and academic performance. Furthermore, when considering well-being, comfortable environments contribute to students’ mental and physical health, promoting an environment conducive to concentration and learning.
Author Contributions
Conceptualization, I.L.N., I.M.d.L. and E.E.B.; methodology, I.L.N., I.M.d.L. and E.E.B.; software, I.L.N. and I.M.d.L.; validation, E.E.B.; formal analysis, E.E.B.; investigation, I.L.N. and I.M.d.L.; resources, I.L.N. and I.M.d.L.; writing—original draft preparation, I.L.N. and I.M.d.L.; writing—review and editing, I.L.N., I.M.d.L. and E.E.B.; visualization, I.L.N., I.M.d.L. and E.E.B.; supervision, E.E.B.; project administration, E.E.B.; funding acquisition, I.L.N., I.M.d.L. and E.E.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the “Coordenação de Aperfeiçoamento de Pessoal de Nível Superior” (CAPES)—financing code 001 and “Conselho Nacional de Desenvolvimento Científico e Tecnológico” (CNPq).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fernández Hernández, F.; Jiménez Navarro, J.P.; Atienza-Márquez, A.; Cejudo López, J.M.; Carrillo Andrés, A. An Experimental and Numerical Model of a Desiccant Façade. A Case of Study of an Office Building in Different Weather Conditions. Energy Build. 2020, 224, 110255. [Google Scholar] [CrossRef]
- Zomorodian, Z.S.; Tahsildoost, M.; Hafezi, M. Thermal Comfort in Educational Buildings: A Review Article. Renew. Sustain. Energy Rev. 2016, 59, 895–906. [Google Scholar] [CrossRef]
- Ghoreishi, K.; Fernández-Gutiérrez, A.; Fernández-Hernández, F.; Parras, L. Retrofit Planning and Execution of a Mediterranean Villa Using On-Site Measurements and Simulations. J. Build. Eng. 2021, 35, 102083. [Google Scholar] [CrossRef]
- Thapa, S.; Indraganti, M. Evaluation of Thermal Comfort in Two Neighboring Climatic Zones in Eastern India—An Adaptive Approach. Energy Build. 2020, 213, 109767. [Google Scholar] [CrossRef]
- Schweiker, M.; André, M.; Al-Atrash, F.; Al-Khatri, H.; Alprianti, R.R.; Alsaad, H.; Amin, R.; Ampatzi, E.; Arsano, A.Y.; Azar, E.; et al. Evaluating Assumptions of Scales for Subjective Assessment of Thermal Environments—Do Laypersons Perceive Them the Way, We Researchers Believe? Energy Build. 2020, 211, 109761. [Google Scholar] [CrossRef]
- Lamberti, G.; Salvadori, G.; Leccese, F.; Fantozzi, F.; Bluyssen, P.M. Advancement on Thermal Comfort in Educational Buildings: Current Issues and Way Forward. Sustainability 2021, 13, 10315. [Google Scholar] [CrossRef]
- Singh, M.K.; Ooka, R.; Rijal, H.B.; Kumar, S.; Kumar, A.; Mahapatra, S. Progress in Thermal Comfort Studies in Classrooms over Last 50 Years and Way Forward. Energy Build. 2019, 188–189, 149–174. [Google Scholar] [CrossRef]
- Lamberti, G.; Fantozzi, F.; Salvadori, G. Thermal Comfort in Educational Buildings: Future Directions Regarding the Impact of Environmental Conditions on Students’ Health and Performance. In Proceedings of the 2020 IEEE International Conference on Environment and Electrical Engineering and 2020 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Madrid, Spain, 9–12 June 2020. [Google Scholar]
- Lovec, V.; Premrov, M.; Leskovar, V.Ž. Practical Impact of the COVID-19 Pandemic on Indoor Air Quality and Thermal Comfort in Kindergartens. A Case Study of Slovenia. Int. J. Environ. Res. Public Health 2021, 18, 9712. [Google Scholar] [CrossRef]
- Yun, H.; Nam, I.; Kim, J.; Yang, J.; Lee, K.; Sohn, J. A Field Study of Thermal Comfort for Kindergarten Children in Korea: An Assessment of Existing Models and Preferences of Children. Build. Environ. 2014, 75, 182–189. [Google Scholar] [CrossRef]
- Dias Pereira, L.; Neto, L.; Bernardo, H.; Gameiro da Silva, M. An Integrated Approach on Energy Consumption and Indoor Environmental Quality Performance in Six Portuguese Secondary Schools. Energy Res. Soc. Sci. 2017, 32, 23–43. [Google Scholar] [CrossRef]
- Hamzah, B.; Gou, Z.; Mulyadi, R.; Amin, S. Thermal Comfort Analyses of Secondary School Students in the Tropics. Buildings 2018, 8, 56. [Google Scholar] [CrossRef]
- Barrett, P.; Davies, F.; Zhang, Y.; Barrett, L. The Impact of Classroom Design on Pupils’ Learning: Final Results of a Holistic, Multi-Level Analysis. Build. Environ. 2015, 89, 118–133. [Google Scholar] [CrossRef]
- Porras-Salazar, J.A.; Wyon, D.P.; Piderit-Moreno, B.; Contreras-Espinoza, S.; Wargocki, P. Reducing Classroom Temperature in a Tropical Climate Improved the Thermal Comfort and the Performance of Elementary School Pupils. Indoor Air 2018, 28, 892–904. [Google Scholar] [CrossRef] [PubMed]
- Guevara, G.; Soriano, G.; Mino-Rodriguez, I. Thermal Comfort in University Classrooms: An Experimental Study in the Tropics. Build. Environ. 2021, 187, 107430. [Google Scholar] [CrossRef]
- Zaki, S.A.; Damiati, S.A.; Rijal, H.B.; Hagishima, A.; Abd Razak, A. Adaptive Thermal Comfort in University Classrooms in Malaysia and Japan. Build. Environ. 2017, 122, 294–306. [Google Scholar] [CrossRef]
- López-Chao, V.; Amado Lorenzo, A.; Saorín, J.L.; De La Torre-Cantero, J.; Melián-Díaz, D. Classroom Indoor Environment Assessment through Architectural Analysis for the Design of Efficient Schools. Sustainability 2020, 12, 2020. [Google Scholar] [CrossRef]
- Schmidt, M.; Moreno, M.V.; Schülke, A.; Macek, K.; Mařík, K.; Pastor, A.G. Optimizing Legacy Building Operation: The Evolution into Data-Driven Predictive Cyber-Physical Systems. Energy Build. 2017, 148, 257–279. [Google Scholar] [CrossRef]
- Du, H.; Lian, Z.; Lai, D.; Liu, W.; Duanmu, L.; Zhai, Y.; Cao, B.; Zhang, Y.; Zhou, X.; Wang, Z.; et al. Method of Determining Acceptable Air Temperature Thresholds in Chinese HVAC Buildings Based on a Data-Driven Model. Energy Build. 2021, 241, 110920. [Google Scholar] [CrossRef]
- Rupp, R.F.; Kim, J.; Ghisi, E.; de Dear, R. Thermal Sensitivity of Occupants in Different Building Typologies: The Griffiths Constant Is a Variable. Energy Build. 2019, 200, 11–20. [Google Scholar] [CrossRef]
- Niza, I.L.; Broday, E.E. An Analysis of Thermal Comfort Models: Which One Is Suitable Model to Assess Thermal Reality in Brazil? Energies 2022, 15, 5429. [Google Scholar] [CrossRef]
- Etemadi, S.; Khashei, M. Etemadi Multiple Linear Regression. Measurement 2021, 186, 110080. [Google Scholar] [CrossRef]
- Silitonga, P.; Bustamam, A.; Muradi, H.; Mangunwardoyo, W.; Dewi, B.E. Comparison of Dengue Predictive Models Developed Using Artificial Neural Network and Discriminant Analysis with Small Dataset. Appl. Sci. 2021, 11, 943. [Google Scholar] [CrossRef]
- Lai, D.; Chen, C. Comparison of the Linear Regression, Multinomial Logit, and Ordered Probability Models for Predicting the Distribution of Thermal Sensation. Energy Build. 2019, 188–189, 269–277. [Google Scholar] [CrossRef]
- Maykot, J.K.; Rupp, R.F.; Ghisi, E. A Field Study about Gender and Thermal Comfort Temperatures in Office Buildings. Energy Build. 2018, 178, 254–264. [Google Scholar] [CrossRef]
- Gobo, J.; Faria, M.; Galvani, E.; Goncalves, F.; Monteiro, L. Empirical Model of Human Thermal Comfort in Subtropical Climates: A First Approach to the Brazilian Subtropical Index (BSI). Atmosphere 2018, 9, 391. [Google Scholar] [CrossRef]
- Wu, Z.; Li, N.; Wargocki, P.; Peng, J.; Li, J.; Cui, H. Adaptive Thermal Comfort in Naturally Ventilated Dormitory Buildings in Changsha, China. Energy Build. 2019, 186, 56–70. [Google Scholar] [CrossRef]
- Talukdar, M.S.J.; Talukdar, T.H.; Singh, M.K.; Baten, M.A.; Hossen, M.S. Status of Thermal Comfort in Naturally Ventilated University Classrooms of Bangladesh in Hot and Humid Summer Season. J. Build. Eng. 2020, 32, 101700. [Google Scholar] [CrossRef]
- Singh, S.; Chani, P.S. Thermal Comfort Analysis of Indian Subjects in Multi-Storeyed Apartments: An Adaptive Approach in Composite Climate. Indoor Built Environ. 2018, 27, 1216–1246. [Google Scholar] [CrossRef]
- Niza, I.L.; Broday, E.E. Thermal Comfort Conditions in Brazil: A Discriminant Analysis through the ASHRAE Global Thermal Comfort Database II. Build. Environ. 2022, 221, 109310. [Google Scholar] [CrossRef]
- Wu, M.; Li, H.; Qi, H. Using Electroencephalogram to Continuously Discriminate Feelings of Personal Thermal Comfort between Uncomfortably Hot and Comfortable Environments. Indoor Air 2020, 30, 534–543. [Google Scholar] [CrossRef]
- Shan, X.; Yang, E.-H.; Zhou, J.; Chang, V.W.-C. Human-Building Interaction under Various Indoor Temperatures through Neural-Signal Electroencephalogram (EEG) Methods. Build. Environ. 2018, 129, 46–53. [Google Scholar] [CrossRef]
- Gładyszewska-Fiedoruk, K.; Sulewska, M.J. Thermal Comfort Evaluation Using Linear Discriminant Analysis (LDA) and Artificial Neural Networks (ANNs). Energies 2020, 13, 538. [Google Scholar] [CrossRef]
- Neale, A.; Kummert, M.; Bernier, M. Discriminant Analysis Classification of Residential Electricity Smart Meter Data. Energy Build. 2022, 258, 111823. [Google Scholar] [CrossRef]
- Bueno, A.M.; Mendes da Luz, I.; Niza, I.L.; Broday, E.E. Hierarchical and K-Means Clustering to Assess Thermal Dissatisfaction and Productivity in University Classrooms. Build. Environ. 2023, 233, 110097. [Google Scholar] [CrossRef]
- Clima Ponta Grossa: Temperatura, Tempo e Dados climatológicos Ponta Grossa. Available online: https://pt.climate-data.org/america-do-sul/brasil/parana/ponta-grossa-4493/ (accessed on 1 August 2023).
- Bozzhigitov, A.; Memon, S.A.; Adilkhanova, I. Sensitivity of Energy Performance to the Selection of PCM Melting Temperature for the Building Located in Cfb Climate Zone. Energy Rep. 2022, 8, 6301–6320. [Google Scholar] [CrossRef]
- Mahecha, R.E.G.; Caldas, L.R.; Garaffa, R.; Lucena, A.F.P.; Szklo, A.; Toledo Filho, R.D. Constructive Systems for Social Housing Deployment in Developing Countries: A Case Study Using Dynamic Life Cycle Carbon Assessment and Cost Analysis in Brazil. Energy Build. 2020, 227, 110395. [Google Scholar] [CrossRef]
- Pereira, P.F.d.C.; Broday, E.E. Determination of Thermal Comfort Zones through Comparative Analysis between Different Characterization Methods of Thermally Dissatisfied People. Buildings 2021, 11, 320. [Google Scholar] [CrossRef]
- ISO 7730; Ergonomics of the Thermal Environment—Analytical Determination and Interpretation of Thermal Comfort Using Calculation of the PMV and PPD Indices and Local Thermal Comfort Criteria. ISO: Genève, Switzerland, 2005.
- ISO 10551; Ergonomics of the Physical Environment—Subjective Judgement Scales for Assessing Physical Environments. ISO: Genève, Switzerland, 2019.
- ISO 9920; Ergonomics of the Thermal Environment—Estimation of Thermal Insulation and Water Vapour Resistance of a Clothing Ensemble. ISO: Genève, Switzerland, 2007.
- ASHRAE—American Society of Heating, Refrigerating and Air Conditioning Engineers. ASHRAE Standard 55-2020 Thermal Environmental Conditions for Human Occupancy; ASHRAE: Atlanta, GA, USA, 2021. [Google Scholar]
- Wang, D.; Song, C.; Wang, Y.; Xu, Y.; Liu, Y.; Liu, J. Experimental Investigation of the Potential Influence of Indoor Air Velocity on Students’ Learning Performance in Summer Conditions. Energy Build. 2020, 219, 110015. [Google Scholar] [CrossRef]
- Fernández-Hernández, F.; Fernández-Gutiérrez, A.; Martínez-Almansa, J.J.; del Pino, C.; Parras, L. Flow Patterns and Heat Transfer Coefficients Using a Rotational Diffuser Coupled with a Radiant Floor Cooling. Appl. Therm. Eng. 2020, 168, 114827. [Google Scholar] [CrossRef]
- ISO 8996; Ergonomics of the Thermal Environment—Determination of Metabolic Rate. ISO: Genève, Switzerland, 2004.
- CBE Thermal Comfort Tool. Available online: https://comfort.cbe.berkeley.edu/ (accessed on 1 August 2023).
- Mičko, P.; Kapjor, A.; Holubčík, M.; Hečko, D. Experimental Verification of CFD Simulation When Evaluating the Operative Temperature and Mean Radiation Temperature for Radiator Heating and Floor Heating. Processes 2021, 9, 1041. [Google Scholar] [CrossRef]
- Iacobucci, D.; Ruvio, A.; Román, S.; Moon, S.; Herr, P.M. How Many Factors in Factor Analysis? New Insights about Parallel Analysis with Confidence Intervals. J. Bus. Res. 2022, 139, 1026–1043. [Google Scholar] [CrossRef]
- Bidmos, M.A.; Dayal, M.R.; Adegboye, O.A. Measurements of the Talus in the Assessment of Population Affinity. Forensic Sci. Int. 2018, 287, 221.e1–221.e7. [Google Scholar] [CrossRef] [PubMed]
- Jović, O. Durbin-Watson Partial Least-Squares Regression Applied to MIR Data on Adulteration with Edible Oils of Different Origins. Food Chem. 2016, 213, 791–798. [Google Scholar] [CrossRef] [PubMed]
- Vuckovic, A.; Osuagwu, B.A. Using a Motor Imagery Questionnaire to Estimate the Performance of a Brain–Computer Interface Based on Object Oriented Motor Imagery. Clin. Neurophysiol. 2013, 124, 1586–1595. [Google Scholar] [CrossRef]
- Yamashita, K.; Kuwashiro, T.; Ishikawa, K.; Furuya, K.; Harada, S.; Shin, S.; Wada, N.; Hirakawa, C.; Okada, Y.; Noguchi, T. Right Entorhinal Cortical Thickness Is Associated with Mini-Mental State Examination Scores from Multi-Country Datasets Using MRI. Neuroradiology 2022, 64, 279–288. [Google Scholar] [CrossRef]
- Maroco, J. Análise Estatística: Com Utilização Do SPSS; Edições Sílabo: Lisbon, Portugal, 2003. [Google Scholar]
- Torriani, G.; Lamberti, G.; Salvadori, G.; Fantozzi, F.; Babich, F. Thermal comfort and adaptive capacities: Differences among students at various school stages. Build. Environ. 2023, 237, 110340. [Google Scholar] [CrossRef]
- Faheem, M.; Bhandari, N.; Tadepalli, S. Adaptive thermal comfort in naturally ventilated hostels of warm and humid climatic region, Tiruchirappalli, India. Energy Built Environ. 2023, 4, 530–542. [Google Scholar] [CrossRef]
- Singh, M.K.; Ooka, R.; Rijal, H.B.; Kumar, S.; de Dear, R. Adaptive thermal comfort in the offices of three climates of North-East India. J. Build. Eng. 2023, 75, 106843. [Google Scholar] [CrossRef]
- Run, K.; Cévaër, F.; Dubé, J.F. Does energy-efficient renovation positively impact thermal comfort and air quality in university buildings? J. Build. Eng. 2023, 78, 107507. [Google Scholar] [CrossRef]
- Jain, N.; Burman, E.; Robertson, C.; Stamp, S.; Shrubsole, C.; Aletta, F.; Barrett, E.; Oberman, T.; Kang, J.; Raynham, P.; et al. Building performance evaluation: Balancing energy and indoor environmental quality in a UK school building. Build. Serv. Eng. Res. Technol. 2020, 41, 343–360. [Google Scholar] [CrossRef]
- Verma, A.; Gupta, V.; Nihar, K.; Jana, A.; Jain, R.K.; Deb, C. Tropical climates and the interplay between IEQ and energy consumption in buildings: A review. Build. Environ. 2023, 242, 110551. [Google Scholar] [CrossRef]
- Yang, L.; Zhao, S.; Gao, S.; Zhang, H.; Arens, E.; Zhai, Y. Gender Differences in Metabolic Rates and Thermal Comfort in Sedentary Young Males and Females at Various Temperatures. Energy Build. 2021, 251, 111360. [Google Scholar] [CrossRef]
- Park, B.R.; Choi, Y.J.; Choi, E.J.; Moon, J.W. Adaptive Control Algorithm with a Retraining Technique to Predict the Optimal Amount of Chilled Water in a Data Center Cooling System. J. Build. Eng. 2022, 50, 104167. [Google Scholar] [CrossRef]
- Soto Muñoz, J.; Trebilcock Kelly, M.; Flores-Alés, V.; Ramírez-Vielma, R. Understanding the Perceived Productivity of Office Occupants in Relation to Workspace Thermal Environment. Build. Res. Inf. 2022, 50, 152–170. [Google Scholar] [CrossRef]
- Parkinson, T.; Schiavon, S.; de Dear, R.; Brager, G. Overcooling of Offices Reveals Gender Inequity in Thermal Comfort. Sci. Rep. 2021, 11, 23684. [Google Scholar] [CrossRef] [PubMed]
- Hair, J.F.; Anderson, R.E.; Black, W.C. Análise Multivariada de Dados; Bookman: Porto Alegre, Brazil, 2005. [Google Scholar]
- Lala, B.; Biju, A.; Vanshita; Rastogi, A.; Dahiya, K.; Kala, S.M.; Hagishima, A. The Challenge of Multiple Thermal Comfort Prediction Models: Is TSV Enough? Buildings 2023, 13, 890. [Google Scholar] [CrossRef]
- Trebilcock, M.; Soto-Muñoz, J.; Figueroa, R. Thermal Comfort in Primary Schools: A Field Study in Chile. In Proceedings of the Windsor Conference 2014: Counting the Cost of Comfort in a Changing World, Windsor, UK, 10–13 April 2014. [Google Scholar]
- Thapa, S. Investigation of Thermal Comfort and Adaptation among the Residents of Cold Climate in the Lower Himalayan Region of Eastern India. Indoor Built Environ. 2022, 31, 1613–1635. [Google Scholar] [CrossRef]
- Dervishi, S.; Baçi, N. Early Design Evaluation of Low-Rise School Building Morphology on Energy Performance: Climatic Contexts of Southeast Europe. Energy 2023, 269, 126790. [Google Scholar] [CrossRef]
- Alghamdi, S.; Tang, W.; Kanjanabootra, S.; Alterman, D. Field Investigations on Thermal Comfort in University Classrooms in New South Wales, Australia. Energy Rep. 2023, 9, 63–71. [Google Scholar] [CrossRef]
- Zhang, S.; Zhu, N. Gender Differences in Thermal Responses to Temperature Ramps in Moderate Environments. J. Therm. Biol. 2022, 103, 103158. [Google Scholar] [CrossRef]
- Kenawy, I.; Elkadi, H. Effects of Cultural Diversity and Climatic Background on Outdoor Thermal Perception in Melbourne City, Australia. Build. Environ. 2021, 195, 107746. [Google Scholar] [CrossRef]
- Arroyo, Y.P.V.; Peñabaena-Niebles, R.; Correa, C.B. Influence of Environmental Conditions on Students’ Learning Processes: A Systematic Review. Build. Environ. 2023, 231, 110051. [Google Scholar] [CrossRef]
- Amoatey, P.; Al-Jabri, K.; Al-Saadi, S.; Al-Harthy, I.; Al-Khuzairi, M. Impact of Indoor Environmental Quality on Students’ Comfort in High School Buildings during the Summer Season in an Extreme Climate. J. Archit. Eng. 2023, 29, 04023014. [Google Scholar] [CrossRef]
- Thapa, S.; Singh, R.; Bundele, M.; Thapa, S.; Thadathil, G.; Kr Jakhar, Y. Study of Thermal Comfort in the Residents of Different Climatic Regions of India—Effect of the COVID-19 Lockdown. Indoor Air 2021, 31, 899–917. [Google Scholar] [CrossRef] [PubMed]
- Rus, T.; Moldovan, R.; Albu, H.; Beu, D. Impact of Pandemic Safety Measures on Students’ Thermal Comfort—Case Study: Romania. Buildings 2023, 13, 794. [Google Scholar] [CrossRef]
- Yang, S.-Q.; Matzarakis, A. Implementation of Human Thermal Comfort and Air Humidity in Köppen-Geiger Climate Classification and Importance towards the Achievement of Sustainable Development Goals. Theor. Appl. Climatol. 2019, 138, 981–998. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).