Abstract
The role of energetic particle precipitation in the formation of thermospheric tides is investigated. Using the Global Self-consistent Model of the Thermosphere, Ionosphere, and Protonosphere (GSM TIP) and two models of energetic particle precipitation, APM (Auroral Precipitation Model) and AIMOS 2.0.-AISstorm (Atmospheric Ionization Module Osnabrück 2.0—Atmospheric Ionization during Substorms), we performed simulations for the period 3–12 September 2017. This period covers both geomagnetically quiet days and the storm of 7–8 September. The analysis shows that migrating tides diurnal wave (DW) and semidiurnal wave (SW) prevail on quiet days for both versions of the simulations. On the day of maximum storm development on 8 September and the day after—9 September, the nonmigrating components of tidal waves, mainly DW0 and SW0, are intensified. There are also increasing differences in the spatial structure of tides between the two versions of simulations, especially between diurnal and semidiurnal tides at 154 km. On the disturbance days, the amplitudes of diurnal and semidiurnal tides at 154 km in the APM version are markedly greater than the corresponding values in the AIMOS version. Thus, it should be noted that the integral characteristics of the ionization function from precipitations are more important for the formation of DW and SW than its spatial structure or the features of temporal variations. A comparison of the total electron content (TEC) maps for the two versions of the simulation showed that the AIMOS version nicely reproduces the experimental data for a quiet time. The APM version is less accurate for quiet time but simulates the quantitative increase to disturbed conditions at high and middle latitudes better. For model reproduction of observed TEC variations at low and equatorial latitudes, it is not enough to consider the thermospheric source of thermospheric tides. In this case, the role of atmosphere–ionosphere coupling is very important.
1. Introduction
The importance of atmospheric tides as factors of the variability of the thermosphere and ionosphere is now widely recognized. Recently, ICON measurements of wind and temperature in the low thermosphere have been used to obtain and specify the tidal spectrum at this altitude [1]. Tidal components are of great importance for the state of the ionosphere, which is formed at altitudes of the E-region, where electric dynamo fields generate the influence of tidal winds. These electric fields, penetrating above, take part in the formation of the temporal and spatial variability of the F-region of the ionosphere [2,3,4]. Part of the tidal spectrum that creates electric fields is formed directly in the thermosphere because of the absorption of EUV radiation and the impact of high-latitude energy and pulse sources. The role of such thermospheric tides increases during geomagnetic disturbances, especially during geomagnetic storms [5,6]. Note that geomagnetic storms affect the entire ionosphere of the Earth. They are the most important phenomenon of space weather in terms of the impact on the atmosphere–ionosphere system. Modeling the state of the thermosphere and ionosphere and the dynamics of the upper atmosphere in the conditions of geomagnetic storms remains the most difficult and not fully solved task [7]. The reasons for this are the uniqueness of each geomagnetic disturbance, manifested in the time of occurrence of disturbances, the dynamics of its development, the spectra and power of the fluxes of solar and magnetospheric particles penetrating the thermosphere and ionosphere, etc. [8,9,10,11].
Important tools for studying atmospheric tides (numerical models of the upper atmosphere and ionosphere) are currently being actively developed [12,13]. It should be noted that, for the most part, the theoretical studies of the dynamics of the upper atmosphere performed earlier in the conditions of geomagnetic disturbances drew attention to two main factors affecting the state of the thermosphere: Joule heating and ion drag. Possible mechanisms included increased dissipation due to increased temperatures, generation of higher order tidal modes by the geomagnetic disturbances, or phase differences between the waves generated by auroral processes and those forced by solar radiation. Thermospheric tides are generated in response to time-varying forcings, which include in situ solar forcing, upward propagating waves from the lower atmosphere, and ion-neutral momentum coupling. Waves with semidiurnal periods may also be generated by high-latitude processes such as magnetospheric convection and Joule heating [14]. The role of high-latitude sources of precipitation in the formation of thermospheric tides has not been studied enough.
Currently, based on the analysis of experimental data, empirical and hybrid models of the spectral characteristics and power of energetic particle precipitation have been created both in quiet and geomagnetic-disturbed conditions [15,16,17,18,19]. The use of new models of energetic particle precipitations in the description of the sources of ionization disturbances and the thermal balance of the upper atmosphere improves the realism of the description of changes occurring in the environment during geomagnetic storms.
The aim of this study was to evaluate the role of the precipitation of energetic particles on the formation of thermospheric tides under quiet and geomagnetically disturbed conditions. In the present work, we studied the September 2017 storm using the Global Self-consistent Model of the Thermosphere, Ionosphere, and Protonosphere (GSM TIP) and energetic particle precipitation models AIMOS [15] and APM [16,20].
2. Description of the Geomagnetic Storm and the Storm Scenario in the GSM TIP Model
2.1. Heliogeophysical Situation
The geomagnetic storm of 7–8 September 2017 was preceded by a coronal mass ejection (CME) that reached the Earth around 23 UTC on 7 September. A strong geomagnetic storm began at 23:25 UTC. Figure 1 shows the behavior of the indices of geomagnetic (Dst, Kp, AE, AL) and solar (F10.7) activity on 3–11 September 2017 [https://omniweb.gsfc.nasa.gov] (accessed on 18 February 2022).
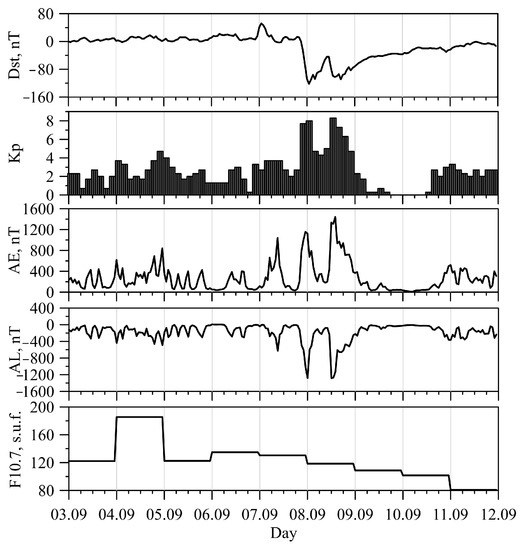
Figure 1.
Time variations in the geomagnetic and solar activity indices Dst, Kp, AE, AL, and F.10.7 during 3–11 September 2017.
It can be seen that two geomagnetic storms took place during this period, on 7 and 8 September. During the first storm, the Dst, Kp, AL, and AE indices reached their extreme values of −130 nT, 7, 1200 nT, and 2600 nT, respectively. During the second storm, the extreme values of Dst and AE reached −120 nT and 2800 nT, respectively. It should be noted that these two storms were preceded by a rather long, relatively quiet geomagnetic period on 3–6 September 2017, during which there were significant changes in the solar activity index F10.7 associated with a set of M and X class solar flares. In addition to strong geomagnetic storms and solar flares, during the period under review, increases in the fluxes of solar and magnetospheric protons of various energies were recorded during the periods of 5, 6–8, and 10–11 September. An analysis of the solar and geomagnetic conditions showed that on 6–7 September, as well as on 10–11 September 2017, after flares and CME, precipitations of mainly solar protons were recorded. In the rest of the time (7–9 September 2017), the appearance of proton precipitations is associated with geomagnetic disturbances. In this study, thermospheric/ionospheric disturbances associated with geomagnetic storms were considered in the period from 3 September to 11 September 2017.
2.2. GSM TIP Model
The study of ionospheric disturbances during a geomagnetic storm was carried out using a global numerical model of the upper atmosphere—GSM TIP [21,22,23]. The GSM TIP model is developed in WD IZMIRAN, Kaliningrad, Russian Federation. The GSM TIP model numerically integrates a system of quasi-hydrodynamic equations of continuity, motion, and heat balance for the neutral and charged components of a multicomponent gas mixture, as well as a three-dimensional equation describing the conservation law of the total current in the ionosphere. In the GSM TIP model, the Earth’s magnetic field is approximated by a tilted dipole. As parameters determining the effect of geomagnetic disturbances on the upper atmosphere, the GSM TIP model uses the cross-polar cap potential (CPCP), Region 2 field-aligned currents (R2 FAC), and precipitation of high-energy particles in the auroral region. The CPCP ΔΦ, which needs to be introduced into these calculations, was set based on its empirical dependence on the index of geomagnetic activity AE [24]. The potential at geomagnetic latitudes of ±75° was set to vary according to the harmonic law with respect to local magnetic time, with a maximum on the dawn side and a minimum on the dusk side. In this case, changes in the size of the polar caps and, consequently, the position of its equatorial boundary during disturbances were not considered. The position of the maxima of R2 FAC, flowing out on the dawn side and flowing in on the dusk side, was set according to [25], depending on the specified potential difference across the polar caps at geomagnetic latitudes, from ±65° at ΔΦ ≤ 40 kV to ±35° at ΔΦ > 200 kV. In addition, according to [26], a 30 min time delay was considered for the R2 FAC variations relative to the variations in CPCP.
Recently, the GSM TIP model was used to study different aspects of the upper atmosphere response to geomagnetic storms [27,28,29]. As was shown in [30,31,32], the GSM TIP model well reproduces temporal evaluation of the storm-time tongue of ionization, the main ionospheric trough, and auroral electrojet. For the simulation of the neutral temperature variability, the GSM TIP model includes the following terms in thermal balance equations: (1) the work of compression and expansion of neutral gas; (2) convective heating; (3) Joule heating; (4) thermal conductivity; (5) heating by solar radiation; (6) infrared radiative cooling by atomic oxygen (O), carbon dioxide (CO2), and nitric oxide (NO); (7) heating by precipitating particles; (8) viscous heating. Thus, the GSM TIP can reproduce the storm-induced thermospheric heating caused by the strengthening of the high-latitude ionospheric electric fields, currents, and auroral particle precipitation.
In this study, we used two options to account for the effect of energetic particle precipitation in the GSM TIP model using two different models: AIMOS and APM. As can be seen (below), the fundamental differences between these two models are as follows: (1) the models are in a different experimental base (constantly updated data from the GOES and POES satellites for a specific event in AIMOS and DMSP data fixed for 1986 for APM), (2) proton and alpha particle precipitations are accounted for in AIMOS, which is not the case in APM, (3) the APM model has a higher temporal resolution. Calculations using the GSM TIP model and two different precipitation models described above were carried out for the conditions of 3–11 September 2017. It is important to note that the performed GSM TIP simulations used constant values of the neutral parameters at the lower boundary (80 km) so that the tides obtained in the model simulations are formed precisely by thermospheric sources.
2.3. AIMOS 2.0—AISStorm Model
The new version of AIMOS (Atmospheric Ionization Model Osnabrück) [15] is a numerical model of atmospheric ionization due to precipitating particles with high spatial resolution and extends the model by separate treatment of substorm periods. This model calculates 3D ionization maps of precipitating protons, electrons, and alpha particles with a 30 min temporal resolution. Note that this study uses 2 h mean values. AIMOS includes a sorting algorithm to assign observations from polar-orbiting POES and Metop satellites to horizontal precipitation cells. For this, AIMOS uses the data from the TED and MEPED detectors. In addition, high-energy protons and alpha particles from the SEM detectors of the GOES satellites are used in the polar cap. The measured energy range is 154 eV–500 MeV for protons, 154 eV–300 keV for electrons, and 4 MeV–500 MeV for alpha particles. Mean flux maps were calculated from 18 years of satellite data (2001–2018) grouped by Kp level, geomagnetic APEX [33] vs. magnetic local time (MLT) location with 1° vs. 3.75° resolution, and substorm activity. Each flux map represents a typical spatial pattern of particle precipitation for one particle channel on the global map. Typical average flow maps from AIMOS are given in [34]. The effective flow for a 30 min interval is determined by overlaying precipitation maps with direct measurements at that time. Considering that only areas with high flux values (auroral oval) are used for scaling, the influence of noise in real-time data is suppressed. For each spectral interval of particles, the ionization profile is calculated by the Monte Carlo method [35], and the atmospheric parameters were taken from the HAMMONIA [36] and NRLMSISE-00 [37] models. The AIMOS model is available at http://www.ionization.de (accessed on 11 October 2021).
2.4. The APM Model
The Empirical Auroral Precipitation Model (APM model) [16,17,20] was developed at the Polar Geophysical Institute based on statistical processing of data from the DMSP F6 and F7 satellites. This model allows a global distribution of the characteristics of precipitating electrons in the coordinates "corrected geomagnetic latitude—magnetic local time" (CGL-MLT) for different levels of magnetic activity, determined by 1 min AL index values, to be obtained. The model is founded on statistical processing of DMSP spacecraft observations. The database contains information on the spatial boundaries and characteristics (average energy and energy flux) of precipitating particles for more than 30,000 DMSP spacecraft passages through the auroral zone. To increase the statistical significance of the results, all satellite passes were divided into eight 3 h intervals of magnetic local time (00-03 MLT, 03-06 MLT, 06-09 MLT, etc.). The standard deviation of the boundary position from the average values is about 2°–3° of latitude, depending on the MLT, the level of magnetic activity, and the type of boundary. According to the level of magnetic activity, the statistical data array was in the range of AL values from 0 to −1500 nT. The APM model is available at http://apm.pgia.ru/ (accessed on 20 October 2021).
In the GSM TIP model, the ionization rates of precipitating electrons are calculated from the values of the spectrum and electron fluxes of the APM model using the approximation described in [38].
3. Processing Method
Global empirical and theoretical models of diurnal variations describing large-scale processes in the thermosphere and ionosphere are based on the idea of the periodicity of variations in environmental parameters depending on longitude and time. This makes it possible to single out planetary scales in the spatiotemporal structure of variations, determined by daily averaged values of parameters and daily variations. In the models, the diurnal variability of the parameters is represented by an expansion into a series in terms of harmonics with periods that are sub-harmonics of a day (tidal variations). In theoretical studies, the spatial structure of tidal variations is determined by the superposition of tidal waves with the corresponding periods. Analysis of the spectral structure of tidal variations of parameters calculated in theoretical models allows us to determine the wave spectra and identify the role of various physical factors in the formation of the global structure of daily variations. This approach made it possible to naturally adapt the observational data within the framework of experimental models and to interpret the results of theoretical and experimental studies in a physically justified way. Spatial and temporal variations of thermospheric parameters for each day of the simulated period were used to analyze the spectral structure of tidal variations. The analysis of the spectral structure of tidal variations was carried out according to the methodology presented in [39,40].
Calculated spatial and temporal variations of atmospheric and ionospheric parameters F (r, θ, , t, nd) for each day nd in the time period under study were presented as a Fourier series expansion
where is the average daily parameter value and is the complex amplitude of tidal variation with period T/n, (T = 24 h); n = 1, 2, 3; r, θ, φ—altitude, latitude, and longitude, t—universal time.
The spectral characteristics of the tidal waves that make up the tidal variations were determined from the Fourier transform of the amplitudes of the tidal variations in longitudes:
is the complex amplitude of a tidal wave with period T/n and zonal wave number s = 0, ±1, ±2, ±3. Thus, the application of (1)–(3) makes it possible to determine the characteristics of tidal waves that determine the structure of variations in the parameters of the thermosphere.
4. Results
Diurnal (DW) and semidiurnal (SW) tidal variations of the neutral temperature for quiet and geomagnetically disturbed conditions on September 2017 are presented in this section.
Figure 2 shows the amplitudes and spectra of diurnal tidal variations at altitudes of 121 and 154 km on a quiet geomagnetic day (6 September 2017), obtained from the results of GSM TIP simulation with the APM and AIMOS models. The latitude–longitude structures of thermospheric diurnal tides are similar for AIMOS and APM models of particle precipitation both at 121 km, and at 154 km. The extrema of diurnal tides lie at higher latitudes at a height of 121 km in comparison to 154 km altitude. At that maximum, a height of 121 km exists at different longitudes for the northern (~150°) and southern (~0°) hemispheres. However, at an altitude of 154 km, these maxima in the northern and southern hemispheres are located at the same longitude (~120°).
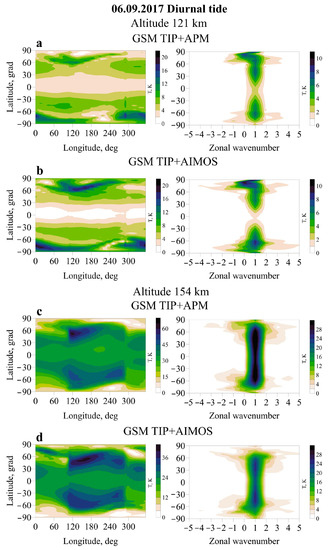
Figure 2.
Spatial distribution of the amplitude of the diurnal tide in temperature and the spectrum of tidal waves at heights of 121 km (a,b) and 154 km (c,d) according to the results of calculations in the GSMTIP + APM (left) and GSMTIP + AIMOS (right) variants on a geomagnetically quiet day on 6 September 2017.
As can be seen, at an altitude of 121 km, the spatial structure of the DW tide and the wave spectrum in both cases are very similar. Solar migrating DW1 and nonmigrating DW2 waves prevail at the mid-latitudes. At the latitudes above 60°, nonmigrating tides with zonal wave numbers s = 0, −1 prevail. The weakening of the DW1 amplitude at the equator should also be noted. Differences in the spatial structure of diurnal tides for both versions of the simulation at an altitude of 154 km are also minimal. At the same time, the area where nonmigrating components have a significant effect on the structure of the tide has expanded to middle latitudes. We also note that the DW amplitude values at the height of 121 km in both versions of the simulation practically coincide, while at the height of 154 km at middle and high latitudes, the tide amplitude in the AIMOS version is less than in the APM version by 15–20 K.
Figure 3 shows the spatial structure and wave spectrum of the diurnal tide during the geomagnetic disturbance period (8–9 September 2017). During the geomagnetic storm (8 September), the structure and amplitude of the diurnal tide changed at an altitude of 121 km, especially for the APM version. At high latitudes, the DW0 is intensified, and for the APM version of the simulation, this wave mode became dominant. At AIMOS, the altitude of 121 km reflects the equatorial displacement of the auroral oval during enhanced Kp levels. As seen at 0° long, the 8 K contour moves from 60° S (9 September) to 45° S. After the end of the storm in September, the amplitudes of diurnal waves decreased, and the tide structure began to return to a quiet distribution. An analysis of the spectral characteristics showed that under the perturbed conditions, the latitudinal region, where the nonmigrating tidal waves have a significant influence, extends to low latitudes and persists after the end of the geomagnetic storm.
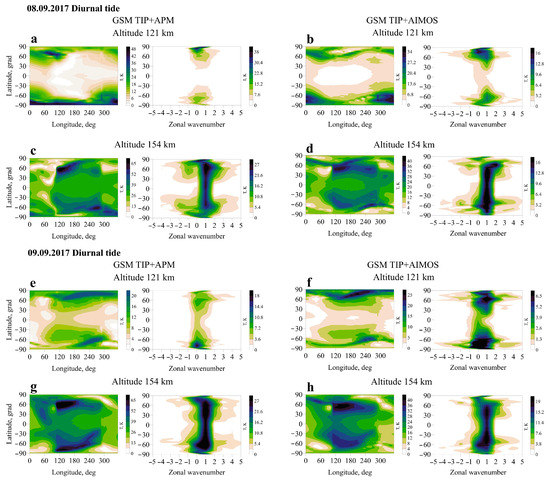
Figure 3.
Spatial distribution of the amplitude of the diurnal tide in temperature and the spectrum of tidal waves at heights of 121 km (a,b,e,f) and 154 km (c,d,g,h) according to the results of calculations in the GSMTIP + APM (left) and GSMTIP + AIMOS (right) variants in a geomagnetic disturbance period on 8–9 September 2017.
At an altitude of 154 km, the response of the diurnal tide to the geomagnetic disturbance is less pronounced in comparison to 121 km (Figure 3c,d,g,h). The amplitude of nonmigrating waves increased at high latitudes; however, the migrating wave DW1 remained prevalent on 8 and 9 September as well. One can also note an increase in the amplitude of the tide on 8 and 9 September at middle and low latitudes in the APM version of the simulation and auroral latitudes in the version with AIMOS. In addition, on the day of the geomagnetic storm in both versions of the simulations, there was a decrease in the tidal amplitude in the longitude sector 0°–120° at middle and high latitudes. Two sharp transitions of thermospheric tide amplitude at ~100° and ~280° are connected with locations of geomagnetic poles, which are accounted for in the dipole approximation of GSM TIP model. The spatial structure of the DW began to return to an undisturbed state after the end of the storm on 9 September 2017. With the obvious similarity of changes in the spatial structure of the diurnal tide, there are significantly higher amplitudes on these days in the APM version, ~70° K, compared to 45° K in AIMOS.
Figure 4 shows the spatial distribution of the amplitude and the spectrum of semidiurnal tidal waves at 121 and 154 km altitudes on 6 September. As can be seen from Figure 4a, in quiet geomagnetic conditions at an altitude of 121 km in both versions of the simulations, the spatial structure of the tide at middle and low latitudes is determined by the symmetric solar-migrating wave SW2, with its maximum located at the equator.
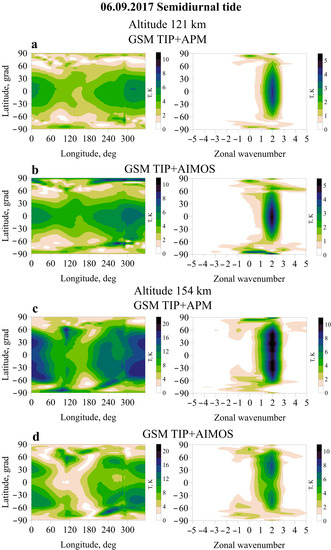
Figure 4.
Spatial distribution of the amplitude of the semidiurnal tide in temperature and the spectrum of tidal waves at heights of 121 km (a,b) and 154 km (c,d) according to the results of calculations in the GSMTIP + APM (left) and GSMTIP + AIMOS (right) variants on a geomagnetically quiet day on 6 September 2017.
At high latitudes, the role of nonmigrating tides SW0 and SW1 is increased. It may also be noted that at 121 km, the high-latitude local maximum of the SW amplitude in GSM TIP simulations using the AIMOS version is associated precisely with nonmigrating tides. The amplitude of the semidiurnal tide at high latitudes is less than the APM version of the simulation. At 154 km (Figure 4c,d), the tidal structure is determined by waves with zonal wave numbers s = −1, 0, 2, the same as at 121 km. The maximum values of the amplitude of the semidiurnal tide are located at low latitudes. Note that the amplitude of the semidiurnal tide at 121 km in the simulations with AIMOS is larger than in the version with APM, and at an altitude of 154 km, it is smaller. Figure 5 shows the same as in Figure 4 but on geomagnetically disturbed days. During the geomagnetic storm (8 September 2017) at an altitude of 121 km, the amplitude of the semidiurnal tide increased from 12 K to 24 K at high latitudes and slightly increased at middle and low latitudes. The amplification of the semidiurnal tide in the APM version is especially noticeable. Disturbances in the structure of the semidiurnal tide in both versions of the simulation occur due to the amplification of nonmigrating tides with wave numbers s = −2, −1, 0, 1, 3 at high and s = 0 at equatorial latitudes. In the APM version of the GSM TIP simulation, the SW0 component becomes dominant at high latitudes. On 9 September, the amplitudes of semidiurnal tides return to pre-storm values in both versions of the simulation; however, the post-storm structure of tidal waves differs markedly from pre-storm ones by the presence of two minima in the longitudinal sectors 30°–60° and 180°–220°. In the spectra of the semidiurnal tide, along with SW2, the SW0 wave is clearly distinguished.
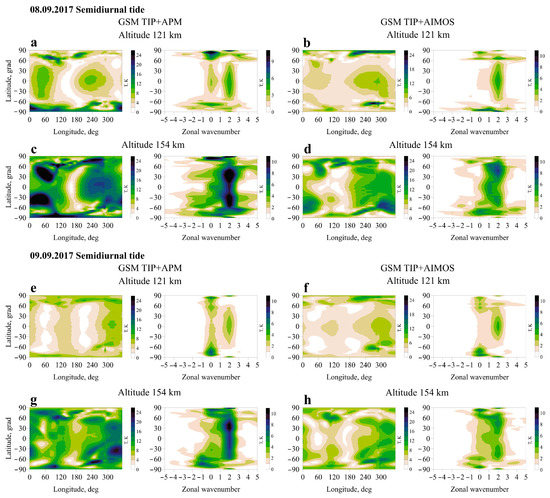
Figure 5.
Spatial distribution of the amplitude of the semidiurnal tide in temperature and the spectrum of tidal waves at heights of 121 km (a,b,e,f) and 154 km (c,d,g,h) according to the results of calculations in the GSMTIP + APM (left) and GSMTIP + AIMOS (right) variants on a geomagnetic disturbance period on 8–9 September 2017.
At an altitude of 154 km, the amplitude of the semidiurnal tide on 8 September increased, especially in the APM version of the simulation, but on 9 September, it returned to the pre-storm values. The changes in the structure of semidiurnal variations on 8 September in the AIMOS version are less pronounced than in the APM version and, like at 121 km, are due to intensification of the nonmigrating components. The influence of nonmigrating tides extends to middle and low latitudes. After the end of the storm on 9 September, the structure of the semidiurnal tide at 154 km differed significantly from the pre-storm tide, qualitatively resembling the structure of the semidiurnal tide at 121 km. In the tidal spectra for both versions of the simulation, the nonmigrating components are preserved; in the APM version it is mainly SW0 and SW1 waves, and it is an SW0 wave in the AIMOS version.
According to Table 1, the amplitude of diurnal and semidiurnal tides increased for both versions of the GSM TIP model simulation at all altitudes (excluding DW tides at 154 km obtained in the AIMOS version of the GSM TIP simulation) during the geomagnetic storm in comparison to quiet conditions. The amplitudes of DW and SW tides at 121 km are very similar in both versions of the GSM TIP model simulation. However, at 154 km altitude, the APM version of the GSM TIP simulation shows greater amplitude DW and SW tides in comparison to the AIMOS version. It should be noted that there are only 12 3 h intervals higher than Kp 7.3 in the solar minimum year 1986, which is used for APM. Thus, the statistical basis is rather poor for the used event.

Table 1.
Maximum amplitudes (K) of diurnal and semidiurnal tides for APM and AIMOS modeling versions.
5. Discussion
Some authors (for example, [41]) showed that tidal winds at ~120 km do not change during magnetic storms. Our results showed that on the day of maximum geomagnetic storm development on 8 September and the day after, the nonmigrating components of tidal waves in temperature, mainly DW0 and SW0, intensified. There were also increasing differences in the spatial structure of tides between the two versions of the simulations, especially between the diurnal tides at 121 km and the semidiurnal tides at 154 km. The particle precipitation effect in the tides is due to thermospheric heating, which occurs due to additional ionization and recombination processes.
Obviously, the vertical structure of thermospheric disturbances depends significantly on the additional ionization source due to energetic particle precipitation. In our calculations, this leads to local increases in the amplitudes of nonmigrating tides in the lower thermosphere of high latitudes.
The use of different precipitation models leads to differences in high-latitude ionization processes, especially during storms. Figure 6 shows the altitudinal profiles of the ionization rate of molecular nitrogen, integrated over all longitudes and latitudes from 90° N to 55° N latitude inclusive(Σ(q(N2)) 1/s⋅cm−1). As can be seen, the height of the maximum Σ(q(N2) in the APM version is ~10 km lower than in the AIMOS version. The ionization rate in the APM variant exceeds that of AIMOS by a factor of about six during the maximum phase of the storm on 8 September. The greatest difference of storm-time disturbances in ionization rate obtained in two versions of the GSM TIP simulations occurred at heights above 130 km. This fact explained the greater differences in thermospheric tides at 154 km altitude obtained in the two versions of the GSM TIP model. The reason probably is the lower energy resolution for POES/Metop in comparison to DMSP.
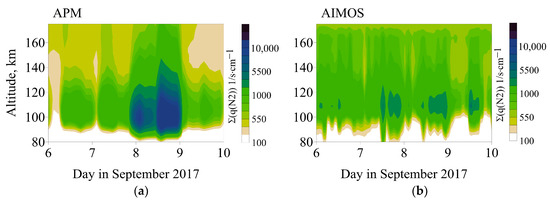
Figure 6.
Altitude profiles of longitude and latitude-integrated molecular nitrogen ionization rates (in logarithmic scale) from 90° N to 60° N for the APM variant (a) and AIMOS (b).
The characteristic differences in the ionization rate of the two versions of the simulations lead, in the end, to differences in the structure and amplitudes of the diurnal and semidiurnal tides generated in the lower thermosphere. Let us consider how, in the versions of the simulation under consideration, the obtained differences in tides form differences in the electron density distribution.
Figure 7a–c shows the total electron content (TEC) values for the two variants of the GSM TIP simulation with the APM and AIMOS models and a map of the experimental TEC for 13 UT 6 September (quiet day). Experimental TEC is Global Ionospheric Maps (GIMs) data produced at the Center for Orbit Determination in Europe (CODE). CODE GIMs are produced using measurements from about 200 GPS/GLONASS stations. Here AIMOS shows the best agreement with experimental TEC in terms of quantity and location. In contrast, APM generates too much at the poles and lacks TEC at low latitudes.
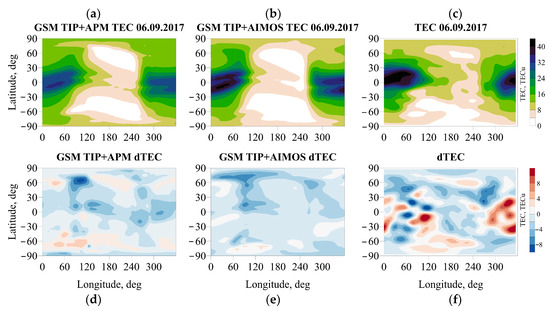
Figure 7.
Total electron content (ionospheric TEC) values for the two versions of the TIP GSM calculation with the APM model (a,d), AIMOS (b,e), and the experimental TEC map at 13 UT 6 September (c) and the ΔTEC disturbance at 13 UT 8 September (f).
Figure 7d–f adds the ΔTEC values between the geomagnetic disturbance day (13 UT 8 September) and the quiet day. The time moment of 13 UT was chosen because the maximum ionospheric effects were observed at this time. These results demonstrate a similar picture of TEC disturbances for the two versions of the precipitation model: interhemispheric asymmetry of TEC disturbances (the largest negative disturbances are formed in the northern hemisphere and the largest positive disturbances in the southern hemisphere) and formation of a belt of negative TEC disturbances in the equator area.
However, some details of TEC disturbances obtained using two different variants of precipitations are different. A more complex structure of TEC disturbances and their bigger amplitudes are formed when energetic particle perturbations are considered according to the APM model. At the same time, a comparison of the model and experimental TEC disturbances shows that the APM version of the GSM TIP simulation corresponds better to the experimental data at high and middle latitudes. Recall that, according to our analysis, the tidal amplitudes increased more during the model storm considering the APM version of the GSM TIP simulation. This fact reflects the existence of a relationship (direct or indirect) between tidal perturbations and TEC disturbances. TEC disturbances are reproduced in the worst way in the modeling results at low latitudes and the equator. This may be due to the lack of consideration in the GSM TIP model of atmospheric tides and their interaction with thermospheric tides generated by the geomagnetic storm. We should note that both model versions significantly underestimate the TEC effect at 60 N/100 E, where the particle forcing should be strong in both models, which might be an indication of a missing direct effect.
The ionization of neutrals by high-energy particle precipitations leads to complex effects on the upper atmosphere/ionosphere. A sharp increase in particle precipitation fluxes leads to a local increase in the electron and ion density in the precipitation zone that leads to an increase in the auroral E-region ionospheric conductivity. The amplitude and structure of disturbances in conductivity are very important for the electric field of magnetospheric convection both at high latitudes and its penetration to low latitudes. Such disturbed electric fields in the ionosphere can form TEC disturbances [41].
6. Conclusions
This paper presents a study of thermospheric tides and the response of the ionosphere to tidal variations during September 2017, performed on the GSM TIP model. The selected period covers quiet days and the days of the geomagnetic storm of 7–8 September. The setting of boundary conditions excluded the penetration of wave processes and their impact on the thermosphere from the underlying layers of the atmosphere. Two versions of the simulation were performed, the scenarios differing only in the description of the ionization by precipitation particles. The first version of the simulation was the APM model, and the second version was AIMOS.
This study showed the following:
1. During a geomagnetic storm, the amplitude of diurnal and semidiurnal tides increases at all altitudes. On quiet days, migrating tides DW1 and SW2 prevailed, and their structure and amplitude in both versions of the simulation mainly coincided. On the day of maximum geomagnetic storm development on 8 September and the day after, the nonmigrating components of tidal waves, mainly DW0 and SW0, intensified. There were also increasing differences in the spatial structure of tides between the two versions of the simulation, especially between the diurnal tides at 121 km and the semidiurnal tides at 154 km. On disturbance days, the amplitudes of diurnal and semidiurnal tides in the APM version are markedly greater than the corresponding values in the AIMOS version of the GSM TIP model.
2. A comparison of the APM and AIMOS ionization function characteristics showed that the amplitude of the ionization rate and, eventually, the total energy that is transferred to the thermosphere are more important for the formation of DW and SW than the spatial structure or temporal resolution of their variations. The APM model, together with the GSM TIP solver for the ionization process, produced greater storm-time disturbances of ionization rates in the lower ionosphere (especially at F1 region heights) in comparison to the AIMOS model. Thus, in the maximum phase of the geomagnetic storm on 8 September, the ionization rate in the APM version exceeds analogous AIMOS values by about six times, which leads to significantly larger tidal wave amplitudes. This difference also affects the values of the ionospheric response changes in the TEC. This leads to greater storm-time disturbances in the amplitude of diurnal and semidiurnal tides obtained in the APM version of the GSM TIP model in comparison to the AIMOS one.
3. Comparison of the TEC maps for the two versions of the simulation showed that AIMOS reproduced the quiet time TEC well, but concerning the TEC disturbance during storms at high and medium latitudes, the amplitude changes, and the qualitative picture is better described in the APM version. At the same time, the TEC disturbances are worst reproduced in simulation results at low latitudes, and there may also be issues inside the main particle precipitation regions. The first may be due to the lack of consideration in the GSM TIP model of atmospheric tides and their interaction with thermospheric tides generated by a geomagnetic storm.
Author Contributions
Data curation, F.S.B.; methodology, F.S.B. and I.V.K.; formal analysis and investigation, F.S.B., O.P.B., I.V.K., M.V.K. and V.V.K.; writing—original draft preparation, F.S.B., O.P.B., I.V.K. and M.V.K.; provision of AIMOS data paper discussion, O.S.Y. and J.M.W.; supervision, E.V.R. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the Ministry of Science and Higher Education of the Russian Federation, agreement 075-15-2021-583 (tidal variation analysis) and RSF, project number 21-17-00208 (model runs and postprocessing).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Forbes, J.M.; Zhang, X.; Hagan, M.E.; England, S.L.; Liu, G.; Gasperini, F. On the Specification of Upward-Propagating Tides for ICON Science Investigations. Space Sci. Rev. 2017, 212, 697–713. [Google Scholar] [CrossRef] [PubMed]
- Kil, H.; Talaat, E.R.; Oh, S.J.; Paxton, L.J.; England, S.L.; Su, S.Y. Wave structures of the plasma density and vertical E × B drift in low-latitude F region. J. Geophys. Res. 2008, 113, A09312. [Google Scholar] [CrossRef]
- Liu, H.; Watanabe, S. Seasonal variation of the longitudinal structure of the equatorial ionosphere: Does it reflect tidal influences from below? J. Geophys. Res. 2008, 113, A08315. [Google Scholar] [CrossRef]
- Truskowski, A.O.; Forbes, J.M.; Zhang, X.; Palo, S.E. New perspectives on thermosphere tides—1. Lower thermosphere spectra and seasonal-latitudinal structures. Earth Planets Space 2014, 66, 136. [Google Scholar] [CrossRef]
- Forbes, J.M.; Zhang, X.; Palo, S.; Russell, J.; Mertens, C.J.; Mlynczak, M. Tidal variability in the ionospheric dynamo region. J. Geophys. Res. 2008, 113, A02310. [Google Scholar] [CrossRef]
- Hagan, M.E.; Maute, A.; Roble, R.G. Tropospheric tidal effects on the middle and upper atmosphere. J. Geophys. Res. 2009, 114, A01302. [Google Scholar] [CrossRef]
- Cai, X.; Wang, W.; Lin, D.; Eastes, R.W.; Qian, L.; Zhu, Q.; Correira, J.; McClintock, W.E.; Gan, Q.; Aryal, S.; et al. Investigation of the Southern Hemisphere mid-high latitude thermospheric ∑O/N2 responses to the Space-X storm. J. Geophys. Res. Space Phys. 2023, 128, e2022JA031002. [Google Scholar] [CrossRef]
- Rees, D. Observations and modelling of ionospheric and thermospheric disturbances during major geomagnetic storms: A review. J. Atmos. Terr. Phys. 1995, 57, 1433–1457. [Google Scholar] [CrossRef]
- Yokoyama, N.; Kamide, Y. Statistical nature of geomagnetic storms. J. Geophys. Res. 1997, 102, 14215–14222. [Google Scholar] [CrossRef]
- Lastovicka, J. Monitoring and forecasting of ionospheric space weather—Effects of geomagnetic storms. J. Atmos. Solar-Terr. Phys. 2002, 64, 697–705. [Google Scholar] [CrossRef]
- Danilov, A.D.; Konstantinova, A.V. Ionospheric Precursors of Geomagnetic Storms. 1. A Review of the Problem. Geomagn. Aeron. 2019, 59, 554–566. [Google Scholar] [CrossRef]
- Fesen, C.G. Tidal effects on the thermosphere. Surv. Geophys. 1992, 13, 269–295. [Google Scholar] [CrossRef]
- Fesen, C.G.; Richmond, A.D.; Roble, R.G. Theoretical effects of geomagnetic activity on thermospheric tides. J. Geophys. Res. 1993, 98, 15599–15612. [Google Scholar] [CrossRef]
- Fesen, C.G.; Richmond, A.D.; Roble, R.G. Auroral effects on midlatitude semidiurnal tides. Geophys. Res. Let. 1991, 18, 412–415. [Google Scholar] [CrossRef]
- Wissing, J.M.; Kallenrode, M.-B. Atmospheric Ionization Module OSnabruck (AIMOS): A 3-D model to determine atmospheric ionization by energetic charged particles from different populations. J. Geophys. Res. 2009, 114, A06104. [Google Scholar] [CrossRef]
- Vorobjev, V.G.; Yagodkina, O.I. Auroral precipitation dynamics during strong magnetic storms. Geomagn. Aeron. 2007, 47, 185–192. [Google Scholar] [CrossRef]
- Vorobjev, V.G.; Yagodkina, O.I. Empirical model of auroral precipitation power during substorms. J. Atmos. Solar-Terr. Phys. 2008, 70, 654–662. [Google Scholar] [CrossRef]
- Zhang, Y.; Paxton, L.J. An empirical Kp-dependent global auroral model based on TIMED/GUVI FUV data. J. Atmos. Solar-Terr. Phys. 2008, 70, 1231–1242. [Google Scholar] [CrossRef]
- Wu, C.; Ridley, A.J.; DeJong, A.D.; Paxton, L.J. FTA: A Feature Tracking Empirical Model of Auroral Precipitation. Space Weather 2021, 19, e2020SW002629. [Google Scholar] [CrossRef]
- Vorobjev, V.G.; Yagodkina, O.I. Effect of magnetic activity on the global distribution of auroral precipitation zones. Geomagn. Aeron. 2005, 45, 438–444. [Google Scholar]
- Namgaladze, A.A.; Korenkov, Y.N.; Klimenko, V.V.; Karpov, I.V.; Surotkin, V.A.; Naumova, N.M. Numerical modelling of the thermosphere-ionosphere-protonosphere system. J. Atmos. Solar-Terr. Phys. 1991, 53, 1113–1124. [Google Scholar] [CrossRef]
- Koren’kov, Y.N.; Klimenko, V.V.; Bessarab, F.S. A study of the interrelationship between ionospheric electrodynamics and thermospheric circulation for a self-consistent description of the Earth’s upper atmosphere. Geomagn. Aeron. 1998, 38, 783–788. [Google Scholar]
- Klimenko, M.V.; Bryukhanov, V.V.; Klimenko, V.V. Numerical simulation of the electric field and zonal current in the Earth’s ionosphere: The dynamo field and equatorial electrojet. Geomagn. Aeron. 2006, 46, 457–466. [Google Scholar] [CrossRef]
- Feshchenko, E.Y.; Maltsev, Y.P. Electric potential distribution in the high-latitude ionosphere under different geophysical conditions. Geomagn. Aeron. 2005, 45, 213–220. [Google Scholar]
- Sojka, J.J.; Zhu, L.; Crain, D.J.; Schunk, R.W. Effect of high-latitude ionospheric convection on Sun-aligned polar caps. J. Geophys. Res. 1994, 99, 8851–8863. [Google Scholar] [CrossRef]
- Kikuchi, T.; Hashimoto, K.K.; Nozaki, K. Penetration of magnetospheric electric fields to the equator during a geomagnetic storm. J. Geophys. Res. 2008, 113, A06214. [Google Scholar] [CrossRef]
- Kotova, D.S.; Klimenko, M.V.; Klimenko, V.V.; Zakharov, V.E. Influence of geomagnetic storms of September 26–30, 2011, on the ionosphere and HF radiowave propagation. II. radiowave propagation. Geomagn. Aeron. 2017, 57, 288–300. [Google Scholar] [CrossRef]
- Ratovsky, K.G.; Klimenko, M.V.; Klimenko, V.V.; Chirik, N.V.; Korenkova, N.A.; Kotova, D.S. After-effects of geomagnetic storms: Statistical analysis and theoretical explanation. Solar-Terr. Physics. 2018, 4, 26–32. [Google Scholar] [CrossRef]
- Ratovsky, K.; Klimenko, M.; Vasilyev, R.; Klimenko, V.; Podlesnyi, A. Vertical plasma transport in the ionosphere over Irkutsk during St. Patrick’s Day geomagnetic storm: Observations and modeling. Adv. Space Res. 2021, 67, 122–132. [Google Scholar] [CrossRef]
- Dmitriev, A.V.; Suvorova, A.V.; Klimenko, M.V.; Klimenko, V.V.; Ratovsky, K.G.; Rakhmatulin, R.A.; Parkhomov, V.A. Predictable and unpredictable ionospheric disturbances during St. Patrick’s Day magnetic storms of 2013 and 2015 and on 8–9 March 2008. J. Geophys. Res. 2017, 122, 2398–2423. [Google Scholar] [CrossRef]
- Klimenko, M.V.; Klimenko, V.V.; Despirak, I.V.; Zakharenkova, I.E.; Kozelov, B.V.; Cherniakov, S.M.; Andreeva, E.S.; Tereshchenko, E.D.; Vesnin, A.M.; Korenkova, N.A.; et al. Disturbances of the thermosphere-ionosphere-plasmasphere system and auroral electrojet at 30°E longitude during the St. Patrick’s Day geomagnetic storm on 17–23 March 2015. J. Atmos. Solar-Terr. Phys. 2018, 180, 78–92. [Google Scholar] [CrossRef]
- Klimenko, M.V.; Zakharenkova, I.E.; Klimenko, V.V.; Lukianova, R.Y.; Cherniak, I.V. Simulation and observations of the polar tongue of ionization at different heights during the 2015 St. Patrick’s Day storms. Space Weather 2019, 17, 1073–1089. [Google Scholar] [CrossRef]
- Richmond, A.D. Ionospheric Electrodynamics Using Magnetic Apex Coordinates. J. Geomagn. Geoelectr. 1995, 47, 191–212. [Google Scholar] [CrossRef]
- Yakovchuk, O.; Wissing, J. Magnetic local time asymmetries in precipitating electron and proton populations with and without substorm activity. Ann. Geophys. 2019, 37, 1063–1077. [Google Scholar] [CrossRef]
- Schröter, J.; Heber, B.; Steinhilber, F.; Kallenrode, M. Energetic particles in the atmosphere: A Monte-Carlo simulation. Adv. Space Res. 2006, 37, 1597–1601. [Google Scholar] [CrossRef]
- Schmidt, G.A.; Ruedy, R.; Hansen, J.E.; Aleinov, I.; Bell, N.; Bauer, M.; Bauer, S.; Cairns, B.; Canuto, V.; Cheng, Y.; et al. Present day atmospheric simulations using GISS ModelE: Comparison to in-situ, satellite and reanalysis data. J. Clim. 2006, 19, 153–192. [Google Scholar] [CrossRef]
- Picone, J.M.; Hedin, A.E.; Drob, D.P.; Aikin, A.C. NRLMSISE-00 empirical model of the atmosphere: Statistical comparisons and scientific issues. J. Geophys. Res. 2002, 107, 1468. [Google Scholar] [CrossRef]
- Deminov, M.G.; Khegai, V.V. Analytical approximation of the ionization rate by auroral electrons. Geomagn. Aeron. 1980, 20, 145–147. [Google Scholar]
- Karpov, I.V.; Bessarab, F.S.; Borchevkina, O.P.; Artemenko, K.A.; Klopova, A.I. Modeling the effect of mesospheric internal gravity waves in the thermosphere and ionosphere during the 2009 sudden stratospheric warming. Geomagn. Aeron. 2018, 58, 509–522. [Google Scholar] [CrossRef]
- Vasiliev, P.A.; Bessarab, F.S.; Karpov, I.V.; Klimenko, V.V.; Klimenko, M.V.; Sukhodolov, T.V.; Rozanov, E.V. Tidal and planetary waves in the lower thermosphere and ionosphere simulated with the eagle model for the January 2009 sudden stratospheric warming conditions. Izv. Atmos. Ocean. Phys. 2019, 55, 178–187. [Google Scholar] [CrossRef]
- Resende, L.C.A.; Shi, J.; Denardini, C.M.; Batista, I.S.; Picanço, G.A.S.; Moro, J.; Chagas, R.A.J.; Barros, D.; Chen, S.S.; Nogueira, P.A.B.; et al. The impact of the disturbed electric field in the sporadic E (Es) layer development over Brazilian region. J. Geophys. Res. Space Phys. 2021, 126, e2020JA028598. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).