NAO Seasonal Forecast Using a Multivariate Air–Sea Coupled Deep Learning Model Combined with Causal Discovery
Abstract
1. Introduction
- An exploration of the relationship between NAO and air–sea variables from a data-driven causal discovery perspective at seasonal time scales.
- The proposed air–sea coupled NAO-MCD deep learning mode achieves high reliability for NAO seasonal forecasts.
- An assessment of the forecast skills of advanced numerical models and machine learning models for the NAO at 1–6-month lead times is presented.
2. Materials and Methods
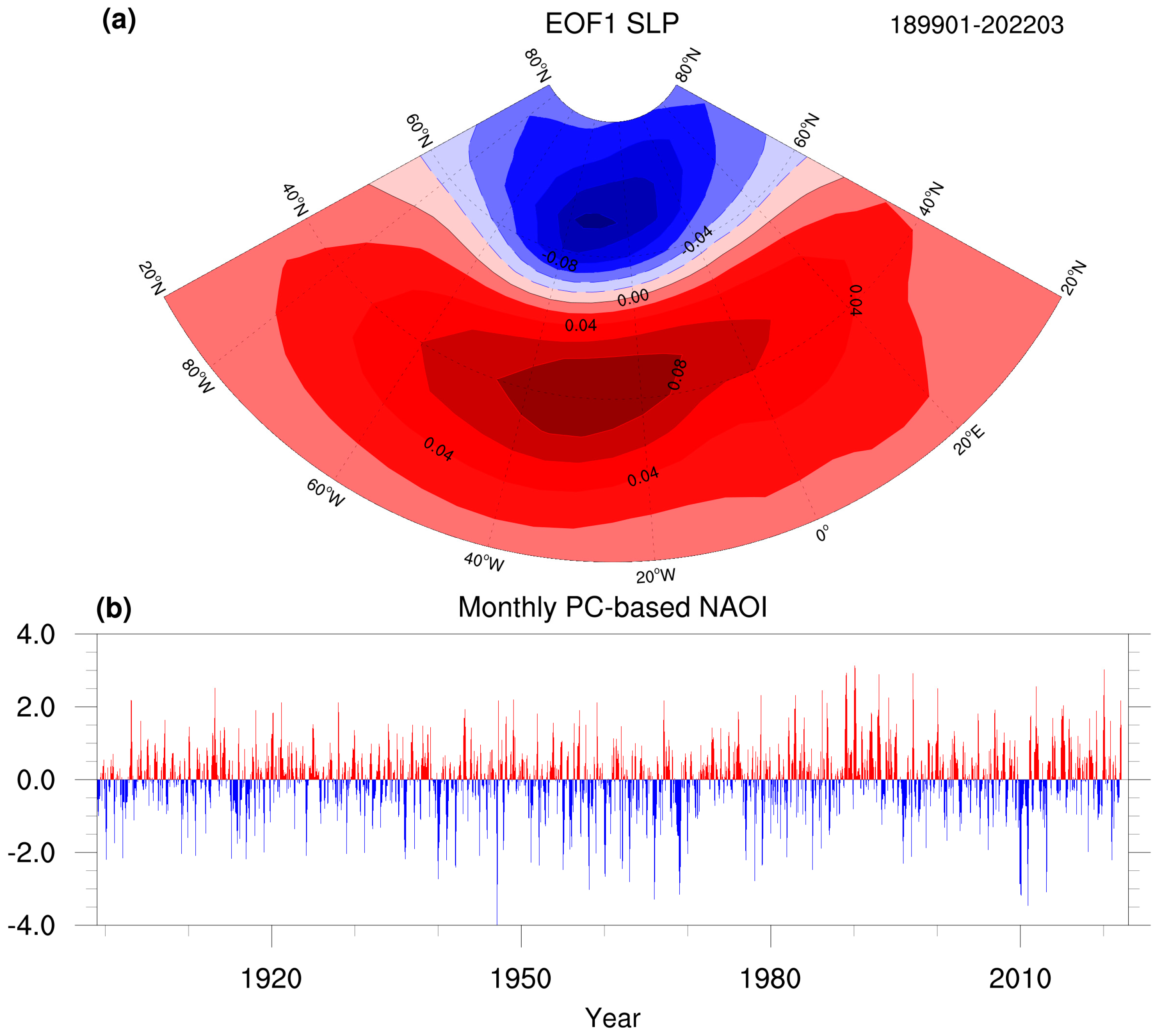
2.1. PC-Based NAO Index
2.2. Problem Formalization
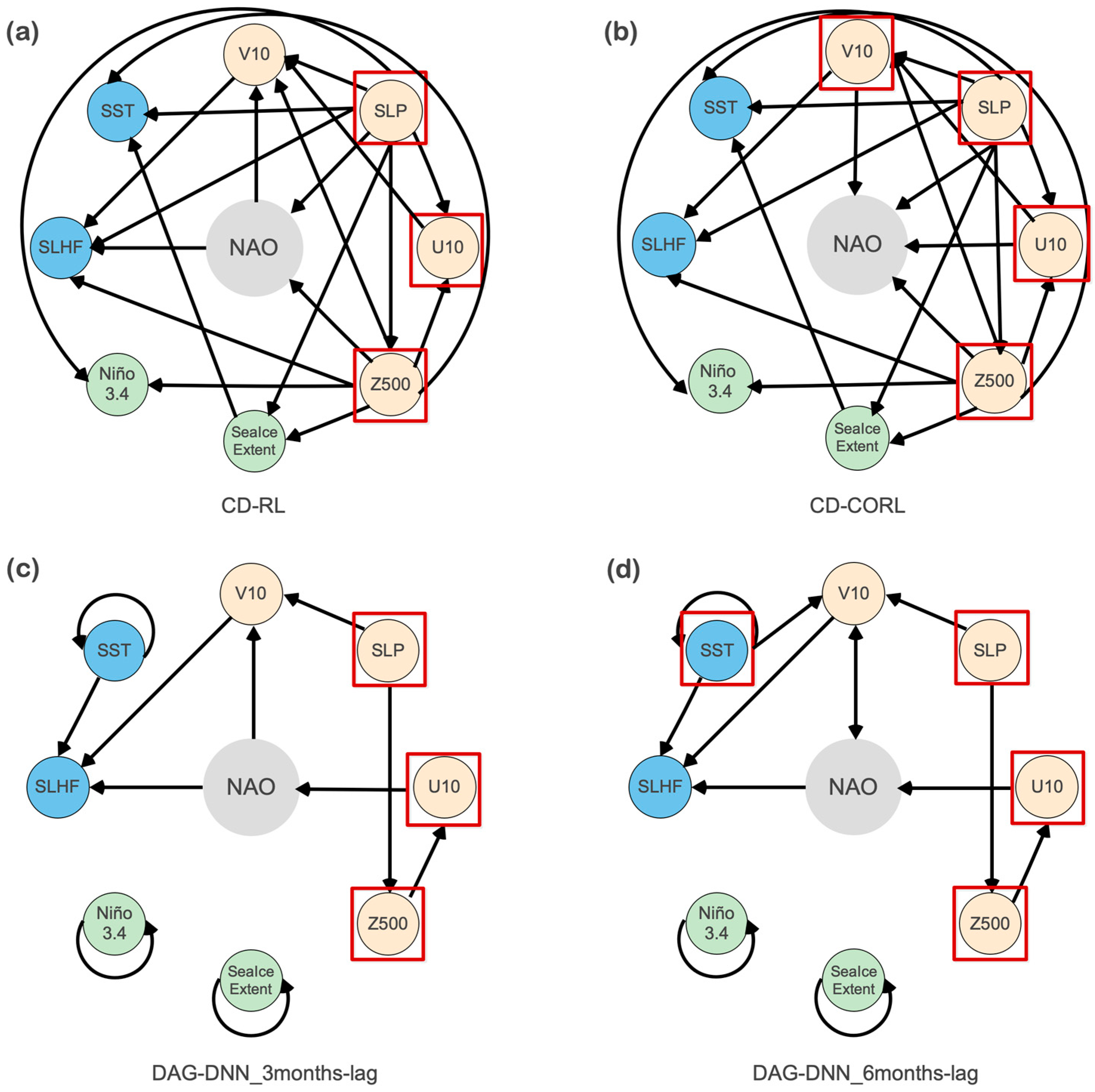
2.3. Data-Driven Causal Discovery Models
2.3.1. CD-RL
2.3.2. CD-CORL
- Action: The selection of variables is considered an action, in which each step selects a variable , resulting in a sequence of variables that constitute the action space , where d is the number of variables.
- State: The encoder directly takes a sample data of each variable as a state , and all the embedded states constitute the space S .
- State transfer: At the current decision step, the specified state transition is connected to the action selected. If the selected variable is , then the state is transferred to state , which is the j-th output from encoder, i.e., , where denote the state taken at the t-th decision step.
2.3.3. DAG-GNN
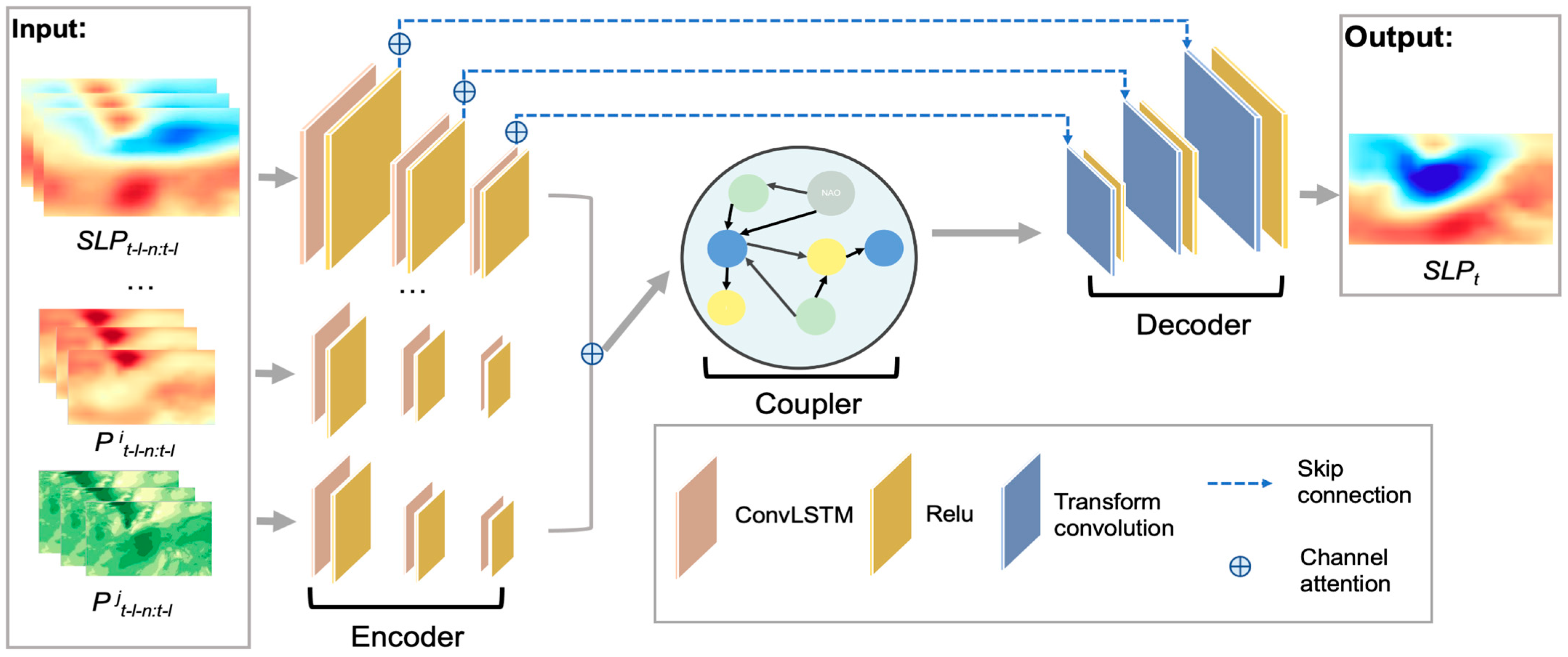
2.4. NAO-MCD: Multivariate Air–Sea Coupled Model for NAO Forecast Combined with Causal Discovery
2.4.1. Encoder
2.4.2. Coupler
2.4.3. Decoder
3. Experiments and Evaluations
3.1. Potential Predictors
3.2. Datasets and Pre-Processing
3.3. Loss Function
3.4. Experiment Setting
3.5. Evaluation Metrics
4. Experimental Results and Analysis
4.1. Results of Causal Discovery and Predictor Selection
4.2. Analysis of Effective Seasonal NAO Forecast of NAO-MCD
4.2.1. Effect of Ensemble Size
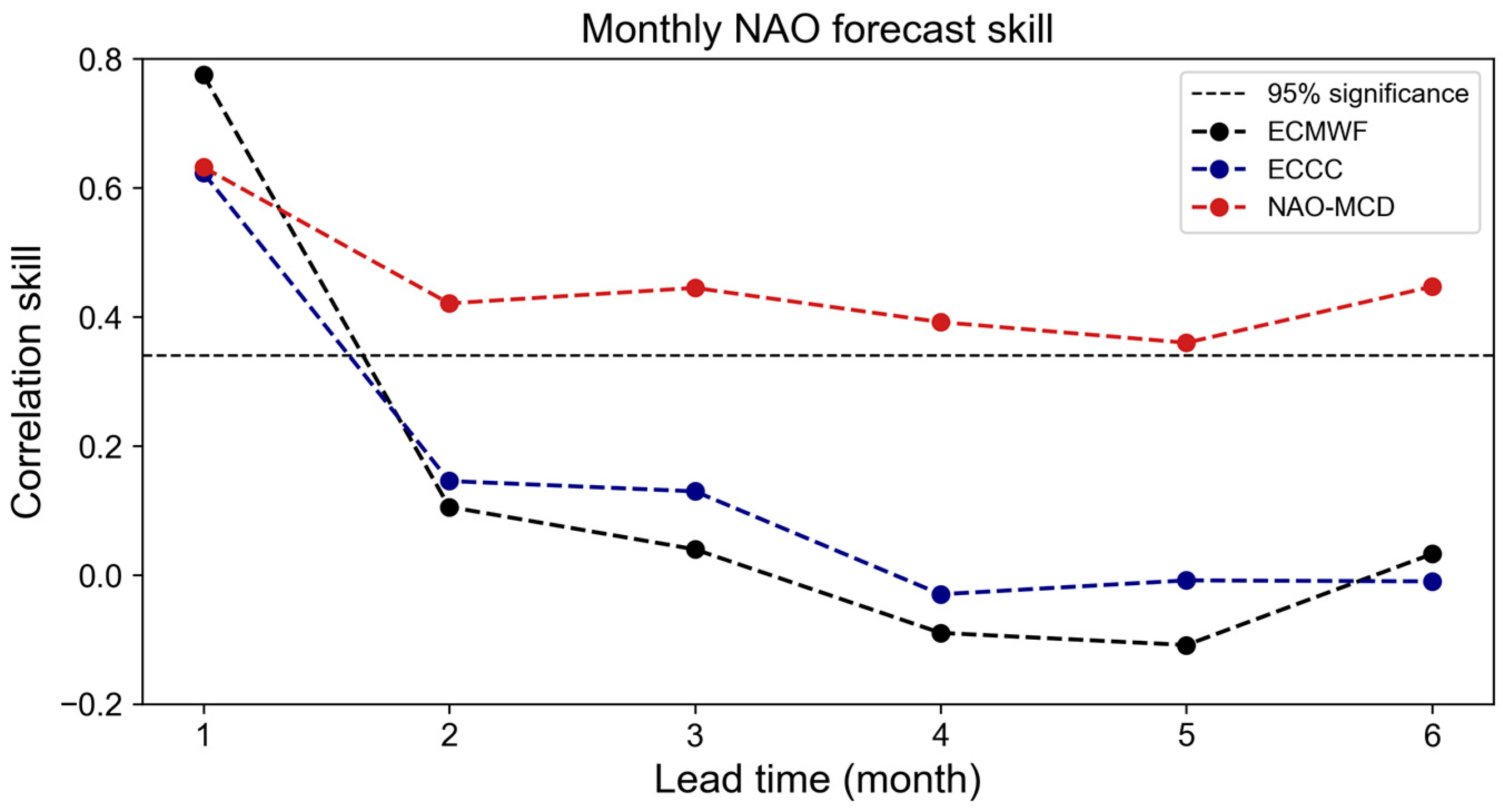
4.2.2. Monthly NAO Forecast
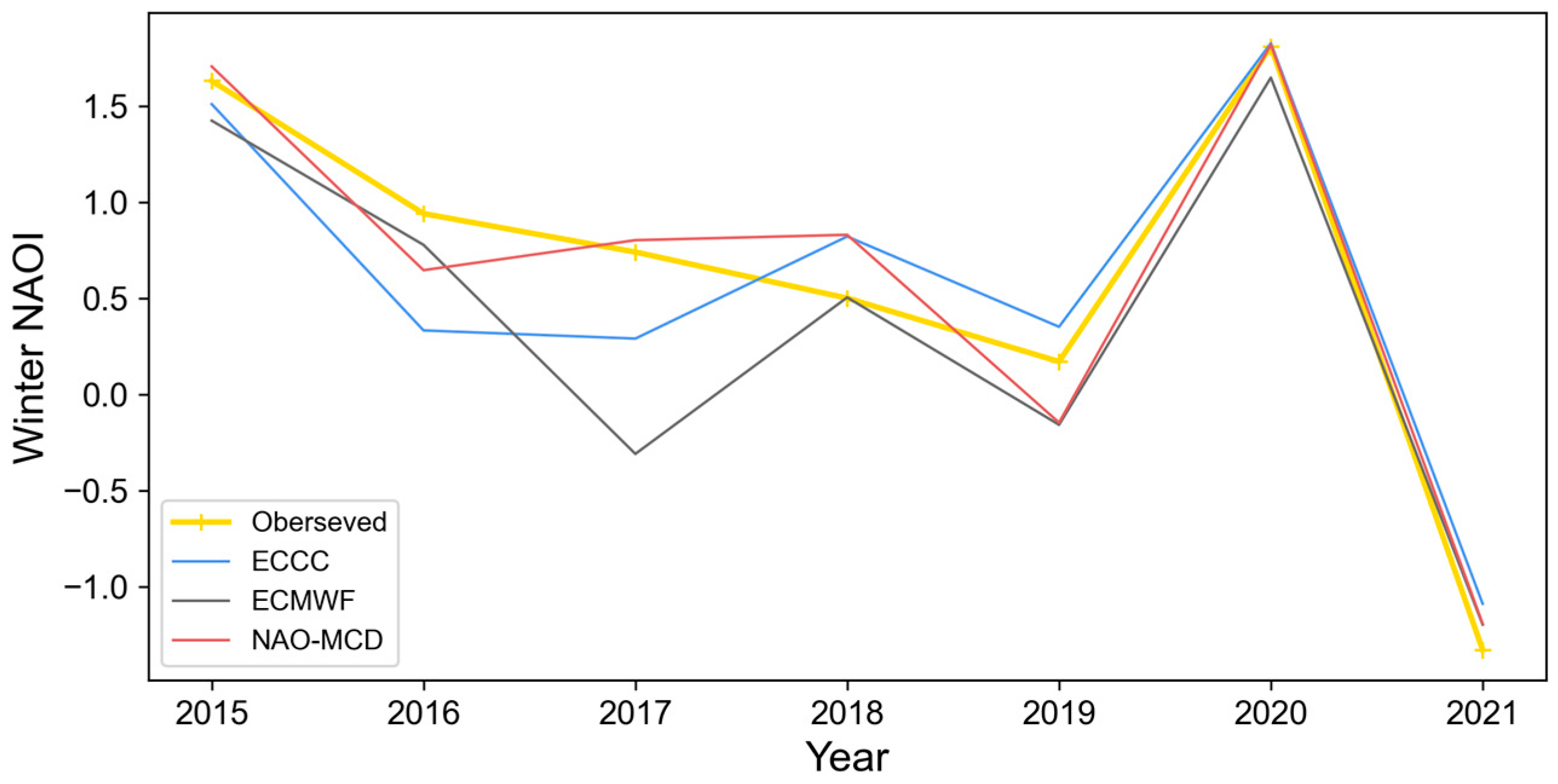
4.2.3. Winter NAO Forecast
4.3. Effectiveness of the NAO-MCD’s Model Structure
4.3.1. Contributions of Different Predictors to the Forecast Skill
4.3.2. Effectiveness of Causal Discovery and the Coupler
4.3.3. Comparison with Other Advanced Deep Learning Models
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hurrell, J.W.; Kushnir, Y.; Visbeck, M. The North Atlantic Oscillation. Science 2001, 291, 603–605. [Google Scholar] [CrossRef]
- Hurrell, J.W. Decadal Trends in the North Atlantic Oscillation: Regional Temperatures and Precipitation. Science 1995, 269, 676–679. [Google Scholar] [CrossRef] [PubMed]
- Hurrell, J.W.; Van Loon, H. Decadal Variations in Climate Associated with the North Atlantic Oscillation. In Climatic Change at High Elevation Sites; Diaz, H.F., Beniston, M., Bradley, R.S., Eds.; Springer: Dordrecht, The Netherlands, 1997; pp. 69–94. [Google Scholar] [CrossRef]
- Donat, M.; Peterson, T.; Brunet, M.; King, A.; Almazroui, M.; Kolli, R.; Boucherf, D.; Al-Mulla, A.; Nour, A.; Aly, A.; et al. Changes in Extreme Temperature and Precipitation in the Arab Region: Long-Term Trends and Variability Related to ENSO and NAO. Int. J. Climatol. 2014, 34. [Google Scholar] [CrossRef]
- Rousi, E.; Rust, H.W.; Ulbrich, U.; Anagnostopoulou, C. Implications of Winter NAO Flavors on Present and Future European Climate. Climate 2020, 8, 13. [Google Scholar] [CrossRef]
- Athanasiadis, P.J.; Bellucci, A.; Scaife, A.A.; Hermanson, L.; Materia, S.; Sanna, A.; Borrelli, A.; MacLachlan, C.; Gualdi, S. A Multisystem View of Wintertime NAO Seasonal Predictions. J. Clim. 2017, 30, 1461–1475. [Google Scholar] [CrossRef]
- Weisheimer, A.; Schaller, N.; O’Reilly, C.; MacLeod, D.A.; Palmer, T. Atmospheric Seasonal Forecasts of the Twentieth Century: Multi-Decadal Variability in Predictive Skill of the Winter North Atlantic Oscillation (NAO) and Their Potential Value for Extreme Event Attribution: Atmospheric Seasonal Forecasts of the Twentieth Century. Q. J. R. Meteorol. Soc. 2017, 143, 917–926. [Google Scholar] [CrossRef] [PubMed]
- Kent, C.; Scaife, A.A.; Dunstone, N. What Potential for Improving Sub-Seasonal Predictions of the Winter NAO? Atmos. Sci. Lett. 2023, 24, e1146. [Google Scholar] [CrossRef]
- Richter, J.H.; Glanville, A.A.; Edwards, J.; Kauffman, B.; Davis, N.A.; Jaye, A.; Kim, H.; Pedatella, N.M.; Sun, L.; Berner, J.; et al. Subseasonal Earth System Prediction with CESM2. Weather Forecast. 2022, 37, 797–815. [Google Scholar] [CrossRef]
- Lin, H. Predictability and Prediction of the North Atlantic Oscillation. In Proceedings of the ECMWF Seminar on Predictability in the European and Atlantic Regions, Reading, UK, 6–9 September 2010. [Google Scholar]
- Tao, L.-J.; Gao, C.; Zhang, R.-H. Model Parameter-Related Optimal Perturbations and Their Contributions to El Niño Prediction Errors. Clim. Dyn. 2019, 52, 1425–1441. [Google Scholar] [CrossRef]
- Hall, R.J.; Scaife, A.A.; Hanna, E.; Jones, J.M.; Erdélyi, R. Simple Statistical Probabilistic Forecasts of the Winter NAO. Weather Forecast. 2017, 32, 1585–1601. [Google Scholar] [CrossRef]
- Strommen, K.; Palmer, T.N. Signal and Noise in Regime Systems: A Hypothesis on the Predictability of the North Atlantic Oscillation. Q. J. R. Meteorol. Soc. 2019, 145, 147–163. [Google Scholar] [CrossRef]
- Yuan, S.; Luo, X.; Mu, B.; Li, J.; Dai, G. Prediction of North Atlantic Oscillation Index with Convolutional LSTM Based on Ensemble Empirical Mode Decomposition. Atmosphere 2019, 10, 252. [Google Scholar] [CrossRef]
- Cuesta, J.E.; Hunt, J.K.; Schull, J. Weekly Climate Indices: Generation and Prediction. 2019. Stanford Research Series. Available online: https://medium.com/comet-ml/stanford-research-series-weekly-climate-indices-generation-and-prediction-8e548babb3a7 (accessed on 10 January 2023).
- Mu, B.; Li, J.; Yuan, S.; Luo, X. The NAO Variability Prediction and Forecasting with Multiple Time Scales Driven by ENSO Using Machine Learning Approaches. Comput. Intell. Neurosci. 2022, 2022, e6141966. [Google Scholar] [CrossRef] [PubMed]
- Siddique, T.; Mahmud, M.S.; Keesee, A.M.; Ngwira, C.M.; Connor, H. A Survey of Uncertainty Quantification in Machine Learning for Space Weather Prediction. Geosciences 2022, 12, 27. [Google Scholar] [CrossRef]
- Ebert-Uphoff, I.; Deng, Y. Causal Discovery for Climate Research Using Graphical Models. J. Clim. 2012, 25, 5648–5665. [Google Scholar] [CrossRef]
- Song, H.; Wang, J.; Tian, J.; Huang, J.; Zhang, Z. Spatio-Temporal Climate Data Causality Analytics—An Analysis of ENSO’s Global Impacts. In Proceedings of the 8th International Workshop on Climate Informatics (CI2018), Boulder, CO, USA, 19–21 September 2018. [Google Scholar]
- Huang, Y.; Kleindessner, M.; Munishkin, A.; Varshney, D.; Guo, P.; Wang, J. Benchmarking of Data-Driven Causality Discovery Approaches in the Interactions of Arctic Sea Ice and Atmosphere. Front. Big Data 2021, 4, 72. [Google Scholar] [CrossRef]
- He, S.; Yang, S.; Chen, D. Accurate Attribution and Seasonal Prediction of Climatic Anomalies Using Causal Inference Theory. J. Clim. 2022, 35, 4111–4124. [Google Scholar] [CrossRef]
- He, S.; Yang, S.; Chen, D. Inferring Causal Structures to Model and Predict ENSO and Its Effect on Asian Summer Monsoon. In Proceedings of the EGU General Assembly 2023, Vienna, Austria, 24–28 April 2023. EGU23-102. [Google Scholar] [CrossRef]
- Jones, P.D.; Osborn, T.J.; Briffa, K.R. Pressure-Based Measures of the North Atlantic Oscillation (NAO): A Comparison and an Assessment of Changes in the Strength of the NAO and in Its Influence on Surface Climate Parameters. In The North Atlantic Oscillation: Climatic Significance and Environmental Impact; American Geophysical Union (AGU): Washington, DC, USA, 2003; pp. 51–62. [Google Scholar] [CrossRef]
- Hurrell, J.W.; Deser, C. North Atlantic Climate Variability: The Role of the North Atlantic Oscillation. J. Mar. Syst. 2010, 79, 231–244. [Google Scholar] [CrossRef]
- Wunsch, C. The Interpretation of Short Climate Records, with Comments on the North Atlantic and Southern Oscillations. Bull. Am. Meteorol. Soc. 1999, 80, 245–256. [Google Scholar] [CrossRef]
- Chevillon, G. Direct Multi-Step Estimation and Forecasting. J. Econ. Surv. 2007, 21, 746–785. [Google Scholar] [CrossRef]
- Pearl, J. Models, Reasoning and Inference; Cambridge University Press: Cambridge, UK, 2000; Volume 19. [Google Scholar]
- Zhu, S.; Ng, I.; Chen, Z. Causal Discovery with Reinforcement Learning. arXiv 2019, arXiv:1906.04477. [Google Scholar]
- Wang, X.; Du, Y.; Zhu, S.; Ke, L.; Chen, Z.; Hao, J.; Wang, J. Ordering-Based Causal Discovery with Reinforcement Learning. arXiv 2021, arXiv:2105.06631. [Google Scholar]
- Yu, Y.; Chen, J.; Gao, T.; Yu, M. DAG-GNN: DAG Structure Learning with Graph Neural Networks. In International Conference on Machine Learning; PMLR: San Diego, CA, USA, 2019; pp. 7154–7163. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.-Y.; Wong, W.-K.; Woo, W. Convolutional LSTM Network: A Machine Learning Approach for Precipitation Nowcasting. In Proceedings of the International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; pp. 802–810. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015; Part III 18. Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Bjerknes, J. Atlantic Air-Sea Interaction. In Advances in Geophysics; Landsberg, H.E., Van Mieghem, J., Eds.; Elsevier: Amsterdam, The Netherlands, 1964; Volume 10, pp. 1–82. [Google Scholar]
- Thompson, D.W.J.; Wallace, J.M. The Arctic Oscillation Signature in the Wintertime Geopotential Height and Temperature Fields. Geophys. Res. Lett. 1998, 25, 1297–1300. [Google Scholar] [CrossRef]
- Woollings, T.; Hannachi, A.; Hoskins, B.; Turner, A. A Regime View of the North Atlantic Oscillation and Its Response to Anthropogenic Forcing. J. Clim. 2010, 23, 1291–1307. [Google Scholar] [CrossRef]
- Laurila, T.K.; Sinclair, V.A.; Gregow, H. Climatology, Variability, and Trends in near-Surface Wind Speeds over the North Atlantic and Europe during 1979–2018 Based on ERA5. Int. J. Climatol. 2021, 41, 2253–2278. [Google Scholar] [CrossRef]
- Clark, R.T.; Bett, P.E.; Thornton, H.E.; Scaife, A.A. Skilful Seasonal Predictions for the European Energy Industry. Environ. Res. Lett. 2017, 12, 024002. [Google Scholar] [CrossRef]
- Feldstein, S.B. The Timescale, Power Spectra, and Climate Noise Properties of Teleconnection Patterns. J. Clim. 2000, 13, 4430–4440. [Google Scholar] [CrossRef]
- Wang, L.; Ting, M.; Kushner, P.J. A Robust Empirical Seasonal Prediction of Winter NAO and Surface Climate. Sci. Rep. 2017, 7, 279. [Google Scholar] [CrossRef]
- Kolstad, E.W.; Screen, J.A. Nonstationary Relationship Between Autumn Arctic Sea Ice and the Winter North Atlantic Oscillation. Geophys. Res. Lett. 2019, 46, 7583–7591. [Google Scholar] [CrossRef]
- Cassou, C. Euro-Atlantic Regimes and Their Teleconnections. In Proceedings of the ECMWF Seminar on Predictability in the European and Atlantic Regions, Reading, UK, 6–9 September 2010; Volume 6, pp. 1–14. [Google Scholar]
- Rodwell, M.J.; Rowell, D.P.; Folland, C.K. Oceanic Forcing of the Wintertime North Atlantic Oscillation and European Climate. Nature 1999, 398, 320–323. [Google Scholar] [CrossRef]
- Zhang, W.; Jiang, F. Subseasonal Variation in the Winter ENSO-NAO Relationship and the Modulation of Tropical North Atlantic SST Variability. Climate 2023, 11, 47. [Google Scholar] [CrossRef]
- Feng, P.-N.; Lin, H.; Derome, J.; Merlis, T.M. Forecast Skill of the NAO in the Subseasonal-to-Seasonal Prediction Models. J. Clim. 2021, 34, 4757–4769. [Google Scholar] [CrossRef]
- Hurrell, J.W.; Kushnir, Y.; Ottersen, G.; Visbeck, M. An Overview of the North Atlantic Oscillation. In The North Atlantic Oscillation: Climatic Significance and Environmental Impact; American Geophysical Union (AGU): Washington, DC, USA, 2003; pp. 1–35. [Google Scholar] [CrossRef]
- Bell, C.J.; Gray, L.J.; Charlton-Perez, A.J.; Joshi, M.M.; Scaife, A.A. Stratospheric Communication of El Niño Teleconnections to European Winter. J. Clim. 2009, 22, 4083–4096. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 Global Reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Fetterer, F.; Knowles, K.; Meier, W.N.; Savoie, M.; Windnagel, A.K. Sea Ice Index, Version 3. 2017. Distributed by National Snow and Ice Data Center. Available online: https://doi.org/10.7265/N5K072F8 (accessed on 15 November 2022).
- Eyring, V.; Bony, S.; Meehl, G.A.; Senior, C.A.; Stevens, B.; Stouffer, R.J.; Taylor, K.E. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) Experimental Design and Organization. Geosci. Model Dev. 2016, 9, 1937–1958. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E.; Long, S.R.; Peng, C.-K. On the Trend, Detrending, and Variability of Nonlinear and Nonstationary Time Series. Proc. Natl. Acad. Sci. USA 2007, 104, 14889–14894. [Google Scholar] [CrossRef]
- Scaife, A.A.; Arribas, A.; Blockley, E.; Brookshaw, A.; Clark, R.T.; Dunstone, N.; Eade, R.; Fereday, D.; Folland, C.K.; Gordon, M.; et al. Skillful Long-Range Prediction of European and North American Winters. Geophys. Res. Lett. 2014, 41, 2514–2519. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2017, arXiv:1412.6980. [Google Scholar] [CrossRef]
- Prechelt, L. Early Stopping—But When? In Neural Networks: Tricks of the Trade, 2nd ed.; Montavon, G., Orr, G.B., Müller, K.-R., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2012; pp. 53–67. [Google Scholar] [CrossRef]
- Thépaut, J.-N.; Dee, D.; Engelen, R.; Pinty, B. The Copernicus Programme and Its Climate Change Service. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; Institute of Electrical and Electronics Engineers: Piscataway, NJ, USA, 2018; pp. 1591–1593. [Google Scholar] [CrossRef]
- Bhatt, U.; Alexander, M.; Battisti, D.; Houghton, D.; Keller, L. Atmosphere-Ocean Interaction in the North Atlantic: Near-Surface Climate Variability. J. Clim. 1998, 11, 1615–1632. [Google Scholar] [CrossRef]
- Osińska, M.; Jędrasik, J. Atlantic Oscillation Indices in Meridional Distribution. Theor. Appl. Climatol. 2020, 141, 1367–1382. [Google Scholar] [CrossRef]
- Woollings, T.; Franzke, C.; Hodson, D.L.R.; Dong, B.; Barnes, E.A.; Raible, C.C.; Pinto, J.G. Contrasting Interannual and Multidecadal NAO Variability. Clim. Dyn. 2015, 45, 539–556. [Google Scholar] [CrossRef]


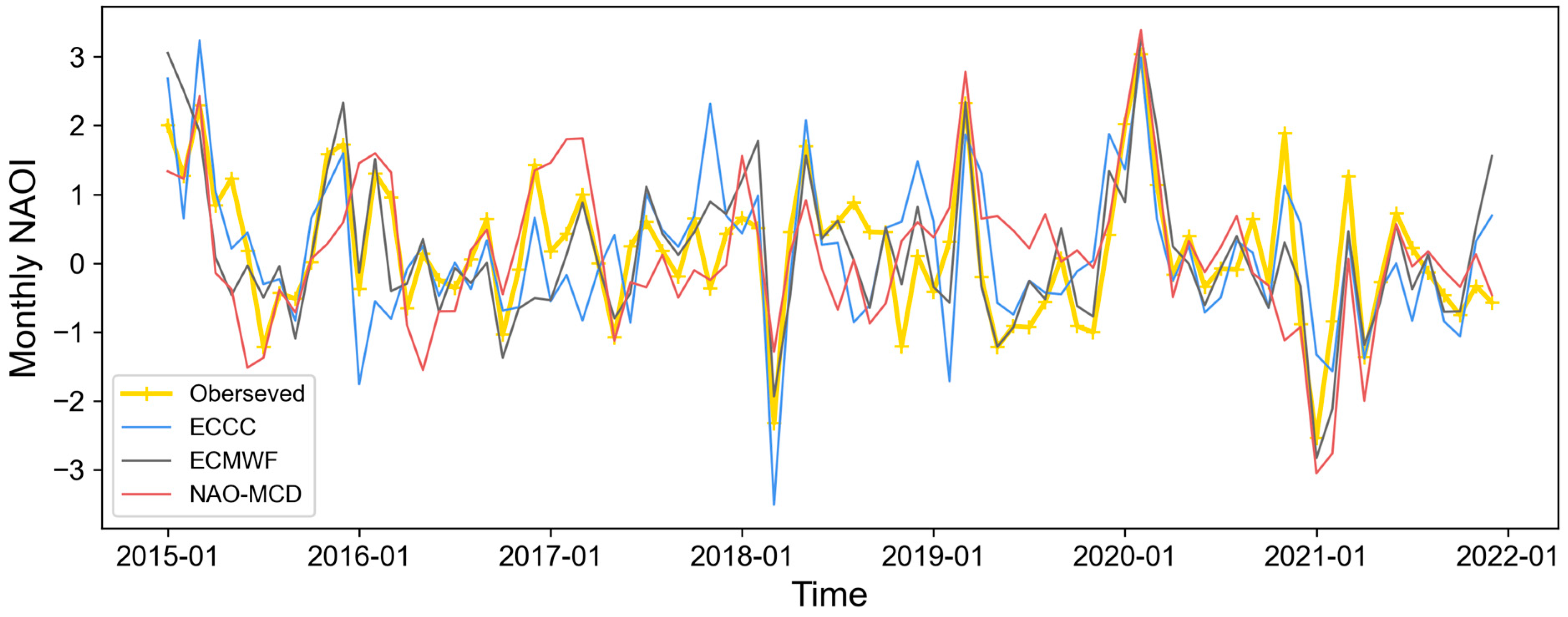
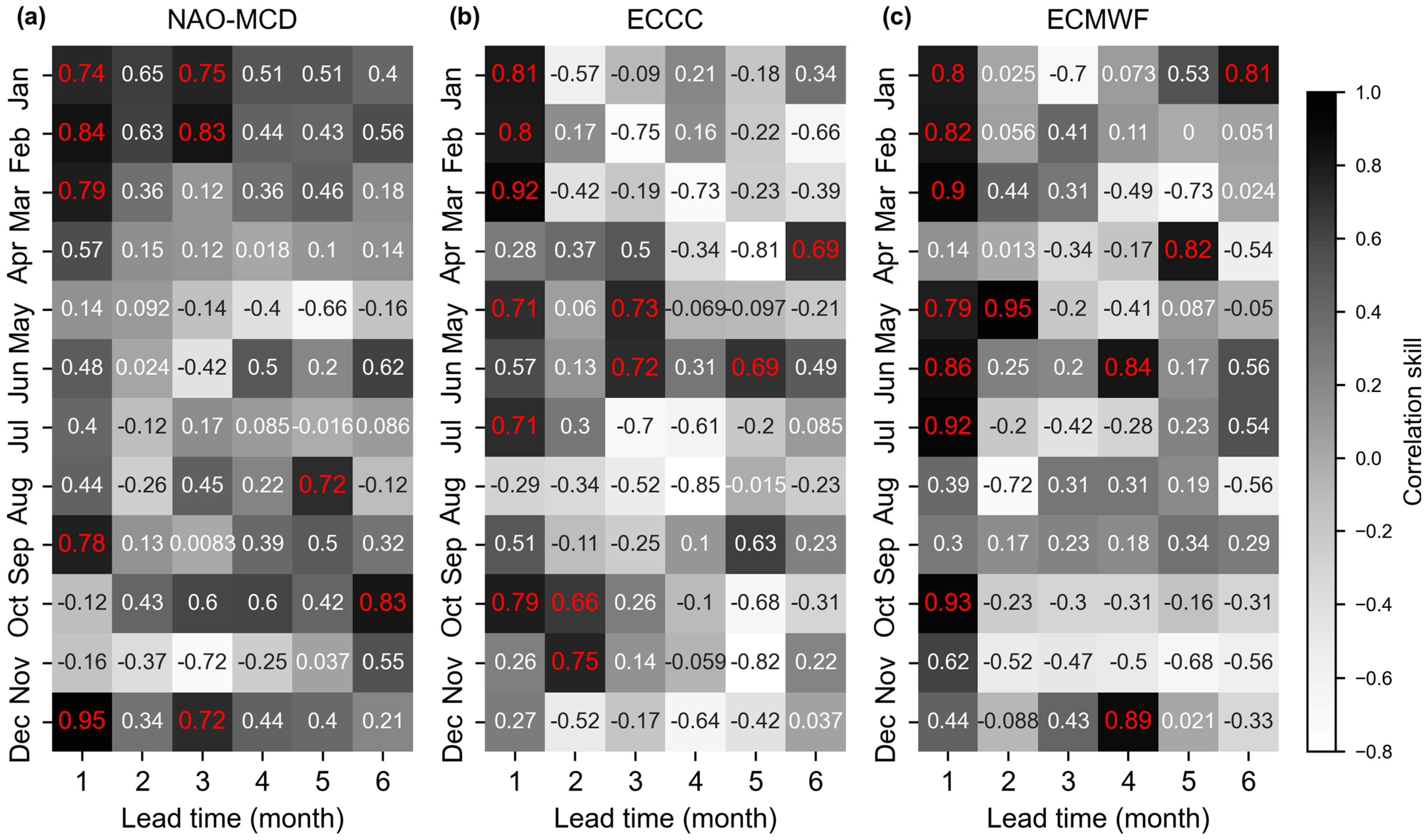
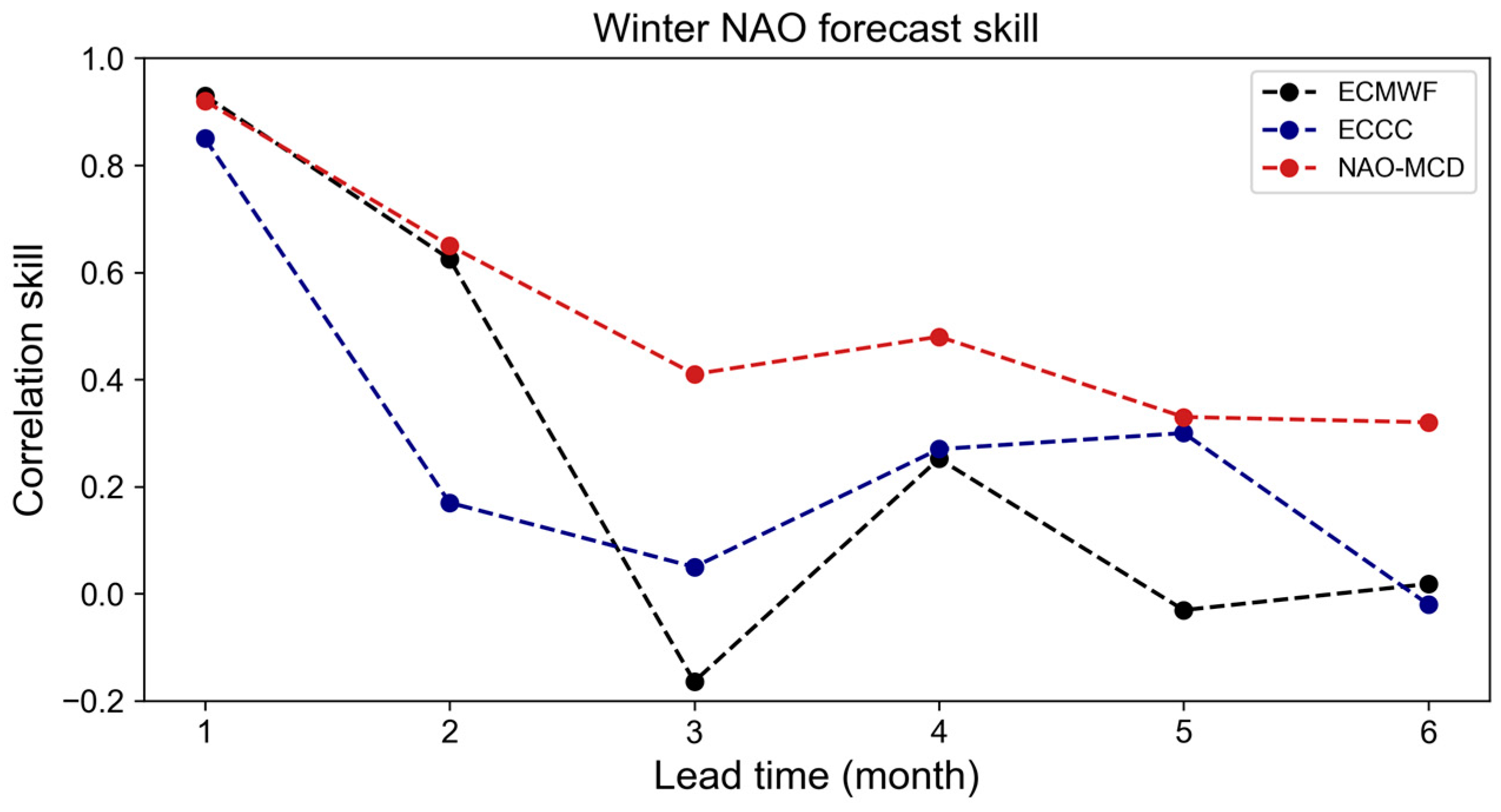
| Variable | Description | Unit |
|---|---|---|
| SLP | Sea-level pressure | hPa |
| Z500 | 500 hPa geopotential height | m |
| V10 | 10 m meridional wind | m·s−1 |
| U10 | 10 m zonal wind | m·s−1 |
| SST | Sea surface temperature | K |
| SLHF | Sea surface latent heat flux | J·m−2 |
| Niño 3.4 | Niño 3.4 ENSO index | - |
| SeaIceExtent | Arctic sea ice extent index | - |
| Variable | Time Range | Data Source | Data Type |
|---|---|---|---|
| SLP | 1899–2021 | NCAR | Observation |
| Z500 | 1899–1949 1950–2021 | CMIP6 Era5 | Model simulation Reanalysis |
| V10 | 1899–1949 1950–2021 | CMIP6 Era5 | Model simulation Reanalysis |
| U10 | 1899–1949 1950–2021 | CMIP6 Era5 | Model simulation Reanalysis |
| SST | 1899–1949 1950–2021 | CMIP6 Era5 | Model simulation Reanalysis |
| SLHF | 1899–1949 1950–2021 | CMIP6 Era5 | Model simulation Reanalysis |
| Niño 3.4 | 1950–2021 | NSIDC | Observation |
| SeaIceExtent | 1950–2021 | NCAR | Observation |
| Member Number | ||||
|---|---|---|---|---|
| 1 | 2 | 6 | 7 | 5 |
| 2 | 3 | 6 | 7 | 5 |
| 3 | 2 | 7 | 7 | 5 |
| 4 | 2 | 6 | 7 | 6 |
| 5 | 3 | 6 | 7 | 6 |
| 6 | 2 | 7 | 7 | 6 |
| SLP | Z500 | V10 | U10 | SST | SLHF | Niño 3.4 | SeaIce Extent | |
|---|---|---|---|---|---|---|---|---|
| correlation coefficient | 0.11 | 0.11 | 0.35 | 0.22 | 0.067 | 0.12 | 0.035 | 0.081 |
| p-value | 0.0068 | 0.0086 | 1.3 × 10−15 | 2.2 × 10−6 | 0.013 | 0.0089 | 0.251 | 0.188 |
| Forecast System Name | Forecast System Version | Forecast Initial Condition | Model Resolution (Model Top) | Available Ensemble Size |
|---|---|---|---|---|
| ECMWF | SEAS5 | 1st of month | TCo319 (~0.36° lat-long)/91 levels in vertical, to 0.01 hPa | 25 |
| ECCC | CanCM4i | 1st of month | T63 (~2.8° lat-long)/35 levels in vertical, to 1 hPa | 10 |
| Phase | Index Values | Number in the Test Set | Number of Correct Forecasts | |||
|---|---|---|---|---|---|---|
| ECMWF | ECCC | NAO-MCD | ||||
| NAO−− | Strong negative | NAOI < −1.0 | 9 | 4 | 3 | 4 |
| NAO++ | Strong positive | NAOI > 1.0 | 15 | 10 | 9 | 9 |
| Perturbed Predictor | Forecast Skill | RSME (hPa) | SSIM (%) |
|---|---|---|---|
| - | 0.589 | 4.063 | 79.674 |
| SLP | 0.587 | 4.087 | 78.642 |
| Z500 | 0.589 | 4.072 | 79.567 |
| V10 | 0.588 | 4.075 | 79.034 |
| U10 | 0.589 | 4.067 | 79.568 |
| SST | 0.589 | 4.070 | 79.535 |
| All | 0.582 | 4.115 | 78.622 |
| Removed Predictor | RSME (hPa)/SSIM (%) | ||
|---|---|---|---|
| 1-Month Lead | 3-Month Lead | 6-Month Lead | |
| - | 4.06/79.67 | 4.18/78.12 | 4.26/77.15 |
| Z500 | 4.18/78.04 | 4.25/76.80 | 4.39/76.02 |
| V10 | 4.31/77.09 | 4.35/75.83 | 4.42/75.11 |
| U10 | 4.39/76.80 | 4.39/75.49 | 4.62/75.21 |
| SST | 4.22/78.60 | 4.37/76.05 | 4.47/74.47 |
| Model | RSME (hPa)/SSIM (%) | ||
|---|---|---|---|
| 1-Month Lead | 3-Month Lead | 6-Month Lead | |
| CNN | 5.36/66.23 | 6.47/63.12 | 7.26/59.15 |
| ConvLSTM | 4.64/70.25 | 4.95/64.77 | 5.39/63.89 |
| NAO-MCD with correlation predictors | 4.24/77.73 | 4.52/76.13 | 4.87/75.02 |
| NAO-MCD without coupler | 4.35/76.79 | 4.52/75.72 | 4.74/74.35 |
| NAO-MCD | 4.18/78.04 | 4.25/76.80 | 4.39/76.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mu, B.; Jiang, X.; Yuan, S.; Cui, Y.; Qin, B. NAO Seasonal Forecast Using a Multivariate Air–Sea Coupled Deep Learning Model Combined with Causal Discovery. Atmosphere 2023, 14, 792. https://doi.org/10.3390/atmos14050792
Mu B, Jiang X, Yuan S, Cui Y, Qin B. NAO Seasonal Forecast Using a Multivariate Air–Sea Coupled Deep Learning Model Combined with Causal Discovery. Atmosphere. 2023; 14(5):792. https://doi.org/10.3390/atmos14050792
Chicago/Turabian StyleMu, Bin, Xin Jiang, Shijin Yuan, Yuehan Cui, and Bo Qin. 2023. "NAO Seasonal Forecast Using a Multivariate Air–Sea Coupled Deep Learning Model Combined with Causal Discovery" Atmosphere 14, no. 5: 792. https://doi.org/10.3390/atmos14050792
APA StyleMu, B., Jiang, X., Yuan, S., Cui, Y., & Qin, B. (2023). NAO Seasonal Forecast Using a Multivariate Air–Sea Coupled Deep Learning Model Combined with Causal Discovery. Atmosphere, 14(5), 792. https://doi.org/10.3390/atmos14050792








