Field Calibration of a Low-Cost Air Quality Monitoring Device in an Urban Background Site Using Machine Learning Models
Abstract
:1. Introduction
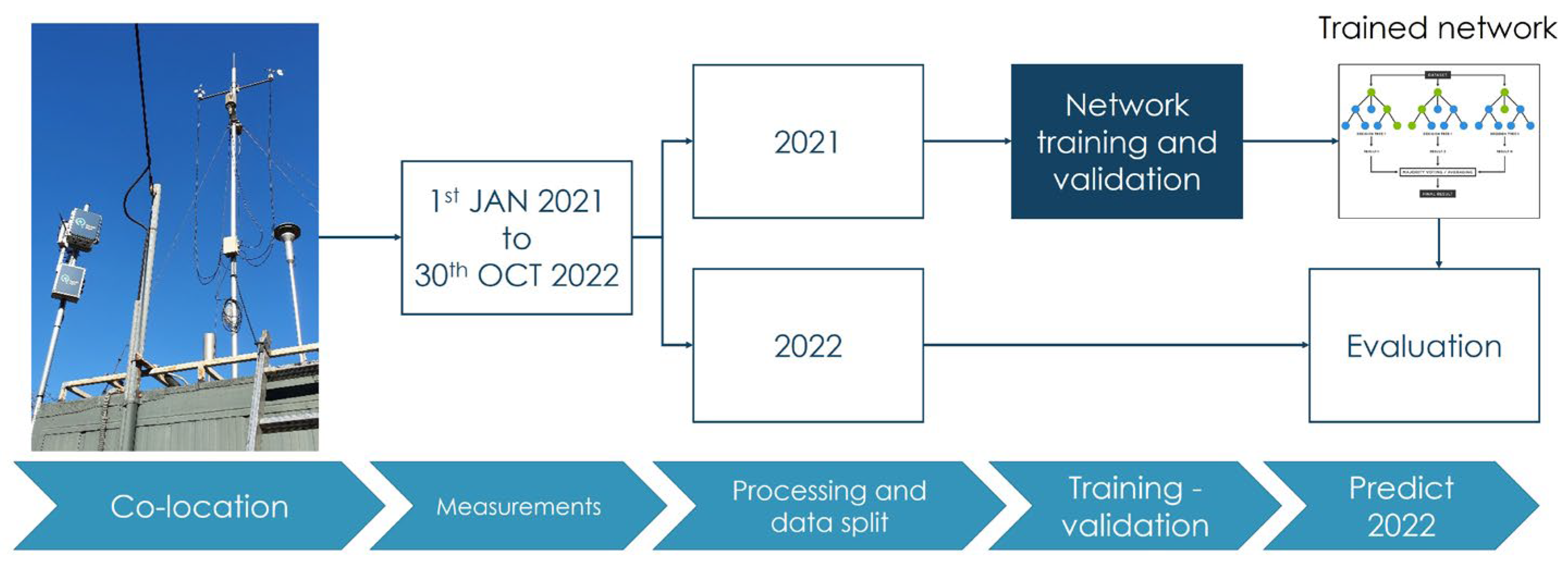
2. Materials and Methods
2.1. Environment Sensing Appliance (ENSENSIA)
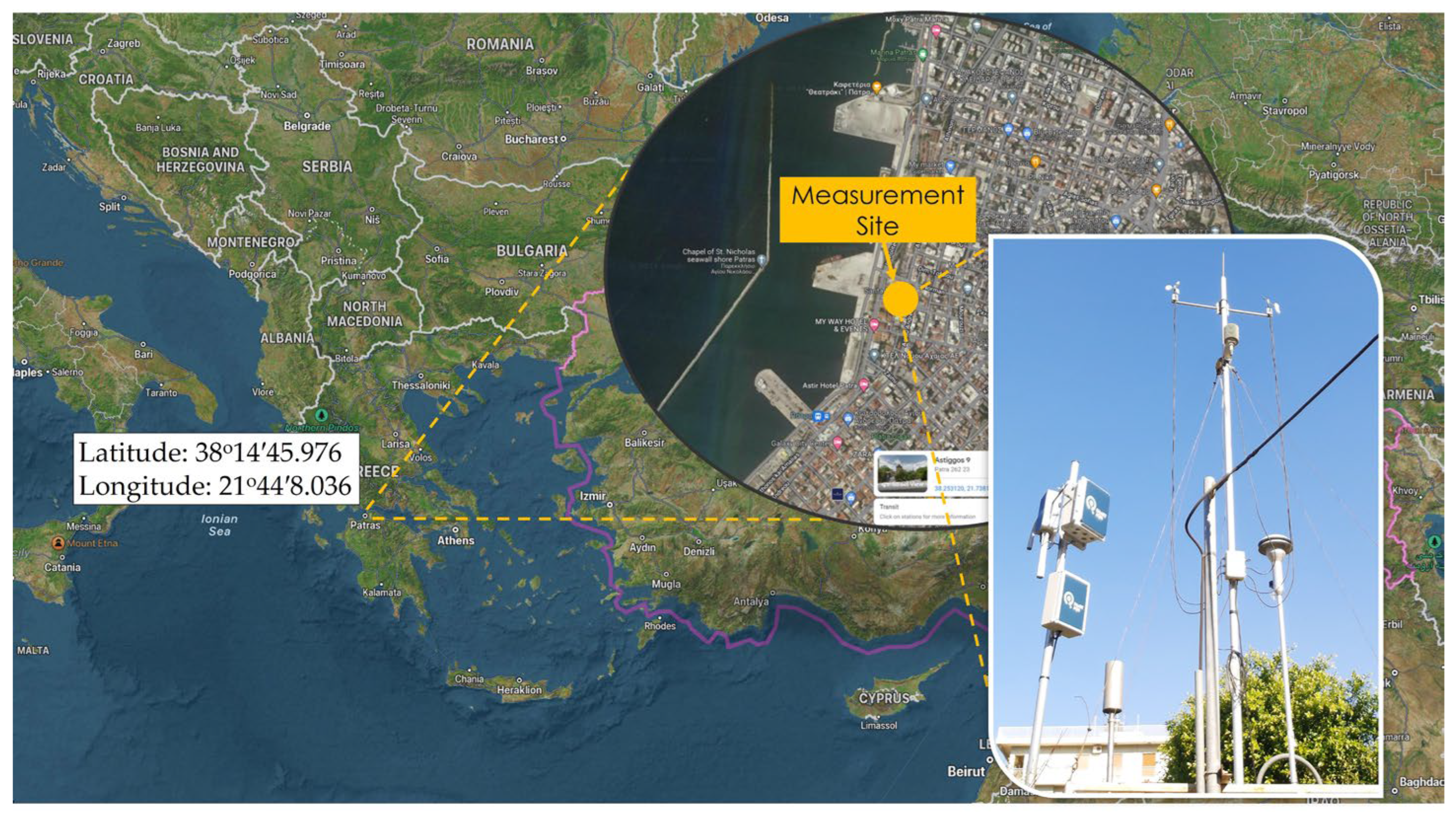
2.2. Measurement Site
2.3. Data Preprocessing
2.4. Machine Learning and Deep Learning
2.4.1. Linear Correction
2.4.2. K-Nearest Neighbors
2.4.3. Random Forest
2.4.4. Artificial Neural Network
2.4.5. Long-Short Term Memory Network
2.4.6. Convolutional Neural Network
2.5. Experiment Setup and Performance Metrics
3. Results
3.1. Nitrogen Dioxide
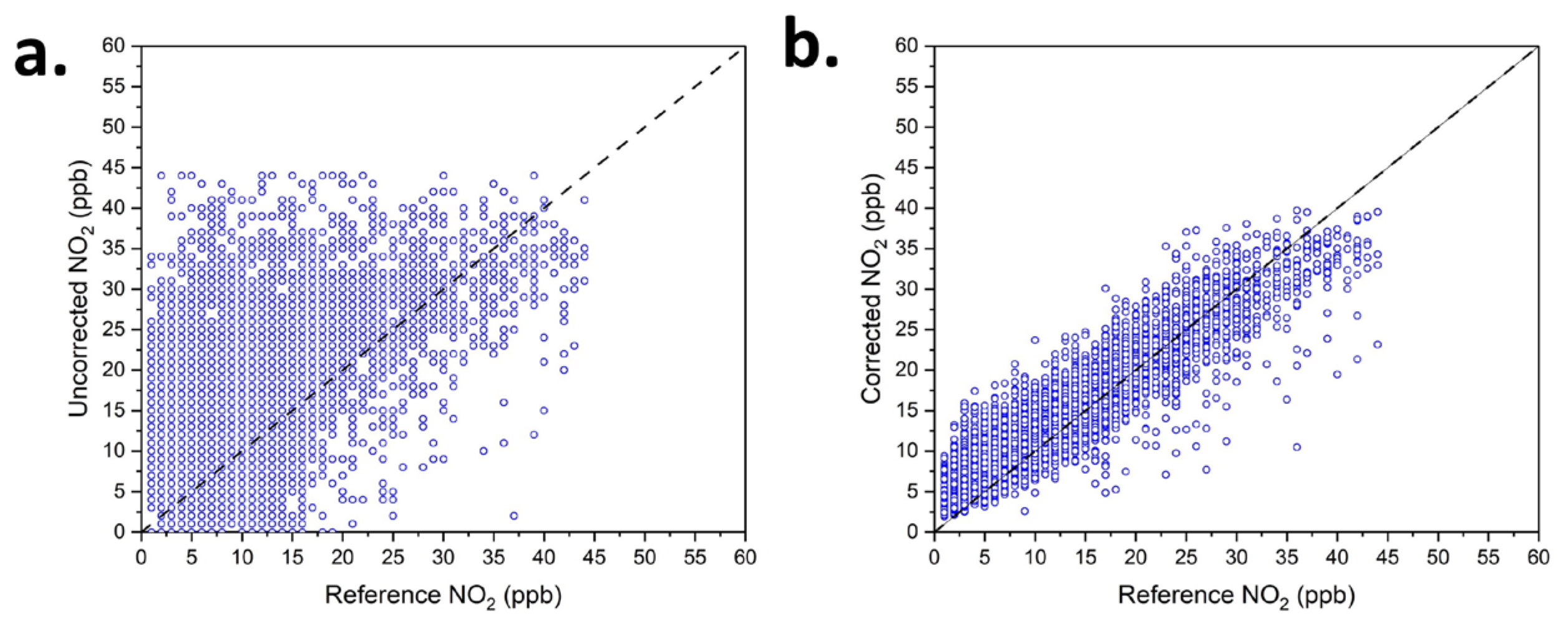
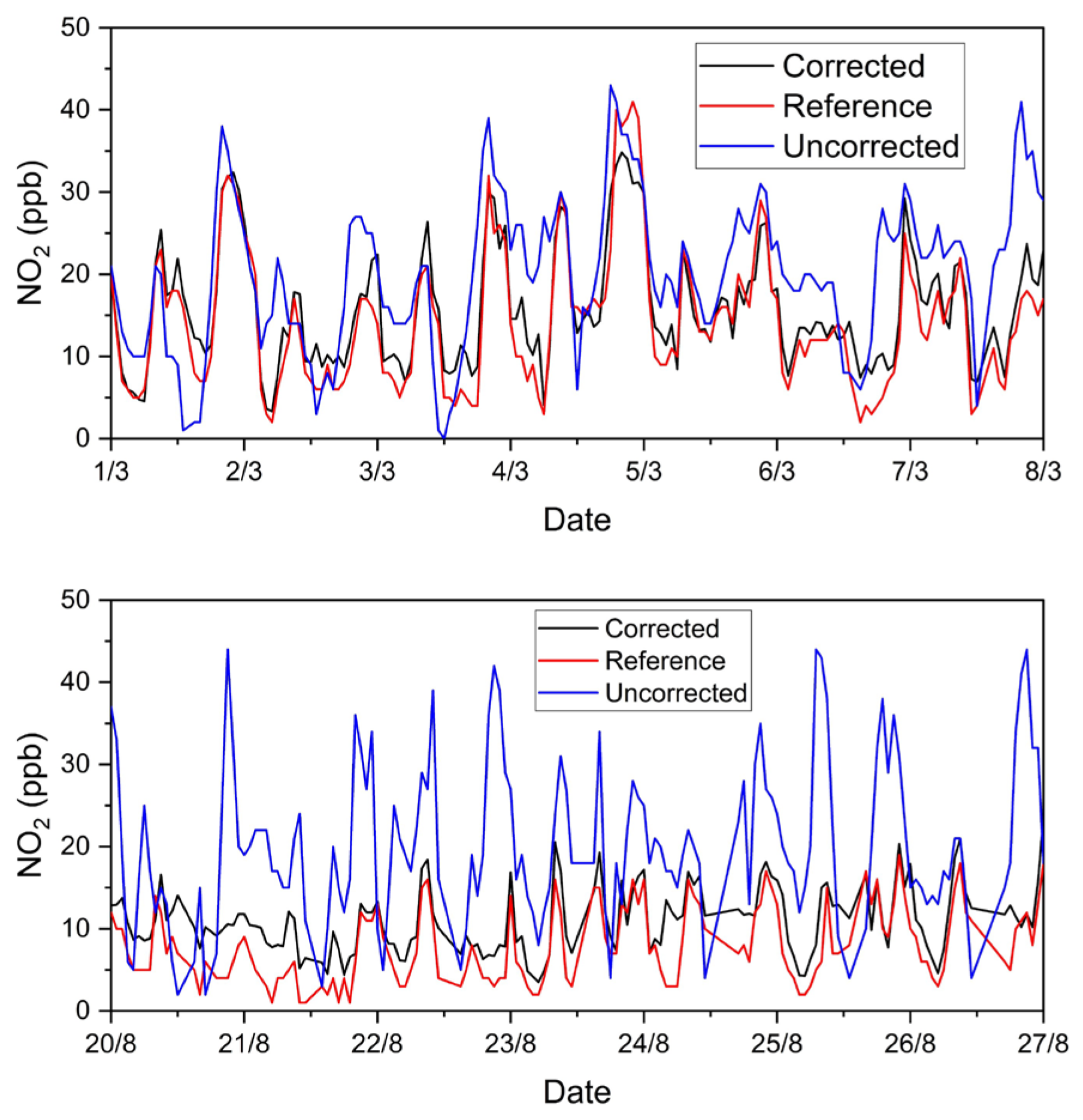
3.1.1. Evaluation of Uncorrected Sensor Readings
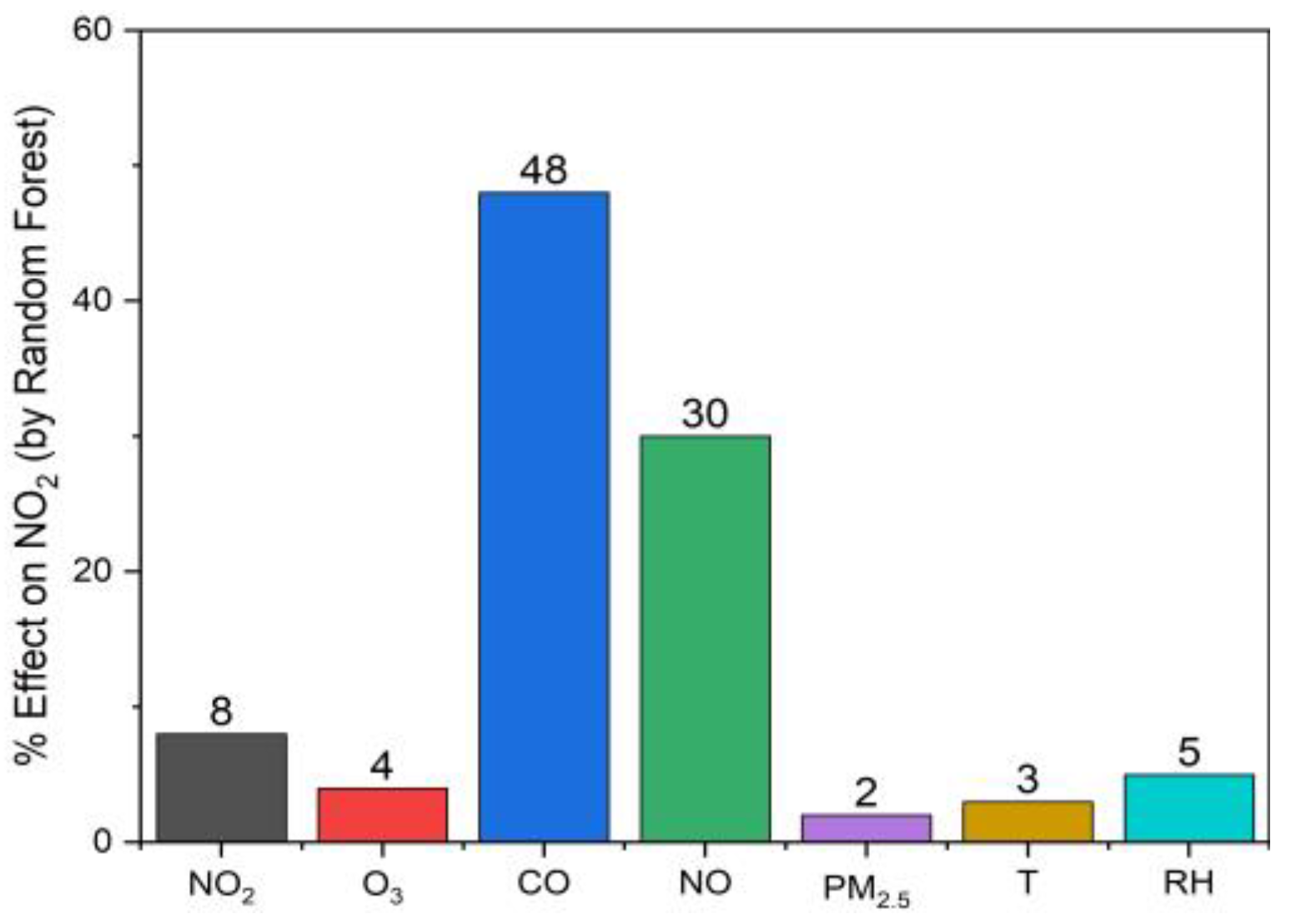
3.1.2. Evaluation of Machine Learning Algorithms
3.2. Ozone
3.2.1. Evaluation of Uncorrected Sensor Readings
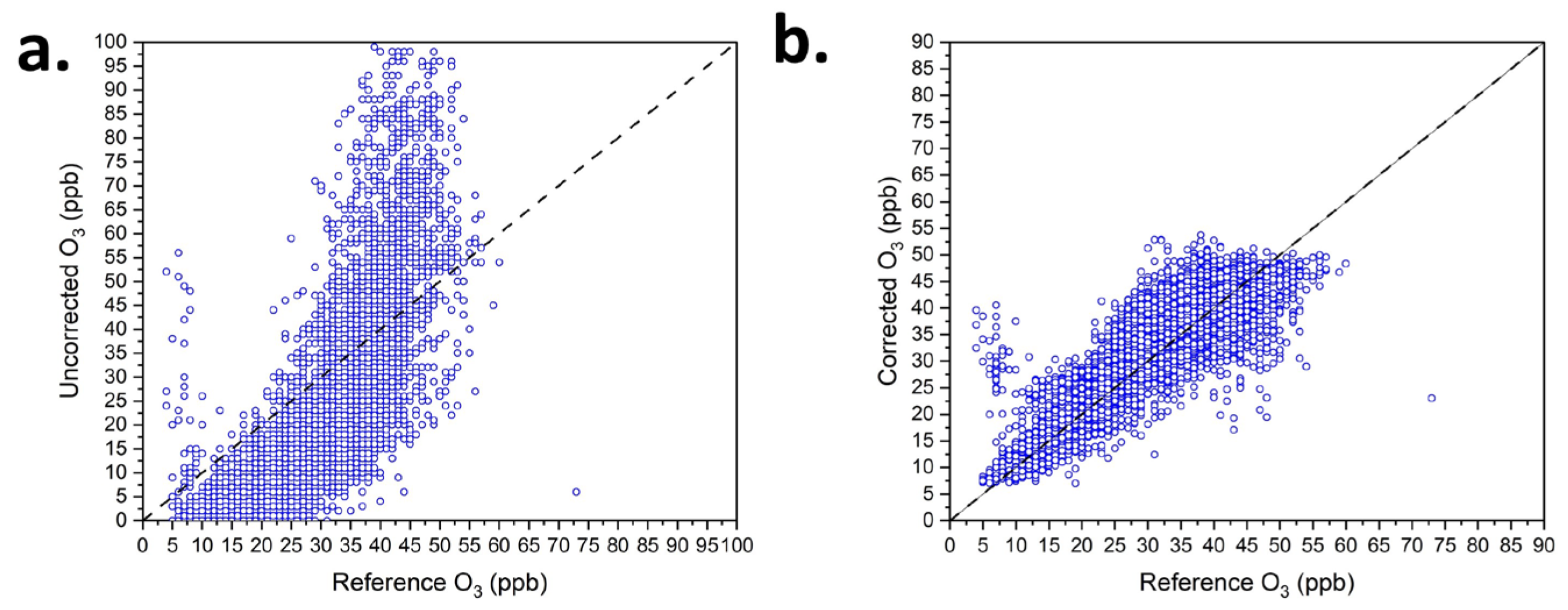
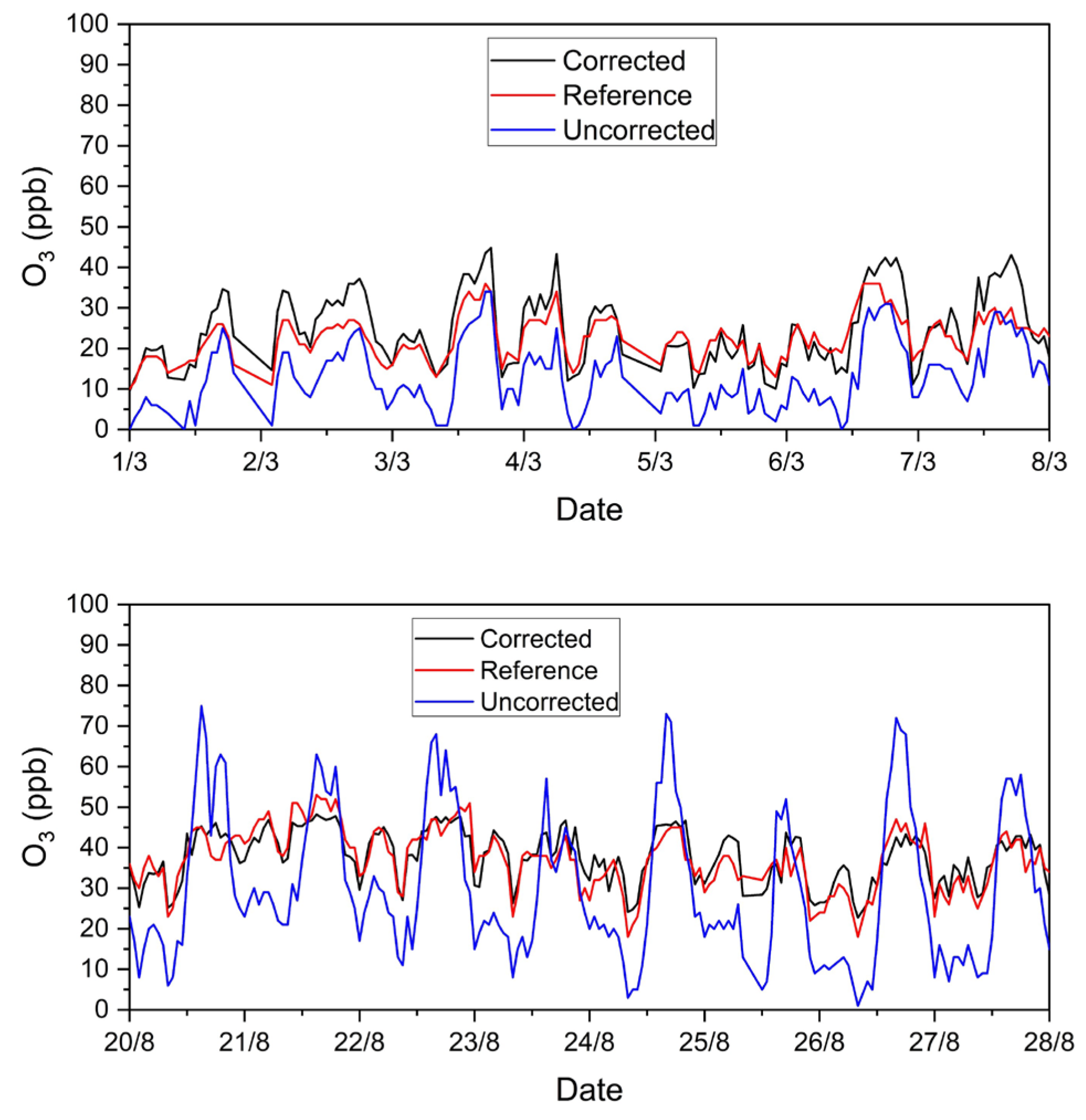
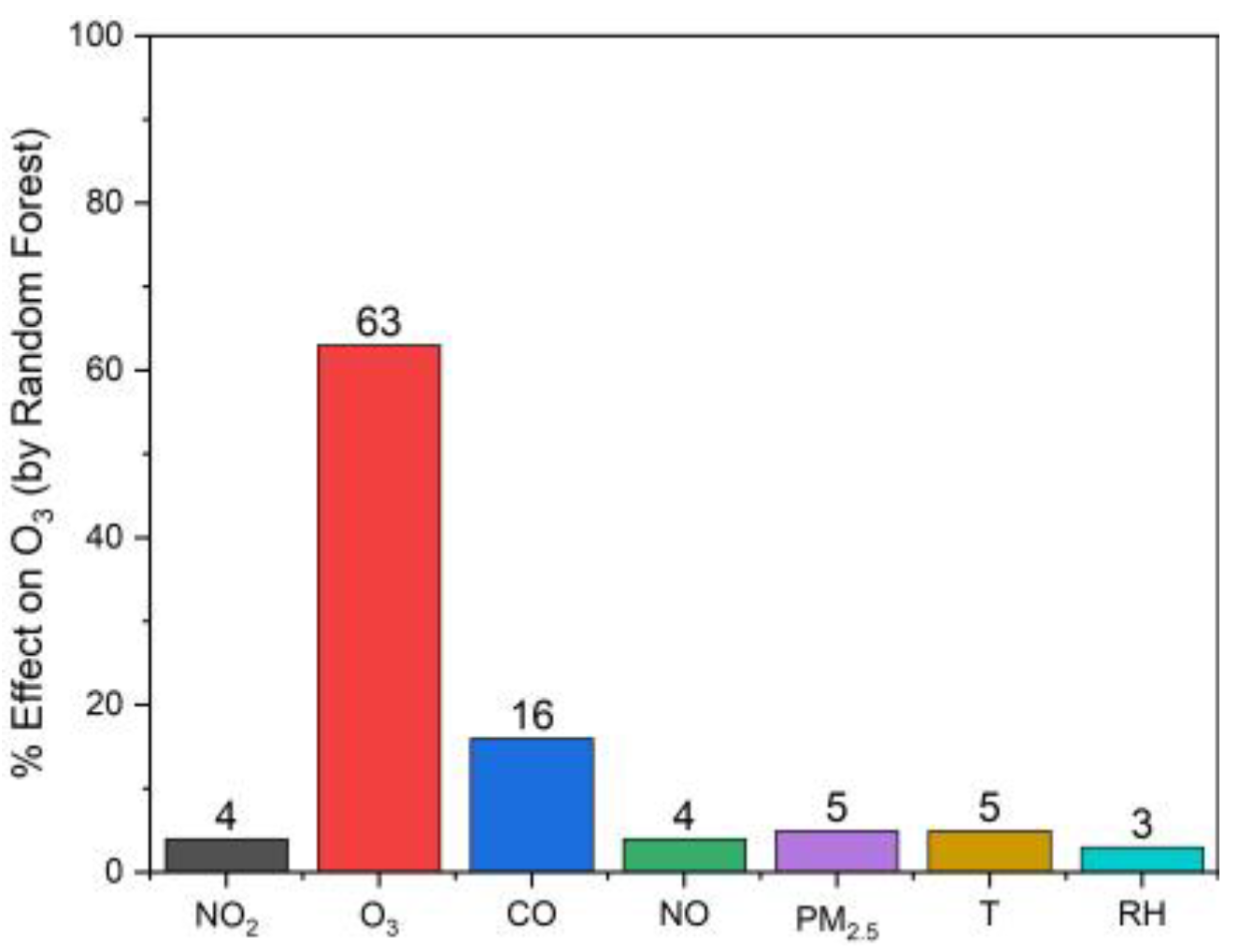
3.2.2. Evaluation of Machine Learning Algorithms
3.3. Comparisons with Previous Studies
4. Conclusions and Discussion
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Malings, C.; Tanzer, R.; Hauryliuk, A.; Saha, P.K.; Robinson, A.L.; Presto, A.A.; Subramanian, R. Fine particle mass monitoring with low-cost sensors: Corrections and long-term performance evaluation. Aerosol Sci. Technol. 2020, 54, 160–174. [Google Scholar] [CrossRef]
- Lelieveld, J.; Haines, A.; Pozzer, A. Age-dependent health risk from ambient air pollution: A modelling and data analysis of childhood mortality in middle-income and low-income countries. Lancet Planet. Health 2018, 2, e292–e300. [Google Scholar] [CrossRef]
- Goldemberg, J.; Martinez-Gomez, J.; Sagar, A.; Smith, K.R. Household air pollution, health, and climate change: Cleaning the air. Environ. Res. Lett. 2018, 13, 030201. [Google Scholar] [CrossRef]
- Nuvolone, D.; Petri, D.; Voller, F. The effects of ozone on human health. Environ. Sci. Pollut. Res. 2018, 25, 8074–8088. [Google Scholar] [CrossRef] [PubMed]
- Atkinson, R.W.; Butland, B.K.; Anderson, H.R.; Maynard, R.L. Long-term concentrations of nitrogen dioxide and mortality: A meta-analysis of cohort studies. Epidemiology 2018, 29, 460. [Google Scholar] [CrossRef]
- Rai, A.C.; Kumar, P.; Pilla, F.; Skouloudis, A.N.; Di Sabatino, S.; Ratti, C.; Yasar, A.; Rickerby, D. End-user perspective of low-cost sensors for outdoor air pollution monitoring. Sci. Total Environ. 2017, 607–608, 691–705. [Google Scholar] [CrossRef]
- Spinelle, L.; Gerboles, M.; Kotsev, A.; Signorini, M. Evaluation of Low-Cost Sensors for Air Pollution Monitoring: Effect of Gaseous Interfering Compounds and Meteorological Conditions; EUR 28601 EN; Publications Office of the European Union: Luxembourg, 2017. [Google Scholar] [CrossRef]
- Schneider, P.; Castell, N.; Vogt, M.; Dauge, F.R.; Lahoz, W.A.; Bartonova, A. Mapping urban air quality in near real-time using observations from low-cost sensors and model information. Environ. Int. 2017, 106, 234–247. [Google Scholar] [CrossRef]
- Kosmopoulos, G.; Salamalikis, V.; Pandis, S.N.; Yannopoulos, P.; Bloutsos, A.A.; Kazantzidis, A. Low-cost sensors for measuring airborne particulate matter: Field evaluation and calibration at a south-eastern European site. Sci. Total Environ. 2020, 748, 141396. [Google Scholar] [CrossRef] [PubMed]
- Giordano, M.R.; Malings, C.; Pandis, S.N.; Presto, A.A.; McNeill, V.F.; Westervelt, D.M.; Beekmann, M.; Subramanian, R. From low-cost sensors to high-quality data: A summary of challenges and best practices for effectively calibrating low-cost particulate matter mass sensors. J. Aerosol Sci. 2021, 158, 105833. [Google Scholar] [CrossRef]
- Zimmerman, N.; Presto, A.A.; Kumar, S.P.N.; Gu, J.; Hauryliuk, A.; Robinson, E.S.; Robinson, A.L.; Subramanian, R. A machine learning calibration model using random forests to improve sensor performance for lower-cost air quality monitoring. Atmos. Meas. Tech. 2018, 11, 291–313. [Google Scholar] [CrossRef]
- van Ratingen, S.; Vonk, J.; Blokhuis, C.; Wesseling, J.; Tielemans, E.; Weijers, E. Seasonal influence on the performance of low-cost NO2 sensor calibrations. Sensors 2021, 21, 7919. [Google Scholar] [CrossRef] [PubMed]
- Han, P.; Mei, H.; Liu, D.; Zeng, N.; Tang, X.; Wang, Y.; Pan, Y. Calibrations of low-cost air pollution monitoring sensors for CO, NO2, O3, and SO2. Sensors 2021, 21, 256. [Google Scholar] [CrossRef] [PubMed]
- Christakis, I.; Hloupis, G.; Stavrakas, I.; Tsakiridis, O. Low cost sensor implementation and evaluation for measuring NO2 and O3 pollutants. In Proceedings of the 2020 9th International Conference on Modern Circuits and Systems Technologies (MOCAST), Bremen, Germany, 7–9 September 2020; pp. 1–4. [Google Scholar]
- Margaritis, D.; Keramydas, C.; Papachristos, I.; Lambropoulou, D. Calibration of low-cost gas sensors for air quality monitoring. Aerosol Air Qual. Res. 2021, 21, 210073. [Google Scholar] [CrossRef]
- Apostolopoulos, I.D.; Fouskas, G.; Pandis, S.N. An IoT integrated air quality monitoring device based on microcomputer technology and leading industry low-cost sensor solutions. In Future Access Enablers for Ubiquitous and Intelligent Infrastructures; Perakovic, D., Knapcikova, L., Eds.; Lecture Notes of the Institute for Computer Sciences, Social Informatics and Telecommunications Engineering; Springer International Publishing: Cham, Switzerland, 2022; Volume 445, pp. 122–140. ISBN 978-3-031-15100-2. [Google Scholar]
- Mohri, M.; Rostamizadeh, A.; Talwalkar, A. Foundations of Machine Learning; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Svetnik, V.; Liaw, A.; Tong, C.; Culberson, J.C.; Sheridan, R.P.; Feuston, B.P. Random forest: A classification and regression tool for compound classification and QSAR modeling. J. Chem. Inf. Comput. Sci. 2003, 43, 1947–1958. [Google Scholar] [CrossRef]
- Quinlan, J.R. Bagging, boosting, and C4.5. In Proceedings of the 13th National Conference on Artificial Intelligence, Portland, Oregon, 4–8 August 1996; Volume 1, pp. 725–730. [Google Scholar]
- Dietterich, T.G. Ensemble methods in machine learning. In Multiple Classifier Systems; Springer: Berlin/Heidelberg, Germany, 2000; pp. 1–15. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Sherstinsky, A. Fundamentals of Recurrent Neural Network (RNN) and Long Short-Term Memory (LSTM) network. Phys. D Nonlinear Phenom. 2020, 404, 132306. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Gu, J.; Wang, Z.; Kuen, J.; Ma, L.; Shahroudy, A.; Shuai, B.; Liu, T.; Wang, X.; Wang, G.; Cai, J.; et al. Recent advances in convolutional neural networks. Pattern Recognit. 2018, 77, 354–377. [Google Scholar] [CrossRef]
- Borrego, C.; Ginja, J.; Coutinho, M.; Ribeiro, C.; Karatzas, K.; Sioumis, T.; Katsifarakis, N.; Konstantinidis, K.; De Vito, S.; Esposito, E.; et al. Assessment of air quality microsensors versus reference methods: The EuNetAir Joint Exercise—Part II. Atmos. Environ. 2018, 193, 127–142. [Google Scholar] [CrossRef]
- Castell, N.; Dauge, F.R.; Schneider, P.; Vogt, M.; Lerner, U.; Fishbain, B.; Broday, D.; Bartonova, A. Can commercial low-cost sensor platforms contribute to air quality monitoring and exposure estimates? Environ. Int. 2017, 99, 293–302. [Google Scholar] [CrossRef] [PubMed]
- Zauli-Sajani, S.; Marchesi, S.; Pironi, C.; Barbieri, C.; Poluzzi, V.; Colacci, A. Assessment of air quality sensor system performance after relocation. Atmos. Pollut. Res. 2021, 12, 282–291. [Google Scholar] [CrossRef]
| Units | Sensor Model | Range | Manufacturer | |
|---|---|---|---|---|
| Ozone | ppb | OX-B431 | 0 to 200 ppb | Alphasense |
| Nitrogen Dioxide | ppb | NO2-B43F | 0 to 200 ppb | Alphasense |
| Nitric Oxide | ppb | NO-B4 | 0 to 200 ppb | Alphasense |
| Carbon Monoxide | ppb | CO-B4 | 0 to 2000 ppb | Alphasense |
| Fine Particle Matter | μg m−3 | PMS5003 | 0 to 500 μg m−3 | Plantower |
| Temperature | Celsius | BME680 | −40 to 85 °C | Bosch Sensortec |
| Relative Humidity | % | BME680 | 0 to 100 % | Bosch Sensortec |
| Method | Parameters | ||
|---|---|---|---|
| KNN | Neighbors: 100 | Leaf Size: 30 | Distance Metric: Euclidean |
| RF | Min. split samples: 2 Bootstrap: Yes | Estimators: 1000 | Criterion: MSE |
| NN | Hidden layers: 2 Activation: Sigmoid | Dropout: 50% | Loss: MSE Optimizer: Stochastic Gradient Descent |
| LSTM | Steps: 24 LSTM units: 60/120 | Dropout: 50% | Loss: MAE Optimizer: Adam |
| CNN | Steps: 24 Layers: 3 Activation: RELU | Filters (size): 24 (kernel = 3), 48 (kernel = 3), 120 (kernel = 3) Dropout: 50% | Loss: MSE Optimizer: Adam |
| R | R2 | ME (ppb) | RMSE (ppb) | MB (ppb) | nME | |
|---|---|---|---|---|---|---|
| Train (2021 Campaign) | 0.47 | 0.22 | 8.6 | 10.7 | 6.2 | 0.65 |
| Test (2022 Campaign) | 0.47 | 0.22 | 9.4 | 11.6 | 7.3 | 0.67 |
| Data | R | R2 | ME (ppb) | RMSE (ppb) | MB (ppb) | nME | |
|---|---|---|---|---|---|---|---|
| LR. | Training (2021) | 0.76 | 0.58 | 4.1 | 6.0 | 0.7 | 0.36 |
| Test (2022) | 0.85 | 0.72 | 3.7 | 4.8 | 1.3 | 0.33 | |
| KNN | Training (2021) | 0.82 | 0.67 | 3.6 | 4.8 | 0.0 | 0.34 |
| Test (2022) | 0.86 | 0.74 | 3.3 | 4.4 | 0.0 | 0.32 | |
| RF | Training (2021) | 0.87 | 0.75 | 3.1 | 4.2 | 0.4 | 0.31 |
| Test (2022) | 0.91 | 0.86 | 3.0 | 3.9 | 1.7 | 0.30 | |
| NN | Training (2021) | 0.81 | 0.68 | 3.9 | 5.3 | 0.0 | 0.34 |
| Test (2022) | 0.83 | 0.69 | 4.0 | 4.9 | 1.0 | 0.34 | |
| CNN | Training (2021) | 0.82 | 0.68 | 3.5 | 5.0 | 0.0 | 0.32 |
| Test (2022) | 0.85 | 0.72 | 3.5 | 4.6 | 1.0 | 0.33 | |
| LSTM | Training (2021) | 0.89 | 0.78 | 2.8 | 3.9 | 0.0 | 0.26 |
| Test (2022) | 0.9 | 0.82 | 3.0 | 3.9 | 1.8 | 0.31 |
| R | R2 | ME (ppb) | RMSE (ppb) | MB (ppb) | nME | |
|---|---|---|---|---|---|---|
| Train (2021 Campaign) | 0.62 | 0.39 | 13.9 | 16.6 | −7.4 | 0.57 |
| Test (2022 Campaign) | 0.72 | 0.52 | 13.0 | 15.5 | −5.9 | 0.55 |
| Data | R | R2 | ME (ppb) | RMSE (ppb) | MB (ppb) | nME | |
|---|---|---|---|---|---|---|---|
| LR. | Training (2021) | 0.74 | 0.56 | 5.9 | 8.0 | −0.2 | 0.48 |
| Test (2022) | 0.83 | 0.69 | 5.2 | 6.6 | 0.0 | 0.39 | |
| KNN | Training (2021) | 0.77 | 0.59 | 5.7 | 7.7 | 0.5 | 0.20 |
| Test (2022) | 0.83 | 0.70 | 5.2 | 6.5 | 3.6 | 0.18 | |
| RF | Training (2021) | 0.80 | 0.65 | 5.1 | 7.1 | 0.0 | 0.18 |
| Test (2022) | 0.83 | 0.69 | 4.3 | 5.8 | 1.3 | 0.15 | |
| NN | Training (2021) | 0.76 | 0.59 | 5.3 | 7.8 | 0.0 | 0.19 |
| Test (2022) | 0.81 | 0.64 | 4.7 | 6.1 | 1.5 | 0.17 | |
| CNN | Training (2021) | 0.77 | 0.60 | 5.2 | 7.7 | −0.3 | 0.19 |
| Test (2022) | 0.83 | 0.68 | 4.6 | 6.1 | 2.0 | 0.16 | |
| LSTM | Training (2021) | 0.82 | 0.67 | 4.6 | 6.9 | 0.0 | 0.16 |
| Test (2022) | 0.79 | 0.63 | 4.6 | 6.7 | 0.6 | 0.16 |
| First Author | Reference | Pollutant | Algorithm | R2 |
|---|---|---|---|---|
| Ratingen | [12] | NO2 | MLR | 0.69–0.84 |
| Han | [13] | NO2 | LSTM, RF | 0.7 |
| Christakis | [14] | NO2 | MLR | 0.84 |
| Margaritis | [15] | NO2 | RF | 0.92 |
| Zimmerman | [11] | NO2 | RF | 0.62 |
| Borrego | [25] | NO2 | RF | 0.93 |
| Castell | [26] | NO2 | LR | 0.42 |
| Zauli-Sajani | [27] | NO2 | RF | 0.84 |
| This study | NO2 | RF | 0.86 | |
| Ratingen | [12] | O3 | MLR | 0.69–0.84 |
| Han | [13] | O3 | LSTM, RF | 0.7 |
| Christakis | [14] | O3 | MLR | 0.87 |
| Margaritis | [15] | O3 | RF | 0.96 |
| Zimmerman | [11] | O3 | RF | 0.86 |
| Borrego | [25] | O3 | RF | 0.84 |
| Castell | [26] | O3 | LR | 0.68 |
| Zauli-Sajani | [27] | O3 | RF | 0.82 |
| This study | O3 | RF | 0.69 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Apostolopoulos, I.D.; Fouskas, G.; Pandis, S.N. Field Calibration of a Low-Cost Air Quality Monitoring Device in an Urban Background Site Using Machine Learning Models. Atmosphere 2023, 14, 368. https://doi.org/10.3390/atmos14020368
Apostolopoulos ID, Fouskas G, Pandis SN. Field Calibration of a Low-Cost Air Quality Monitoring Device in an Urban Background Site Using Machine Learning Models. Atmosphere. 2023; 14(2):368. https://doi.org/10.3390/atmos14020368
Chicago/Turabian StyleApostolopoulos, Ioannis D., George Fouskas, and Spyros N. Pandis. 2023. "Field Calibration of a Low-Cost Air Quality Monitoring Device in an Urban Background Site Using Machine Learning Models" Atmosphere 14, no. 2: 368. https://doi.org/10.3390/atmos14020368
APA StyleApostolopoulos, I. D., Fouskas, G., & Pandis, S. N. (2023). Field Calibration of a Low-Cost Air Quality Monitoring Device in an Urban Background Site Using Machine Learning Models. Atmosphere, 14(2), 368. https://doi.org/10.3390/atmos14020368






