GHG Global Emission Prediction of Synthetic N Fertilizers Using Expectile Regression Techniques

Abstract

Agriculture accounts for a large percentage of nitrous oxide ($N_{2}O$) emissions, mainly due to the misapplication of nitrogen-based fertilizers, leading to an increase in the greenhouse gas (GHG) footprint. These emissions are of a direct nature, released straight into the atmosphere through nitrification and denitrification, or of an indirect nature, mainly through nitrate leaching, runoff, and $N_{2}O$ volatilization processes. $N_{2}O$ emissions are largely ascribed to the agricultural sector, which represents a threat to sustainability and food production, subsequent to the radical contribution to climate change. In this connection, it is crucial to unveil the relationship between synthetic N fertilizer global use and $N_{2}O$ emissions. To this end, we worked on a dataset drawn from a recent study, which estimates direct and indirect $N_{2}O$ emissions according to each country, by the Intergovernmental Panel on Climate Change (IPCC) guidelines. Machine learning tools are considered great explainable techniques when dealing with air quality problems. Hence, our work focuses on expectile regression (ER) based-approaches to predict $N_{2}O$ emissions based on N fertilizer use. In contrast to classical linear regression (LR), this method allows for heteroscedasticity and omits a parametric specification of the underlying distribution. ER provides a complete picture of the target variable’s distribution, especially when the tails are of interest, or in dealing with heavy-tailed distributions. In this work, we applied expectile regression and the kernel expectile regression estimator (KERE) to predict direct and indirect $N_{2}O$ emissions. The results outline both the flexibility and competitiveness of ER-based techniques in regard to the state-of-the-art regression approaches.

1. Introduction

The food and drink industry is the largest producing sector globally, and due to the increased consumer demand for processed food products, it has led to consequential impacts on health and the environment [1]. Biotic and abiotic components of the environment are targeted by air pollution, which is considered one of our era’s greatest scourges. Every substance, solid, liquid, or gas, if being produced in higher concentrations while reducing the quality of our environment, is defined as a pollutant [2]. According to the World Health Organization (WHO), 99% of humans are breathing air that exceeds WHO guideline limits and contains high levels of pollutants, while low- and middle-income countries are subject to the highest exposures. Air quality is closely linked to the Earth’s climate and ecosystem, and is known to be the single largest environmental health risk factor globally. Many of the drivers of air pollution are also sources of greenhouse gas (GHG) emissions [3].

Particulate matter (PM) can be formed directly in the atmosphere by physicochemical reactions between pollutants already present in the atmosphere or can be directly emitted from anthropogenic activities and natural sources to the atmosphere. 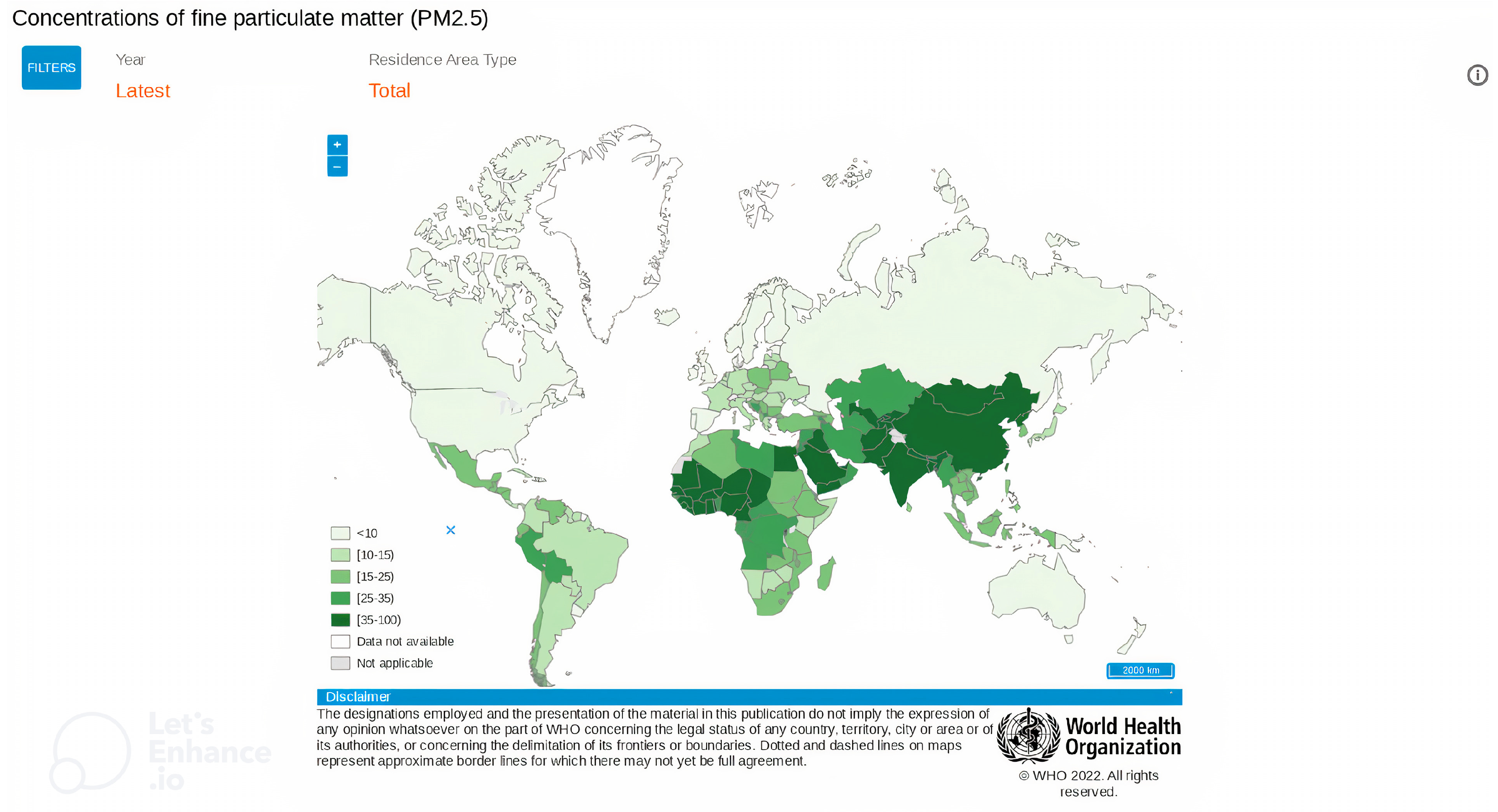The United States Environmental Protection Agency defined PM as a term for particles, whose penetration depends on their diminutive size, ranging from particles with diameters of 10 μm (μm) or smaller, called $P{M}_{10}$, and extremely fine particles with diameters that are generally 2.5 μm (μm) and smaller $P{M}_{2.5}$ [2]. PM is most likely condensed in cities and industrialized areas, as it is geographically shown in Figure 1. PM concentrations levels are represented by color grading, where the intense green represents the highest mean values of these concentrations (μg/m${}^3$) The increase in atmospheric $P{M}_{2.5}$ concentration, air movement patterns, and exposure of populations, result in health and economic effects. Food system emissions alone account for about 22.4% of global mortality due to degraded air quality and 1.4% of global crop production losses [4]. A recent study [5] in the United States estimated that 4300 cases annually of premature mortality happen due to maize production. In fact, higher mortality rates were observed within the top five maize-producing states (Iowa, Illinois, Nebraska, Minnesota, and Indiana). Moreover, increased concentrations of $P{M}_{2.5}$ are driven by emissions of ammonia NH3, which result from nitrogen (N) fertilizer use [5].

Industrial facilities, such as power stations, refineries, petrochemicals, chemical and fertilizer industries, and metallurgical, and other industrial plants, are major sources of pollutants emissions. GHG emissions from the agricultural sector increased by 10.1% from 1990 to 2018 and accounted for 9.9% of total US greenhouse gas emissions [6]. In fact, agricultural $N_{2}O$ emissions are projected to continue to rise [7]. Agricultural crop production, including farms and the supply chains that produce the chemical and energy inputs, contribute majorly to the emissions of GHGs, which include carbon dioxide ($C{O}_2$), nitrous oxide ($N_{2}O$), methane ($C{H}_4$), and black carbon [4]. Nitrous oxide being one of the most impacting GHG, was chosen in this study. It is estimated that $N_{2}O$ emissions in the US account for approximately 75% of total emissions. The truth is that the increased value brought about by nitrogen-based fertilizer applications is outweighed by the expenses of environmental nitrogen pollution, such as the eutrophication of rivers, loss of biodiversity, global warming, and stratospheric ozone depletion, even though N is a limiting component for agricultural production [8].

With the growing rate of big data evolution and its complexity, various prediction methods based on machine learning technologies have been developed for air quality problems [9,10]. Multiple linear regression (MLR) is one of the most popular tools capable of incorporating complex non-linear relationships between the concentration of air pollutants and meteorological variables [11].

This work is based on Greenhouse Gas Emissions from Global Production and the use of Synthetic Nitrogen Fertilizers in the Agriculture dataset, from the Figshare repository, from the year 2018. The authors also used this dataset in a recently published work [12], where they estimated GHG emissions due to synthetic N fertilizer manufacture, transportation, and field use in agricultural systems. Most studies have tackled the GHG emission problems; while integrating ML tools basically focus on $C{O}_2$ or $C{H}_4$ emissions [13], very few papers are based on ($N_{2}O$) emissions. In fact, this gas is 300 times more harmful to the climate than ($C{O}_2$) and steadily increases in the atmosphere, with agriculture being the largest contributor, and nitrogen the most used synthetic fertilizer [14].

In this study, we propose two expectile-based regression approaches, namely, expectile regression (ER) and the kernel expectile regression estimator (KERE). Due to their flexibility in application, heavy-tailed distributions and outliers are of interest. In this context, and based on the fact that only a few countries are considered agricultural-producing countries, there is a concentration of information in the tail of the distribution. We used expectile-based regression to take advantage of the parameterized nature, which allows for modeling different aspects of the distribution rather than the simple mean.

The rest of this manuscript is structured as follows: Section 2 briefly outlines the works and studies related to our research. Section 3 and Section 4 investigate and analyze the dataset. Thereof, Section 5 assembles the results and the discussion. Finally, Section 6 portrays concluding remarks and states future works.

2. Background and Related Works

In the last decades, climate changes are becoming more frequent with longer shifts in temperature and weather patterns [15,16]. According to the United Nations reports, human activities are the main drivers of climate change, such as the agricultural production system, which significantly contributes to GHG emissions, such as nitrous oxide $N_{2}O$ [17,18].

2.1. Nitrogen Based-Fertilizers Use and Climate Change

The increasing usage of nitrogen-based fertilizers has a significant influence on the worldwide agricultural soils’ rapid emissions of $N_{2}O$ [19]. It represents a major contributing factor to the current rise in the global average temperature and a significant impact on agricultural productivity [20]. On the other hand, in the agricultural sector, there is significant $N_{2}O$ discharge, mostly as a result of the usage of nitrogen-based fertilizers as a crop productivity booster [20], or through their manufacturing processes [21]. According to the Food and Agriculture Organization(FAO), the usage of synthetic N-based fertilizers is expected to grow to 50% by 2050 [12]. In 2019, $N_{2}O$ levels in the atmosphere have grown by more than 20% from 270 parts per billion in 1750 to 332 parts per billion [14]. Global concerns surround the steadily rising levels of $N_{2}O$ in the atmosphere [21], as a strong greenhouse gas with a long lifetime (around 121 years) [7]. This gas is responsible for rising temperatures altering the patterns of the world’s weather, which can cause severe abiotic phenomena, such as droughts and heavy rains.

2.1.1. Nitrogen-Based Fertilizers

Nitrogen supply and crop demand must be synchronized in order to maintain optimal plant growth and reduce environmental losses, with regard to other outside factors [22]. The 4R nutrient stewardship community suggests that nitrogen-based fertilizers must reduce GHG emissions while minimizing any harm to the air quality. The 4Rs concept involves applying fertilizers using the right source, at the right rate, at the right time, and at the right place for each crop [23]. The main sources of nitrogen-based fertilizers are typically divided into ammonium-based ($N{H}_4^{+}$) and nitrate-based ($N{O}_3^{-}$) [24]: ammonium nitrate (AN) $(33,5\%\mathtt{N})$; Urea $(46\%\mathtt{N})$; ammonium sulfate (AS) $(21\%\mathtt{N})$; calcium ammonium nitrate (CAN) $(27\%\mathtt{N})$ [25]. Other nitrogen–phosphate (NP) and nitrogen–phosphate–potassium (NPK) fertilizers, which are widely used, such as mono-ammonium phosphate (MAP) with $11\%$ of N, di-ammonium phosphate (DAP) with $18\%$ of N and ammonium sulfate ($21\%$ of N) [22].

2.1.2. Nitrous Oxide: A Side Effect of Nitrogen-Based Fertilizers Use

N is one of the major macro-nutrients other than P and K, which are crucial for plant growth and development. Under climate-change conditions, enhancing agricultural output and quality while minimizing environmental losses has become an arduous challenge [26]; hence, leading to the usage of synthetic N fertilizers, in order to improve crop production by providing the plant with the necessary nutrient. N is particularly a limiting factor for crop growth, it has an important role within plant cells, which ensures better results in terms of yield and quality as well [8]. Having multiple synergistic interactions with other nutrients, and in accordance with Liebig’s law of the minimum, nitrogen is the first probable nutrient deficiency to occur [27]. The agricultural sector is once again the most impacted by the temperature rise brought on by $N_{2}O$ emissions. Research has indicated that it is responsible for 15% of greenhouse gas emissions [20]. According to FAO estimates for the year 2019, nitrogen-based fertilizer field application contributed to 8.3% of world GHG emissions, while fertilizer manufacturing accounted for 0.7% [12]. In other words, the fertilizer supply chain (from the manufacturing to the field application) distributes the whole nitrogen cycle and, thereby, efforts must be taken to lessen the quantity of $N_{2}O$ emitted into the atmosphere [28].

2.1.3. Nitrogen Dynamics in Soil and $N_{2}O$ Emissions Pathways

Soils naturally release $N_{2}O$ due to the microbiological processes that are a part of the nitrogen cycle [29]. As shown in Figure 2, nitrogen-based fertilizers when applied to the soil, some of it is taken up by the plant, while the rest is converted by soil microorganisms or lost through volatilization/leaching. The greatest sources of indirect $N_{2}O$ emissions come from agricultural $N{O}_3^{-}$ leaching and runoff, which account for around 30% of the nitrogen lost from agricultural soils [28]. On the other hand, denitrification and nitrification through microorganisms involve the direct emissions pathway of $N_{2}O$. Under aerobic conditions, the conversion of $N{H}_4^{+}$ to $N{O}_3^{-}$ occurs under the name of nitrification, while the denitrification process takes place involving the conversion of $N{O}_3^{-}$ to $N_2$, with $N_{2}O$ acting as an intermediate product [30].

2.2. Machine Learning Tools for Air Quality Predictions: Nitrous Oxide Emissions

When it comes to air quality prediction, tools, such as artificial intelligence (AI) and machine learning (ML), have gained remarkable attention due to their potential to help in GHG emission predictions.

Table 1. Machine learning models used recently for predicting $N_{2}O$ and GHG emissions.

Ref	Title	ML Model	GHG Emissions
[11]	Air-pollution prediction in a smart city, deep learning approach	Hybrid CNN-LSTM	Combining historical and meteorological data of pollutants to predict $P{M}_{2.5}$ concentrations in Beijing, China.
[31]	Global riverine nitrous oxide emissions: The role of small streams and large rivers	Data-driven random forest ML (RFML)	Integrating a data-driven ML model with a physically based up-scaling model to identify $N_{2}O$ global emissions, from streams and rivers.
[32]	Machine learning approach to simulate soil $C{O}_2$  Fluxes under cropping systems	Regression models: KNN, SVR, and RF.	Including ML models for regression purposes in order to predict soil GHG emissions without the biogeochemical expertise.
[33]	A new approach for predicting nitrification and its fraction of  $N_{2}O$  emissions in global terrestrial ecosystems	Stochastic gradient boosting (SGB)	Integrating an ML-SGB model to estimate and predict the global nitrification rate ($R_{\mathit{nit}}$) and $N_{2}O$ emissions from the process of nitrification.
[34]	Untangling soil weather drivers of daily $N_{2}O$  emissions and fertilizer management mitigation strategies in no-till corn	Conditional inference tree (CIT)	Using a ML-CIT model to identify the main soil–weather drivers of daily $N_{2}O$ hot moments and fertilizer management options to mitigate them.
[35]	Machine learning improves predictions of agricultural nitrous oxide ($N_{2}O$) emissions from intensively managed cropping systems	Random forest	Coupling an ML-RF model with a cropping system model to predict daily soil $N_{2}O$ emissions.

summarizes various recent and convenient works that integrated ML tools for $N_{2}O$ emissions.

3. Dataset

The dataset was acquired from the Figshare repository, entitled Greenhouse Gas Emissions from Global Production and Use of Nitrogen-based Fertilizer in Agriculture. This dataset contains information used to analyze the impact of synthetic N fertilizer production, transportation, and use on global anthropogenic greenhouse gas emissions. The main sources are Agrifootprint 6.0 (AFP6), Food and Agriculture Organization Corporate Statistical Database (FAOSTAT), and International Fertilizer Association (IFASTAT).

3.1. Data Description

The data were derived from a recent study [12], where they estimated GHG emissions per capita terms for the year 2018, due to multiple synthetic N fertilizer parameters, namely, manufacture, transportation, and field use in agricultural systems. This field-level dataset available on $N_{2}O$ soil emissions was estimated based on global $N_{2}O$ direct emission factors (EFs). From the literature, EFs for indirect $N_{2}O$ soil emissions and N fertilizer manufacturing and transportation were extracted. The original dataset is organized in a .xlsx format file, with eight tables. We extracted data from tables 2 and 5 as shown in Figure 3.

To calculate the amount of global GHG emissions generated through the processes of synthetic N fertilizer production, transportation, and agricultural use, they followed the IPCC guidelines for national GHG inventories. They accordingly calculated the emissions at the country level on the basis of the activity data they collected and the appropriate EFs. The IPCC guidelines divide the agricultural $N_{2}O$ source into three categories: direct emissions from agricultural land, emissions from animal waste management systems, and indirect emissions associated with volatilized/leached N that are removed in biomass or otherwise exported from agricultural land. Each is estimated to contribute by one-third, while indirect emissions account for approximately two-thirds.

3.2. Data Pre-Processing

In this section, we present the transformations and aggregations applied to the data, in order to explore the relationship between N synthetic fertilizer sources, and $N_{2}O$ direct and indirect emissions. This will allow us to set up the necessary structure to achieve the objective of this work.

• Scaling and missing values: Features with percentage values are calculated to indicate the amount of each nitrogen source used. This will allow for adequate and informative exploratory analysis in later stages. In addition, entries with missing values were removed.
• Standardizing: Standardization is crucial in feature extraction; especially when features vary in large units or when reported in different measures. To this end, the data are standardized using the following formula: $(X-\mu )/\sigma$, where X is the explanatory variable, $\mu$ and $\sigma$ are the mean and standard deviations, respectively. In addition, the total amount of nitrogen used per country was removed due to the direct correlation with the N sources. Moreover, the corresponding features of indirect emissions generated by leaching/run-off and volatilization were added to indicate indirect emissions generally.
• Exploratory data analysis: To explore the data, two initial investigations are performed. First, the linear regression approach is applied to standardized data to extract feature importance. Second, we investigate the most important features by a distribution graph. In Figure 4, it is apparent that most of the features exude initial signs of heavy-tailed behaviors, which are due to the disparities in agricultural activities (per country).

4. Data Analysis

Generally, ML techniques can be categorized into supervised, unsupervised, semi-supervised, and reinforcement learning. Supervised ML approaches deal with a particular case of problems where each data sample is paired to a label. In particular, regression-type approaches generate an underlying function that provides a real value for each data sample. In this work, the goal is to explore the relationship between $N_{2}O$ gas emissions (direct and indirect), the quantity of applied nitrogen, and synthetic fertilizer sources. To this end, we present the following workflow, based on expectile regression models as our learning approach.

4.1. Expectile-Based Regression

4.1.1. Linear Expectile Regression

Linear expectile regression (ER) was first introduced by Newey and Powell in risk measurement [36]. This approach can be defined as the generalization of conditional expectation to model the relationship between a dependent variable and the covariates [37]. Multiple studies were conducted to explore ER performance, particularly when dealing with heavy-tailed distribution [38]. Although the ER provides a complete picture of the data [39], its statistical properties are under-explored in contrast with other methods, such as linear regression and quantile regression [40,41].

Given Y a random variable, the expectile of level $\tau$ denoted by ${\mu }_{\tau }$ is defined as follows:

$${\mu }_{\tau }\left(Y\right)=\underset{\tau \in \mathbb{R}}{min}\mathbb{E}\left({\varphi }_{\tau }(Y-\tau )\right),$$

(1)

where

$${\varphi }_{\tau }\left(u\right)=\left\{\begin{array}{cc}\tau u^2,\hfill & u<0\hfill \\ (1-\tau )u^2\hfill & u\ge 0.\hfill \end{array}\right.$$

${\varphi }_{\tau }$ is the asymmetric least square (ALS) loss function that assigns weights $\tau$ and $1-\tau$ to positive and negative deviations, respectively. Figure 5 provides example curves of ${\varphi }_{{\tau }_i}$ and expectile values ${\mu }_{{\tau }_i}$ with respect to different expectile levels ${\tau }_i$, respectively.

Let us suppose that we have n samples $({\mathbf{y}}_i,{\mathbf{x}}_i)$, where ${\mathbf{x}}_i={(1,{\mathbf{x}}_{i,1},\dots ,{\mathbf{x}}_{i,p})}^T$ are the covariates. The expectiles defined in Equation (1) are used to set up the expectile regression, which assumes a linear model of the following form:

$${\mu }_{\tau }\left({\mathbf{y}}_i\right|{\mathbf{x}}_i)={\mathbf{x}}_i^T{\beta }_{\tau }$$

(2)

The estimated coefficients ${\widehat{\beta }}_{\tau }$ can be obtained by minimizing the empirical loss function:

$${\displaystyle \frac{1}{n}}\sum _{i=1}^n{\varphi }_{\tau }({\mathbf{y}}_i-{\mathbf{x}}_i^T{\beta }_{\tau }).$$

(3)

To solve the optimization problem in Equation (3), we suggest the following Algorithm 1 based on using iterative reweighted least squares (IRLS) [42]:   

Algorithm 1: ALS for estimating ER coefficients.

Input: Measured dataset ${\left\{(x_i,y_i)\right\}}_{i=1}^m$.

1. Initialize ${\beta }_{\tau ,0}$.

2. Use the empirical loss function in Equation (3);

3. Update the coefficient using the algorithm of IRLS [42],

Output: The coefficients’ estimates $\widehat{\mathsf{\beta }}$.

   The linear expectile regression has shown great performance in contrast with classical approaches of regression [36]. However, we may encounter more complex datasets for which ER might be too restrictive in terms of errors. To this end, researchers have developed more flexible methods namely: expectile regression with boosting (ER-boosting) [43] and non-parametric estimator of conditional expectiles based on local linear polynomials with a one-dimensional covariate [44].

4.1.2. Kernel Expectile Regression Estimator (KERE)

In this work, we adopt a recent flexible method introduced in a modern study [45], based on exploiting the properties of the reproducing kernel Hilbert spaces (RKHS) [46]. Let ${\mathbb{H}}_K$ denote a Hilbert space generated by a predefined kernel K. Given n samples $({\mathbf{y}}_i,{\mathbf{x}}_i)$, the kernel expectile regression estimator is derived from the following optimization problem:

$$({\widehat{f}}_n\left(\mathbf{x}\right),{\widehat{\alpha }}_0)=\arg \underset{f\in {\mathbb{H}}_K,{\alpha }_0\in \mathbb{R}}{min}\sum _{i=1}^n{\varphi }_{\tau }({\mathbf{y}}_i-{\alpha }_0-f\left({\mathbf{x}}_i\right))+\lambda {\parallel f\parallel }_{{\mathbb{H}}_K}^2,$$

(4)

where f spans the Hilbert space, ${\parallel f\parallel }_{{\mathbb{H}}_K}^2$ is the norm of f in ${\mathbb{H}}_K$, ${\alpha }_0$ is the intercept and $\lambda$ is the regularization parameter.

Although Equation (4) lies in an infinite dimensional space, the dimension of this formulation is reduced by using the representer theorem and the reproducing property [47]. Thus, the optimization parameter f in Equation (4) and its RKHS norm are expressed as follows:

$$f\left(\mathit{x}\right)=\sum _{k=1}^n{\alpha }_{k}K({\mathit{x}}_k,\mathit{x}),{\parallel f\parallel }_{{\mathbb{H}}_K}^2=\sum _{i=1}^n\sum _{j=1}^n{\alpha }_i{\alpha }_{j}K({\mathbf{x}}_i,{\mathbf{x}}_j).$$

(5)

where K is the kernel function and ${\alpha }_k\in \mathbb{R}$.

To this end, Equation (4) can be reformulated as follows:

$$\left\{{\widehat{\alpha }}_i\right\}=\underset{{\alpha }_i\in \mathbb{R}}{\mathrm{argmin}}\sum _{i=1}^n{\varphi }_{\tau }\left({\mathbf{y}}_i-{\alpha }_0-\sum _{j=1}^n{\alpha }_{j}K({\mathbf{x}}_i,{\mathbf{x}}_j)\right)+\lambda \sum _{i=1}^n\sum _{j=1}^n{\alpha }_i{\alpha }_{j}K({\mathbf{x}}_i,{\mathbf{x}}_j).$$

(6)

A compact formulation of Equation (6) using matrix notations is introduced as follows:

$$\widehat{\mathit{\alpha }}=\underset{\mathit{\alpha }\in {\mathbb{R}}^{n+1}}{\mathrm{argmin}}\sum _{i=1}^n{\varphi }_{\tau }(y_i-{\mathit{K}}_i\mathit{\alpha })+\lambda {\mathit{\alpha }}^T\mathit{K}\mathit{\alpha },$$

(7)

where

$${\mathit{K}}_i=(1,K({\mathit{x}}_i,{\mathit{x}}_1),\dots ,K({\mathit{x}}_i,{\mathit{x}}_n)){\mathit{K}}_0=\left(\begin{array}{cc}0& 0_{n\times 1}\\ 0_{n\times 1}& K\end{array}\right)$$

(8)

$$\mathit{K}=\left(\begin{array}{ccc}K({\mathit{x}}_1,{\mathit{x}}_1)& \cdots & K({\mathit{x}}_1,{\mathit{x}}_n)\\ K({\mathit{x}}_2,{\mathit{x}}_1)& \cdots & K({\mathit{x}}_2,{\mathit{x}}_n)\\ ⋮& \ddots & ⋮\\ K({\mathit{x}}_n,{\mathit{x}}_1)& \cdots & K({\mathit{x}}_n,{\mathit{x}}_n)\end{array}\right)$$

(9)

The proposed algorithm to solve Equation (7) relies on using maximization–minimization (MM) approaches [48]. The key idea is to find a surrogate function through the Taylor expansion that majorizes the objective function. Optimizing this surrogate function will either improve the value of the objective function or leave it unchanged.

Using the MM approach to solve Equation (7) yields the following formulation for iteratively updating $\mathit{\alpha }=\left({\alpha }_0,{\alpha }_1,\cdots ,{\alpha }_n\right)$.

$${\mathit{\alpha }}^{(t+1)}={\mathit{\alpha }}^{\left(t\right)}+{\mathit{K}}_u^{-1}\left(-\lambda {\mathit{K}}_0{\mathit{\alpha }}^{\left(t\right)}+{\displaystyle \frac{1}{2}}\sum _{i_1}^n{\varphi }_{\tau }\left(r_i^{\left(t\right)}\right){\mathit{K}}_i\right),$$

(10)

where ${\mathit{K}}_u^{-1}$ is the inverse matrix of ${\mathit{K}}_u$ defined as follows:

$$\begin{array}{c}\hfill {\mathit{K}}_u=max(1-\tau ,\tau )\left(\begin{array}{ccc}n& {\mathbf{1}}^T\mathit{K}& \\ \mathit{K}\mathbf{1}& \mathit{K}\mathit{K}+{\displaystyle \frac{\lambda }{max(1-\tau ,\tau )}}\mathit{K}\end{array}\right).\end{array}$$

Algorithm 2 summarizes the steps to reach the KERE estimates $\widehat{\mathit{y}}$ of the output $\mathit{y}$.

Algorithm 2: Kernel expectile regression estimator.

Input: Dataset ${\left\{(x_i,y_i)\right\}}_{i=1}^m$, kernel function $K(.,.)$, tolerance $ϵ$, maximum iterations $i_{max}$.

1: Calculate the kernel matrix $\mathit{K}={\left(K({\mathit{x}}_i,{\mathit{x}}_j)\right)}_{i,j}$.

2: Initialize ${\alpha }^{\left(0\right)}$, $r_i^{\left(0\right)}$ and $t\stackrel{}{\leftarrow }0$.

3: While $r_i^{\left(t\right)}\ge ϵ$ and $t\le i_{max}$:

● Calculate updated residue $r_i^{\left(t\right)}=y_i-{\mathit{K}}_i{\mathit{\alpha }}^{\left(\mathbf{t}\right)}$

● Update ${\mathit{\alpha }}^{\left(t\right)}$ based on Equation (10).

● $t\stackrel{}{\leftarrow }t+1$

4: Calculate the output estimator ${\widehat{y}}_i={\alpha }_0^{\left(t\right)}+{\displaystyle \sum _{j=1}^n}{\alpha }_j^{\left(t\right)}K\left({\mathit{x}}_j,{\mathit{x}}_i\right)$

Output: The vector of estimates $\widehat{\mathit{y}}$.

4.2. Experimental Setup

In this work, we evaluated some of the expectile-based approaches, namely, expectile regression (ER) [36] and kernel expectile regression estimator (KERE) [45] on the GHG emission dataset. As detailed in Section 4, both ER and KERE depend on the chosen expectile level w. To depict the performance relative to the expectile level, we construct multiple models of ER and KERE using multiple expectile levels spanning the following values:

$$\tau \in \left\{0.01,0.05,0.1,0.2,0.25,0.5,0.7,0.75,0.8,0.95\right\}.$$

In addition, KERE models require the kernel function to be selected. Although various kernels are available for use, we choose the well-known radial basis family (RBF) kernel defined in Equation (11).

$$K\left(\mathit{x},\mathit{y}\right)=e^{\frac{1}{{\sigma }^2}\left|\right|\mathit{x}-{\mathit{y}\left|\right|}^2},$$

(11)

where $\sigma$ stands for the bandwidth.

To select the best hyperparameters for KERE models, we perform two dimensional 8-fold cross-validation to select the optimal hyperparameters $(\lambda ,\sigma )$, where $\lambda$ and $\sigma$ stand for the regularization parameter and the RBF kernel bandwidth, respectively. Moreover, the maximum number of iterations $i_{max}$ and the tolerance value $ϵ$ is fixed to 4000 and ${10}^{-6}$, respectively.

Furthermore, we select the KERE model corresponding to the expectile level of interest being $w=0.7$ to conduct a benchmark comparison with state-of-the-art regression models.

Table 2. The benchmark regression-based approaches used to predict direct and indirect Nitrogen emissions.

Technique	Hyperparameters
Support vector machine (SVM)	Kernel function, its parameters, and regularization C.
Lasso regression	Regularization parameter $\lambda$.
Light gradient boosting Machine	Boosting approach.
Random forest regressor	Number of trees and features.
K-neighbor regressor	Number of neighbors.
Extra trees regressor	Number of trees and features.
AdaBoost regressor	Learning rate.
Gradient boosting regressor	Learning rate $\eta$.
Decision tree regressor	Minimum sample leaf, maximum depth, split rule.
MLP regressor	Number of layers
Huber regressor	Strength parameter $\alpha$.
Ridge regression	Regularization parameter $\lambda$.

summarizes the selected regression methods to be compared with KERE, as well as their respective characteristics. We also conduct an 8-fold cross-validation to tune each model’s hyperparameter.

The evaluation process is two-fold. First, we compare ER and KERE models using a customized error metric, namely, mean absolute deviation (MAD) (w) defined below. This type of error reflects the model fit with an emphasis on the tails by assigning weights $\tau$ and 1 −$\tau$ to positive and negative deviations, respectively. Second, a subset of the KERE models is selected to be compared with state-of-the-art regression approaches using mean absolute error (MAE) and root-mean-square error (RMSE).

• Mean absolute deviation MAD (w):

  $$\mathrm{MAD}\left(w\right)={\displaystyle \frac{1}{n}}\sum _{i=1}^n{\varphi }_w\left(\mathit{y}-\widehat{\mathit{y}}\right)$$
• Mean absolute error (MAE):

  $$\mathrm{MAE}={\displaystyle \frac{1}{n}}\sum _{i=1}^n|\mathit{y}-\widehat{\mathit{y}}|$$
• Root-mean-square error (RMSE):

  $$\mathrm{RMSE}={\displaystyle \frac{1}{n}}\sum _{i=1}^n\sqrt{{\displaystyle \frac{1}{n}}{\left(\mathit{y}-\widehat{\mathit{y}}\right)}^2}$$

4.3. Benchmark Methods

In order to assess the performance of the kernel expectile regression estimator on the proposed dataset, we compare it to twelve other benchmark regression approaches. As detailed in Table 2, we use support vector regression, lasso, light gradient boosting machine, random forest, K-neighbor, extra trees, AdaBoost, gradient boosting, decision tree, Huber, multilayer perceptron, and ridge regressors. Table 2 summarizes the techniques considered as well as their hyperparameters to be tuned using K-fold cross-validation.

4.4. Computational Software

The computational software for this study was written using both RStudio and Python. RStudio was used for comparing kernel expectile regression estimator and linear expectile regression. Both approaches were implemented using “KERE” and “Expectreg” libraries [49], respectively. On the other hand, Python was used to compute the comparison with regression benchmark approaches detailed in Table 2. The benchmark comparison was conducted using the PyCaret library (version 3.0.0rc4), specifically PyCaret.regression module.

All of the aforementioned regression techniques were computed using an 8-fold cross-validation to tune the corresponding hyperparameters. The advantage of the PyCaret library in Python is the agility of its classes, particularly Compare_models in setting up the proper framework for a fair comparison.

5. Results and Discussion

Firstly, we report the results of two expectile-based approaches, namely kernel expectile regression estimator (KERE) and expectile regression (ER). The two methods were applied to predict both $N_{2}O$ direct and indirect emissions. First, KERE and ER are compared on both the training and testing phases. We evaluate the models primarily using mean absolute deviation error (MAD), which varies with respect to the expectile level. In addition, we report the mean absolute error (MAE), root-mean-square error (RMSE), and R². Second, we chose the KERE model corresponding to the expectile level $w=0.7$ for comparison with state-of-the-art regression approaches using R², MAE, and RMSE.

We report the results for both the training and testing of KERE and ER regarding the direct emissions in

Table 3. Direct emissions. The training MAD, RMSE, and MAE metrics for both KERE and ER are reported with respect to the various expectile levels ranging between $0.01$ and $0.99$.

w	MAD		RMSE		MAE		${\mathit{R}}^2$
	KERE	ER	KERE	ER	KERE	ER	KERE	ER
0.01	0.008	0.008	0.919	0.924	0.248	0.290	0.54	0.16
0.05	0.026	0.040	0.726	0.880	0.203	0.280	0.92	0.23
0.1	0.088	0.079	0.938	0.850	0.273	0.276	0.10	0.25
0.15	0.040	0.112	0.511	0.830	0.160	0.275	0.94	0.27
0.2	0.054	0.144	0.505	0.814	0.168	0.280	0.84	0.28
0.25	0.046	0.174	0.417	0.800	0.151	0.287	0.93	0.30
0.3	0.043	0.202	0.371	0.788	0.136	0.299	0.94	0.30
0.4	0.053	0.252	0.356	0.769	0.153	0.328	0.92	0.31
0.5	0.044	0.290	0.297	0.762	0.136	0.364	0.94	0.31
0.6	0.068	0.316	0.355	0.772	0.184	0.410	0.88	0.31
0.7	0.056	0.324	0.331	0.810	0.190	0.476	0.90	0.30
0.75	0.043	0.320	0.331	0.848	0.185	0.524	0.91	0.30
0.8	0.041	0.308	0.333	0.906	0.206	0.586	0.90	0.29
0.95	0.067	0.241	0.837	1.483	0.739	1.085	0.69	0.25

and

Table 4. Direct emissions. The testing MAD, RMSE and MAE metrics for both KERE and ER are reported with respect to the various expectile levels ranging between $0.01$ and $0.99$.

w	MAD		RMSE		MAE		${\mathit{R}}^2$
	KERE	ER	KERE	ER	KERE	ER	KERE	ER
0.01	0.015	9.307	1.205	3.395	0.412	0.924	0.033	0.005
0.05	0.074	32.14	1.136	5.996	0.413	1.286	0.197	0.002
0.1	0.144	59.868	1.200	8.280	0.421	1.595	0.064	0.001
0.15	0.206	80.011	1.080	9.796	0.432	1.787	0.197	0.0007
0.2	0.308	97.211	1.133	11.097	0.466	1.962	0.058	0.0006
0.25	0.316	114.24	1.057	12.399	0.448	2.142	0.198	0.0005
0.3	0.367	130.65	1.053	13.706	0.458	2.326	0.194	0.0004
0.4	0.461	157.004	1.048	16.198	0.465	2.696	0.182	0.0003
0.5	0.541	171.65	1.040	18.528	0.487	3.066	0.187	0.0002
0.6	0.663	169.59	1.080	20.565	0.511	3.406	0.112	0.0002
0.7	0.663	147.29	1.032	22.097	0.524	3.707	0.187	0.0001
0.75	0.691	126.833	1.040	22.438	0.529	3.818	0.175	0.0001
0.8	0.708	101.666	1.047	22.427	0.574	3.903	0.168	0
0.95	0.589	25.094	1.266	22.229	1.010	4.393	0.120	0.0001

, respectively. It is noticeable that KERE outperforms ER in all reported metrics, namely MAD, RMSE, and MAE. This is because KERE is able to depict non-linear behavior utilizing the kernel trick. In addition, ER approach reports an increasing MAD error as the expectile levels increase, whereas KERE stays relatively stable as the expectile level increases. This is reflected by the mean absolute deviation of ER (0.8) being 0.308 compared to KERE (0.7) being 0.041. In addition, it is apparent that R² values drop significantly between training and testing for both KERE and ER which highlights the failure to explain the direct emissions variance.

One KERE model corresponding to expectile level $w=0.7$ is selected from Table 4 to be compared with the benchmark approaches summarized in Table 1.

Table 5. The benchmark regression-based approaches used to predict direct nitrogen emissions.

Phase	Training			Testing
Technique	MAE	RMSE	R	MAE	RMSE	R
Support Vector Regression	1.118	1.199	−13.56	0.494	1.270	0.02
Lasso Regression	0.418	0.736	− 0.505	0.593	1.302	−0.024
Light Gradient Boosting Machine	0.3998	0.715	−0.452	0.575	1.270	0.025
Random Forest Regressor	0.243	0.745	−0.12	0.448	1.3625	−0.1216
K Neighbors Regressor	0.255	0.702	−0.08	0.454	1.268	0.028
Extra Trees Regressor	0.253	0.720	−0.05	0.445	1.320	−0.053
AdaBoost Regressor	0.305	0.776	−0.41	0.489	1.247	0.060
Gradient Boosting Regressor	0.411	0.727	−0.46	0.585	1.288	−0.003
Decision Tree Regressor	0.249	0.748	−0.129	0.448	1.362	−0.121
Huber Regressor	0.311	0.767	−1.60	1.098	5.179	−15.21
MLP Regressor	0.513	1.105	−22.19	1.137	3.587	−6.77
Ridge Regression	0.415	0.732	−0.80	0.643	1.369	−0.13
Kernel expectile regression 1	0.190	0.331	0.90	0.524	1.032	0.187

¹ KERE model with respect to expectile level = 0.7.

summarizes the performance of the benchmark regressors in contrast with KERE models, where $R^2$, MAE and RMSE are reported.

It is shown that the KERE R-squared values are slightly low but significantly better than the rest of the regression approaches (18%). We can argue that the usage of fewer fertilizers implies less factors implicated in the agricultural processes. For example, in small countries where agriculture is not the main activity, the source of N-based fertilizers does not necessarily explain $N_{2}O$ emissions. However, when N-based fertilizers are applied in bigger quantities, the source explains more about the direct emissions.

Secondly, we report the performance analysis of KERE and ER with respect to indirect emissions.

Table 6. Indirect emissions. The training MAD, RMSE, and MAE metrics for both KERE and ER are reported with respect to the various expectile levels ranging between $0.01$ and $0.99$.

w	MAD		RMSE		MAE		${\mathit{R}}^2$
	KERE	ER	KERE	ER	KERE	ER	KERE	ER
0.01	0.012	0.013	1.137	1.162	0.160	0.256	0.93	0.18
0.05	0.044	0.064	0.943	1.089	0.139	0.271	0.98	0.42
0.1	0.093	0.118	0.951	1.017	0.155	0.283	0.82	0.50
0.15	0.213	0.164	1.190	0.958	0.189	0.290	0.08	0.53
0.2	0.068	0.203	0.580	0.910	0.106	0.295	0.99	0.54
0.25	0.066	0.235	0.511	0.872	0.103	0.300	0.99	0.55
0.3	0.064	0.261	0.460	0.841	0.100	0.303	0.99	0.55
0.4	0.107	0.296	0.504	0.802	0.136	0.309	0.92	0.55
0.5	0.056	0.311	0.336	0.789	0.104	0.315	0.99	0.55
0.6	0.052	0.305	0.301	0.802	0.118	0.324	0.98	0.55
0.7	0.099	0.279	0.448	0.842	0.181	0.338	0.88	0.55
0.75	0.049	0.257	0.285	0.875	0.154	0.348	0.98	0.54
0.8	0.048	0.228	0.296	0.920	0.179	0.362	0.97	0.53
0.95	0.073	0.083	0.948	1.194	0.517	0.535	0.6	0.48

and

Table 7. Indirect emissions. The testing MAD, RMSE, and MAE metrics for both KERE and ER are reported with respect to the various expectile levels ranging between $0.01$ and $0.99$.

w	MAD		RMSE		MAE		${\mathit{R}}^2$
	KERE	ER	KERE	ER	KERE	ER	KERE	ER
0.01	0.0004	0.0005	0.092	0.175	0.132	0.092	0.122	0.004
0.05	0.005	0.053	0.104	0.281	0.182	0.104	0.123	0.887
0.1	0.008	0.313	0.105	0.614	0.258	0.105	0.350	0.933
0.15	0.001	0.678	0.082	0.911	0.317	0.082	0.839	0.943
0.2	0.024	1.054	0.180	1.163	0.366	0.180	0.116	0.945
0.25	0.032	1.410	0.209	1.384	0.408	0.209	0.139	0.945
0.3	0.035	1.754	0.226	1.593	0.448	0.226	0.139	0.944
0.4	0.032	2.344	0.234	1.982	0.528	0.234	0.356	0.941
0.5	0.035	2.739	0.265	2.340	0.608	0.265	0.115	0.937
0.6	0.040	2.891	0.318	2.679	0.695	0.318	0.158	0.929
0.7	0.046	2.762	0.391	3.010	0.792	0.391	0.306	0.917
0.75	0.031	2.581	0.352	3.177	0.846	0.352	0.114	0.908
0.8	0.030	2.316	0.387	3.349	0.905	0.387	0.113	0.897
0.95	0.051	0.843	1.010	3.824	1.230	1.010	0.253	0.821

summarize the performance evaluation of both approaches in the training and testing phases. The MAD, RMSE, and MAE metrics are reported with respect to the various expectile levels. Similar to the models reported previously, KERE models significantly outperform ER models. The MAD evaluation metric of KERE and ER on the testing set is 0.046 and 2.762 corresponding to expectile level $w=0.7$. Whereas KERE and ER report an MSE metric of 0.391 and 3.010 with respect to the same expectile level.

Similar to the previously mentioned results, the KERE model corresponding to the expectile level $w=0.7$ is selected to be compared with the benchmark regression methods by reporting MAE, RMSE, and R². As outlined in

Table 8. The benchmark regression-based approaches used to predict indirect nitrogen emissions.

Phase	Training			Testing
Technique	MAE	RMSE	R	MAE	RMSE	R
Huber Regressor	0.0736	0.2891	−0.2846	0.210	1.564	0
Support Vector Regression	0.8994	1.0082	NA	0.308	1.544	0.01
AdaBoost Regressor	0.085	0.312	−0.028	0.446	2.009	−0.65
Lasso Regression	0.1489	0.3416	−8.487	0.279	1.566	0
Decision Tree Regressor	0.0845	0.3213	−0.1150	0.227	1.576	−0.02
Extra Trees Regressor	0.0835	0.3196	−0.0401	0.225	1.575	−0.02
Gradient Boosting Regressor	0.1481	0.3408	−8.4346	0.449	1.990	−0.62
K Neighbors Regressor	0.0903	0.3217	−0.859	0.237	1.573	−0.01
Random Forest Regressor	0.1333	0.5300	0.1415	0.225	1.574	−0.01
Light Gradient Boosting Machine	0.2286	0.7311	−338.59	0.279	1.566	0
Ridge Regression	0.1600	0.4165	−17.72	0.311	1.578	−0.02
MLP Regressor	0.415	0.732	−0.80	0.733	2.557	−1.68
Kernel Expectile Regression 1	0.154	0.285	0.90	0.524	0.98	0.18

¹ KERE model with respect to expectile level = 0.7.

, the selected KERE model performed significantly better, especially with regard to the RMSE metric evaluation.

Reporting the training and testing results for both direct and indirect emissions outlined the out-performance of kernel expectile regressions estimator approach to its counterpart Expectile Regression, especially with regard to MAD evaluation error. Furthermore, the KERE model corresponding to expectile level $w=0.7$ was selected to focus on the data closer to the tail of the data. The latter corresponds to the range of medium to large countries, showing that such a model, in addition to being flexible, performs better than all other considered benchmark regression approaches.

The KERE technique is indeed an explainable approach, allowing us to explore the relationship between synthetic N fertilizers use and global $N_{2}O$ emissions. Reducing N rates is not the main factor for reducing GHG emissions, mainly nitrous oxide. The adoption of lower N rates underestimates $N_{2}O$ emissions [50], as there are many factors at stake, such as the management of fertilizer applications while enhancing N use efficiency (NUE). N-based fertilizers vary depending on the N-form they contain, either ammonium $N{H}_4^{+}$ or nitrate $N{O}_3^{-}$. 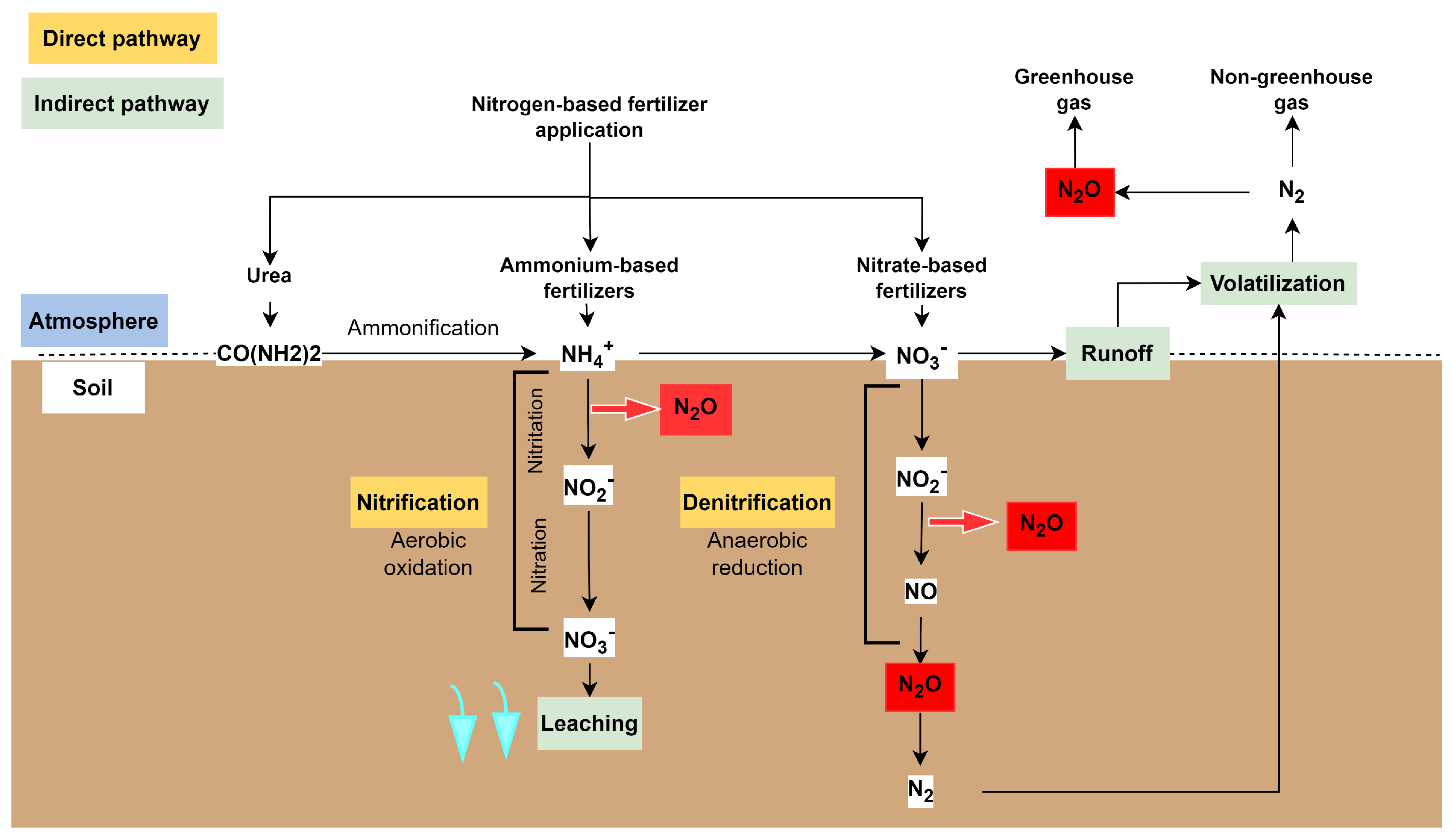In fact, $N{H}_4^{+}$ is the starting point by which the soil microorganisms perform the nitrification process to form $N{O}_3^{-}$, from which other soil microorganisms convert it to $N_2$ gas through the process of denitrification, while emitting the $N_{2}O$ gas during the whole process and this is the direct pathway of the $N_{2}O$ emissions. Referring to Figure 2 which highlights N pathways, and based on a modern study [51], it appears that there is a positive correlation between soil moisture content and cumulative $N_{2}O$ emissions. When water content is high in the soil, it was suggested that the required conditions for denitrification are met, leading to higher $N{O}_3^{-}$ concentrations in the soils, providing N substrate for the production of $N_{2}O$. In fact, floods and rain may have an impact on GHG emissions, increasing precipitation may enhance soil $N_{2}O$ emissions [52].

A first on-farm study [50] was conducted to report $N_{2}O$ response to multiple fertilizer rates on production-scale fields. They observed linear and nonlinear increases in $N_{2}O$ depending on the study locations and year. However, the nonlinear exponential response models best represented the overall $N_{2}O$ response to N fertilizer across all site years. A more recent study [53] also demonstrated the nonlinear relationship between the application of nitrogen-based fertilizers and $N_{2}O$ emissions, explaining how it changes depending on the meteorological circumstances, while the correlation between the $N_{2}O$ emissions and the N-fertilizer rate used remains unclear. In another study, it has been proven that monitoring nitrogen application alone is not capable of stimulating $N_{2}O$ emissions as much as the combination of nitrogen addition and rainfall reduction [54]. Nonetheless, nitrogen fertilization is an external factor; other management practices generate $N_{2}O$ as a side effect of their applications, such as irrigation or tillage practices or even the crop type used. Cropping systems have an impact on soil quality and soil GHG emissions. In a recent study [55], the importance of combining winter cover crop cultivation for single cropping systems with reduced N fertilizer application was investigated. This work supports our results; the cropping system and N rate application impact the GHG emissions and $N_{2}O$ direct emissions. In comparison with traditional cotton cultivation, where $N_{2}O$ and other GHG emissions were increased, it appears that both cover cropping with reduced N helped to mitigate soil GHG emissions. Furthermore, the geographical disposition may have an impact as well. For example, countries, such as China, the USA, Canada, India, and Brazil are known for their enormous agricultural production, hence, diverse soil characteristics, diverse climates, and various crop types are greatly responsible for the increase of GHG emissions. From another point of view, and in the case of China, rice represents the most economically important crop, where rice paddies are an excellent environment for the biological activities of nitrification and denitrification processes which have been accelerated especially in flooded soils, leading to enormous $N_{2}O$ production as described by [56]. Other N-fertilization management techniques have an impact on $N_{2}O$ emissions, with an increase in N fertilizer’s use, adopting the 4R Nutrient Stewardship has a significant potential to lower $N_{2}O$ emissions [57].

The results also show that the source of N synthetic fertilizers does not contribute as much to indirect emissions of $N_{2}0$. When it comes to indirect emissions, research has proven that the leaching and runoff of nitrate from the application of synthetic N fertilizers is a substantial indirect source of $N_{2}O$ emissions from groundwater. This indicates that indirect emissions are not related to the source of N fertilizer itself, but depend mainly on the N content in agricultural soils that could be lost through leaching/Runoff [58].

6. Conclusions and Future Works

The food supply chain is a salient contributor to global emissions of air pollutants. These major air pollutant compounds, such as $N_{2}O$, are emitted by different stages of the food system, from food production, processing, packaging, transport, retail, consumption, and disposal. This work used an explainable approach in order to explore the relationship between synthetic N fertilizers and global $N_{2}O$ emissions.

According to our results and the findings within the literature, we conclude, two major points:

• Using the kernel expectile regression estimator approach is highly suitable when dealing with air quality related data.
• Integrating additional external factors is highly recommended, for more accurate results and in order to interpret our outputs.

Based upon the results from the KERE method, the source of N-based fertilizers is not capable of explaining $N_{2}O$ emissions on their own. On the one hand, the disparity in the degree of $N_{2}O$ emissions between countries, where many national GHG inventories employ the IPCC’s first-tier method, which uses a set of global default emission factors (EF) to estimate the $N_{2}O$ emissions depending on varying geography. On the other hand, N-fertilizer sources and quantities are not the only major contributors in nitrous oxide emissions, in fact, a significant portion of greenhouse gas emissions is now caused by farming activities either directly or indirectly, leading to a decay in air quality. Agricultural practices are of great importance; hence, we propose that reducing the usage of synthetic N fertilizers is not the most suitable solution to reduce $N_{2}O$ emissions. However, there is a need to monitor nitrogen-based fertilizer usage, while keeping an eye on the whole farming management practices, such as conventional tillage, which is a major contributor in $N_{2}O$ emissions, and no-tillage can decrease the $N_{2}O$ emissions, in the presence of different fertilizer treatments. Furthermore, our research suggests the necessity for a more specified and detailed estimation of $N_{2}O$ emissions, based on each country for a longer period of time. In order to establish a more effective study, we also encourage agribusinesses, organizations, and farmers to empower data availability. Bridging the gap between research and industry is a challenging step. Gaining insight from the data is very important; hence, increasing the usage of explainable machine learning tools is of great significance toward integrating interpretability for air quality models.