Effect of Catalyst Inlet Flow Field Distribution Characteristics on Outlet NO Concentration Distribution in SCR Denitration Reactor Based on Monte Carlo Method
Abstract
:1. Introduction
2. Research Method
2.1. Numerical Calculation Model
+ 0.1614AB − 2.955AC + 0.2458BC
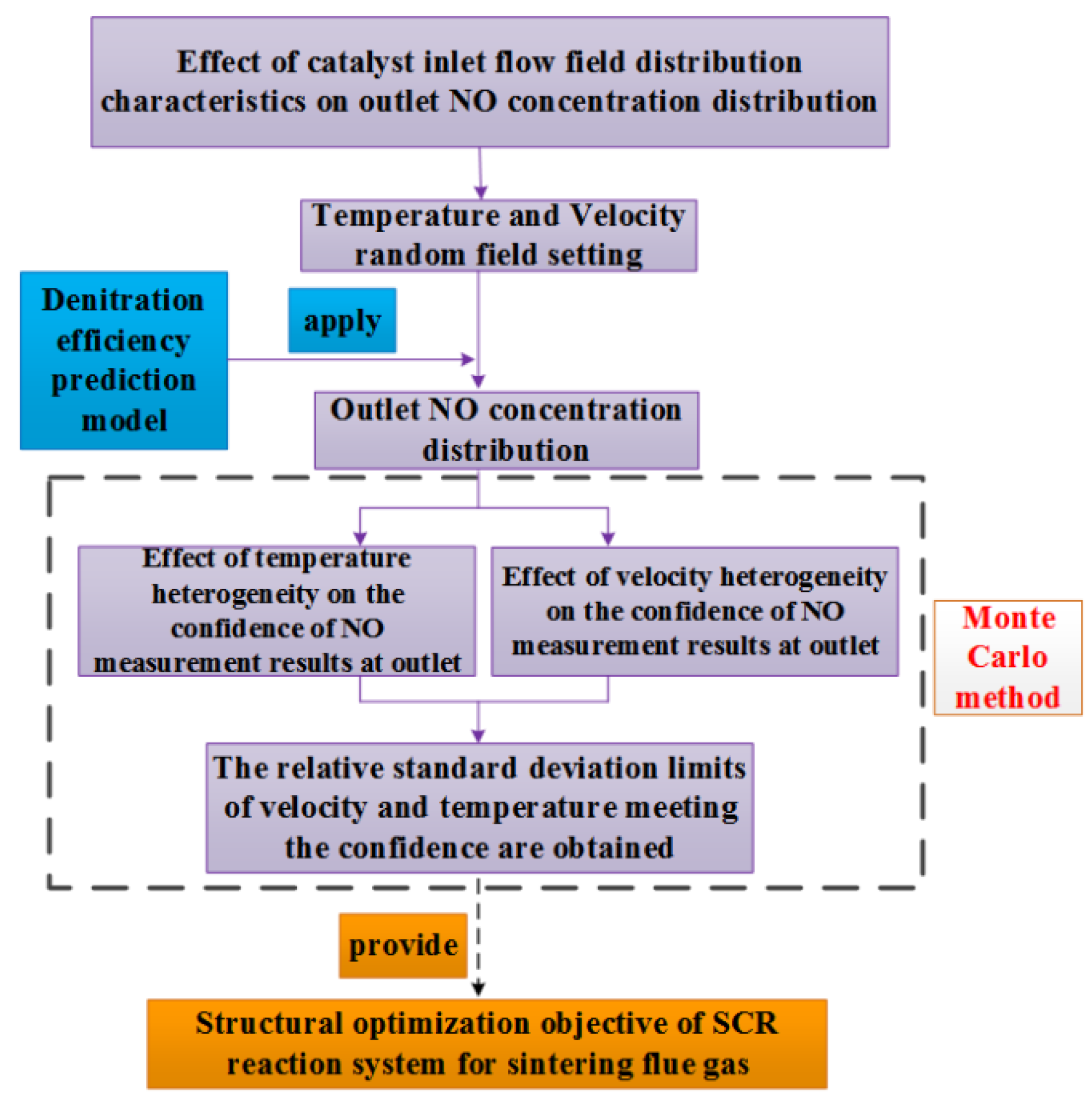
2.2. Introduction to Research Ideas and Concepts
2.2.1. Monte Carlo Method
2.2.2. Research Routes
2.2.3. Concept Introduction
3. Results and Discussion
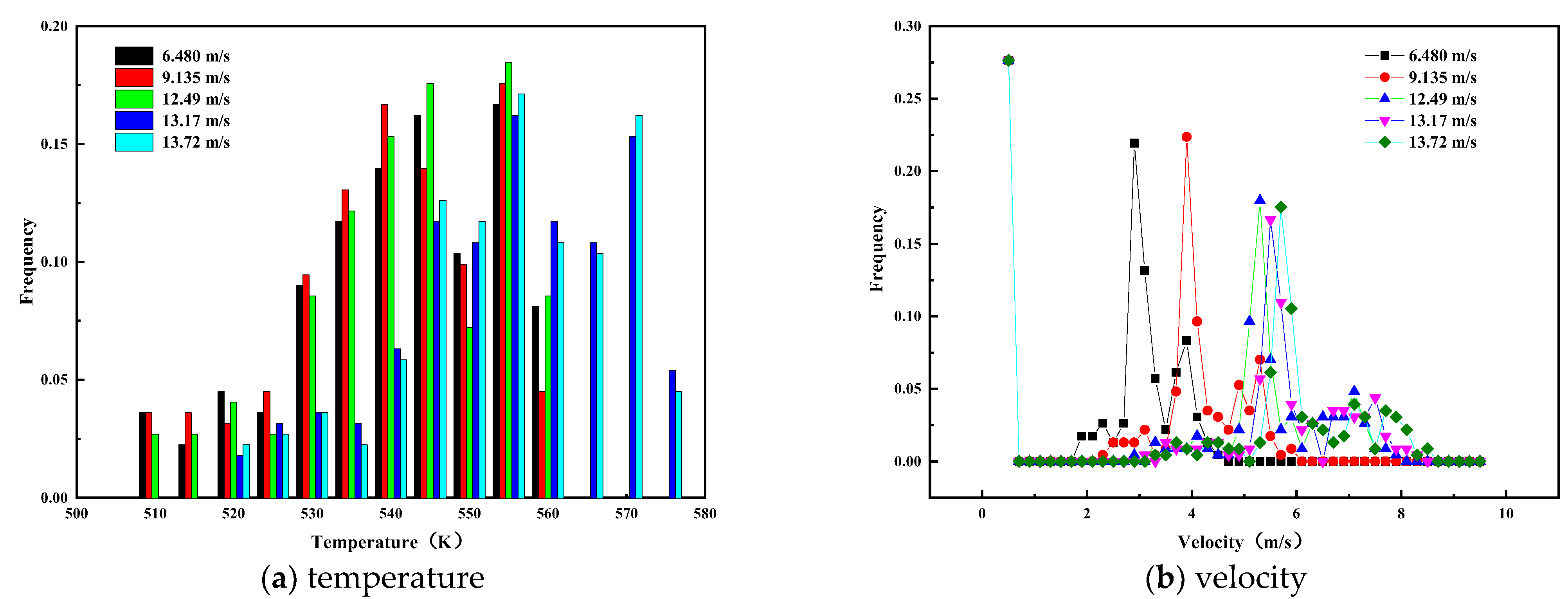
3.1. Random Field Distribution of Velocity and Temperature
3.1.1. Determination of Velocity and Temperature Random Fields
3.1.2. Setting of Velocity and Temperature Random Fields
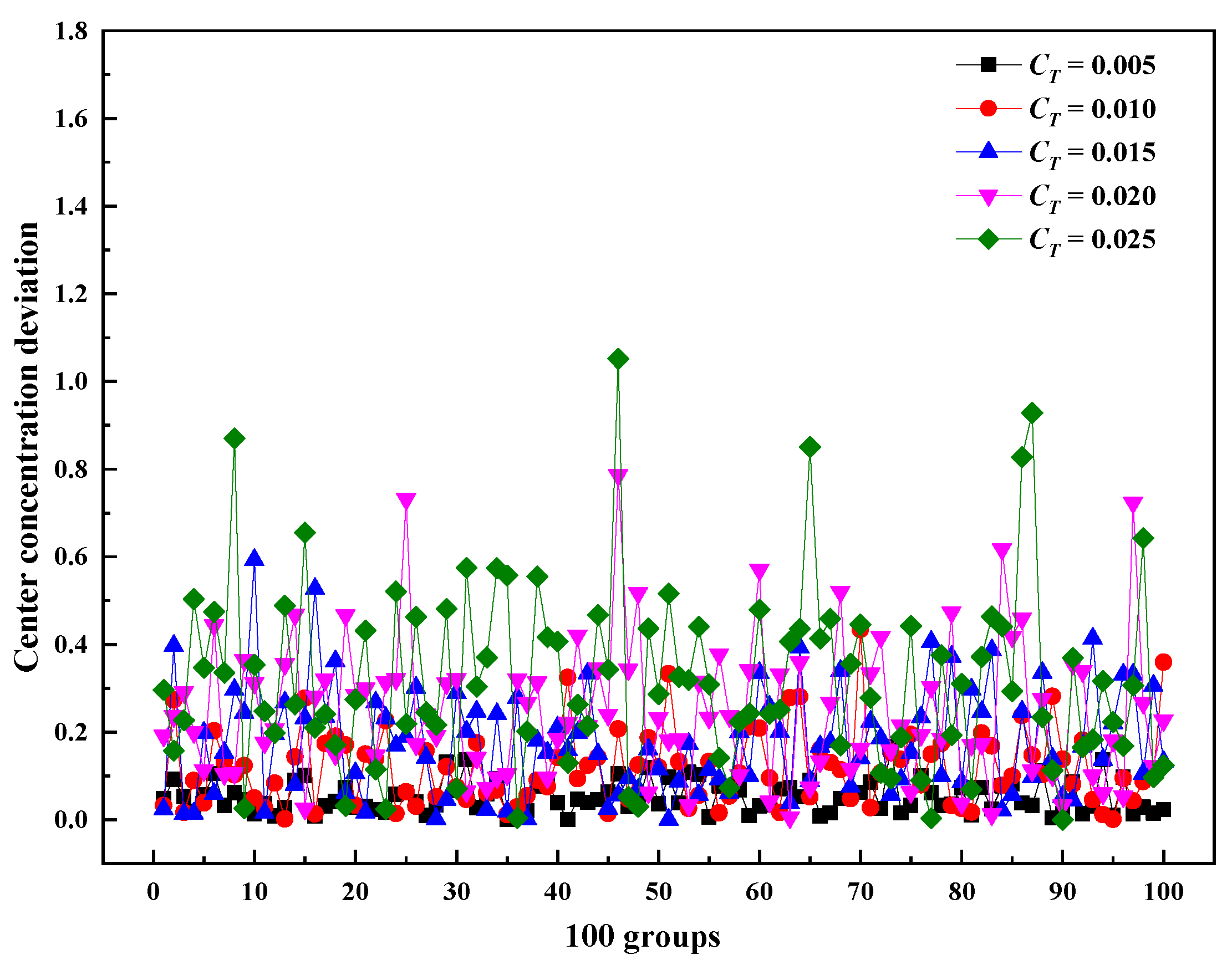
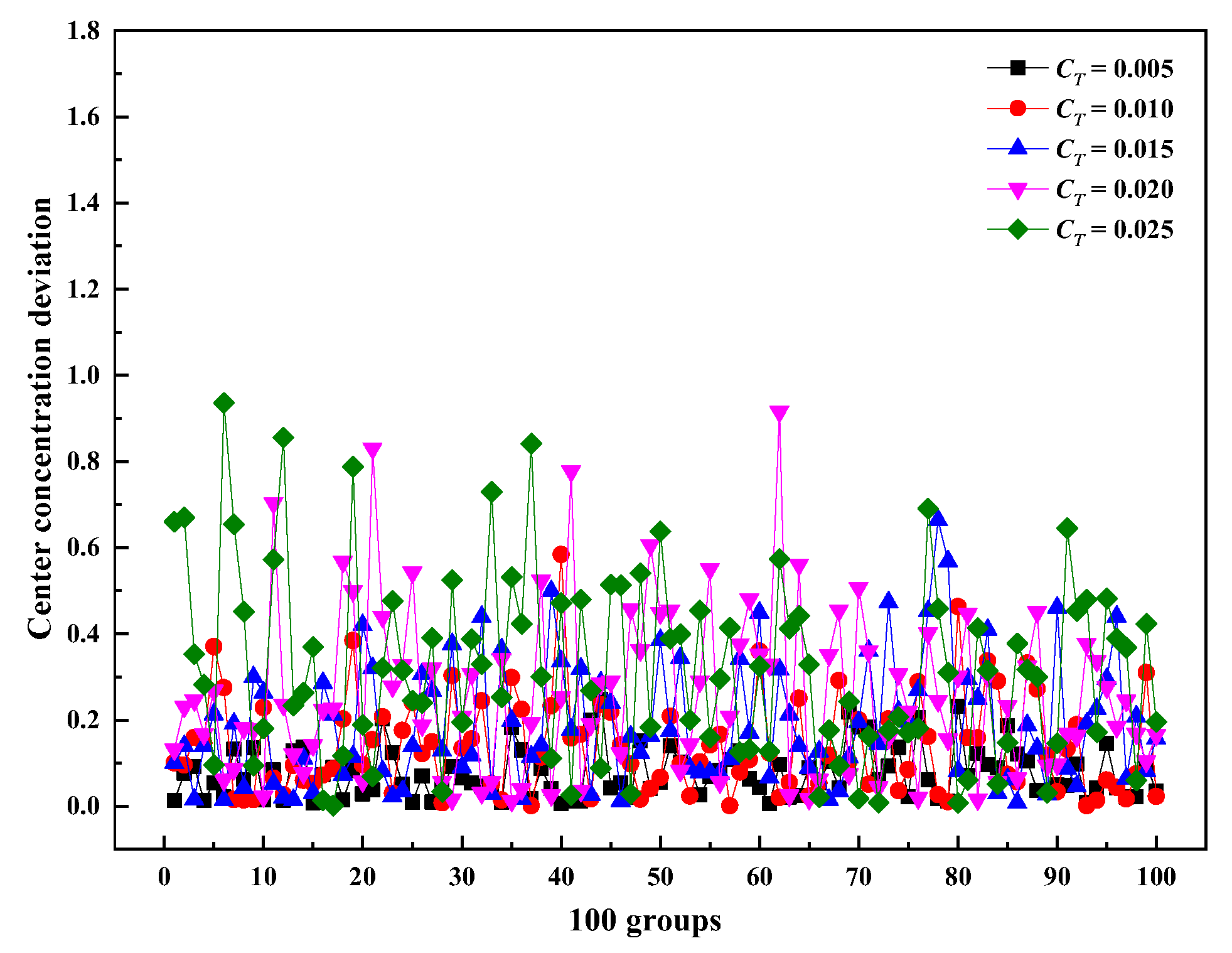
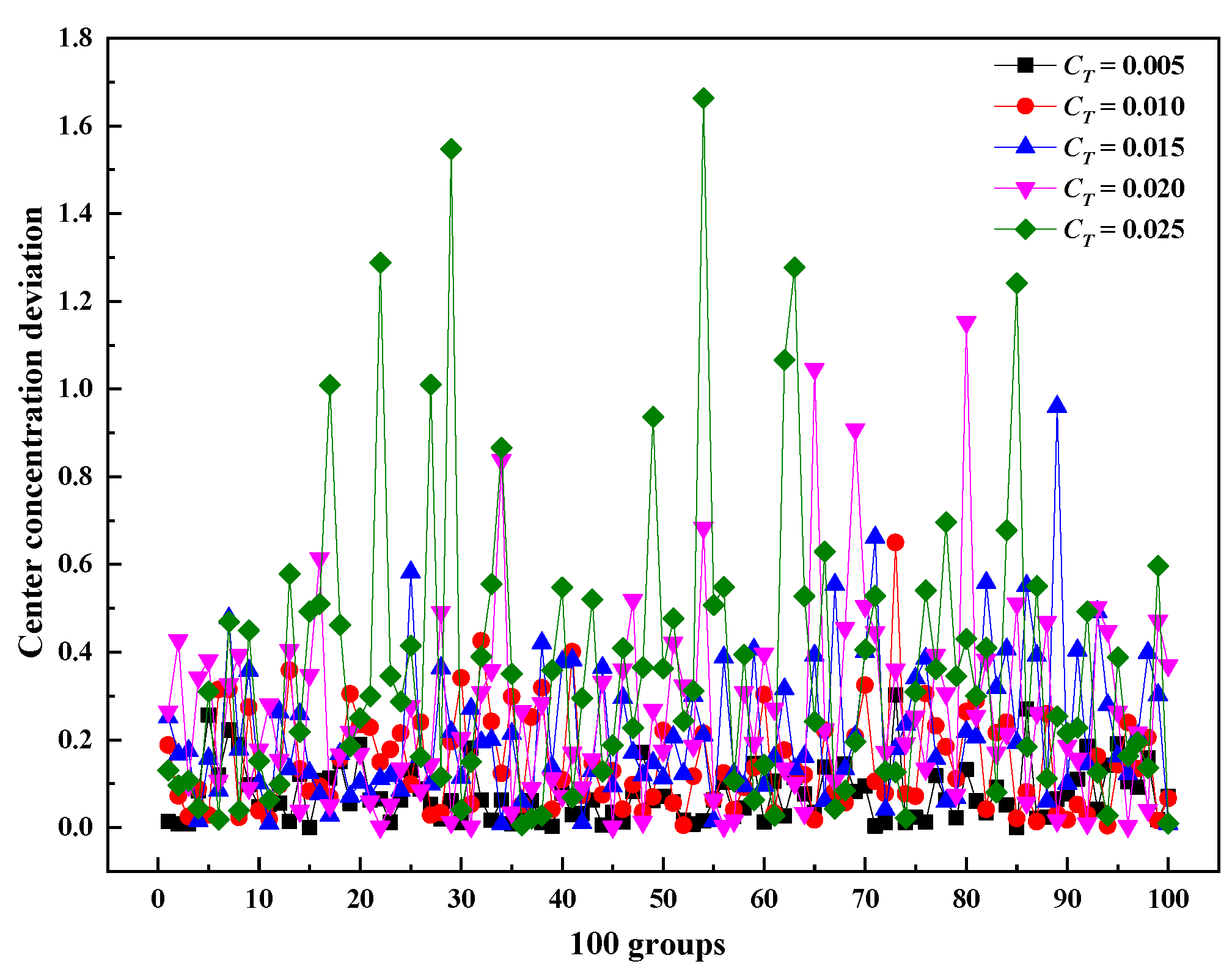
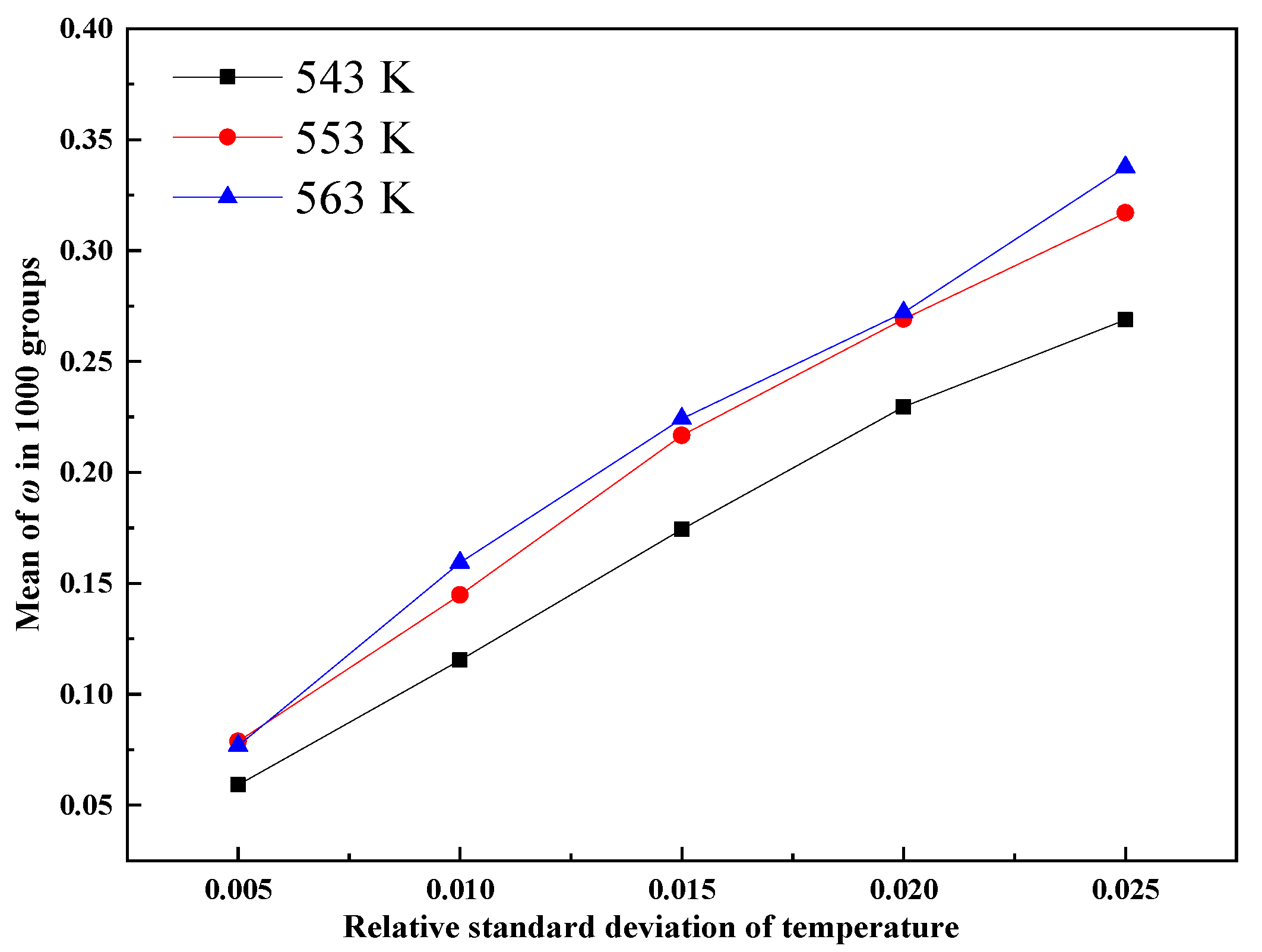
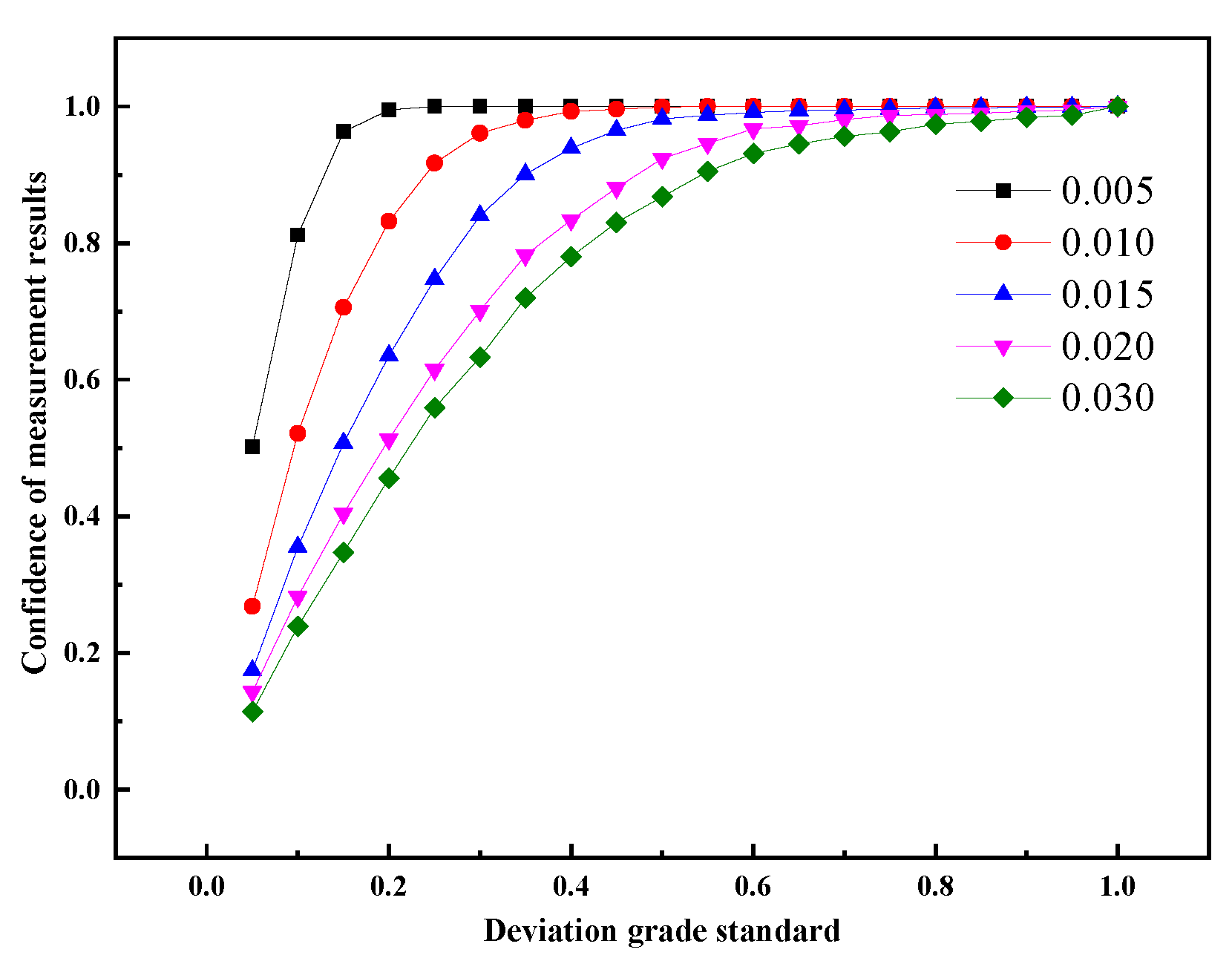
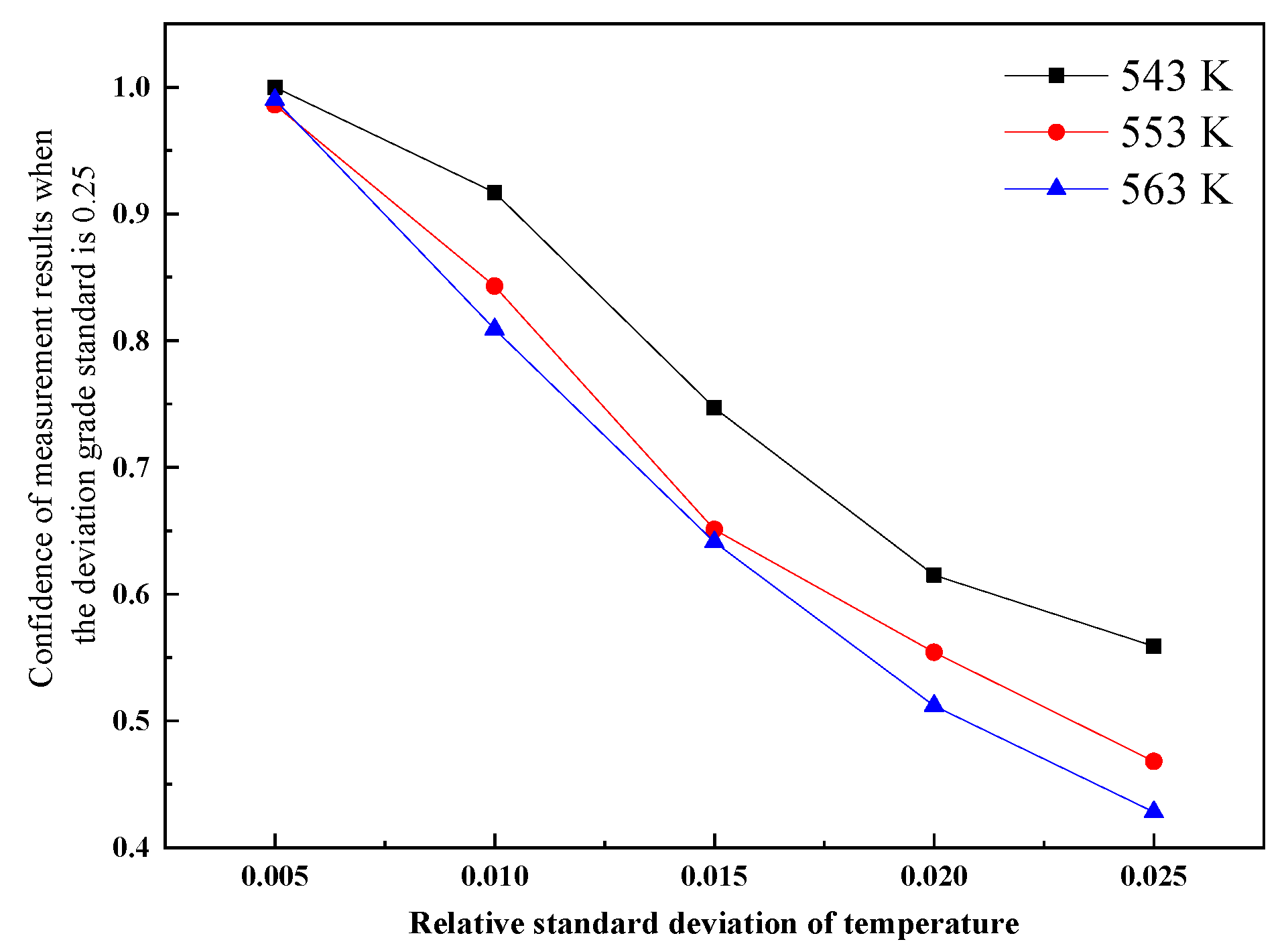
3.2. Effect of Nonuniform Temperature on the Confidence of NO Measurement Results at the Outlet
3.2.1. Different Averaged Values of Temperature
3.2.2. Different Averaged Values of Velocity
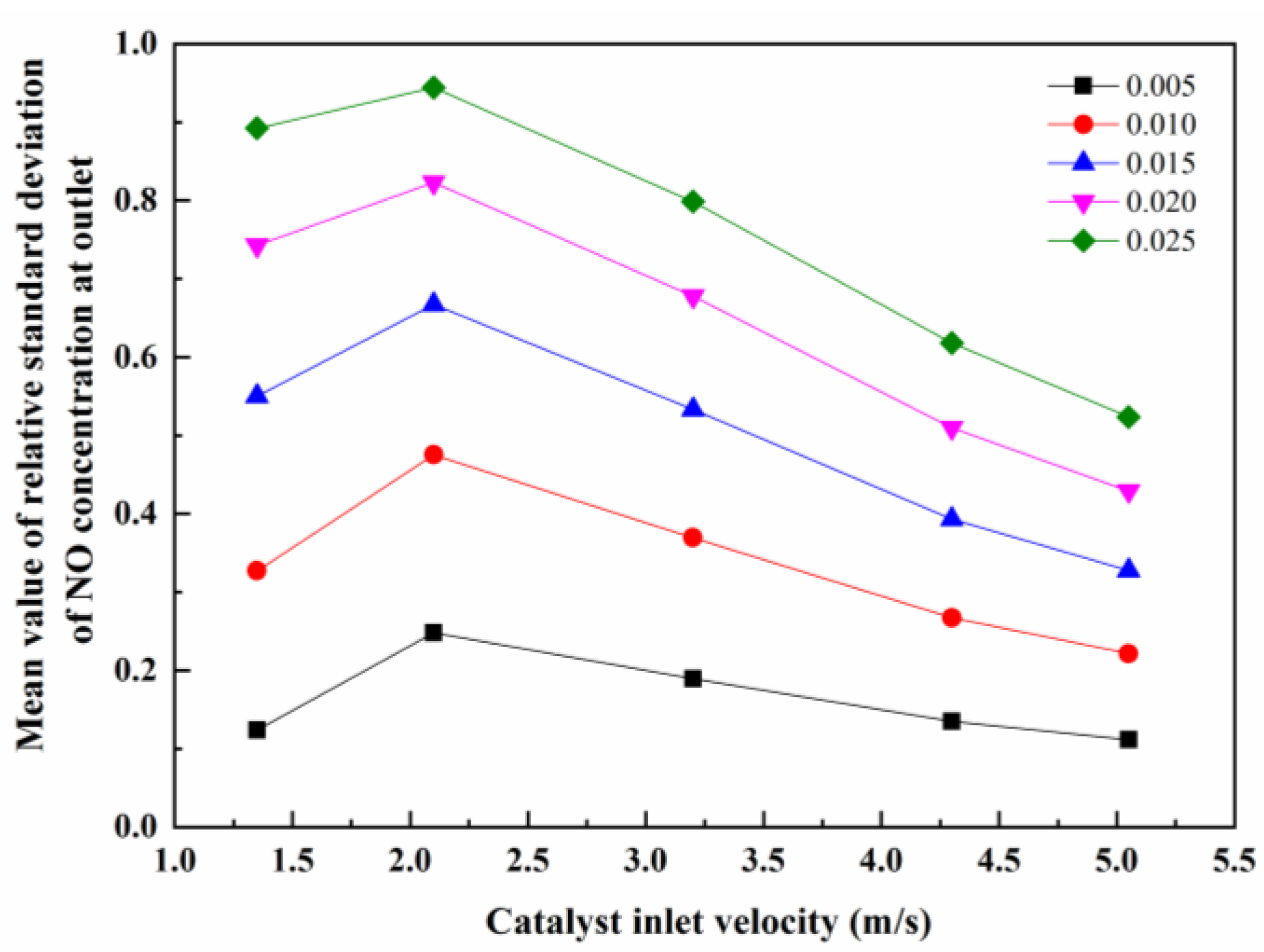
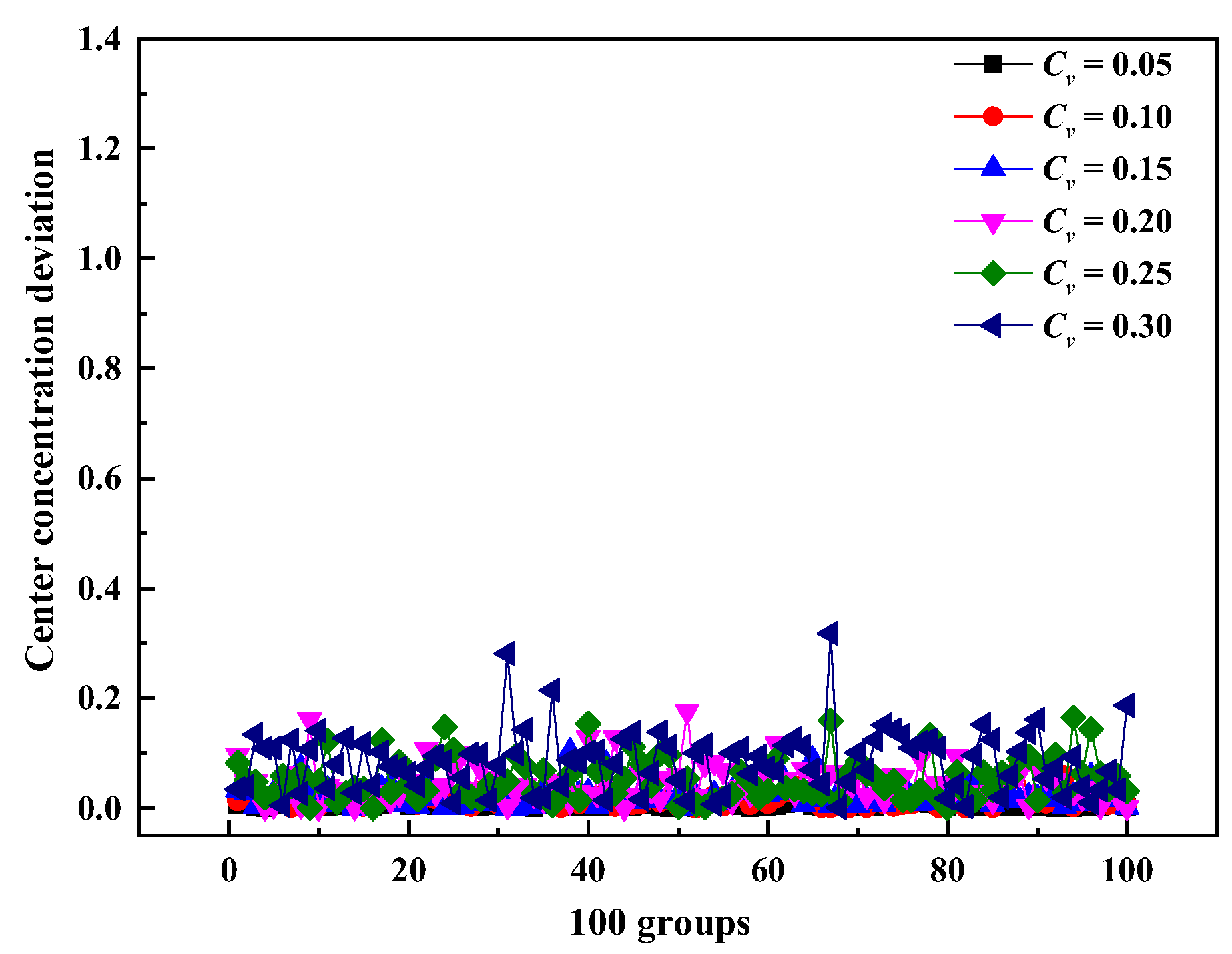
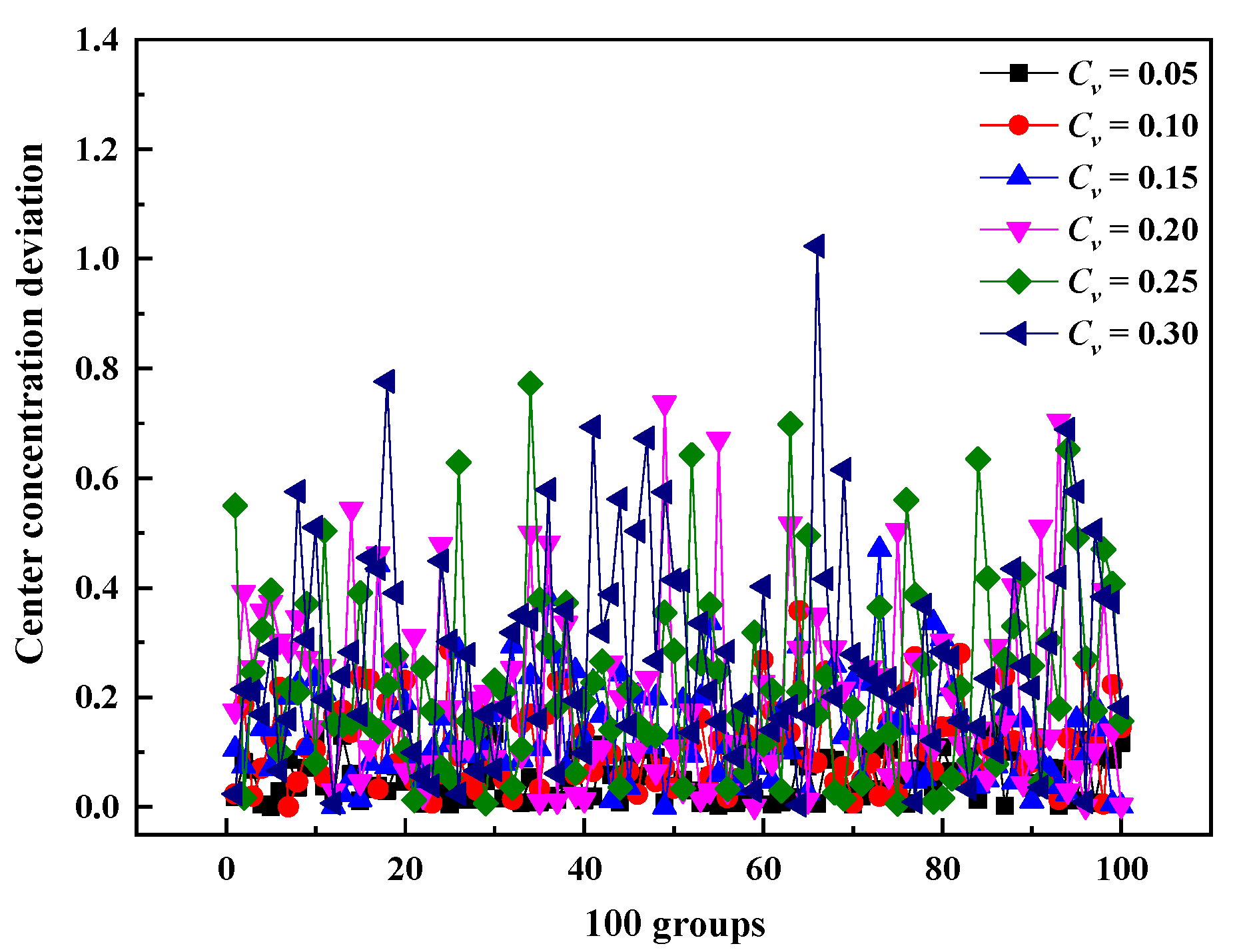
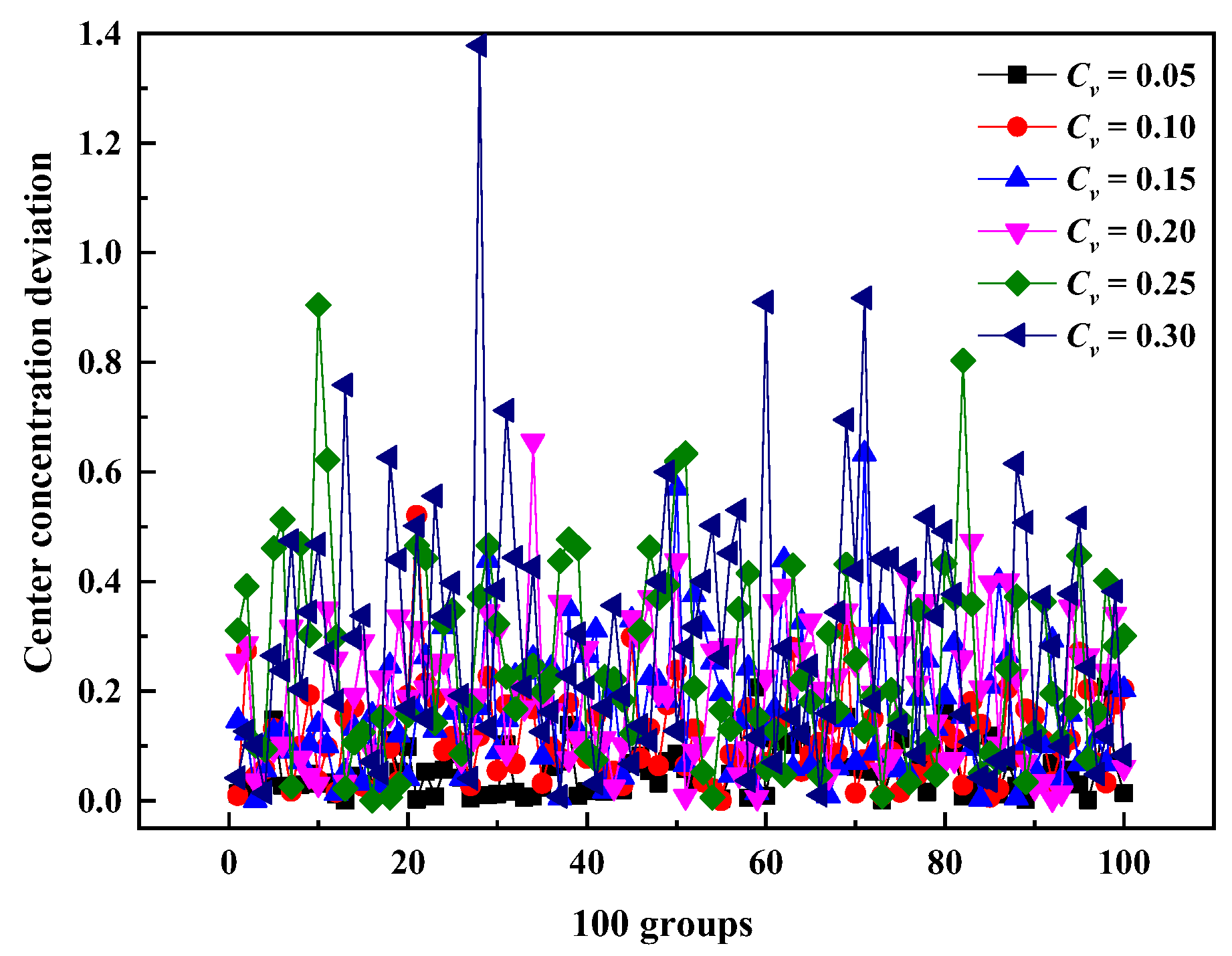
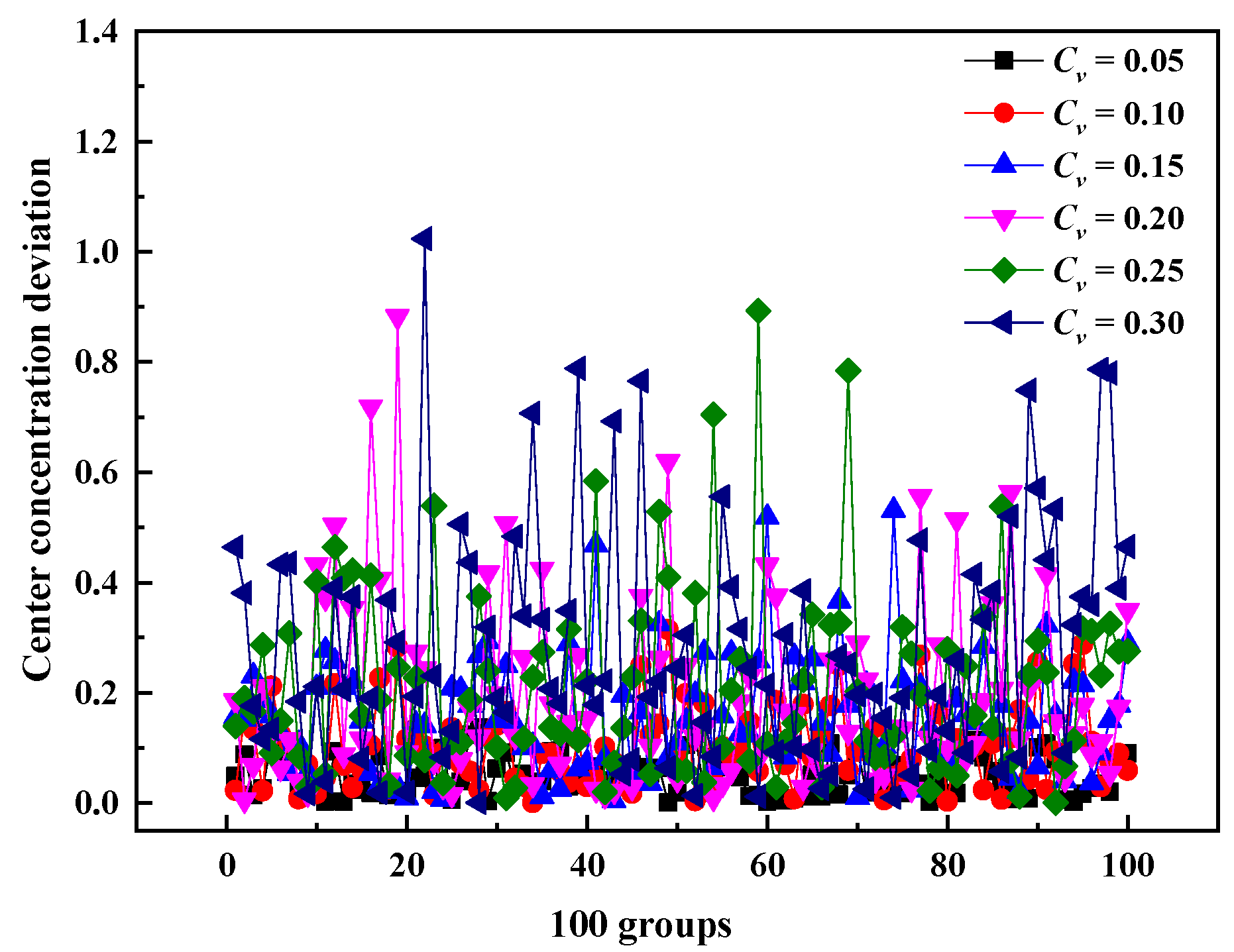
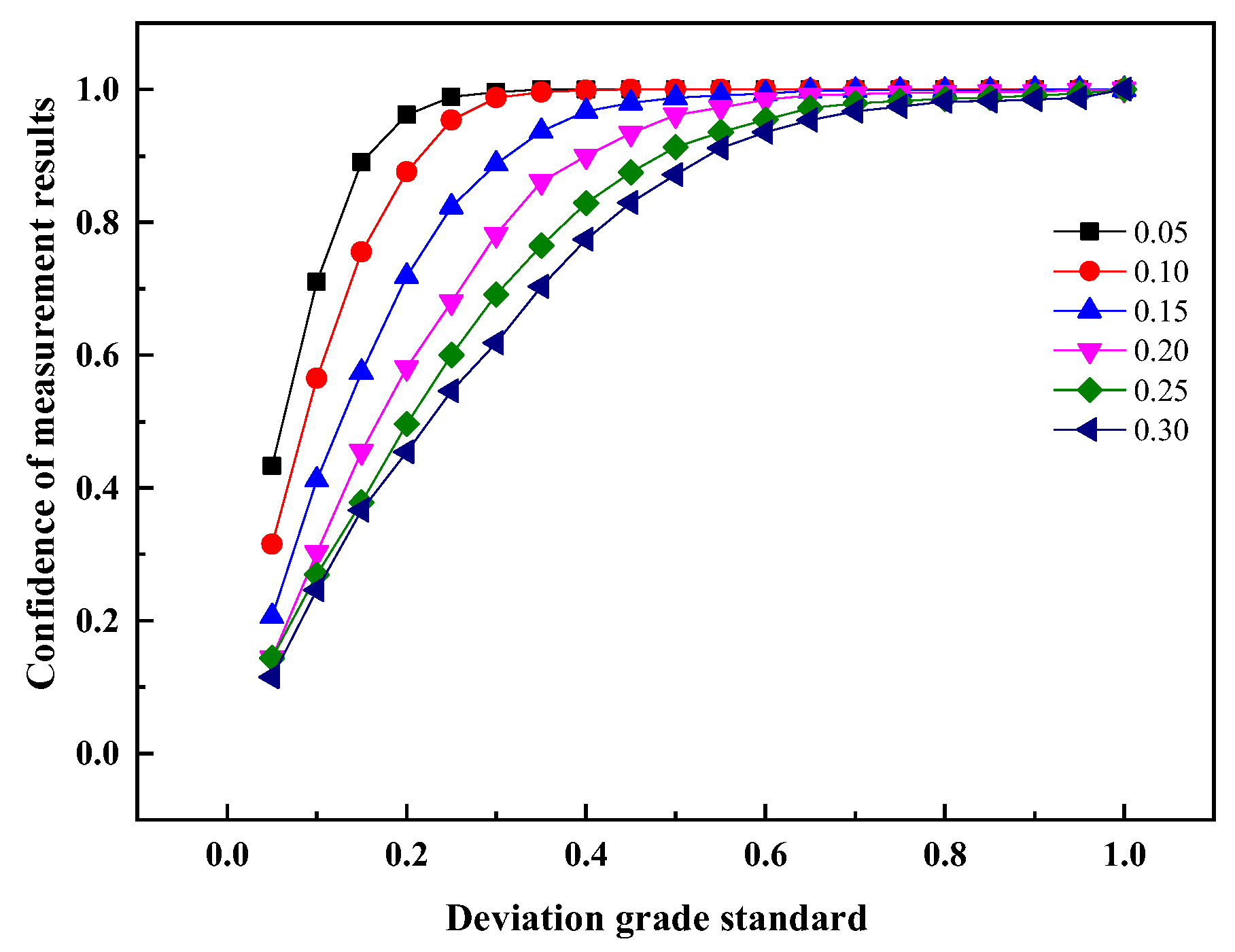
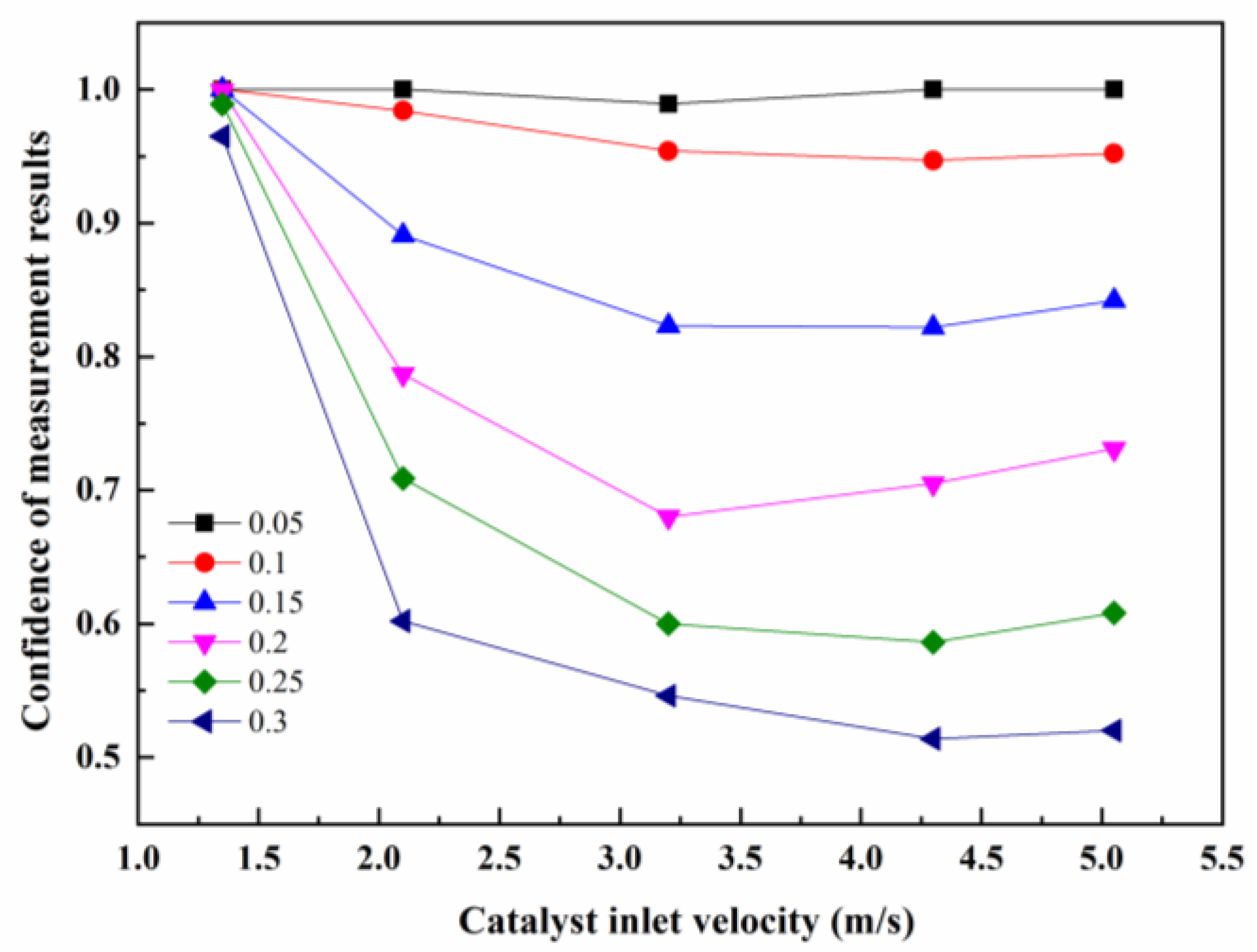
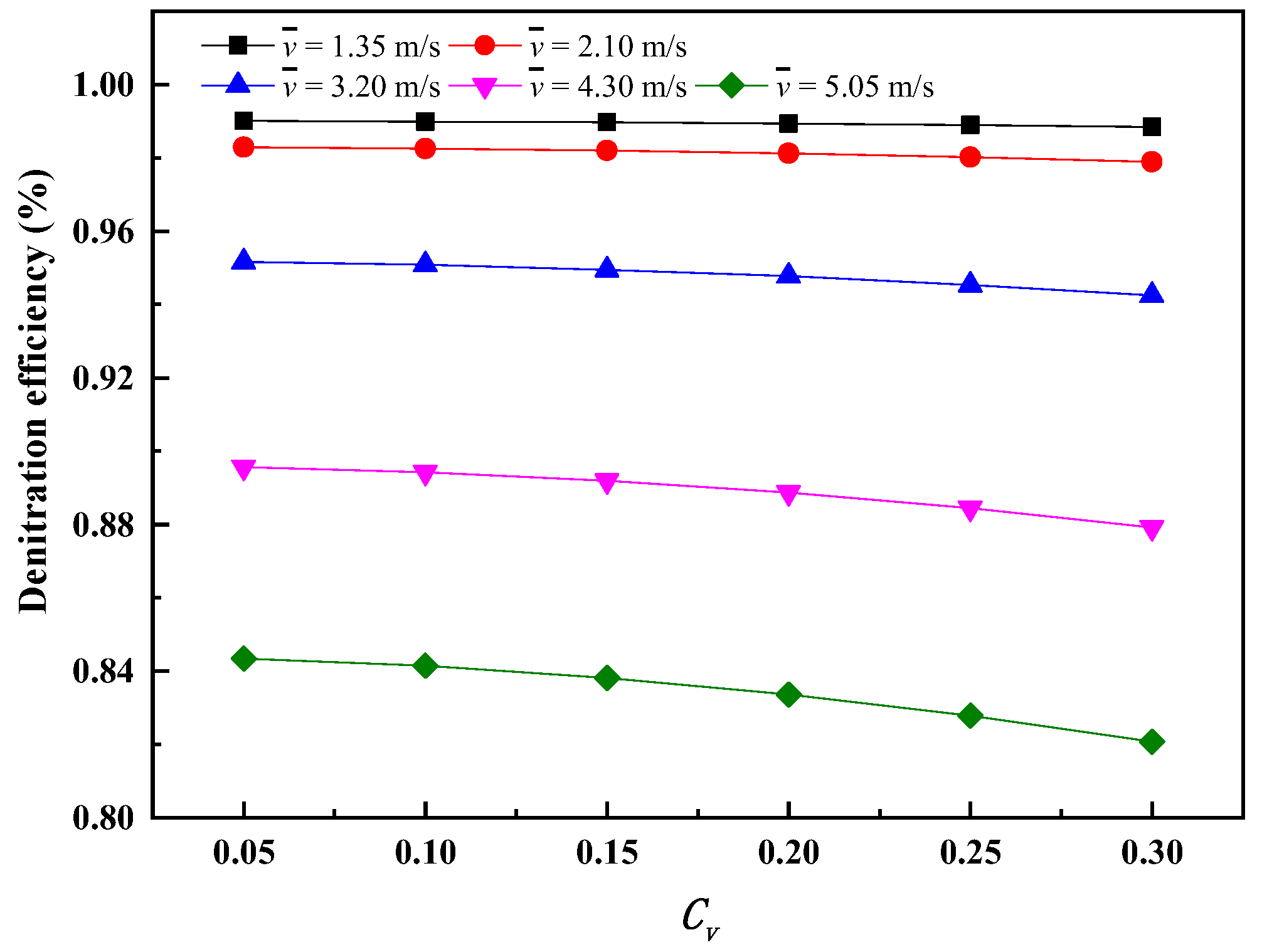
3.3. Effect of Nonuniform Velocity on the Confidence of NO Measurement Results at the Outlet
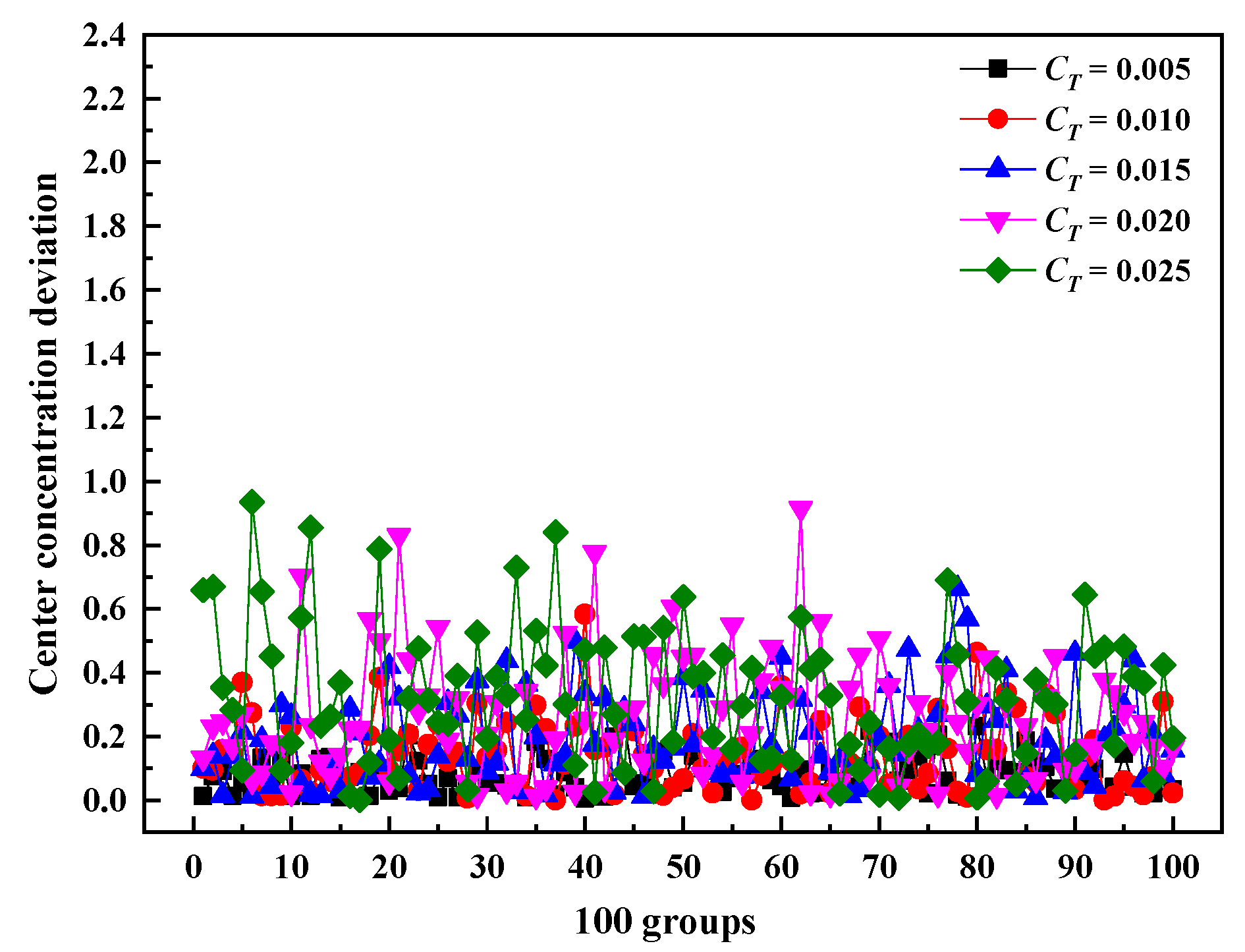
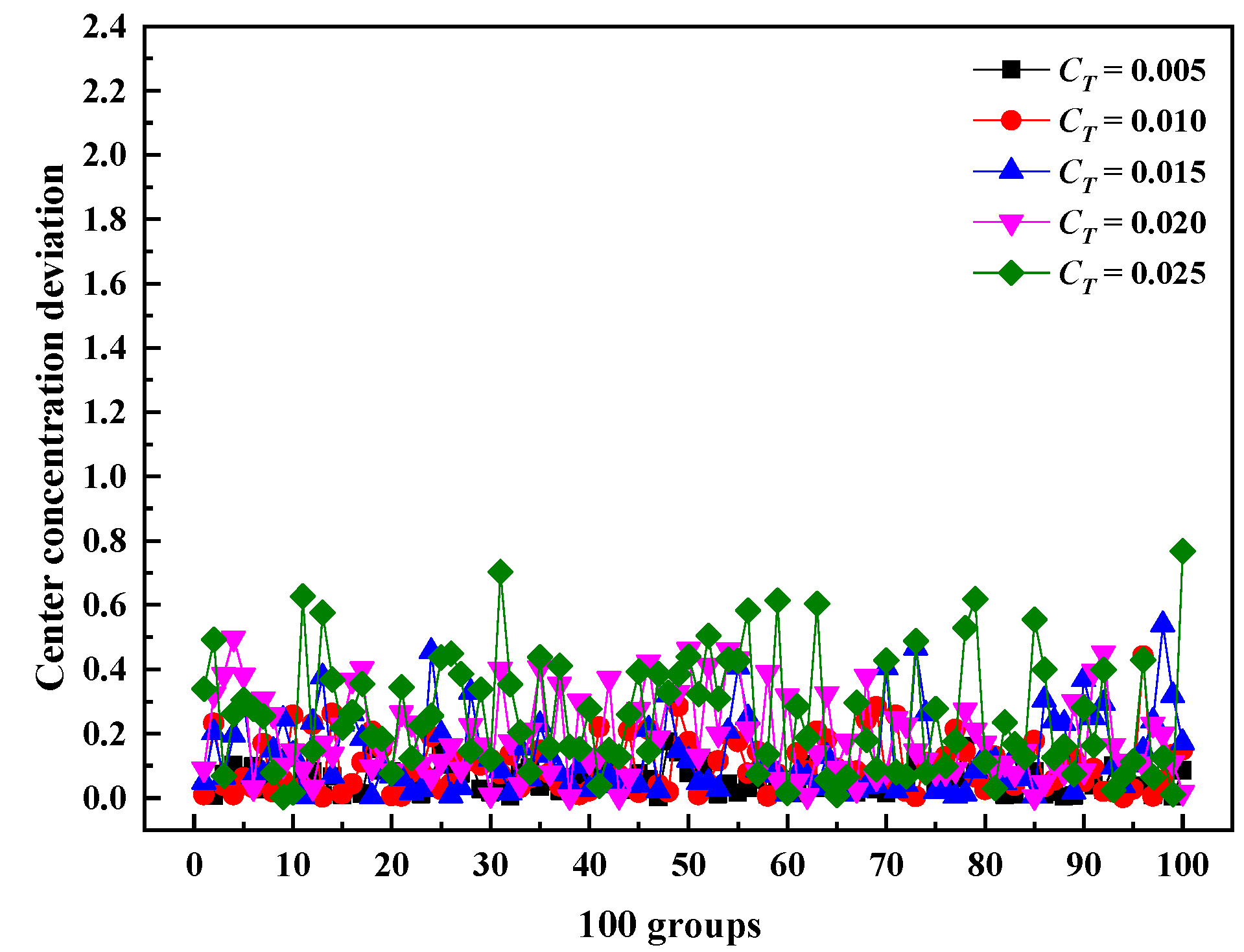
3.4. Effect of Nonuniform Temperature and Velocity on Denitration Efficiency
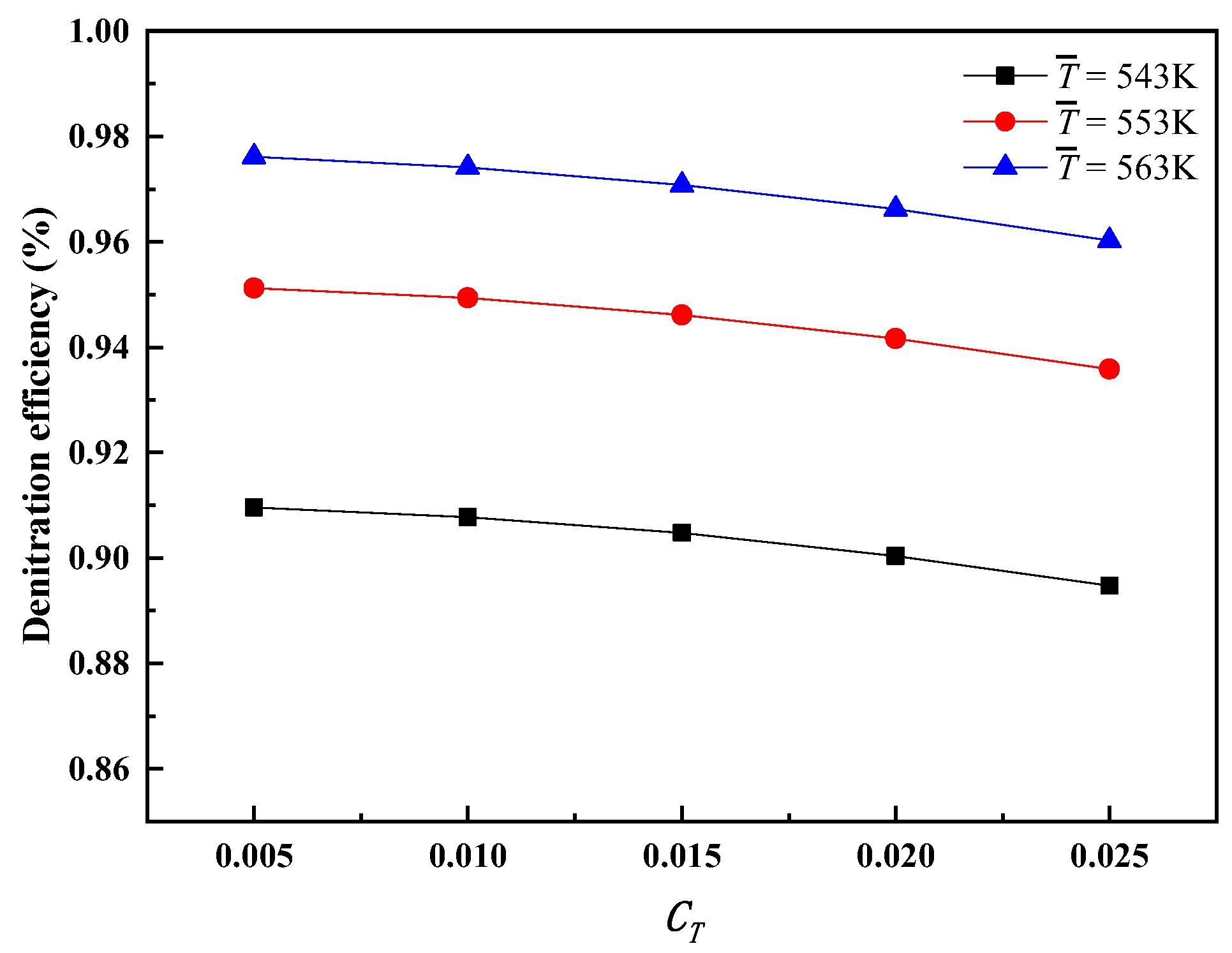
3.4.1. Effect of Nonuniform Temperature on Denitration Efficiency
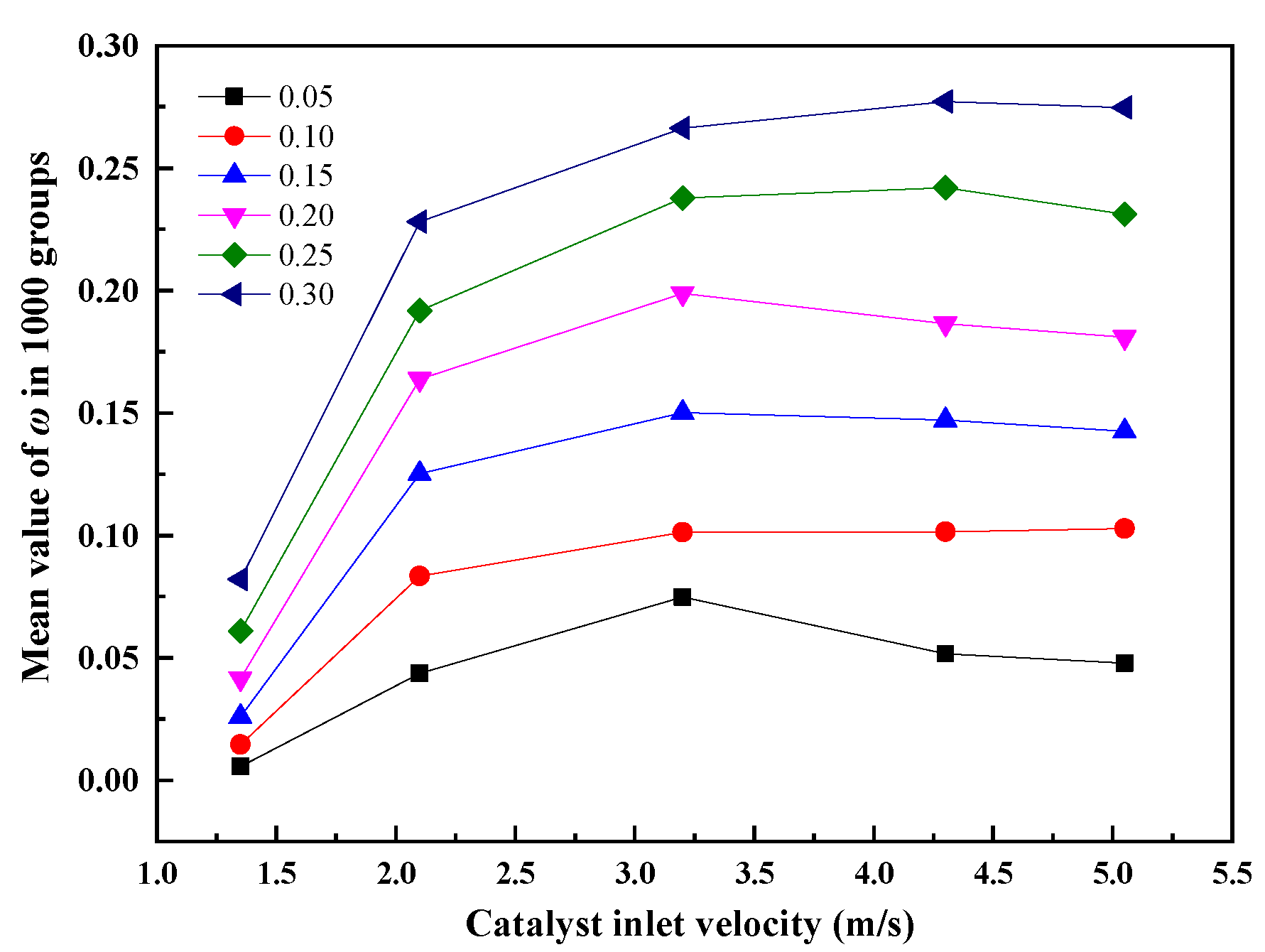
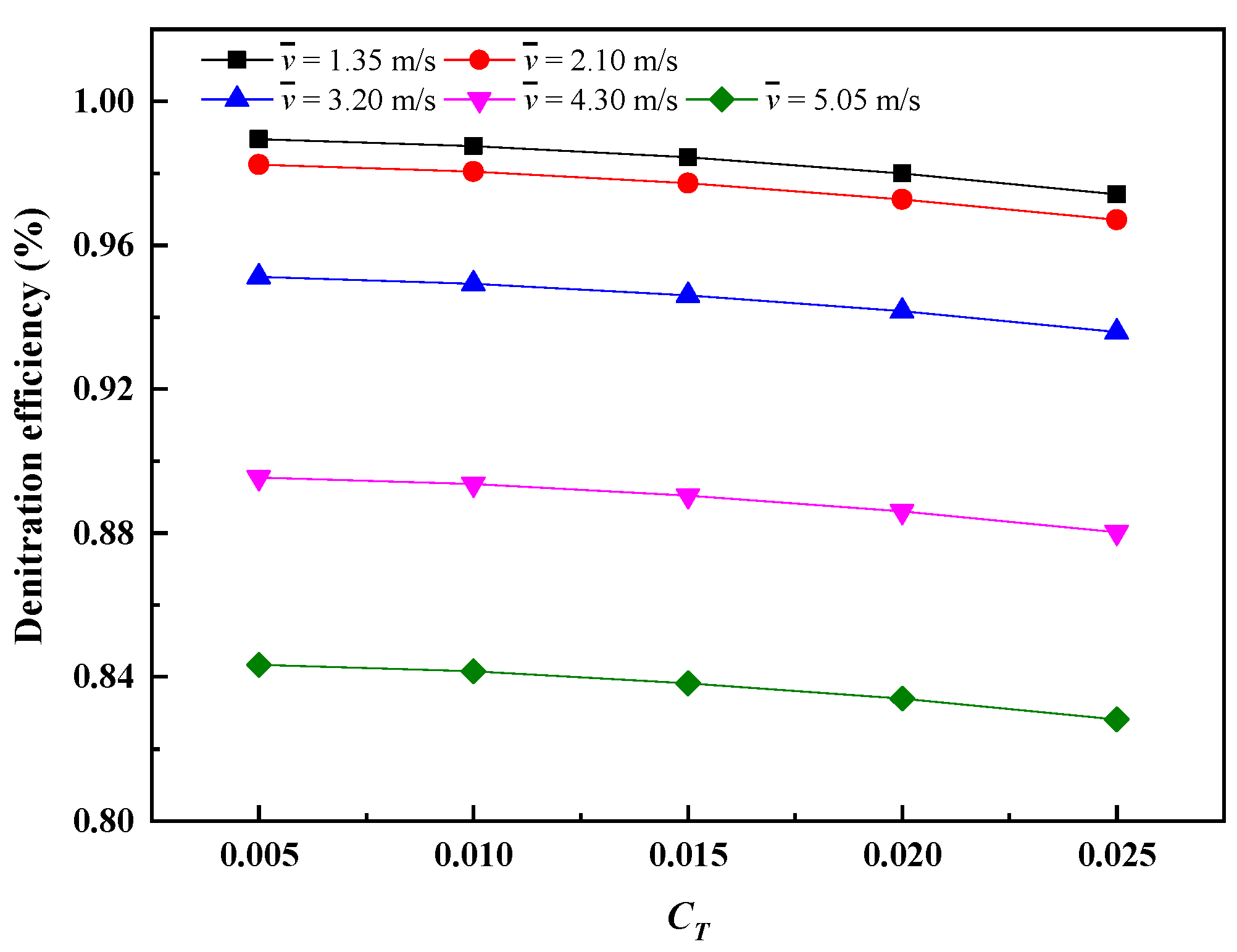
3.4.2. Effect of Nonuniform Velocity on Denitration Efficiency
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, Z.J.; Zheng, Z.; Gao, X.Q. Operation optimization of the steel manufacturing process: A brief review. Int. J. Miner. Metall. Mater. 2021, 28, 1274–1287. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Zhang, J.L.; Liu, Z.J.; Du, C.B. Recent Advances and Research Status in Energy Conservation of Iron Ore Sintering in China. Miner. Met. Mater. Soc. 2017, 69, 2404–2411. [Google Scholar] [CrossRef]
- Ye, L.; Lu, P.; Chen, D.; Chen, D.; Wu, H.; Dai, W.; Gan, Y.; Xiao, J.; Xie, Z.; Li, Z.; et al. Activity enhancement of acetate precursor prepared on MnOx-CeO2 catalyst for low-temperature NH3-SCR: Effect of gaseous acetone addition. Chin. Chem. Lett. 2021, 32, 2509–2512. [Google Scholar] [CrossRef]
- Meng, H. Deep desulfurization of sintering flue gas in iron and steel works based on low-temperature oxidation. Open Chem. 2020, 18, 1370–1380. [Google Scholar] [CrossRef]
- Shen, B.; Ma, H.; Yan, Y.J. Mn-CeOx/Ti-PILCs for selective catalytic reduction of NO with NH3 at low temperature. J. Environ. Sci. 2012, 24, 499–506. [Google Scholar] [CrossRef]
- Kobayashi, M.; Kuma, R.; Morita, A. Low temperature selective catalytic reduction of NO by NH3 over V2O5 supported on TiO2–SiO2–MoO3. Catal. Lett. 2006, 112, 37–44. [Google Scholar] [CrossRef]
- Wang, Y.; Tan, H.; Dong, K.; Liu, H.; Xiao, J.; Zhang, J. Study of ash fouling on the blade of induced fan in a 330 MW coal-fired power plant with ultra-low pollutant emission. Appl. Therm. Eng. 2017, 118, 283–291. [Google Scholar] [CrossRef]
- Theinnoi, K.; Tsolakis, A.; Sitshebo, S.; Cracknell, R.F.; Clark, R.H. Fuels combustion effects on a passive mode silver/alumina HC-SCR catalyst activity in reducing NOx. Chem. Eng. J. 2010, 158, 468–473. [Google Scholar] [CrossRef]
- Zhang, K.; Zhao, J.; Zhu, Y. MPC case study on a selective catalytic reduction in a power plant. J. Process Control 2018, 62, 1–10. [Google Scholar] [CrossRef]
- Tan, P.Q.; Zhang, S.C.; Wang, S.Y.; Hu, Z.Y.; Lou, D.M. Simulation on catalytic performance of fresh and aged SCR catalysts for diesel engines. J. Energy Inst. 2020, 93, 2280–2292. [Google Scholar] [CrossRef]
- Li, Z.; Lee, Y.S.; Chen, J.; Qian, Y. Developing variable moving window PLS models: Using case of NOx emission prediction of coal-fired power plants. Fuel 2021, 296, 120441. [Google Scholar] [CrossRef]
- Liu, G.; Zhang, Y.; Shen, D.; Yuan, B.; Li, R.; Sun, Y. Anticipatory NH3 injection control for SCR system based on the prediction of the inlet NOx concentration. J. Energy Inst. 2021, 94, 167–175. [Google Scholar] [CrossRef]
- Yao, J.; Zhong, Z.; Zhu, L. Porous Medium Model in Computational Fluid Dynamics Simulation of a Honeycombed SCR DeNOx Catalyst. Chem. Eng. Technol. 2015, 38, 283–290. [Google Scholar] [CrossRef]
- Yang, J.; Ma, H.; Yamamoto, Y.; Yu, J.; Xu, G.; Zhang, Z.; Suzuki, Y. SCR catalyst coated on low-cost monolith support for flue gas denitration of industrial furnaces. Chem. Eng. J. 2013, 230, 513–521. [Google Scholar] [CrossRef]
- Yue, G.; Qiu, T.; Lei, Y. Experimental demonstration of NOx reduction and ammonia slip for diesel engine SCR system. Environ. Sci. Pollut. Res. 2022, 29, 1118–1133. [Google Scholar] [CrossRef]
- Zhang, Y.; Lou, D.; Tan, P.; Hu, Z.; Fang, L. Effect of SCR downsizing and ammonia slip catalyst coating on the emissions from a heavy-duty diesel engine. Energy Rep. 2022, 8, 749–757. [Google Scholar] [CrossRef]
- Cheng, T.; Zheng, C.; Yang, L.; Wu, H.; Fan, H. Effect of selective catalytic reduction denitrification on fine particulate matter emission characteristics. Fuel 2019, 238, 18–25. [Google Scholar] [CrossRef]
- Sohn, J.; Hwang, I.S.; Hwang, J. Improvement of ammonia mixing in an industrial scale selective catalytic reduction De-NOx system of a coal-fired power plant: A numerical analysis. Process Saf. Environ. Prot. 2021, 147, 334–345. [Google Scholar] [CrossRef]
- Tian, X.; Xiao, Y.; Zhou, P.; Zhang, W.; Chu, Z.; Zheng, W. Study on the mixing performance of static mixers in selective catalytic reduction (SCR) systems. J. Mar. Eng. Technol. 2015, 14, 57–60. [Google Scholar] [CrossRef] [Green Version]
- Ye, D.; Wang, X.; Wang, R.; Gao, S.; Liu, H.; Wang, H. Optimizing flow field in an SCR system of a 600 MW power plant: Effects of static mixer alignment style. Waste Dispos. Sustain. Energy 2021, 3, 339–346. [Google Scholar] [CrossRef]
- Wang, L.; Qian, F.; Zhu, J.; Huang, N.; Xu, B.; Wu, H. Multi-scale simulation of flow characteristics in selective catalytic reduction honeycomb catalyst. Chin. J. Process Eng. 2020, 20, 134–140. [Google Scholar] [CrossRef]
- Ye, M.; Qian, F.; Gao, Y.; Lu, J.; Han, Y.; Huang, N.; Xu, B.; Wu, H. CFD analysis of influencing factors on SCR denitration efficiency of sintering flue gas based on response surface methodology. Atmos. Pollut. Res. 2021, 12, 101107. [Google Scholar] [CrossRef]
- Frenkel, D.; Schrenk, K.J.; Martiniani, S. Monte Carlo sampling for stochastic weight functions. Proc. Natl. Acad. Sci. USA 2017, 114, 6924–6929. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kunsch, R.J.; Rudolf, D. Optimal confidence for Monte Carlo integration of smooth functions. Adv. Comput. Math. 2019, 45, 3095–3122. [Google Scholar] [CrossRef] [Green Version]
- Dammalapati, S.; Aghalayam, P.; Kaisare, N. Modeling the Effect of Nonuniformities from Urea Injection on SCR Performance Using CFD. Ind. Eng. Chem. Res. 2019, 58, 20247–20258. [Google Scholar] [CrossRef]
- Cho, J.M.; Choi, J.W.; Hong, S.H.; Kim, K.C.; Na, J.H.; Lee, J.Y. Application of computational fluid dynamics analysis for improving performance of commercial scale selective catalytic reduction. Korean J. Chem. Eng. 2006, 23, 43–56. [Google Scholar] [CrossRef]
- HJ 75-2017; Technical Specification for Continuous Monitoring of Flue gas (SO2, NOx and Particulate Matter) Emission from Fixed Pollution Sources. Ministry of Environmental Protection, Chinese Academy of Environmental Sciences: Beijing, China, 2017.
- Rogers, K.; Nolan, P.S. SCR Reactor Performance Profiling and Results Analysis; The U.S. EPA/DOE/EPRI Combined Power Plant Air Pollutant Control Symposium: Chicago, IL, USA, 2001; pp. 20–23.
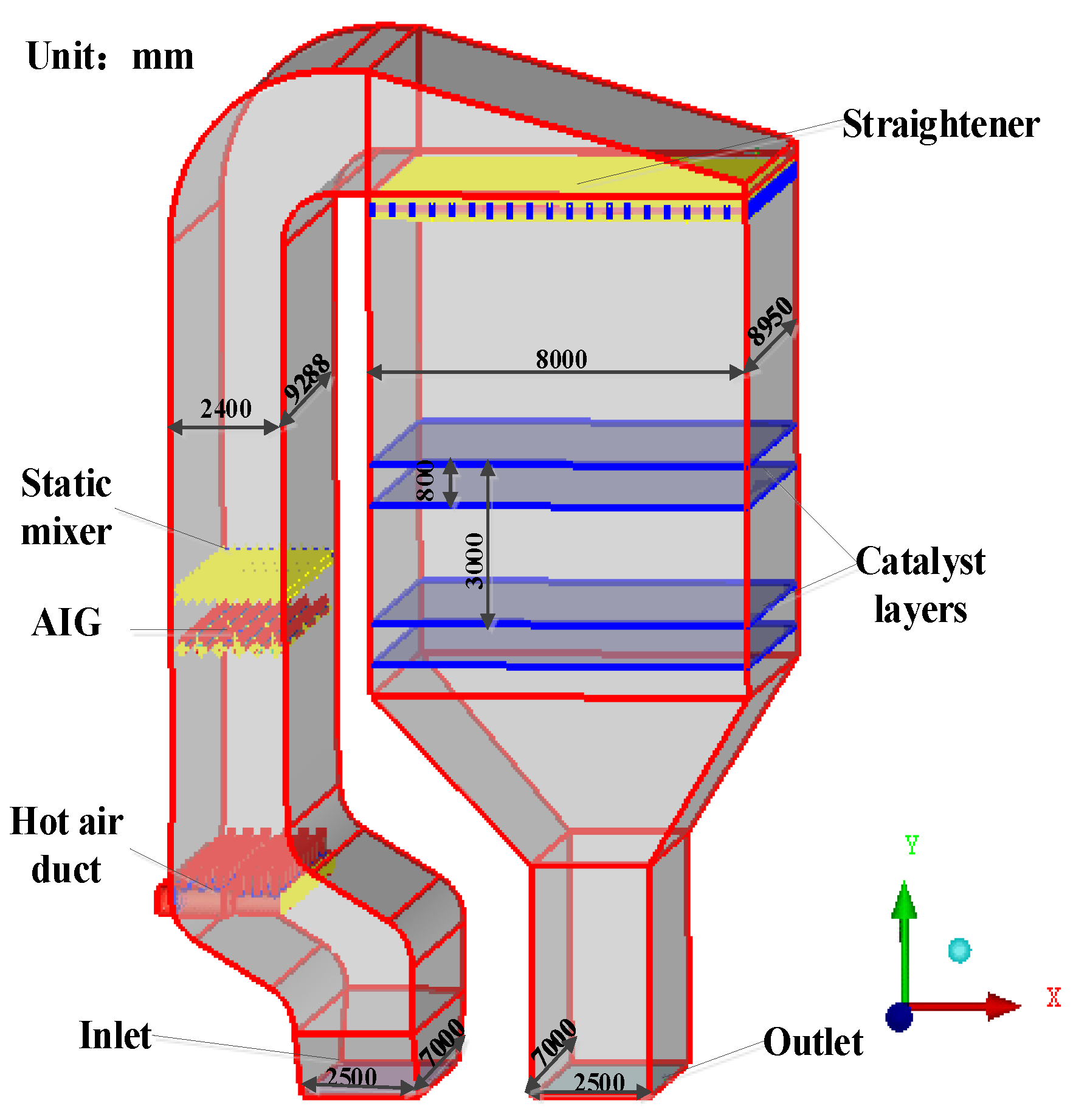













| SCR Reactor | Size |
|---|---|
| Inlet section size/(mm × mm) | 2500 × 7000 |
| Section size of flue collector/(mm × mm) | 2400 × 9288 |
| Section size of reactor bulk/(mm × mm) | 8000 × 8950 |
| Outlet section size/(mm × mm) | 2500 × 7000 |
| Thickness of catalyst layer/(mm) | 800 |
| Porosity of catalyst | 0.718 |
| Reactor height/(mm) | 20,000 |
| Case | Mean of Catalyst Inlet Temperature (K) | Relative Standard Deviation of Temperature | Catalyst Inlet Velocity (m/s) |
|---|---|---|---|
| Case T1~T5 | 543 | 0.005, 0.010, 0.015, 0.020, 0.025 | 3.2 |
| Case T6~T10 | 553 | 0.005, 0.010, 0.015, 0.020, 0.025 | 3.2 |
| Case T11~T15 | 563 | 0.005, 0.010, 0.015, 0.020, 0.025 | 3.2 |
| Case | Mean of Catalyst Inlet Temperature (K) | Relative Standard Deviation of Temperature | Catalyst Inlet Velocity (m/s) |
|---|---|---|---|
| Case 1~5 | 553 | 0.005, 0.010, 0.015, 0.020, 0.025 | 1.35 |
| Case 6~10 | 553 | 0.005, 0.010, 0.015, 0.020, 0.025 | 2.1 |
| Case 11~15 (T6~T10) | 553 | 0.005, 0.010, 0.015, 0.020, 0.025 | 3.2 |
| Case 16~20 | 553 | 0.005, 0.010, 0.015, 0.020, 0.025 | 4.3 |
| Case 21~25 | 553 | 0.005, 0.010, 0.015, 0.020, 0.025 | 5.05 |
| Case | Mean Catalyst Inlet Velocity | Relative Standard Deviation of Velocity | Catalyst Inlet Temperature |
|---|---|---|---|
| Case v1~v6 | 1.35 | 0.05, 0.10, 0.15, 0.20, 0.25, 0.30 | 553 |
| Case v7~v12 | 2.1 | 0.05, 0.10, 0.15, 0.20, 0.25, 0.30 | 553 |
| Case v13~v18 | 3.2 | 0.05, 0.10, 0.15, 0.20, 0.25, 0.30 | 553 |
| Case v19~v24 | 4.3 | 0.05, 0.10, 0.15, 0.20, 0.25, 0.30 | 553 |
| Case v25~v30 | 5.05 | 0.05, 0.10, 0.15, 0.20, 0.25, 0.30 | 553 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, W.; Ye, M.; Gao, Y.; Sun, Y.; Qian, F.; Lu, J.; Wu, S.; Huang, N.; Xu, B. Effect of Catalyst Inlet Flow Field Distribution Characteristics on Outlet NO Concentration Distribution in SCR Denitration Reactor Based on Monte Carlo Method. Atmosphere 2022, 13, 931. https://doi.org/10.3390/atmos13060931
Sun W, Ye M, Gao Y, Sun Y, Qian F, Lu J, Wu S, Huang N, Xu B. Effect of Catalyst Inlet Flow Field Distribution Characteristics on Outlet NO Concentration Distribution in SCR Denitration Reactor Based on Monte Carlo Method. Atmosphere. 2022; 13(6):931. https://doi.org/10.3390/atmos13060931
Chicago/Turabian StyleSun, Wanying, Mengmeng Ye, Yihua Gao, Yi Sun, Fuping Qian, Jinli Lu, Shenghua Wu, Naijing Huang, and Bing Xu. 2022. "Effect of Catalyst Inlet Flow Field Distribution Characteristics on Outlet NO Concentration Distribution in SCR Denitration Reactor Based on Monte Carlo Method" Atmosphere 13, no. 6: 931. https://doi.org/10.3390/atmos13060931
APA StyleSun, W., Ye, M., Gao, Y., Sun, Y., Qian, F., Lu, J., Wu, S., Huang, N., & Xu, B. (2022). Effect of Catalyst Inlet Flow Field Distribution Characteristics on Outlet NO Concentration Distribution in SCR Denitration Reactor Based on Monte Carlo Method. Atmosphere, 13(6), 931. https://doi.org/10.3390/atmos13060931





