Meaningful Trend in Climate Time Series: A Discussion Based On Linear and Smoothing Techniques for Drought Analysis in Taiwan
Abstract
:1. Introduction
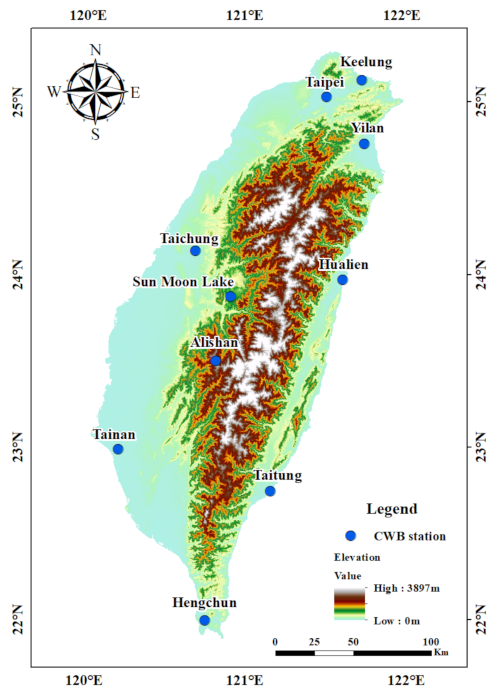
2. Study Region and Data
3. Methodology
3.1. Standardized Precipitation Index (SPI)
3.2. Smoothing Technique: Regularized Minimal-Energy Tensor-Product Spline (RMTS)
3.3. Trend Detection Based On Linear and Smoothing Techniques
3.3.1. Linear Regression
3.3.2. Locally Weighted Least Squares Regression
3.3.3. Test for Trend Using First Derivatives
4. Results and Discussion
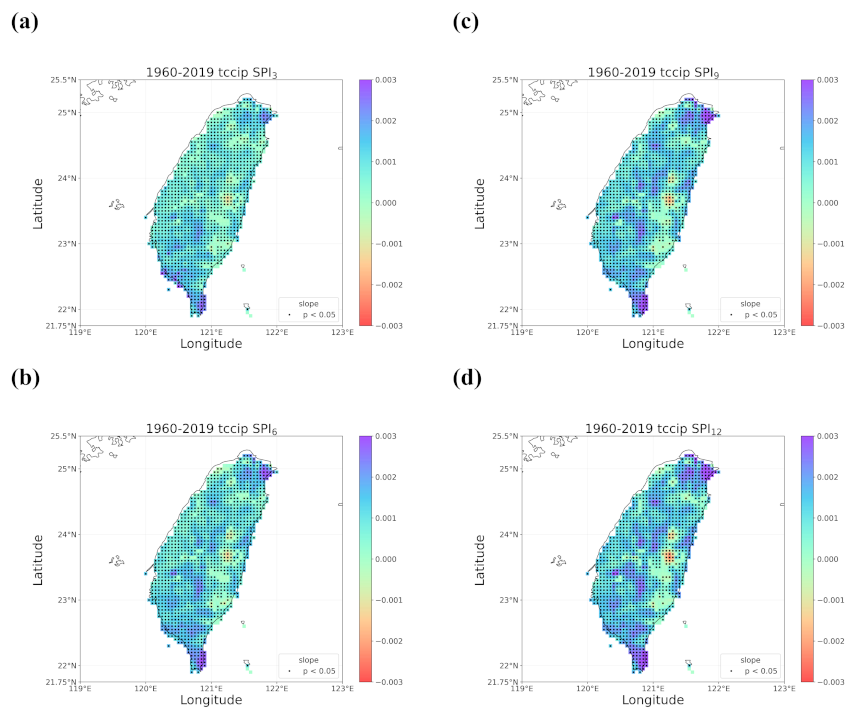
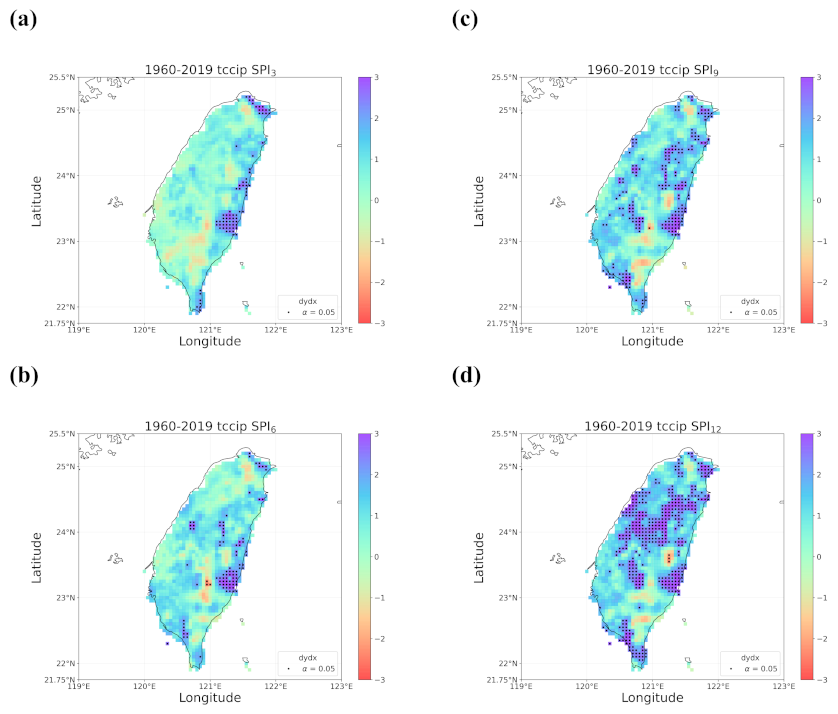
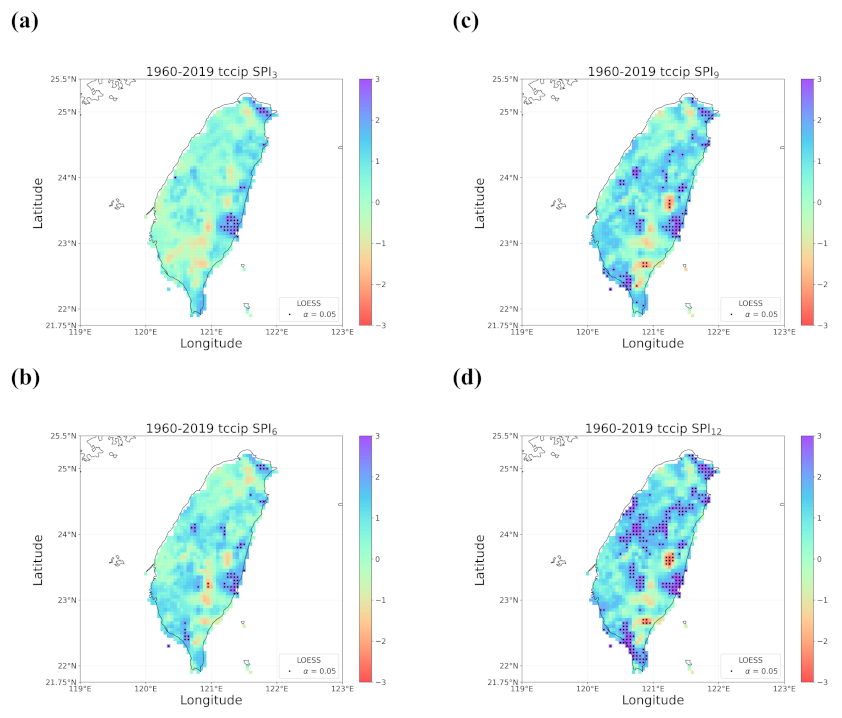
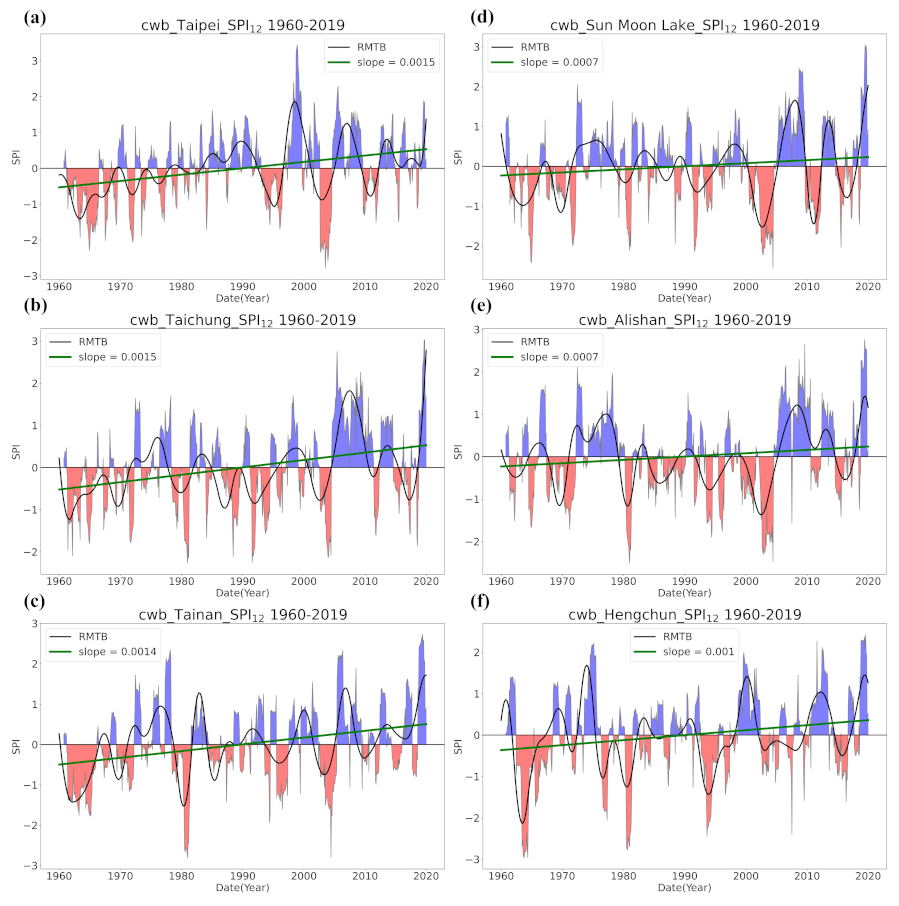
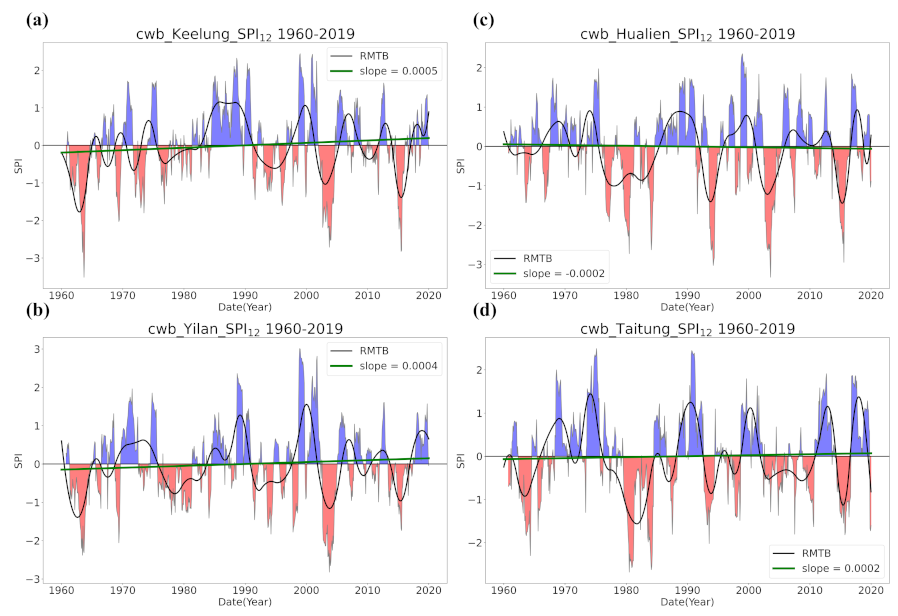
4.1. Overall Trend in Taiwan’s Drought from 1960 to 2019
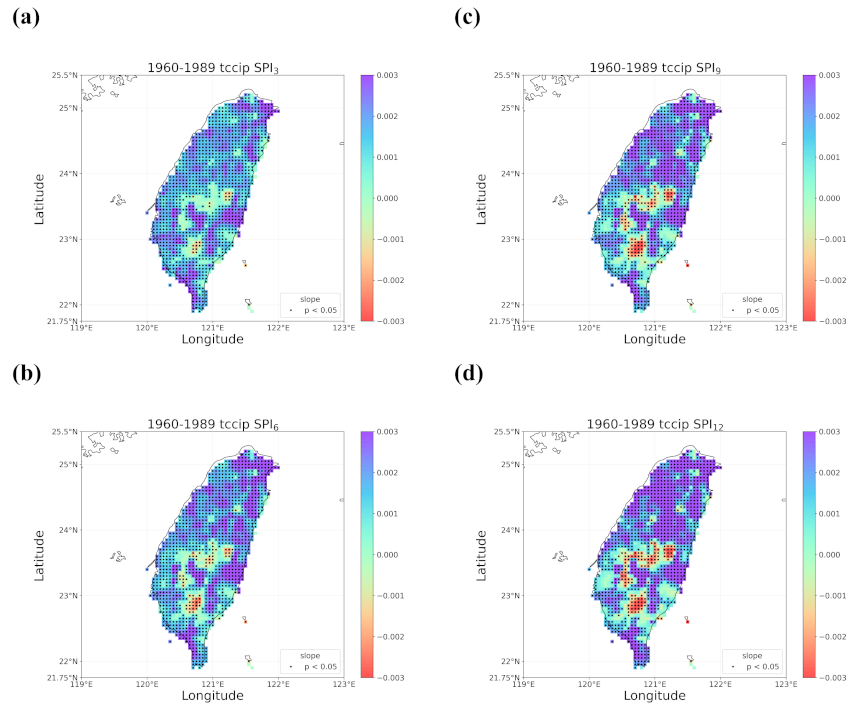
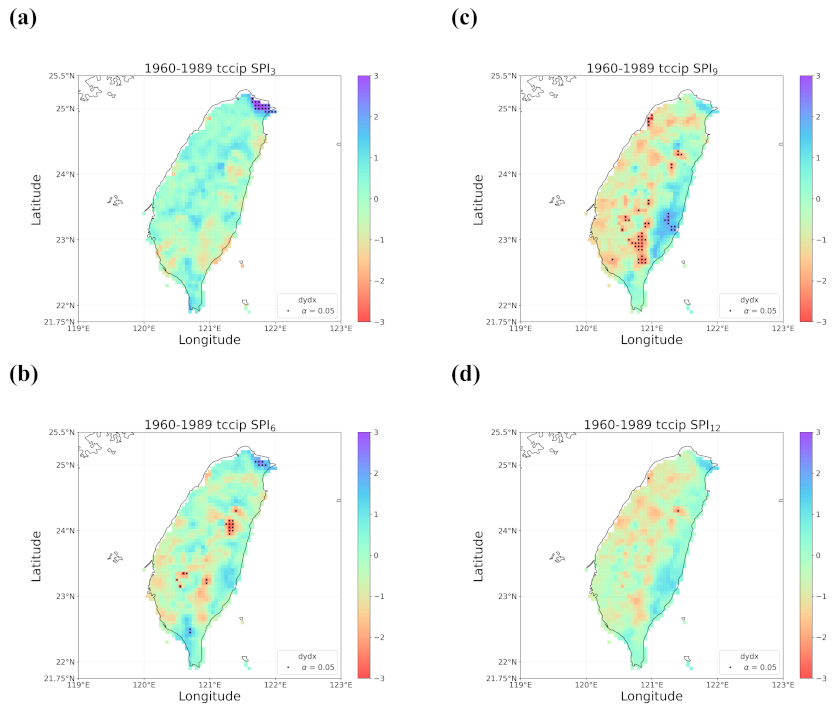
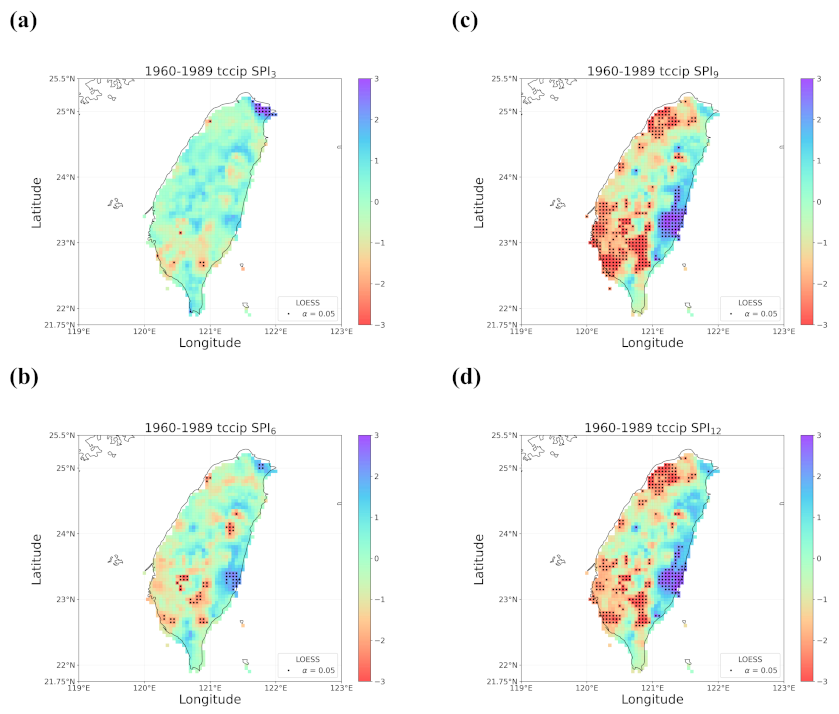
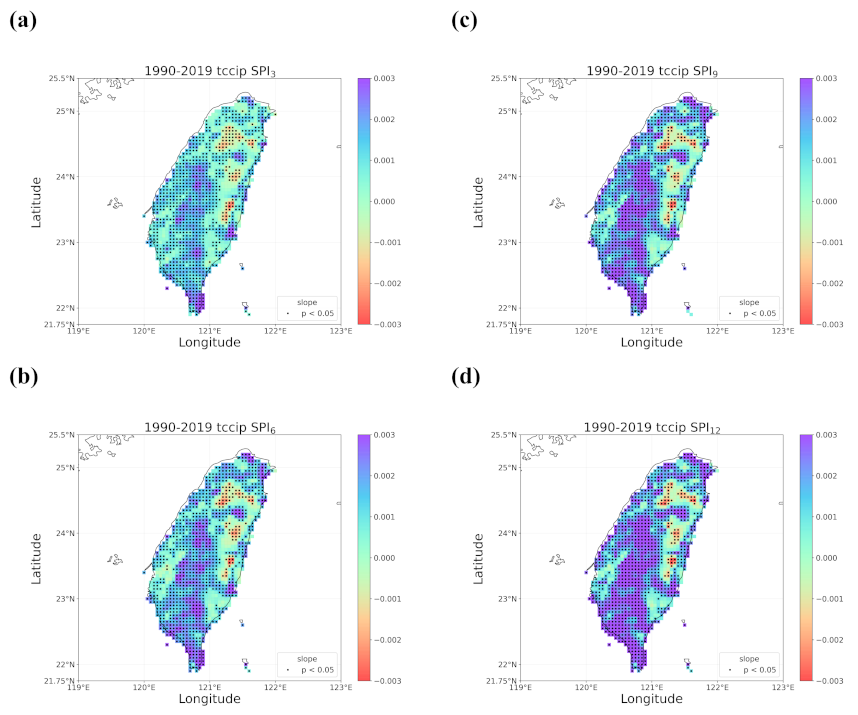
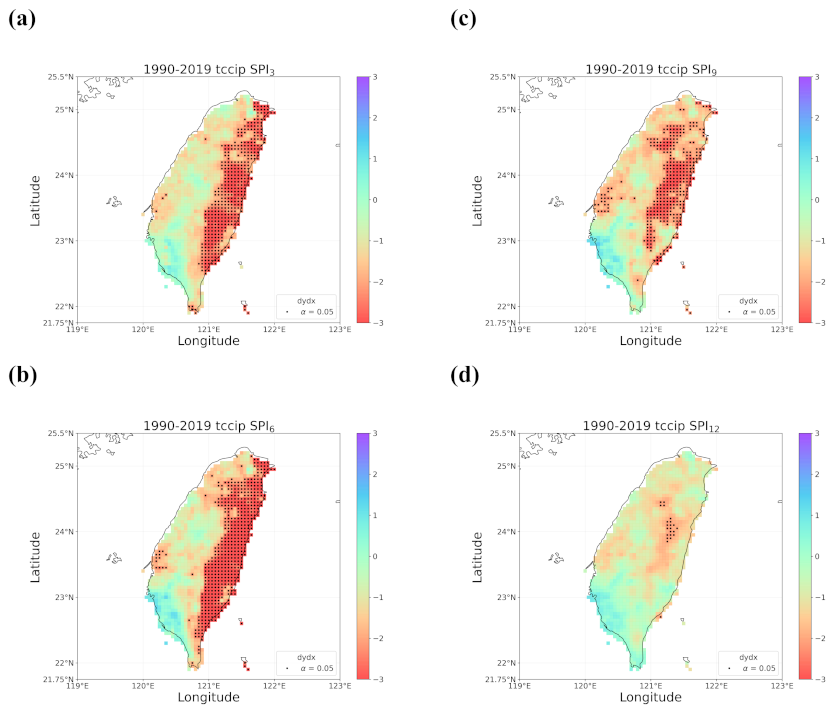
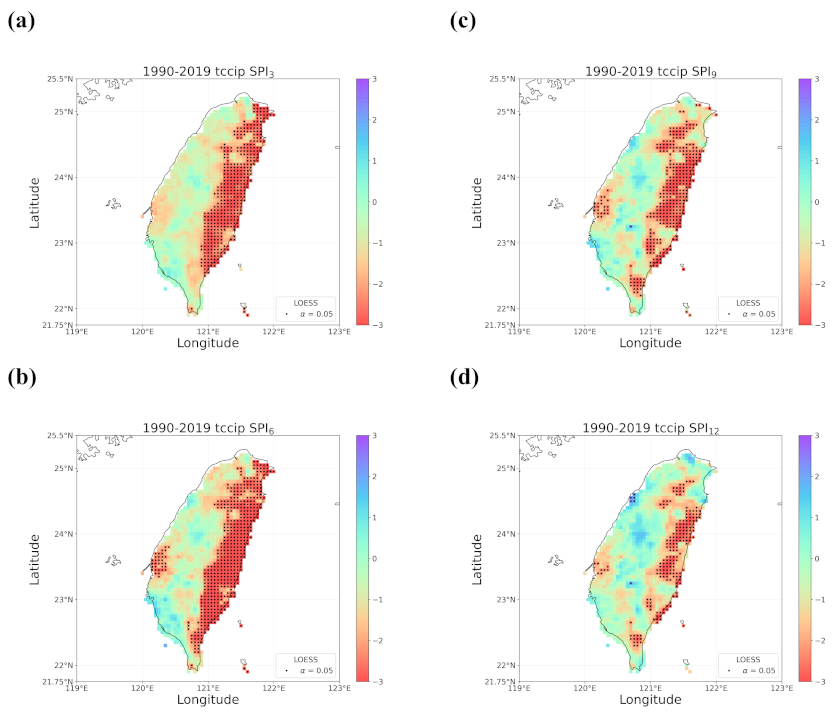
4.2. Trends in the Earlier and Later 30 Years
4.3. Discussion of Meaningful Trends
5. Conclusions and Recommendations
- Trend detection using LR showed great differences from that using the smoothing techniques, and LR seemed to be less robust as it falsely identified too many grids with significant trends and non-Gaussian residuals. LR trend lines were not found meaningful in many occasions of our case examining the SPI series in Taiwan since the data did not present much linearity.
- When all the methods reached a consensus in the patterns of detected trends with significance, intuitively we could have more confidence in such detected trends. By calculating pattern correlations as the quantification metric of pattern similarity between detected trends, we found that the recent drying trend at the shorter time scales over eastern Taiwan in 1990–2019 should be the most trustworthy.
- Regardless of the methods, detected trends in the entire period (1960–2019), the earlier 30 years (1960–1989), or the later 30 years (1990–2019) were all different. While the general wetting trend was identified over a great portion of Taiwan’s territory in the past 60 years, some migrations of drying or wetting trends actually took place in different time intervals.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Seager, R.; Naik, N.; Vogel, L. Does global warming cause intensified interannual hydroclimate variability? J. Clim. 2012, 25, 3355–3372. [Google Scholar] [CrossRef] [Green Version]
- Madsen, H.; Lawrence, D.; Lang, M.; Martinkova, M.; Kjeldsen, T.R. Review of trend analysis and climate change projections of extreme precipitation and floods in Europe. J. Hydrol. 2014, 519, 3634–3650. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.J.; Chen, C.C.; Lo, M.H.; Juang, J.Y.; Chang, C.M. Central Taiwan’s hydroclimate in response to land use/cover change. Environ. Res. Lett. 2020, 15, 034015. [Google Scholar] [CrossRef]
- Bhuyan, M.D.I.; Islam, M.M.; Bhuiyan, M.E.K. A trend analysis of temperature and rainfall to predict climate change for northwestern region of Bangladesh. Am. J. Clim. Chang. 2018, 7, 115–134. [Google Scholar] [CrossRef] [Green Version]
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Theil, H. A rank-invariant method of linear and polynomial regression analysis. Indag. Math. 1950, 12, 173. [Google Scholar]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Pettitt, A.N. A non-parametric approach to the change-point problem. J. R. Stat. Soc. Ser. C Appl. Stat. 1979, 28, 126–135. [Google Scholar] [CrossRef]
- Jiang, S.; Wang, M.; Ren, L.; Xu, C.Y.; Yuan, F.; Liu, Y.; Shen, H. A framework for quantifying the impacts of climate change and human activities on hydrological drought in a semiarid basin of Northern China. Hydrol. Process. 2019, 33, 1075–1088. [Google Scholar] [CrossRef]
- Animashaun, I.M.; Oguntunde, P.G.; Akinwumiju, A.S.; Olubanjo, O.O. Rainfall analysis over the Niger central hydrological area, Nigeria: Variability, trend, and change point detection. Sci. Afr. 2020, 8, e00419. [Google Scholar] [CrossRef]
- Harka, A.E.; Jilo, N.B.; Behulu, F. Spatial-temporal rainfall trend and variability assessment in the Upper Wabe Shebelle River Basin, Ethiopia: Application of innovative trend analysis method. J. Hydrol. Reg. Stud. 2021, 37, 100915. [Google Scholar] [CrossRef]
- Chen, S.T.; Kuo, C.C.; Yu, P.S. Historical trends and variability of meteorological droughts in Taiwan/Tendances historiques et variabilité des sécheresses météorologiques à Taiwan. Hydeol. Sci. J. 2009, 54, 430–441. [Google Scholar] [CrossRef]
- Shih, D.S.; Chen, C.J.; Li, M.H.; Jang, C.S.; Chang, C.M.; Liao, Y.Y. Statistical and numerical assessments of groundwater resource subject to excessive pumping: Case study in Southwest Taiwan. Water 2019, 11, 360. [Google Scholar] [CrossRef] [Green Version]
- Yeh, H.F. Using integrated meteorological and hydrological indices to assess drought characteristics in southern Taiwan. Hydrol. Res. 2019, 50, 901–914. [Google Scholar] [CrossRef]
- Lee, Y.C.; Wang, C.C.; Weng, S.P.; Chen, C.T. Future Projections of Meteorological Drought Characteristics in Taiwan. Atmos. Sci. 2019, 47, 66–91. [Google Scholar]
- Henny, L.; Thorncroft, C.D.; Hsu, H.H.; Bosart, L.F. Extreme Rainfall in Taiwan: Seasonal Statistics and Trends. J. Clim. 2021, 34, 4711–4731. [Google Scholar] [CrossRef]
- Mudelsee, M. Trend analysis of climate time series: A review of methods. Earth Sci. Rev. 2019, 190, 310–322. [Google Scholar] [CrossRef]
- Gray, K.L. Comparison of Trend Detection Methods; University of Montana: Missoula, MT, USA, 2007. [Google Scholar]
- Chen, C.J.; Lee, T.Y. Variations in the correlation between teleconnections and Taiwan’s streamflow. Hydrol. Earth Syst. Sci. 2017, 21, 3463–3481. [Google Scholar] [CrossRef] [Green Version]
- Li, P.L.; Lin, L.F.; Chen, C.J. Hydrometeorological Assessment of Satellite and Model Precipitation Products over Taiwan. J. Hydrometeorol. Meteorol. 2021, 22, 2897–2915. [Google Scholar] [CrossRef]
- Hwang, J.T.; Martins, J.R.R.A. A fast-prediction surrogate model for large datasets. Aerosp. Sci. Technol. 2018, 75, 74–87. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; Volume 17, pp. 179–183. [Google Scholar]
- Guenang, G.M.; Kamga, F.M. Computation of the Standardized Precipitation Index (SPI) and its use to assess drought occurrences in Cameroon over recent decades. J. Appl. Meteorol. Climatol. 2014, 53, 2310–2324. [Google Scholar] [CrossRef]
- Bouhlel, M.A.; Hwang, J.T.; Bartoli, N.; Lafage, R.; Morlier, J.; Martins, J.R.R.A. A Python surrogate modeling framework with derivatives. Adv. Eng. Softw. 2019, 135, 102662. [Google Scholar] [CrossRef] [Green Version]
- Cleveland, W.S. Robust locally weighted regression and smoothing scatterplots. J. Am. Stat. Assoc. 1979, 74, 829–836. [Google Scholar] [CrossRef]
- James, F.C.; McCulloch, C.E.; Wiedenfeld, D.A. New approaches to the analysis of population trends in land birds. Ecology 1996, 77, 13–27. [Google Scholar] [CrossRef] [Green Version]
- Bryhn, A.C.; Dimberg, P.H. An operational definition of a statistically meaningful trend. PLoS ONE 2011, 6, e19241. [Google Scholar] [CrossRef] [Green Version]
- Shapiro, S.S.; Wilk, M.B. An analysis of variance test for normality (complete samples). Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- Muhlbauer, A.; Spichtinger, P.; Lohmann, U. Application and comparison of robust linear regression methods for trend estimation. J. Appl. Meteorol. Climatol. 2009, 48, 1961–1970. [Google Scholar] [CrossRef]
- DelSole, T.; Yang, X. Field significance of regression patterns. J. Clim. 2011, 24, 5094–5107. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis. Proc. R. Soc. Lond. A 1971, 454, 903–995. [Google Scholar] [CrossRef]
| Time Period | SPI3 | SPI6 | SPI9 | SPI12 |
|---|---|---|---|---|
| 1960–2019 | (0.03, 0.02, 0.67) | (0.04, 0.05, 0.74) | (0.09, 0.10, 0.66) | (0.19, 0.22, 0.68) |
| 1960–1989 | (0.04, 0.06, 0.79) | (0.03, 0.22, 0.44) | (0.26, 0.23, 0.37) | (0.01, 0.19, 0.08) |
| 1990–2019 | (0.32, 0.36, 0.91) | (0.40, 0.38, 0.86) | (0.49, 0.52, 0.71) | (0.28, 0.40, 0.13) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, S.-H.; Mahmud, K.; Chen, C.-J. Meaningful Trend in Climate Time Series: A Discussion Based On Linear and Smoothing Techniques for Drought Analysis in Taiwan. Atmosphere 2022, 13, 444. https://doi.org/10.3390/atmos13030444
Huang S-H, Mahmud K, Chen C-J. Meaningful Trend in Climate Time Series: A Discussion Based On Linear and Smoothing Techniques for Drought Analysis in Taiwan. Atmosphere. 2022; 13(3):444. https://doi.org/10.3390/atmos13030444
Chicago/Turabian StyleHuang, Shih-Han, Khalid Mahmud, and Chia-Jeng Chen. 2022. "Meaningful Trend in Climate Time Series: A Discussion Based On Linear and Smoothing Techniques for Drought Analysis in Taiwan" Atmosphere 13, no. 3: 444. https://doi.org/10.3390/atmos13030444
APA StyleHuang, S.-H., Mahmud, K., & Chen, C.-J. (2022). Meaningful Trend in Climate Time Series: A Discussion Based On Linear and Smoothing Techniques for Drought Analysis in Taiwan. Atmosphere, 13(3), 444. https://doi.org/10.3390/atmos13030444







