Abstract
We studied the correlations between the migrating and non-migrating tides and solar cycle in the mesosphere and lower thermosphere (MLT) regions between 60S and 60N, which are in LAT-LON Earth coordinates, by analyzing the simulation datasets from the thermosphere and ionosphere extension of the Whole Atmosphere Community Climate Model (WACCM-X). A least squares fitting method was utilized to obtain the daily mean migrating tides and non-migrating tides. The Pearson linear correlation coefficient was used to analyze the correlations between tides and solar activity. Our analysis shows that the negative correlations between tides and solar activity are mostly impacted by the first symmetrical structure of the tidal modes for both migrating and non-migrating components. The coefficient of molecular thermal conductivity for the first symmetrical structure is small at low solar flux, so the tides dissipate more slowly when the F10.7 cm radio flux level is low. Thus, the amplitudes of tidal variations under a solar minimum condition are larger than those under a solar maximum condition. The correlation between tides and solar activity could also be influenced by some other factors, such as geomagnetic activity and the density of carbon dioxide on Earth. The tidal variations can be influenced by westward background wind, which grows stronger as geomagnetic activity rises. Further, dissipation of the tides decreases because the heat conduction and molecular viscosity are weakened in the cooling thermosphere caused by increasing , which results in larger tidal amplitudes under the solar maximum condition. It is found that the correlations between tides and solar cycle vary at different altitudes and latitudes. The negative correlations are most possibly influenced by the first symmetrical structure of tidal variations and may also be impacted by geomagnetic activity. The positive correlations are impacted by the density of .
1. Introduction
Atmospheric solar tides are global-scale horizontal oscillations with periods that are related to a solar day. The periods of solar tides are usually 24 h, 12 h, 8 h, and 6 h, and the solar tides with these periods are called diurnal, semidiurnal, terdiurnal, and quarterdiurnal tides [1]. The solar tides can also be classified into migrating tides and non-migrating tides. The migrating tides are sun-synchronous and propagate westward with the subsolar point. The non-migrating tides are out of the subsolar point, which means the tides can propagate westward, eastward, or stay stationary [2]. Zonal wavenumber means the number of complete waveforms in the same latitude circle, and the zonal wavenumbers of migrating tides should be equal to the frequency () counterparts [3]. For instance, the zonal wavenumber of migrating diurnal tides should be , where the value of the zonal wavenumber is equal to the frequency of the diurnal tides and the sign of the zonal wavenumber represents the tides propagating westward (positive eastward). Thus, the migrating diurnal, semidiurnal, terdiurnal, and quarterdiurnal tides are DW1, SW2, TW3, and QW4, respectively, and the non-migrating diurnal tides are DE1, DE2, DW2, DE3, DW3, DE4, DW4, and so on. “D” represents diurnal tides, “E” represents eastward, and “W” represents westward. The number represents the zonal wavenumber. The non-migrating semidiurnal, terdiurnal, and quarterdiurnal tides can be classified in the same manner. To distinguish the longitude information of the migrating and non-migrating tides, the meteor radar stations are not enough. Thus, the complete longitude information was not obtained until Challenging Minisatellite Payload (CHAMP) satellite and Sounding of the Atmosphere using Broadband Emission Radiometry (SABER) on the Thermosphere–Ionosphere–Mesosphere Energetics and Dynamics (TIMED) satellite were launched [4,5]. The amplitudes of the diurnal tides and semidiurnal tides are usually large, and the amplitudes of the terdiurnal tides and quarterdiurnal tides are comparatively small [3]. The amplitudes of the diurnal tides are stronger at low latitudes, whereas the counterparts of the semidiurnal tides are stronger at middle and high latitudes [1,6]. DW1 dominates in equinoxes and summer in the low-latitude regions and SW2 peaks during March to October at southern middle latitudes [7]. Research regarding terdiurnal tides and quarterdiurnal tides is rare because of the small amplitudes of these waves. TW3 shows the maximum in April and December in the middle latitudes of the northern hemisphere [8]. The amplitudes of non-migrating tides are usually weaker than those of migrating tides; however, the non-migrating tides still play an important role in atmosphere dynamical processes [9,10,11]. For example, non-migrating diurnal tide DE3 is responsible for the zonal wavenumber-4 structure in the mesosphere and lower thermosphere (MLT) and is crucial in global tidal wind-driven dynamo [12]. DE3 peaks in June through November, which is consistent with DE2 [13]. Sometimes, the non-migrating diurnal tides can be comparable in strength with migrating tides.
Migrating tides are excited by solar radiation absorption by water vapor and water molecules in the troposphere, solar ultraviolet radiation by in the stratosphere, and oxygen and nitrogen molecules in the thermosphere [14]. Meanwhile, non-migrating tides are not only excited by solar radiation but also excited by latent heat release generated by convection in the tropical regions and nonlinear interaction with planetary waves [3,7,13]. Thus, generation of tides is linked closely with solar radiation, and it is well-founded to expect that atmospheric tides are related to solar activities, which are influenced by solar radiation.
The F10.7 cm index is one of the most widely used indices of solar activity [15]. A 10.7 cm solar flux measurement is a criterion of the strength of solar radio emission in a 100 MHz wide band centered on 2800 MHz, which refers to a wavelength of 10.7 cm [16]. It can be applied as a simple solar activity level indicator or as a proxy for other solar emissions or quantities that are more difficult to obtain, such as extreme ultraviolet (EUV) irradiance [16]. Thus, we use the F10.7 cm index as the index of solar activity in this paper. In previous studies, the relationship between 11-year solar cycle activities and atmospheric tides has been explored. Sprenger, et al. [17] found a relationship between tides and solar cycle at the middle-latitude region. The semidiurnal tides showed a negative correlation with solar cycle during winter below 100 km. Later, many researchers also reported correlations between atmospheric tides and solar cycle. Namboothiri, et al. [18] found that semidiurnal tides showed negative correlations between 79 km and 97 km using the observation obtained from MF radar at Saskatoon, Canada (52N, 107W) from 1969 to 1990, which was consistent with the study reported by Sprenger, Schminder and Physics [17]. Bremer, et al. [19] observed a weak negative correlation between semidiurnal tides and solar cycle, although the level of significance did not reach 95%. The strong linear response between mean winds and semidiurnal tides and solar activities between 80 km and 100 km at several northern hemisphere locations was investigated by Wilhelm, et al. [20]. Further, diurnal tides show a weak response to solar cycle in this research. The relationship between thermospheric tides and solar activities above 200 km was reported by Gong, et al. [21]. The amplitudes of the diurnal tidal waves and semidiurnal tidal waves have been found to be positive and negative, respectively, correlated with the increasing solar cycle at Puerto Rico (18.3N, 66.7W) between 1984 and 2015 [21]. Andrioli, et al. [22] observed enhanced diurnal and semidiurnal tidal amplitudes during solar minimum activity at Cachoeira Paulista (22.7S; 45W) between 80 km and 100 km from 1999 to 2019. However, some studies reported that there is no significant correlation between zonal wind tides and solar activities [23,24,25]. Long-term research regarding migrating and non-migrating tidal waves is rare for limited observations. The study reported by Chang, et al. [26] exhibited a negative correlation between DW1 and TW3 and solar cycle, whereas the amplitudes of SW2 show a weak positive correlation with the influence of solar activity at 97 km between 2007 and 2011. Most of the previous studies showed correlations between zonal wind tides and solar cycle at single stations, and the interest of our study is the global distribution of correlations between zonal wind tides and solar cycle and the possible reasons.
In our present study, the correlations between migrating tides DW1, SW2, TW3, and the typical non-migrating tides DE2, DE3, SE2, and SE3 and solar activities are explored by analyzing the global zonal wind simulation data from the specified dynamics thermosphere and ionosphere extension of the Whole Atmosphere Community Climate Model (SD-WACCM-X), which will be discussed in detail in the next section. We study the influence of the solar cycle on the mesosphere and lower thermosphere region tides and further discuss modulation of solar activity on tides by calculating the correlations between the migrating tides, the non-migrating tides, and geomagnetic activity (index kp) and carbon dioxide .
2. Dataset and Analysis
2.1. SD-WACCM-X
The thermosphere and ionosphere extension of the Whole Atmosphere Community Climate Model (WACCM-X) is configured based on the National Center for Atmospheric Research (NCAR) Whole Atmosphere Community Climate Model (WACCM). The WACCM-X is a whole atmosphere and ionosphere model with the coupling of ocean, atmosphere, sea, and land surface. The top boundary of WACCM-X is extended to ~500–700 km altitude. A detailed description of the first version of the WACCM-X is provided by Liu, et al. [27]. In our study, we used the current version of the WACCM-X, which is described in Liu, et al. [28].
The specified dynamics WACCM-X (SD-WACCM-X) used in our study can simulate specific events by constraining the model meteorology with Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2) data. This model is configured with a horizontal resolution of 1.9° latitude and 2.5° longitude, a temporal resolution of 1 h, and 145 vertical pressure levels. The output simulations from 2003 to 2019 are chosen to study the correlation between the migrating tides, the non-migrating tides, and F10.7 cm index, kp index, and the density of . The comparison between WACCM-X and SABER has already been performed by some researchers [8,29,30]. Further, the results from WACCM-X and TIDI are also compared and discussed in more detail in the next section. Generally, the SD-WACCM-X presents consistent tidal behaviors with observation. The F10.7 cm index and kp index are obtained from OMNI data, and data are obtained from SD-WACCM-X.
2.2. Methodology
The global zonal wind simulation data are obtained from SD-WACCM-X. The hourly dataset is binned by longitudes and latitudes. The least squares fitting method [31] is utilized to obtain the daily mean migrating tides and non-migrating tides. The fitting equation is expressed as
where A and B are amplitudes of tides; represents the frequency of tides; s is the zonal wavenumber of the fitted tides; and are the UT time and longitudes of the samplings, respectively. C represents the background zonal wind. Then, the daily mean migrating tides and non-migrating tides are smoothed with a span of 365 days to remove the seasonal variations.
The correlation coefficient is Pearson linear correlation coefficient [32], which represents as
where X and Y represent the array to be calculated correlation; a and b represent the index of the array; n means the length of the array. The result shows the degree of correlation, which ranges from 1 to 1. The sign represents the negative (positive) correlation. To calculate the correlation between tides and solar cycle, X represents the migrating or non-migrating tides and Y represents F10.7 cm index.
Spatial structure is the structure in a certain range of altitude and latitude. The migrating and non-migrating tides data are three-dimensional data, which are altitude, latitude, and time. The data are averaged by time to display the spatial structure.
3. Results
3.1. Migrating Tides
Figure 1 shows the migrating tides at the equator from 2003 to 2019 and F10.7 cm index. Figure 1a illustrates migrating diurnal tide DW1 at the equator from 2003 to 2019. The white solid line represents the 10.7 cm solar radio flux (F10.7), which is a measurement of the intensity of solar radio emissions with a wavelength of 10.7 cm (a frequency of 2800 MHz). F10.7 is a general indicator of solar magnetic activity, solar ultraviolet and X-ray emissions, and even solar irradiance. F10.7 is used for a wide range of applications, including astronomy, climate modeling, geophysics, meteorology, communications, satellite systems, and so on [33]. Thus, the 10.7 cm solar radio flux is a useful index of solar activity as a proxy for solar extreme ultraviolet radiation. As reported by Hathaway [34], the solar minimum between solar cycle 23 and 24 is approximately from 2007 to 2009. Figure 1a shows a positive correlation between DW1 and F10.7 cm index above 160 km at the equator, whereas the correlation becomes weak at 30N, as shown in Figure 1b. Figure 1c,d exhibits the negative relationship between SW2 and solar activity above 120 km. Meanwhile, Figure 1e,f shows the positive correlation and negative correlation between TW3 and F10.7 cm index above 120 km at the equator and 30N, respectively. Thus, it is not hard to find that the migrating tidal variations are influenced strongly by solar cycle, and the relationships between different tidal waves and solar cycle vary at different latitudes.

Figure 1.
Migrating tidal variations from 2003 to 2019 for (a,b) DW1, (c,d) SW2, and (e,f) TW3 at (a,c,e) equator and (b,d,f) 30N. The white solid line presents the daily mean F10.7 cm index from 2003 to 2019.
To further analyze the relationships between tides and solar activities, we calculate the correlations using the Pearson linear correlation method. Figure 2 exhibits the correlation coefficients between DW1, SW2, TW3, and solar cycle and the spatial structure of tidal waves. The correlation between amplitude of tides and F10.7 cm index at the equator and 30° N, which are displayed in Figure 1, are also included in Figure 2, and the correlations between DW1 and F10.7 cm index at the equator and 30° N are almost the same. The correlations are positive above 130 km and are negative below 130 km. The correlations between SW2 and F10.7 cm index at the equator and 30° N are also almost the same. The correlations are positive below 130 km and are negative above 130 km. Further, the correlations between TW3 and F10.7 cm index at the equator and 30° N are different. The correlations at the equator are positive above 130 km, and the correlations at 30° N are negative above 120 km. The correlation coefficients of DW1 and F10.7 cm index are displayed in Figure 2a. The migrating tide DW1 below approximately 140 km at latitudes from 50S to 50N shows a negative correlation with solar cycle. Further, the DW1 above around 140 km at latitudes from 60S to 60N displays a positive correlation with solar cycle. The strong negative correlation between DW1 and F10.7 cm index exists at approximately 120 km from 40S to 10S and from 10N to 40N, and the maximum of the negative correlation is approximately 0.5, which appears at 20N and 20S at 120 km. Meanwhile a strong positive correlation between them appears above 140 km from 30S to 30N. The positive correlation peaks above around 160 km from 20S to 20N, and the maximum of the positive correlation is 0.8. The correlation coefficients are symmetrical in both hemispheres. The reason why the correlations between tidal waves and solar activities vary from different heights and latitudes is the key point of this paper and will be discussed later. Figure 2b displays the spatial structure of DW1, which is dominant at approximately 100 km at about 30N and 30S. The spatial structure of DW1 is also symmetrical in both hemispheres. Wu, Ortland, Killeen, Roble, Hagan, Liu, Solomon, Xu, Skinner, and Niciejewski [29] displayed the migrating diurnal tides obtained by TIDI from 2002 to 2007, which can be compared with our results in this paper. The maximum of the spatial structure from TIDI is between 20° N and 50° N and between 20° S and 50° S [29], which is consistent with the spatial structure of WACCM-X DW1 in zonal wind shown in Figure 2b. Figure 2c shows the correlation coefficients of SW2 and F10.7 cm index from 2003 to 2019. The migrating tide SW2 below approximately 130 km at latitudes from 60S to 60N shows a positive correlation with solar activity. Meanwhile, the SW2 above around 130 km at latitudes from 60S to 60N displays a negative correlation with solar cycle, which is opposite to the counterpart of DW1. The negative correlation coefficients are larger than the positive and they are not symmetrical in hemispheres. The maximum of the negative correlation coefficients is 0.7 and the maximum of the positive correlation coefficients is 0.5. Figure 2d exhibits the spatial structure of SW2, and the amplitudes of SW2 are large at approximately 120 km between 60S and 0 and between 30N and 60N. The spatial structure of SW2 is asymmetrical in hemispheres. Figure 2e shows the correlation coefficients of TW3 and F10.7 cm index from 2003 to 2019. The migrating tide TW3 below approximately 120 km between 60S and 15S and between 15N and 60N displays a negative correlation with solar cycle, whereas the TW3 between 15S and 15N displays a positive correlation with solar cycle at the same height. The maximum of the negative correlation coefficients is 0.6 and the maximum of the positive correlation coefficients is only 0.2, which is much smaller than other correlation coefficients. Figure 2f shows the spatial structure of TW3, which is much weaker than the strength of DW1 and SW2. The amplitudes of TW3 are stronger between 60S and 15S and between 15N and 60N above 120 km. Further, the amplitudes of TW3 in the southern hemisphere are a bit stronger than their counterparts in the northern hemisphere.

Figure 2.
The correlation between migrating tidal variations (a) DW1, (c) SW2, and (e) TW3 and F10.7 cm index between 60S and 60 N from 2003 to 2019. The spatial structure between 60 S and 60 N from 2003 to 2019 for (b) DW1, (d) SW2, and (f) TW3.
3.2. Non-Migrating Tides
Studies on the characteristic of non-migrating tides are rare, and non-migrating tides DE2, DE3, SE2, and SE3 are studied in this paper. Figure 3 displays the correlation coefficients between the non-migrating diurnal tides and F10.7 cm index and their spatial structures. Figure 3a shows the correlation between DE2 and F10.7 cm index, which varies with altitude and latitude. The positive relationship with them is shown at approximately 60S above 110 km and displays a rapid descent in height until 120 km between 0 and 30S. The positive correlation in the northern hemisphere is found between 0 and 50N from 80 km to 100 km. Further, the negative correlation is shown above 120 km from 0 to 50N in the northern hemisphere, and the coefficients in the southern hemisphere descend with altitude from 60S to the equator. The maximum of the negative correlation is 0.7, which appears from 20S to 10N above 170 km. At the same time, the maximum of the positive correlation coefficients is 0.5, which appears at approximately 50S at 120 km. The relationship between DE2 and solar cycle is completely different from DW1. The reason that caused these phenomena will be discussed in the next section. Figure 3b displays the correlation coefficients between DE3 and F10.7 cm index, which are almost negative above 110 km from 60S to 60N. The correlation coefficients below 100 km are rather weak and less regular. The maximum of the negative correlation coefficients is 0.7 and the maximum of the positive correlation coefficients is 0.5. The spatial structures of DE2 and DE3 shown in Figure 3c,d are both dominant from 100 km to 140 km between 30S and 30N. Wu, Ortland, Killeen, Roble, Hagan, Liu, Solomon, Xu, Skinner and Niciejewski [30] displayed non-migrating diurnal tides DE3 in zonal wind obtained from TIDI. The spatial structure of DE3 from TIDI is dominant between 30° S and 10° N at approximately 100 km. The spatial structure of DE3 from WACCM-X shown in Figure 3d is also dominant between 30° S and 20° N at approximately 100 km, which is nearly consistent with observations. It is obvious that the amplitude of DE3 is much stronger than that of DE2. The amplitude of DE2 in the northern hemisphere is stronger than that in the southern hemisphere, and the spatial structure of DE3 is nearly symmetric in both hemispheres. The amplitude of DE3 in the southern hemisphere is larger than in the northern near the equator.

Figure 3.
The correlation between non-migrating tidal variations (a) DE2 and (b) DE3 and F10.7 cm index between 60S and 60 N from 2003 to 2019. The spatial structure between 60 S and 60 N from 2003 to 2019 for (c) DE2 and (d) DE3.
Figure 4 displays the correlation between the non-migrating semidiurnal tides and F10.7 cm index. The correlation coefficients of SE2 and F10.7 cm index, which are a little weaker than the coefficients of diurnal tides, are shown in Figure 4a. Negative correlation coefficients are exhibited above approximately 130 km between 0 and 60N. At the same time, the negative correlation coefficients in the southern hemisphere are found above 120 km between 0 and 60S. The positive correlation coefficients are displayed below the regions of the negative correlation coefficients except the equator region. The maximum of the negative correlation coefficients is 0.4, which is comparatively smaller than the negative correlation coefficients of other tides. The maximum of the positive correlation coefficients is also 0.4. The correlations between SE2 and solar cycle are weaker than other tides. Figure 4b shows the negative relationship between SE3 and F10.7 cm index from 60 km to 180 km. The negative correlation coefficients are exhibited almost above approximately 120 km between 60S and 60N, whereas the positive correlation coefficients are below 120 km. The maximum of the negative correlation coefficients is 0.7 and the maximum of the positive correlation coefficients is 0.4. Figure 4c,d displays the spatial structures of SE2 and SE3, which are similar to each other. The structures of SE2 and SE3 are both dominant above 100 km between 50S and 15S and 15N and 50N. Figure 4c shows that the amplitudes of SE2 peak at approximately 40S and 40N, and Figure 4d shows the maximum of SE3 is at 40S and 30N. The amplitude of SE2 in the northern hemisphere is stronger than that in the southern hemisphere, which is opposite to SE3.
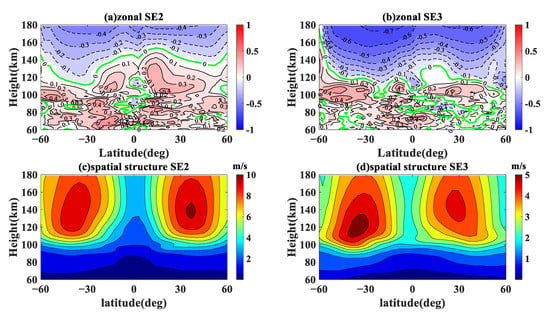
Figure 4.
The correlation between non-migrating tidal variations (a) SE2 and (b) SE3 and F10.7 cm index between 60S and 60 N from 2003 to 2019. The spatial structure between 60 S and 60 N from 2003 to 2019 for (c) SE2 and (d) SE3.
3.3. Seasonal Variation
Figure 5 shows the seasonal variations in migrating tides DW1, SW2, and TW3. The seasonal variations in DW1 at 100 km between 60S and 60N from 2003 to 2019 are displayed in Figure 5a. The remarkably strong amplitudes of the migrating tides DW1 are notable in February to April between 40S and 10S and 10N and 40N, and two small peaks of DW1 amplitudes are shown in July and October, respectively, at the same regions. The seasonal variation is almost symmetrical in the northern and southern hemispheres, and Figure 5d shows the same seasonal variations in DW1 at 140 km, which are totally different from the seasonal variations at 100 km. In Figure 5d, large amplitudes are found from March to August between 60S and 30S and two other weak peaks from February to April and from October to December between 30N and 60N, which are asymmetrical in both hemispheres. As shown in Figure 2a, the correlations with DW1 and solar cycle are different at 100 km and 140 km, which is consistent with the seasonal variation in DW1. Figure 5b,e displays the seasonal variations in SW2 at 100 km and 140 km. At 100 km, the amplitudes of SW2 reach the maximum in January and December between 60S and approximately 30S and in May and September between 30N and 60N, respectively. However, the amplitudes at 140 km peak in June and July between 60S and 30S and peak in January and December between 30N and 60N. Apparently, the results are nearly opposite in different hemispheres at these two altitudes. The correlations of SW2 and solar activity are also contrary at 100 km and 140 km, as displayed in Figure 2c. Seasonal variations in TW3 at 100 km and 140 km are exhibited in Figure 5c,f. In Figure 5c, the amplitudes of TW3 at 100 km show the maximum in January to February and November to December between 60S and 30S and peak in June to August between 30N and 60N. At the same time, the seasonal variations also peak in March and September at the equator. Figure 5f shows the large amplitudes in January, March, and October between 60S and 30S and in January, March to August, November, and December between 30N and 60N. Further, a weak peak is found in June and July between 30S and the equator. The seasonal variations at 100 km are similar to the variations at 140 km in the high-latitude regions of the southern hemisphere, whereas the variations at 100 km are different from those at 140 km in other regions.
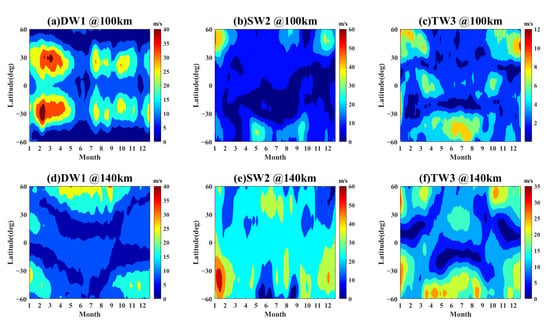
Figure 5.
Seasonal variations of migrating tides (a,d) DW1, (b,e) SW2, and (c,f) TW3 at (a–c) 100 km, and (d–f) 140 km between 60S and 60 N from 2003 to 2019.
Observed from the above results, the correlations between the migrating tides and solar cycle are consistent at different altitudes when the seasonal variations in the migrating tides are consistent. The results indicate that the relationship between the migrating tides and solar cycle may be influenced by the seasonal variation in the migrating tides. The zonal winds at different altitudes have the same seasonal variations when they have the same correlation with solar activity and vice versa. The reasons for the different seasonal variations at different altitudes will be the focus of the following discussion.
Figure 6 shows the seasonal variations in non-migrating tides DE2, DE3, and SE2, SE3. The seasonal variations in DE2 at 100 km and 140 km between 60S and 60N from 2003 to 2019 are displayed in Figure 6a,b. The large amplitudes of the non-migrating tides DE2 at 100 km are notable all year around 30S and 30N, and they peak in spring and winter in the southern hemisphere and in August to October in the northern hemisphere. Further, notable amplitudes are found in January, February, May, June, July, August, November, and December between 30S and 30N. The seasonal variations in winter are lager than the summer counterparts, and they are almost symmetrical in the northern and southern hemispheres. As exhibited in Figure 3a, the correlations with DE2 and solar cycle are different at 100 km and 140 km, which is consistent with the seasonal variation in DE2. Figure 6c,d shows the seasonal variations in DE3 at 100 km and 140 km, respectively. The amplitudes of DE3 reach the maximum in January and July, August, and September around the equator at both 100 km and 140 km. Apparently, the correlations are the same at these two altitudes, as displayed in Figure 3b. The seasonal variations in SE2 at 100 km and 140 km are exhibited in Figure 6e,f. The amplitudes of SE2 at 100 km show the maximum in March and November between 60N and approximately 30N and in April, August, and November between 10S and 60S. Figure 6f shows notable amplitudes in March, October, and November between 60N and 10N and in September and November between 10S and 60S. The seasonal variations at 100 km are different from the variations at 140 km, which is consistent with the correlations. The seasonal variations of SE3 at 100 km and 140 km are shown in Figure 6g,h. The amplitudes of SE3 at 100 km are dominant all year except in winter between 30S and 45S. Figure 6h shows large amplitude in January, March, April to June, and December around 30N and in January, May to August, and December around 30S. The seasonal variations at 100 km vary from the variations at 140 km, which is consistent with the correlations.

Figure 6.
Seasonal variations in non-migrating tides (a,b) DE2, (c,d) DE3, and (e,f) SW2, (g,h) SE3 at (a,c,e,g) 100 km, and (b,d,f,h) 140 km between 60S and 60 N from 2003 to 2019.
4. Discussion
4.1. Seasonal Variation
4.1.1. Migrating Tides
The present work displays the relationship between the different migrating and non-migrating tides and solar activity utilizing 17-year wind simulation data from SD-WACCM-X. This long-term relationship reveals some characteristics of zonal tidal variations from stratosphere to thermosphere, which will be discussed in the following parts. The seasonal variation in tides may be one of the influence factors for the correlation between tides and solar cycle. Further, the seasonal variation in tides has been taken into account before analyzing the solar cycle correlation.
As displayed in Figure 5, the seasonal variations correspond to the spatial structure shown in Figure 2. At approximately 100 km, migrating tide DW1 is dominant at the regions around 30N and 30S. The seasonal variation in DW1 also shows the same characteristic, and it is not difficult to find that the negative correlation is strong between 40S and 40N at approximately 110 km. The shape of the negative correlation regions is similar to the spatial structure of DW1. The same situation is also found in SW2 and TW3. The amplitudes of SW2 are large above 110 km, and the negative correlation between SW2 and solar activity is displayed above around 120 km. The amplitudes of TW3 are strong between 60S and 15S and between 15N and 60N above 120 km. A negative correlation of TW3 is found in the same regions. To sum up, the negative correlations between the migrating tides and solar cycle are always found where the migrating tides are dominant. Oberheide, et al. [35] studied the vertical structures of DW1 and SW2 using Hough Mode Extension (HME) fitting. HME is an extension of the classical Hough mode and represents the solution of Laplace’s tidal equation with dissipation and mean winds [36]. HME1 and HME2 represent the first symmetrical structure and the first asymmetrical structure, respectively, and HME3 and HME4 represent the second symmetrical structure and the second asymmetrical structure by that analogy. The diurnal and semidiurnal tides are well described by using HME1, HME2, HME3, and HME4 fitting. Oberheide, Forbes, Zhang and Bruinsma [35] found that the structure of DW1 was linked closely with HME1, which dissipated above approximately 110 km to 120 km. The short vertical wavelength of HME1 is the reason why HME1 cannot propagate upward to the thermosphere. This finding is consistent with the spatial structure shown in Figure 2b. The spatial structure of DW1 displayed in Figure 2b also shows that the tide dominates at approximately 100 km and dissipates above approximately 110 km to 120 km, which confirms the HMEs analyses. Oberheide, et al. [37] found that HME1 dissipates slowly when the F10.7 cm radio flux level is low because the coefficients of molecular thermal conductivity of HMEs are proportional to the temperature [14], and the higher order HMEs also dissipate slowly when the solar activity level is low. However, the impact caused by higher order HMEs is smaller than HME1 because the coefficient of molecular dissipation is in direct proportion to the square of the vertical wavelength. It is well-known that the temperature is high at high solar flux. Therefore, the winds dissipate more quickly when the solar flux level is high. Thus, it can be inferred that the amplitudes of DW1 during the time of low solar activity are larger than those during the time of high solar activity. Therefore, the negative correlations between DW1 and F10.7 cm radio flux are shown at the regions dominated by the maximum of spatial structure. Further, it is well-known that the migrating tides are excited by solar radiation, and the tides in the thermosphere are influenced strongly by solar radiation, which is related with solar activity. However, there is a negative correlation above 120 km where HME1 of DW1 has dissipated. Hence, the relationship between DW1 and solar cycle may also be influenced by some other factors, which will be discussed in the next section.
As for SW2, it is governed by HME1 and HME2 in the thermosphere above 100 km [35], and HME1 and HME2 are dominant at different months. As discussed above, the coefficients of molecular thermal conductivity in HME1 and HME2 of SW2 are also related with temperature [14]. The negative correlations are also present in the large-amplitude SW2 regions, which is consistent with our conclusion, and the vertical wavelength of HME2 for SW2 is shorter than HME1 [35]. Hence, HME1 of SW2 is dominant at higher altitudes for shorter vertical wavelength and dissipates more easily in MLT. The spatial structure of SW2 displayed in Figure 2d shows the tide dominates between approximately 110 and 130 km, which also confirms the HMEs analyses. Positive correlations are shown between 100 km and 120 km, where there is control by HME1 and HME2 of SW2. The coefficient of molecular dissipation is in direct proportion to the square of the vertical wavelength, which leads to the smaller amplitudes of HME2. Oberheide, Forbes, Häusler, Wu and Bruinsma [37] also showed that the amplitudes of HME1 vary considerably at different solar flux than HME2. It is reasonable to speculate that the correlation coefficient between HME2 of SW2 and solar activity is lower than HME1, and DW1 in the MLT has been proven to be almost excited by troposphere radiative heating, whereas SW2 is influenced by multiple sources, including chemical heating and ozone heating [38]. This otherness may also account for the different characteristic of the correlations of DW1 and SW2.
The HME fitting for TW3 is very complicated and more wave modes are needed to fit TW3 well. HME1, HME2, and HME4 all contribute to TW3 in MLT regions, and higher order HMEs dissipate more quickly for their short vertical wavelengths [35]. Thus, HME1 of TW1 may govern at higher altitudes. As shown in Figure 2e,f, the negative relationship between TW3 and solar cycle is almost present in the regions where the spatial space of TW3 reaches the maximum above 120 km. As a result, no matter which HME dominates the tides, the dominance areas of spatial structures shown in Figure 2 are areas of negative correlations.
As discussed above, we dope out that the negative correlations between migrating tides and solar activity are most possibly present in the regions where HME1s of the migrating tides dominate, and HME1s of the migrating tides usually dissipate more slowly during low solar activity time. However, some other factors also impact the correlations, which will be discussed in the next section.
4.1.2. Non-Migrating Tides
DE2 and DE3 are both governed by HME1s, which propagate upward to the thermosphere with less dissipation because of their long vertical wavelengths. As shown in Figure 3a, the negative relationship between DE2 and solar activity appears in the regions where the spatial structure of DE2 reaches the maximum above 100 km, and positive correlations are present below the strong HME1 of DE2. It may be caused by other factors for the small amplitudes of DE2 in this region. The negative correlations between DE3 and solar cycle displayed in Figure 3b are also present above 100 km between 50S and 50N, where the HME1 of DE3 is dominant. SE2 and SE3 are both governed by HME1 and HME2, and HME2 contributes more in the MLT regions. The negative relationships between SE2, SE3, and solar activity appear in the regions where the spatial structures of SE2 and SE3 are dominant above 120 km in Figure 4, and the positive correlations are present below 120 km, which may be caused by other factors.
4.2. Impact of CO2 and Geomagnetic Activity
4.2.1. Migrating Tides
Increasing leading to thermosphere cooling has been proven [39], and dissipation of the tides decreases with weaker heat conduction and molecular viscosity in the cooling thermosphere [40]. As a result, the density of has an impact on the correlation between tides and solar activity cycle. At the same time, geomagnetic activity, which plays a role in tidal waves, is linked closely with solar activity [41,42,43]. The geomagnetic activity may also influence the correlations between tides and solar activity. The tides usually have two sources, one in situ and one propagating from below. The source in situ is usually the solar radiation, which is related with and kp index. The impact of and kp on tides is generated in situ, and the impact of HME1 is propagating from below. The geomagnetic index kp and are added to further study the reason for the different correlations between migrating and non-migrating tides and solar activity at different altitudes and latitudes. Figure 7 displays the correlations between the migrating tides and F10.7 cm index, geomagnetic index kp, and between 60 km and 180 km from 2003 to 2019. It is well-known that geomagnetic activity is linked closely with solar activity [41,42,43]. The geomagnetic activity is strong when the solar activity is strong, which shows a positive relationship between geomagnetic activity and solar activity, and the geomagnetic activity is also related with tidal waves. The westward wind increases with the geomagnetic activity increasing [44]. From the above we can infer that the westward wind will increase during the time of high solar activity. At the same time, the dissipation of tidal waves will also increase when the background westward wind increase. As a result, the geomagnetic activity has an impact on the negative correlations between tides and solar activity. Figure 7b shows the correlations between DW1 and kp, which exhibit a negative relationship between 30S and 30N from about 110 km to 140 km. The negative correlation at approximately 120 km from 40S to 40N displayed in Figure 7a may be influenced by the negative correlations in Figure 7b.

Figure 7.
The correlation between migrating tidal variations (a–c) DW1, (d–f) SW2, and (g–i) TW3, and (a,d,g) F10.7 cm index, (b,e,h) kp index, and (c,f,i) between 60 S and 60 N from 2003 to 2019. The green curve means the zero lines.
Moreover, the high solar activity accounts for the increasing . Increasing leading to thermosphere cooling has been proven [39,45,46,47], and the dissipation of the tides decreases for the weaker heat conduction and molecular viscosity in the cooling thermosphere [40]. The tides will increase when the dissipation of the tides decreases. Thus, has an impact on the positive correlations between tidal waves and solar cycle, and Figure 7c shows the relatively stronger positive correlations between DW1 and above approximately 130 km and 140 km. It can be inferred above that amplitudes of DW1 increase when density of increases. Hence, the positive correlations present above 130 km and 140 km in Figure 7a may be influenced by the positive correlations in Figure 7c. The positions of the maximum of the positive correlations in Figure 7c are almost the same with the counterparts in Figure 7a, which further verifies the above speculation. The structures of the correlations for kp and displayed in Figure 7e–i are all consistent with this conclusion. As a result, the positive relationships between migrating tides and solar cycle are possibly influenced by the density of and the negative relationships between migrating tides and solar cycle are possibly influenced by geomagnetic activity.
4.2.2. Non-Migrating Tides
Figure 8 shows the correlations between non-migrating diurnal tides DE2 and DE3 and F10.7 cm index, geomagnetic index kp, and between 60 km and 180 km from 2003 to 2019. In Figure 8b,e, the negative correlations are shown in the regions where the negative correlations display in Figure 8a,d. The speculation we discussed above is also verified in the non-migrating tides. In Figure 8c,f, the positive correlations are present below 100 km. The thermosphere cooling caused by appears in the thermosphere, and the density of in the mesosphere shows little impact on the relationships between the non-migrating diurnal tides and the solar cycle. The impact of tides’ own structures and geomagnetic activity is stronger than the impact of

Figure 8.
The correlation between non-migrating tidal variations (a–c) DE2, (d–f) DE3, and (a,d) F10.7 cm index, (b,e) kp index, and (c,f) between 60 S and 60 N from 2003 to 2019. The green curve means the zero lines.
Figure 9 represents the correlations between non-migrating semidiurnal tides SE2 and SE3 and F10.7 cm index, geomagnetic index kp, and between 60 km and 180 km from 2003 to 2019. In Figure 9a, the negative correlations above 140 km may be influenced by geomagnetic activity shown in Figure 9b, which is consistent with our speculation. Figure 9c exhibits strong positive correlations between SE2 and between 15S and 45N above 100 km, which is not consistent with the speculation raised above. It can be indicated that the impact of HME1 of SE2 is stronger than the counterparts from 2003 to 2019, and the negative correlations above 140 km shown in Figure 9a are relatively smaller than those of other tides. The structures of the correlations for kp and displayed in Figure 9e,f are all consistent with this speculation.

Figure 9.
The correlation between non-migrating tidal variations (a–c) SE2, (d–f) SE3, and (a,d) F10.7 cm index, (b,e) kp index, and (c,f) between 60 S and 60 N from 2003 to 2019. The green curve means the zero lines.
5. Summary
We studied the global distribution of the correlations between migrating and non-migrating tides and solar cycle in the MLT regions between 60S and 60N by analyzing the simulation data obtained from SD-WACCM-X. The SD-WACCM-X dataset displays that the correlations vary from different altitudes and latitudes and the possible influence factors.
Our analysis shows that the negative correlations between tides and solar activity are mostly impacted by structures for both migrating and non-migrating components. Oberheide, Forbes, Häusler, Wu and Bruinsma [37] found that HME1 or other HMEs dissipate slowly when the F10.7 cm radio flux level is low, and the impact caused by higher order HMEs is much smaller than HME1 because the coefficient of molecular dissipation is in direct proportion to the square of the vertical wavelength. Therefore, the negative correlations between tides and F10.7 cm radio flux are shown at the regions dominated by HME1, and the migrating and non-migrating tides are both excited by solar radiation, which is related to solar activity [3,7,13]. As a result, the maximum of the spatial structures has an impact on the negative correlations between migrating and non-migrating tides and solar cycle.
The correlation between tide and solar activity could also be influenced by some other factors, such as geomagnetic activity and . The negative correlation between tidal waves and solar cycle is possibly influenced by geomagnetic activity. It is well-known that geomagnetic activity is linked closely with solar activity [41,42,43]. The geomagnetic index kp is lower during the time of low solar activity. Tidal variations can also be influenced by westward background wind, which increases as magnetic activity rises [44]. The positive correlations between tidal waves and solar activities are possibly influenced by the density of . The dissipation of the tides decreases with increasing , which results in larger tidal amplitudes [39,40], and the high solar activity accounts for the increasing .
The negative correlations are most possibly influenced by the first symmetrical structure of tidal variations and may also be impacted by geomagnetic activity. The positive correlations are impacted by the density of . We also found that the impact of HME1 regarding tidal variations is stronger than the counterparts. The correlations between the migrating tides and non-migrating tides and solar cycle are influenced mostly by HME1 of tides and geomagnetic activity.
Author Contributions
Conceptualization, S.G. and R.S.; software, R.S.; validation, R.S., S.G. and X.D.; formal analysis, R.S.; investigation, R.S.; resources, S.G. and X.D.; writing—original draft preparation, R.S.; writing—review and editing, R.S., S.G. and N.L.; funding acquisition, S.G. and X.D. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the National Natural Science Foundation of China (41831071 and 41874181), the B-type Strategic Priority Program of the Chinese Academy of Sciences (Grant XDB41000000), the Chinese Meridian Project.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
WACCM-X is an open-source software model, and its source code is publicly available at https://escomp.github.io/CESM/versions/master/html/downloading_cesm.html accessed on 18 October 2019. The atmospheric forcing data, which were regridded from the MERRA-2 dataset and used to run the SD-WACCM-X, can be downloaded at https://rda.ucar.edu/datasets/ds313.3/?hash=access, accessed on 18 October 2019. The OMNI data F10.7 cm index and kp index were obtained from the GSFC/SPDF OMNIWeb interface at https://omniweb.gsfc.nasa.gov accessed on 12 March 2022.
Acknowledgments
The numerical calculations in this paper were conducted on the supercomputing system in the Supercomputing Center of Wuhan University.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lindzen, R.S.; Chapman, S. Atmospheric tides. Space Sci. Rev. 1969, 10, 3–188. [Google Scholar] [CrossRef]
- Miyahara, S.; Miyoshi, Y. Migrating and non-migrating atmospheric tides simulated by a middle atmosphere general circulation model. Adv. Space Res. 1997, 20, 1201–1207. [Google Scholar] [CrossRef]
- Hagan, M.E.; Forbes, J.M. Migrating and nonmigrating diurnal tides in the middle and upper atmosphere excited by tropospheric latent heat release. J. Geophys. Res. Atmos. 2002, 107, ACL 6-1–ACL 6-15. [Google Scholar] [CrossRef]
- Häusler, K.; Luhr, H.; Hagan, M.E.; Maute, A.; Roble, R.G. Comparison of CHAMP and TIME-GCM nonmigrating tidal signals in the thermospheric zonal wind. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
- Remsberg, E.; Lingenfelser, G.; Harvey, V.; Grose, W.; Russell, J., III; Mlynczak, M.; Gordley, L.; Marshall, B.T. On the verification of the quality of SABER temperature, geopotential height, and wind fields by comparison with Met Office assimilated analyses. J. Geophys. Res. Atmos. 2003, 108. [Google Scholar] [CrossRef]
- Manson, A.H.; Meek, C.E.; Teitelbaum, H.; Vial, F.; Schminder, R.; Kürschner, D.; Smith, M.J.; Fraser, G.J.; Clark, R.R. Climatologies of semi-diurnal and diurnal tides in the middle atmosphere (70–110 km) at middle latitudes (40–55). J. Atmos. Terr. Phys. 1989, 51, 579–593. [Google Scholar] [CrossRef]
- Sridharan, S. Seasonal Variations of Low-Latitude Migrating and Nonmigrating Diurnal and Semidiurnal Tides in TIMED-SABER Temperature and Their Relationship With Source Variations. J. Geophys. Res. Space Phys. 2019, 124, 3558–3572. [Google Scholar] [CrossRef]
- Yue, J.; Xu, J.; Chang, L.C.; Wu, Q.; Liu, H.-L.; Lu, X.; Russell, J., III. Global structure and seasonal variability of the migrating terdiurnal tide in the mesosphere and lower thermosphere. J. Atmos. Solar-Terr. Phys. 2013, 105, 191–198. [Google Scholar] [CrossRef]
- Liu, H.-L.; Wang, W.; Richmond, A.; Roble, R.G. Ionospheric variability due to planetary waves and tides for solar minimum conditions. J. Geophys. Res. Space Phys. 2010, 115. [Google Scholar] [CrossRef]
- Pedatella, N.M.; Forbes, J.M. Evidence for stratosphere sudden warming-ionosphere coupling due to vertically propagating tides. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Chang, L.C.; Palo, S.E.; Liu, H.L. Short-term variation of the s= 1 nonmigrating semidiurnal tide during the 2002 stratospheric sudden warming. J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef]
- Lieberman, R.S.; Oberheide, J.; Talaat, E.R. Nonmigrating diurnal tides observed in global thermospheric winds. J. Geophys. Res. Space Phys. 2013, 118, 7384–7397. [Google Scholar] [CrossRef]
- Häusler, K.; Lühr, H. Nonmigrating tidal signals in the upper thermospheric zonal wind at equatorial latitudes as observed by CHAMP. Ann. Geophys. 2009, 27, 2643–2652. [Google Scholar] [CrossRef]
- Forbes, J.M.; Garrett, H.B. Theoretical studies of atmospheric tides. Rev. Geophys. 1979, 17, 1951–1981. [Google Scholar] [CrossRef]
- Balan, N.; Bailey, G.J. Equatorial plasma fountain and its effects: Possibility of an additional layer. J. Geophys. Res. Space Phys. 1995, 100, 21421–21432. [Google Scholar] [CrossRef]
- Tapping, K.F. The 10.7 cm solar radio flux (F10. 7). Space Weather 2013, 11, 394–406. [Google Scholar] [CrossRef]
- Sprenger, K.; Schminder, R. Solar cycle dependence of winds in the lower ionosphere. J. Atmos. Terr. Phys. 1969, 31, 217–221. [Google Scholar] [CrossRef]
- Namboothiri, S.; Manson, A.; Meek, C. Variations of mean winds and tides in the upper middle atmosphere over a solar cycle, Saskatoon, Canada, 52°N, 107°W. J. Atmos. Terr. Phys. 1993, 55, 1325–1334. [Google Scholar] [CrossRef]
- Bremer, J.; Schminder, R.; Greisiger, K.; Hoffmann, P.; Kürschner, D.; Singer, W. Solar cycle dependence and long-term trends in the wind field of the mesosphere/lower thermosphere. J. Atmos. Solar-Terr. Phys. 1997, 59, 497–509. [Google Scholar] [CrossRef]
- Wilhelm, S.; Stober, G.; Brown, P. Climatologies and long-term changes in mesospheric wind and wave measurements based on radar observations at high and mid latitudes. Ann. Geophys. 2019, 37, 851–875. [Google Scholar] [CrossRef]
- Gong, Y.; Lv, X.; Zhang, S.; Zhou, Q.; Ma, Z. Climatology and seasonal variation of the thermospheric tides and their response to solar activities over Arecibo. J. Atmos. Solar-Terr. Phys. 2021, 215, 105592. [Google Scholar] [CrossRef]
- Andrioli, V.F.; Xu, J.; Batista, P.P.; Resende, L.C.A.; Da Silva, L.A.; Marchezi, J.P.; Li, H.; Wang, C.; Liu, Z.; Guharay, A. New Findings Relating Tidal Variability and Solar Activity in the Low Latitude MLT Region. J. Geophys. Res. Space Phys. 2022, 127. [Google Scholar] [CrossRef]
- Guharay, A.; Batista, P.; Andrioli, V. Investigation of solar cycle dependence of the tides in the low latitude MLT using meteor radar observations. J. Atmos. Solar-Terr. Phys. 2019, 193. [Google Scholar] [CrossRef]
- Dhadly, M.S.; Emmert, J.T.; Drob, D.P.; McCormack, J.P.; Niciejewski, R.J. Short-Term and Interannual Variations of Migrating Diurnal and Semidiurnal Tides in the Mesosphere and Lower Thermosphere. J. Geophys. Res. Space Phys. 2018, 123, 7106–7123. [Google Scholar] [CrossRef]
- Baumgaertner, A.; McDonald, A.; Fraser, G.; Plank, G. Long-term observations of mean winds and tides in the upper mesosphere and lower thermosphere above Scott Base, Antarctica. J. Atmos. Solar-Terr. Phys. 2005, 67, 1480–1496. [Google Scholar] [CrossRef]
- Chang, L.C.; Lin, C.H.; Liu, J.Y.; Balan, N.; Yue, J.; Lin, J.T. Seasonal and local time variation of ionospheric mi-grating tides in 2007–2011 FORMOSAT-3/COSMIC and TIE-GCM total electron content. J. Geophys. Res. Space Phys. 2013, 118, 2545–2564. [Google Scholar] [CrossRef]
- Liu, H.-L.; Foster, B.T.; Hagan, M.E.; McInerney, J.M.; Maute, A.; Qian, L.; Richmond, A.; Roble, R.G.; Solomon, S.; Garcia, R.R.; et al. Thermosphere extension of the Whole Atmosphere Community Climate Model. J. Geophys. Res. Space Phys. 2010, 115. [Google Scholar] [CrossRef]
- Liu, H.; Bardeen, C.G.; Foster, B.T.; Lauritzen, P.; Liu, J.; Lu, G.; Marsh, D.R.; Maute, A.; McInerney, J.M.; Pedatella, N.M.; et al. Development and Validation of the Whole Atmosphere Community Climate Model With Thermosphere and Ionosphere Extension (WACCM-X 2.0). J. Adv. Model. Earth Syst. 2018, 10, 381–402. [Google Scholar] [CrossRef]
- Wu, Q.; Ortland, D.A.; Killeen, T.L.; Roble, R.G.; Hagan, M.E.; Liu, H.-L.; Solomon, S.C.; Xu, J.; Skinner, W.R.; Niciejewski, R.J. Global distribution and interannual variations of mesospheric and lower thermospheric neutral wind diurnal tide: 2. Nonmigrating tide. J. Geophys. Res. Space Phys. 2008, 113. [Google Scholar] [CrossRef]
- Wu, Q.; Ortland, D.; Killeen, T.; Roble, R.; Hagan, M.; Liu, H.L.; Solomon, S.; Xu, J.; Skinner, W.; Niciejewski, R.J. Global distribution and interannual variations of mesospheric and lower thermospheric neutral wind diurnal tide: 1. Migrating tide. J. Geophys. Res. Space Phys. 2008, 113. [Google Scholar] [CrossRef]
- Wu, N.L.; Hays, P.B.; Skinner, W.R. A Least Squares Method for Spectral Analysis of Space-Time Series. J. Atmos. Sci. 1995, 52, 3501–3511. [Google Scholar] [CrossRef]
- Lee Rodgers, J.; Nicewander, W.A. Thirteen ways to look at the correlation coefficient. Am. Stat. 1988, 42, 59–66. [Google Scholar] [CrossRef]
- Huang, C.; Liu, D.-D.; Wang, J.-S. Forecast daily indices of solar activity, F10.7, using support vector regression method. Res. Astron. Astrophys. 2009, 9, 694–702. [Google Scholar] [CrossRef]
- Hathaway, D.H. The Solar Cycle. Living Rev. Sol. Phys. 2015, 12, 1–87. [Google Scholar] [CrossRef]
- Oberheide, J.; Forbes, J.; Zhang, X.; Bruinsma, S.L. Climatology of upward propagating diurnal and semidiurnal tides in the thermosphere. J. Geophys. Res. Space Phys. 2011, 116. [Google Scholar] [CrossRef]
- Hong, S.-S.; Lindzen, R.S. Solar Semidiurnal Tide in the Thermosphere. J. Atmos. Sci. 1976, 33, 135–153. [Google Scholar] [CrossRef]
- Oberheide, J.; Forbes, J.; Häusler, K.; Wu, Q.; Bruinsma, S.L. Tropospheric tides from 80 to 400 km: Propagation, interannual variability, and solar cycle effects. J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef]
- Zhang, X.; Forbes, J.M.; Hagan, M.E. Longitudinal variation of tides in the MLT region: 1. Tides driven by tropospheric net radiative heating. J. Geophys. Res. Space Phys. 2010, 115. [Google Scholar] [CrossRef]
- Zhang, S.; Holt, J.M.; Erickson, P.J.; Goncharenko, L.P.; Nicolls, M.J.; McCready, M.; Kelly, J. Ionospheric ion temperature climate and upper atmospheric long-term cooling. J. Geophys. Res. Space Phys. 2016, 121, 8951–8968. [Google Scholar] [CrossRef]
- Liu, H.; Tao, C.; Jin, H.; Nakamoto, Y. Circulation and Tides in a Cooler Upper Atmosphere: Dynamical Effects of CO2 Doubling. Geophys. Res. Lett. 2020, 47. [Google Scholar] [CrossRef]
- Legrand, J.-P.; Simon, P.J.A. Some solar cycle phenomena related to the geomagnetic activity from 1868 to 1980. I-The shock events, or the interplanetary expansion of the toroidal field. Astron. Astrophys. 1985, 152, 199–204. [Google Scholar]
- Legrand, J.; Simon, P. Solar cycle and geomagnetic activity: A review for geophysicists. Part I. The contributions to geomagnetic activity. Ann. Geophys. 1989, 7, 565–578. [Google Scholar]
- Obridko, V.N.; Kanonidi, K.D.; Mitrofanova, T.A.; Shelting, B.D. Solar activity and geomagnetic disturbances. Geomagn. Aeron. 2013, 53, 147–156. [Google Scholar] [CrossRef]
- Yi, W.; Reid, I.M.; Xue, X.; Murphy, D.J.; Vincent, R.A.; Zou, Z.; Chen, T.; Wang, G.; Dou, X. First Observations of Antarctic Mesospheric Tidal Wind Responses to Recurrent Geomagnetic Activity. Geophys. Res. Lett. 2021, 48, e2020GL089957. [Google Scholar] [CrossRef]
- Kogure, M.; Liu, H.; Tao, C. Mechanisms for Zonal Mean Wind Responses in the Thermosphere to Doubled CO2 Concentration. J. Geophys. Res. Space Phys. 2022, 127. [Google Scholar] [CrossRef]
- Mlynczak, M.G.; Hunt, L.A.; Thomas Marshall, B.; Martin-Torres, F.J.; Mertens, C.J.; Russell, J.M., III; Remsberg, E.E.; López-Puertas, M.; Picard, R.; Winick, J.; et al. Observations of infrared radiative cooling in the thermosphere on daily to mul-tiyear timescales from the TIMED/SABER instrument. J. Geophys. Res. Space Phys. 2010, 115. [Google Scholar] [CrossRef]
- Liu, H.; Tao, C.; Jin, H.; Abe, T. Geomagnetic activity effects on CO2-driven trend in the thermosphere and ionosphere: Ideal model experiments with GAIA. J. Geophys. Res. Space Phys. 2021, 126, e2020JA028607. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).