On the Nature and Origin of Atmospheric Annual and Semi-Annual Oscillations
Abstract
1. Introduction
2. The Pressure Data and Method of Analysis
2.1. Step 1 (Embedding Step)
2.2. Step 2 (Decomposition in Singular Values (SVD))
2.3. Step 3 (Reconstruction)
2.4. Step 4 (The Diagonal Mean, Aka the Hankelization Step)
3. The SSA Pressure Components
- 1 year ( ∼93 hPa),
- 0.5 years (∼65 hPa),
- 0.33 years (∼44 hPa),
- 0.25 years (∼21 hPa).
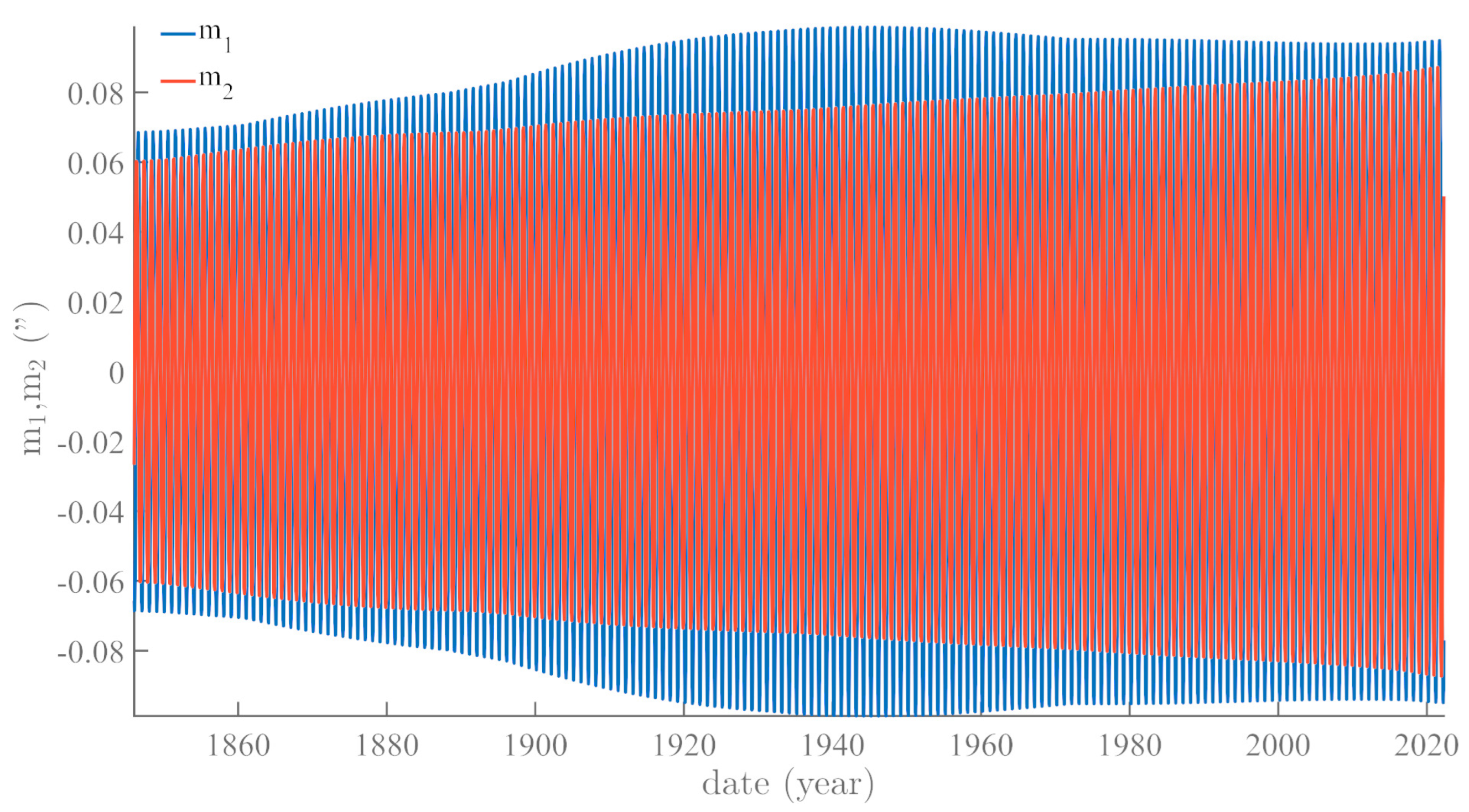
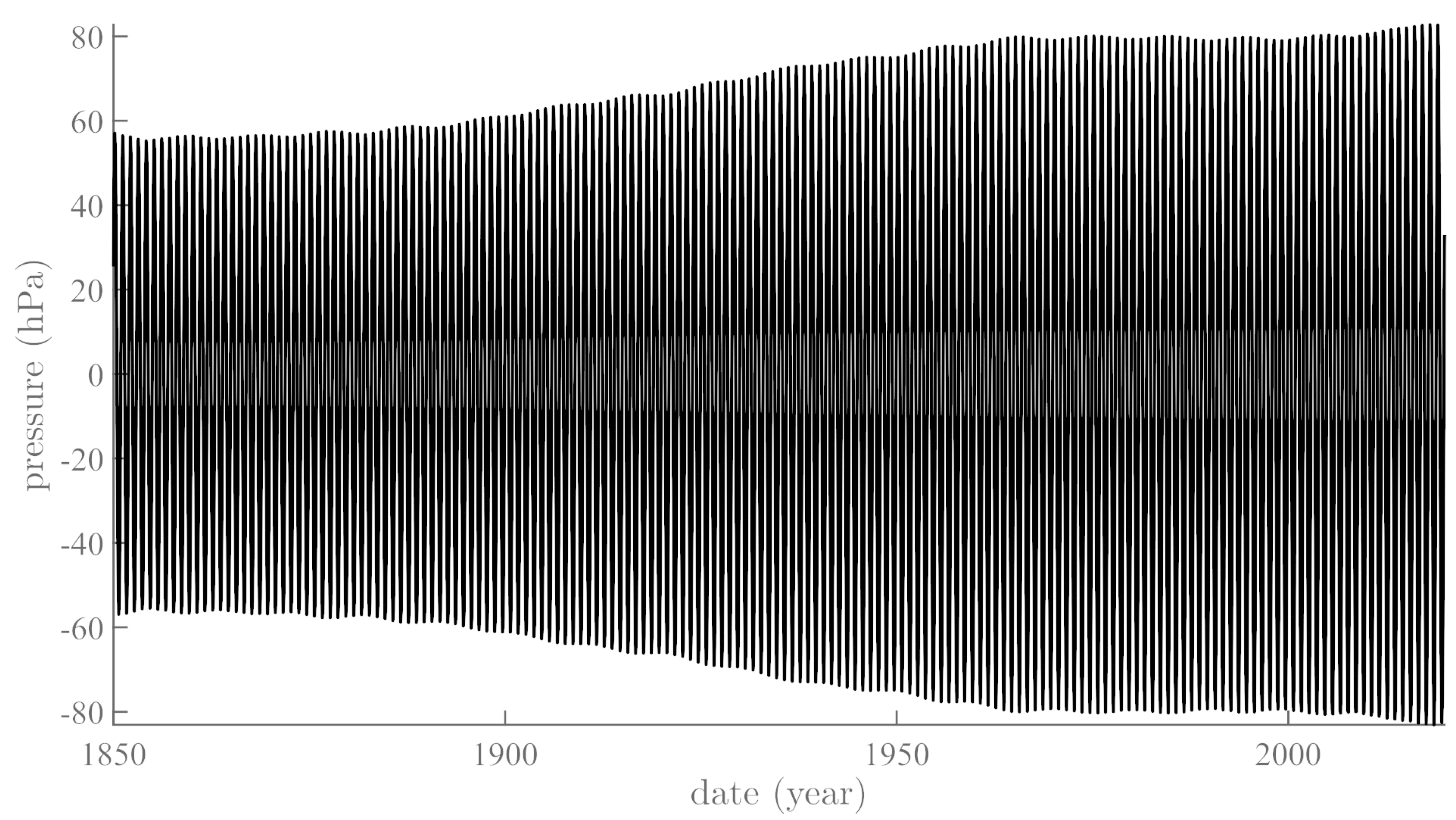
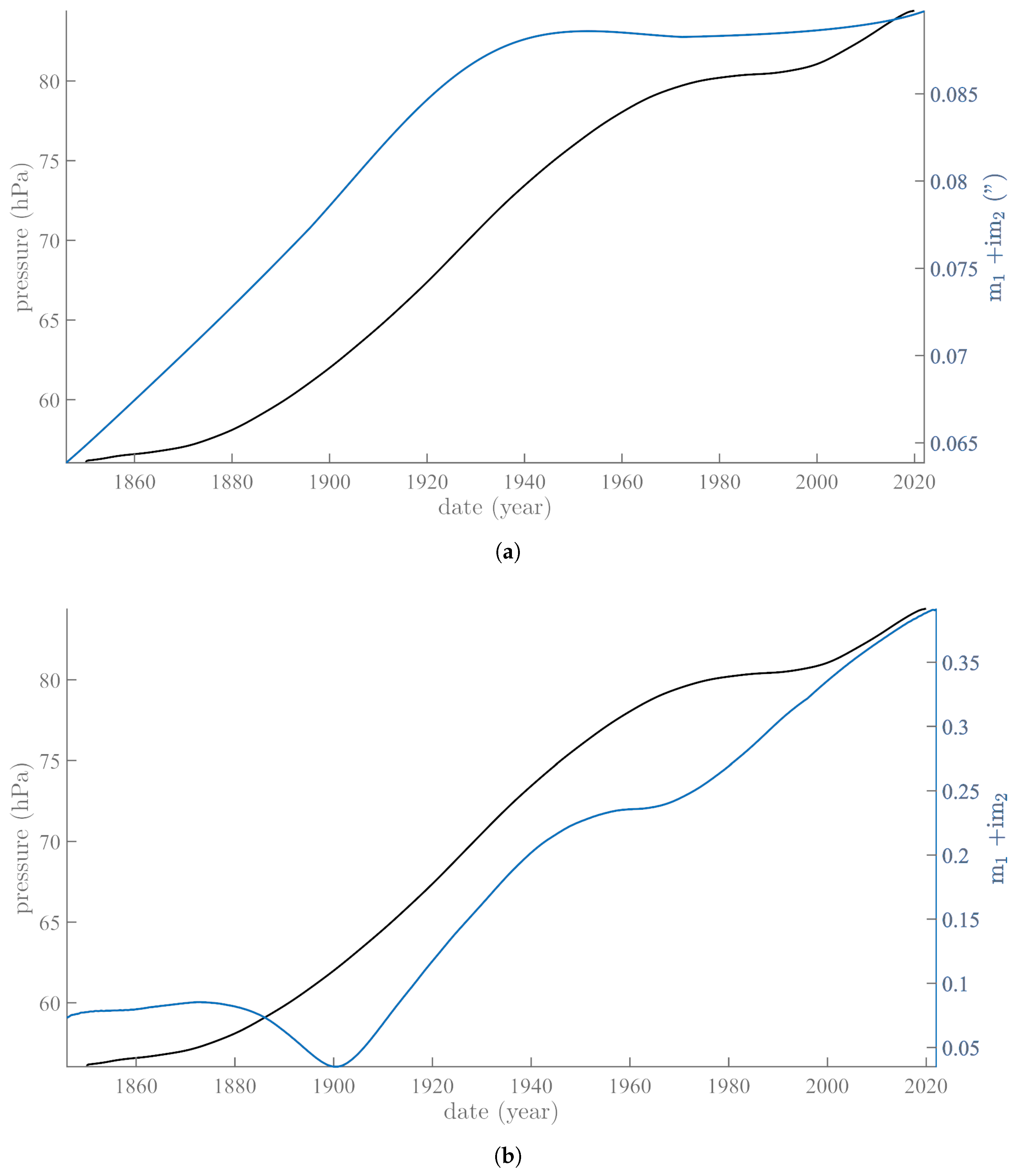
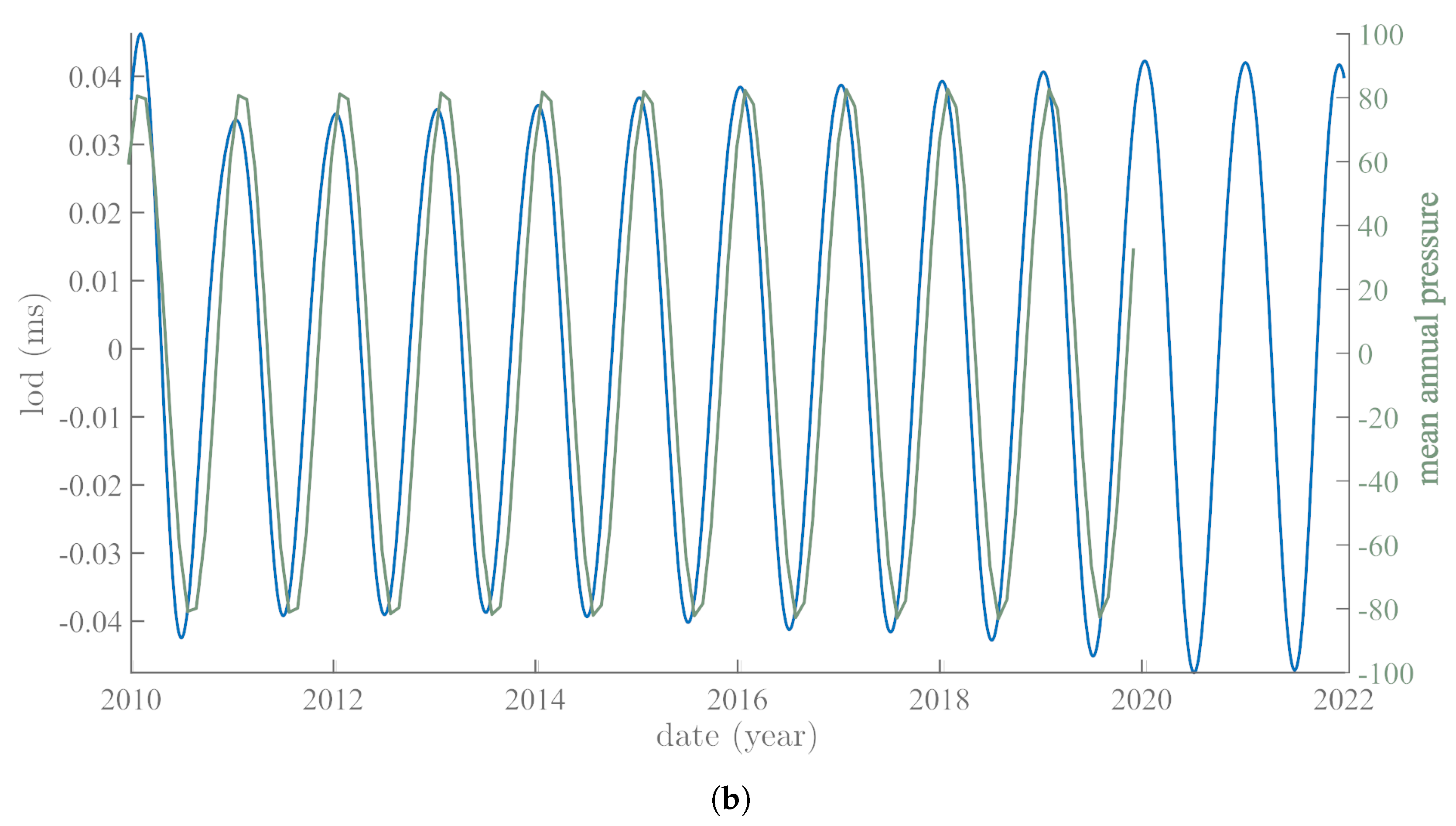
4. Annual and Semi-Annual SSA Pressure Components and Variations in Polar Motion: Time Analysis
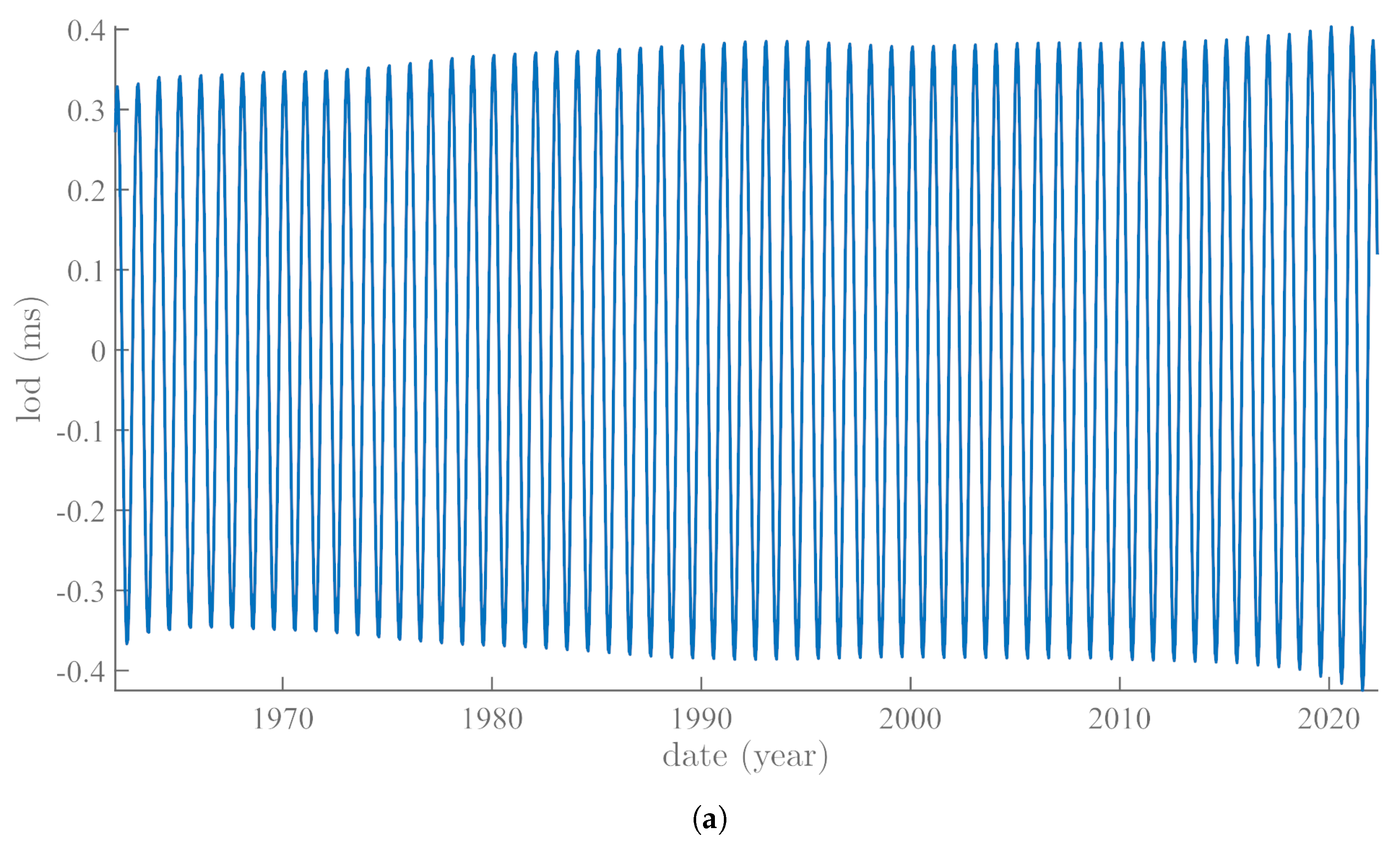
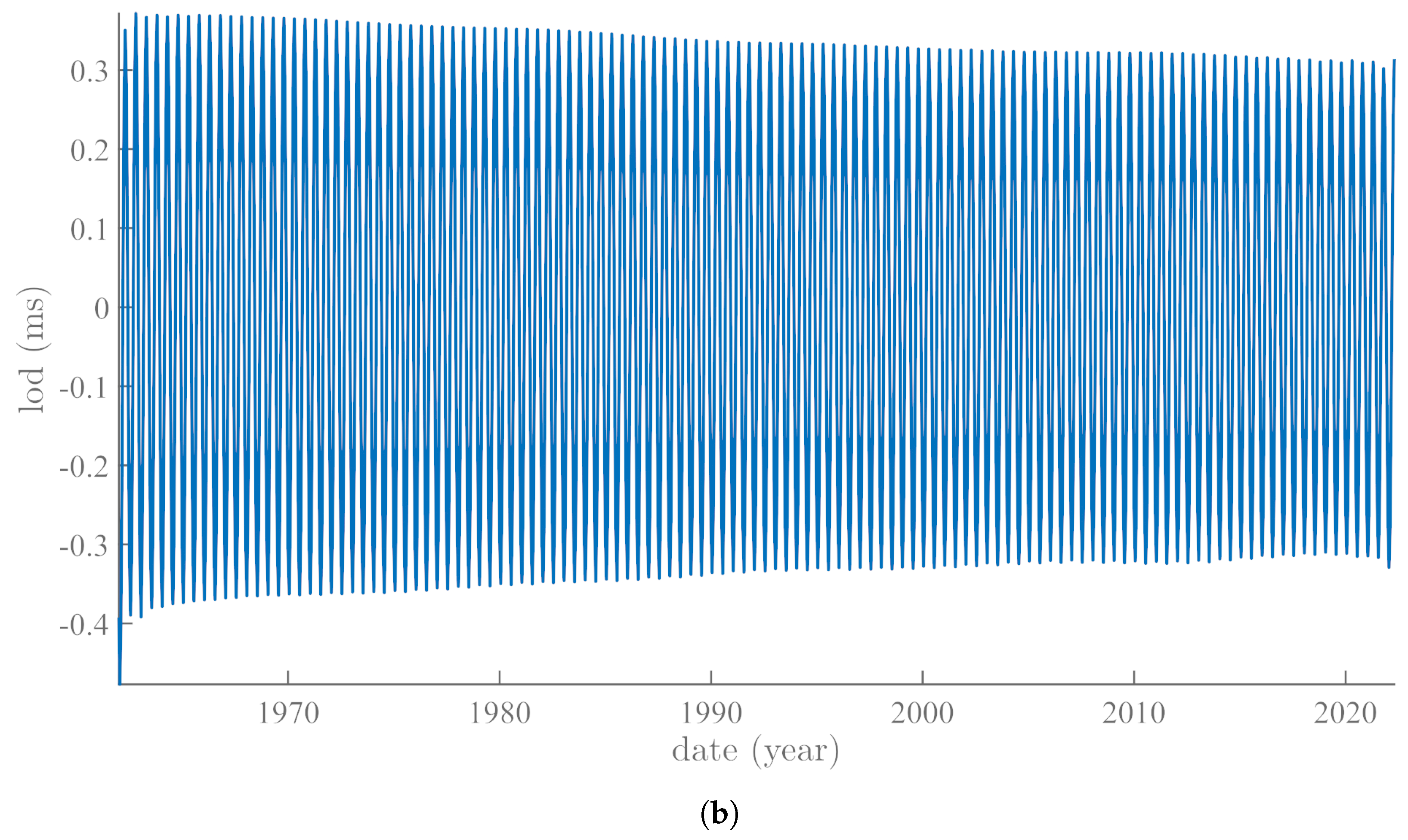
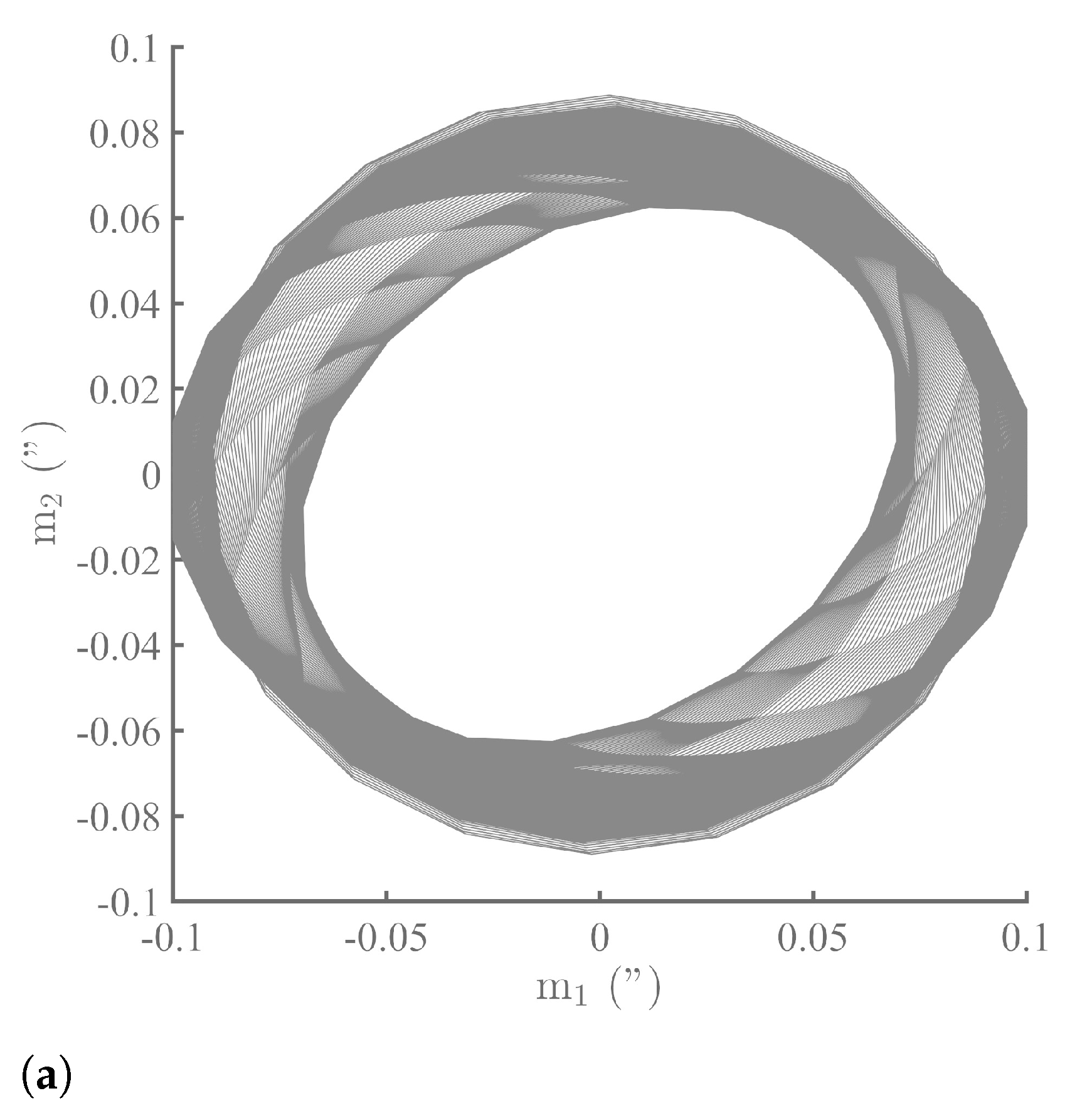
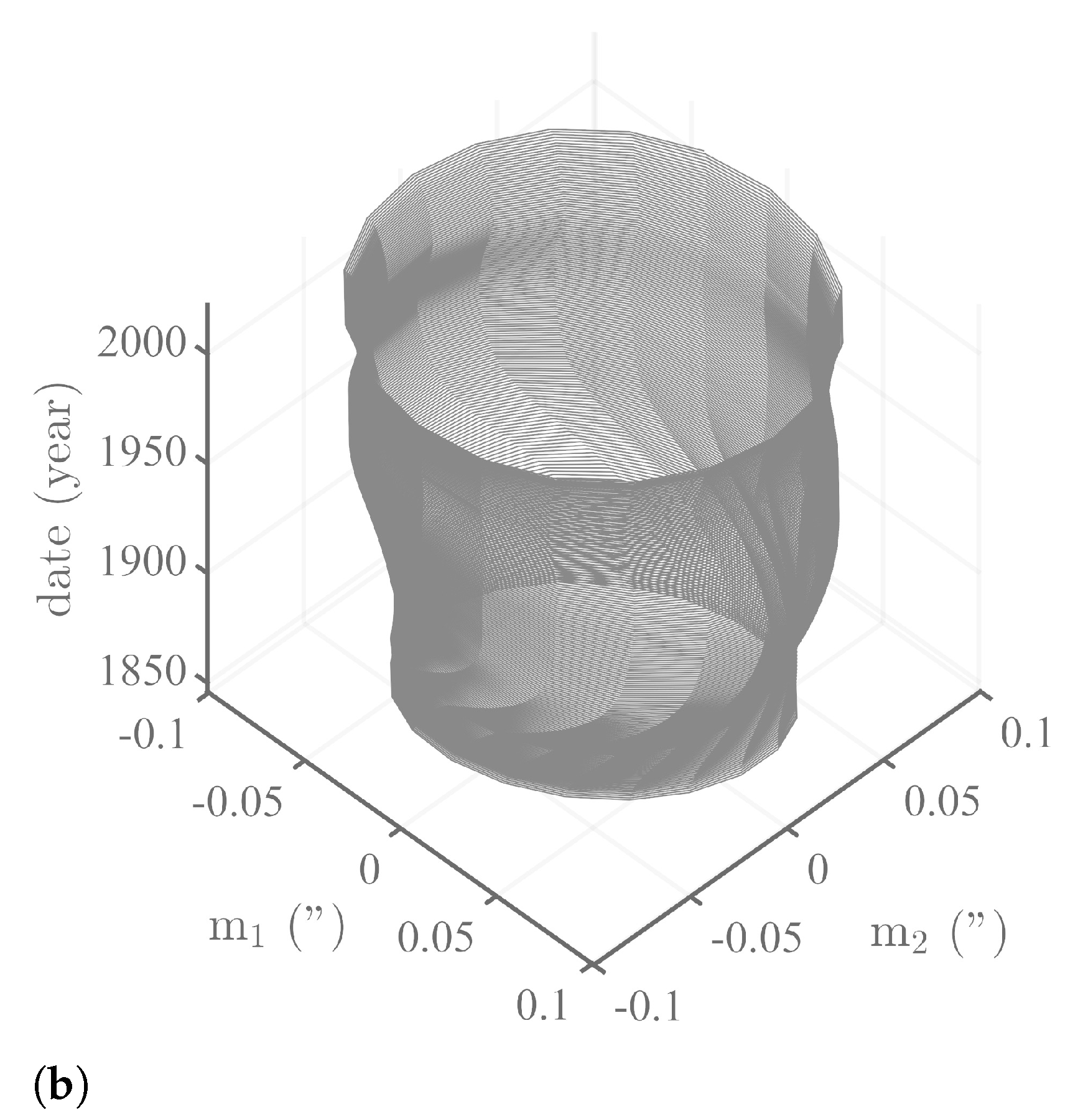
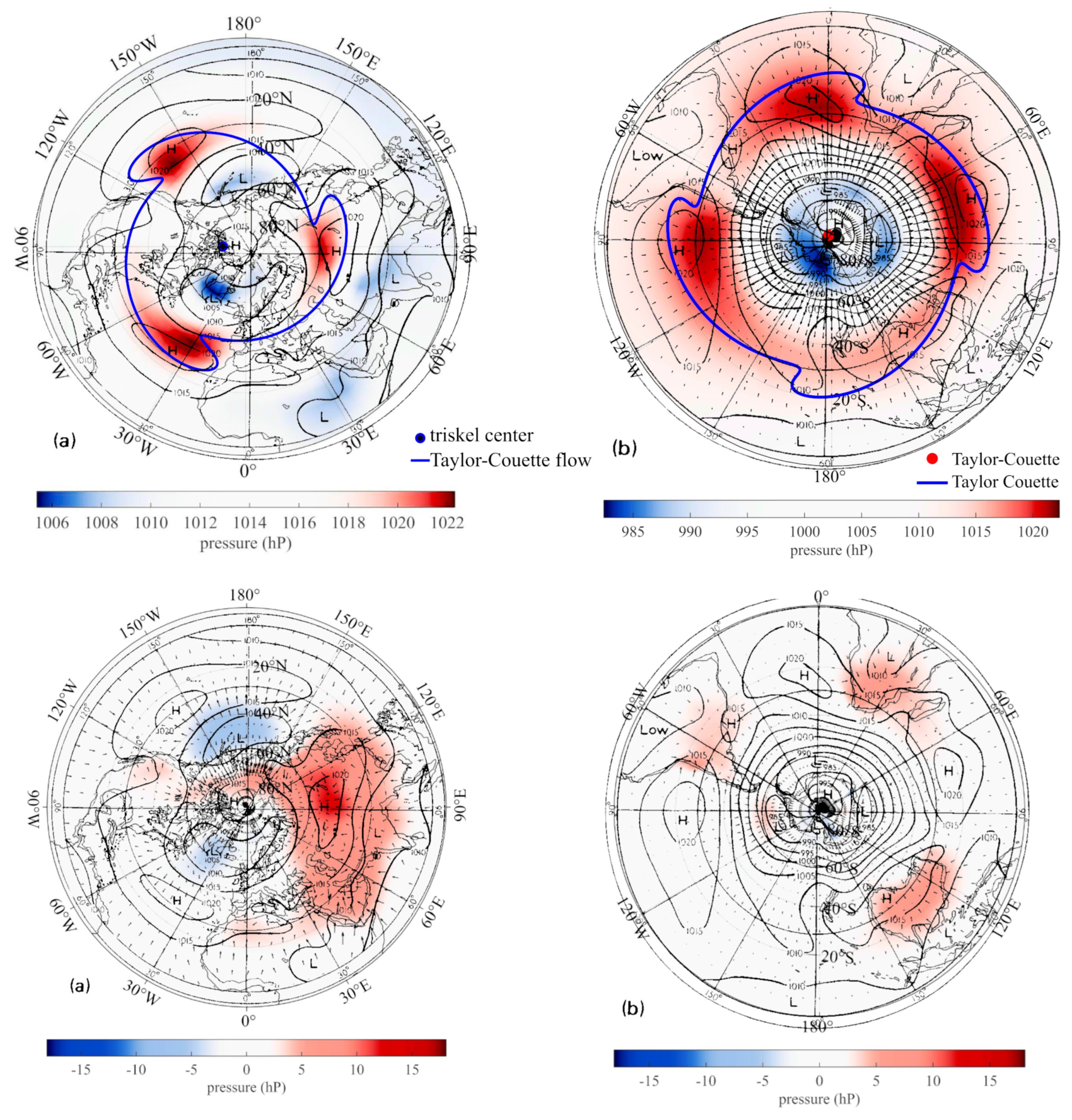
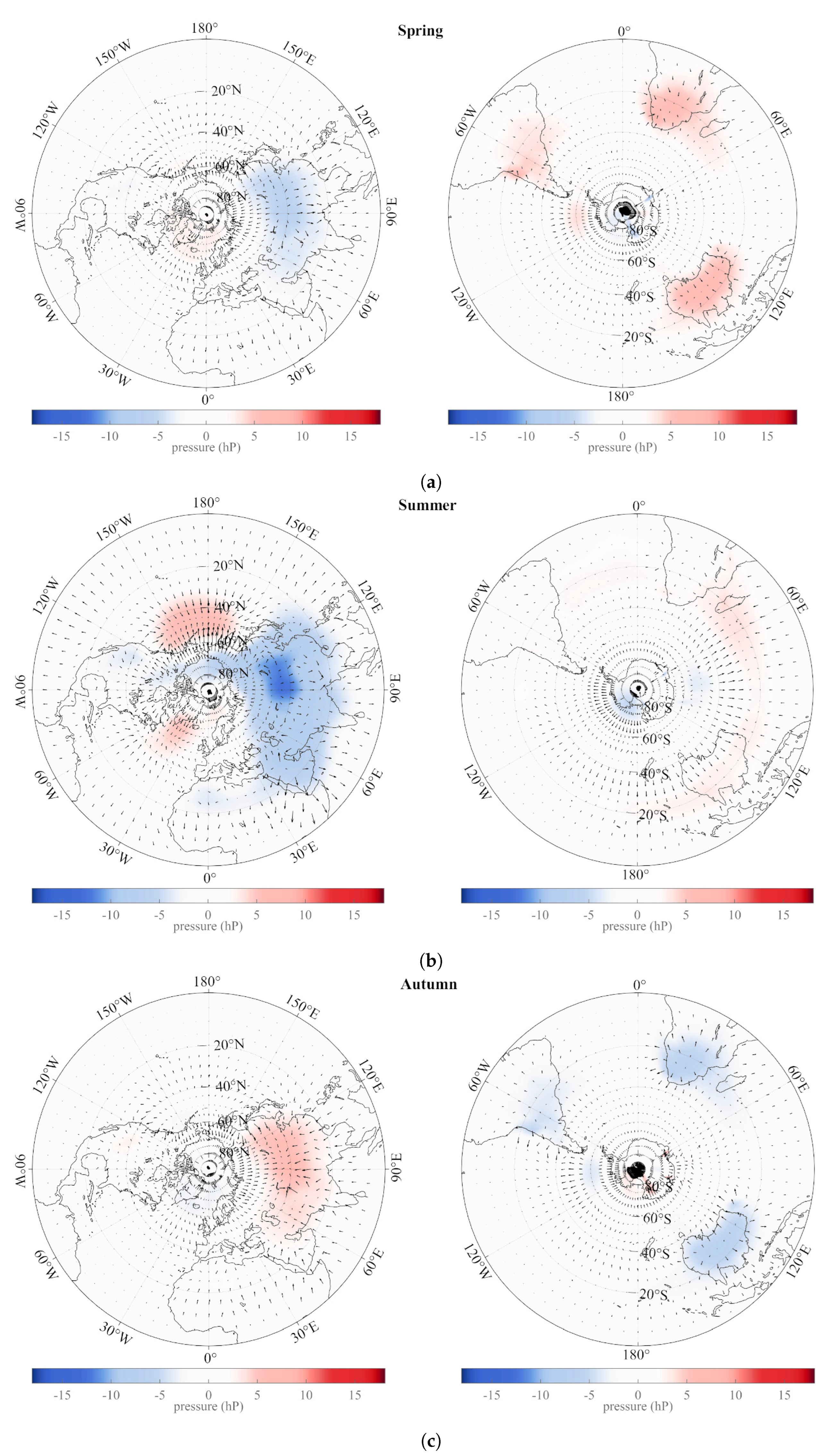
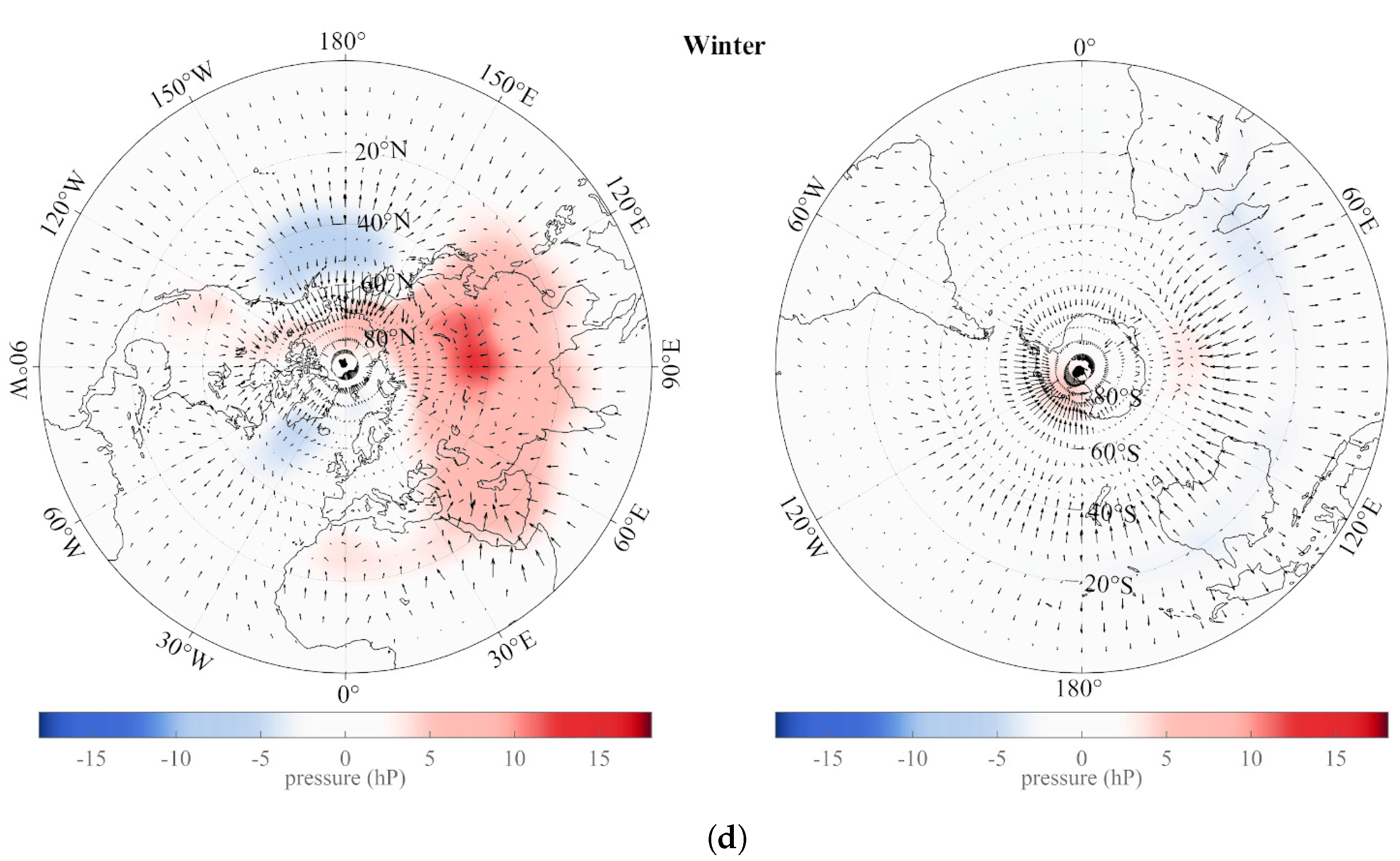
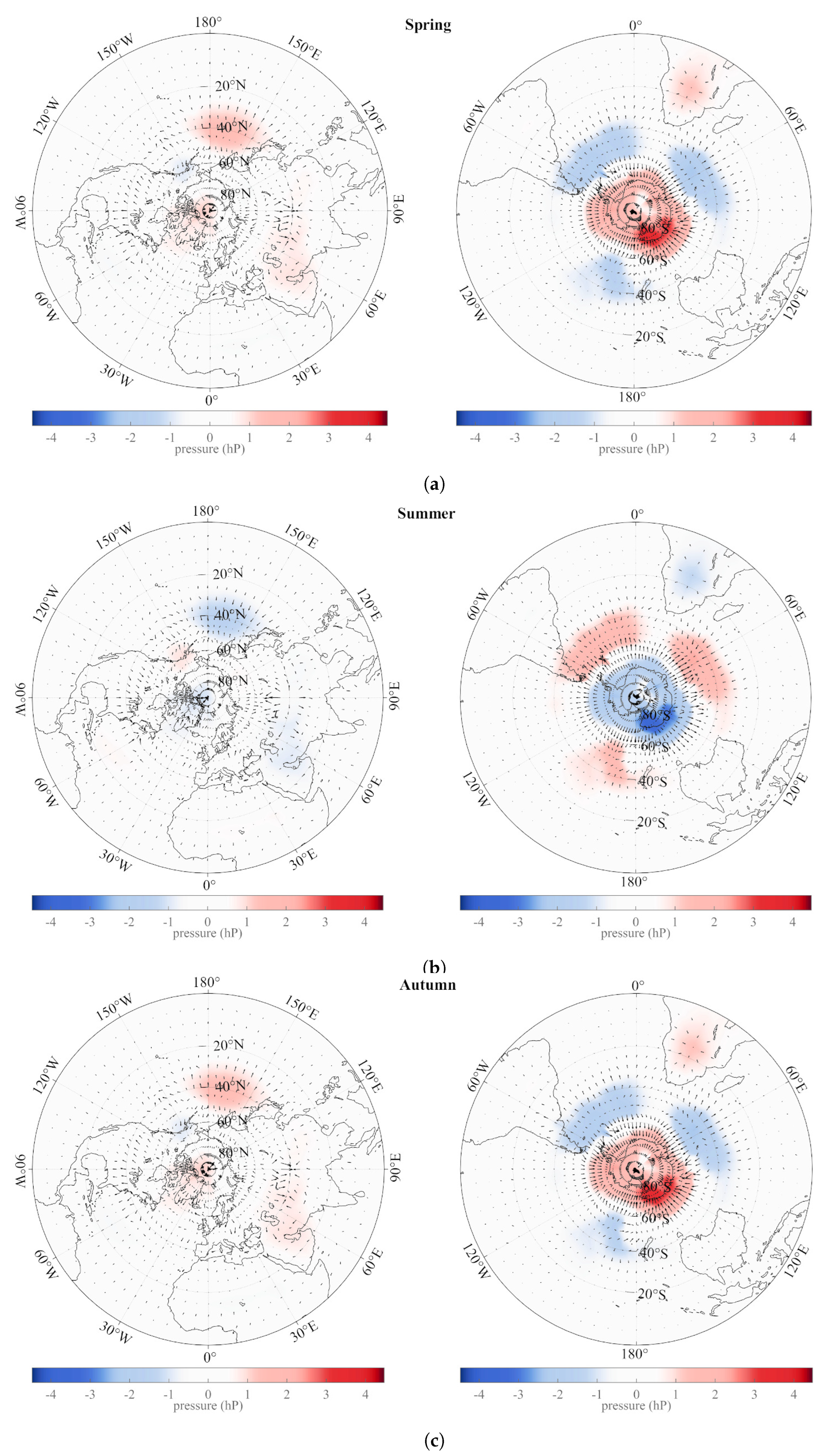
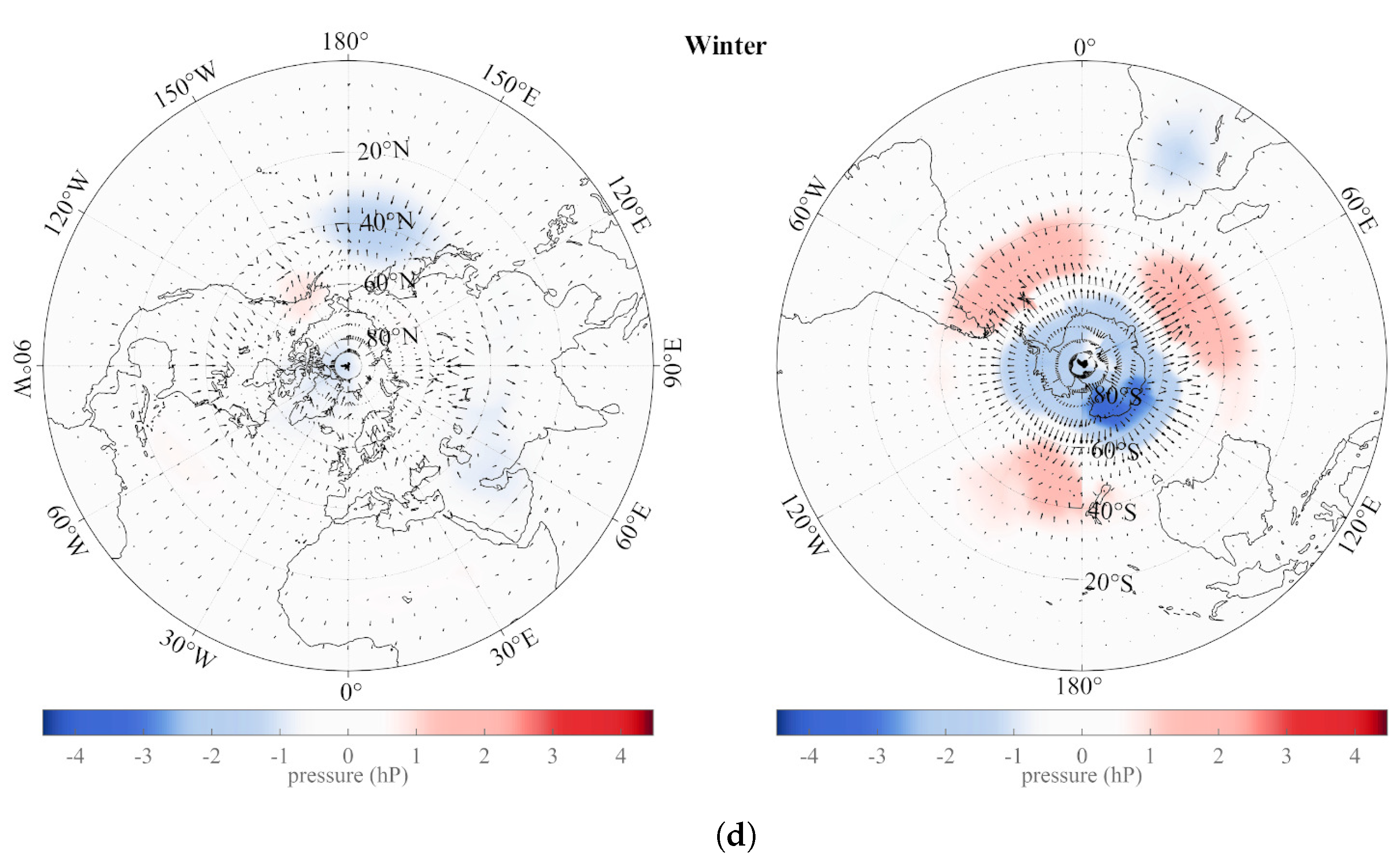
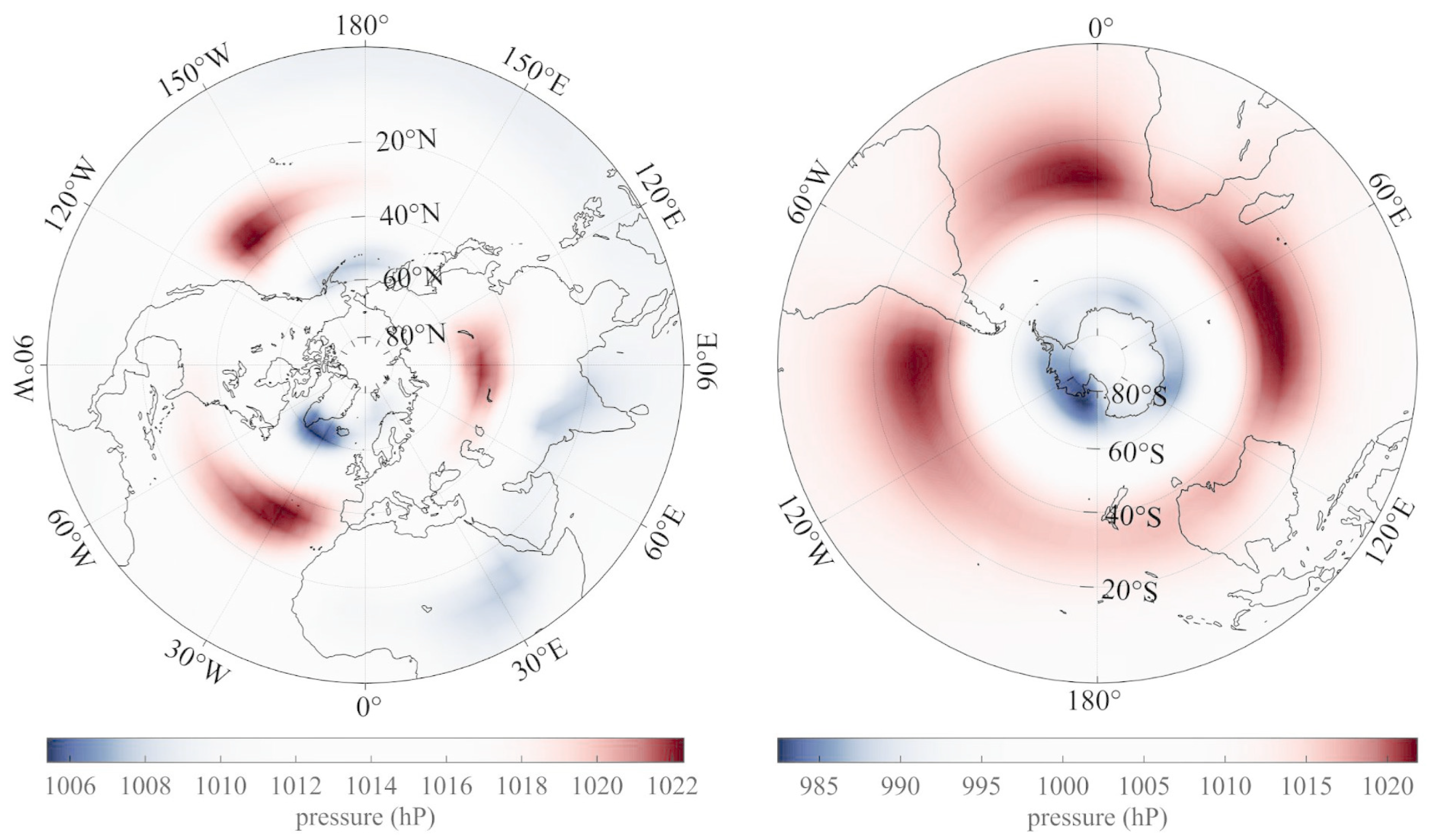
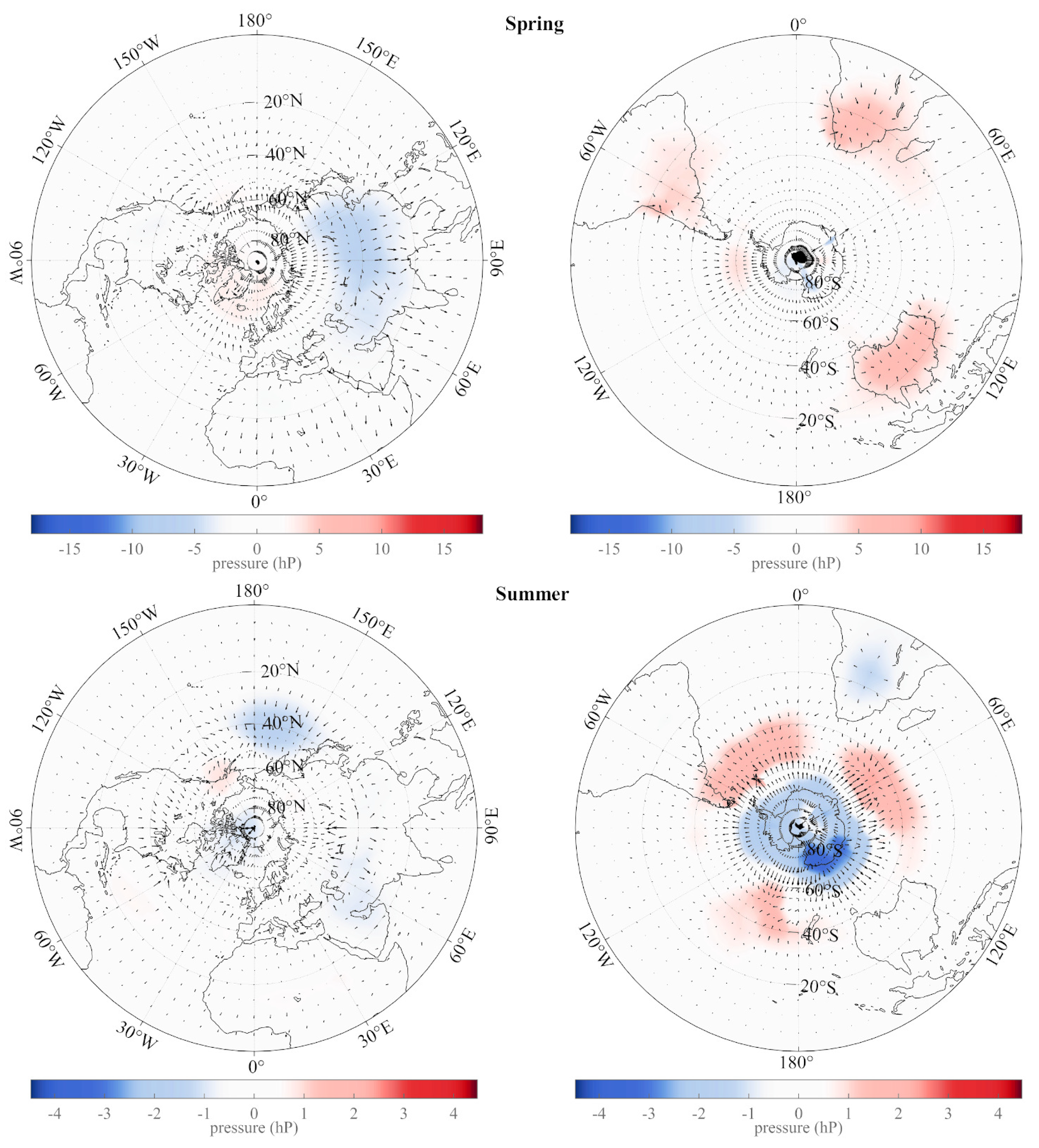
5. The Annual and Semi-Annual SSA Pressure Components: Spatial Analysis
6. Discussion
6.1. Symmetries and Forcings
6.2. Sun–Earth Distance and Phases
7. Sketch of a Mechanism
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Lopes, F.; Courtillot, V.; Le Mouël, J.L.; Gibert, D. Triskeles and Symmetries of Mean Global Sea-Level Pressure. Atmosphere 2022, 13, 1354. [Google Scholar] [CrossRef]
- Chandler, S.C. On the variation of latitude, I. Astron. J. 1891, 11, 59–61. [Google Scholar] [CrossRef]
- Chandler, S.C. On the variation of latitude, II. Astron. J. 1891, 11, 65–70. [Google Scholar] [CrossRef]
- Markowitz, W. Concurrent astronomical observations for studying continental drift, polar motion, and the rotation of the Earth. In Symposium-International Astronomical Union; Cambridge University Press: Cambridge, UK, 1968; Volume 32, pp. 25–32. [Google Scholar]
- Stoyko, A. Mouvement seculaire du pole et la variation des latitudes des stations du SIL. In Symposium-International Astronomical Union; Cambridge University Press: Cambridge, UK, 1968; Volume 32, pp. 52–56. [Google Scholar]
- Kirov, B.; Georgieva, K.; Javaraiah, J. 22-year periodicity in solar rotation, solar wind parameters and earth rotation. In Solar variability: From core to outer frontiers, Proceedings of the 10th European Solar Physics Meeting, Prague, Czech Republic, 9–14 September 2002; Wilson, A., Ed.; ESA SP-506; ESA Publications Division: Noordwijk, The Netherlands, 2002; Volume 1, pp. 149–152. ISBN 92-9092-816-6. [Google Scholar]
- Lambeck, K. The Earth’s Variable Rotation: Geophysical Causes and Consequences; Cambridge University Press: Cambridge, UK, 2005; ISBN 05-2167-330-5. [Google Scholar]
- Zotov, L.; Bizouard, C. On modulations of the Chandler wobble excitation. J. Geodyn. 2012, 62, 30–34. [Google Scholar] [CrossRef]
- Markowitz, W.; Guinot, B. Continental Drift, Secular Motion of the Pole, and Rotation of the Earth; Springer Science & Business Media: Dordrecht, Holland, 2013; Volume 32. [Google Scholar]
- Chao, B.F.; Chung, W.; Shih, Z.; Hsieh, Y. Earth’s rotation variations: A wavelet analysis. Terra Nova 2014, 26, 260–264. [Google Scholar] [CrossRef]
- Zotov, L.; Bizouard, C.; Shum, C.K. A possible interrelation between Earth rotation and climatic variability at decadal time-scale. Geod. Geodyn. 2016, 7, 216–222. [Google Scholar] [CrossRef]
- Lopes, F.; Le Mouël, J.L.; Gibert, D. The mantle rotation pole position. A solar component. Comptes Rendus Geosci. 2017, 349, 159–164. [Google Scholar] [CrossRef]
- Le Mouël, J.L.; Lopes, F.; Courtillot, V. Sea-Level Change at the Brest (France) Tide Gauge and the Markowitz Component of Earth’s Rotation. J. Coast. Res. 2021, 37, 683–690. [Google Scholar] [CrossRef]
- Lopes, F.; Le Mouël, J.L.; Courtillot, V.; Gibert, D. On the shoulders of Laplace. Phys. Earth Planet. Inter. 2021, 316, 106693. [Google Scholar] [CrossRef]
- Lopes, F.; Courtillot, V.; Le Mouël, J.L.; Gibert, D. On two formulations of polar motion and identification of its sources. arXiv 2022, arXiv:2204.11611v1. [Google Scholar] [CrossRef]
- Gleissberg, W. A long-periodic fluctuation of the sunspot numbers. Observatory 1939, 62, 158. [Google Scholar]
- Jose, P.D. Sun’s motion and sunspots. Astron. J. 1965, 70, 193–200. [Google Scholar] [CrossRef]
- Coles, W.A.; Rickett, B.J.; Rumsey, V.H.; Kaufman, J.J.; Turley, D.G.; Ananthakrishnan, S.A.J.W.; Sime, D.G. Solar cycle changes in the polar solar wind. Nature 1980, 286, 239–241. [Google Scholar] [CrossRef]
- Charvatova, I.; Strestik, J. Long-term variations in duration of solar cycles. Bull. Astron. Inst. Czechoslov. 1991, 42, 90–97. [Google Scholar]
- Scafetta, N. Empirical evidence for a celestial origin of the climate oscillations and its implications. J. Atmos. Sol.-Terr. Phys. 2010, 72, 951–970. [Google Scholar] [CrossRef]
- Le Mouël, J.L.; Lopes, F.; Courtillot, V. Identification of Gleissberg cycles and a rising trend in a 315-year-long series of sunspot numbers. Sol. Phys. 2017, 292, 1–9. [Google Scholar] [CrossRef]
- Usoskin, I.G. A history of solar activity over millennia. Living Rev. Sol. Phys. 2017, 14, 1–97. [Google Scholar] [CrossRef]
- Scafetta, N. Solar oscillations and the orbital invariant inequalities of the solar system. Sol. Phys. 2020, 295, 1–19. [Google Scholar] [CrossRef]
- Courtillot, V.; Lopes, F.; Le Mouël, J.L. On the prediction of solar cycles. Sol. Phys. 2021, 296, 1–23. [Google Scholar] [CrossRef]
- Scafetta, N. Reconstruction of the interannual to millennial scale patterns of the global surface temperature. Atmosphere 2021, 12, 147. [Google Scholar] [CrossRef]
- Wood, C.A.; Lovett, R.R. Rainfall, drought and the solar cycle. Nature 1974, 251, 594–596. [Google Scholar] [CrossRef]
- Mörth, H.T.; Schlamminger, L. Planetary motion, sunspots and climate. In Solar-Terrestrial Influences on Weather and Climate; Springer: Dordrecht, The Netherlands, 1979; pp. 193–207. [Google Scholar]
- Mörner, N.A. Planetary, solar, atmospheric, hydrospheric and endogene processes as origin of climatic changes on the Earth. In Climatic Changes on a Yearly to Millennial Basis; Springer: Dordrecht, The Netherlands, 1984; pp. 483–507. [Google Scholar]
- Schlesinger, M.E.; Ramankutty, N. An oscillation in the global climate system of period 65–70 years. Nature 1994, 367, 723–726. [Google Scholar] [CrossRef]
- Lau, K.M.; Weng, H. Climate signal detection using wavelet transform: How to maketime series sing. Bull. Am. Meteorol. Soc. 1995, 76, 2391–2402. [Google Scholar] [CrossRef]
- Courtillot, V.; Gallet, Y.; Le Mouël, J.L.; Fluteau, F.; Genevey, A. Are there connections between the Earth’s magnetic field and climate? Earth Planet. Sci. Lett. 2007, 253, 328–339. [Google Scholar] [CrossRef]
- Courtillot, V.; Le Mouël, J.L.; Kossobokov, V.; Gibert, D.; Lopes, F. Multi-decadal trends of global surface temperature: A broken line with alternating ˜30 years linear segments? Atmos. Clim. Sci. 2013, 3, 34080. [Google Scholar] [CrossRef]
- Le Mouël, J.L.; Lopes, F.; Courtillot, V. A solar signature in many climate indices. J. Geophys. Res. Atmos. 2019, 124, 2600–2619. [Google Scholar] [CrossRef]
- Scafetta, N.; Milani, F.; Bianchini, A. A 60-year cycle in the Meteorite fall frequency suggests a possible interplanetary dust forcing of the Earth’s climate driven by planetary oscillations. Geophys. Res. Lett. 2020, 47, e2020GL089954. [Google Scholar] [CrossRef]
- Connolly, R.; Soon, W.; Connolly, M.; Baliunas, S.; Berglund, J.; Butler, C.J.; Zhang, W. How much has the Sun influenced Northern Hemisphere temperature trends? An ongoing debate. Res. Astron. Astrophys. 2021, 21. [Google Scholar] [CrossRef]
- Guinot, B. Variation du pôle et de la vitesse de rotation de la Terre. In Traité de Géophysique Interne, Tome I: Sismologie et Pesanteur; Masson & Cie, Éditeurs: Paris, France, 1973. [Google Scholar]
- Ray, R.D.; Erofeeva, S.Y. Long-period tidal variations in the length of day. J. Geophys. Res. Solid Earth 2014, 119, 1498–1509. [Google Scholar] [CrossRef]
- Le Mouël, J.L.; Lopes, F.; Courtillot, V.; Gibert, D. On forcings of length of day changes: From 9-day to 18.6-year oscillations. Phys. Earth Planet. Inter. 2019, 292, 1–11. [Google Scholar] [CrossRef]
- Dumont, S.; Silveira, G.; Custódio, S.; Guéhenneux, Y. Response of Fogo volcano (Cape Verde) to lunisolar gravitational forces during the 2014–2015 eruption. Phys. Earth Planet. Inter. 2021, 312, 106659. [Google Scholar] [CrossRef]
- Petrosino, S.; Dumont, S. Tidal modulation of hydrothermal tremor: Examples from Ischia and Campi Flegrei volcanoes, Italy. Front. Earth Sci. 2022, 9, 775269. [Google Scholar] [CrossRef]
- Stephenson, F.R.; Morrison, L.V. Long-term changes in the rotation of the Earth: 700 BC to AD 1980. Philos. Trans. R. Soc. A 1984, 313, 47–70. [Google Scholar] [CrossRef]
- Hulot, G.; Le Huy, M.; Le Mouël, J.L. Influence of core flows on the decade variations of the polar motion. Geophys. Astrophys. Fluid Dyn. 1996, 82, 35–67. [Google Scholar] [CrossRef]
- Deng, S.; Liu, S.; Mo, X.; Jiang, L.; Bauer-Gottwein, P. Polar drift in the 1990s explained by terrestrial water storage changes. Geophys. Res. Lett. 2021, 48, e2020GL092114. [Google Scholar] [CrossRef]
- Gross, R.S.; Fukumori, I.; Menemenlis, D. Atmospheric and oceanic excitation of the Earth’s wobbles during 1980–2000. J. Geophys. Res. Solid Earth 2003, 108. [Google Scholar] [CrossRef]
- Bizouard, C.; Seoane, L. Atmospheric and oceanic forcing of the rapid polar motion. J. Geod. 2010, 84, 19–30. [Google Scholar] [CrossRef]
- Chen, J.; Wilson, C.R.; Kuang, W.; Chao, B.F. Interannual oscillations in earth rotation. J. Geophys. Res. Solid Earth 2019, 124, 13404–13414. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifchitz, E.M. Mechanism: Course of Theoretical Physics; Mir Edition: Moscow, Russia, 1984. [Google Scholar]
- Wilson, C.R.; Haubrich, R.A. Meteorological excitation of the Earth’s wobble. Geophys. J. Int. 1976, 46, 707–743. [Google Scholar] [CrossRef]
- Spitaler, R. Die ursache der breitenschwankungen; Wien, K.-K., Ed.; Hof- und staatsdruckerei: Vienna, Austria, 1897. [Google Scholar]
- Spitaler, R. Die periodischen Luftmassenvershiebungen und ihr Einfluss auf dieLagenanderungen der Erdachse (Breitenschwankungen). Petermanns Mitteilungen Erganxungsband 1901, 29, 137. [Google Scholar]
- Jeffreys, H. Causes contributory to the Annual Variation of Latitude. (Plate 8). Mon. Not. R. Astron. Soc. 1916, 76, 499–525. [Google Scholar] [CrossRef]
- Munk, W.; Mohamed, M. Atmospheric excitation of the Earth’s wobble. Geophys. J. Int. 1961, 4, 339–358. [Google Scholar] [CrossRef]
- Allan, R.; Ansell, T. A new globally complete monthly historical gridded mean sea level pressure dataset (HadSLP2): 1850–2004. J. Clim. 2006, 19, 5816–5842. [Google Scholar] [CrossRef]
- Golyandina, N.; Zhigljavsky, A. Singular Spectrum Analysis for Time Series; Springer: Berlin, Germany, 2013; ISBN 978-3642349126. [Google Scholar]
- Lemmerling, P.; Van Huffel, S. Analysis of the structured total least squares problem for hankel/toeplitz matrices. Numer. Algorithms 2001, 27, 89–114. [Google Scholar] [CrossRef]
- Golub, G.H.; Reinsch, C. Singular value decomposition and least squares solutions. In Linear Algebra; Springer: Berlin/Heidelberg, Germany, 1971; pp. 134–151. [Google Scholar]
- Usoskin, I.G.; Solanki, S.K.; Schüssler, M.; Mursula, K.; Alanko, K. Millennium-scale sunspot number reconstruction: Evidence for an unusually active Sun since the 1940s. Phys. Rev. Let. 2017, 91, 211101. [Google Scholar] [CrossRef]
- Schwabe, H. Sonnenbeobachtungen im Jahre 1843. Von Herrn Hofrath Schwabe in Dessau. Astron. Nachrichten 1844, 21, 233. [Google Scholar]
- Adhikari, S.; Ivins, E.R. Climate-driven polar motion: 2003–2015. Sci. Adv. 2016, 2, e1501693. [Google Scholar] [CrossRef]
- Vondrák, J.; Ron, C.; Pesek, I.; Cepek, A. New global solution of Earth orientation parameters from optical astrometry in 1900–1990. Astron. Astrophys. 1995, 297, 899. [Google Scholar]
- Gibert, D.; Holschneider, M.; Le Mouël, J.L. Wavelet analysis of the Chandler wobble. J. Geophys. Res. Solid Earth 1998, 103, 27069–27089. [Google Scholar] [CrossRef]
- Gibert, D.; Le Mouël, J.L. Inversion of polar motion data: Chandler wobble, phase jumps, and geomagnetic jerks. J. Geophys. Res. Solid Earth 2008, 113. [Google Scholar] [CrossRef]
- Laplace, P.S. Traité de Mécanique Céleste; de l’Imprimerie de Crapelet: Paris, France, 1799. [Google Scholar]
- Lamb, H.H. Climate: Present, Past and Future. 1. Fundamentals and Climate Now; Methuen Publishing: London, UK, 1972. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Fluid Mechanics: Courses of Theoretical Physics; Pergamon Press: Oxford, UK, 1987; Volume 6. [Google Scholar]
- Chandrasekhar, S. Hydrodynamic and Hydromagnetic Stability; Oxford University Press: Oxford, UK, 1961; ISBN 978-0486640716. [Google Scholar]
- Frisch, U. Turbulence: The Legacy of AN Kolmogorov; Cambridge University Press: Cambridge, UK, 1995; ISBN 0521457130. [Google Scholar]
- Landau, L.D. On the problem of turbulence. Dokl. Akad. Nauk USSR 1944, 44, 311. [Google Scholar]
- Schrauf, G. The first instability in spherical Taylor-Couette flow. J. Fluid Mech. 1986, 166, 287–303. [Google Scholar] [CrossRef]
- Mamun, C.K.; Tuckerman, L.S. Asymmetry and Hopf bifurcation in spherical Couette flow. Phys. Fluids 1995, 7, 80–91. [Google Scholar] [CrossRef]
- Nakabayashi, K.; Tsuchida, Y. Flow-history effect on higher modes in the spherical Couette system. J. Fluid Mech. 1995, 295, 43–60. [Google Scholar] [CrossRef]
- Hollerbach, R.; Junk, M.; Egbers, C. Non-axisymmetric instabilities in basic state spherical Couette flow. Fluid Dyn Res. 2006, 38, 257. [Google Scholar] [CrossRef]
- Mahloul, M.; Mahamdia, A.; Kristiawan, M. The spherical Taylor–Couette flow. Eur. J. Mech.-B/Fluids 2016, 59, 1–6. [Google Scholar] [CrossRef]
- Garcia, F.; Seilmayer, M.; Giesecke, A.; Stefani, F. Modulated rotating waves in the magnetised spherical Couette system. J. Nonlinear Sci. 2019, 29, 2735–2759. [Google Scholar] [CrossRef]
- Mannix, P.M.; Mestel, A.J. Bistability and hysteresis of axisymmetric thermalconvection between differentially rotating spheres. J. Fluid Mech. 2021, 911. [Google Scholar] [CrossRef]
- Rayleigh, L. On convection currents in a horizontal layer of fluid, when the higher temperature is on the under side. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1916, 32, 529–546. [Google Scholar] [CrossRef]
- Taylor, G.I., VIII. Stability of a viscous liquid contained between two rotating cylinders. Philos. Trans. R. Soc. A 1923, 223, 289–343. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Courtillot, V.; Le Mouël, J.-L.; Lopes, F.; Gibert, D. On the Nature and Origin of Atmospheric Annual and Semi-Annual Oscillations. Atmosphere 2022, 13, 1907. https://doi.org/10.3390/atmos13111907
Courtillot V, Le Mouël J-L, Lopes F, Gibert D. On the Nature and Origin of Atmospheric Annual and Semi-Annual Oscillations. Atmosphere. 2022; 13(11):1907. https://doi.org/10.3390/atmos13111907
Chicago/Turabian StyleCourtillot, Vincent, Jean-Louis Le Mouël, Fernando Lopes, and Dominique Gibert. 2022. "On the Nature and Origin of Atmospheric Annual and Semi-Annual Oscillations" Atmosphere 13, no. 11: 1907. https://doi.org/10.3390/atmos13111907
APA StyleCourtillot, V., Le Mouël, J.-L., Lopes, F., & Gibert, D. (2022). On the Nature and Origin of Atmospheric Annual and Semi-Annual Oscillations. Atmosphere, 13(11), 1907. https://doi.org/10.3390/atmos13111907





