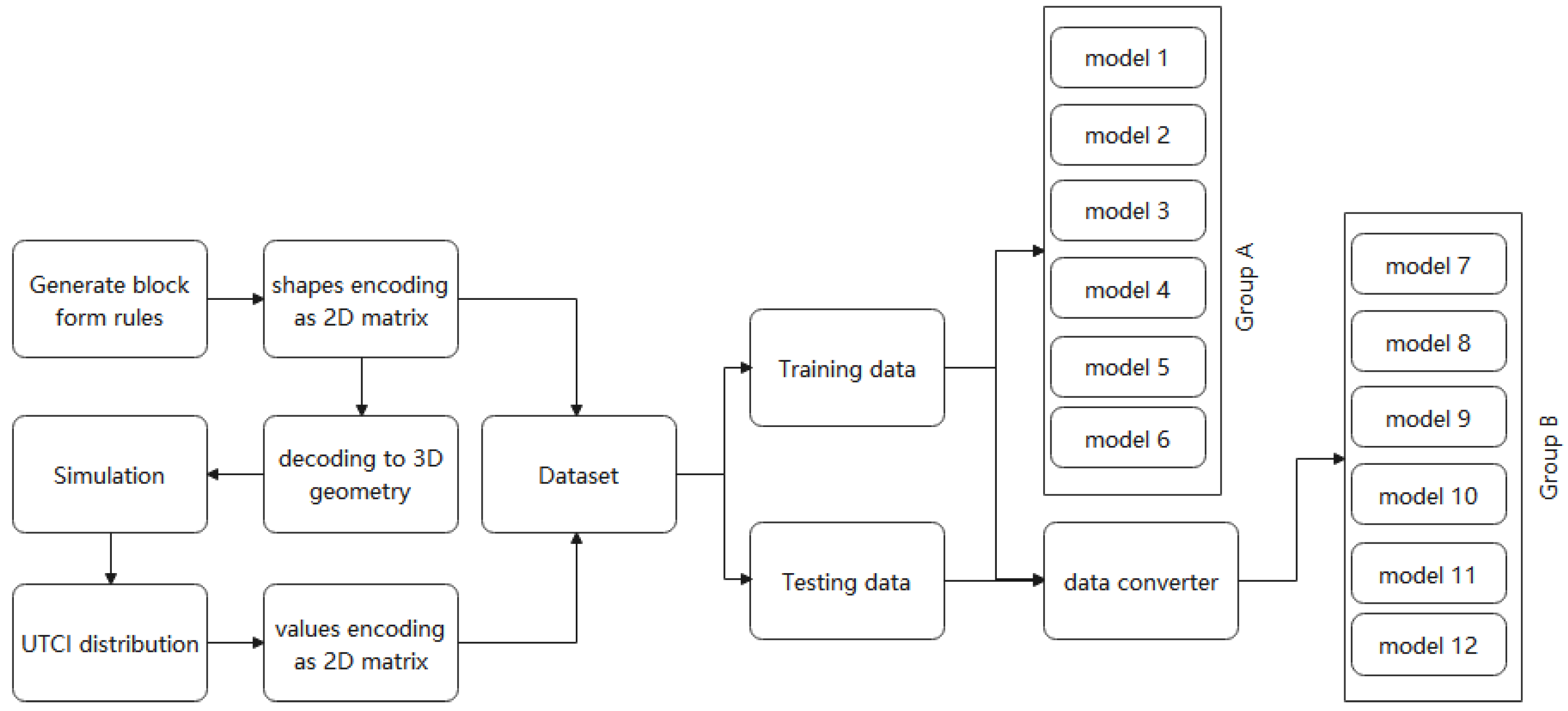
To predict the UTCI distribution for outdoor sites through the convolutional neural network workflow shown in
Figure 2, I used the grasshopper platform to generate 2400 sets of block scenarios as a data source. First, the coding rules of the building form were set (see
Section 2.1), and the distribution of UTCI and the block form were turned into a two-dimensional encoding to form a dataset (see
Section 2.2). Next, based on the two fundamental theories mentioned above, six kinds of neural network models were separately established, the same dataset was used to train them, and the final hyperparameter model was obtained (see
Section 2.3). These models’ training processes and performance were then evaluated and compared.
2.1. Translation of Architectural Design Scheme Performance Problems
Due to the creative characteristics of architects, they may create different forms of solutions to potential design problems. In this process, the primary problem of prediction requires a translation method to automatically convert potential design solutions into languages that computers can read.
Traditional three-dimensional solid models can be expressed in many ways, such as parametric and feature-based modeling, sweeping, implicit representation, constructive solid geometry, and cell decomposition [
39]. However, these methods are not all applicable to machine learning computing. To summarize the related literature,
Table 2 describes the primary methods of the three major schemes in the field.
The first method, parameter representation, is suitable for simple block forms. For example, Han abstracted a typical one-sided daylight simulation scene in office buildings into a standard room unit, and described it by parameters such as room depth, width, height, window orientation, window–wall ratio, and window size. Artificial neural networks, extreme gradient boosting, random forest, and support vector regression algorithms were used to establish the mapping relationship between building parameters and the daylight distribution, and the R2 score of the prediction results for the test set was 0.996, and so better fulfilled the need for indoor daylight distribution prediction in ordinary office buildings [
19,
41,
42]. Second, constructive solid geometry, in terms of computational science, refers to complex geometry calculated by Boolean operations from basic geometries. In alternative performance algorithms, the complex building volume is usually decomposed into variants of different meta-models in the area. Then, the performance of the meta-model is separately calculated to obtain comprehensive data on complex buildings. Zhu developed a method that disassembles complex urban blocks into five types of box units and then calculates the annual solar radiation of each unit using radiance. Finally, each box unit’s geometric parameters and boundary conditions are imported into the neural networks for training to construct the calculation networks of the meta-model to determine the energy consumption of complex blocks [
43]. This method can control the timing within a few minutes for hundreds of thousands of buildings, and the cooling and heating load can be controlled within 6–10%. The third method is cell decomposition, which decomposes the building forms into a finite number of cells. According to the different data structures, this method can be expressed as point clouds, depth maps, or octrees. For example, Mokhtar converted a 3D graph into a height map on a Cartesian grid, and the gray image level was used to represent it. Then, the steady-state RANS equations with a turbulence model of realizable k-ε were used to solve the cases to obtain airflow distributions. The PIX2PIX model was used to establish the mapping between the building form and the wind environment of a building site with these labeled data, which enabled the rapid calculation of the CFD of the site [
9].
Architecture is a space-based discipline. The relationship between the performance of an environment, and the building form is also important. In the process of converting building form into a computer language, the above three methods have limitations. Parameter representation and constructive solid geometry employ feature vectors, which are generally variables with different physical meanings, such as the width and depth of a room, and the height and width of a window. The process of conversion requires a certain syntax to be followed, which can be difficult to resolve if the variables are outside the scope of the syntax. Therefore, in practice, these two methods are more suitable for performance analysis scenarios with low spatial sensitivity and simple building forms, such as indoor lighting and energy consumption calculations. The UTCI distribution of an outdoor site involved in this study is directly tied to the surrounding geometrical morphology, making cell decomposition a more suitable trans-algorithm. In this method, the topological relationships of the spatial information are preserved as much as possible, but compared with the previous two methods, the recoded data have a larger dimension and lower information density, and the types of each data dimension of the matrix are the same. As such, I used cell decomposition to analyze the building form and performance prediction.
2.2. Case Description and Database Establishment
The training of machine learning models requires a large amount of training data. In this study, to form a database, I generated many random building forms through grasshopper script and calculated the UTCI distribution of these cases.
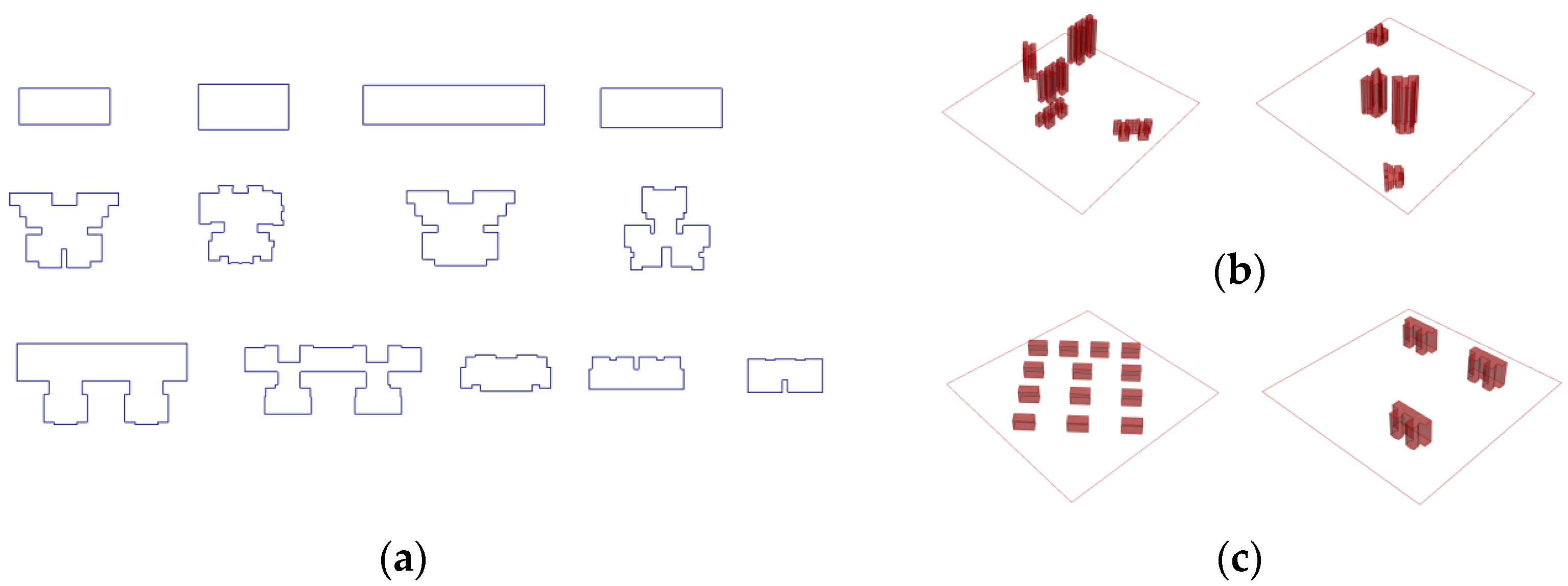
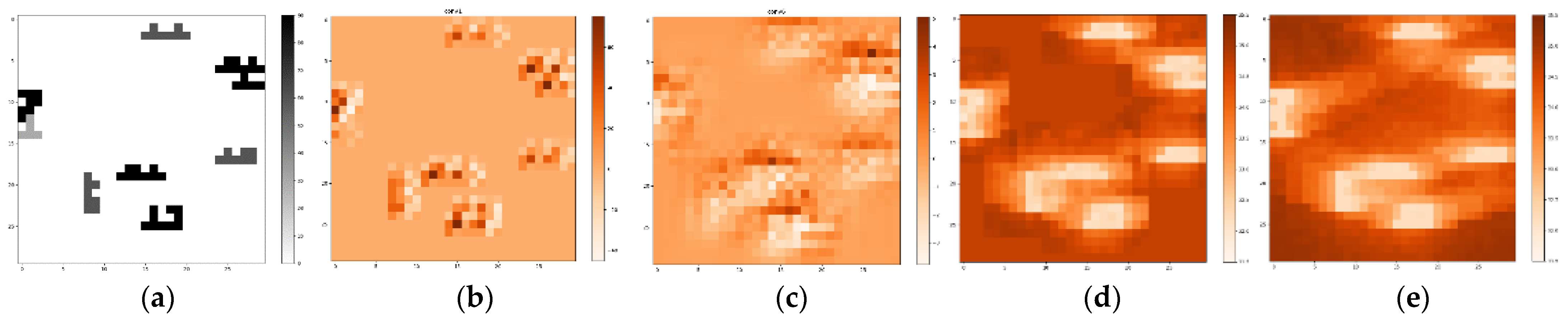
To ensure the data were more closely related to the actual underlying buildings (
Figure 3a), I referred to the Standard for Urban Residential Area Planning and Design, with 150–250 m being appropriate for enclosed residential units. The target site was slightly expanded to a rectangle of 300 m
2. The architectural form at the site was freestyle (
Figure 3b) and determinant (
Figure 3c). By randomly setting the building height, location, and orientation, the architectural forms of 2400 residential blocks were generated.
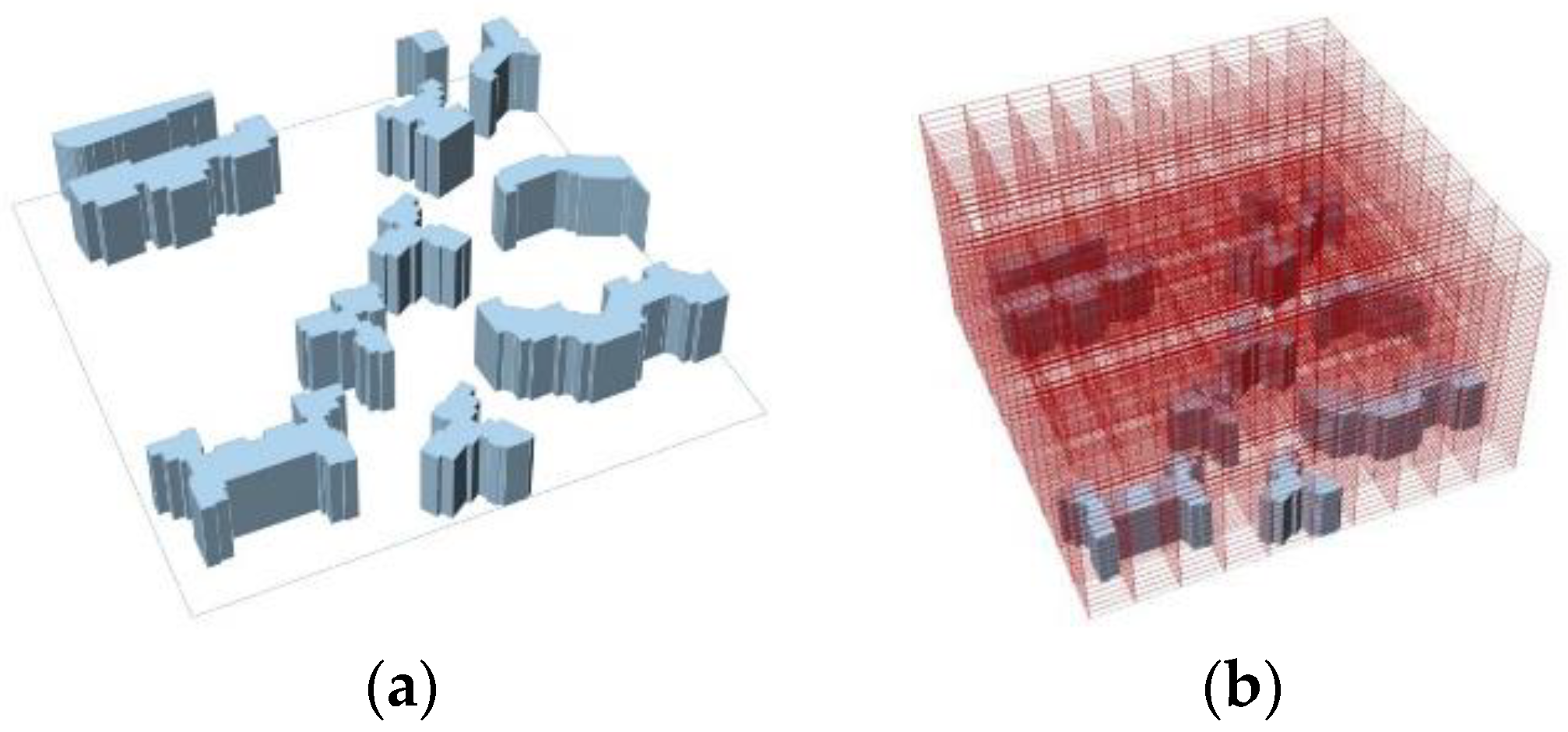
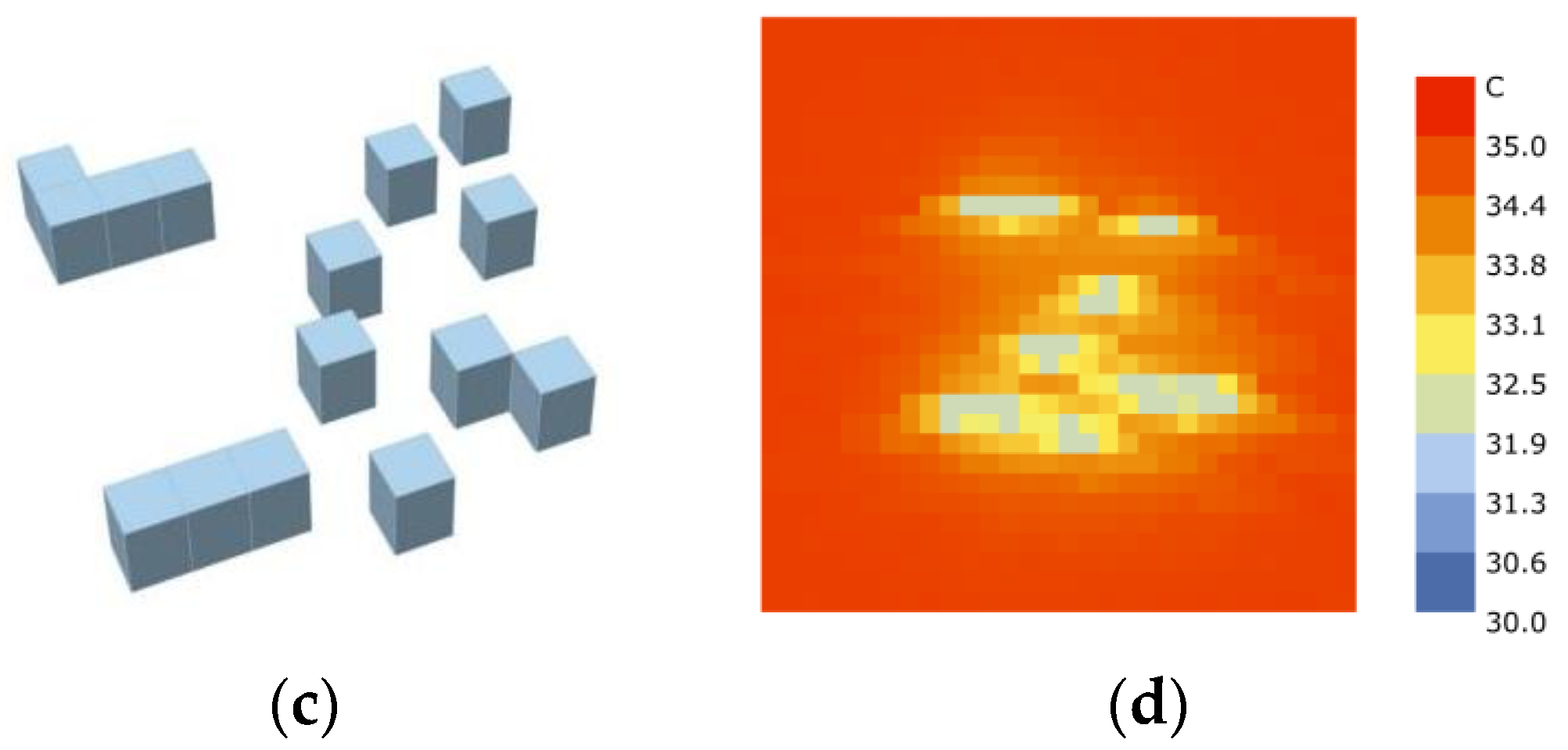
As described in
Section 2.1, I used the cell decomposition method to set the coding rules of building form, which considered each unit as 10 × 10 × 1 m, and built an orthogonal Cartesian coordinate system for the site. I determined the units in the site one by one. If the unit center was located inside the building geometry, the unit body was retained and marked as 1; otherwise, it was marked as 0. Subsequently, numbers in the Z-direction were added up and converted into a 2D matrix, which was denoted as
Si, where
i is the serial number of cases. Each number in the matrix represented the height of the geometry in the position. Finally, the 2D matrix representing the shape was re-decoded into a 3D shape, and UTCI was calculated to obtain the computed value matrix (
Figure 4).
UTCI was proposed by Cost Acition730 in 2009, which is an evaluation index for the thermal comfort of the human body under heat stress based on the theory of thermal physiological exchange [
22,
23,
44,
45,
46,
47]. In this study, UTCI calculation tools were provided by grasshopper and ladybug (
Table 3). The calculation principle of the average radiant temperature in the calculation process can be found in [
48]. The wind speed, relative humidity, and dry bulb temperature were directly acquired from typical meteorological data files. The calculation surface was a horizontal plane 1.5 m above the ground, and the analysis grid was 0.5 m. The summer solstice day was selected as the typical calculation day (22 June). The weather datafile was downloaded from
https://www.ladybug.tools/epwmap accessed on 1 september 2021; these data were derived from the Department of Energy (
https://www.energy.gov/ accessed on 1 september 2021). On the typical day, I used hourly radiation, wind speed, and temperature data. Then, the average UTCI distribution value in the preceding matrix was calculated as the representative value of this position, which was converted into a two-dimensional matrix, denoted as
Ri, where
i is the serial number of the building case.
The building form data matrix Si and the site UTCI distribution matrix Ri jointly constituted sequence i in the dataset, forming an original dataset with a total of 2400 data pieces. The data order was disrupted and divided into training and testing data in 0.7 and 0.3 ratios. All the model training and testing in the study was calculated based on this dataset.
2.3. Construction of Neural Network Model
Based on the discussion in
Section 1.2 and
Section 1.3, compared with the traditional machine learning methods that directly rely on the iterative fitting of massive data to form a prediction model, the robustness of a model framework based on physical laws and prior knowledge is higher.
Many studies [
38,
49,
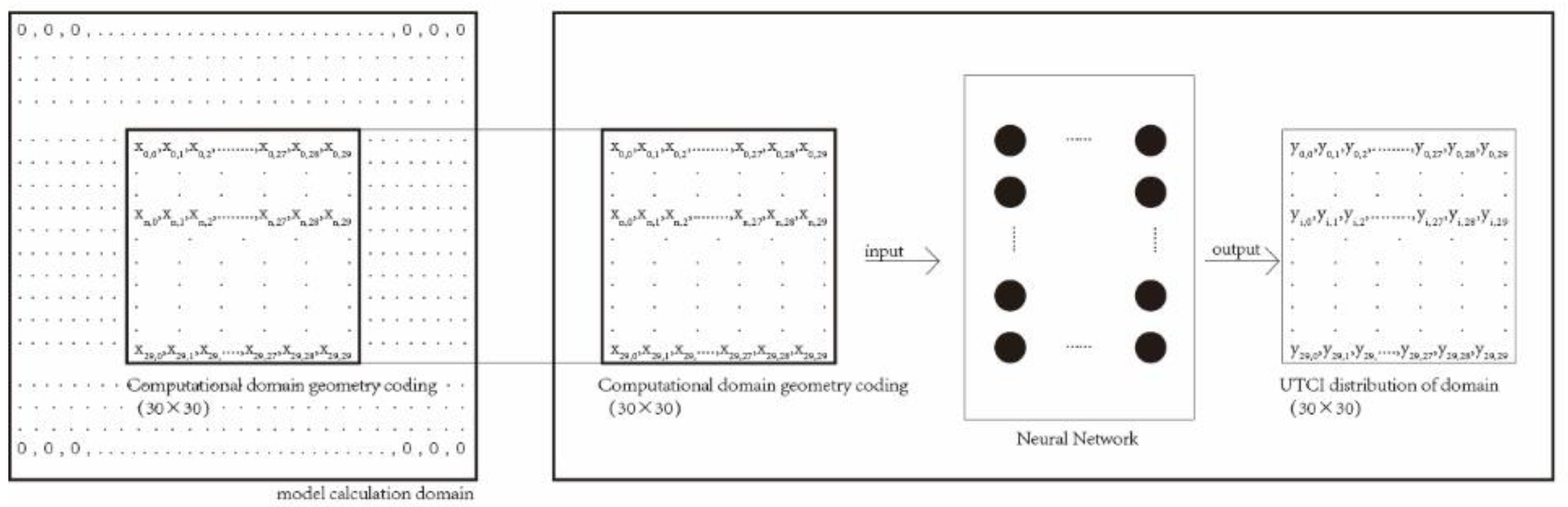
50] have proven that (1) for the space of the building site, the UTCI distribution is closely related to the building form; (2) for a point in space, the UTCI of this point is influenced by the architectural form of its environment. This connection is constant and does not change with changes in space. According to these two theories, I constructed two groups of neural network models, Groups A and B. The calculation methods of the two groups of models are shown in
Figure 5 and
Figure 6, with the schematic diagrams for Groups A and B, respectively.
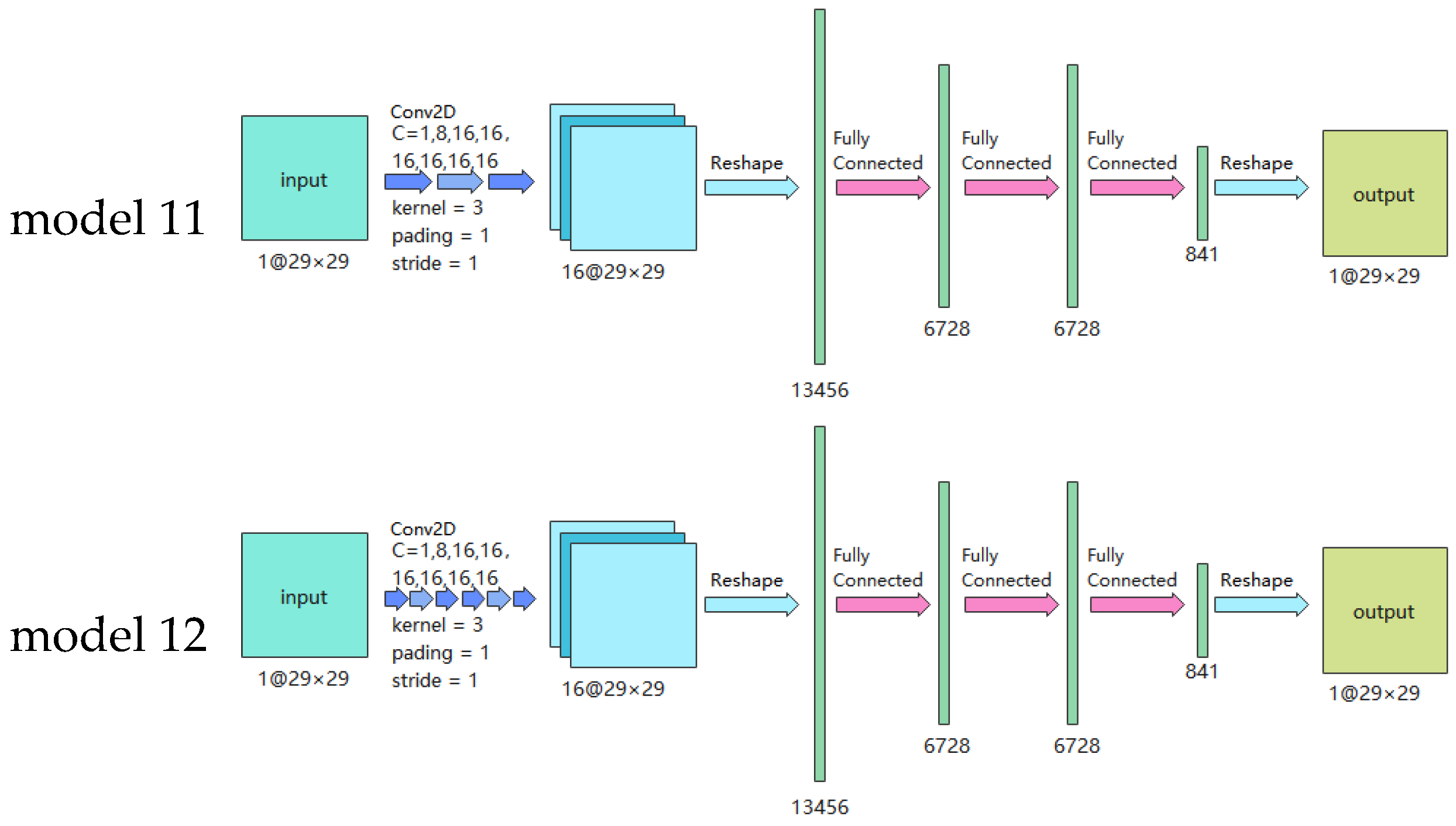
Group A regarded the block space as a whole, and the input of the model was the block space form coding, Si, with dimensions of 30 × 30. The output was the UTCI distribution of the pedestrian height plane, Ri, which had the same dimensions of 30 × 30. and from the Group A dataset (, ).
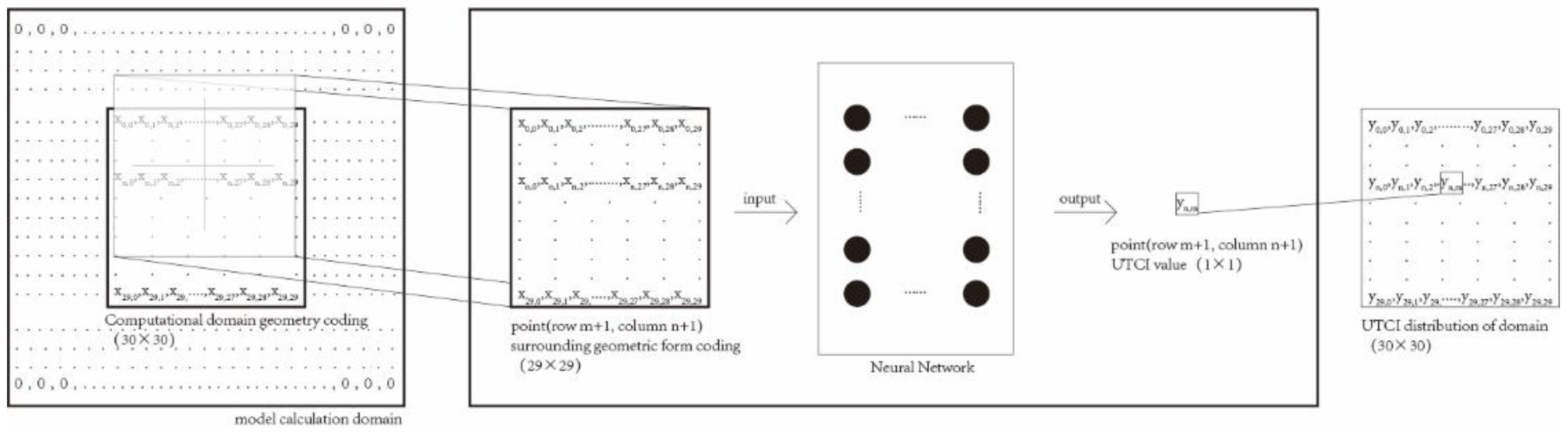
Group B regarded the block space as a discrete measurement point and calculations were made point-by-point based on the surrounding information of the measurement point. The input port of its model encodes the geometric block information in a specific range of surrounding blocks, denoted as , and the dimension was 29 × 29. The model’s output was the UTCI value of the point, which was recorded as , and the dimension was 1.
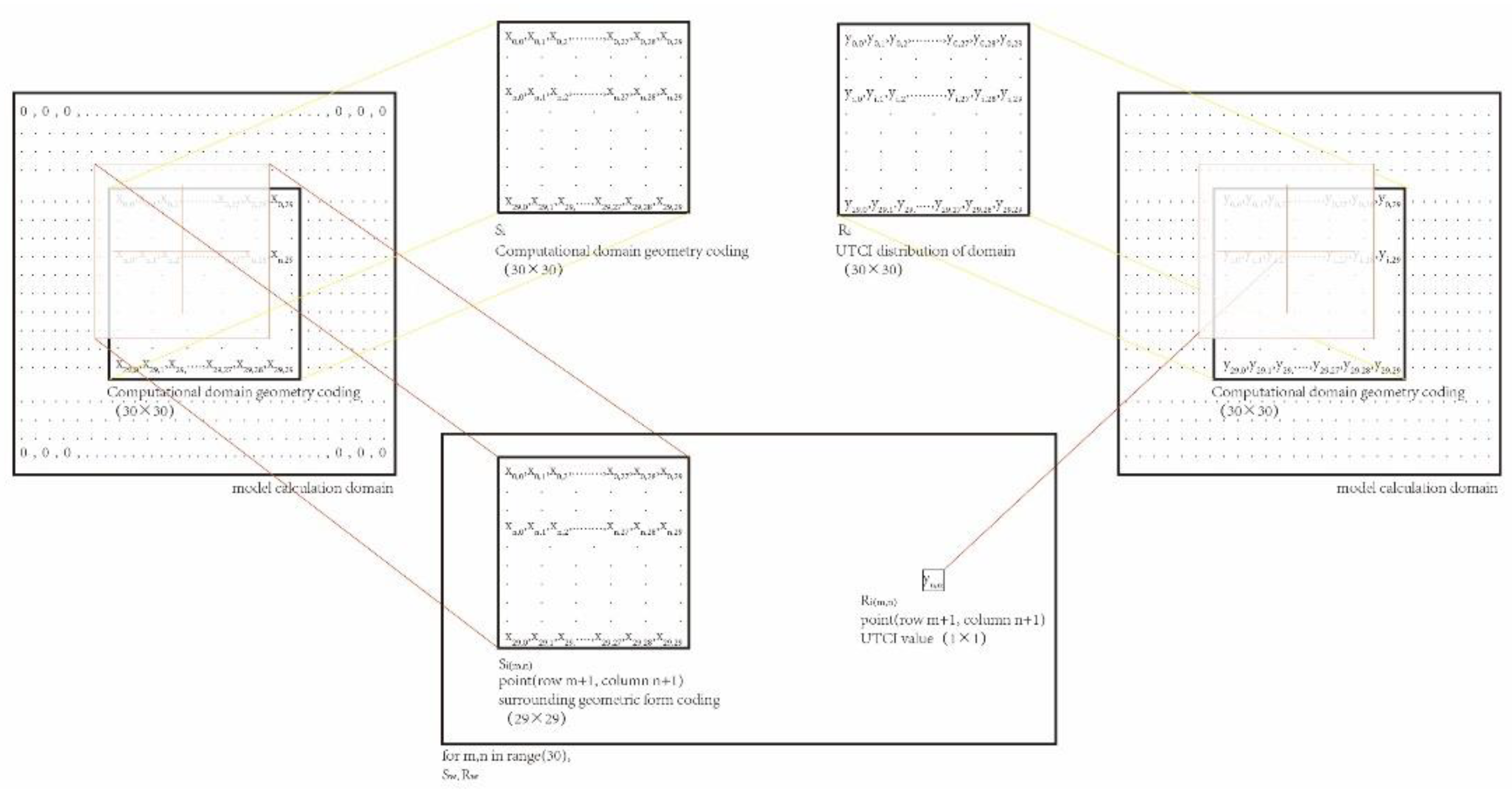
Both
and
were transformed from the original
, as shown in
Figure 7. Specifically, for the
ith site case, the matrix corresponding to a point
in the space of row m and column n in
should be a 29 × 29 matrix consisting of
to
. The data corresponding to
were the values
in row m and column n of
. After data rule conversion, each building site case could be converted into 900 sets of data, and a total of 1,749,539 pieces of data were obtained after removing duplicate data, forming the Group B dataset (
).
The role of the critical steps in a system can be judged and analyzed by adjusting the hyperparameters of models [
28,
29]. Therefore, for the two groups of models above, as shown in
Table 4 and
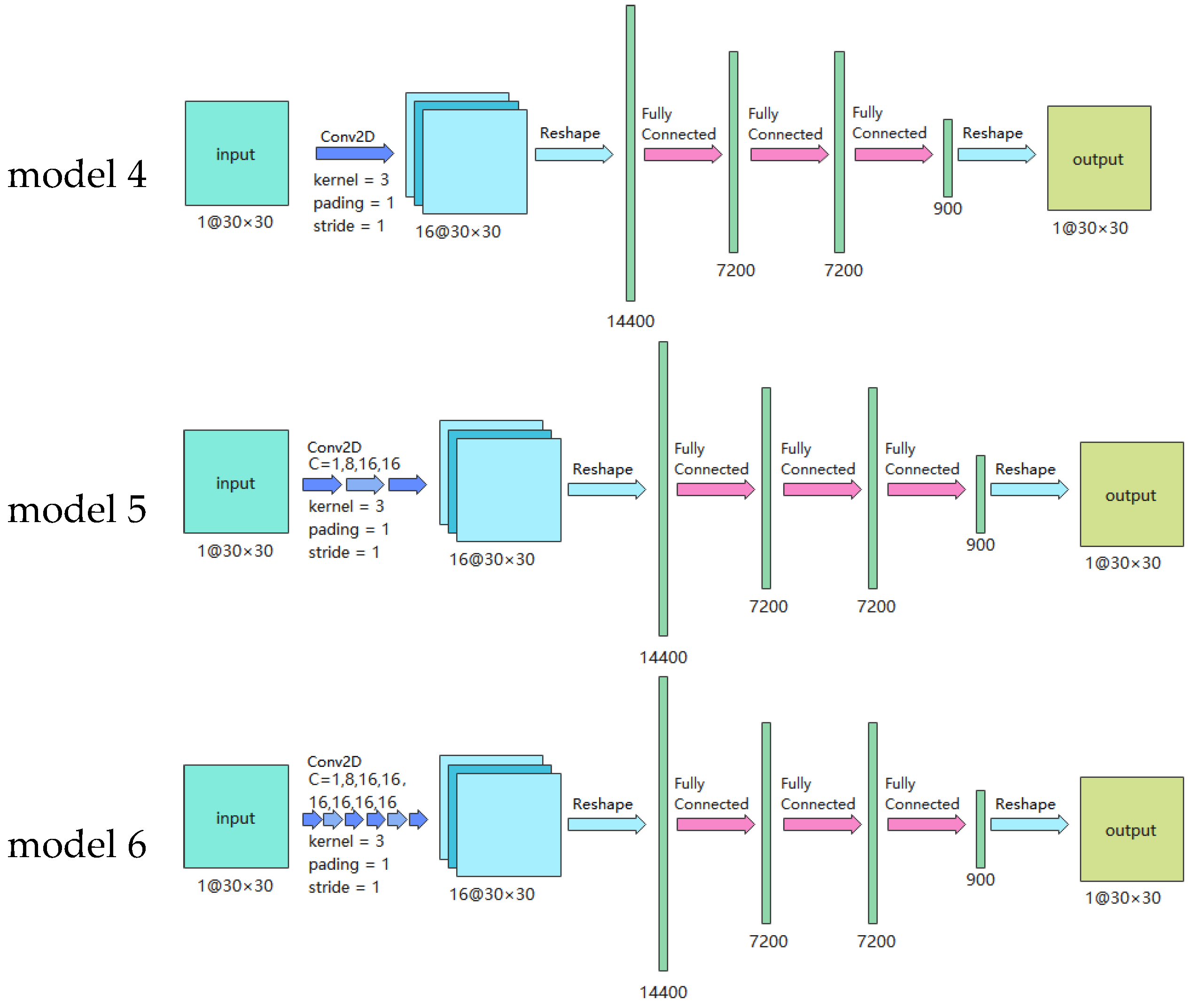
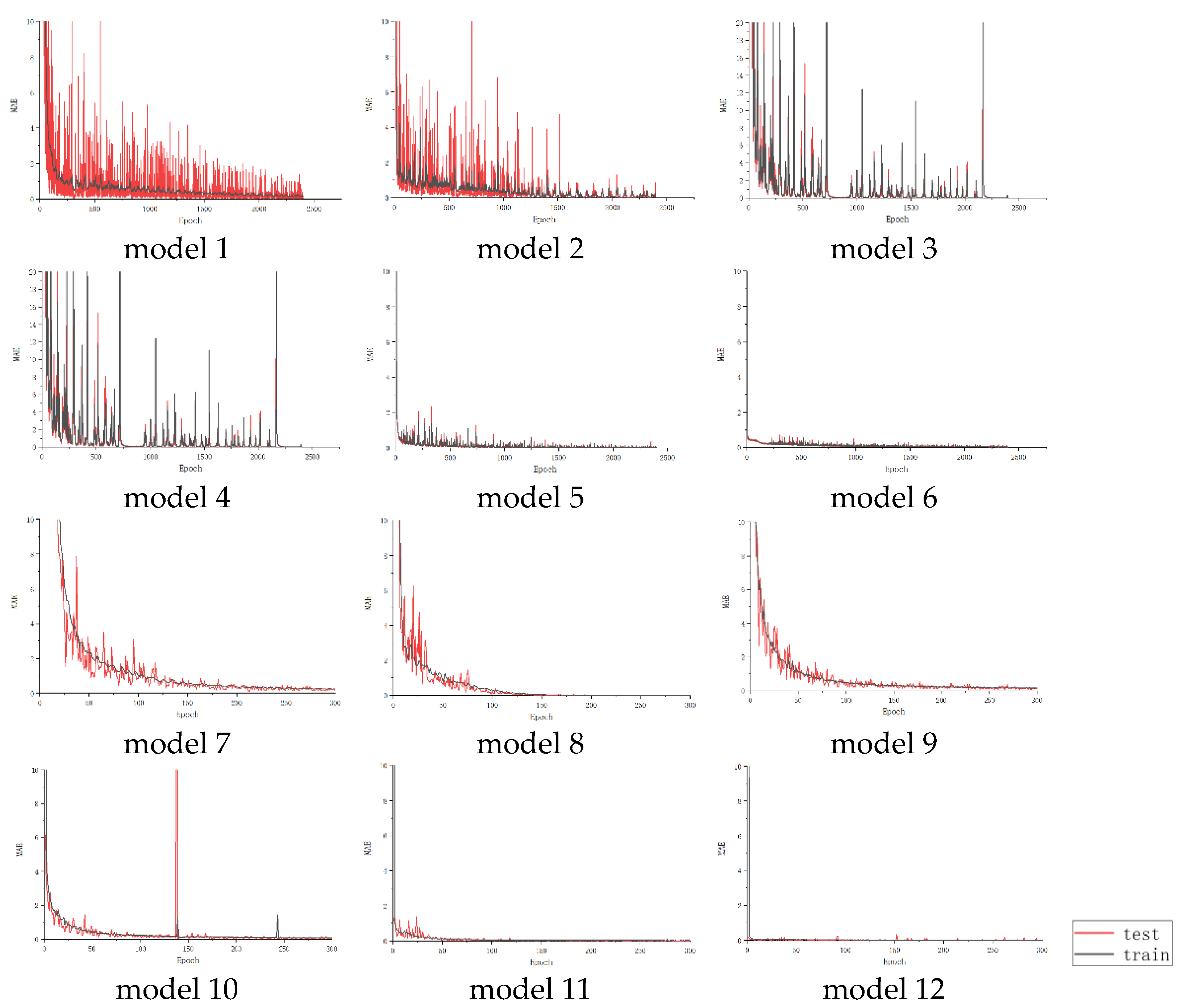
Table 5, different types of neural networks, different numbers of neural network layers, and different sizes of convolution kernel were separately used to construct neural network models, and each method formed six neural network models. Except for the different input and output layers, the other hidden layers of the two groups were set according to the same multiple and appeared in pairs. Specifically, models 1 and 7 were the benchmark models of the two groups, using one fully connected layer; models 2 and 8 had three fully connected layers; models 3, 4, 9, and 10, had one additional convolutional layer, with the convolution kernel matrix set as (3 × 3) and (9 × 9). Models 5, 6, 11, and 12 used three and six layers with 3 × 3 convolution kernels. After a series of settings, both groups of models had the same number of training parameters, as shown in
Table 6 and
Table 7. The neural network model structures are shown in
Figure 8 and
Figure 9. The generated code associated with the model can be downloaded from
https://github.com/architsama/UTCI_distribution (accessed on 23 August 2022).
To ensure the consistency of the neural network training environment, all other parameters of each neural network model were uniformly set: the loss function used was the mean-square error (MSE), as shown in Equation (1). As the optimizer, I used Adam [
51], the batch size for the training was 128, and the learning rate was 0.001. To facilitate comparison with other study results in the same field, I introduced a dimensionless index, the R2 score, to evaluate the degree of model regression effectiveness, as shown in Equation (2). Its value is usually between 0 and 1, where the closer the value to 1, the more accurately the model fits the data. I also introduced the index root-mean-squared error (RMSE) to facilitate lateral comparisons of model accuracy.
where
is the output predicted by each model;
is the average value of the calculation;
is the value of the calculation; m is the number of cases in the dataset.
A computer equipped with AMD Ryzen 7 4800H CPU and NVIDIA GeForce RTX 2060 GPU was used to complete the training of 12 kinds of neural networks under the above two frameworks of Groups A and B. The neural network was implemented using the Python 3.7 programming language and the machine learning framework Pytorch. The cumulative running time of all model training was approximately 120 h.