Abstract
The phenological phases of field crops have shifted to earlier times in the Czech Republic in recent decades; additionally, they have shown correlations with temperatures from previous spring months. Using a thermal time model called PhenoClim, the correlations between temperatures and phenophases allow us to evaluate the strongest predictors (i.e., maximum temperature) and indicators of base temperatures and growing degree days for the selected phenophases of winter wheat (Triticum aestivum L.). With the help of this model, it is possible to explain 0.6–0.82% of the phase variability and to estimate the onset of phenophases for the selected time period and stations (with the RMSE values of 9.4 days for jointing, 4.3 days for heading, and 5.3 days for full ripeness). To further refine the modeled onsets of phenophases, we used satellite data, specifically the normalized difference vegetation index and the enhanced vegetation index 2 from MODIS; based on these vegetation indices, the start of the growing season (SOS) was determined. After including SOS to model PhenoClim, we modeled the onsets of phenophases, with average accuracies ranging from 6.2 to 15.2. By combining the thermal time model and remote sensing data, specifically the data concerning the determination of SOS, we can refine the modeling of the onset of full ripeness in some locations.
1. Introduction
Phenology is an important indicator for assessment of the impacts of climate change [1], owing to its relationship with air temperature [2,3]. Other factors influencing phenology include the length of the photoperiod and the availability of water [4]. Each phenological phase (phenophase) has optimal temperature limits that are required to reach specific phenophase [5]. Temperature models are usually based on the base temperature (Tbase) and growing degree day (GDD) values for each phenophase [6]. A challenge in studying phenophases and their onsets estimation of the onsets of phenophases with the highest possible accuracies [6,7,8] for further use in growth models [9] under current and future climatic conditions [10,11]. Based on models of the onset of phenophases, it is possible to evaluate the length of the vegetation period [12] or the length of the period between the onsets of individual phenophases [8].
In recent decades, the use of satellite imagery has come to the forefront in phenology assessments. Both optical [13] and radar satellite data [14] are used for this purpose. Some studies have combined both sets of satellite data to identify phenophases and achieve more accurate results than the results obtained using each set separately [15]. Satellite images enable evaluation of the growth and development of vegetation on a much larger spatial scale than can be achieved with ground observations. However, ground observations (by humans or cameras) play an important role and serve to calibrate satellite data [7]. Phenological metrics (phenometrics) obtained by the functional analysis of vegetation indices (VIs) are used As indicators of the timing of phenophases. Basic phenometrics include the start of the growing season (SOS), also called the green-up date, onset of greenness, or spring phenology; the length of the growing season (LOS); and the end of the growing season (EOS), also called the end of senescence, end of greenness, dormancy, or autumn phenology [16].
Phenological studies most often describe shifts in the onsets of phenophases to an earlier time and their relationships with climatic variables (most often temperature); however, recent studies have dealt with chilling units and the length of the day [17]. Many studies have evaluated wild plant species [18,19,20], and some have reviewed field crops, e.g., rape [21,22] and rice [23]. Fewer publications have examined the relationships between phenophases and satellite data in field crops [13,24,25] than those that have examined wild plants. Therefore, in this study, we focused on the phenology of a field crop (winter wheat), in particular, the phenophases of jointing, heading, and full ripeness. The main objectives of this study are (1) to evaluate the trends in the onsets of selected phenophases for field crops (winter wheat), (2) to establish the most accurate temperature model for determination of selected phenophases, (3) to determine the dates of phenophases (jointing, heading, and full ripeness) based on temperature models for selected areas, and (4) to determine the start of the growing season (SOS) using VIs and its relationship with the temperature model.
2. Materials and Methods
2.1. Stations and Phenological and Meteorological Data
Phenological data from 28 stations in the Czech Republic at varying altitudes (from 171 to 647 m a.s.l.) were used in the present study, covering the period from 1961 to 2021. The experimental stations represent the soil and climatic conditions of the region; the same set of experimental fields was used in almost all cases. These data were visual ground-based phenological observations of winter wheat (Triticum aestivum L.) from official state trials of the registered and considered cultivars at small-plot experimental stations of the Central Institute for Supervising and Testing in Agriculture (Figure 1). Phenological dates were assessed by highly trained staff. Because the same set of 30–40 winter wheat cultivars (depending on the year) was grown at each site, the so-called standard cultivar phenological dates were used. The standard for the variety trials was always selected with respect to the previous standard cultivar. The dates of onset of three phenophases were evaluated: jointing (BBCH31), heading (BBCH51), and full ripeness (BBCH89). The completeness of data in individual years depended on each station and phenophase. For some stations, data were available for the entire period of 1961–2021, whereas for some stations, data were unavailable in some years. In most cases, data were available for the last thirty years or more, but at several stations, only a short-term series of observations (approx. 11–17 years) was available. Long-term series of observations are generally used as part of phenological studies (approx. 20–30 years), but in this study, a short-term series of observations was also used in order to include as much accurate information as possible about the onsets of phenophases in the model in an effort to increase the spatial resolution of the stations. The geographical coordinates of all stations and the availability of phenological data at each of them are shown in Table 1. A detailed overview of the available years is shown in Table A1.
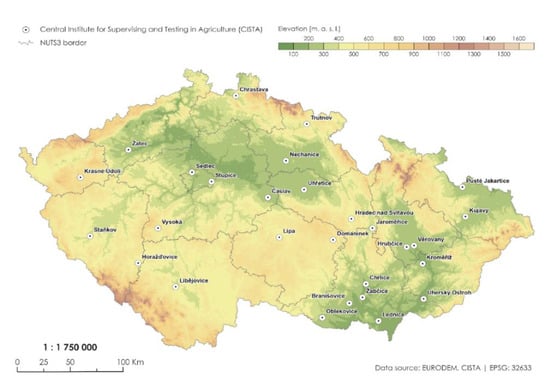
Figure 1.
Overview map of the 28 stations with visual ground-based phenological observations.

Table 1.
An overview of the experimental stations from the Central Institute for Supervising and Testing in Agriculture with phenological observations and geographic coordinates (altitude (m.a.s.l.), latitude, and longitude), as well as the total number of years of ground phenological observations for each station. The observation stations are arranged according to altitude.
Correlation coefficients (r, Pearson coefficient) were used as the primary indicators of the strength of the relationships between given variables. The trends represent the slope of the linear regression between the phenological date and the year. Any significance in the observed trends was assessed using a t-test. All tests were performed with the statistical/programming tool R 3.6.1. [26] and AnClim software [27].
Meteorological data for the observation stations were retrieved from maps interpolated based on 268 climatological stations and 787 precipitation stations in the Czech Republic for the period from 1961 to 2021. The required values for the average (Tmean), maximum (Tmax), and minimum (Tmin) air temperature, as well as precipitation values, were extracted from this map. Input climatological data were quality-controlled, homogenized, and confirmed to not contain missing values [28,29,30,31].
2.2. PhenoClim Model
PhenoClim is a model that allows for modeling of the onsets of phenophases in locations or time periods with only meteorological parameters [10,32]. It is a temperature model or a so-called thermal time model that works with one climate variable (Tmax, Tmean, and Tmin) and uses statistical variables to determine the most suitable values of GDD and Tbase. The beginning of temperature summation during model calibration was determined using temperature conditions (Tmin = 0 °C, Tmax = 5 °C, and Tmean = 2.5 °C).
For each phenophase, the best meteorological predictor was searched for, which was determined using the root mean square error (RMSE). The values of Tbase and GDD are needed to reach a certain phenophase and were simultaneously calculated with the RMSE. Different calibration and validation datasets were used for the analysis, and a total of 168 model runs were calculated for each phenophase. Using the lowest RMSE value, the 10 best model runs were determined; these values were averaged, and the most suitable model was determined for each phenophase. PhenoClim made it possible to include the length of the photoperiod in the calculations and simultaneously consider the snow cover. According to the basic settings of the model, the photoperiod for winter wheat was defined as a short day of 7 h and a long day of 13 h following the approach used by Trnka et al. (2014) [33]. The beginning of the temperature summation was adjusted based on the day length coefficient. When the day length was less than 7 h, the value of the coefficient was 0, and there was no temperature summation. This phenomenon occurred only after crossing the 7 h mark. The snow cover was calculated using seven parameters, which were key for snow accumulation and melting [34]. Both of these functionalities reduced the resulting RMSE values and thus improved the accuracy of the model. PhenoClim was further used (based on the calculated models with the smallest error and the established SOS) to model the dates of the phenophases for sites for which there was no ground-based phenological monitoring.
2.3. Remote Sensing Data
The satellite data came from the Moderate Resolution Imaging Spectroradiometer (MODIS) sensor that was carried on the polar-orbiting Terra satellite, i.e., the MOD09GQ product, with a spatial resolution of 250 m, which was available through the LP DAAC Data Pool [35]. For the Czech Republic territory, four images were downloaded, and three layers were extracted from each image: two bands (red and infrared) and a quality layer. Each band was covered with a layer of quality, and the grids with the highest qualities were selected. After selection, the values of the normalized difference vegetation index (NDVI) and enhanced vegetation index 2 (EVI2) were calculated as follows:
where ρRed and ρNIR are the reflectance values in the red and near-infrared (IR) bands, respectively. The factor G is determined by the c value, and c is derived by linearly fitting ρRed = c × ρNIR [36].
Based on the filter, which works with a ± seven-day time window, the values of the vegetation indices were interpolated in a daily step. Pixels containing only winter wheat vegetation in the period from 2015 to 2020 were selected near stations where visual ground-based phenological observations were available. Based on information from the Land Parcel Identification System (LPIS) database, the plots and pixels containing only with winter wheat were identified. A minimum of five and a maximum of ten available pixels within a radius of five kilometers from the station at approximately the same altitude were required for further analysis of a station. NDVI and EVI2 values were calculated for these pixels. The index values were averaged, and the average values for each station were smoothed using the Gaussian ordinate method with a period = 10. AnClim software [27] was used to smooth the curves, facilitating the used of this method. The adjusted daily index values were converted into Z-score values. A Z-score threshold between 0.00 and 0.60 (in the 0.05 step) was determined at eight stations because data were available for these stations each year between 2015 and 2020. Each of these threshold values corresponded to a threshold for determination of a possible SOS. The conversion of VIs values to Z-score values made it possible to take into account the interannual variability of VI values when determining the SOS. The SOS was determined separately for each station and year. This phenomenon indicated that for each year at one station, 13 days were determined as possible days for the SOS. The established SOS for the individual thresholds was used in the PhenoClim model as the day of the start of temperature summation to calculate the onset of the phenophase. The onsets of phenophases for each threshold in the time period of 2015–2020 were modeled based on the best predictor, GDD, Tbase, and SOS. The onsets of the phenophases modeled in this six-year time period were compared to ground observations. For modeled onsets of phenophases, the RMSE value was calculated for each threshold, and the best threshold of the Z-score coefficient was determine based on the lowest value.
3. Results
The first outputs revealed trends in the phenophase dates of winter wheat. At almost all studied stations (28 stations overall, with three phenophases each), phenophases were shifted to earlier times, and at some stations, these shifts were statistically significant. The lowest change and significance levels in trends were detected for the phenophase jointing, which was mostly caused by short observation periods (e.g., Kromeriz: 12 years or Sedlec: 13 years). However, the heading and full ripeness phenophases were observed for longer periods (reaching 61 years), and trends were frequently significant. The dates of observed phenophases (jointing, heading, and full ripeness) advanced by an average of 2.1–3.4 days per decade (Table 2). The shifting of phenophases to an earlier date differed according to the given phenophase but was observed at almost all stations. Shifts to later dates were observed at only three stations (nonsignificant). The largest significant trends (by 5.9–6.9 days per decade) were calculated for the jointing phenophase (at three stations), as well as the full ripeness phenophase (at Stupice station). The most significant trends were calculated for the full ripeness phenophase (trends were detected for 18 stations among a total of 28 stations); however, for the jointing phenophase, only 11 stations presented with significant trends (Table 2).

Table 2.
Linear trends for observed jointing, heading, and ripening phenophases among the 28 observation stations. Positive values of trends indicate a shift in the onsets of phenophases to a later date, and negative values indicate a shift to an earlier date. The values of the correlation coefficients describe the relationships among observed and modeled terms of the phenophases and, which were statistically significant in all cases. * Significant trend at α = 0.05; ** significant trend at α = 0.01; *** significant trend at α = 0.001.
According to the lowest RMSE value, the best predictor for the onsets of phenophases was Tmax calculated by the model PhenoClim for all three phenophases. The value of RMSE (based on the average of the 10 best models) moved in a range of 4.3–9.4 days. The lowest RMSE (4.3 days) was detected by the set of models for the heading phenophase, and the largest RMSE (9.4 days) was detected for the jointing phenophase. Two main parameters subsequently used for the modeling of the terms of phenophases were Tbase and GDD (Table 3).

Table 3.
RMSE values for given phenophases with the corresponding growing degree day (GDD) and base temperature (Tbase) values for the best predictor (Tmax) as calibration results of the PhenoClim model. R2 is the value of the coefficient of determination, and r is the value of the correlation coefficient.
Using the model setting (the best predictor, GDD, and Tbase) for each phenophase, the onsets of phenophases were modeled for the 28 experimental stations for the period from 1961 to 2021. The lowest correlation (between observed and modeled terms of phenophases) was calculated for the jointing phenophase (r = 0.45–0.87), with only one station with no significance. The correlations for the remaining two phenophases (heading and full ripeness) between observed and modeled onsets were high and significant at all stations (r = 0.68–0.96) (Table 2). A comparison of observed and modeled phases is displayed for station Chrlice for illustration in Figure 2. The line graphs on the left side of Figure 2 show the time course of observed and modeled onsets of individual phenophases in the period from 1961 to 2021. The scatterplots on the right side of the figure show the relationship between observed and modeled onsets of individual phenophases.
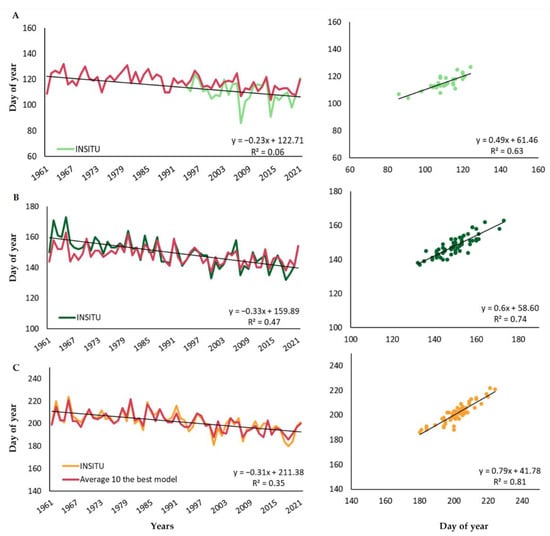
Figure 2.
Comparison between the observed and modeled jointing (A), heading (B), and full ripeness (C) phenophases for Chrlice station. The red curves in the line graphs represent the modeled onsets of phenophases in the period from 1961 to 2021, and the colored curves (light green, dark green, and yellow) represent the ground-observed onsets of phenophases.
Based on the NDVI and EVI2 values, the SOS was determined for eight experimental stations in individual years during the period from 2015 to 2020 for each phenophase. After including SOS in the model, the RMSE value was calculated for the modeled onsets of phenophases, based on which the best threshold of Z-score was determined. Among the average values of eight stations, the best threshold for both vegetation indices was found to have a Z-score of 0. The average RMSE value for this threshold moved within the range of 6.2 to 15.2 (Table 4). The lowest average RMSE value was found for the full ripeness phenophase by using the SOS determined by EVI2. For the jointing and heading phenophases, improved results were obtained by using SOS from NDVI; nevertheless, the average RMSE values were higher than for the full ripeness phenophase. The best threshold Z-score and corresponding RMSE value differed for individual stations; an overview is shown in Table A2 and Table A3, highlighting that for the jointing phenophase and full ripeness phenophase at some stations, the accuracy of the model was improved when SOS was included relative to when it was excluded. A comparison of the observed and modeled values with and without the start of the season is displayed for the Chrlice station for illustration in Figure 3.

Table 4.
The average RMSE values describe the accuracy with which the model calculated the onsets of jointing, heading, and full ripeness phenophases. The lowest average RMSE values are highlighted with a gray background. Thr-0 to Thr-0.6 are the thresholds of the Z-score for the model with SOS, NDVI is the normalized difference vegetation index, and EVI2 is the enhanced vegetation index 2.
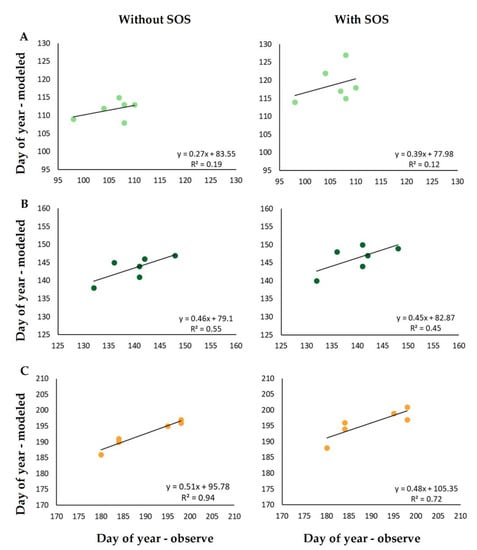
Figure 3.
Comparison between observed and modeled values excluding the start of the season (left side) and a comparison between the observed and modeled values including the start of the season based on a Z-score being 0 (right side) for the jointing (A), heading (B), and full ripeness (C) phenotypes at Chrlice station in the time period from 2015 to 2020.
4. Discussion
Ground observations are among the most accurate methods for determining phenophases and are necessary for the calibration and evaluation of the model. In order to ensure that the model to considered as much accurate information as possible about the onsets of phenophases and that this was high-spatial-resolution information, we decided to use phenological data from stations with available short-term observations (e.g., Sedlec (13 years)), in addition to phenological data from stations with available long-term observations. Previous studies dealing with the phenology of winter wheat showed changes in trends comparable to those reported here, e.g., app. by 1.1–2.7 days/decade during the period from 1981 to 2009 [37] or by 0.8–1.8 days/decade during the period from 1935 to 2004 [38]. We observed an average shift of 2.1–3.4 days during the period from 1961 to 2021. Which may be the reason for a more pronounced shift compared to the mentioned studies given the global increase in temperature in recent decades? One reason could be a different time period that was evaluated. Compared to the aforementioned studies, in this study, we included data from the last 30 years in our analysis at most stations, with a mor pronounced increase in the temperature than in previous years; temperature is considered one of the main factors influencing the onset of phenophases. Earlier onsets of phenophases have also been reported in other field crops. In Germany [22], in the period from 1979 to 2013 shifts in winter rape of 4.8 days/decade and in winter rye by 1.3 days/decade were reported; in a study of oats in the period from 1959 to 2009, researchers reported a shift in an average of 0.2–3.3 days/decade [39]. The results of these studies showed that the shifts in the onsets of phenophases are species-specific. The abovementioned changes in the onsets of phenophases and in the lengths of time between individual phenophases led to reductions in the growth period and negatively impacted the yields of field crops [40]. Given that temperature affects the onsets of the phenophases of field crops [37], knowledge about the effects of climate change on their phenological development is needed to optimize the farming system and increase the productivity of field crops [1]. Additionally, owing to climate change, increasing temperatures, and potentially more frequent occurrences of extreme temperature conditions, it is necessary to adapt to these conditions and mitigate their impact. One possible solution is the inclusion of varieties with higher temperature requirements [40,41] and increased resistance to drought and heat [42] in the sowing procedure. The results of studies dealing with the temperature requirements of field crops or changes in the onsets of phenophases can thus be crucial for the decision making of breeding companies. Another possible measure to mitigate the negative impacts of climate change is shifting the date of sowing [41,42]. The mentioned measures are mainly based on the relationship between phenology and temperature; temperature is generally considered to be one of the main factors influencing the onsets of phenophases. In our case, Tmax was identified as the best predictor of the onsets of phenological terms. In addition to air temperature, photoperiod plays an important role in plant phenology, which is important in spring phenology to prevent damage from spring frosts and in autumn phenology to stop plant growth [2]. Considering these two main factors influencing the onsets of phenophases and in an effort to obtain more robust results, photoperiod was also included in the calculations during the calibration of the PhenoClim model. In addition to climatic conditions, the phenologies of field crops are influenced by changes in management, although few studies have been conducted on this topic. Such influences include the type of cultivar (early vs. late), which is related to the density of planting and the date of sowing [22]. For example, a later sowing date can have distinct effects on winter (positive) and spring (negative) wheat [41]. In this case, we did not include other factors in the calculations, but they could be the subject of follow-up studies to provide more realistic information about plant behavior.
The results of the PhenoClim model based only on temperature thresholds and photoperiod showed relatively high accuracies in terms of predicting heading and full ripeness, similar to the results of a study conducted in southeastern USA [6]. Using the same temperature thresholds, researchers modeled three phenological stages for eight winter wheat cultivars during the period from 1999 to 2010 and achieved a similar accuracy (average RMSE in the range of 5.2–7.1 days), as in our study. The results of studies focused on predicting the onset of key phenophases based on GDD and Tbase could be helpful for crop management practices, such as fertilization, irrigation, pesticide applications, and harvest scheduling. Possibilities of further use of predicting the prediction of the onsets of phenophases of field crops were presented in a study conducted in Denmark [43] based on field experiments of spring barley and winter wheat during the period from 1991 to 2018 to assess the viability of growing cover crops on the basis of harvest date prediction in the current season. In the first step, the ability of the model to predict the maturity date was determined with an accuracy RMSE of 5.5 days for both evaluated crops. Then, based on a calibrated sum of temperatures between maturity and harvest (400 °C for barley and 450 °C for wheat), the model predicted the harvest date and, with an RMSE error of 6.6 days for spring barley and 9.3 days for winter wheat. The model was capable of predicting the date and harvests, which could be helpful for planning autumn work in the field and the possible establishment of cover crops [43].
Finally, a combination of the PhenoClim thermal model and the SOS derived from remote sensing showed that it was possible to model the onset of the full ripeness phenophase with a relatively high accuracy. At half of the assessed stations, even higher accuracy was achieved when SOS was considered than when only the thermal model was used. A similar accuracy in estimating the maturity date of winter wheat was achieved by combining the sum of temperatures and EVI2, achieving an RMSE of 7.3 with a coefficient of determination value of 0.48 (i.e., r = 0.69) [25]. Furthermore, a method for monitoring and predicting heading and flowering dates of winter wheat was proposed based on a combination of temperature sums and NDVI [24]. Researchers used the dynamic threshold method to determine phenological metrics. The RMSE value for the prediction of the onset of heading was in the range of 4.76–6.13 days, and that for the estimation of flowering was in the range of 5.30–6.41 days. In this case, for the heading phenophase, by combining both methods, the accuracy of the model was one day less than that for the full ripeness phenophase, which can be considered a relatively satisfactory accuracy. The lowest accuracy of the model was for the jointing phenophase, probably as a result of the limited amount of phenological input data for this phenophase, given the overall poorer results in the other analyses. With information derived from remote sensing data, it is possible to include another variable in the temperature models reflecting the actual state of the vegetation on a large spatial scale. Additionally, this information can be derived practically in real time, enabling estimation of the onsets of phenophases in a given season. The results of this study could be of practical use for planning field work (e.g., fertilization and pest control).
5. Conclusions
Analysis of long-term phenological data of winter wheat in the period from 1961 to 2021 showed shifts in the onsets of phenophases to earlier dates for all shifts with statistical significance. The maximum air temperature was shown to be the best predictor of phenophase onsets for model tools. Using models based on temperature thresholds to determine phenophases, it was possible fundamentally approach to methods based on traditional ground observations. Combining remote sensing data with temperature models resulted in decreased accuracy of phenophase onset determination in most cases; however, in the case of the heading and full ripeness phenophase, this deterioration did not exceed an average of four days (for full ripeness, even better results were obtained at four stations), indicating a still high ability of the model to predicting the onsets of phenophases.
Author Contributions
Conceptualization, P.D., M.T. and Z.Ž.; methodology, P.D., L.B. and M.T.; software, J.B. (Jan Balek); validation, P.D.; formal analysis, P.D. and L.B.; investigation, J.B. (Jakub Bohuslav) and E.P.; resources, M.T. and Z.Ž.; data curation, L.H. and D.S.; writing—original draft preparation, P.D.; writing—review and editing, P.D. and L.B.; visualization, M.B.; supervision, L.B., M.T. and Z.Ž.; project administration, P.D., M.T. and Z.Ž.; funding acquisition, M.T. and Z.Ž. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the Internal Grant Agency of the Faculty of AgriSciences at Mendel University in Brno as part of the research project AF-IGA2021-IP036, “Onset of phenological phases of winter wheat and spring barley—using ground data, modeling and remote sensing”. The contributions of D.S. and M.T. were funded by the Ministry of Education, Youth and Sports of the Czech Republic as part of the SustES project “Adaptation strategies for sustainable ecosystem services and food security under adverse environmental conditions” (CZ.02.1.01/0.0/0.0/16_019/0000797), which provided essential data and software access.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The contributions of Petra Dížková and Jakub Bohuslav were financially supported by grant no. AF-IGA2021-IP036. The authors are grateful to Reinhart Ceulemans, (University of Antwerp, Belgium) for a thorough prereview of the paper and critical comments that considerably improved the manuscript. The Central Institute for Supervising and Testing in Agriculture provided the ground-based phenological data set.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
An overview of experimental stations of the Central Institute for Supervising and Testing in Agriculture with phenological observations and their geographic coordinates (altitude (m.a.s.l.), latitude, and longitude). In the right half of the table, the time periods in which ground observations were available for each phenophase and each station are listed. The period column indicates a specific time period or year. The year column is the total number of years of ground observations for each station.
Table A1.
An overview of experimental stations of the Central Institute for Supervising and Testing in Agriculture with phenological observations and their geographic coordinates (altitude (m.a.s.l.), latitude, and longitude). In the right half of the table, the time periods in which ground observations were available for each phenophase and each station are listed. The period column indicates a specific time period or year. The year column is the total number of years of ground observations for each station.
| Station | Altitude (m) | Latitude | Longitude | Jointing | Heading | Full Ripeness | |||
|---|---|---|---|---|---|---|---|---|---|
| Period | Years | Period | Years | Period | Years | ||||
| Lednice | 171 | 48°47′59″ | 16°48′12″ | 1994–2021 | 28 | 1976–2021 | 46 | 1976–2021 | 46 |
| Zabcice | 182 | 49°0′41″ | 16°36′9″ | 2000–2021 | 22 | 2000–2021 | 22 | 2000–2021 | 22 |
| Branisovice | 190 | 48°57′46″ | 16°25′54″ | 1995; 2000–2021 | 23 | 1994–1997; 1999–2021 | 27 | 1994–1995; 1999–2021 | 25 |
| Chrlice | 190 | 49°7′52″ | 16°39′9″ | 1994–2021 | 28 | 1961–2021 | 61 | 1961–2021 | 61 |
| Uhersky Ostroh | 196 | 48°59′8″ | 17°23′23 | 1994–2021 | 28 | 1963–1965; 1967–1976; 1978–2021 | 57 | 1963–1965; 1967–2021 | 58 |
| Kromeriz | 201 | 49°17′52″ | 17°23′35″ | 1994–2002; 2004–2005; 2008 | 12 | 1994–1998; 2000–2002; 2004–2005; 2008 | 11 | 1994–1998; 2000–2002; 2004–2005; 2007–2008 | 12 |
| Verovany | 204 | 49°27′39″ | 17°17′16″ | 1994–2021 | 28 | 1970–2021 | 52 | 1970–2021 | 52 |
| Hrubcice | 210 | 49°27′0″ | 17°11′35″ | 1997; 2000–2021 | 23 | 1995–1998; 2000–2021 | 26 | 1997; 2000–2021 | 23 |
| Zatec | 233 | 50°19′37″ | 13°32′44″ | 1993–1997; 1999–2018 | 25 | 1993–1997; 1999–2018 | 25 | 1993–1997; 1999–2018 | 25 |
| Uhretice | 237 | 49°58′44″ | 15°52′2″ | 2000–2021 | 22 | 2000–2021 | 22 | 2000–2021 | 22 |
| Nechanice | 239 | 50°14′14″ | 15°37′57″ | 1992–2021 | 30 | 1992–2021 | 30 | 1992–2021 | 30 |
| Oblekovice | 250 | 48°50′18″ | 16°4′53″ | 1994–2021 | 28 | 1961–1978; 1980–2021 | 60 | 1961–1978; 1980–2021 | 60 |
| Kujavy | 258 | 49°42′11″ | 17°58′21″ | 1992–1998; 2000–2021 | 29 | 1992–1998; 2000–2021 | 29 | 1992–1998; 2000–2021 | 29 |
| Stupice | 277 | 50°3′12″ | 14°38′51″ | 2000–2021 | 22 | 1994–2021 | 28 | 1994–1997; 1999–2021 | 27 |
| Caslav | 290 | 49°54′39″ | 15°23′22″ | 1993–2021 | 29 | 1993–2021 | 29 | 1993–2021 | 29 |
| Puste Jakartice | 295 | 49°58′0″ | 17°56′55″ | 1994–2021 | 28 | 1969–2021 | 53 | 1969–2021 | 53 |
| Sedlec | 300 | 50°8′2″ | 14°23′29″ | 1992–2004 | 13 | 1992–2004 | 13 | 1992–2004 | 13 |
| Chrastava | 345 | 50°49′1″ | 14°58′7″ | 1994–2021 | 28 | 1977–2021 | 45 | 1977–2021 | 45 |
| Stankov | 370 | 49°33′7″ | 13°4′8″ | 1993–2021 | 29 | 1993–2021 | 29 | 1993–2021 | 29 |
| Trutnov | 414 | 50°33′39″ | 15°54′45″ | 1992–1998; 2000–2021 | 29 | 1992–1998; 2000–2021 | 29 | 1992–1998; 2000–2021 | 29 |
| Jaromerice | 425 | 49°37′32″ | 16°45′6″ | 1993–2021 | 29 | 1993–2021 | 29 | 1993–2021 | 29 |
| Libejovice | 434 | 49°6′51″ | 14°11′36″ | 1994–2002; 2004–2011 | 17 | 1961–2002; 2004–2011 | 50 | 1961–2002; 2004–2011 | 50 |
| Horazdovice | 450 | 49°19′14″ | 13°42′3″ | 1994–1998; 2000–2021 | 27 | 1973–1981; 1983–1987; 1989–1992; 1994–1998; 2000–2021 | 45 | 1973–1981; 1983–1987; 1989–1992; 1994–1998; 2000–2021 | 45 |
| Hradec nad Svitavou | 450 | 49°42′41″ | 16°28′50″ | 1992–1998; 2000–2021 | 29 | 1992–1998; 2000–2021 | 29 | 1992–1998; 2000–2021 | 29 |
| Lipa | 505 | 49°33′21″ | 15°32′10″ | 1994–2021 | 28 | 1961–1978; 1980–2021 | 60 | 1961–1978; 1980–1985; 1987–2021 | 59 |
| Domaninek | 570 | 49°31′41″ | 16°14′11″ | 1994–2021 | 28 | 1961–2021 | 61 | 1961–2021 | 61 |
| Vysoka | 590 | 49°38′3″ | 13°57′9″ | 1992–2021 | 30 | 1992–2021 | 30 | 1992–2021 | 30 |
| Krasne Udoli | 647 | 50°4′20″ | 12°55′16″ | 1994; 1996–2002; 2004–2010 | 15 | 1965–1992; 1994; 1996–2000; 2002; 2004–2010 | 42 | 1965–1992; 1994; 1996–2002; 2004–2010 | 43 |

Table A2.
The RMSE values describe the accuracy modeled at the onsets of the jointing, heading, and full ripeness phenophases. Thr-0 to Thr-0.6 columns indicated the RMSE values for the modeled onsets of phenophases, including the start of the growing season derived from NDVI. The lowest values for each station are highlighted with a light gray background. A dark gray background highlights the station; the model including SOS is better than the model without SOS.
Table A2.
The RMSE values describe the accuracy modeled at the onsets of the jointing, heading, and full ripeness phenophases. Thr-0 to Thr-0.6 columns indicated the RMSE values for the modeled onsets of phenophases, including the start of the growing season derived from NDVI. The lowest values for each station are highlighted with a light gray background. A dark gray background highlights the station; the model including SOS is better than the model without SOS.
| JOINTING | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Station | Model without SOS | Thr 0 | Thr 0.05 | Thr 0.1 | Thr 0.15 | Thr 0.2 | Thr 0.25 | Thr 0.3 | Thr 0.35 | Thr 0.4 | Thr 0.45 | Thr 0.5 | Thr 0.55 | Thr 0.6 |
| RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | |
| Branisovice | 11.3 | 17.7 | 36.3 | 18.7 | 20.9 | 21.1 | 22.7 | 21.9 | 21.9 | 22.2 | 22.4 | 22.7 | 23.2 | 23.2 |
| Caslav | 11.4 | 22.9 | 23.5 | 23.8 | 24.3 | 24.8 | 25.0 | 25.3 | 25.8 | 26.2 | 26.4 | 26.6 | 27.0 | 27.3 |
| Hrubcice | 10.6 | 20.3 | 20.3 | 20.4 | 20.8 | 20.2 | 20.2 | 20.5 | 20.8 | 21.8 | 22.9 | 23.0 | 23.6 | 23.9 |
| Chrlice | 6.9 | 13.2 | 13.4 | 13.6 | 14.0 | 14.7 | 15.2 | 16.4 | 16.7 | 16.8 | 17.6 | 18.8 | 19.4 | 19.6 |
| Oblekovice | 10.2 | 9.7 | 10.0 | 9.6 | 9.9 | 10.3 | 11.5 | 11.5 | 11.9 | 11.9 | 12.2 | 12.8 | 13.0 | 13.1 |
| Puste Jakartice | 10.4 | 15.7 | 15.8 | 15.5 | 16.1 | 16.3 | 16.5 | 16.8 | 17.0 | 17.7 | 18.4 | 18.5 | 18.8 | 19.7 |
| Uhretice | 13.6 | 6.0 | 5.8 | 5.8 | 6.0 | 6.0 | 6.1 | 6.1 | 6.3 | 5.9 | 5.9 | 5.8 | 5.9 | 6.2 |
| Verovany | 6.2 | 11.7 | 12.0 | 12.2 | 12.2 | 12.5 | 12.9 | 13.3 | 13.6 | 13.7 | 14.5 | 15.0 | 15.4 | 15.8 |
| Average | 10.1 | 14.6 | 17.1 | 15.0 | 15.5 | 15.7 | 16.3 | 16.4 | 16.7 | 17.0 | 17.5 | 17.9 | 18.3 | 18.6 |
| HEADING | ||||||||||||||
| Station | model without SOS | Thr 0 | Thr 0.05 | Thr 0.1 | Thr 0.15 | Thr 0.2 | Thr 0.25 | Thr 0.3 | Thr 0.35 | Thr 0.4 | Thr 0.45 | Thr 0.5 | Thr 0.55 | Thr 0.6 |
| RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | |
| Branisovice | 2.4 | 5.0 | 5.0 | 5.0 | 5.6 | 5.8 | 6.0 | 6.0 | 6.0 | 6.2 | 6.2 | 6.5 | 6.5 | 6.7 |
| Caslav | 4.8 | 9.6 | 9.9 | 10.2 | 10.6 | 10.6 | 11.0 | 11.3 | 11.3 | 11.6 | 12.3 | 12.3 | 12.3 | 12.5 |
| Hrubcice | 2.8 | 5.8 | 6.2 | 6.0 | 6.1 | 5.9 | 5.7 | 5.7 | 5.6 | 5.8 | 6.4 | 6.6 | 6.8 | 7.2 |
| Chrlice | 4.9 | 6.1 | 6.1 | 6.5 | 6.5 | 6.7 | 7.1 | 7.5 | 8.1 | 8.1 | 8.3 | 9.2 | 9.6 | 9.7 |
| Oblekovice | 4.9 | 7.9 | 7.9 | 7.6 | 7.8 | 8.1 | 8.6 | 8.7 | 9.1 | 9.1 | 9.1 | 9.5 | 9.5 | 9.7 |
| Puste Jakartice | 5.8 | 8.0 | 8.0 | 8.2 | 8.2 | 8.2 | 8.4 | 8.4 | 8.4 | 8.9 | 9.2 | 9.5 | 9.8 | 10.2 |
| Uhretice | 4.5 | 9.4 | 9.6 | 9.6 | 9.6 | 9.8 | 10.2 | 10.4 | 10.6 | 10.9 | 10.9 | 11.1 | 11.4 | 11.6 |
| Verovany | 5.4 | 10.4 | 10.6 | 10.6 | 10.6 | 10.9 | 10.9 | 11.1 | 11.3 | 11.4 | 11.7 | 12.2 | 12.6 | 12.8 |
| Average | 4.4 | 7.8 | 7.9 | 8.0 | 8.1 | 8.2 | 8.5 | 8.7 | 8.8 | 9.0 | 9.3 | 9.6 | 9.8 | 10.1 |
| FULL RIPENESS | ||||||||||||||
| Station | model without SOS | Thr 0 | Thr 0.05 | Thr 0.1 | Thr 0.15 | Thr 0.2 | Thr 0.25 | Thr 0.3 | Thr 0.35 | Thr 0.4 | Thr 0.45 | Thr 0.5 | Thr 0.55 | Thr 0.6 |
| RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | |
| Branisovice | 7.5 | 10.0 | 10.1 | 10.3 | 11.0 | 11.1 | 11.2 | 11.2 | 11.2 | 11.5 | 11.5 | 11.8 | 11.8 | 11.9 |
| Caslav | 2.8 | 5.7 | 6.4 | 6.4 | 6.6 | 7.1 | 7.3 | 7.3 | 7.9 | 8.1 | 8.4 | 8.3 | 8.6 | 8.7 |
| Hrubcice | 3.4 | 6.4 | 6.4 | 6.1 | 6.3 | 5.8 | 5.6 | 5.6 | 5.5 | 5.5 | 6.0 | 6.1 | 6.1 | 6.3 |
| Chrlice | 4.6 | 4.5 | 4.5 | 4.2 | 4.2 | 4.1 | 4.2 | 3.9 | 3.9 | 3.6 | 3.9 | 4.1 | 4.4 | 4.2 |
| Oblekovice | 9.5 | 9.3 | 9.4 | 9.3 | 9.4 | 9.6 | 9.9 | 9.9 | 10.3 | 10.3 | 10.3 | 10.5 | 10.5 | 10.7 |
| Puste Jakartice | 4.0 | 4.5 | 4.7 | 4.3 | 4.1 | 4.0 | 3.9 | 3.9 | 4.1 | 4.0 | 4.2 | 4.3 | 4.3 | 4.8 |
| Uhretice | 2.3 | 5.7 | 6.0 | 6.0 | 6.2 | 6.2 | 6.2 | 6.2 | 6.4 | 6.2 | 6.0 | 6.4 | 6.4 | 6.5 |
| Verovany | 6.1 | 4.7 | 4.7 | 4.9 | 4.6 | 4.6 | 4.7 | 4.6 | 4.7 | 4.9 | 4.7 | 4.9 | 5.2 | 5.4 |
| Average | 5.0 | 6.4 | 6.5 | 6.4 | 6.6 | 6.6 | 6.6 | 6.6 | 6.7 | 6.8 | 6.9 | 7.1 | 7.2 | 7.3 |

Table A3.
The RMSE values describe the accuracy modeled at the onset of the jointing, heading, and full ripeness phenophases. Thr-0 to Thr-0.6 indicate the RMSE values for modeled onsets of phenophases, including the start of the growing season derived from EVI2. The lowest values for each station are highlighted with a light gray background. A dark gray background highlights the station; the model including SOS is better than the model without SOS.
Table A3.
The RMSE values describe the accuracy modeled at the onset of the jointing, heading, and full ripeness phenophases. Thr-0 to Thr-0.6 indicate the RMSE values for modeled onsets of phenophases, including the start of the growing season derived from EVI2. The lowest values for each station are highlighted with a light gray background. A dark gray background highlights the station; the model including SOS is better than the model without SOS.
| JOINTING | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Station | Model without SOS | Thr 0 | Thr 0.05 | Thr 0.1 | Thr 0.15 | Thr 0.2 | Thr 0.25 | Thr 0.3 | Thr 0.35 | Thr 0.4 | Thr 0.45 | Thr 0.5 | Thr 0.55 | Thr 0.6 |
| RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | |
| Branisovice | 11.3 | 17.7 | 36.3 | 18.7 | 20.9 | 20.9 | 21.1 | 21.9 | 21.9 | 22.2 | 22.4 | 22.7 | 23.2 | 23.2 |
| Caslav | 11.4 | 22.9 | 23.4 | 23.8 | 24.3 | 24.8 | 25.0 | 25.3 | 25.8 | 26.2 | 26.4 | 26.6 | 27.0 | 27.3 |
| Hrubcice | 10.6 | 21.5 | 21.8 | 22.0 | 22.5 | 22.4 | 22.8 | 23.4 | 23.8 | 23.9 | 24.6 | 24.7 | 25.0 | 25.4 |
| Chrlice | 6.9 | 15.4 | 16.2 | 16.2 | 16.8 | 17.0 | 17.1 | 17.8 | 18.3 | 18.6 | 19.4 | 20.0 | 20.3 | 20.3 |
| Oblekovice | 10.2 | 11.0 | 11.0 | 12.0 | 12.4 | 12.6 | 12.9 | 12.9 | 13.1 | 13.6 | 13.8 | 14.5 | 15.1 | 15.2 |
| Puste Jakartice | 10.4 | 15.7 | 15.8 | 15.5 | 16.1 | 16.3 | 16.5 | 16.8 | 17.0 | 18.0 | 18.4 | 18.5 | 18.8 | 19.7 |
| Uhretice | 13.6 | 5.2 | 5.0 | 5.2 | 5.3 | 5.2 | 5.3 | 5.6 | 5.9 | 6.2 | 6.4 | 6.4 | 6.8 | 6.8 |
| Verovany | 6.2 | 12.5 | 12.5 | 12.9 | 13.1 | 13.5 | 13.8 | 14.3 | 14.5 | 15.3 | 16.2 | 16.8 | 16.9 | 17.4 |
| Average | 10.1 | 15.2 | 17.8 | 15.8 | 16.4 | 16.6 | 16.8 | 17.2 | 17.6 | 18.0 | 18.5 | 18.8 | 19.1 | 19.4 |
| HEADING | ||||||||||||||
| Station | Model without SOS | Thr 0 | Thr 0.05 | Thr 0.1 | Thr 0.15 | Thr 0.2 | Thr 0.25 | Thr 0.3 | Thr 0.35 | Thr 0.4 | Thr 0.45 | Thr 0.5 | Thr 0.55 | Thr 0.6 |
| RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | |
| Branisovice | 2.4 | 5.0 | 5.0 | 5.0 | 5.6 | 5.8 | 6.0 | 6.0 | 6.0 | 6.2 | 6.2 | 6.5 | 6.5 | 6.7 |
| Caslav | 4.8 | 9.6 | 9.9 | 10.2 | 10.6 | 10.6 | 11.0 | 11.3 | 11.3 | 11.6 | 12.3 | 12.3 | 12.3 | 12.5 |
| Hrubcice | 2.8 | 6.2 | 6.5 | 6.6 | 6.6 | 6.5 | 6.7 | 6.7 | 7.2 | 7.4 | 7.7 | 7.7 | 7.9 | 8.1 |
| Chrlice | 4.9 | 7.0 | 7.1 | 7.5 | 7.9 | 8.2 | 8.2 | 8.5 | 8.7 | 9.0 | 9.6 | 10.1 | 10.4 | 10.4 |
| Oblekovice | 4.9 | 7.9 | 7.9 | 8.7 | 8.9 | 9.1 | 9.5 | 9.5 | 9.5 | 9.8 | 9.8 | 10.3 | 10.7 | 11.0 |
| Puste Jakartice | 5.8 | 8.0 | 8.0 | 8.2 | 8.2 | 8.2 | 8.4 | 8.4 | 8.4 | 9.1 | 9.2 | 9.5 | 9.8 | 10.2 |
| Uhretice | 4.5 | 8.7 | 9.6 | 9.6 | 9.7 | 10.0 | 10.4 | 10.7 | 10.7 | 11.1 | 11.5 | 11.5 | 12.0 | 12.2 |
| Verovany | 5.4 | 10.7 | 10.7 | 10.9 | 10.9 | 11.3 | 11.5 | 11.5 | 12.0 | 12.5 | 12.9 | 13.6 | 13.6 | 14.0 |
| Average | 4.4 | 7.9 | 8.1 | 8.3 | 8.6 | 8.7 | 8.9 | 9.1 | 9.3 | 9.6 | 9.9 | 10.2 | 10.4 | 10.6 |
| FULL RIPENESS | ||||||||||||||
| Station | Model without SOS | Thr 0 | Thr 0.05 | Thr 0.1 | Thr 0.15 | Thr 0.2 | Thr 0.25 | Thr 0.3 | Thr 0.35 | Thr 0.4 | Thr 0.45 | Thr 0.5 | Thr 0.55 | Thr 0.6 |
| RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | RMSE (Days) | |
| Branisovice | 7.5 | 10.0 | 10.1 | 10.3 | 11.0 | 11.1 | 11.2 | 11.2 | 11.2 | 11.5 | 11.5 | 11.8 | 11.8 | 11.9 |
| Caslav | 2.8 | 5.7 | 6.4 | 6.4 | 6.6 | 7.1 | 7.3 | 7.3 | 7.9 | 8.1 | 8.4 | 8.3 | 8.6 | 8.7 |
| Hrubcice | 3.4 | 6.2 | 6.0 | 6.3 | 6.6 | 6.3 | 6.4 | 6.3 | 6.8 | 6.8 | 6.8 | 7.0 | 7.4 | 7.5 |
| Chrlice | 4.6 | 3.8 | 3.9 | 3.8 | 3.8 | 3.9 | 3.6 | 3.7 | 3.7 | 4.0 | 4.2 | 4.4 | 4.4 | 4.6 |
| Oblekovice | 9.5 | 9.6 | 9.6 | 10.1 | 10.2 | 10.4 | 10.4 | 10.4 | 10.5 | 10.9 | 10.9 | 11.4 | 11.9 | 12.1 |
| Puste Jakartice | 4.0 | 4.5 | 4.7 | 4.3 | 4.1 | 4.0 | 3.9 | 3.9 | 4.1 | 4.0 | 4.3 | 4.3 | 4.3 | 4.8 |
| Uhretice | 2.3 | 5.0 | 5.3 | 5.3 | 5.3 | 5.5 | 5.6 | 6.1 | 6.1 | 6.1 | 6.5 | 6.5 | 6.9 | 6.9 |
| Verovany | 6.1 | 4.4 | 4.4 | 4.4 | 4.6 | 4.4 | 4.6 | 4.7 | 4.9 | 5.6 | 5.6 | 6.2 | 6.4 | 6.4 |
| Average | 5.0 | 6.2 | 6.3 | 6.3 | 6.5 | 6.6 | 6.6 | 6.7 | 6.9 | 7.1 | 7.3 | 7.5 | 7.7 | 7.9 |
References
- Sujetoviene, G.; Velica, R.; Kanapickas, A.; Kriauciuniene, Z.; Romanovskaja, D.; Baksiene, E.; Vaguseviciene, I.; Klepeckas, M.; Juknys, R. Climate-change-related long-term historical and projected changes to spring barley phenological development in Lithuania. J. Agric. Sci. 2018, 156, 1061–1069. [Google Scholar] [CrossRef]
- Fu, Y.S.; Li, X.X.; Zhou, X.C.; Geng, X.J.; Guo, Y.H.; Zhang, Y.R. Progress in plant phenology modeling under global climate change. Sci. China-Earth Sci. 2020, 63, 1237–1247. [Google Scholar] [CrossRef]
- Xiao, L.J.; Liu, B.; Zhang, H.X.; Gu, J.Y.; Fu, T.Y.; Asseng, S.; Liu, L.L.; Tang, L.; Cao, W.X.; Zhu, Y. Modeling the response of winter wheat phenology to low temperature stress at elongation and booting stages. Agric. For. Meteorol. 2021, 303, 13. [Google Scholar] [CrossRef]
- Oteros, J.; Garcia-Mozo, H.; Botey, R.; Mestre, A.; Galan, C. Variations in cereal crop phenology in Spain over the last twenty-six years (1986–2012). Clim. Chang. 2015, 130, 545–558. [Google Scholar] [CrossRef]
- Porter, J.R.; Gawith, M. Temperatures and the growth and development of wheat: A review. Eur. J. Agron. 1999, 10, 23–36. [Google Scholar] [CrossRef]
- Salazar-Gutierrez, M.R.; Johnson, J.; Chaves-Cordoba, B.; Hoogenboom, G. Relationship of base temperature to development of winter wheat. Int. J. Plant Prod. 2013, 7, 741–762. [Google Scholar]
- Zhou, M.; Ma, X.; Wang, K.K.; Cheng, T.; Tian, Y.C.; Wang, J.; Zhu, Y.; Hu, Y.Q.; Niu, Q.S.; Gui, L.J.; et al. Detection of phenology using an improved shape model on time-series vegetation index in wheat. Comput. Electron. Agric. 2020, 173, 13. [Google Scholar] [CrossRef]
- Zhao, F.; Yang, G.J.; Yang, X.D.; Cen, H.Y.; Zhu, Y.H.; Han, S.Y.; Yang, H.; He, Y.; Zhao, C.J. Determination of Key Phenological Phases of Winter Wheat Based on the Time-Weighted Dynamic Time Warping Algorithm and MODIS Time-Series Data. Remote Sens. 2021, 13, 1836. [Google Scholar] [CrossRef]
- Kostková, M.; Hlavinka, P.; Pohanková, E.; Kersebaum, K.C.; Nendel, C.; Gobin, A.; Olesen, J.E.; Ferrise, R.; Dibari, C.; Takac, J.; et al. Performance of 13 crop simulation models and their ensemble for simulating four field crops in Central Europe. J. Agric. Sci. 2021, 159, 69–89. [Google Scholar] [CrossRef]
- Černá, H.; Bartošová, L.; Trnka, M.; Bauer, Z.; Štěpánek, P.; Možný, M.; Dubrovský, M.; Žalud, Z. The analysis of long-term phenological data of apricot tree (Prunus armeniaca L.) in southern Moravia during 1927–2009. Acta Univ. Agric. Silvic. Mendel. Brun. 2012, 60, 9–18. [Google Scholar] [CrossRef]
- Marcinkowski, P.; Piniewski, M. Effect of climate change on sowing and harvest dates of spring barley and maize in Poland. Int. Agrophys. 2018, 32, 265–271. [Google Scholar] [CrossRef]
- Bhutto, S.A.; Wang, X.Y.; Wang, J. The start and end of the growing season in Pakistan during 1982–2015. Environ. Earth Sci. 2019, 78, 10. [Google Scholar] [CrossRef]
- Song, Y.; Wang, J.; Yu, Q.; Huang, J.X. Using MODIS LAI Data to Monitor Spatio-Temporal Changes of Winter Wheat Phenology in Response to Climate Warming. Remote Sens. 2020, 12, 786. [Google Scholar] [CrossRef]
- Steele-Dunne, S.C.; McNairn, H.; Monsivais-Huertero, A.; Judge, J.; Liu, P.W.; Papathanassiou, K. Radar Remote Sensing of Agricultural Canopies: A Review. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2249–2273. [Google Scholar] [CrossRef]
- Mercier, A.; Betbeder, J.; Baudry, J.; Le Roux, V.; Spicher, F.; Lacoux, J.; Roger, D.; Hubert-Moy, L. Evaluation of Sentinel-1 & 2 time series for predicting wheat and rapeseed phenological stages. ISPRS J. Photogramm. Remote Sens. 2020, 163, 231–256. [Google Scholar] [CrossRef]
- Caparros-Santiago, J.A.; Rodriguez-Galiano, V.; Dash, J. Land surface phenology as indicator of global terrestrial ecosystem dynamics: A systematic review. ISPRS J. Photogramm. Remote Sens. 2021, 171, 330–347. [Google Scholar] [CrossRef]
- Menzel, A.; Yuan, Y.; Matiu, M.; Sparks, T.; Scheifinger, H.; Gehrig, R.; Estrella, N. Climate change fingerprints in recent European plant phenology. Glob. Chang. Biol. 2020, 26, 2599–2612. [Google Scholar] [CrossRef] [PubMed]
- Parmesan, C.; Yohe, G. A globally coherent fingerprint of climate change impacts across natural systems. Nature 2003, 421, 37–42. [Google Scholar] [CrossRef]
- Buntgen, U.; Piermattei, A.; Krusic, P.J.; Esper, J.; Sparks, T.; Crivellaro, A. Plants in the UK flower a month earlier under recent warming. Proc. R. Soc. B-Biol. Sci. 2022, 289, 9. [Google Scholar] [CrossRef]
- Bartošová, L.; Dížková, P.; Bauerová, J.; Hájková, L.; Fischer, M.; Balek, J.; Bláhová, M.; Možný, M.; Zahradníček, P.; Štěpánek, P.; et al. Phenological Response of Flood Plain Forest Ecosystem Species to Climate Change during 1961–2021. Atmosphere 2022, 13, 978. [Google Scholar] [CrossRef]
- Hájková, L.; Možný, M.; Oušková, V.; Bartošová, L.; Dížková, P.; Žalud, Z. Meteorological Variables That Affect the Beginning of Flowering of the Winter Oilseed Rape in the Czech Republic. Atmosphere 2021, 12, 1444. [Google Scholar] [CrossRef]
- Rezaei, E.E.; Siebert, S.; Ewert, F. Climate and management interaction cause diverse crop phenology trends. Agric. For. Meteorol. 2017, 233, 55–70. [Google Scholar] [CrossRef]
- Bai, H.Z.; Xiao, D.P.; Zhang, H.; Tao, F.L.; Hu, Y.H. Impact of warming climate, sowing date, and cultivar shift on rice phenology across China during 1981–2010. Int. J. Biometeorol. 2019, 63, 1077–1089. [Google Scholar] [CrossRef]
- Huang, X.; Zhu, W.Q.; Wang, X.Y.; Zhan, P.; Liu, Q.F.; Li, X.Y.; Sun, L.X. A Method for Monitoring and Forecasting the Heading and Flowering Dates of Winter Wheat Combining Satellite-Derived Green-up Dates and Accumulated Temperature. Remote Sens. 2020, 12, 3536. [Google Scholar] [CrossRef]
- Zhao, F.; Yang, G.J.; Yang, H.; Long, H.L.; Xu, W.M.; Zhu, Y.H.; Meng, Y.; Han, S.Y.; Liu, M. A Method for Prediction of Winter Wheat Maturity Date Based on MODIS Time Series and Accumulated Temperature. Agriculture 2022, 12, 945. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019; Available online: https://www.R-project.org/ (accessed on 8 October 2022).
- Štěpánek, P. AnClim—Software for Time Series Analysis; Department of Geography, Faculty of Natural Sciences, Masaryk University: Brno, Czech Republic, 2008. [Google Scholar]
- Štěpánek, P.; Zahradníček, P.; Brázdil, R.; Tolasz, R. Metodologie Kontroly a Homogenizace Časových řad v Klimatologii; ČHMÚ: Prague, Czechia, 2012; 118p, ISBN 978-80-86690-97-1. [Google Scholar]
- Štěpánek, P.; Zahradníček, P.; Huth, R. Interpolation techniques used for data quality control and calculation of technical series: An example of a Central European daily time series. Időjárás 2011, 115, 87–98. [Google Scholar]
- Štěpánek, P.; Zahradníček, P.; Farda, A. Experiences with data quality control and homogenization of daily records of various meteorological elements in the Czech Republic in the period 1961–2010. Időjárás 2013, 117, 123–141. [Google Scholar]
- Squintu, A.A.; van der Schrier, G.; Štěpánek, P.; Zahradníček, P.; Tank, A.K. Comparison of homogenization methods for daily temperature series against an observation-based benchmark dataset. Theor. Appl. Climatol. 2020, 140, 285–301. [Google Scholar] [CrossRef]
- Bartošová, L.; Bauer, Z.; Trnka, M.; Štěpánek, P.; Žalud, Z. Climatic factors and their influence on onset and duration of phenological phases of chosen plants at locations south Moravia during 1961–2007. Acta Univ. Agric. Silvic. Mendel. Brun. 2010, 58, 35–44. [Google Scholar] [CrossRef]
- Trnka, M.; Rötter, R.P.; Ruiz-Ramos, M.; Kersebaum, K.C.; Olesen, J.E.; Žalud, Z.; Semenov, M.A. Adverse weather conditions for European wheat production will become more frequent with climate change. Nat. Clim. Chang. 2014, 4, 637–643. [Google Scholar] [CrossRef]
- Trnka, M.; Kocmankova, E.; Balek, J.; Eitzinger, J.; Ruget, F.; Formayer, H.; Hlavinka, P.; Schaumberger, A.; Horakova, V.; Možný, M.; et al. Simple snow cover model for agrometeorological applications. Agric. For. Meteorol. 2010, 150, 1115–1127. [Google Scholar] [CrossRef]
- Vermote, E.; Wolfe, R. MOD09GQ MODIS/Terra Surface Reflectance Daily L2G Global 250 m SIN Grid V006 [Data Set]; NASA EOSDIS Land Processes DAAC; United States Geological Survey: Reston, VA, USA, 2015. [Google Scholar] [CrossRef]
- Zeng, L.L.; Wardlow, B.D.; Xiang, D.X.; Hu, S.; Li, D.R. A review of vegetation phenological metrics extraction using time-series, multispectral satellite data. Remote Sens. Environ. 2020, 237, 20. [Google Scholar] [CrossRef]
- Xiao, D.P.; Tao, F.L.; Liu, Y.J.; Shi, W.J.; Wang, M.; Liu, F.S.; Zhang, S.; Zhu, Z. Observed changes in winter wheat phenology in the North China Plain for 1981–2009. Int. J. Biometeorol. 2013, 57, 275–285. [Google Scholar] [CrossRef]
- Hu, Q.; Weiss, A.; Feng, S.; Baenziger, P.S. Earlier winter wheat heading dates and warmer spring in the US Great Plains. Agric. For. Meteorol. 2005, 135, 284–290. [Google Scholar] [CrossRef]
- Siebert, S.; Ewert, F. Spatio-temporal patterns of phenological development in Germany in relation to temperature and day length. Agric. For. Meteorol. 2012, 152, 44–57. [Google Scholar] [CrossRef]
- Xiao, D.P.; Qi, Y.Q.; Li, Z.Q.; Wang, R.D.; Moiwo, J.P.; Liu, F.S. Impact of thermal time shift on wheat phenology and yield under warming climate in the Huang-Huai-Hai Plain, China. Front. Earth Sci. 2017, 11, 148–155. [Google Scholar] [CrossRef]
- Liu, Y.J.; Chen, Q.M.; Ge, Q.S.; Dai, J.H.; Dou, Y. Effects of climate change and agronomic practice on changes in wheat phenology. Clim. Chang. 2018, 150, 273–287. [Google Scholar] [CrossRef]
- Eitzinger, J.; Trnka, M.; Semeradová, D.; Thaler, S.; Svobodová, E.; Hlavinka, P.; Siska, B.; Takac, J.; Malatinska, L.; Nováková, M.; et al. Regional climate change impacts on agricultural crop production in Central and Eastern Europe—Hotspots, regional differences and common trends. J. Agric. Sci. 2013, 151, 787–812. [Google Scholar] [CrossRef]
- Pullens, J.W.M.; Sorensen, C.A.G.; Olesen, J.E. Temperature-based prediction of harvest date in winter and spring cereals as a basis for assessing viability for growing cover crops. Field Crop. Res. 2021, 264, 11. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).