Abstract
Recent work attributing decadal regime changes in temperature to radiative forcing is extended to atmospheric moisture. Temperature, and specific and relative humidity (T, q, RH) from the HadISDH data set were analyzed for regime shifts using the bivariate test. Most shifts in q and T for global and northern hemisphere (NH), and tropical land occurred within a year of each other. Only one shift of q was recorded in the southern hemisphere (SH). RH increased in the NH in 1990–91 and decreased in a series of shifts from the late 1990s, while in the SH decreased from 2001. The tropics have remained neutral, shifting negative over land and positive over the ocean. The global decreases in 2001 and 2011 was −0.56%. Global RH from 32 climate models from the CMIP5 RCP4.5 archive all contained regime shifts but only 4 reached or exceeded the observed decreases by 2100, the earliest in 2056. Regime shifts in RH and fire danger over Australia are consistent with the SH decreases in RH, shifting within one year of global fire season length in 2002, showing that impacts are also being underestimated by current analyses. Methods for nonlinear attribution and the contributing processes for nonlinear change are discussed. These results show that developing a better understanding of nonlinear change in moisture-related climate risk is an urgent task.
1. Introduction
Decadal step changes have been detected in global mean surface temperature (GMST) and regional temperatures using a number of different change-point methods [1,2,3,4,5,6]. Using inverse modeling, these have been identified as climate regime changes where the nonlinear component is externally forced [4,7]. Similar changes are evident in coupled ocean-atmosphere climate models from the Climate Model Intercomparison Projects CMIP3 and CMIP5 [7].
These results have been severely tested, where a severe test of hypothesis H is successful if it passes statistical tests with probative criteria that its rivals fail—a result that would be very improbable were H false [8]. Hypothesis H is that on decadal timescales, climate responds to forcing via a series of abrupt shifts. This was tested against null hypothesis that the forced component is a gradual, monotonic trend [7]. The latter is the standard view of climate change, recently re-endorsed in the IPCC Sixth Assessment Report (AR6) with high confidence [9].
Of the six tests applied during testing, regime shifts passed all, whereas gradual change did not [7]. Two were crucial:
(1) The timing of shifts in GMST from CMIP3 and CMIP5 ensembles of historical forcing reproduced the observed pattern of regional and global shifts drawn from five observational records with high probability (p < 0.01). Decadal variability is considered to be random, but if it was, this outcome from two successive generations of models would be the almost impossible. Time series were divided into fast and slow components of change by summing internal trends between break points and shifts as the distance between end points of those trends. If the timing of shifts is accepted as being forced, but still due to internal variability, the rapid warming component in observed GMST is too large and the gradual component too small to explain the forced component of total change. For five records 1880–2020, shift to total warming ratios are 0.65 to 0.92.
(2) Time series of GMST 1861–2095 from 94 models in the CMIP5 RCP4.5 ensemble were divided into shifts and internal trends. Regressed against equilibrium climate sensitivity (ECS) 2006–2095, the r2 for shifts was 0.53 compared to 0.18 for trends, giving the fast-warming component 2.9 times the power of slow warming in predicting model ECS [8]. For 1861–2095, the r2 values were 0.36 for shifts and 0.07 for trends, 5.2 times the power.
Instead of the atmosphere warming gradually, during steady-state regimes, excess heat is stored in the ocean where it accumulates. On reaching a critical threshold, heat is suddenly released, producing a rapid response in atmospheric feedback, hence the close relationships between rapid warming and ECS. From the second half of the 20th century, these shifts were initiated in tropical sea surface temperatures before propagating to land and higher latitudes [10]. Decadal variability is often the trigger.
Due to the nonlinearity of the hydrological cycle, atmospheric moisture can often be more important than direct temperature effects. Atmospheric moisture influences the hydrometeorological spectrum from very wet to very dry conditions. For example, higher atmospheric moisture content at higher temperatures increases maximum precipitable water and rainfall intensity [11,12,13]. Moisture deficits are also important, where a lack of moisture at higher temperatures contributes to flash droughts and greater respiratory stress for vegetation [14,15]. Fire climates feature towards the dry end of the hydrological spectrum, where low atmospheric moisture and high rainfall variability greatly increase fire risks [16,17]. Understanding how atmospheric moisture may respond to a changing climate is therefore very important [18,19,20,21].
This paper focuses on regime shifts in relative humidity. It starts by analyzing observations, then goes on to survey shifts in CMIP5 models. We explore methods for nonlinear attribution before showing how regime shifts in RH have affected fire climates in Australia and globally. The results should concern researchers, policy makers and practitioners to the regime-like structure of atmospheric moisture so that impacts can be better anticipated and planning put in place. Instances where regime changes in climate models differ substantially from observations also indicate weaknesses that need to be accounted for when projecting future change.
2. Materials and Methods
Shifts in mean were detected using the multi-step bivariate test utilizing the bivariate test developed by Maronna and Yohai [22] to detect multiple shifts in the time series [23,24]. The bivariate test was developed to test mean shifts in serially independent data. It tests a time series against a random reference where the null hypothesis is no step change, and against a reference variable where the null hypothesis is no relative change from the reference. Let be a stationary reference time series and be a test time series that measures for a single shift at some time i0, where the test result is the Ti0 statistic for maximum i0 in year 0 of the change.
The Ti0 statistic measures against the null of no change in the mean with p < 0.05 thresholds of 7.4, 7.8, 8.2 and 8.7 for i = 15, 20, 30, 40, and p < 0.01 thresholds of 9.3, 9.8, 10.7 and 11.6 for i = 15, 20, 30, 40, respectively. Error sampling using the random reference applies 100 iterations, whereas the relative test uses the available data only once. The multi-step version has been extensively and rigorously tested in a wide range of conditions, providing reliable results in the presence of moderate trends and autocorrelation [24].
A variety of other tests, such as the ADF, and tests for data stationarity and whiteness were sourced from the Real Statistics resource pack [25].
The main data set analyzed for shifts was the HadISDH land [26,27], marine [28,29] and blended data 1973–2020, as anomalies during 1981–2010. HadISDH is a global gridded monthly mean surface humidity dataset. Quality controlled and homogenized/bias-adjusted monthly mean anomalies were provided alongside uncertainty estimates (2σ limits for sampling, coverage, station and combined uncertainties). The land data were derived from the sub-daily temperature and dewpoint quality-controlled data from land stations with sufficiently long records. The marine data were obtained from ships, moored buoys and ocean platforms [29]. Three variables were analyzed for shifts: temperature (T), specific humidity (q) and relative humidity (RH). It has previously been examined for trends [26,28,30,31,32] and compared with the climate model output [33]. Testing was conducted for annual data to detect the shift and obtain p-values against a random reference, then monthly data analyzed to pinpoint the timing.
The data covered publicly available areal averages covering global, northern and southern hemisphere extra tropics and the tropical regions. Domains covered were global 70° S to 70° N, each hemisphere 20–70° and tropics 20° S to 20° N. There were significant data gaps in these records due to incomplete coverage, particularly over the SH ocean [28]. Annual means were initially analyzed using the multi-step bivariate test, but then expanded to allow shifts within the first and last six years of the record and those at p < 0.05, both restrictions within the automated program. This was because of the record’s relatively short length (48 years). Having analyzed longer records and those from other sources, we relaxed the rules near the beginning of the record (e.g., the mid-to-late 1970s following the 1976 Pacific shift), and also towards the end. The initial multistep bivariate test results can be downloaded as Supplementary Material and the updated results are shown in the next section.
Projected global mean relative humidity 1861–2100 from 32 models from the CMIP5 RCP4.5 ensemble was downloaded from the KNMI data repository for the r1p1 (realization 1) and also analyzed for regime shifts. The results are also in the Supplementary Materials.
3. Results
3.1. Observations
The main regime shifts in temperature during the 1973–2020 period occurred in the tropical oceans in 1976–77, the extratropics shortly after in 1978–79, the northern hemisphere in 1987–88, globally in 1995–98, southern hemisphere oceans in 2009–10 and globally in 2014–15 [7,10,24]. T and q from HadISDH are shown in Table 1. Not all shifts in T register a corresponding shift in q but most do. Note that shifts calculated by the bivariate test are an estimate of the change in mean as calculated by the test—these are typically close to the arithmetic mean. T generally preceded q except in between 1994–95 and 1997–98. This marks a period of successive regime shifts in a complex event. Detailed analysis of temperature connects a phase shift in the Atlantic Multidecadal Oscillation (AMO) and regime shift western Pacific Warm Pool in 1995 [10], a link confirmed elsewhere [34]. It was followed in two months by a shift in q in the NH ocean, which preceded any shifts in SST (excepting the warm pool). This established a regime shift in tropical regions and warming in the 1997–98 El Niño propagated this more widely. This was followed by a negative phase shift in the Pacific Decadal Oscillation (PDO), then by three La Niña events through to 2001–02. Changes in q are larger in the tropics compared to the extratropics because of the greater water-holding capacity of the warmer atmosphere, rather than the size of the temperature shifts, which are generally larger in the higher latitudes.

Table 1.
Bivariate test result (Ti0), year of shift, month of shift, p-value for regime changes in specific humidity (g kg−1) and month of shift in temperature from HadISDH data.
For RH, shifts are fewer with timing that generally follows shifts in T and q, often with a delay (Table 2).

Table 2.
Bivariate test result (Ti0), year of shift, month of shift, p-value for regime changes in relative humidity (%) from HadISDH data.
Regimes for the three variables are compared in Figure 1 and Figure 2, illustrated by their internal trends. Global and tropical averages are shown in Figure 1. The timing of regime change in T and q in the global average are closely linked, with the change in T being larger. The tropical averages show T and q moving in unison, showing that the tropics are very efficient in mobilizing atmospheric moisture with warming compared to the extra-tropics. The tropics show limited response in RH until the recent decade, when RH over tropical land reduced. RH decreased in 2012 by 0.40 and over the ocean in 2017 by 0.43, showing no change in the blended record.
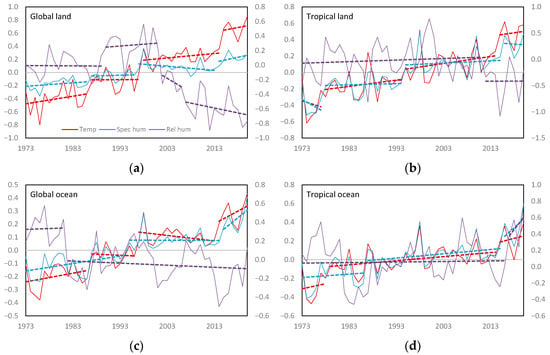
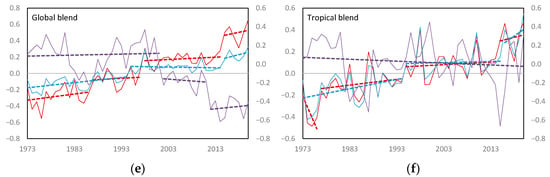
Figure 1.
Annual anomalies (1981–2010) and regimes showing internal trends (dashed lines) for global and tropical average temperature (T), specific humidity (q) and relative humidity (RH) for (a) global land, (b) tropical land, (c) global ocean, (d) global ocean, (e) global blend and (f) tropical blend (Willett et al. 2020). Units are °C for temperature and g kg−1 for specific humidity on the left axis and % for relative humidity on the right axis. Solid lines are annual values and dashed lines internal trends between shift points.
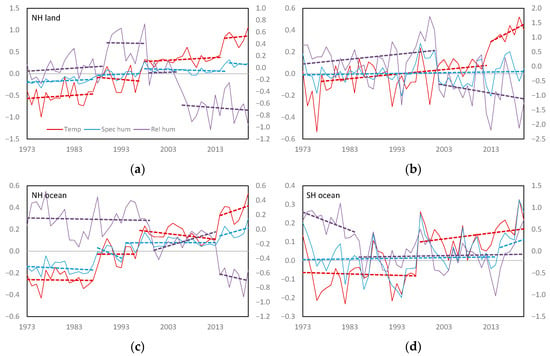
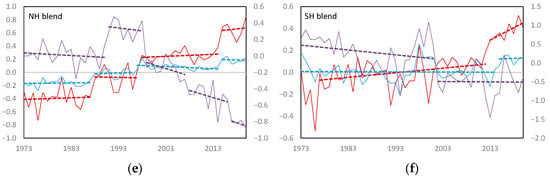
Figure 2.
Annual anomalies (1981–2010) and regimes showing internal trends for northern and southern hemisphere average temperature (T), specific humidity (q) and relative humidity (RH) for (a) NH land, (b) SH land, (c) NH ocean, (d) SH ocean, (e) NH blend and (f) SH blend (Willett et al. 2020). Units are °C for temperature and g kg−1 for specific humidity on the left axis and % for relative humidity on the right axis. Solid lines are annual values and dashed lines internal trends between shift points.
Globally, T increased only slightly faster than q over the ocean, whereas over land, the increase has been larger. This is expected because of the greater partitioning of sensible and latent heat over land. The blended record is partway between the two, but shows a greater influence of land than the ocean. Consistent with this, RH responds more strongly over land and generally follows T and q. Global ocean RH decreased by 0.39 from 1982, then has remained relatively constant, although shows large variability.
Figure 2 shows the hemispheric responses. The NH shows the strong influence of land on atmospheric moisture. The 1987–88 regime shift was to warmer, wetter conditions, producing an increase in RH. This reversed with the next regime shift in the late 1990s. A further downward shift in RH out of phase with T and q over land occurred in 2005–06. RH over the ocean decreased in 2013–14 as part of the recent global shift that coincided with the phase shift in the PDO. The blended data shows the influence of both ocean and land producing long-term gradual change at p > 0.05.
The SH shows fewer regime changes. Shifts in T were fewer with limited change in q except for increases in the ocean and blended records in 2015. RH over the ocean decreased in the mid-1980s. RH over land was sustained until following the 1997–98 shift in temperature, shifting down in late 2001. The cause of this delay was due to the shift in T in 1997–98 being followed by a large La Niña and negative phase shift in the PDO perhaps delaying onset for several years following the shifts in T and q. This downward shift is present in the blended data set, showing the influence of land on the result, despite its relatively small area.
We briefly surveyed longer-term data sets for their ability to represent known regime shifts. Global vapor pressure (1901–2018) over land from the CRU_ts4.03 data set [35] showed upward shifts in 1930 (p < 0.01), 1979 (p < 0.05), 1987 (p < 0.05), 1998 (p < 0.01), and 2015 (p < 0.1). The dates 1979, 1998 and 2015 line up with known shifts in air temperature over land, 1987 registers in the NH and 1930 was a shift date for the HadCRUt data set until recent years [10] (it now separates into 1920–21 and 1936–37). We did not use RH from this data set because its correlation with HadISDH 1973–2018 for the SH is poor (0.14), whereas correlation for specific humidity is good (0.95). We did not analyze reanalysis data in detail for similar reasons.
Exploring Uncertainty
This section explored the sensitivity of these results to uncertainties. The two main types were error and structural uncertainty. Error uncertainty describes the relationship between the test itself and the internal variability within the data. Structural uncertainty contains measurement methods, including instrumentation, coverage and reading frequency, along with data quality management and uncertainty management techniques. The HadISDH data were supplied with 2σ estimates of sample, coverage, station and overall uncertainty. These ranges were constructed by the Monte Carlo sampling of uncertainty ranges at each time step on a 5° grid [26], and were averaged for the regional estimates. The differences between the HadCRUt and HadISDH data sets were mainly structural.
Structural uncertainty affected by the means of measurement and treatment is inherent in any type of environmental measurement. It differs between different treatments, so while it can be explored internally and between different methodologies, the overall uncertainty with respect to the “true” change is very difficult to gauge. This led Thorne et al. [36] to conclude that at least three independent constructions were required to explore such uncertainty. Given there is only one high-quality record of atmospheric moisture, this is not possible here.
As trend and shift analysis represent the signal-to-noise relationship very differently, we assessed the sensitivity of both to a combination of structural and error analysis. Results that are sensitive to various types of uncertainty need to be treated more circumspectly than those that are robust. We analyzed global mean land RH, for both shifts and trends. As noted in Table 2, this time series shifted in 1990, 2002 and 2007 for the median estimate, so we also analyzed the 2σ upper and lower limits. Note that because these limits are measures of annual uncertainty, the likelihood of producing a mean linear or nonlinear response at the 2σ limit is remotely small.
Table 3 shows the shift size and trends for the lower, median and upper limits. The variation between shifts is much lower than trends from the same data, with total estimated change for shifts in the range of −0.51 to −0.71 compared to −0.58 to −0.99 for trends. By not accounting for the positive change in 1990, trend analysis estimates a greater decrease than the bivariate analysis, with a wide range of uncertainty. This increase is routinely interpreted as climate variability. Attribution is discussed in Section 3.3.

Table 3.
Estimates of shifts and trends for the lower limit, median and upper limit estimate for global mean relative humidity (%) over land from the HadISDH data. Trends are % change per decade. All shifts are p < 0.01, except * p < 0.05 and ** p < 0.1. Total change for shifts is the sum of mean change between regimes and for trends is the gradient over the full period (in bold).
Different sampling strategies on the 1990 shift were then assessed. Two tests applied Gaussian sampling on an annual basis for station and overall uncertainty. Station uncertainty is about half of overall uncertainty. This was followed by bias sampling of overall uncertainty, where the same random sample was applied over the whole time series. For the original test that sampled the median only using a randomized reference time series (n = 100) reported in Table 2, the Ti0 variable was 11.96 ± 0.72, the year 1990 ± 0.47 and shift size 0.29 ± 0.01 (Table 4). For the subsequent uncertainties, the Ti0 variable decreased slightly but remained p < 0.01 and the standard deviation increased by a factor of 2–4 for each variable, still minor compared to overall change. The mean changes remained fairly constant while their uncertainty expanded, being constrained by the central limit theorem.

Table 4.
Estimates of shifts for an example regime change using different sampling strategies for structural uncertainty for global mean relative humidity (%) over land 1973–2001, showing the change and standard deviation. All changes are p < 0.01.
We then explored the relative confidence limits for steps and trends over the whole range of uncertainty for global mean RH over land, where the range of confidence for the upper and lower 2σ confidence limits for the whole distribution were calculated. We distinguish steps from shifts where shifts refer to the size of the change only, whereas steps calculate the arithmetic mean change between each shift. Both the bivariate test and least squares trend analysis are based on the assumption of normally distributed serially independent data, so their total area covered is 41.8 RH %years for trends and 41.6 for steps, compared to the measured range of 28.6 RH %years. The results are shown in Figure 3. Both charts show the median RH with the 2σ range, the 2σ confidence limits for the median and the 2σ confidence limits for the entire range for trends (Figure 3a) and steps (Figure 3b). The range for steps clearly fits the data better than that for trends.
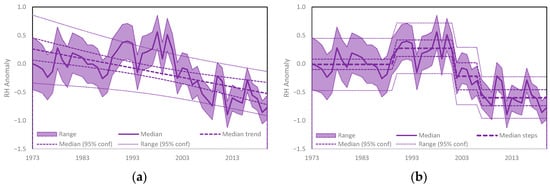
Figure 3.
Median annual anomalies (1981–2010) and the 2σ uncertainty range (shaded area) showing (a) the median trend with 95% trend confidence limits and the 95% annual anomaly range limits assuming change is gradual and (b) as for (a) but considered as regimes (1973–2020).
This is a very important result because trends are fitted to the data based on initial assumptions about the nature of change, whereas steps are based on detection—if there are no steps present below a nominated probability, they do not register. The only optimization is to ensure that all the steps within specified limits are detected.
In this example, the trend data captured 79% of the 2σ uncertainty for the observed range, but 46% of its confidence range was blank space. The step data captured 92% of the observed uncertainty and 37% of its confidence range was blank. Considering only the median estimate for observations, trends captured 27% of the 2σ sigma range and steps 37%. For this narrower band, the confidence range for trends was 42% blank space and for steps was 18%. Testing the residuals of the entire time series for stationarity and whiteness, showed both trends and steps are stationary according to the ADF test, but steps were statistically white according to the Box–Pierce and Ljung–Box tests (p > 0.3), whereas trends were not (p < 1 × 10−8). Overall shifts have a much better fit to the data than trends.
We did not include uncertainty estimates with our results because of the difficulty in separating error from structural uncertainties. However, we showed that detected shifts analyzed as simple steps in mean provided a better fit.
3.2. Comparison with Climate Models
A total of 32 records of RH 70° S to 70° N from CMIP5 RCP4.5 models were analyzed for regime shifts and compared with the global blended record. RH produced by the models is much less responsive to historical forcing than observations. Figure 4 shows all 32 records for the period in 1973–2020, with a common baseline of 1981–2010, shown as a running 11-month mean. Few show any appreciable movement and none reproduce the shifts shown in observations.
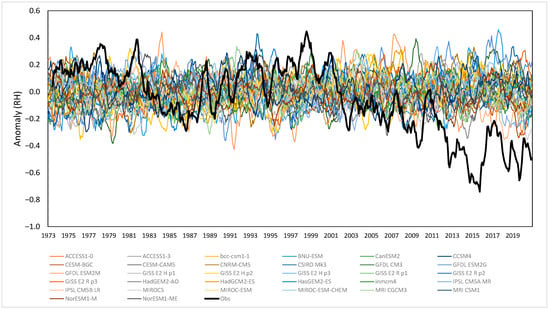
Figure 4.
Simulated RH 70° S to 70° N from CMIP5 RCP4.5 compared with observed RH for blended global RH from Had ISDH. Period 1973–2020 with a baseline of 1981–2010, shown as a running 11-month mean.
Over the full period in 1861–2100, the 32 simulations produced 105 shifts, with 19 records decreasing and 13 increasing. The observed time series shifted by −0.27 in December 2001 and −0.29 in November 2011, a total reduction of −0.56. Only four of the records exceeded this decrease by the decade in 2091–2100. We tested the timing of when the first and second shifts were exceeded by negative regime shifts in the model ensemble. Two models, IPSL CM5A and CM5B, shifted below the first (−0.27 in 2001) in 2014 and 2016, respectively. Eleven more models exceeded that value after 2049. Only three models shifted below the total reduction of −0.56, in 2056, 2075 and 2088, one more meeting it by 2100.
The observed and model time series to 2100 are shown in Figure 5. The 1973–2000 regime in the observations has been readjusted by −0.10 to match the 1981–2010 baseline in the models. The observed response occurred in the presence of a top of the atmosphere energy imbalance of about 0.5 W m2, increasing to about 0.95 W m2 in 2012–13, under atmospheric forcing about three times that amount [37]. The equivalent model response occurs earliest in 2056 with the models stabilizing at a forcing of 4.5 W m2 from around 2060 [38].
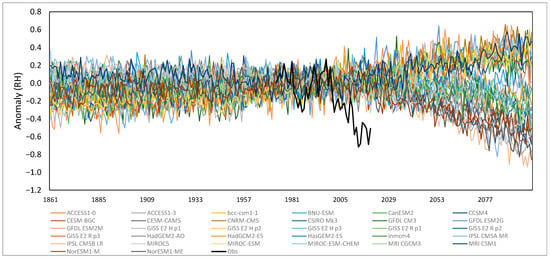
Figure 5.
Simulated annual RH 70° S to 70° N from CMIP5 RCP4.5 (1861–2100) with a baseline of 1981–2010 compared with observed RH for blended global RH from Had ISDH (1973–2020). Observations have been adjusted by −0.10.
These underestimates have been noted by Dunn et al. [33] and Douville and Plazzotta [39]. The latter focused on the NH midlatitudes, linking the recent drying to long-term reduction in CMIP5 models. This was a model-to-model comparison, using reanalysis and SST-forced simulations of historical climate and comparing those with the CMIP5 models run using historical forcing. The Dunn et al. [33] study was restricted to the land-only HadISDH data, and used reanalysis and an SST-forced atmospheric GCM for a fuller assessment of observations to 2014. The latter was unable to reproduce the post 2000 reductions. Historical runs of CMIP5 models from nine groups where historical forcing extended to 2012–14 all failed to match the observations and were inconclusive about the direction of forced change [33]. The models in Figure 4 follow RCP4.6 from 2006 but show similar results.
3.3. Attribution
The differences between observed and modelled RH have been noted previously [18,33], but since the release of the global high-quality HadISDH data set combining ocean and land observations, have become very apparent [28]. RH is one of the most difficult ways to measure climatic variables, along with closely related evaporation measures, especially transpiration [32,40]. If assessed as trend changes, the relatively brief 48-year record presents issues in terms of constraining the associated uncertainties. Non-linear responses are routinely attributed to decadal variability [18,41,42], but if they become an accepted response to forcing, attribution of change within the HadISDH data becomes more straightforward. Most of the uncertainty previously linked to variability converts to signal, and the trends between breakpoints, as pictured in Figure 4 and Figure 5, are generally not statistically meaningful. The 48-year length of the HadISDH record contained zero to three shifts in each time series. The three variables tested produced 36 trends, whereas they provided 31 shifts for T, 25 for q and 20 for RH. Of those internal trends, only one of each variable registered p < 0.05. The models were also very step-like, with global RH showing eight internal trends p < 0.05 and three p < 0.01 associated with the 105 total shifts.
Whether RH is responding to changes in rainfall minus evaporation (P-E) changes over the ocean, or due to soil moisture and vegetation feedbacks over land has also been difficult to assess [32]. The relationship between regime shifts in T, q and RH, can help shed light on that. A feature of the bivariate test is that if related variables shift in unison, no breakpoint is recorded, because even though both records are nonstationary, they share the same relative changes in mean. If shifts are multiplicative and/or out of phase, then they can be detected against a nonstationary reference. This technique was first used by Jones [4] to identify shifts in continental temperature independent of land-surface moisture feedbacks. Here, it was used to identify those feedbacks.
We analyzed three pairs for each of the regions in Table 1 and Table 2, where the first was used as the reference and the second, the test variable. Pairs tested were T–q, T–RH and q–RH. The T–q pairs for the most part recorded no meaningful result, therefore most of the shifts between T and q in Table 1 (the blue and red lines in Figure 1 and Figure 2) are additive. The exceptions are the SH ocean in 1985 shifting down by −0.12 kg m−1 at p < 0.01, an increase over the whole NH of 0.07 kg m−1 in 1988 at p < 0.05, and increase of 0.13 kg m−1 at p < 0.05 over the tropical ocean in 2017 that may be temporary—related to successive La Niña events, an increase of 0.10 kg m−1 in 1995 at p < 0.1 over tropical land and −0.08 kg m−1 at p < 0.1 over global land in 2004 (Table 5). The SH ocean decrease was unrelated to temperature and was not reflected on land so may have been be due to a decrease in oceanic rainfall, or to limited spatial coverage. The other shifts may represent changing moisture distribution.

Table 5.
Bivariate test result (Ti0), year of shift, and p-value for regime changes in pairs with the reference first for temperature (T) specific humidity (q in g kg−1) and relative humidity (RH in %) from HadISDH data. NR is no result, given for p > 0.1 values.
Many of the relationships between T and q with RH shown in Table 5 are multiplicative, reflecting feedback effects, especially with the transition of moisture from ocean to land, and internally on land may be due to changes in rates of moisture recycling. If moisture supply does not keep up with increases in T, RH will decrease. Regime shifts from Table 2 that continue through to Table 5 reflect such changes, and new shifts may indicate other processes in play, such as rainfall changes.
Two events are notable—the first in the late 1980s and the second in the late 1990s. Although Reid et al. [6] addressed the global impacts of the late-1980s shift, our analyses show that its main impact was over NH land, especially Eurasia [24]. Moisture over NH and global land registered as a shift in q in 1987 but was delayed in RH until 1990 (Table 2). These shifts are unusual in representing an increase and are almost totally absent from Table 5, showing that the impact was additive with no additional feedback over land.
The 1990s event was Initiated by a shift in q in the NH ocean in mid-1994 at p < 0.01, timing that is difficult to interpret. However, q showed no net shift from T in Table 1, which shifted in 1997, so can be physically linked. A shift in q in 1995 over the tropics coincided with a relative increase in RH over tropical land and the land-ocean average. Widespread shifts in 1997–98 temperature were reflected in smaller shifts in q in the extratropics. These were followed by relative decreases in RH 1998–2002 in the NH ocean and land, and subsequently SH land. A second shift registered over NH land in 2007, which may have been due to land-based feedback with a nonlinear response shown in Table 5.
Further decreases in RH relative to q occurred over SH in 2012, following two very wet years, and relative to both T and q over the NH ocean in 2014, on top of shifts in both. These are linked to the shifts that ended the extended regime dating from 1997–98 (the so-called hiatus), which influenced the SH followed by the NH. Additional reductions in RH occurred over the NH ocean and land and SH land, while the tropics registered an increase over the ocean and decrease over the land. A contemporary increase in q suggests this latter decrease and that over SH land is largely a land-temperature feedback, whereas the NH shows reductions in RH over both ocean and land.
Other Studies
In AR5 (2013), the IPCC reported that near surface humidity had very likely increased since the 1970s but had since abated over land in recent years (medium confidence) [41]. In AR6, large-scale decreases in RH over land since 2000 were assessed as very likely [40]. The reduction was attributed to greater warming over land and altered circulation patterns, but that is not consistent with the evidence from the regime shifts detailed above, which includes an oceanic origin and subsequent land-based feedback. However, AR6 only analyzed RH over land, lacking access to the latest data from HadISDH containing the updated ocean and land-ocean blended data [28].
Under sustained radiative forcing, the ocean warms the land, even though the land warms by a greater amount [31,42,43]. The ocean is also the dominant source of atmospheric moisture. Ninety percent of the moisture originating from the ocean rains out over the ocean, and ten percent falls on land [44]. Two-thirds of that is then recycled over land [44,45]. Continental precipitation can be mapped as to whether it is largely of oceanic origin or recycled continental [45]. Continental regions with seasonally alternating hot, dry and wet climates tend to be in zones with rainfall of oceanic origin, including regions of Mediterranean climate, tropical wet and dry season climates and some alpine and boreal climates [44,45,46].
Chadwick et al. [47] used a simple model to scale specific humidity over the ocean with that on land, which reproduced land patterns fairly well. Using a similar approach with the same data set, the transport of moist static energy from the ocean to the land produced a fractional response, decreasing RH over drier land areas [30]. According to Chadwick et al. [47], the adjustment timescale of moisture over land in response to transport from the oceans is much faster than the warming timescale of the surface oceans under climate change. However, they were assuming the ocean warms gradually at a slower rate than the atmosphere, whereas it maintains steady state until regime shifts produce rapid warming in SST and the overhead atmosphere.
Both these studies analyzed their results as trends. For temperature and specific and relative humidity 40° S to 40° N (their Figure 1), the Byrne and O’Gorman [31] model predicted the observed trend for all three over land. Their results captured the variability and shift for specific humidity but not fully for relative humidity. This may partly be due to the different sources of land and ocean data. Their land data was derived from HadISDH and the ocean data from the ERA-interim reanalysis [31]. The pattern and timing of large-scale shifts in relative humidity are therefore consistent with the changing relationship between rainfall and evaporation over oceanic source regions for moisture, combined with surface feedback effects over land.
Figure 5 shows 5° × 5° grid-based trends for two periods, 1973–1999 and 2000–2019, almost picking up the 2002 break [26] (Willet et al. 2014; data for 2020). This conveniently captured the main break around the year 2000, so the first period in 1999 contained positive trends over the NH land, whereas the second was dominated by negative trends over midlatitude land and positive trends over some ocean areas, the tropics and high latitudes. Many of the negative regions were in the mid-latitude belts of Mediterranean climates where the vast majority of their moisture is of oceanic origin [45,46]. However, a large part of continental Eurasia where terrestrial recycling is high [44] was also affect by reductions in RH (Figure 6).
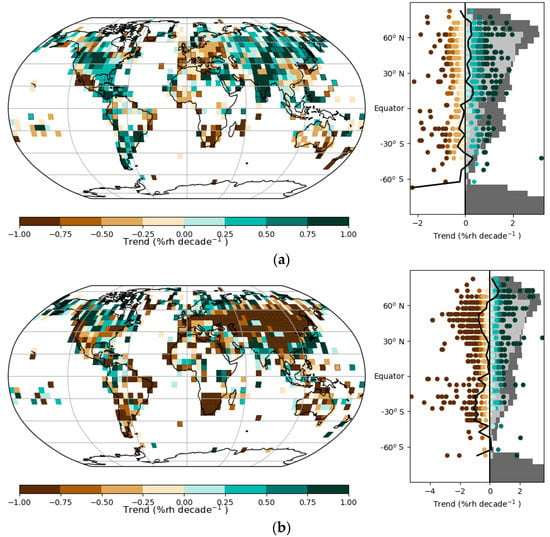
Figure 6.
Trends for blended land and marine RH from the HadISDH dataset [26,28,30] showing trends (a) 1973–1999 and (b) 2000–2019 (center) on a 5° by 5° grid with latitudinal spread of results to the right, where light grey shows proportion coverage (source https://www.metoffice.gov.uk/hadobs/hadisdh/trendmaterialBLEND.html, accessed 20 June 2020).
The advantage of being able to use regime shifts with precise timing means that if forcing can be or has been attributed to the driving variable, and a causal relationship has been established with subsequent variables, then successive regime shifts can be attributed to the original forced response. This offers a great deal more precision than allowed by trends, and the use of inverse analysis as shown in Table 5, means that observations can be relied upon much more strongly, with models being used for support.
The alternative is to use trend analysis, but in the presence of large variability obtaining a statistically meaningful result can be difficult. This is illustrated by the recent AR6 findings on the attribution of changes in observed RH, which is limited to decreases in the midlatitude NH continents in summer with medium confidence [48], despite having evidence of more widespread changes. The sensitivity analysis in Section 3.1 shows that steps reproduce the known uncertainty much more closely.
3.4. Impacts
The impact of regime shifts in moisture is illustrated by a recent analysis of changes in fire danger in Australia and its links to global fire season length [49]. In Australia, fire danger is calculated using McArthur’s Forest Fire Danger Index (FFDI) [50,51,52]. This is constructed from daily maximum temperature (Tmax), 3 p.m. relative humidity, 3 p.m. windspeed and a drought factor. Due to the difficulty in obtaining continuous high-quality records for RH and 3 p.m. windspeed, multiple linear regression relationships for high quality fire season Tmax, rainfall anomalies, cloud cover and area above the 10th percentile of Tmax from the Australian Bureau of Meteorology were used to estimate annual the FFDI indices for total FFDI and days above high, very high and severe FFDI [49]. They were developed using a homogenized nine-station state average for Victoria, Australia 1972–73 to 2009–10, then evaluated for states and territories against a national time series 1973–2017 consisting of 39 stations [52,53]. The results show that for five regions with representative station coverage, a close match was achieved with station-based estimates of average annual FFDI (r2 0.84–0.88) and days of severe fire danger (r2 0.68–0.81) [49].
All regions showed regime shifts in FFDI indices, except for Western Australia and the Northern Territory, regions that span very different climates (tropical/arid zone/temperate and tropical/arid zone). Timing ranged from 1996–97 in Victoria, 2001–02 and 2002–03 in south-west Western Australia, Tasmania, South Australia and New South Wales aand 2012–13 in Queensland. Testing of input variables showed that regime shifts in FFDI occurred only when there was a downward shift in RH that was accompanied or closely followed by a shift in fire season Tmax. The shift in RH was therefore enhancing fire season Tmax through drier conditions. The changes in fire season Tmax generally followed those in mean, which also usually preceded the change in RH. Testing for regime shifts in other inputs showed that wind and other variables were not involved. A fire climate can therefore be defined as the external climatic influences on fire regimes based on the atmospheric moisture content and fire season maximum temperature of a region. Changes in these key variables can therefore be used to project large-scale influences on future fire danger independent of local conditions.
The hemisphere-wide reduction in RH over SH land of −1.1% in 2002 from HadISDH and −2.4% across Australia in 2001 is shown in Figure 7. The Australian median daily average FFDI calculated from Lucas and Harris [54] was compared with global fire season length, a mean anomaly constructed from the number of days when fire danger was above its median value from three analysis data sets for three fire danger variables, covering the US, Canada and Australian FFDI 1979–2013 [55]. Both shifted up in 2002. The Australian record measures a 15% increase, but in some regions, days above severe fire danger have more than doubled [47].
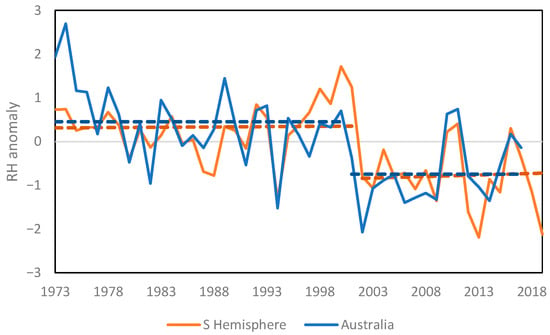
Figure 7.
Mean daily average anomalies for RH from Southern Hemisphere land (HadISDH) and Australia [54], the latter as standard anomalies.
This example shows that shifts in moisture and fire regimes over Australia can be linked to broader-scale regime shifts. There is potential to expand this type of analysis to a range of moisture-related variables. This would include the investigation of fire climates across more regions, changes in soil moisture and drought, ecosystem function, plant growth, surface water balance, and physiological comfort for animal species. They translate into widespread impacts in ecology, agricultural systems, human health and extreme events, including water and fire-related extremes.
4. Discussion
The introduction of the high-quality blended land-ocean data set for HadISDH 1973–2020 [28] provides the opportunity to analyze the data for regime shifts in moisture. Previous work has identified and attributed regime shifts in temperature [4,7] but a lack of confidence in the quality of observed atmospheric moisture data has prevented its extension to relative humidity until now. The analysis here is restricted to the four major zones of publicly available data: the NH and SH extratropics 20–70°, the tropical zone to 20°, and the global average below 70°. These large areas capture the major regional characteristics while averaging out more localized data quality issues, especially those related to lower sampling rates over the ocean.
Area averages capture the average shift over a region. Where regimes are present in the data, uneven sampling of quality-controlled data does not run the risk of detecting shifts where none exist, but it does increase the uncertainty around shift size and timing. Regime shifts are not evenly distributed over a region [24], but spatial data needs to be of sufficiently high quality at the scale being investigated for patterns of regime change to be identified. The uncertainty analysis carried out in Section 3.1 shows that steps provide a more accurate description of change than trends for the example given, which is representative of the overall data.
4.1. Attribution Methods
Measuring shifts and trends uses the same data, but provides very different information. Trends measure long-run change but convey limited information about the signal until sufficient time has elapsed to discount other influences. Different methods of data preparation, such as the removal of various types of noise, will vary the results but usually not the direction [56]. Alternatively, if present, a series of regime shifts can be identified in a single sequence, providing more information.
How forcing is allocated using linear and nonlinear methods is also very different. The standard method treats the forced change as gradual and variations from that signal as stochastic or forced stochastic if forcing is considered to increase the frequency of random events [48]. Trend analysis requires the signal to rise beyond the noise, a process that has become known as signal emergence [57,58]. The separation of signal from noise and its exploration in model ensembles measures stochastic uncertainty [59,60]. For example, comparing satellite estimates of the lower tropospheric atmospheric temperature with compatible model simulations led to the conclusion that a minimum 17-year period was required for signal emergence [61]. A further examination of the statistical emergence of the anthropogenic global fingerprint (spatial pattern) in model ensembles concluded the time of emergence was 8–15 years in the troposphere and 1–3 years in the stratosphere [59]. These longer periods reflect the presence of decadal variations in the troposphere, absent from the stratosphere.
Regime shifts that can be linked to nonlinear shifts in T measure the forced response directly, with the proviso that accompanying shifts in variability mode or unforced circulation changes may complicate the signal, though to a lesser degree than how decadal variability affects trends. Regime shifts affecting causal relationships, such as T→q→RH can also be explored via shift sequences. The nonlinear attribution methods outlined in Section 3.3 allow attribution to be carried out using observations, provided they are of sufficiently quality and extent. This reduces the present reliance on models for direct attribution and increases the emphasis on process studies, especially (i) where various types of forcing may affect regime shifts differently (e.g., stratospheric and tropospheric ozone), (ii) through feedback effects (especially those over land affecting moisture) and (iii) to separate the forced and free components of regime shifts. The latter can arise when mode change in decadal oscillations and forced change combine; e.g., the AMO-PDO in 1995–98 and the PDO in 2012–14.
For standard, linear attribution when observations are limited, models generally are preferred because they provide a more complete spatial and temporal record. For example, two-tier attribution methods were used to compare trends in reanalysis model output with climate model output under various forcings to attribute the decrease in NH midlatitude RH [39]. A significant proportion of attribution studies compare trends in reanalysis data with models subject to historical forcing in preference to observations for reasons of quality and coverage.
However, for nonlinear attribution, the performance of complex climate models and reanalyses in reproducing regime shifts has been inadequate for most variables tested [62]. For example, both the NCEP/NCAR R1 and the Twentieth Century Reanalysis V3 contain regime shifts in radiative fluxes, moisture and temperature but show limited skill in reproducing historical change [62]. An initial survey of RH for R1 1948–2022 shows an inhomogeneity at the beginning of the satellite records in 1979, followed by negative shifts in global mean RH in 1989, 1996 and 2012 of −1.88% compared to the observed −0.56%. The longer V3 record 1880–2015 shows negative shifts in 1893, 1921 and 1960 totaling −0.44% followed by a minor positive trend, so does not reproduce any of the recent change. Simmons et al. [63] showed the ERA interim and ERA40 RH agreed with global and continental trends to 2008, but an initial analysis of RH in ERA50 to 2021 contains positive shifts in 1957 and 1972, a large negative shift in 1988, positive in 2006 and negative in 2018, the latter at p < 0.05. The 1988 and 2006 shifts are in the opposite direction to observations.
The underestimation of modeled changes in RH detailed in Section 3.2 raises serious concerns about their capacity to adequately represent future moisture changes. The incomplete coverage of HadISDH shown in Figure 5 compared to the same overall domain in Figure 3 and Figure 4 may introduce some bias, but these are mostly over the SH ocean. However, using trend analysis of observations as a constraint for future projections, which underestimates the impact of observed downward shift, Douville and Plazzotta [39] found that most of the CMIP5 models underestimated NH midlatitude reductions under the much stronger RCP8.5 forcing.
There is further evidence that models need to be forced harder to produce the changes seen historically. Heede et al. [64] forced a coupled model with abrupt changes in CO2 doubling from 2× to 16×. They showed that assuming that evaporative damping controlled the surface response, the mixed layer model responses followed the Clausius-Clapeyron relationship, whereas the coupled models did not. This indicates a less efficient response, which would result in reduced RH, but these relationships did not diverge greatly until 4 × CO2 forcing was imposed. Furthermore, energy balance constraints restrict the hydrological response to 2–3% of the ideal 7% response per °C predicted by Clausius–Clapeyron relationship [18,65]. Therefore, to reproduce the observed response, coupled models need to be forced much harder than the observed climate.
Trends are most suitable for estimating long-term change, because the additive nature of radiative forcing provides the overall boundary conditions within which the nonlinear dissipative system operates. Overall projected change remains largely altered, but regime shifts and trends are similar to stairs and ramps reaching the same destination—how these rapid shifts affect climate impacts is a critical factor that is largely being overlooked [2,66]. Ensemble means become less important in favor of the statistics of regime shift size, frequency and behavior. This also alters how signal statistical emergence can be calculated—via observations first and individual model statistics second, with ensemble averages being less relevant. Using regime shifts in high quality observational data for attributing forced change will allow attribution to be made with high confidence more rapidly than has been possible to date because of the additional information provided by shifts compared to trends. However, the use of models to understand underlying processes, and in additive analyses that test different elements of forcing, remains essential.
4.2. Contributing Processes and Mechanisms
A set of related papers explore the processes and mechanisms behind regime shifts [62,67]. These focus on the Pacific Ocean heat engine, a heat pump (reverse heat engine) that uses the kinetic energy embodied in the Coriolis Effect to transport heat from the cool reservoir in the eastern Pacific to the hot reservoir of the Western Pacific Warm Pool. This acts as a thermoregulator teleconnected to the broader climate network of decadal oscillations, including the PDO and AMO, which in turn is linked to the Atlantic Meridional Overturning Circulation, resulting in a network of fast to very slow dissipation processes [10]. A major role of the heat pump is to govern the dissipation of heat from the equator to the poles via meridional heat transfer. This involves the dissipation of both moist and dry heat to the poles, the balance between the two influencing available atmospheric moisture.
The asymmetry between the two hemispheres, the high proportion of land in the NH and ocean in the SH, has a significant effect on the balance between heat and moisture given both hemispheres have to emit the same amount of energy to space [62]. The heat engine, which includes ENSO and PDO, and other oscillations are emergent features of coupled systems not present in mixed layer models. These emerged with the advent of ocean-atmosphere coupling [62]. Normally, this network maintains steady-state conditions, but if forced, can reach a critical point where the dissipative processes reorganize to a new regime. Warmer if forcing is positive and cooler if negative.
Further evidence of a complex system response comes from model experiments driven by observed SST. Douville et al. [68] drove the CNRM-CM6-1 atmospheric model with SST and ice extent. Figure 1 shows a clear downward regime shift in RH N of 60° S just before 2000. The NH midlatitudes show rapid increases in the late 1980s, followed by a decrease a decade later [68]. They also undertook process studies, identifying the ocean influence of reduced moisture over land, along with further reductions over land due to the physiological responses to CO2 being included in the land surface model [68]. The inclusion of CO2 effects in this model produced greater declines in RH than its predecessor [68]. These outcomes are consistent with the results in Table 5.
Patch or pacemaker experiments that take a small part of the ocean, running it within a coupled model to assess its influence on the broader climate can also produce regime shifts. Kosaka and Xie [69] tested the findings from previous studies identifying the IPO/PDO as the main driver of the staircase in GMST. They used historical SST covering the eastern Pacific 20° S–20° N and 175° E to the American coast 1870–2014 to drive the GFDL CM2.1 coupled model under historical forcing. This region covers the cool reservoir of the Pacific Ocean heat engine. Based on their results, they concluded that this region is a major driver of Pacific decadal variability [69]. Testing their results for regime shifts, a ten-member ensemble average produced shifts in temperature close to the historical average, in 1977, 1986 and 1997 [62], consistent with the dates in Table 1. This shows the central-eastern Pacific plays a major role in mediating the observed regime shifts [62].
The timing and location of shifts in RH and FFDI indicate that regime shifts are part of tropical expansion. Zonal gradients in temperature pressure and wind stress have increased, increasing the Walker circulation [64], along with increased meridional winds [70]. Mean meridional transport shows nonlinear expansion of the Hadley Cell and transport generally in the late 1990s [71]. These are not seen in the historical simulations of the CMIP5 ensemble [72]. In addition to the pacemaker experiment described above, a recent application of higher resolution in the tropical Pacific also produced PDO behavior more closely, resolving individual eddies [73]. Finer ocean resolution in the tropics may therefore help to overcome the limited responses seen in coupled models (Figure 4 and Figure 5). The addition of realistic physiological processes over land, amplifying regime shifts in RH will also contribute to more realistic regime shifts.
The early indications are that these issues are present in CMIP6 coupled models. Lee et al. [74] project with medium confidence widespread decreased near surface RH over land and moderate increases over the ocean. High confidence (>80% model agreement) is given to some areas of tropical and subtropical land [74]. However, RH has undergone two forced shifts in the late 1990s and in 2014 over the NH ocean, which has reasonable coverage in the HadISDH dataset, so a reversal would be required for this to eventuate. The model consensus over Australia in 2081–2100 under SSP7.0 is −2–0% as shown in Lee et al. [74] (their Figure 4.23) and the observed change in Figure 7 is −2.4%. Note also that the fire regimes changes initiated in the late 1990s/early 2000s in southern Australia are generally close to or equal to the upper limit of change projected for 2030, and the shift in RH/fire season Tmax feedback relationship was the main initiator of these changes [49].
These all point to observed atmospheric moisture being much more responsive to forcing than seen in climate models. Recent changes are being misdiagnosed as decadal climate variability and consequently current and future moisture-related areas of climate risk are being underestimated.
5. Conclusions
Analyses of the recently released land, ocean and blended HadISDH data set [26,28,30] for regime shifts in 1973–2020 show that shifts in specific humidity (q) are closely linked to those in temperature, especially in the tropics and northern hemisphere. All shifts in q were positive, and all regions showed shifts except for the SH land and blended records. For RH, net change between the first to last regime (records containing zero to three regime changes, Table 5) were −0.58 for global land, marine −0.39 and blend −0.56; for NH land −0.63, marine −0.80 and blend −0.83; SH land −1.18, marine −0.77 and blend −0.80; and tropical land −0.40, marine 0.43 and blend no change. The SH and NH changes balance each other, and the tropics show a decrease on land, and increase over the ocean for no net change. Testing RH against temperature and specific humidity shows that some changes were nonlinear, especially those from the late 1990s onwards. These are due to reductions in net moisture transport with respect to temperature over the ocean, which combines with positive land-surface feedbacks over land.
Coupled climate models from CMIP5 produce regime changes in atmospheric moisture (32 models, 170 shifts, with 19 decreasing and 13 increasing), but they significantly underestimate current and future changes in RH. The observed time series shifted by −0.27 in December 2001 and −0.29 in November 2011, a total reduction of −0.56. No model reproduced these reductions and only four of the records met or exceeded this decrease by 2100, the first in 2054.
Analyzing shifts instead of trends in RH provides much greater confidence in the nature and direction of change compared to the findings in AR6. Reductions over the NH and ocean, SH land and global average are forced because of their links with the T→q→RH sequence. When that is translated into impacts, we find that those related to atmospheric dryness, with fire climate being a specific example, are being underestimated.
Using trend analysis to make climate projections reveals a weakness in that the method discards information pertaining to forced nonlinear change, so we have outlined some initial methods for using nonlinear analysis for attributing and projecting climate. Accounting for rapid shifts in atmospheric moisture in detection and attribution, in assessing changing climate risks and in improving model performance in this area are all urgent tasks.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/atmos13101577/s1, MSBV test results.xlsx.
Author Contributions
Conceptualization, R.N.J.; methodology, R.N.J. and J.H.R.; software, J.H.R. and R.N.J.; writing—original draft preparation, R.N.J.; writing—review and editing, R.N.J. and J.H.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
HadISDH is a global gridded monthly mean surface humidity dataset. Quality controlled and homogenized/bias adjusted monthly mean anomalies (relative to a 1991–2020 base period) produced by the UK Met Office Hadley Centre. Downloadable timeseries are linked to the following page https://www.metoffice.gov.uk/hadobs/hadisdh/. The land data is version 4.3.1.2020 and ocean and blended data 1.1.0.2020. Data downloaded 20 July 2020. Licensing information for the data and Figure 6 can be found at https://www.nationalarchives.gov.uk/doc/open-government-licence/version/3/. CMIP5 RCP4.5 RH was obtained from the WMO KNMI climate explorer https://climexp.knmi.nl/selectfield_cmip5.cgi downloaded 20 July 2020. The downloaded timeseries were from the r1p1 realization for each model. CMIP5 archives are made available by the modeling groups, the Program for Climate Model Diagnosis and Intercomparison (PCMDI) and the WCRP’s Working Group on Coupled Modeling (WGCM). The U.S. Department of Energy’s Program for Climate Model Diagnosis and Intercomparison provides coordinating support and led development of software infrastructure in partnership with the Global Organization for Earth System Science Portals.
Acknowledgments
The authors acknowledge the inputs of two anonymous reviewers.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Belolipetsky, P.V.; Bartsev, S.; Ivanova, Y.; Saltykov, M. Hidden staircase signal in recent climate dynamic. Asia-Pac. J. Atmos. Sci. 2015, 51, 323–330. [Google Scholar] [CrossRef]
- Jones, R.N.; Young, C.K.; Handmer, J.; Keating, A.; Mekala, G.D.; Sheehan, P. Valuing Adaptation under Rapid Change; National Climate Change Adaptation Research Facility: Gold Coast, QLD, Australia, 2013; p. 182. [Google Scholar]
- Reid, P.C.; Beaugrand, G. Global synchrony of an accelerating rise in sea surface temperature. J. Mar. Biol. Assoc. UK 2012, 92, 1435–1450. [Google Scholar] [CrossRef]
- Jones, R.N. Detecting and attributing nonlinear anthropogenic regional warming in southeastern Australia. J. Geophys. Res. 2012, 117, D04105. [Google Scholar] [CrossRef]
- Belolipetsky, P.V. The Shifts Hypothesis—An alternative view of global climate change. arXiv 2014, arXiv:1406.5805. [Google Scholar]
- Reid, P.C.; Hari, R.E.; Beaugrand, G.; Livingstone, D.M.; Marty, C.; Straile, D.; Barichivich, J.; Goberville, E.; Adrian, R.; Aono, Y. Global impacts of the 1980s regime shift. Global Change Biol. 2016, 22, 682–703. [Google Scholar] [CrossRef] [PubMed]
- Jones, R.N.; Ricketts, J.H. Reconciling the signal and noise of atmospheric warming on decadal timescales. Earth Syst. Dyn. 2017, 8, 177–210. [Google Scholar] [CrossRef]
- Mayo, D.G. Statistical Inference as Severe Testing; Cambridge University Press: Cambridge, UK, 2018; p. 486. [Google Scholar]
- IPCC. Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Masson-Delmotte, V., Zhai, P., Priani, A., Connors, S., Péan, C., Berger, S., Eds.; Cambridge University Press: Cambridge, UK, 2021.
- Jones, R.N.; Ricketts, J.H. The Pacific Ocean heat engine. Earth Syst. Dyn. Discuss. 2021, 2021, 1–47. [Google Scholar] [CrossRef]
- Pall, P.; Allen, M.; Stone, D.A. Testing the Clausius–Clapeyron constraint on changes in extreme precipitation under CO2 warming. Clim. Dyn. 2007, 28, 351–363. [Google Scholar] [CrossRef]
- O’Gorman, P.A.; Muller, C.J. How closely do changes in surface and column water vapor follow Clausius–Clapeyron scaling in climate change simulations? Environ. Res. Lett. 2010, 5, 025207. [Google Scholar] [CrossRef]
- Kim, S.; Sharma, A.; Wasko, C.; Nathan, R. Linking total precipitable water to precipitation extremes globally. Earth’s Future 2022, 10, e2021EF002473. [Google Scholar] [CrossRef]
- Parker, T.; Gallant, A.; Hobbins, M.; Hoffmann, D. Flash drought in Australia and its relationship to evaporative demand. Environ. Res. Lett. 2021, 16, 064033. [Google Scholar] [CrossRef]
- Otkin, J.A.; Zhong, Y.; Hunt, E.D.; Christian, J.I.; Basara, J.B.; Nguyen, H.; Wheeler, M.C.; Ford, T.W.; Hoell, A.; Svoboda, M. Development of a flash drought intensity index. Atmosphere 2021, 12, 741. [Google Scholar] [CrossRef]
- Beer, T.; Williams, A. Estimating Australian forest fire danger under conditions of doubled carbon dioxide concentrations. Clim. Change 1995, 29, 169–188. [Google Scholar] [CrossRef]
- Rodriguez-Iturbe, I. Ecohydrology: A hydrologic perspective of climate-soil-vegetation dynamies. Water Resour. Res. 2000, 36, 3–9. [Google Scholar] [CrossRef]
- Allan, R.; Barlow, M.; Byrne, M.P.; Cherchi, A.; Douville, H.; Fowler, H.J.; Gan, T.Y.; Pendergrass, A.G.; Rosenfeld, D.; Swann, A.L. Advances in understanding large-scale responses of the water cycle to climate change. Ann. N. Y. Acad. Sci. 2020, 1472, 49–75. [Google Scholar] [CrossRef]
- Davis, R.E.; McGregor, G.R.; Enfield, K.B. Humidity: A review and primer on atmospheric moisture and human health. Environ. Res. 2016, 144, 106–116. [Google Scholar] [CrossRef] [PubMed]
- Gimeno, L.; Dominguez, F.; Nieto, R.; Trigo, R.; Drumond, A.; Reason, C.J.; Taschetto, A.S.; Ramos, A.M.; RameshKumar, M.; Marengo, J. Major mechanisms of atmospheric moisture transport and their role in extreme precipitation events. Annu. Rev. Environ. Resour. 2016, 41, 117–141. [Google Scholar] [CrossRef]
- Dai, A. Drought under global warming: A review. Wiley Interdiscip. Rev. Clim. Change 2011, 2, 45–65. [Google Scholar] [CrossRef]
- Maronna, R.; Yohai, V.J. A bivariate test for the detection of a systematic change in mean. J. Am. Stat. Assoc. 1978, 73, 640–645. [Google Scholar] [CrossRef]
- Ricketts, J.H. A probabilistic approach to climate regime shift detection based on Maronna’s bivariate test. In Proceedings of the 21st International Congress on Modelling and Simulation (MODSIM2015), Gold Coast, QLD, Australia, 29 November–4 December 2015; pp. 1310–1316. [Google Scholar]
- Ricketts, J.H. Understanding the Nature of Abrupt Decadal Shifts in a Changing Climate. Ph.D. Thesis, Victoria University, Melbourne, VIC, Australia, 2019. [Google Scholar]
- Zaiontz, C. Real Statistics Resource Pack, v6.0. 2018. Available online: www.real-statistics.com (accessed on 29 September 2019).
- Willett, K.; Dunn, R.; Thorne, P.; Bell, S.; De Podesta, M.; Parker, D.; Jones, P.; Williams, C., Jr. HadISDH land surface multi-variable humidity and temperature record for climate monitoring. Clim. Past 2014, 10, 1986–2006. [Google Scholar] [CrossRef]
- Smith, A.; Lott, N.; Vose, R. The integrated surface database: Recent developments and partnerships. Bull. Am. Meteorol. Soc. 2011, 92, 704–708. [Google Scholar] [CrossRef]
- Willett, K.M.; Dunn, R.J.; Kennedy, J.J.; Berry, D.I. Development of the HadISDH marine humidity climate monitoring dataset. Earth Syst. Sci. Data 2020, 12, 2853–2880. [Google Scholar] [CrossRef]
- Freeman, E.; Woodruff, S.D.; Worley, S.J.; Lubker, S.J.; Kent, E.C.; Angel, W.E.; Berry, D.I.; Brohan, P.; Eastman, R.; Gates, L. ICOADS Release 3.0: A major update to the historical marine climate record. Int. J. Climatol. 2017, 37, 2211–2232. [Google Scholar] [CrossRef]
- Willett, K.M.; Williams, C.N., Jr.; Dunn, R.J.; Thorne, P.W.; Bell, S.; de Podesta, M.; Jones, P.D.; Parker, D.E. HadISDH: An updateable land surface specific humidity product for climate monitoring. Clim. Past. 2013, 9, 657–677. [Google Scholar] [CrossRef]
- Byrne, M.P.; O’Gorman, P.A. Trends in continental temperature and humidity directly linked to ocean warming. Proc. Natl. Acad. Sci. USA 2018, 115, 4863–4868. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Nieto, R.; Gimeno, L.; Azorin-Molina, C.; Drumond, A.; El Kenawy, A.; Dominguez-Castro, F.; Tomas-Burguera, M.; Peña-Gallardo, M. Recent changes of relative humidity: Regional connections with land and ocean processes. Earth Syst. Dyn. 2018, 9, 915–937. [Google Scholar] [CrossRef]
- Dunn, R.J.; Willett, K.M.; Ciavarella, A.; Stott, P.A. Comparison of land surface humidity between observations and CMIP5 models. Earth Syst. Dyn. 2017, 8, 719. [Google Scholar] [CrossRef]
- Sun, C.; Kucharski, F.; Li, J.; Jin, F.-F.; Kang, I.-S.; Ding, R. Western tropical Pacific multidecadal variability forced by the Atlantic multidecadal oscillation. Nat. Commun. 2017, 8, 1–10. [Google Scholar] [CrossRef]
- University of East Anglia Climatic Research Unit; Harris, I.C.; Jones, P.D. CRU TS4.03: Climatic Research Unit (CRU) Time-Series (TS) Version 4.03 of High-Resolution Gridded Data of Month-By-Month Variation in Climate (Jan. 1901–Dec. 2018), Centre for Environmental Data Analysis. 2020. Available online: https://catalogue.ceda.ac.uk/uuid/10d3e3640f004c578403419aac167d82 (accessed on 20 April 2020).
- Thorne, P.W.; Parker, D.E.; Christy, J.R.; Mears, C.A. Uncertainties in Climate Trends: Lessons from Upper-Air Temperature Records. Bull. Am. Meteorol. Soc. 2005, 86, 1437–1442. [Google Scholar] [CrossRef]
- Loeb, N.G.; Johnson, G.C.; Thorsen, T.J.; Lyman, J.M.; Rose, F.G.; Kato, S. Satellite and ocean data reveal marked increase in Earth’s heating rate. Geophys. Res. Lett. 2021, 48, e2021GL093047. [Google Scholar] [CrossRef]
- Thomson, A.; Calvin, K.; Smith, S.; Kyle, G.P.; Volke, A.; Patel, P.; Delgado-Arias, S.; Bond-Lamberty, B.; Wise, M.; Clarke, L.; et al. RCP4.5: A pathway for stabilization of radiative forcing by 2100. Clim. Change 2011, 109, 77–94. [Google Scholar] [CrossRef]
- Douville, H.; Plazzotta, M. Midlatitude summer drying: An underestimated threat in CMIP5 models? Geophys. Res. Lett. 2017, 44, 9967–9975. [Google Scholar] [CrossRef]
- Gulev, S.K.; Thorne, P.W.; Ahn, J.; Dentener, F.J.; Domingues, C.M.; Gerland, S.; Gong, D.; Kaufman, D.S.; Nnamchi, H.C.; Quaas, J.; et al. Changing state of the climate system. In Climate Change 2021: Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M.I., et al., Eds.; Cambridge University Press: Cambridge, UK, 2021; pp. 287–422. [Google Scholar]
- Hartmann, D.L.; Tank, A.M.G.K.; Rusticucci, M.; Alexander, L.V.; Brönnimann, S.; Charabi, Y.; Dentener, F.J.; Dlugokencky, E.J.; Easterling, D.R.; Kaplan, A.; et al. Observations: Atmosphere and Surface. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; pp. 159–254. [Google Scholar]
- Boer, G. The ratio of land to ocean temperature change under global warming. Clim. Dyn. 2011, 37, 2253–2270. [Google Scholar] [CrossRef]
- Dommenget, D. The Ocean’s Role in Continental Climate Variability and Change. J. Clim. 2009, 22, 4939–4952. [Google Scholar] [CrossRef]
- Gimeno, L.; Drumond, A.; Nieto, R.; Trigo, R.M.; Stohl, A. On the origin of continental precipitation. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Gimeno, L.; Stohl, A.; Trigo, R.M.; Dominguez, F.; Yoshimura, K.; Yu, L.; Drumond, A.; Durán-Quesada, A.M.; Nieto, R. Oceanic and terrestrial sources of continental precipitation. Rev. Geophys. 2012, 50. [Google Scholar] [CrossRef]
- Van der Ent, R.J.; Savenije, H.H.; Schaefli, B.; Steele-Dunne, S.C. Origin and fate of atmospheric moisture over continents. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Chadwick, R.; Good, P.; Willett, K. A simple moisture advection model of specific humidity change over land in response to SST warming. J. Clim. 2016, 29, 7613–7632. [Google Scholar] [CrossRef]
- Eyring, V.; Gillett, N.; Achutarao, K.; Barimalala, R.; Barreiro Parrillo, M.; Bellouin, N.; Cassou, C.; Durack, P.; Kosaka, Y.; McGregor, S.; et al. Human Influence on the Climate System. In Climate Change 2021: Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M.I., et al., Eds.; Cambridge University Press: Cambridge UK, 2021. [Google Scholar]
- Jones, R.N.; Ricketts, J.H. Constructing and Assessing Fire Climates for Australia; Victoria University: Melbourne, VIC, Australia, 2021; p. 65. [Google Scholar]
- Luke, R.H.; McArthur, A.G. Bushfires in Australia; Australian Government Publishing Service: Canberra, ACT, Australia, 1978; p. 359.
- McArthur, A.G. Fire Behaviour in Eucalypt Forests; Forestry and Timber Bureau: Canberra, ACT, Australia, 1967; p. 36. [Google Scholar]
- Noble, I.; Gill, A.; Bary, G. McArthur’s fire-danger meters expressed as equations. Aust. J. Ecol. 1980, 5, 201–203. [Google Scholar] [CrossRef]
- Harris, S.; Lucas, C. Understanding the variability of Australian fire weather between 1973 and 2017. PLoS ONE 2019, 14, e0222328. [Google Scholar] [CrossRef]
- Lucas, C.; Harris, S. Seasonal McArthur Forest Fire Danger Index (FFDI) Data for Australia: 1973–2017. 2019. Mendeley Data. Available online: https://data.mendeley.com/datasets/xf5bv3hcvw/2 (accessed on 7 February 2020).
- Jolly, W.M.; Cochrane, M.A.; Freeborn, P.H.; Holden, Z.A.; Brown, T.J.; Williamson, G.J.; Bowman, D.M.J.S. Climate-induced variations in global wildfire danger from 1979 to 2013. Nat. Commun. 2015, 6, 7537. [Google Scholar] [CrossRef]
- Li, J.; Thompson, D.W.; Barnes, E.A.; Solomon, S. Quantifying the lead time required for a linear trend to emerge from natural climate variability. J. Clim. 2017, 30, 10179–10191. [Google Scholar] [CrossRef]
- Hawkins, E.; Sutton, R. Time of emergence of climate signals. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Chen, D.; Rojas, M.; Samset, B.; Cobb, K.; Diongue Niang, A.; Edwards, P.; Emori, S.; Faria, S.; Hawkins, E.; Hope, P. Framing, context, and methods. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Masson-Delmotte, V., Zhai, V., Pirani, A., Conners, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M.I., et al., Eds.; Cambridge University Press: Cambridge UK, 2021. [Google Scholar]
- Santer, B.D.; Fyfe, J.C.; Solomon, S.; Painter, J.F.; Bonfils, C.; Pallotta, G.; Zelinka, M.D. Quantifying stochastic uncertainty in detection time of human-caused climate signals. Proc. Natl. Acad. Sci. USA 2019, 116, 19821–19827. [Google Scholar] [CrossRef]
- James, R.; Washington, R.; Schleussner, C.F.; Rogelj, J.; Conway, D. Characterizing half-a-degree difference: A review of methods for identifying regional climate responses to global warming targets. Wiley Interdiscip. Rev. Clim. Change 2017, 8, e457. [Google Scholar] [CrossRef]
- Santer, B.D.; Mears, C.; Doutriaux, C.; Caldwell, P.; Gleckler, P.J.; Wigley, T.M.L.; Solomon, S.; Gillett, N.P.; Ivanova, D.; Karl, T.R.; et al. Separating signal and noise in atmospheric temperature changes: The importance of timescale. J. Geophys. Res. 2011, 116, D22105. [Google Scholar] [CrossRef]
- Jones, R.N.; Ricketts, J.H. Climate as a complex, self-regulating system. Earth Syst. Dyn. Discuss. 2021, 2021, 1–47. [Google Scholar] [CrossRef]
- Simmons, A.J.; Willett, K.M.; Jones, P.D.; Thorne, P.W.; Dee, D.P. Low-frequency variations in surface atmospheric humidity, temperature, and precipitation: Inferences from reanalyses and monthly gridded observational data sets. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
- Heede, U.K.; Fedorov, A.V.; Burls, N.J. Time Scales and Mechanisms for the Tropical Pacific Response to Global Warming: A Tug of War between the Ocean Thermostat and Weaker Walker. J. Clim. 2020, 33, 6101–6118. [Google Scholar] [CrossRef]
- Held, I.M.; Soden, B.J. Robust responses of the hydrological cycle to global warming. J. Clim. 2006, 19, 5686–5699. [Google Scholar] [CrossRef]
- Ebi, K.L.; Ziska, L.H.; Yohe, G.W. The shape of impacts to come: Lessons and opportunities for adaptation from uneven increases in global and regional temperatures. Clim. Change 2016, 139, 341–349. [Google Scholar] [CrossRef]
- Ricketts, J.; Jones, R. Severe Testing and Characterization of Change Points in Climate Time Series. In Recent Advances in Numerical Simulations; InTech Open: London, UK, 2021; p. 209. [Google Scholar] [CrossRef]
- Douville, H.; Decharme, B.; Delire, C.; Colin, J.; Joetzjer, E.; Roehrig, R.; Saint-Martin, D.; Oudar, T.; Stchepounoff, R.; Voldoire, A. Drivers of the enhanced decline of land near-surface relative humidity to abrupt 4xCO2 in CNRM-CM6-1. Clim. Dyn. 2020, 55, 1613–1629. [Google Scholar] [CrossRef]
- Kosaka, Y.; Xie, S.-P. The tropical Pacific as a key pacemaker of the variable rates of global warming. Nat. Geosci. 2016, 9, 669–673. [Google Scholar] [CrossRef]
- Hu, S.; Fedorov, A.V. Cross-equatorial winds control El Niño diversity and change. Nat. Clim. Change 2018, 8, 798–802. [Google Scholar] [CrossRef]
- Lucas, C.; Rudeva, I.; Nguyen, H.; Boschat, G.; Hope, P. Variability and changes to the mean meridional circulation in isentropic coordinates. Clim. Dyn. 2022, 58, 257–276. [Google Scholar] [CrossRef]
- Kociuba, G.; Power, S.B. Inability of CMIP5 models to simulate recent strengthening of the Walker circulation: Implications for projections. J. Clim. 2015, 28, 20–35. [Google Scholar] [CrossRef]
- Constantinou, N.C.; Hogg, A.M. Intrinsic oceanic decadal variability of upper-ocean heat content. J. Clim. 2021, 34, 6175–6189. [Google Scholar] [CrossRef]
- Lee, J.-Y.; Marotzke, J.; Bala, G.; Cao, L.; Corti, S.; Dunne, J.P.; Engelbrecht, F.; Fischer, E.; Fyfe, J.C.; Jones, C.; et al. Future global climate: Scenario-based projections and near-term information. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Masson-Delmotte, V., Zhai, V., Pirani, A., Conners, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M.I., et al., Eds.; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).