Sugarcane Yield Forecast in Ivory Coast (West Africa) Based on Weather and Vegetation Index Data
Abstract
1. Introduction
2. Studied Area and Data
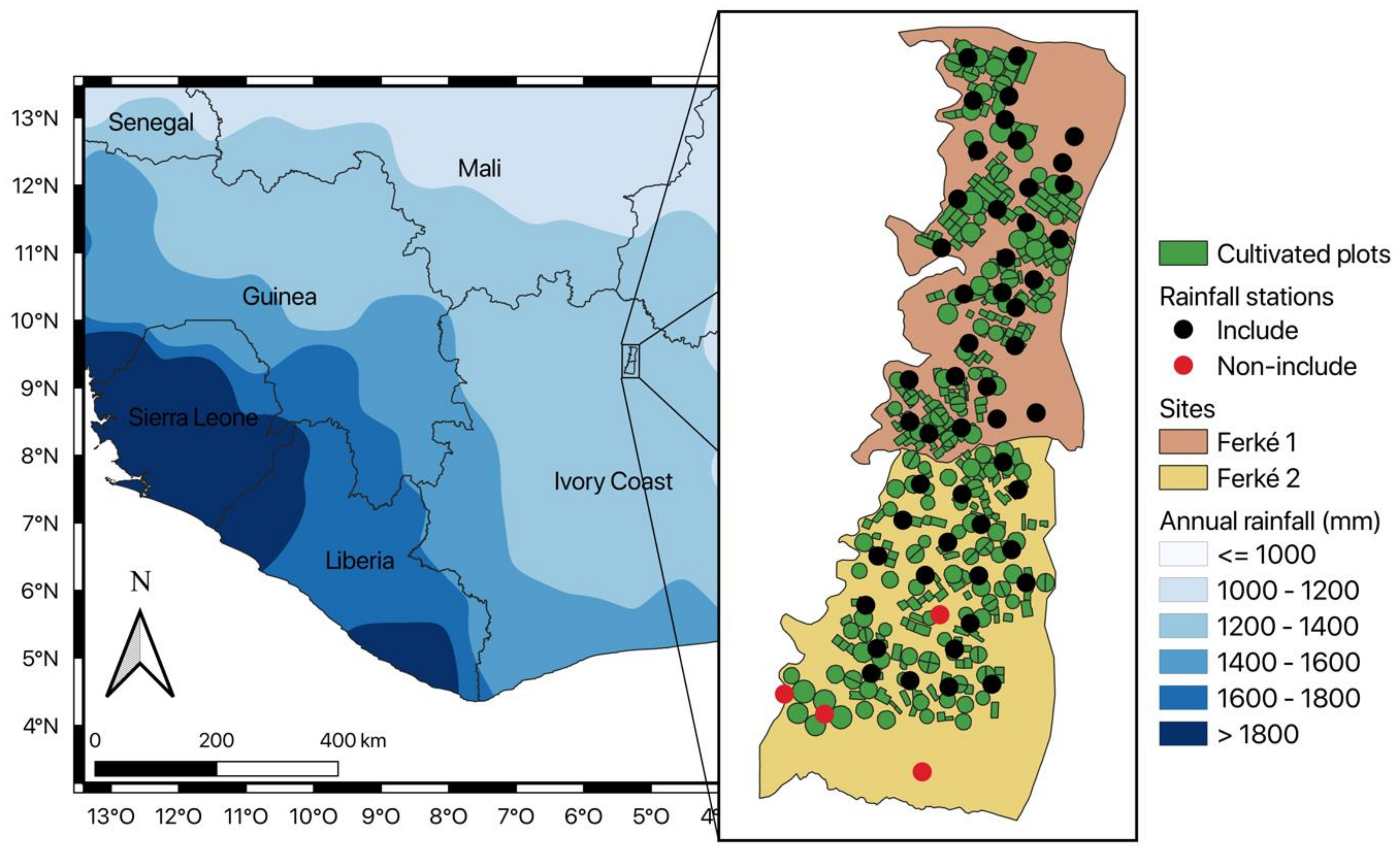
2.1. Studied Area
2.2. Data
2.2.1. Sugarcane Yield
2.2.2. Meteorological Data
2.2.3. Satellite Data
3. Methodology
3.1. Trends and Breaks in Rainfall Data
3.2. Explanatory and Yield Forecating Models
3.2.1. Forecast from Climate Variables at the Plot Level
Explanatory Model
Forecasting Model
3.2.2. Forecast of Mean Sugarcane Yields of Ferké 1 and 2 from Climate Variables
Explanatory Model
Forecasting Model
3.2.3. Forecasting from Satellite Variables at the Plot Level
Explanatory Model
Forecasting Model
3.3. Comparison of the Models
4. Results and Discussion
4.1. Trends and Change-Points in Data
4.2. Explanatory and Yield-Forecasting Models
4.2.1. Explanatory and Forecasting Models Using Climate Variables and Cropping Practices at the Plot Scale
Explanatory Model
Forecasting Model
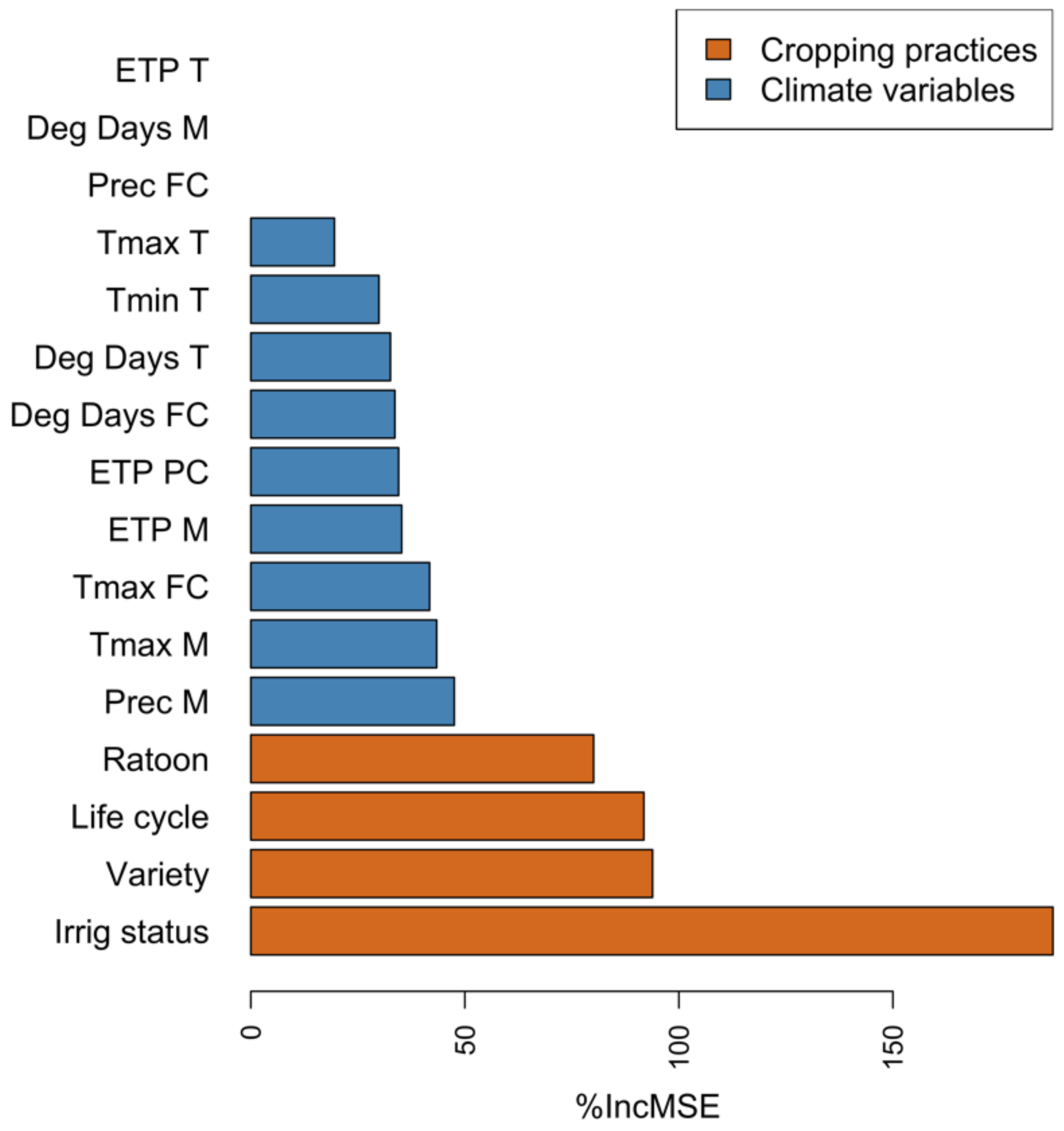
Cropping Practices
4.2.2. Explanatory and Forecasting Models Using Climate Data at the Scale of Ferké 1 and Ferké 2
Explanatory Model
Forecasting Model
4.2.3. Explanatory and Forecasting Models Using Satellite Data
Explanatory Model
Forecasting Model
4.3. Overall Assessment of the Forecasting Models
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- World Bank. Agriculture, Forestry, and Fishing, Value Added (% of GDP)—Cote d’Ivoire. Available online: https://data.worldbank.org/indicator/NV.AGR.TOTL.ZS?locations=CI (accessed on 7 September 2020).
- FAO. World Food and Agriculture—Statistical Pocketbook 2019; Food & Agriculture Organization: Rome, Italy, 2019; ISBN 978-92-5-131849-2. [Google Scholar]
- Ransinghe, R.; Ruane, A.C.; Vautard, R.; Arnell, N.; Coppola, E.; Cruz, F.A.; Dessai, S.; Islam, A.S.; Rahimi, M.; Carrascal, D.R.; et al. Climate Change Information for Regional Impact and for Risk Assessment. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Masson Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M.I., Eds.; IPCC: Geneva, Switzerland; Cambridge University Press: Cambridge, UK, 2021; In Press. [Google Scholar]
- Konan, E.A.; Pene, C.B.; Dick, E. Caractérisation Agro-Climatique Du Périmètre Sucrier de Ferké 2 Au Nord de La Côte d’Ivoire. J. Appl. Biosci. 2017, 116, 11532–11545. [Google Scholar] [CrossRef][Green Version]
- Noufé, D.; Mahé, G.; Kamagaté, B.; Servat, É.; Tié, A.G.B.; Savané, I. Climate Change Impact on Agricultural Production: The Case of Comoe River Basin in Ivory Coast. Hydrol. Sci. J. 2015, 60, 1972–1983. [Google Scholar] [CrossRef][Green Version]
- Sanogo, S.; Fink, A.H.; Omotosho, J.A.; Ba, A.; Redl, R.; Ermert, V. Spatio-Temporal Characteristics of the Recent Rainfall Recovery in West Africa. Int. J. Climatol. 2015, 35, 4589–4605. [Google Scholar] [CrossRef]
- Sultan, B.; Defrance, D.; Iizumi, T. Evidence of Crop Production Losses in West Africa Due to Historical Global Warming in Two Crop Models. Sci. Rep. 2019, 9, 12834. [Google Scholar] [CrossRef]
- Parkes, B.; Defrance, D.; Sultan, B.; Ciais, P.; Wang, X. Projected Changes in Crop Yield Mean and Variability over West Africa in a World 1.5 K Warmer than the Pre-Industrial Era. Earth Syst. Dyn. 2018, 9, 119–134. [Google Scholar] [CrossRef]
- Marin, F.R.; Jones, J.W.; Singels, A.; Royce, F.; Assad, E.D.; Pellegrino, G.Q.; Justino, F. Climate Change Impacts on Sugarcane Attainable Yield in Southern Brazil. Clim. Chang. 2013, 117, 227–239. [Google Scholar] [CrossRef]
- Singels, A.; Jones, M.; Marin, F.; Ruane, A.; Thorburn, P. Predicting Climate Change Impacts on Sugarcane Production at Sites in Australia, Brazil and South Africa Using the Canegro Model. Sugar Tech 2014, 16, 347–355. [Google Scholar] [CrossRef]
- Linnenluecke, M.K.; Nucifora, N.; Thompson, N. Implications of Climate Change for the Sugarcane Industry. WIREs Clim. Chang. 2018, 9, e498. [Google Scholar] [CrossRef]
- Zhao, D.; Li, Y.-R. Climate Change and Sugarcane Production: Potential Impact and Mitigation Strategies. Int. J. Agron. 2015, 2015, e547386. [Google Scholar] [CrossRef]
- Vaughan, C.; Muth, M.F.; Brown, D.P. Evaluation of Regional Climate Services: Learning from Seasonal-Scale Examples across the Americas. Clim. Serv. 2019, 15, 100104. [Google Scholar] [CrossRef]
- World Meteorological Organization. 2019 State of Climate Services; World Meteorological Organization: Geneva, Switzerland, 2019; p. 44. [Google Scholar]
- Vaughan, C.; Dessai, S. Climate Services for Society: Origins, Institutional Arrangements, and Design Elements for an Evaluation Framework. Wiley Interdiscip. Rev. Clim. Chang. 2014, 5, 587–603. [Google Scholar] [CrossRef] [PubMed]
- Akwango, D.; Obaa, B.B.; Turyahabwe, N.; Baguma, Y.; Egeru, A. Effect of Drought Early Warning System on Household Food Security in Karamoja Subregion, Uganda. Agric. Food Secur. 2017, 6, 43. [Google Scholar] [CrossRef]
- Ouedraogo, M.; Zougmore, R.; Barry, S.; Some, L. The Value and Benefits of Using Seasonal Climate Forecasts in Agriculture: Evidence from Cowpea and Sesame Sectors in Climate-Smart Villages of Burkina Faso (Info Note, pp. 1–4). Available online: https://www.researchgate.net/publication/292987809_The_value_and_benefits_of_using_seasonal_climate_forecasts_in_agriculture_evidence_from_cowpea_and_sesame_sectors_in_climate-smart_villages_of_Burkina_Faso (accessed on 29 September 2020).
- Vaughan, C.; Hansen, J.; Roudier, P.; Watkiss, P.; Carr, E. Evaluating Agricultural Weather and Climate Services in Africa: Evidence, Methods, and a Learning Agenda. WIREs Clim. Chang. 2019, 10, e586. [Google Scholar] [CrossRef]
- Keating, B.A.; Robertson, M.J.; Muchow, R.C.; Huth, N.I. Modelling Sugarcane Production Systems I. Development and Performance of the Sugarcane Module. Field Crops Res. 1999, 61, 253–271. [Google Scholar] [CrossRef]
- Singels, A.; Donaldson, R.A. A Simple Model of Unstressed Sugarcane Canopy Development. Proc. S. Afr. Sug. Technol. Ass. 2000, 74, 151–154. [Google Scholar]
- Cardozo, N.P.; Sentelhas, P.C. Climatic Effects on Sugarcane Ripening under the Influence of Cultivars and Crop Age. Sci. Agric. 2013, 70, 449–456. [Google Scholar] [CrossRef]
- Scarpari, M.S.; de Beauclair, E.G.F. Physiological Model to Estimate the Maturity of Sugarcane. Sci. Agric. 2009, 66, 622–628. [Google Scholar] [CrossRef]
- Everingham, Y.; Sexton, J.; Skocaj, D.; Inman-Bamber, G. Accurate Prediction of Sugarcane Yield Using a Random Forest Algorithm. Agron. Sustain. Dev. 2016, 36, 27. [Google Scholar] [CrossRef]
- Hammer, R.G.; Sentelhas, P.C.; Mariano, J.C.Q. Sugarcane Yield Prediction through Data Mining and Crop Simulation Models. Sugar Tech 2020, 22, 216–225. [Google Scholar] [CrossRef]
- De Oliveira, M.P.G.; Bocca, F.F.; Rodrigues, L.H.A. From Spreadsheets to Sugar Content Modeling: A Data Mining Approach. Comput. Electron. Agric. 2017, 132, 14–20. [Google Scholar] [CrossRef]
- Bégué, A.; Todoroff, P.; Pater, J. Multi-Time Scale Analysis of Sugarcane within-Field Variability: Improved Crop Diagnosis Using Satellite Time Series? Precis. Agric. 2008, 9, 161–171. [Google Scholar] [CrossRef]
- Robson, A. Developing Sugarcane Yield Prediction Algorithms from Satellite Imagery. In Proceedings of the 34th Conference of the Australian Society of Sugar Cane Technologists, Cairns, Australia, 1–4 May 2012; Volume 34, p. 11. [Google Scholar]
- Albergel, J.; Lévêque, C.; Aubertin, C. Le nord de la Côte d’Ivoire, un milieu approprié aux aménagements de petite et moyenne hydraulique. In L’eau en Partage: Les Petits Barrages de Côte d’Ivoire; Cecchi, P., Ed.; Latitudes 23; IRD: Paris, France, 2007; pp. 45–57. [Google Scholar]
- Gaudin, R. Incidence de l’eau sur la culture de la canne. Agric. Dév. 1999, 24, 5–8. [Google Scholar]
- Humbert, R.P. The Growing of Sugar Cane; Elsevier Pub. Co.: Amsterdam, The Netherlands; New York, NY, USA, 1968. [Google Scholar]
- Deressa, T.; Hassan, R.; Poonyth, D. Measuring the Impact of Climate Change on South African Agriculture: The Case of Sugarcane Growing Regions. Agrekon 2005, 44, 524–542. [Google Scholar] [CrossRef]
- Hunsigi, G. Production of Sugarcane: Theory and Practice; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; ISBN 978-3-642-78133-9. [Google Scholar]
- Dias, H.B.; Sentelhas, P.C. Evaluation of Three Sugarcane Simulation Models and Their Ensemble for Yield Estimation in Commercially Managed Fields. Field Crops Res. 2017, 213, 174–185. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The Climate Hazards Infrared Precipitation with Stations—A New Environmental Record for Monitoring Extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef]
- Romero, R.; Guijarro, J.A.; Ramis, C.; Alonso, S. A 30-Year (1964–1993) Daily Rainfall Data Base for the Spanish Mediterranean Regions: First Exploratory. Int. J. Clim. 1998, 18, 541–560. [Google Scholar] [CrossRef]
- Teegavarapu, R.S.V.; Chandramouli, V. Improved Weighting Methods, Deterministic and Stochastic Data-Driven Models for Estimation of Missing Precipitation Records. J. Hydrol. 2005, 312, 191–206. [Google Scholar] [CrossRef]
- Weier, J.; Herring, D. Measuring Vegetation (NDVI and EVI); NASA Earth Observatory: Washington, DC, USA.
- Didan, K.; Munoz, A.B.; Huete, A. MODIS Vegetation Index User’s Guide (MOD13 Series); Vegetation Index and Phenology Lab, University of Arizona: Tucson, AZ, USA, 2015; p. 35. [Google Scholar]
- Fernandes, J.L.; Ebecken, N.F.F.; Esquerdo, J.C.D.M. Sugarcane Yield Prediction in Brazil Using NDVI Time Series and Neural Networks Ensemble. Int. J. Remote Sens. 2017, 38, 4631–4644. [Google Scholar] [CrossRef]
- Dubey, S.K.; Gavli, A.S.; Yadav, S.K.; Sehgal, S.; Ray, S.S. Remote Sensing-Based Yield Forecasting for Sugarcane (Saccharum officinarum L.) Crop in India. J. Indian Soc. Remote Sens. 2018, 46, 1823–1833. [Google Scholar] [CrossRef]
- Shao, Y.; Lunetta, R.S.; Wheeler, B.; Iiames, J.S.; Campbell, J.B. An Evaluation of Time-Series Smoothing Algorithms for Land-Cover Classifications Using MODIS-NDVI Multi-Temporal Data. Remote Sens. Environ. 2016, 174, 258–265. [Google Scholar] [CrossRef]
- Kandasamy, S.; Baret, F.; Verger, A.; Neveux, P.; Weiss, M. A Comparison of Methods for Smoothing and Gap Filling Time Series of Remote Sensing Observations—Application to MODIS LAI Products. Biogeosciences 2013, 10, 4055–4071. [Google Scholar] [CrossRef]
- Klisch, A.; Atzberger, C. Operational Drought Monitoring in Kenya Using MODIS NDVI Time Series. Remote Sens. 2016, 8, 267. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The Relationship of Drought Frequency and Duration to Time Scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; p. 6. [Google Scholar]
- Debortoli, N.; Dubreuil, V.; Heinke, C.; Filho, S.R. Tendances et ruptures des séries pluviométriques dans la région méridionale de l’Amazonie brésilienne. In 25e Colloque de l’AIC; Université Joseph Fourier: Grenoble, French, 2012; pp. 201–206. [Google Scholar]
- Soro, G.; Noufé, D.; Goula Bi, T.; Shorohou, B. Trend Analysis for Extreme Rainfall at Sub-Daily and Daily Timescales in Côte d’Ivoire. Climate 2016, 4, 37. [Google Scholar] [CrossRef]
- Binbol, N.; Adebayo, A.; Kwon-Ndung, E. Influence of Climatic Factors on the Growth and Yield of Sugar Cane at Numan, Nigeria. Clim. Res. 2006, 32, 247–252. [Google Scholar] [CrossRef]
- Skocaj, D.M.; Everingham, Y.L. Identifying Climate Variables Having the Greatest Influence on Sugarcane Yields in the Tully Mill Area. In Proceedings of the Australian Society of Sugar Cane Technologists; Bruce, R.C., Ed.; Australian Society of Sugar Cane Technologists: Mackay, Australia, 2014; Volume 36, pp. 53–61. [Google Scholar]
- Bégué, A.; Lebourgeois, V.; Bappel, E.; Todoroff, P.; Pellegrino, A.; Baillarin, F.; Siegmund, B. Spatio-Temporal Variability of Sugarcane Fields and Recommendations for Yield Forecast Using NDVI. Int. J. Remote Sens. 2010, 31, 5391–5407. [Google Scholar] [CrossRef]
- Kutner, M.H. Applied Linear Statistical Models, 5th ed.; The McGraw-Hill/Irwin Series Operations and Decision Sciences; McGraw-Hill Irwin: Boston, MA, USA, 2005; ISBN 978-0-07-238688-2. [Google Scholar]
- Saithanu, K.; Mekparyup, J. Forecasting Sugar Cane Yield in the Northeast of Thailand with MLP Models. Glob. J. Pure Appl. Math. 2015, 11, 2161–2164. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and Regression by RandomForest. R News 2002, 2, 18–22. [Google Scholar]
- Ferraciolli, M.A.; Bocca, F.F.; Rodrigues, L.H.A. Neglecting Spatial Autocorrelation Causes Underestimation of the Error of Sugarcane Yield Models. Comput. Electron. Agric. 2019, 161, 233–240. [Google Scholar] [CrossRef]
- Beguería, S. Validation and Evaluation of Predictive Models in Hazard Assessment and Risk Management. Nat. Hazards 2006, 37, 315–329. [Google Scholar] [CrossRef]
- Sacré Regis, M.D.; Mouhamed, L.; Kouakou, K.; Adeline, B.; Arona, D.; Koffi Claude, A.K.; Talnan Jean, H.C.; Salomon, O.; Issiaka, S. Using the CHIRPS Dataset to Investigate Historical Changes in Precipitation Extremes in West Africa. Climate 2020, 8, 84. [Google Scholar] [CrossRef]
- Barry, A.A.; Caesar, J.; Klein Tank, A.M.G.; Aguilar, E.; McSweeney, C.; Cyrille, A.M.; Nikiema, M.P.; Narcisse, K.B.; Sima, F.; Stafford, G.; et al. West Africa Climate Extremes and Climate Change Indices: West Africa Climate Extremes. Int. J. Climatol. 2018, 38, e921–e938. [Google Scholar] [CrossRef]
- Kruger, A.C.; Sekele, S.S. Trends in Extreme Temperature Indices in South Africa: 1962–2009. Int. J. Climatol. 2013, 33, 661–676. [Google Scholar] [CrossRef]
- Vincent, L.A.; Aguilar, E.; Saindou, M.; Hassane, A.F.; Jumaux, G.; Roy, D.; Booneeady, P.; Virasami, R.; Randriamarolaza, L.Y.A.; Faniriantsoa, F.R.; et al. Observed Trends in Indices of Daily and Extreme Temperature and Precipitation for the Countries of the Western Indian Ocean, 1961–2008. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Bocca, F.F.; Rodrigues, L.H.A. The Effect of Tuning, Feature Engineering, and Feature Selection in Data Mining Applied to Rainfed Sugarcane Yield Modelling. Comput. Electron. Agric. 2016, 128, 67–76. [Google Scholar] [CrossRef]
- Saithanu, K.; Sittisorn, P.; Mekparyup, J. Estimation of Sugar Cane Yield in the Northeast of Thailand with MLR Model. Burapha Sci. J. วารสารวิทยาศาสตร์บูรพา 2017, 22, 197–201. [Google Scholar]
- Konan, E.A.; Péné, C.B.; Dick, E. Main Factors Determining the Yield of Sugarcane Plantations on Ferralsols in Ferké 2 Sugar Complex, Northern Ivory Coast. J. Emerg. Trends Eng. Appl. Sci. 2017, 8, 244–256. [Google Scholar]
- Pagani, V.; Stella, T.; Guarneri, T.; Finotto, G.; van den Berg, M.; Marin, F.R.; Acutis, M.; Confalonieri, R. Forecasting Sugarcane Yields Using Agro-Climatic Indicators and Canegro Model: A Case Study in the Main Production Region in Brazil. Agric. Syst. 2017, 154, 45–52. [Google Scholar] [CrossRef]
- Blackburn, F. Sugar-Cane; London and New York (Tropical Agriculture Series); Longman: Harlow, UK, 1984. [Google Scholar]
- James, G. Sugarcane, 2nd ed.; World Agriculture Series; Blackwell Science: Oxford, UK, 2004; ISBN 978-0-632-05476-3. [Google Scholar]
- Ferraro, D.O.; Rivero, D.E.; Ghersa, C.M. An Analysis of the Factors That Influence Sugarcane Yield in Northern Argentina Using Classification and Regression Trees. Field Crops Res. 2009, 112, 149–157. [Google Scholar] [CrossRef]
- Greenland, D. Climate Variability and Sugarcane Yield in Louisiana. J. Appl. Meteorol. 2005, 44, 1655–1666. [Google Scholar] [CrossRef]
- Samui, R.P.; John, G.; Kulkarni, M.B. Impact of Weather on Yield of Sugarcane at Different Growth Stages. J. Agric. Phys. 2003, 3, 119–125. [Google Scholar]
- Shrivastava, P. Impact of Weather Changes on Sugarcane Production. Res. Environ. Life Sci. 2014, 7, 243–246. [Google Scholar]
- Son, N.T.; Chen, C.F.; Chen, C.R.; Minh, V.Q.; Trung, N.H. A Comparative Analysis of Multitemporal MODIS EVI and NDVI Data for Large-Scale Rice Yield Estimation. Agric. For. Meteorol. 2014, 197, 52–64. [Google Scholar] [CrossRef]








| Type of Variables | Variables | Description | Unit |
|---|---|---|---|
| Cropping practices | Irrig_status * | Irrigation status | |
| Ratoon * | Number of plant regrowth | ||
| CoupeN * | Date of harvest | Date | |
| Age * | Life cycle length | Month | |
| Var * Surface | Sugarcane variety Surface of the plot | ||
| Quality of production | Suc | Sugar content | Percent |
| ENA | Percentage of internodes attacked by caterpillars | Percent | |
| Climate variables | Tmin | Minimal temperature | °C |
| Tmax | Maximal temperature | °C | |
| Trange | Temperature range | °C | |
| Prec | Accumulated precipitation | Mm | |
| ETP | Potential evapotranspiration | Mm | |
| RHmean | Mean relative humidity | Percent | |
| Rg | Global insolation radiation | W.m−2 | |
| DegDays | Cumulated degree days | degree.day | |
| Satellite variables | Int_NDVI | Integrated NDVI | 10−3 |
| Max_NDVI | Maximal annual NDVI | 10−3 | |
| Int_EVI | Integrated EVI | 10−3 | |
| Max_EVI | Maximal annual EVI | 10−3 |
| Indices | Index Definition | Unit |
|---|---|---|
| Rainfall data | ||
| PRECTOT | Average rainfall on rainy days (> 1mm) | mm.day−1 |
| SPI12 | 12-month SPI index taken in December | |
| Temperature data | ||
| Tmoy | Mean annual temperature | °C |
| Tmin | Minimal annual temperature | °C |
| Tmax | Maximal annual temperature | °C |
| Sugarcane yields | ||
| Yields | Sugarcane yields | Tons/ha |
| Article | Studied Area | Model Used | Main Variables | Performances |
|---|---|---|---|---|
| Binbol et al. [47] | Nigeria | Evaporation Minimum temperature | R2 = 0.68 | |
| Skocaj and Everingham [48] | Australia | Linear regression Stepwise model | Rainfall at the end of growing season | 0.37 < R2 < 0.94 |
| Everingham et al. [23] | Australia | Random Forest | Forecast of El Niño phenomena | 0.67 < R2 < 0.79 |
| Hammer et al. [24] | Brazil | Three machine learning models | Number of ratoons | 0.64 < R2 < 0.66 |
| Bégué et al. [49] | Reunion island | Satellite imagery | NDVI | R2 = 0.75 |
| Robson [27] | Australia | Satellite imagery | GNDVI | 0.4 < R2 < 0.7 |
| Indices | Change-Points | Trends |
|---|---|---|
| Rainfall data | ||
| PRECTOT | No change-point | No trend |
| SPI12 | No change-point | No trend |
| Temperature data | ||
| Tmoy | No change-point | Significant increasing trend at the 1% threshold in Ferké 1 and 2 |
| Tmin | No change-point | Significant increasing trend at the 5% threshold in Ferké 1 and 2 |
| Tmax | No change-point | Significant increasing trend at the 5% threshold in Ferké 1 and 2 |
| Sugarcane yields | ||
| Yields | No change-point | No trend |
| Sugarcane Yields | ||
|---|---|---|
| Coefficient | p-Value | |
| Prec in maturation phase | 0.0481 *** | (0.0000) |
| Prec in pre-growth phase | −0.0139 *** | (0.0001) |
| Max temp in high growth phase | −3.2336 *** | (0.0000) |
| Max temp in maturation phase | −1.3556 *** | (0.0000) |
| Max temp in pre-growth phase | 1.5727 *** | (0.0000) |
| N | 5097 | |
| R2 (cropping practices) | 0.5114 | |
| R2 (all variables) | 0.5413 | |
| Sugarcane Yields (T/Ha) | ||
|---|---|---|
| Coefficient | p-Value | |
| (Intercept) | −37.68 | (0.23) |
| Minimal temperature | 5.33 ** | (0.00) |
| N | 24 | |
| R2 | 0.38 | |
| p-Value | R2 | RMSE | |
|---|---|---|---|
| Int_NDVI | <2.10−16 | 0.35 | 17.19 |
| Max_NDVI | <2.10−16 | 0.16 | 19.57 |
| Int_EVI | <2.10−16 | 0.43 | 14.31 |
| Max_EVI | <2.10−16 | 0.31 | 15.67 |
| Cropping Practices and Climate Variables at the Plot Level (Accuracy = 58%) | ||||
|---|---|---|---|---|
| Yields | Forecast | |||
| High | Medium | Low | ||
| Observed | High | 756 | 926 | 16 |
| Medium | 358 | 1225 | 115 | |
| Low | 68 | 620 | 1011 | |
| Climate variables averaged at the zone level (accuracy = 54%) | ||||
| Yields | Forecast | |||
| High | Medium | Low | ||
| Observed | High | 7 | 1 | 0 |
| Medium | 4 | 2 | 2 | |
| Low | 0 | 4 | 4 | |
| Cropping practices and integral of the EVI from January to August (accuracy = 65%) | ||||
| Yields | Forecast | |||
| High | Medium | Low | ||
| Observed | High | 190 | 184 | 4 |
| Medium | 66 | 293 | 18 | |
| Low | 7 | 112 | 259 | |
| Models | Indices | Sugarcane Yields | ||
|---|---|---|---|---|
| High | Medium | Low | ||
| Climate variables at the scale of Ferké 1/Ferké 2 (Section 3.2.2) | Sensitivity | 88% | 25% | 50% |
| Specificity | 75% | 69% | 88% | |
| Cropping practices and climate variables at the plot scale (Section 3.2.1) | Sensitivity | 45% | 72% | 60% |
| Specificity | 87% | 54% | 96% | |
| Cropping practices and integral of the EVI from January to August (Section 3.2.3) | Sensitivity | 50% | 78% | 69% |
| Specificity | 90% | 61% | 98% | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pignède, E.; Roudier, P.; Diedhiou, A.; N’Guessan Bi, V.H.; Kobea, A.T.; Konaté, D.; Péné, C.B. Sugarcane Yield Forecast in Ivory Coast (West Africa) Based on Weather and Vegetation Index Data. Atmosphere 2021, 12, 1459. https://doi.org/10.3390/atmos12111459
Pignède E, Roudier P, Diedhiou A, N’Guessan Bi VH, Kobea AT, Konaté D, Péné CB. Sugarcane Yield Forecast in Ivory Coast (West Africa) Based on Weather and Vegetation Index Data. Atmosphere. 2021; 12(11):1459. https://doi.org/10.3390/atmos12111459
Chicago/Turabian StylePignède, Edouard, Philippe Roudier, Arona Diedhiou, Vami Hermann N’Guessan Bi, Arsène T. Kobea, Daouda Konaté, and Crépin Bi Péné. 2021. "Sugarcane Yield Forecast in Ivory Coast (West Africa) Based on Weather and Vegetation Index Data" Atmosphere 12, no. 11: 1459. https://doi.org/10.3390/atmos12111459
APA StylePignède, E., Roudier, P., Diedhiou, A., N’Guessan Bi, V. H., Kobea, A. T., Konaté, D., & Péné, C. B. (2021). Sugarcane Yield Forecast in Ivory Coast (West Africa) Based on Weather and Vegetation Index Data. Atmosphere, 12(11), 1459. https://doi.org/10.3390/atmos12111459








