Evaluation of the CRU TS3.1, APHRODITE_V1101, and CFSR Datasets in Assessing Water Balance Components in the Upper Vakhsh River Basin in Central Asia
Abstract
:1. Introduction
2. Materials and Methods
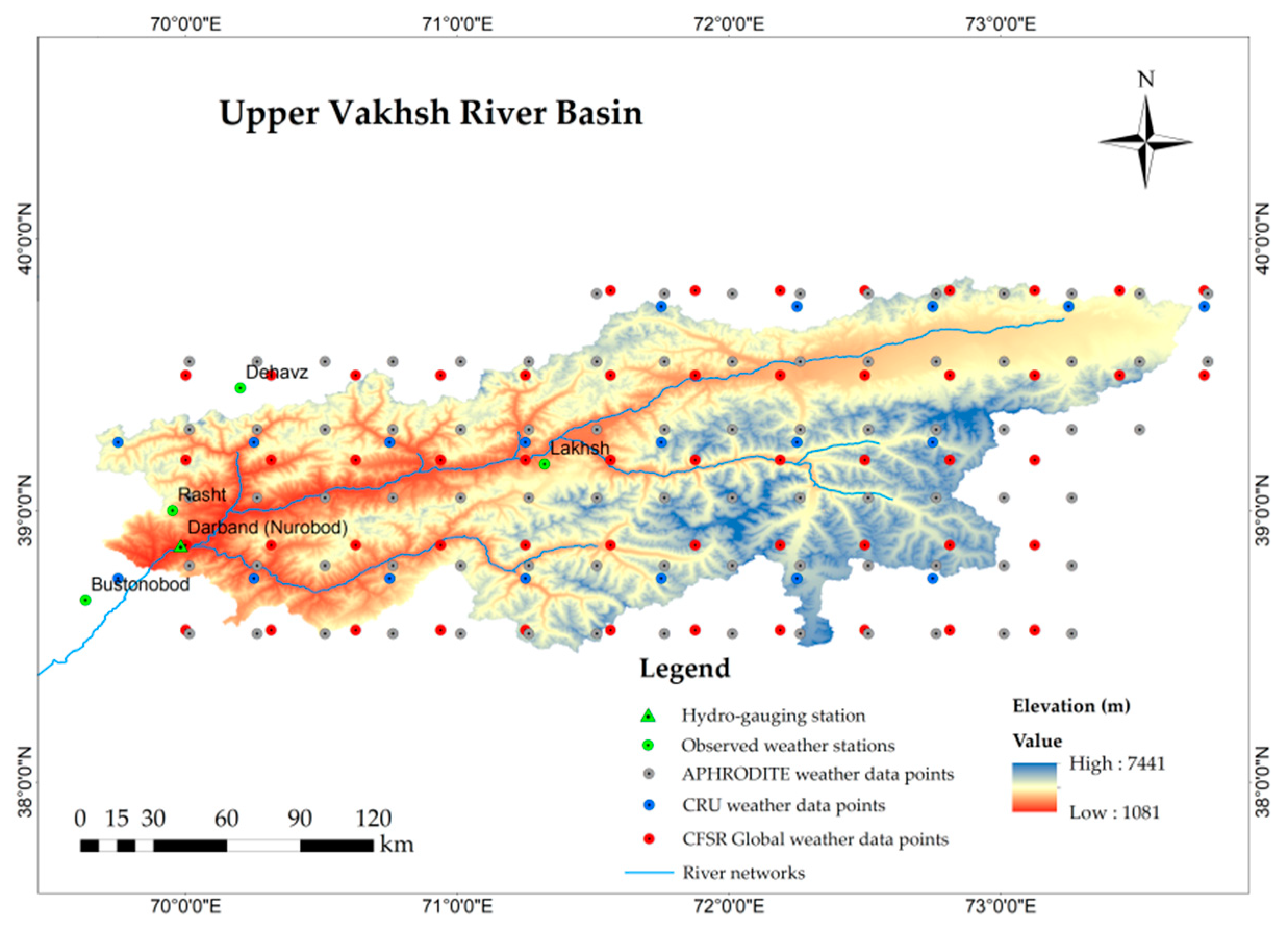
2.1. Study Area
2.2. Data
| Land Cover Types | Area (% of Basin) | Area (km2 of Basin) | FAO Soil Name | Area (% of Basin) | Area (km2 of Basin) |
|---|---|---|---|---|---|
| Pasture | 6.57 | 1935.31 | Acrisols | 22.06 | 6495.10 |
| Agriculture | 6.58 | 1938.49 | Gleysols | 25.47 | 7499.95 |
| Forest | 1.16 | 340.38 | Leptosols | 9.17 | 2701.29 |
| Grassland | 48.63 | 14,318.06 | Phaeozems | 7.13 | 2099.55 |
| Shrubland | 4.30 | 1267.29 | Rock outcrops | 20.46 | 6024.15 |
| Urban | 0.03 | 8.07 | Eutric cambisols | 0.68 | 199.90 |
| Bare land | 16.84 | 4957.09 | Gelic gleysols | 0.02 | 7.33 |
| Water body | 0.14 | 42.08 | Glaciers | 15.00 | 4417.40 |
| Ice and snow | 15.75 | 4637.89 | |||
| Total | 100 | 29,444.66 | 100 | 29,444.66 |
3. Methodology
Model Assessment
4. Results
4.1. Parameter Sensitivity Analysis
4.2. Calibration and Validation
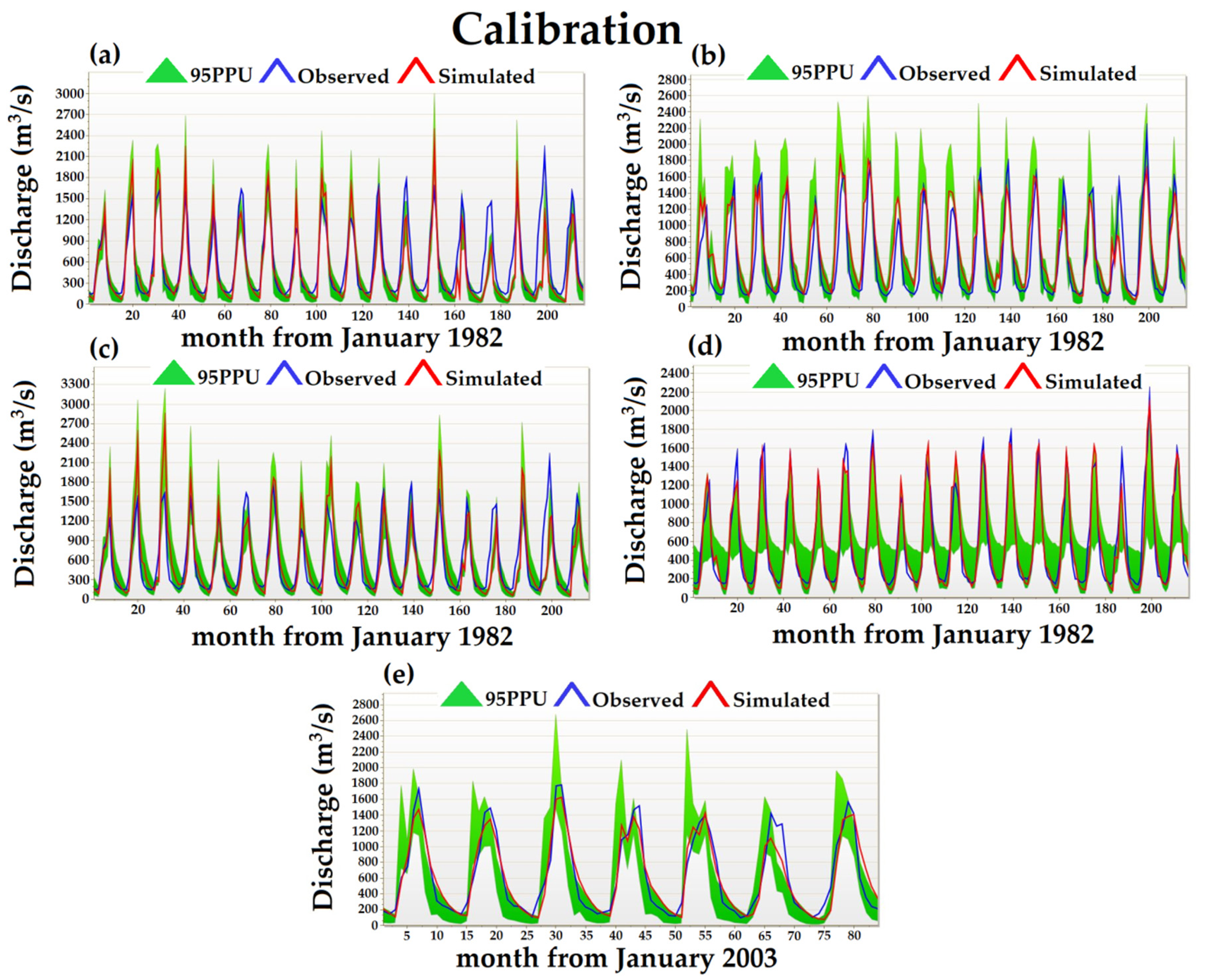

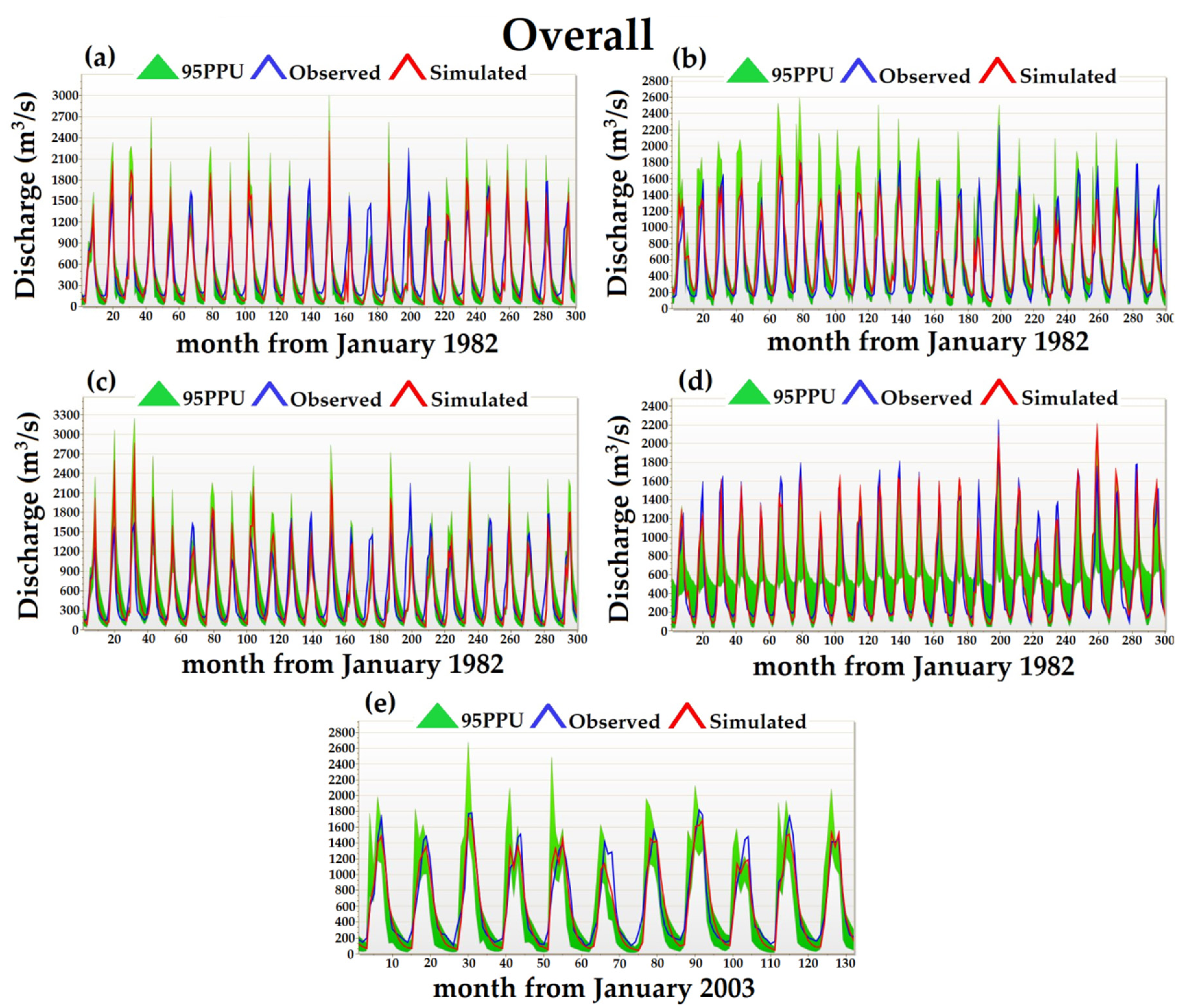
4.3. Performance of the Hydrological Model
| Data Source\Statistical Indices | R2 | NSE | PBIAS (%) | RSR | MSE (%) | KGE | P-Factor | R-Factor |
|---|---|---|---|---|---|---|---|---|
| Calibration | ||||||||
| Combination of the APHRODITE_V1101 and CFSR data (1982–1999) | 0.76 | 0.70 | 14.80 | 0.55 | 7.78 | 0.80 | 0.66 | 0.66 |
| Combination of the APHRODITE_V1101 and CRU TS3.1 data (1982–1999) | 0.79 | 0.74 | −17.70 | 0.77 | 6.72 | 0.77 | 0.66 | 0.79 |
| CFSR data (1982–1999) | 0.71 | 0.64 | −0.31 | 0.60 | 9.12 | 0.81 | 0.75 | 0.95 |
| CRU TS3.1 data (1982–1999) | 0.92 | 0.91 | 1.32 | 0.29 | 2.23 | 0.95 | 0.82 | 1.01 |
| Observational data (2003–2009) | 0.90 | 0.90 | 0.69 | 0.31 | 2.54 | 0.90 | 0.69 | 0.80 |
| Data source | Validation | |||||||
| Combination of the APHRODITE_V1101 and CFSR data (2000–2006) | 0.83 | 0.77 | 17.22 | 0.48 | 6.01 | 0.81 | 0.67 | 0.66 |
| Combination of the APHRODITE_V1101 and CRU TS3.1 data (2000–2006) | 0.79 | 0.78 | 1.30 | 0.46 | 5.54 | 0.80 | 0.70 | 0.66 |
| CFSR data (2000–2006) | 0.85 | 0.83 | 9.58 | 0.42 | 4.48 | 0.87 | 0.79 | 0.89 |
| CRU TS3.1 data (2000–2006) | 0.89 | 0.88 | −6.09 | 0.35 | 3.18 | 0.91 | 0.80 | 1.08 |
| Observational data (2010–2013) | 0.94 | 0.93 | 5.51 | 0.26 | 2.04 | 0.93 | 0.81 | 0.76 |
| Data source | Overall | |||||||
| Combination of the APHRODITE_V1101 and CFSR data (1982–2006) | 0.78 | 0.72 | 15.00 | 0.53 | 7.20 | 0.81 | 0.66 | 0.67 |
| Combination of the APHRODITE_V1101 and CRU TS3.1 data (1982–2006) | 0.76 | 0.74 | −10.80 | 0.51 | 6.70 | 0.78 | 0.68 | 0.75 |
| CFSR data (1982–2006) | 0.74 | 0.68 | 2.00 | 0.56 | 8.10 | 0.83 | 0.75 | 0.95 |
| CRU TS3.1 data (1982–2006) | 0.90 | 0.90 | 0.29 | 0.31 | 2.51 | 0.95 | 0.81 | 1.02 |
| Observational data (2003–2013) | 0.92 | 0.91 | 5.21 | 0.29 | 2.34 | 0.93 | 0.73 | 0.78 |
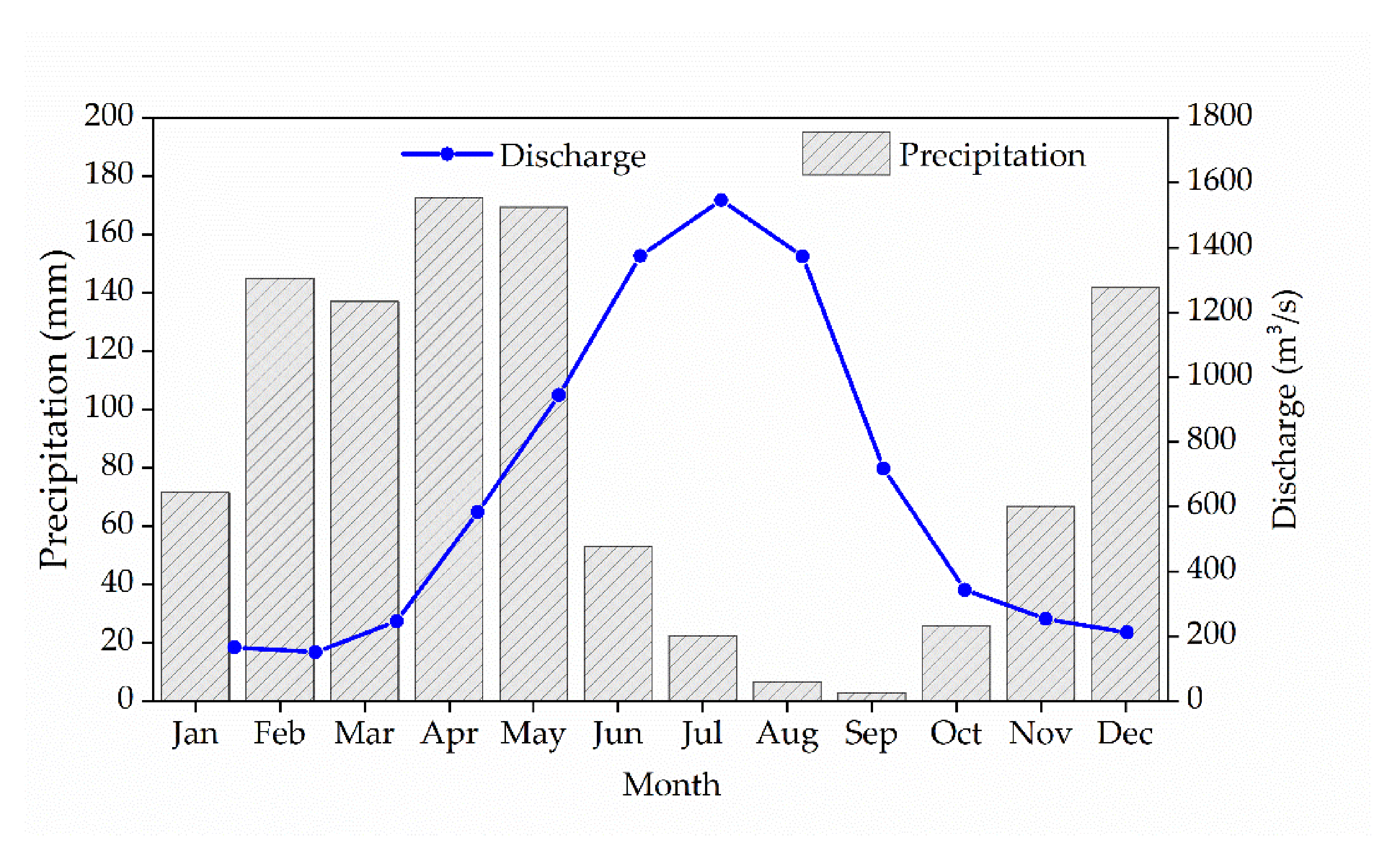
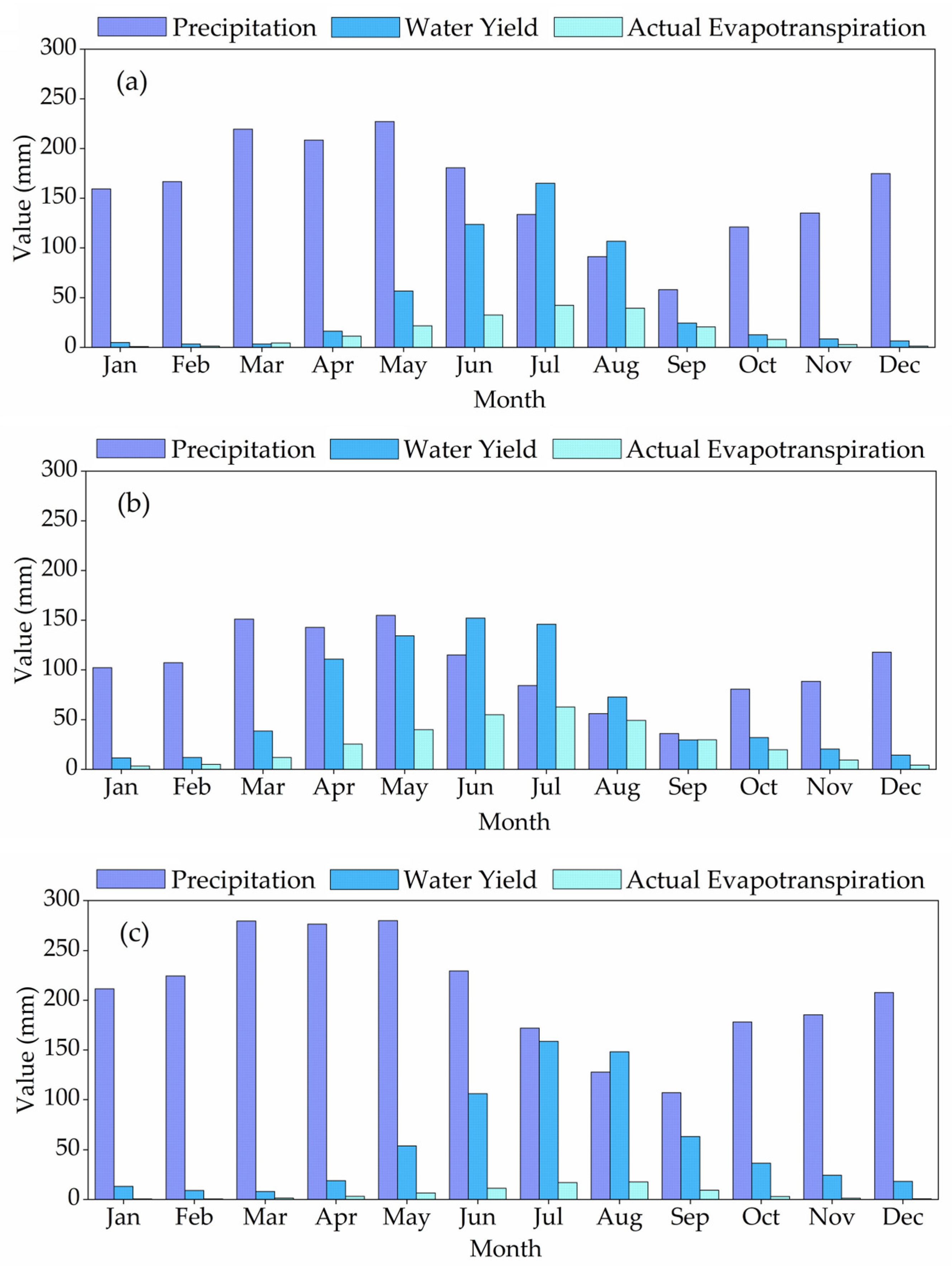
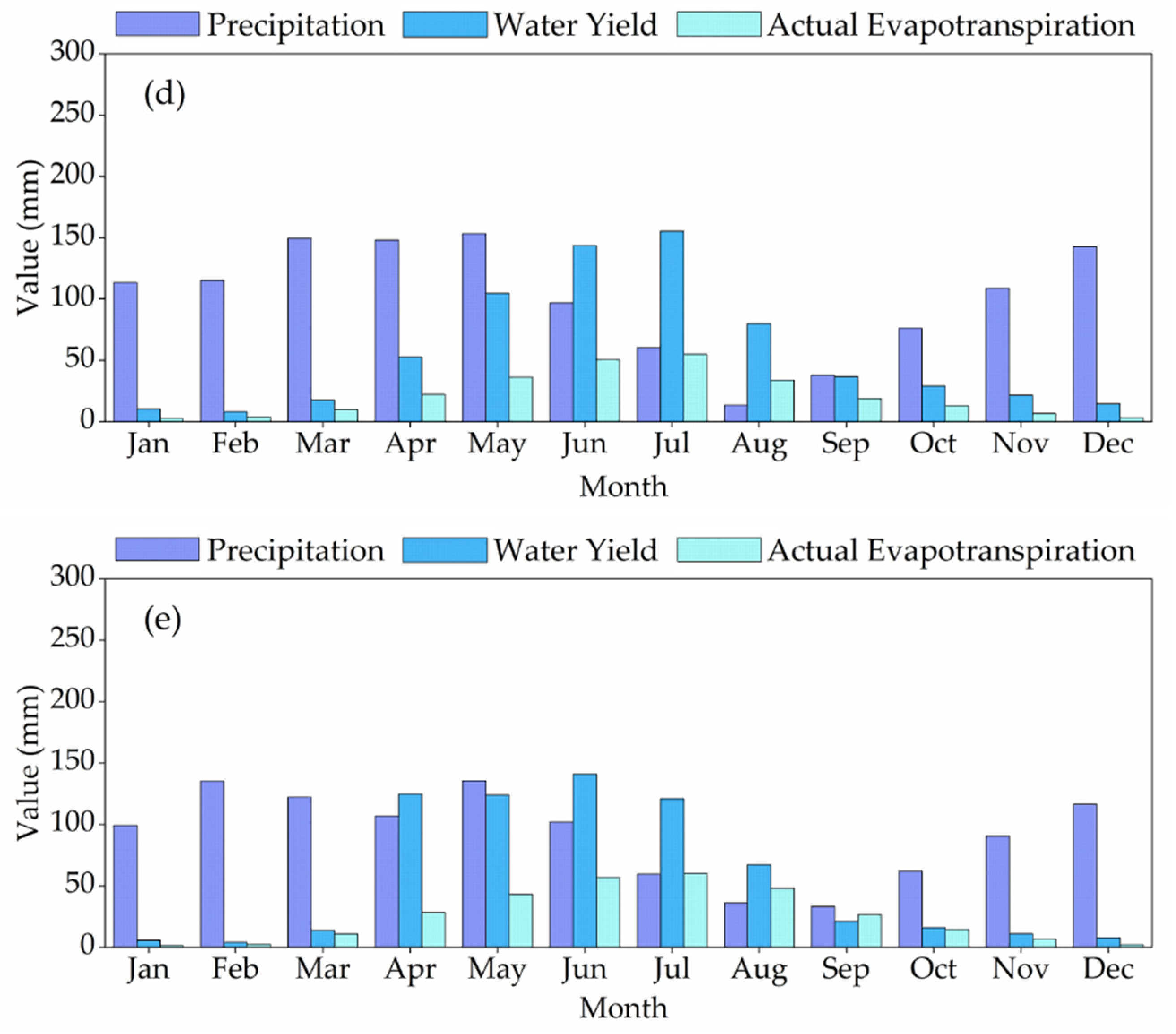
4.4. Water Balance of the Upper Vakhsh River Basin in Central Asia
4.5. Snowmelt Contribution to the Streamflow of the Upper Vakhsh River Basin, Using the SWAT Model
5. Discussion
Uncertainties and Limitations
6. Conclusions
- (a)
- The results of the study indicated that the applied gridded datasets, such as CRU TS3.1, AHPRODITE_V1101, and CFSR, can be used as alternative climate data in an assessment of the hydrology in the UVRB.
- (b)
- We observed that the CFSR datasets performed worse than APHRODITE_V1101+CFSR, APHRODITE_V1101+CRU TS3.1, and observational datasets.
- (c)
- Aquifer percolation fraction (RCHRG_DP), baseflow alpha-factor (ALPHA_BF), moist bulk density (SOL_BD), SCS runoff curve number for moisture condition-II (CN2), and effective hydraulic conductivity in main channel alluvium (CH_K2) were determined to be the most sensitive factors for streamflow simulation using the SWAT model in the UVRB.
- (d)
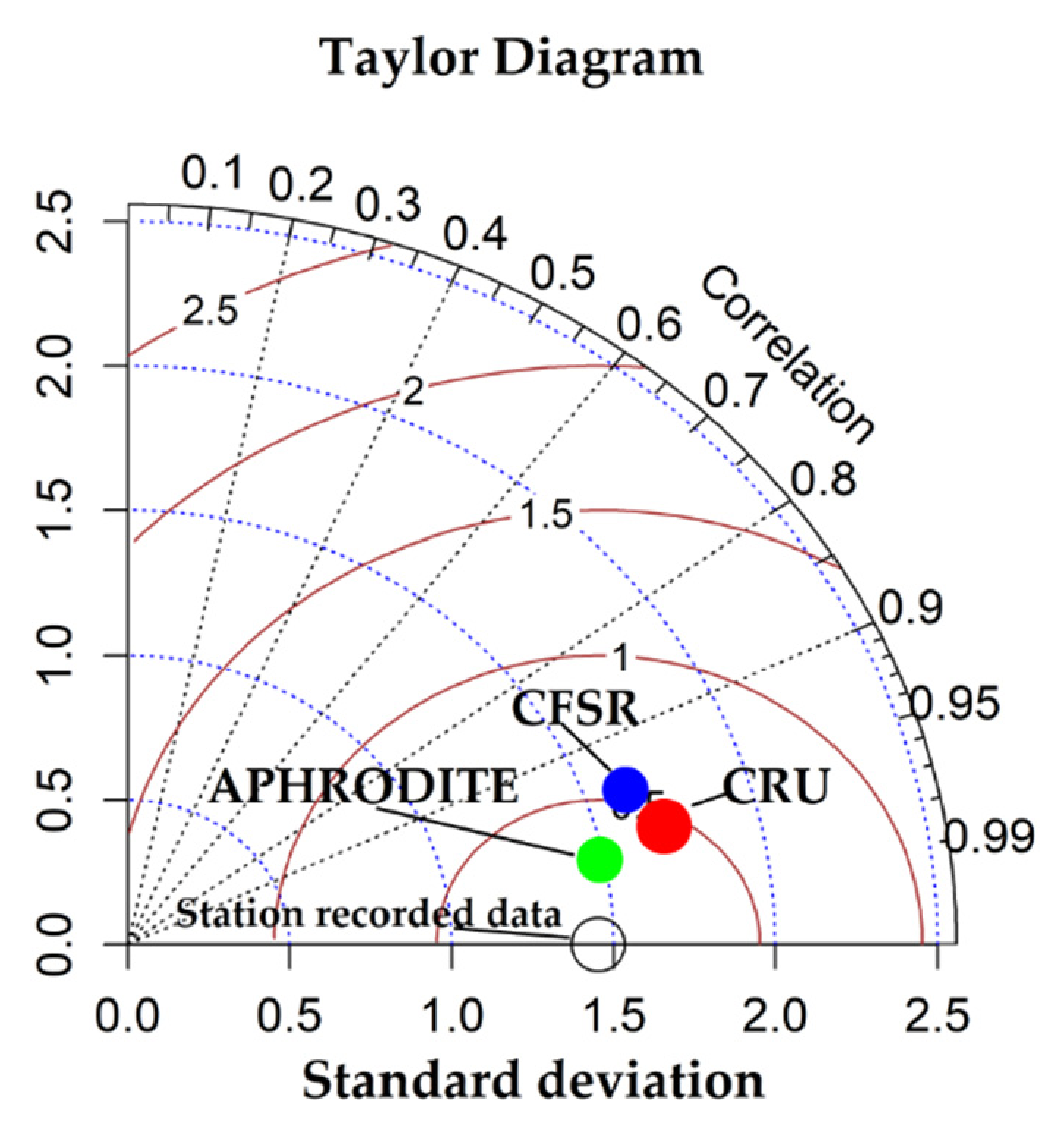
- APHRODITE_V1101+CFSR showed “good” [71] results in simulating the monthly observed streamflow (with NSE = 0.70 and 0.72 for calibration and for overall period, respectively, and PBIAS = 14.8% and 15% for calibration and for overall period, respectively). The APHRODITE_V1101+CRU TS3.1 gave “good” results for calibration and overall periods (NSE = 0.74 and 0.74, respectively), with “satisfactory” [71] (PBIAS = −17.7%) and “good” (PBIAS = −10.80%) underestimation of streamflow. This combination showed “very good” [71] results (NSE = 0.78) for the validation period with a “very good” overestimation of streamflow (PBIAS of 1.30%). The CFSR datasets presented “good” results (NSE = 0.68) with a “very good” (PBIAS of 2%) overestimation of streamflow and, for the validation period, CFSR provided “very good” results (NSE = 0.83) with a “very good” overestimation of streamflow (PBIAS of 9.58%). The CRU TS3.1 datasets gave “very good” results for calibration, validation and overall scales (NSE = 0.91, 0.88 and 0.91, and PBIAS = 0.32%, 6.09%, and 0.29%, respectively). The observational datasets for calibration, validation and overall provided “very good” results (NSE = 0.90, 0.93 and 0.91 and PBIAS = 0.69%, 5.51%, and 5.21%, respectively). The better performance corresponds to observational datasets with higher NSE values, followed by the CRU TS3.1 datasets.
- (e)
- The coefficient of determination (R2) showed an acceptable (>0.6) [103] correlation between the observed and simulated monthly streamflow during calibration, validation, and overall scales (R2 ranges from 0.74 to 0.94) for all five datasets.
- (f)
- For APHRODITE_V1101+CFSR, APHRODITE_V1101+CRU TS3.1, CFSR, CRU TS3.1, and observational datasets, the SWAT model simulated mean annual precipitation of the UVRB as 1875.9 mm, 1236.9 mm, 2479 mm, 1215.9 mm, and 1098.5 mm, respectively, with 93.82% (1760.11 mm), 70.41% (870.85 mm), 96% (2379.86 mm), 86.52% (1051.98 mm), and 76.16% (836.65 mm) as snowfall, out of which 29.70% (522.72 mm), 72.19% (628.63 mm), 25.88% (615.80 mm), 68.51% (720.67 mm), and 68.87% (576.19 mm), respectively, melts and facilitates snowmelt runoff in the basin.
- (g)
- The UVR basin evapotranspiration is 9.93% (APHRODITE_V1101+CFSR), 25.52% (APHRODITE_V1101+CRU TS3.1), 2.9% (CFSR), 21.08% (CRU TS3.1), and 27.28% (observational datasets) (186.3 mm, 315.7 mm, 72.1 mm, 256.4 mm, and 299.7 mm out of 1875.9 mm, 1236.9 mm, 2479 mm, 1215.9 mm, and 1098.5 mm, respectively). Overall, less evapotranspiration occurs in December, January, and February.
- (h)
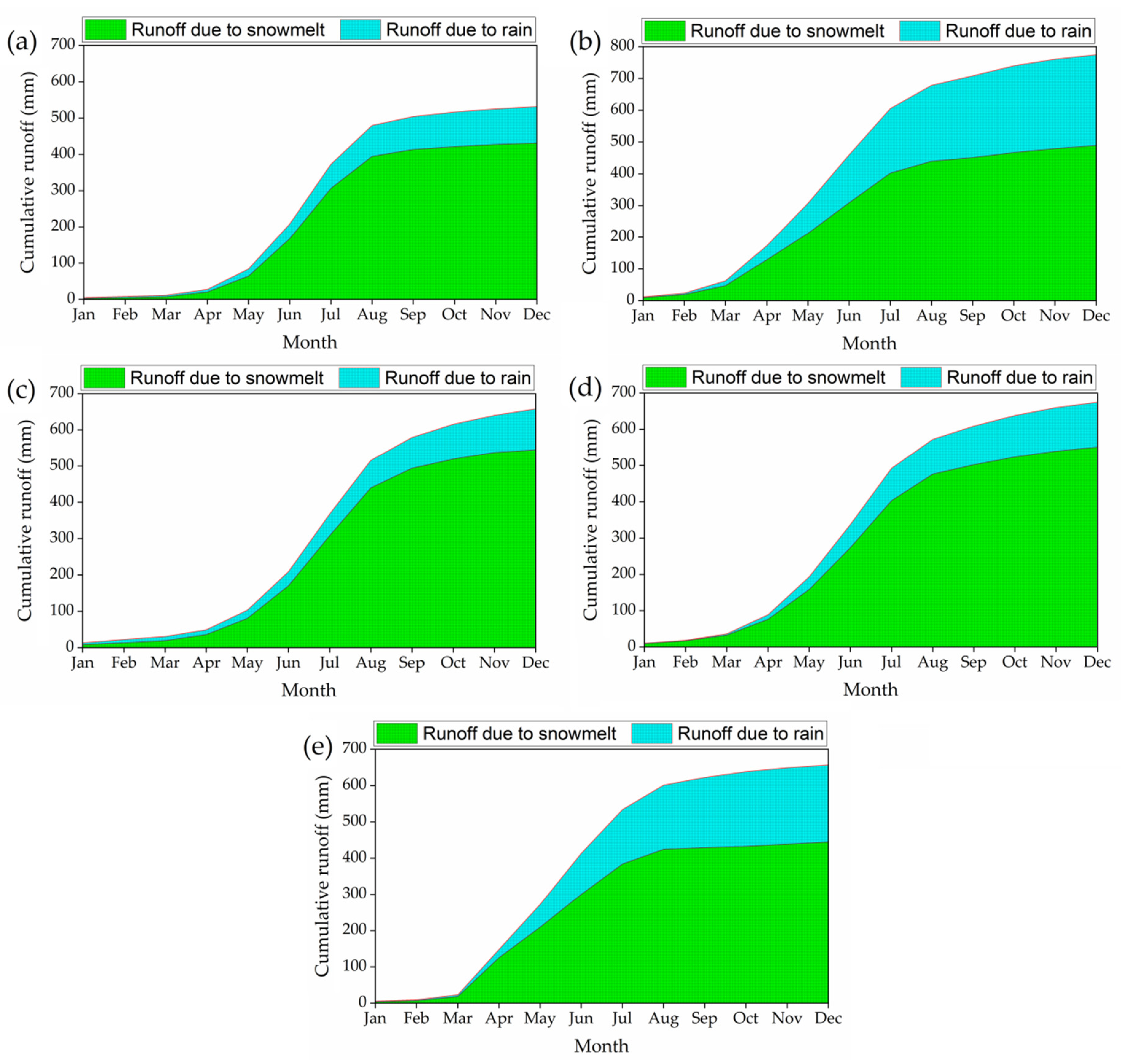
- From 1982 to 2006, the simulation of five different weather products (APHRODITE_V1101+CFSR, APHRODITE_V1101+CRU TS3.1, CFSR, CRU TS3.1) and observational datasets in the UVR basin showed that snowmelt runoff contributes approximately 81.06%, 63.12%, 82.79%, 81.66%, and 67.67%, respectively, of annual runoff. Snowmelt runoff contributes the most to overall runoff in spring and summer.
- (i)
- The annual flow contribution of rain was estimated at 18.94%, 36.88%, 17.21%, 18.34%, and 32.33% using APHRODITE_V1101+CFSR, APHRODITE_V1101+CRU TS3.1, CFSR, CRU TS3.1, and observational datasets.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chiphang, N.; Bandyopadhyay, A.; Bhadra, A. Assessing the Effects of Snowmelt Dynamics on Streamflow and Water Balance Components in an Eastern Himalayan River Basin Using SWAT Model. Environ. Model. Assess. 2020, 25, 861–883. [Google Scholar] [CrossRef]
- Dhami, B.; Himanshu, S.K.; Pandey, A.; Gautam, A.K. Evaluation of the SWAT model for water balance study of a mountainous snowfed river basin of Nepal. Environ. Earth Sci. 2018, 77, 21. [Google Scholar] [CrossRef]
- Schuol, J.; Abbaspour, K. Using monthly weather statistics to generate daily data in a SWAT model application to West Africa. Ecol. Model. 2007, 201, 301–311. [Google Scholar] [CrossRef]
- Liu, Z.J.; Weller, D.E.; Jordan, T.E.; Correll, D.L.; Boomer, K.B. Integrated Modular Modeling of Water and Nutrients From Point and Nonpoint Sources in the Patuxent River Watershed 1. JAWRA J. Am. Water Resour. Assoc. 2008, 44, 700–723. [Google Scholar] [CrossRef]
- Abbott, M.; Bathurst, J.; Cunge, J.; O’connell, P.; Rasmussen, J. An introduction to the European Hydrological System—Systeme Hydrologique Europeen,“SHE”, 2: Structure of a physically-based, distributed modelling system. J. Hydrol. 1986, 87, 61–77. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment part I: Model development 1. JAWRA J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Holtan, H.N.; Lopez, N.C. USDAHL-70 Model of Watershed Hydrology; US Department of Agriculture, U.S. Government Printing Office: Washington, DC, USA, 1971. [Google Scholar]
- Fontaine, T.; Cruickshank, T.; Arnold, J.; Hotchkiss, R. Development of a snowfall–snowmelt routine for mountainous terrain for the soil water assessment tool (SWAT). J. Hydrol. 2002, 262, 209–223. [Google Scholar] [CrossRef]
- Abbaspour, K. User Manual for SWAT-CUP, SWAT Calibration and Uncertainty Analysis Programs; Swiss Federal Institute of Aquatic Science and Technology: Eawag, Switzerland, 2007. [Google Scholar]
- Debele, B.; Srinivasan, R.; Gosain, A. Comparison of process-based and temperature-index snowmelt modeling in SWAT. Water Resour. Manag. 2010, 24, 1065–1088. [Google Scholar] [CrossRef]
- Pradhanang, S.M.; Anandhi, A.; Mukundan, R.; Zion, M.S.; Pierson, D.C.; Schneiderman, E.M.; Matonse, A.; Frei, A. Application of SWAT model to assess snowpack development and streamflow in the Cannonsville watershed, New York, USA. Hydrol. Process. 2011, 25, 3268–3277. [Google Scholar] [CrossRef]
- Troin, M.; Caya, D. Evaluating the SWAT’s snow hydrology over a Northern Quebec watershed. Hydrol. Process. 2014, 28, 1858–1873. [Google Scholar] [CrossRef]
- Zhang, L.; Jin, X.; He, C.; Zhang, B.; Zhang, X.; Li, J.; Zhao, C.; Tian, J.; DeMarchi, C. Comparison of SWAT and DLBRM for hydrological modeling of a mountainous watershed in arid northwest China. J. Hydrol. Eng. 2016, 21, 04016007. [Google Scholar] [CrossRef]
- Omani, N.; Srinivasan, R.; Karthikeyan, R.; Reddy, V.; Smith, P.K. Impacts of climate change on the glacier melt runoff from five river basins. Trans. ASABE 2016, 59, 829–848. [Google Scholar]
- Dile, Y.T.; Srinivasan, R. Evaluation of CFSR climate data for hydrologic prediction in data-scarce watersheds: An application in the Blue Nile River Basin. JAWRA J. Am. Water Resour. Assoc. 2014, 50, 1226–1241. [Google Scholar] [CrossRef]
- Tolera, M.B.; Chung, I.-M.; Chang, S.W. Evaluation of the climate forecast system reanalysis weather data for watershed modeling in Upper Awash basin, Ethiopia. Water 2018, 10, 725. [Google Scholar] [CrossRef] [Green Version]
- Adeogun, A.G.; Sule, B.F.; Salami, A.W.; Daramola, M.O. Validation of SWAT model for prediction of water yield and water balance: Case study of upstream catchment of Jebba dam in Nigeria. Int. J. Math. Comput. Phys. Comput. Eng. 2014, 8, 264–270. [Google Scholar]
- Gupta, A.; Himanshu, S.K.; Gupta, S.; Singh, R. Evaluation of the SWAT Model for Analysing the Water Balance Components for the Upper Sabarmati Basin. In Advances in Water Resources Engineering and Management; Springer: Singapore, 2020; pp. 141–151. [Google Scholar]
- Goswami, S.B.; Kar, S.C. Simulation of water cycle components in the Narmada River basin by forcing SWAT model with CFSR data. Meteorol. Hydrol. Water Manag. Res. Oper. Appl. 2018, 13–25, 6. [Google Scholar] [CrossRef]
- Himanshu, S.K.; Pandey, A.; Shrestha, P. Application of SWAT in an Indian river basin for modeling runoff, sediment and water balance. Environ. Earth Sci. 2017, 76, 3. [Google Scholar] [CrossRef]
- Nasiri, S.; Ansari, H.; Ziaei, A.N. Simulation of water balance equation components using SWAT model in Samalqan Watershed (Iran). Arab. J. Geosci. 2020, 13, 421. [Google Scholar] [CrossRef]
- Yin, Z.; Feng, Q.; Zou, S.; Yang, L. Assessing variation in water balance components in mountainous inland river basin experiencing climate change. Water 2016, 8, 472. [Google Scholar] [CrossRef] [Green Version]
- Pritchard, H.D. Asia’s glaciers are a regionally important buffer against drought. Nature 2017, 545, 169–174. [Google Scholar] [CrossRef]
- Siderius, C.; Biemans, H.; Wiltshire, A.; Rao, S.; Franssen, W.; Kumar, P.; Gosain, A.; Van Vliet, M.; Collins, D. Snowmelt contributions to discharge of the Ganges. Sci. Total Environ. 2013, 468, S93–S101. [Google Scholar] [CrossRef] [PubMed]
- Duan, Y.; Liu, T.; Meng, F.; Luo, M.; Frankl, A.; De Maeyer, P.; Bao, A.; Kurban, A.; Feng, X. Inclusion of modified snow melting and flood processes in the swat model. Water 2018, 10, 1715. [Google Scholar] [CrossRef] [Green Version]
- Mohammed, I.N.; Bolten, J.D.; Srinivasan, R.; Lakshmi, V. Satellite observations and modeling to understand the Lower Mekong River Basin streamflow variability. J. Hydrol. 2018, 564, 559–573. [Google Scholar] [CrossRef] [PubMed]
- Tan, M.L.; Samat, N.; Chan, N.W.; Roy, R. Hydro-meteorological assessment of three GPM satellite precipitation products in the Kelantan River Basin, Malaysia. Remote Sens. 2018, 10, 1011. [Google Scholar] [CrossRef] [Green Version]
- Li, D.; Christakos, G.; Ding, X.; Wu, J. Adequacy of TRMM satellite rainfall data in driving the SWAT modeling of Tiaoxi catchment (Taihu lake basin, China). J. Hydrol. 2018, 556, 1139–1152. [Google Scholar] [CrossRef]
- Malsy, M.; aus der Beek, T.; Flörke, M. Evaluation of large-scale precipitation data sets for water resources modelling in Central Asia. Environ. Earth Sci. 2015, 73, 787–799. [Google Scholar] [CrossRef]
- Hajihosseini, H.; Hajihosseini, M.; Morid, S.; Delavar, M.; Booij, M.J. Hydrological assessment of the 1973 treaty on the transboundary Helmand River, using the SWAT model and a global climate database. Water Resour. Manag. 2016, 30, 4681–4694. [Google Scholar] [CrossRef]
- Luo, M.; Meng, F.; Liu, T.; Duan, Y.; Frankl, A.; Kurban, A.; De Maeyer, P. Multi–model ensemble approaches to assessment of effects of local Climate Change on water resources of the Hotan River Basin in Xinjiang, China. Water 2017, 9, 584. [Google Scholar] [CrossRef]
- Liu, J.; Shanguan, D.; Liu, S.; Ding, Y. Evaluation and hydrological simulation of CMADS and CFSR reanalysis datasets in the Qinghai-Tibet Plateau. Water 2018, 10, 513. [Google Scholar] [CrossRef] [Green Version]
- Luo, X.; Fan, X.; Ji, X.; Li, Y. Evaluation of corrected APHRODITE estimates for hydrological simulation in the Yarlung Tsangpo–Brahmaputra River Basin. Int. J. Climatol. 2019, 40, 4158–4170. [Google Scholar] [CrossRef]
- Tan, M.L.; Gassman, P.W.; Cracknell, A.P. Assessment of three long-term gridded climate products for hydro-climatic simulations in tropical river basins. Water 2017, 9, 229. [Google Scholar] [CrossRef] [Green Version]
- Xu, H.; Xu, C.-Y.; Chen, S.; Chen, H. Similarity and difference of global reanalysis datasets (WFD and APHRODITE) in driving lumped and distributed hydrological models in a humid region of China. J. Hydrol. 2016, 542, 343–356. [Google Scholar] [CrossRef]
- Singh, L.; Saravanan, S. Evaluation of various spatial rainfall datasets for streamflow simulation using SWAT model of Wunna basin, India. Int. J. River Basin Manag. 2020, 20, 1–25. [Google Scholar] [CrossRef]
- Shen, Y.J.; Shen, Y.; Fink, M.; Kralisch, S.; Brenning, A. Unraveling the Hydrology of the glacierized Kaidu Basin by integrating multisource data in the Tianshan Mountains, Northwestern China. Water Resour. Res. 2018, 54, 557–580. [Google Scholar] [CrossRef]
- Yatagai, A.; Krishnamurti, T.; Kumar, V.; Mishra, A.; Simon, A. Use of APHRODITE rain gauge–based precipitation and TRMM 3B43 products for improving Asian monsoon seasonal precipitation forecasts by the superensemble method. J. Clim. 2014, 27, 1062–1069. [Google Scholar] [CrossRef]
- Li, L.; Ngongondo, C.S.; Xu, C.-Y.; Gong, L. Comparison of the global TRMM and WFD precipitation datasets in driving a large-scale hydrological model in southern Africa. Hydrol. Res. 2013, 44, 770–788. [Google Scholar] [CrossRef]
- Gulakhmadov, A.; Chen, X.; Gulahmadov, N.; Liu, T.; Davlyatov, R.; Sharofiddinov, S.; Gulakhmadov, M. Long-Term Hydro–Climatic Trends in the Mountainous Kofarnihon River Basin in Central Asia. Water 2020, 12, 2140. [Google Scholar] [CrossRef]
- Vaghefi, S.A.; Abbaspour, N.; Kamali, B.; Abbaspour, K.C. A toolkit for climate change analysis and pattern recognition for extreme weather conditions–Case study: California-Baja California Peninsula. Environ. Model. Softw. 2017, 96, 181–198. [Google Scholar] [CrossRef]
- Touseef, M.; Chen, L.; Yang, K.; Chen, Y. Long-Term Rainfall Trends and Future Projections over Xijiang River Basin, China. Adv. Meteorol. 2020, 2020, 6852148. [Google Scholar] [CrossRef] [Green Version]
- Yatagai, A.; Kamiguchi, K.; Arakawa, O.; Hamada, A.; Yasutomi, N.; Kitoh, A. APHRODITE: Constructing a long-term daily gridded precipitation dataset for Asia based on a dense network of rain gauges. Bull. Am. Meteorol. Soc. 2012, 93, 1401–1415. [Google Scholar] [CrossRef]
- Palazzi, E.; Von Hardenberg, J.; Provenzale, A. Precipitation in the Hindu-Kush Karakoram Himalaya: Observations and future scenarios. J. Geophys. Res. Atmos. 2013, 118, 85–100. [Google Scholar] [CrossRef]
- Fuka, D.R.; Walter, M.T.; MacAlister, C.; Degaetano, A.T.; Steenhuis, T.S.; Easton, Z.M. Using the Climate Forecast System Reanalysis as weather input data for watershed models. Hydrol. Process. 2014, 28, 5613–5623. [Google Scholar] [CrossRef]
- Cuceloglu, G.; Ozturk, I. Assessing the Impact of CFSR and Local Climate Datasets on Hydrological Modeling Performance in the Mountainous Black Sea Catchment. Water 2019, 11, 2277. [Google Scholar] [CrossRef] [Green Version]
- Worqlul, A.W.; Yen, H.; Collick, A.S.; Tilahun, S.A.; Langan, S.; Steenhuis, T.S. Evaluation of CFSR, TMPA 3B42 and ground-based rainfall data as input for hydrological models, in data-scarce regions: The upper Blue Nile Basin, Ethiopia. Catena 2017, 152, 242–251. [Google Scholar] [CrossRef]
- Jarvis, A.; Reuter, H.I.; Nelson, A.; Guevara, E. Hole-Filled SRTM for the Globe Version 4. 2008. Available online: http://srtm.csi.cgiar.org (accessed on 16 July 2020).
- Food and Agriculture Organization; International Institute for Applied Systems Analysis; International Soil Reference and Information Centre. JRC: Harmonized World Soil Database (Version 1.2); FAO: Rome, Italy; IIASA: Laxenburg, Austria, 2012. [Google Scholar]
- Arino, O.; Ramos Perez, J.J.; Kalogirou, V.; Bontemps, S.; Defourny, P.; Van Bogaert, E. Global Land CoverMap for 2009 (GlobCover 2009); European Space Agency: Paris, France; University College London: London, UK, 2012. [Google Scholar]
- Yacoub, C.; Foguet, A.P. Slope effects on SWAT modeling in a mountainous basin. J. Hydrol. Eng. 2013, 18, 1663–1673. [Google Scholar] [CrossRef] [Green Version]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool Theoretical Documentation Version 2009; Texas Water Resources Institute: Temple, TX, USA, 2011. [Google Scholar]
- Gassman, P.W.; Reyes, M.R.; Green, C.H.; Arnold, J.G. The soil and water assessment tool: Historical development, applications, and future research directions. Trans. ASABE 2007, 50, 1211–1250. [Google Scholar] [CrossRef] [Green Version]
- Cronshey, R. Urban Hydrology for Small Watersheds; US Department of Agriculture, Soil Conservation Service, Engineering Division: Washington, DC, USA, 1986. [Google Scholar]
- Hydrology, S. National Engineering Handbook; US Soil Conservation Service: Washington, DC, USA, 1972. [Google Scholar]
- Hock, R. Temperature index melt modelling in mountain areas. J. Hydrol. 2003, 282, 104–115. [Google Scholar] [CrossRef]
- Rahman, K.; Maringanti, C.; Beniston, M.; Widmer, F.; Abbaspour, K.; Lehmann, A. Streamflow modeling in a highly managed mountainous glacier watershed using SWAT: The Upper Rhone River watershed case in Switzerland. Water Resour. Manag. 2013, 27, 323–339. [Google Scholar] [CrossRef] [Green Version]
- Ruan, H.; Zou, S.; Yang, D.; Wang, Y.; Yin, Z.; Lu, Z.; Li, F.; Xu, B. Runoff simulation by SWAT model using high-resolution gridded precipitation in the upper Heihe River Basin, Northeastern Tibetan Plateau. Water 2017, 9, 866. [Google Scholar] [CrossRef] [Green Version]
- Omani, N.; Srinivasan, R.; Karthikeyan, R.; Smith, P.K. Hydrological modeling of highly glacierized basins (Andes, Alps, and Central Asia). Water 2017, 9, 111. [Google Scholar] [CrossRef] [Green Version]
- Garee, K.; Chen, X.; Bao, A.; Wang, Y.; Meng, F. Hydrological modeling of the upper indus basin: A case study from a high-altitude glacierized catchment Hunza. Water 2017, 9, 17. [Google Scholar] [CrossRef] [Green Version]
- Gulakhmadov, A.; Chen, X.; Gulahmadov, N.; Liu, T.; Anjum, M.N.; Rizwan, M. Simulation of the Potential Impacts of Projected Climate Change on Streamflow in the Vakhsh River Basin in Central Asia under CMIP5 RCP Scenarios. Water 2020, 12, 1426. [Google Scholar] [CrossRef]
- Yang, J.; Reichert, P.; Abbaspour, K.C.; Xia, J.; Yang, H. Comparing uncertainty analysis techniques for a SWAT application to the Chaohe Basin in China. J. Hydrol. 2008, 358, 1–23. [Google Scholar] [CrossRef]
- Xu, C.Y.; Chen, D. Comparison of seven models for estimation of evapotranspiration and groundwater recharge using lysimeter measurement data in Germany. Hydrol. Process. Int. J. 2005, 19, 3717–3734. [Google Scholar] [CrossRef]
- Earls, J.; Dixon, B. A comparison of SWAT model-predicted potential evapotranspiration using real and modeled meteorological data. Vadose Zone J. 2008, 7, 570–580. [Google Scholar] [CrossRef]
- Priestley, C.H.B.; Taylor, R. On the assessment of surface heat flux and evaporation using large-scale parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Samani, Z.A. Reference crop evapotranspiration from temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Penman, H. Evaporation: An introductory survey. Neth. J. Agric. Sci. 1956, 4, 9–29. [Google Scholar] [CrossRef]
- Monteith, J. The state and movement of water in living organisms. In Proceedings of the 19th Symposia of the Society for Experimental Biology; Cambridge University Press: London, UK, 1965; pp. 205–234. [Google Scholar]
- Li, Z.; Yang, Y.; Kan, G.; Hong, Y. Study on the applicability of the Hargreaves potential evapotranspiration estimation method in CREST distributed hydrological model (version 3.0) applications. Water 2018, 10, 1882. [Google Scholar] [CrossRef] [Green Version]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef] [Green Version]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- KGE Package ‘hydroGOF’. 2020. Available online: https://cran.r-project.org/web/packages/hydroGOF/hydroGOF.pdf (accessed on 9 September 2020).
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Santhi, C.; Harmel, R.; Van Griensven, A.; Van Liew, M.W. SWAT: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1491–1508. [Google Scholar] [CrossRef]
- Abbaspour, K. SWAT-CUP 2012: SWAT Calibration and Uncertainty Programs-A User Manual, 2012; Eawag–Swiss Federal Institute of Aquatic Science and Technology: Dübendorf, Switzerland, 2015. [Google Scholar]
- Ahmed, E.; Al Janabi, F.; Zhang, J.; Yang, W.; Saddique, N.; Krebs, P. Hydrologic Assessment of TRMM and GPM-Based Precipitation Products in Transboundary River Catchment (Chenab River, Pakistan). Water 2020, 12, 1902. [Google Scholar] [CrossRef]
- Salles, L.; Satgé, F.; Roig, H.; Almeida, T.; Olivetti, D.; Ferreira, W. Seasonal effect on spatial and temporal consistency of the new GPM-based IMERG-v5 and GSMaP-v7 satellite precipitation estimates in Brazil’s central plateau region. Water 2019, 11, 668. [Google Scholar] [CrossRef] [Green Version]
- Abbaspour, K.C.; Johnson, C.; Van Genuchten, M.T. Estimating uncertain flow and transport parameters using a sequential uncertainty fitting procedure. Vadose Zone J. 2004, 3, 1340–1352. [Google Scholar] [CrossRef]
- Schuol, J.; Abbaspour, K.C.; Srinivasan, R.; Yang, H. Estimation of freshwater availability in the West African sub-continent using the SWAT hydrologic model. J. Hydrol. 2008, 352, 30–49. [Google Scholar] [CrossRef]
- Anand, J.; Gosain, A.; Khosa, R.; Srinivasan, R. Regional scale hydrologic modeling for prediction of water balance, analysis of trends in streamflow and variations in streamflow: The case study of the Ganga River basin. J. Hydrol. Reg. Stud. 2018, 16, 32–53. [Google Scholar] [CrossRef]
- Fletcher, T.D.; Andrieu, H.; Hamel, P. Understanding, management and modelling of urban hydrology and its consequences for receiving waters: A state of the art. Adv. Water Resour. 2013, 51, 261–279. [Google Scholar] [CrossRef]
- Hu, Z.; Hu, Q.; Zhang, C.; Chen, X.; Li, Q. Evaluation of reanalysis, spatially interpolated and satellite remotely sensed precipitation data sets in central Asia. J. Geophys. Res. Atmos. 2016, 121, 5648–5663. [Google Scholar] [CrossRef] [Green Version]
- Arsenault, R.; Essou, G.R.; Brissette, F.P. Improving hydrological model simulations with combined multi-input and multimodel averaging frameworks. J. Hydrol. Eng. 2017, 22, 04016066. [Google Scholar] [CrossRef]
- Duan, W.; Chen, Y.; Zou, S.; Nover, D. Managing the water-climate-food nexus for sustainable development in Turkmenistan. J. Clean. Prod. 2019, 220, 212–224. [Google Scholar] [CrossRef]
- Duan, W.; Takara, K. Impacts of Climate and Human Activities on Water Resources and Quality; Springer Nature: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Schuol, J.; Abbaspour, K.C.; Yang, H.; Srinivasan, R.; Zehnder, A.J. Modeling blue and green water availability in Africa. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef] [Green Version]
- Deng, H.; Chen, Y. Influences of recent climate change and human activities on water storage variations in Central Asia. J. Hydrol. 2017, 544, 46–57. [Google Scholar] [CrossRef]
- Li, Z.; Chen, Y.; Fang, G.; Li, Y. Multivariate assessment and attribution of droughts in Central Asia. Sci. Rep. 2017, 7, 1–12. [Google Scholar] [CrossRef]
- Eini, M.R.; Javadi, S.; Delavar, M.; Monteiro, J.A.; Darand, M. High accuracy of precipitation reanalyses resulted in good river discharge simulations in a semi-arid basin. Ecol. Eng. 2019, 131, 107–119. [Google Scholar] [CrossRef]
- Grusson, Y.; Anctil, F.; Sauvage, S.; Sánchez Pérez, J.M. Testing the SWAT model with gridded weather data of different spatial resolutions. Water 2017, 9, 54. [Google Scholar] [CrossRef] [Green Version]
- Pathak, S.; Ojha, C.; Shukla, A.; Garg, R. Assessment of Annual Water-Balance Models for Diverse Indian Watersheds. J. Sustain. Water Built Environ. 2019, 5, 04019002. [Google Scholar] [CrossRef]
- Thapa, B.R.; Ishidaira, H.; Pandey, V.P.; Shakya, N.M. A multi-model approach for analyzing water balance dynamics in Kathmandu Valley, Nepal. J. Hydrol. Reg. Stud. 2017, 9, 149–162. [Google Scholar] [CrossRef]
- Leta, O.T.; El-Kadi, A.I.; Dulai, H.; Ghazal, K.A. Assessment of climate change impacts on water balance components of Heeia watershed in Hawaii. J. Hydrol. Reg. Stud. 2016, 8, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Budhathoki, A.; Babel, M.S.; Shrestha, S.; Meon, G.; Kamalamma, A.G. Climate change impact on water balance and hydrological extremes in different physiographic regions of the West Seti River Basin, Nepal. Ecohydrol. Hydrobiol. 2020, 21, 79–95. [Google Scholar] [CrossRef]
- Ferguson, R. Snowmelt runoff models. Prog. Phys. Geogr. 1999, 23, 205–227. [Google Scholar] [CrossRef]
- Harrison, G.P.; Whittington, H. Vulnerability of hydropower projects to climate change. IEE Proc. Gener. Transm. Distrib. 2002, 149, 249–255. [Google Scholar] [CrossRef] [Green Version]
- Alekseevskii, N.; Zavadskii, A.; Krivushin, M.; Chalov, S. Hydrological monitoring at international rivers and basins. Water Resour. 2015, 42, 747–757. [Google Scholar] [CrossRef]
- Ta, Z.; Yu, Y.; Sun, L.; Chen, X.; Mu, G.; Yu, R. Assessment of Precipitation Simulations in Central Asia by CMIP5 Climate Models. Water 2018, 10, 1516. [Google Scholar] [CrossRef] [Green Version]
- Yang, D.; Gao, B.; Jiao, Y.; Lei, H.; Zhang, Y.; Yang, H.; Cong, Z. A distributed scheme developed for eco-hydrological modeling in the upper Heihe River. Sci. China Earth Sci. 2015, 58, 36–45. [Google Scholar] [CrossRef]
- Shaw, E.M.; Beven, K.J.; Chappell, N.A.; Lamb, R. Hydrology in Practice; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Harris, I.; Jones, P.D.; Osborn, T.J.; Lister, D.H. Updated high-resolution grids of monthly climatic observations–the CRU TS3. 10 Dataset. Int. J. Climatol. 2014, 34, 623–642. [Google Scholar] [CrossRef] [Green Version]
- Sorooshian, S.; AghaKouchak, A.; Arkin, P.; Eylander, J.; Foufoula-Georgiou, E.; Harmon, R.; Hendrickx, J.M.; Imam, B.; Kuligowski, R.; Skahill, B. Advanced concepts on remote sensing of precipitation at multiple scales. Bull. Am. Meteorol. Soc. 2011, 92, 1353–1357. [Google Scholar] [CrossRef]
- Conti, F.L.; Hsu, K.-L.; Noto, L.V.; Sorooshian, S. Evaluation and comparison of satellite precipitation estimates with reference to a local area in the Mediterranean Sea. Atmos. Res. 2014, 138, 189–204. [Google Scholar] [CrossRef] [Green Version]
- Santhi, C.; Arnold, J.G.; Williams, J.R.; Dugas, W.A.; Srinivasan, R.; Hauck, L.M. Validation of the swat model on a large rwer basin with point and nonpoint sources 1. JAWRA J. Am. Water Resour. Assoc. 2001, 37, 1169–1188. [Google Scholar] [CrossRef]

| Year | Observation | Simulated-1 | Simulated-2 | Simulated-3 | Simulated-4 | ||||
|---|---|---|---|---|---|---|---|---|---|
| Flow (m3/s) | Flow (m3/s) | Rate (%) | Flow (m3/s) | Rate (%) | Flow (m3/s) | Rate (%) | Flow (m3/s) | Rate (%) | |
| 1982 | 519.42 | 518.25 | −0.23 | 731.39 | 28.98 | 608.03 | 14.57 | 541.45 | 4.07 |
| 1983 | 573.58 | 663.75 | 13.58 | 727.21 | 21.13 | 760.64 | 24.59 | 550.86 | −4.13 |
| 1984 | 644.50 | 707.10 | 8.85 | 734.60 | 12.27 | 890.92 | 27.66 | 577.44 | −11.61 |
| 1985 | 595.75 | 595.67 | −0.01 | 765.99 | 22.23 | 657.31 | 9.37 | 603.96 | 1.36 |
| 1986 | 492.25 | 492.34 | 0.02 | 633.18 | 22.26 | 515.41 | 4.49 | 492.89 | 0.13 |
| 1987 | 683.42 | 562.95 | −21.40 | 949.26 | 28.01 | 545.32 | −25.32 | 658.34 | −3.81 |
| 1988 | 711.75 | 685.50 | −3.83 | 924.93 | 23.05 | 764.24 | 6.87 | 666.43 | −6.80 |
| 1989 | 443.08 | 440.85 | −0.51 | 688.96 | 35.69 | 568.37 | 22.04 | 454.13 | 2.43 |
| 1990 | 624.67 | 684.65 | 8.76 | 791.25 | 21.05 | 805.38 | 22.44 | 620.63 | −0.65 |
| 1991 | 565.17 | 586.13 | 3.58 | 796.42 | 29.04 | 659.22 | 14.27 | 633.34 | 10.76 |
| 1992 | 650.42 | 507.05 | −28.27 | 773.53 | 15.92 | 597.96 | −8.77 | 661.16 | 1.62 |
| 1993 | 694.67 | 449.89 | −54.41 | 744.46 | 6.69 | 551.77 | −25.90 | 678.11 | −2.44 |
| 1994 | 631.81 | 638.18 | 1.00 | 811.60 | 22.15 | 745.32 | 15.23 | 641.08 | 1.45 |
| 1995 | 568.18 | 377.26 | −50.61 | 592.66 | 4.13 | 491.28 | −15.65 | 606.12 | 6.26 |
| 1996 | 638.31 | 285.13 | −123.87 | 595.88 | −7.12 | 382.11 | −67.05 | 634.59 | −0.59 |
| 1997 | 600.54 | 472.78 | −27.02 | 439.89 | −36.52 | 623.95 | 3.75 | 422.12 | −42.27 |
| 1998 | 828.35 | 368.49 | −124.79 | 710.06 | −16.66 | 474.37 | −74.62 | 773.38 | −7.11 |
| 1999 | 673.37 | 459.95 | −46.40 | 702.52 | 4.15 | 533.08 | −26.32 | 667.83 | −0.83 |
| 2000 | 572.29 | 472.56 | −21.10 | 567.44 | −0.85 | 563.35 | −1.59 | 517.43 | −10.60 |
| 2001 | 564.96 | 610.16 | 7.41 | 568.66 | 0.65 | 677.75 | 16.64 | 500.73 | −12.83 |
| 2002 | 726.54 | 617.11 | −17.73 | 693.48 | −4.77 | 558.38 | −30.12 | 698.52 | −4.01 |
| 2003 | 656.57 | 587.33 | −11.79 | 695.84 | 5.64 | 573.49 | −14.49 | 893.66 | 26.53 |
| 2004 | 649.40 | 568.10 | −14.31 | 704.03 | 7.76 | 555.56 | −16.89 | 779.52 | 16.69 |
| 2005 | 695.60 | 472.60 | −47.19 | 587.79 | −18.34 | 593.18 | −17.27 | 660.14 | −5.37 |
| 2006 | 647.45 | 477.57 | −35.57 | 405.19 | −59.79 | 646.72 | −0.11 | 668.40 | 3.13 |
| Components | Calibration (1982–1999) | Validation (2000–2006) | Overall (1982–2006) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a | b | c | d | e | a | b | c | d | e | a | b | c | d | e | |
| Precipitation | 1940.5 | 1287.8 | 2608.7 | 1188.8 | 1077.2 | 1709.6 | 1106.1 | 2145.4 | 1285.5 | 1104.1 | 1875.9 | 1236.9 | 2479 | 1215.9 | 1098.5 |
| Snowfall | 1830.24 | 926.38 | 2498.15 | 1027.98 | 827.7 | 1579.83 | 728.25 | 2075.87 | 1114.06 | 856.11 | 1760.11 | 870.85 | 2379.86 | 1051.98 | 836.65 |
| Snowmelt | 525.24 | 664.73 | 612.49 | 700.66 | 570.48 | 518.31 | 523.78 | 586.88 | 759.7 | 672.69 | 525.54 | 625.65 | 619.19 | 718.21 | 574.41 |
| Sublimation | 105.07 | 140.26 | 43.41 | 165.83 | 150.08 | 124.33 | 121.3 | 63.36 | 171.03 | 59.73 | 110.83 | 134.95 | 49.95 | 167.57 | 156 |
| Surface runoff Q | 46.1 | 295.28 | 94.32 | 27.69 | 244.04 | 173.16 | 226.6 | 76.31 | 37.27 | 284.41 | 46.54 | 276.79 | 90.56 | 30.73 | 243.22 |
| Lateral soil Q | 408.14 | 387.13 | 331.26 | 384.37 | 294.81 | 278.43 | 331.83 | 309.39 | 418.27 | 369.63 | 413.34 | 371.49 | 331.92 | 394.21 | 307.92 |
| Ground water (deep AQ) Q | 70.93 | 128.18 | 180.68 | 120.7 | 96.12 | 82.46 | 107.48 | 161.2 | 131.13 | 132.42 | 70.57 | 122.34 | 179.25 | 123.78 | 103.83 |
| Revap or shallow aquifer recharges | 41.96 | 53.23 | 32.06 | 124.19 | 51.08 | 59.61 | 57.35 | 44.06 | 131.79 | 49.44 | 39.95 | 48.98 | 35.11 | 124.45 | 46.47 |
| Deep aquifer recharge | 70.98 | 128.16 | 180.74 | 121.12 | 96.37 | 82.47 | 105.12 | 161.68 | 130.19 | 131.16 | 70.64 | 121.64 | 179.4 | 123.83 | 103.57 |
| Total aquifer recharge | 106.04 | 173.12 | 274.57 | 360.35 | 130.19 | 111.4 | 142.01 | 245.61 | 387.34 | 177.18 | 105.53 | 164.33 | 272.53 | 368.4 | 139.91 |
| Total water yield | 529.52 | 811.05 | 669.31 | 651.75 | 634.98 | 534.05 | 665.94 | 591.31 | 721.27 | 786.48 | 534.72 | 771.24 | 661.98 | 672.11 | 654.97 |
| Percolation out of soil | 106.05 | 173.12 | 274.59 | 360.64 | 130.22 | 111.39 | 141.87 | 245.58 | 386.49 | 177.24 | 105.54 | 164.28 | 272.53 | 368.4 | 139.9 |
| Actual evapotranspiration | 179.3 | 310.6 | 64.7 | 254.2 | 296.3 | 207.4 | 328.8 | 88.6 | 261.5 | 142.9 | 186.3 | 315.7 | 72.1 | 256.4 | 299.7 |
| Potential evapotranspiration | 390.1 | 672.7 | 160.3 | 673.6 | 668.2 | 436.7 | 692.5 | 220.3 | 693.1 | 297 | 403.1 | 678.3 | 177.1 | 679.1 | 668.6 |
| Month | Rainfall (mm) (a) | Snowmelt (mm) (b) | Net Rainfall Input (a + b) | Water Yield (mm) | Snowmelt Contribution (mm) | Monthly Snowmelt Contribution to the Streamflow (%) |
|---|---|---|---|---|---|---|
| Combination of the APHRODITE_V1101 and CFSR datasets | ||||||
| January | 0.08 | 0.10 | 0.18 | 4.79 | 2.64 | 55.19 |
| February | 0.10 | 0.33 | 0.43 | 3.27 | 2.51 | 76.78 |
| March | 2.27 | 4.85 | 7.12 | 3.35 | 2.28 | 68.10 |
| April | 6.23 | 26.13 | 32.36 | 16.32 | 13.18 | 80.75 |
| May | 18.86 | 63.04 | 81.90 | 56.58 | 43.55 | 76.97 |
| June | 26.07 | 131.06 | 157.13 | 123.71 | 103.18 | 83.41 |
| July | 32.56 | 172.81 | 205.37 | 165.00 | 138.84 | 84.15 |
| August | 21.28 | 101.46 | 122.74 | 106.71 | 88.21 | 82.66 |
| September | 4.37 | 16.68 | 21.05 | 24.44 | 19.36 | 79.24 |
| Octpber | 3.22 | 4.86 | 8.08 | 12.69 | 7.63 | 60.13 |
| November | 0.40 | 0.94 | 1.34 | 8.39 | 5.88 | 70.07 |
| December | 0.35 | 0.48 | 0.83 | 6.45 | 3.72 | 57.66 |
| Total | 115.79 | 522.72 | 638.51 | 531.70 | 430.99 | |
| Combination of the APHRODITE_V1101 and CRU TS3.1 datasets | ||||||
| January | 2.35 | 9.22 | 11.57 | 11.56 | 9.22 | 79.70 |
| February | 2.88 | 13.56 | 16.44 | 11.98 | 9.88 | 82.49 |
| March | 15.51 | 40.87 | 56.38 | 38.55 | 27.94 | 72.49 |
| April | 37.49 | 104.65 | 142.14 | 110.93 | 81.68 | 73.63 |
| May | 68.70 | 113.25 | 181.95 | 134.35 | 83.62 | 62.24 |
| June | 70.65 | 122.18 | 192.83 | 152.15 | 96.41 | 63.36 |
| July | 65.80 | 116.29 | 182.09 | 145.97 | 93.22 | 63.86 |
| August | 43.56 | 45.86 | 89.42 | 72.72 | 37.30 | 51.29 |
| September | 20.86 | 13.01 | 33.87 | 29.57 | 11.36 | 38.42 |
| Octpber | 23.10 | 23.74 | 46.84 | 31.93 | 16.18 | 50.68 |
| November | 10.21 | 15.01 | 25.22 | 20.50 | 12.20 | 59.52 |
| December | 4.95 | 10.97 | 15.92 | 14.33 | 9.88 | 68.92 |
| Total | 366.06 | 628.63 | 994.69 | 774.54 | 488.88 | |
| Month | Rainfall (mm) (a) | Snowmelt (mm) (b) | Net Rainfall Input (a + b) | Water Yield (mm) | Snowmelt Contribution (mm) | Monthly Snowmelt Contribution to the Streamflow (%) |
|---|---|---|---|---|---|---|
| CFSR datasets | ||||||
| January | 0.04 | 0.06 | 0.10 | 13.26 | 8.20 | 61.81 |
| February | 0.19 | 0.22 | 0.41 | 9.04 | 4.88 | 54.01 |
| March | 1.00 | 3.46 | 4.46 | 8.09 | 6.28 | 77.57 |
| April | 3.64 | 23.25 | 26.89 | 18.93 | 16.37 | 86.47 |
| May | 13.12 | 63.62 | 76.74 | 53.86 | 44.65 | 82.90 |
| June | 24.06 | 135.85 | 159.91 | 106.03 | 90.08 | 84.95 |
| July | 29.53 | 197.33 | 226.86 | 158.66 | 138.01 | 86.98 |
| August | 19.84 | 156.09 | 175.93 | 148.17 | 131.46 | 88.72 |
| September | 5.22 | 30.26 | 35.48 | 63.33 | 54.01 | 85.29 |
| Octpber | 1.95 | 4.68 | 6.63 | 36.37 | 25.68 | 70.60 |
| November | 0.29 | 0.80 | 1.09 | 24.32 | 17.84 | 73.38 |
| December | 0.24 | 0.17 | 0.41 | 18.16 | 7.48 | 41.18 |
| Total | 99.12 | 615.80 | 714.92 | 658.22 | 544.93 | |
| CRU TS3.1 datasets | ||||||
| January | 0.69 | 5.77 | 6.46 | 10.35 | 9.25 | 89.32 |
| February | 0.57 | 10.05 | 10.62 | 8.20 | 7.76 | 94.63 |
| March | 4.04 | 32.84 | 36.88 | 17.68 | 15.74 | 89.05 |
| April | 17.96 | 88.73 | 106.69 | 52.67 | 43.80 | 83.17 |
| May | 37.72 | 136.36 | 174.08 | 104.58 | 81.92 | 78.33 |
| June | 40.37 | 160.78 | 201.15 | 143.77 | 114.91 | 79.93 |
| July | 31.73 | 159.57 | 191.30 | 155.30 | 129.54 | 83.41 |
| August | 5.07 | 56.39 | 61.46 | 79.87 | 73.28 | 91.75 |
| September | 8.41 | 20.02 | 28.43 | 36.66 | 25.81 | 70.42 |
| Octpber | 9.28 | 26.40 | 35.68 | 29.17 | 21.58 | 73.99 |
| November | 5.85 | 16.09 | 21.94 | 21.73 | 15.93 | 73.33 |
| December | 2.21 | 7.66 | 9.87 | 14.63 | 11.35 | 77.60 |
| Total | 163.90 | 720.67 | 884.57 | 674.61 | 550.89 | |
| Month | Rainfall (mm) (a) | Snowmelt (mm) (b) | Net Rainfall Input (a + b) | Water Yield (mm) | Snowmelt Contribution (mm) | Monthly Snowmelt Contribution to the Streamflow (%) |
|---|---|---|---|---|---|---|
| Observational datasets | ||||||
| January | 0.09 | 0.32 | 0.41 | 5.47 | 4.28 | 78.20 |
| February | 0.53 | 1.14 | 1.67 | 3.96 | 2.71 | 68.35 |
| March | 5.23 | 25.77 | 31.00 | 13.80 | 11.47 | 83.13 |
| April | 25.72 | 152.84 | 178.56 | 124.85 | 106.87 | 85.60 |
| May | 57.90 | 120.70 | 178.60 | 123.98 | 83.79 | 67.58 |
| June | 63.90 | 115.64 | 179.54 | 140.94 | 90.78 | 64.41 |
| July | 44.26 | 100.51 | 144.77 | 120.89 | 83.93 | 69.43 |
| August | 29.86 | 45.71 | 75.57 | 67.34 | 40.73 | 60.49 |
| September | 18.11 | 4.68 | 22.79 | 21.00 | 4.31 | 20.55 |
| Octpber | 12.64 | 3.81 | 16.45 | 15.77 | 3.65 | 23.14 |
| November | 3.32 | 4.08 | 7.40 | 10.95 | 6.04 | 55.16 |
| December | 0.32 | 0.97 | 1.29 | 7.61 | 5.72 | 75.18 |
| Total | 261.88 | 576.19 | 838.07 | 656.57 | 444.28 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gulakhmadov, A.; Chen, X.; Gulakhmadov, M.; Kobuliev, Z.; Gulahmadov, N.; Peng, J.; Li, Z.; Liu, T. Evaluation of the CRU TS3.1, APHRODITE_V1101, and CFSR Datasets in Assessing Water Balance Components in the Upper Vakhsh River Basin in Central Asia. Atmosphere 2021, 12, 1334. https://doi.org/10.3390/atmos12101334
Gulakhmadov A, Chen X, Gulakhmadov M, Kobuliev Z, Gulahmadov N, Peng J, Li Z, Liu T. Evaluation of the CRU TS3.1, APHRODITE_V1101, and CFSR Datasets in Assessing Water Balance Components in the Upper Vakhsh River Basin in Central Asia. Atmosphere. 2021; 12(10):1334. https://doi.org/10.3390/atmos12101334
Chicago/Turabian StyleGulakhmadov, Aminjon, Xi Chen, Manuchekhr Gulakhmadov, Zainalobudin Kobuliev, Nekruz Gulahmadov, Jiabin Peng, Zhengyang Li, and Tie Liu. 2021. "Evaluation of the CRU TS3.1, APHRODITE_V1101, and CFSR Datasets in Assessing Water Balance Components in the Upper Vakhsh River Basin in Central Asia" Atmosphere 12, no. 10: 1334. https://doi.org/10.3390/atmos12101334
APA StyleGulakhmadov, A., Chen, X., Gulakhmadov, M., Kobuliev, Z., Gulahmadov, N., Peng, J., Li, Z., & Liu, T. (2021). Evaluation of the CRU TS3.1, APHRODITE_V1101, and CFSR Datasets in Assessing Water Balance Components in the Upper Vakhsh River Basin in Central Asia. Atmosphere, 12(10), 1334. https://doi.org/10.3390/atmos12101334







